DISCOVERING CAUSALITIES FROM CARDIOTOCOGRAPHY SIGNALS USING IMPROVED CONVERGENT CROSS MAPPING WITH GAUSSIAN PROCESSES

Abstract

Convergent cross mapping (CCM) is designed for causal discovery in coupled time series, where Granger causality may not be applicable because of a separability assumption. However, CCM is not robust to observation noise which limits its applicability on signals that are known to be noisy. Moreover, the parameters for state space reconstruction need to be selected using grid search methods. In this paper, we propose a novel improved version of CCM using Gaussian processes for discovery of causality from noisy time series. Specifically, we adopt the concept of CCM and carry out the key steps using Gaussian processes within a non-parametric Bayesian probabilistic framework in a principled manner. The proposed approach is first validated on simulated data, and then used for understanding the interaction between fetal heart rate and uterine activity in the last two hours before delivery and of interest in obstetrics. Our results indicate that uterine activity affects the fetal heart rate, which agrees with recent clinical studies.

1. INTRODUCTION

During labor, a fetus can be deprived of adequate levels of oxygen and can become hypoxic and acidotic. If the oxygen supply drops below a certain threshold, asphyxia occurs, and this can lead to permanent brain damage or even death of the fetus [1]. Cardiotocography (CTG) is the most widely used technology for monitoring the well-being of fetuses during labor. CTG comprises of the fetal heart rate (FHR) and uterine activity (UA) signals, which are both recorded and visually inspected by clinicians [2]. The purpose of CTG is to alert obstetricians of such alterations in blood flow and oxygen content that are reflected in the CTG patterns for appropriate and timely intervention. The interpretation of FHR recordings is a highly intricate and complex task with high inter- and intra-variable evaluations among obstetricians, notwithstanding the availability of various clinical guidelines from both the National Institute of Child Health and Human Development (NICHD) and the International Federation of Gynecology and Obstetrics (FIGO) [3, 4]. In fact, the current guidelines for FHR evaluation have been criticized for simplistic interpretation [5]. The reliable interpretation of CTG tracings requires better understanding of the interaction between FHR and UA signals. In this paper, we address the problem of making inference about causality from CTG signals, which interestingly, has largely been overlooked in the literature.

The gold standard for identifying causal relationships is using controlled randomized experiments. In many situations, however, these experiments cannot be performed [6]. When we work with signals, their samples are usually stored in the form of time series. The samples are ordered in time, which helps in addressing the detection of causality because cause should occur before the effect [7, 8]. The Granger causality is the best known concept for discovering causalities [9]. The concept relies on two fundamental principles: (a) the effect does not precede its cause in time, and (b) the causing series contains unique information about the series being caused that is not available otherwise. However, when two time series are dynamically coupled, the second principle of the Granger causality is violated, and consequently, the causal discovery results may be unreliable [10].

Another approach for determining causality is known as convergent cross mapping (CCM), which was proposed in [11]. The method is designed for coupled time series and is based on state space reconstruction (SSR). We recall that in dynamical systems theory two time series are causally related if they are from the same dynamical system, or equivalently, share a common attractor manifold $\mathcal{M}$. Further, the signature of the causing series is embedded in the effect series [11]. Although CCM has been successfully applied to perform causal inference in many communities, e.g., social media [12] and neuroscience [13], it can be shown that CCM is sensitive to observation noise [14]. To improve the applicability of CCM, some variants of CCM have been proposed, e.g. [15, 16].

In this paper, we propose a fully Gaussian process (GP)-based version of CCM. The GP-based SSR step is capable of automatic learning an attractor manifold of better quality from noisy observations in a principled manner, unlike the original SSR method in CCM where the parameters for reconstruction are usually selected with grid search. For the cross mapping step, the GP-based method is able to provide cross mapping results under a probabilistic framework. More importantly, because of the Bayesian nature of the GP framework, the GPs are data efficient and robust to overfitting. As a result, our GP-based CCM can provide better convergence which is critical in distinguishing causation from correlation. We first validated the GP based approach using the well-studied Lorenz system with and without observation noise. Then we implemented the original CCM and the GP-based CCM, respectively, on a segment of real CTG recordings. The results of the original CCM are ambiguous, whereas the results of the GP-based CCM clearly indicate that the changes in the UA signal cause changes in the FHR signal, and not vice versa. Our finding is consistent with recent clinical studies [17].

2. BACKGROUND

2.1. Takens’ Theorem

The CCM framework is built on Takens’ theorem proposed by Floris Takens in [18], which is of great importance in attractor reconstruction, i.e., the reconstruction of the state space of a system. When the conditions of the theorem are satisfied, the theorem provides guarantees that, generically, the information about hidden states of a dynamical system can be reconstructed from a single observation variable of the system. Next, we state the theorem:

Theorem 1 (Takens’ theorem) Let $\mathcal{M}$ be a compact manifold of (integer) dimension d. Then for generic pairs (ϕ, y), where

• $\varphi :\mathcal{M}\to \mathcal{M}$ is a C²-diffeomorphism of $\mathcal{M}$ in itself,

• $\text{y}:\mathcal{M}\to ℝ$ is a C²-differentiable function, the map ${\Phi }_{(\varphi ,y)}:\mathcal{M}\to {ℝ}^{2d+1}$ given by

  $${\Phi }_{(\varphi ,y)}(x):=\left(y(x),y(\varphi (x)),y\left({\varphi }^2(x)\right),\dots ,y\left({\varphi }^{2d}(x)\right)\right)$$

  is an embedding of $\mathcal{M}$ in ${ℝ}^{2d+1}$.

The most common choice of ϕ is a delay by a constant τ. A fundamental contribution of Takens’ theorem is the claim that for a reliable reconstruction of a manifold $\mathcal{M}$ of dimension d, it is sufficient to have a delay embedding of dimension E = 2d + 1.

2.2. Convergent Cross Mapping

The CCM framework is composed of two steps. The first step is state space construction (SSR) using each time series. Given a time series x(t), a shadow manifold ${\mathcal{M}}_x^{\text{DE}}$ of dimension E, as an estimate or reconstruction of latent attractor manifold ${\mathcal{M}}_x$, is constructed using delay embedding. The point corresponding to time instant t on ${\mathcal{M}}_x^{\text{DE}}$ is an E-dimensional vector $m_x^{\text{DE}}(t)={[x(t),x(t-\tau ),\dots ,x(t-(E-1)\tau )]}^{\top }$. If two time series, x(t) and y(t), are from the same dynamical system, ${\mathcal{M}}_x^{\text{DE}}$ and ${\mathcal{M}}_y^{\text{DE}}$ should be topologically similar, since they both are diffeomorphic to the true manifold $\mathcal{M}$.

In the second step, given two shadow manifolds ${\mathcal{M}}_x^{\text{DE}}$ and ${\mathcal{M}}_y^{\text{DE}}$ their correspondence is tested for causal discovery. Specifically, given a point in ${\mathcal{M}}_y^{\text{DE}}\in {ℝ}^{N\times E}$, CCM will find its E + 1 nearest neighbors (the minimum number of points to bound a simplex in ${ℝ}^E$) in ${\mathcal{M}}_y^{\text{DE}}$ and their corresponding time indices and then test whether these time indices can be used to identify nearby points on ${\mathcal{M}}_x^{\text{DE}}$, and vice versa. This is implemented using cross mapping with simplex projection, i.e., estimating x(t) with ${\mathcal{M}}_y^{\text{DE}}$ denoted as $\widehat{x}(t)|{\mathcal{M}}_y^{\text{DE}}$, and vice versa. Essentially, the CCM test measures the extent to which the historical record of one time series can reliably estimate states of the other time series. If x(t) is a stochastic driver or cause of y(t) (e.g., x is an environmental driver and y is a population variable), information about the states of x can be recovered from the observations of y, but not vice versa.

Furthermore, the CCM takes convergence into consideration that not only distinguishes CCM from general cross prediction, but also allows for distinguishing causation from simple correlation. The convergence means that cross-mapped estimates improve in estimation capacity, which is usually measured by correlation, with the length of time-series, L (sample size used to construct the history). If the Pearson correlation coefficient (PCC), denoted as ρ, is adopted as a capacity metric and the conditions of Takens’ theorem are satisfied, it can be proved that the PCC as a function of L will converge to 1 as L approaches infinity. In practice, because of observation noise and finite number of observations, the correlation will only converge to a value less than 1 [11].

The choice of reconstruction parameters E and τ need to be carefully selected. In many situations, the true manifold $\mathcal{M}$ that is responsible for generating the data is usually unknown. As a result, we do not have any knowledge about the true dimension d of the manifold $\mathcal{M}$ (or E = 2d + 1). In practice, the common approach of choosing E is using false nearest neighbours [19] in a grid search manner, which is not principled. In theory, τ is a free parameter and can be arbitrarily selected. However, because in reality the number of observation is finite, the value of τ will actually affect the quality of ${\mathcal{M}}^{\text{DE}}$ in term of capturing the underlying dynamics of the system. One common approach for choosing τ is based on mutual information and is also obtained by a grid search [20].

2.3. Gaussian Processes

In machine learning literature, GPs provide powerful and flexible Bayesian nonparametric framework for modeling functions and mappings, and they have been successfully applied in both supervised and unsupervised learning [21, 22]. By definition, a GP indexed by x is a stochastic process in which every finite collection of random variables has a multivariate normal distribution, and it is completely specified by its mean function m(x) and covariance function k_f(x, x′), which are defined by $m(x)=\mathbb{E}[f(x)]$, and $k_f\left(x,x^{\prime }\right)=\mathbb{E}\left[(f(x)-m(x))\left(f\left(x^{\prime }\right)-m\left(x^{\prime }\right)\right)\right]$. Conceptually, a real valued function f(x) can be seen as a vector with infinite dimensionality. Therefore, GPs are suitable for specifying the prior distribution of a latent function f(x), and our prior knowledge and assumption about f(x) can be conveniently encoded in the design of the covariance function without assuming any analytical form of f(x). To reduce the number of hyperparameters, a GP is often assumed to be zero mean, and we write f(x) ~ GP(0, k_f(x, x′)). The covariance function k_f(x, x′) is of great importance because it maps the distance, or similarity, between the inputs x and x′ to the covariance between the outputs f(x) and f(x′).

3. MODEL DESCRIPTION

3.1. State Space Reconstruction

Given a time series, we first construct a shadow manifold ${\mathcal{M}}^{\text{init}}$ using delay embedding, with τ = 1 (delay by one sample) and E that is relatively large, e.g., E = 20. The intuition of it is that, a relatively large E ensures the conditions in Takens’ theorem to be satisfied, and τ = 1 is the minimum delay, which suggests that there is no information loss regarding the underlying dynamics. Consequently, ${\mathcal{M}}^{\text{init}}$ is of high dimension and the variables from the different dimensions are highly correlated. Therefore, ${\mathcal{M}}^{\text{init}}$ is not suitable for simplex projection where E+1 nearest neighbours need to be identified because the Euclidean distance in high dimensions is large, and neighbours in high dimensions are sparse.

We use the Bayesian GP latent variable model (GPLVM) [23], to infer the low dimensional manifold ${\mathcal{M}}^{\text{GP}}$ that is responsible for generating ${\mathcal{M}}^{\text{init}}$. Let ${\mathcal{M}}^{\text{init}}\in {ℝ}^{N\times Q}$ be a matrix whose rows lie in ${\mathcal{M}}^{\text{init}}$ and similarly, ${\mathcal{M}}^{\text{GP}}\in {ℝ}^{N\times E}$ is a matrix with rows that lie in ${\mathcal{M}}^{\text{GP}}$. The generative process can then be expressed as follows:

$$M^{\text{init }}=f\left(M^{\text{GP}}\right)+\mathit{ϵ},$$ (1)

where $\mathit{ϵ}\in {ℝ}^{N\times Q}$ is a matrix whose rows are zero mean Gaussian with covariance ${\sigma }_{ϵ}^{2}I$. Since our purpose is not to predict how the system will evolve on the attractor manifold in the future, we initialize each dimension in f as an independent draw from a GP, i.e., f ~ GP(0, k(x, x′)), where the covariance function is a Q-dimensional radial basis function (RBF), which has the following form:

$$k\left(x,x^{\prime }\right)={\sigma }_f^2\text{ exp }\left(-\frac{1}{2}\sum _{q=1}^Q\frac{1}{{\mathcal{l}}_q}{\left(x_q-x_q^{\prime }\right)}^2\right).$$ (2)

The learning requires maximizing the marginal likelihood given by:

$$p\left(M^{\text{init}}\right)=\int p\left(M^{\text{init}}|M^{\text{GP}}\right)p\left(M^{\text{GP}}\right)d{M}^{\text{GP}}.$$ (3)

Unlike the GP regression framework, this marginal likelihood is intractable because M^GP and M^init are related by the covariance function in a highly nonlinear manner, and in general, nonlinear mapping will not preserve Gaussianity. This is handled in [23] by employing variational inference, and approximating the true posterior p(M^GP | M^init) by a Gaussian variational distribution q(M^GP), from which a tractable lower bound on the marginal likelihood was obtained and then adopted for learning.

In our work, the mean of q(M^GP) is used as reconstructed attractor manifold, and the covariance q(M^GP) is adopted for measuring the uncertainty in the learning. In the covariance function, shown in (2), each dimension q is associated with $r_q=\frac{1}{{\mathcal{l}}_q}$, which can be seen as an importance weight of dimension q in the modeling. Since ℓ_q as a hyperparameter will be automatically learned from the data, this is known as automatic relevance determination (ARD). We initialize Q = E, and use ARD for learning the dimension of ${\mathcal{M}}^{\text{GP}}$. The values of the importance weights of irrelevant or redundant embedding dimensions will be close to zero, and the final learned Q will be much smaller than E.

3.2. Cross Mapping

Let the two reconstructed attractor manifolds be ${\mathcal{M}}_x^{\text{GP}}$ and ${\mathcal{M}}_y^{\text{GP}}$ and that they correspond to two time series x(t) and y(t), respectively. We will use them to discover causality by using GP-based cross mapping. For convenience, we only discuss the cross mapping of $\widehat{x}(t)|{\mathcal{M}}_y^{\text{GP}}$ using GP regression framework.

For each time instant t₀ in L − E + 1 ≤ t₀ ≤ L, we first find $m_y^{\text{GP}}\left(t_0\right)$ and its corresponding Q + 1 nearest neighbours for t < t₀ on ${\mathcal{M}}_y^{\text{GP}}$, denoted as ${\left\{m_y^{\text{GP}}\left(t_{n_i}^0\right)\right\}}_{i=1}^{Q+1}$, where $t_{n_i}^0$ is time index of the ith nearest neighbor of $m_y^{\text{GP}}\left(t_0\right)$. Then we train a GP regression model to learn the mapping from ${\tilde{y}}_{t_0}={\left[y\left(t_{n_1}^0\right),y\left(t_{n_2}^0\right),\dots ,y\left(t_{n_{Q+1}}^0\right)\right]}^{\top }$ to y(t₀), using the generative process as follows:

$$y\left(t_0\right)=g\left({\tilde{y}}_{t_0}\right)+\eta ,$$ (4)

where g is governed by a GP with zero mean and covariance function k_g(x, x′) which is a Q + 1 dimensional RBF, and $\eta ~\mathcal{N}\left(0,{\sigma }_{\eta }^2\right)$ is a white Gaussian noise.

Let $\tilde{Y}={\left\{{\tilde{y}}_{t_i}\right\}}_{i=1}^N$ denote the collection of all input vectors, and K_gg the covariance matrix obtained by evaluating the covariance function for $\tilde{Y}$, i.e., $K_{gg}=k_g(\tilde{Y},\tilde{Y})$. Then the prior probability density function (pdf) of g given $\tilde{Y}$ is given by

$$p(g|\tilde{Y},\mathit{\theta })=\mathcal{N}\left(g|0,K_{gg}\right).$$ (5)

The hyperparameters θ in the covariance function and the noise variance ${\sigma }_{\eta }^2$ are learned in the training stage by maximizing the (tractable) model evidence,

$$\begin{gathered} \text{log }p(y|\tilde{Y},\mathit{\theta })=\text{log }\mathcal{N}\left(y|0,K_{gg}+{\sigma }_{\eta }^{2}I\right) \\ =-\frac{1}{2}{y}^T{K}^{-1}y-\frac{1}{2}\text{log}|K|-\frac{N}{2}\text{log }2\pi , \end{gathered}$$ (6)

where $K=K_{gg}+{\sigma }_{\eta }^{2}I$. If we have test inputs ${\tilde{y}}_{*}$, the predictive pdf $p\left(g_{*}|{\tilde{y}}_{*},\tilde{Y},y,\mathit{\theta }\right)$ will be Gaussian with a mean given by:

$$E\left(g_{*}\right)=\left[k_g\left({\tilde{y}}_{*},\tilde{Y}\right)\right]K^{-1}y.$$ (7)

Since we need to perform cross mapping, we modify (7) as

$$\widehat{x}\left(t_0\right)=\left[k_g\left({\tilde{x}}_{t_0},\tilde{Y}\right)\right]K^{-1}y,$$ (8)

where ${\tilde{x}}_{t_0}$ is formed from x(t) and corresponding to the ordered time indices of the neighbours of $m_y^{\text{GP}}\left(t_0\right)$ on ${\mathcal{M}}_x^{\text{GP}}$. The variance of the cross mapping can also be computed readily [21]. If x drives y, the estimation capacity of $\widehat{x}(t)|{\mathcal{M}}_y^{\text{GP}}$, which is usually measured by the correlation coefficient ρ between $\widehat{x}(t)$ and x(t), will be improved with the increase of L and will converge.

4. EXPERIMENTS AND RESULTS

4.1. Synthetic Data

We first validate our GP-based method on the well-known Lorenz system defined by

$$\begin{gathered} dx/dt=a(y-x), \\ dy/dt=x(c-z)-y, \\ dz/dt=xy-bz. \end{gathered}$$ (9)

The system is nonlinear, non-periodic, three-dimensional and deterministic.

We generated a Lorenz attractor (a set of chaotic solutions of the Lorenz system) $\mathcal{M}$ of length 365 with (9) and a classic set of parameter values a = 10, $b=\frac{8}{3}$, and c = 28, along with the three time series obtained by projecting points in $\mathcal{M}$ to the X, Y and Z axes shown in Fig. 1.

Fig. 1.

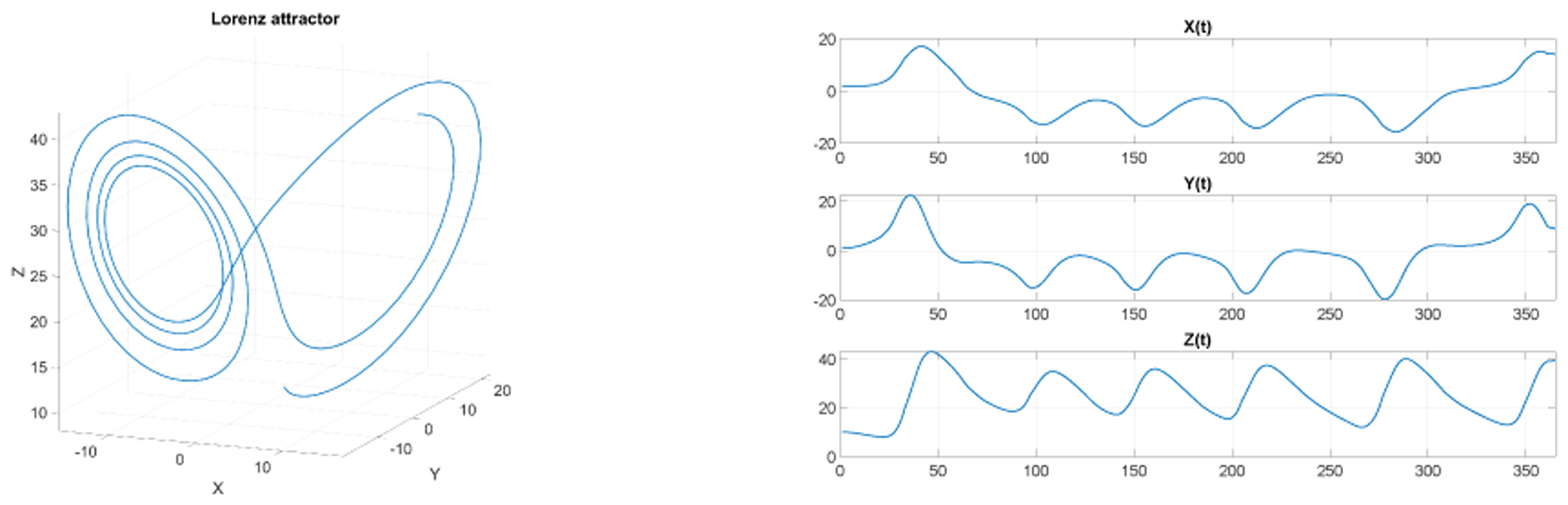
Synthetic data, the Lorenz attactor $\mathcal{M}$ (left) along with the three time series obtained by projecting $\mathcal{M}$ to X, Y and Z axis (right).

To make our experiments more realistic, we added white Gaussian noise $e~\mathcal{N}\left(0,{\sigma }_e^2\right)$, and we set ${\sigma }_e^2=0$, 1 and 9, respectively. Then we implemented the original CCM and our GP-based method to discover causality between X(t) and Y (t). Recall that in the original CCM, the SSR parameters are selected using grid search [19, 20]. From (9), we know that the true causal relationship is that X(t) is a cause of Y (t), and Y (t) is also a cause of X(t).

The comparison of SSR results for Y (t) are shown in Fig. 2, where we see that the GP-based SSR consistently provided better reconstructions. This was especially the case for ${\sigma }_e^2=9$, where the ${\mathcal{M}}_Y^{\text{DE}}$ is essentially unrecognizable, whereas ${\mathcal{M}}_Y^{\text{GP}}$ is still topologically similar to $\mathcal{M}$. It is worth noting that when ${\sigma }_e^2=0$, i.e., noise-free, the ${\mathcal{M}}_Y^{\text{DE}}$ is distorted, especially for the curves within the left lobe, whereas, in ${\mathcal{M}}_Y^{\text{GP}}$ there is no such distortion. Moreover, the true dimensionality of $\mathcal{M}$ is correctly estimated with and without observation noise.

Fig. 2.

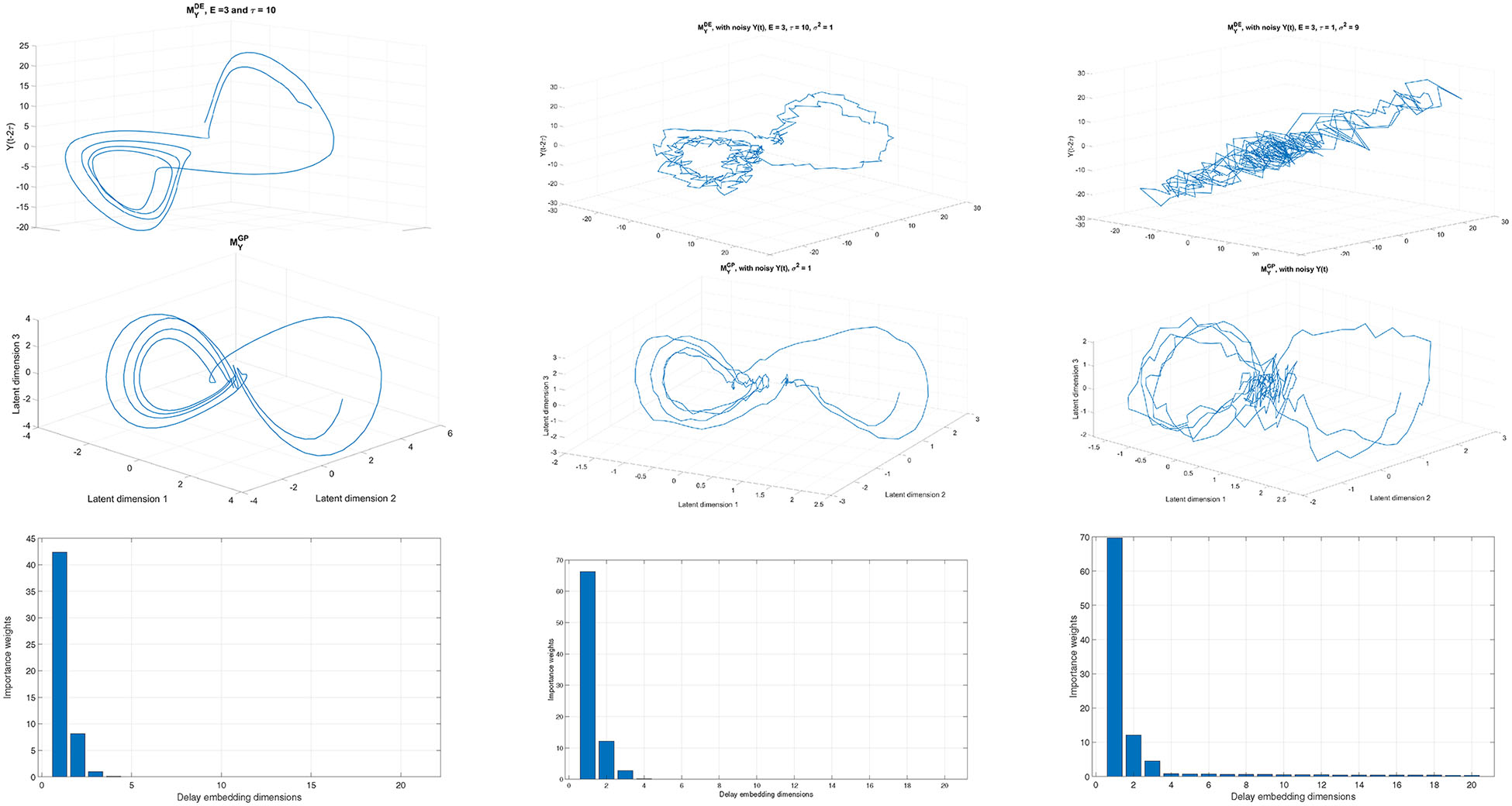
Attactor manifold reconstruction results for the synthetic dataset using delay embedding with optimal setting (top), and GP-based method (bottom) along with the importance weight of each dimension in ${\mathcal{M}}_Y^{\text{init}}$ that reveals the dimensionality of ${\mathcal{M}}_Y^{\text{GP}}$ (middle). From left to right, the variance of observation noise is ${\sigma }_e^2=0$, 1, and 9, respectively.

Finally, the test results of both methods are summarized in Fig. 3. We can see that both methods are able to identify the correct causal relationship when ${\sigma }_e^2=0$. However, for ${\sigma }_e^2=1$ and 9, the GP-based method demonstrated better convergence, which is crucial for distinguishing causation from correlation.

Fig. 3.

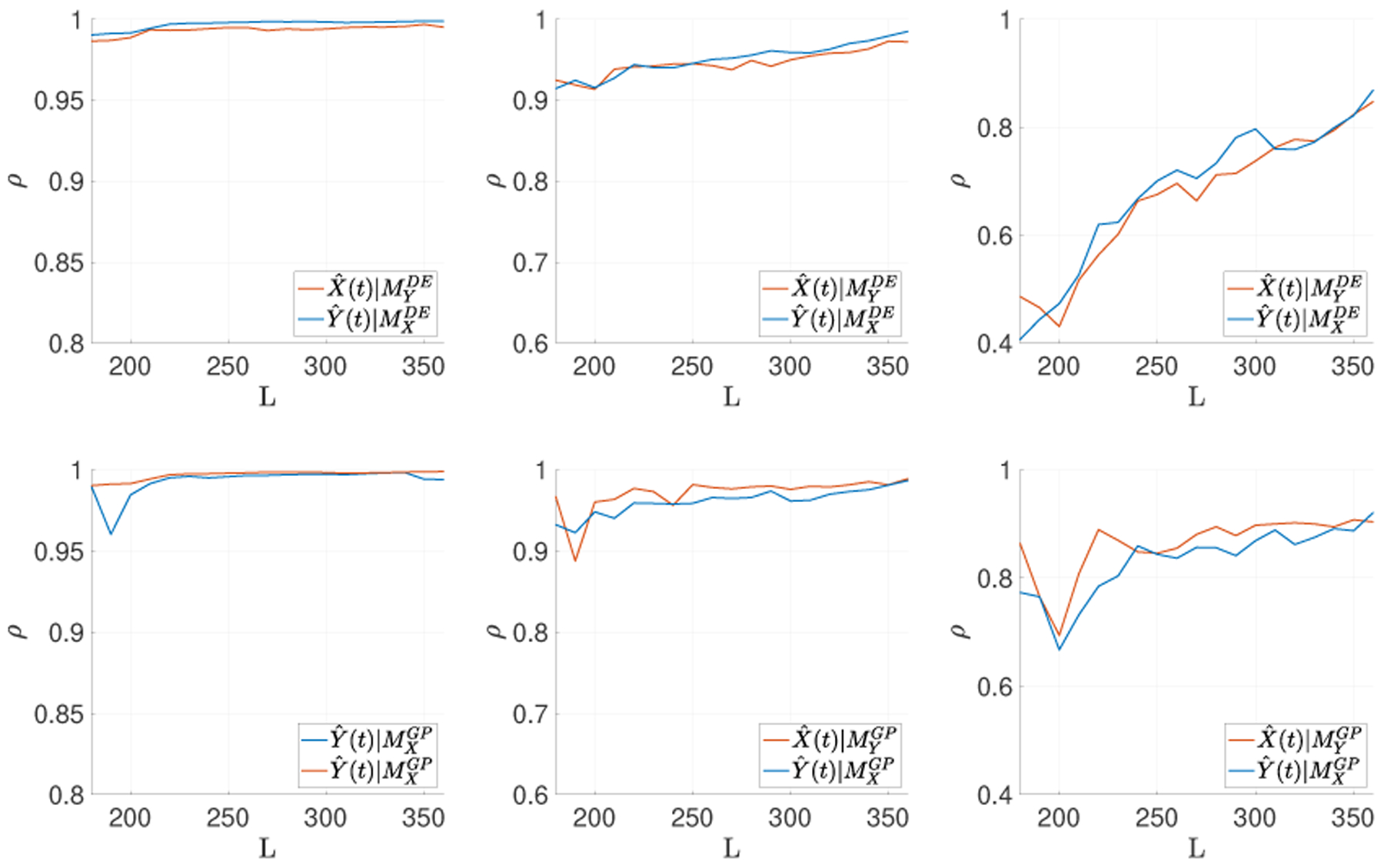
The test results on synthetic data using the orginal CCM (top), and the GP-based method (bottom). From left to right, the variance of the observation noise is ${\sigma }_e^2=0$, 1, and 9, respectively. The time series length L is increased from 180 to 360 with a step size of 10.

4.2. Real CTG Segment

In our experiments with real CTG data, we selected data records from an open access database that were acquired at the obstetrics ward of the University Hospital in Brno, Czech Republic. A detailed description of the database can be found in [24]. We applied our GP-based method on a real CTG segment of length 480 samples, which corresponds to a duration of 2 minutes (the sampling rate for both FHR and UA signals was 4 Hz). The FHR and UA signals and their corresponding attractor manifolds obtained by the GP-based method are shown in Fig. 4. Although the FHR and UA recordings are very different, their attactor manifolds are similar.

Fig. 4.

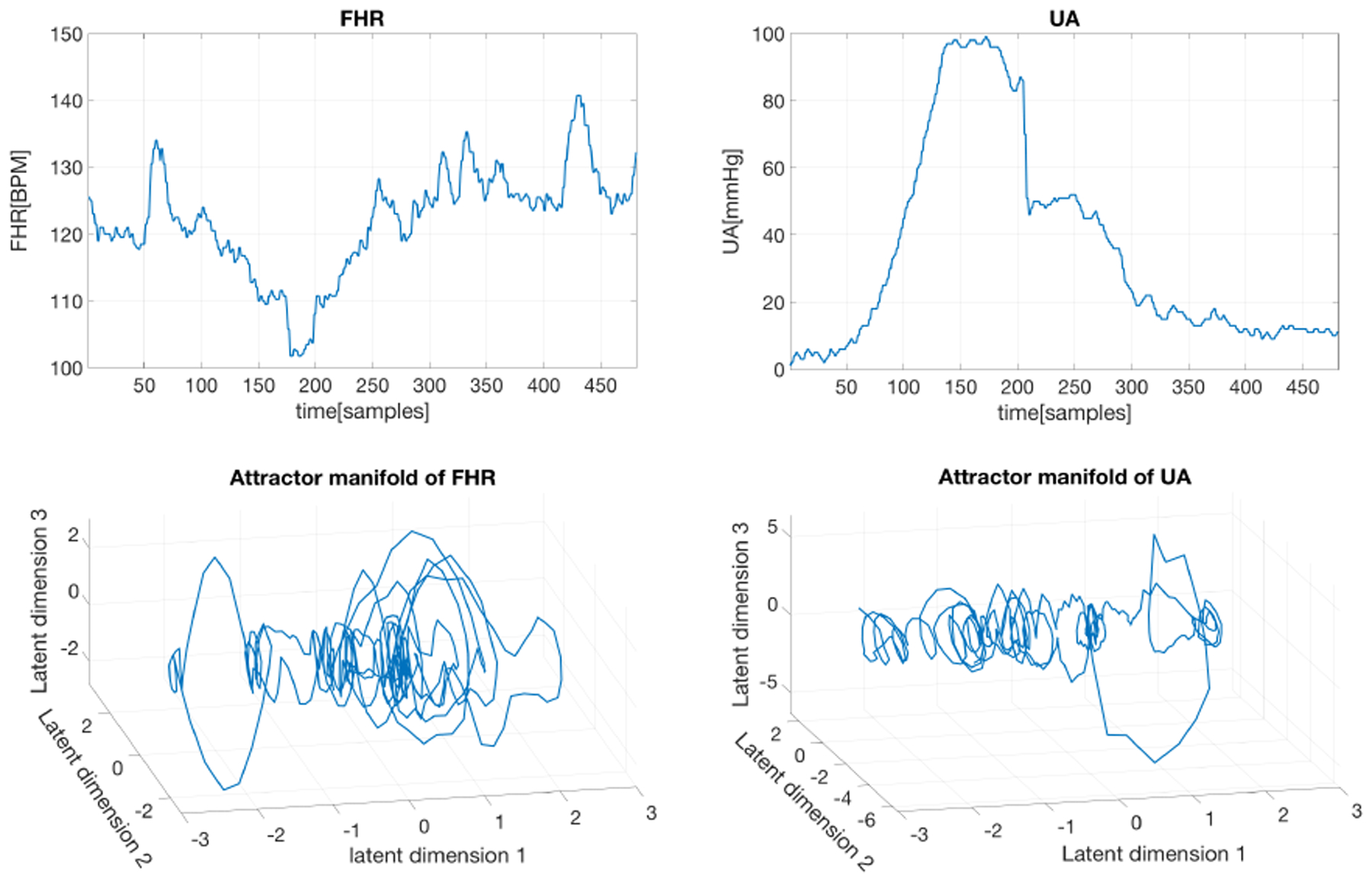
Raw FHR and UA segments (top), and their corresponding reconstructed attractor manifolds with the GP-based method (bottom).

The test results of the CTG segment using the original CCM and our GP-based method are shown in Fig. 5, where X denotes UA signal and Y denotes FHR signal. The results of the original CCM is ambiguous, since for both directions, the correlation coefficient shows decreasing trend, after L = 400. Moreover, there was no convergence for both directions. The test results of the GP-based method clearly showed that changes in the UA signal is a cause of changes in the FHR signal and not vice versa. For cross mapping from UA to FHR ($\widehat{Y}(t)|{\mathcal{M}}_X^{\text{GP}}$), the correlation coefficient showed high variance and no convergence, which indicates that FHR is not a cause of UA. Meanwhile, in the cross mapping from FHR to UA ($\widehat{X}(t)|{\mathcal{M}}_Y^{\text{GP}}$), the correlation coefficient showed small variance, and was gradually improved with L, and finally converged around 0.99. This suggests that changes in the UA signal cause changes in the FHR signal. This finding is consistent with clinical studies [17].

Fig. 5.

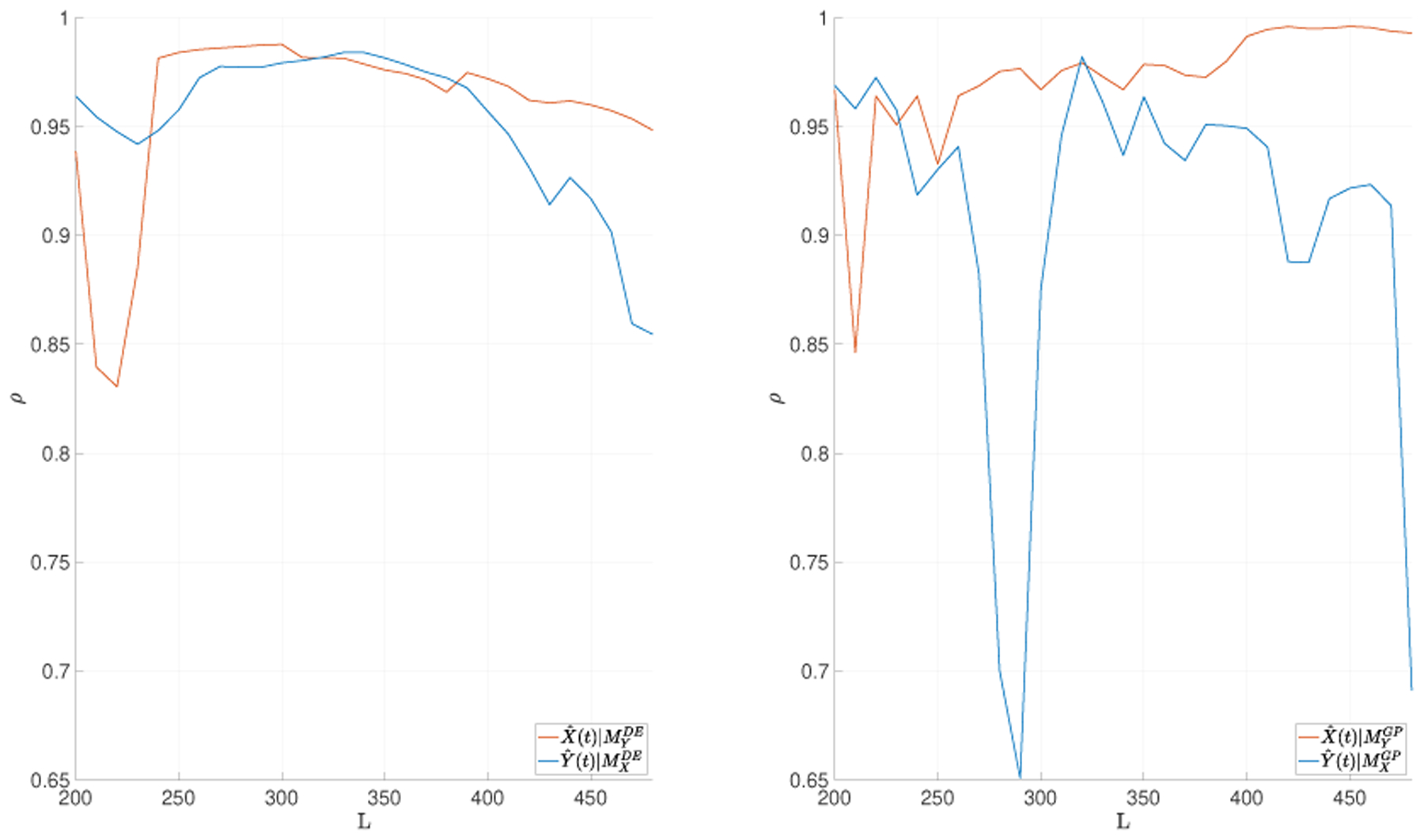
The test results on CTG segment using original CCM (left), and the GP-based method (right), where X denotes UA signal, and Y denotes FHR signal. The time series length L is increased from 200 to 480 with a step size of 10.

5. CONCLUSION

In this paper, we proposed a fully GP-based version of CCM for casual discovery that is robust to observation noise. Both the SSR and cross mapping steps are carried out using GPs within the Bayesian nonparametric probabilistic framework, which is data efficient and robust to overfitting. The method is also capable of properly handling uncertainties. We first validated our approach on synthetic data with different levels of noise variance and found that the GP-based CCM demonstrated better convergence, which is critical for distinguishing causation from correlation. Then we applied the GP-based CCM on a segment of real CTG recordings, and the results indicate that uterine activity affects fetal heart rates. The proposed method can readily be adopted for causal discovery in other areas, e.g., neuroscience.