An extended fuzzy decision-making framework using hesitant fuzzy sets for the drug selection to treat the mild symptoms of Coronavirus Disease 2019 (COVID-19)

Abstract

The whole world is presently under threat from Coronavirus Disease 2019 (COVID-19), a new disease spread by a virus of the corona family, called a novel coronavirus. To date, the cases due to this disease are increasing exponentially, but there is no vaccine of COVID-19 available commercially. However, several antiviral therapies are used to treat the mild symptoms of COVID-19 disease. Still, it is quite complicated and uncertain decision to choose the best antiviral therapy to treat the mild symptom of COVID-19. Hesitant Fuzzy Sets (HFSs) are proven effective and valuable structures to express uncertain information in real-world issues. Therefore, here we used the hesitant fuzzy decision-making (DM) method. This study has chosen five methods or medicines to treat the mild symptom of COVID-19. These alternatives have been ranked by seven criteria for choosing an optimal method. The purpose of this study is to develop an innovative Additive Ratio Assessment (ARAS) approach to elucidate the DM problems. Next, a divergence measure based procedure is developed to assess the relative importance of the criteria rationally. To do this, a novel divergence measure is introduced for HFSs. A case study of drug selection for COVID-19 disease is considered to demonstrate the practicability and efficacy of the developed idea in real-life applications. Afterward, the outcome shows that Remdesivir is the best medicine for patients with mild symptoms of the COVID-19. Sensitivity analysis is presented to ensure the permanence of the introduced framework. Moreover, a comprehensive comparison with existing models is discussed to show the advantages of the developed framework. Finally, the results prove that the introduced ARAS approach is more effective and reliable than the existing models.

Graphical abstract

1. Introduction

Wuhan, China, faced a serious threat during early December 2019, which twisted public health and globally wreaked chaos. The pneumonia cases originated as a novel beta coronavirus, named Coronavirus Disease 2019 (COVID-19) or Severe Acute Respiratory Syndrome-Corona Virus-2 (SARS-CoV-2) or 2019-nCoV. The diffusive rapidity of the COVID-19 epidemic was uncertain; therefore, the Chinese government actively channelized Wuhan’s traffic to control the spread of the epidemic [1]. In expressions of the number of confirmed COVID-19 cases, the United States, India, Brazil, Russia, and France are the five most-affected countries. The World Health Organization (WHO) affirmed the condition of a pandemic by March 2020. Thus far, various nations and regions have been locked-down and used firm social distancing procedures to discontinue virus propagation. To date, the COVID-19 has speedily spread all over the globe, affecting over 62,570,316 people (report of November 29, 2020) [2]. The virus that the source of COVID-19 is mostly transmitted through droplets produced when an individual with COVID-19 coughs, sneezes or exhales. Coronavirus is riskier for low-immunity people, old age, diabetes, and medical problems, particularly related to the lungs [3], [4], [5], [6]. The spread of viruses can be affected by various reasons, including climate, population density, medical-care facilities, and others [7].

“Coronaviruses are a large family of viruses which may cause different types of infections in animals or humans. In humans, they mainly produce respiratory tract infections ranging from the common cold to more severe diseases such as Middle East Respiratory Syndrome (MERS) and Severe Acute Respiratory Syndrome (SARS) [8], [9], [10] ”. Sequencing and phylogenetic studies have revealed that the COVID-19 strain is diligently associated with a group of human and bat SARS-like coronaviruses [4], [11], [12]. It is believed that the COVID-19 made its genesis from bats into higher life chains [13], [14], [15]. Initially reported cases of COVID-19 were related to Haman seafood and live-animal shops. Nonetheless, no animal source has been recognized to till now, and spillover actions may remain to happen. Though bats might be the source of COVID-19, it is substantial to find the mediator species to stop the pandemic from spreading globally.

The COVID-19 was recognized in December 2019, so due to insufficient data and medical technologies, namely clinical trials, it is still in a precarious phase of assessment. Previously, it is quite difficult to apply the available disease data directly to existing mathematical tools and answer how successful the ongoing medical response is. For the treatment process, doctors, experts, or medical sections should implement tests, strategies or choose an optimal scheme to evade further growth of the crisis. The developing strategy division must take quick and effective decisions. In this situation, while making decisions, people are generally bound logically in place of fully reasonable. Therefore, it is significant to find apt Decision-Making (DM) models that recognize human activities to offer people effective ways of reacting to emergencies. Dealing with vague and uncertain data in realistic settings has every time been a difficulty. Numerous tools have been discovered to tackle the intricacy and ambiguity obtained in daily-life procedures, namely, the doctrine of Fuzzy Sets (FSs) and their generalization. At present, the Hesitant Fuzzy Sets (HFSs) are recognized as a latent procedure to elucidate the ambiguity that is ultimately available in intricate DM issues. Focused on the fruitfulness of HFSs, this study is conducted under the HFSs. Even though several Multi-Criteria Decision-Making (MCDM) problems have been initiated under the environment of HFSs, there is no study on developing the Additive Ratio Assessment (ARAS) framework with hesitant fuzzy information and employing divergence measure. Also, no study has employed the concepts of HF-divergence measure to estimate the criteria weights for evaluating drug selection problems for patients with mild symptoms of COVID-19 disease. Aiming at the situation that the weight of Decision Experts (DEs) and criteria are unknown, new expert weight and criteria weight calculation models are discussed, which can systematically employ the significance of DEs and their assessment’s rationality. The proposed model can efficiently exclude the effect of extreme DE opinions on the assessment outcomes, further explain the problem of large modifications in DEs opinions or evade several DEs being purposely influenced. The objective of the work is explained as follows:

• •An extended ARAS method is introduced within the context of HFSs to handle the complex MCDM problems.
• •An innovative procedure is proposed to evaluate the attribute weights using the introduced HF-divergence measure.
• •Further, a case study of drug selection for mild symptoms of COVID-19 is discussed to express the applicability and usefulness of the developed ARAS framework within the HFSs context.
• •Comparison and sensitivity assessment are made to interpret the outcomes.

The structure of this paper is as follows. Section 2 focuses on reviewing the literature of the proposed study. Section 3 delivers the fundamental notions of HFSs. Section 3.1 develops a new HF-divergence measure and some interesting axioms. Section 4 presents a novel HF-ARAS approach based on a divergence measure. Section 5 discusses a case study to prove the superiority of the developed model. In the end, Section 6 presents the overall conclusions and recommendations for future research.

2. Literature review

The current section provided an overview of COVID-19 disease and related works of HFSs and the ARAS approach.

2.1. COVID-19 disease

The COVID-19 is an acute and new disease for public health that is infectious. Current evidence shows that the asymptomatic period of COVID-19 infection ranges from two days and two weeks. During this time, the infected person may not develop any symptoms and may not be alert for their infection, yet they can transmit the disease to other people. “In the novel COVID-19 strain, the nucleotide sequence of the external codomain in the spike protein receptor-binding domain is different from that of the 2003 Severe acute respiratory syndrome Coronavirus (SARS-CoV). When individual bat coronavirus spike genes were introduced into SARS-CoV infectious clones, the SARS-CoV/bat-CoV spike viruses could bind to the human, bat, or civet Angiotensin-Converting Enzyme-2 (ACE2) cellular receptor [16] ”. Analysis of the interaction between the spike protein and the host ACE2 receptor might expose insights on how the virus disabled the species barrier to arrive at advanced life chains. From the public health and socio-economic viewpoint, we immediately need to discover a useful vaccine and antiviral therapeutics to discontinue the chain of the COVID-19 pandemic.

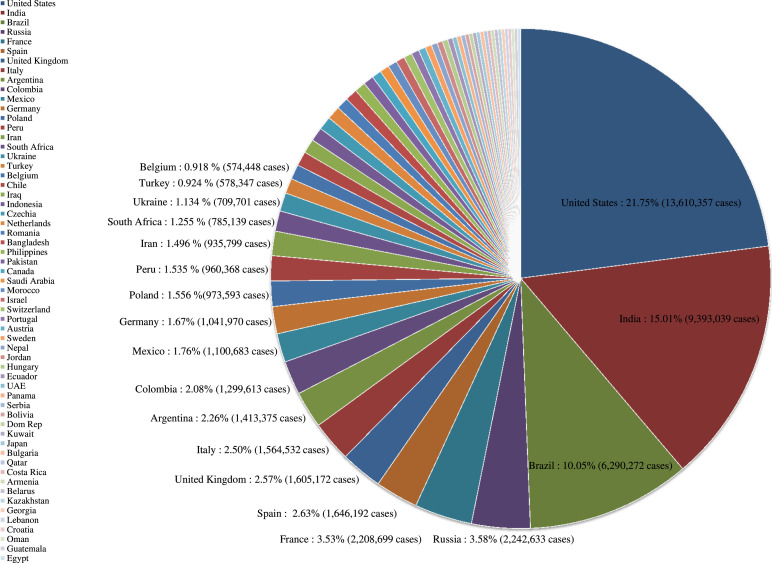
The CODIV-19 is spreading rapidly that is being transmitted by infected people, making it more challenging to control its spread worldwide [17], [18], [19]. The spreading of COVID-19 cases is depicted in Fig. 1 [2]. Here, several ample preventive procedures, such as social distancing, have to be considered globally to decrease infection spread. Nevertheless, the only option to end the COVID-19 pandemic is the development of an effective vaccine. The incubation period of COVID-19 is from contact with the infected person to the appearance of the symptoms. Fever, cough, nausea, and shortness of breath are common symptoms of COVID-19 [20]. For example, most viral chest diseases, H1N1 (Hemagglutinin Type 1 and Neuraminidase Type 1), H5N1 (Hemagglutinin Type 5 and Neuraminidase Type 1), and influenza, have the same symptoms as COVID-19, which may lead to the wrong diagnosis. For the diagnosis of COVID-19, the most common tools used are the Polymerase Chain Reaction (PCR), assay, or a chest Computed Tomography (CT) scan. The PCR method can directly detect viral nucleic acids, while in the CT scan method, volumes of infection on one or both sides of the lung is being determined [21]. A turning point for this epidemic would be the development of a vaccine. However, WHO estimates that this could take 18 months [22]. Until this time, symptomatic treatments have been used to treat the symptoms of the virus. Therefore, maintaining social distancing and awareness will be preventive measures until a vaccine is developed. Simultaneously, effective infection systems procedures remain perilous for treating and controlling COVID-19 infections. Nour et al. [23] gave a Convolutional Neural Network (CNN) architecture-based model to detect positive COVID-19 cases to support everyday clinical applications automatically. Aydin and Yurdakul [24] constructed a three-phase model using machine learning procedures and data envelopment analysis to evaluate the performances of 142 nations against the COVID-19 outbreak. Marques et al. [25] proposed a medical decision support system using CNN for COVID-19 diagnosis. Mohammed et al. [26] discussed a model to support the health organizations for choosing the COVID-19 diagnosis tool. Hazarika and Gupta [27] concentrated on modeling and forecasting the spread of COVID-19 in the top 5 worst-hit nations (Brazil, India, Peru, Russia, and the USA) according to the reports on July 10, 2020, using Wavelet Coupled Random Vector Functional Link Network (WCRVFL) network.

Fig. 1.

Distribution of cases all over the world.

Worldometer [2].

In recent times, the study of COVID-19 transmission hasgained attractive attention from researchers and practitioners. Sameni [28] presented a Susceptible–Infected–Recovered​ (SIR) family of compartmental methodologies to understand the epidemic patterns of COVID-19. Ahmadi et al. [29] studied the COVID-19 outbreak by considering geographical and climatological parameters. Zhu and Chen [30] proposed a statistical disease model to analyze the early outbreak in China. Boldog et al. [31] introduced an integrated tool for assessing the risk of COVID-19 outbreaks in countries outside of China. Yang and Wang [32] established a mathematical model, which considers the multiple transmission pathways for transmitting and spreading the COVID-19 epidemic in Wuhan, China. Chen et al. [2] suggested a scientific methodology, which simulated the potential risk of transmission of SARS-CoV-2 from the reservoir to individual and from individual to individual. To study the spread trend of COVID-19, several scholarly articles have been presented in the literature [33], [34], [35].

Since 2020, the COVID-19 has been spreading on a large amount worldwide, which has greatly impacted human life. To recognize COVID-19 and diminish its effect, researchers have prepared research and workable models. Abdo et al. [36] discussed the comprehensive procedure of COVID-19 by evaluating the nonlinear fractional differential equations. Melin et al. [37] gave a multiple collaborative CNN tool with fuzzy sets (FSs), which successfully enhanced the predictable consequence of the COVID-19 time series. Crokidakis [38] applied a Susceptible–Infectious–Quarantined–Recovered (SIQR) tool to examine the Rio fever rate data to analyze the efficacy of social isolation in handling the COVID-19 pandemic. Melin et al. [39] examined the COVID-19 spread globally from a spatial viewpoint. Contreras et al. [40] recognized a multi-group Susceptible–Exposed–Infected–Recovered–Asymptomatic (SEIRA) tool to support the people developing the strategies. Boccaletti et al. [41] mentioned that through sharing and integrating applied mathematics with different doctrines, namely, virology, machine learning, the damaging impact of the pandemic can be lessened. Abdel-basst et al. [42] advocated a model with the pathogenic set, Best–Worst​ Method (BWM), and Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) methods to distinguish between COVID-19 and different four viral chest diseases under an uncertain setting.

Recently, numerous studies on COVID-19 diagnosis, treatment, control, and impact have been performed in the literature. Devaux et al. [43] discussed the promising tools of chloroquine interference with COVID-19. Zhang et al. [44] examined whether various Chinese medical herbs can handle COVID-19 contamination. Phan et al. [45] discovered procedures for the detection and clinical diagnosis of COVID-19. Lupia et al. [46] précised the clinical diagnosis of COVID 19 with recommendations for patients with antibiotic treatment. Shen et al. [47] summarized the presently accessible detection tools for COVID-19 to support investigators in introducing enhanced procedures for recognizing infection. Kooraki et al. [48] investigated radiology can assist scientists with the detection of COVID-19. Bonilla-Aldana et al. [49] assembled data about COVID-19 utilizing an Internet-based reporting model to advance its effectiveness during the pandemic. McKibbin and Fernando [50] and Anderson et al. [51] examined the effects of COVID-19 on macroeconomic consequences in different scenarios and the effect of government policies in dealing with the COVID-19 pandemic, respectively.

Gupta et al. [52] proposed a stacked deep CNN InstaCovNet-19 to detect COVID-19 and pneumonia. Karthik et al. [53] proposed a custom CNN architecture to enable automated learning of such latent features to a particular class of pneumonia/COVID-19. Ezzat et al. [54] developed a Gravitational Search Algorithm (GSA) model-driven DenseNet121-COVID-19 with a hybrid CNN design. Ghosh and Bhattacharya [55] discussed a precise data-driven tool for the infection spread to recognize and interpret COVID-19 data by optimized cellular automata to provide an exceptional platform. Ashraf and Abdullah [56] introduced several tools to deal with the emergency condition of COVID-19 using spherical fuzzy sets. Issa and Elaziz [57] developed the enhancement of Fragmented Local Aligner Technique (FLAT) to produce acceptable Longest Common Consecutive Subsequence (LCCS) with proficient performance in an equitable time. Wu et al. [58] proposed an approach to plan emergency production procedures for a medical mask producer during the COVID-19 pandemic in China. Hernandez-Matamoros et al. [59] developed an Autoregressive Integrated Moving Average (ARIMA) tool for 145 nations, which are spread scattered into six regions to predict the COVID-19 cases. This study reviews the literature with a novel COVID-19 diagnosis framework that utilizes HF-divergence measure-based ARAS under HFSs. We combined the divergence measure with the ARAS model to obtain a reliable structure that implements under an uncertain setting for evaluating the medicine to treat the patient with mild symptoms of COVID-19.

2.2. Hesitant Fuzzy Sets (HFSs)

In the DM procedure, the DEs might assess the Belongingness Degree (BD) of an object to a set of various distinct degrees in numerous real-life circumstances because of their individual attention, time restrictions, and deficiency of information. For example, suppose a group of DEs is required to offer the BD of a particular opinion to an adult age cluster. In that case, the first DE wishes 0.65, another 0.70, and the last one does not recommend the BD due to the time restrictions and deficiency of knowledge/information/data [60]. To handle this issue, the doctrine of HFSs was given by Torra and Narukawa [61], which offers the BD to comprise various distinct assessment degrees. As the extension of FSs, HF sets have gained much interest from the researchers in dealing with the ambiguity in daily life problems. It is represented by a BD and signified by a set of possible degrees. Recently, it is revealing that the HFSs have powerfully associated with the existing FSs, namely, Intuitionistic Fuzzy Sets (IFSs) [62], Type-2 Fuzzy Sets (T2FSs) [63], and Fuzzy Multi Sets (FMSs) [64]. As stated by Torra [60], the prime concern to invent HFSs is that when describing the BD of an object, the complexity of generating the BD is not a margin of error (previously seen in IFSs) or specific possibility distribution (previously seen in T2FSs) on the possibility degrees, but a possible degrees’ set. Owing to the association with mentioned extended FSs, HFSs are distinguished as IFSs when it is a non-void closed interval; in specific concerns, HFSs can describe FMSs, even if the laws for FMSs do not implement properly to HFSs.

Next, numerous researchers have concentrated on the HFSs context. For instance, Xia and Xu [65] and Xia et al. [66] presented a set of Aggregation Operators (AOs) on HFSs. Xu and Xia [67] pioneered the distance measure on HFSs and discussed the relationship between different information measures [68]. He et al. [69] and Sun [70] presented the power geometric and normalized geometric Bonferroni mean operators and used them to handle MCDM problems for HFSs. Liao et al. [71] introduced the HF-correlation measures. Li et al. [72] and Hu et al. [73] discussed several hesitant fuzzy information measures. Cuiping et al. [74] developed several novel prioritized aggregation operators. Yu [75] firstly proposed the concept of hesitant fuzzy Heronian mean operators. Lv et al. [76] firstly suggested the conception of a feature vector and then studied the hesitant fuzzy information measures. Wang [77] used a combination of similarity measures and applied the synthetical procedure for HFSs. In addition, they used their formula for clustering analysis within the HFSs context.

Currently, HFSs has extensively been employed in MCDM problems because of their usefulness in articulating ambiguous information. Afterward, numerous MCDM models have been presented to elucidate DM problems under the HFSs environment. Xu & Zhang [78] and Liao & Xu [79] discussed the TOPSIS and the VlseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR) approaches to solve the MCDM for HFSs. Liu et al. [80] initiated the HF cognitive maps and showed how to explore the risk factors that arise in an electric power system. Mousavi et al. [81] introduced the Hesitant Fuzzy Elimination and Choice Expressing the REality (HF-ELECTRE) technique to assess the renewable energy source assessment problem. Rani et al. [82] evaluated and ranked sustainable suppliers by employing the Hesitant Fuzzy Step-wise Weight Assessment Ratio Analysis-Complex Proportional Assessment (HF-SWARA-COPRAS) methodology. Lan et al. [83] suggested an MCDM model with new priority degree formula on HFSs. With the implementation of the HF-COPRAS method, Mishra et al. [84] assessed and presented the ranking order of the service quality alternatives for vehicle insurance companies. Cheng [85] recommended novel autocratic DM using group recommendations for HFSs to deal with the green hotel assessment problems. In a further study, Mishra et al. [86] designed an innovative framework within the HFSs environment to evaluate and prioritize green supplier alternatives. In the literature, several other models have been discussed within the HFSs setting [87], [88].

Wu et al. [89] used a Decision Making Trial and Evaluation Laboratory (DEMATEL) to compute the significance of customer needs, and the VIKOR approach ranked the characteristics of an electric vehicle on HFSs. It is worthy to say that various theoretical and practical reasoning can be simplified with the help of Uniformly Typical Hesitant Fuzzy Sets (UTHFSs), which was articulated by Alcatud and Torra [90]. Farhadinia and Herrera-Viedma [91] re-defined the Extended HFSs (EHFSs) by the Cartesian product of HFSs. Liao et al. [92] proposed a Choquet integral-based Gained And Lost Dominance Score (GLDS) model to deal with the two significant concerns concerning the interactions among criteria and the behavior preference of DEs in MCDM problems. Wang et al. [93] extended the Group Emergency DM (GEDM) method using HFNs.

Kaya and Erginel [94] presented a new approach that integrates SWARA and the Sustainable Quality Function Deployment (SQFD) model to improve the sustainable airport quality under HFSs. Mokhtia et al. [95] adapted the Ridge, Least Absolute Shrinkage and Selection Operator (LASSO), and Elastic Net regression models for the assignment of assessing feature. Colak and Kaya [96] proposed a hybrid model consisting of Delphi, Analytic Hierarchy Process (AHP), and VIKOR approaches to evaluate Turkey’s energy storage alternatives under a hesitant fuzzy environment. Mardani et al. [97] developed a combined structure with the SWARA, SWOT (Strengths, Weaknesses, Opportunities, Threats), Weighted Aggregated Sum Product Assessment (WASPAS), and HFSs to assess the digital technologies intervention to control the COVID-19 outbreak. Wu et al. [98] gave a trust-based Social Network Group Decision Making (SNGDM) approach with HPRs to the Water–Energy–Food (WEF) nexus assessment. Mo et al. [99] proposed the Hesitant Fuzzy Satisfaction With Life Scale (HFSWLS), consisting of numerous possible cognitive degree judgments to describe the uncertainties and hesitancies. Narayanamoorthy et al. [100] gave a framework with Multi-Objective Optimization based on Simple Ratio Analysis (MOOSRA) on HFSs, evaluating the best alternative bio-medical waste disposal treatment methods. In the process of MCDM, criteria weights pay attention to expose the DEs preferences, and also, the DE weights contribute to the ranking methods for handling the problem. When the DE assigns values of attributes, they have some hesitation. To evade the particular concern, we have to utilize the HFSs in the proposed approach. From this motivation part, we propose a procedure to compute the criteria weights based on HF-divergence measure and DE weights for HFSs.

2.3. Additive Ratio Assessment (ARAS) approach

Zavadskas and Turskis [101] sowed the initial seed for the ARAS framework based on the intuitive concept of complex domains with contradictory attributes illustrated via easy relative comparisons. This method has intuitive and straightforward procedures that yield sensible, adequate and relatively exact results in selection from diversified alternatives based on their performance measures that are put forward as weighted assessment criteria. It gives the notion of an optimality degree to find the rank. The comprehensive investigation of the ARAS model is presented in Table 1. ARAS’s benefits are (i) Straight and proportional association with attribute weights [101], [102], [103]. (ii) capability to determine highly difficult problems [104], [105], [106]. (iii) flexible and scalable [104], [106]. (iv) effectiveness [104], [105], [106], [107]. (v) adaptable to different fuzzy environments [106]. Its weaknesses are discussed as (i) Prioritizations of DEs may impact the alteration between the utility values [108]. (ii) Dependency on initial data-type and aims of participants [105], [108]. (iii) Dependency on the knowledge level of DEs and their assessment process [105], [106], [108].

Table 1.

Existing studies on the ARAS approach.

Author(s)	Year	The objective of the paper	Fuzzy extensions	Benchmark	GDM
Zavadskas & Turskis [101]	2010	Pioneer the ARAS approach	–	ARAS method	Yes
Turskis & Zavadskas [109]	2010	To select the logistic center’s location	FSs	Combined AHP & ARAS method	Yes
Kutut et al. [103]	2013	To maintain historic city center buildings	–	ARAS method	No
Keršulienė and Turskis [102]	2014	To choose the chief accountant	FSs	Fuzzy ARAS, AHP	Yes
Stanujkic [104]	2015	To generalize the ARAS model in the Interval-Valued Fuzzy Sets (IVFSs)	IVFSs	IVF-ARAS	Yes
Zavadskas et al. [105]	2015	To choose deep-water sea Port	FSs	AHP, Fuzzy ARAS	Yes
Karabasevic et al. [110]	2016	To better select personnel	FSs	SWARA, ARAS	Yes
Zavadskas et al. [108]	2017	To evaluate managerial issues consisting of cost-effective management	FSs	ARAS and TOPSIS with FSs	Yes
Büyüközkan and Göçer [106]	2018	To evaluate digital supply Chains	Interval-Valued Intuitionistic Fuzzy Sets (IVIFSs)	IVIF-AHP, ARAS	Yes
Dahooie et al. [111]	2018	To assess projects	IVFSs	SWARA, Interval-valued ARAS	Yes
Büyüközkan and Güler [112]	2020	To assess the digital maturity scores of the firms	HFSs	HFL-AHP, HFL-ARAS	Yes
Iordache et al. [107]	2019	To choose the underground hydrogen storage location	Interval Type-2 Hesitant Fuzzy Sets (IT2HFSs)	IT2HF-ARAS	Yes
Liao et al. [113]	2019	To select the digital finance supplier selection	Hesitant Fuzzy Linguistic Term Sets (HFLTSs)	HFL-BWM and ARAS	Yes
Büyüközkan and Güler [114]	2020	To select the smartwatch	HFLTSs	HFL-SAW-ARAS	Yes
Ghenai et al. [115]	2020	To select renewable energy systems	–	Combined SWARA and ARAS method	Yes
Goswami and Mitra [116]	2020	To select the best mobile model	–	Integrated AHP COPRAS and ARAS	Yes
Mishra et al. [117]	2020	To select the personnel selection	IFSs	IF- ARAS method	Yes

Afterward, various extensions of ARAS methodology have been fruitfully implemented in different uncertain areas [104]. Turskis and Zavadskas [109] discussed an integrated method by combining AHP and ARAS approaches for logistic center location problems with fuzzy information. Buyukozkan and Gocer [93] developed combined AHP and ARAS methods under IVIFSs and utilized them to evaluate the digital supply chain selection problem. Mishra et al. [117] integrated the framework with ARAS approach, divergence measure, improved score function, and IF-aggregation operators to choose the best Information Technology (IT) personnel selection. Although many existing studies related to HFSs have been presented in Section 2.2, there is no work in the literature related to the ARAS framework within the HFSs environment to assess the drug alternatives for the mild symptoms of COVID-19.

From the above discussion, numerous scholars have worked on fuzzy MCDM. Also, a few scholars have discussed the implementation with HF-MCDM. There is not, however, a model in MCDM with an integrated weighting procedure under HFSs. To fill this research gap, we propose a weighting model and ranking model, which consider DEs hesitation and ambiguity when providing the degrees for assessing the suitable option. Furthermore, the implementation of drug selection for treating the patient has contained a lot of hesitant and vague expressions with some vague criteria. When DE gives the degrees for criteria, he needs to describe his knowledge of hesitation; HFSs help to assign the BDs in terms of HFNs. Therefore, the application of drug selection for treating the patient of COVID-19 with HFNs is considered the main motivation of our study.

3. Basic concepts

This section firstly confers various important and elementary concepts about HFSs. Further, new divergence measure is proposed for HFSs.

Definition 1

A HFS $U$ in the finite universe $\Omega$ can be denoted by a belongingness degree (BD) $h_U$, which draws each object z to the finite discourse $\Omega$ to a subset of values in $[0,1]$. Xia and Xu [66] defined the mathematical form of HFS as

$$U=\left\{〈z,h_U\left(z\right)〉:z\in \Omega \right\},$$ (1)

where $h_U\left(z\right)$ is named as Hesitant Fuzzy Number (HFN), signifying the possible BDs of object $z\in \Omega$ to the set U, which holds $h_U\left(z\right)=\left\{\xi :\xi \in h_U\left(z\right)\right\}$.

Definition 2

Let $h,h_1,h_2\in HFNs\left(\Omega \right)$. Then, operations on HFNs are given by [60], [66]

(i) $h^c={\cup }_{\xi \in h}\left\{1-\xi \right\}$,

(ii) $h_1\cup h_2={\cup }_{{\xi }_1\in h_1,{\xi }_2\in h_2}max\left\{{\xi }_1,{\xi }_2\right\}$,

(iii) $h_1\cap h_2={\cup }_{{\xi }_1\in h_1,{\xi }_2\in h_2}min\left\{{\xi }_1,{\xi }_2\right\}$,

(iv) $\lambda h={\cup }_{\xi \in h}\left\{1-{\left(1-\xi \right)}^{\lambda }\right\},\lambda >0$,

(v) $h^{\lambda }={\cup }_{\xi \in h}\left\{{\xi }^{\lambda }\right\},\lambda >0$,

(vi) $h_1\oplus h_2={\cup }_{{\xi }_1\in h_1,{\xi }_2\in h_2}\left\{{\xi }_1+{\xi }_2-{\xi }_1{\xi }_2\right\}$,

(vii) $h_1\otimes h_2={\cup }_{{\xi }_1\in h_1,{\xi }_2\in h_2}\left\{{\xi }_1{\xi }_2\right\}$.

Definition 3

The score function and the variance of the HFN $h_1$ are given by [66], [79]

$$\mathbb{S}\left(h_1\right)=\frac{1}{g_{h_1}}\sum _{\gamma \in h_1}\xi \text{ and }\upsilon \left(h_1\right)=\frac{1}{g_{h_1}}\sqrt{\sum _{{\xi }_i,{\xi }_j\in h_1}{\left({\xi }_i-{\xi }_j\right)}^2},$$ (2)

where $g_{h_1}$ is the number of objects in $h_1$.

Definition 4 [66], [79] —

Consider a set of HFNs $E=\left\{h_1,h_2,\dots ,\right)\left(h_n\right\}$, then the HF-weighted average (HFWA) operator is given as

$$HFWA\left(h_1,h_2,\dots ,h_n\right)=\stackrel{n}{\underset{j=1}{\oplus }}{\omega }_j{h}_j={\cup }_{{\xi }_1\in h_1,{\xi }_2\in h_2,\dots ,{\xi }_n\in h_n}\left\{1-\prod _{j=1}^n{\left(1-{\xi }_j\right)}^{{\omega }_j}\right\}.$$ (3)

Definition 5 [68] —

Let $U,V\in HFSs\left(\Omega \right)$. The function $D:HFS\left(\Omega \right)\times HFS\left(\Omega \right)\to \mathbb{R}$ is called an HF-divergence measure if it holds

(J1) $D\left(U,V\right)\ge 0$,

(J2) $D_1\left(U,V\right)=0\iff U=V$.

3.1. New divergence measure for HFSs

There are various models to compute the criteria weights and categorize those models into subjective and objective ways. The subjective way defines weights purely based on the thought or decisions of DEs, whereas the objective way chooses weights using mathematical assessments, which neglect the subjective decision information of DEs. This combination incapacitates the shortcoming which arises in either a subjective way or an objective way. In this study, for estimating objective weights, HF-divergence measures based procedure is developed. Here, a new HF-divergence measure is proposed.

Let $U,V\in HFSs\left(\Omega \right)$. Then, a novel divergence measure for HFSs is defined by

$$D_1\left(U,V\right)=\frac{1}{n}\sum _{i=1}^n\left(\frac{1}{g_h\left(\sqrt{2}-1\right)}\sum _{j=1}^{g_h}\left(\sqrt{\frac{{\left(h_U^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_V^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}}\right)\right)\left(\left(-\frac{h_U^{\sigma \left(j\right)}\left(z_i\right)+h_V^{\sigma \left(j\right)}\left(z_i\right)}{2}\right)\right),$$ (4)

Theorem 1

Let $U,V\in HFSs\left(\Omega \right)$ . Then the measure $D_1\left(U,V\right)$ is valid HF-divergence measure.

Proof

(i) For any two real number $\alpha ,\beta \in \mathbb{R}$, the following inequality holds ${\left(\frac{{\alpha }^2+{\beta }^2}{2}\right)}^{1∕2}\ge \frac{\alpha +\beta }{2}$. Since $0\le h_U^{\sigma \left(j\right)}\left(z_i\right),h_V^{\sigma \left(j\right)}\left(z_i\right)\le 1$, which implies that $\sqrt{\frac{{\left(h_U^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_V^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}}\ge \frac{h_U^{\sigma \left(j\right)}\left(z_i\right)+h_V^{\sigma \left(j\right)}\left(z_i\right)}{2}$, for each $1\le i\le n$,$1\le j\le g_h$. Therefore, from Eq. (4), we obtain $D_1\left(U,V\right)\ge 0$.

(ii) Suppose that $U=V$, therefore, $h_U^{\sigma \left(j\right)}\left(z_i\right)=h_V^{\sigma \left(j\right)}\left(z_i\right),\forall i=1\left(1\right)n,j=1,2,\dots ,g_h$. Then, Eq. (4) becomes

$$D_1\left(U,V\right)=\frac{1}{n}\sum _{i=1}^n\left(\frac{1}{g_h\left(\sqrt{2}-1\right)}\sum _{j=1}^{g_h}\left[{\left(\frac{{\left(h_U^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_V^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}\right)}^{1∕2}\right)\right)\left(\left(-\frac{h_U^{\sigma \left(j\right)}\left(z_i\right)+h_V^{\sigma \left(j\right)}\left(z_i\right)}{2}\right]\right)=0.$$

Conversely, assume $D_1\left(U,V\right)=0$,

$$\iff \frac{1}{n}\sum _{i=1}^n\left(\frac{1}{g_h\left(\sqrt{2}-1\right)}\sum _{j=1}^{g_h}\left[{\left(\frac{{\left(h_U^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_V^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}\right)}^{1∕2}\right)\right)\left(\left(-\frac{h_U^{\sigma \left(j\right)}\left(z_i\right)+h_V^{\sigma \left(j\right)}\left(z_i\right)}{2}\right]\right)=0,$$

$$\iff {\left(\frac{{\left(h_U^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_V^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}\right)}^{1∕2}-\frac{h_U^{\sigma \left(j\right)}\left(z_i\right)+h_V^{\sigma \left(j\right)}\left(z_i\right)}{2}=0.$$

This is possible if and only if $h_U^{\sigma \left(j\right)}\left(z_i\right)=h_V^{\sigma \left(j\right)}\left(z_i\right)$, $i=1\left(1\right)n,j=1,2,\dots ,g_h$. This proves that $U=V$.

Since measure $D_1\left(U,V\right)$ holds all the essential postulates of Definition 5. Hence, $D_1\left(U,V\right)$ is a valid divergence measure for HFSs.

Theorem 2

Let $U,V,T\in HFSs\left(Y\right)$ , then the measure $D_1\left(U,V\right)$ satisfies the following axioms:

• (i) $D_1\left(U,V\right)=D_1\left(V,U\right)$ ,
• (ii) $D_1\left(U,V\right)\le D_1\left(U,T\right)$
• (iii) $D_1\left(V,T\right)\le D_1\left(U,T\right)$ , for $U\subseteq V\subseteq T$ .

Proof

(i) It is straightforward.

(ii) Let $U\subseteq V\subseteq T$, then for any $1\le i\le n$, $1\le j\le g_h,\forall z_i\in \Omega$, $h_U^{\sigma \left(j\right)}\left(z_i\right)\le h_V^{\sigma \left(j\right)}\left(z_i\right)\le h_T^{\sigma \left(j\right)}\left(z_i\right),$  we obtain

$$D_1\left(U,V\right)=\frac{1}{n}\sum _{i=1}^n\left(\frac{1}{g_h\left(\sqrt{2}-1\right)}\sum _{j=1}^{g_h}\left[{\left(\frac{{\left(h_U^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_V^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}\right)}^{1∕2}\right)\right)\left(\left(-\frac{h_U^{\sigma \left(j\right)}\left(z_i\right)+h_V^{\sigma \left(j\right)}\left(z_i\right)}{2}\right]\right)\le \frac{1}{n}\sum _{i=1}^n\left(\frac{1}{g_h\left(\sqrt{2}-1\right)}\sum _{j=1}^{g_h}\left[{\left(\frac{{\left(h_U^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_T^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}\right)}^{1∕2}\right)\right)\left(\left(-\frac{h_U^{\sigma \left(j\right)}\left(z_i\right)+h_T^{\sigma \left(j\right)}\left(z_i\right)}{2}\right]\right)=D_1\left(U,T\right).$$

Thus, $D_1\left(U,V\right)\le D_1\left(U,T\right),\forall T\in HFS\left(\Omega \right)$.

Similarly, we can verify axiom (iii).

Theorem 3

Let $U,V,T\in HFSs\left(\Omega \right)$ . Then the measure $D_1\left(U,V\right)$ holds the given axioms:

(i) $D_1\left(U\cup V,U\cap V\right)=D_1\left(U,V\right);$

(ii) $D_1\left(U\cup V,T\right)\le D_1\left(U,T\right)+D_1\left(V,T\right),\forall T\in HFS\left(\Omega \right);$

(iii) $D_1\left(U\cap V,T\right)\le D_1\left(U,T\right)+D_1\left(V,T\right),\forall T\in HFS\left(\Omega \right);$

Proof

To prove (i)–(iii), we partition the universe of discourse $\Omega$ into two disjoint sets ${\Omega }_1$ and ${\Omega }_2$, where ${\Omega }_1=\left\{z_i\left|z_i\in \Omega ,U\left(z_i\right)\subseteq \right)\right)\left(V\left(z_i\right)\right\}$ and ${\Omega }_2=\left\{z_i\left|z_i\in \Omega ,V\left(z_i\right)\subseteq U\left(z_i\right)\right)\right\}$. Based on these considerations, we further propose some properties of the divergence measure, which are explained as follows:

$$D_1\left(U\cup V,U\cap V\right)=\frac{1}{n}\sum _{i=1}^n\left(\frac{1}{g_h\left(\sqrt{2}-1\right)}\right)\times \sum _{j=1}^{g_h}\left(\sqrt{\frac{{\left(h_{U\cup V}^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_{U\cap V}^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}}\right)\left(\left(-\frac{h_{U\cup V}^{\sigma \left(j\right)}\left(z_i\right)+h_{U\cap V}^{\sigma \left(j\right)}\left(z_i\right)}{2}\right)\right),=\frac{1}{n}\sum _{y_i\in {\Omega }_1}\left(\frac{1}{g_h\left(\sqrt{2}-1\right)}\sum _{j=1}^{g_h}\left(\sqrt{\frac{{\left(h_V^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_U^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}}\right)\right)\left(\left(-\frac{h_V^{\sigma \left(j\right)}\left(z_i\right)+h_U^{\sigma \left(j\right)}\left(z_i\right)}{2}\right)\right)+\frac{1}{n}\sum _{y_i\in {\Omega }_2}\left(\frac{1}{g_h\left(\sqrt{2}-1\right)}\sum _{j=1}^{g_h}\left(\sqrt{\frac{{\left(h_U^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_V^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}}\right)\right)\left(\left(-\frac{h_U^{\sigma \left(j\right)}\left(z_i\right)+h_V^{\sigma \left(j\right)}\left(z_i\right)}{2}\right)\right)=\frac{1}{n}\sum _{i=1}^n\left(\frac{1}{g_h\left(\sqrt{2}-1\right)}\sum _{j=1}^{g_h}\left(\sqrt{\frac{{\left(h_U^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_V^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}}\right)\right)\left(\left(-\frac{h_U^{\sigma \left(j\right)}\left(z_i\right)+h_V^{\sigma \left(j\right)}\left(z_i\right)}{2}\right)\right)=D_1\left(U,V\right).$$

It implies that $D_1\left(U\cup V,U\cap V\right)=D_1\left(U,V\right)$. Hence, axiom (i) is proved.

Again, from Eq. (4), we get

$$D_1\left(U\cup V,T\right)=\frac{1}{n}\sum _{i=1}^n\left(\frac{1}{g_h\left(\sqrt{2}-1\right)}\right)\times \sum _{j=1}^{g_h}\left(\sqrt{\frac{{\left(h_{U\cup V}^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_T^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}}\right)\left(\left(-\frac{h_{U\cup V}^{\sigma \left(j\right)}\left(z_i\right)+h_T^{\sigma \left(j\right)}\left(z_i\right)}{2}\right)\right)=\frac{1}{n}\sum _{y_i\in {\Omega }_1}\left(\frac{1}{g_h\left(\sqrt{2}-1\right)}\sum _{j=1}^{g_h}\left(\sqrt{\frac{{\left(h_V^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_T^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}}\right)\right)\left(\left(-\frac{h_V^{\sigma \left(j\right)}\left(z_i\right)+h_T^{\sigma \left(j\right)}\left(z_i\right)}{2}\right)\right)+\frac{1}{n}\sum _{y_i\in {\Omega }_2}\left(\frac{1}{g_h\left(\sqrt{2}-1\right)}\sum _{j=1}^{g_h}\left(\sqrt{\frac{{\left(h_U^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_T^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}}\right)\right)\left(\left(-\frac{h_U^{\sigma \left(j\right)}\left(z_i\right)+h_T^{\sigma \left(j\right)}\left(z_i\right)}{2}\right)\right),\forall T\in HFS\left(\Omega \right)\le \frac{1}{n}\sum _{i=1}^n\left(\frac{1}{g_h\left(\sqrt{2}-1\right)}\sum _{j=1}^{g_h}\left(\sqrt{\frac{{\left(h_U^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_T^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}}\right)\right)\left(\left(-\frac{h_U^{\sigma \left(j\right)}\left(z_i\right)+h_T^{\sigma \left(j\right)}\left(z_i\right)}{2}\right)\right)+\frac{1}{n}\sum _{i=1}^n\left(\frac{1}{g_h\left(\sqrt{2}-1\right)}\sum _{j=1}^{g_h}\left(\sqrt{\frac{{\left(h_V^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_T^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}}\right)\right)\left(\left(-\frac{h_V^{\sigma \left(j\right)}\left(z_i\right)+h_T^{\sigma \left(j\right)}\left(z_i\right)}{2}\right)\right),\forall T\in HFS\left(\Omega \right).$$

It implies that $D_1\left(U\cup V,T\right)\le D_1\left(U,T\right)+D_1\left(V,T\right),\forall T\in HFS\left(\Omega \right)$. Hence, the property (ii) is proved.

Similarly, we can prove the property (iii).

Theorem 4

Let $U,V,T\in HFSs\left(\Omega \right)$ . Then $D_1\left(U\cap V,T\right)+D_1\left(U\cup V,T\right)=D_1\left(U,T\right)+D_1\left(V,T\right)$ .

Proof

To prove the result, we partition the universe of discourse $\Omega$ into two disjoint sets ${\Omega }_1$ and ${\Omega }_2$, where ${\Omega }_1=\left\{z_i\left|z_i\in \Omega ,U\right)\right)\left(\left(z_i\right)\subseteq V\left(z_i\right)\right\}$ and ${\Omega }_2=\left\{z_i\left|z_i\in \Omega ,V\left(z_i\right)\subseteq U\left(z_i\right)\right)\right\}$. Based on these considerations; we further propose some properties of the divergence measure, which are explained as follows:

$$D_1\left(U\cup V,T\right)=\frac{1}{n}\sum _{i=1}^n\left(\frac{1}{g_h\left(\sqrt{2}-1\right)}\right)\times \sum _{j=1}^{g_h}\left(\sqrt{\frac{{\left(h_{U\cup V}^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_T^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}}\right)\left(\left(-\frac{h_{U\cup V}^{\sigma \left(j\right)}\left(z_i\right)+h_T^{\sigma \left(j\right)}\left(z_i\right)}{2}\right)\right)=\frac{1}{n}\sum _{y_i\in {\Omega }_1}\left(\frac{1}{g_h\left(\sqrt{2}-1\right)}\sum _{j=1}^{g_h}\left(\sqrt{\frac{{\left(h_V^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_T^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}}\right)\right)\left(\left(-\frac{h_V^{\sigma \left(j\right)}\left(z_i\right)+h_T^{\sigma \left(j\right)}\left(z_i\right)}{2}\right)\right)+\frac{1}{n}\sum _{y_i\in {\Omega }_2}\left(\frac{1}{g_h\left(\sqrt{2}-1\right)}\sum _{j=1}^{g_h}\left(\sqrt{\frac{{\left(h_U^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_T^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}}\right)\right)\left(\left(-\frac{h_U^{\sigma \left(j\right)}\left(z_i\right)+h_T^{\sigma \left(j\right)}\left(z_i\right)}{2}\right)\right).$$

Also,

$$D_1\left(U\cap V,T\right)=\frac{1}{n}\sum _{i=1}^n\left(\frac{1}{g_h\left(\sqrt{2}-1\right)}\right)\times \sum _{j=1}^{g_h}\left(\sqrt{\frac{{\left(h_{U\cap V}^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_T^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}}\right)\left(\left(-\frac{h_{U\cap V}^{\sigma \left(j\right)}\left(z_i\right)+h_T^{\sigma \left(j\right)}\left(z_i\right)}{2}\right)\right)=\frac{1}{n}\sum _{y_i\in {\Omega }_1}\left(\frac{1}{g_h\left(\sqrt{2}-1\right)}\sum _{j=1}^{g_h}\left(\sqrt{\frac{{\left(h_U^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_T^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}}\right)\right)\left(\left(-\frac{h_U^{\sigma \left(j\right)}\left(z_i\right)+h_T^{\sigma \left(j\right)}\left(z_i\right)}{2}\right)\right)+\frac{1}{n}\sum _{y_i\in {\Omega }_2}\left(\frac{1}{g_h\left(\sqrt{2}-1\right)}\sum _{j=1}^{g_h}\left(\sqrt{\frac{{\left(h_V^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_T^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}}\right)\right)\left(\left(-\frac{h_V^{\sigma \left(j\right)}\left(z_i\right)+h_T^{\sigma \left(j\right)}\left(z_i\right)}{2}\right)\right).$$

Thus, by adding these equations, we obtain

$$D_1\left(U\cap V,T\right)+D_1\left(U\cup V,T\right)=D_1\left(U,T\right)+D_1\left(V,T\right).$$

Theorem 5

Let $U,V,T\in HFSs\left(\Omega \right)$ , then

$$max\left\{D_1\left(U\cup T,V\cup T\right),D_1\left(U\cap T,V\cap T\right)\right\}\le D_1\left(U,V\right)\text{ for every }T\in HFS\left(\Omega \right).$$

Proof

To verify this, we divide $\Omega$ into the given eight subsets:

$$\Omega =\left\{z_i\in \Omega |U\left(z_i\right)\le V\left(z_i\right)=T\left(z_i\right)\right\}\cup \left\{z_i\in \Omega |U\left(z_i\right)=T\left(z_i\right)\le V\left(z_i\right)\right\}$$

$$\cup \left\{z_i\in \Omega |U\left(z_i\right)\le V\left(z_i\right)<T\left(z_i\right)\right\}\cup \left\{z_i\in \Omega |U\left(z_i\right)\le T\left(z_i\right)<V\left(z_i\right)\right\}$$

$$\cup \left\{z_i\in \Omega |V\left(z_i\right)<U\left(z_i\right)\le T\left(z_i\right)\right\}\cup \left\{z_i\in \Omega |V\left(z_i\right)\le T\left(z_i\right)<U\left(z_i\right)\right\}$$

$$\cup \left\{z_i\in \Omega |T\left(z_i\right)<U\left(z_i\right)\le V\left(z_i\right)\right\}\cup \left\{z_i\in \Omega |T\left(z_i\right)<V\left(z_i\right)<U\left(z_i\right)\right\},$$

which are denoted by ${\Delta }_1,{\Delta }_2,\dots ,{\Delta }_8$. On the basis of Kobza [118] and Mishra et al. [86], for every ${\Delta }_k;k=1\left(1\right)8$,

$${\left(\frac{{\left(h_U^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_V^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}\right)}^{1∕2}\ge \frac{h_U^{\sigma \left(j\right)}\left(z_i\right)+h_V^{\sigma \left(j\right)}\left(z_i\right)}{2},\text{ for any }1\le i\le n,1\le j\le g_h.$$

Thus, from Theorem 2, axiom (ii), we get $D_1\left(U\cap T,V\cap T\right)\le D_1\left(U,V\right)$ and $D_1\left(U\cup T,V\cup T\right)$ $\le D_1\left(U,V\right)$, $\forall T\in HFS\left(\Omega \right)$.

Hence,

$$max\left\{D_1\left(U\cup T,V\cup T\right),D_1\left(U\cap T,V\cap T\right)\right\}\le D_1\left(U,V\right),\forall T\in HFS\left(\Omega \right).$$

Usually, each object $z_i\in \Omega$ weight should be considered, so we present the weighted HF-divergence measure.

$$D_2\left(U,V\right)=\sum _{i=1}^n\left(\frac{{\omega }_i}{g_h\left(\sqrt{2}-1\right)}\right)\times \sum _{j=1}^{g_h}\left(\sqrt{\frac{{\left(h_U^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_V^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}}\right)\left(\left(-\frac{h_U^{\sigma \left(j\right)}\left(z_i\right)+h_V^{\sigma \left(j\right)}\left(z_i\right)}{2}\right)\right),$$ (5)

Next, we observe that the HF-divergence measures Eqs. (4), (5) are discrete, if both the discourse and weight are continuous, such that $z_i\in \Omega =\left[a,b\right]$, is $\omega \left(z_i\right)$, where $\omega \left(z_i\right)\in \left[0,1\right]$ and ${\int }_a^b\omega \left(z_i\right)d{z}_i=1$, then we present a continuous weighted HF-divergence measure as follows:

$$D_3\left(U,V\right)={\int }_a^b\left(\frac{\omega \left(z_i\right)}{g_h\left(\sqrt{2}-1\right)}\sum _{j=1}^{g_h}\left(\sqrt{\frac{{\left(h_U^{\sigma \left(j\right)}\left(z_i\right)\right)}^2+{\left(h_V^{\sigma \left(j\right)}\left(z_i\right)\right)}^2}{2}}\right)\right)\left(\left(-\frac{h_U^{\sigma \left(j\right)}\left(z_i\right)+h_V^{\sigma \left(j\right)}\left(z_i\right)}{2}\right)\right)d{z}_i.$$ (6)

4. Hesitant fuzzy ARAS (HF-ARAS) framework

Here, we initiate a new HF-ARAS framework to deal with the complex MCDM problems. The developed HF-ARAS framework is based on the operations of HFNs, score function, and HF-divergence measure. The implementation processes of the proposed framework are described in the following steps (see Fig. 2):

Fig. 2.

Graphical representation of proposed HF-ARAS framework.

Step 1: Initiate the alternative and criteria.

A group of $\mathrm{\ell }$ DEs $\alpha =\left\{{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_{\mathrm{\ell }}\right\}$ decides the $m$ option $\left\{M_1,M_2,\dots ,M_m\right\}$ and $n$ attributes $\left\{S_1,S_2,\dots ,S_n\right\}$, respectively. Based on insufficient and uncertain information related to options, the DEs give HFNs to weigh his/her judgment on $M_i$ over the attribute $S_j$.

Step 2: Estimate crisp DEs weights $\left({\lambda }_k\right)$.

To calculate the DEs’ weights, consider that the significant degrees of DEs are articulated as LVs specified in forms of HFNs. Let $h_k\left(z\right)=\left\{\xi :\xi \in h_k\left(z\right)\right\}$ be the rating of DEs by the experts in the form of HFN; then the $k$th DE weight is computed by

$${\lambda }_k=\frac{\sum _{{\gamma }_a\in h}{\xi }_a}{\sum _{k=1}^{\mathrm{\ell }}\left(\sum _{{\gamma }_a\in h}{\xi }_a\right)},k=1\left(1\right)\mathrm{\ell },a=1,2,\dots ,g_h,\text{ where }{\lambda }_k\ge 0\text{ and }\sum _{k=1}^{\mathrm{\ell }}{\lambda }_k=1.$$ (7)

Step 3: Calculate the aggregated HF-decision matrix (AHF-DM).

To generate AHF-DM, we aggregate all the individuals’ matrices. To do this, let $Z=\left(h_{ij}\right),\forall i,j$ be the AHF-DM, where $Z={\oplus }_{k=1}^{\ell }{\lambda }_k{Z}_k$, and

$$h_{ij}={\cup }_{{\xi }_1\in h_{ij}^k,{\xi }_2\in h_{ij}^k,\dots ,{\xi }_a\in h_{ij}^k}\left\{1-\prod _{k=1}^{\mathrm{\ell }}{\left(1-{\xi }_a^k\right)}^{{\lambda }_k}\right\}.$$ (8)

Step 4: Compute the criteria weights.

To calculate criteria weights, we recommend a process using introduced HF-divergence measure as

Step 4.1: Calculate the support degree $sup\left(h_{ij},h_{it}\right)$ between the evaluation criteria $S_j$ and $S_t$ in the AHF-DM.

$$sup\left(h_{ij},h_{it}\right)=1-D_1\left(h_{ij},h_{it}\right),i=1\left(1\right)m,j,t=1\left(1\right)n,j\ne t$$ (9)

where $D_1\left(h_{ij},h_{it}\right)$ is the HF-divergence measure given by Eq. (4).

Step 4.2: Evaluate the total support degree $T\left(h_{ij}\right)$ for every $h_{ij}$ over the attribute $S_j$.

$$T\left(h_{ij}\right)=\sum _{t=1;j\ne t}^{n}sup\left(h_{ij},h_{ik}\right).$$ (10)

Step 4.3: Compute the rationality degree ${\delta }_j$ of each criterion $S_j$.

$${\delta }_j=\frac{1}{m\left(n-1\right)}\sum _{i=1}^m\sum _{j=1}^{n}T\left(h_{ij}\right);{\delta }_j\in \left[0,1\right].$$ (11)

Step 4.4: Estimate the comprehensive degree ${\xi }_j$ of criteria $S_j$.

$${\xi }_j=\frac{{\delta }_j}{\sum _{j=1}^n{\delta }_j};0\le {\xi }_j\le 1.$$ (12)

Step 4.5: Compute the importance degree $\left({\kappa }_j\right)$ of each criterion $S_j$.

For this, create the individual importance degree matrix $\left({\eta }^k\right)$ for $k$th DE by using the process.

$${\eta }^k={\left({\eta }_1^k,{\eta }_2^k,\dots ,{\eta }_n^k\right)}_{1\times n}^T,$$ (13)

where ${\eta }_j^k$ is the importance degree of criterion $S_j$ given by $k$th DE. To estimate the subjective weight, we get

$${\kappa }_j=HFW{A}_{\lambda }\left({\eta }^1,{\eta }^2,\dots ,{\eta }^{\mathrm{\ell }}\right).$$ (14)

Let ${\eta }^k=\left(h_j^k\right)$ be the decision matrix provided by the DEs to compute the subjective weights of criteria, where $h_j^k=\left\{{\gamma }_k:{\gamma }_k\in h_j^k\right\},k=1\left(1\right)\mathrm{\ell }$ is an HFN. Then, we find the overall importance degree as follows:

$${\kappa }_j={\left(h_j\right)}^{\ast }={\cup }_{{\gamma }_1\in h_1^k,{\gamma }_2\in h_2^k,\dots ,{\gamma }_n\in h_n^k}\left\{1-\prod _{k=1}^{\mathrm{\ell }}{\left(1-{\gamma }_k\right)}^{{\lambda }_k}\right\}.$$ (15)

Here, ${\kappa }_j={\left(h_j\right)}^{\ast }$ is a HFN.

Step 4.6: Evaluate the overall importance degree $\left({\eta }_j\right)$ of criteria $S_j$.

Next, we calculate the score value $\mathbb{S}\left({\kappa }_j\right)$ by Eq. (1). Thus, we calculate the importance degree as follows:

$${\eta }_j=\frac{\mathbb{S}\left({\kappa }_j\right)}{\sum _{j=1}^n\mathbb{S}\left({\kappa }_j\right)};j=1\left(1\right)n.$$ (16)

Step 4.7: Compute the attribute weights.

With the use of Eqs. (13), (17), the formula for the computation of combined weight is

$$w_j=\vartheta {\delta }_j+\left(1-\vartheta \right){\eta }_j,$$ (17)

where ${\delta }_j$ represents the rationality degree of $j$th criterion, ${\eta }_j$ represents the importance degree of $j$th criterion, $\vartheta \left(0\le \vartheta \le 1\right)$ shows the adjustment coefficient, and it can be chosen based on the actual demand of DM and $0\le w_j\le 1$. To compute the criteria weights, the maximum the coefficient $\vartheta$ value, the superior the influence of rationality degree of assessment, while minimizing the coefficient $\vartheta$ value, the lesser the influence of importance degree of criteria and vice versa.

Step 5: Determine the optimal performance rating.

The optimal significance rating $\left(M_0\right)$ can be evaluated by

$$M_0=\left\{\begin{array}{c}max{h}_{ij},j\in S_b\hfill \\ min{h}_{ij},j\in S_n\hfill \end{array}\right)$$ (18)

where $S_b$ and $S_n$ are the benefit and cost criteria sets, respectively.

Step 6: Make the normalized AHF-DM.

In the HF-ARAS framework, AHF-DM $Z=\left(h_{ij}\right),\forall i,j$ is transformed into normalizing AHF-DM $\mathbb{N}=\left({\overline{h}}_{ij}\right);\forall i,j$ by the linear method as

$${\overline{h}}_{ij}=\left\{\begin{array}{c}\frac{h_{ij}}{\underset{i}{max}\mathbb{S}\left(h_{ij}\right)},j\in S_b\hfill \\ 1-\frac{h_{ij}}{\underset{i}{max}\mathbb{S}\left(h_{ij}\right)},j\in S_n.\hfill \end{array}\right)$$ (19)

Step 7: Create a weighted normalized HF-decision matrix.

This step is similar to the classical ARAS approach. To determine the weighted normalized AHF-DM, ${\mathbb{N}}_w={\left({\tilde{h}}_{ij}\right)}_{m\times n}$, the formula is applied as

$${\tilde{h}}_{ij}=\stackrel{n}{\underset{j=1}{\oplus }}{w}_j{\overline{h}}_{ij}={\cup }_{{\overline{\xi }}_1\in {\overline{h}}_{i1},{\overline{\xi }}_2\in {\overline{h}}_{i2},\dots ,{\overline{\xi }}_n\in {\overline{h}}_{in}}\left\{1-\prod _{j=1}^n{\left(1-{\overline{\xi }}_j\right)}^{w_j}\right\}.$$ (20)

Step 8: Estimation of score degrees

Based on Eq. (2), the score degrees of weighted normalized AHF-DM ${\mathbb{N}}_w={\left({\tilde{h}}_{ij}\right)}_{m\times n}$ is calculated as below:

$$\mathbb{S}\left({\tilde{h}}_{ij}\right)=\frac{1}{g_{{\tilde{h}}_{ij}}}\sum _{\tilde{\xi }\in {\tilde{h}}_{ij}}\tilde{\xi }.$$ (21)

Step 9: Calculate the overall performance rating and utility degree

With the use of the following expression, the overall performance rating is computed as

$$P_i=\sum _{j=1}^n\mathbb{S}\left({\tilde{h}}_{ij}\right),i=1\left(1\right)m.$$ (22)

The greatest value of $P_i$ determines the best option, while the lowest value of $P_i$ determines the worst option. This means that the preferences of options can be estimated based on $P_i$.

To find the most appropriate option(s), it is necessary to assess an optimal option as well as essential to obtain the relative impact of considered options over the optimal option. To do this, the utility degree $U_i$ of an option $M_i$ is evaluated by

$$U_i=\frac{P_i}{M_0};i=1\left(1\right)m.$$ (23)

It is clear that $U_i\in \left[0,1\right]$ and it is ranked in an increasing order, which provides the required priority order. The relative importance of an appropriate alternative is calculated based on the utility degree.

Step 10: Select the suitable option.

The largest value $U_i$ of an option $M_i$ is the desirable one. Hence, the most optimal option is assessed as

$$M^{\ast }=\left\{M_i|\underset{i}{max}{U}_i;i=1\left(1\right)m\right\},$$ (24)

where $M^{\ast }$ is the most appropriate option.

5. Case study

The COVID-19 is a fresh strain that has been recognized in humans in recent times and officially named COVID-19. Corona characterizes crown-like spikes on the external surface of the virus [119]. This virus, closely associated with SARS-CoV and MERS-CoV, has a range of clinical manifestations [120]. Several existing antiviral agents can be predicted to preclude the mild symptoms of COVID-19 infections [121]. Though, in the case of antiviral drugs, up to now, there is no specific drug. Favipiravir is an antiviral utilized for treating influenza in Japan. It discriminatory inhibits viruses from their genetic material. Lopinavir/Ritonavir (LPV/RTV) is a combination of two medications utilized to treat HIV/AIDS. Affirmation for COVID-19, MERS, and SARS is, however, to the spectacle, it can recover clinical consequences or prevent infection. The experiment proposes to recognize and approve any benefit for COVID-19 patients.

In comparison, there are indicators from laboratory tests that the combination may be effectual against COVID-19. Also, the mixture of Lopinavir/Ritonavir with Interferon-beta (LPV/RTV-IFNb) marginally decreased viral masses without influencingother disease factors. Remdesivir (GS-5734), a nucleotide analog prodrug, was earlier tested for SARS, MERS, and Ebola [122]. As per the experimental investigation, it has been found that Remdesivir is safe and effective for patients with mild symptoms of COVID-19 [123]. Hydroxychloroquine (HCQ) and chloroquine (CQ) are broadly preferred antimalarial medicines that stimulate immunomodulatory things and are also utilized to prevent autoimmune circumstances. Wang et al. [124] testified that CQ successfully prevents SARS-CoV-2 in vitro. HCQ was obtained to be more intoxicating than CQ in vitro. The reports lessening from the global outbreak of COVID-19 have assessed these medicines’ possible utility in governing cytokine discharge syndrome in severely ill patients. Although there is not a suitable medication for treating COVID-19 and thus, all antiviral drugs need to be further investigated in clinical trials.

As per the WHO report on November 29, 2020, there have been estimated more than 62,570,316 cases of COVID-19 across the world, causing more than 1,466,426 deaths. Approximately 44,671,725 persons have recovered [2]. As per the reported data, most people with COVID-19 will have the subsequent symptoms and signs: Fever (83%–99%), Cough (59%–82%), Fatigue (44%–70%), Anorexia (40%–84%), Shortness of breath (31%–40%), Sputum production (28%–33%) and Myalgias (11%–35%) [14], [125], [126], [127], [128], [129].

Here, we prefer five medicines as alternatives [13] to control the COVID-19 patients, namely, LPV/RTV-IFNb ($M_1$), Favipiravir ($M_2$), LPV/RTV ($M_3$), Remdesivir ($M_4$), Hydroxychloroquine ($M_5$). Antiviral drugs should be chosen not only for their impact on signs but also for their performance and probable side effects. Thus, we take seven parameters Anorexia ($S_1$), Cough ($S_2$), Fatigue ($S_3$), Fever ($S_4$), Myalgia ($S_5$), Shortness of breath ($S_6$), and Sputum production ($S_7$) [14], [111], [112], [113], [114], [115]. For selecting an ideal drug, we present the assessment values in the term of LVs and hesitant fuzzy preference degrees in Table 2, which are taken from Mousavi et al. [68] and Mishra et al. [73]. In this study, according to the considered criteria, a self-generated questionnaire is developed to provide the related doctors and patients. The questionnaires are generated-based on LVs and mentioned in Table 2. Afterward, we prepare a list of doctors and patients who fulfill the criteria; these nominated doctors have treated the patient, and patients have suffered COVID-19. The doctors are qualified virologist who studies and understand virus behavior in the human body. These doctors also had training from the medical council regarding drug usage on patients with COVID-19 symptoms and possessed 7 to 10 years of experience in the medical field. The names of doctors and the hospital(s) they serve are kept anonymous for ethical reasons. The first two authors of this paper requested seven doctors initially for data related to the research problem being considered, of which three doctors agreed to provide data with a prime confidentiality understanding. Next, the Delphi surveys are accomplished from February 2020 to June 2020 by providing questionnaires to the doctors and patients to assemble data about the issue to achieve consensus or gain understanding. Datasheets, in the form of questionnaires, were given to these doctors, and the purpose of this data acquisition was clarified to each doctor. Based on their advice and suggestion, the questionnaire was revised, and the collected linguistic data was normalized to maintain anonymity. Final datasheets that are used in this study were again shared with the doctors for acknowledgment and cross-checked. After this procedure, subjective randomness was mitigated by associating corresponding belongingness degrees to the preferences. Finally, this information was utilized by the proposed model for assessment. The procedure of the introduced model to assess the antiviral drugs for treating the patient with mild symptoms of COVID-19 as follows:

Table 2.

Assessment ratings of criteria and drug options.

LVs	Hesitant preference degrees in the form of intervals	DEs risk preference
		Pessimist	Modest	Optimist
Extremely preferred (EP)	[0.90, 1.00]	0.9	0.95	1.00
Strongly preferred (SP)	[0.80, 0.90]	0.80	0.85	0.90
Preferred (P)	[0.65, 0.80]	0.65	0.725	0.80
Medium (M)	[0.50, 0.65]	0.50	0.575	0.65
Undesirable (U)	[0.35, 0.50]	0.35	0.425	0.50
Strongly undesirable (SU)	[0.20, 0.35]	0.2	0.275	0.35
Extremely undesirable (EU)	[0.00, 0.20]	0.00	0.10	0.20

Consider the DEs’ weights are in the form of LVs as {P, M, SP}. By utilizing Table 2 and Eq. (7), the numeric weights ${\lambda }_k:k=1,2,3$ of DEs are achieved as {${\lambda }_1=0.3372$, ${\lambda }_2=0.2674$, ${\lambda }_3=0$.3953}. As per the experts ${\alpha }_k:k=1\left(1\right)3$, the five drugs’ performance matrices on seven attributes are specified in Table 3 in terms of LVs.

Table 3.

The evaluation matrix regarding five medicines in the form of LVs.

Criteria	DEs	${\mathrm{M}}_1$	${\mathrm{M}}_2$	${\mathrm{M}}_3$	${\mathrm{M}}_4$	${\mathrm{M}}_5$
S 1	${\alpha }_1$	P	M	M	SP	M
	${\alpha }_2$	M	P	SP	M	P
	${\alpha }_3$	P	P	M	P	M
S 2	${\alpha }_1$	M	P	P	P	P
	${\alpha }_2$	M	M	M	P	P
	${\alpha }_3$	P	U	P	M	M
S 3	${\alpha }_1$	U	M	M	M	U
	${\alpha }_2$	M	U	M	P	P
	${\alpha }_3$	M	P	M	M	P
S 4	${\alpha }_1$	P	M	M	M	M
	${\alpha }_2$	M	M	P	M	M
	${\alpha }_3$	P	P	P	P	P
S 5	${\alpha }_1$	M	M	U	M	SU
	${\alpha }_2$	U	SU	U	P	M
	${\alpha }_3$	U	M	M	P	P
S 6	${\alpha }_1$	U	U	SU	P	U
	${\alpha }_3$	M	U	P	M	P
	${\alpha }_3$	SU	M	U	U	SU
S 7	${\alpha }_1$	U	M	SU	P	M
	${\alpha }_2$	U	U	M	U	SU
	${\alpha }_3$	SU	SU	U	M	U

With the use of Eq. (8), all three DMs’ opinions are aggregated, and then AHF-DM is constructed in Table 4.

Table 4.

The AHF-DM for drugs selection.

Criteria	${\mathrm{M}}_1$	${\mathrm{M}}_2$	${\mathrm{M}}_3$	${\mathrm{M}}_4$	${\mathrm{M}}_5$
${\mathrm{S}}_1$	0.684	0.666	0.696	0.804	0.604
${\mathrm{S}}_2$	0.608	0.554	0.633	0.649	0.690
${\mathrm{S}}_3$	0.512	0.572	0.549	0.680	0.615
${\mathrm{S}}_4$	0.633	0.608	0.633	0.624	0.644
${\mathrm{S}}_5$	0.450	0.476	0.454	0.729	0.548
${\mathrm{S}}_6$	0.423	0.454	0.469	0.600	0.547
${\mathrm{S}}_7$	0.370	0.373	0.401	0.604	0.381

With the use of formulae (9)–(12), the rationality and comprehensive degrees of the criteria $S_{\mathrm{j}}$ are computed in Table 5. The overall importance degree and score values are computed in Table 6 by utilizing Eqs. (13)–(16).

Table 5.

Rationality degree of AHF-DM for drug selection.

Criteria	${\mathrm{M}}_1$	${\mathrm{M}}_2$	${\mathrm{M}}_3$	${\mathrm{M}}_4$	${\mathrm{M}}_5$	${\delta }_j$	${\xi }_j$
${\mathrm{S}}_1$	3.991	3.990	3.991	3.964	3.974	0.6637	0.1431
${\mathrm{S}}_2$	3.995	3.983	3.996	3.990	3.994	0.6653	0.1434
${\mathrm{S}}_3$	3.977	3.991	3.989	3.970	3.989	0.6639	0.1431
${\mathrm{S}}_4$	4.000	3.998	4.000	3.999	3.999	0.6666	0.1437
${\mathrm{S}}_5$	3.955	3.965	3.957	3.876	3.971	0.6575	0.1418
${\mathrm{S}}_6$	3.970	3.982	3.985	3.959	3.980	0.6625	0.1428
${\mathrm{S}}_7$	3.965	3.967	3.974	3.880	3.970	0.6585	0.1420

Table 6.

Importance degrees of the preferred criteria.

Criteria	LVs is specified by DEs			HFNs is specified by DEs			$\mathbb{S}\left({\kappa }_j\right)$	${\eta }_j$
	${\alpha }_1$	${\alpha }_2$	${\alpha }_3$	$D_1$	$D_2$	$D_3$
${\mathrm{S}}_1$	M	M	P	0.50	0.575	0.725	0.644	0.1569
${\mathrm{S}}_2$	SP	P	P	0.80	0.725	0.65	0.752	0.1832
${\mathrm{S}}_3$	P	M	M	0.65	0.575	0.50	0.600	0.1462
${\mathrm{S}}_4$	SP	SP	SP	0.85	0.80	0.85	0.855	0.2083
${\mathrm{S}}_5$	U	SU	U	0.35	0.275	0.425	0.377	0.0918
${\mathrm{S}}_6$	U	U	M	0.35	0.425	0.50	0.454	0.1106
${\mathrm{S}}_7$	SU	M	U	0.35	0.50	0.35	0.423	0.1030

Based on Table 5, Table 6 and Eq. (17), the combined attribute weights is calculated and given as

$$w_j=\{0.150,0.163,0.145,0.176,0.117,0.127,0.123\}.$$

Next, we determine the optimal performance ratings of drug options by using the (18). The obtained optimal performance ratings of drug options are

$$M_0=\{0.804,0.690,0.680,0.644,0.729,0.600,0.604\}.$$

As all considered criteria are of cost types; thus, there is no need to normalize them. Table 7 presents the weighted evaluation matrix of five drug options for COVID-19 disease. Using Eq. (23), the degree of utility or relative quality ${\mathit{U}}_i$ is computed as follows: $U_1=0.703$, $U_2=0.698$, $U_3=0.741$, $U_4=0.976$, $U_5=0.787$. Then, the preference order for the drug options is determined as $M_4\succ M_5\succ M_3\succ M_1\succ M_2$. Based on (24), the desirable drug option is Remdesivir (${\mathit{M}}_4$).

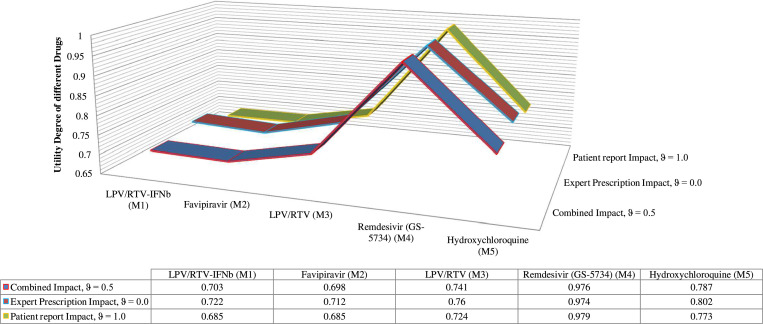
5.1. Sensitivity analysis

In this study, a sensitivity assessment is made to certify the developed framework and their drug selection problem for COVID-19 disease. Here, some clinical trials have been launched to recognize the COVID-19 virus better and search for the appropriate drug to treat infection symptoms successfully. In this study, we have selected three diverse values of coefficient ‘$\vartheta$’. On the basis of different values of the parameter $\vartheta$, we have calculated the utility degrees $U_i\in \left[0,1\right],\left(i=1\left(1\right)5\right)$ of the drug options, and then we obtain that the order of drug options is the same in each criterion set; which as $M_4\succ M_5\succ M_3\succ M_1\succ M_2$. Hence, it is found that the best drug assessment is depending on the given coefficient ‘$\vartheta$’ values. At $\vartheta =0.0$, we have obtained the preferences of the options based on expert or doctor’s prescription. At $\vartheta =1.0$, we have obtained the ranking of the drug options based on patient report. At $\vartheta =0.5$, we find the preferences based on the combined impact of doctor’s prescriptions and patient reports. Based on the obtained result and Fig. 3, we can conclude that the drug option Remdesivir ($M_4$) is most appropriate for mild symptoms of COVID-19 patients according to the medical experts, drug performance on patients, and their combined opinions. Thus, the developed HF-ARAS model has sufficient stability over different attribute weight sets.

Fig. 3.

Variation of drugs selection over different impact degrees.

Table 7.

The weighted evaluation matrix regarding five medicines in terms of HFNs.

Criteria	${\mathrm{M}}_0$	${\mathrm{M}}_1$	${\mathrm{M}}_2$	${\mathrm{M}}_3$	${\mathrm{M}}_4$	${\mathrm{M}}_5$
${\mathrm{S}}_1$	0.217	0.159	0.152	0.164	0.217	0.130
${\mathrm{S}}_2$	0.174	0.142	0.123	0.151	0.157	0.174
${\mathrm{S}}_3$	0.152	0.099	0.116	0.109	0.152	0.129
${\mathrm{S}}_4$	0.166	0.162	0.152	0.162	0.158	0.166
${\mathrm{S}}_5$	0.141	0.067	0.073	0.068	0.141	0.089
${\mathrm{S}}_6$	0.110	0.067	0.074	0.077	0.110	0.096
${\mathrm{S}}_7$	0.107	0.055	0.056	0.061	0.107	0.057
${\mathit{P}}_i$	1.067	0.751	0.745	0.791	1.042	0.840

5.2. Comparative study

In this subsection, we have performed a comparison to prove the practicality of the proposed HF-ARAS method. For this, we have taken HF-TOPSIS [78] and HF-COPRAS [84] approaches to solve the above-discussed drug selection problem. The procedural procedure of HF-TOPSIS [78] is presented as follows:

Steps 1–4: These steps are similar to the above-discussed model

Step 5: Estimate the HF-ideal solution (IS) and HF-anti-ideal solution (HF-AIS)

Now, we compute HF-IS and HFA-IS, given as ${\sigma }^{+}$ $=$ {0.804, 0.690, 0.680, 0.644, 0.729, 0.600, 0.604} and ${\sigma }^{-}$ $=$ {0.604, 0.554, 0.512, 0.608, 0.450, 0.423, 0.370}, respectively.

Step 6: Assess the closeness index (CI) of each option to HF-IS as

$$CI\left(M_i\right)=\frac{{\mathrm{\Upsilon }}_i^{-}}{{\mathrm{\Upsilon }}_i^{+}+{\mathrm{\Upsilon }}_i^{-}},$$ (25)

wherein ${\mathrm{\Upsilon }}_i^{+}={\sum }_{j=1}^n{D}_1\left(h_{ij},h_j^{+}\right)$ and ${\mathrm{\Upsilon }}_i^{-}={\sum }_{j=1}^n{D}_1\left(h_{ij},h_j^{-}\right)$.

Then, we estimate the divergences between $M_{\mathrm{i}}$ and HF-IS options with HF-AIS over ${\mathit{S}}_{\mathrm{j}}$ by Eq. (5). Further, we find CI by using Eq. (25), which as

$$CI\left(M_1\right)=0.0496,CI\left(M_2\right)=0.0527,CI\left(M_3\right)=0.1253,$$

$$CI\left(M_4\right)=0.9904\text{ and }CI\left(M_5\right)=0.3348.$$

Step 7: Preference order of options according to the increasing values of CI (${\mathit{M}}_{\mathrm{i}}$)

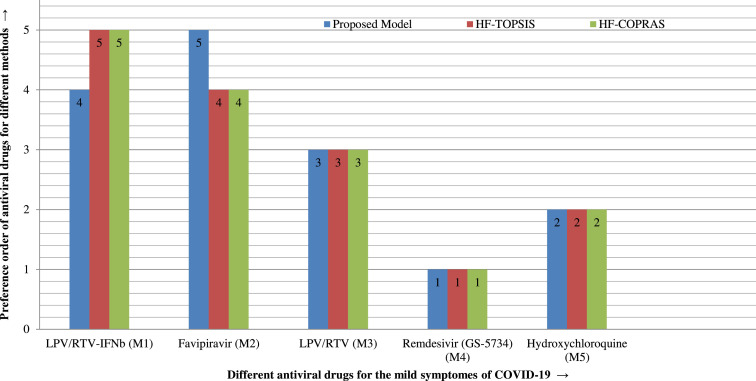
According to the values of CIs, the priority order of alternatives is $M_4\succ M_5\succ M_3\succ M_2\succ M_1$, thus, $M_4$ (Remdesivir) is an optimal antiviral drug for the mild symptoms of COVID-19.

Next, the procedural steps for the HF-COPRAS method are discussed as [84]

Steps 1–4: These steps are similar to the above-discussed method.

Step 5: Aggregate the benefit and cost attributes in the decision matrix by using Eq. (4). Since all attributes are of non-benefit-type, therefore, we analyze the following index for each option to minimize the risk preference ${\beta }_i={\oplus }_{j=1}^n{w}_j{h}_{ij},i=1\left(1\right)m$. Also, the index value is the same as the relative degree of each option. Therefore, we get ${ƛ}_1=0.554$, ${ƛ}_2=0.551$, ${ƛ}_3=0.574$, ${ƛ}_4=0.682$ and ${ƛ}_5=0.597$.

Step 6: Compare the relative degrees of the five drugs based on the priority ${ƛ}_i$ and get the preference order of these five drug options as ${ƛ}_4\succ {ƛ}_5\succ {ƛ}_3\succ {ƛ}_2\succ {ƛ}_1$. The ranking reflects that the drug $M_4$ (Remdesivir) is the optimal one among the others.

Step 7: Estimate the “utility degree” ${\hslash }_i=\frac{{ƛ}_i}{{ƛ}_{max}}\times 100\text{\%}$, which reflects the utility degree between each drug and the best drug to treat the mild symptoms of the COVID-19 patients. Then, we obtain ${\hslash }_1=81.220$, ${\hslash }_2=80.700$, ${\hslash }_3=84.141$,${\hslash }_4=100.000$ and ${\hslash }_5=87.533$.

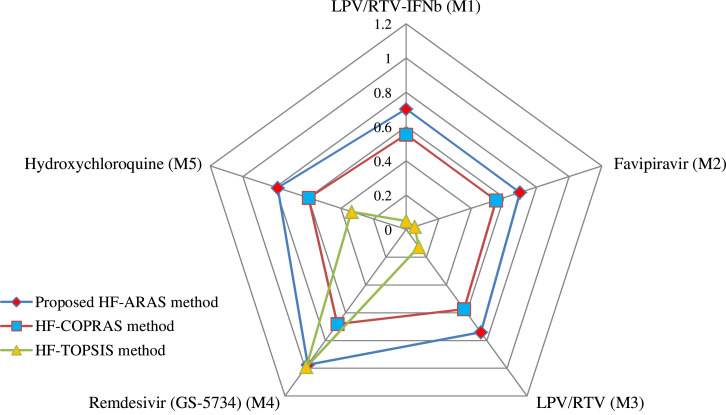
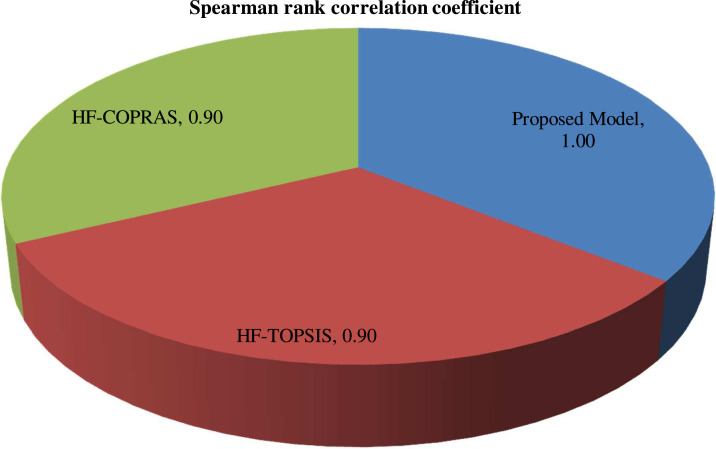
Here, we found that the concluding preferences of the drug options achieved by HF-TOPSIS and HF-COPRAS approaches are the same, i.e., $M_4\succ M_5\succ M_3\succ M_2\succ M_1$, and the most suitable drug for COVID-19 mild symptom is $M_4$ (Remdesivir). Hence, from Fig. 4, we can observe that the most appropriate drug option, i.e., Remdesivir ($M_4$) is the same drug with all the discussed methodologies, whilst the options’ ranking order slightly varies with different methods. From Fig. 5, it is observed that the introduced framework is highly reliable with the extant models under HFSs. To preserve consistency in the model-related comparison, we discuss the methods, namely, Zhang & Xu [78] and Mishra et al. [84]. The Spearman correlation values (SCVs) of the introduced model with HF-TOPSIS, HF-COPRAS, and proposed utility degree measures are given by (0.90, 0.90, 1.00). The SCV is calculated to these preference order to delineate the steadiness of the introduced model. Also, Fig. 6 depicts the prioritization order from different methods with HFSs and discusses diverse aspects to distinguish the efficacy of the introduced model.

Fig. 4.

Comparison of the proposed approach with different existing approaches.

Fig. 5.

Correlation plot of the introduced model with existing approaches.

Fig. 6.

Comparison of the priority order of antiviral drugs alternative with various approaches.

On the basis of this comparative study, we have listed some advantages of the proposed model in the following points (see Table 8):

Table 8.

Comparison of different parameters with various methodologies.

Aspects	Xu and Zhang [78]	Mishra et al. [84]	Mardani et al. [97]	Proposed framework
Approaches	TOPSIS method	COPRAS method	SWARA-WASPAS method	ARAS methodology
Alternatives/criteria assessment	HFSs	HFSs	HFSs	HFSs
Aggregation process	Arithmetic	Arithmetic	Arithmetic, Geometric	Arithmetic, geometric
Theme of prioritization	Compromise solution	Compromise solution	Utility theory	Utility theory
Criteria weights	Assumed	Shapley function-based procedure	SWARA method	The proposed method based on divergence measure
MCDM process	Single	Single	Group	Group
Hesitation degree in assessments	Included	Included	Included	Included
Expert weights	Assumed	Assumed	Computed	Computed (Using Scoring model)
Normalization type	Vector	Linear	Linear	Linear, Vector
Optimal drug option	${\mathit{M}}_4$	${\mathit{M}}_4$	${\mathit{M}}_4$	${\mathit{M}}_4$

In the proposed method, an innovative criteria weights-determination procedure is introduced, which can systematically employ the significance of criteria and their estimation’s rationality. The proposed procedure can successfully exclude the influence of DE opinions on the assessment outcomes, further handle the issue of considerable alterations in DEs’ opinions or evade several DEs being purposely operated.

It is based on a broader standard of ARAS with information measures to solve drug selection problems in comparison to HF-TOPSIS [78] and HF-COPRAS [84] methods. Because the HF-ARAS method considers improved score values (deviations) from optimal alternative, while the other methods only consider a single criterion of the minimum distance from IS (ideal point) and AIS (anti-ideal point).

The implementation of the HF-ARAS method’s hesitant fuzzy and aggregation operator facilitates obtaining the utility-based solution (score model) for the drug selection problem only when compared with existing methods [78], [84]. The proposed method can be effortlessly employed utilizing commercially existing software like MATLAB and other associated mathematical programming tools.

6. Conclusions

The present work’s objective is to offer an innovative framework to evaluate the drug selection problem for mild symptoms of COVID-19 disease on HFSs. This study is divided into two folds: firstly, a new divergence measure and its properties have been introduced to measure the discrimination for HFSs. Secondly, a modified hesitant fuzzy ARAS (HF-ARAS) method has been proposed. In this process, a procedure using a developed divergence measure is introduced to calculate the attribute weights. Further, the efficacy and usefulness of this introduced framework have been demonstrated by the assessment of drugs for patients with mild symptoms of the COVID-19. To validate the permanence of the developed framework, sensitivity analysis has also been presented. A comparison and sensitivity assessment has been taken to confirm the validity and steadiness of the obtained results. The outcomes reveal that the HF-ARAS model has good proficiency and is well-consistent with extant approaches. There are a number of possibilities to extend the developed methodology.

The practicality of the introduce-ARAS model is evaluated by the case study of treating mild symptoms of COVID-19. According to the preference order of options, Remdesivir is the best drug for treating patients with mild symptoms of COVID-19. This ranking is based on the doctor’s recommendation; the patient reports with seven parameters Anorexia, Cough, Fatigue, Fever, Myalgia, Shortness of breath, and Sputum production. Remdesivir medicine reduces the health risk of patients and secures human health from the effects of viral diseases. Further, the developed framework can be generalized to q-Rung Orthopair Fuzzy Sets (q-ROFSs), Probabilistic Linguistic Term Sets (PLTSs), Neutrosophic Sets (SVNSs), and Bipolar Complex Fuzzy Sets (BCFSs), and can be employed to select the optimal antiviral therapy for the mild symptoms of COVID-19.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

CRediT authorship contribution statement

Arunodaya Raj Mishra: Conceptualization, Formal analysis, Visualization, Methodology, Resources, Writing - original draft, References, Review & editing. Pratibha Rani: Conceptualization, Methodology, Validation, Writing - original draft, Comparative study and sensitivity analysis. R. Krishankumar: Formal analysis, Validation, Sensitivity analysis, Writing - review & editing. K.S. Ravichandran: Resources, Visualization, Supervision, Proofread, Drafting. Samarjit Kar: Resources, Visualization, Supervision, Proofread, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.