Evaluation of dose-volume histogram prediction for organ-at risk and planning target volume based on machine learning

Sheng xiu Jiao; Ming li Wang; Li xin Chen; Xiao-wei Liu

doi:10.1038/s41598-021-82749-5

. 2021 Feb 4;11:3117. doi: 10.1038/s41598-021-82749-5

Evaluation of dose-volume histogram prediction for organ-at risk and planning target volume based on machine learning

Sheng xiu Jiao ¹, Ming li Wang ², Li xin Chen ^2,^✉, Xiao-wei Liu ^1,^✉

PMCID: PMC7862493 PMID: 33542427

Abstract

The purpose of this work is to evaluate the performance of applying patient dosimetric information induced by individual uniform-intensity radiation fields in organ-at risk (OAR) dose-volume histogram (DVH) prediction, and extend to DVH prediction of planning target volume (PTV). Ninety nasopharyngeal cancer intensity-modulated radiation therapy (IMRT) plans and 60 rectal cancer volumetric modulated arc therapy (VMAT) plans were employed in this study. Of these, 20 nasopharyngeal cancer cases and 15 rectal cancer cases were randomly selected as the testing data. The DVH prediction was performed using two methods. One method applied the individual dose-volume histograms (IDVHs) induced by a series of fields with uniform-intensity irradiation and the other method applied the distance-to-target histogram and the conformal-plan-dose-volume histogram (DTH + CPDVH). The determination coefficient R² and mean absolute error (MAE) were used to evaluate DVH prediction accuracy. The PTV DVH prediction was performed using the IDVHs. The PTV dose coverage was evaluated using D₉₈, D₉₅, D₁ and uniformity index (UI). The OAR dose was compared using the maximum dose, V₃₀ and V₄₀. The significance of the results was examined with the Wilcoxon signed rank test. For PTV DVH prediction using IDVHs, the clinical plan and IDVHs prediction method achieved mean UI values of 1.07 and 1.06 for nasopharyngeal cancer, and 1.04 and 1.05 for rectal cancer, respectively. No significant difference was found between the clinical plan results and predicted results using the IDVHs method in achieving PTV dose coverage (D_98, D_95, D₁ and UI) for both nasopharyngeal cancer and rectal cancer (p-values ≥ 0.052). For OAR DVH prediction, no significant difference was found between the IDVHs and DTH + CPDVH methods for the R², MAE, the maximum dose, V₃₀ and V₄₀ (p-values ≥ 0.087 for all OARs). This work evaluates the performance of dosimetric information of several individual fields with uniform-intensity radiation for DVH prediction, and extends its application to PTV DVH prediction. The results indicated that the IDVHs method is comparable to the DTH + CPDVH method in accurately predicting the OAR DVH. The IDVHs method quantified the input features of the PTV and showed reliable PTV DVH prediction, which is helpful for plan quality evaluation and plan generation.

Subject terms: Cancer therapy, Radiotherapy

Introduction

With the continuous development of artificial intelligence and machine learning technology, a medical computerized clinical decision support and assistance systems based on more available clinical data have played an increasingly important role in helping clinicians make clinical decisions^{1, 2}. In the field of radiotherapy, making dose-volume histogram (DVH) or dose distribution of organ at risk (OAR) predictions based on prior plan data could provide a valuable dose-volume reference that could help planners determine whether the quality of a treatment plan could be further improved^3–11 and could be used as the dose-volume optimization input constraints in a treatment planning system (TPS) to assist in plan generation^12–17. In addition, a machine learning method could predict the dose-volume parameter such as dose distribution index for treatment plan evaluation which is helpful for fast plan quality evaluation¹⁸.

The use of geometric information in predicting credible DVH has been widely studied; the representative patient geometric information descriptors are the overlap volume histogram (OVH) and the distance-to-target histogram (DTH). The OVH and DTH quantify the spatial relationship between OARs and the target^19–24. Recently, an OAR DVH prediction method based on patient dosimetric information was proposed^25–27, which indicated that using dosimetric information can improve DVH prediction.

In the treatment planning process, the dose-volume constraints of OAR and planning target volume (PTV) are needed for inverse optimization processes, and the PTV DVH prediction is beneficial for achieving clinically acceptable plans. By selecting a reference expansion target, Babier et al. used the OVH to predict the OAR and PTV DVH with the goal of automatically generating treatment plans for oropharynx patients²⁸. The geometric information for the OAR, such as the DTH, was calculated based on the spatial relationship between the OAR and PTV and used to predict the OAR DVH. A few studies have reported PTV DVH prediction using DTH.

From another point of view, the individual DVHs of different fields containing the direction-dependent dosimetric information should be helpful for the DVH prediction. However, the effectiveness of the PTV DVH prediction and the OAR DVH prediction accuracy using the individual DVHs of different fields is unknown. This work is to evaluate the performance of using the individual DVHs of different fields in OAR DVH prediction, and to aim to give a method for PTV DVH prediction.

Methods

In this work, the clinical treatment plans were used as the training and testing data. The different DVH prediction methods based on the geometric and dosimetric information were used to predict OAR DVH. The PTV DVH prediction was performed using only the dosimetric information. The prediction performance was evaluated using the dosimetric parameters, determination coefficient R² and mean absolute error (MAE).

Patient data

Following the Sun Yat-sen University Cancer Center Internal Review Board (IRB) approval (Approval No: YB2018-06), ninety90 nasopharyngeal carcinoma IMRT plans and 60 rectal cancer VMAT plans previously generated at our center were used as the database. Twenty nasopharyngeal carcinoma cases and 15 rectal cancer cases were randomly selected as the testing cases. The remaining cases were used as the training data. The informed consents have been obtained from all patients, and all patient data has been fully anonymized. All methods were performed in accordance with the relevant guidelines and regulations of the Sun Yat-sen University Cancer Center.

According to the guidelines of the Radiation Therapy Oncology Group (RTOG) protocols 0225 and 0615 for nasopharyngeal carcinoma and the RTOG protocol 0822 for rectal cancer, the dose-volume constraints for each structure were obtained and illustrated in Table 1. The nasopharyngeal carcinoma 9-field IMRT plans were generated with 6-MV photon beams using the Eclipse TPS (Varian Medical Systems, Palo Alto, USA, version 11.0). The gantry angles were: 160°, 120°, 80°, 40°, 0°, 200°, 240°, 280° and 320°. The target prescription dose of the nasopharyngeal carcinoma plan was 70 Gy in 32 fractions. Three PTVs, PTV70, PTV60 and PTV54 in the nasopharyngeal carcinoma IMRT plan were expanded by 3 mm from the corresponding clinical target volume (CTV70, CTV60 and CTV54). The OARs included the brainstem, spinal cord, chiasm, bilateral lens, bilateral optic nerve, bilateral parotid and bilateral temporal lobe. The rectal cancer plans were generated for double 6-MV VMAT arcs using the MONACO TPS (Elekta CMS, Maryland Heights, MO, version 5.10). The target prescription dose was 50 Gy in 25 fractions. Two PTVs, PTV50 and PTV45 in the rectal cancer VMAT plan were expanded by 5 mm from the CTV50 and CTV45, respectively. The OARs included the bladder, colon, bilateral femoral head and small intestine.

Table 1.

The required dose optimization constraints for generating a radiation therapy plan.

Nasopharyngeal carcinoma IMRT plan		Rectal cancer VMAT plan
Structure	Constraint	Structure	Constraint
PTV70	D₀ ≤ 75 Gy	PTV50	D₀ ≤ 55 Gy
–	D₁₀₀ ≥ 71 Gy	–	D₉₇ ≥ 51 Gy
–	D₉₇ ≥ 72 Gy	–	–
PTV60	D₁₀₀ ≥ 60 Gy	PTV45	D₁₀₀ ≥ 45 Gy
PTV54	D₁₀₀ ≥ 54 Gy	–	–
Brainstem	D₀ ≤ 60 Gy	Bladder	V₅₀ ≤ 50%
Spinal cord	D₀ ≤ 50 Gy	–	V₆₀ ≤ 20%
Chiasm	D₀ ≤ 60 Gy	Colon	D₀ ≤ 50 Gy
Lens	D₀ ≤ 10 Gy	–	–
Optic nerve	D₀ ≤ 60 Gy	Small intestine	D₀ ≤ 50 Gy
Parotid	V₃₀ ≤ 50%	–	V₅₀ ≤ 5%
Temporal lobe	D₀ ≤ 72 Gy	Femoral head	V₅₀ ≤ 5%

Open in a new tab

V_x volume receiving greater than x Gy, D_y the dose to the highest y% of volume.

DVH prediction method

The dosimetric information from individual fields with uniform-intensity radiation, termed the individual dose-volume histograms (IDVHs), was used to predict the OAR DVH and PTV DVH. Another method applied the DTH and the conformal plan dose-volume histogram (CPDVH) to predict the OAR DVH, which is referred to as the DTH + CPDVH method²⁶. Table 2 shows the input features of the OAR and PTV used in this work.

Table 2.

The geometric and dosimetric features of the OAR and PTV used in this study.

Structures

Features

Description

OAR

DTH

CPDVH

IDVHs

Distance-to-target histogram

Conformal plan dose-volume histogram

Individual dose-volume histograms

PTV

IDVHs

Individual dose-volume histograms

Open in a new tab

Each OAR has three features (DTH, CPDVH and IDVHs). The PTV has a single dosimetric feature (IDVHs).

IDVHs method

The input of the IDVHs method was the IDVHs, which represents the individual dose-volume histograms of 9 fields without interfields dose superposition. For the nasopharyngeal carcinoma cases, the process of calculating the individual field dose was as follows: each field was fitted to the PTV54 and the dose was calculated using 6-MV photon beams in an Eclipse TPS. Nine equally spaced fields were used in the dose calculation. The slice thickness of the CTs was 0.3 cm. For VMAT technology with many fields, calculating the dose of a large number of individual fields is time consuming. To solve this problem, this work applied 9 equally spaced fields to calculate the dosimetric information in the rectal cancer cases. The individual field dose was calculated for 6-MV photon beams using the MONACO TPS. Each field was fitted to the PTV45. The slice thickness of the CTs was 0.3 cm. Each field had the same weight.

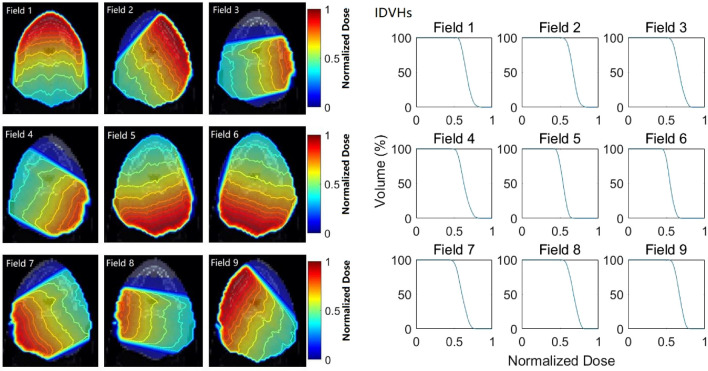
Figure 1 illustrates the dose distributions of the 9 individual fields with uniform-intensity irradiation at the same CT slice of a nasopharyngeal carcinoma patient and the corresponding IDVHs of a highlighted structure. The IDVH dose was normalized to the maximum dose of all individual fields. As shown in Fig. 1, the dose fall-off rate information of each individual field could be clearly presented, which differs from previous reports on the small dose fall-off rate of the PTV boundary regions after interfield dose superposition²⁶.

The dose distributions of the 9 individual fields with uniform-intensity irradiation at the same CT slice of a nasopharyngeal carcinoma patient (left) and the IDVHs of a highlighted structure (right).

For the IDVHs method, the input consisted of 9 parts. Each part sampled 50 points from the cumulative DVH of each field at an equal-interval dose. Thus, the input of the IDVHs method was 450 dimensional. The DVH prediction model was a generalized regression neural network (GRNN)²⁹, which was constructed using a neural network toolbox nntool of MATLAB (version R2018b, Math Works, Natick, MA). Of note, that the OAR and PTV were trained separately because the large difference of the DVH distribution of the OAR and PTV, and the multimodels may better predict the DVH³⁰.

DTH + CPDVH method

The DTH is used as the descriptor to quantify the spatial relationship between the OAR and PTV and represents the fractional volume of the OAR within a certain distance from the PTV surface²¹. To obtain the dosimetric information of each nasopharyngeal carcinoma patient, a 9-fields conformal plan was established. The process was as follows: the conformal plans were generated for 9 equally spaced fields with 6-MV photon beams. Each field was fitted to the PTV54 and had the same weight. All nasopharyngeal carcinoma conformal plans were developed using an Eclipse TPS. For the rectal cancer patients, the conformal plans were generated for 9 equally spaced fields with 6-MV photon beams. Each field was fitted to the PTV45 and had the same weight. All the rectal cancer conformal plans were developed using the MONACO TPS.

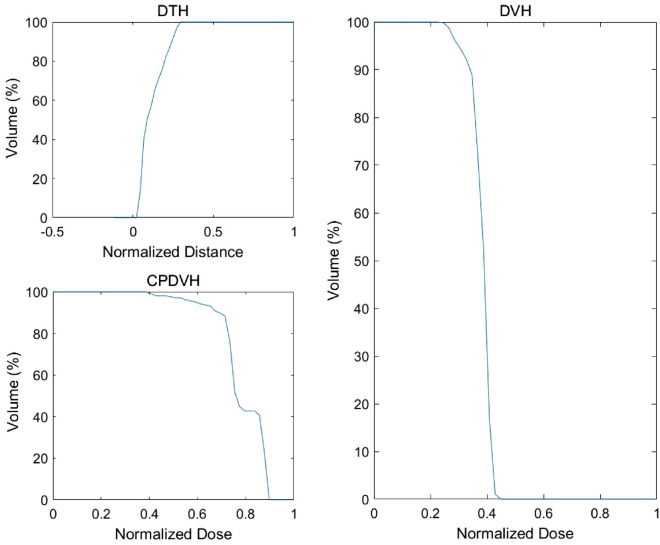
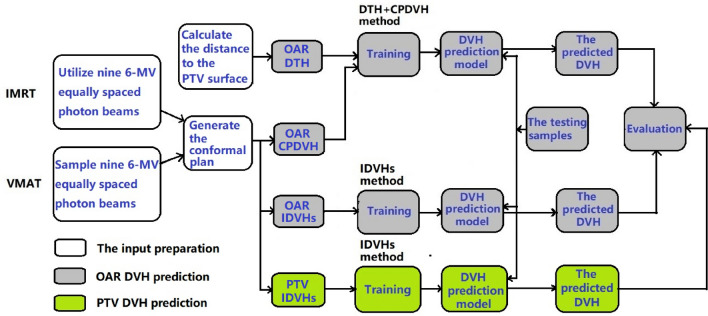
In Fig. 2, the DTH distance was normalized to the maximum distance of all OARs. The CPDVH dose was normalized to the PTV maximum dose of all the conformal plans. The DVH dose was normalized to the PTV maximum dose of all the IMRT or VMAT plans. The input of the DTH + CPDVH method was 100 dimensional, which included 50 points from the cumulative DTH at equal-interval distance and 50 points from cumulative CPDVH at equal-interval dose. The DVH prediction model was GRNN. Figure 3 shows a flowchart of the OAR and PTV DVH prediction process.

Flowchart showing the DVH prediction process.

DVH prediction error

The DVH prediction accuracy of the DTH + CPDVH method and the IDVHs method was evaluated using the determination coefficient R² and MAE. The closer R² is to 1.0, and the closer MAE is to 0, the closer the predicted value is to the actual value. The parameter D₉₈, D₉₅, D₁ and uniformity index (UI) were used to evaluate the PTV dose coverage. D_y is the dose to the highest y% of the volume. The OAR dosimetric result of the DTH + CPDVH prediction method and the IDVHs prediction method were evaluated using the maximum dose, V₃₀ and V₄₀. V_x represents the volume receiving greater than x Gy.

R^{2} = 1 - \frac{\sum_{i = 1}^{50} {(V_{i, T P S} - V_{i, p r e d})}^{2}}{\sum_{i = 1}^{50} {(V_{i, T P S} - \bar{V_{T P S}})}^{2}}

M A E = \frac{1}{50} \sum_{i = 1}^{50} |V_{i, T P S} - V_{i, p r e d}|

U I = \frac{D_{5}}{D_{95}}

$V_{i, T P S}$ is the ith volume value in the DVH curve that was achieved by the TPS and $V_{i, p r e d}$ is the ith volume value in the DVH curve that was predicted by the DTH + CPDVH or IDVHs method. The UI values closer to 1 indicate better homogeneity³¹. Significant differences were tested using SPSS (version 17, IBM-SPSS Statistics, Inc., Chicago, IL). The Wilcoxon signed rank test was utilized to compare the difference. A p-value < 0.05 was considered statistically significant.

Results

OAR DVH prediction accuracy of the IDVHs method

The means and standard deviations of the R² and MAE values for all testing cases are illustrated in Table 3. For nasopharyngeal cancer, the IDVHs method had a mean R² ranging from 0.87 to 0.97 at all OARs with standard deviations ≤ 0.20. The IDVHs method had a mean R² ≥ 0.92 for 5 out of 7 OARs in the 20 nasopharyngeal cancer test cases. The IDVHs method achieved a mean MAE value in the range from 1.16 to 7.95% with standard deviations ≤ 6% at all OARs. The IDVHs method produced a mean MAE ≤ 4.5% for 5 out of 7 OARs in the 20 nasopharyngeal cancer test cases. No significant differences in the R² and MAE values between the DTH + CPDVH method and IDVHs method were found for the OARs in the 20 nasopharyngeal cancer test cases (p-value ≥ 0.218).

Table 3.

The means and standard deviations of R² and MAE of the DTH + CPDVH method and IDVHs method for 20 nasopharyngeal cancer patients and 15 rectal cancer patients.

OAR	R²			MAE (%)
OAR	DTH + CPDVH	IDVHs	p-value	DTH + CPDVH	IDVHs	p-value
Nasopharyngeal cancer
Brainstem	0.97 ± 0.03	0.97 ± 0.03	0.647	3.52 ± 1.99	3.63 ± 2.24	0.650
Spinal cord	0.97 ± 0.03	0.97 ± 0.03	0.616	3.20 ± 1.50	3.22 ± 1.48	0.906
Chiasm	0.88 ± 0.24	0.87 ± 0.13	0.438	7.12 ± 8.00	7.95 ± 5.37	0.218
Lens	0.92 ± 0.08	0.92 ± 0.09	0.586	1.11 ± 0.88	1.16 ± 1.10	0.632
Optic nerve	0.89 ± 0.18	0.88 ± 0.16	0.679	6.84 ± 4.16	7.05 ± 4.82	0.831
Parotid	0.97 ± 0.03	0.97 ± 0.02	0.433	4.98 ± 3.12	4.34 ± 1.71	0.332
Temporal lobe	0.97 ± 0.07	0.97 ± 0.03	0.758	2.38 ± 1.95	2.41 ± 2.22	0.970
Rectal cancer
Bladder	0.98 ± 0.03	0.97 ± 0.03	0.190	2.20 ± 1.42	2.36 ± 1.70	0.221
Colon	0.95 ± 0.04	0.95 ± 0.04	0.722	6.13 ± 3.48	5.89 ± 3.50	0.937
Femoral head	0.96 ± 0.06	0.96 ± 0.06	0.990	4.59 ± 3.85	4.77 ± 3.01	0.865
Small intestine	0.95 ± 0.05	0.95 ± 0.06	0.463	4.86 ± 2.73	4.52 ± 3.59	0.807

Open in a new tab

The p-value between the DTH + CPDVH method and the IDVH method was given, and the difference was considered statistically significant if the p-value was less than 0.05.

For rectal cancer, the IDVHs method achieved a mean R² value ≥ 0.95 at the bladder, colon, bilateral femoral head and small intestine with standard deviation ≤ 0.06. The IDVHs method achieved a mean MAE value ≤ 6% at the bladder, colon, bilateral femoral head and small intestine with standard deviations ≤ 4%. No significant differences between the DTH + CPDVH method and IDVHs method in the R² and MAE values were found for the OAR in 15 rectal cancer test cases (p-value ≥ 0.190).

Table 4 illustrates the mean absolute difference between dosimetric parameter achieved by the TPS and dosimetric parameter predicted by the DTH + CPDVH or IDVHs method in 20 nasopharyngeal cancer and 15 rectal cancer test cases. The mean absolute difference between the IDVHs method and the TPS ranged from 1.20 to 2.84 Gy at the maximum dose D₀ of the brainstem, spinal cord, chiasm, bilateral lens and bilateral optic nerve for the 20 nasopharyngeal cancer test cases. The mean absolute difference between the IDVHs method and the TPS ranged from 1.6 to 2.64% at V₃₀ and V₄₀ of bilateral parotid and bilateral temporal lobe for the 20 nasopharyngeal cancer test cases.

Table 4.

Mean absolute difference between the dosimetric parameter achieved by the TPS and the dosimetric parameter predicted by the DTH + CPDVH or IDVHs method.

OAR	Parameters	Δ_DTH+CPDVH	Δ_IDVHs	p-value
Nasopharyngeal cancer
Brainstem	D₀ (Gy)	2.48 ± 2.23	2.44 ± 2.28	0.204
Spinal cord	D₀ (Gy)	2.96 ± 2.16	2.16 ± 1.74	0.179
Chiasm	D₀ (Gy)	2.08 ± 2.52	2.24 ± 3.02	0.324
Lens	D₀ (Gy)	1.28 ± 0.84	1.20 ± 1.02	0.763
Optic nerve	D₀ (Gy)	2.84 ± 4.47	2.84 ± 4.06	0.458
Parotid	V₄₀ (%)	3.20 ± 4.54	2.64 ± 2.51	0.518
Temporal lobe	V₃₀ (%)	1.80 ± 2.68	1.60 ± 2.99	0.601
Rectal cancer
Bladder	V₄₀ (%)	8.97 ± 7.14	9.54 ± 7.28	0.691
Colon	V₄₀ (%)	2.76 ± 2.48	3.19 ± 2.56	0.814
Femoral head	V₄₀ (%)	0.92 ± 0.71	1.08 ± 1.00	0.733
Small intestine	V₃₀ (%)	4.27 ± 3.35	2.89 ± 3.82	0.087

Open in a new tab

For the DTH + CPDVH method, Δ_DTH+CPDVH =|P_DTH+CPDVH-P_TPS|; for the IDVHs method, Δ_IDVHs =|P_IDVHs-P_TPS|, where Δ represents the absolute difference between the dosimetric parameter achieved by the TPS and the dosimetric parameter predicted by the prediction method in the testing cases. P represents the corresponding parameter. The data shown are the means and standard deviations of the respective parameters for the 20 nasopharyngeal cancer and 15 rectal cancer test cases.

For the 15 rectal cancer test cases, the mean absolute difference between the IDVHs method and the TPS at V₃₀ and V₄₀ ranged from 1.08% to 9.54% for all OARs. The mean absolute difference between the IDVHs method and the TPS at V₃₀ and V₄₀ was not more than 3.5% at the colon, bilateral femoral head and small intestine with standard deviations ≤ 4%. As shown in Table 4, no significant differences were found between the DTH + CPDVH method and the IDVHs method for all OARs (p-value ≥ 0.087). Both methods achieved a comparable predicted result.

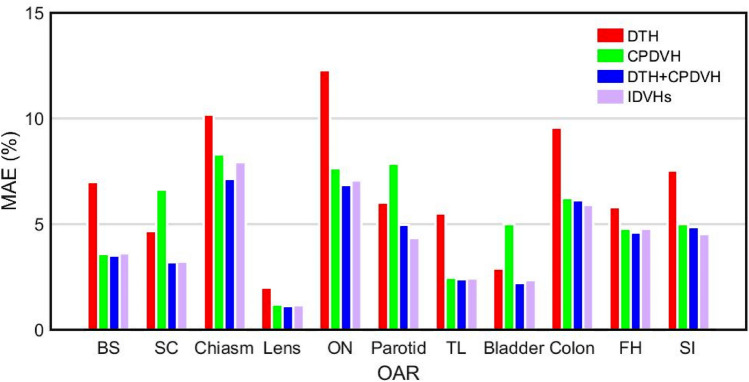
Figure 4 illustrates the mean MAE value of different DVH prediction methods in the 20 nasopharyngeal cancer and 15 rectal cancer cases. As shown in Fig. 4, both the IDVHs and DTH + CPDVH methods achieved comparable mean MAE value, which was consistent with the results of OAR dosimetric parameters prediction of the two methods.

The mean MAE of different prediction methods. BS brainstem, SC spinal cord, ON optic nerve, TL temporal lobe, FH femoral head, SI small intestine.

PTV DVH prediction accuracy of the IDVHs method

The comparison between the PTV dose coverage generated by the TPS and the PTV dose coverage predicted by the IDVHs method was shown in Table 5. For the PTV70, PTV60 and PTV54 of nasopharyngeal cancer, the mean absolute percentage difference between the plans generated by the TPS vs predicted by the IDVHs method in D₉₈, D₉₅ and D₁ ranged from 1.06% to 3.15% in the 20 nasopharyngeal cancer test cases with standard deviations ≤ 3%. For the PTV50 and PTV45 of the rectal cancer cases, the mean absolute percentage difference between the plans generated by the TPS vs predicted by the IDVHs method in D₉₈, D₉₅ and D₁ ranged from 0.85% to 3.74% in the 15 rectal cancer test cases with standard deviations ≤ 4%.

Table 5.

Comparison between the PTV dose coverage achieved by the TPS and the PTV dose coverage predicted by the IDVHs method.

Structures	Parameters	TPS (Mean ± SD)	IDVHs (Mean ± SD)	diff (%)	p-value
Nasopharyngeal cancer
PTV70	D₉₈ (Gy)	69.85 ± 1.25	69.56 ± 1.28	2.63 ± 2.08	0.836
	D₉₅ (Gy)	70.76 ± 0.54	70.22 ± 1.95	2.11 ± 1.58	0.307
	D₁ (Gy)	75.60 ± 1.00	75.55 ± 0.85	1.06 ± 1.09	0.848
	UI	1.07 ± 0.03	1.06 ± 0.02	2.02 ± 1.46	0.296
PTV60	D₉₈ (Gy)	61.33 ± 0.94	61.95 ± 1.32	2.12 ± 1.72	0.052
PTV60	D₉₅ (Gy)	62.88 ± 1.07	63.17 ± 1.55	2.57 ± 2.43	0.201
PTV54	D₉₈ (Gy)	53.60 ± 1.62	53.88 ± 1.34	3.15 ± 2.36	0.562
PTV54	D₉₅ (Gy)	55.44 ± 1.37	55.65 ± 1.15	2.45 ± 2.21	0.236
Rectal cancer
PTV50	D₉₈ (Gy)	50.83 ± 1.04	50.69 ± 1.74	2.95 ± 2.87	0.286
	D₉₅ (Gy)	51.59 ± 0.94	51.13 ± 1.66	2.57 ± 2.86	0.396
	D₁ (Gy)	54.10 ± 0.62	54.12 ± 0.62	0.85 ± 0.76	0.550
	UI	1.04 ± 0.02	1.05 ± 0.03	2.63 ± 2.68	0.650
PTV45	D₉₈ (Gy)	46.11 ± 0.74	45.86 ± 0.99	3.74 ± 3.85	0.753
PTV45	D₉₅ (Gy)	47.05 ± 0.83	46.85 ± 1.76	3.22 ± 3.63	0.995

Open in a new tab

The data shown are the means and standard deviations of the respective parameters for the 20 nasopharyngeal cancer and 15 rectal cancer patients. diff represents the mean absolute percentage difference between the PTV dose coverage achieved by the TPS and the PTV dose coverage predicted by the IDVHs method. (diff =|P_IDVHs-P_TPS|/P_TPS × 100%), where, P represents the corresponding parameter.

For the PTV70 in the nasopharyngeal cancer cases, the TPS and IDVHs method achieved UI values of 1.07 ± 0.03 and 1.06 ± 0.02, respectively. For the PTV50 in the rectal cancer cases, the TPS and IDVHs method achieved UI values of 1.04 ± 0.02 and 1.05 ± 0.03, respectively. No significant difference was found in the UI values between the TPS and IDVHs method. Likewise, no significant difference was found in PTV dose coverage at D₉₈, D₉₅ and D₁ between the TPS and IDVHs method for both nasopharyngeal cancer and rectal cancer cases.

Supplemental Fig. 1 shows the comparison between the predicted PTV DVH using the IDVHs method versus the TPS. Two PTVs, PTV70 of the nasopharyngeal cancer cases and PTV50 of the rectal cancer cases, are shown in detail. As shown in Supplemental Fig. 1, for the nasopharyngeal cancer, the predicted DVHs of PTV70 are close to the DVHs achieved by the TPS in 18/20 test cases, except for cases #1 and #10. For the rectal cancer, except for cases #1, #8 and #12, most predicted DVHs of PTV50 are close to the DVHs achieved by the TPS in the 15 test cases.

Supplemental Fig. 2 illustrates the R² value of different PTVs of all the testing cases. Regarding the R² value, 17/20 cases in PTV70, 20/20 cases in PTV60, 11/20 cases in PTV54, 11/15 cases in PTV50 and 13/15 cases in PTV45 are located at within 0.9 ~ 1. The IDVHs method achieved a mean R² value at PTV70, PTV60, PTV54, PTV50 and PTV45 of 0.95, 0.98, 0.93, 0.92 and 0.95, respectively.

Discussion

The difference between the method using only the DTH and the IDVHs method or the DTH + CPDVH method at the mean MAE value is rather large (see Fig. 4). The use of a set of individual DVHs (IDVHs) improves the prediction accuracy of the DVHs of OARs that are partially surrounded or overlapped by PTV (such as spinal cord, parotid and bladder), and they cannot be predicted accurately employing the superimposed dosimetric information (such as the CPDVH). The results show that the better OAR DVH prediction using a set of individual DVHs containing the direction-dependent dosimetric information.

The patient geometric information-based three-dimensional (3D) dose prediction model has been widely studied and reported in recent years and can provide the predicted dosimetric results for OAR and PTV^6–9. Fan et al. applied a deep learning-based model to predict the 3D dose distribution for head-and-neck cancer and no significant difference was found between the predicted plan (Pred) and the manually optimized plan (MO) at D₉₅ of PTV₆₀ (mean, 59.4 Gy vs 59.6 Gy, p = 0.05) and PTV₅₄ (mean, 53.9 Gy vs 53.7 Gy, p = 0.28)⁸. For comparison, the difference between the predicted plan and the manually optimized plan at D₉₅ of different PTVs was calculated as follows: ε =|Pred-MO|/MO × 100%, where Pred represented the average D₉₅ of PTVs in the predicted plans; MO represented the average D₉₅ of PTVs in the manually optimized plans. Compared with their results⁸, the difference between the 3D dose prediction method and the IDVHs method at D₉₅ of different PTVs was (PTV₆₀, ε, 0.34% vs 0.46%) and (PTV₅₄, ε, 0.37% vs 0.38%). Recently, Song et al. proposed a deep neural network to predict the 3D dose of rectal cancer patients, and the results showed that no significant difference between the DeepLabv3 + prediction results (Dose_DeepLabv3+) and the Dose_approved was found at D₉₈ of PTV₅₀ (mean, 49.19 Gy vs 49.07 Gy, p = 0.23)¹⁰. Compared with their prediction results⁹, the difference between the deep neural network method and the IDVHs method at D₉₈ of PTV₅₀ was (ε, 0.24% vs 0.28%). The predicted PTV dosimetric results of this study are comparable to the results of Fan et al.⁸ and Song et al.⁹.

Considering that the geometry differences for distinct diseases may affect the DVH prediction accuracy of the IDVHs method, in this work, DVH prediction was studied for nasopharyngeal carcinoma of the head-and-neck and rectal cancer of the abdomen. The results showed the feasibility and effectiveness of predicting the OAR and PTV DVH in these two diseases using the IDVHs method. Future studies on the predictive value of the IDVHs method in other diseases are warranted.

For the IMRT plan with a fixed irradiation angle, the irradiation field arrangement could be used to establish the corresponding conformal plan to extract the features of the OAR and target. For other diseases using a 5-fields or 7-fields arrangement, the corresponding field arrangement of the conformal plan can be adjusted accordingly. The VMAT plan, which samples many irradiation fields to calculate the dosimetric information, is time consuming. Perhaps, sampling less equally spaced irradiation fields can achieve similar prediction accuracy with 9 equally spaced fields. The difference in prediction accuracy when sampling different equally spaced irradiation fields will be studied in the future.

Conclusion

This work evaluated the performance of the IDVHs method in predicting both the OAR and PTV DVH for IMRT and VMAT plans. The results indicated that the IDVHs method is comparable to the DTH + CPDVH method in accurately predicting the OAR DVH. The IDVHs method quantified the input features of the PTV and showed reliable PTV DVH prediction. Therefore, the IDVHs method can provide more comprehensive guidance information for radiotherapy treatment plan quality evaluation and plan generation.

Supplementary Information

Supplementary Information^{(687.6KB, docx)}

Acknowledgements

This work was supported by the National Natural Science Foundation of China (U1832128 and 11375278) and Guangdong Esophageal Cancer Institute Science and Technology Program (No. M201813).

Author contributions

J.S.X. Developed the DVH prediction model, analysed data and wrote the manuscript. W.M.L. Provided training and test samples, analysed data. C.L.X. Analysed data and revised manuscript. L.X.W. Designed the study and revised manuscript. All authors contributed to the editing and revising of the manuscript.

Data availability

The datasets generated and/or analysed during the current study are available from the corresponding author on request.

Competing interests

The authors declare no competing interests.

Footnotes

Publisher's note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Contributor Information

Li xin Chen, Email: chenlx@sysucc.org.cn.

Xiao-wei Liu, Email: stslxw@mail.sysu.edu.cn.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-021-82749-5.

References

1.Mahadevaiah G, Bermejo I, Jaffray D, Deller A, Wee L. Artificial intelligence-based clinical decision support in modern medical physics: Selection, acceptance, commissioning, and quality assurance. Med. Phys. 2020;47(5):e228–e235. doi: 10.1002/mp.13562. [DOI] [PMC free article] [PubMed] [Google Scholar]
2.Siddique S, Chow JCL. Artificial intelligence in radiotherapy. Rep. Pract. Oncol. Radiother. 2020;25(4):656–666. doi: 10.1016/j.rpor.2020.03.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
3.Tol JP, Dahele M, Delaney AR, Slotman BJ, Verbakel WF. Can knowledge-based DVH predictions be used for automated, individualized quality assurance of radiotherapy treatment plans? Radiat. Oncol. 2015;10:234. doi: 10.1186/s13014-015-0542-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
4.Moore KL, Brame RS, Low DA, Mutic S. Experience-based quality control of clinical intensity-modulated radiotherapy planning. Int. J. Radiat. Oncol. Biol. Phys. 2011;81:545–551. doi: 10.1016/j.ijrobp.2010.11.030. [DOI] [PubMed] [Google Scholar]
5.Valdes G, Simone CB, Chen J, Lin A, Yom SS, Pattison AJ, Solberg TD. Clinical decision support of radiotherapy treatment planning: A data-driven machine learning strategy for patient-specific dosimetric decision making. Radiother. Oncol. 2017;125(3):392–397. doi: 10.1016/j.radonc.2017.10.014. [DOI] [PubMed] [Google Scholar]
6.Qi M, Li Y, Wu A, Jia Q, Guo F, Lu X, Kong F, Mai Y, Zhou L, Song T. Region-specific three-dimensional dose distribution prediction: A feasibility study on prostate VMAT cases. J. Radiat. Res. Appl. Sci. 2020;13(1):485–495. doi: 10.1080/16878507.2020.1756185. [DOI] [Google Scholar]
7.Nguyen D, Long T, Jia X, Lu W, Gu X, Iqbal Z, Jiang S. A feasibility study for predicting optimal radiation therapy dose distributions of prostate cancer patients from patient anatomy using deep learning. Sci. Rep. 2019;9(1):1076. doi: 10.1038/s41598-018-37741-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Fan J, Wang J, Chen Z, Hu C, Zhang Z, Hu W. Automatic treatment planning based on three-dimensional dose distribution predicted from deep learning technique. Med. Phys. 2018;46(1):370–381. doi: 10.1002/mp.13271. [DOI] [PubMed] [Google Scholar]
9.Song Y, Hu J, Liu Y, Hu H, Huang Y, Bai S, Yi Z. Dose prediction using a deep neural network for accelerated planning of rectal cancer radiotherapy. Radiother. Oncol. 2020;149:111–116. doi: 10.1016/j.radonc.2020.05.005. [DOI] [PubMed] [Google Scholar]
10.Wu B, Ricchetti F, Sanguineti G, et al. Patient geometry-driven information retrieval for IMRT treatment plan quality control. Med. Phys. 2009;36:5497–5505. doi: 10.1118/1.3253464. [DOI] [PubMed] [Google Scholar]
11.Johanna SM, Jens S. Dose-volume histogram prediction using density estimation. Phys. Med. Biol. 2015;60:6923–6936. doi: 10.1088/0031-9155/60/17/6923. [DOI] [PubMed] [Google Scholar]
12.Good D, Lo J, Lee WR, Wu QJ, Yin FF, Das SK. A knowledge-based approach to improving and homogenizing intensity modulated radiation therapy planning quality among treatment centers: An example application to prostate cancer planning. Int. J. Radiat. Oncol. Biol. Phys. 2013;87:176–181. doi: 10.1016/j.ijrobp.2013.03.015. [DOI] [PubMed] [Google Scholar]
13.Tol JP, Delaney AR, Dahele M, Slotman BJ, Verbakel WF. Evaluation of a knowledge-based planning solution for head and neck cancer. Int. J. Radiat. Oncol. Biol. Phys. 2015;91(3):612–620. doi: 10.1016/j.ijrobp.2014.11.014. [DOI] [PubMed] [Google Scholar]
14.Sharpe MB, Moore KL, Orton CG. Within the next ten years treatment planning will become fully automated without the need for human intervention. Med. Phys. 2014;41(12):120601. doi: 10.1118/1.4894496. [DOI] [PubMed] [Google Scholar]
15.Krayenbuehl J, Norton I, Studer G, Guckenberger M. Evaluation of an automated knowledge based treatment planning system for head and neck. Radiat. Oncol. 2015;10:226. doi: 10.1186/s13014-015-0533-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
16.Wu H, Jiang F, Yue H, Zhang H, Wang K, Zhang Y. Applying a RapidPlan model trained on a technique and orientation to another: A feasibility and dosimetric evaluation. Radiat. Oncol. 2016;11:108. doi: 10.1186/s13014-016-0684-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Chang ATY, Hung AWM, Cheung FWK, Lee MCH, Chan OSH, Philips H, Cheng YT, Ng WT. Comparison of planning quality and efficiency between conventional and knowledge based algorithms in nasopharyngeal cancer patients using intensity-modulated radiotherapy. Int. J. Radiat. Oncol. Biol. Phys. 2016;95:981–990. doi: 10.1016/j.ijrobp.2016.02.017. [DOI] [PubMed] [Google Scholar]
18.Ng F, Jiang R, Chow JCL. Predicting radiation treatment planning evaluation parameter using artificial intelligence and machine learning. IOP SciNotes. 2020;1(1):014003. doi: 10.1088/2633-1357/ab805d. [DOI] [Google Scholar]
19.Kazhdan M, Simari P, McNutt T, et al. A shape relationship descriptor for radiation therapy planning. Lecture Notes Comput. Sci. 2009;5762:100–108. doi: 10.1007/978-3-642-04271-3_13. [DOI] [PubMed] [Google Scholar]
20.Appenzoller LM, Michalski JM, Thorstad WL, Mutic S, Moore KL. Predicting dose-volume histograms for organs-at-risk in IMRT planning. Med. Phys. 2012;39:7446–7461. doi: 10.1118/1.4761864. [DOI] [PubMed] [Google Scholar]
21.Zhu X, Ge Y, Li T, Thongphiew D, Yin FF, Wu QJ. A planning quality evaluation tool for prostate adaptive IMRT based on machine learning. Med. Phys. 2011;38:719–726. doi: 10.1118/1.3539749. [DOI] [PubMed] [Google Scholar]
22.Yuan L, Ge Y, Lee WR, Yin FF, Kirkpatrick JP, Wu QJ. Quantitative analysis of the factors which affect the interpatient organ-at-risk dose sparing variation in IMRT plans. Med. Phys. 2012;39:6868–6878. doi: 10.1118/1.4757927. [DOI] [PubMed] [Google Scholar]
23.Wall PDH, Carver RL, Fontenot JD. An improved distance-to-dose correlation for predicting bladder and rectum dose-volumes in knowledge-based VMAT planning for prostate cancer. Phys. Med. Biol. 2018;63:015035. doi: 10.1088/1361-6560/aa9a30. [DOI] [PubMed] [Google Scholar]
24.Wu B, Pang D, Lei S, Gatti J, Tong M, McNutt T, Kole T, Dritschilo A, Collins S. Improved robotic stereotactic body radiation therapy plan quality and planning efficacy for organ-confined prostate cancer utilizing overlap-volume histogram-driven planning methodology. Radiother. Oncol. 2014;112:221–226. doi: 10.1016/j.radonc.2014.07.009. [DOI] [PubMed] [Google Scholar]
25.Ma M, Kovalchuk N, Buyyounouski MK, Xing L, Yang Y. Dosimetric features-driven machine learning model for DVH prediction in VMAT treatment planning. Med. Phys. 2019;46(2):857–867. doi: 10.1002/mp.13334. [DOI] [PubMed] [Google Scholar]
26.Jiao S, Chen L, Zhu J, Wang M, Liu X. Prediction of dose-volume histograms in nasopharyngeal cancer IMRT using geometric and dosimetric information. Phys. Med. Biol. 2019;64:2304. doi: 10.1088/1361-6560/ab50eb. [DOI] [PubMed] [Google Scholar]
27.Zhuang Y, Han J, Chen L, Liu X. Dose-volume histogram prediction in volumetric modulated arc therapy for nasopharyngeal carcinomas based on uniform-intensity radiation with equal angle intervals. Phys. Med. Biol. 2019;64(23):2303. doi: 10.1088/1361-6560/ab5433. [DOI] [PubMed] [Google Scholar]
28.Babier A, Boutilier JJ, Mcniven AL, et al. Knowledge-based automated planning for oropharyngeal cancer. Med. Phys. 2018;45(7):2875–2883. doi: 10.1002/mp.12930. [DOI] [PubMed] [Google Scholar]
29.Specht DF. A general regression neural networks IEEE Trans. Neural Netw. 1991;2:568–576. doi: 10.1109/72.97934. [DOI] [PubMed] [Google Scholar]
30.Chin Snyder K, Kim J, Reding A, Fraser C, et al. Development and evaluation of a clinical model for lung cancer patients using stereotactic body radiotherapy (SBRT) within a knowledge-based algorithm for treatment planning. J. Appl. Clin. Med. Phys. 2016;17(6):263–275. doi: 10.1120/jacmp.v17i6.6429. [DOI] [PMC free article] [PubMed] [Google Scholar]
31.Nwankwo O, Mekdash H, Sihono DSK, Wenz F, Glatting G. Knowledge-based radiation therapy (KBRT) treatment planning versus planning by experts: Validation of a KBRT algorithm for prostate cancer treatment planning. Radiat. Oncol. 2015;10:111. doi: 10.1186/s13014-015-0416-6. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information^{(687.6KB, docx)}

Data Availability Statement

The datasets generated and/or analysed during the current study are available from the corresponding author on request.

[CR1] 1.Mahadevaiah G, Bermejo I, Jaffray D, Deller A, Wee L. Artificial intelligence-based clinical decision support in modern medical physics: Selection, acceptance, commissioning, and quality assurance. Med. Phys. 2020;47(5):e228–e235. doi: 10.1002/mp.13562. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR2] 2.Siddique S, Chow JCL. Artificial intelligence in radiotherapy. Rep. Pract. Oncol. Radiother. 2020;25(4):656–666. doi: 10.1016/j.rpor.2020.03.015. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR3] 3.Tol JP, Dahele M, Delaney AR, Slotman BJ, Verbakel WF. Can knowledge-based DVH predictions be used for automated, individualized quality assurance of radiotherapy treatment plans? Radiat. Oncol. 2015;10:234. doi: 10.1186/s13014-015-0542-1. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR4] 4.Moore KL, Brame RS, Low DA, Mutic S. Experience-based quality control of clinical intensity-modulated radiotherapy planning. Int. J. Radiat. Oncol. Biol. Phys. 2011;81:545–551. doi: 10.1016/j.ijrobp.2010.11.030. [DOI] [PubMed] [Google Scholar]

[CR5] 5.Valdes G, Simone CB, Chen J, Lin A, Yom SS, Pattison AJ, Solberg TD. Clinical decision support of radiotherapy treatment planning: A data-driven machine learning strategy for patient-specific dosimetric decision making. Radiother. Oncol. 2017;125(3):392–397. doi: 10.1016/j.radonc.2017.10.014. [DOI] [PubMed] [Google Scholar]

[CR6] 6.Qi M, Li Y, Wu A, Jia Q, Guo F, Lu X, Kong F, Mai Y, Zhou L, Song T. Region-specific three-dimensional dose distribution prediction: A feasibility study on prostate VMAT cases. J. Radiat. Res. Appl. Sci. 2020;13(1):485–495. doi: 10.1080/16878507.2020.1756185. [DOI] [Google Scholar]

[CR7] 7.Nguyen D, Long T, Jia X, Lu W, Gu X, Iqbal Z, Jiang S. A feasibility study for predicting optimal radiation therapy dose distributions of prostate cancer patients from patient anatomy using deep learning. Sci. Rep. 2019;9(1):1076. doi: 10.1038/s41598-018-37741-x. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR8] 8.Fan J, Wang J, Chen Z, Hu C, Zhang Z, Hu W. Automatic treatment planning based on three-dimensional dose distribution predicted from deep learning technique. Med. Phys. 2018;46(1):370–381. doi: 10.1002/mp.13271. [DOI] [PubMed] [Google Scholar]

[CR9] 9.Song Y, Hu J, Liu Y, Hu H, Huang Y, Bai S, Yi Z. Dose prediction using a deep neural network for accelerated planning of rectal cancer radiotherapy. Radiother. Oncol. 2020;149:111–116. doi: 10.1016/j.radonc.2020.05.005. [DOI] [PubMed] [Google Scholar]

[CR10] 10.Wu B, Ricchetti F, Sanguineti G, et al. Patient geometry-driven information retrieval for IMRT treatment plan quality control. Med. Phys. 2009;36:5497–5505. doi: 10.1118/1.3253464. [DOI] [PubMed] [Google Scholar]

[CR11] 11.Johanna SM, Jens S. Dose-volume histogram prediction using density estimation. Phys. Med. Biol. 2015;60:6923–6936. doi: 10.1088/0031-9155/60/17/6923. [DOI] [PubMed] [Google Scholar]

[CR12] 12.Good D, Lo J, Lee WR, Wu QJ, Yin FF, Das SK. A knowledge-based approach to improving and homogenizing intensity modulated radiation therapy planning quality among treatment centers: An example application to prostate cancer planning. Int. J. Radiat. Oncol. Biol. Phys. 2013;87:176–181. doi: 10.1016/j.ijrobp.2013.03.015. [DOI] [PubMed] [Google Scholar]

[CR13] 13.Tol JP, Delaney AR, Dahele M, Slotman BJ, Verbakel WF. Evaluation of a knowledge-based planning solution for head and neck cancer. Int. J. Radiat. Oncol. Biol. Phys. 2015;91(3):612–620. doi: 10.1016/j.ijrobp.2014.11.014. [DOI] [PubMed] [Google Scholar]

[CR14] 14.Sharpe MB, Moore KL, Orton CG. Within the next ten years treatment planning will become fully automated without the need for human intervention. Med. Phys. 2014;41(12):120601. doi: 10.1118/1.4894496. [DOI] [PubMed] [Google Scholar]

[CR15] 15.Krayenbuehl J, Norton I, Studer G, Guckenberger M. Evaluation of an automated knowledge based treatment planning system for head and neck. Radiat. Oncol. 2015;10:226. doi: 10.1186/s13014-015-0533-2. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR16] 16.Wu H, Jiang F, Yue H, Zhang H, Wang K, Zhang Y. Applying a RapidPlan model trained on a technique and orientation to another: A feasibility and dosimetric evaluation. Radiat. Oncol. 2016;11:108. doi: 10.1186/s13014-016-0684-9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR17] 17.Chang ATY, Hung AWM, Cheung FWK, Lee MCH, Chan OSH, Philips H, Cheng YT, Ng WT. Comparison of planning quality and efficiency between conventional and knowledge based algorithms in nasopharyngeal cancer patients using intensity-modulated radiotherapy. Int. J. Radiat. Oncol. Biol. Phys. 2016;95:981–990. doi: 10.1016/j.ijrobp.2016.02.017. [DOI] [PubMed] [Google Scholar]

[CR18] 18.Ng F, Jiang R, Chow JCL. Predicting radiation treatment planning evaluation parameter using artificial intelligence and machine learning. IOP SciNotes. 2020;1(1):014003. doi: 10.1088/2633-1357/ab805d. [DOI] [Google Scholar]

[CR19] 19.Kazhdan M, Simari P, McNutt T, et al. A shape relationship descriptor for radiation therapy planning. Lecture Notes Comput. Sci. 2009;5762:100–108. doi: 10.1007/978-3-642-04271-3_13. [DOI] [PubMed] [Google Scholar]

[CR20] 20.Appenzoller LM, Michalski JM, Thorstad WL, Mutic S, Moore KL. Predicting dose-volume histograms for organs-at-risk in IMRT planning. Med. Phys. 2012;39:7446–7461. doi: 10.1118/1.4761864. [DOI] [PubMed] [Google Scholar]

[CR21] 21.Zhu X, Ge Y, Li T, Thongphiew D, Yin FF, Wu QJ. A planning quality evaluation tool for prostate adaptive IMRT based on machine learning. Med. Phys. 2011;38:719–726. doi: 10.1118/1.3539749. [DOI] [PubMed] [Google Scholar]

[CR22] 22.Yuan L, Ge Y, Lee WR, Yin FF, Kirkpatrick JP, Wu QJ. Quantitative analysis of the factors which affect the interpatient organ-at-risk dose sparing variation in IMRT plans. Med. Phys. 2012;39:6868–6878. doi: 10.1118/1.4757927. [DOI] [PubMed] [Google Scholar]

[CR23] 23.Wall PDH, Carver RL, Fontenot JD. An improved distance-to-dose correlation for predicting bladder and rectum dose-volumes in knowledge-based VMAT planning for prostate cancer. Phys. Med. Biol. 2018;63:015035. doi: 10.1088/1361-6560/aa9a30. [DOI] [PubMed] [Google Scholar]

[CR24] 24.Wu B, Pang D, Lei S, Gatti J, Tong M, McNutt T, Kole T, Dritschilo A, Collins S. Improved robotic stereotactic body radiation therapy plan quality and planning efficacy for organ-confined prostate cancer utilizing overlap-volume histogram-driven planning methodology. Radiother. Oncol. 2014;112:221–226. doi: 10.1016/j.radonc.2014.07.009. [DOI] [PubMed] [Google Scholar]

[CR25] 25.Ma M, Kovalchuk N, Buyyounouski MK, Xing L, Yang Y. Dosimetric features-driven machine learning model for DVH prediction in VMAT treatment planning. Med. Phys. 2019;46(2):857–867. doi: 10.1002/mp.13334. [DOI] [PubMed] [Google Scholar]

[CR26] 26.Jiao S, Chen L, Zhu J, Wang M, Liu X. Prediction of dose-volume histograms in nasopharyngeal cancer IMRT using geometric and dosimetric information. Phys. Med. Biol. 2019;64:2304. doi: 10.1088/1361-6560/ab50eb. [DOI] [PubMed] [Google Scholar]

[CR27] 27.Zhuang Y, Han J, Chen L, Liu X. Dose-volume histogram prediction in volumetric modulated arc therapy for nasopharyngeal carcinomas based on uniform-intensity radiation with equal angle intervals. Phys. Med. Biol. 2019;64(23):2303. doi: 10.1088/1361-6560/ab5433. [DOI] [PubMed] [Google Scholar]

[CR28] 28.Babier A, Boutilier JJ, Mcniven AL, et al. Knowledge-based automated planning for oropharyngeal cancer. Med. Phys. 2018;45(7):2875–2883. doi: 10.1002/mp.12930. [DOI] [PubMed] [Google Scholar]

[CR29] 29.Specht DF. A general regression neural networks IEEE Trans. Neural Netw. 1991;2:568–576. doi: 10.1109/72.97934. [DOI] [PubMed] [Google Scholar]

[CR30] 30.Chin Snyder K, Kim J, Reding A, Fraser C, et al. Development and evaluation of a clinical model for lung cancer patients using stereotactic body radiotherapy (SBRT) within a knowledge-based algorithm for treatment planning. J. Appl. Clin. Med. Phys. 2016;17(6):263–275. doi: 10.1120/jacmp.v17i6.6429. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR31] 31.Nwankwo O, Mekdash H, Sihono DSK, Wenz F, Glatting G. Knowledge-based radiation therapy (KBRT) treatment planning versus planning by experts: Validation of a KBRT algorithm for prostate cancer treatment planning. Radiat. Oncol. 2015;10:111. doi: 10.1186/s13014-015-0416-6. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Evaluation of dose-volume histogram prediction for organ-at risk and planning target volume based on machine learning

Sheng xiu Jiao

Ming li Wang

Li xin Chen

Xiao-wei Liu

Abstract

Introduction

Methods

Patient data

Table 1.

DVH prediction method

Table 2.

IDVHs method

Figure 1.

DTH + CPDVH method

Figure 2.

Figure 3.

DVH prediction error

Results

OAR DVH prediction accuracy of the IDVHs method

Table 3.

Table 4.

Figure 4.

PTV DVH prediction accuracy of the IDVHs method

Table 5.

Discussion

Conclusion

Supplementary Information

Acknowledgements

Author contributions

Data availability

Competing interests

Footnotes

Contributor Information

Supplementary Information

References

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases