The Use Of Genetic Correlation And Mendelian Randomization Studies To Increase Our Understanding of Relationships Between Complex Traits.

Abstract

Purpose of the review:

Increasing access to large-scale genetic datasets in population-based studies allows for genetic association studies as a means to examine previously known and novel relationships among complex traits. In this review, we discuss two widely used approaches to leverage genetic data to study the links between traits: Genome-wide genetic correlation and Mendelian Randomization (MR) studies.

Recent findings:

Both genetic correlation and MR studies have provided important novel insights. However, although they are less sensitive to many sources of bias present in traditional, observational epidemiology, they still rely on assumptions that in practice might be difficult to assess. To overcome this, development of novel methods less sensitive to these assumptions is an active area of research.

Summary:

We believe that as population-based genetic datasets grow larger and novel methods allowing for weaker forms of current assumptions become available, genetic correlation and MR studies will become an integral part of genetic epidemiology studies.

INTRODUCTION

Genome-wide association studies (GWAS) have generated thousands of single-nucleotide polymorphism (SNP)-trait associations. These results have already provided several new insights into disease etiology, and they provide initial clues for further investigations[1]. In addition to being a successful tool for identifying individual risk factors for disease, GWAS have also offered novel approaches to obtain novel insights into shared etiology across traits. For example, the estimated genome-wide genetic correlation between Estrogen Receptor (ER)+ and ER− breast cancer is modest (r_g=0.60)[2], similar to the genetic correlation between lung and head and neck cancer (r_g=0.57)[3]. This is in agreement with findings from GWAS, where ER+ and ER− breast cancer share some, but not all, genome-wide significant variants[2]. They also agree with observational studies[4] demonstrating differential effects of non-genetic risk factors for ER+ and ER− breast cancer and highlight the importance of considering etiological heterogeneity across disease subtypes. Furthermore, GWAS can allow us to revisit associations in observational epidemiology. For example, by substituting observational measures of a trait with its genetic predictors, we can partially overcome inherent issues in observational epidemiology such as confounding and reverse causation. Such Mendelian Randomization (MR) studies (see below) have provided evidence against a causal role of high-density lipoprotein (HDL) cholesterol in coronary artery disease (CAD), despite evidence of an inverse relationship in observational studies[5, 6].

In this review, we will discuss two popular genetic approaches that help increase our knowledge about associations between traits; genome-wide genetic correlation and MR studies. The overarching goal with genome-wide genetic correlation analysis is to quantify the correlation of effect estimates across SNPs between two traits, whilst the goal with MR studies is to leverage genetic information to estimate a causal effect of one trait on another. Here, we will describe these two approaches in more detail, including their advantages and disadvantages, and also discuss their similarities and differences. Throughout the manuscript, we will focus our discussion on two-sample designs, that is, when the two traits of interest have been assessed in two independent populations[7]. For example, a two-sample genetic correlation (or MR) study assessing the relationship between body mass index (BMI) and prostate cancer would use BMI GWAS summary statistics from UK Biobank and prostate cancer GWAS summary statistics from the PRACTICAL consortium, where there is no overlap between UK Biobank and PRACTICAL participants.

GENETIC CORRELATION STUDIES

Genetic correlation studies estimate the correlation in allele effects between two traits across causal SNPs in the genome. The genetic correlation r_g can be defined as $\frac{{\sum }_k{b}_k{c}_k}{\sqrt{{\sum }_k{b}_k^2}\sqrt{{\sum }_k{c}_k^2}}$, where b_k is the per-allele effect of SNP k from a multivariable regression of trait Y₁ on all SNPs in an infinite sample from a given population, and c_k is the same for trait Y₂. In practice, when the sample sizes for studies of Y₁ and Y₂ are typically smaller than the number of SNPs to be analyzed, multivariable regression cannot be used to estimate b_k or c_k; additional assumptions are needed[8]. When individual-level data is available, the genome-wide genetic correlation between two traits can be estimated using bivariate genome-based restricted maximum likelihood (GREML) analysis[9] on GWAS data of independent individuals as implemented in the widely-used GCTA software[10]. In the absence of individual-level data, genetic correlations between two traits can be estimated by the increasingly used cross-trait LD score regression (LDSC)[11]. LDSC relies on the fact that SNP-specific association statistics include the effects of all SNPs in linkage disequilibrium (LD) with that SNP. Thus, for a polygenic trait, SNPs in high-LD regions will on average have higher χ² statistics than SNPs in low-LD regions. We can estimate the genetic correlation between two traits using the relationship $E\left[{\beta }_j{\gamma }_j\right]=\frac{{\rho }_g}{M}{l}_j+\frac{N_s\rho }{N_{\text{Y}1}{N}_{\text{Y}2}}$, where β_j and γ_j is the effect size for SNP j on trait Y₁ and trait Y₂ respectively, ρ_g is the genetic covariance, M is the number of SNPs, N₁ and N₂ are sample sizes for trait Y₁ and Y₂ respectively, N_s is the number of overlapping samples, ρ is the phenotypic correlation between overlapping samples and l(j, c) is the LD Score of SNP j, defined as l(j, c) ≔ ∑_k∈c r²(j, k))[12]. The genetic covariance ρ_g is estimated by the slope obtained from a linear regression of β_jγ_j on l(j, c). We can obtain l(j, c) from external reference databases such as 1000 Genomes[13], with the caveat that the genetic ancestry between the study samples and reference panel needs to match. To obtain the genetic correlation r_g, we can normalize the genetic covariance ρ_g by the estimated SNP heritabilities for the two traits: $r_g=\frac{{\rho }_g}{h_{g1}^2{h}_{g2}^2}$, where $h_{g_1}^2$ and $h_{g_2}^2$ are the SNP heritabilities for trait Y₁ and Y₂, respectively[11]. LDSC is attractive in that it allows for overlap of individuals between studies and is computationally fast. In fact, even in situations when individual-level data is available, LDSC might be preferable due to computational feasibility. However, LDSC is less precise than GREML analysis and requires that the external LD reference panel matches the study population[14]. Genetic correlation analyses assume each of the traits under study has a genetic component, so traits with no convincing evidence that $h_g^2>0$ should not be included in these analyses.

Both GREML and LDSC are more powerful when the true genetic architecture across traits is polygenic with many causal SNPs of low effect. In contrast, if the genetic architecture is driven by a few SNPs with large effects, it can be more efficient to only analyze those. It is important to note that a negligible genome-wide genetic correlation does not necessarily negate local genetic correlations between two traits. This might happen if the genetic correlation between two traits is positive in some regions of the genome but negative in others. Thus, it might be of interest to complement any genome-wide genetic correlation studies with local genetic correlation analyses to obtain a more in-depth understanding of the genetic overlap between two traits. Local genetic correlations can be estimated using ρ-HESS, which relies on GWAS summary statistics and an external LD panel[15]. In contrast to LDSC, ρ-HESS requires information about any phenotypic correlation and sample overlap between two traits, which can be estimated by LDSC. For a more in-depth review of genetic correlation studies, please see van Rheenen et al. [16].

Genetic correlations can be difficult to interpret, as they can be consistent with several different causal structures (Figure 1). As an example, assume that we observe a genetic correlation between traits Y₁ and Y₂. The observed genetic correlation could either be due to a causal relationship between Y₁ and Y₂ (Figure 1a), but could also be due to their shared association with an (un)observed risk factor X which is also associated with G (Figure 1b). For example, the observed genetic correlation (r_g=0.57) [3] between lung (LC) and head neck cancer (HNC) likely reflects (at least partially) the underlying genetic association with smoking HNC ← G_smoking → LC. Another example is the observed genetic correlation between HDL and CAD which may be mediated by triglycerides (T): HDL←G→T→CAD. In this case, the observed genetic correlation between HDL and CAD does not reflect a causal relationship between HDL and CAD, but rather the pleiotropic effects on G on HDL and T. The genetic correlation between two traits can also be driven by multiple common causes, of which some can have opposite effect on the two outcomes (Figure 1c). In this case, the genome-wide genetic correlation may be negligible since some genetic loci will show positive genetic correlation between Y₁ and Y₂, while some will show negative genetic correlations. Thus, if the genetic correlation analysis was restricted to the loci in either G₁ or G₂ the magnitude could differ from 0. This is a situation where calculating local genetic correlations[15] can be particularly useful, as it would allow for identifying specific loci that are correlated due to individual shared common causes (e.g. X₁, Figure 1c).

Figure 1:

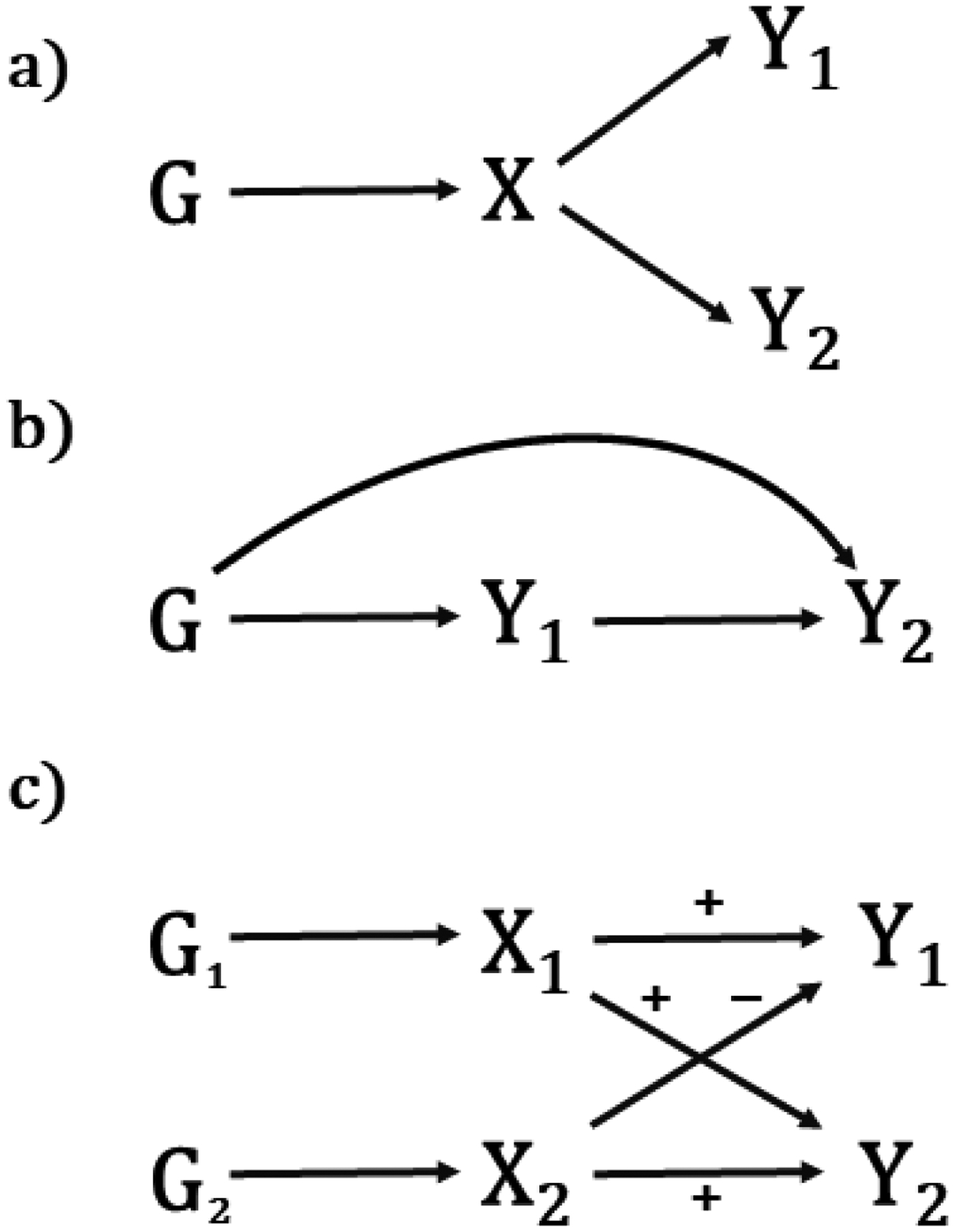
Potential sources of genetic correlation. (a) Traits Y₁ and Y₂ share a common cause X under genetic control. (b) Trait Y₁ causes trait Y₂. (c) Traits Y₁ and Y₂ share two common causes, X₁ and X₂, one of which has the same directions of effect on both traits, the other of which has opposite directions. In this case, the genome-wide genetic correlation may be close to 0, although when restricted to the loci in G₁ or G₂ the magnitude could be away from 0.

MENDELIAN RANDOMIZATION STUDIES

MR studies assume that genotypes are distributed randomly with respect to any confounders between a potential risk factor X and an outcome Y[17]. To assess the causal effect of X on Y, we use genetic variants (G_X) that have been robustly associated with X as a proxy for X (robustly often translates to genome-wide significant). We then test for association between the instrumental variable X_g and Y, where X_g can be described as the “genetically predicted X”. Naturally, the stronger genetic component that X has, the more representative X_G can be. As more SNP-trait associations are identified through GWAS and other large-scale genetic association studies, the instrumental variables that serve as proxies for X are becoming stronger, increasing the statistical power of MR studies. For the primary analysis, we recommend to include only SNPs that have shown association with X on a genome-wide significant level in the target population. Here, “target population” refers to a population similar to the MR study population, where the outcome Y is measured. For example, if the MR study population is of Asian ancestry, we recommend to use SNPs that have been associated with the risk factor X on a genome-wide significant level in an Asian population, or, if Y is assessed in postmenopausal women, we recommend selecting G_x to be SNPs associated with X in postmenopausal women. Choosing genome-wide significant markers helps alleviate “weak instrument bias,” which occurs when the instrument either is not associated with the exposure at all or the instrument-exposure association is measured imprecisely. However, even in the absence of weak instrument bias, genetic instruments are often modestly correlated with exposures: even though we can be confident that the association between the instrument and exposure is not chance sampling error and that we are estimating that association accurately, the correlation can still be small (correlations under 0.3 are common). This has implications for power and the interpretation of non-significant MR tests of exposure-outcome associations, which may reflect limited power rather than absence of a causal effect of exposure on outcome. See [18, 19] for discussions of power calculations for MR studies.

MR studies typically assume a linear model for X_g as a function of SNP genotypes: X_g = ∑_k b_kG_k, where b_k is the per-allele effect of SNP k on X. Although initially proposed in the setting where X and Y are both measured on the same set of subjects, recent studies have taken advantage of the availability of summary statistics from large GWAS of X and Y—the sample sizes from consortia of studies that have measured either X or Y often far exceeds the sample size of studies where both X and Y have been measured[20]. The ratio estimate $(\widehat{\beta })$ of the effect of X on Y using summary statistics on genetic variants k=1,…,K can be calculated as $\widehat{\beta }=\frac{{\sum }_k{b}_k{c}_k{\sigma }_{Y_k}^{-2}}{{\sum }_k{b}_k^2{\sigma }_{Y_k}^{-2}}$ where c_k is the per-allele effect of SNP k on Y, and ${\sigma }_{Y_k}$ is the standard error for c_k. The standard error for $\widehat{\beta }$ is given by: $\text{se}(\widehat{\beta })=\sqrt{\frac{1}{{\sum }_k{x}_k^2{\sigma }_{Y_k}^{-2}}}$. Under certain assumptions as discussed in this section[21], $\widehat{\beta }$ can then be interpreted as the causal effect on Y associated with one unit change in X.

Although MR studies alleviate some shortcomings with observational studies—notably they are robust to unmeasured confounding between X and Y and reverse causation—they come with caveats. In addition to the requirement that there exist robust genetic predictors of X, MR studies also assume that there is no confounding factor that affects both G_x and Y (e.g. population stratification). One of the largest concerns with MR studies in practice is the assumption of no pleiotropy, that is, G_X can only be associated with Y through X and not through any other pathway. As more genetic associations are discovered, widespread pleiotropy (i.e. the same SNP is associated with multiple traits) is becoming more apparent. Thus, the more genetic variants included in an MR study, the higher risk of introducing bias due to pleiotropy. In a situation where G_x is also associated with C, another risk factor for Y, we can no longer assume that G_x affects Y only through its association with X, and thus, one of the fundamental assumptions of MR studies is violated. Since traditional MR approaches rely on the assumption of no pleiotropy, naively applying standard inverse-variance weighted approaches for polygenic traits is subject to bias. For example, a naïve MR analysis of age at menarche and breast cancer risk showed no evidence of association (Odds Ratio (OR) =1.00, 95% Confidence Interval (CI)=0.96–1.05)[22]. However, given the known shared genetic basis between BMI and age at menarche[23], the authors further adjusted their MR analysis for genetically predicted BMI and observed evidence for a causal inverse association between age at menarche and breast cancer (OR=0.94, 95% CI (95% CI: 0.89–0.98). Specifically, the authors reweighted the individual age of menarche SNPs for its effect on BMI rather than age at menarche, thereby controlling for the effect of genetically predicted BMI induced by SNPs associated with age at menarche. Further discussion of the relationship between age at menarche, BMI and breast cancer can be found in Burgess et al. [24].

These results illustrate some of the limitations with MR analysis when multiple correlated factors are associated with the outcome. Many alternative MR approaches have been proposed to tackle pleiotropy, including MR Egger regression[25], multivariable MR analysis[26], the weighted median approach[27], and MR-PRESSO[28] (Table 1). In practice, it is not possible to verify that all assumptions of MR studies are met. Further, each of these alternative approaches come with additional assumptions that are often difficult to verify in practice, and thus the most appropriate method for analyzing the data will be situation-dependent. Therefore, we recommend using a range of MR methods, as consistency in the results across the various methods provides support for a robust finding. Regardless of method(s) used, it is important the investigator recognizes the assumptions made in the analyses, and interpret the results with those assumptions in mind. There are many reviews discussing the pitfalls of MR studies and alternative approaches[29, 30, 21, 17].

Table 1:

Methods to address pleiotropy in MR studies

Method	Description	Advantages	Disadvantages	Reference
MR Egger	Provides unbiased estimates of the true effect even in the presence of pleiotropy.	Does not require the instrumental variables to be valid.	Relies on the InSIDE (INstrument Strength Independent of the Direct Effect) assumption.	[25]
Multivariable MR analysis	Allows for simultaneous assessment of multiple correlated risk factors with a shared genetic basis, such as lipids.	Allows for inclusion of pleiotropic variants when the variants are associated with the risk factors under study.	Subject to the same assumptions as traditional MR analysis, including no pleiotropic associations with any factors that are not considered in the primary analysis.	[26]
Weighted median estimator	Calculates a weighted median of the individual SNP-specific estimates.	Does not rely on the InSIDE assumption.	Requires that at least 50% of the instrument variables are valid.	[27]
MR-PRESSO	Corrects for horizontal pleiotropic effects by removing outliers.	MR-PRESSO can be used in the context of other MR approaches such as MR Egger	Sensitive to the InSIDE assumption. Requires that at least 50% of the instrument variables are valid. Requires simulations, and thus is not as computationally fast as other methods.	[28]

BIAS IN GENETIC CORRELATION AND MR STUDIES

All genetic association studies including genetic correlation and MR studies are subject to collider bias, which can arise if both traits under study are independently associated with a third variable which is controlled for in the analysis, introducing a spurious association between the two traits. Day and colleagues estimated that the extent of collider bias is inversely related to the strength of the association between the exposure and the collider[31]. A specific case of collider bias is selection bias, where, even though genetic variants associated with Y₁ are not associated with Y₂ (and vice versa) in the general population, they are in the sample under study. For example, an MR study of BMI and breast cancer prognosis among breast cancer cases would be subject to collider bias if there are variants associated with both breast cancer incidence and prognosis, but not BMI (in the general population) (Figure 2). Since BMI is associated with breast cancer risk, variants associated with BMI will be correlated with other risk variants among breast cancer cases—violating MR assumptions and potentially inducing a spurious association between BMI and breast cancer prognosis[28]. The impact of selection bias in MR studies is in most cases small, but can be substantial if the selection effects are large[32]. Collider bias has received much attention lately, since it might cause biased effects in large population-based samples such as UK Biobank[33–35]. In particular, the participant rate for UK Biobank was only 5%, and important population characteristics such as smoking, educational attainment and overall mortality differ from the general population. Specifically, UK Biobank participants are less likely to smoke, have higher educational attainment and lower mortality compared to the general population. Thus, due to collider bias we would expect to see upward biased genetic correlations between factors associated with participation in UK Biobank (such as smoking and education attainment). For example, a genetic risk score for BMI was associated with UK Biobank assessment center even after adjusting for 40 principal components[35]. These results could either be due to residual population stratification or collider bias, as both assessment center and BMI are associated with participation in UK Biobank[36]. As these large resources of data are increasingly being used, we urge to consider how representative a study population is of the general population when drawing conclusion and discussing generalizability.

Figure 2:

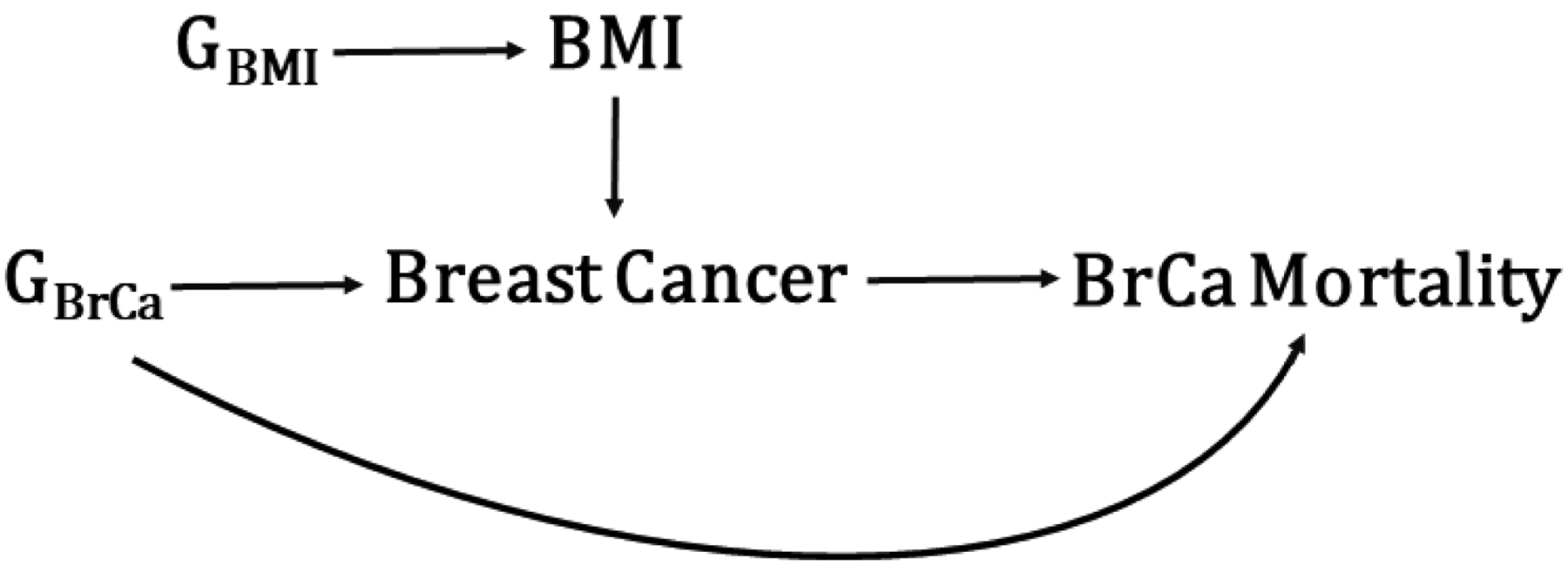
Example of collider bias. An MR study of BMI and breast cancer mortality among breast cancer cases would be subject to collider bias if there are variants associated with both breast cancer incidence and prognosis, but not BMI (in the general population). Since BMI is associated with breast cancer risk, variants associated with BMI (G_BMI) will be correlated with other risk variants (G_BrCa) among breast cancer cases—violating MR assumptions and potentially inducing a spurious association between BMI and breast cancer mortality.

Other potential sources of bias that affect both genetic correlation and MR studies include population stratification, dynastic effects and assortative mating. As with any genetic association study, population stratification needs to be considered by, for example, including principal components in the analytical model[37]. Dynastic effects refer to the fact that any genetic effects on a trait inherited from parent to offspring can be exacerbated by any trait-associated environments that the parents provide the offspring with. Morris et al[38] discusses the example of genetic variants associated with educational attainment. If the parents carry genetic variants positively associated with educational attainment, they might also be more apt to have books in the home, which might further increase the educational attainment for the offspring. Thus, the genetic propensity to high education among the parents will not only be genetically inherited by the offspring, but can also provide an education-stimulating environment. Assortative mating is simply stating the fact that we are more likely to choose a spouse that is similar to ourselves, thus inducing non-random mating patterns in the population. For a more in-depth discussion of these issues, we refer to Morris et al[38].

DIRECTIONAL ANALYSIS

Statistically significant evidence from naive MR analysis does not necessarily implicate that X is causal for Y (G_X→X→Y), but may instead reflect a common shared genetic factor that is not mediated by either of the traits (X←G_x→Y). It is therefore important to also carefully consider alternative causal pathways (e.g. by constructing DAGs) and recognize that any conclusions about causality will be based on the assumptions made by the investigator. Bidirectional MR studies is a tool to assess any assumptions made about the direction of causal relationships. Briefly, in bidirectional MR analysis for two traits, we first assess if SNPs associated with X is also associated with Y and then if SNPs associated with Y are also associated with X. If the former but not latter is true, we have evidence that X causes Y. For example, SNPs associated with BMI have been shown to also be associated with circulation C-reactive protein (CRP) levels, but SNPs associated with circulating CRP levels are not associated with BMI[39]. Based on these results, it is more likely that BMI affects CRP levels than the other way around. An important caveat in bidirectional MR analysis is that the SNPs for X and Y have to be independent of each other in order to receive valid results.

Similarly, a drawback with genome-wide genetic correlation analyses is that they only provide an estimate of the correlation, but give no information about the direction of the correlation (i.e. does X cause Y or does Y cause X?). Recently developed statistical methods have addressed this shortcoming by relying on genome-wide data to identify directional genetic correlations that support either mediated or pleiotropic causal models for pairs of traits[40, 41]. Joseph Pickrell and colleagues developed a statistical framework that uses the correlation between trait-specific effect sizes of genome-wide significant SNPs for pairs of phenotypes[40]. The genome is first divided into independent regions, and given GWAS summary statistics on two traits, they calculate the likelihood for a range of causal and non-causal models within each region. They then assess if SNPs having an effect on X also have an effect of Y and vice versa. As an example, they found that SNPs influencing BMI had correlated effects on triglyceride levels, whereas the reverse was not true, suggesting that increased BMI is a cause for increased triglyceride levels. Using the same approach, they also found that hypothyroidism causes lower stature. We applied this approach on a set of 38 non-cancer traits and 6 solid cancers, with the aim of identifying potential causal relationships[3]. We detected four putative directional genetic correlations where SNPs associated with the non-cancer trait showed correlated effect estimates with cancer but the reverse was not true (circulating HDL concentrations and breast cancer, schizophrenia and breast cancer, age at natural menopause and breast cancer, and lupus and prostate cancer).

The latent causal variable method assumes that there is a latent causal variable (LCV) that mediates the genetic relationship between two traits[41]. The relative strength of the genetic correlation between the LCV and the two traits can help assess if one trait is more likely to be the causing the other. If the LCV is more strongly genetically correlated with X than Y, there is evidence that X is partially genetically causal for Y. Although the underlying mathematical model differs from the method developed by Pickrell and colleagues, the LCV model similarly assesses if SNPs affecting X show correlated effects on Y, and vice versa. The LCV model was used to propose an inverse causal role of LDL on bone mineral density, supported by the observation that statin use increases bone mineral density. These results were subsequently supported in MR studies as well[42].

MULTI-ETHNIC CONSIDERATIONS

Both MR and genetic correlation studies are vulnerable to ancestral heterogeneity and population stratification. To our knowledge, this is an underdeveloped area in terms of methodology. Brown and colleagues[43] developed a Bayesian approach (Popcorn), that estimates genome-wide transethnic genetic correlations between two non-admixed populations, using GWAS summary statistics only. However, we are not aware of any methods that allow for genetic correlation analysis in admixed populations, where LD patterns are more complex. In multi-ethnic MR studies, it is important to assess if the MR assumptions hold. For example, it is not clear if a study of circulating CRP levels and cardiovascular disease in an African-American population can rely on obtaining instrumental variables (SNPs) from CRP association studies conducted in European ancestry individuals.

CONCLUSIONS

Both genetic correlation and MR analyses have provided novel insights into epidemiology studies, both confirming and refuting previous associations from observational studies. Leveraging germline genetics helps us overcome many shortcomings in observational epidemiology and can lend important support for causal inference. As large datasets and results are becoming publicly available (e.g. Biobanks), both genetic correlation and MR analyses are poised to continue to increase in popularity. For example, UK Biobank recently released biomarker data on all 500,000 participants, which will allow for causal assessments of biomarkers (e.g. hormones, vitamin D, IGF-1) and disease. In particular, as more data on potential risk factors for disease become available, genetic correlation and MR studies will be important tools to disentangle correlated risk factors.

MR studies have helped shed light on previously debated observed relationships. In addition to refuting a causal relationship between HDL and CHD[5, 6], it has also helped identify an inverse effect of genetically predicted BMI and both pre- and postmenopausal breast cancer risk [44]. As mentioned earlier, failure to account for horizontal pleiotropy can severely bias the results, as with the case of age at menarche and breast cancer [23]. Yarmolinsky and colleagues conducted a comprehensive MR study of twelve previously suggested risk factors and ovarian cancer histotypes [45]. They also assessed violation of MR assumptions by using five different MR approaches. Their analyses demonstrated inconsistent results across both histotypes and MR approach. The most consistent result was for genetic susceptibility to endometriosis and invasive epithelial ovarian cancer, which was supported by three of the MR approaches. Both naïve and MR-Egger analyses supported an association between BMI and invasive epithelial ovarian cancer, but inconsistency in results across other MR approaches pointed towards violations of the MR assumptions. When stratifying the analysis by ovarian cancer histotypes, they further observed evidence of associations for multiple risk factors across histotypes, and these results were often supported across MR approaches. This study showcases the importance of applying multiple MR approaches to identify any evidence of assumption violation, as well as the importance of considering etiological heterogeneity across disease subtypes.

Both MR and genetic correlation studies have their merits. Genetic correlation analysis quantifies the correlation in alleles effects across the entire genome and is particularly powerful when the underlying genetic architecture is polygenic with multiple causal variants, all with small effect. In addition, novel methods for estimating local genetic correlations, can give insights into specific regions in the genome that contributes disproportionally to a shared genetic basis. MR studies can provide information about direction of association. Development of new statistical methodology for MR studies, in particular novel methods that are less sensitive to the classical MR assumptions, is a very active field of research. Indeed, multiple alternative approaches that is robust to one or several assumptions have already been developed. Further, MR studies only requires genetic data on a limited set of SNPs rather than genome-wide genotype data.

In general, methods for MR analyses have been more developed than for genetic correlation analyses. We expect that developing novel methods relating to both MR and genetic correlation analyses will be a highly active area of research over the next few years. Here, we discussed two recently proposed methods that build on MR and genetic correlation analyses to assess causality[40, 41]. An important area for improvement is research on how to apply MR and genetic correlation studies on multi-ethnic populations, in particular for admixed populations which exhibit long-range LD, where current genome-wide genetic correlation analysis can create bias. A recent study highlighted the health disparity associated with implementing polygenic risk scores (PRS) developed in a specific ancestral population into clinical practice, as in general, PRS perform poorly across ancestries[46]. The unambiguously most important factor to overcome this is to shift the focus on genetic discovery from European-ancestry populations to other ethnicities. In addition, efforts towards developing novel methods that assess genetic correlations and causal relationships across ancestries will help us understand to which extent we can leverage genetic findings across ancestral populations.

In conclusion, genome-wide genetic correlation and MR studies have made important contributions to further understand relationships between complex traits. However, both approaches are sensitive to confounding which, if ignored, can lead to biased results. Further, both approaches are notoriously data hungry, requiring large datasets. We believe that as large genetic and outcome datasets (e.g. Biobanks) are made publicly available, and as statistical methodology is being further developed, these studies will play a central role in genetic epidemiology.