Agreement of two pre-trained deep-learning neural networks built with transfer learning with six pathologists on 6000 patches of prostate cancer from Gleason2019 Challenge

Abstract

Introduction: While the visual inspection of histopathology images by expert pathologists remains the golden standard method for grading of prostate cancer the quest for developing automated algorithms for the job is set and deep-learning techniques have emerged on top of other approaches. Methods: Two pre-trained deep-learning networks, obtained with transfer learning from two general purpose classification networks – AlexNet and GoogleNet, originally trained on a proprietary dataset of prostate cancer were used to classify 6000 cropped images from Gleason2019 Challenge. Results: The average agreement between the two networks and the six pathologists was found to be substantial for AlexNet and moderate for GoogleNet. When tested against the majority vote of the six pathologists the agreement was perfect and moderate for AlexNet, and GoogleNet, respectively. Despite our expectations, the average inter-pathologist agreement was moderate, while between the two networks it was substantial. Resulted accuracy for AlexNet and GoogleNet when tested against the majority vote as ground truth was of 85.51% and 74.75%, respectively. This result was higher than the score obtained on the dataset that they were trained on, showing their generalization capabilities. Conclusions: Both the agreement and the accuracy indicate a better performance of AlexNet over GoogleNet, making it suitable for clinical deployment thus could potentially contribute to faster, more accurate and with higher reproducibility prostate cancer diagnosis.

⧉ Introduction

Prostate cancer is a leading cause of morbidity and mortality for men [1]. Prostate cancer treatment is based on the visual assessment of prostate biopsies by pathologists [2], which could be considered as an imperfect diagnostic tool.

There have been many attempts to stratify the prostate cancer outcome based on the morphological aspect; however, only two of them emerged – the Gleason grading system (GGS), and Srigley grading system (SGS). Even though we have discussed different advantages of the SGS [3], the GGS remains the most commonly used and widely accepted option.

Together with more recent revisions [4,5], the GGS [6] (initially published in 1966) stratifies prostate cancers based on architectural patterns as their biological reflection. The system classifies prostate cancer growth patterns in five classes. The final GGS score is computed as the sum of the two most commonly classes and ranges between two and 10.

In theory, the GGS describes five classes and subclasses. Classes 1 and 2 generally present a good prognostic and are not considered in this study. The other three classes are briefly described as follows [6,7,8,9].

The moderate differentiation class is pattern 3, and originally had three subclasses. The aspect of subtype 3A includes isolated glands of medium size, with a variable shape, consisting of elongations, twists and angles that can also have sharp angles. Subtype 3B is described similar, but with smaller tumor glands. The last subtype – 3C – is described as ducts or ducts expanded with sieve or intra-luminal papillary tumor masses.

The poorly differentiated high-grade proliferation class is pattern 4 and includes two subclasses. The tumor proliferation in subtype 4A is composed of cells that may have either a fused microacinar arrangement or a cribriform or a papillary one. Specifically, tumor cells form either infiltrative masses with a totally irregular appearance or strings or cords of epithelial malignant cells. Subtype 4B is described similar, this time the malignant cells have a clear cytoplasm.

The weakest differentiated class is pattern 5, and it also includes two subclasses. The aspects seen in subtype 5A are similar to the “comedo”-type of intraductal breast carcinoma, they are tumor masses in which the cells have a chordal or cylindrical arrangement, with a cribriform, papillary appearance (very similar with subtype 3C) or solid, with smooth, rounded edges, whose central area is typically occupied by necrotic detritus. Anaplastic tumor cells that distribute in tumoral areas with irregular edges describe subtype 5B.

The recent revisions redistributed some aspects from the original system. Thus, pattern 3 remained with only two subtypes mainly (original 3A and 3B). Pattern 4 included cribriform glands larger than benign glands and with an irregular border, finally consisting of poorly formed glands of either cribriform or fused architecture [4,5].

A common problem of the GGS is the inter-observer and intra-observer variability, as the reported discordance show as much as 30% to 53% [10,11,12,13,14,15,16], and with poor differences between classes in feature extraction algorithms [17,18,19]. Different studies show that pathologists that routinely interpret urology slides have higher rates of inter-observer agreement than general ones, while the diagnosis from more experience pathologists show a more accurate class assessment [15]. Despite its limitations, GGS remains the most widely used system in standardized patient management [20].

Because using the GSS is a demanding task and, at the same time, the output shows a high variability, the development of automated systems for assessing tumoral architecture rapidly emerged. Different techniques have been proposed, ranging from simple morphological architecture descriptors [21] to neural networks [22] and deep-learning (DL) techniques [23], the later showing the best performance.

Aim

This paper describes the behavior of two DL algorithms, obtained with transfer learning from general purpose deep-learning (neural) networks (DLNs) on a private dataset, assessed on a public dataset of GGS classified images of prostate cancer labeled by six different pathologists.

⧉ Materials and Methods

Deep-learning classification system

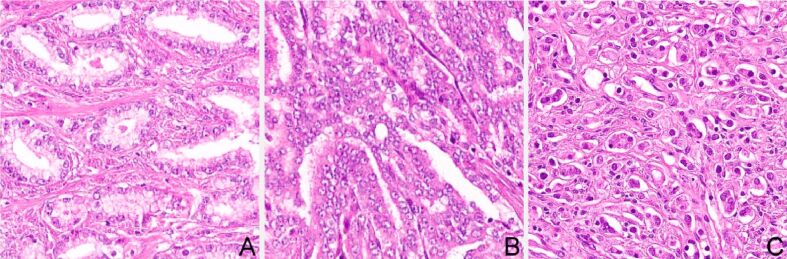
Two DLNs were imported from previous work [24]. The two algorithms used transfer learning from two well-known DL pre-trained networks AlexNet [25] and GoogleNet [26]. A total of 439 Hematoxylin–Eosin (HE) images were classified according to GGS, as follows: Gleason pattern 2 (n=57), Gleason pattern 3 (n=166), Gleason pattern 4 (n=182), and Gleason pattern 5 (n=34). The dataset had no image with pattern 1. The images, 32-bit red, green, blue (RGB) color space, were cropped at 512×512 pixels from whole slide images scanned with Leica Aperio AT2, using a 20× apochromatic objective. The two pre-trained networks were imported with their structural layers together with their weights obtained on the described dataset. Samples of the original dataset are presented in Figure 1.

Figure 1.

Training dataset sample: (A) Gleason pattern 3; (B) Gleason pattern 4; (C) Gleason pattern 5. Hematoxylin–Eosin (HE) staining: (A–C) ×200

Datasets

The dataset used for the classification task was extracted from the Gleason2019 Grand Challenge [27]. The challenge originally aimed at the automatic Gleason grading of prostate cancer from HE-stained histopathology images. The data consisted in a set of tissue micro-array (TMA) images. Each TMA image was annotated in detail by six expert pathologists (named P1 to P6).

The original challenge had two tasks: pixel-level Gleason grade prediction and core-level Gleason score prediction with two leading objectives: (i) establish a benchmark for assessing and comparing the state-of-the-art image analysis and machine learning-based algorithms for this challenging task and (ii) evaluate the accuracy and robustness of these computerized methods against the opinion of multiple human experts [28].

Methodology

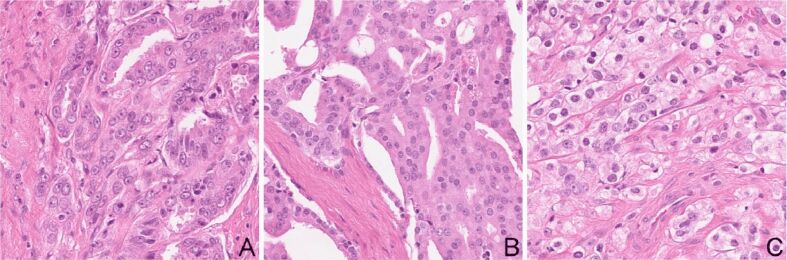
A cropping algorithm was developed that cropped patches of 1000×1000 pixels from the TMA images from the dataset. The size of the crop was established so that it fits the size of the images in the original dataset that the DLNs were trained on. The algorithm scanned each TMA image with a window of 1000×1000 pixels and the resulted images was saved only if one of the pathologists labeled it with a unique pattern. Labels from each of the six pathologists were logged. Two thousand images were randomly selected from patterns 3, 4, and 5. Samples of each pattern can be seen in Figure 2.

Figure 2.

Testing dataset sample: (A) Gleason pattern 3; (B) Gleason pattern 4; (C) Gleason pattern 5 equivalent. HE staining: (A–C) ×200

Next each of the obtained image was resized to 227×227 and 224×224 pixels to match the input layer of the AlexNet and GoogleNet, respectively.

In the end, each of the 6000 images labeled by at least one of the pathologists as Gleason pattern 3 (n=2000), Gleason pattern 4 (n=2000), and Gleason pattern 5 (n=2000) were labeled by the two pre-trained networks. The results were logged for statistical analysis.

Statistical analysis

In order to measure the inter-rater reliability Cohen’s kappa coefficient (κ) [29] was used. Cohen’s kappa coefficient (κ) is a statistic designed for categorical items, meant to be a more robust measure than the simple percent agreement as it takes into account the possibility of the agreement occurring by chance. P-value for kappa is not reported, because even relatively low values of kappa can nonetheless be significantly different from zero [30], but irrelevant to its meaning.

Magnitude guidelines for kappa coefficient have been set, however they are not universally accepted. A common interpretation [31] characterize values <0 as indicating no agreement and 0–0.20 as slight, 0.21–0.40 as fair, 0.41–0.60 as moderate, 0.61–0.80 as substantial, and 0.81–1 as almost perfect agreement. Other studies [32] characterize kappas over 0.75 as excellent, 0.40 to 0.75 as fair to good, and less than 0.40 as poor. There is no evidence to support any interpretation other than intuition and common sense. For interpretation, we have used the stratification proposed by Landis & Koch [31].

For each image, the majority vote was established as the class with the most votes (mode) from the six pathologists. As recommended by the Gleason2019 Grand Challenge organizers [28], this could stand as a ground truth, but there is no objective reason for this consideration.

The classification accuracy of the two DLNs was assessed against the majority vote seen as ground truth.

⧉ Results

The two DLNs successfully provided labels for each of the 6000 images.

Cohen’s kappa coefficient (κ) results between each of the six pathologists are presented in Table 1, between each of the two DLNs and the six pathologists are presented in Table 2, and between the two DLNs in Table 3.

Table 1.

Cohen’s kappa coefficient (κ) between the pathologists (P1 to P6)

	P1	P2	P3	P4	P5	P6
P1	1	0.2285	0.5959	0.3679	0.8090	0.4758
P2	0.2285	1	0.2804	0.1636	0.2713	0.2532
P3	0.5959	0.2804	1	0.7229	0.7692	0.2893
P4	0.3679	0.1636	0.7229	1	0.5087	0.0724
P5	0.8090	0.2713	0.7692	0.5087	1	0.4515
P6	0.4758	0.2532	0.2893	0.0724	0.4515	1

Table 2.

Cohen’s kappa coefficient (κ) between the pathologists (P1 to P6) and the DLNs

	P1	P2	P3	P4	P5	P6
AlexNet	0.9220	0.2480	0.6630	0.4207	0.8818	0.5295
GoogleNet	0.7741	0.2050	0.4005	0.2208	0.5876	0.3638

DLNs: Deep-learning networks

Table 3.

Cohen’s kappa coefficient (κ) between the DLNs

	GoogleNet
AlexNet	0.7109

DLNs: Deep-learning networks

Resulted Cohen’s kappa coefficient (κ) between the majority vote against the six pathologists are presented in Table 4, while against the two DLNs in Table 5. Mean and standard deviation (SD) of Cohen’s kappa coefficient between the six pathologists was 0.42±0.22, while Cohen’s kappa coefficient (κ) between the two networks was 0.7109.

Table 4.

Cohen’s kappa coefficient (κ) between the pathologists (P1 to P6) and the majority vote

	P1	P2	P3	P4	P5	P6
Majority vote	0.7652	0.3169	0.8207	0.5524	0.9166	0.4153

Table 5.

Cohen’s kappa coefficient (κ) between the DLNs and the majority vote

	AlexNet	GoogleNet
Majority vote	0.8355	0.5561

DLNs: Deep-learning networks

Mean and SD pathologists’ agreement coefficient was 0.42±0.23, this being interpreted as moderate, and raging between slight and substantial. Individual agreements classes between each of the six pathologists were interpreted as slight (n=2), fair (n=6), moderate (n=4), substantial (n=2), perfect (n=1). Note that pathologists P1 and P5 had a perfect agreement, and P3 and P5 together with P3 and P4 had a substantial agreement. This will later influence the majority vote, and individual agreement with it.

Mean and SD agreement coefficient between the two DLNs and the six pathologists were 0.61±0.26 and 0.43±0.22 for AlexNet and GoogleNet, respectively. AlexNet individual agreement classes were interpreted as substantial, ranging from fair to perfect, with individual agreements classes fair (n=1), moderate (n=2), substantial (n=1), and perfect (n=2). GoogleNet individual agreement classes were interpreted as moderate, ranging from fair to substantial, with individual agreements classes fair (n=4), moderate (n=1), and substantial (n=1).

The agreement coefficient between the two DLNs was 0.71 and it was interpreted as substantial.

Mean and SD agreement coefficient between the six pathologists and the majority of their vote was 0.63±0.24, this being interpreted as substantial and ranging between fair and perfect. Individual agreements classes between the six pathologists and the majority vote were interpreted as fair (n=1), moderate (n=2), substantial (n=1), perfect (n=2).

Note that even if pathologists P1 and P5 had a perfect one on one agreement when compared to the majority vote, P1 dropped a class and the agreement become substantial with the group, while P3 ascended a class form substantial to perfect, while P5 kept his perfect agreement. This shows that no matter the experience or expertise when tested against a majority vote the individual has no advantage. Also note that AlexNet and P1 had an agreement coefficient of 0.9220 (perfect), and since AlexNet was trained on the expertise of a two specialized uropathologists, if, and only if the network generalized correctly, the most experienced pathologist was P1.

Mean agreement coefficient between the two DLNs and the majority vote were 0.8355 and 0.5561 for AlexNet and GoogleNet, respectively. They were interpreted as perfect and moderate.

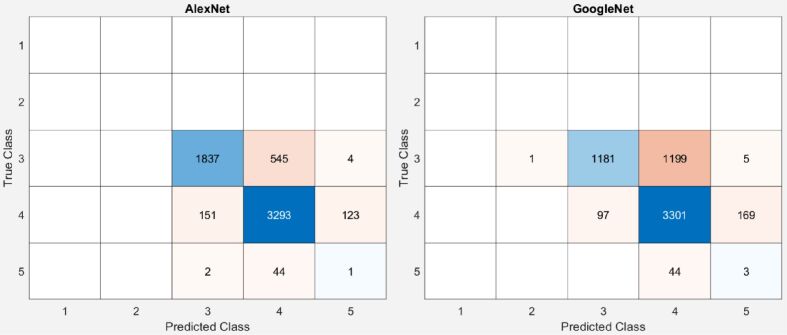
More than that, as resulted from the GGS patterns described in the introduction, there is similitude between the subclasses. However, the similitude from 4A and 4B could not affect our class estimation the ones between 5A and 3C could. As resulted from Figure 3, both networks mainly misclassified pattern 5 as 4, only AlexNet misclassified two images of pattern 5 as pattern 3, once again leading us to the assumption that the unbalanced training dataset is the origin of the misclassification.

Figure 3.

Confusion Gleason Grading System (GGS) matrices of AlexNet and GoogleNet. True Class is set as the majority vote of the six pathologists

Both networks had their best agreement with P1, this stating, once again that P1 had the most experience or similar with the pathologists that labeled the training dataset.

Resulted accuracy for AlexNet and GoogleNet when tested against the majority vote as ground truth was 85.51% and 74.75%, respectively. The resulted confusion matrices are presented in Figure 3.

⧉ Discussions

Previously developed DLNs were used to label crops of prostate TMA images using GGS and their result were compared to the results from six pathologists.

The two DLNs behaved differently, though they were trained on the same dataset, AlexNet outperformed GoogleNet. Even on the original dataset AlexNet outperformed GoogleNet [20], with an accuracy of 61.17% versus 60.9%. From the multiple aspects that could make this difference possible two of them stand out as evidence: the larger size and simpler architecture of AlexNet and the larger input layer size. AlexNet has a depth of only eight layers, while GoogleNet has 22. AlexNet has 61 million parameters, while GoogleNet has only seven. It seems that AlexNet generalized better. Let us note that the networks perform better on the current dataset. Taking in consideration the class distribution and the confusion matrices (Figure 3), this could just be a matter of an unbalanced dataset.

As presented by Tolkach et al. (2020) [23], the optimal minimal dimension of tumors for representative grading is 560×560 μm, and their images were cropped to 600×600 pixels having about 150 μm, acquired using a 20× magnification, which makes our 1000×1000 pixels size image larger than the required minimum, thus optimal for its use.

In a similar designed study [33], on the external test dataset, the designed system obtained a high agreement with the reference standard set independently by two pathologists (quadratic Cohen’s kappa 0.723 and 0.707) and within inter-observer variability (kappa 0.71). Their system was trained on much larger dataset, and obtained very good results on Gleason pattern 5, unlike ours.

For assigning Gleason grades, another similar DL system [34] achieved a mean pairwise kappa of 0.62, which was within the range of the corresponding values for the expert pathologists (0.60–0.73). Again, the training and testing datasets were much larger, the grading was done following the International Society of Urological Pathology (ISUP) [5]. From the confusion matrices presented, we note that ISUP grade 5 (last) had a lower accuracy, similar to our study where Gleason pattern 5 (last) had the lowest accuracy, and probably related to the naturally unbalanced training dataset.

With automated Gleason grading and Gleason pattern region segmentation tasks, the reported inter-annotator agreements between the model and the pathologists from another study [35], also quantified using Cohen’s quadratic kappa statistic, was 0.77 on average. This time, the study uses the GGS patterns which are combined to give scores, but the main focus of the study was set on the segmentation task, rather than on the classification task.

A very similar approach to ours was presented in another paper [36], but instead of using histologically stained images, the research uses magnetic resonance imaging (MRI) pictures. The pre-trained GoogleNet network was used, and the reported accuracy for the simple task of stating if a prostate contains or not malignant tissue reported accuracy was 100%. This shows, once again, the robustness of transfer learning.

Trained on 112 million pathologist-annotated image patches from 1226 slides, and evaluated on a different dataset of 331 slides, another DL algorithm reported good accuracy [37]. No agreement was computed, but compared to a reference standard provided by genitourinary pathology experts, the mean accuracy among 29 general pathologists was 0.61% on the validation set, while the proposed DL technique had a significantly higher diagnostic accuracy of 0.70%. The reported accuracy is much smaller than the one obtained by AlexNet on our dataset and higher than the one obtained by GoogleNet.

Using a small and unbalanced dataset, like the one used in our training dataset, another report [38] stated that automated grade groups determination method agreement with a genitourinary pathologist was substantial (κ=0.70), but this refers to the overall sample. Inter-class differentiation accuracy was reported as over 90%.

A model [39] trained and tested on the same image dataset from where we have extracted our testing dataset that used DeepLabV3+ [40], with a pre-trained MobileNetV2 [41] and Adam optimizer [42], reported a kappa score of 0.56, with the pathologists’ annotations on the test subset which was higher than the one found between the pathologists (0.55). The smaller agreement compared to our method could result from the smaller patch size of 512×512 pixels that they had used, and by the fact they had reported on all the dataset instead of reporting on randomly selected images.

Study limitations

This study has limitations. First, there is no ground truth. Though the GGS has specific morphological description for each of the patterns, there is no superior way of assessing the pattern score, other than the pathologists’ visual assessment. Second, there is only one training and one testing dataset. More than that the training dataset is private. Third, though both datasets are stained using HE technique, there is no way of quantifying the quality and quantity of the staining process. This drawback could be overcome with a color stain normalization technique, as previously proposed [43]. Fourth, additional aspects, such as non-adenocarcinoma variants, other GGS classes or benign prostate tissue were not taken in consideration.

⧉ Conclusions

Mean and SD of Cohen’s kappa coefficient between the two DLNs and the six pathologists that labeled the images was 0.61±0.42 and 0.43±0.22 for AlexNet and GoogleNet, respectively, while when tested against the majority vote Cohen’s kappa coefficient was 0.8355 and 0.5561 for the two networks. Results are promising, and the pre-trained networks show better inter-observability variation than human pathologists, making the better-performer – AlexNet – suitable for clinical deployment, and thus could potentially contribute to faster, more accurate and with higher reproducibility prostate cancer diagnosis.

Conflict of interests

The authors declare that they have no conflict of interests.