Fairy circles reveal the resilience of self-organized salt marshes

Self-organized fairy circles reveal the resilience of emerging salt marsh ecosystems.

Abstract

Spatial patterning is a fascinating theme in both theoretical and experimental ecology. It reveals resilience and stability to withstand external disturbances and environmental stresses. However, existing studies mainly focus on well-developed persistent patterns rather than transient patterns in self-organizing ecosystems. Here, combining models and experimental evidence, we show that transient fairy circle patterns in intertidal salt marshes can both infer the underlying ecological mechanisms and provide a measure of resilience. The models based on sulfide accumulation and nutrient depletion mechanisms reproduced the field-observed fairy circles, providing a generalized perspective on the emergence of transient patterns in salt marsh ecosystems. Field experiments showed that nitrogen fertilization mitigates depletion stress and shifts plant growth from negative to positive in the center of patches. Hence, nutrient depletion plays an overriding role, as only this process can explain the concentric rings. Our findings imply that the emergence of transient patterns can identify the ecological processes underlying pattern formation and the factors determining the ecological resilience of salt marsh ecosystems.

INTRODUCTION

Spatial self-organized patterns are widespread across many ecosystems, such as arid ecosystems (1–3), mussel beds (4–6), freshwater and salt marshes (7–9), coral reefs (10), peatlands (11), and sorted patterned grounds (12). Both experiments and theoretical models have highlighted that these self-organizing patterns can reveal the underlying mechanisms driving ecosystem resilience (3). Spatial patterns were proposed as an indicator for ecological resilience that could function as a general first warning for impending regime shifts, as well as could be potentially useful to infer environmental changes for many ecosystems (2, 13–15). So far, regular patterns have been attributed to scale-dependent alternation between facilitation and inhibitory interactions, also called scale-dependent feedbacks (10). These processes lead to persistent and stable regular patterns, despite the ecosystems occurring outside of thermodynamic equilibrium (3, 16, 17). Hitherto, less attention has been devoted to ecosystem patterns that have not yet reached a persistent pattern state, hereafter called transient patterns. Understanding system behavior away from persistent patterns may yield a more realistic interpretation of such “young” or inherently less stable system dynamics (18, 19). Transient dynamics can be universal in nature, as was found in, for example, crescent-like patches of Asphodelus ramosus observed in the northern Negev, in both nonspatially and spatially dynamic systems (18, 20–22). Hence, interpretation of transient patterns in the context of self-organized ecosystems may be very effective in identifying the underlying mechanisms of pattern formation and in assessing environmental stresses.

Self-organization theory has successfully helped us to understand the mechanisms underlying spotted, striped, and labyrinth patterns, starting with the seminal work of Alan Turing (16, 17, 23, 24). Recently, fairy circles or other ring-type patterns (hereafter FCs) resulting from spatial self-organization have attracted much attention in Australian and Namibian dryland ecosystems (3, 25–28), as well as seagrass and dryland ecosystems (29, 30) (see a summary in Table 1 for more details). However, there is still substantial debate about what ecological processes trigger these observed circles. Using a multiscale hybrid model, it was shown that these marked FC patterns could be attributed to subterranean termites (3, 28). However, other studies highlight that positive feedback between biomass and water can also be used to reproduce this FC pattern, without the need to include termite activity (27, 30, 31). Although both theoretical and empirical studies have, to a certain extent, addressed stable FCs, the functioning and underlying mechanisms of these unique FC patterns have remained elusive. It is clear that progress in this field requires a better link between observed patterns and underlying processes in these diverse ecosystems to elucidate the underlying mechanisms governing FC patterns in ecology (3, 28, 32). Here, we address this problem using large-scale FC-like patterns that are newly found in Chinese coastal salt marshes (but are also found in other coastal salt marshes worldwide; fig. S1), which may provide a unique opportunity to explore the mechanisms underlying FC patterns.

Table 1. Studies reporting spatiotemporal behaviors and ecological processes of FCs in the different ecosystems.

Transience is in contrast to the persistent Turing-like patterning that is persistent with a characteristic spatial scale, whereas FCs in salt marshes quickly disappear and become a spatial homogeneous vegetation state. NMR, no mechanism reported there.

Ecosystems	Saptiotemporal behaviors*	Mechanisms	Ecological processes	Repulsion/collision	Source
Salt marshes	Transient; irregular or random	Damping waves	Nutrient depletion on the inner side of the rings	Collision between FCs	This study
	Transient; irregular or random	Fast-slow dynamics	Sulfide inhibition	Collision between FCs	This study
	Transient; irregular or random	NMR	Sediment deposition at edges, an irregularly flooded	–	(37, 62)
Seagrass meadow	Irregular or random	NMR	Toxic sulfide accumulating on the inner side of the rings	–	(44)
	Persistent; irregular	Turing principle	Demographic imbalances with facilitative and competitive interactions	Repulsion between FCs	(29)
Namibia	Persistent; regular or random	Turing principle	Termite-vegetation interaction or strong interaction between plants	Repulsion between FCs	(25, 27, 28, 31)
Dryland vegetation	Persistent; regular	Turing principle	Overland water flow is intercepted at a patch periphery and plants with large lateral expand	Repulsion between FCs	(30)

*The terms regular, irregular, or random refer to the landscapes of individuals’ FCs in the two-dimensional space.

In salt marsh pioneer zones, a multitude of patterns can occur simultaneously, including spots, rings, and concentric ring patterns (see Fig. 1 and figs. S1 and S2 for global distribution). To gain an understanding of intertidal salt marsh FCs, where the patterns display remarkable transient dynamic behavior, we combined field data, process-based mathematical modeling, and drone images and assessed the ecosystem resilience and stability with theoretical models. We observed a development of spatial patterns changing from spots to ring-type patterns (Fig. 1, E and F), from rings to concentric circles (fig. S4, A and B), and ultimately to a homogeneous vegetation as a succession of transient pattern, a phenomenon that has received limited attention in the field of spatial self-organization (1–4, 33, 34). In this study, we ask (i) how transient patterns can be used to infer distinctive ecological processes, and (ii) whether transient patterns better reflect the relationship between pattern and process, to elucidate which specific ecological feedback triggers the observed patterns. We report that inspecting the transient spatiotemporal behaviors of the vegetation patterns in a salt marsh ecosystem (dominated by Scirpus mariqueter) in China revealed that both nutrient depletion and sulfide accumulation and toxicity are likely factors limiting vegetation development in intertidal salt marshes along the Chinese coastline (Fig. 1 and figs. S1 and S2). We also present two simple mathematical models of clonal plant growth that yield self-organized FC patterns consistent with the observed spatiotemporal behaviors. These transient FCs reveal high ecosystem resilience in terms of its ability to reach or return to a vegetated state following disturbances due to the global attraction. In contrast, persistent Turing-like FCs may indicate the presence of alternative stable states and a possible collapse to a degraded state once a tipping point is approached.

Fig. 1. Widespread spatial distributions of FC patterns and the typical spatiotemporal dynamics in intertidal salt marshes of the Chinese coast.

(A) South of Hangzhou Bay, coexistence of spots, and FC patterns in S. alterniflora. (B) Yangtze Estuary North Branch, spots, and FCs in S. alterniflora in April 2017. (C) CDNR, FCs in S. mariqueter in October 2018. (D) Nanhui shoal of Shanghai, coexistence of spots, FCs, and concentric rings in S. mariqueter in July 2018. (E) Temporal evolution of representative FC patterns within an annual cycle. Drone images of FC patterns for S. mariqueter in Nanhui shoal, Shanghai (30°59′50.99″N, 121°56′33.29″E). (F) Drone images in May and September 2019 showing transition from spot to FC patterns. (G) Two main hypotheses and corresponding mathematical models explaining the observed FC patterns in the salt marsh ecosystems. Model I describes a fast-slow system between plants and hydrogen sulfide (H₂S) that could function as an inhibitor to plant growth. Model II represents the nutrient depletion hypothesis when high densities of plants appear at the center of patches. The models are described mathematically in the right panels (see Materials and Methods and table S1 for more detailed definitions of the variables and parameters in the models). Photo credit: Li-Xia Zhao (A to D) and Quan-Xing Liu (E and F).

Observed patterns, hypotheses, and mathematical models

Coastal salt marshes display three types of spatial patterns: spots, ring patterns, and concentric rings (see Fig. 1, A to D, and figs. S1 and S2). We have studied the temporal dynamics of these salt marsh rings with the use of drones. Our observation highlighted that in contrast to persistent Turing-like patterns, in which patches repel each other, the ring patterns revealed clear merging behavior even within one growing season (Fig. 1E and figs. S2 and S6). This previously unidentified merging feature also clearly distinguished these spatial patterns from previously reported FC patterns that similarly result from a Turing process [also called scale-dependent feedback (3, 26–29)]. Also, FCs in this salt marsh ecosystem display concentric rings that have not been reported in other types of ecosystems (Fig. 1F and fig. S4). While FCs have been studied in specific seagrass systems in the context of self-organization theory [see (29), where spots were also called FCs], they have not yet been considered in a more general framework, comparing persistent with transient patterns.

Using mathematical models, we investigate whether nutrient depletion and sulfide toxicity were potential mechanisms explaining transient FC formation, and how they influenced ecosystem resilience (see Materials and Methods for more details). On intertidal mudflats, plants can trap suspended particles and stabilize sediments, thereby facilitating their own growth. However, this positive feedback also results in a negative feedback as organic matter accumulates in the sediment. Anaerobic decomposition involving sulfate-reducing bacteria yields toxic sulfides (35–37) that lead to plant die-off if sulfide accumulation is high enough. Hence, the plant-sulfide feedback framework describes a mechanism whereby sulfide concentrations increase from a process beneficial to plants but form a negative feedback to plant growth (Fig. 1G, H1—Model I). However, competition for nutrients among plants and resulting nutrient depletion provide a second mechanism that could trigger the die-off/degradation of plants at the center and the emergence of FCs. The edges of patches continue to expand outward into bare sediments, but their growth is limited inside the circles by depletion of nutrients (Fig. 1G, H2—Model II). It is noteworthy that in salt marsh ecosystems, these two feedbacks are potentially complementary to each other. We suggest that sulfide accumulation could potentially play a more important role in mudflats than in sandy salt marshes. We use dynamic models I and II, which mathematically coupled to these two hypotheses, respectively, to explore associated spatiotemporal behaviors. For detailed definitions of the variables and parameters in the models (Fig. 1G, right), see table S1 and Materials and Methods.

RESULTS

Two potential mechanisms for FC patterns

To investigate these hypotheses, we collected sediment and plant biomass samples from FC patches of the native species S. mariqueter (hereafter Scirpus) and the invasive species Spartina alterniflora (hereafter Spartina) on the intertidal mudflats at Chongming Island, Shanghai. With respect to the sediment samples, the explanatory variables we used to account for plant biomass include four physical variables [elevation, salinity, water content (wet), and clay], a chemical variable (sulfide), two nutrient variables [dissolved organic carbon (DOC) and ${\text{NH}}_4^{+}$], and an environmental variable (wet as a reflection of moisture level). We compared the in situ differences among these physical, chemical, and nutrient variables at different locations within FCs following the radial direction (named as center, on-ring, and outer bare flats; Fig. 2A). Note that we also named the boundary edges of spotted patterns as on-ring for consistency. All variables revealed relatively homogeneous levels (and detailed concentrations in fig. S7), independent of the specific location variables relative to the FC patterns, but two of these seven variables clearly varied over space: ammonium and sulfide concentration (${\text{NH}}_4^{+}$, F_2,5 = 13.58, P < 0.01; sulfide, F_2,12 = 7.34, P < 0.01; Fig. 2, B and C). Because the locations of the center, on-ring, and outer bare flats represent post-establishment, mid-establishment, and pre-establishment phases of plants, respectively, negative values imply a negative effect on plant growth (Fig. 2D). For FC patterns, soil nitrogen was found to be significantly lower in the degrading center of patches (Tukey post hoc test, P < 0.01, n = 3; Fig. 2, C and D), whereas sulfide levels were significantly higher in the center (Tukey post hoc test, P < 0.01, n = 6; Fig. 2, B to D). This evidence was further supported by correspondence analysis. The first and second axes of the correspondence analysis plot explained 79.4 and 20.6% of the variation, respectively (fig. S3). Relative abundance of ammonium was negatively correlated with the on-ring location but positively correlated with center and outer locations. Sulfide concentrations were positively correlated with the on-ring and outer locations but negatively correlated with the center location. Therefore, the field survey strongly supports our hypotheses of the pattern-forming mechanisms, i.e., both plant-sulfide and plant-nutrient feedbacks are operating simultaneously and in conjunction in our sedimentation-governed salt marshes.

Fig. 2. In situ field measurements and salt marsh grass transplantations used to test the potential mechanisms that trigger FC pattern formation in salt marsh ecosystems.

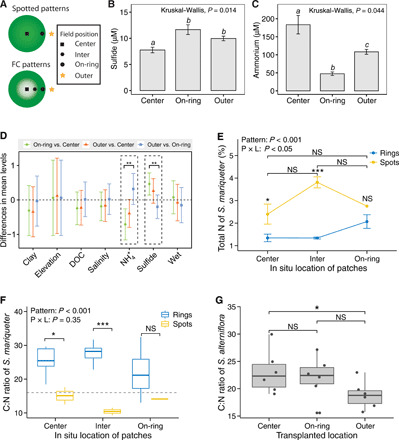
(A) Schematic illustration of measuring positions in spot and FC patterns to infer the potential mechanisms of FC patterns. (B and C) Concentration changes of the sulfide and ammonium in the center, on-ring, and outer of ring-type patterns. Letters above bars indicate significant differences (P < 0.05). (D) Physical, chemical, and sediment properties were sampled along a spatial gradient of FC patterns. Black dashed boxes indicate statistically significant properties at P < 0.05, while error bars indicate ±SD (n = 7). The detailed concentrations at each position were shown in fig. S7. (E) Total nitrogen composition of S. mariqueter leaves collected at different locations. Error bars indicate ±1 SD from the patch means (n = 6 patches). Pattern (P) × location (L), F_2,23 = 4.27, P = 0.03. (F) Stoichiometric changes in the C:N ratio of plant leaves of S. mariqueter at three different locations (n = 6). Pattern × location, F_2,23 = 1.12, P = 0.35. A reference stoichiometric ratio C:N of 16:1 is indicated by the dashed black line. (G) Leaf C:N stoichiometric analysis of S. alterniflora seedlings transplanted into different locations in ring-type patterns of S. alterniflora. Box plots depict the median (horizontal line), first and third quartiles (box), and the lowest and highest data points within 1.5-fold of the interquartile range of the first and third quartiles, respectively. Significant differences are denoted by different symbols, with ***P < 0.001, **P < 0.01, *P < 0.05, and “NS” for P > 0.05 (see tables S2 to S4 for detailed statistical analyses).

The cellular abundances of total C and N are most often discussed in terms of the C:N ratio. Carbon is, by far, the most dominant element in the biomass. The stoichiometric C:N ratio and nitrogen concentration in leaves indicate the level of effective nutrient depletion. If we examine in situ data on Scirpus and Spartina in terms of total carbon, total nitrogen, and C:N ratio, we find that there was higher biomass on-ring than in the center and in-between (between the center and on-ring; see Fig. 2A) locations for well-developed ring-type patterns [fig. S3B; one-way analysis of variance (ANOVA), F_2,24 = 6.11, P < 0.01; see table S1], whereas there were no significant differences for initial spotted patterns (F_2,6 = 2.01, P > 0.05; fig. S3B). For both spots and ring-type patterns, the biomass displayed an increasing trend from the center to outward edges. In contrast, total leaf nitrogen of Scirpus from the center to outward edges showed different trends between the spots and ring-type patterns (Fig. 2E; see tables S2 to S4 for details). Although we detected no statistically significant differences among three locations for nitrogen (F_2,6 = 2.04, P = 0.17; table S2), these differing trends still imply the potential for nutrient-dependent mechanisms to affect ring-type pattern formation (F_2,24 = 33.25, P < 0.001) because the ring-type patterns developed from the spotted patterns (see Fig. 1F) and concentric circles developed from rings (fig. S4B). More direct evidence is given by the significant interaction effect (F_2,23 = 4.27, P < 0.05). Figure 2F shows the stoichiometric C:N ratio measured in random leaf samples from spots and ring-type patterns (representative spots and ring-type patterns are shown in fig. S1). The C:N ratio was clearly higher overall in ring-type patterns than in spotted patterns, implying that nitrogen becomes a limiting factor governing plant growth after transition from the spotted pattern (F_1,23 = 21.57, P < 0.001; Fig. 2F). We further explored how variations of C:N ratio change in the Spartina ring-type patterns with transplant experiments. The stoichiometric C:N ratio of Spartina in Fig. 2G follows a similar trend, with a strong contrast between the center and outward edges, implying nutrient depletion from the center to the outward edges in ring-type patterns (Wilcox test, P = 0.041, n = 6; Fig. 2G).

Experimental and theoretical validation of the nutrient depletion mechanism

To explore the consequences of sulfide and nutrient control specifically for ring-type and concentric ring–type patterns, we compared the experimental evidence with numerical simulations. Field surveys did not provide evidence that the plant-sulfide toxicity feedback can explain the concentric ring–type patterning (no significant differences in porewater sulfide between locations within this pattern; Fig. 3A, upper right). However, the sulfide concentrations between vegetated (inter and on-ring) and un-vegetated (center and outer) locations in ring-type patterns showed significant differences (Fig. 3A, top left). The ammonium analyses suggest that nutrient depletion plays a more dominant role in explaining both ring-type and concentric ring–type patterns (Fig. 3A, bottom). Significant difference was found in the ammonium concentration in the porewater between the various locations between the center and the outer flats. The spatial-lag behavior should be noted between the ring-type and concentric ring–type patterns, where depletion is the highest on-ring in the ring-type patterns and in the center in concentric rings. This suggests the presence of a transient development from ring-type patterns to concentric ring–type patterns.

Fig. 3. Theoretical models and field experiments to confirm underlying mechanisms.

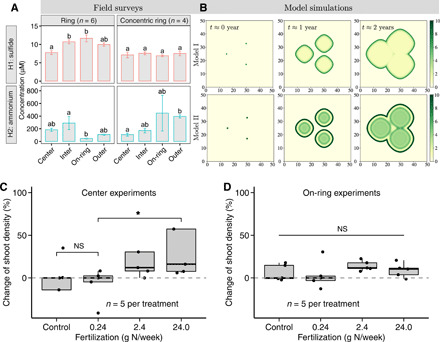
(A) Spatial variations of H₂S and ${\text{NH}}_4^{+}$ concentrations collected from ring-type patterns and concentric rings, respectively. Different lowercase letters above error bars represent statistically different groups identified by post hoc least significant difference tests with level of significance set at P < 0.05. The error bars indicate mean ± SE (n = 7, the numbers of sampled patches) (see tables S5 and S6 for detailed explanation of statistical parameters). (B) Theoretical simulations of models I and II, respectively, for FC pattern formation. Both models were implemented starting from the same initial conditions (three solutions). The color bars depict the plant biomass per square meter (g/m²). Left to right: Spatial patterns corresponding to each time point at yearly increments from seed colonization. The parameters used in these numerical simulations are shown in table S1. These simulations are shown over time in movies S1 and S2, respectively. (C and D) Effect of fertilization on plant growth in terms of the percentage change of net shoot density at the patch center and on the rings, respectively. Box plots depict the median (horizontal line), first and third quartiles (box), and the lowest and highest data points within 1.5-fold of the interquartile range of the first and third quartiles, respectively. Significant differences are denoted by P values using the nonparametric Wilcoxon rank sum test followed by post hoc comparison.

We compare the above analysis with three important observations drawn from the two models, as is schematically illustrated in Fig. 1G. First, simulations using the plant-sulfide feedback in model I are able to reproduce the FC or ring patterns observed in the field. However, this mechanism is not able to generate concentric ring patterns, thus deviating from the observed patterns in the field in some cases (Fig. 3B, top panels). Second, the plant-nutrient feedbacks in model II are able to explain the transient development from spotted to ring-type to concentric ring patterns (Fig. 3B and fig. S4D). Third, both models demonstrate the FC patterns resulting from the expansion of isolated patches. It should be emphasized that this phenomenon is distinctly different from previously described Turing-like self-organization patterns, where FCs would repel each other and coexist as distinct patches in a steady state (see Fig. 4C and fig. S6 and the Supplementary Materials for a detailed description on the modified sulfide-plant model with scale-dependent feedback mechanisms). Despite their simplicity, the models were able to capture the major features of the observed spatial patterns in intertidal salt marshes (Fig. 1, A to F, and figs. S1 and S2). Consistent with model predictions (see movies S1 and S2), the survey areas with FC patterns became completely vegetated salt marshes in a transient phase with FCs.

Fig. 4. Attraction and stabilities of the homogeneous vegetation state, as well as resilience of transient FCs and persistent Turing-like FCs.

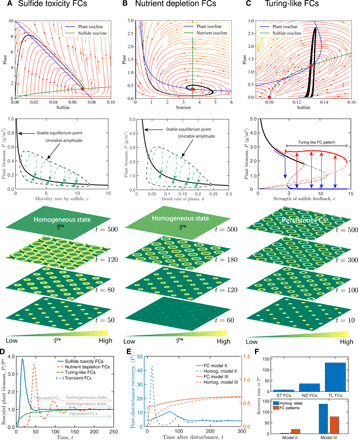
(A to C) Dynamics behaviors of three self-organized mechanisms of FC patterning. Top row: Attraction and stability of the positive equilibrium (vegetation state) with the phase portrait of system kinetics for transient and persistent FCs. Both transient FCs are global asymptotic stability, whereas persistent FCs are local asymptotic stability. Middle row: Bifurcation diagrams showing the amplitudes of FC patterned solutions and their stability were plotted in terms of plant biomass as a function of the parameter, c. Solid lines mark stable portions of the branch; dashed lines mark unstable portions. Bottom row: Typical spatial patterns and transition from the same spatial regular seedling clusters to FCs or a homogeneous steady state. (D) Trajectories of the distinctive patterned models when they return to pre-disturbance equilibrium after a temporary disturbance. (E) Recovery speed of the transient FCs and persistent FCs for self-organized patterns and spatial homogeneous scenarios. For all simulations, the plants were seeded at 40% of their positive equilibrium point (P*, red solid circles as shown in the top row). (F) Statistical comparisons for the recovery time of FC patterns among simulation models as well as the homogeneous state. Here, time was taken for 95% recovery to P*. ST FCs, sulfide toxicity FCs; ND FCs, nutrient depletion FCs; TL FCs, Turing-like FCs. The actual phase planes were shown for models with parameter values listed in table S1.

The nutrient depletion hypothesis is further confirmed by experiment with nitrogen fertilization. For both the control and lower nitrogen addition treatments, the plants at the patch centers display a negative growth rate (P = 0.92, n = 5). However, the high-nitrogen addition treatments mitigate the depletion stress and shift plant growth from negative to positive (ca. 24.0 g N per week; P < 0.05, n = 5; Fig. 3C). Overall, we observe a considerably positive response to increased nitrogen fertilizer, in support of the nutrient limitation hypothesis. On the contrary, there is no significant effect of nitrogen fertilization in the on-ring locations (P = 0.69, n = 5; Fig. 3D). Hence, plant growth was found to be significantly depressed by nutrient depletion at the patch centers compared to the outer ring, implying that the nutrient depletion likely depresses or even prevents plant growth in the middle of the rings.

Stability and resilience of the self-organized FCs

Self-organized patterns are commonly linked to increase the resilience of the ecosystems that display them (i.e., in terms of fast recovery in response to disturbances). We explore whether the transient FCs provide insight in the resilience of the salt marsh ecosystem in relation to environmental disturbances. First, the stability of the desired state (such as homogeneous vegetation dominated state) is directly related to its resilience (e.g., returning to a pre-disturbance state) following a disturbance (38, 39). To compare the resilience of the transient with that of persistent FC patterns, we further build the scale-dependent feedback model III based on the proposed sulfide toxicity model I (see Materials and Methods for details), which generated the Turing-like FC patterns (Fig. 4C and fig. S6). Phase portraits of partial differential equation (PDE) models reveal that transient FCs have a global attraction basin of the vegetation state (Fig. 4, A and B), whereas persistent Turing-like FCs typically have a local attraction basin (Fig. 4C). The latter type typically has an alternative stable state, resulting from self-reinforcing positive feedbacks. Our analysis reveals that ecosystems with persistent FC patterns can more easily flip into an alternative stable state when nonlinear feedback, the interaction of species or processes, or stochastic forcing by a fluctuating environment prevents ecosystem emergence and recovery.

Second, the global attraction and stability of transient FC patterns directly stimulate a fast return and hence high resilience for returning to a pre-disturbance state (Fig. 4D). The self-organized FC peaks and global attractions of vegetation state explain the observed performance of transient patterns. Theoretical results clearly reveal that the rate of recovery of ecosystem with transient FCs (with either sulfide toxicity and nutrient depletion feedbacks) is about twofold higher than ecosystems with Turing-like FC patterns (Fig. 4F, top). The recovery time of system with transient FC patterns is slightly shorter than the homogeneous scenarios, but overall, it is significantly quicker than in systems with Turing-like FC patterns (Fig. 4F, bottom). Furthermore, it is noteworthy that the systems with transient FCs ultimately evolve to a homogeneous state, as is observed in our study sites.

FCs indicate an Allee effect in salt marsh establishment

To explore the spatiotemporal dynamics of the clonal expansion behavior leading to FC patterns at the large scale, we obtained remote sensing imagery taken in 2010, 2012, 2013, 2014, 2015, and 2018 of a specific salt marsh dominated by the clonal plant Zizania latifolia. Remote sensing data reveal salt marsh establishment from a bare mudflat state with a few successfully established patches to the final densely vegetated salt marsh. The salt marsh ecosystem is shown to pass through transient spatiotemporal development from spots to ring-type patterns (Fig. 5A). This clonal expansion behavior is consistent with our model predictions. The expansion of patches clearly reveals two key ecological processes from their demographic dynamics (Fig. 5B). Positive size dependence, an Allee effect, is shown in the multiyear data but reflects the size of vegetation patch instead of population density. There is previous evidence supporting the demographic Allee effect in S. alterniflora, with reduced per capita population growth rate at the low densities found at the front of invasions (40, 41). This Allee effect argument is supported with the field-observed patterns, in which FC patterns of S. mariqueter can effectively prevent invasion of S. alterniflora over the short term (see fig. S4). As time passes, FC patterns may potentially influence the strength of Allee effects (weak versus strong Allee effects). For example, in some plants (such as S. mariqueter and S. alterniflora here), high rates of seed set in 1 year can lead to reduced growth and reproduction the following year, demonstrating a negative and therefore weak Allee effect (42). On the other hand, plant patches demonstrate strong local facilitation, which is considered a crucial process for salt marshes to withstand tidal waves (34, 43), as within the clumps, plant expansion is facilitated, underpinning the Allee effect (40, 41). Hence, the FC patterns here may result from Allee processes, where a more adaptive spatial structure develops as a consequence of self-organization processes that capture more resources, and makes more effective use of the resources, increasing plant to survival.

Fig. 5. Observed spatiotemporal behavior of FC patterns obtained from 2012, 2013, 2014, 2015, and 2018 satellite images and patch growth curves.

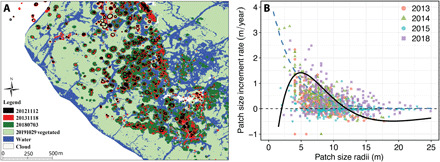
(A) The satellite images show the spots spanning over many meters in the radial direction from their centers and forming the FC patterns over time. Satellite images were taken from Google Earth of the Shanghai coastal area at coordinate 31°14′14.94″N, 121°49′38.25″E, where the dominant species is Z. latifolia within the focused area. (B) Patch size growth rate versus patch size in the radial direction, where the data were extracted from these satellite images. The growth rate reveals a stretched Allee-like effect behavior (solid black curve) rather than one based on positive feedback alone (blue dashed curve). Curves were calculated (fit lines) using the mathematical formulas f(x) = r(x − N₁)(1 − x/N₂) exp(−α x) (AIC = 1631.9, R² = 0.49, P < 0.001) and a positive feedback g(x) = exp(−0.29x + 1.56) (AIC = 1361.8, R² = 0.43, P < 0.001) with parameters r = 2.2, α = 0.2, N₁ = 2.0, and N₂ = 12.0. The fixed points of f(x) = 0 correspond to the critical sizes needed to survive (see table S7 for detailed statistical properties of exponential model and Allee effect model).

DISCUSSION AND OUTLOOK

FC mechanisms in salt marsh ecosystems

The present study identifies two potentially complementary mechanisms that contribute to FC formation (including ring-type patterns and concentric ring–type patterns) in salt marsh ecosystems. The first ecological process presumes that following the initial expansion of plants on intertidal mudflats, there is a gradual accumulation of toxic sulfide in the sediment, creating what can be considered a system with “fast-slow” dynamic system (model I). This model is supported by field data revealing sulfide accumulation in the sediment here as well as previous evidence in eelgrass fairy rings (Zostera marina L.) (44), although the measured concentrations would not be toxic immediately. This plant-sulfide feedback could principally be a ubiquitous phenomenon in intertidal salt marshes and aquatic ecosystems. The toxic sulfide accumulation in the sediment due to low iron availability in this carbonate-rich environment acts as inhibiting agent to cause the apparent die-off of plant shoots on the inner and center side of the patches, shaping the ring-type patterns (Fig. 3, A and B). Yet, despite its obvious presence in the field, this mechanism cannot explain the formation of concentric circles. We therefore propose an alternative or additional process in the form of nutrient depletion (model II), which is able to explain both the ring-type and concentric ring–type patterns and which is strongly supported by experimental evidence. Our field evidence suggests that although both sulfide toxicity and nutrient depletion are present in our study area, nutrient depletion plays an overriding role, as only this process can explain the concentric rings.

Our study proposes a principally different mechanism for FC formation in salt marshes compared to what was previously proposed for FCs in arid systems, for instance, in Namibia (25–28). One explanation is that the Namibian FCs are driven by water limitation and hence follow the principle of scale-dependent feedback. A second explanation emphasizes the importance of termites, which, due to their semiregular spacing, also align to the principle of scale dependence (28, 32). With both explanations, patterns characterize a system with approximately persistent patterned states, although likely taking extensive periods to develop. The patterns observed in salt marshes are transient, and their principal dynamics follow that of a limit cycle (18, 45), where periods of expansive growth are followed by accumulation of toxic substances and nutrient depletion, which then lead to plant collapse at short-term transients. In a spatially expanding systems, this manifests itself as concentric rings, which can be a transient feature as the systems slowly find an equilibrium characterized by modest growth limited by mild sulfide toxicity and low nutrient levels, operating separately or in conjunction. The patterns that are observed even allow the observer to distinguish between the types of growth limitation, providing a crucial insight into the processes shaping ecosystem resilience (see Fig. 4).

Many important aspects with regard to ecosystem functioning remain unknown for self-organized FC patterns in salt marshes (see Fig. 1 and fig. S1). For instance, do transient FC patterns provide comparable emergent properties with respect to ecosystem resilience as was found with Turing-like patterns? There have been many recent studies on the implications of pattern formation along gradients of environmental stress, such as in semiarid zones (1–3), salt marsh grasses (34), intertidal mussels (6), and shoreline barnacles (46, 47). A common denominator in these studies is that individuals can better facilitate the growth and survival of their neighbors through various mechanisms, but under less harsh environments, they compete with each other (48). Failure of this facilitative process can result in abrupt boundaries when harsh conditions are encountered because individuals cannot persist below a threshold size. This type of Allee processes together with negative density dependence can explain some marked self-organized patterns observed in nature in environmentally harsh or stressful habitats, such as semiarid vegetation (13, 14), peatlands (11), and mussel beds (4, 48). Specifically, in our salt marsh ecosystem, this Allee effect may limit patch establishment and expansion, as plant density plays a crucial role in overcoming establishment (49, 50). Here, using the developmental dynamics of pattern formation, the data suggest that FCs can be used to characterize the strength of Allee effects on salt marsh ecosystems (Fig. 5B). Yet, further experimental evidence is needed to support this hypothesis.

Transient patterns versus persistent patterns

Our study highlights the importance of studying the transient dynamics of self-organization in ecosystems, providing a window into the mechanisms that are shaping the landscape. Existing literature (3, 24–29) has focused on self-organization in persistent patterns. Transient behavior has largely been ignored in ecology [only a few studies in most recent literature (18, 19, 22)]. These studies suggest that pattern transitions such as from spots to rings require environmental degeneration to occur (2, 12, 17, 26–29). In our study, however, this transition can emerge without any change in environmental conditions. A second characteristic difference between persistent Turing-like patterns and the transient patterns described in this paper is that the transient FC patterns can display merging behavior with neighboring FCs. In self-organization models that build on water depletion, FCs were found to repel each other [see fig. S6 for our model here and also (27) for Namibian FCs]. This highlights how a comparison of the difference in pattern characteristic involving both transient patterns and persistent ones can help distinguish the mechanisms that underlie pattern formation and ecosystem development (Table 1).

Salt marshes are vulnerable ecosystems that may undergo sudden shifts in area extent affecting a multitude of coastal processes (51, 52). The causes of degradation are often unknown and predict that degradation will continue into the future. Understanding the potential mechanisms and spatial hallmarks of resilience is profoundly important to salt marsh restorations given ongoing climate change and expanding anthropogenic activities (53–55). Yet, there is limited understanding of how to infer the resilience of salt marshes. Here, we have studied transient FC patterns and explored the underlying ecological processes, revealing that expansion speed is limited to nutrient limitation. With regard to ecosystem resilience, our models (see movies S1 and S2) and field evidence (see Figs. 4 and 5A) suggest that salt marsh ecosystems will develop toward homogeneous vegetative state after the transient phase with FC patterns. It is worthy to note that FC patterns in this study are different from the FCs reported for dryland ecosystems (3, 26–30). FCs, as found in drylands, reflect a persistent state with stable patterns, and it is likely difficult to return them to a homogeneous vegetation/shrub state. Therefore, our study here reveals that the transient FC patterns reflect the high resilience of the self-organized salt marshes (Fig. 4D).

Collectively, our results underline the value of addressing transient spatiotemporal patterns in ecosystems, as they provide a window into the formative processes of ecosystem development, providing a range of possible indicators that have hitherto received less attention in the self-organization literature (1–4, 25–33). Our results also highlight the complexity of ecological feedback responses and the possibility of their co-occurrence and complementarity in driving distinct patterning mechanisms at both the local and ecosystem scales. As our world is rapidly changing because of climate change and other human impacts, understanding of the transient dynamics might become increasingly important (18, 21, 22). Given the complexity generated by the interactions of a multitude of ecological processes occurring at different spatial scales, transient patterns may provide a crucial needed window into the processes that shape the resilience of ecosystems worldwide.

MATERIALS AND METHODS

FC patterns in intertidal salt marshes

Intertidal salt marshes establish starting from only a few patches on bare mudflats at very early stages. These clump-like patterns are crucial for survival because of the impact of wave action (see Fig. 5A and fig. S2A). Hence, salt marshes in our survey area display dense spotted patterns by a couple of months. FCs emerge after these dense spotted patterns spread from a diameter of only a few meters to dozens of meters. These processes are found in vegetation dominated by S. mariqueter, S. alterniflora, and Z. latifolia in coastal and intertidal salt marsh ecosystems, Shanghai, China. Note that these species are dispersed through both clonal reproduction and seedlings, where seedlings can be passively transported by the wind and tidal waves.

Field survey and experiment locations

From April 2018 to July 2019, we conducted field experiments and took aerial images with drones in salt marshes in China (31°30′10.85″N, 121°59′11.50″E). Field transplant experiments were established in S. alterniflora patches in northern Chongming Island (on the north branch of the Yangtze River), Shanghai. Sediment samples for estimating nutrient and sulfide concentrations, sulfate-reducing bacteria, and sulfide-oxidizing bacteria were collected from FCs in Chongming Dongtan Nature Reserve (CDNR) in southern Chongming Island. In north Nanhui shoal (on the south branch of the Yangtze River), we only collected sediment samples for measuring nutrients and sulfide. The native S. mariqueter is the dominant species in the pioneer zone of salt marsh ecosystems at these locations. These areas can be inundated during spring tides or during high-tide phases during neap tide, during which heterogeneous distribution of nutrient and other geochemical factors can occur at the local scale. Nitrogen concentration in the tidal water of ${\text{NO}}_x^{-}$ and ${\text{NH}}_4^{+}$ are ca. 80 and 10 μM, respectively, in Chongming Island. To investigate the dynamics of FCs in natural ecosystems, high-resolution images (ca. 0.02 m) were taken with drones in April 2018.

Transplant experiment in S. alterniflora

To test the role of nutrient depletion in FC patterning, we conducted transplant experiments in salt marsh with Spartina on the north branch of the Yangtze River (Fig. 1B). We selected seven ring-type patterns in Spartina and transplanted Spartina seedlings (20 to 30 seedlings per plot) into the patch center (center), into the rings themselves (on-ring), and outer bare land close to patch (outer) in the radial direction. For all treatments, we transplanted Spartina tussocks (clumps) with a consistent sediment sample volume of 25 × 25 × 20 cm³ in April 2018. All transplant plots (25 × 25 cm²) were marked with PVC (polyvinyl chloride) tubes. Every 2 weeks, we measured the density and height of transplanted plants and randomly selected plots of the same size and density around the transplant plots (ca. 50-cm distances from each other) for plant growth references (in situ plots used as the control treatment). At the same time, we took soil samples for measuring total organic carbon and total nitrogen at a depth of 0 to 10 cm around transplant plots (ca. 10-cm distances) to estimate nutrient depletion. In August 2018, we measured temperature, water content, conductivity, redox potential, and pH at the depth of ca. 10 cm around transplant plots. We also collected leaf samples of Spartina for measuring stoichiometric C:N ratio.

Experimental design and sample analyses

To investigate the potential relationship between sulfide and nutrient depletion, and FC patterns, i.e., both ring-type and concentric ring formations, we compared ring-type patterns with spotted patches in CDNR (n = 2 and n = 6 for spot and ring patches, respectively, in May 2019) and concentric rings in Nanhui shoal (Fig. 1D; n = 4). At each patch, we took four sediment cores with PVC tubes (diameter of 10 cm and height of 20 cm) at the patch center (center), on the ring itself (on-ring), intermediate position from the center to the ring (inter), and outer bare land (outer). For every sediment core, we collected pore water samples using 20-ml syringes connected to Rhizon samplers (0.6 μm), which were placed at the five depths of 1, 3, 5, 10, and 15 cm, respectively. We separated these pore water samples into three parts. First, we extracted a 0.5-ml sample for measuring sulfide concentration with a 1-ml syringe and injected it into 2.0 ml of 10% Zn acetate solution immediately to avoid oxidation (56). Second, we filtered and diluted the samples following the operation protocol for testing DOC (n = 7 for each location) with an element analyzer (Thermo Fisher Scientific Inc., USA). Last, the remaining pore water in the samples was filtered and diluted to 16.0 ml for analyzing nutrient concentrations, including ammonia, nitrite, nitrate, and phosphate with a segmented element analyzer (Skalar Inc., The Netherlands). In this study, only nitrogen in the form of ammonium was used for further analysis, as the other nutrients were difficult to detect because of low concentrations. To analyze the effect of sediment dynamics at the patch scales, we set 10 markers from the patch center to edge at 1.0-m intervals in spots and ring-type patches (three replicates) and measured elevational change every 2 weeks. At corresponding distances, sediment samples were taken from the CDNR and sliced at each depth (1, 3, 5, 10, and 15 cm, respectively) and frozen at −80°C. After being freeze-dried in the laboratory, sediment grain size was measured using a particle size analyzer (Beckman Coulter, LS13320, USA).

Fertilization experiment

To directly demonstrate our hypothesis that nutrient limitation causes observed FCs for Scirpus in the salt marshes dominated by this species, we conducted nitrogen fertilization experiments in the center and in on-ring locations in case of the spotted patches (n = 5 for per treatment) at location CDNR from July to September 2020. The N addition treatments were set to 0 (control), 0.24, 2.4, and 24.0 g N per week for the developed spotted patches (diameters, ca. 10.0 to ca. 15.0 m). At each treatment, four radial directions within a “+” shape were assigned to four-factor fertilization treatments. Four plots of ca. 1 × 1 m² with approximately equal plant density were fertilized at the center and on the ring along the radial direction for spotted patches to evaluate the effect of the N addition evaluation. Then, we measured plant density and height of each plot every 2 weeks. The growth rate of plants was assessed by the formula of $\text{GR}=\frac{N(t+1)-N(t)}{N(t)}\times 100\%$ for treatment experiments. Here, N(t) is the plant density at time t.

Statistical analysis

We used the nonparametric Kruskal-Wallis test in post hoc comparisons to test the differences between the average concentrations of sulfide and ammonium at different locations within patches (e.g., location in center, on-ring, and outer). We use correspondence analysis to extract key factors explaining variation in the collected samples and one-way ANOVA with locations and patterns as fixed factors to test the stoichiometric C:N ratio in the in situ experiments. We tested the effects of locations and patterns as fixed factors on the concentration of sulfide and ammonium using one-way ANOVA with Tukey post hoc multiple comparisons. The nonparametric Wilcoxon rank sum test was used to test the effect of fertilization gradient on plant density change in the center and on-ring of patches, respectively, and to compare the effects of plants and locations on the concentration of nitrate and C:N ratio when sample size was small. All statistical calculations (mean, SE, and SD) were carried out using R (version 3.6; www.r-project.org) studio software. Pairwise t tests were applied when testing the effect of the transplant experimental sample with the emmeans and ggpubr packages. For tests across different locations within FCs (e.g., center, inter, and on-ring) and spatial patterns (ring-type and spots), the Tukey post hoc test was applied. Significant differences were designated between two locations according to the following scale: ***P < 0.001, **P < 0.01, *P < 0.05, and “NS” (not significant) for P > 0.05.

Mathematical models

Here, we focus on the two main mechanisms to explain the observed FCs of clonal plants on intertidal salt marshes, namely, sulfide toxicity and nutrient depletion (Fig. 1H). We developed a set of PDEs or, more precisely, two coupled reaction-diffusion equations for the biomass of plants and concentration of sulfide or nutrients, respectively. We formulated these two mechanisms in terms of upscaled continuous densities, thus allowing for description and comparison of spatial and temporal behaviors at much larger spatial scales. The mathematical models are structured as follows.

Sulfide toxicity model

The plant biomass and the sulfide concentration are defined as P(z, t) and S(z, t) at position z = (x, y) and time t, respectively. The change in growth rate of plant biomass in a spatial grid cell can be expressed as

$$\frac{\mathrm{\partial }P}{\mathrm{\partial }t}=\mathit{rP}(1-\frac{P}{K})-\mathit{cPS}+D_p\mathrm{\Delta }P$$ (1a)

The first term describes plant population growth as following a classical logistic-shaped growth curve, where r is the intrinsic growth rate of the plants and K is the plant carrying capacity. Organic matter can enrich hydrogen sulfide (H₂S) in intertidal salt marshes, which is toxic and leads to healthy plant die-off (35, 37). Hence, the loss of plants is assumed to increase with increasing sulfide concentration and plant biomass (57). This is represented by the term cPS, where mortality is proportionally caused by sulfide concentration. Field surveys on clonal dispersal traits for salt marsh plant species S. mariqueter and S. alterniflora have revealed that plant lateral expansion through vegetative reproduction could be described by random walk (58, 59). Hence, we apply a standard diffusion process to describe plant dispersal with a parameter of diffusion coefficient D_p.

Changes in sulfide concentration are described as

$$\frac{\mathrm{\partial }S}{\mathrm{\partial }t}=\mathrm{\xi }[\mathrm{\epsilon }P-d\frac{k_{\mathrm{s}}}{P+k_{\mathrm{s}}}S]+D_{\mathrm{s}}\mathrm{\Delta }S$$ (1b)

where ξ is a dimensionless parameter to control the time scale for the variables of the plant biomass and sulfide concentration. Parameter ε is the effective generation rate of hydrogen sulfide production arising from plant biomass. Parameter d is the maximum escape rate of sulfide through the mud-air interface, and k_s represents the effect of plants in promoting sulfide enrichment by producing DOC for promoting bioactivity of sulfate-reducing bacteria. D_s represents the horizontal dispersion rate of sulfide concentration, mainly due to the gradient of dense concentration (∆ represents the nabla operator, second spatial derivative, $\text{∆}=\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}+\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{y}^2}$), which is modeled with a diffusion approximation. Now, the computational model used for describing the dynamics of sulfide toxicity can be well explained with these two coupled PDEs (Eqs. 1a and 1b). The temporal evolution of spatial patterns can then be simulated by numerically integrating differential equations using in-house–developed OpenCL or Python software. The definitions and units of the variables and parameters are summarized in table S1. We name this set of two equations (Eqs. 1a and 1b) as model I. Note that model I is a fast-low dynamics system controlled by the time scale parameter of ξ for sulfide concentrations.

Nutrient depletion model

Similar to the plant-sulfide feedback model, we now build a theoretical model styled on plant-nutrient feedbacks. It should be noted that the main process here governs plant growth involving nutrient concentration. The variable P(x, t) can be described by a dominant balance between growth, mortality, and diffusion processes

$$\frac{\mathrm{\partial }P}{\mathrm{\partial }t}=\frac{\mathit{rN}}{k_1+N}P-\mathit{dP}+D_p\mathrm{\Delta }P$$ (2a)

The first term in Eq. 2a corresponds to growth dynamics, where r is the maximum growth when nutrients are sufficient, and k₁ represents the half-saturation constant of nutrients in promoting plant growth rate. Note that this growth rate is assumed to increase with higher nutrient concentration. Plant mortality is assumed to be proportional to plant biomass with the constant d. Here, we also use the standard diffusion behavior for plants, D_p∆P.

Nutrients N are added to the sediment by inflow of surface water during high tide and recycling through the organic matter decomposition of dead plant material on intertidal salt marshes. The nutrients are mainly depleted from the sediment through plant water uptake. Then, changes in nutrient describing the above processes can be considered as follows

$$\frac{\mathrm{\partial }N}{\mathrm{\partial }t}=I_{\text{in}}+\mathit{sdP}-c\frac{\mathit{rN}}{k_1+N}P+D_{\mathrm{n}}\mathrm{\Delta }N$$ (2b)

Here, I_in is the nutrient deposition rate by high tides, and s is the effective conversion factor from dead plants to nutrients (here, 0 < s < 1.0). Parameter c is the maximum nutrient uptake rate by plants (here, c < 1.0), and D_n represents the horizontal dispersion coefficient of nutrients. Table S1 provides an overview of the parameter values used, their interpretations, and units. We name this set of two equations (Eqs. 2a and 2b) as model II.

Scale-dependent model for Turing-like FCs

To distinguish differences in dynamic behavior between the transient FCs and persistent FC patterns, we build a model based on the scale-dependent feedback process between sulfide and plants that reproduces Turing-like FCs. The model describes that sulfide concentration inhibits plant growth, whereas plants can reproduce through a natural cloning process and facilitate the production of sulfide. This simple scale-dependent model can be expressed as follows

$$\frac{\mathrm{\partial }P}{\mathrm{\partial }t}=\frac{r}{S} \frac{P^2}{k_{\mathrm{p}}^2+P^2}-\mathit{cPS}+D_{\mathrm{p}}{\nabla }^{2}P$$ (3a)

$$\frac{\mathrm{\partial }S}{\mathrm{\partial }t}=s_{\text{in}}+\mathrm{\epsilon }{P}^2-\mathit{dS}+D_{\mathrm{s}}{\nabla }^{2}S$$ (3b)

We name this set of equations (Eqs. 3a and 3b) as model III (or Turing-like FCs) in the main text. More detailed explanations on variables and parameters are present in text S1 and table S1.

Stability and resilience

Stability corresponds to the tendency of a system to remain in a given (spatial) configuration despite the imposition of an external disturbance. The local or global stability of the proposed FCs models was obtained by studying the phase portrait and bifurcation structure of three models using the methods described in (5, 33). The global stability of the equilibria of systems (1) and (2) shows that the largest eigenvalues λ_1,2 of Jacobian matrix hold the conditions of ℛe{λ_1,2(k)} < 0 for all wave number k. However, a positive equilibrium is locally stable if its eigenvalues hold the conditions ℛe{λ_1,2(k)} > 0 for a nonnegative wave number k. The latter is termed diffusion-driven instabilities or Turing patterns resulting from positive feedback. This also creates an alternative stable state and leads to collapse when a large disturbance pushes the system beyond a threshold such that it cannot return to the original stable vegetation state (1, 2, 8). All bifurcation analyses were obtained with pde2path package (60).

Stability is commonly referred to that reflecting different aspects of resilience. Two types of resilience are commonly discussed in ecology (38, 39). Ecological resilience can be measured by the magnitude of disturbance that can be absorbed before the system changes its structure, i.e., stability of the equilibrium (38). Going beyond these stability properties, the degree of the system’s engineering resilience is traditionally quantified by the magnitude or speed of returning time to a pre-disturbance state after a temporary disturbance (5, 15, 39). Thus, we further assessed the resilience as the return time when the self-organized FCs of proposed models were disturbed by 40% reduction of biomass from that characterizing their positive equilibrium. We compared the recovery time between transient FCs and persistent FC patterns with the same methods for the spatially homogeneous state and the state characterized by spatially self-organized patterns.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/6/eabe1100/DC1