Myosin-driven actin-microtubule networks exhibit self-organized contractile dynamics

Microtubules enable organized myosin-driven contraction by providing flexural rigidity and enhanced connectivity to actin networks.

Abstract

The cytoskeleton is a dynamic network of proteins, including actin, microtubules, and their associated motor proteins, that enables essential cellular processes such as motility, division, and growth. While actomyosin networks are extensively studied, how interactions between actin and microtubules, ubiquitous in the cytoskeleton, influence actomyosin activity remains an open question. Here, we create a network of co-entangled actin and microtubules driven by myosin II. We combine dynamic differential microscopy, particle image velocimetry, and particle tracking to show that both actin and microtubules undergo ballistic contraction with unexpectedly indistinguishable characteristics. This contractility is distinct from faster disordered motion and rupturing that active actin networks exhibit. Our results suggest that microtubules enable self-organized myosin-driven contraction by providing flexural rigidity and enhanced connectivity to actin networks. Beyond the immediate relevance to cytoskeletal dynamics, our results shed light on the design of active materials that can be precisely tuned by the network composition.

INTRODUCTION

The cytoskeleton is a dynamic composite network of proteins that not only provides cells with mechanical support but also markedly restructures to enable essential biological processes such as cell division, growth, mobility, and intracellular transport (1–3). These diverse dynamics and properties are enabled by the inherent activity of the actin filaments, microtubules, and motor proteins that comprise the cytoskeleton. One ubiquitous interaction that the cytoskeleton uses to self-organize and produce active work is the association of the motor protein myosin II with actin filaments. These actomyosin complexes generate contractile motion and force by myosin II minifilaments pulling actin filaments past each other to drive cell migration, signaling, adhesion, protrusion, and retraction (4–7).

A critical parameter that influences the large-scale activity of actomyosin networks is the connectivity of the network, which can be tuned via actin cross-linking proteins (8–10). In vitro studies have shown that actin networks must be cross-linked above a critical percolation threshold to sustain ordered contractility across the network (8–11). Without additional cross-linkers linking actin filaments together, actomyosin activity in disordered actin networks can induce both contractile and extensile forces, resulting in flow and rupturing of the actin network (12, 13). In vitro studies have shown that in this regime, myosin II restructures actin into disconnected foci and that the system exhibits disordered motion rather than organized contraction (14). Additional cross-linkers allow myosin II motors to generate internal stress more efficiently in the network as they mobilize actin (15–17). In response to this stress, actin filaments can buckle, shorten, or even break, leading to self-organized network contraction (18).

Microtubules can also undergo active rearrangement via interactions with motor proteins such as the family of kinesins (19–21). Studies on kinesin-driven microtubule networks have shown that the kinesin-microtubule interaction generally leads to extensile rather than contractile motion and often results in flow rather than coarsening or restructuring (20–23), although microtubule contraction has been observed as well (19, 24).

While active actin networks and microtubule networks have been intensely studied over the last decade (4, 25), how the presence of one filament type affects the active dynamics of the other remains an open question (26). At the same time, interactions between actin and microtubules are pervasive in the cell and are particularly important for regulating cell shape during migration, division, and intracellular transport (27). Thus, understanding how the composite nature of the cytoskeleton affects its motor-driven activity is of critical importance. Furthermore, we have previously shown that in vitro systems of co-entangled actin and microtubules exhibit emergent mechanical properties, absent in single-component networks, which could be harnessed for the design of materials with novel properties useful in engineering and biomedical applications (28–30). Hence, incorporating activity into this system could provide a powerful platform for engineering active nonequilibrium materials.

Here, we create an active composite network of co-entangled actin filaments and microtubules that exhibits contractility driven by myosin II minifilaments. We use two-color confocal fluorescence microscopy to visualize the network reorganization during motor activity. We use particle image velocimetry (PIV) and dynamic differential microscopy (DDM), complemented by particle-tracking experiments, to characterize the active network dynamics. We show that microtubules enable organized and uniform contraction of actomyosin networks that otherwise exhibit disjointed and disordered dynamics. Actin-microtubule networks also exhibit slower and more sustained contraction than actomyosin alone while still supporting nearly ballistic contractility characterized by steady directed motion. Furthermore, our particle-tracking experiments show that particles embedded in active actin-microtubule networks exhibit two distinct transport modes dependent on the time scale probed. At small time scales, particles move subdiffusively, similar to that in steady-state networks, while at larger time scales, the motion is ballistic, akin to actomyosin networks. Our findings suggest that actin-microtubule interactions may play an important role in tuning actomyosin activity in cells and could be exploited in cytoskeleton-inspired active matter to tune not only the stiffness of the material but also the spatial and temporal scales of activity.

RESULTS

Designing an active actin-microtubule network

We designed active actin-microtubule networks using myosin II to drive activity (movies S1 to S3). While active actin networks and microtubule networks have been intensely investigated in recent years (4, 25), to our knowledge, active matter composed of both actin filaments and microtubules has yet to be realized. We previously determined optimal buffers and polymerization conditions to copolymerize actin and microtubules to form composite networks that are homogeneous and in which the two filament types are coentangled with one another (28–30). Here, we incorporate myosin II activity into these networks to bring this system one step closer to the cellular cytoskeleton and to provide new design principles for active biomaterials. We focus on networks with equal molarity of actin and tubulin, since we have previously shown that networks with this actin-to-tubulin ratio exhibit strong resistance to imposed stress while maintaining a high degree of filament mobility (29). This combination of resilience and mobility provides an ideal platform for designing active materials that can respond to stimuli while maintaining structure.

To produce activity, we incorporate myosin II minifilaments at a 1:12 myosin:actin molar ratio, similar to the ratios used in previous in vitro actomyosin studies (10, 14). As we are motivated in part by materials design, we focus on this ratio as it produces the highest degree of activity without resulting in network destruction or irreproducible activity. However, we note that actomyosin network destruction, as previously demonstrated in vitro (4), likely plays an important role in biological processes such as cell migration and neuronal growth (5, 31, 32). In future work, we will systematically tune myosin:actin ratios and protein concentrations to map the phase space of possible network dynamics.

To control the duration and location of myosin II activity, we incorporate a saturating concentration of blebbistatin into the networks that deactivate myosin II activity except when exposed to ~400- to 500-nm light (33). We use two-color fluorescence confocal microscopy to image the actin and microtubule networks and initiate activity. We use 488-nm light to simultaneously visualize the actin channel and activate myosin-driven activity, and we use 561-nm light to image microtubules. As we describe below, this three-dimensional system exhibits robust and uniform myosin-driven contractility.

Actin-microtubule contraction is synchronized and organized

Figure 1A shows images from a representative time series of an actin-microtubule network undergoing myosin-driven activity over the course of 6 min. The top row displays dual-color images with both the actin and microtubule channels visualized, while the bottom two rows show the separate actin and microtubule channels. From the images, it is clear that myosin II activity causes the network to move and rearrange. We see more clustering at later time points, as well as conformational changes and mobility of some of the brighter structures. Unexpectedly, despite the fact that myosin II only binds to actin, the two networks remain well integrated and microtubules colocalize and move with the actin filaments. While we only analyze the contraction dynamics for 6 min, we see the well-incorporated composite network contract for up to 30 min.

Fig. 1. Design and characterization of active actin-microtubule networks.

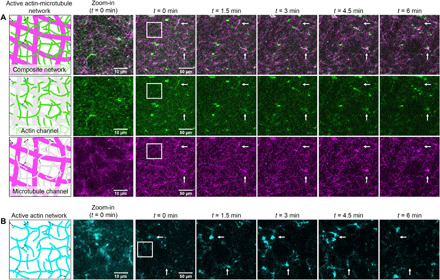
(A) (Column 1) Cartoon depictions of an active actin-microtubule network composed of actin filaments (green/gray), microtubules (magenta/gray), and myosin minifilaments (black). As depicted, the actin filaments and microtubules are co-entangled with one another, and the myosin can bind to actin to generate activity. (Column 2) Zoomed-in regions of images shown in column 3. (Columns 3 to 7) 256 × 256 pixel confocal microscopy images of an active actin-microtubule network at five equally spaced time points of a 6-min time series (movie S1). Two-color images in the top row display both actin (green) and microtubules (magenta) in the composite network. The second and third rows separately show the actin (movie S2) and microtubule (movie S3) channels, respectively. Either actin or microtubules are shaded gray in the corresponding cartoons to reflect the imaging channel not shown. Arrows in the images point to examples of colocalized actin filaments and microtubules moving and reconfiguring due to myosin activity. (B) Cartoon depiction and corresponding confocal micrographs of an active actin network (movie S4). Actin filaments are colored cyan to differentiate from the actin channel in the actin-microtubule networks. The network is prepared identically to the active actin-microtubule network but lacks microtubules. Arrows in the images point to examples of actin moving and reconfiguring due to myosin activity.

As a control, to determine the effect of actin-microtubule interactions on actomyosin activity, we created active networks with the tubulin removed but with all other reagents and conditions fixed (movie S4). As shown in Fig. 1B, these active actin networks undergo substantially more restructuring and rupturing during myosin activity, as actin filaments form bright bundles and foci and leave large voids in the network. The horizontal set of arrows shows a large bundle of actin forming then disappearing from the plane of view, while the vertical set of arrows indicates a region where a bundle of actin enters then exits the plane of view. Hence, microtubules appear to provide stabilization to actomyosin networks and enable slower, more controlled actomyosin activity. Static actin-microtubule networks, either without light activation or without myosin, showed no network rearrangement over the 6 min of imaging (movies S5 and S6). Microtubule networks with and without myosin II also showed no network rearrangement (movies S7 and S8), indicating that myosin II does not associate with microtubules and that actin is needed as a substrate for myosin II activity.

To determine the direction of motion of the filaments in the active networks, we used PIV analysis to generate velocity vector fields at different times during activity. Figure 2A shows the velocity fields for the actin (top row) and microtubule (bottom row) channels of an active actin-microtubule network. At each time point and for each channel, the velocity vectors point toward the center of the activated region, showing that the network is contracting over time. The velocity fields for actin and microtubules are quite similar at each time point, demonstrating that the microtubules and actin move together. Furthermore, the velocity fields for all time points are similar, pointing inward with similar magnitudes, indicating that the network is undergoing controlled and organized contraction.

Fig. 2. PIV shows that microtubules enable organized myosin-driven contraction.

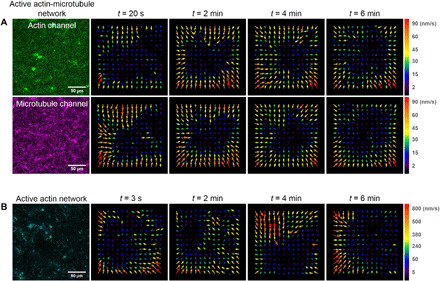
(A) Velocity vector fields of the actin channel (green, top row) and microtubule channel (magenta, middle row) of the active actin-microtubule network shown in Fig. 1 at four time points during the 6-min time series. Velocity fields were generated using PIV analysis with a lag time of 20 s. Velocity fields for both channels show consistent motion directed toward the center region of the field of view throughout the movie duration. Different arrow colors correspond to different speeds as indicated in the color scale to the right of vector fields. (B) Velocity vector fields of the active actin network (cyan), generated via PIV analysis with a lag time of 3 s, show faster and more disordered motion than the actin-microtubule network throughout the duration of the time series.

Unlike the composite network, the active actin network, shown in Fig. 2B, exhibits velocity fields that quickly change direction and magnitude over time. Moreover, while the velocity fields for the composite actin-microtubule networks were computed using frames that were 20 s apart, the actin networks needed frames that were only 3 s apart. When we tried to use longer lag times, the velocity fields were dominated by noise and important features of the network escaped the field of view. This result implied that the contraction speed was faster and less controlled in the actin network compared with the composite. While the composite network exhibits characteristics of controlled network-wide contraction, the actin network ruptured and contracted toward different foci that moved in a disordered fashion over time, as previously reported for actomyosin networks without additional cross-linkers (12, 13). This difference suggests that microtubules can organize actomyosin activity and slow it down.

Microtubules slow actomyosin activity sevenfold

To further quantify the active dynamics of myosin-driven networks, we use differential dynamic microscopy (DDM) to analyze the time series of images. DDM is useful for investigating diffusive and active dynamics of soft materials such as those found in biological systems (34), including cytoskeleton complexes (35–37). In our own previous work, we have used DDM to study the passive transport of tracers within static actin-microtubule networks and found that these networks exhibit subdiffusive behavior (38). Here, we first use DDM analysis to generate image structure functions D(q, Δt) at varying wave numbers q, as described in Materials and Methods. Figure 3A shows D(q, Δt) curves for an active actin-microtubule network, increasing with lag time for three representative wave numbers. At each wave number, D(q, Δt) curves are largely indistinguishable between the actin and microtubule channels, demonstrating the correlated motion of the two filaments. As the lag time increases, D(q, Δt) increases and then begins to plateau, at which point density fluctuations in the network are considered no longer correlated. By fitting D(q, Δt) with an exponential function, as described in Materials and Methods, we extract a characteristic decay time τ for fluctuations of a given wave number (Fig. 3C). This time roughly corresponds to the lag time at which D(q, Δt) reaches a plateau. As shown, both actin and microtubule channels appear to approach this plateau at similar lag times. However, D(q, Δt) for active actin networks reach plateaus more quickly than active actin-microtubule networks, indicating faster dynamics (Fig. 3B). In contrast to the active networks, D(q, Δt) for inactive actin-microtubule networks, as well as networks without actin, exhibits no plateau and can thus not be fit to extract a decay time (figs. S1 and S2). This lack of a plateau indicates that the dynamics of the inactive networks are much slower than active networks and do not rearrange appreciably over the experimental time frame.

Fig. 3. DDM demonstrates that actin and microtubules in active actin-microtubule networks exhibit nearly indistinguishable contraction dynamics that are slower than in actin networks.

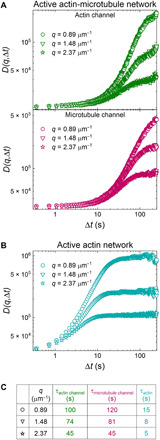
(A) Representative image structure functions D(q, Δt) for the actin channel (green, top) and microtubule channel (magenta, middle) of an active actin-microtubule network for wave numbers of q = 0.89 (circles, highest curves), 1.48 (triangles, middle curves), and 2.37 μm⁻¹ (stars, lowest curves). Note the similarity between curves for the actin and microtubule channels. (B) Representative image structure functions for the active actin network for the same three q values shown in (A). Note that D(q, Δt) curves for the active actin network approach plateaus at shorter lag times than for the actin-microtubule network and, as such, have shorter decay times. (C) Decay times τ for all curves plotted in (A) and (B), determined via fitting each curve to an exponential function (see Materials and Methods). Decay times roughly correlate with when D(q, Δt) curves reach a plateau and decrease as q increases. Decay times for the actin and microtubule channels of the actin-microtubule network are in close agreement and an order of magnitude longer than those for the actin network.

To more fully capture the dynamics of the active networks, we evaluate the dependence of the decay time τ on the wave number q. Figure 4A shows the average τ(q) curves for both the actin and microtubules of the active composite network as well as for the actin network. The curves for both actin and microtubules of the composite are nearly identical, signifying that the dynamics of both types of filaments are highly correlated. Comparing the actin network to the composite, we see that for any given wave number, the characteristic decay time of the actin network is significantly smaller than that of the actin-microtubule network, showing that the density fluctuations decay faster. This result supports our PIV analysis that shows that the actin networks exhibit much faster dynamics compared with actin-microtubule networks.

Fig. 4. DDM reveals that microtubules slow down and organize ballistic motion of myosin-driven cytoskeleton networks.

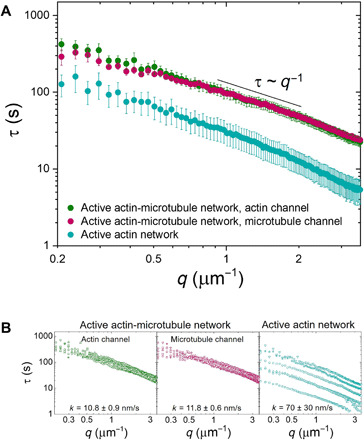
(A) Average characteristic decay time τ versus wave number q for the actin channel (green) and microtubule channel (magenta) of an active actin-microtubule network and an active actin network (teal). All curves appear to roughly follow the scaling τ~q⁻¹ for larger q values, indicating ballistic motion. Smaller τ(q) values for all wave numbers show that the active actin network exhibits faster motion than the actin-microtubule network. (B) Individual τ versus q curves from which the average curves displayed in (A) were computed. Fitting each curve to τ~1/kq provides an effective speed k for each filament and each network, which is listed in the corresponding plots. The large spread in active actin data compared to the active actin-microtubule data shows that the microtubules are able to organize actomyosin activity and enable controlled contraction. Data shown are from six different replicates.

The shape of the τ(q) functions reveals the type of motion the active networks exhibit and the corresponding rate of motion. If τ~1/kq, then the system exhibits ballistic motion and k represents the speed. If τ~1/kq², then the system exhibits diffusive motion and k represents the diffusion coefficient. All curves for actin and microtubules in composite or actin networks exhibit roughly q⁻¹ dependence, signifying ballistic motion. We find exponents of −1.15 ± 0.03 and −0.85 ± 0.05 for the actin channel and microtubule channel of the composite network, respectively. An exponent of −1.00 ± 0.03 is found for the active actin network.

We fixed the scaling exponent to −1 to determine an effective speed k from the relation τ~1/kq. We compute contraction speeds of 10.8 ± 0.9 and 11.8 ± 0.6 nm/s for the actin and microtubules in the composite network, compared with 70 ± 30 nm/s for the active actin network (Fig. 4B). Note that the speeds for both actin and microtubules in the composite network are identical, within error, while the motion of the actomyosin network is ~7× faster. Furthermore, the large SE for the actomyosin network speed suggests a wide variation in activity.

Each average curve displayed in Fig. 4A is computed from six different regions of interest in two different networks, displayed in Fig. 4B. The curves for both channels of the actin-microtubule network are overlapping with very little spread in the data, suggesting that the contraction dynamics are highly controlled and reproducible. Conversely, the active actin network exhibits a wider spread in τ versus q curves, demonstrating the highly variable activity that actomyosin networks display in the absence of microtubules.

Particles exhibit both subdiffusion and ballistic transport in active actin-microtubule networks

To provide another independent measure of dynamics to complement our DDM results, we perform particle tracking analysis, as described in Materials and Methods. We compute mean squared displacements (MSDs) of beads embedded in each network as a function of lag time Δt. Particles undergoing normal Brownian diffusion exhibit a scaling of MSD~Δt¹, whereas ballistic motion manifests as MSD~Δt² and subdiffusion manifests as MSD~Δt^α with α < 1. To determine the extent to which the network dynamics deviate from Brownian diffusion, we plot MSD/Δt versus Δt curves on a log-log scale (Fig. 5). Subdiffusive MSDs have a negative slope, while superdiffusive or ballistic MSDs have a positive slope. As expected, particles in the inactive actin-microtubule network exhibit purely subdiffusive behavior for all experimental lag times, with MSD~Δt^0.6. This exponent is similar to that reported previously for similar actin-microtubule networks (38). Particles in the active actin network exhibit subdiffusive behavior for the first ~2 to 3 s, after which the motion is nearly ballistic (MSD~Δt^1.7). Particle dynamics in the active actin-microtubule network appear similar to the inactive network for the first ~30 s, with MSD~Δt^0.7, after which it transitions to nearly ballistic behavior similar to the active actin network, with MSD~Δt^1.55. This result demonstrates that thermally driven network fluctuations dictate the mechanics of the active composite network for shorter time scales, while motor-driven contraction controls the motion at larger time scales. This separability of dynamics could play important roles in dictating how the cytoskeleton responds to mechanical and chemical stimuli.

Fig. 5. Particles in active actin-microtubule networks exhibit subdiffusive behavior at short lag times, while near-ballistic motor-driven behavior dominates their long-time dynamics.

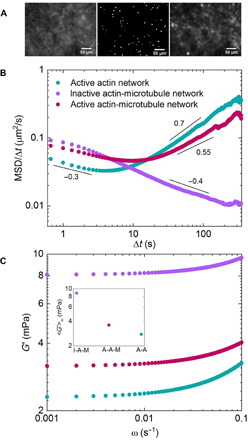
(A) Sample image from one of the movies (movie S9) used for particle-tracking analysis of active actin-microtubule networks (center). Images of microtubules in the network before (left) and after (right) experiments. Scale bars, 50 μm. (B) Mean squared displacements (MSDs) of microspheres embedded in cytoskeleton networks, determined via particle-tracking algorithms, divided by the corresponding lag time (Δt) as a function of Δt. MSD/Δt curves for active actin-microtubule (magenta), active actin (teal), and inactive actin-microtubule (purple) networks are shown. Scaling bars and corresponding numbers show approximate power-law scaling of MSD/Δt curves. Particles in inactive actin-microtubule networks exhibit subdiffusive behavior over the entire experimental window, while in active actin networks, they exhibit near-ballistic dynamics over the majority of the experimental lag times. In active actin-microtubule networks, on the other hand, particles exhibit subdiffusion similar to inactive networks for short lag times but transition to dynamics similar to active actin networks at large lag times. (C) Elastic moduli G′(ω) derived from the MSDs shown in (B). The frequency range shown corresponds to the time scales over which active dynamics (i.e., ballistic motion) are evident in (B). Inset shows <G′>, averaged over all frequencies shown, for each G′(ω) curve displayed. Color code is shown in (B).

To determine the impact of microtubules on the elasticity of actomyosin networks, we evaluate the frequency-dependent elastic modulus, G′(ω), from our particle tracking data using standard microrheology methods described in Materials and Methods (38–42). Figure 5C displays G′(ω) for the frequency range in which active dynamics dominate, as determined from MSDs. As shown, the elastic modulus of the active actin-microtubule network is ~30% higher than the actomyosin network, demonstrating that microtubules stiffen actomyosin networks. However, the inactive network is >2× stiffer than the active networks, indicating that motor activity helps to fluidize the rigid networks. In our previous microrheology studies on steady-state actin-microtubule networks, we showed that actin networks were actually more elastic than actin-microtubule networks due to the increased mesh size and reduced entanglement density of the composite system (38). We further showed that actin-microtubule networks with actin cross-linked by static cross-linkers were ~2× stiffer than those without cross-linkers (30). These steady-state results are at odds with our current results, which show that active actin-microtubule networks are more elastic than actin networks and that active actin cross-linking (by myosin II motors) reduces the elasticity of inactive actin-microtubule networks without cross-linkers. Hence, the motor activity appears to dominate the mechanical response over the connectivity that the increased entanglement density and cross-linking provide.

DISCUSSION

Our collective results demonstrate that microtubules play an essential role in regulating actomyosin dynamics. Specifically, co-entangled actin-microtubule networks driven by myosin II exhibit organized and controlled contraction dynamics. In contrast, similar actomyosin networks that lack microtubules undergo fast, multidirectional motion and network rupturing. While previous studies have shown that in actomyosin networks, actin cross-linking above the percolation threshold is required for organized contraction dynamics, we show here that microtubules can also enable self-organized contractile activity.

There are several ways that microtubules may modulate actomyosin contraction. Microtubules have a ~100× greater persistence length than actin filaments, so a network of microtubules entangled within an actomyosin network may mechanically couple the composite network over larger length scales. Such connectivity is a necessary condition for actomyosin contraction (8). In this manner, microtubules replicate the function of cross-linkers in biasing network activity toward contraction, by increasing network connectivity and facilitating propagation of local myosin activity across a larger range of the network. Previous studies have also shown that in actin-microtubule composites, actin filaments provide lateral reinforcement to microtubules, which are then able to bear larger compressive loads and stabilize the network (43). This interplay may explain why the presence of microtubules both organizes actomyosin activity and slows the rate of network rearrangement.

Last, previous studies have shown that filament rigidity plays an important role in determining whether motor-driven activity is contractile or extensile and the dimensionality of the dynamics (9). Specifically, increasing filament rigidity can reduce the dimensionality of the contraction and also allow for extensile motion at low connectivity and contraction at high connectivity. Hence, the rigidity of the microtubules itself could serve to reduce the degrees of freedom of the dynamics, leading to more organized and controlled motion while, at the same time, offering extensile feedback during contraction to slow the rate of contraction. This interplay between rigidity and connectivity in tuning the active dynamics of myosin-driven networks suggests that a composite network of both rigid microtubules and semiflexible actin filaments can confer contractility and activity that cannot be reproduced in single-filament active systems.

In the cell, the cytoskeleton is a nonequilibrium composite network that self-organizes and restructures to enable processes as diverse as cell motility, mechanosensing, and intracellular transport (4, 8). Many of these processes rely on interactions between actin and microtubules (6, 26, 44, 45) as well as active rearrangement and force generation via motor proteins such as myosin II (4). Here, we present the synthesis and characterization of an active composite network of actin and microtubules with activity driven by myosin motors. We couple PIV with DDM to show that myosin-driven actin-microtubule networks exhibit robust ballistic contractility that is more organized and slower than networks that lack microtubules. Furthermore, while myosin only associates with actin, the dynamics of the actin filaments and microtubules in the network are nearly indistinguishable, suggesting that they are strongly coupled and that the presence of the microtubules can serve to tune the dynamics of actomyosin networks. These findings indicate that in cells, actomyosin contraction may be regulated via microtubules, in addition to chemical cross-linkers. Our particle-tracking analysis also shows that active actin-microtubule networks exhibit subdiffusive behavior at short lag times, similar to inactive networks, and near-ballistic behavior, similar to actomyosin networks, at long time scales. This result suggests that actin-microtubule interactions can allow for multifunctionality of active systems—i.e., exhibiting either steady-state or active responses depending on the time scale. Last, the marked difference in the microheological behavior of active actin-microtubule networks compared with steady-state in vitro cytoskeleton systems (30, 38) highlights the principle role that nonequilibrium activity plays in the measured dynamics.

Our results provide novel insights into the role of actin-microtubule interactions in controlling motor-driven cellular processes, and the myriad of ways in which the cytoskeleton can modulate self-organized activity. Furthermore, our active system provides a powerful modular platform for introducing and independently tuning various cytoskeleton components (e.g., filaments, motor proteins, cross-linkers, and environmental conditions) in a systematic manner to directly link network composition with the resulting active dynamics. Last, the ability to introduce reproducible, self-organized activity into a three-dimensional composite network breaks new ground for designing tunable, self-driven, and self-organized active biomaterials.

MATERIALS AND METHODS

Cytoskeleton protein preparation

Rabbit skeletal actin, porcine brain tubulin, and rhodamine-labeled tubulin were obtained from Cytoskeleton (AKL99, T240, and TL590M), and Alexa Fluor 488–labeled actin was obtained from Thermo Fisher Scientific (A12373). Unlabeled actin was reconstituted to 2 mg/ml in 5 mM tris-HCl (pH 8.0), 0.2 mM CaCl₂, 0.2 mM adenosine 5′-triphosphate (ATP), 5% (w/v) sucrose, and 1% (w/v) dextran. Labeled actin was reconstituted to 1.5 mg/ml in 5 mM tris (pH 8.1), 0.2 mM CaCl₂, 0.2 mM dithiothreitol (DTT), 0.2 mM ATP, and 10% (w/v) sucrose. Unlabeled and labeled tubulin were reconstituted to 5 mg/ml with 80 mM piperazine-N,N′-bis(2-ethanesulfonic acid) (PIPES) (pH 6.9), 2 mM MgCl₂, 0.5 mM EGTA, and 1 mM guanosine 5′-triphosphate (GTP). All cytoskeleton proteins were flash frozen in aliquots and stored at −80°C.

Myosin preparation

Rabbit skeletal myosin II (Cytoskeleton, #MY02) was reconstituted to 10 mg/ml in 25 mM PIPES (pH 7.0), 1.25 M KCl, 2.5% sucrose, 0.5% dextran, and 1 mM DTT, flash frozen in aliquots, and stored at −80°C. To remove enzymatically dead myosin, 16.7 μM actin was polymerized on ice for 1 hour in 550 mM KCl, 10 mM imidazole (pH 7), 2 mM tris (pH 8), 1 mM MgCl₂, 1 mM EGTA, 0.5 mM DTT, 0.4 mM ATP, 0.1 mM CaCl₂, and 8.3 μM phalloidin. After polymerization, 1 mM ATP and 2.8 μM myosin II were added to the actin, and the entire suspension was centrifuged at 4°C for 30 min at 32,000 revolutions per minute. Immediately after centrifuging, the supernatant was removed and stored on ice. Because enzymatically dead myosin binds to actin filaments but does not unbind, the supernatant of the centrifuged solution should contain primarily active myosin.

Cytoskeleton network assembly

Active actin-microtubule networks were polymerized from 2.9 μM each of actin monomers and tubulin dimers in 100 mM PIPES, 2 mM MgCl₂, and 2 mM EGTA supplemented with 0.1% Tween 20, 1 mM ATP, 1 mM GTP, 2.9 μM phalloidin, and 5 μM taxol (46). The addition of phalloidin and taxol stabilizes the actin filaments and microtubules and inhibits treadmilling and other dynamic instabilities (47, 48). To image actin and microtubules, 18% of actin monomers and 10% of tubulin dimers were labeled with Alexa Fluor 488 and rhodamine, respectively. We chose this labeling method, rather than doping in preformed labeled filaments, to enable direct visualization of the network dynamics and morphology, rather than relying on tracer filaments as reporters. The caveat to this technique is that individual filaments cannot be resolved, as each filament is too sparsely labeled and the network is too dense [~0.8-μm mesh size (30)]. Hence, the images in Fig. 1 show network structure but not individual filaments. After the networks were polymerized for 1 hour at 37°C, an oxygen scavenging system [glucose (45 μg/ml), 0.005% β-mercaptoethanol, glucose oxidase (43 μg/ml), and catalase (7 μg/ml)] was added to reduce photobleaching during fluorescence imaging, 0.24 μM myosin was added to introduce network activity, and 50 μM blebbistatin was added to inhibit myosin activity until imaging began. While we do not directly visualize the myosin in the networks, based on the uniformity of the contraction that we see in actin-microtubule networks, we expect myosin II minifilaments to be evenly distributed. Furthermore, if we estimate ~400 myosin II proteins per minifilament (14), then a 1:12 myosin:actin molar ratio gives a ~1:4800 myosin minifilament:actin monomer ratio. Hence, each myosin II minifilament that cross-links two actin filaments together is spaced apart by ~2400 monomers. With a length per actin monomer of ~2.7 nm (49–51), we expect that myosin II minifilaments are spaced apart by ~6 μm. Previous work on actomyosin networks with a comparable myosin:actin ratio showed similar spacing between minifilaments (14).

Sample preparation

All samples were loaded into a thin rectangular chamber, formed by adhering a silanized glass coverslip to a glass slide using two strips of heated parafilm (~70-μm thickness). The chambers were immediately sealed with epoxy and then imaged. To prevent myosin from adhering to the surface, coverslips were passivated with silane as follows. Coverslips were first plasma cleaned for 30 min and then immersed in a succession of acetone, ethanol, 0.1 M KOH, and water baths. Once completely dry, coverslips were immersed in 2% dimethyldichlorosilane, successively immersed in ethanol and water to remove the excess silane, and then dried before use. Coverslips were used within a month of silanization (52).

Confocal microscopy

A Nikon A1R laser scanning confocal microscope was used to image networks with a 60× 1.4 numerical aperture (NA) objective (Nikon) and multiple laser lines and filters to allow for two-color imaging. Microtubules were imaged using a 561-nm laser with 561-nm excitation and 595-nm emission filters. Actin was imaged using a 488-nm laser with 488-nm excitation and 525-nm emission filters. The 488-nm light also served to inactivate the blebbistatin and initiate myosin activity. Time series were taken in the middle of the ~70-μm-thick chamber for 6 min at a frame rate of 2.78 frames per second (fps). Examples of the time series are shown in movies S1 to S3, and representative 256 × 256 pixel images (212 × 212 μm) are shown in Fig. 1. Experiments were performed on six different replicates.

Particle image velocimetry

To determine the direction of motion of the filaments during activity, PIV analysis was performed using the PIV ImageJ plugin (53). This analysis iteratively measured the cross-correlation in image intensity between regions of two images in a time series spaced a lag time Δt apart. We chose to perform PIV analysis during four equally spaced time points spanning the 6-min time series. Each image was divided into 64 regions, from which we generated a field of 64 vectors, each representing the optic flow of a specified region. We chose Δt = 20 s for active actin-microtubule networks and Δt = 3 s for active actin networks, because the actin-microtubule and actin networks moved a similar distance during these time differences, and motion due to thermal noise was negligible.

Differential dynamic microscopy

We performed DDM analysis on each time series using custom Python scripts (54). DDM analysis determines how quickly density fluctuations decay by taking Fourier transforms of the difference between images separated by a given lag time Δt (55). The average Fourier transform squared of all image differences for a given lag time yields the image structure function D(q, Δt). For systems that exhibit a plateau at long lag times, we fit D(q, Δt) to the following model

$$\mathit{D}(\mathit{q},\mathrm{\Delta }\mathit{t})=\mathit{A}(\mathit{q})\times (1-\mathit{f}(\mathit{q},\mathrm{\Delta }\mathit{t}))+\mathit{B}(\mathit{q})$$

where, q is the wave vector, A(q) is the amplitude, B(q) is the background, and f(q, Δt) is the intermediate scattering function, which contains the dynamics of the system.

To determine the type of motion and the corresponding rate, we model each intermediate scattering function as an exponential

$$\mathit{f}(\mathit{q},\mathrm{\Delta }\mathit{t})={({\mathit{e}}^{-(\mathit{q})/\mathrm{\Delta }\mathit{t}})}^{\mathrm{\gamma }}$$

where τ is the decay time and γ is the scaling factor. We evaluate the decay time τ as a function of q to characterize the type of motion. For example, if τ~1/kq, then the system exhibits ballistic motion and k represents the corresponding velocity. If τ~1/kq², then the system exhibits diffusive motion and k represents the diffusion coefficient. The factor γ stretches or compresses the exponential, and typical values are shown in table S1. γ < 1 characterizes a stretched exponential, while γ > 1 characterizes a compressed exponential. Compressed exponentials are indicative of systems undergoing slow ballistic relaxation of internal dipole stresses over larger length scales (56), which is consistent with stresses generated by myosin motor activity.

Particle tracking

As a complementary method for observing active network dynamics, 1-μm polystyrene microspheres were embedded in networks and tracked using custom Python scripts (57). The beads were labeled with Alexa Fluor 488–bovine serum albumin to visualize and prevent nonspecific binding to the proteins or surfaces. Time series of beads were collected at 2.78 fps for 6 min using an Olympus IX73 inverted fluorescence microscope with a 20× 0.4 NA objective, 480/535-nm excitation/emission filters, and a Hamamatsu ORCA-Flash 2.8 complementary metal-oxide semiconductor (CMOS) camera (180 nm per pixel). To verify network formation and reconfiguration from myosin activity, images of the microtubules in the networks were taken before and after each time series using 578/603-nm excitation/emission filters. The bead concentration was such that ~50 beads were tracked in each 1920 × 1440 pixel field of view (346 × 259 μm) (movie S9). We use custom Python scripts to measure the frame-to-frame x and y displacements of the beads and compute the MSD of the ensemble of beads for lag times of 0.33 s < Δt < 343.3 s. From the MSDs, we also compute the elastic modulus G′ as a function of frequency ω using previously described microrheology methods that relate MSDs to the complex shear modulus via the generalized Stokes-Einstein relation (38–42).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/6/eabe4334/DC1

View/request a protocol for this paper from Bio-protocol.