Nonlinear elasticity and damping govern ultrafast dynamics in click beetles

Significance

Click beetles are among animals that amplify mechanical power output using springs and latches to perform ultrafast movements. Studies involving these animals have been limited to observing the kinematics of the movements. Here, we study the kinematics and dynamics of the extremely fast bending maneuver performed by click beetles (i.e., the clicking motion). First, we identify the latching, loading, and release phases of the clicking motion using high-speed synchrotron X-ray imaging. Second, we discover a portion of the spring mechanism that the beetles use to store and quickly release energy. Finally, using specialized analytical methods, we characterize the damping and elastic forces that govern the release phase, which explains why the beetles can rapidly perform this click without significant damage.

Abstract

Many small animals use springs and latches to overcome the mechanical power output limitations of their muscles. Click beetles use springs and latches to bend their bodies at the thoracic hinge and then unbend extremely quickly, resulting in a clicking motion. When unconstrained, this quick clicking motion results in a jump. While the jumping motion has been studied in depth, the physical mechanisms enabling fast unbending have not. Here, we first identify and quantify the phases of the clicking motion: latching, loading, and energy release. We detail the motion kinematics and investigate the governing dynamics (forces) of the energy release. We use high-speed synchrotron X-ray imaging to observe and analyze the motion of the hinge’s internal structures of four Elater abruptus specimens. We show evidence that soft cuticle in the hinge contributes to the spring mechanism through rapid recoil. Using spectral analysis and nonlinear system identification, we determine the equation of motion and model the beetle as a nonlinear single-degree-of-freedom oscillator. Quadratic damping and snap-through buckling are identified to be the dominant damping and elastic forces, respectively, driving the angular position during the energy release phase. The methods used in this study provide experimental and analytical guidelines for the analysis of extreme motion, starting from motion observation to identifying the forces causing the movement. The tools demonstrated here can be applied to other organisms to enhance our understanding of the energy storage and release strategies small animals use to achieve extreme accelerations repeatedly.

Some of the fastest and most extraordinary motions of the animal kingdom are employed by small animals to hunt, locomote, or escape predators. Fleas, froghoppers, mantis shrimps, trap-jaw ants, and click beetles are capable of achieving accelerations up to ${\mathrm{10}}^6$ m/${\mathrm{s}}^2$ repeatedly (1–6). Such extreme motions cannot be generated directly by muscles, animals’ most common actuators (7). Instead, some animals have evolved complex structures and materials to overcome this actuation limitation by amplifying the mechanical power output of the muscles with springs and latches. Such systems allow elastic energy to be slowly stored, and, upon release of the latch, very fast recoil of the spring powers the motion. The difference between the energy storage and release timescales results in mechanical power output amplification. Trap-jaw ants, for example, store elastic energy slowly ($\sim$400 ms) by deforming parts of their exoskeleton when loading their mandibles to the open position. In contrast, the elastic recoil of the distributed exoskeletal springs occurs more than 600 times faster ($\sim$0.6 ms), resulting in the mandibles snapping shut (1, 8, 9). Fast elastic recoil of body elements is also used by some plants to disperse seeds and pollen, to feed, or to defend themselves (10–12). The Venus flytrap, for instance, captures insects by closing two jaw-like shell lobes in $\sim$100 ms (10).

Identifying the energy release mechanisms animals use to amplify mechanical power output is challenging because springs in most organisms are internal and distributed throughout the body. As a result, very few spring mechanisms have been identified in power-amplified biological systems, also referred to as latch-mediated spring-actuated (LaMSA) organisms (13). Most studies on such systems focus on kinematics, that is, the analysis of the position, velocity, and acceleration time series. Variations in these metrics help describe the different body part movements and their interaction with one another. However, kinematics-based analyses do not enable the identification of the forces that cause the movement (kinetics), which is critical to explaining how extreme accelerations are generated. By combining kinematics with kinetics, that is, considering the dynamics, we can derive the equations of motion, identify the governing forces, and detail their contributions that lead to ultrafast motions. Dynamics-based analyses are also essential to simulating a system’s response to external stimuli and evaluating the effects of microscale and mesoscale properties, such as material composition and architecture, on the energy storage and dissipation strategies.

In this paper, we focus on click beetles (Coleoptera: Elateridae), an under-studied group of animals that use springs and latches to amplify mechanical power output (Fig. 1A) and whose spring mechanism is unknown. Click beetles have fascinated scientists because of a unique morphological adaptation, the thoracic hinge, that enables them to bend their body along the hinge (Fig. 1A, black arrow), and then to accelerate their center of mass by unbending (Fig. 1A, dashed arrow) extremely quickly (3). When the click beetle’s body is unconstrained and on a hard surface, this fast unfolding motion results in a jump (3, 14, 15). The body bending and unbending motion is referred to as the click or clicking motion because it generates an audible “clicking” sound, similar to snapping one’s fingers. The thoracic hinge is composed of two conformal parts: the peg and the mesosternal lip (Fig. 1A), which together form a mechanical latch (4). When the latch is engaged, the beetle stores elastic energy in a still unknown distributed spring; the recoil of the spring leads to the clicking motion (3, 4, 16). Although the kinematics of the jump have been studied (3, 14–18), as have the latch geometry and mechanics (4), the unique clicking motion that enables the jump has not been described, let alone analyzed in detail. Specifically, the phases of the click have never been determined, nor have the elastic energy storage and release mechanisms. As the clicking motion happens at a much faster timescale than the jump, it requires specialized analysis tools to characterize the movement (kinematics) and the forces (dynamics).

Fig. 1.

Phases of the clicking motion and characterization of the peg tip and the soft cuticle displacement during the loading and energy release phases. (A) Adult E. abruptus click beetle general appearance (with legs removed) and lateral view projections of the hinge extracted from the X-ray recordings. Lateral view projections show the interaction between the peg, the mesosternal lip, and the cavity during the clicking motion. The landmark points tracked at the peg tip (green star), along the soft cuticle situated behind the peg (blue markers), and along the upper part of the cavity (yellow markers) are highlighted. The clicking motion can be divided into three phases: latching (i and ii), loading (iii and iv), and energy release (v–viii). During the latching phase, the peg slides along the cavity (i) and latches on the mesosternal lip (ii). Then, the loading phase begins as the soft cuticle contracts (iii). While the soft cuticle is contracting (i.e., displacing dorsally), the peg slowly rotates about the contact with the mesosternal lip (iii and iv, purple arrow). At the end of the contraction (iv), the latch is released (unlatching, v), and the peg slips and slides along the mesosternal cavity as the soft cuticle recoils (vi). During the energy release phase, the peg oscillates along the mesosternal cavity (vi and vii), until coming to a rest inside the cavity (viii). When the peg reaches the interior of the cavity, the soft cuticle and the mesosternal lip come in contact (vii and viii). Colored arrows indicate the movement direction of the peg (i and v–vii) and the soft cuticle (iii and vi). (B) Position of the peg tip of specimen 1 in x and y coordinates during the clicking motion. At t = 0.208 s, the peg is unlatched, and fast oscillations occur. (C) Fast damped oscillations of the peg tip in x and y coordinates during the energy release phase. (D) Duration of the energy release phase of the clicks of the four E. abruptus specimens. (E) Displacement of the soft cuticle and duration of the loading phase for the four specimens. The blue colors represent the start of the loading phase (0 s), and the red colors represent positions at the end of the loading phase (0.15 s). (F) Recoil of the soft cuticle at the beginning of the energy release and duration of the unlatching and elastic recoil for specimens 1 and 2. The blue colors (t = 0.1545 s) represent the start of the energy release phase (unlatching), and the red colors represent the first contact between the soft cuticle and the mesosternal lip, that is, the end of the elastic recoil at t = 0.1553 s. Error bars represent ± 1 SD.

In this study, we ask the following questions: 1) What are the phases of the clicking motion? 2) What are the elastic energy storage and release mechanisms in click beetles? 3) Can the energy release mechanism be inferred from the latch dynamics during the energy release phase? This study describes, in detail, the loading phase of the clicking motion and analyzes the energy release kinematics and dynamics in click beetles. This work expands our knowledge of power-amplified systems in nature, and provides a path for the analysis of the dynamics of ultrafast motions by applying physics-based analytical tools such as spectral analysis and nonlinear system identification.

Results

Clicking Motion Phases.

The high-speed X-ray recordings of the hinge allow for the visualization and identification of the phases of the clicking motion. The clicking motion can be divided into three phases: latching, loading, and energy release (Fig. 1). Prior to the click, the peg is at rest in the cavity (Fig. 1 A, i). The latching phase starts as the beetle rotates the anterior body (head and prothorax) dorsally (Fig. 1A, black arrow). The rotation produces a bend in the body such that the head and thorax are angled upward relative to the posterior body (Fig. 1A). The peg slides anteriorly out of the cavity (Fig. 1 A, i), and sets in place on the mesosternal lip, forming a “latch” (Fig. 1 A, ii) (4).

During the loading phase, the bend in the body is maintained as the latch is locked, and energy is stored in the system. The latch is maintained by the contact of conformal surfaces between the peg and the mesosternal lip (Fig. 1 A, ii–iv and Movie S1) (4). The loading phase is characterized by the large dorsally directed deformation of the soft cuticle (Fig. 1 A, iii and iv and E), and by the slow rotation of the peg about the contact surface with the mesosternal lip (Fig. 1 A, iii and iv, purple arrow, and Fig. 1B). The contraction of the soft cuticle during the loading phase of specimen 1 is shown in Fig. 1E. The contraction duration lasted, on average, 160 ms for specimen 1, 235 ms for specimen 2, 33 ms for specimen 3, and 243 ms for specimen 4 (Fig. 1E).

At the end of the soft cuticle contraction, the peg slips, unlocking the latch and beginning the energy release phase (Fig. 1 A, v–viii, B, and C). The energy release phase consists of unlocking the latch (Fig. 1 A, v), a rapid initial energy release referred to as elastic recoil (Fig. 1 A, vi), and energy dissipation through oscillatory motion (Fig. 1 A, vii and viii). The unlocking of the latch (Fig. 1 A, v) involves shearing of the conformal surfaces of the peg and mesosternal lip until they are no longer in contact, an extremely fast process (about 0.1 ms). As these two surfaces slide past each other, the head and thorax rotate counter to the direction of loading, bending the body in the opposite direction (Fig. 1A, dashed arrow). The peg slides along the mesosternal cavity, and the soft cuticle displaces ventrally in about 0.8 ms (Fig. 1 A, vi and F). The movement continues in an oscillatory fashion (Fig. 1 A, vii, B, and C), as the peg swings in and out of the cavity multiple times before coming to rest in the cavity (Fig. 1 A, viii and Movie S2). The energy release phase lasted, on average, 13.8 ms for specimen 1, 17.4 ms for specimen 2, 7.4 ms for specimen 3, and 8.8 ms for specimen 4 (Fig. 1D).

Energy Release Kinematics.

During the energy release, the soft cuticle quickly displaces, and the peg swings in and out of the mesosternal cavity, until coming to rest at the starting position. Here we focus on the deformation of the soft cuticle (Fig. 1F) and the oscillations of the peg tip (Fig. 1A, green star, and Fig. 1C) to describe and quantify the energy release kinematics.

The soft cuticle displaces ventrally at the beginning of the energy release phase and comes in contact with the mesosternal lip in less than 1 ms (Fig. 1F). The short duration of this displacement (less than 1 ms) of the soft cuticle compared to the loading displacement timescale (33 ms to 243 ms; Fig. 1E) suggests that the observed displacement at the beginning of the energy release is an elastic recoil, defined as a fast release of stored elastic energy.

The position of the peg tip during the energy release phase of specimen 1 is shown in Fig. 1C. The high-speed recordings show that, throughout the oscillations of the energy release phase, the peg and the upper surface of the cavity remain in contact (Fig. 1A and Movie S2). The trajectory of the peg is thus constrained by the cavity’s geometry, with the peg tip following an arc along the upper surface of the cavity (Fig. 2A).

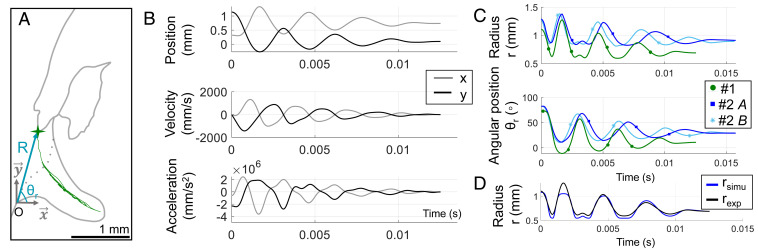
Fig. 2.

Kinematics of the energy release phase. (A) The trajectory of the peg tip as the peg oscillates (i.e., swings along the cavity) during the energy release phase is shown in green. O is the origin of the Cartesian ($x$ and $y$) and the polar (${\theta }_r$ and $r$) coordinates, fixed at the edge of the cavity. (B) Position, velocity, and acceleration of the peg tip of specimen 1 during the energy release phase in Cartesian coordinates. (C) Position of the peg tip in polar coordinates during the energy release phase of specimen 1 (one click, referred to as “1”) and specimen 2 (two clicks, referred to as “2A” and “2B”). (D) Experimental and simulated $r$ response during the energy release phase. The simulated radius, $r$, is recovered from the experimental angular position of the peg tip, ${\theta }_r$, and the cavity’s geometry mapping.

The peg kinematics during the energy release phase were measured by tracking the position of the peg tip per Fig. 1A. These calculations assume that the trajectory is planar throughout the energy release, which is consistent with the overall sagittal motion observed. During the energy release, the peg tip reaches a maximum velocity of 1.8 m/s, which corresponds to about 1,000 peg lengths per s (peg length is $\sim$1.8 mm) and a maximum acceleration of 5.2 $\times \hspace{0.17em}{\mathrm{10}}^3$ m/${\mathrm{s}}^2$, or 530 times the gravitational acceleration (SI Appendix, Table S2).

During the energy release, the main body motion is a rotation of the head and prothorax around the hinge in the sagittal plane. The kinematics was analyzed using polar coordinates to explain the rotational motion (Fig. 2C). The origin of the polar coordinates is colocated with the origin in Cartesian coordinates, namely, at the edge of the cavity. The radius $r$ represents the distance of the peg tip relative to the origin, and the angle ${\theta }_r$ represents the rotation of the anterior body (head and thorax) about the origin, calculated as $r=\sqrt{x^2+y^2}$ and ${\theta }_r=arctan\left(y/x\right)$, where x and y are the horizontal and vertical positions in Cartesian coordinates (Fig. 2 A and B). The oscillations previously observed in the x and y coordinates (Figs. 1 B and C and 2B) are visible in the polar coordinates, $r$ and ${\theta }_r$ (Fig. 2C).

Energy Release Dynamics.

After unlatching, the motion of the peg is used to identify the dynamics of the energy release (Movie S2 and Fig. 1 A, vii–viii). More specifically, the kinematics of a component of the latch, namely, the peg tip, is used to characterize the dynamics of the energy release phase. We modeled the click beetle as a one-degree-of-freedom system and analyzed the spectral signature of the angular position of the peg tip. Then, we applied nonlinear system identification methods to identify the forces driving this motion.

One-degree-of-freedom system analysis.

The movements of the peg along the cavity are spatially constrained by the cavity’s geometry (see Energy Release Kinematics). Thus, the radius $r$ and angular position of the peg tip ${\theta }_r$ are not independent but are coupled by the cavity’s geometry. As such, the motion of the peg can be fully described using one independent parameter, the radius $r$ or the angular position ${\theta }_r$, and the cavity’s geometry, which represents a nonlinear mapping that couples $r$ and ${\theta }_r$. Therefore, we modeled the system as an oscillator with one degree of freedom, using the angular position ${\theta }_r$ as the independent parameter because it represents the anterior body’s oscillations. The nonlinear spatial mapping of the cavity’s geometry was obtained by tracing the upper part of the cavity in the X-ray images, following the yellow landmarks shown in Fig. 1A. Fig. 2D compares the experimental response of $r$ to its response derived from the experimental response of the angular position of the peg tip ${\theta }_r$ and of the cavity’s geometry mapping. The period of oscillation and the amplitude of the $r$ response can be recovered from the cavity’s geometry mapping and the experimental angular position ${\theta }_r$ (Fig. 2D), supporting the assumption that the peg oscillations can be modeled as a one-degree-of-freedom oscillator. We attribute the deviations in amplitude in Fig. 2D to resolution limits in measuring the cavity’s geometry. For the remainder of the paper, the angular position of the peg tip, ${\theta }_r$, is shifted to set the final equilibrium position to zero and facilitate the dynamics analysis calculations. The shifted angular position of the tip is referred to as $\theta$ (Fig. 3A).

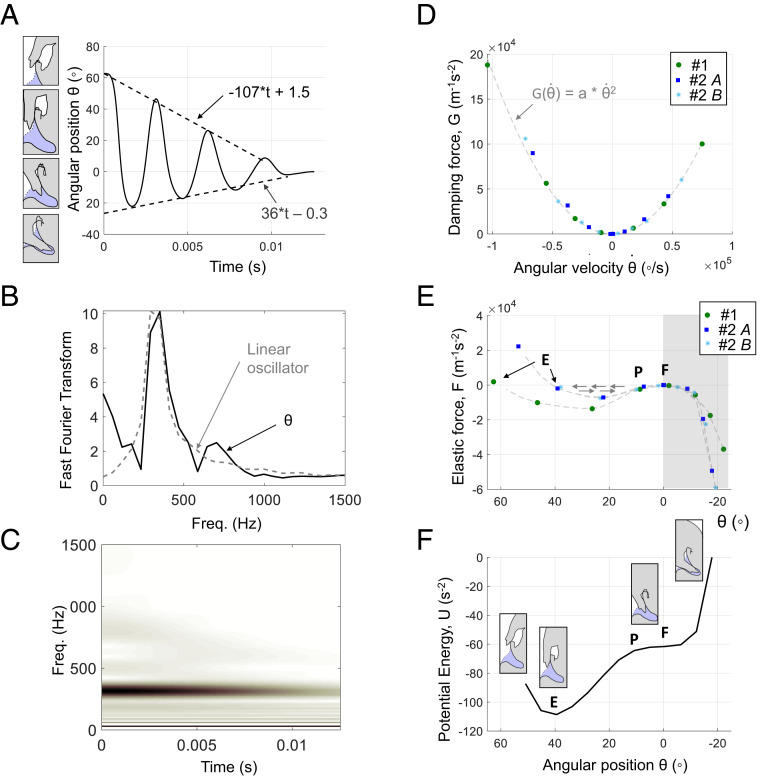
Fig. 3.

The angular position of the peg tip kinematics, spectral analysis, and nonlinear system identification during the energy release phase. (A) Representative angular position of the peg tip $\theta$ as a function of time during the energy release (specimen 1) with the final equilibrium position set to zero. Two linear decay rates with different slopes are observed for all specimens. The peg tip oscillations are asymmetric with respect to the final (resting) equilibrium. (B) Discrete Fourier transform of the angular $\theta$ response of specimen 1 and of a linear time-invariant oscillator. The fast Fourier transform of the angular position response, $\theta$, shows the fundamental frequency at 352 Hz, a second harmonic at 703 Hz, and a zero frequency. In comparison, the Fourier transform of the linear time-invariant oscillator (the dashed line) shows a fundamental frequency only. (C) The wavelet transform plot of the $\theta$ response of specimen 1 shows the decay in amplitude of the fundamental frequency and the second harmonic as time increases. (D) The normalized damping force for all responses (specimen 1 and 2) is nonlinear and follows the same quadratic curve, with a coefficient $a=1.8^{*}10^{-5}$. (E) The normalized elastic force is also nonlinear and shows two regions, for negative and positive positions of the peg tip $\theta$. A very stiff region is shown for negative $\theta$ and corresponds to the angles where the soft cuticle and the mesosternal lip are in contact. A region of negative stiffness is observed between 0° and $\mathrm{25}°$ (note that the x axis is decreasing). The elastic force curve is characteristic of a snap-through buckling system, where P, E, and F are three equilibrium points. P is commonly referred to as the critical point, and F is the final equilibrium point (resting position at the end of the motion). (F) Representative potential energy curve (specimen 2, release A). The two equilibria F and E are stable, and P is unstable. The motion sketches represent the positions of the peg at the different $\theta$ angles during the energy release phase.

Spectral analysis of the $\theta$ response.

The angular position of the peg tip $\theta$ during the energy release phase of specimen 1 is shown in Fig. 3A. For all clicks recorded, the angular position, $\theta$, is asymmetrical with respect to the final equilibrium, and two linear decay envelopes are fitted. The Fourier and the wavelet transforms are used to uncover the spectral behavior of the angular position response, $\theta$. The Fourier transform shows that the dominant frequencies of the angular position response signal are at 0, 352, and 703 Hz (Fig. 3B), which are also revealed in the wavelet transform plot (Fig. 3C). The zero frequency observed in the angular position response $\theta$ reflects the asymmetry of the system, previously shown in Fig. 3A. The frequency of 352 Hz is the fundamental frequency (or first harmonic) and has the highest amplitude in the Fourier transform plot and the darkest shade in the wavelet transform plot (Fig. 3 B and C). The frequency of 703 Hz is the second harmonic. The wavelet transform indicates how the frequencies vary with time. Fig. 3C shows that the amplitude decays, as indicated by the lighter shades of the fundamental frequency (352 Hz) and the second harmonic (703 Hz), as time increases. Amplitude decay with time is characteristic of a damped system.

The kinematic and spectral analyses suggest that the response of the angular position of the peg tip response, $\theta$, can be modeled as a damped oscillator with a single degree of freedom. Thus, the general form of the equation of motion can be formulated as

$$a_{\theta }+G\left(\stackrel{.}{\theta }\right)+F\left(\theta \right)=0,$$ [1]

where $G$ is the total normalized velocity-dependent force, which is often related to damping or energy-dissipative forces, and $F$ is the total normalized displacement-dependent force, which is often related to elastic or energy-storing forces. $a_{\theta }$ is the circumferential acceleration defined as $a_{\theta }=r\stackrel{.}{\theta }+2\stackrel{.}{r}\stackrel{.}{\theta }$, and $\stackrel{.}{\theta }$ is the time derivative of the $\theta$ coordinate. $a_{\theta }$, $\stackrel{.}{\theta }$, and $\theta$ are known from the angular kinematics (Figs. 2 and 3A). The damping and elastic forces $G$ and $F$ are yet to be determined.

Damping and elastic force characterization using nonlinear system identification.

The normalized damping force, G, and the normalized elastic force, F, can be estimated from the experimental kinematic data following the restoring force method (19). This method enables the identification of nonlinear forces that are dependent on velocity (e.g., damping forces) and displacement (e.g., elastic forces) in the presence of inertial terms (19). Per Eq. 1, at $\theta =0$, $G\left(\stackrel{.}{\theta }\right)=-a_{\theta }$, and, at $\stackrel{.}{\theta }=0$, $F\left(\theta \right)=-a_{\theta }$. Fig. 3 D and E shows that both forces are nonlinear and follow the same trends for all clicks analyzed.

For all clicks recorded from specimens 1 and 2, the damping force follows a quadratic curve (Fig. 3D). The nonlinear elastic force shown in Fig. 3E features two regions. The first region is defined from $\theta =-22°$ to $0°$ and corresponds to the positions of the peg inside the cavity. In this region, the mesosternal lip is in contact with the soft cuticle (Fig. 1 A, vii and viii), and thus the stiffness is large relative to the second region, as indicated by the steep slope in the shaded region of Fig. 3E. The second region is defined from $\theta$ = 0° to $\mathrm{63}°$, and corresponds to the positions of the peg outside and at the entrance of the cavity, where there is no contact between the soft cuticle and the mesosternal lip. Within this second region, between $\theta$ = 0° and $\mathrm{25}°$, the slope of the elastic force–displacement curve becomes negative (note that the x axis in Fig. 3E is decreasing), which is indicative of negative stiffness. A positive slope (i.e., positive stiffness) is observed again in the rest of the second region (i.e., $\theta$ values between 25° and $\mathrm{63}°$). The overall shape of the elastic force (Fig. 3E) is characteristic of snap-through buckling (20). Snap-through buckling is a mode of instability that enables a system to pass rapidly from one equilibrium position to another nonadjacent equilibrium position that may be physically distant. A snap-through buckling system exhibits two stable equilibria and one unstable equilibrium. Equilibrium points are indicated 1) by a maxima or minima in the energy plot (Fig. 3F) and 2) with points at which the force (Fig. 3E) is zero. The stability of the equilibrium points is determined by the curvature of the energy plot; positive concavity indicates a stable equilibrium, while negative concavity indicates an unstable equilibrium. This condition is reflected in the potential energy curve by two “valleys” (positive concavity) and one “hill” (negative concavity). Here, points F, P, and E are approximate positions of equilibrium points defined by the rotation angles at which the force is approximately zero. The potential energy landscape (Fig. 3F) shows that P, commonly referred to as the critical point, is unstable, and that E and the final resting equilibrium, F, are stable. A critical point refers to the unstable equilibrium point, where an infinitesimal change in load causes rapid movement toward a stable equilibrium. Thus, during the energy release phase, the peg snaps between the potential energy local minima F and E in Fig. 3 E and F.

The identification method (restoring force method) used is validated by estimating the circumferential acceleration for all releases (SI Appendix, Fig. S2). The estimated F and G functions predict well the frequency and the decay of the circumferential acceleration, except for the first 0.001 s of the release, which represents the transient response. The transient response corresponds to the unlatching phase (Fig. 1A, v and C.), which is not modeled in this study. The circumferential accelerations for the three clicks are reproduced based on the forces identified in Fig. 3 D and F for specimen 2 release A (SI Appendix, Fig. S2). SI Appendix, Fig. S2 shows the model’s predictive capability to reproduce similar movements not used to generate the model.

Discussion

In this study, we identified and quantified the phases of the clicking motion and uncovered part of the spring mechanism in click beetles. In-depth analysis of the movement (kinematics) and the forces (dynamics) during the energy release phase enabled the formulation of the equation of motion and the characterization of the elastic and damping forces that govern the ultrafast release.

Studying the clicking motion using high-speed synchrotron X-ray revealed three distinct phases of the click, namely, latching, loading, and energy release. The relatively long duration of the loading phase (160 and 235 ms in specimens 1 and 2) compared to the overall duration of the energy release phase (13.8 and 17.4 ms), indicates that energy is released much faster than it is stored. The time difference between the energy storage and release supports that click beetles can amplify mechanical power during the clicking motion. Therefore, like other biological power-amplified systems, click beetles rely on latch-mediated spring mechanisms (13) to amplify muscle mechanical power output. The use of spring mechanisms enables fast dissipation of energy through elastic recoil, specifically, fast release of stored elastic energy via passive elements. For animals, the advantage of using spring mechanisms as actuators is that they are not limited by muscle contraction speed (21). However, prior to this study, the spring mechanisms of click beetles were unknown, limiting our understanding of their capability to store and release elastic energy.

High-speed X-ray images of the hinge reveal large displacements of the soft cuticle during the loading and energy release phases. Additionally, the very fast displacement of the soft cuticle at the beginning of the energy release phase is characteristic of an elastic recoil. Thus, the soft cuticle in the hinge is likely to be a component of the distributed spring mechanism that click beetles use to power the motion. Other parts of the exoskeleton may also be able to store and release elastic energy and will be studied further in the future using a different experimental setup. The click beetle’s exoskeletal spring system is comparable to other power-amplified systems where the difference in energy storage and release duration is also significant. For example, the trap-jaw ants in the genus Ondotomachus store elastic energy in $\sim$400 ms and release it in less than 1 ms (22). Thus, like trap-jaws ants and mantis shrimps, click beetles belong to a category of animals that use their exoskeleton as a spring to power the motion (22–24).

In the click beetle, the elastic recoil of the soft cuticle results in an energy release phase that is extremely dynamic, exhibiting multiple oscillations over a very short timescale. Spectral analysis techniques were used to study the angular position of the peg tip as a function of both frequency and time. Analyzing both the frequency and time histories of the motion enabled us to derive the general form of the equation of motion, namely, a single nonlinear differential equation in terms of the angular position, including a damping term and an elastic term (Eq. 1). Nonlinear terms in the equation of motion indicate that the forces acting on the system, the elastic and damping forces, do not increase (or decrease) proportionally throughout the motion. Compared to a linear, time-invariant, spring-mass, damped oscillator, which is the simplest representation of a single-degree-of-freedom oscillator (Fig. 3B, dashed line), the angular position of the peg tip (Fig. 3B, solid line) exhibits two frequencies in addition to the fundamental frequency or first harmonic (i.e., the largest component at 352 Hz): a zero frequency (i.e., a large component at 0 Hz) and a second harmonic. The zero frequency means that the angular position response is asymmetric, and the second harmonic indicates the existence of a quadratic nonlinearity (25). The asymmetry of the angular position response, $\theta$, may be due to the contact between the mesosternal lip and the soft cuticle when the peg is inside the cavity, constraining the motion for negative $\theta$ positions (Fig. 1 A, vii and viii; see Energy Release Kinematics). While most analyses of extreme motions have been limited to investigations of kinematics (13, 26), here, we consider the frequency response of the motion to investigate the dynamics of the energy release. The spectral analysis informs our choice of an appropriate equation of motion structure and enables us to connect the discovered phenomena (asymmetry in the position graph) with physical observations (dynamic contact between two body parts).

During the energy release, the elastic and damping terms (F and G in Eq. 1) of the one-degree-of-freedom oscillator that describe the angular position of the peg tip were determined using nonlinear system identification. The restoring force system identification method is capable of extracting the total displacement and velocity-dependent forces, referred to as the elastic and damping forces. However, the exact source and constraints that contribute to each of these forces would require additional experiments. Nonetheless, characterizing the elastic and damping forces reveals the fast energy actuation and energy dissipation strategies used by click beetles to overcome muscle velocity limitations. For example, understanding the elastic recoil strategy is fundamental to explain the material and musculoskeletal properties required to generate extremely fast energy release. Additionally, uncovering damping strategies can inform fatigue and damage considerations in power-amplified systems.

The overall shape of the elastic force, which features a negative stiffness region (Fig. 3E), is characteristic of snap-through buckling systems (20). Our analysis shows that snap-through buckling is the dominant elastic recoil mechanism governing the angular position of the peg during the energy release phase. In the click beetle, the use of snap-through buckling as the elastic recoil strategy enables the peg to move between physically distant points extremely quickly, with only a small change in applied forces, effectively leveraging energy transfer to move between low-energy states. Snap-through buckling has also been observed in other plants and animals. For example, the Venus flytrap uses snap-through buckling as the governing energy release mechanism to shut its jaw-like shells (10). Unlike the visible snap-through buckling of the Venus flytrap shells, no visible snapping or deformations were observed in the hinge of the click beetles in this study. Thus, there is a need to examine other parts of the cuticle in the future to uncover the portions of the body that may snap during the energy release phase.

The damping force is of quadratic form (Fig. 3D), which confirms the existence of a nonlinear quadratic term in the equation of motion as predicted by the spectral analysis. A damping force of quadratic form is usually characteristic of air damping (27). However, quadratic damping could also arise due to the contact between the soft cuticle and the mesosternal lip (Fig. 1 A, vii) during the energy release oscillations, or due to the contact between the peg and very low stiffness compliant elastic anatomical elements such as hairs, which have been previously observed on the upper part of the cavity (4). Although the linear decay of Fig. 3A may indicate that the primary damping mechanism is dry friction (Coulomb friction), both the frequency analysis and nonlinear system identification demonstrate that the damping is quadratic. Previous work by some of the authors has shown that the surfaces of the peg and the mesosternal cavity in contact during the energy release are very smooth (4). Consequently, dry friction is not likely the primary mechanism of energy dissipation. The quadratic damping profile may explain why click beetles can perform the clicking motion repeatedly without apparent external damage in the hinge, which would have been expected if dry friction was the primary source of energy dissipation.

Uncovering the elastic and damping forces driving the release provides several key insights. First, we show that the clicking motion can be modeled as a single-degree-of-freedom system during the release phase. This model structure allows us to infer the energy release dynamics from observations and analysis of the hinge’s motion, specifically, by analyzing the motion of the soft cuticle and latch dynamics. Second, the forces identified during the release are nonlinear. Knowledge of the dissipation forces profile (quadratic) and the elastic force profile (snap-through buckling, an asymmetric instability) will guide future studies to investigate the bending and deformation of the soft cuticle, and the contact between the soft cuticle and the hinge, and to look for shell-like structures in the hinge. Snap-through buckling is commonly observed in thin shells, and the material properties of such structures are of primary interest for studies on fatigue and damage mitigation.

This paper integrates biological knowledge with physics-based experimental and analytical tools to examine the click beetle’s ultrafast clicking motion. The tools applied in this study allow for the analysis of LaMSA organisms as integrated dynamic systems. This study provides a pathway for the analysis of ultrafast motion starting from traditional motion observations (kinematics) and leading to uncovering the dynamics. The use of synchrotron imaging enables subsequent dynamical analysis without the use of invasive measurements, which are difficult to conduct at this small scale and would likely alter the system and its response. The procedures outlined in this study provide an analysis and modeling scaffold for researchers studying organisms that use springs and latches to amplify mechanical power output. Such a scaffold may also lead to the design and fabrication of power-amplified engineered systems. In-depth understanding of the forces governing extreme maneuvers will enable the creation of a new generation of insect-inspired robots capable of generating and sustaining high-acceleration movements. Such robots will also serve as research platforms to answer critical questions about their biological counterparts.

Experimental Methods

Click Beetle Collection.

In July 2018, four click beetles (Elater abruptus Say, 1825) were collected on permanent research sites owned by the University of Illinois at Urbana–Champaign in Champaign County, with permission from the university’s Committee of Natural Areas. The beetles were captured alive using modified black cross-vane panel traps (AlphaScents), coated with the fluoropolymer dispersion Fluon®PTFE (AGC Chemicals Americas, Inc.) to improve trapping efficiency (28). An experimental lure provided by Jocelyn G. Millar, Department of Entomology, University of California, Riverside, was used. The live insects were kept in plastic containers with bark and soil, and were fed sugar and water ad libitum using a 1.7-mL microcentrifuge tube (Denville Scientific) filled with 10% sucrose solution capped with a cotton ball. The animals were identified to species following Roache (1960), Johnson (2003), and Evans (2014) (29–31). Voucher specimens were deposited in the Illinois Natural History Survey Insect Collection, Prairie Research Institute, the University of Illinois at Urbana–Champaign.

Motion Capture Setup.

The clicking motion of the hinge was recorded with both synchrotron X-ray imaging and visible-light imaging at beamline 32-ID of the Advanced Photon Source (APS), Argonne National Laboratory. Synchrotron X-ray imaging offers the possibility to view and record the motion of internal structures in living insects at the millimeter to centimeter scale with micrometer-scale spatial resolution (32). Images were created using monochromatic X-rays (25 keV), a scintillator screen, and a 5× microscope objective, providing a 2.4 × 3.6 mm field of view. Two high-speed cameras (Photron FASTCAM SA-Z) were used to simultaneously record the motion of the hinge using X-ray and visible light (Fig. 4C). Trials were recorded at frame rates of 1,000, 20,000, and 30,000 frames per second (fps). The visible-light images were used to monitor the insects and confirm that the observed movements were clicks.

Fig. 4.

Click beetle morphology and experimental setup. (A) The body of a click beetle can be divided into two subunits, linked by a thoracic hinge: the head and prothorax, and the mesothorax, metathorax, and abdomen. (B) Sketch highlighting the anatomical components of the hinge in the sagittal plane: the peg, the mesosternal lip, and the mesosternal cavity. (C) Experimental setup used to image the hinge during the clicking motion. The beetles were placed in a custom vise and constrained from the abdomen to the mesothorax; the thoracic hinge, the prothorax, and the head were free to move. One high-speed camera provided the X-ray view and was focused on the hinge to record the lateral view in the sagittal plane of the peg and mesosternal lip during the click motion. A second high-speed camera provided a visible-light view, used to monitor the animals and validate that the recorded head motions were clicks.

Individual beetles were anesthetized using nitrogen and mounted in a custom vise (Fig. 4C). The vise was composed of two parallel adjustable plates between which the beetles were fixed using dental wax (Utility Wax Rods Round, Kerr Corporation). Only the abdomen was constrained, leaving the head, prothorax, and hinge free to move. Thus, the beetles were able perform the same bending and unbending motions (Fig. 1A) as before a jump. Only the energy release phase movements were altered by constraining the body. Each individual was positioned perpendicular to the X-ray source, such that the side of the body faced the beam and the head was up, providing a lateral view in projection (Fig. 4C). X-ray images captured the mesothorax, the hinge, and about 1/4 of the prothorax during the clicking motion. The clicking motion was triggered by exposing the animal to the beam; when the beam was turned on, beetles immediately began clicking for multiple cycles. Multiple recordings were made for each specimen (SI Appendix, Table S1). One clicking motion (latching, loading, and release) was recorded for each specimen 1 and 2 at 20,000 fps and 30,000 fps, respectively; a second release motion was recorded for specimen 2 (20,000 fps). Seven clicking motions of specimen 3 and eight clicking motions of specimen 4 were recorded at 1,000 fps (SI Appendix, Table S1). The animals were still alive after filming, based on leg and antenna movements, but were unable to perform the click with further stimulus. The mass of each individual was measured after each trial using a Precision Standard scale (Ohaus) with an accuracy of 1 mg. The body length was measured from the base to the apex using calipers (Mitutoyo Absolute). The mass and body length of the four specimens recorded are reported in SI Appendix, Table S1.

Motion Analysis.

The high-speed synchrotron X-ray videos were analyzed using ProAnalyst (Xcitex). The 1,000-fps images were obtained at a lower radiation level, which enabled multiple clicks per recording. The 1,000-fps recordings captured the relatively slow movements during the click (latching and loading phases), but were not able to resolve the fast release, due to motion blur in the energy release phase. The 30,000- and 20,000-fps recordings (specimens 1 and 2) were used to observe the full range of the loading and energy release phases (Movies S1 and S2). Previous work by Bolmin et al. (4) detailed the latch mechanics; thus we focused on the analysis of loading and energy release phases. Anatomical landmarks around the hinge were used to track the motion, frame by frame. Specifically, the position of the peg tip was digitized for all phases of motion. Additionally, the position of the cuticle dorsal to the peg, referred to as the “soft cuticle,” was tracked during the loading phase. This part of the cuticle is soft in comparison to the peg’s stiffer cuticle, which is critical for the latch to be maintained (4). Relative softness of the cuticle may be due to a higher content of cuticular proteins like resilin or less cross-linkages between the chitin and proteins, making the cuticle less sclerotized (33), or it may be thinner. To our knowledge, the exact chemical structure of the click beetle’s soft cuticle is not known.

Fig. 1A shows the landmark points used for tracking with respect to the peg, the mesosternal lip, and the cavity in the field of view of the X-ray camera. The position of each tracker was extracted in Cartesian coordinates using ProAnalyst and imported into Matlab (Mathworks). The position of the peg tip in Cartesian coordinates of specimen 1, recorded at 30,000 fps, was filtered using a low-pass filter (cutoff frequency, 800 Hz) in Matlab, and the position of specimen 2, recorded at 20,000 fps, was interpolated in ProAnalyst. The velocity and acceleration of the peg tip were calculated using the custom derivative function “deriv” from the System Identification Programs for AirCraft toolbox in Matlab (34). The derivatives were smoothed using a local quadratic least-squares fit to each data point and its four neighboring points. The angular position of the peg tip was shifted to reach zero at the equilibrium position at the end of the oscillations for the dynamics analysis, to facilitate the calculations. The synchrotron X-ray images were also used to acquire morphological data, including the cavity’s geometry (Fig. 1A), necessary for the analysis of the energy release dynamics.

Restoring Force Method and Model Validation.

The normalized damping force G and the normalized elastic force F were derived using the restoring force method (19). We assume that no external force is applied to the system during the release (free response). The equations of motion in polar coordinates can be formulated as $a_{\theta }=\sum {\mathcal{F}}_{\theta }$, where ${\mathcal{F}}_{\theta }$ are the normalized forces tangent to the motion, and $a_{\theta }=r\stackrel{.}{\theta }+2\stackrel{.}{r}\stackrel{.}{\theta }$. As the polar coordinates $r$ and $\theta$ are linked through the cavity’s geometry, we define the polynomial functions $F$ and $G$ such that

$$r\stackrel{.}{\theta }+2\stackrel{.}{r}\stackrel{.}{\theta }+F\left(\theta \right)+G\left(\stackrel{.}{\theta }\right)=0.$$ [2]

F and G were evaluated at the points where $\theta$ and $\stackrel{.}{\theta }$ are zero such that, at $\theta =0$, $G\left(\stackrel{.}{\theta }\right)=-a_{\theta }$, and, at $\stackrel{.}{\theta }=0,F\left(\theta \right)=-a_{\theta }$ after fitting a piecewise cubit hermit interpolating polynomial (“pchip” function in Matlab) to the experimental data for each click.

Eq. 2 was used to predict the functions G and F (SI Appendix, Fig. S2). G and F outputted by the system identification analysis for specimen 2’s release A were used to reconstruct the circumferential acceleration for specimen 1’s release and specimen 2’s release B. SI Appendix, Fig. S2A shows the comparison between the experimentally driven circumferential acceleration (i.e., $a_{\theta }=r_{2A}{\stackrel{.}{\theta }}_{2A}+2{\stackrel{.}{r}}_{2A}{\stackrel{.}{\theta }}_{2A}$) and the modeled circumferential acceleration (i.e., $a_{\theta }=-F_{2A}\left({\theta }_{2A}\right)-G_{2A}\left({\stackrel{.}{\theta }}_{2A}\right)$) for specimen 2 release A. SI Appendix, Fig. S2 B and C validates the system identification approach by comparing the experimentally driven circumferential acceleration using $\theta$ and $r$ for specimen 1 and specimen 2 release B to the specimen 2 release A modeled circumferential acceleration (i.e., $a_{\theta }=-F_{2A}\left({\theta }_i\right)-G_{2A}\left(\stackrel{.}{{\theta }_i}\right)$, i = 1 or 2B).

G was estimated by fitting a quadratic polynomial through the data for all clicks. F was estimated for each click by fitting a piecewise cubit hermit interpolating polynomial. The circumferential acceleration was predicted based on the function G and on the function F estimated from specimen 2’s release A’s data. G and F are the lumped velocity-dependent and displacement-dependent forces. Various constraints and forces may contribute to either or both of these functions.

Data Availability.

Video files and raw excel data have been deposited at https://doi.org/10.13012/B2IDB-8033264_V1.