Abstract
A widespread brain disorder of present days is depression which influences 264 million of the world’s population. Depression may cause diverse undesirable consequences, including poor physical health, suicide, and self-harm if left untreated. Depression may have adverse effects on the personal, social, and professional lives of individuals. Both neurologists and researchers are trying to detect depression by challenging brain signals of Electroencephalogram (EEG) with chaotic and non-stationary characteristics. It is essential to detect early-stage depression to help patients obtain the best treatment promptly to prevent harmful consequences. In this paper, we proposed a new method based on centered correntropy (CC) and empirical wavelet transform (EWT) for the classification of normal and depressed EEG signals. The EEG signals are decomposed to rhythms by EWT and then CC of rhythms is computed as the discrimination feature and fed to K-nearest neighbor and support vector machine (SVM) classifiers. The proposed method was evaluated using EEG signals recorded from 22 depression and 22 normal subjects. We achieved 98.76%, 98.47%, and 99.05% average classification accuracy (ACC), sensitivity, and specificity in a 10-fold cross-validation strategy by using an SVM classifier. Such efficient results conclude that the method proposed can be used as a fast and accurate computer-aided detection system for the diagnosis of patients with depression in clinics and hospitals.
Keywords: Electroencephalogram, Depression, Empirical wavelet transform, Centered correntropy, Computer-aided detection
Introduction
Depression is a mental disorder that affects the social and individual life of people of all ages and genders. Depression is known as an intolerable state which can be treated by medicines for anti-depression, significant physical activity, and psychotherapy. All around the world, over 264 million people suffer from depression [1], however, 80% of the people with depression illness have not been treated because of their lack of awareness of depression symptoms [2]. If a person with depression illness is not identified in the early stages, he or she may lead to worse behaviors, such as self-harm or suicide attempts. There is no specific age group for this disorder. The symptoms of depression can be identified by clinical interview or psychiatric questioning [2]. The symptoms of mental disorder, like depression for patients with various languages, lifestyles, religions, and cultures, are not constant [3]. On another hand, the severity of symptoms is depended on the depression stage (mild, moderate or severe, melancholic, or psychotic). Hence, it appears that the identification of depression is highly dependent on the experience of the psychiatrists or counselors and subjective involvement. Thus, a reliable method for the identification of depression disorder without human intervention is highly desirable.
Understanding brain function is one of the most difficult challenges for physicians and neurologists. Magnetic resonance imaging (MRI) and positron emission tomography (PET) scans have been widely used in brain cognition investigations over the last two decades. Although MRI [4] and PET scan can detect depression, they are expensive and not widely used in clinics or in developing countries. An example of an MRI is shown in Fig. 1 for depression and normal subjects.
Fig. 1.
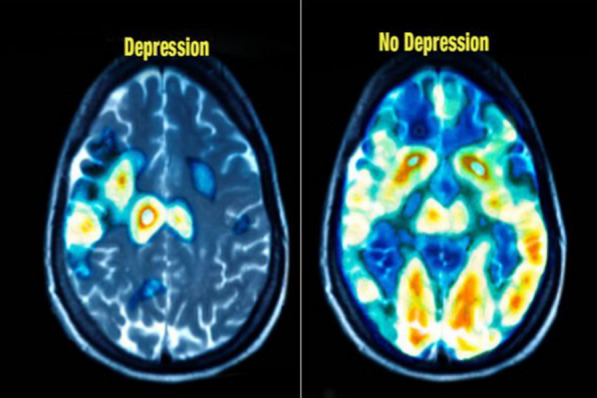
An example of depression and normal brain by MRI. (Image is from https://healthpoint.pk/)
Nowadays, Electroencephalogram (EEG) signals have become an available tool for brain cognition [5, 6]. Although, the EEG signal is complex and non-stationary due to its inexpensive accessibility in developing countries and clinics. Furthermore, due to easy acquisition, it can be used instead of MRI and PET scans in brain cognition researches. EEG signal is known as powerful biomarker in many brain disorders detection, including: Alzheimer [7], dementia [8], epilepsy [9], alcoholism [10], attention deficit hyperactivity deficit (ADHD) syndrome [11], autism [12], Parkinson’s disease [13], sleep studies [14], schizophrenia [15, 16], analysis of emotional states [17, 18], and brain-computer interfaces (BCI) [19–23].
Since neurons do not function properly in depressed subjects, the synapse has a lower concentration of receptors and neurotransmitter release has decreased compared to healthy subjects [24, 25]. Depression EEG signals are therefore less complex (more predictability) than standard EEG signals [26].
In recent decades, research has been conducted to identify the effects of depression on EEG signals. In [26], the normal and depressed EEG signal is decomposed to eight-level using the discrete wavelet transform (DWT) to extract five EEG rhythms. Subsequently, relative wavelet entropy (RWE) and various entropy feature are extracted from DWT coefficients as discrimination features and fed to a two-layer feed-forward artificial neural network (ANN) classifier to characterize EEG signals in normal and depression group [26] resulting in 98.11% classification accuracy (ACC). In [6], the complexity and nonlinearity of EEG signals collected from frontal lobes from patients diagnosed with major depressive disorder (MDD) and normal subjects have been investigated using the wavelet-chaos methodology. They extracted EEG rhythms by employing Daubechies order 4 (db4) filter bank and then computed Higuchi’s fractal dimension (HFD) and Katz’s fractal dimension (KFD) from sub-bands of ordinary and depression as features. Finally, the extracted features are fed to the enhanced probabilistic neural network (EPNN), to discriminate the MDD and normal EEG signals. Their method achieved a classification ACC of 91.3%.
In [27], differences between male and female depressive brain dynamics are investigated based on a spatio-temporal analysis of relative convergence (STARC) of EEG signals. In other words, they used nonlinear features with statistical analysis to show a significant difference between the EEG signals of the sexes with depression. In [24], EEG rhythms power, detrended fluctuation analysis (DFA), HFD, correlation dimension, Lyapunov exponent are extracted from EEG signals of 45 normal and 45 depressed patients as features. After that, the genetic algorithm selected the 16 significant features and fed them to SVM, k-nearest neighbor (KNN), and logistic regression (LR) classifiers. They reported 90.05% classification ACC in the categorization of normal subjects and depression patients.
In [25], wavelet packet decomposition (WPD) with db8 filter bank is decomposed to normal and depressed EEG signals. The entropy-based features including approximate entropy (ApEn), sample entropy (SampEn), Renyi entropy (REN), and bispectral phase entropy (Ph) are computed from EEG subbands. The student`s t test acquired significant features and fed to the PNN classifier resulting in 99.5% classification ACC.
In [28], the detection of depression is investigated using nonlinear features extracted from EEG signals. The features are ranked corresponding to their t-value and the SVM classifier input. Their method resulted in an classification ACC of 98%. Furthermore, they proposed a novel index for the diagnosis of depression. In [29], the EEG-derived synchronization likelihood features are applied as an input to an SVM classifier that resulted in 98% classification ACC. In [30], a new method has been proposed based on kernel eigen-filter-bank common spatial patterns for the detection of depression EEG signals with an ACC of 81.23%.
In linear predictive coding (LPC) methodology, several discrimination features are extracted and used in a classifier that resulted in 94.30% ACC in normal and depressed EEG signal classifications [31]. In [32], EEG signals are decomposed into rhythms by Fourier transform, and then power, frequency, asymmetry, and coherence are extracted from rhythms as features for discrimination between normal and depression signals.
In [33], a novel approach for automated classification of normal and depression EEG signals have been proposed based on a deep convolutional neural network (CNN) that resulted in 93.54% and 95.96% classification ACC for left and right hemispheres, respectively. Recently, in [34] the authors designed a new bandwidth-duration localized (BDL) three-channel orthogonal wavelet filter bank (TCOWFB) to analyzing bio-signal. Furthermore, in [34], normal and depression EEG signals are decomposed into 3 levels using BDL TCWFB and computed the logarithm of norm from sub-bands as discrimination features. After that, the SVM classifier achieved 99.02% and 99.54% classification ACC for the left and right hemispheres, respectively. The literature review [6, 24, 26, 29] suggests that the complexity of rhythms can be used as a significant parameter to diagnose normal and depressed EEG signals. For this purpose, we have computed the nonlinear features from EEG signal rhythms in this study.
Detection of the frequency components was the first challenge in signal processing applications. In the early nineteenth century, Fourier transforms detected the signal frequency component by rewrite the signal function in the exponential form [35] though there was no relationship between time and frequency in the Fourier transform. In the early twentieth century, the wavelet transform is proposed for representing the signal in the time–frequency plane [35]. Besides, the wavelet function is not necessarily exponential, it can be employed for time–frequency analysis of those signals which are not combinations of exponential functions [35].
Although, wavelet transform with various wavelet functions can provide significant time–frequency decomposition for non-stationary signals, but the biggest defect of wavelet transform is its non-adaptive decomposition that is due to the constant of decomposition bank filter for any input signal [36]. In the late twentieth century, empirical mode decomposition (EMD) is proposed as an adaptive method for analyzing nonlinear and non-stationary signals [37]. Generally, EMD decomposes input signals to different intrinsic mode functions (IMFs) and it is reversible, which means the sum of obtained IMFs and the residual signal synthesizes the original input signal [15]. The EMD algorithm is employed for many signal processing applications, with some limiting factors, such as time-consumption, noise-sensitive, and lack of closed-form mathematical expression.
A new approach called empirical wavelet transform (EWT) had been proposed to extract IMFs of input non-stationary signals by generating an adaptive filter bank to overcome the mentioned drawbacks of DWT and EMD [36]. EWT, unlike DWT, is an adaptive method for the analyses of non-stationary signals [36]. Adaptive EWT with a similar goal like EMD is not noise sensitive which is capable of analyzing noisy signals more accurately than EMD and also EWT has a mathematical expression that makes it faster than the EMD algorithm [16]. Even though EWT like DWT decomposes the input signal by filter bank but EWT filter bank bandwidths differ according to the information signal spectrum while DWT filter bank is constant to any input signals. EWT filter bank bandwidths are determined that correspond to adequate segmentation of the data signal frequencies [36]. Several methods for suitable segmentation of the information signal spectrum according to specific applications have been proposed [38–40].
In our previous studies [19, 21, 22, 41], we proposed EWT based algorithms for the detection of different motor imagery EEG signals. Based on the remarkable results obtained in our previous work, in this work, we again used EWT for the detection of normal and depressed signals. In this study, EWT is used as processing tools for delta, theta, alpha, beta, and gamma rhythms extraction that occupies spectrum in the range of [0, 4], [4, 8], [8, 13], [13, 30] and [30, 60] Hz. Although DWT, WPD, and Butterworth filter can extract EEG rhythms [6, 25–28], EWT can achieve this goal in a single step which shows the superiority of this method. The centered correntropy is computed as the discrimination feature to measurement the complexity of rhythms and can quantify the correlation in the nonlinear domain [42–44]. Clinically significant features are obtained using the Kruskal–Wallis statistical test and fed to SVM and KNN classifiers with different kernel functions and K values consecutively.
The paper is arranged successively. Section 2 is a review of DWT and EWT. Section 3 explains the proposed method, which consists of data acquisition, rhythm separation by DWT and EWT, centered correntropy, and classification methods. The results of the proposed method are presented in Sect. 4, and the discussion on the results is described in Sect. 5. Finally, we have a conclusion in Sect. 6.
A review of DWT and EWT
Nowadays, the wavelet transform has become a useful tool in biomedical signal processing applications. In DWT, the bandwidth of scaling function and wavelet function, in the first level decomposition is [0, ] and [, ], respectively. In the same way, for the second level decomposition, the bandwidth of scaling function and wavelet function is [0, ] and [, ], respectively. In general, for DWT, in n-th level decomposition, the bandwidth of scaling function and wavelet function is [0, ] and [, ], respectively. In other words, bandwidths in DWT are fixed for all rates of decomposition which means that the DWT is not flexible as per the incoming signal [19, 21, 22]. The removal of non-adaptive DWT by producing adaptive wavelets corresponding to the input signal spectrum is suggested by EWT [36]. Figure 2 shows the EWT steps for adaptively decomposing the input signal.
Fig. 2.
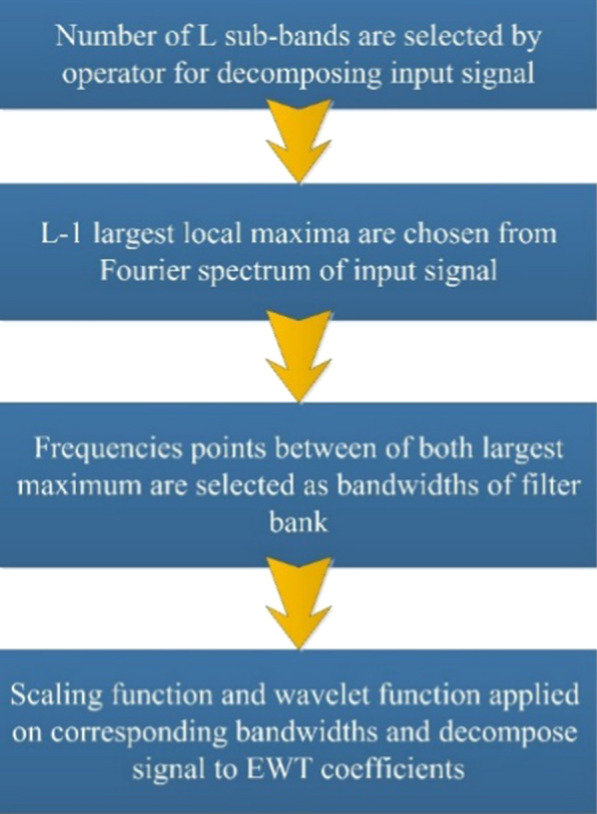
Steps of EWT for the adaptive decomposition of an input signal
In [36] the operator obtains several isolated sub-bands (L). Using the Fourier transform, the reference frequency range is shown in [0, π]. L-1 local frequency spectrum maxima are picked, and midpoints of each set of local maxima are then used as EWT filter bank bandwidths, which helps to adjust EWT filter banks [36, 41]. The EWT filter bank is created based on the most recent Littlewood–Paley, and Meyers wavelets after differentiation of the range of frequencies [35]. In the Fourier domain, the scaling function and wavelet function of the EWT filter bank is defined as [36]:
| 1 |
| 2 |
where , is the bandwidth of EWT filter bank, and is,
| 3 |
Moreover, makes sure the EWT coefficients are in space.
The factor tightens the filter bank structure resulting in the lowest overlap of bandwidths with lower and upper frequencies. Moreover, the parameter makes ignorable stop-band ripples for the EWT filter bank with the ability to solve mode-mixing problems. Similar to DWT, the inner product of the input signal with wavelet function as well as scaling function gives detail and approximation coefficients respectively.
Proposed method
The proposed system for the automatic detection of depression is demonstrated in Fig. 3. First, the EWT is applied to EEG signals to extracting rhythms. Secondly, the CC is computed as the discrimination feature from rhythms, and finally, statistically significant features obtained by Kruskal–Wallis statistical test are fed to SVM and KNN classifiers to categorize the normal and depressed group.
Fig. 3.
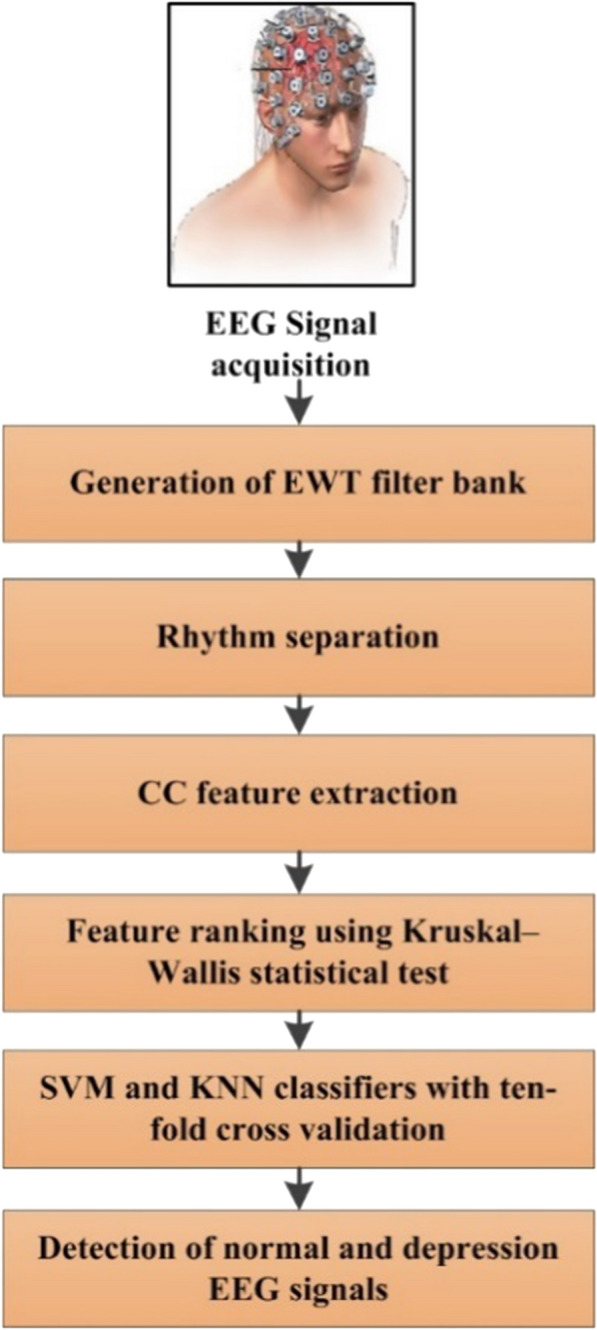
Steps of our proposed method for automatic detection of normal and depression EEG signals
Data acquisition
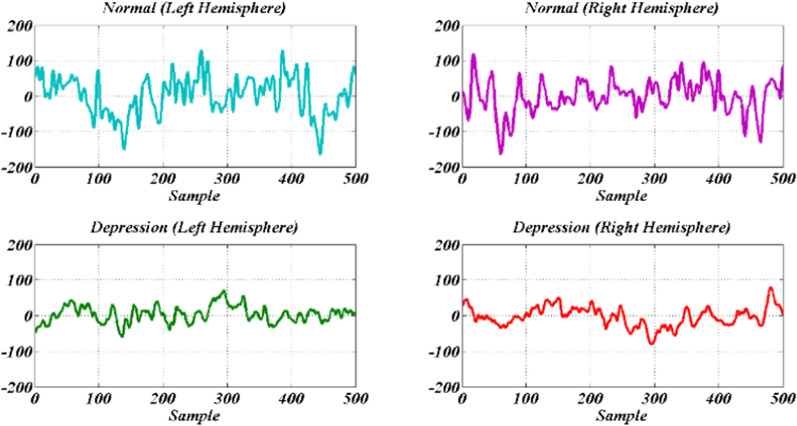
This study employed 22 healthy (16 men and 6 women) subjects without brain disease and 22 depressed subjects (10 men and 12 women) which candidate to being admitted to the hospital. The age of the volunteers was between 23 and 58 years. The data acquisition from each subject was performed in the resting state with open and closed eyes for 10 min. EEG was recorded with a bipolar montage from the left and right hemispheres. Eye moving and blinking as well as muscle artifacts were discarded visually. Also, the EEG signals sampled at a rate of 256 Hz and 50 Hz power line intrusion was eliminated with a notch filter. Due to the non-stationary nature of EEG signals, each EEG record is divided into segments of 500 samples with a length of about 2 s. This experiment was approved by the Research Ethics Committee of AJA University of Medical Sciences (Approval ID: IR.AJAUMS.REC.1399.049), Tehran, Iran. Representative samples of regular and depressed EEG signals for both hemispheres are shown in Fig. 4.
Fig. 4.
Sample EEG signals of normal (up) and depressed subjects (down) for left and right hemispheres
Separating rhythms by DWT and EWT
The EWT has been recommended to analyze and to adaptively decompose the non-stationary signals like bio-signals [16]. EWT has already been used in the detection of epilepsy [45], Parkinson’s [13], and glaucoma [40] by the EEG signal. EWT creates an adaptive filter bank by significant segmentation of the data signal spectrum. For substantial segmentation of the input signal spectrum, several methods, including: ‘local maxima’ [36], ‘histogram’ [46], and ‘scale-space’ [47] have been proposed. In this paper, EWT is used as an adaptive processing method for the extraction of five EEG rhythms. For this purpose, the Fourier spectrum of input EEG signal is segmented corresponding to frequency bandwidths of the delta, theta, alpha, beta, and gamma rhythms. Thus, the cut off frequencies () in the EEG signal spectrum should be chosen to resulting [0, 4], [4, 8], [8, 13], [13, 30], and [30, 60] boundaries corresponding to frequency bandwidth of delta, theta, alpha, beta, and gamma rhythms in Fourier domain, respectively.
The value was experimentally set at 0.2376 in EWT (see Sect. 2) to reduce the mode mixing as well as to avoid the sub-bands overlapping. Using the EWT filter bank, tighter frames are generated with small transition bands for the filters and negligible stop-band and pass-band ripples [36, 40]. The precise segregation of rhythm by EWT contributes to less aliasing. Figure 5 displays the filter bank created to distinguish EEG rhythms in which the first five filters distinguish delta, theta, alpha, beta, and gamma rhythms. It must be noted that rate information larger than 60 Hz is known as interference.
Fig. 5.
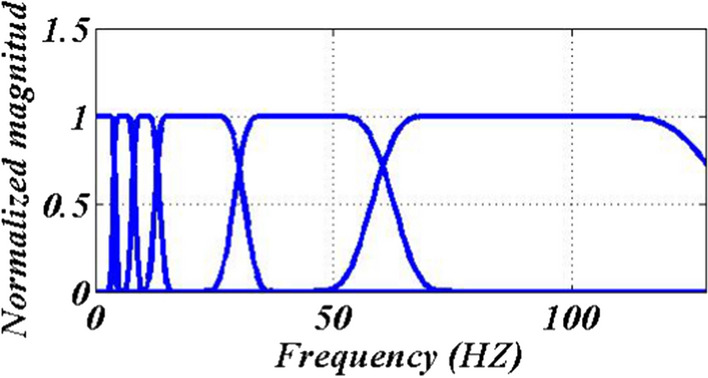
Designed filter bank
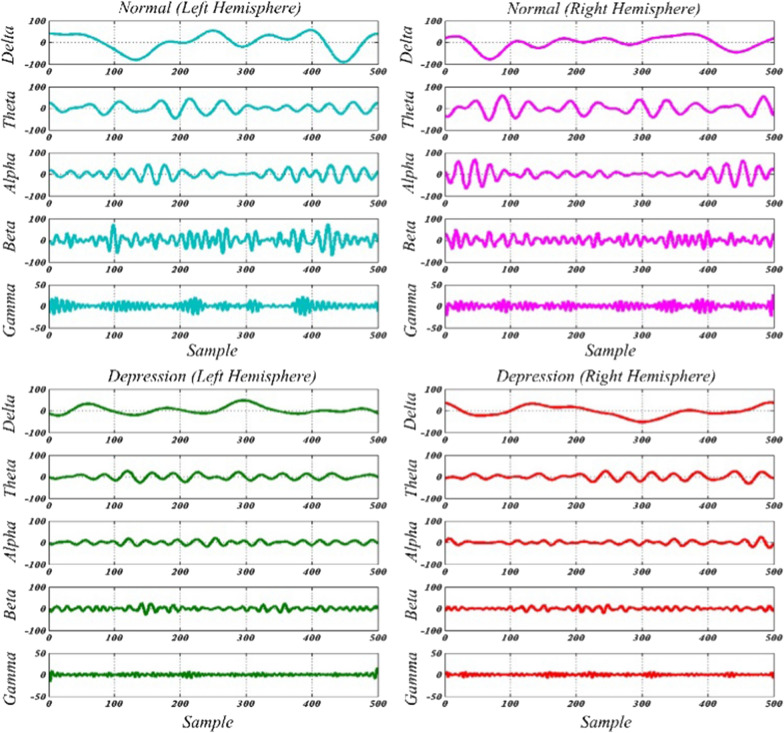
Figure 6 shows the five rhythms obtained in the EWT domain for EEG signals of normal and depressed subjects for both hemispheres. Though DWT has been used to extract EEG rhythms in [6, 24, 26, 27, 29] but none have mentioned the defects of DWT. In this paper, DWT defects are investigated for this application and compared to EWT. For this purpose, all EEG signals (normal and depressed of both hemispheres) are decomposed into five levels by DWT with ‘db4’ wavelet function. As described in Sect. 2, the five-level decomposition of EEG signals, resulted in one approximation and five details.
Fig. 6.
Five rhythms of normal and depression EEG signals for both hemispheres
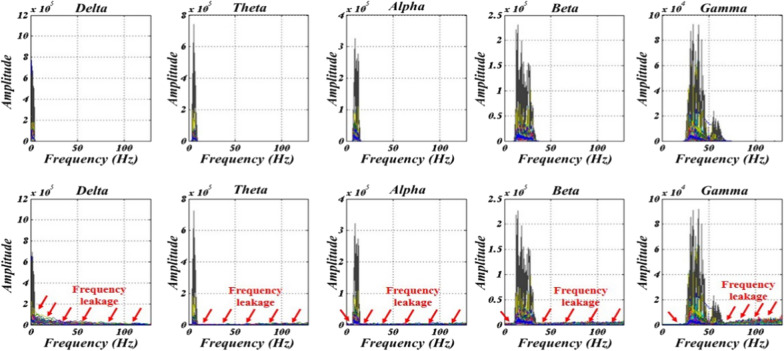
Detail 1 has a frequency band [64, 128] Hz that is higher than the bandwidth of gamma rhythm and can be ignored as noise. Gamma, beta, alpha, and theta rhythms were assigned to details 2, 3, 4, and 5 with frequency bands of [32, 64], [16, 32], [8, 16], and [4, 8] Hz, respectively. The delta rhythm was also attributed to the approximation with the frequency band of [0, 4] Hz. The Fourier spectrum of extracted rhythms for EEG signals (depression and normal of both hemispheres) is depicted in Fig. 7.
Fig. 7.
Shown the spectrum of the obtained delta, theta, alpha, beta, and gamma rhythms (1st–5th rows) by using DWT (1st column) and EWT (2nd column) for EEG signals
In this regard, the main drawback was the frequency leakage for all DWT outputs due to the existing stop-band ripple compared with EWT with no leakage. On the other hand, EWT can extract EEG rhythms by the one-step process while DWT requires five-level decomposition. Besides, some decomposition levels for extraction rhythms in DWT can be more by increasing sampling frequency (see Sect. 2). In addition, in the method of separation of EWT rhythms by adjusting the sampling frequency, the number of steps does not differ and are constant since bandwidth cut-off frequencies are constant for every sampling frequency (i.e. ).
Centered correntropy
Correlation is employed for measuring the similarity between the two random variables [40, 42, 43]. Correntropy is a quantity that measures the correlation in the nonlinear domain [42, 43]. Correntropy is an essential tool to extract the behaviors of the signal in the time-domain. Correntropy can be defined as follows [42, 43]:
| 4 |
| 5 |
where, N, k, and are the length of x(n), delay, mean correntropy, and the Gaussian kernel function with band-width, respectively.
So, CC can be computed as,
| 6 |
In this study, we test k for different values, where for k = 2 resulted in the best performance in depressed EEG detection. By setting k = 2, we extracted two CC features from each rhythm named and due to the first and second delay; also is fixed to 1. CC is computed from the decomposed delta, theta, alpha, beta, and gamma rhythm as discrimination features for the classification of normal and depressed EEG signals. CC has been used previously for the detection of alcohol in EEG signals [48] and sleeps apnea in ECG signals [49].
Classification
In this paper, the usefulness of SVM and KNN classifiers are investigated in the classification of normal and depressed EEG signals. A brief review of SVM and KNN classifiers are provided in the following sub-sections.
Support vector machine (SVM)
SVM is a nonlinear and supervised classifier that has been used widely in designing CAD systems [50]. In the SVM classifier, training data is mapped to a higher dimensional space using a kernel function. After that, a linear optimal hyperplane separates the classes corresponding to training data labels and classifies the test data [51]. In this paper, the radial basis function (RBF) is mapped the features on higher-dimensional space because of its better performance in comparison with other kernel functions [52]. The selection of the significant kernel function has a direct effect on classifier performance. So, the scaling factor of RBF is changed from 0.5 to 1.5, with 0.1 steps to choose the best kernel function.
K nearest neighbour (KNN)
KNN is a supervised classifier with fast implementation [53]. In the KNN classifier, any testing data belongs to a group that has more members among K training neighbors. Hence, the distance measurement method and the number of K are two factors influencing the correctness of the KNN algorithm [54, 55]. In this paper, Euclidean and City block distances are applied; also, we varied K from 2 to 9 with step 1. (i.e., ).
Results
Considering the non-stationary feature of the EEG signals, each EEG record in this work was divided into segments with 500 samples. Typical samples of normal and depressed EEG signals for the left and right hemispheres are demonstrated in Fig. 4. First, EEG signals are decomposed to rhythm using EWT. Figure 5 shows the designed EWT filter bank and Fig. 6 shows the decomposed rhythms, respectively. Then, centered correntropy is computed as discrimination features from normal and depression rhythms. Table 1 shows the mean and standard deviation (std) of computed features.
Table 1.
The results (mean, standard deviation, and p values) of centered correntropy computed from rhythms of left and right hemisphere EEG signals
| Rhythm feature | Left | |||
|---|---|---|---|---|
| Normal | Depression | p value | ||
| Delta | 0.3861 ± 0.0088 | 0.3831 ± 0.0048 | 0 | |
| 0.1977 ± 0.0865 | 0.2301 ± 0.0447 | 2.025 | ||
| Theta | 0.3770 ± 0.0135 | 0.3825 ± 0.0045 | 1.666 | |
| 0.1460 ± 0.0606 | 0.1148 ± 0.0324 | 1.741 | ||
| Alpha | 0.3700 ± 0.0142 | 0.3840 ± 0.0042 | 0 | |
| 0.1136 ± 0.0429 | 0.0593 ± 0.0198 | 0 | ||
| Beta | 0.3670 ± 0.0133 | 0.3868 ± 0.0027 | 0 | |
| 0.0628 ± 0.0251 | 0.0215 ± 0.0068 | 0 | ||
| Gamma | 0.2776 ± 0.0566 | 0.3656 ± 0.0076 | 0 | |
| 0.0635 ± 0.0236 | 0.0234 ± 0.0079 | 0 | ||
| Rhythm feature | Right | |||
|---|---|---|---|---|
| Normal | Depression | p value | ||
| Delta | 0.3870 ± 0.0076 | 0.3837 ± 0.0046 | 0 | |
| 0.1948 ± 0.0835 | 0.2251 ± 0.0444 | 8.401 | ||
| Theta | 0.3779 ± 0.0114 | 0.3831 ± 0.0042 | 9.897 | |
| 0.1436 ± 0.0582 | 0.1108 ± 0.0310 | 1.500 | ||
| Alpha | 0.3715 ± 0.0131 | 0.3846 ± 0.0037 | 0 | |
| 0.1095 ± 0.0435 | 0.0566 ± 0.0180 | 0 | ||
| Beta | 0.3672 ± 0.0139 | 0.3875 ± 0.0022 | 0 | |
| 0.0625 ± 0.0260 | 0.0198 ± 0.0061 | 0 | ||
| Gamma | 0.2755 ± 0.0542 | 0.3684 ± 0.0068 | 0 | |
| 0.0659 ± 0.0235 | 0.0219 ± 0.0073 | 0 | ||
It is clear from Table 1 that the mean value of in depression rhythms (expect of the delta) is more significant than normal rhythms in the left and right hemispheres. On the other hand, the mean value of in normal rhythms (expect of the delta) is higher than depression rhythms in the left and right hemispheres. Also, the std value of the extracted features in depression rhythms is significantly lesser than the normal rhythms for both the left and right hemispheres.
The ability of extracted features in discrimination of normal and depression EEG signals is evaluated by using Kruskal–Wallis statistical test corresponding to their p value. The lesser p value indicates better discrimination between normal and depression EEG signals. The p value of features extracted from EEG signals of the left and right hemispheres are given in Table 1. It can be observed from Table 1 that the p value of all rhythms is pretty good (zero or less than zero) that shows the power of centered correntropy of rhythms in discriminating between the normal and depressed EEG signals.
So, all extracted features are fed to SVM and KNN classifiers in the 10-fold cross-validation (CV) strategy. In particular, the performances of the classifiers are graded in one of the four different situations mentioned as follows:
True Positive (TP): the number of depression EEG signals detected as depression EEG signals.
True Negative (TN): the number of normal EEG signals detected as normal EEG signals.
False Positive (FP): the number of normal EEG signals detected as depression EEG signals.
False Negative (FN): the number of depression EEG signals detected as normal EEG signals.
Accuracy (ACC) measures the algorithm’s ability to distinguish between depression and normal signals. While the sensitivity (SEN), and specificity (SPE) calculate that the classifier is capable of accurately determining depression and normal instances respectively [34]. These can be defined as:
| 7 |
| 8 |
| 9 |
Also, the Matthews correlation coefficient (MCC) is a quality of binary classification performance and defined as [34]:
| 10 |
In this paper, a 10-fold CV is applied for the training and testing of classifiers [29, 33]. In 10-fold CV, input data is broken into ten subsets. Then, at any time, one subset is used as testing data, and the remaining subsets are used as training data. So all subsets were used as training data once and nine-time as testing data. Eventually, the mean value is disclosed for the objective parameters. In this work, features are given as an input to both KNN and SVM classifiers in a 10-fold CV strategy.
The performance of centered correntropy of rhythms as a discrimination feature in the classification of EEG signals for both hemispheres are written in Tables 2, 3 and 4, respectively.
Table 2.
Performance of SVM classifier with RBF kernel function in the classification of centered correntropy features
| Objective parameters | Hemisphere | |
|---|---|---|
| Left | Right | |
| ACC (%) | 98.33 | 98.76 |
| SEN (%) | 98.02 | 98.47 |
| SPE (%) | 98.65 | 99.05 |
| MCC | 0.96 | 0.97 |
| RBF parameter | 0.8 | 0.6 |
Table 3.
Performance of KNN classifier with City block distance in the classification of centered correntropy features
| Objective parameters | Hemisphere | |
|---|---|---|
| Left | Right | |
| ACC (%) | 97.63 | 98.37 |
| SEN (%) | 96.39 | 97.39 |
| SPE (%) | 98.87 | 99.39 |
| MCC | 0.95 | 0.96 |
| Number of K | 4 | 6 |
Table 4.
Performance of KNN classifier with Euclidean distance in the classification of centered correntropy features
| Objective parameters | Hemisphere | |
|---|---|---|
| Left | Right | |
| ACC (%) | 97.41 | 98.30 |
| SEN (%) | 96.13 | 97.44 |
| SPE (%) | 98.69 | 99.16 |
| MCC | 0.94 | 0.96 |
| Number of K | 4 | 4 |
It is evident from Tables 2, 3 and 4 that the SVM classifier with RBF kernel function showed a classification ACC of 98.33% and 98.76%, SEN of 98.02% and 98.47%, SPE of 98.65% and 99.05% in the detection of normal and depression EEG signals for left and right hemispheres, respectively. The KNN classifier with City block distance can classify the normal and depression EEG signals with 97.63% and 98.37% ACC, 96.39%, and 97.39% SEN, 98.87%, and 99.36% SPE in the left and right hemispheres, respectively. Also, the KNN classifier with Euclidean distance resulted in 97.41% and 98.30% ACC, 96.13%, and 97.44% SEN, 98.69%, and 99.16% SPE in the left and right hemispheres, respectively.
It can be observed that ACC, SEN, and MCC of SVM classifier with RBF kernel is slightly better than KNN classifier with both Euclidean and City block distances in the classification of normal and depressed EEG signals of left and right hemispheres as shown in Tables 2, 3 and 4. On the other hand, the classification SPE of the KNN classifier with both city block and Euclidean distance is better than the SVM classifier. Also, the value of classification ACC in the right hemisphere is better than the left hemisphere.
Area of under receiver operating characteristic curve (AUC) quantifies the capability of the proposed framework in the binary classification task, i.e., depressed and normal EEG signals classification [21, 22, 56]. For comparison of the performance of the used classifiers, the AUC value for the SVM classifier with RBF kernel and KNN classifier with city block and Euclidean distance is shown in Fig. 8.
Fig. 8.
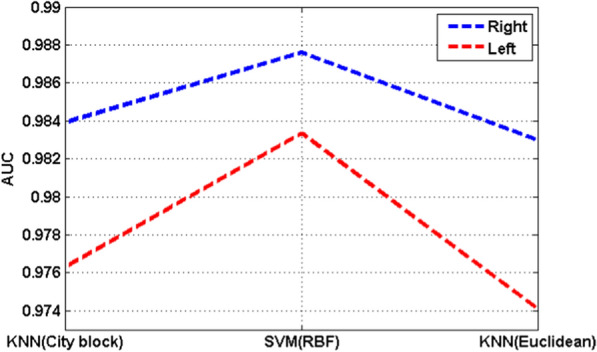
Values of AUC for various classifiers
It can be observed that the AUC in the right hemisphere is higher than the left hemisphere which indicates that the EEG signals recorded from the right side of the brain are better than the left side in depression detection application. Besides, the value of AUC for the SVM classifiers with RBF classifier in both hemispheres is higher than the KNN classifier with city block and Euclidean distance which indicates that the SVM classifier performs better in depressed and normal EEG signals classification tasks compared to the KNN classifier.
The algorithm computational time of every EEG with 500 samples, including the generation of EWT filter bank, rhythm separation, and centered correntropy computation using i5-M480 CPU (2.67 GHz), 6 GB RAM, and MATLAB 2014a is 0.3 s which indicates the simplicity of the proposed method. Also, our proposed method required less than 0.2 s for the classification of an input test signal, which is fast due to the less number of arrays of the feature vector. The algorithm time can be further reduced by using a powerful PC and other computationally efficient software packages. In terms of delay time compared with other studies, we are unable to find such a measure for most of the studies in Table 5 so we are not able to compare delay time with other studies.
Table 5.
Comparison with previous studies for automated depression detection
| Reference/year | Subjects normal (N) vs. depressed (D) | Processing method | Number of channels | Classifier | CV | Performance (%) | ||
|---|---|---|---|---|---|---|---|---|
| ACC | SEN | SPE | ||||||
| [26], Subha et al. 2012 | 15 N vs. 15 D | Rhythm separation by DWT + RWE + entropy features | 2 | ANN | No | 98.11 | 98.73 | 97.50 |
| [6], Ahmadlou et al. 2012 | 12 N vs. 12 D | Rhythm separation by DWT + HFD and KFD | 7 | EPNN | No | 91.30 | – | – |
| [27], Ahmadlou et al. 2012 | “11 male and 11 female depressed subjects” | Rhythm separation by DWT + STARC | 19 | – | – | They founded that there is a significant difference between gender with depression. | ||
| [24],Hosseinifard et al. 2013 | 45 N vs. 45 D | Rhythm separation by butterworth filter + DFA, HFD, Correlation dimension and Lyapunov exponent | 19 | LR | LOO | 90.05 | – | – |
| [25], Faust et al. 2014 | 15 N vs. 15 D | WPD + ApEn, SampEn, REN and Ph | 2 | PNN | No |
Left: 98.20 Right: 99.50 |
Left:97.10 Right: 99.20 |
Left: 99.40 Right: 99.70 |
| [28], Acharya et al. 2015 | 15 N vs. 15 D | Nonlinear features | 2 | SVM | No | 98.00 | 97.00 | 98.50 |
| [29], Mumtaz et al. 2017 | 30 N vs. 34 D | Synchronization likelihood | 19 | SVM | 10-Fold | 98 | 99.90 | 95 |
| [30], Liao et al. 2017 | 20 N vs. 20 D | Kernel Eigen-Filter-Bank Common Spatial Patterns + principal component analysis | 8 | SVM | LOO | 81.23 | – | – |
| [31], Bairy et al. 2017 | 15 N vs. 15 D | LPC | 2 | BT | LOO | 94.30 | 91.46 | 97.45 |
| [32], Knott et al. 2001 | 70 N vs. 23 D | Rhythm separation by Fourier Transform + rhythms power + frequency + asymmetry + coherence | 19 | JR | No | 91.3 | – | – |
| [57], Bachmann et al. 2018 | 13 N vs. 13 D | three linear and three nonlinear features: Spectral asymmetry index, alpha band power variability, relative gamma power, HFD, DFA, and Lempel–Ziv complexity | 2 | LR | LOO | 92 | – | – |
| [33], Acharya et al. 2018 | 15 N vs. 15 D | Deep learning + 13 layer convolution neural network | 2 | CNN | 10-Fold |
Left: 93.54 Right: 95.96 |
Left: 91.89 Right: 94.99 |
Left: 95.18 Right: 96.00 |
| [34], Sharma et al. 2018 | 15 N vs. 15 D | BDL TCWFB + logarithm of L2 norm | 2 | SVM | 10-Fold |
Left: 99.02 Right: 99.54 |
Left: 98.66 Right: 98.66 |
Left: 99.38 Right: 99.38 |
|
Present study 2020 |
22 N vs. 22 D | Rhythm separation by EWT + CC | 2 | SVM | 10-Fold |
Left: 98.33 Right: 98.76 |
Left: 98.02 Right: 98.47 |
Left: 98.65 Right: 99.05 |
| KNN | 10-Fold |
Left: 97.63 Right: 98.37 |
Left: 96.39 Right: 97.39 |
Left: 98.87 Right: 99.36 |
||||
The bold notations indicate the results obtained by our proposed strategy
Discussion
The proposed framework is applied to the EEG signals acquired from 22 normal and 22 depressed subjects. The FP1-T3 and FP2-T4 bipolar channels from the left and right halves of the brain provided all EEG signals. We showed that EWT could separate rhythms precisely in comparison with DWT. Also, separated rhythms by designed EWT filter banks do not show frequency leakage while in rhythms separated by DWT, the frequency leakage is very high; meaning that pretty less aliasing occurs through our designed EWT filter bank. We discarded all frequencies higher than 60 Hz considering them as noise. In other words, our designed EWT filter bank could extract EEG rhythms without any data pre-processing for noise removal.
After separation of the EEG signals to rhythms, centered corentropy is computed as a discrimination features. The selection of suitable delay is accomplished by testing the various values of k, where k = 2 resulted in the best performance for the classification of normal and depressed EEG signals. The selection of k = 2 results in the extraction of two features from each rhythm (i.e., and ). So, the feature vector has ten elements. Most of the computed p values are zero or less than zero indicating that all of the extracted features from the left and right hemispheres can provide significant discrimination between normal and depressed EEG signals. We found that the std value of the extracted features in depression rhythms is significantly lesser than the normal rhythms for both the left and right hemispheres. Since the centered correntropy is a quantity to measure the correlation in the nonlinear domain, we can say that fewer std values of extracted centered correntropy from the depressed EEG rhythms correlate more with each other compared with the normal EEG rhythms. Similarly, in [33, 34], this consequence helped to find that the depression EEG signals have less complexity (more predictability) than the normal EEG signals.
The performance of the proposed method is reported in the 10-fold CV strategy to ensure its reliability. We have found that ACC of SVM classifier with RBF kernel is better than the KNN classifier with city-block and euclidean distances for both hemispheres. Our proposed method resulted in 98.33% and 98.76% classification ACC for the left and right hemispheres, respectively.
The proposed method showed that EEG signals acquired from the right hemisphere are better than the left hemisphere in the diagnostic of depression disorder. Similar consequences have been obtained in [25, 26, 28, 31, 33, 34] which are used a similar approach for recording the EEG signals (i.e. the FP1-T3 channels on the left and FP2-T4 channels on the right half of the brain). In other words, the right EEG signals are enough for the detection of depression. However, we cannot expand this consequence for other studies that deployed other channels for the detection of depressed EEG signals. Although in the MRI scan, the significant difference between normal and depressed brain happens in the right hemisphere (see Fig. 1).
In Table 5, we compared our method with previous studies for the classification of normal and depressed subject’s EEG signals. As seen in Table 5, “BDL TCWFB + logarithm of L2 norm” [34], provides the highest classification ACC of 99.02% and 99.54% for left and right halves respectively. The “WPD + ApEn, SampEN, REN and Ph” [25] achieved 98.2% and 99.5% average identification accuracies for the left and right half of the brain respectively. The studies [26] and [28] achieved overall 98.1% and 98% classification accuracies. In a study [29], a classification ACC of 98% was achieved with the synchronization likelihood approach. In our proposed framework, we achieved 98.3% and 99.5% classification ACC for the left and right half of the brain, respectively. Although there is no significant difference between the proposed study and [25, 26, 28, 29, 34] in terms of classification accuracies however there are some disadvantages in previous studies such as, some studies require more number of features, more number of channels, pre-processing step, computationally in-efficient and last but not least, some studies missed 10-fold CV which may cause over-fitting problem. Further looking into Table 5, the proposed algorithm provide up to 16.4% and 17.14% classification improvement in comparison with other studies.
The advantages of our proposed method compared to previous studies are written bellow:
The proposed EWT filter bank can decompose rhythms in a single-step process (even with the varying sampling frequency), while DWT and WPD require several decomposition levels (number of decomposition levels is changed by the increase or decrease of sampling frequency). Besides, the frequency leakage of the EWT filter bank is very lesser than DWT. In other words, EWT has a higher frequency resolution than DWT in rhythm separation applications.
The proposed method does not require any pre-processing step, because the designed EWT filter bank for rhythms separation can discard any frequency component higher than 60 Hz considering them as noise, which makes the proposed method faster and simpler while in all previous studies [24, 26, 28, 33, 34] pre-processing techniques like Butterworth or notch filter were used for removing noise from the EEG signals.
The proposed method achieved a high classification ACC of 98.33% and 98.76% for left and right EEG signals in a 10-fold CV strategy that shows the proposed method is more reliable and efficient while results have been reported in [6, 25, 26, 28, 32] without any CV and in [24, 30, 31, 57] by leave-one-out (LOO) CV technique.
We extracted cantered correntropy as features for the diagnosis of depression, while in [6, 24–28, 32, 57], various types of features have been extracted for the diagnosis that makes these studies computationally expensive. The proposed method computes only two features from five rhythms for classifying normal and depressed EEG signals. In other words, our feature vector has ten elements, while elements of feature vectors in [26] were 20, in [24] were 30, [28] were 15 and in [29] were 100 showing that their methods are more complicated than the proposed framework.
The proposed method used only two channels (bipolar recording) of EEG for discrimination and classification of normal and depression signals while [6] used seven channels, in [24, 27, 29, 32] nineteen channels, and in [30] eight channels were used for the classification.
The proposed method using SVM classifier with RBF kernel function achieved proper MCC of 0.96 and 0.97 in the classification of normal and depression EEG signals collected from the left and right hemispheres, respectively; which indicate the effectiveness of binary classification.
The proposed method achieved the highest classification ACC compared to previous studies except for [25] and [34]. Although classification ACC of our method is very slightly less than [25] and [34], in [25] four entropies are computed from the WPD coefficient as features vs our method extracted only centered correntropy. Besides, in [25], the total variational filtering algorithm and notch filter are applied as pre-processing while our proposed framework does not require any pre-processing. In [34], EEG signals are decomposed to three levels by TCOWFB and then logarithm of norm has been computed as a discrimination feature. In [34], the number of decomposition levels is changed with the change of sampling frequency. Also, they decompose EEG signal in four-steps (i.e., first EEG signals are filtered by a notch filter and then decomposed to three levels), but in our method, EEG signal is decomposed by one step and the number of decomposition level does not change and also not requires any pre-processing assuring the merits of our method.
Another advantage of our proposed method is that it does not depend on psychiatrist experience or psychological counseling and it can be used easily by physicians and nurses. Although physicians make the final diagnosis, this system can be advantageous for the physician for an accurate diagnosis of depression. Based on the experiments, early-stage detection of muscular and cardiac diseases is also possible using the proposed method by processing the electromyogram (EMG) and ECG signals.
Conclusion
In this work, we proposed a new, user-friendly and efficient method for the diagnosis of normal and depressed EEG signals based on the computation of centered correntropy from rhythms in the EWT domain using an SVM classifier. Also, we showed that the frequency leakage of EWT is remarkably lower than DWT in rhythms separation application. Our proposed method resulted in 98.76% average classification ACC with a 10-fold CV strategy to prevent the over-fitting that is outstanding in comparison with state-of-the-art papers not only in terms of SEN, SPE, and ACC but also concerning the elimination of pre-processing step, rhythms extraction, and feature vector length affecting the algorithm complexity. Thus, the proposed system can be used easily by physicians and nurses in hospitals and clinics for the correct diagnosis of depression. The parameters for the SVM and KNN classifiers are chosen empirically in this study, in future automated parameter selection method will make this method more adaptive.
Acknowledgements
Hesam Akbari and Muhammad Tariq Sadiq are co-first authors.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Compliance with ethical standards
Conflict of interest
The authors declare that they have no conflict of interest.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Hesam Akbari and Muhammad Tariq Sadiq are Co-first authors.
Contributor Information
Hesam Akbari, Email: st_h.akbari@azad.ac.ir.
Muhammad Tariq Sadiq, Email: muhammad.sadiq1@ee.uol.edu.pk.
Ateeq Ur Rehman, Email: ateeq.rehman@gcu.edu.pk.
References
- 1.(WHO), W.H.O. Depression. https://www.who.int/news-room/fact-sheets/detail/depression. Accessed 30 Jan 2020.
- 2.Kaur P, Siuly S, Miao Y. Detection of depression from brain signals: A review study. In International conference on health information science. Springer, Berlin; 2018.
- 3.Behere PB, et al. Religion and mental health. Indian J Psychiatry. 2013;55(Suppl 2):S187. doi: 10.4103/0019-5545.105526. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- 4.Zeng LL, et al. Unsupervised classification of major depression using functional connectivity MRI. Hum Brain Mapp. 2014;35(4):1630–1641. doi: 10.1002/hbm.22278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Subha DP, et al. EEG signal analysis: a survey. J Med Syst. 2010;34(2):195–212. doi: 10.1007/s10916-008-9231-z. [DOI] [PubMed] [Google Scholar]
- 6.Rehman AU, Sadiq MT, Shabbir N, Jafri GA. Opportunistic cognitive MAC (OC-MAC) protocol for dynamic spectrum access in WLAN environment. Int J Comput Sci Issues. 2013;10(6):45. [Google Scholar]
- 7.Duan F, et al. Topological network analysis of early Alzheimer’s disease based on resting-state EEG. IEEE Trans Neural Syst Rehabil Eng. 2020;28:2164–2172. doi: 10.1109/TNSRE.2020.3014951. [DOI] [PubMed] [Google Scholar]
- 8.Ieracitano C, et al. A novel multi-modal machine learning based approach for automatic classification of EEG recordings in dementia. Neural Netw. 2020;123:176–190. doi: 10.1016/j.neunet.2019.12.006. [DOI] [PubMed] [Google Scholar]
- 9.Akbari H, Esmaili SS. A novel geometrical method for discrimination of normal, interictal and ictal EEG signals A novel geometrical method for discrimination of normal, interictal and ictal EEG signals.
- 10.Farsi L, et al. Classification of alcoholic EEG signals using a deep learning method. IEEE Sens J. 2020;21(3):3552–3560. [Google Scholar]
- 11.Moghaddari M, Lighvan MZ, Danishvar S. Diagnose ADHD disorder in children using convolutional neural network based on continuous mental task EEG. Comput Methods Prog Biomed. 2020;197:105738. doi: 10.1016/j.cmpb.2020.105738. [DOI] [PubMed] [Google Scholar]
- 12.Tawhid M, Siuly S, Wang H. Diagnosis of autism spectrum disorder from EEG using a time–frequency spectrogram image-based approach. Electron Lett. 2020;56:1372–1375. [Google Scholar]
- 13.Oung QW, et al. Empirical wavelet transform based features for classification of Parkinson’s disease severity. J Med Syst. 2018;42(2):29. doi: 10.1007/s10916-017-0877-2. [DOI] [PubMed] [Google Scholar]
- 14.Cai Q, et al. A graph-temporal fused dual-input convolutional neural network for detecting sleep stages from EEG signals. IEEE Trans Circu Syst II: Express Briefs. 2020 doi: 10.1109/TCSII.2020.3014514. [DOI] [Google Scholar]
- 15.Siuly S, et al. A computerized method for automatic detection of schizophrenia using EEG signals. IEEE Trans Neural Syst Rehabil Eng. 2020;28:2390–2400. doi: 10.1109/TNSRE.2020.3022715. [DOI] [PubMed] [Google Scholar]
- 16.Khare SK, et al. Classification of schizophrenia patients through empirical wavelet transformation using electroencephalogram signals. Bristol: IOP Publishing; 2020. [Google Scholar]
- 17.Khare SK, Bajaj V. An evolutionary optimized variational mode decomposition for emotion recognition. IEEE Sens J. 2020;21:2035–2042. [Google Scholar]
- 18.Khare SK, Bajaj V, Sinha G. Adaptive tunable Q wavelet transform based emotion identification. IEEE Trans Instrum Meas. 2020;69(12):9609–9617. [Google Scholar]
- 19.Sadiq MT, et al. Motor imagery BCI classification based on novel two-dimensional modelling in empirical wavelet transform. Electron Lett. 2020;56(25):1367–1369. [Google Scholar]
- 20.Sadiq MT, et al. Identification of motor and mental imagery EEG in two and multiclass subject-dependent tasks using successive decomposition index. Sensors. 2020;20(18):5283. doi: 10.3390/s20185283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sadiq MT, et al. Motor imagery EEG signals classification based on mode amplitude and frequency components using empirical wavelet transform. IEEE Access. 2019;7:127678–127692. [Google Scholar]
- 22.Sadiq MT, et al. Motor imagery EEG signals decoding by multivariate empirical wavelet transform-based framework for robust brain-computer interfaces. IEEE Access. 2019;7:171431–171451. [Google Scholar]
- 23.Sadiq MT, et al. A matrix determinant feature extraction approach for decoding motor and mental imagery EEG in subject specific tasks. IEEE Trans Cogn Dev Syst. 2020 doi: 10.1109/TCDS.2020.3040438. [DOI] [Google Scholar]
- 24.Hosseinifard B, Moradi MH, Rostami R. Classifying depression patients and normal subjects using machine learning techniques and nonlinear features from EEG signal. Comput Methods Prog Biomed. 2013;109(3):339–345. doi: 10.1016/j.cmpb.2012.10.008. [DOI] [PubMed] [Google Scholar]
- 25.Faust O, et al. Depression diagnosis support system based on EEG signal entropies. J Mech Med Biol. 2014;14(03):1450035. [Google Scholar]
- 26.Puthankattil SD, Joseph PK. Classification of EEG signals in normal and depression conditions by ANN using RWE and signal entropy. J Mech Med Biol. 2012;12(04):1240019. [Google Scholar]
- 27.Ahmadlou M, Adeli H, Adeli A. Spatiotemporal analysis of relative convergence of EEGs reveals differences between brain dynamics of depressive women and men. Clin EEG Neurosci. 2013;44(3):175–181. doi: 10.1177/1550059413480504. [DOI] [PubMed] [Google Scholar]
- 28.Acharya UR, et al. A novel depression diagnosis index using nonlinear features in EEG signals. Eur Neurol. 2015;74(1–2):79–83. doi: 10.1159/000438457. [DOI] [PubMed] [Google Scholar]
- 29.Mumtaz W, et al. A machine learning framework involving EEG-based functional connectivity to diagnose major depressive disorder (MDD) Med Biol Eng Comput. 2018;56(2):233–246. doi: 10.1007/s11517-017-1685-z. [DOI] [PubMed] [Google Scholar]
- 30.Liao S-C, et al. Major depression detection from EEG signals using kernel eigen-filter-bank common spatial patterns. Sensors. 2017;17(6):1385. doi: 10.3390/s17061385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bairy GM, et al. Automated diagnosis of depression electroencephalograph signals using linear prediction coding and higher order spectra features. J Med Imaging Health Inform. 2017;7(8):1857–1862. [Google Scholar]
- 32.Knott V, et al. EEG power, frequency, asymmetry and coherence in male depression. Psychiatry Res: Neuroimaging. 2001;106(2):123–140. doi: 10.1016/s0925-4927(00)00080-9. [DOI] [PubMed] [Google Scholar]
- 33.Acharya UR, et al. Automated EEG-based screening of depression using deep convolutional neural network. Comput Methods Programs Biomed. 2018;161:103–113. doi: 10.1016/j.cmpb.2018.04.012. [DOI] [PubMed] [Google Scholar]
- 34.Sharma M, et al. An automated diagnosis of depression using three-channel bandwidth-duration localized wavelet filter bank with EEG signals. Cogn Syst Res. 2018;52:508–520. [Google Scholar]
- 35.Daubechies I. Ten lectures on wavelets. San Diego: SIAM; 1992. [Google Scholar]
- 36.Gilles J. Empirical wavelet transform. IEEE Trans Signal Process. 2013;61(16):3999–4010. [Google Scholar]
- 37.Huang NE, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc R Soc Lond. Ser A: Math Phys Eng Sci. 1971;1998(454):903–995. [Google Scholar]
- 38.Amezquita-Sanchez JP, Adeli H. A new music-empirical wavelet transform methodology for time–frequency analysis of noisy nonlinear and non-stationary signals. Digit Signal Process. 2015;45:55–68. [Google Scholar]
- 39.Hu Y, et al. An enhanced empirical wavelet transform for noisy and non-stationary signal processing. Digit Signal Process. 2017;60:220–229. [Google Scholar]
- 40.Maheshwari S, Pachori RB, Acharya UR. Automated diagnosis of glaucoma using empirical wavelet transform and correntropy features extracted from fundus images. IEEE J Biomed Health Inform. 2016;21(3):803–813. doi: 10.1109/JBHI.2016.2544961. [DOI] [PubMed] [Google Scholar]
- 41.Sadiq MT, Yu X, Yuan Z. Exploiting dimensionality reduction and neural network techniques for the development of expert brain–computer interfaces. Expert Syst Appl. 2020;164:114031. [Google Scholar]
- 42.Liu W, Pokharel PP, Príncipe JC. Correntropy: properties and applications in non-Gaussian signal processing. IEEE Trans Signal Process. 2007;55(11):5286–5298. [Google Scholar]
- 43.Rao M, et al. A test of independence based on a generalized correlation function. Signal Process. 2011;91(1):15–27. [Google Scholar]
- 44.Ghofrani S, Akbari H. Comparing nonlinear features extracted in EEMD for discriminating focal and non-focal EEG signals. In Tenth international conference on signal processing systems. 2019. International Society for Optics and Photonics.
- 45.Akbari H, Ghofrani S. Fast and accurate classification F and NF EEG by using SODP and EWT. Int J Image Graph Signal Process. 2019;11(11):29–35. [Google Scholar]
- 46.Sadiq MT, Shabbir N, Kulesza WJ. Spectral subtraction for speech enhancement in modulation domain. Int J Comput Sci Issues. 2013;10(4):282. [Google Scholar]
- 47.Gilles J, Heal K. A parameterless scale-space approach to find meaningful modes in histograms—application to image and spectrum segmentation. Int J Wavelets Multiresolut Inf Process. 2014;12(06):1450044. [Google Scholar]
- 48.Patidar S, et al. An integrated alcoholic index using tunable-Q wavelet transform based features extracted from EEG signals for diagnosis of alcoholism. Appl Soft Comput. 2017;50:71–78. [Google Scholar]
- 49.Nishad A, Pachori RB, Acharya UR. Application of TQWT based filter-bank for sleep apnea screening using ECG signals. J Ambient Intell Humaniz Comput. 2018 doi: 10.1007/s12652-018-0867-3. [DOI] [Google Scholar]
- 50.Siuly S, et al. A new framework for automatic detection of patients with mild cognitive impairment using resting-state EEG signals. IEEE Trans Neural Syst Rehabil Eng. 2020;28(9):1966–1976. doi: 10.1109/TNSRE.2020.3013429. [DOI] [PubMed] [Google Scholar]
- 51.Al Ghayab HR, et al. A feature extraction technique based on tunable Q-factor wavelet transform for brain signal classification. J Neurosci Methods. 2019;312:43–52. doi: 10.1016/j.jneumeth.2018.11.014. [DOI] [PubMed] [Google Scholar]
- 52.Supriya S, et al. Automated epilepsy detection techniques from electroencephalogram signals: a review study. Health Inf Sci Syst. 2020;8(1):1–15. doi: 10.1007/s13755-020-00129-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Siuly S, Li Y, Zhang Y. EEG signal analysis and classification. Berlin: Health Information Science, Springer; 2016. [Google Scholar]
- 54.Taran S, Bajaj V, Siuly S. An optimum allocation sampling based feature extraction scheme for distinguishing seizure and seizure-free EEG signals. Health Inf Sci Syst. 2017;5(1):7. doi: 10.1007/s13755-017-0028-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Akhter MP, Jiangbin Z, Naqvi IR, Abdelmajeed M, Mehmood A, Sadiq MT. Document-level text classification using single-layer multisize filters convolutional neural network. IEEE Access. 2020;8:42689–42707. [Google Scholar]
- 56.Anuragi A, Sisodia DS, Pachori RB. Automated alcoholism detection using fourier-bessel series expansion based empirical wavelet transform. IEEE Sens J. 2020;20(9):4914–4924. [Google Scholar]
- 57.Bachmann M, et al. Methods for classifying depression in single channel EEG using linear and nonlinear signal analysis. Comput Methods Prog Biomed. 2018;155:11–17. doi: 10.1016/j.cmpb.2017.11.023. [DOI] [PubMed] [Google Scholar]