Bayesian modeling of dependence in brain connectivity data

SUMMARY

Brain connectivity studies often refer to brain areas as graph nodes and connections between nodes as edges, and aim to identify neuropsychiatric phenotype-related connectivity patterns. When performing group-level brain connectivity alternation analyses, it is critical to model the dependence structure between multivariate connectivity edges to achieve accurate and efficient estimates of model parameters. However, specifying and estimating dependencies between connectivity edges presents formidable challenges because (i) the dimensionality of parameters in the covariance matrix is high (of the order of the fourth power of the number of nodes); (ii) the covariance between a pair of edges involves four nodes with spatial location information; and (iii) the dependence structure between edges can be related to unknown network topological structures. Existing methods for large covariance/precision matrix regularization and spatial closeness-based dependence structure specification/estimation models may not fully address the complexity and challenges. We develop a new Bayesian nonparametric model that unifies information from brain network areas (nodes), connectivity (edges), and covariance between edges by constructing the function of covariance matrix based on the underlying network topological structure. We perform parameter estimation using an efficient Markov chain Monte Carlo algorithm. We apply our method to resting-state functional magnetic resonance imaging data from 60 subjects of a schizophrenia study and simulated data to demonstrate the performance of our method.

1. Introduction

Neuroimaging research is increasingly focused on studying brain connectivity and its relationship with neuropsychiatric phenotypes (Bullmore and Sporns, 2009; Biswal and others, 2010; Craddock and others, 2013; Stam, 2014). Functional brain connectivity measures synchronized activation of brain signals between neural processing units from distinct brain locations. The brain signals are measured by biomedical techniques including functional magnetic resonance imaging (fMRI), magnetoencephalography, and electroencephalography. The basic element in these brain connectivity data is the connectivity edge that connects two brain areas of distinct spatial coordinates (nodes), which is naturally linked to other edges to form network topology (Simpson and others, 2012; Sporns, 2014; Chen and others, 2015; Simpson and Laurienti, 2016). Therefore, brain connectivity data are multi-dimensional and characterized by complex dependence structures reflecting highly sophisticated neurophysiology and organized network topology (Shou and others, 2014; Ahn and others, 2015; Chiang and others, 2017; Durante and Dunson, 2018; Xia and Li, 2017).

In brain connectivity studies, our aim is to identify brain connectivity patterns that are associated with pathological and behavior phenotypes via statistical analyses. However, statistical analyses used in brain connectivity studies often ignore correlations between the multivariate connectivity edges, which may lead to inaccurate parameter estimation and statistical testing results. Advanced statistical models may mitigate these shortcomings by correctly specifying and estimating the dependence between brain imaging features (Bowman, 2005; Derado and others, 2010).

Statistically, functional brain connectivity data can be formulated by a weighted and symmetric matrix: 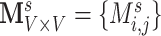for a subject 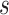(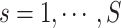), where each entry 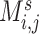represents the connectivity measurement between brain areas 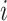and 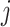(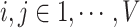). Thus, 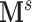represents a graph that consists of 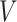nodes and 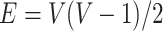weighted edges. The most commonly used metrics for 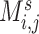are correlation coefficient, partial correlation coefficient, and mutual information coefficient among many choices (Kim and others, 2015). Statistical models have been developed to estimate brain connectivity and test their association with neuropsychiatric phenotypes (Kim and others, 2014; Lindquist and others, 2014; Ahn and others, 2015; Zhang and others, 2015; Chen and others, 2016; Han and others, 2016; Qiu and others, 2016; Chiang and others, 2017; Fiecas and others, 2017; Durante and Dunson, 2018; Xia and Li, 2017 among others). Edge-wise statistical inference is desirable because edge-wise findings are localized and more straightforward to interpret (Zalesky and others, 2010; Craddock and others, 2013; Simpson and others, 2015). The connectivity edge matrix 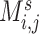can be transformed into a vector 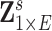with 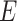edges that follows a multivariate distribution. For example, let 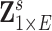be a vector of commonly used Fisher’s Z transformed correlation coefficients that follow a multivariate normal distribution 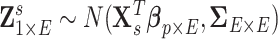, where 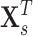represents 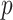subject-specific clinical and demographic covariates and 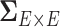is the covariance matrix between connectivity edges. Clearly, correctly specifying and estimating dependence structure between connectivity edges can increase the accuracy of model parameter estimates and statistical tests on individual edges (Bowman, 2005; Derado and others, 2010).

It has been a long-term challenge to estimate the covariance matrix 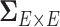between connectivity edges because: (i) the dimensionality of parameters in 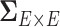is as high as 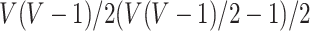, for example, when 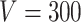the number of parameters in 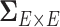is greater than 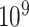; (ii) it is difficult to define the spatial closeness between a pair of edges with four nodes, and the geometric distances between the four nodes do not predict the correlation/dependency between a pair of edges; and (iii) each connectivity edge is constrained by two nodes, and a group of correlated edges can be constrained by a small set of nodes with organized yet latent network topology (Figure 1). The direct estimation of large sample covariance is not reliable, and it is hard to achieve the inverse calculation that is required for inferences (Fan and others, 2016). Although numerous methods have been developed to estimate node-based variables for large precision matrix shrinkage estimation, e.g. 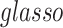(Cai and others, 2011; Fan and others, 2016), these may not be directly applicable to estimating 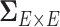because they may not address the impact of spatial and network topological properties on the covariance between edges. On the other hand, the widely used spatial modeling strategies that specify dependence structure/parameters via spatial closeness (mainly used in localized brain activity analysis) (Bowman, 2005; Bowman and others, 2008; Derado and others, 2010; Brown and others, 2014) may not be well suited for connectivity analysis because dependencies between connectivity edges are not necessarily driven by their spatial closeness but are definitely driven by the (latent) organized and biologically meaningful network topological structures that are not constrained by spatial adjacency (see section 3.2). Simpson and Laurienti (2015) proposed a two-part mixed effect model for whole-brain connectivity data analysis that accounts for covariance among connectivity edges via the local and global network/graph descriptive statistics. However, the explicit dependence structure of connectivity edges (which edges are more correlated with each other) in the mixed model is unknown, and such information may further be incorporated in the mixed model as more specific random effects.

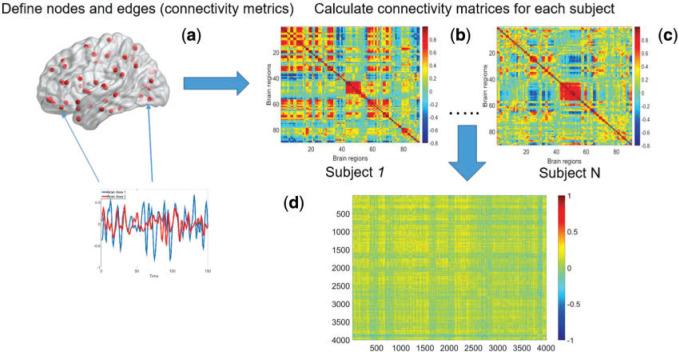
Fig. 1.

Demonstration of calculating covariance matrix between connectivity edges across subjects: (a) a brain connectivity edge is calculated based on two brain areas (nodes) of a study subject, e.g. correlation or partial correlation metrics; (b) and (c) a connectivity matrix is calculated (90 AAL brain regions and 4005 edges for each subject; (d) across all subjects, the covariance matrix between edges is a 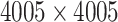matrix.

To address these challenges, we propose a Bayesian nonparametric model to estimate 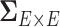that integrates multiple layers of information including nodes, edges, and correlations between edges by leveraging the latent network topological information. It has been well documented that brain connectivity data show organized and biologically meaningful network topological structures (Bullmore and Sporns, 2009; Rubi-nov and Sporns, 2010; Simpson and others, 2015), and these structures can be related to the covariance structure (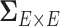). Our empirical data analyses on multiple brain connectivity data sets suggest that connectivity edges within organized networks are more correlated than edges outside the networks. These results are neurophysiologically plausible, because many brain functional networks show synchronized patterns at activation and resting (Biswal and others, 2010; Craddock and others, 2013; Stam, 2014).

However, it is difficult to identify the latent network structure where the inside network edges are more correlated. Conventional network detection methods (e.g. Newman 2006) assign nodes into clusters based on the similarities between nodes. Yet, in our application, these methods cannot be directly used to cluster edges into networks based on the similarity (correlation) between edges, because edges are constrained by nodes and a cluster of edges may be randomly distributed in the brain and may not be biologically meaningful. We develop a new Bayesian nonparametric model to estimate the network structure (assigning nodes into clusters) based on the sample covariance matrix between connectivity edges. Note that for the purposes of our model, the term “network” for the covariance matrix is estimated based on the sample covariance matrix between connectivity edges across subjects, which is different from the commonly used term “network/graph topological properties or descriptive statistics” (e.g. modularity and small-worldness) referring to values that are calculated or estimated by using the mean values of edges from the connectivity matrix of a single subject or the average connectivity matrix across subjects in a study (Bullmore and Sporns, 2009; Craddock and others, 2013). We develop an efficient Markov chain Monte Carlo (MCMC) algorithm to estimate the massive parameters and overcome computational challenges involved with the calculation of inverses and determinants of large matrices. Finally, we demonstrate the use of our proposed model in an fMRI data set to identify schizophrenia disorder related functional brain connectivity patterns, followed by simulation studies to evaluate the performance and utility of our proposed method.

2. Methods

Following a formerly described strategy to estimate parameters of the large covariance matrix of spatial–temporal imaging data (Bowman, 2005; Derado and others, 2010), we focus on the residual matrix 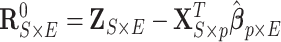, where 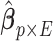can be estimated unbiasedly by using the general linear model. We calculate 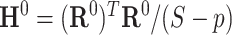and separately estimate the correlation matrix 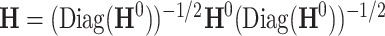and standard deviations 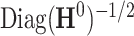by assuming independence between the two components of the covariance matrix (Barnard and others, 2000). 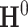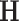The dimension of and is 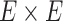. Our Bayesian non-parametric model takes 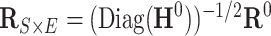and 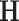as the input data, and estimates the correlation matrix 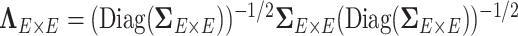with a network topological structure and (Fan and others, 2016).

2.1. Model specification

First, we let 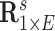follow a multivariate normal distribution with zero mean and a unknown dependence structure 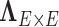. The correlation matrix is a function of the network structure and the correlation parameters 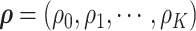. 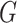is the random measure of the network structure (i.e. the network assignment of brain areas). 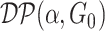represents a Dirichlet process with base measure 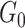and scalar precision 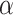, which is used to identify the latent 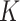networks ( 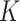is unknown).

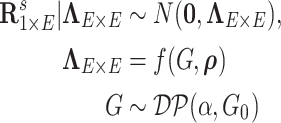(2.1)

We specify the network topological structure-based covariance matrix function as

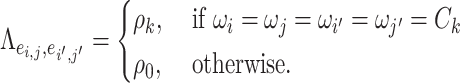(2.2)

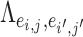is an entry of 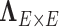that denotes the correlation between the edge 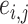(i.e. the brain connectivity edge connecting brain regions 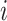and 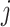, 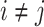) and edge 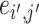. Let 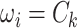be an indicator variable for the network membership of brain region 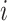. For a pair of edges 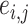and 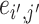, we denote 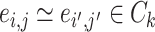(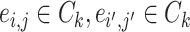) if and only if 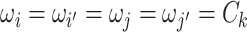and the two edges are in the same network. Given the network memberships of the nodes, 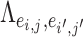is determined by the “locations” of these two edges in the network topology. Formula 2.2 represents a commonly used parametric covariance specification method in neuroimaging statistics, setting an exchangeable dependence structure for imaging features in a spatially and/or temporally close “neighborhood” (Bowman, 2005; Derado and others, 2010; Risk and others, 2016). The assumption of exchangeable dependence structure is often empirically examined by exploratory data analysis in these applications. Likewise, we validate this assumption using our example data sets and several other fMRI data sets (not presented here due to the page limit). The results show distinct distributions of empirical correlations among edges inside vs. outside automatically detected networks with 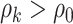(see details in Section 3.1 and Figures 2 and 4). Unlike the previous methods where the “neighborhood” is directly defined based on the spatial and temporal adjacency, the “neighborhood” networks in our method are automatically detected mainly based on the input data and dependence structure specification 2.2. Specifically, when we assign each node 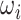(instead of each edge) to one network 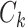, and a connectivity edge 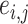can be therefore assigned to a network based on the memberships of its two nodes. Therefore, a network structure more accurately reflecting the latent dependence structure leads to a better-estimated covariance matrix and thus the increased value of likelihood function, and the posterior sampling procedure will converge when the dependence networks and covariance matrix are optimally estimated.

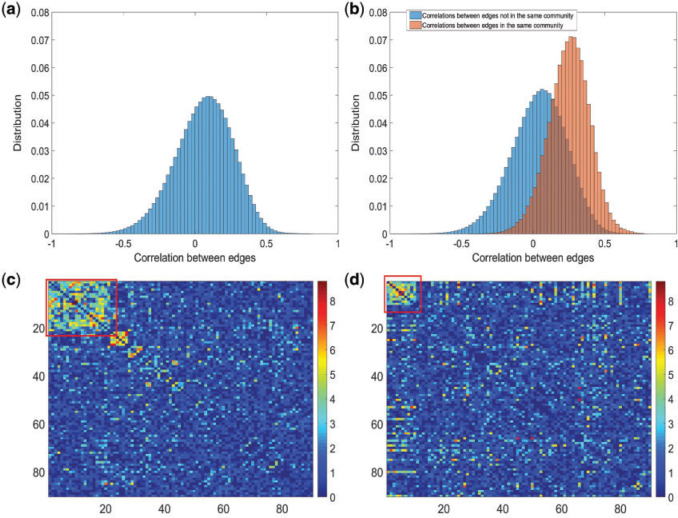
Fig. 2.

(a) Histogram of 8 018 010 correlations between all 4005 edges. (b) Reflects our estimated network topology and correlation matrix in that 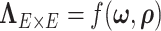, and the correlations between edges in the same networks are more correlated than correlations between edges not in the same community. (c) and (d) Inferences with dependence structure between edges vs. inferences with independence assumption: the disease-related connectivity network is larger when accounting for dependence structure between edges and agrees better with findings in previous studies. Each entry in the heatmaps is—log transformed 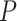-value of an edge between the column and row nodes and a hotter point indicates more significant difference between diagnosis groups. We order the brain regions by listing regions in the diagnosis group related-network first.

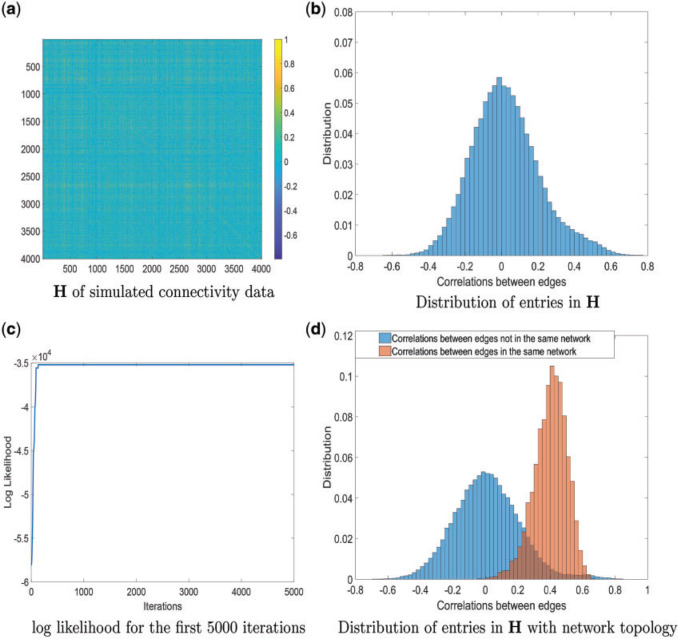
Fig. 4.

(a) and (b) The simulated connectivity data and input data correlation H are demonstrated.(c) Log likelihood of the first 5000 samples of the MCMC, which converges quickly as well. (d) Distributions of entries in H based on estimated network topology.

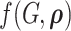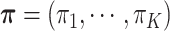By using the above heuristic, we develop a new Dirichlet process model (DPM) to detect underlying networks. We specify the distributions of parameters in . As suggested by Neal (2000), a DPM can be represented by taking the limit as the number of components goes to infinity. Let Discrete() denote a discrete distribution and let each brain area have probability of being in network (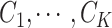). Let Dirichlet(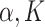) be a Dirichlet distribution with parameter 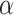. Then DPM in 2.1 is equivalent to the following model.

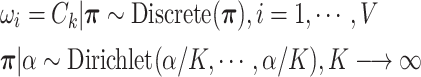(2.3)

In addition, we assume that 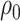, 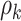follow normal distributions with hyperparameters .

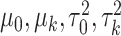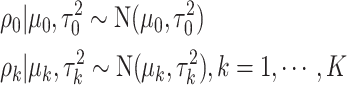(2.4)

The community network structure is widely used and well-documented in brain connectivity network studies and infinite mixture models with a stochastic block structure are often used for statistical modeling (Pavlovic and others, 2014; Sporns, 2016; Bryant and others, 2017). However, the underlying covariance-related network structure is difficult to estimate, and neither infinite mixture model nor DPM can be directly applied, because they are conventionally used to estimate node community memberships based on the similarities between nodes. Nor can we directly cluster edges into network communities based on the sample edge covariance matrix (similarities between edges), because this may yield clusters of edges that are distributed in the brain without any network topological structure (without the constraint of clustered nodes) and are thus not biologically meaningful. Therefore, our proposed Bayesian nonparametric model is novel and learns network structure (node allocation) by using the sample covariance (adjacency) matrix among edges as input data.

Given the prior distributions of community structure 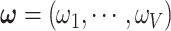, 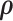and function 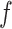, the posterior probability of 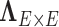can be written as:

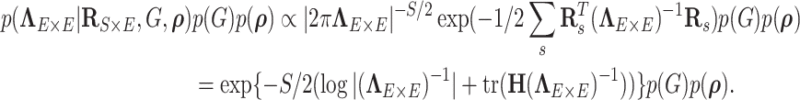(2.5)

The value of likelihood function changes substantially when moving a node from one community 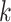to another 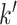because the covariance entries of 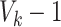+ 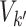edge pairs change correspondingly in 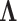. This property ensures that the posterior sampling of DPM can quickly converge.

The parametric dependence structure specification in 2.2 is widely used and practically effective for multivariate imaging features (Bowman, 2005; Derado and others, 2010), and 2.2 is more flexible because the “neighborhood” structure is learned via DPM instead of using assumptions (e.g. spatial smoothness). One alternative strategy is to specify the prior distribution of each entry of the covariance matrix to follow a normal distribution 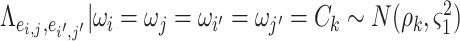(Khondker and others, 2013). However, this may lead to the problematic inversion of 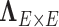and difficulty in MCMC calculation, and an intractable number of parameters. In contrast, the model specification of 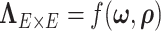in 2.2 ensures that the covariance matrix is positive definite (see proof in the supplementary material available at Biostatistics online).

2.2. Posterior computation

We implement the posterior computation of 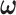and 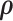by MCMC. Specifically, we have the full conditional distribution of 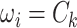given 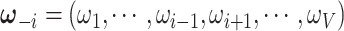, 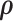and data :

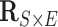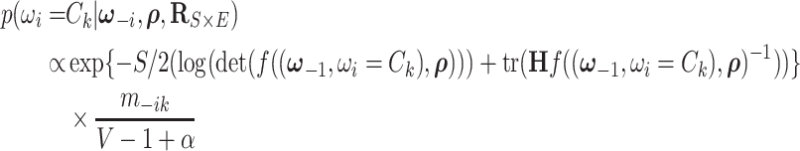(2.6)

where 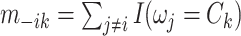represents the number of nodes in community 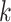, and

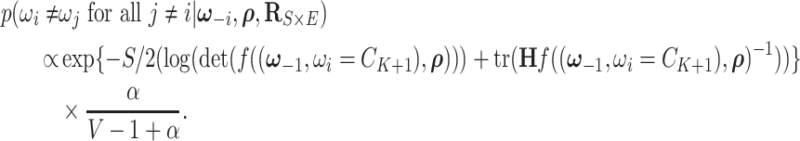(2.7)

The calculation of 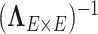is implemented using the Sherman–Morrison formula (Press, 2007):

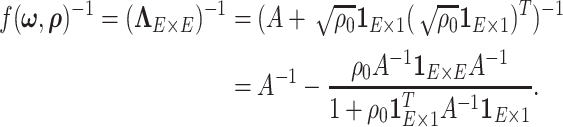(2.8)

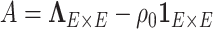is block diagonal and each block is compound symmetric, and thus the calculation is straightforward. Similarly, the determinant can be calculated by the matrix determinant lemma (Harville, 1998): 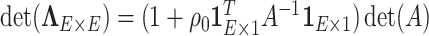. By applying these results, the posterior can be efficiently sampled.

The full conditionals of 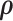are given by

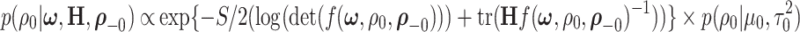(2.9)

where 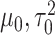are selected based on the empirical distribution of the entries in H.

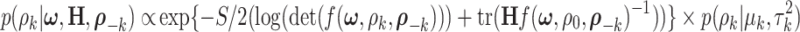(2.10)

where 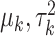are selected based on the empirical distribution of the entries in H. The Metropolis–Hasting algorithm is used for posterior sampling for .

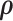Alternatively, 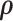can be estimated based on the empirical distribution of the entries in H given the estimated network topology 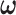, and then 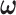is updated based on 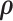. This iterative procedure often converges quickly because the network topology estimation is very robust to the numeric values of 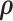, which can greatly improve the computational efficiency and yield similar results. Last, we calculate the covariance matrix between edges 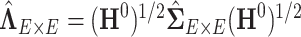and the inversion 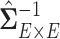by using the Sherman–Morrison formula.

3. Application to investigate altered functional connectivity patterns by Schizophrenia

We applied the proposed method to the analysis of the resting state fMRI data. The study recruited 30 individuals with schizophrenia (age = 39.73 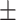13.79 years) and 30 matched healthy controls (age = 39.73 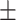14.16 years) matched on age (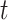=0.27, 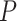=0.78) and sex ratio (=0.09, 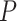=0.77). All participants were evaluated using the Structured Clinical Interview for the DSM-IV diagnoses. The fMRI data acquisition and preprocessing steps are included in supplementary material available at Biostatistics online. The preprocessed brain images was divided into 90 anatomical automatic labeling (AAL) regions as nodes, and each region-wise time series was calculated based on weighted average of voxels within a 10 mm sphere around the centroid of each region. Fisher’s Z-transformed correlation coefficients were calculated between time series of all region pairs as metrics for edges (Tzourio-Mazoyer and others, 2002, Kim and others, 2015).

3.1. Estimating network-based covariance matrix between edges

Each of the 60 subjects had a connectivity matrix of 4005 edges connecting the 90 nodes. We applied the proposed Bayesian model to estimate the 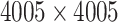covariance matrix between all edges. We first calculated the residual matrix 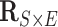and correlation matrix 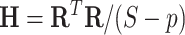. The Bayesian non-parametric model was implemented to identify the latent network topological structure and the covariance matrix based on the input data 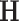. We set the hyperparameters based on the empirical analysis of distribution of all entries in 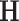, and let 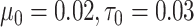and 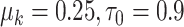expressing a reasonable prior belief that 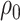is likely around 0 and the value of 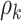depends on the network structure. We set the initial value of 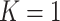and performed MCMC sampling for 5000 iterations with 1000 burn-in.

The MCMC converged quickly and the infinite mixture model suggested 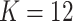, with two large communities of 37 and 16 nodes, respectively. We found that edges in the community networks were more correlated. The 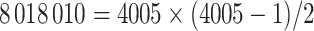correlations between all 4005 edges are demonstrated in the normalized histogram in Figure 2a. We further compared the distributions of correlations between edges (entries in H) within the same networks and otherwise; as shown in Figure 2b edges within the same networks were more correlated than edges not in the same network. We also found that the posterior distributions of 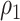and 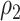are similar (with posterior mode values of 0.28 and 0.29). We also compared models with and 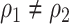using likelihood ratio test based on estimated network structure, and the results (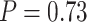) indicated that the correlations of edges in the two networks were similar. In contrast, the empirical distribution of correlations between edges not in the same covariance network was close to the null distribution (Figure 2b). We further formally tested whether the distribution of correlations among outside network edges differed from the null distribution using the strategy outlined by Schäferand Strimmer (2005). We performed local fdr analysis on the Fisher’s Z-transformed correlation coefficients of outside network edges. None of the correlations had a q value 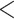0.2 and non-null components were not detected (Efron, 2004). Therefore, the non-null component of correlations between connectivity edges can be mostly explained by edges inside networks. These results further verify that our dependence structure specification of 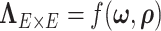in equation 2.2 is sound and that the Bayesian model is effective to identify the latent network structure. Prior research (e.g. Power and others, 2010) reveals that brain connectome show network-based development, which further supports the network-based covariance structure specification.

The major hyperparameter that is subject to user’s choice in our model is the Dirichlet process concentration parameter 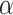, while 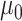and 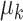are determined by the empirical data statistics. We evaluated the model performance by letting 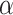equal to 0.1, 1, 10, and 100. The results indicated that our model is robust to the choices of 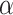as we obtained similar results of edge-dependence networks (the two large networks were unchanged, see supplementary material available at Biostatistics online). The computational time using an i7 3.4G HZ CPU and 64 G RAM desktop was roughly 3.5 h.

3.2. Implications of covariance networks

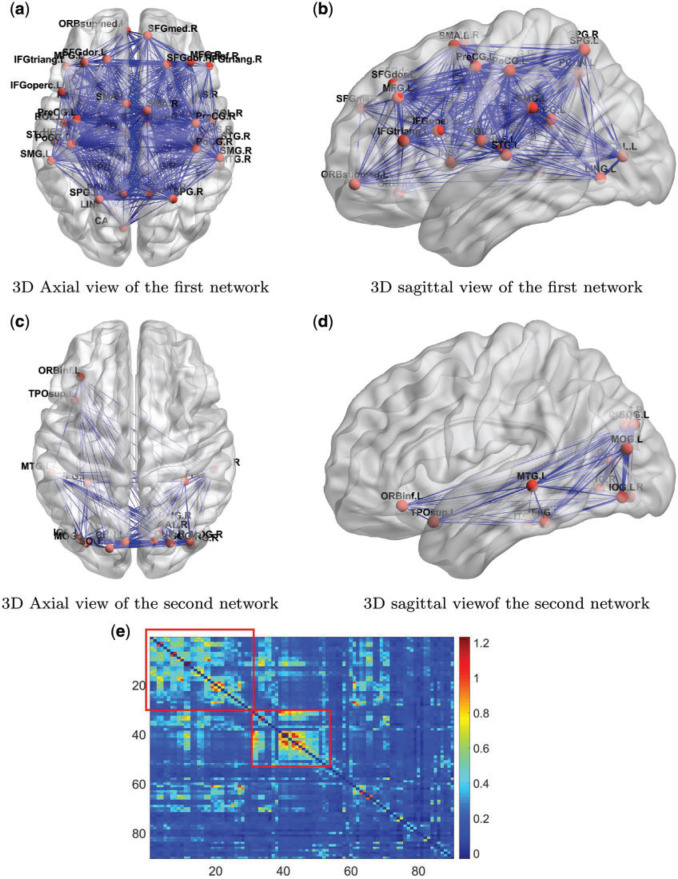
We next explored the detected community networks based on the covariance between edges with a focus on the two large community networks. The first network consists of 37 nodes (Table 2 in the supplementary material available at Biostatistics online), including the medial prefrontal cortices, posterior cingulate cortices, inferior parietal lobules, lateral temporal cortices, and the precuneus (Figure 3). Interestingly, the first network largely overlapped with the default mode network (DMN), which is a well-known network of interacting brain regions when experimental subjects are at wakeful rest (Greicius and others, 2003; Stam, 2014). Our new finding, by applying the proposed model, is that edges in the DMN are more correlated with each other than other edge pairs. Network two is illustrated in Figures 3c and 3d, which mainly includes brain areas in the occipital cortices, cuneus left and right, three temporal and one inferior frontal brain region (Table 3 in the supplementary material available at Biostatistics online). The interactive regions in the second network are mainly related to the visual function. The rest of the 10 networks were relatively small, consisting of only three or four spatially adjacent nodes. The correlations of the edges in these networks have a little impact on the 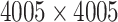covariance matrix estimation.

Fig. 3.

(a) and (b) Three-dimensional demonstration of the first network of DMN are shown. (c) and (d) Three-dimensional demonstration of the second network of DMN are shown. The width of an edge is proportional to the mean connectivity strength across all subjects. (e) A heatmap shows the average brain connectivity matrix across all experimental subjects with the networks based on edge covariance matrix estimation. The correlated edges in the covariance networks show higher mean value.

Figure 3e shows the mean functional connectivity metrics (Fisher’s Z-transformed correlation coefficients) across all subjects. A large proportion of edges tend to show higher connectivity strengths (edge mean values) within the covariance networks, although the networks were identified only using the sample covariance between edges (independent of the mean values). Note that clustering/community detection results based on mean values of the connectivity matrix may extract different networks, and edges in those networks may not be correlated.

We also found that correlation between a pair of edges was not related to the spatial closeness of the four coordinates in our example data. We used the minimum distance sum between four nodes of a pair of edges as a measure of distance between edges, and the correlation between spatial distance and edge correlation was 0.13. On the other hand, many pairs of edges in the DMN are distant in space yet highly correlated. If edges in a cluster of spatially close nodes are more correlated, our Bayesian model can also identify these nodes as a network (e.g. a network of regions within the frontal lobe), because the likelihood function for 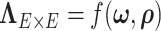is greater when the network is correctly estimated. Therefore, our proposed model is more general, flexible, and data-driven and is capable of capturing the spatial and network topological property of a brain network.

3.3. Results: connectivity patterns associated with Schizophrenia

We calculated 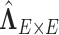using mode values of 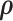and stable 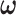and the inverse matrix for statistical inferences on individual connectivity edges testing 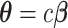. For this case study, our aim was to examine whether connectivity patterns are associated with diagnostic group. Following the strategy by Derado and others (2010), we incorporated the estimated covariance matrix (“neighborhood” information) into the general linear model to account for dependencies of connectivity edges. The analysis results provide a vector of test-statistics (and corresponding 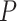-values) for all 4005 edges that are subject to multiple-test control. Since edges are correlated and constrained by nodes and network topology, the conventional false discovery rate (FDR) control method may not be applicable. Thus, we applied the network based inference tools to adjust multiple comparisons of the testing results, for example, those described by Zalesky and others (2010) and Chen and others (2015). These tools are an extension of the most commonly used cluster-extent based multiple comparison correction methods in neuroimaging studies (Woo and others, 2014), which define a cluster as a set of topologically connected connectivity edges showing group-wise difference. Zalesky and others (2010) identifies a cluster of the maximally connected component in the thresholded connectome map by greedy search, while Chen and others (2015) implements shrinkage on cluster sizes and taking in to account the number and effect sizes of edges in the cluster. Permutation tests are then performed based on the cluster extent/information to achieve corrected statistical inference.

The hypothesis testing results based on our estimated dependence structure identified 292 edges with P-values 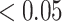verses 213 edges for the model with the general linear model ( 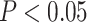is not used for final inferences). We claim that our method accounting for dependencies between edges improves the power of statistical tests because, not only more small 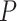-value edges were detected by our method, but these edges showed more organized network topological structure in the following analyses. We applied network-level inference adjusting for multiple tests as described by Chen and others (2015) to the vector of testing results and Figure 2c shows one significant brain connectivity network of 21 nodes that is associated with diagnostic group by using our estimated covariance matrix (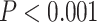). The disease-related brain connectivity network includes the medial premotor, cingulate and parietal cortex, precentral and postcentral cortex, occipital association cortex, and left superior frontal, superior temporal, and insular cortices (see Table 4 in the supplementary material available at Biostatistics online). Connectivity strengths were reduced in the schizophrenic group. The results strongly coincide with the edge-wise findings in well-documented precedent studies of functional connectivity and schizophrenia Lynall and others (2010) (although Lynall and others, 2010 only reported a handful of disease-related connections between region pairs without an organized subnetwork). The overall network level inferential results show reduced interconnections between DMN, the salience network, and the executive network in patients with schizophrenia. Therefore, we are the first to report schizophrenia-related connectivity patterns in topologically organized networks, thereby synchronizing isolated previous findings of individual edges into a well-organized network. In contrast, Figure 2d shows a smaller significant brain connectivity network (nodes) that is associated with diagnosis group based on the general linear model (without considering the covariance between edges) analysis results. In summary, the proposed approach can assist in detecting the underlying true phenotype related brain connectivity networks by providing more powerful statistical tests on edges.

4. Simulations

In the simulation study, we generated brain connectivity data showing that edges within the latent network community are more correlated across subjects. We focused on examining whether our Bayesian model could identify the latent network topology of covariance and correctly specify the dependence structure between edges, using the sample covariance matrix as the input data. Specifically, we simulated a brain connectivity data set with a moderate sample size (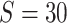), and assumed a latent stochastic block model with the total number of nodes 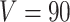(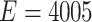), which includes three blocks with sizes 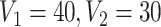, and 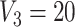. Then 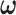in the covariance function 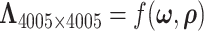is determined by the above stochastic block model, and we further set 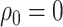and 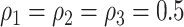. Last, we generated the connectivity data 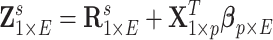, where 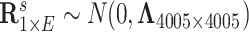. We calculated 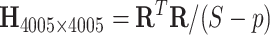as the input data as demonstrated in Figure 4. Note that the sample covariance matrix H is the input matrix for large covariance and precision matrix methods (e.g. glasso). We then tuned from 0.3 to 0.7 and repeated each setting for 20 times to evaluate the performance of our model at different levels of .

We applied our Bayesian non-parametric model to the sample covariance of brain connectivity data H to identify the latent network topology and estimate the dependence structure. The results show satisfactory performance of our model. When 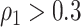, the accuracy of latent network topology detection was 100%, decreasing to 94.1% and 72.6% for 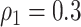and 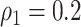respectively. With accurately estimated 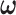, the dependence structure of 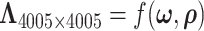can be estimated efficiently. We also note that MCMC converges very quickly after a few iterations (See Figure 2 in the supplementary material available at Biostatistics online). The reason is that moving one node from one network to another changes the covariance between many edges, and the likelihood value undergoes a relative large change. Figure 4 shows the network topology identification along the MCMC iterations for two initial settings: (i) all nodes belong to one network and (ii) each node is a singleton network. In both settings, the MCMC sampling of our model can quickly allocate the nodes to the true networks, and the likelihood approaches the maximum in the first couple of hundred iterations based on 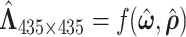(Figure 4c). Figure 4d shows the distributions of entries in H with network topology information and the two distributions. Clearly, the simulated data sets mimic the data example well. Like the data example, our results are not affected by the choice of 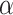from 0.1 to 100.

In addition, our method is robust to the deviation of estimated 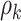. For instance, at the starting iterations of posterior samples 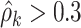(when ), the true community network structure can still be accurately detected by DPM. Then, will converge to the true value and the covariance matrix can be precisely estimated. Therefore, a more efficient alternative MCMC algorithm is: (i) first, to estimate the covariance network topology and 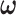with reasonable initial values of from the empirical data; (ii) next, to update the estimates of 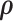based on 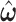; and (iii) finally to iterate until convergence. In practice, we found the performance of these two algorithms to be very similar, because 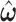is estimated equivalently.

Last, we compared our method with two commonly used methods that estimate covariance between high-dimensional variables: 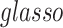and constrained 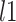minimization for inverse matrix estimation (CLIME) (Cai and others, 2011). There are 303 810, 94 395, 17 955, inside network edge pairs in the three networks with 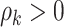, which are considered positive correlations between edges. We used false positive (FP) 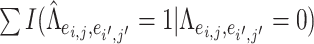and false negative (FN) 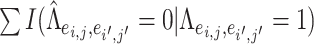as evaluation metrics instead of Frobenius norm. In practice, the FP and FN metrics are more important than the Frobenius norm, because the FP and FN metrics indicate whether edges borrow strength from each other correctly for statistical inferences in the regression model. For instance, 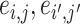can borrow strength from each other if 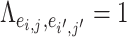and thus 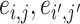are “neighbors” (Derado and others, 2010). For 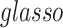and CLIME, the non-zero entries of the estimated edge precision matrix are considered as estimated positive dependence entries. For our Bayesian model, we consider inside network edge pairs as estimated positive dependence entries.

The results in Table 1 show that our method outperforms the competing models. The possible reasons are (i) that our method utilizes the latent network topology to guide the construction of the large covariance matrix between connectivity edges, and thus correlations between edges in the network can borrow strength from each other to reduce the FP and FN findings and (ii) that it does not rely on the sparsity assumption.

Table 1.

Covariance/precision matrix estimation results: median along with 25% and 75% quantiles of FP and FN

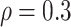
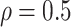
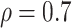
	FP		FN		FP		FN		FP		FN
Method	Median	Quantiles	Median	Quantiles	Median	Quantiles	Median	Quantiles	Median	Quantiles	Median	Quantiles
glasso	126 584.5	(98 627, 162 315)	94 151	(76 345, 113 682)	19 861	(16 837, 21 971.5)	5464	(4897, 7133)	2123.5	(485, 3529)	1302	(887, 1695)
CLIME	139 363	(88 532, 175 943.5)	113 595	(69 533, 146 298)	12 601.5	(8266, 15 302)	5298	(4396, 6157.5)	1575	(891.5, 1856)	917	(393.5, 1231)
NetCov	164	(18, 284)	26	(0, 82)	11	(1, 44)	0	(0, 9)	0	(0, 0)	0	(0, 0)

5. Discussion

In neuroimaging statistics, addressing dependence structures between multivariate imaging features is a fundamental issue. Various well-established theories and methods exist to model spatial and temporal dependence between localized brain activations and node variables (Bowman and others, 2008; Derado and others, 2010; Brown and others, 2014; Eloyan and others, 2014; Sweeney and others, 2016). However, there has been a lack of statistical methods to model the dependence between brain connectivity (edge-based) features.

In the statistical literature, the dependence structure of multivariate imaging variables are often pre-specified by leveraging biologically plausible assumptions. For example, the spatial and temporal closeness is used to specify the parametric covariance structure and the correlation between any two imaging features is determined by a function of the spatial and/or temporal distance between them (higher correlations between features closer to each other). In that, the massive number of parameters in the large covariance matrix are reduced to a handful of parameters in the covariance-distance function (Derado and others, 2010). However, the dependence structure of connectivity edges cannot be directly specified by the spatial closeness between edges. We propose a more flexible framework that assumes the dependence structure between edges is related to an unknown network structure, and jointly estimates the latent network structure and model parameters using a Bayesian model. The application of Bayesian non-parametric model is also novel because we estimate the network structure (the allocation of nodes) based on the sample covariance matrix between edges, which is distinct from conventional community detection algorithms and assigns nodes to communities based on the similarity between nodes. The model is scalable because a correctly specified network structure tends to substantially increase likelihood functions, which facilitates efficient MCMC sampling of DPM and quick convergence. The proposed method outperforms existing large covariance/precision matrix estimation (regularization) methods by leveraging the network properties of brain connectivity data. In some applications, the covariance network structure may not exist, and then the MCMC iterations tend not to converge and the posteriors of 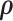vary around zero, and thus the parametric covariance model is not available and the general linear model can be applied for inference.

Nodes and edges. The definition of nodes and edges is important for brain connectivity analysis. In our application, we choose AAL as the brain atlas because it has been the most commonly used brain atlas (Stanley, 2013) and is compatible to the findings of previous connectivity studies in schizophrenia research (Lynall and others, 2010; Fornito and others, 2012). Since our network detection is based solely on correlations among connectivity edges, comparing our results to the documented networks can assist in model validation. For the same reason, we chose the most commonly used correlation coefficients as the connectivity metric, although other metrics (e.g. partial correlation) have similar patterns of correlations between edges. To ensure the reliability of the connectivity edges, we recommend using an fMRI time sequence longer than 12 min (Birn and others, 2013).

The results of case study reveal two networks where edges are more correlated. The first network mainly consists of nodes in the DMN and the second network is related to the visual function. Although similar networks (biologically meaningful) have been reported and discussed, we are the first to report edges within those networks are more correlated with each other. We further utilize the network topology-oriented covariance structure to analyze the association between brain connectivity patterns and the neuropsychiatric phenotype. The results also show interesting findings that interconnections between three important well-known networks DMN, Salience network, and executive network are altered in patients.

In summary, the proposed Bayesian non-parametric model provides a viable means to model dependence between edge-based brain connectivity variables by learning latent network topology from the sample edge covariance matrix. Our model assumption that edge pairs within networks are more correlated is validated by empirical data analyses and is neurophysiologically plausible (for example, the DMN in the data example is well justified). The proposed method demonstrates accurate and robust performance in our simulation study and empirical data. Modeling dependence between connectivity edges can increase the relative efficiency of statistical inferences, which will often lead to more powerful statistical tests and reveal neuropsychiatric phenotype-related brain connectivity networks with higher accuracy. In this article, we focus on inter-region connectivity, which is mostly used in current brain connectivity analysis and network research. Yet, it can be naturally integrated with previous work (e.g. Chen and others, 2016) to link voxel-level connectivity to region-level connectivity using a hierarchical model. The software package of the proposed method is available at https://github.com/shuochenstats/Bayes-Nonpara-Network.

Funding

Support was received from NIH grants MH116948, MH112180, MH105561, EB01561, GM12406, and MH108148.