Summary
This article considers Bayesian approaches for incorporating information from a historical model into a current analysis when the historical model includes only a subset of covariates currently of interest. The statistical challenge is 2-fold. First, the parameters in the nested historical model are not generally equal to their counterparts in the larger current model, neither in value nor interpretation. Second, because the historical information will not be equally informative for all parameters in the current analysis, additional regularization may be required beyond that provided by the historical information. We propose several novel extensions of the so-called power prior that adaptively combine a prior based upon the historical information with a variance-reducing prior that shrinks parameter values toward zero. The ideas are directly motivated by our work building mortality risk prediction models for pediatric patients receiving extracorporeal membrane oxygenation (ECMO). We have developed a model on a registry-based cohort of ECMO patients and now seek to expand this model with additional biometric measurements, not available in the registry, collected on a small auxiliary cohort. Our adaptive priors are able to use the information in the original model and identify novel mortality risk factors. We support this with a simulation study, which demonstrates the potential for efficiency gains in estimation under a variety of scenarios.
Keywords: Bias-variance tradeoff, Combining information, Hierarchical shrinkage, Power prior, Regularized horseshoe prior
1. Introduction
When a statistical model is published, there are often already models for the same outcome. Although the new model and the existing models may each differ in their target populations, underlying sets of predictors, or in other ways (e.g. Becker and Wu, 2007), there is usually some historical information available when the new model was built. In that sense, this framework of sequential but independent model development is not fully utilizing available historical information. In this article, we propose Bayesian approaches that incorporate the posterior distribution from the historical model into a prior for the new model when the set of historical covariates is strictly nested within the set of the new covariates.
Our motivation for this work is a short-term mortality risk prediction model (“Ped-RESCUERS”) for pediatric patients receiving extracorporeal membrane oxygenation (ECMO) support using information on 1611 pediatric patients treated between the years 2009 and 2012 (Barbaro and others, 2016). The source population was the Extracorporeal Life Support Organization (ELSO), an international registry of ECMO patients, and the pertinent data are limited to patient clinical characteristics (weight, age, sex, primary diagnosis, co-morbidities, complications, and pre-ECMO supportive therapies) and ECMO-specific measurements (blood gas measurements and ventilator settings). In total, Ped-RESCUERS uses eleven predictors. Patient-specific biometric measurements of renal, hepatic, neurological, and hematological dysfunction that may be associated with mortality on ECMO are not generally collected in the ELSO registry. We posited a list of eleven such additional potential risk factors and collected them on a cohort of 178 non-overlapping patients at three ECMO-providing centers. The data consist of both the eleven risk factors in PED-RESCUERS and eleven biometric measurements not in the registry. We require a model that potentially includes all 22 covariates as predictors. We report on these new data in Barbaro and others (2018). However, given the ratio of sample size to number of covariates and the subsequent variability in estimates, it is more statistically incumbent to make use of the information from the original large cohort of patients with unmeasured biometric measurements. Yet, the process of doing so may introduce bias, due to the different predictors included in each model. It is these competing objectives we seek to balance so as to increase overall efficiency, i.e. decrease root mean squared error (RMSE).
In other cases, there may only be very limited historical information, meaning that the number of historical predictors is much less than the total number of potential predictors under study. It is reasonable to expect that incorporating even such limited historical information should result in a model that is non-inferior to a modeling approach ignoring the historical information entirely. For example, one alternative to a prior based solely on historical data would be to regularize estimation and prediction with a prior that shrinks parameters toward zero, as in the Bayesian Lasso (Park and Casella, 2008) and others (Griffin and Brown, 2005; Armagan and others, 2013). Based on this logic, an ideal strategy combines these approaches: incorporating whatever historical information is available and, for those parameters about which it is not informative, controlling variability by shrinking them to zero in the “usual” way.
We achieve this here through an extension of the power prior, which includes the historical data likelihood, raised to a power 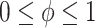 (Ibrahim and Chen, 2000; Ibrahim and others, 2015). Setting
(Ibrahim and Chen, 2000; Ibrahim and others, 2015). Setting 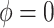 or
or 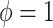 corresponds, respectively, to ignoring the historical likelihood entirely or a fully Bayesian update. Using
corresponds, respectively, to ignoring the historical likelihood entirely or a fully Bayesian update. Using 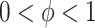 allows for partial borrowing of the historical likelihood in the presence of heterogeneity, and this can be made adaptive by considering a hyperprior on
allows for partial borrowing of the historical likelihood in the presence of heterogeneity, and this can be made adaptive by considering a hyperprior on 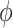 itself (Duan and others, 2006; Neuenschwander and others, 2009). The novel idea in our approach is to use
itself (Duan and others, 2006; Neuenschwander and others, 2009). The novel idea in our approach is to use 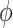 to vary the relative contributions of the historical prior (
to vary the relative contributions of the historical prior (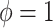 ) and a variance-reducing prior that shrinks to zero (
) and a variance-reducing prior that shrinks to zero (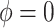 ).
).
In the classical power prior, the historical and current models include the same predictors. In one extension, Chen and others (1999) approach a related problem by constructing a second, artificial historical likelihood that uses a constant for the outcome and copies of the added covariates from the current data. This has the effect of shrinking the corresponding regression parameters toward zero and so is actually more similar to a typical shrinkage-to-zero prior. Ibrahim and others (2002) consider the general setting of fitting generalized linear models (GLMs) using power priors when values are missing in covariates of the historical and/or current datasets. Crucially, both the historical and current likelihoods condition on the same set of covariates, and missingness is ancillary to the main statistical problem.
Beyond the power prior, there exist alternative approaches for incorporating historical information. A meta-analysis statistically combines univariable or multivariable associations from multiple studies based upon each analysis’ variance or covariance matrix (Walker and others, 2008; Chen and others, 2012; Jackson and Riley, 2014). The main advantage of a meta-analysis is its simplicity, even when combining more than two models, because only summaries statistics are required. Among other assumptions, however, all models to be combined must include the same predictors. Recently, several authors have proposed strategies for incorporating summary-level historical information via constraints on the likelihood (Chatterjee and others, 2016; Grill and others, 2017; Cheng and others, 2018). Antonelli and others (2017) propose Bayesian approaches for borrowing information from the dataset with additional covariates to improve estimation of the average causal effect in the dataset with fewer covariates. Relative to previous important work in this area, we highlight two distinctive features of our approach. First, we account for the underlying uncertainty in the historical information by using the posterior variance from the historical model as the prior variance for the current model. Second, we explicitly ignore any historical information about the intercept, which, in the case of a binary outcome, borrows information, while still allowing for differences in the underlying true prevalence between the historical and the current models.
The proceeding sections develop the ingredients of our approach that combines historical-based prior shrinkage and shrinkage to zero. Section 2 reviews the “regularized horseshoe prior” (Carvalho and others, 2009, 2010; Piironen and Vehtari, 2015, 2017a, 2017b), which is the shrinkage-to-zero prior that we use. Section 3 outlines the construction of two historical-based priors derived from models fit to a subset of the current set of covariates under consideration. Section 4 proposes how to adaptively combine the historical information with the shrinkage prior. Sections 5 and 6 demonstrate our methods with a simulation study and analysis of the motivating ECMO mortality risk prediction model, respectively. Section 7 concludes with a discussion.
2. Shrinkage-to-zero priors
Let 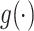 denote the link function of a GLM and
denote the link function of a GLM and 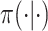 and
and 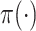 denote conditional and marginal distributions, respectively. We will use the prior/posterior nomenclature to indicate whether conditioning is on data. Capital and lowercase letters, respectively, indicate random data and observed data; all types of Greek letters will be reserved for parameters. Standard font will be used for scalar or vector valued quantities, and boldface font will be reserved for matrix-valued quantities.
denote conditional and marginal distributions, respectively. We will use the prior/posterior nomenclature to indicate whether conditioning is on data. Capital and lowercase letters, respectively, indicate random data and observed data; all types of Greek letters will be reserved for parameters. Standard font will be used for scalar or vector valued quantities, and boldface font will be reserved for matrix-valued quantities.
A GLM for an outcome 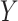 is fit to a length-
is fit to a length-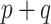 vector of covariates
vector of covariates 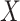 ,
, 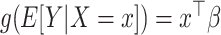 , using
, using 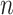 datapoints,
datapoints, 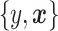 . The covariates
. The covariates 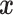 are standardized to their empirical mean and empirical standard deviation. We do not distinguish between the first
are standardized to their empirical mean and empirical standard deviation. We do not distinguish between the first 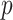 and the final
and the final 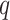 elements of
elements of 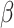 yet (these identify the original and added elements, respectively) but will do so in subsequent sections. The vector
yet (these identify the original and added elements, respectively) but will do so in subsequent sections. The vector 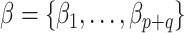 is of primary interest. Given the likelihood
is of primary interest. Given the likelihood 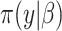 and prior
and prior 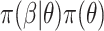 , with
, with 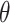 a vector of hyperparameters that is conditionally independent of
a vector of hyperparameters that is conditionally independent of 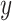 given
given 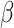 , the posterior is
, the posterior is 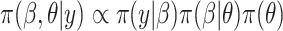 . Often, the prior
. Often, the prior 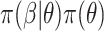 is selected to regularize parameters by shrinking estimates toward zero, reducing variance at a cost of some bias, thereby increasing efficiency. Many such shrinkage priors can be written as products of conditionally independent normal priors on
is selected to regularize parameters by shrinking estimates toward zero, reducing variance at a cost of some bias, thereby increasing efficiency. Many such shrinkage priors can be written as products of conditionally independent normal priors on 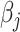 : e.g.,
: e.g., 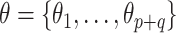 and
and 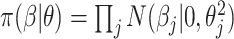 . For example, if each
. For example, if each 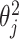 is independently inverse-gamma distributed with a common shape and scale parameter equal to
is independently inverse-gamma distributed with a common shape and scale parameter equal to 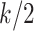 , each
, each 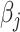 is marginally Student-
is marginally Student-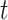 distributed with
distributed with 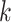 degrees of freedom (e.g. Gelman and others, 2014). A different choice of
degrees of freedom (e.g. Gelman and others, 2014). A different choice of 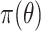 conferring more adaptive shrinkage properties is the “regularized horseshoe” (Carvalho and others, 2009, 2010; Piironen and Vehtari, 2015, 2017a, 2017b). Given constants
conferring more adaptive shrinkage properties is the “regularized horseshoe” (Carvalho and others, 2009, 2010; Piironen and Vehtari, 2015, 2017a, 2017b). Given constants 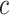 ,
, 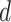 and hyperparameters
and hyperparameters 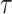 ,
, 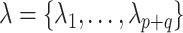 , the hyperprior is
, the hyperprior is 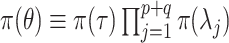 , where
, where 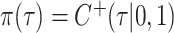 ,
, 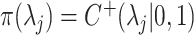 for
for 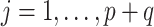 , and
, and 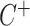 indicates the positive half-Cauchy distribution. Letting
indicates the positive half-Cauchy distribution. Letting 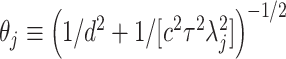 , the conditional prior for
, the conditional prior for 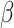 is then
is then
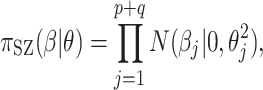 |
(2.1) |
The SZ subscript indicates “shrinkage to zero”. The hyperparameter 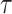 globally shrinks
globally shrinks 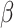 , while the
, while the 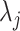 s multiplicatively offset
s multiplicatively offset 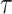 and thus admit large individual variance components. The original horseshoe (Carvalho and others, 2009) implicitly used
and thus admit large individual variance components. The original horseshoe (Carvalho and others, 2009) implicitly used 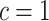 and
and 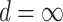 , i.e.
, i.e. 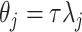 , and others have since generalized it. First, Piironen and Vehtari (2017a) suggested considering alternative values of
, and others have since generalized it. First, Piironen and Vehtari (2017a) suggested considering alternative values of  , which scales the global shrinkage, by linking its value to an implicit assumption about the a priori effective number of non-zero parameters in the model, say
, which scales the global shrinkage, by linking its value to an implicit assumption about the a priori effective number of non-zero parameters in the model, say 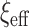 . The relationship is given by
. The relationship is given by 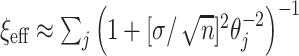 , where
, where 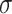 is the dispersion. So, for example, if
is the dispersion. So, for example, if 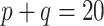 ,
, 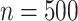 and
and 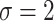 , under the original horseshoe, the prior mean of
, under the original horseshoe, the prior mean of 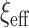 is
is 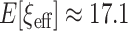 . If instead
. If instead 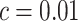 , then
, then 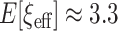 . Typically, using
. Typically, using 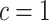 codifies a prior belief that most of the
codifies a prior belief that most of the 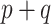 parameters are non-zero, which is unlikely when
parameters are non-zero, which is unlikely when 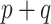 itself is large. Further, the expression for
itself is large. Further, the expression for 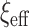 highlights that the choice of
highlights that the choice of 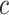 ought to scale with
ought to scale with 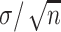 , all other things being equal. Larger sample sizes warrant smaller values of
, all other things being equal. Larger sample sizes warrant smaller values of 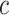 . Based on this, the authors recommend selecting
. Based on this, the authors recommend selecting 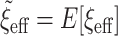 and then, assuming
and then, assuming 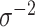 is fixed, numerically solving
is fixed, numerically solving 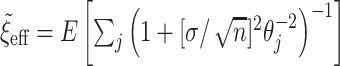 for
for 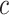 (
(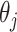 is a function of
is a function of 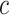 ), where the expectation is taken with respect to
), where the expectation is taken with respect to 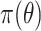 . The result will usually be
. The result will usually be 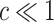 .
.
Subsequent work by Piironen and Vehtari (2017b) argued that the original horseshoe tends to under-shrink large elements of 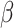 , which can also result in numerical difficulties, known as “divergent transitions”, as a result of a stochastic search through heavy tails (Piironen and Vehtari, 2015). As a solution, they suggest to soft-truncate its tails with a diffuse normal prior with variance
, which can also result in numerical difficulties, known as “divergent transitions”, as a result of a stochastic search through heavy tails (Piironen and Vehtari, 2015). As a solution, they suggest to soft-truncate its tails with a diffuse normal prior with variance 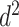 . Choosing a finite-valued
. Choosing a finite-valued 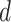 results in the regularized horseshoe prior. Our strategy for choosing the hyperparameters
results in the regularized horseshoe prior. Our strategy for choosing the hyperparameters 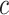 and
and 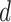 in this paper is to set
in this paper is to set 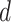 equal to a large value,
equal to a large value, 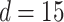 , and then numerically solve
, and then numerically solve 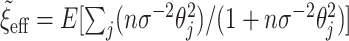 for
for 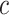 , as before. A large
, as before. A large 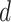 has minimal effect in the middle of the horseshoe prior but effectively thins out the heavy tails. We further discuss
has minimal effect in the middle of the horseshoe prior but effectively thins out the heavy tails. We further discuss 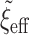 in Section 5. The prior in (2.1) is the hierarchical shrinkage prior that we will extend in Section 4 to adaptively incorporate historical information. But first, Section 3 considers the prerequisite non-adaptive prior using the historical information alone.
in Section 5. The prior in (2.1) is the hierarchical shrinkage prior that we will extend in Section 4 to adaptively incorporate historical information. But first, Section 3 considers the prerequisite non-adaptive prior using the historical information alone.
3. Historical shrinkage prior
Separate 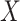 into
into 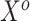 and
and 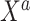 , of length
, of length 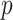 and
and 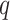 , respectively. The original covariates
, respectively. The original covariates 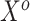 were measured in the historical analysis, and the added covariates
were measured in the historical analysis, and the added covariates 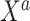 were not. We are interested in modeling
were not. We are interested in modeling 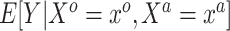 , but the historical model only estimates the smoothed version
, but the historical model only estimates the smoothed version 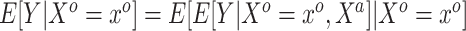 . The historical analysis conveys information about
. The historical analysis conveys information about
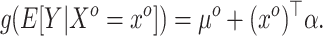 |
(3.1) |
This knowledge is quantified by the posterior distribution of 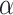 given the historical data, about which one likely only has access to summary statistics, e.g. the mean and covariance matrix. Our interest is not in Model (3.1) but rather the embiggened model
given the historical data, about which one likely only has access to summary statistics, e.g. the mean and covariance matrix. Our interest is not in Model (3.1) but rather the embiggened model
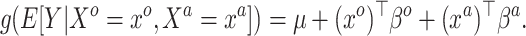 |
(3.2) |
We have a dataset of 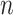 observations,
observations, 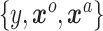 and a likelihood function
and a likelihood function 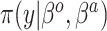 . A standard analysis of
. A standard analysis of 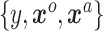 alone might employ a shrinkage-to-zero prior as described in Section 2; that prior does not distinguish between historical and current covariates. Keeping in mind our ultimate goal of incorporating the historical information we have about
alone might employ a shrinkage-to-zero prior as described in Section 2; that prior does not distinguish between historical and current covariates. Keeping in mind our ultimate goal of incorporating the historical information we have about 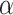 , this section lays out an alternative prior formulation based upon the historical analysis. We will then combine these priors in Section 4.
, this section lays out an alternative prior formulation based upon the historical analysis. We will then combine these priors in Section 4.
3.1. Naive Bayesian update
A naive Bayesian (NB) update would directly apply the historical posterior on 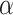 as a prior on
as a prior on 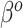 , since these parameters correspond to the same set of covariates, namely
, since these parameters correspond to the same set of covariates, namely 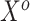 . More formally, one might use
. More formally, one might use 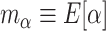 and
and 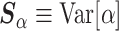 as the respective prior mean and variance for
as the respective prior mean and variance for 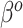 . Then, given an optional scaling hyperparameter
. Then, given an optional scaling hyperparameter 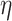 , a conditional prior might be
, a conditional prior might be
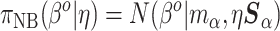 |
(3.3) |
However, Model (3.1) cannot hold for all patterns 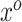 if Model (3.2) is the true generating model unless
if Model (3.2) is the true generating model unless 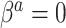 (or, if for some fixed
(or, if for some fixed 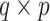 matrix of weights
matrix of weights 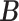 ,
, 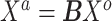 almost surely. In the special case that
almost surely. In the special case that 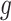 is the identity link, this condition may be relaxed to equality in expectation, i.e.
is the identity link, this condition may be relaxed to equality in expectation, i.e. 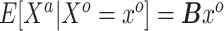 ). Thus, in general, the naive Bayesian is implicitly assuming that
). Thus, in general, the naive Bayesian is implicitly assuming that 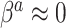 , so as to be able to equate
, so as to be able to equate 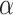 and
and 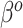 in (3.3). To be consistent with this assumption,
in (3.3). To be consistent with this assumption, 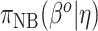 should be accompanied by a prior on
should be accompanied by a prior on 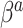 that strongly shrinks to zero. We discuss this further in Section 4.
that strongly shrinks to zero. We discuss this further in Section 4.
3.2. Sensible Bayesian update
Although the naive Bayesian update may improve efficiency, by construction it assumes 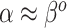 and
and 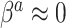 . In general
. In general 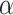 and
and 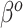 are not equal, neither in value nor interpretation. Further, it is illogical to begin with a strong prior assumption that
are not equal, neither in value nor interpretation. Further, it is illogical to begin with a strong prior assumption that 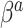 - corresponding to the novel set of covariates of interest, is approximately zero. The naive Bayesian update will introduce bias when
- corresponding to the novel set of covariates of interest, is approximately zero. The naive Bayesian update will introduce bias when 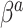 is far from zero. A more sensible Bayesian update would place the prior on the many-to-few mapping from
is far from zero. A more sensible Bayesian update would place the prior on the many-to-few mapping from 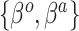 to
to 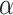 . Based on derivations below, we show that this mapping can be approximated by
. Based on derivations below, we show that this mapping can be approximated by 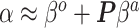 , where
, where 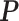 is a certain
is a certain 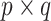 projection matrix. To see this, begin by iterating the conditional expectation of
projection matrix. To see this, begin by iterating the conditional expectation of 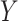 given
given 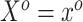 :
:
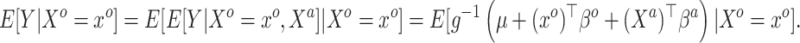 |
Applying Model (3.1), i.e. taking 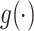 of both sides, which—because the true(r) model is (3.2)—will only be an approximation of the conditional mean of
of both sides, which—because the true(r) model is (3.2)—will only be an approximation of the conditional mean of  given
given 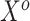 , we obtain the following:
, we obtain the following:
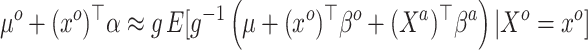 |
(3.4) |
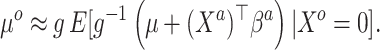 |
(3.5) |
This relates the available historical model with the current model. In particular, (3.5) obtains an approximation for the historical (and misspecified) intercept 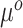 by plugging in
by plugging in 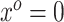 , which is predicated on
, which is predicated on 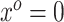 falling within the observed support of
falling within the observed support of 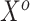 and achieved by centering the covariates. This is useful because taking the difference between (3.4) and (3.5) completely removes
and achieved by centering the covariates. This is useful because taking the difference between (3.4) and (3.5) completely removes 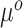 from the equation:
from the equation:
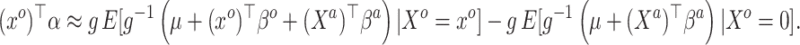 |
(3.6) |
Equation (3.6) is the basis of the sensible Bayesian update: it links Model (3.2) to a function of the parameters from Model (3.1), about which there is historical information. Furthermore, like the naive Bayesian update, the sensible Bayesian update avoids borrowing information on the historical intercept 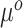 . This relaxes a critical assumption: we do not require that the historical and current data generating models are identical but, less restrictively, that the underlying true values of
. This relaxes a critical assumption: we do not require that the historical and current data generating models are identical but, less restrictively, that the underlying true values of 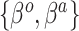 are equal.
are equal.
When the link function 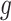 is non-linear, constructing a prior based upon (3.6) would necessitate a Jacobian adjustment, and the adaptive priors that we subsequently develop in Section 4 would require numerically integrating over this Jacobian at each iteration of the Markov Chain, rendering such an approach computationally intractable. Practically, then, we must further approximate the mapping to obviate the Jacobian adjustment. Moving
is non-linear, constructing a prior based upon (3.6) would necessitate a Jacobian adjustment, and the adaptive priors that we subsequently develop in Section 4 would require numerically integrating over this Jacobian at each iteration of the Markov Chain, rendering such an approach computationally intractable. Practically, then, we must further approximate the mapping to obviate the Jacobian adjustment. Moving 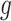 across the integrals,
across the integrals,
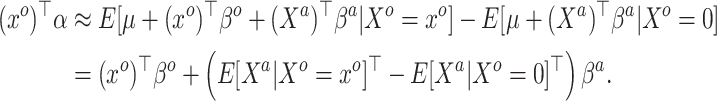 |
(3.7) |
For a given 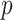 -length vector
-length vector 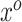 , we can use Equation (3.7) to link a
, we can use Equation (3.7) to link a 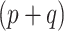 -dimensional set of parameter values
-dimensional set of parameter values 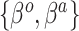 to a linear combination of
to a linear combination of 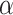 , capturing one dimension of information about
, capturing one dimension of information about 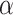 . With a linearly independent set of
. With a linearly independent set of 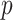 vectors
vectors 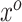 , we can create the desired
, we can create the desired 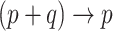 mapping and capture the available
mapping and capture the available 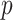 dimensions of information.
dimensions of information.
In theory, (3.7) holds for any arbitrary vector 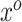 . However, as a consequence of the derivations in this section, we intuitively understand
. However, as a consequence of the derivations in this section, we intuitively understand 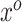 to correspond to a vector of the original covariates. This is important because we need to be able to calculate or approximate the expectations in the mapping. Let
to correspond to a vector of the original covariates. This is important because we need to be able to calculate or approximate the expectations in the mapping. Let 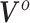 denote a
denote a 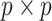 matrix of linearly independent columns, with the
matrix of linearly independent columns, with the 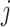 th row representing a hypothetical pattern of the original covariates. Analogously, let
th row representing a hypothetical pattern of the original covariates. Analogously, let 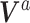 denote a
denote a 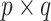 matrix of
matrix of 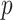 hypothetical patterns of the added covariates. Then, the length-
hypothetical patterns of the added covariates. Then, the length-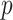 vectorized mapping is
vectorized mapping is
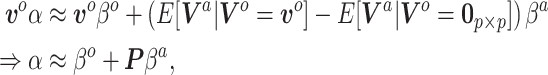 |
(3.8) |
where 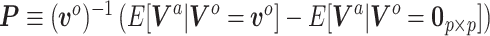 . Analogous to the naive Bayesian update,
. Analogous to the naive Bayesian update,
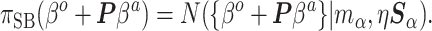 |
(3.9) |
In calculating the posterior,  and
and 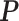 are treated as fixed and known constants. Section S1 of supplementary material available at Biostatistics online describes in detail how to construct
are treated as fixed and known constants. Section S1 of supplementary material available at Biostatistics online describes in detail how to construct 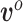 and how to use multiple imputation with chained equations (MICE) to calculate a Monte Carlo estimate of the integral in (3.8).
and how to use multiple imputation with chained equations (MICE) to calculate a Monte Carlo estimate of the integral in (3.8).
Contrasting the distributions in (3.3) and (3.9), the latter incorporates a linear offset to account for the differences between Models (3.1) and (3.2). The sensible Bayesian update thus approximates and adjusts for the difference between 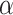 and
and 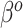 . However, the prior in (3.9) will still be insufficient on its own, as it only informs
. However, the prior in (3.9) will still be insufficient on its own, as it only informs 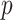 dimensions of a
dimensions of a 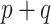 parameter space. We return to this point in Section 4. In summary, both ideas merit further consideration: the sensible Bayesian is intuitively preferable by adjusting for model misspecification, and the naive Bayesian avoids modeling the distribution of
parameter space. We return to this point in Section 4. In summary, both ideas merit further consideration: the sensible Bayesian is intuitively preferable by adjusting for model misspecification, and the naive Bayesian avoids modeling the distribution of 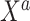 given
given 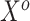 .
.
4. Adaptive weighting
Alone, neither type of prior from Section 2 or 3 would be acceptable in the context of this article: the shrinkage-to-zero prior in Section 2 ignores the historical data, and the priors in Section 3 may be incomplete, particularly when the historical information is limited to a small number of covariates. In this section, we develop combined versions of the historical priors that adaptively vary between the priors in Sections 2 and 3. Called “naive adaptive Bayes” (NAB) and “sensible adaptive Bayes” (SAB), these seek to incorporate the historical information without sacrificing potential efficiency gains coming from shrinking to zero. We describe the two adaptive priors before formally defining them. Both share the following commonalities. Similar to the power prior, a hyperparameter 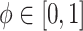 weights the historical information by inversely scaling the variance
weights the historical information by inversely scaling the variance 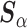 ; larger (smaller) values of
; larger (smaller) values of 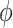 reflect greater (less) incorporation of the historical information. When
reflect greater (less) incorporation of the historical information. When 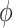 is equal to zero, both NAB and SAB reduce to the shrinkage-to-zero prior in (2.1).
is equal to zero, both NAB and SAB reduce to the shrinkage-to-zero prior in (2.1).
4.1. Naive adaptive Bayes
Where NAB and SAB differ is at 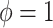 , which corresponds to full use of the historical information. NAB extends the
, which corresponds to full use of the historical information. NAB extends the 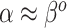 assumption of its non-adaptive counterpart in Section 2.1. Therefore, the historical prior on
assumption of its non-adaptive counterpart in Section 2.1. Therefore, the historical prior on 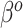 in (3.3) is fully used when
in (3.3) is fully used when 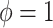 , and additional shrinkage of
, and additional shrinkage of 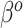 is unnecessary. Moreover,
is unnecessary. Moreover, 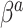 is strongly shrunk to zero, because that is generally the only parameterization for which
is strongly shrunk to zero, because that is generally the only parameterization for which 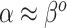 . The hyperparameters of NAB are
. The hyperparameters of NAB are 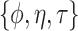 (scalars) and
(scalars) and 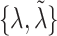 (vectors). The pre-specified constants are scalars
(vectors). The pre-specified constants are scalars 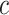 ,
, 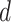 , and
, and 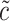 . For notational simplicity, define
. For notational simplicity, define 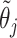 to be
to be
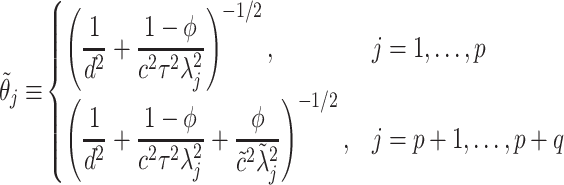 |
Then, the NAB conditional prior is
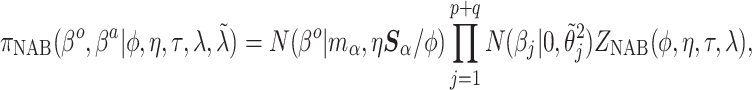 |
(4.1) |
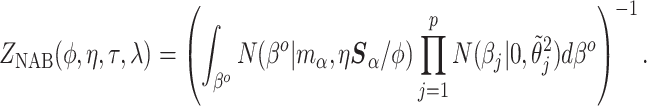 |
(4.2) |
As desired, the impact of the shrinkage-to-zero prior decreases with 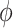 .
. 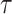 and
and 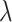 are the same as in Section 2.1, and the constants
are the same as in Section 2.1, and the constants 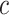 and
and 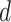 are selected as previously described. We set
are selected as previously described. We set 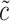 equal to 0.05, i.e. a small number, reflecting the assumption that
equal to 0.05, i.e. a small number, reflecting the assumption that 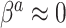 when
when 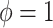 ; however, we introduce an auxiliary hyperparameter
; however, we introduce an auxiliary hyperparameter 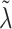 , allowing for non-zero elements of
, allowing for non-zero elements of 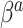 if warranted by the data. The hyperparameter
if warranted by the data. The hyperparameter 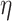 separately controls the historical prior shrinkage. Hyperpriors for
separately controls the historical prior shrinkage. Hyperpriors for 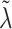 and
and 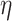 are discussed below. The constant
are discussed below. The constant 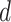 guarantees propriety of the posterior for any
guarantees propriety of the posterior for any 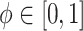 . To summarize, NAB varies between standard shrinkage to zero (
. To summarize, NAB varies between standard shrinkage to zero (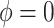 ) and a Bayesian update under the assumption that
) and a Bayesian update under the assumption that 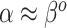 and
and 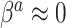 (
(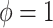 ).
).
Remark 1
The normalizing constant
in (4.2) ensures that the prior is proper for any configuration of the hyperparameters and must be calculated when any of the hyperparameters are random. Its analytic expression is derived in Section S2 of supplementary material available at Biostatistics online. The integral calculation must be updated at each step of the Markov Chain. This would become computationally intractable in the presence of a Jacobian from a non-linear transformation and is why we approximated the mapping as in (3.7).
Remark 2
A reviewer observed the similarity between NAB and the class of “penalized complexity” priors of Simpson and others (2017), both of which use the extreme end of the hyperparameter support (
, in our notation) to essentially recapitulate some pre-specified simple model and prevent overfitting. Penalized complexity priors are defined for a much broader context and thus allow for more general base models, as opposed to our specific objective of incorporating historical information.
4.2. Sensible adaptive Bayes
For SAB, the modified prior in (3.9) is fully employed when 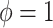 , and any additional shrinkage of
, and any additional shrinkage of 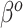 to zero is weak. However, because the sensible Bayesian update adjusts for the difference between
to zero is weak. However, because the sensible Bayesian update adjusts for the difference between 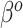 and
and 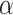 , it is not necessary to assume that
, it is not necessary to assume that  . Thus, in SAB, the value of
. Thus, in SAB, the value of 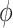 does not affect the contribution of the variance-reducing prior on
does not affect the contribution of the variance-reducing prior on 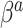 . Defining the SAB hyperparameter
. Defining the SAB hyperparameter 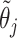 to be
to be
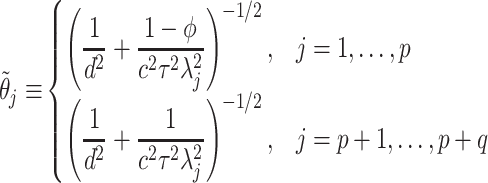 |
the SAB conditional prior is
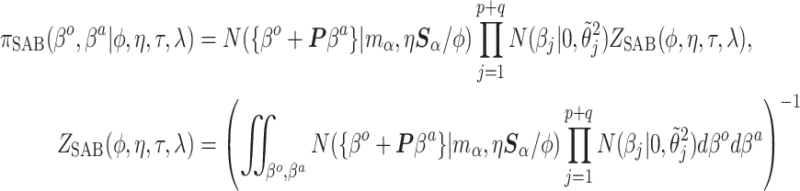 |
(4.3) |
An expression for 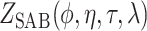 is derived in Section S3 of supplementary material available at Biostatistics online. As with NAB, a finite-valued
is derived in Section S3 of supplementary material available at Biostatistics online. As with NAB, a finite-valued 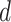 ensures that
ensures that 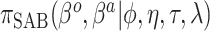 is proper for any
is proper for any 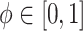 .
.
4.3. Hyperpriors
We describe here our choices of hyperprior for the hyperparameters 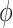 ,
, 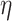 , and, for NAB,
, and, for NAB, 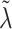 . The hyperpriors on the global and local shrinkage components,
. The hyperpriors on the global and local shrinkage components, 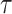 and
and 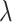 , remain as given in Section 2.
, remain as given in Section 2.
The hyperparameter 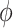 distributes prior weight between shrinkage to zero (
distributes prior weight between shrinkage to zero (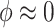 ) and historical shrinkage (
) and historical shrinkage (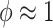 ). We consider two hyperprior options. The first, called agnostic, is uniform over the unit interval. The second is a truncated normal distribution with mean and standard deviation of 1 and 0.25, respectively. This is optimistic because the mode is
). We consider two hyperprior options. The first, called agnostic, is uniform over the unit interval. The second is a truncated normal distribution with mean and standard deviation of 1 and 0.25, respectively. This is optimistic because the mode is 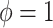 , encouraging full use of the historical information.
, encouraging full use of the historical information.
The hyperparameter 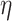 independently controls the historical prior shrinkage. This could simply be set to 1; we used an inverse-gamma distribution with shape and scale equal to 2.5.
independently controls the historical prior shrinkage. This could simply be set to 1; we used an inverse-gamma distribution with shape and scale equal to 2.5.
Finally, the hyperparameter vector 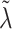 , used by NAB, controls the prior scale of
, used by NAB, controls the prior scale of  when
when 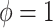 . As with
. As with 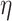 , each element of
, each element of 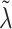 could be set to 1, which would give that
could be set to 1, which would give that 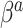 is normal with standard deviation
is normal with standard deviation 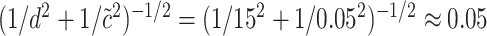 when
when 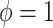 . We instead model the components of
. We instead model the components of 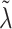 as inverse-gamma, each with shape and scale equal to 0.5, allowing for some elements of
as inverse-gamma, each with shape and scale equal to 0.5, allowing for some elements of 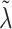 to be large.
to be large.
5. Simulation study
We conducted a simulation study of logistic regression to evaluate our proposed methodology against a variety of data generating scenarios. All analyses were conducted in the R statistical environment (R Core Team, 2016; Wickham, 2009; van Buuren and Groothuis-Oudshoorn, 2011) and its interface with Stan (Carpenter, 2017; Stan Development Team, 2017, 2018), which numerically characterizes posterior distributions using Hamiltonian Monte Carlo. Code to reproduce the simulation study is available at https://github.com/psboonstra/AdaptiveBayesianUpdates.
Varying between each scenario were the fixed, unknown values of 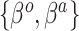 to be estimated (ten possibilities described in Table 2, ranging from
to be estimated (ten possibilities described in Table 2, ranging from 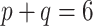 to 100 predictors), the sample size of the historical data analyses (
to 100 predictors), the sample size of the historical data analyses (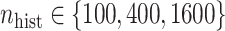 ), and the sample size of the current data analyses (
), and the sample size of the current data analyses (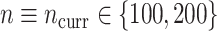 ). For each of the 60 unique data generating scenarios, we independently sampled 128 “historical” and “current” datasets of size
). For each of the 60 unique data generating scenarios, we independently sampled 128 “historical” and “current” datasets of size 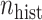 and
and 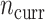 , respectively. To generate the data, preliminary values of
, respectively. To generate the data, preliminary values of 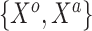 were sampled from multivariable normal distributions with constant correlation equal to 0.2. After this, half of the elements of each of
were sampled from multivariable normal distributions with constant correlation equal to 0.2. After this, half of the elements of each of 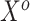 and
and 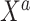 were transformed using the sign function, i.e.
were transformed using the sign function, i.e.  . Then, given the resulting
. Then, given the resulting 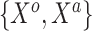 vector,
vector, 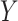 was sampled from a logistic regression with parameters
was sampled from a logistic regression with parameters 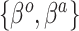 fixed at one of the values in the third column of Table 2. The true generating value of the intercept in the historical data model (
fixed at one of the values in the third column of Table 2. The true generating value of the intercept in the historical data model (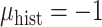 ) was larger than that of the current data model (
) was larger than that of the current data model (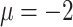 ), yielding different marginal prevalences of the outcome. Each historical dataset consisted of
), yielding different marginal prevalences of the outcome. Each historical dataset consisted of 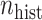 independent draws of
independent draws of 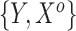 , whereas each current dataset consisted of
, whereas each current dataset consisted of 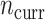 independent draws of
independent draws of 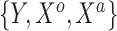 . In summary, the historical and current generating models differ in the true value of the intercept; the historical and current datasets structurally differ in that the former does not use
. In summary, the historical and current generating models differ in the true value of the intercept; the historical and current datasets structurally differ in that the former does not use 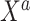 .
.
Table 2.
Summary of fixed, true values of 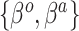 from the generating logistic regression model,
from the generating logistic regression model, 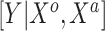 used in the simulation study as well as the asymptotic true values of
used in the simulation study as well as the asymptotic true values of 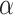 from the misspecified reduced model,
from the misspecified reduced model, 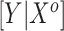
| Label |
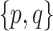
|
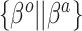
|
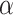
|
|---|---|---|---|
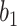
|
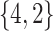
|
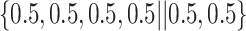
|
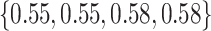
|
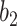
|
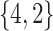
|
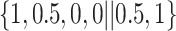
|
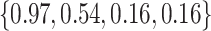
|
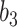
|
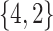
|
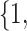 - -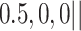 - -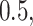 - -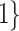
|
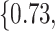 - -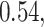 - -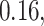 - -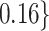
|
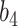
|
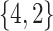
|
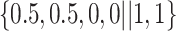
|
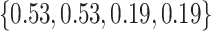
|
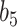
|
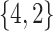
|
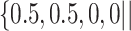 - -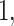 - -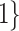
|
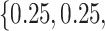 - -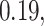 - -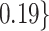
|
|
|
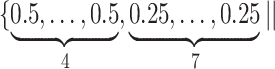
|
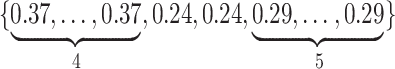
|
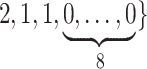
|
|||
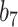
|
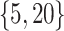
|
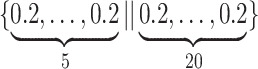
|
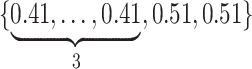
|
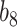
|
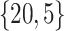
|
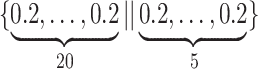
|
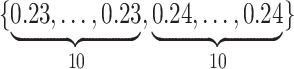
|
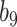
|
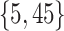
|
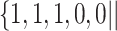
|
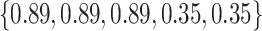
|
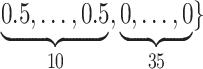
|
|||
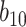
|
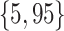
|
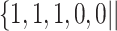
|
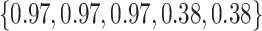
|
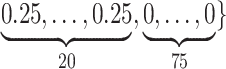
|
The “ ” symbol is used to distinguish between elements of
” symbol is used to distinguish between elements of 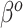 and
and 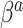 .
.
Remark 3
The intercept
in Model (3.1) is distinct from
described in the preceding paragraph: the former denotes the intercept from the asymptotically misspecified sub-model, and the latter is the true intercept from Model (3.2) that actually generated the historical data.
The fourth column of Table 2 gives the asymptotic parameter values from the misspecified logistic regression of 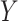 on
on 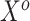 , which the historical data analysis estimates. To emulate the historical analysis, an initial Bayesian logistic regression was fit to the historical outcomes
, which the historical data analysis estimates. To emulate the historical analysis, an initial Bayesian logistic regression was fit to the historical outcomes 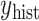 to estimate Model (3.1). We applied a regularized horseshoe prior on
to estimate Model (3.1). We applied a regularized horseshoe prior on 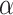 using (2.1) with
using (2.1) with 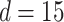 and
and 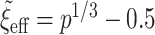 ,
, 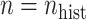 , and
, and 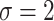 to determine the value of
to determine the value of 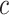 . So, for example, when
. So, for example, when 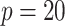 , the assumed effective number of non-zero parameters was
, the assumed effective number of non-zero parameters was 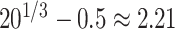 , and when
, and when 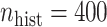 , solving
, solving 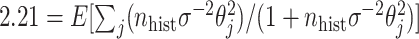 yields
yields 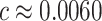 . Fixing
. Fixing 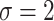 corresponds to the largest dispersion in a logistic GLM and usually results in slightly less than
corresponds to the largest dispersion in a logistic GLM and usually results in slightly less than 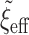 effective parameters compared with
effective parameters compared with 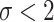 (Piironen and Vehtari, 2017a). We obtained samples from the historical posterior distribution
(Piironen and Vehtari, 2017a). We obtained samples from the historical posterior distribution 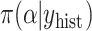 and estimated
and estimated 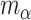 and
and 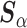 , the ingredients for the adaptive priors in the current data analysis. Then, the “current” analysis was conducted: a second Bayesian logistic regression to estimate the larger model in (3.2), using the current outcomes
, the ingredients for the adaptive priors in the current data analysis. Then, the “current” analysis was conducted: a second Bayesian logistic regression to estimate the larger model in (3.2), using the current outcomes 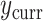 . Each of the five priors in the third column of Table 1 was paired with the likelihood of
. Each of the five priors in the third column of Table 1 was paired with the likelihood of 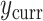 , yielding five posterior distributions to be compared. Four of these were adaptive Bayesian updates from in Section 4: two adaptive priors times two distinct hyperpriors on
, yielding five posterior distributions to be compared. Four of these were adaptive Bayesian updates from in Section 4: two adaptive priors times two distinct hyperpriors on 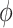 . The other was the regularized horseshoe in (2.1) and was used as a reference; we call this approach ‘Standard’. We used
. The other was the regularized horseshoe in (2.1) and was used as a reference; we call this approach ‘Standard’. We used 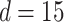 and
and 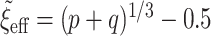 ,
, 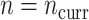 , and
, and 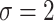 to solve for
to solve for 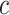 . All of the adaptive priors are equivalent to Standard when
. All of the adaptive priors are equivalent to Standard when 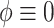 . For SAB, we estimated
. For SAB, we estimated 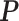 (3.9) using Monte Carlo methods based upon 100 independent draws from MICE. We measured performance using
(3.9) using Monte Carlo methods based upon 100 independent draws from MICE. We measured performance using 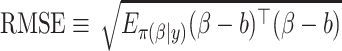 , where
, where 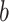 is the fixed, true value of the regression coefficient vector, and the expectation is taken over both the original and added covariates. For each of the adaptive Bayesian updates, we calculated its RMSE ratio with respect to Standard, such that ratios less than one indicate relatively better performance of the adaptive update. For each unique data generating mechanism, we report the distribution of 128 RMSE ratios. The top panel of Figure 1 plots the RMSE ratios from the first 5 rows of Table 2, for which
is the fixed, true value of the regression coefficient vector, and the expectation is taken over both the original and added covariates. For each of the adaptive Bayesian updates, we calculated its RMSE ratio with respect to Standard, such that ratios less than one indicate relatively better performance of the adaptive update. For each unique data generating mechanism, we report the distribution of 128 RMSE ratios. The top panel of Figure 1 plots the RMSE ratios from the first 5 rows of Table 2, for which 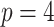 and
and 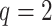 , and the bottom panel plots the ratios from the final 5 rows, for which
, and the bottom panel plots the ratios from the final 5 rows, for which 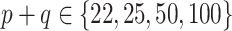 .
.
Table 1.
Summary of posterior distributions evaluated in the simulation study
| Labels | Likelihood | Prior | Prior equation | Hyperprior: 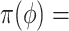
|
|---|---|---|---|---|
| Standard |
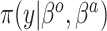
|
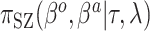
|
Equation (2.1) | — |
| NAB(agnostic) |
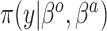
|
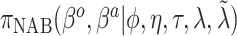
|
Equation (4.1) | Unif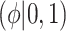
|
| NAB(optimist) |
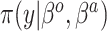
|
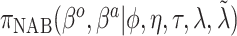
|
Equation (4.1) |
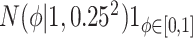
|
| SAB(agnostic) |
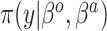
|
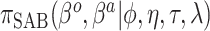
|
Equation (4.3) | Unif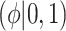
|
| SAB(optimist) |
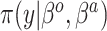
|
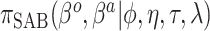
|
Equation (4.3) |
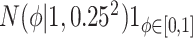
|
Because the same likelihood is used for all methods, any differences are due to priors used. The “Standard” approach is precisely the regularized horseshoe prior and used as a benchmark for comparing performance.
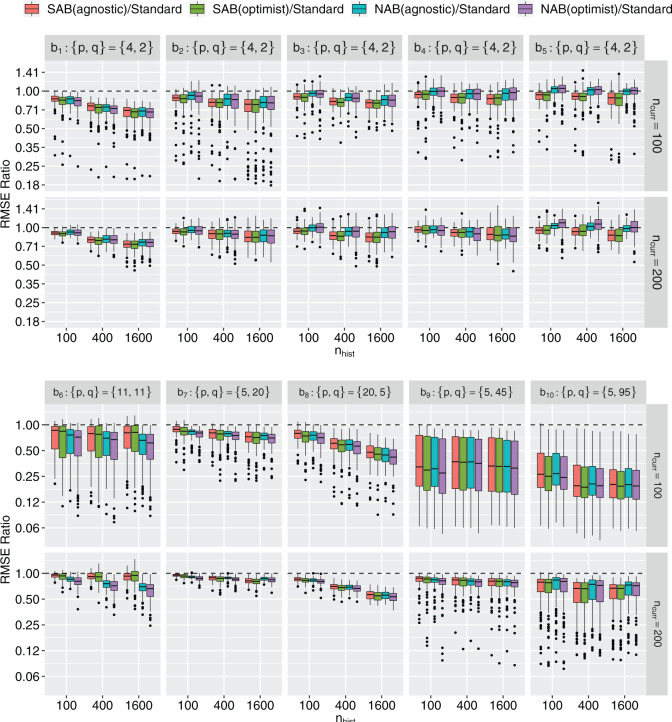
Fig. 1.
Boxplots of RMSE ratios ( -axis, on the log
-axis, on the log -scale) comparing four adaptive priors that make use of the historical information against a standard hierarchical shrinkage prior, plotted against varying sample sizes of the historical data (
-scale) comparing four adaptive priors that make use of the historical information against a standard hierarchical shrinkage prior, plotted against varying sample sizes of the historical data (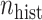 ;
; 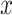 -axis) for ten true values of the regression coefficients (
-axis) for ten true values of the regression coefficients (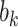 ,
, 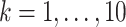 ; columns) taken from Table 2 and varying sample sizes of the current data (
; columns) taken from Table 2 and varying sample sizes of the current data (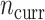 ; rows). Each boxplot compares the posteriors across 128 independent datasets. Smaller ratios indicate better performance of the corresponding adaptive prior.
; rows). Each boxplot compares the posteriors across 128 independent datasets. Smaller ratios indicate better performance of the corresponding adaptive prior.
More historical data, i.e. larger 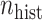 , improved the relative performance of the adaptive updates. For example, across coefficient settings
, improved the relative performance of the adaptive updates. For example, across coefficient settings 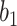 –
–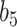 , with
, with 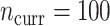 , the middle quartiles of the SAB(agnostic)/Standard RMSE ratio were
, the middle quartiles of the SAB(agnostic)/Standard RMSE ratio were 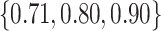 when
when 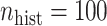 versus
versus 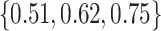 when
when 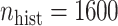 . The NAB-type updates also improved with increasing
. The NAB-type updates also improved with increasing 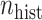 , but, in absolute terms, they did not always improve upon Standard, e.g. for
, but, in absolute terms, they did not always improve upon Standard, e.g. for 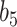 the quartiles of the RMSE ratio were
the quartiles of the RMSE ratio were 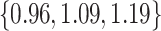 when
when 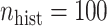 and
and 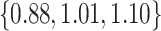 when
when 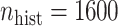 .
.
More current data, i.e. larger 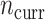 , hurt the typical relative performance of the adaptive updates, all other aspects being fixed, but also decreased the variability between datasets. This can be seen in Figure 1: when
, hurt the typical relative performance of the adaptive updates, all other aspects being fixed, but also decreased the variability between datasets. This can be seen in Figure 1: when 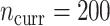 (the second and fourth rows), the boxplots move closer to 1.00 and with less spread relative to
(the second and fourth rows), the boxplots move closer to 1.00 and with less spread relative to 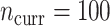 (the first and third rows, respectively). A fixed amount of historical data becomes relatively less valuable in the presence of more current data.
(the first and third rows, respectively). A fixed amount of historical data becomes relatively less valuable in the presence of more current data.
The adaptive priors were relatively less useful when 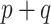 was small: across all datasets in the top panel of Figure 1, for which
was small: across all datasets in the top panel of Figure 1, for which 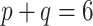 , the middle quartiles of the RMSE ratios for NAB(agnostic) was
, the middle quartiles of the RMSE ratios for NAB(agnostic) was 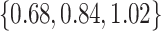 , and for SAB(agnostic) it was
, and for SAB(agnostic) it was 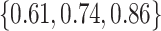 ; across all datasets in the bottom panel, for which
; across all datasets in the bottom panel, for which 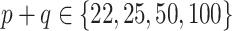 , these were
, these were 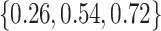 and
and 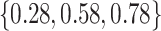 , respectively. Comparing the adaptive priors, NAB outperformed SAB in scenarios for which the integral required by the latter, i.e. (3.8), was difficult to estimate well, e.g.
, respectively. Comparing the adaptive priors, NAB outperformed SAB in scenarios for which the integral required by the latter, i.e. (3.8), was difficult to estimate well, e.g. 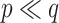 .
.
Figures S1 and S2 of supplementary material available at Biostatistics online plot the separate RMSE ratios for 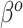 and
and 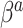 , respectively. There is a clear trend of improving performance for estimating
, respectively. There is a clear trend of improving performance for estimating 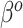 , which is to be expected given its relationship to
, which is to be expected given its relationship to 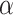 . For the small
. For the small 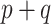 settings, the SAB-type updates were about equivalent to the standard approach in estimating
settings, the SAB-type updates were about equivalent to the standard approach in estimating 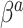 , and the NAB-type updates were worse. Interestingly, in the larger
, and the NAB-type updates were worse. Interestingly, in the larger 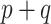 settings, the adaptive priors were marginally better at estimating
settings, the adaptive priors were marginally better at estimating 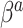 than the standard approach. Our findings were relatively unchanged upon increasing the shape and scale of
than the standard approach. Our findings were relatively unchanged upon increasing the shape and scale of 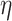 , which scales
, which scales 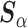 , to 25 (Figure S3 of supplementary material available at Biostatistics online). Finally, Table S1 of supplementary material available at Biostatistics online summarizes the running time of each prior considered. The SAB-type updates were slowest to run, owing in part to the required imputation step.
, to 25 (Figure S3 of supplementary material available at Biostatistics online). Finally, Table S1 of supplementary material available at Biostatistics online summarizes the running time of each prior considered. The SAB-type updates were slowest to run, owing in part to the required imputation step.
6. Application: mortality risk prediction in pediatric ECMO patients
We demonstrate our methods on the data example discussed in the introduction. Ped-RESCUERS was fit to 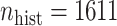 historical patients, and
historical patients, and 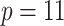 risk factors for short-term mortality were included. Our current data consists of
risk factors for short-term mortality were included. Our current data consists of 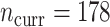 patients, on which we have measured both the
patients, on which we have measured both the 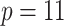 original and the
original and the 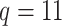 added covariates, all of which are defined in Table S2 of supplementary material available at Biostatistics online. The overall mortality rate in the Ped-RESCUERS cohort was 40.8%; in the current cohort it was 26.4%.
added covariates, all of which are defined in Table S2 of supplementary material available at Biostatistics online. The overall mortality rate in the Ped-RESCUERS cohort was 40.8%; in the current cohort it was 26.4%.
We fit the following seven Bayesian logistic regression models. Ped-RESC is the model from Barbaro and others (2016) based upon the original covariates fit to the 1611 patients. Ped-RESC2 is this same model fit to the current 178 patients, using weakly informative Cauchy priors on the regression coefficients; we include this model so as to be able to assess differences due to study populations. The other five priors are as considered in the simulation study: a regularized horseshoe prior on all 22 parameters (“Standard”), and agnostic and optimistic versions for each of the SAB and NAB priors. For all five priors, we used 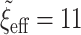 to reflect an optimistic prior assumption that 11 of the 22 parameters are non-zero. To account for sporadic missingness in the current data (about 4% in total), we used a pseudo-Bayesian strategy proposed by Zhou and Reiter (2010). We first imputed 100 datasets using MICE. Then, for each completed dataset and each prior, we sampled 400 draws from the posterior distribution of the parameters conditional upon that completed dataset, concatenating these across imputations to construct a sample of
to reflect an optimistic prior assumption that 11 of the 22 parameters are non-zero. To account for sporadic missingness in the current data (about 4% in total), we used a pseudo-Bayesian strategy proposed by Zhou and Reiter (2010). We first imputed 100 datasets using MICE. Then, for each completed dataset and each prior, we sampled 400 draws from the posterior distribution of the parameters conditional upon that completed dataset, concatenating these across imputations to construct a sample of 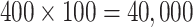 posterior draws “averaged” over the imputations. The log-odds ratios (ORs), i.e. elements of
posterior draws “averaged” over the imputations. The log-odds ratios (ORs), i.e. elements of 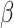 , were standardized with respect to the observed distribution of the 178 current patients, allowing for a comparison of magnitudes both between and within priors.
, were standardized with respect to the observed distribution of the 178 current patients, allowing for a comparison of magnitudes both between and within priors.
Table 3 gives the posterior medians of the ORs. Also included is the larger of (i) 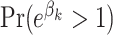 and (ii)
and (ii) 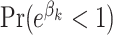 . Bolded results correspond to those with a
. Bolded results correspond to those with a 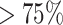 probability of falling above or below 1, a simple binary indicator of variable importance. The first two blocks of rows correspond to the original covariates, and the second two blocks of rows correspond to the added covariates. Figure 2 presents boxplots of the posterior distributions of all ORs.
probability of falling above or below 1, a simple binary indicator of variable importance. The first two blocks of rows correspond to the original covariates, and the second two blocks of rows correspond to the added covariates. Figure 2 presents boxplots of the posterior distributions of all ORs.
Table 3.
Posterior medians of standardized odds ratios (ORs) and, in parentheses, variable importance probabilities given as percentages, defined as the larger of (i) the posterior probability that an OR exceeds one and (ii) the posterior probability that an OR falls below one
| Model | pH | PaCO (mmHg) (mmHg) |
MAP(CMV) | MAP(HFOV) | Admit hours | Intubated hours |
|---|---|---|---|---|---|---|
(cmH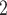 O) O) |
(cmH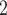 O) O) |
pre-ECMO (log) | pre-ECMO (log) | |||
| PedRESC | 0.46(100.0%) | 0.70(96.3%) | 1.37(93.9%) | 1.43(98.6%) | 1.42(99.3%) | 1.62(99.5%) |
| PedRESC2 | 0.37(96.0%) | 0.67(76.9%) | 1.54(74.1%) | 1.59(83.4%) | 1.64(86.8%) | 2.30(95.7%) |
| Standard | 0.99(58.8%) | 1.01(58.9%) | 1.01(55.6%) | 1.02(60.8%) | 1.01(58.4%) | 1.96(90.6%) |
| NAB(Agn) | 0.58(94.5%) | 0.88(70.1%) | 1.29(84.3%) | 1.39(93.0%) | 1.33(91.5%) | 1.71(98.3%) |
| NAB(Opt) | 0.55(97.5%) | 0.82(78.4%) | 1.33(88.7%) | 1.41(96.2%) | 1.36(95.7%) | 1.67(99.0%) |
| SAB(Agn) | 0.90(73.7%) | 1.02(56.9%) | 1.10(69.2%) | 1.14(77.4%) | 1.03(59.2%) | 2.25(99.0%) |
| SAB(Opt) | 0.86(76.9%) | 1.02(56.1%) | 1.13(71.4%) | 1.15(78.4%) | 1.02(58.1%) | 2.25(99.4%) |
| Model | Malignancy | Pre-ECMO | DX:Asthma | DX:Bronchiolitis | DX:Pertussis | |
| milrinone | ||||||
| PedRESC | 1.22(95.1%) | 1.29(95.8%) | 0.75(93.9%) | 0.58(100.0%) | 1.33(99.5%) | |
| PedRESC2 | 1.21(71.1%) | 1.31(76.6%) | 0.05(99.2%) | 0.76(75.1%) | 2.07(97.9%) | |
| Standard | 1.00(50.8%) | 1.00(51.4%) | 0.94(69.8%) | 0.98(63.6%) | 1.33(85.2%) | |
| NAB(Agn) | 1.15(80.7%) | 1.17(81.5%) | 0.70(91.4%) | 0.65(95.4%) | 1.43(98.8%) | |
| NAB(Opt) | 1.17(87.0%) | 1.21(87.8%) | 0.71(93.6%) | 0.63(98.2%) | 1.40(99.4%) | |
| SAB(Agn) | 1.03(59.2%) | 0.99(54.9%) | 0.96(60.6%) | 0.61(96.4%) | 1.50(96.8%) | |
| SAB(Opt) | 1.03(59.5%) | 0.99(52.6%) | 0.97(60.0%) | 0.57(97.9%) | 1.49(96.9%) | |
| Model | Abnormal | Bilirubin | ALT U/L (log) | Extent of | Extent of | Extent of |
| pupillary resp. | mg/dL (log) | leukocyt. (log) | leukopen. (log) | thrombocytopen. (log) | ||
| PedRESC | — | — | — | — | — | — |
| PedRESC2 | — | — | — | — | — | — |
| Standard | 0.99(56.4%) | 1.07(72.5%) | 5.60(99.8%) | 1.04(68.7%) | 0.97(66.6%) | 1.01(55.1%) |
| NAB(Agn) | 0.99(55.1%) | 1.05(71.5%) | 4.88(99.6%) | 1.03(63.8%) | 0.98(62.5%) | 1.01(54.3%) |
| NAB(Opt) | 0.99(54.6%) | 1.04(69.6%) | 4.92(99.5%) | 1.02(63.1%) | 0.98(61.5%) | 1.01(54.1%) |
| SAB(Agn) | 0.99(57.5%) | 1.13(75.5%) | 4.87(99.8%) | 1.05(66.4%) | 0.95(66.5%) | 1.01(55.3%) |
| SAB(Opt) | 0.99(57.8%) | 1.12(75.2%) | 4.60(99.7%) | 1.04(64.6%) | 0.96(65.1%) | 1.01(55.3%) |
| Model | INR | VIS (log) | Lactate | PF ratio (log) | Pre-ECMO acute | |
| mMol/L (log) | kidney injury | |||||
| PedRESC | — | — | — | — | — | |
| PedRESC2 | — | — | — | — | — | |
| Standard | 1.02(62.0%) | 1.01(57.9%) | 1.57(85.6%) | 0.94(71.4%) | 1.00(53.7%) | |
| NAB(Agn) | 1.01(57.9%) | 1.01(53.2%) | 1.10(77.6%) | 0.96(68.8%) | 1.00(50.2%) | |
| NAB(Opt) | 1.01(56.7%) | 1.00(53.0%) | 1.07(75.1%) | 0.97(67.6%) | 1.00(50.0%) | |
| SAB(Agn) | 1.05(66.8%) | 1.02(59.1%) | 1.94(90.7%) | 0.87(77.2%) | 1.00(52.8%) | |
| SAB(Opt) | 1.05(66.8%) | 1.02(60.1%) | 1.97(90.6%) | 0.88(76.8%) | 1.00(51.9%) |
Results in bold have percentages exceeding 75.0%.
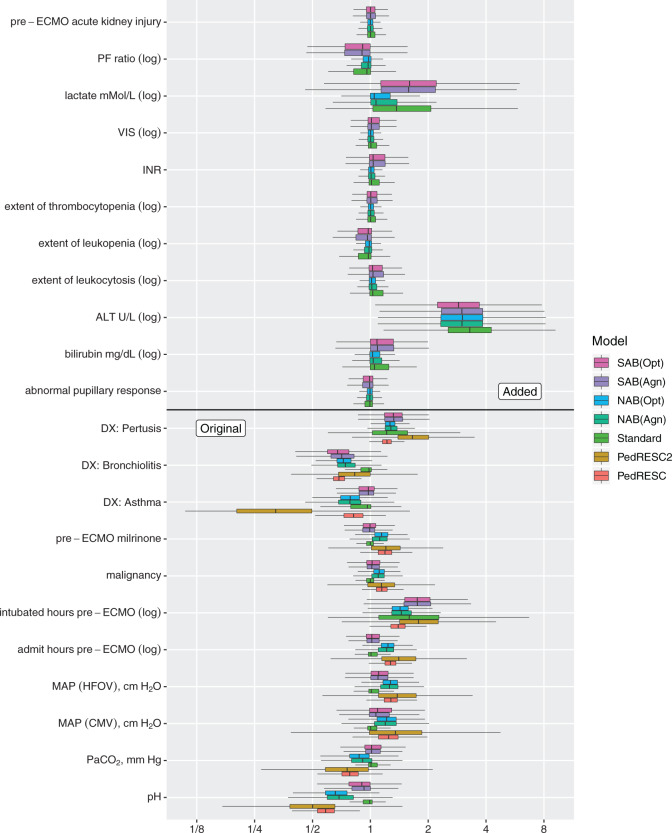
Fig. 2.
Boxplots of posterior draws of odds ratios (ORs) from seven Bayesian logistic models using different priors. All models estimate ORs corresponding to the original covariates (the bottom eleven rows). Five models (all except “PedRESC” and “PedRESC2”) estimate ORs corresponding to the added covariates (the top eleven rows).
Comparing PED-RESC and PED-RESC2, the direction and magnitude of the observed associations in the sets of original covariates were consistent between the two cohorts, with one exception: in PED-RESC2, no patients with a primary diagnosis of asthma died, i.e. the data were quasi-complete separated. All variable importance probabilities were generally closer to 1 in PED-RESC, due to its larger sample size. The regularized horseshoe (Standard) shrinks nearly all ORs, both original and added, close to one. This is one consequence of the size of 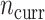 relative to
relative to 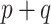 . In contrast, all of the adaptive priors recover some of the original associations from PED-RESC.
. In contrast, all of the adaptive priors recover some of the original associations from PED-RESC.
Using the NAB-type priors, the importance probabilities for the original risk factors were all greater than 75%, as well as those of added covariates of ALT and lactate. These two were also important according to Standard. Neither of the SAB priors found PaCO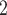 , MAP(CMV), admit hours pre-ECMO, malignancy, preECMO milrinone, or DX:Asthma to be important and, among the added covariates, identified bilirubin, ALT, lactate, and PF ratio as important. The posterior means of
, MAP(CMV), admit hours pre-ECMO, malignancy, preECMO milrinone, or DX:Asthma to be important and, among the added covariates, identified bilirubin, ALT, lactate, and PF ratio as important. The posterior means of 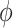 were 0.61 and 0.64, respectively, for the agnostic versions of NAB and SAB, and 0.84 and 0.82, respectively, for the optimistic versions.
were 0.61 and 0.64, respectively, for the agnostic versions of NAB and SAB, and 0.84 and 0.82, respectively, for the optimistic versions.
From Figure 2, there are two general differences between Standard and the adaptive priors. For the two original covariates that Standard also identified as important (DX:Pertussis and intubated hours pre-ECMO), the posterior variability of the adaptive priors is smaller than Standard. Among the remaining original covariates, the adaptive priors have larger posterior variability than Standard; this is a consequence of the shrinkage-to-zero prior, which yields small posterior variance for coefficients that it identifies as likely to be zero-valued. This does not mean Standard is automatically preferred, because some of this shrinkage likely reflects an inability to reliably estimate parameters rather than confidence that they are truly zero. In general, the SAB-type priors deviate more from PED-RESC than the NAB-type priors: NAB shrinks 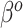 directly towards the PED-RESC estimates, whereas SAB shrinks a linear combination of
directly towards the PED-RESC estimates, whereas SAB shrinks a linear combination of 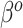 and
and 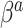 toward the PED-RESC estimates.
toward the PED-RESC estimates.
7. Discussion
We have proposed novel adaptive Bayesian updates of a GLM when the historical model only includes a subset of the covariates of interest. The priors, with acronyms ‘NAB’ or ‘SAB’, adaptively combine prior information from the historical model, including underlying statistical uncertainty, with variance-reducing shrinkage to zero. Thus, they are flexible enough for use in many contexts, ranging from the historical information being highly informative about a few parameters to being weakly informative about most parameters, as evidenced by our simulation study. They generally outperformed or matched in performance a standard approach that ignores historical information. We demonstrated these ideas in our motivating case study for predicting short-term mortality risk in pediatric ECMO patients.
Specifically, we combined a registry-based mortality risk prediction model (the historical model) fit to 1611 patients’ data with a broader model that includes biometric measurements (the current model) recorded on 178 patients. A standard shrinkage prior shrunk most ORs, both original and added, to one, which is typical behavior for such priors in the presence of substantial uncertainty. Taking into account a clinical perspective, it seems unlikely that only two of the eleven original covariates identified by Ped-RESCUERS remain as risk factors for mortality after including the added biometric measurements. Agreeing more with our clinical expectation, the adaptive updates included between five and all eleven of the original Ped-RESCUERS risk factors and also identified two (NAB) or four (SAB) of the added covariates as likely risk factors. Some of this “loss” of importance may be due to correlation between the original and added covariates: PaCO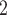 and lactate are negatively correlated, both associated with the degree of acidosis in the body. Similarly, bilirubin and ALT both measure liver damage, which may explain that the NAB priors focused on ALT alone whereas SAB found both bilirubin and ALT to be important. One surprising non-finding was SAB’s failure to identify malignancy as a meaningful risk factor. NAB did identify malignancy as important, and this is more consistent with the Ped-RESCUERS model as well as our expectation based upon clinical experience and intuition.
and lactate are negatively correlated, both associated with the degree of acidosis in the body. Similarly, bilirubin and ALT both measure liver damage, which may explain that the NAB priors focused on ALT alone whereas SAB found both bilirubin and ALT to be important. One surprising non-finding was SAB’s failure to identify malignancy as a meaningful risk factor. NAB did identify malignancy as important, and this is more consistent with the Ped-RESCUERS model as well as our expectation based upon clinical experience and intuition.
The SAB prior depends upon both a simplifying functional approximation (3.6) and an imputation model for 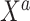 given
given 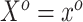 (3.7). In simulated scenarios for which the imputation model was readily estimated and had sufficient predictive ability, namely
(3.7). In simulated scenarios for which the imputation model was readily estimated and had sufficient predictive ability, namely 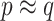 , these approximations yielded considerable efficiency gains. Its advantage over NAB was most evident in coefficient setting
, these approximations yielded considerable efficiency gains. Its advantage over NAB was most evident in coefficient setting 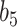 , in which the true value of
, in which the true value of 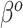 differed from the misspecified true value of
differed from the misspecified true value of 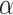 , and so NAB was substantially worse than Standard because the former was biased. Subsequent investigations have also suggested that SAB improves as
, and so NAB was substantially worse than Standard because the former was biased. Subsequent investigations have also suggested that SAB improves as 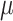 is closer to zero. In contrast, in settings
is closer to zero. In contrast, in settings 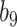 and
and 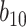 , for which
, for which 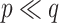 and NAB slightly outperformed SAB, the need for imputation was likely to the detriment of SAB (although it still outperformed Standard). Such
and NAB slightly outperformed SAB, the need for imputation was likely to the detriment of SAB (although it still outperformed Standard). Such 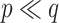 and small
and small 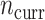 scenarios would correspond, for example, to an exploration of adding a panel of biomarkers,
scenarios would correspond, for example, to an exploration of adding a panel of biomarkers, 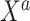 , which are available on just a few subjects, to an established risk prediction model,
, which are available on just a few subjects, to an established risk prediction model, 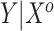 . In that setting, the covariates
. In that setting, the covariates 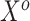 are probably weak predictors of
are probably weak predictors of 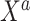 . Empirically, we have found that estimating
. Empirically, we have found that estimating 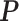 with 100 imputations worked as a good rule of thumb. Of course, there may be underlying differences between the current and historical populations in the true
with 100 imputations worked as a good rule of thumb. Of course, there may be underlying differences between the current and historical populations in the true 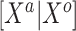 distribution that no amount of current data or number of imputations could recover. NAB is free of this particular distributional assumption and therefore not automatically inferior to SAB in all scenarios, despite the implied value judgment in our nomenclature of ‘naive’ versus ‘sensible’. The only difference between the historical priors in (3.3) and (3.9) being the additive offset
distribution that no amount of current data or number of imputations could recover. NAB is free of this particular distributional assumption and therefore not automatically inferior to SAB in all scenarios, despite the implied value judgment in our nomenclature of ‘naive’ versus ‘sensible’. The only difference between the historical priors in (3.3) and (3.9) being the additive offset 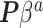 in (3.9), replacing it with
in (3.9), replacing it with 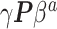 ,
, 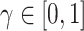 , may be one way to leverage the advantages of both adaptive priors. Importantly, both NAB and SAB ignore information on the historical intercept, meaning that they assume that the historical and current models share
, may be one way to leverage the advantages of both adaptive priors. Importantly, both NAB and SAB ignore information on the historical intercept, meaning that they assume that the historical and current models share 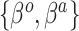 in common but not necessarily the full data-generating mechanism
in common but not necessarily the full data-generating mechanism 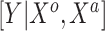 .
.
Shrinkage methods classically make a bias-variance tradeoff to improve overall performance: bias in the direction of zero in exchange for a reduction in variance to improve efficiency. In contrast, the adaptive Bayesian updates we propose, which balance between historical-based shrinkage and shrinkage to zero, are making a bias-bias tradeoff. Both extremes of the adaptive priors (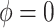 and
and 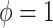 ) reduce variance, and the question is rather one of determining, which type of shrinkage is less biased.
) reduce variance, and the question is rather one of determining, which type of shrinkage is less biased.
Supplementary Material
Acknowledgments
The authors thank two referees, the Associate Editor and the Coordinating Editor for their thorough reviews and helpful comments. Conflict of Interest: None declared.
Funding
This work was partially supported by the National Institutes of Health [P30 CA046592; R01 CA129102] and the Extracorporeal Life Support Organization.
References
- Antonelli J., Zigler C. and Dominici F. (2017). Guided Bayesian imputation to adjust for confounding when combining heterogeneous data sources in comparative effectiveness research. Biostatistics 18, 553–568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armagan A., Dunson D. B. and Lee J. (2013). Generalized double Pareto shrinkage. Statistica Sinica 23, 119–143. [PMC free article] [PubMed] [Google Scholar]
- Barbaro R. P., Boonstra P. S., Kuo K. W., Selewski D. T., Bailly D. K., Stone C. L., Chow J., Annich G. M., Moler F. W. and Paden M. L. (2018). Evaluating pediatric mortality risk prediction among children receiving extracorporeal respiratory support. ASAIO Journal 10.1097/mat.0000000000000813. [DOI] [PubMed] [Google Scholar]
- Barbaro R. P., Boonstra P. S., Paden M. L., Roberts L. A., Annich G. M., Bartlett R. H., Moler F. W. and Davis M. M. (2016). Development and validation of the pediatric risk estimate score for children using extracorporeal respiratory support (Ped-RESCUERS). Intensive Care Medicine 42, 879–888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becker B. J. and Wu M.-J. (2007). The synthesis of regression slopes in meta-analysis. Statistical Science 22, 414–429. [Google Scholar]
- Carpenter B. (2017). Stan: a probabilistic programming language. Journal of Statistical Software 76, 1–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carvalho C. M., Polson N. G. and Scott J. G. (2010). The horseshoe estimator for sparse signals. Biometrika 97, 465–480. [Google Scholar]
- Carvalho C. M., Polson N. G. and Scott J. G. (2009). Handling sparsity via the horseshoe In: van Dyk D. and Welling M. (editors), Proceedings of the Twelfth International Conference on Artificial Intelligence and Statistics, Volume 5 Proceedings of Machine Learning Research, Clearwater Beach, Florida USA: PMLR, pp. 73–80. [Google Scholar]
- Chatterjee N., Chen Y.-H., Maas P. and Carroll R. J. (2016). Constrained maximum likelihood estimation for model calibration using summary-level information from external big data sources. Journal of the American Statistical Association 111, 107–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen H., Manning A. K. and Dupuis J. (2012). A method of moments estimator for random effect multivariate meta-analysis. Biometrics 68, 1278–1284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen M.-H., Ibrahim J. G. and Yiannoutsos C. (1999). Prior elicitation, variable selection and Bayesian computation for logistic regression models. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 61, 223–242. [Google Scholar]
- Cheng W., Taylor J. M. G.,Vokonas P. S.,Park S. K. and Mukherjee B. (2018). Improving estimation and prediction in linear regression incorporating external information from an established reduced model. Statistics in Medicine 37, 1515–1530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duan Y., Ye K. and Smith E. P. (2006). Evaluating water quality using power priors to incorporate historical information. Environmetrics 17, 95–106. [Google Scholar]
- Gelman A., Carlin H. B., Stern H. S., Dunson D. B., Vehtari A. and Rubin D. B. (2014). Bayesian Data Analysis, 3rd edition. Boca Raton, FL: CRC Press. [Google Scholar]
- Griffin J. E. and Brown P. J. (2005). Alternative prior distributions for variable selection with very many more variables than observations Working Paper 10, University of Warwick. Centre for Research in Statistical Methodology. [Google Scholar]
- Grill S., Ankerst D. P., Gail M. H., Chatterjee N. and Pfeiffer R. M. (2017). Comparison of approaches for incorporating new information into existing risk prediction models. Statistics in Medicine 36, 1134–1156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ibrahim J. G. and Chen M.-H. (2000). Power prior distributions for regression models. Statistical Science 15, 46–60. [Google Scholar]
- Ibrahim J. G., Chen M.-H., Gwon Y. and Chen F. (2015). The power prior: theory and applications. Statistics in Medicine 34, 3724–3749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ibrahim J. G., Chen M.-H. and Lipsitz S. R. (2002). Bayesian methods for generalized linear models with covariates missing at random. Canadian Journal of Statistics 30, 55–78. [Google Scholar]
- Jackson D. and Riley R. D. (2014). A refined method for multivariate meta-analysis and meta-regression. Statistics in Medicine 33, 541–554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuenschwander B., Branson M. and Spiegelhalter D. J. (2009). A note on the power prior. Statistics in Medicine 28, 3562–3566. [DOI] [PubMed] [Google Scholar]
- Park T. and Casella G. (2008). The Bayesian lasso. Journal of the American Statistical Association 103, 681–686. [Google Scholar]
- Piironen J. and Vehtari A. (2015). Projection predictive variable selection using Stan+R. arXiv preprint arXiv:1508.02502. https://arxiv.org/abs/1508.02502v1. [Google Scholar]
- Piironen J. and Vehtari A. (2017a). On the hyperprior choice for the global shrinkage parameter in the horseshoe prior. In: Singh A. and Zhu J. (editors), Proceedings of the 20th International Conference on Articial Intelligence and Statistics, Volume 54, Proceedings of Machine Learning Research Fort Lauderdale, FL, USA: PMLR, pp. 905–913. [Google Scholar]
- Piironen J. and Vehtari A. (2017b). Sparsity information and regularization in the horseshoe and other shrinkage priors. Electronic Journal of Statistics 11, 5018–5051. [Google Scholar]
- R Core Team. (2016). R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; https://www.R-project.org/. [Google Scholar]
- Simpson D., Rue H., Riebler A., Martins T. G. and Sørbye S. H. (2017). Penalising model component complexity: A principled, practical approach to constructing priors. Statistical Science 32, 1–28. [Google Scholar]
- Stan Development Team (2017). Stan Modeling Language User’s Guide and Reference Manual, Version 2.17.0. http://mc-stan.org/.
- Stan Development Team (2018). RStan: the R interface to Stan. R package version 2.17.3. [Google Scholar]
- van Buuren S. and Groothuis-Oudshoorn K. (2011). mice: Multivariate imputation by chained equations in R. Journal of Statistical Software 45, 1–67. [Google Scholar]
- Walker E., Hernandez A. V. and Kattan M. W. (2008). Meta-analysis: Its strengths and limitations. Cleveland Clinic Journal of Medicine 75, 431–439. [DOI] [PubMed] [Google Scholar]
- Wickham H. (2009). ggplot2: Elegant Graphics for Data Analysis. New York, NY: Springer. [Google Scholar]
- Zhou X. and Reiter J. P. (2010). A note on Bayesian inference after multiple imputation. The American Statistician 64, 159–163. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.