Abstract
The analysis of area-level aggregated summary data is common in many disciplines including epidemiology and the social sciences. Typically, Markov random field spatial models have been employed to acknowledge spatial dependence and allow data-driven smoothing. In the context of an irregular set of areas, these models always have an ad hoc element with respect to the definition of a neighborhood scheme. In this article, we exploit recent theoretical and computational advances to carry out modeling at the continuous spatial level, which induces a spatial model for the discrete areas. This approach also allows reconstruction of the continuous underlying surface, but the interpretation of such surfaces is delicate since it depends on the quality, extent and configuration of the observed data. We focus on models based on stochastic partial differential equations. We also consider the interesting case in which the aggregate data are supplemented with point data. We carry out Bayesian inference and, in the language of generalized linear mixed models, if the link is linear, an efficient implementation of the model is available via integrated nested Laplace approximations. For nonlinear links, we present two approaches: a fully Bayesian implementation using a Hamiltonian Monte Carlo algorithm and an empirical Bayes implementation, that is much faster and is based on Laplace approximations. We examine the properties of the approach using simulation, and then apply the model to the classic Scottish lip cancer data.
Keywords: Change of support problem, Ecological bias, Hamiltonian Monte Carlo, Markovian Gaussian random fields
1. Introduction
When modeling residual spatial dependence, it is appealing to formulate modeling in terms of an underlying continuous spatial surface, and this is the usual approach for point-referenced data. Continuous modeling becomes more difficult when the data contain regional aggregates at varying spatial resolutions. In epidemiological studies, data is often aggregated for reporting or anonymization. While there exists a wealth of techniques to model regional data at a fixed resolution (Cressie and Wikle, 2011; Banerjee and others, 2014), these models do not extend in a straightforward fashion to situations where more than one resolution is used. In this article, we develop methods for dealing with such situations. We describe two motivating settings.
In the first scenario, we suppose we have areal data only. In epidemiology and the social sciences this situation is the most common, since such data usually satisfy confidentiality constraints, and typically arises from aggregation over a disjoint, irregular partition of the study map, based on administrative boundaries. As an example, we consider incident lip cancer counts observed in 56 counties in Scotland over the years 1975–1980. These data provide a good test case, since they have been extensively analyzed in the literature; see Wakefield (2007) and the references there-in. In this setting, we may view the continuous underlying surface as a device to induce a spatial prior for the areas that avoids the usual arbitrary element of defining neighbors over an irregular geography.
The second scenario, we consider is one in which one data source is available as area level averages over a set of areas but is supplemented with data collected from surveys at known locations. Our interest in this problem arises from spatial modeling of demographic indicators in a developing world context. One source of data is the census, which provides data at the aggregate level, e.g. the average or sum of a variable over an administrative areal unit. In many countries, demographic and health information is collected via surveys, such as Demographic and Health Surveys (DHS; Corsi and others, 2012), and these provide a second source of data. These surveys are typically stratified cluster designs with countries being stratified into coarse areas and into urban/rural, with enumeration areas (EAs) sampled within strata, and then households sampled within EAs. In these surveys, the locations of the EAs, i.e. the GPS coordinates, are often available. In each of these examples, we assume that there is a latent, continuous Gaussian random field (GRF) that varies in space,  where
where  is our study region of interest.
is our study region of interest.
The situation with which we are concerned with in this article is closely related to the change of support problem (COSP; Bradley and others, 2016; Cressie and Wikle, 2011; Gelfand, 2010; Gotway and Young, 2002). This problem occurs when one would like to make inference at a particular spatial resolution, but the data are available at another resolution. Much of this work focuses on normal data, with block kriging being used. For example, Fuentes and Raftery (2005) combine point and aggregate pollution data, with the latter consisting of outputs from numerical models, produced over a gridded surface. Berrocal and others (2010) considered the same class of problem, but added a time dimension and used a regression model with coefficients that varied spatially to relate the observed data to the modeled output. Moraga and others (2017) develop a similar framework to ours and use a stochastic partial different equation (SPDE) approach in order to relate two levels of pollution data. Specifically, the model they propose relates the continuous surface to the area (grid) level by taking an unweighted average of the surface at various points within each grid. We extend this work in several regards: most importantly, our model can accommodate non-normal outcomes and we also allow for a more complex relationship between the point-level process and the aggregated data. Therefore, we are able to address a wider range of situations.
Diggle and others (2013) take a different approach for discrete data and model various applications using log-Gaussian Cox processes, including the reconstruction of a continuous spatial surface from aggregate data. Their approach is based on Markov chain Monte Carlo (MCMC) and follows Li and others (2012) in simulating random locations of cases within areas, which is a computationally expensive step. Recently, Taylor and others (2015, 2018) have focused on improving computation for this scenario and extended the framework to include spatiotemporal models.
A related problem to the COSP, is the modeling of areal data over time, but with boundary changes. Lee and others (2017) analyze space-time data on male bladder cancer in Nova Scotia; the spatial aggregation changes over time, with the older data tending to be of aggregate form and the point data being the norm in more recent years. Building on previous work (Fan and others, 2011; Li and others, 2012; Nguyen and others, 2012), they use a local EM algorithm in conjunction with a local polynomial to model the risk surface.
We propose a three-stage Bayesian hierarchical model that can combine point and areal data by assuming a common underlying smooth, continuous surface. We use the SPDE approach of Lindgren and others (2011) to model the latent field, which allows for computationally efficient inference. The article is structured as follows. In Section 2, we describe the model and in Section 3 the computational details. A simulation study in Section 4 considers a number of scenarios including point data, areal data, and a combination of the two. In Section 5, we illustrate the non-linear areal data only situation for the famous Scotland lip cancer example. Section 6 contains concluding remarks.
2. Model description
We propose a general model framework for inference that can be used for data collected at points, over areas, or a combination of the two. We describe the likelihood first for normal and then for Poisson data (as an illustration of a non-normal outcome), before concluding with a discussion of the model for the latent spatial surface.
2.1. Normal responses
In general, models are specified at the point level. We describe the normal model in the context of modeling household wealth over a spatial region. Since we will be concerned with observations at the area-level we will introduce general notation. The region of interest,  , is divided into
, is divided into 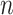 disjoint areas denoted
disjoint areas denoted 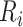 , with
, with  households in area
households in area 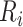 ,
, 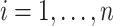 . Let
. Let  denote the
denote the  -th response associated with location
-th response associated with location 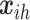 (e.g. longitude and latitude), with covariate information
(e.g. longitude and latitude), with covariate information 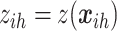 ,
,  ; we assume a single covariate only for notational simplicity, with the extension to multiple covariates being straightforward. The household-level model is
; we assume a single covariate only for notational simplicity, with the extension to multiple covariates being straightforward. The household-level model is 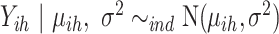 , with
, with  and
and 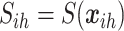 being the spatial random effect, where the spatial model is a GRF. We have assumed the measurement error variance
being the spatial random effect, where the spatial model is a GRF. We have assumed the measurement error variance 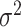 is the same for each response but this can easily be relaxed. When data are available from a census we observe the average response in each of the areas
is the same for each response but this can easily be relaxed. When data are available from a census we observe the average response in each of the areas 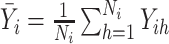 . The induced area-level model is
. The induced area-level model is  where,
where,
 |
(2.1) |
2.2. Poisson responses
In the second case, we consider, we assume that only the sum of all binary events,  , is observed and recorded in area
, is observed and recorded in area 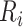 . The individual-level model is
. The individual-level model is  We assume a rare event scenario, along with a log-linear model, so that,
We assume a rare event scenario, along with a log-linear model, so that,  . We sum over all cases to give,
. We sum over all cases to give,  , where,
, where,
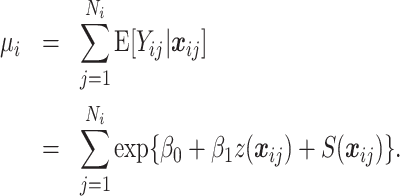 |
(2.2) |
If we have non-rare outcomes and only observe the sum then the situation is far more difficult to deal with since the sum of binomials with varying probabilities is a convolution of binomials. If we observe the individual outcomes 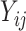 (and not just the sum), then we can model each as binomial (so that we do not have to resort to the convolution). The common situation with disease counts and expected numbers are available across a set of areas is considered in Section 5.
(and not just the sum), then we can model each as binomial (so that we do not have to resort to the convolution). The common situation with disease counts and expected numbers are available across a set of areas is considered in Section 5.
2.3. Model for the latent process
We assume a zero-mean latent GRF. There are many choices for describing how the form of the covariance changes with distance, but we follow Stein (1999) and others who make a strong argument for the Matérn covariance function defined as,
 |
(2.3) |
where  denotes Euclidean distance,
denotes Euclidean distance, 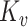 is the modified Bessel function of the second kind and order
is the modified Bessel function of the second kind and order  ,
,  is a scaling parameter, and
is a scaling parameter, and  is a variance parameter. We define the practical range
is a variance parameter. We define the practical range 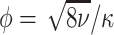 as the distance at which the correlation drops to approximately 0.1. In general, it is difficult to learn about the smoothness parameter
as the distance at which the correlation drops to approximately 0.1. In general, it is difficult to learn about the smoothness parameter  , and so it is conventional to fix this parameter; we follow this convention and set
, and so it is conventional to fix this parameter; we follow this convention and set 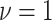 .
.
3. Computation
There are two steps to the computation, first the continuous latent surface is discretized in a convenient fashion (Section 3.1) and second the posterior is approximated. We begin with the normal case (Section 3.2) before turning to the more difficult Poisson case (Section 3.3).
3.1. Approximating the latent process
The major hurdle to the more widespread modeling of spatial data with a continuous surface has been the computation. In particular, inverting and finding the determinant of the Matérn covariance matrix, which is in general not sparse, has been a roadblock when the number of points is not small. However, recent work by Lindgren and others (2011) and Simpson and others (2012) detail the connection between GRFs and Gaussian Markov random fields (GMRFs). They first note that GRFs with a Matérn covariance function are solutions to a particular SPDE, and under certain relatively non-restrictive choices this produces a Markovian GRF (MGRF). They then show it is possible to obtain a representation of the solution to the SPDE using a GMRF.
We follow the SPDE approach and approximate the GRF over a triangulation of the domain (called the mesh) by a weighted sum of basis functions,
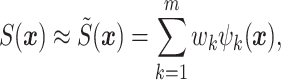 |
(3.1) |
where 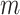 is the number of mesh points in the triangulation,
is the number of mesh points in the triangulation, 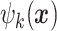 is a basis function, and
is a basis function, and 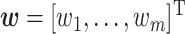 is a collection of weights. The distribution of the weights
is a collection of weights. The distribution of the weights 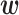 is jointly Gaussian with mean
is jointly Gaussian with mean  and sparse
and sparse 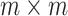 precision matrix,
precision matrix, 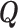 , depending on spatial hyperparameters
, depending on spatial hyperparameters 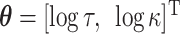 where
where  ; hence,
; hence,  is a GMRF. The form of
is a GMRF. The form of  is chosen so that the resulting distribution for
is chosen so that the resulting distribution for 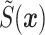 approximates the distribution of the solution to the SPDE, and thus the form will depend on the basis functions. The basis functions are chosen to be piecewise linear functions; that is,
approximates the distribution of the solution to the SPDE, and thus the form will depend on the basis functions. The basis functions are chosen to be piecewise linear functions; that is, 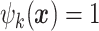 at the
at the  -th vertex of the mesh and
-th vertex of the mesh and 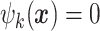 at all other vertices,
at all other vertices, 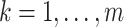 . This results in a set of pyramids, each with typically a six- or seven-sided base. Therefore, the spatial prior consists of functions that are weighted linear combinations of these pyramids, with the weights having a multivariate normal distribution. The sparsity of
. This results in a set of pyramids, each with typically a six- or seven-sided base. Therefore, the spatial prior consists of functions that are weighted linear combinations of these pyramids, with the weights having a multivariate normal distribution. The sparsity of 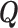 eases computation.
eases computation.
For inference, the discretized version of the spatial prior is combined with the likelihood. In the setting, where we have known locations, it follows from (3.1) that the value of the spatial random effect at an observation point,  , can be approximated by a weighted average of the value of the GMRF on the three nearest mesh vertices. We can write,
, can be approximated by a weighted average of the value of the GMRF on the three nearest mesh vertices. We can write, 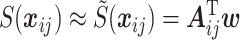 , where
, where 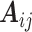 is an
is an 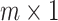 -vector of weights that corresponds to the
-vector of weights that corresponds to the  -th row of a sparse projection matrix
-th row of a sparse projection matrix 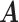 . The nonzero entries of
. The nonzero entries of 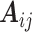 , which correspond to the mesh points comprising the triangle containing
, which correspond to the mesh points comprising the triangle containing 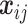 , are calculated using Barycentric interpolation. In the case where the observation location,
, are calculated using Barycentric interpolation. In the case where the observation location,  , is at a mesh vertex,
, is at a mesh vertex,  contains one non-zero entry that is equal to one.
contains one non-zero entry that is equal to one.
For the normal response model with areal data, we use a fully Bayesian approach, since a fast computational strategy is available. Specifically, the integrated nested Laplace approximation (INLA), an approach for analyzing latent Gaussian models (Rue and others, 2009), can be used. INLA works by using a combination of Laplace approximations along with numerical integration to obtain approximations to the posterior marginals. The SPDE approach has also been implemented in the R package R-INLA (Lindgren and Rue, 2015). For the Poisson response model, R-INLA cannot be used for data aggregated over areas; instead, we consider approaches that involve empirical Bayes (EB), Laplace approximations, MCMC, or hybrid combinations of these techniques.
3.2. Normal responses
The likelihood is normal with mean (2.1), and for simplicity we assume no covariates. The key to implementation is to approximate the integrated residual spatial area risk using the mesh. We do not observe the exact locations of all households in each area, so we incorporate population information through gridded population density and weight the approximated spatial surface at the mesh points accordingly. Defining 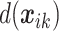 to be the “relative” population density at location
to be the “relative” population density at location 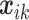 satisfying
satisfying  and
and  , we obtain,
, we obtain,
 |
(3.2) |
where  is the number of mesh points in area
is the number of mesh points in area 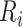 and
and 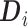 is an
is an 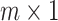 vector with up to
vector with up to  nonzero entries
nonzero entries 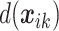 .
.
This type of model can be fit using INLA, since 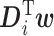 is Gaussian. See Appendix A of the supplementary material available at Biostatistics online for details on the implementation in the context of the simulation that we describe in Section 4.
is Gaussian. See Appendix A of the supplementary material available at Biostatistics online for details on the implementation in the context of the simulation that we describe in Section 4.
3.3. Poisson responses
For areal Poisson data, we have the model  . We use a weighted average of the exponentiated spatial random effect at the mesh points contained in the area to form
. We use a weighted average of the exponentiated spatial random effect at the mesh points contained in the area to form 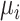 . That is, and again ignoring covariates, we approximate the integral (2.2), to give
. That is, and again ignoring covariates, we approximate the integral (2.2), to give
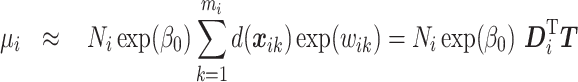 |
(3.3) |
where 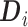 is an
is an 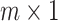 vector, as defined in Section 3.2 and
vector, as defined in Section 3.2 and 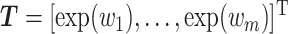 .
.
Due to the structure of this model, it is not possible to use the R-INLA software for fitting, but we describe three alternatives. First, a quick approximation is offered by EB with a Laplace approximation being used to integrate out the spatial random effects. To implement this, we use the R package TMB (which stands for Template Model Builder; Kristensen 2014). This is very efficient and estimates of the spatial hyperparameters and fixed effects can be computed within minutes. Second, we resort to MCMC methods. It is well known that in the Gaussian Process context, MCMC methods can be inefficient (Filippone and others, 2013). We opt to use a Hamiltonian Monte Carlo (HMC; Neal, 2011) transition operator for updating  . Specifically, we first update the spatial hyperparameters
. Specifically, we first update the spatial hyperparameters  using a random walk proposal and then jointly update
using a random walk proposal and then jointly update 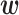 and
and 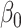 using HMC. Finally, we consider a hybrid approach where estimates for the spatial hyperparameters
using HMC. Finally, we consider a hybrid approach where estimates for the spatial hyperparameters 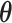 are found using the empirical Bayes approach and then, conditional on these estimates, posteriors for
are found using the empirical Bayes approach and then, conditional on these estimates, posteriors for 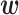 and any fixed effects are explored using MCMC methods. Details of these algorithms in the context of the Scotland example can be found in Appendix C of the supplementary material available at Biostatistics online.
and any fixed effects are explored using MCMC methods. Details of these algorithms in the context of the Scotland example can be found in Appendix C of the supplementary material available at Biostatistics online.
In both the simulation and the real data example, we use relatively vague priors; see Appendices A and C of the supplementary material available at Biostatistics online for details.
4. Simulation study in the normal response case
4.1. Set up
We illustrate the method for normal responses via a simulation considering observations associated with points and observations associated with areas. As a motivating example, we assume the aim is to construct a poverty surface; understanding the spatial structure of poverty and poverty-related factors is of considerable interest (e.g. Gething and others, 2015; Minot and Baulch, 2005; Okwi and others, 2007). Poverty has many different facets, and we take the wealth index (Rutstein and Johnson, 2004) as our measure, which serves as a surrogate for long-term standard of living. The wealth index is comprised of several variables such as household ownership of consumables, access to drinking water, and toilet facilities. The score is then standardized to have mean 0 and standard deviation 1. We simulate a surface of the average wealth index score within households.
We will consider situations in which the wealth index is measured at point locations and we also consider incorporating census data, which provides the average wealth index at the area-level. Observations associated with points are taken from a design that is informed by the Kenya DHS (Kenya National Bureau of Statistics, 2015). It is simplified in that we do not consider stratification or explicit cluster sampling for the 400 locations, which correspond to the centroids of enumeration areas (EAs) from the Kenya 2008 DHS. The dots on the plots in Figure 1 indicate the locations of these sampling points. We emphasize that these are point locations. It would be straightforward to extend the simulation and model to acknowledge the complex design, see Wakefield and others (2018).
Fig. 1.
Mesh (left) and latent spatial surface (right) used for the simulations. The mesh extends beyond the border of Kenya to avoid boundary effects. The black dots represent the locations of the 400 enumeration areas.
Let  index the administrative areas in Kenya and
index the administrative areas in Kenya and 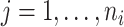 represent the EAs in area
represent the EAs in area 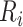 . Hence,
. Hence,  . Furthermore, let
. Furthermore, let 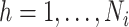 index the households included in the census in area
index the households included in the census in area 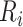 and let
and let  be the number of households surveyed at the
be the number of households surveyed at the 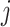 th location (EA) in
th location (EA) in 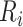 . For our simulation, the number of households participating in a survey,
. For our simulation, the number of households participating in a survey,  , ranges from 41 to 81, with mean 55 to give 21 946 households in total. We let
, ranges from 41 to 81, with mean 55 to give 21 946 households in total. We let 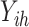 be the wealth index of household
be the wealth index of household  in area
in area 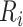 . As assumed in the DHS, all households in EA
. As assumed in the DHS, all households in EA  have the same location.
have the same location.
We consider the data generating mechanism, 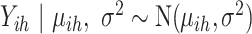 for
for 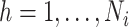 ,
, 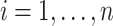 . Thus, for census data we assume the following model for the average wealth index in area
. Thus, for census data we assume the following model for the average wealth index in area 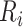 ,
,
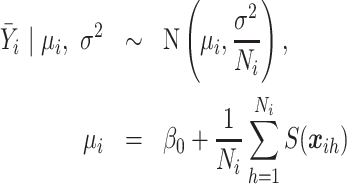 |
(4.1) |
where 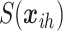 is the value of the spatial random effect at geographic location
is the value of the spatial random effect at geographic location  . For survey data we assume the following model for the average household wealth index taken at EA
. For survey data we assume the following model for the average household wealth index taken at EA  in area
in area 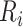 ,
,
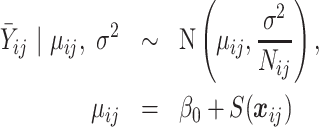 |
(4.2) |
where 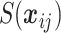 is the spatial random effect evaluated at the centroid,
is the spatial random effect evaluated at the centroid,  , of the EA. In this setting,
, of the EA. In this setting, 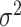 represents measurement error.
represents measurement error.
We assume that the spatial model is a MGRF with Matérn covariance controlled by variance parameter  and scale parameter
and scale parameter  . We set
. We set  ,
, 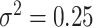 , and
, and  . To simulate the spatial surface, we use the SPDE approach, which requires a triangulated mesh. This mesh is shown in the left panel of Figure 1 with
. To simulate the spatial surface, we use the SPDE approach, which requires a triangulated mesh. This mesh is shown in the left panel of Figure 1 with  mesh points; these mesh points are approximately 15 km apart in the interior of Kenya. We set
mesh points; these mesh points are approximately 15 km apart in the interior of Kenya. We set 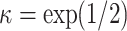 , which corresponds to a practical range of
, which corresponds to a practical range of  degrees. The simulated average household wealth index surface, i.e.,
degrees. The simulated average household wealth index surface, i.e.,  , is shown in the right panel of Figure 1, where the spatial effect
, is shown in the right panel of Figure 1, where the spatial effect  approximates
approximates 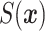 .
.
To simulate data at the 400 EAs, we approximate (4.2) by 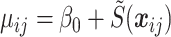 where
where 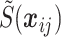 is the simulated spatial effect at EA
is the simulated spatial effect at EA 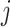 in area
in area  . To simulate the census data we use gridded population estimates from SEDAC (Center for International Earth Science Information Network - CIESIN - Columbia University, 2016), which are available on an (approximately) 1 km square grid at the equator. The gridded population estimates are then transformed to household estimates by dividing the population estimates by 3.9, the mean size of households in 2014 (Kenya National Bureau of Statistics, 2015). We then approximate (4.1) by
. To simulate the census data we use gridded population estimates from SEDAC (Center for International Earth Science Information Network - CIESIN - Columbia University, 2016), which are available on an (approximately) 1 km square grid at the equator. The gridded population estimates are then transformed to household estimates by dividing the population estimates by 3.9, the mean size of households in 2014 (Kenya National Bureau of Statistics, 2015). We then approximate (4.1) by 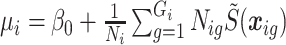 where
where 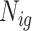 is the household estimate for grid cell
is the household estimate for grid cell  in area
in area 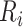 ,
,  is the household estimate for area
is the household estimate for area  , and
, and 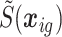 is the simulated spatial effect at the centroid of grid cell
is the simulated spatial effect at the centroid of grid cell  .
.
We consider five different scenarios with varying levels of information available on location: (i) survey data only, (ii) census data up to county level ( ) only, (iii) both survey data and census data up to county level, (iv) census data up to provincial level (
) only, (iii) both survey data and census data up to county level, (iv) census data up to provincial level ( ) only, and (v) both survey data and census data up to provincial level. When we analyze survey and census data together, we assume the two data sources are independent, which in practice means that the surveyed population is only a small fraction of the total population.
) only, and (v) both survey data and census data up to provincial level. When we analyze survey and census data together, we assume the two data sources are independent, which in practice means that the surveyed population is only a small fraction of the total population.
To assess accuracy of the reconstruction under each scenario, we compute the mean squared error (MSE) and mean absolute error (MAE) of the spatial effect surface by
 |
respectively, where 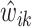 is the posterior mean and
is the posterior mean and 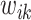 is the “true” value of the spatial effect at mesh point
is the “true” value of the spatial effect at mesh point 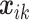 . Both the MSE and MAE are given in Table 1 for all five scenarios. The top row of Figure 2 gives the sampling locations/areas, with each column corresponding to a different sampling scheme, and the middle and bottom rows the posterior means and standard deviations of the spatial effect surface.
. Both the MSE and MAE are given in Table 1 for all five scenarios. The top row of Figure 2 gives the sampling locations/areas, with each column corresponding to a different sampling scheme, and the middle and bottom rows the posterior means and standard deviations of the spatial effect surface.
Table 1.
Posterior median and 95% credible intervals (CI) for parameters, mean squared error (MSE), and mean absolute error (MAE) of the surfaces in the simulation under five scenarios: 400 surveys with exact location (Surveys), census data at the county level (47 Areas), both survey and census data at the county level (Surveys + 47 Areas), census data at the provincial level (8 Areas), and both survey and census data at the provincial level (Surveys + 8 Areas)
| Scenario |
 : : 
|
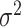 : : 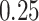
|
 : : 
|
 : : 
|
MSE | MAE |
|---|---|---|---|---|---|---|
| Surveys | 0.0614 | 0.292 | 2.16 | 0.894 | 0.206 | 0.333 |
( 0.549, 0.635) 0.549, 0.635) |
(0.235, 0.365) | (1.56, 3.12) | (0.515, 1.65) | |||
| 47 Areas | 0.198 | 0.213 | 2.08 | 0.687 | 0.339 | 0.463 |
( 0.334, 0.728) 0.334, 0.728) |
(0.0618, 0.367) | (1.37, 3.24) | (0.388, 1.27) | |||
| Surveys + 47 Areas | 0.0529 | 0.323 | 2.11 | 0.833 | 0.170 | 0.316 |
( 0.519, 0.575) 0.519, 0.575) |
(0.262, 0.401) | (1.56, 3.03) | (0.500, 1.50) | |||
| 8 Areas |
 0.0108 0.0108 |
0.211 | 1.10 | 0.654 | 0.551 | 0.602 |
( 0.511, 0.444) 0.511, 0.444) |
(0.0617, 0.364) | (0.383, 2.30) | (0.317, 1.76) | |||
| Surveys + 8 Areas | 0.0571 | 0.298 | 2.17 | 0.879 | 0.201 | 0.330 |
( 0.552, 0.616) 0.552, 0.616) |
(0.241, 0.371) | (1.58, 3.15) | (0.516, 1.63) |
Fig. 2.
Comparison of results under the five scenarios: 400 surveys with exact location (Surveys), census data at the county level (47 Areas), both survey and census data at the county level (Surveys + 47 Areas), census data at the provincial level (8 Areas), and both survey and census data at the provincial level (Surveys + 8 Areas). Top row is the data available under each scenario. Black dots are the locations of the enumeration areas and black borders correspond to the various boundaries (47 counties and 8 provinces). Middle row is the predicted (posterior mean) of the spatial surface. Bottom row is the posterior standard deviation of the predicted surface.
4.2. Survey data
In the first scenario, we consider the situation in which we have survey data available from 400 EAs. To fit the model using R-INLA, we construct the projection matrix 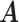 as described in Section 3.1. We fit model (4.2) using the SPDE approach. Computational details can be found in Appendix A of the supplementary material available at Biostatistics online.
as described in Section 3.1. We fit model (4.2) using the SPDE approach. Computational details can be found in Appendix A of the supplementary material available at Biostatistics online.
Posterior medians and 95% credible intervals (CIs) for the parameters are presented in Table 1 and the predicted spatial random effect surface is depicted in Figure 2 (left column). In general, the posterior medians are relatively close to their true values and all CIs cover the true value, though are fairly wide. The predicted spatial surface (posterior mean) over Kenya is visually similar to the true spatial surface, though there is some attenuation. Regions of Kenya that have a higher spatial effect are predicted to be lower and vice versa; this shrinkage to the mean phenomenon is well known in the spatial literature (Section 6.4 of Diggle and Ribeiro, 2007). We also see that the posterior standard deviation of the spatial effect is lower in the vicinity of the 400 EAs and higher elsewhere. The posterior median and 2.5th and 97.5th percentiles of the predicted average household wealth index is depicted in Figure 1 (left column) of the supplementary material available at Biostatistics online and we see similar patterns.
4.3. Census data (47 counties)
We next consider a situation in which we have census data for each of the 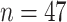 counties in Kenya. To implement (4.1), we approximate
counties in Kenya. To implement (4.1), we approximate 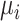 using (3.2), which requires the population density at the mesh points. To determine the population estimate corresponding to the grid containing the mesh point, we used gridded population estimates from SEDAC. Figure 2 of the supplementary material available at Biostatistics online shows which mesh points have higher than average population density in each of the
using (3.2), which requires the population density at the mesh points. To determine the population estimate corresponding to the grid containing the mesh point, we used gridded population estimates from SEDAC. Figure 2 of the supplementary material available at Biostatistics online shows which mesh points have higher than average population density in each of the 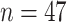 counties.
counties.
The results are presented in Table 1 and depicted in Figure 2 (second column). Again, we see that the posterior medians are relatively close to the true values. The predicted spatial surface is similar to the truth and is very similar to the predicted surface estimated for the point data. In general, the posterior standard deviation of the spatial effect is higher under this scenario than when we had information from 400 surveys. This is also evident when comparing the 2.5th and 97.5th percentile of the predicted average household wealth index, displayed in Figure 1 (middle column) of the supplementary material available at Biostatistics online.
4.4. Survey and census data (47 counties)
Another scenario that might arise is one in which we have both survey data at 400 EAs and census data available for 47 counties. Thus, we simply combine the methods from Sections 4.2 and 4.3. The results are presented in Table 1 and displayed in Figure 2 (third column) and Figure 1 (right column) of the supplementary material available at Biostatistics online. Overall, there is a slight improvement over the survey information only case. We note that there are some identifiability problems when estimating the two variance parameters, which manifests itself here with  being overestimated and
being overestimated and  underestimated.
underestimated.
4.5. Census data (8 provinces)
In order to evaluate the effect when area information is known at a greater aggregate level than previously considered, we examine a situation where we only have census data available for each of the  provinces in Kenya. Implementation-wise, this scenario is analogous to the one previously described in Section 4.3. Results are presented in Table 1 and a depiction of the posterior mean and standard deviation along with a map displaying the eight provinces is in Figure 2 (fourth column). In this scenario, inference for the parameters is severely deteriorated when compared with the previous cases. In particular, the CIs are much wider than in the previous scenarios and the MSE and MAE are substantially larger.
provinces in Kenya. Implementation-wise, this scenario is analogous to the one previously described in Section 4.3. Results are presented in Table 1 and a depiction of the posterior mean and standard deviation along with a map displaying the eight provinces is in Figure 2 (fourth column). In this scenario, inference for the parameters is severely deteriorated when compared with the previous cases. In particular, the CIs are much wider than in the previous scenarios and the MSE and MAE are substantially larger.
4.6. Survey and census data (8 provinces)
The last scenario we consider is similar to that in Section 4.4, where we have survey and census data available (at the provincial level). Parameter estimates are presented in Table 1 and the posterior mean and standard deviation of the random effect is depicted in Figure 2 (last column). Again, identifiability issues are evident in inference for the variances. The spatial effect surface is similar to the surveys-only scenario.
In terms of the MSEs, the values are 0.206, 0.339, and 0.170 when we have survey data with geographic coordinates, census data at the county-level ( ), and a combination. In this simulation, there is a loss of accuracy when we only have census data, but it is not dramatic. However, when we aggregate at the provincial-level (
), and a combination. In this simulation, there is a loss of accuracy when we only have census data, but it is not dramatic. However, when we aggregate at the provincial-level ( ) the MSE is 0.551 and when we additionally incorporate survey data the MSE is 0.201. In general, we see a modest improvement when incorporating the census data over just using survey data. The improvement is significantly better when we used county-level census data rather than provincial-level census data. Similar trends hold for the mean absolute errors.
) the MSE is 0.551 and when we additionally incorporate survey data the MSE is 0.201. In general, we see a modest improvement when incorporating the census data over just using survey data. The improvement is significantly better when we used county-level census data rather than provincial-level census data. Similar trends hold for the mean absolute errors.
5. Application to Scottish lip cancer data
We use the Scotland lip cancer data as an illustrative example of how the method can be applied to areal data. A common model for spatial smoothing for such data is the Besag–York–Mollié (BYM) model (Besag and others, 1991). They propose a discrete spatial model where 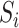 is decomposed into two components,
is decomposed into two components,  . Here,
. Here, 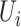 is assigned an intrinsic conditional autoregressive prior,
is assigned an intrinsic conditional autoregressive prior,
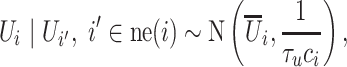 |
where  are the spatial random effects of the neighbors of
are the spatial random effects of the neighbors of 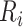 ,
, 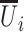 is the mean spatial random effect of the neighbors,
is the mean spatial random effect of the neighbors, 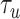 determines the spatial variability, and
determines the spatial variability, and  is the number of neighbors. The other component
is the number of neighbors. The other component  allows for independent shocks in each area,
allows for independent shocks in each area,  . Unfortunately, this specification for the random effects depends on defining a somewhat arbitrary neighborhood structure. As an alternative, we consider spatial modeling via an underlying latent GRF. This may be viewed simply as a mechanism to induce spatial dependence between the areas, and then report the aggregate estimates only. More optimistically, one may report the continuously indexed surface, but this is an intrinsically dangerous endeavor.
. Unfortunately, this specification for the random effects depends on defining a somewhat arbitrary neighborhood structure. As an alternative, we consider spatial modeling via an underlying latent GRF. This may be viewed simply as a mechanism to induce spatial dependence between the areas, and then report the aggregate estimates only. More optimistically, one may report the continuously indexed surface, but this is an intrinsically dangerous endeavor.
Let 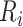 denote county
denote county 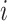 ,
, 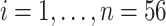 and let
and let 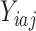 be the binary male lip cancer indicator in stratum (age-band)
be the binary male lip cancer indicator in stratum (age-band) 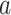 of county
of county 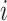 at location
at location 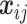 ,
,  where
where  is the male population in county
is the male population in county 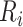 age group
age group 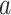 . In the usual case, the available data correspond to summed disease counts
. In the usual case, the available data correspond to summed disease counts 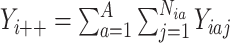 and expected numbers
and expected numbers 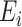 ; these expected numbers are often pre-calculated as
; these expected numbers are often pre-calculated as 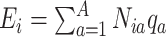 , where
, where  is a reference risk for stratum
is a reference risk for stratum 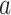 . The
. The  may be taken from a previous time period or calculated (via internal standardization) in advance. The rarity of many diseases, and the lack of stratum-specific information, means that simplifying modeling assumptions are needed, as we now describe.
may be taken from a previous time period or calculated (via internal standardization) in advance. The rarity of many diseases, and the lack of stratum-specific information, means that simplifying modeling assumptions are needed, as we now describe.
We proceed as in the no strata case and assume for a rare disease 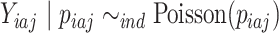 , for
, for  , individuals in strata
, individuals in strata 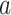 , county
, county 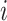 , where
, where  with
with 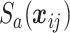 representing the spatial random effect for strata
representing the spatial random effect for strata 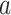 at location
at location 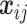 . This leads to
. This leads to 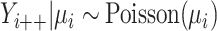 , and, proceeding as before,
, and, proceeding as before,
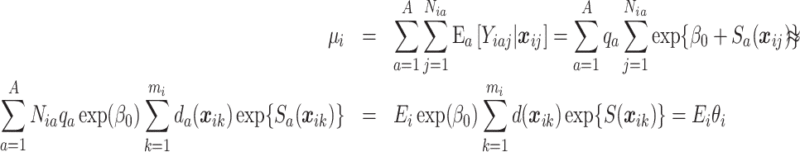 |
where the first equality on the last line follows from assuming a common residual spatial risk surface across stratum (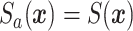 ) and common population density across stratum (
) and common population density across stratum ( ). This allows us to separate the age-standardization from the risk surface estimation to give the data model. Standardization in this fashion leads to the spatial modeling of the relative risk,
). This allows us to separate the age-standardization from the risk surface estimation to give the data model. Standardization in this fashion leads to the spatial modeling of the relative risk,  , an aggregate summary. The standardized incidence ratio (SIR) is
, an aggregate summary. The standardized incidence ratio (SIR) is 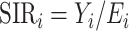 and is the MLE of
and is the MLE of 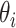 from the Poisson model with mean
from the Poisson model with mean  . The SIRs are depicted in the top left hand panel of Figure 3. It is evident from the map that there is large variability in the area relative risks, with apparent strong spatial dependence.
. The SIRs are depicted in the top left hand panel of Figure 3. It is evident from the map that there is large variability in the area relative risks, with apparent strong spatial dependence.
Fig. 3.
Top left: the SIR estimates of the relative risks of lip cancer in 56 counties of Scotland. Top right: relative risk estimates (posterior medians) from the BYM model. Bottom left: relative risk estimates (posterior medians) from aggregating results from the hybrid EB/MCMC approach. Bottom right: relative risk estimates (posterior medians) from aggregating results from the fully Bayesian approach.
Inference for this model proceeds as discussed in Section 3.3. The mesh used is shown in Figure 4 with  mesh points, which results in mesh points that are
mesh points, which results in mesh points that are  6.3 km apart. We determined the relative population density for each
6.3 km apart. We determined the relative population density for each 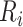 in the same manner as we did for the Kenya simulation and mesh points associated with higher relative population densities are shown in Figure 4.
in the same manner as we did for the Kenya simulation and mesh points associated with higher relative population densities are shown in Figure 4.
Fig. 4.
Left: mesh used for Scotland analysis, consisting of  mesh points. Middle: distribution of population in Scotland. The gray circles represent mesh points where the population density is larger than average for that area. Right: the predicted continuous relative risk surface from using the fully Bayesian approach.
mesh points. Middle: distribution of population in Scotland. The gray circles represent mesh points where the population density is larger than average for that area. Right: the predicted continuous relative risk surface from using the fully Bayesian approach.
We considered several different computational strategies, which are described more fully in Appendix C of the supplementary material available at Biostatistics online. Briefly, we implemented an EB approach in which the spatial random effects were integrated out using Laplace approximations, a fully Bayesian approach (using HMC), and a hybrid of these two in which HMC was used, with the spatial hyperparameters  fixed at the EB estimates. For the fully Bayesian approach, we initialized four chains, used a burn in of 10 000 iterations, ran an additional 1 000 000 iterations and thinned them to ultimately save 1000 iterations from each chain. For the hybrid approach, we also initialized four chains, used a burn in of 500 iterations, and ran an additional 1000 iterations for each chain. Convergence summaries for both the fully Bayesian and hybrid approach are given in Appendix D of the supplementary material available at Biostatistics online.
fixed at the EB estimates. For the fully Bayesian approach, we initialized four chains, used a burn in of 10 000 iterations, ran an additional 1 000 000 iterations and thinned them to ultimately save 1000 iterations from each chain. For the hybrid approach, we also initialized four chains, used a burn in of 500 iterations, and ran an additional 1000 iterations for each chain. Convergence summaries for both the fully Bayesian and hybrid approach are given in Appendix D of the supplementary material available at Biostatistics online.
Estimates and 95% CIs for the parameters 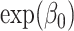 ,
,  , and
, and  are presented in Table 1 of the supplementary material available at Biostatistics online for the three different computational strategies. There is good agreement across the three approaches, though we notice that the posterior CIs tend to be wider when using the fully Bayesian computational strategy, which is not surprising given the assumption of asymptotic normality used to construct the CIs in the EB approach.
are presented in Table 1 of the supplementary material available at Biostatistics online for the three different computational strategies. There is good agreement across the three approaches, though we notice that the posterior CIs tend to be wider when using the fully Bayesian computational strategy, which is not surprising given the assumption of asymptotic normality used to construct the CIs in the EB approach.
We also obtain predictions and posterior standard deviations of 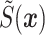 , displayed in Figure 6 of the supplementary material available at Biostatistics online. We note that the posterior standard deviation of the surface is smallest in regions of Scotland where the population is greatest, and larger elsewhere. Furthermore, the posterior standard deviation tends to be a little lower for the hybrid approach than for the fully Bayesian approach, which is not surprising given that the spatial hyperparameters were fixed in the hybrid approach. The predicted continuous relative risk surface using the fully Bayesian approach (posterior median) is presented in Figure 4. As expected, we see that the continuous relative risk surface is largest in the counties with higher SIRs, and lowest in the counties with the smallest SIRs.
, displayed in Figure 6 of the supplementary material available at Biostatistics online. We note that the posterior standard deviation of the surface is smallest in regions of Scotland where the population is greatest, and larger elsewhere. Furthermore, the posterior standard deviation tends to be a little lower for the hybrid approach than for the fully Bayesian approach, which is not surprising given that the spatial hyperparameters were fixed in the hybrid approach. The predicted continuous relative risk surface using the fully Bayesian approach (posterior median) is presented in Figure 4. As expected, we see that the continuous relative risk surface is largest in the counties with higher SIRs, and lowest in the counties with the smallest SIRs.
We obtain relative risk estimates (posterior medians), as well as 95% CIs for each of the 56 counties from this model by aggregating (with respect to the population density) the continuous relative risk surface within each county. To obtain estimates of the desired quantiles in both the fully Bayesian and hybrid approach, for each county 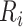 we obtain
we obtain 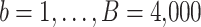 draws from the “aggregated” relative risk surface,
draws from the “aggregated” relative risk surface, 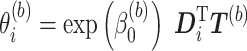 , where
, where 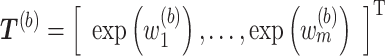 (see (3.3)). As before,
(see (3.3)). As before, 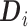 has at most
has at most  nonzero entries that correspond to the population density estimates,
nonzero entries that correspond to the population density estimates,  . From here, we can obtain the desired summary measures. Posterior medians are presented in Figure 3 and the 95% CIs are displayed in Figure 7 of the supplementary material available at Biostatistics online. We see that the relative risk estimates are nearly identical for both computational strategies and are similar to the SIRs, but that the estimates are shrunk towards the overall mean, which is as expected.
. From here, we can obtain the desired summary measures. Posterior medians are presented in Figure 3 and the 95% CIs are displayed in Figure 7 of the supplementary material available at Biostatistics online. We see that the relative risk estimates are nearly identical for both computational strategies and are similar to the SIRs, but that the estimates are shrunk towards the overall mean, which is as expected.
We also compare our results to those obtained using the BYM model. Parameter estimates are in Appendix D of the supplementary material available at Biostatistics online. The predicted relative risks (posterior medians) for each county are presented in Figure 3, and the 95% CIs are presented in Figure 7 of the supplementary material available at Biostatistics online. The results are very similar to the continuous model.
For the fully Bayesian approach using HMC (using our own code), it took approximately a week to fit the model using a computing cluster. This can be improved tremendously by using the hybrid approach. It takes on the order of minutes to obtain the empirical Bayes estimates and about 10 min to run the HMC.
6. Discussion
In this article, we propose a Bayesian hierarchical model that can accommodate observations taken at different spatial resolutions. To this end, we assume a continuous spatial surface, which we model using the SPDE approach.
In the simulation example, we considered surveys taken at point locations and census data associated with areas. When the only data available was census data at the county-level, there was not a substantial loss in accuracy when comparing it to a situation in which we had survey (point) data. In general, we would not expect this to hold when comparing point data to areal data as the loss of information depends on the strength of the spatial dependence, the number and geographical configuration of the areas, and on the amount and quality of the survey data. When the size of the areas increased (comparing 47 counties to 8 provinces), estimates for the spatial parameters and the overall household wealth index were highly variable and the predicted spatial surface was much less nuanced.
With point data, we are not able to learn anything about the surface at a spatial resolution which is less than the distance between the two closest points. If we only have areal data, the situation is far worse. Hence, one should not over-interpret fine spatial scale structure. In both the point and areal data cases, model checking is difficult. For areal data, one may simply view the model as a method to induce an area-level spatial prior. The results can be presented at the area-level, as we did with the Scottish lip cancer example; with area-level data only, we can only check the model at the aggregate level.
We also applied our method to the Scotland lip cancer dataset. Overall, there were very minor differences in the relative risk estimates for each county when comparing our continuous spatial model to a discrete spatial model (i.e. the BYM model) but again there is strong spatial dependence in these data (which explains in part the popularity of these data). However, we note that modeling a continuous surface is particularly attractive in that it is not subject to definitions of administrative boundaries, which can often be arbitrary, and a continuous risk surface, in general, more accurately reflects disease etiology. Furthermore, it can easily be adapted to situations where we might also have point level covariate data. In the latter case, the use of the models we have described avoids the ecological fallacy, which occurs when area-level associations differ from the individual-level counterparts. To avoid ecological bias, one requires point level covariates but the availability of such data is increasing (Gething and others, 2015).
For normal outcomes, all computation can be performed quickly using R-INLA. In the simulation example, it took about 2 min to fit each of the models on a standard laptop. For Poisson outcomes, computation is much more difficult. There has been an increased interest in implementing sparse matrix operations in Stan, which would improve usability of this method. In general, there is still a need for computationally efficient MCMC schemes for Gaussian process data.
In the simulation study we considered, we looked at combining survey (point) data and census (areal) data. However, with older DHS surveys exact geographic coordinates are not available. Instead, it is only known in which area of the country the survey was taken. This is different from the problem we considered in that, instead of observing outcomes that are associated with an entire area (census data), outcomes are for a specific point in the area, but that exact location is unknown. Therefore, the methods proposed here would need to be altered to accommodate this type of situation.
7. Software
All code and input data used in the simulation and application is available on github (https://github.com/wilsonka/pointless-spatial-modeling).
Supplementary Material
Acknowledgments
The authors would like to thank Dan Simpson for numerous helpful conversations and Jim Thorson for advice on TMB. Conflict of Interest: None declared.
Funding
Both authors were supported by R01CA095994 from the National Institutes of Health.
References
- Banerjee, S., Carlin, B. P. and Gelfand, A. E. (2014). Hierarchical Modeling and Analysis for Spatial Data, 2nd edition. Boca Raton, FL: CRC Press. [Google Scholar]
- Berrocal, V. J., Gelfand, A. E. and Holland, D. M. (2010). A spatio-temporal downscaler for output from numerical models. Journal of Agricultural, Biological, and Environmental Statistics 15, 176–197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Besag, J., York, J. and Mollié, A. (1991). Bayesian image restoration with two applications in spatial statistics. Annals of the Institute of Statistics and Mathematics 43, 1–59. [Google Scholar]
- Bradley, J. R., Wikle, C. K. and Holan, S. H. (2016). Bayesian spatial change of support for count-valued survey data with application to the American Community Survey. Journal of the American Statistical Association 111, 472–487. [Google Scholar]
- Center for International Earth Science Information Network - CIESIN - Columbia University. (2016). Gridded Population of the World, Version 4 (GPWv4): Population count. Palisades, NY: NASA Socioeconomic Data and Applications Center (SEDAC) 10.7927/H4PG1PPM (accessed 3 June 2016). [DOI] [Google Scholar]
- Corsi, D. J., Neuman, M., Finlay, J. E. and Subramanian, S. V. (2012). Demographic and health surveys: a profile. International Journal of Epidemiology 41, 1602–1613. [DOI] [PubMed] [Google Scholar]
- Cressie, N. A. C. and Wikle, C. K. (2011). Statistics for Spatio-Temporal Data. Hoboken, NJ: John Wiley and Sons. [Google Scholar]
- Diggle, P. J., Moraga, P., Rowlingson, B. and Taylor, B. M. (2013). Spatial and spatio-temporal log-Gaussian Cox processes: extending the geostatistical paradigm. Statistical Science 28, 542–563. [Google Scholar]
- Diggle, P. J. and Ribeiro, P. J. (2007). Model Based Geostatistics. New York: Springer. [Google Scholar]
- Fan, C. P. S., Stafford, J. and Brown, P. E. (2011). Local-EM and the EMS algorithm. Journal of Computational and Graphical Statistics 20, 750–766. [Google Scholar]
- Filippone, M., Zhong, M. and Girolami, M. (2013). A comparative evaluation of stochastic-based inference methods for Gaussian process models. Machine Learning 93, 93–114. [Google Scholar]
- Fuentes, M. and Raftery, A. E. (2005). Model evaluation and spatial interpolation by Bayesian combination of observations with outputs from numerical models. Biometrics 61, 36–45. [DOI] [PubMed] [Google Scholar]
- Gelfand, A. E. (2010). Misaligned spatial data. In: Gelfand, A. E., Diggle, P. J., Fuentes, M. and Guttorp, P. (editors), Handbook of Spatial Statistics. Boca Raton, FL: CRC Press, pp. 517–539. [Google Scholar]
- Gething, P., Tatem, A., Bird, T. and Burgert-Brucker, C. R. (2015). Creating spatial interpolation surfaces with DHS data. Technical Report, ICF International. DHS Spatial Analysis Reports No. 11. [Google Scholar]
- Gotway, C. A. and Young, L. J. (2002). Combining incompatible spatial data. Journal of the American Statistical Association 97, 632–648. [Google Scholar]
- Kenya National Bureau of Statistics. (2015). Kenya Demographic and Health Survey 2014. Technical Report, Kenya National Bureau of Statistics. [Google Scholar]
- Kristensen, K. (2014). TMB: General random effect model builder tool inspired by ADMB. R package version. [Google Scholar]
- Lee, J. S. W., Nguyen, P., Brown, P. E., Stafford, J. and Saint-Jacques, N. (2017). A local-EM algorithm for spatio-temporal disease mapping with aggregated data. Spatial Statistics 21, 75–95. [Google Scholar]
- Li, Y., Brown, P., Gesink, D. C. and Rue, H. (2012). Log Gaussian Cox processes and spatially aggregated disease incidence data. Statistical Methods in Medical Research 21, 479–507. [DOI] [PubMed] [Google Scholar]
- Lindgren, F. and Rue, H. (2015). Bayesian spatial modelling with R-INLA. Journal of Statistical Software 63, 1–25. [Google Scholar]
- Lindgren, F., Rue, H. and Linström, J. (2011). An explicit link between Gaussian fields and Gaussian Markov random fields: the stochastic differential equation approach (with discussion). Journal of the Royal Statistical Society, Series B 73, 423–498. [Google Scholar]
- Minot, N. and Baulch, B. (2005). Spatial patterns of poverty in Vietnam and their implications for policy. Food Policy 30(5), 461–475. [Google Scholar]
- Moraga, P., Cramb, S. M., Mengersen, K. L. and Pagano, M. (2017). A geostatistical model for combined analysis of point-level and area-level data using INLA and SPDE. Spatial Statistics 21, 27–41. [Google Scholar]
- Neal, R. M. (2011). MCMC using Hamiltonian dynamics. In: Brooks, S., Gelman, A., Jones, G. L. and Meng, X. L. (editors), Handbook of Markov Chain Monte Carlo, Volume 2 Boca Raton, FL: Chapman and Hall/CRC Press, pp. 113–162. [Google Scholar]
- Nguyen, P., Brown, P. E. and Stafford, J. (2012). Mapping cancer risk in southwestern Ontario with changing census boundaries. Biometrics 68, 1228–1237. [DOI] [PubMed] [Google Scholar]
- Okwi, P. O., Ndeng’e, G., Kristjanson, P., Arunga, M., Notenbaert, A., Omolo, A., Henninger, N., Benson, T., Kariuki, P. and Owuor, J. (2007). Spatial determinants of poverty in rural Kenya. Proceedings of the National Academy of Sciences of the United States of America 104, 16769–16774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rue, H., Martino, S. and Chopin, N. (2009). Approximate Bayesian inference for latent Gaussian models using integrated nested Laplace approximations (with discussion). Journal of the Royal Statistical Society, Series B 71, 319–392. [Google Scholar]
- Rutstein, S. O. and Johnson, K. (2004). The DHS wealth index. DHS Comparative Reports No. 6, Calverton, Maryland, USA: http://dhsprogram.com/pubs/pdf/CR6/CR6.pdf. [Google Scholar]
- Simpson, D., Lindgren, F. and Rue, H. (2012). Think continuous: Markovian Gaussian models in spatial statistics. Spatial Statistics 1, 16–29. [Google Scholar]
- Stein, M. L. (1999). Interpolation of Spatial Data: Some Theory for Kriging. New York, NY: Springer. [Google Scholar]
- Taylor, B. M., Andrade-Pacheco, R. and Sturrock, H. J. W. (2018). Continuous inference for aggregated point process data. Journal of the Royal Statistical Society: Series A (Statistics in Society) Advance online publication. 10.1111/rssa.12347. [DOI] [Google Scholar]
- Taylor, B. M., Davies, T. M., Rowlingson, B. and Diggle, P. J. (2015). Bayesian inference and data augmentation schemes for spatial, spatiotemporal and multivariate log-Gaussian Cox processes in R. Journal of Statistical Software 63, 1–48. [Google Scholar]
- Wakefield, J. C. (2007). Disease mapping and spatial regression with count data. Biostatistics 8, 158–183. [DOI] [PubMed] [Google Scholar]
- Wakefield, J., Fuglstad, G.-A.,Riebler, A., Godwin, J., Wilson, K. and Clark, S. J. (2018). Estimating under five mortality in space and time in a developing world context. Statistical Methods in Medical Research. Advance online publication. 10.1177/0962280218767988. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.






