Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2019 Aug 13;36(3):859–864. doi: 10.1093/bioinformatics/btz639

Machine learning empowers phosphoproteome prediction in cancers

Hongyang Li 1,✉, Yuanfang Guan 2,✉
Editor: Jonathan Wren
PMCID: PMC7868059  PMID: 31410451

Abstract

Motivation

Reversible protein phosphorylation is an essential post-translational modification regulating protein functions and signaling pathways in many cellular processes. Aberrant activation of signaling pathways often contributes to cancer development and progression. The mass spectrometry-based phosphoproteomics technique is a powerful tool to investigate the site-level phosphorylation of the proteome in a global fashion, paving the way for understanding the regulatory mechanisms underlying cancers. However, this approach is time-consuming and requires expensive instruments, specialized expertise and a large amount of starting material. An alternative in silico approach is predicting the phosphoproteomic profiles of cancer patients from the available proteomic, transcriptomic and genomic data.

Results

Here, we present a winning algorithm in the 2017 NCI-CPTAC DREAM Proteogenomics Challenge for predicting phosphorylation levels of the proteome across cancer patients. We integrate four components into our algorithm, including (i) baseline correlations between protein and phosphoprotein abundances, (ii) universal protein–protein interactions, (iii) shareable regulatory information across cancer tissues and (iv) associations among multi-phosphorylation sites of the same protein. When tested on a large held-out testing dataset of 108 breast and 62 ovarian cancer samples, our method ranked first in both cancer tissues, demonstrating its robustness and generalization ability.

Availability and implementation

Our code and reproducible results are freely available on GitHub: https://github.com/GuanLab/phosphoproteome_prediction.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Protein phosphorylation is an essential and the most frequent post-translational modification (PTM) in eukaryotes (Ardito et al., 2017; Li et al., 2013; Pawson and Scott, 2005). It is a reversible process controlled by protein kinases and phosphatases (Hunter, 1995). The functions of target proteins are therefore activated, deactivated or modified through the addition or removal of the covalently bound phosphate groups. Protein phosphorylation extends the repertoire of 20 amino acids through modifying their structures and physicochemical characteristics (Hunter, 2012). Together with other PTMs, protein phosphorylation dynamically and flexibly regulates protein function and signaling pathways in many cellular processes.

Technical advancements in quantitative phosphoproteomics by mass spectrometry (MS) allow for identification and quantitation of phosphorylation sites at the system level (Grimsrud et al., 2010). Unique signaling pathways and networks in various systems have been elucidated by phosphoproteomics (Liu et al., 2018a, b; Tan et al., 2017; Wilson et al., 2018). In particular, the phosphoproteomics-based approaches have been widely used to investigate cancer cells and develop personalized treatment (McGrail et al., 2018; Wiredja et al., 2018; Wu et al., 2019; Yang et al., 2018; Zagorac et al., 2018). In addition to phosphoproteomics, proteomic, transcriptomic and genomic profiles have been integrated to study cancers (Dimitrakopoulos et al., 2018; Kan et al., 2018; Li et al., 2018c; Rappoport and Shamir, 2018).

However, MS-based phosphoproteomics approach is time consuming and requires expensive instruments and specialized expertise (Ramroop et al., 2018; Trost and Kusalik, 2011), limiting its wider use especially in developing countries (Aslam et al., 2017). More importantly, in contrast to standard proteome analysis, phosphoproteomics analysis requires a relatively large amount of starting protein samples, further limiting its application when the sample amount is limited in clinical studies (Post et al., 2017). An alternative approach is in silico prediction of phosphoproteomic data from the corresponding proteomic, transcriptomic and genomic data. Many efforts have been made to predict protein phosphorylation sites based on protein sequences (Cao et al., 2018; Hjerrild and Gammeltoft, 2006; Luo et al., 2019; Trost and Kusalik, 2011; Wei et al., 2017). Unfortunately, these sequence-based approaches are not suitable for predicting phosphoproteomic profiles across patients, since samples with identical protein sequences are indistinguishable and the signaling networks related to cancers are not considered. In fact, the phosphoproteomic profiles varied dramatically across ovarian cancer patients and were associated with different survival rates (Zhang et al., 2016). Therefore, there is a great demand for computational models that can predict phosphoproteomic profiles from other omics data.

The Cancer Genome Atlas (TCGA), National Cancer Institute (NCI) and Clinical Proteomic Tumor Analysis Consortium (CPTAC) (Ellis et al., 2013) provide a large collection of genomic, transcriptomic, proteomic and phosphoproteomic data in many cancer types, which is an invaluable source for studying the regulation of protein phosphorylation in human. In 2017, the Dialogue on Reverse Engineering Assessment and Method (DREAM) (Stolovitzky et al., 2007) organized the NCI-CPTAC Proteogenomics Challenge (https://www.synapse.org/#!Synapse:syn8228304/wiki/413428), which was a benchmark competition for an unbiased evaluation of computational methods on held-out datasets (Guan, 2019). In this paper, we present a novel machine learning algorithm, which ranked first in sub-challenge 3 of predicting phosphoproteomic profiles in both breast and ovarian cancer patients. We developed four models, considering the correlations across omics data, the universal protein–protein interactions and the dependency of multiple phosphorylation sites of the same protein.

2 Materials and methods

2.1 Data collection and challenge overview

For both breast and ovarian cancers, the phosphoproteome and proteome data were acquired using the isobaric Tags for Relative and Absolute Quantification (iTRAQ) protein quantification method. These data were downloaded from CPTAC data portal. For breast cancer, 77 samples were analyzed at the Broad Institute (BI); for ovarian cancer, 69 samples were analyzed at Pacific Northwest National Laboratory (PNNL). The details about proteomic and phosphoproteomic data generation are described in Supplementary Information. The corresponding transcriptomic data for the same cancer samples were downloaded from TCGA firehose. The copy number variation (CNV) of DNA data were downloaded from the CPTAC publications (Mertins et al., 2016; Zhang et al., 2016). The aim of this DREAM challenge is to develop computational methods for predicting unseen phosphoproteomic profiles in both breast and ovarian cancer patients, given the corresponding CNV, transcriptomic and proteomic profiles (Fig. 1A). The breast cancer proteome and phosphoproteome consist of 10 005 proteins and 31 981 phosphorylation sites from 4763 unique proteins, respectively. The ovarian cancer proteome and phosphoproteome consist of 7061 proteins and 10 057 phosphorylation sites from 2865 unique proteins, respectively. There are three types of amino acids being phosphorylated: (i) Serine (29 868/8610 sites in breast/ovarian cancer); (ii) Threonine (5633/1410 sites in breast/ovarian cancer); and (iii) Tyrosine (816/164 sites in breast/ovarian cancer). Of note, the phosphorylation site in this study is only a limited subset of the entire cancer phosphoproteome, which was estimated to have around 230 000 phosphorylation sites from 13 000 phosphoproteins in humans (Vlastaridis et al., 2017).

Fig. 1.

Fig. 1.

Open in a new tab

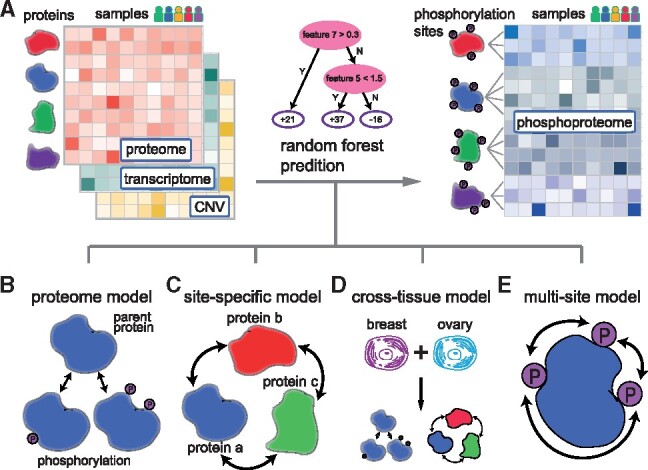
Overview of the algorithm design for predicting phosphoproteome across cancer samples. (A) In this study, we aim to predict phosphoproteome (blue) based on the proteome (red), transcriptome (green) and copy number variations of DNA (yellow). In each of these omics matrices, the columns represent samples from different cancer patients and the rows represent different genes/proteins/phosphorylation sites. We used the random forest model to learn the nonlinear interactions between proteins and predict the phosphorylation levels of the proteome. Four models were developed to address this problem. (B) In the ‘proteome’ model, the abundance of a phosphorylation site was approximated by its parent protein abundance. (C) In the ‘site-specific’ model, we trained a random forest model for each phosphorylation site, resulting in a total of 31 981 and 10 057 models for all phosphorylation sites in breast and ovarian cancer, respectively. The input features are the abundances of all proteins and the random forest model learned the protein–protein interactions in regulating protein phosphorylation. (D) In the ‘cross-tissue’ model, we combined samples from these two cancer tissues and trained the random forest model in the same way as the ‘site-specific’ model. (E) In the ‘multi-site’ model, the prediction for a phosphorylation site was refined as the weighted average of all phosphorylation sites from the same protein. The weights were calculated based on the rate of missing values of a phosphorylation site. (Color version of this figure is available at Bioinformatics online.)

2.2 The ‘proteome’ model

The phosphorylation level of a protein was associated with the protein level itself, since the phosphopeptides were derived from their parent protein. Therefore, we first developed a simple ‘proteome’ model, in which the protein level was directly used as the prediction for the phosphorylation level (Fig. 1B). If multiple phosphorylation sites came from the same parent protein, then the predictions were identical. Therefore, the limitation of this model is that it cannot distinguish different phosphorylation sites from the same protein.

2.3 The ‘site-specific’ model

The phosphorylation of a protein was regulated by functional pathways within a cell. We built a site-specific model to capture the universal protein–protein interactions in an implicit way, instead of using prior knowledge to define protein–protein interactions. In particular, the proteomic data can be represented by an m-by-n matrix X,

[x11x12⋯x1nx21x22…x2n⋮⋮⋱⋮xm1⋯⋯xmn]

where rows represent proteins and columns represent samples. An element xij denotes the protein level of gene i from sample j. Similarly, the phosphoproteomic data can be represented by an s-by-n matrix Y,

[y11y12⋯y1ny21y22…y2n⋮⋮⋱⋮ys1⋯⋯ysn]

where rows represent phosphorylation sites and columns represent samples. An element yij denotes the level of phosphorylation site i from sample j. For each phosphorylation site, we created a ‘site-specific’ random forest (RF) model (Breiman, 2001), with 100 trees and the maximum depth of 3 (Fig. 1C). As one of the tree-based models, RF has been widely used and reported to avoid overfitting and capture nonlinear interactions between features (Li et al., 2018a, b, c, d). For example, for a phosphorylation site i, the observed phosphorylation levels from all samples (yi1, yi2, …, yin) were used as labels. For a sample k, we used expression levels of all m proteins (x1k, x2k, …, xmk) as the corresponding features. In this way, we trained a RF model using n samples for site i. Similarly, for a different phosphorylation site j, we created a different model since the observed labels from all samples (yj1, yj2, …, yjn) were different, although the feature space was identical. We therefore called this a ‘site-specific’ model. The total numbers of feature proteins were 6956 and 3217 in breast and ovarian cancers, respectively. These models were implemented using the function called ensemble.RandomForestRegressor of Python module scikit learn.

2.4 The ‘cross-tissue’ model

We further created a ‘cross-tissue’ model (Fig. 1D). Similar to the site-specific model, we used RF as the base learner and all protein levels as features. We combined samples from these two cancer tissues, resulting in a much larger training dataset of 174 samples (105 breast and 69 ovarian cancer samples). The number of input feature proteins was 3147, which was the number of common feature proteins between these two cancer tissues.

2.5 The ‘multi-site’ model

The phosphorylation sites of the same protein are often correlated. Therefore, we created a ‘multi-site’ model to integrate the information of multiple phosphorylation sites (Fig. 1E). Of note, there were missing values in the phosphoproteome matrix and the missing rates varied a lot across different phosphorylation sites. We calculated the weighted average prediction of multiple sites based on the missing rates:

ymulti=∑i=1k(ni×yi)∑i=1kni

where ni is the number of non-missing training samples for site i, yi is the prediction value for site i and k is the total number of phosphorylation sites for a protein. We assumed that the prediction for a phosphorylation site with less missing values was more reliable, and therefore assigned larger weight. The weight was proportional to the number of non-missing values.

2.6 Cross validation and model ensemble

To systematically evaluate the performance of different models, we applied five-fold cross validation on the 105 breast and 69 ovarian cancer samples. For each cancer tissue, the samples were randomly partitioned into 5 non-overlapping subsets. In each validation, four subsets were used to train a model, and the remaining one subset was used to validate the performance of this model. The final prediction of our method was the ensemble of four models mentioned above in 2.2–2.5, with the ensemble weights of 4, 5, 5 and 2, respectively.

2.7 Model evaluation

For each phosphorylation site, the performance was evaluated by the Pearson’s correlation between observed and predicted abundances across all samples. Then the average correlation of all phosphorylation sites was used as the primary evaluation score. In addition, the Normalized Root Mean Square Error (NRMSE) was used as the secondary metric to compare models.

The formula for computing the Pearson correlation r is as follows:

r=1nobs−1∑i=1nobs(xi−x¯)(yi−y¯)SxSy

The formula for computing NRMSE is as follows:

NRMSE=∑i=1nobs(yi−xi)2/nobsymax−ymin

The observed and predicted values are denoted by y and x, respectively. Sy and Sx are their standard deviations. For each protein, nobs is the number of observed samples, and ymax and ymin are the maximal and minimal value across all samples.

2.8 Statistical analysis

For each model, we randomly sampled 1000 phosphorylation sites without replacement to calculate the Pearson’s correlation and NRMSE for a total of 50 times using R (version 3.4.3). In this way, 50 values of correlation or NRMSE were obtained. Then the two-sided Wilcoxon signed-rank test was performed to compare the performances of two models.

3 Results

3.1 Overview of the phosphoproteomic data

The phosphoproteomic data contained 31 981 phosphorylation sites (from 4763 unique proteins) and 10 057 phosphorylation sites (from 2865 unique proteins) in breast and ovarian cancers, respectively. The coverage of breast cancer was much higher and about three times as much as the coverage of ovarian cancer, due to the experimental and analytical differences between the two data providers. In terms of the number of phosphorylation sites, there were three types of observed peptides: (i) mono-phosphorylated, (ii) dual-phosphorylated and (iii) tri-phosphorylated. In both breast and ovarian cancers, the dominant observations came from the mono-phosphorylated peptides (Fig. 2A and B). As we expected, most phosphorylations were found on serine or threonine, and only a small portion (<3%) was tyrosine phosphorylation (Fig. 2C and D). In addition, the number of unique phosphorylation sites greatly varied across proteins, and the overall distributions were shown in Supplementary Figure S1. We further investigated the relationships among multiple phosphorylation sites of the same protein, which had an average correlation of 0.682. This indicates that when phosphorylation sites came from the same parent protein, they were intrinsically correlated. The correlations described in this section were calculated by the observed experimental data, instead of our predictions in following sections. Intriguingly, we found that phosphorylation sites close to each other had stronger correlations (Supplementary Fig. S2). For phosphorylation sites within the distance of 5 amino acids, the average correlation was 0.856 (left bar in Supplementary Fig. S2C). In contrast, for phosphorylation sites far away from each other (more than 50 amino acids), the average correlation was much lower, only 0.613 (right bar in Supplementary Fig. S2C). This observation is consistent with the report that proximal phosphorylation sites have cooperativity and tend to occur as dense clusters (Schweiger and Linial, 2010). Notebly, the data used in this study were steady-state measurements of the proteome and phosphoproteome in cancer samples. However, reversible protein phosphorylation is highly dynamic and the phosphorylation level can change rapidly without any changes in the protein abundance level (Mann et al., 2002; Vogel and Marcotte, 2012). Our models trained on the steady-state data are not suitable for predicting the dynamic phosphoproteome of cells under perturbation.

Fig. 2.

Fig. 2.

Open in a new tab

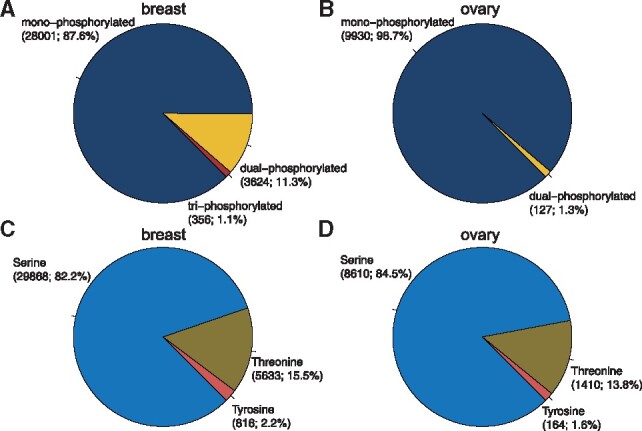
The distributions of different types of phosphorylated peptides and amino acids. Considering the number of phosphorylation sites per peptide, we observed mono-phosphorylated, dual-phosphorylated and tri-phosphorylated peptides in (A) breast and (B) ovary. The major types were the mono-phosphorylated peptides in bother cancer tissues. The tri-phosphorylated peptide was not observed in ovary, which might result from the lower coverage in the ovary dataset. Considering the amino acid types, we observed phosphorylated serine, threonine and tyrosine in both (C) breast and (D) ovarian samples

3.2 Direct approximation for phosphoproteome from multi-omics data

We first tested the performance of three simple models, in which multi-omics data were directly used as approximations. The protein level, the mRNA level and CNV of DNA were used, and the prediction correlation were shown in Figure 3A and B. For both breast and ovarian cancers, the correlations of predictions using CNV or mRNA levels were very low. In contrast, using protein level as approximation had relatively higher correlation around 0.3. This was expected because the phosphorylation sites were derived from their parent proteins. In addition, the NRMSEs between predictions and observations were also calculated and the protein level had low prediction errors (Fig. 3C and D). To test whether the performances were significantly different, the Wilcoxon signed-rank tests were performed and P-values were shown between models. These results indicated that the proteome contained more information than the transcriptome or CNV for predicting the phosphoproteome. We therefore used only protein levels as predictions in our first ‘proteome’ model (Fig. 1B).

Fig. 3.

Fig. 3.

Open in a new tab

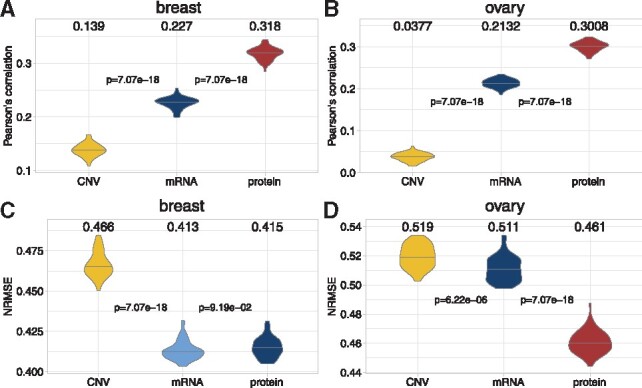
Approximation for phosphoprotein level from CNV, mRNA or protein levels. For each cancer sample, we directly used the CNV, mRNA or protein levels as the approximation for the corresponding phosphoprotein level. The Pearson’s correlations between these approximations and experimental observations were calculated in (A) breast and (B) ovary. The Wilcoxon signed-rank tests were performed for every pair of adjacent models, and the P-values were shown between two violin plots. Similarly, the NRMSE were also calculated in (C) breast and (D) ovary

3.3 Integrating universal protein–protein interactions improves prediction performance

To consider the protein–protein interactions in regulating phosphorylation, we developed a ‘site-specific’ model in which all protein levels were used as features to make predictions (see details in Section 2). When we built this model, a key question was which proteins should be selected as feature proteins. We first selected the top 10, 100 and 1000 expressed proteins, and the results were shown in Supplementary Figure S3. As the number of feature proteins increased, the prediction correlations became higher. We further integrated prior knowledge and selected feature proteins associated with GO terms (GO-0001932 regulation of protein phosphorylation, GO-0006468 protein phosphorylation, GO-0042325 regulation of phosphorylation and GO-0016310 phosphorylation). Intriguingly, compared with the model using all proteins as features, using prior knowledge did not improve performance. These results indicate that protein phosphorylation regulation are complex and involves multiple direct and indirect protein–protein interactions. Our method modeled all possible interactions in an implicit way and achieved higher performance than models using a subset of proteins as features. We further selected top 10, 100 and 1000 proteins with the highest variances across samples (Supplementary Fig. S4). Similarly, the prediction correlation became higher when the number of feature proteins increased. The model with top 1000 proteins with the highest variances achieved comparable performance with the model using all proteins as features.

3.4 Cross-tissue modeling improves prediction performance

We further developed a ‘cross-tissue’ model to investigate the relationship between breast and ovarian phosphoproteome through combining samples (see details in Section 2). This model significantly improved the prediction correlations in both tissues, compare to the single-tissue ‘proteome’ and ‘site-specific’ models (the blue violins in Fig. 4). We also compared the cross-tissue performance against the performance on the held-out datasets used in the final evaluation during the DREAM Proteogenomics Challenge, which were comparable (Supplementary Fig. S5).

Fig. 4.

Fig. 4.

Open in a new tab

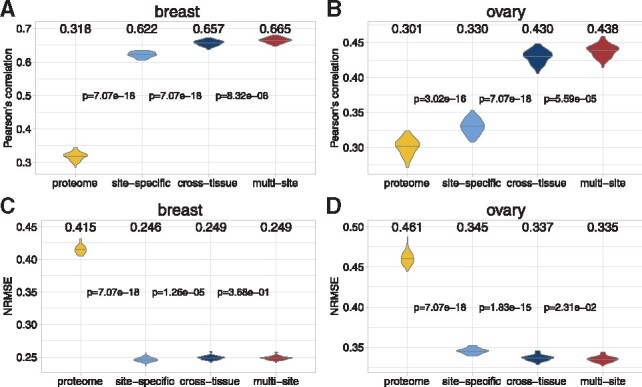
The prediction performance of four models used in our approach. From left to right, the performance of the ‘proteome’, ‘site-specific’, ‘cross-tissue’ and ‘multi-site’ models were compared in violin plots. Among the four models, the ‘site-specific’ and ‘cross-tissue’ models used random forest as the base learner. For the ‘site-specific’ model, the number of input features are 6956 and 3217 respectively in the breast and ovarian cancer. For the ‘cross-tissue’ model, the number of input features is 3147, which is the number of common feature proteins between these two cancer tissues. The Pearson’s correlations between these approximations and experimental observations were calculated in (A) breast and (B) ovary. The Wilcoxon signed-rank tests were performed for every pair of adjacent models, and the P-values were shown between two violin plots. Similarly, the NRMSE were also calculated in (C) breast and (D) ovary

3.5 Leveraging information of multiple phosphorylation sites refines predictions

By carefully examining the phosphoproteomic data and prediction results, we found that phosphorylation sites with more missing observations were relatively harder to predict. In fact, some phosphorylation sites had low occupancy and were not easily detected or mapped to the reference (Dephoure et al., 2013). Therefore, the machine learning models for these hard-to-detect sites were less accurate, due to the missing values. Since multiple phosphorylation sites of the same proteins were correlated, we developed a ‘multi-site’ model to overcome this issue and refine the predictions. In particular, we assembled the predictions for all the phosphorylation sites of a protein based on the quality of the data—a site with less missing values had a larger weight (see details in Section 2). This model further improved the prediction correlations significantly in both cancers (red ‘multi-site’ model in Fig. 4). We also calculated the improvements (Δcorrelation and ΔNRMSE) for phosphorylation sites with different missing rates. As we expected, sites with more missing values had larger increases in correlation and decreases in NRMSE in both cancers (Fig. 5). In summary, by integrating multi-source information, we developed four models (‘proteome’, ‘site-specific’, ‘cross-tissue’ and ‘multi-site’) to predict the phosphoprotein abundances in breast and ovarian cancers.

Fig. 5.

Fig. 5.

Open in a new tab

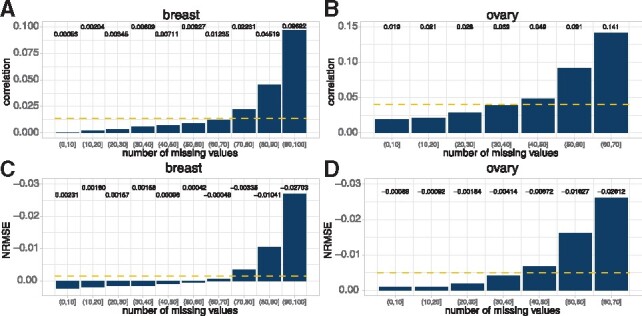
The improvement of phosphorylation sites with different missing rates using the ‘multi-site’ model. The phosphorylation sites were categorized based on the number of missing values in the training data. In general, phosphorylation sites with more missing values gained larger increase in correlation in (A) breast and (B) ovary and larger decrease in NRMSE in (C) breast and (D) ovary. The yellow dashed lines represent the average improvement values. (Color version of this figure is available at Bioinformatics online.)

We further investigated the top features of our models, and compared them with known protein–protein interactions to understand the regulation of protein phosphorylation. For each phosphorylation site, we first calculated the feature importance of all feature proteins and selected top 100 contributing proteins. Then we downloaded the interaction dataset from BioGRID (Release 3.5.174; organism: Homo sapiens) (Stark et al., 2006). For each phosphorylated protein of interest, we compared the top 100 contributing proteins from our model with the known interacting proteins annotated by the BioGRID dataset. Fisher’s exact test was performed to calculate the significance of enrichment. We found 741 (breast cancer) and 160 (ovarian cancer) cases in which the top feature proteins were significantly overlapped with the reported interacting proteins. The P-values, overlapping proteins and top 100 feature proteins of these cases are provided as Supplementary Material. In these cases, the random forest model captured and leveraged the relationship between phosphorylation sites and the regulating proteins. In other cases, although the top feature proteins were not significantly overlapped with the known interacting proteins, they may potentially become interacting candidates to be validated experimentally in the future.

4 Discussion

With the advancements of omics technologies, our understanding of regulatory mechanisms underlying human diseases has been revolutionized over the past decades (Karczewski and Snyder, 2018). Multi-omics based approaches have been used in clinical cancer research and precision medicine (Yoo et al., 2018; Yu and Snyder, 2016). However, a key question in basic research is how to understand the relationships among the observed multi-omics data. Many pioneering efforts have been made to study the genomic, transcriptomic, proteomic and phosphoproteomic characteristics of various cancers (Mertins et al., 2016; Robertson et al., 2017; Zhang et al., 2014; Zhang et al., 2016). Yet the observed correlations between mRNA and protein levels across cancer samples are typically very low (Vogel and Marcotte, 2012), and there is a lack of investigations into the correlation between proteomic and phosphoproteomic data. This indicates that there are many unknown elements in regulating the protein and phosphoprotein abundances at the system level.

In this work, we characterized the correlations between the CNV, mRNA, protein and phosphoprotein levels in breast and ovarian cancer samples, and developed a state-of-the-art approach for predicting phosphoproteome. Notably, instead of using a subset of proteins defined by phosphorylation-related GO terms, we used all proteins as features to achieve better performance. This indicates that the associations among proteins universally exist, and using prior knowledge to define a subset of feature proteins may not be helpful in terms of predicting phosphoproteome. Moreover, we developed a novel strategy to harness the cross-tissue regulatory information, which has not been investigated in the field of phosphoproteome. The ideas embedded in our models are insightful for future omics approaches development in cancer research.

Supplementary Material

btz639_Supplementary_Data
Click here for additional data file. (936KB, zip)

Acknowledgements

We thank the NCI-CPTAC Proteogenomics DREAM Challenge data contributors and organizers: The Clinical Proteomic Tumor Analysis Consortium (CPTAC), Mi Yang (RWTH Aachen University), Zhi Li (New York University), Francesca Petralia (Mount Sinai), Pei Wang (Mount Sinai), Tom Yu (Sage Bionetworks), Xiaoyu Song (Mount Sinai), Reza Ghanadan (DARPA), Henry Rodriguez (NCI), Samuel Payne (PNNL), Gustavo Stolovitzky (IBM Research & Mount Sinai), Paul Boutros (Ontario Institute of Cancer Research), David Fenyo (New York University), Julio Saez-Rodriguez (RWTH-Aachen University & EMBL-EBI). We thank Dr Gilbert Omenn for discussions about proteome and phosphoproteome in cancers.

Author contribution

HL and YG implemented the top-scoring algorithm. HL carried out post-challenge analysis and experiments. HL wrote the manuscript. All authors read and approved the manuscript.

Funding

This work was supported by NSF-US14-PAF07599 (CAREER: On-line Service for Predicting Protein Phosphorylation Dynamics Under Unseen Perturbations NSF) and 19AMTG34850176 (American Heart Association and Amazon Web Services3.0 Data Grant Portfolio: Artificial Intelligence and Machine Learning Training Grants).

Conflict of Interest: Y.G. receives personal payment from Eli Lilly and Company, Genentech Inc, F. Hoffmann-La Roche AG and Cleerly Inc; holds equity shares at Cleerly Inc and Ann Arbor Algorithms Inc; receives research support from Merck KGaA as research contracts and Ryss Tech as unrestricted donations.

Contributor Information

Hongyang Li, Department of Computational Medicine and Bioinformatics, University of Michigan, Ann Arbor, MI 48109, USA.

Yuanfang Guan, Department of Computational Medicine and Bioinformatics, University of Michigan, Ann Arbor, MI 48109, USA.

References

  1. Ardito F.  et al. (2017) The crucial role of protein phosphorylation in cell signaling and its use as targeted therapy (Review). Int. J. Mol. Med., 40, 271–280. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Aslam B.  et al. (2017) Proteomics: technologies and their Applications. J. Chromatogr. Sci., 55, 182–196. [DOI] [PubMed] [Google Scholar]
  3. Breiman L. (2001) 10.1023/A: 1010933404324. Mach. Learn., 45, 5–32.
  4. Cao M.  et al. (2018) Computational prediction and analysis of species-specific fungi phosphorylation via feature optimization strategy. Brief. Bioinform., 10.1093/bib/bby122. [DOI] [PubMed] [Google Scholar]
  5. Dephoure N.  et al. (2013) Mapping and analysis of phosphorylation sites: a quick guide for cell biologists. Mol. Biol. Cell, 24, 535–542. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Dimitrakopoulos C.  et al. (2018) Network-based integration of multi-omics data for prioritizing cancer genes. Bioinformatics, 34, 2441–2448. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Ellis M.J.  et al. (2013) Connecting genomic alterations to cancer biology with proteomics: the NCI Clinical Proteomic Tumor Analysis Consortium. Cancer Discov., 3, 1108–1112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Grimsrud P.A.  et al. (2010) Phosphoproteomics for the masses. ACS Chem. Biol., 5, 105–119. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Guan Y. (2019) Waking up to data challenges. Nat. Mach. Intell., 1, 67–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Hjerrild M., Gammeltoft S. (2006) Phosphoproteomics toolbox: computational biology, protein chemistry and mass spectrometry. FEBS Lett., 580, 4764–4770. [DOI] [PubMed] [Google Scholar]
  11. Hunter T. (1995) Protein kinases and phosphatases: the Yin and Yang of protein phosphorylation and signaling. Cell, 80, 225–236. [DOI] [PubMed] [Google Scholar]
  12. Hunter T. (2012) Why nature chose phosphate to modify proteins. Philos. Trans. R. Soc. Lond. B Biol. Sci., 367, 2513–2516. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Kan Z.  et al. (2018) Multi-omics profiling of younger Asian breast cancers reveals distinctive molecular signatures. Nat. Commun., 9, 1725. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Karczewski K.J., Snyder M.P. (2018) Integrative omics for health and disease. Nat. Rev. Genet., 19, 299–310. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Li X.  et al. (2013) Elucidating human phosphatase-substrate networks. Sci. Signal, 6, rs10.. [DOI] [PubMed] [Google Scholar]
  16. Li H.  et al. (2018a) Accurate prediction of personalized olfactory perception from large-scale chemoinformatic features. Gigascience, 7, 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Li H.  et al. (2018b) Anchor: trans-cell type prediction of transcription factor binding sites. Genome Res, 29, 281–292. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Li H.  et al. (2018c) Network Propagation Predicts Drug Synergy in Cancers. Cancer Res., 78, 5446–5457. [DOI] [PubMed] [Google Scholar]
  19. Li H.  et al. (2018d) TAIJI: approaching experimental replicates-level accuracy for drug synergy prediction. Bioinformatics, 35, 2338–2339. [DOI] [PubMed] [Google Scholar]
  20. Liu J.J.  et al. (2018a) In vivo brain GPCR signaling elucidated by phosphoproteomics. Science, 360, eaao4927. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Liu J.J.  et al. (2018b) Phosphoproteomic approach for agonist-specific signaling in mouse brains: mTOR pathway is involved in κ opioid aversion. Neuropsychopharmacology, 44, 939. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Luo F.  et al. (2019) DeepPhos: prediction of protein phosphorylation sites with deep learning. Bioinformatics, 35, 2766. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Mann M.  et al. (2002) Analysis of protein phosphorylation using mass spectrometry: deciphering the phosphoproteome. Trends Biotechnol., 20, 261–268. [DOI] [PubMed] [Google Scholar]
  24. McGrail D.J.  et al. (2018) Multi-omics analysis reveals neoantigen-independent immune cell infiltration in copy-number driven cancers. Nat. Commun., 9, 1317. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Mertins P.  et al. (2016) Proteogenomics connects somatic mutations to signalling in breast cancer. Nature, 534, 55–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Pawson T., Scott J.D. (2005) Protein phosphorylation in signaling—50 years and counting. Trends Biochem. Sci., 30, 286–290. [DOI] [PubMed] [Google Scholar]
  27. Post H.  et al. (2017) Robust, sensitive, and automated phosphopeptide enrichment optimized for low sample amounts applied to primary hippocampal neurons. J. Proteome Res., 16, 728–737. [DOI] [PubMed] [Google Scholar]
  28. Ramroop J.R.  et al. (2018) Impact of phosphoproteomics in the era of precision medicine for prostate cancer. Front. Oncol., 8, 28.. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Rappoport N., Shamir R. (2018) Multi-omic and multi-view clustering algorithms: review and cancer benchmark. Nucleic Acids Res., 46, 10546–10562. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Robertson A.G.  et al. (2017) Comprehensive molecular characterization of muscle-invasive bladder cancer. Cell, 171, 540–556.e25. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Schweiger R., Linial M. (2010) Cooperativity within proximal phosphorylation sites is revealed from large-scale proteomics data. Biol. Direct., 5, 6.. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Stark C.  et al. (2006) BioGRID: a general repository for interaction datasets. Nucleic Acids Res., 34, D535–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Stolovitzky G.  et al. (2007) Dialogue on reverse-engineering assessment and methods: the DREAM of high-throughput pathway inference. Ann. N. Y. Acad. Sci, 1115, 1–22. [DOI] [PubMed] [Google Scholar]
  34. Tan H.  et al. (2017) Integrative proteomics and phosphoproteomics profiling reveals dynamic signaling networks and bioenergetics pathways underlying T cell activation. Immunity, 46, 488–503. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Trost B., Kusalik A. (2011) Computational prediction of eukaryotic phosphorylation sites. Bioinformatics, 27, 2927–2935. [DOI] [PubMed] [Google Scholar]
  36. Vlastaridis P.  et al. (2017) Estimating the total number of phosphoproteins and phosphorylation sites in eukaryotic proteomes. Gigascience, 6, 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Vogel C., Marcotte E.M. (2012) Insights into the regulation of protein abundance from proteomic and transcriptomic analyses. Nat. Rev. Genet., 13, 227–232. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Wei L.  et al. (2017) PhosPred-RF: a novel sequence-based predictor for phosphorylation sites using sequential information only. IEEE Trans. Nanobiosci., 16, 240–247. [DOI] [PubMed] [Google Scholar]
  39. Wilson G.M.  et al. (2018) Identifying novel signaling pathways: an exercise scientists guide to phosphoproteomics. Exerc. Sport Sci. Rev., 46, 76–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Wiredja D.D.  et al. (2018) Abstract 2698: phosphoproteomics-guided anticancer drug combination design with a novel small-molecule PP2A activator. Cancer Res., 78, 2698–2698. [Google Scholar]
  41. Wu X.  et al. (2019) Integrating phosphoproteomics into kinase-targeted cancer therapies in precision medicine. J. Proteomics, 191, 68–79. [DOI] [PubMed] [Google Scholar]
  42. Yang W.  et al. (2018) Personalization of prostate cancer therapy through phosphoproteomics. Nat. Rev. Urol., 15, 483–497. [DOI] [PubMed] [Google Scholar]
  43. Yoo B.C.  et al. (2018) Clinical multi-omics strategies for the effective cancer management. J. Proteomics, 188, 97–106. [DOI] [PubMed] [Google Scholar]
  44. Yu K.-H., Snyder M. (2016) Omics profiling in precision oncology. Mol. Cell. Proteomics, 15, 2525–2536. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Zagorac I.  et al. (2018) In vivo phosphoproteomics reveals kinase activity profiles that predict treatment outcome in triple-negative breast cancer. Nat. Commun., 9, 3501.. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Zhang B.  et al. (2014) Proteogenomic characterization of human colon and rectal cancer. Nature, 513, 382–387. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Zhang H.  et al. (2016) Integrated proteogenomic characterization of human high-grade serous ovarian cancer. Cell, 166, 755–765. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

btz639_Supplementary_Data
Click here for additional data file. (936KB, zip)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES