A Deep Spatial Context Guided Framework for Infant Brain Subcortical Segmentation

Abstract

Accurate subcortical segmentation of infant brain magnetic resonance (MR) images is crucial for studying early subcortical structural growth patterns and related diseases diagnosis. However, dynamic intensity changes, low tissue contrast, and small subcortical size of infant brain MR images make subcortical segmentation a challenging task. In this paper, we propose a spatial context guided, coarse-to-fine deep convolutional neural network (CNN) based framework for accurate infant subcortical segmentation. At the coarse stage, we propose a signed distance map (SDM) learning UNet (SDM-UNet) to predict SDMs from the original multi-modal images, including T1w, T2w, and T1w/T2w images. By doing this, the spatial context information, including the relative position information across different structures and the shape information of the segmented structures contained in the ground-truth SDMs, is used for supervising the SDM-UNet to remedy the bad influence from the low tissue contrast in infant brain MR images and generate high-quality SDMs. To improve the robustness to outliers, a Correntropy based loss is introduced in SDM-UNet to penalize the difference between the ground-truth SDMs and predicted SDMs in training. At the fine stage, the predicted SDMs, which contains spatial context information of subcortical structures, are combined with the multi-modal images, and then fed into a multi-source and multi-path UNet (M2-UNet) for delivering refined segmentation. We validate our method on an infant brain MR image dataset with 24 scans by evaluating the Dice ratio between our segmentation and the manual delineation. Compared to four state-of-the-art methods, our method consistently achieves better performances in both qualitative and quantitative evaluations.

1. Introduction

Accurate segmentation of subcortical structures from the magnetic resonance (MR) brain images plays an important role in various neuroimaging studies [1–3]. As manual delineation of subcortical structures is very time-consuming, expertise needed, and difficult to reproduce, many previous studies have put efforts into automatic segmentation and achieved significant progress for adult brain MR images [4–7]. However, as shown in Fig. 1, the automatic subcortical segmentation in the infant brain MR images is still challenging, due to their dynamic intensity changes, low tissue contrast, and small structural size [8]. Fully automatic subcortical segmentation methods in infants are urgently needed for many neurodevelopmental researches, such as studying the early growth pattern of subcortical structures [9–11] and the diagnosis of related brain disorders [12].

Fig. 1.

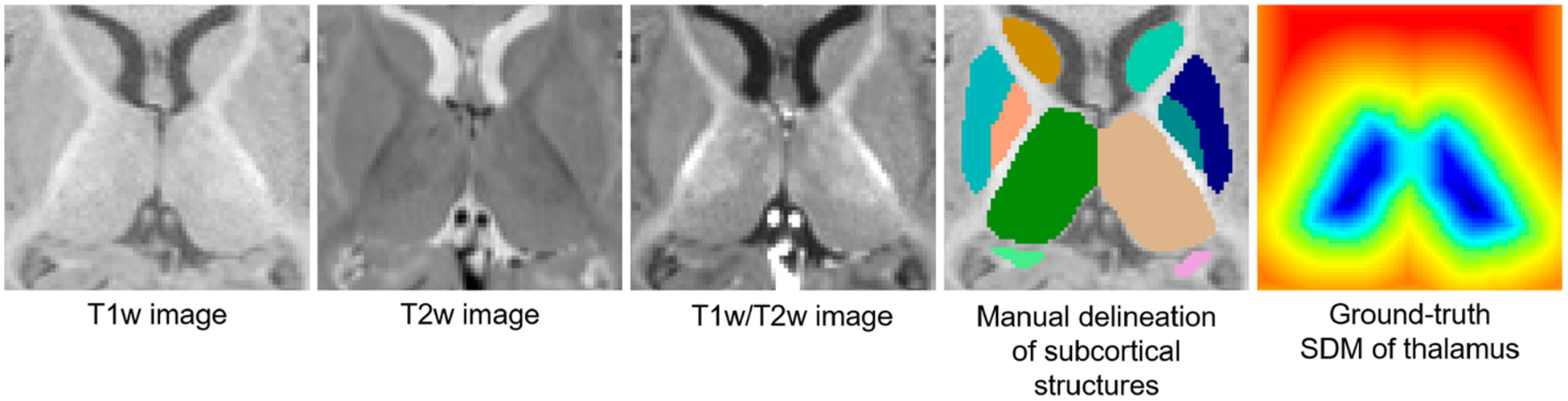
T1w, T2w, and T1w/T2w images of a 6-month subject, the associated manual delineation, and the ground-truth signed distance map (SDM) of the thalamus. Evidently, the boundaries of subcortical structures are fuzzy due to the low contrast in T1w and T2w images. In the T1w/T2w image, the contrast of tissues increased; thus, more distinguishable boundaries can be observed. The ground-truth SDM of each subcortical structure is calculated from the manual delineation.

Recently, the context-guided convolutional neural networks (CNN) based methods have achieved many successes in medical image segmentation tasks [13,14]. These methods try to use the distance maps, which encodes the spatial context information, including the position, shape, and relationship among different segmentation targets, to improve the segmentation accuracy. However, their distance maps are constructed based on the intermediate segmentation results, which may accumulate the segmentation errors to the constructed distance maps. With the inaccurately constructed distance maps to guide the segmentation, the segmentation performance would be degraded. To address this issue, [15] proposed to directly generate the signed distance map (SDM) in a regressionbased network. Then, the boundary of the segmentation target can be computed through the Heaviside function. In doing so, the context information contained in the ground-truth SDMs can be used to directly supervise the network to generate high-quality segmentation results. In [15], the L₁ loss between the predicted SDM and the ground-truth SDM was used for the training, thus improving the robustness of the network. However, the L₁ loss is non-differentiable at zero and may lead to an unstable training process in multi-class segmentation tasks [16], which is thus not suitable for the subcortical segmentation task.

Motivated by these works, in this paper, we propose a spatial context guided, coarse-to-fine deep CNN based framework for accurate 3D subcortical segmentation on infant brain MR images. At the coarse stage, a SDM learning UNet (SDM-UNet) is proposed to directly learn the SDM of each subcortical structure from the original multi-modal MR images, including the T1w, T2w, and T1w/T2w images. In this way, the proposed SDM-UNet can leverage the spatial context information, including the relative position information across different subcortical structures and the shape information of the segmented subcortical structures contained in the ground-truth SDMs, to mitigate the bad influence from the low tissue contrast in infant brain MR images and generate high-quality SDMs. Meanwhile, a Correntropy based loss [17] is introduced in the SDM-UNet to further improve the robustness to outliers under the premise of a stable training process. At the fine stage, a multi-source and multi-path UNet (M2-UNet) is built to rationally encode and effectively fuse the multi-modal information and the spatial context information, which is included in the previously predicted SDMs, to produce the refined subcortical segmentation results. To our best knowledge, this is the first work of using spatial context information for the segmentation of the subcortical structures in infant brain MR images.

2. Method

The framework of our method is presented in Fig. 2, which includes two networks for two stages, respectively. In the following, we will introduce each stage and its corresponding network in detail.

Fig. 2.

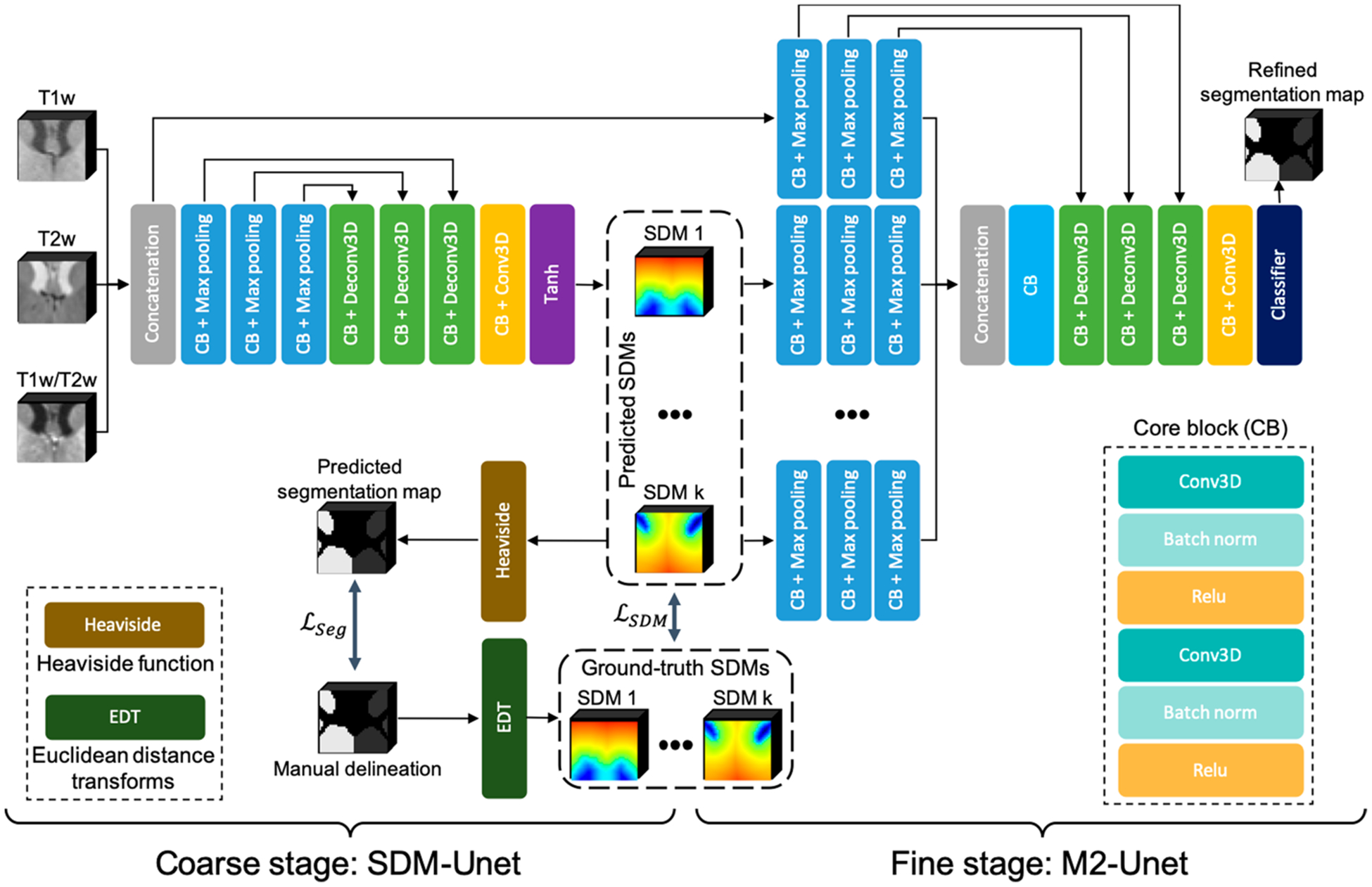
A schematic illustration of the proposed framework, consisting of SDM-UNet at coarse stage and M2-UNet at fine stage.

Coarse Stage SDM-UNet:

To generate high-quality SDMs for improving the segmentation performance in the fine stage, we proposed a SDM learning UNet (SDM-UNet) to directly learn the SDM of each subcortical structure from multi-modal MR images, including T1w, T2w, and T1w/T2w images. By doing this, we can use the spatial context information contained in the ground-truth SDMs to supervise the SDM-UNet, which can help alleviate the bad influence from the low tissue contrast in the infant brain MR images and achieve superior performance on the estimation of SDMs, where the ground-truth SDMs are calculated from the manual delineations via the Euclidean distance transforms. Meanwhile, we can also precisely convert the SDMs to the segmentation maps through the Heaviside function. Therefore, during the training, we convert the predicted SDMs to the predicted segmentation maps and introduce a segmentation loss to penalize the difference between the manual delineations and the predicted segmentation maps to further improve the performance of the proposed SDM-UNet.

The proposed SDM-UNet has an encoder-decoder architecture, which is shown in Fig. 2, and the multi-modal MR images are used as multi-channel input. Skip connections are employed to recover essential details that are possibly lost in the down-sampling process of the encoder.

For a specific subcortical structure in the 3D image, its corresponding SDM can be computed using the following formula, which is a mapping from ${ℝ}^3$ to $ℝ$:

$$\varphi (\text{x})=\{\begin{array}{r}\hfill 0,\text{x}\in \mathcal{B}\\ \hfill -\underset{\text{y}\in \mathcal{B}}{\text{inf}}\Vert \text{x}-\text{y}{\Vert }_2,\text{x}\in {\Omega }_{\text{in}}\\ \hfill +\underset{\text{y}\in \mathcal{B}}{\text{inf}}\Vert \text{x}-\text{y}{\Vert }_2,\text{x}\in {\Omega }_{\text{out}}\end{array}$$ (1)

where x is the coordinate of any point in the 3D image; y is the coordinate of any point on the subcortical structure boundary $\mathcal{B}$, Ω_in and Ω_out denote the region inside (negative value) and outside (positive value) a subcortical structure, respectively. Based on this definition, we can use the Euclidean distance transforms to calculate the ground-truth SDMs of each subcortical structure from the manual delineation.

Once the ground-truth SDMs are calculated, they can be introduced into a SDM learning loss, which encourages the SDM-UNet to predict the SDMs from the original multi-modal MR images. In the learning of the SDMs, the conventional ways [15,18] use the L₁ loss instead of L₂ loss to achieve better robustness to outliers. However, L₁ loss is not differentiable at zero, which severely reduces the training stability. To alleviate the impact of outliers and overcome the shortage of L₁ loss, we apply a Correntropy based loss (Closs) [19] to penalize the difference between the predicted and the ground-truth SDM. Correntropy is a nonlinear distance measure in the original input space, and defines an L₂ distance in kernel space by mapping the input space to a reproducing kernel Hilbert space (RKHS) [20]. For a K-class segmentation task, the SDM learning loss is defined as follows:

$${\mathcal{L}}_{\text{SDM}}=\sum _{k=1}^K\left(1-\text{exp }\left(-\frac{{\left({\text{p}}_k-{\text{q}}_k\right)}^2}{2{\sigma }^2}\right)\right),$$ (2)

where σ is the tunable kernel bandwidth, p_k and q_k represent the predicted and ground-truth SDM belonging to the k-th class. Compared to the L₁ or L₂ norm-based similarity losses, the Correntropy based loss is not only robust to outliers but also stable in training because it is differentiable everywhere [21].

To further utilize the label information in the manual delineation, we convert the predicted SDM to a predicted segmentation map via a smooth approximation of the Heaviside function [22], and introduce a segmentation loss to help improve the prediction of the SDM. We use the following smooth approximation of the Heaviside function to obtain the predicted segmentation maps:

$${\text{s}}_k=\frac{1}{1+e^{-{\text{p}}_k/m}},$$ (3)

where s_k denotes the predicted segmentation map belonging to the k-th class, and m is an approximation parameter. A larger m means a closer approximation. Once the predicted segmentation maps are obtained, the Dice loss [23] is used as the segmentation loss to measure the overlapping between the predicted segmentation maps and the manual delineations:

$${\mathcal{L}}_{\text{Seg}}=\sum _{k=1}^K\left(1-\frac{2\sum _{i=1}^N{\text{s}}_{k,i}{\text{t}}_{k,i}}{\sum _{i=1}^N{\text{s}}_{k,i}+\sum _{i=1}^N{\text{t}}_{k,i}}\right),$$ (4)

where N is the number of voxels, t_k,i and s_k,i represent the i-th voxel in the k-th manual delineation and predicted segmentation map, respectively.

By integrating the above loss terms, the joint loss ${\mathcal{L}}_{\text{SDM-UNet}}$ is defined as:

$${\mathcal{L}}_{\text{SDM-UNet}}={\mathcal{L}}_{\text{SDM}}+\lambda {\mathcal{L}}_{\text{Seg}},$$ (5)

where λ is the loss weight. By minimizing this loss, the proposed SDM-UNet can be stably trained to generate high-quality SDM, which is used as the spatial context information to guide the training of the following M2-UNet to further improve the segmentation accuracy.

Fine Stage M2-UNet:

In order to leverage the spatial context information generated by SDM-UNet, we propose a multi-source and multi-path UNet, namely M2-UNet, at the fine stage to achieve the refined segmentation. The proposed M2-UNet can effectively integrate the multi-modal information and the spatial context information by encoding the multi-modal MR images and SDMs through different encoder paths, which is detailed as follows.

The input of the M2-UNet includes two parts: a) the original multi-modal MR images, which are used as multi-channel input; b) the predicted SDMs from the coarse stage. Different from the multi-modal MR images, the SDMs of different subcortical structures illustrate distinct spatial context information. Therefore, in order to effectively integrate the spatial context information of the subcortical structures, we propose to construct an individual encoder path for the SDMs of each subcortical structure, which can make full use of each encoder path to better extract the high-level features of each subcortical structure.

As the extracted high-level feature maps could better complement each other than the source images [13], we propose to perform a cross-source convolution to aggregate the outputs of all encoder paths. Specifically, the outputs of each encoder path are concatenated and fed to an additional convolutional layer at the beginning of the decoder path. As the cross-source convolution performs across different sources, it assigns different weights to each source and merges the extracted high-level features in the output feature maps. In doing so, the proposed cross-source convolution layer can model the relationships across different source images and achieve a better fusion of the extracted high-level features.

Moreover, because there are total (K + 1) encoder paths in the M2-UNet, employing the skip connections for each encoder path will significantly increase the complexity of the network. It is worth noting that, compared to the SDMs of each subcortical structure, multi-modal MR images accommodate exhaustive intensity information [24]. Hence, in order to recover more useful details with less complicated network architecture, we only employ the skip connections for the encoder path of the multi-modal MR images. Herein, we still use the aforementioned Dice loss for the M2-UNet training.

3. Experiments

Dataset and Experimental Setup:

The proposed network is evaluated on a real infant dataset, which includes 24 infant MRI scans (with both T1w and T2w images) from the UNC/UMN Baby Connectome Project (BCP) [25]. The resolution of the T1w and T2w images is 0.8 × 0.8 × 0.8mm³. These 24 subjects are divided into two age groups (6 and 12 months), and each group has 12 scans. The subcortical structures of all 24 subjects are manually delineated by two experienced experts. For each subject, the T2w image was linearly aligned onto the T1w image [26]. Then, T1w/T2w image is obtained by dividing the T1w image by the T2w image at each voxel. Intensity inhomogeneity is corrected in all images by [27]. To simplify the network, we merged the bilaterally symmetric subcortical structures into six classes (thalamus, caudate, putamen, pallidum, hippocampus, and amygdala). We performed random flipping of image patches for augmenting the data. In order to validate our method, a stratified 5-fold cross-validation strategy is employed, and each fold consists of 16 training images, 4 validation images, and 4 testing images.

Parameters of SDM-UNet and M2-UNet are experimentally set as: learning rate of Adam optimizer = 0.0001, kernel size of each network = 4, stride = 2, λ = 0.1, and σ = 0.8. m is set to 1500. The segmentation was performed in a patch-wise manner, with the patch size of 32 × 32 × 32.

The proposed method was compared with the following methods: a commonly used software package FIRST in FSL [26]; three state-of-the-art deep learning segmentation methods including V-Net [23], LiviaNet [4], SA-Net [15] and the method involving only the proposed SDM-UNet. In order to ensure a fair comparison, the three MR modalities are used as multi-channel input to all learning-based methods. The segmentation results were quantitatively evaluated by the Dice similarity coefficient (DSC) (mean and standard deviation).

Evaluation Results:

In Fig. 3, we visually compared the subcortical segmentation results of the manual delineation and the six automatic methods on a 6-month T1w infant brain MR image. Evidently, the proposed method obtained overall segmentation results more consistent with the manual results. Meanwhile, the proposed method and SDM-UNet can more precisely segment the amygdala and hippocampus than the other competing methods. Compared to SDM-UNet, the proposed method generates segmentation results that are more accurate for most of the subcortical structures, suggesting that the proposed M2-UNet exerts a positive effect in improving the segmentation performance.

Fig. 3.

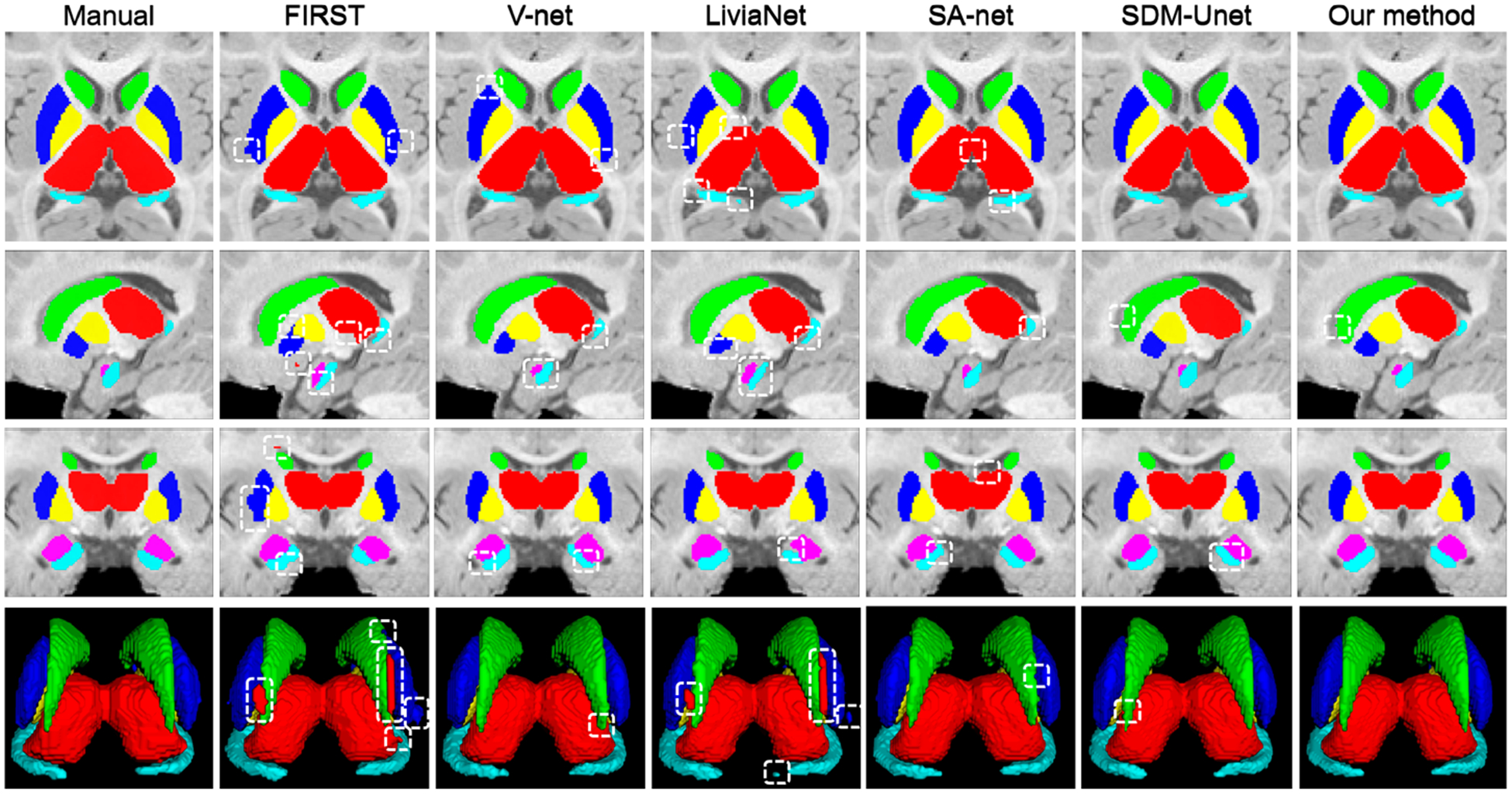
Visual comparison of the segmentation results of the six subcortical structures on a 6-month T1w image, obtained from manual delineation and six automatic methods. The apparent segmentation errors are indicated by boxes.

The DSC values of the segmentation of the six subcortical structures are summarized in Table 1, where we have at least three observations.

Table 1.

The DSC values of the six subcortical structures in each age group.

	Month	FIRST	V-Net	LiviaNet	SA-Net	SDM-UNet	Our method
Thalamus	6	83.85 ± 2.73	94.65 ± 0.68	94.89 ± 0.91	94.12 ± 0.32	94.33 ± 0.36	96.10 ± 0.22
	12	87.37 ± 1.52	95.26 ± 0.42	94.75 ± 1.34	95.14 ± 0.58	95.00 ± 0.48	96.23 ± 0.32
Caudate	6	84.62 ± 1.61	88.45 ± 1.46	92.35 ± 1.28	92.39 ± 0.42	92.36 ± 0.33	94.25 ± 0.54
	12	87.76 ± 1.59	92.78 ± 0.46	91.78 ± 1.89	94.21 ± 0.77	94.12 ± 0.35	94.71 ± 0.43
Putamen	6	74.76 ± 1.93	89.94 ± 2.63	90.69 ± 1.66	91.64 ± 1.26	92.48 ± 1.31	94.60 ± 1.11
	12	83.12 ± 2.82	92.86 ± 1.29	92.44 ± 1.40	93.26 ± 0.82	93.47 ± 0.96	95.51 ± 0.54
Pallidum	6	78.09 ± 2.78	88.35 ± 1.94	89.08 ± 1.82	90.14 ± 1.27	91.01 ± 1.50	92.82 ± 0.98
	12	83.56 ± 1.46	90.72 ± 0.81	90.43 ± 1.22	91.99 ± 0.67	92.23 ± 0.88	94.24 ± 0.91
Hippocampus	6	66.73 ± 4.25	87.27 ± 2.15	86.49 ± 1.46	88.18 ± 1.19	88.71 ± 0.74	90.52 ± 0.86
	12	80.47 ± 2.97	90.14 ± 1.56	90.54 ± 0.89	89.42 ± 1.33	90.34 ± 0.46	92.02 ± 1.28
Amygdala	6	49.33 ± 5.95	83.58 ± 5.99	79.66 ± 3.99	85.79 ± 2.73	86.51 ± 2.89	89.06 ± 1.91
	12	55.12 ± 3.56	85.71 ± 2.41	86.21 ± 2.05	86.20 ± 1.39	87.89 ± 1.31	89.64 ± 1.29
Mean DSC	6	72.90 ± 3.21	88.71 ± 2.48	88.86 ± 1.85	90.38 ± 1.20	90.90 ± 1.19	92.89 ± 0.94
	12	79.56 ± 2.32	91.25 ± 1.16	91.03 ± 1.47	91.70 ± 0.93	92.18 ± 0.74	93.73 ± 0.80

First, compared to the state-of-the-art methods, our method has remarkably better segmentation results for all six subcortical structures in each age group (improved the overall DSC by 2.51% (p−value = 2.3e⁻⁴) and 2.03% (p−value = 1.7e⁻⁵) on 6-month and 12-month images, respectively). Although promising segmentation for amygdala and hippocampus is hard to obtain due to their relatively smaller size, our method still achieves significantly higher DSC values on these two structures (p−value = 1.3e⁻⁴, compared with SA-Net). The results suggest that our method can effectively leverage the spatial context information to improve the segmentation performance.

Second, the DSC values of 6-month images are generally lower than those of 12-month images. This is because the 6-month brain images have the lowest contrast for different subcortical structures, which is conformal with the previous studies [8,28,29]. Meanwhile, the proposed method shows the highest consistency of the segmentation on the 6 and 12 months infant brain MR images. This further implies that incorporating the SDM of each specific subcortical structure can help remedy the bad influence from the low tissue contrast of 6-month MR images and verifies that our method is effective in the task of subcortical segmentation of infant brain MR images.

Third, when compared to state-of-the-art methods, the proposed SDM-UNet achieves better segmentation results (p − value = 1.8e⁻⁴, compared with SA-Net), which indicates that our SDM-UNet can generate more trustworthy SDMs to effectively guide the training of the following M2-UNet to acquire improved segmentation accuracy. Moreover, when compared to SDM-UNet, our method also achieved markedly improved DSC values on all the subcortical structures (from 90.90% to 92.89% (p−value = 5.4e⁻⁶) and 92.18% to 93.73% (p−value = 3.1e⁻⁵) on 6 and 12 months images, respectively), which reveals the effectiveness of the proposed framework in refining the segmentation.

Both the qualitative evaluation in Fig. 3 and the quantitative evaluation in Table 1 suggest that our method yields superior performance on automatic subcortical segmentation of infant brain MR images.

4. Conclusion

In this work, we propose a spatial context guided, coarse-to-fine deep CNN-based framework for the accurate 3D subcortical segmentation in infant brain MR images. At the coarse stage, to mitigate the bad influence from the low tissue contrast in infant brain MR images, we construct a signed distance map (SDM) learning UNet (SDM-UNet), which is supervised by the spatial context information contained in the ground-truth SDMs, to generate high-quality SDMs from the original multi-modal images, including T1w, T2w, and T1w/T2w images. Moreover, a Correntropy based loss is introduced in the SDM-UNet to improve the robustness to the outliers under the premise of a stable training process. At the fine stage, for simultaneously leveraging the multi-modal MR images and the SDMs predicted at the coarse stage to achieve improved segmentation accuracy, a multi-source and multi-path UNet (M2-UNet) is constructed to rationally encode and effectively integrate the multi-modal appearance information and the spatial context information contained in the predicted SDMs. Experimental results demonstrate that, compared to four state-of-the-art methods, our method achieves higher accuracy in the segmentation of subcortical structures of infant brain MR images.