Designing a sustainable closed-loop pharmaceutical supply chain in a competitive market considering demand uncertainty, manufacturer’s brand and waste management

Abstract

Pharmaceutical supply chain (PSC) is one of the most important healthcare supply chains and the recent pandemic (COVID-19) has completely proved it. Also, the environmental and social impacts of PSCs are undeniable due to the daily entrance of a large amount of pharmaceutical waste into the environment. However, studies on closed-loop PSCs (CLPSC) are rarely considered real-world requirements such as competition among diverse brands of manufacturers, the dependency of customers’ demand on products’ price and quality, and diverse reverse flows of end-of-life medicines. In this study, a scenario-based Multi-Objective Mixed-Integer Linear Programming model is developed to design a sustainable CLPSC, which investigates the reverse flows of expired medicines as three classes (must be disposed of, can be remanufactured and can be recycled). To study the competitive market and deal with demand uncertainty, a novel scenario-based game theory model is proposed. The demand function for each brand depends on the price and quality provided. Then, a hybrid solution approach is provided by combining the LP-metrics method with a heuristic algorithm. Furthermore, a real case study is investigated to evaluate the application of the model. Finally, sensitivity analysis and managerial insights are provided. The numerical results show that the proposed classification of reverse flows leads to proper waste management, making money, and reducing both disposal costs and raw material usage. Moreover, competition increases PSCs performance and improves the supply of products to pharmacies.

Supplementary Information

The online version contains supplementary material available at 10.1007/s10479-021-03961-0.

Introduction

Over the last decade, reverse logistics has attracted the attention of many researchers due to the increasing importance of saving raw materials, reducing environmental impacts and government regulations (Kapukaya et al. 2019). Disposal of industrial waste is always one of the most important issues in urban life. With the advent of the industrial revolution, these problems emerged as a result of waste introduction in the environment and its impacts on human health (Krumwiede and Sheu 2002). Recently, with the advent of the coronavirus, waste management of health masks and gloves is a global challenge for managers and government officials.

Since medicines contain complex chemical constituents, medical wastes are classified in the group of the most dangerous waste (Weraikat et al. 2016a). Inefficient methods in the treatment of pharmaceutical waste and lack of reverse logistics initiatives lead to unauthorized disposal and crucial environmental problems including water pollution, soil contamination, and production of toxic and non-toxic wastes (Harijani et al. 2017). Therefore, forming a proper reverse logistics network is essential for PSCs. However, studies on reverse PSCs are still at the conceptual level and do not cover all various return flows of expired medicines (Viegas et al. 2019). In other words, there is still a clear trend toward the development of waste management models in the field of PSCs.

Medicines have a definite lifetime/shelf-life and will be expired/discarded thereafter. These medicines can be stored in pharmacies, or distribution centers (DCs) for a limited time. Nevertheless, they may expire in pharmacies before being delivered to customers. So, there is a serious risk of selling outdated medicines in pharmacies (Narayana et al. 2019). A proper reverse logistics is therefore required to collect outdated medicines to recycle, remanufacture or destroy them by using specific methods. Since the performance of forward and reverse supply chains (SC) are highly correlated, appropriate integration of both forward and reverse flows is imperative (Vahdani et al. 2012). This way, a CLPSC has been introduced to merge forward and reverse flows. An efficient CLPSC structure helps to reduce the negative environmental impacts by adopting eco-friendly transportation systems and collecting industrial wastes (Amin and Zhang 2013). Moreover, in recent years, governmental laws and regulatory requirements for the disposal of pharmaceutical products on one hand, and social responsibilities, economic benefits, and gaining public image, on the other hand, have forced companies in competitive markets to focus on environmental and social issues as well as promoting their sustainable behavior (Kumar et al. 2019).

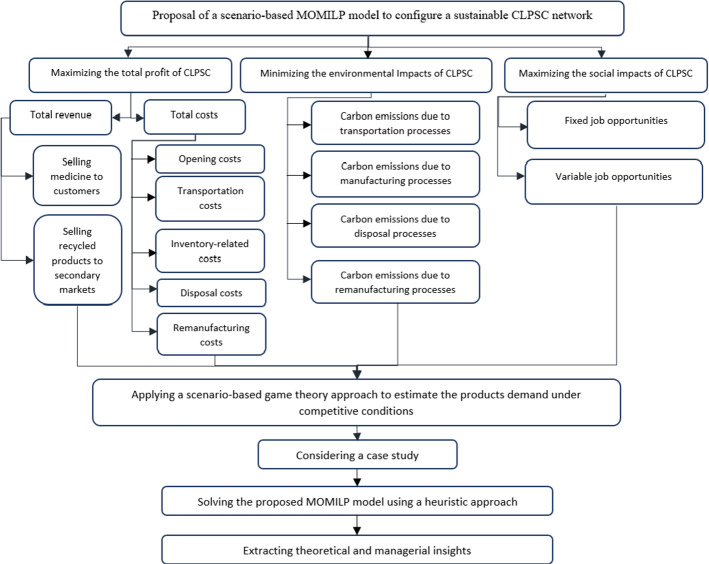
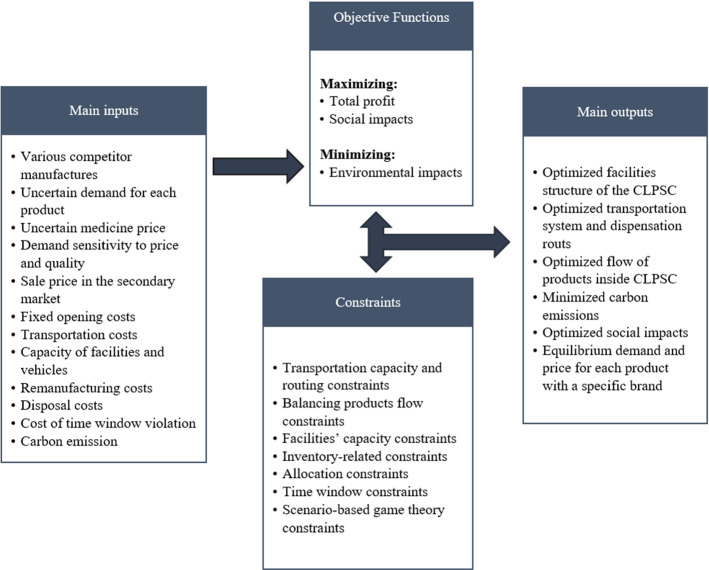
In this study, a scenario-based MOMILP model is proposed to design a sustainable multi-echelon CLPSC network. While there is a broad range of studies dedicated to PSC management, to the best of our knowledge, the problem of managing a sustainable closed-loop PSC considering some main real-world features such as different manufacturers’ brands, different reverse flows, the dependence of demand on quality and price, and competition in the market is rare. The proposed model aims to address the aforementioned features while maximizing the total profit, minimizing environmental damages and optimizing the social impacts of the CLPSC. This research applies a scenario-based game theory approach to deal with demand uncertainty, which is significant and can stabilize the competitive position of chain members. The proposed multi-objective model is then converted to a single-objective form using the LP-metrics method. Due to the complexity of the proposed model, a heuristic approach is applied to solve the model, especially in large scales. The framework of the research problem is depicted in Fig. 1.

Fig. 1.

Framework of the present research

The remainder of the paper is organized as follows. In Sect. 2 review of relevant studies is provided. Section 3 explains the research framework, assumptions, and the proposed model. Section 4 describes the solution methodology. In Sect. 5, a real case study and the numerical results are presented. Finally, Sect. 6 presents conclusions about the findings of the research and future directions.

Literature review

This section dedicates to investigate some related previous researches in the literature along with research gaps in two separate sub-sections.

Related studies

The PSC is one of the most sophisticated and critical SCs which is directly related to the life and health of people. PSC faces many challenges, such as inventory management, waste management, insufficient and uncertain information on demand, inventory shortage, and the expiration of medicines (Chen et al. 2019). Many studies have addressed these challenges in PSC models to some extent. Zandieh et al. (2018) studied a four-echelon PSC designed to minimize total cost and environmental gas emissions as well as maximize social welfare by considering the unemployment ratio in local and main DCs as regional factors. Zahiri et al. (2017) designed a PSC network under uncertainty, in which many backup technologies were utilized to manufacture products. The model aimed to minimize total cost, maximize social effects and minimize environmental impacts as well as non-resiliency. By considering a deterministic demand function, Timajchi et al. (2019) introduced an inventory-routing model for a PSC, which consisted of several hospitals and a radio-pharmacy center. Some main features embedded in the Timajchi et al. (2019)’s model are backordered demand, lost sales, accident risk, and product’s deterioration. Franco and Alfonso-Lizarazo (2019) proposed two mixed-integer programming models that the first one considered PSC costs as well as the products expiration date. While the second model tried to achieve the best expiration dates of required products to minimize the number of expired medicines. In Mousazadeh et al. (2015), TH and ɛ-constraint methods were applied to gain strategic and tactical results. Minimizing total cost and unmet demand were aimed for a pharmaceutical case study with a high degree of epistemic uncertainty.

However, the mentioned articles are mainly targeted sustainability issues, they have less paid attention to suitable planning for treatment of the pharmaceutical wastes. As well, a few numbers of researches have studied the issue of sustainability in the context of CLPSCs. Despite the importance of pharmaceutical products recycling, the issues of reverse logistics and closed-loop of pharmaceutics have rarely been noticed by researchers. In other words, early studies on reverse logistics and environmental issues in PSCs have been more at the conceptual level. Abbas and Farooquie (2018) worked conceptually on returning unsold/unwanted medicines from retailers to producers. These medicines included items that either did not match prescription or they had expired. Susarla and Karimi (2012) presented a Mixed-Integer Linear Programming (MILP) model for a globally integrated network of multinational pharmaceutical enterprises, in which the international tax coefficient and waste disposal were embedded. Narayana et al. (2019) investigated the Taguchi method in a dynamic model of two brands with reverse processes. They derived that contrary to the improvement of reverse characteristics, safety stock cannot affect market flooding alleviating. Taleizadeh et al. (2019) mentioned that customer engagement in the collection of unwanted pharmaceuticals, reselling them with a lower price or transferring them to developing countries can increase SC’s profitability and sustainability. Alizadeh et al. (2020) designed a forward and reverse network for medical disposable supplies to maximize total profit as well as minimize biological risks. Liu et al. (2020) developed a bi-level programming model for recycling pharmaceutical products with governmental encourages considering sustainability aspects. In another study, a multi-mode capacitated transportation system was considered in a forward and backward relief supply chain to minimize total costs and maximize the whole reliability (Madani et al. 2020). Ahlaqqach et al. (2018) designed a CLPSC network to optimize the goals of economics, social responsibility and transportation risk of End Of Life (EOL) pharmaceutical products.

The reverse logistics policies in real-world PSCs are highly sensitive to the product’s characteristics. However, most studies on PSCs’ reverse logistics have neglected this issue and considered return flows as a percentage of the forward flows. Regardless of the returned product’s characteristics, they also assumed that a percentage of the total return flows could be recycled. Weraikat et al. (2016b) investigated a PSC in which the decentralized negotiation process was used for collecting unwanted medicines in customer areas. A constant percentage was considered for products’ recycling in their model. Weraikat et al. (2016b) proposed a reverse PSC to find the effect of customer's incentives on facilitating the return of leftover medicines and improve the sustainability of a drug SC. They divided the return flows into three categories and assigned a percentage of the total return flow to each category to determine the size of each category. To increase the reliability of a four-layer green SC, Moslemi et al. (2017) concentrated on the pharmaceutical products priority for each hospital. As well, the raw materials used to produce medicines could be supplied from either recycled material (with lower prices) or normal ones.

In today’s business environment, the competitive advantages of companies are determined by indicators such as speed and accuracy in service, customer satisfaction and loyalty, lower supply chain costs and ultimately lower finished product costs (Grigoroudis et al. 2013). The goal of pharmacies in the PSC is to fulfill customers’ requirements in a productive way.

However, accurately estimating the demand or flow of a product in a PSC is a complex issue since the demand for medicines is highly sensitive to the price and quality of the product. In today's uncertain world, miscalculation of these parameters can lead to inventories surpluses or shortages in pharmacies. This can not only cause financial losses and a high volume of expired products but also have a significant impact on the patient's health. However, previous studies have rarely attempted to deal with uncertainty in CLPSCs.

Table 1 summarizes some main studies on PSC management. Inspire from real-world and considering Table 1, this paper deals with the problem of “designing and planning a sustainable CLPSC in an uncertain and competitive environment” and by considering some real-world requirements such as (1) sensitivity of customer demand to price and quality, (2) brand diversity of pharmaceutical product, (3) medicine waste management and, (4) integration of forward and backward products’ flows by Simultaneous Pickup and Delivery (SPD) which is rarely addressed in the literature.

Table 1.

Comparison of the proposed study with closely related studies

Paper	Model			Product		Product classification	Period		Capacities		Picked up and delivery	Network structure			Uncertainty	Methods
	SO	BO	MO	S	M		S	M	Facility	Transportation		F	R	CL
Susarla and Karimi (2012)	●				●			●	●			●				LP-metric method
Mousazadeh et al. (2015)		●			●			●	●			●			●	CPLEX
Weraikat et al. (2016a)	●				●			●	●				●			Lagrangian relaxation
Weraikat et al. (2016b)	●				●			●	●				●			Lagrangian relaxation
Zahiri et al. (2017)			●		●			●	●			●			●	Evolutionary algorithm
Moslemi et al. (2017)			●		●			●	●	●				●		NSGAII
Ahlaqqach et al. (2018)			●		●			●	●					●		IBM ILOG CPLEX
Imran et al. (2018)			●		●			●	●			●			●	branch and bound
Nematollahi et al. (2018)		●					●					●				Heuristic
Sabouhi et al. (2018)	●			●				●	●			●			●	Possibilistic chance-constrained programming
Zandieh et al. (2018)			●		●			●	●			●				NSGA-II
Narayana et al. (2019)	●				●			●	●				●			Runge–Kutta fourth order
Roshan et al. (2019)			●		●			●	●			●			●	AUGMECON-2
Chen et al. (2019)	●			●			●					●				Evaluation algorithm
Nasrollahi and Razmi (2019)		●			●			●	●			●			●	NSGA-II
Taleizadeh et al. (2019)	●			●			●						●		●	GAMS
Franco and Alfonso-Lizarazo (2019)		●			●			●				●			●	Sample path
Timajchi et al. (2019)		●		●				●	●	●		●				Hybrid genetic algorithm
Alizadeh et al. (2020)		●			●		●		●	●				●		Bounded De Novo programming
Liu et al. (2020)	●				●	●	●						●			Smoothing method
Current study			●		●	●		●	●	●	●			●	●	Hybrid method

SO single-objective, BO bi-objective, MO multi-objective, S single, M multi, F forward, R reverse, CL closed-loop

Research gap analysis and contributions

The literature shows that there are a few papers which studied pharmaceutical closed-loop supply chains, especially by quantitative approaches. To the best of our knowledge, the CLPSCs are rarely studied from a waste management perspective too. In the current study to concentrate on the waste management requirements in CLPSCs, medicines and their wastes are classified by their characteristics and components in three classes.

Furthermore, to the best of our knowledge, there is no study, which investigates the impact of price and quality of medicines on the PSC network design and performance. This research applies a novel scenario-based game theory approach to estimate the amount of demand due to competition between price and quality. Also, this paper is among the first attempts that design and analyze a CLPSC in an uncertain and competitive market. This way, a novel scenario-based MOMILP model is proposed to integrate sustainable CLPSC network designing and Vehicle Routing Problem with Simultaneous Pickup and Delivery (VRPSPD) under uncertainty.

Based on the literature and Table 1, some main features that distinguish this paper from existing research are as follows:

• Designing a new multi-product, multi-period sustainable CLPSC network, which is considered both strategic decisions (i.e., determining numbers and optimized locations of remanufacturers and disposal centers) and tactical decisions (i.e., the assignment of pharmacies to DCs, and optimum flow of products in the network).

• Designing a sustainable CLPSC for medicines with expiration date and by integrating requirements of pharmaceutical waste management. For this purpose, all possible reverse flows are classified into three categories according to the product type: disposal, remanufacturing, and recycling flows.

• Designing and analyzing a CLPSC under competitive conditions by taking into account different brands of manufacturers. This way, the sensitivity of customer’s demand to the product’s price and quality is considered by applying a scenario-based game theory approach.

• Integrating concepts of CLPSC and capacitated VRPSPD inspired by the real world.

Problem description

Modeling framework

In this study, a multi-product multi-period sustainable CLPSC network is configured that consists of multiple manufacturers, DCs and pharmacies in the forward network, addition to disposal centers and remanufacturers in the reverse network. Medicines, with a specified lifetime, are transferred from manufacturers to DCs. The medicines can be sent to pharmacies at the same period or be stored in DCs for several periods before their expiration date and then be transferred to pharmacies. Vehicles in each period transfer medicines from DCs to the pharmacies assigned to them, and simultaneously collect expired products from pharmacies. Then, depending on the type of outdated medicines, decisions are made to transfer them to the related centers. Three categories of reverse flows are taken into consideration in the proposed model.

The first category of return flows includes expired medicines that are hazardous to the environment, humans, and animals. This kind of return flow can contaminate water or be ingested by animals and harm them. Therefore, they should be sent to the disposal centers and their proper disposal is of significant importance. The second class of disposals can be remanufactured and brought back to the forward PSC. Since the reprocessing cycle of these products can be much shorter and cheaper than the initial production cycle, remanufacturing of these products is very beneficial, they should, therefore, be sent to remanufactures. Finally, the last category is related to the products that are recyclable and can be used in non-pharmaceutical SCs. They can be transferred to DCs to be sold in secondary markets. Moreover, considering the uncertainty of medicines’ demand which is sensitive to price and quality, a scenario-based competition has been taken into account. This way, each brand’s demand is determined according to its price and quality. The competition is examined under three scenarios; optimistic, most likely and pessimistic.

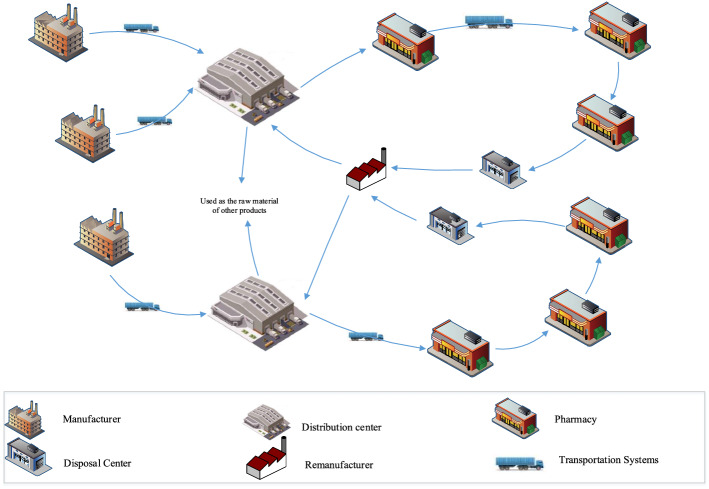
The proposed model aims at maximizing total profit and social impacts of the PSC, in addition to minimizing carbon emissions, through determining the optimum routes and flows of medicines from DCs to pharmacies as well as the number and location of remanufacturers and disposal centers. Figure 2 illustrates a schematic view of the considered CLPSC.

Fig. 2.

Schematic view of the proposed CLPSC

The main assumptions considered are as follows:

• The production capacity of manufacturers and remanufacturers is unlimited.

• The total vehicle load at any point of a route cannot exceed the vehicle capacity.

• Each pharmacy has a time window and can be served by only one DC.

• The demand of each pharmacy is a function of customer’s willingness to buy a medicine considering its price and quality.

• Perishability is just allowed in pharmacies.

• Each medicine has a definite shelf-life, which will expire thereafter, and should be immediately collected after expiration.

• Each medicine is entered into a DC with its full lifetime and leaves DC (to deliver to a pharmacy) with a remaining shelf-life.

The conceptual outline of the proposed CLPSC is depicted in Fig. 3.

Fig. 3.

Conceptual outline of the proposed CLPSC

Proposed MOMILP

In this section, notations and then the proposed mathematical model are presented.

Sets

$m\in \{1,\cdots ,M\}$

Set of manufacturers.

$j\in \{1,\cdots ,J\}$

Set of DCs.

$r\in \{1,\cdots ,R\}$

Set of pharmacies.

$d\in \{1,\cdots ,D\}$

Set of disposal centers.

$c\in \{1,\cdots ,C\}$

Set of remanufacturers.

$n\in \{M,J,D,R,C\}$

Set of nodes.

$p\in \{1,\cdots ,P\}$

Set of products.

$g\in \{1,\cdots ,G\}$

Set of vehicles.

$t,k\in \{1,\cdots ,T\}$

Set of periods of time.

$i_p\in \{1,\cdots ,I={\mathit{SL}}_p\}$

Set of remaining lifetimes of products.

$s\in S$

Set of scenarios.

Parameters

${\mathit{FTC}}_g$

Transportation cost of vehicle g per unit of distance.

${\mathit{IDC}}_{\mathit{jt}}$

Unit inventory cost in DC j in period t.

${\mathit{IRC}}_{\mathit{rt}}$

Unit inventory cost in pharmacy r in period t.

${\mathit{EXC}}_{\mathit{pmt}}$

Unit expiration cost of product p with brand of manufacturer m in period t.

${\mathit{SHC}}_{\mathit{pmrt}}$

Unit lost sale cost of product p with brand of manufacturer m in pharmacy r in period t.

${\mathit{CRM}}_c$

Fixed opening cost of remanufacturer c.

${\mathit{CD}}_d$

Fixed opening cost of disposal center d.

${\mathit{RMCE}}_{\mathit{pm}}$

Unit remanufacturing cost of product p with brand of manufacturer m.

${\mathit{DCE}}_{\mathit{pm}}$

Unit disposal cost of product p with brand of manufacturer m.

${\mathit{CTW}}_r$

Cost of time window violation in pharmacy r.

${\mathit{Tt}}_{n{n}^{\prime }}$

Travel time from node n to $n^{\prime }$

${\mathit{VC}}_g$

Maximum capacity of vehicle g.Maximum capacity of vehicle g.

${\mathit{ID}}_j^{\mathit{max}}$

Maximum allowable inventory level in DC j.

${\mathit{IR}}_r^{\mathit{max}}$

Maximum allowable inventory level in pharmacy r.

${\mathit{CEV}}_g$

Amount of carbon emitted per unit of distance by vehicle g.

${\mathit{CEM}}_{\mathit{mp}}$

Carbon emitted by producing a unit of product p in manufacturer m.

${\mathit{CERM}}_{\mathit{cp}}$

Carbon emitted by remanufacturing a unit of product p in remanufacturer c.

${\mathit{CED}}_{\mathit{dp}}$

Carbon emitted by disposing of a unit of product p in disposal center d.

${\mathit{EBRM}}_p$

Environmental benefit results from remanufacturing a unit of product p.

${\mathit{EBD}}_p$

Environmental benefit results from disposal of a unit of product p.

${\mathit{FJO}}_d$

Number of fixed jobs created by opening disposal center d.

${\mathit{FJO}}_c$

Number of fixed jobs created by opening remanufacturer c.

${\mathit{VJO}}_d$

Number of variable jobs required for disposing of a unit of product in disposal center d.

${\mathit{VJO}}_c$

Number of variable jobs required for processing a unit of product in remanufacturer c.

${\mathit{SL}}_p$

Shelf life of product p.

${\mathit{DS}}_{n{n}^{\prime }}$

Distance between node n and $n^{\prime }$

$D_{\mathit{pmrts}}^{\ast }$

Equilibrium demand for product p with brand of manufacturer m in pharmacy r in period t under scenario s.

$V_{\mathit{pmrs}}^{\ast }$

Equilibrium price of product p with brand of manufacturer m in pharmacy r under scenario s.

${\mathit{ISEX}}_p$

Sale price of a unit of product p in the secondary market.

${\mathit{xy}}_p$

1 if product p must be disposed of; 0, otherwise.

${\mathit{xz}}_p$

1 if product p is recyclable; 0, otherwise.

${\mathit{yz}}_p$

1 if product p is reproducible; 0, otherwise.

L

A large number.

$P_S$

Occurrence probability of scenario s.

Decision variables

$Y_{jn{n}^{\prime }gts}$

1 if in the path of vehicle g assigned to DC j, node $n^{\prime }$ is met after node n under scenario s; 0, otherwise.

$Z_{\mathit{ds}}$

1 if disposal center d is selected under scenario s; 0, otherwise.

$H_{\mathit{cs}}$

1 if remanufacturer c is selected under scenario s; 0, otherwise.

${\mathit{FPM}}_{\mathit{pmjts}}^{i_p}$

Flow of product p with remaining lifetime $i_p$ that is sent from manufacturer m to DC j in period t under scenario s.

${\mathit{FPR}}_{\mathit{pmjrkts}}^{i_p}$

Flow of product p of manufacturer m that is received by DC j in period k and then sent to pharmacy r in period t with remaining lifetime $i_p$ under scenario s.

${\mathit{NVM}}_{\mathit{gmjts}}$

Number of vehicle g transferring products from manufacturer m to DC j in period t under scenario s.

${\mathit{NVJ}}_{\mathit{gjts}}$

Number of vehicle g transferring products from DC j to pharmacies in period t under scenario s.

${\mathit{ID}}_{\mathit{pmjts}}$

Inventory level of product p with brand of manufacturer m in DC j in period t under scenario s.

${\mathit{IR}}_{\mathit{pmrts}}$

Inventory level of product p with brand of manufacturer m in pharmacy r in period t under scenario s.

${\mathit{AT}}_{\mathit{rts}}$

Product’s delivery time to pharmacy r in period t under scenario s.

${\mathit{LS}}_{\mathit{pmrts}}$

Lost sale amount of product p with brand of manufacturer m in pharmacy r in period t under scenario s.

${\mathit{REX}}_{\mathit{pmrkts}}$

Amount of product p with brand of manufacturer m received by pharmacy r in period k and expired in period t under scenario s.

${\mathit{SP}}_{\mathit{pmrkts}}$

Amount of product p with brand of manufacturer m received by pharmacy r in period k and sold in period t under scenario s.

$Q_{\mathit{jnts}}$

Total load of vehicle g assigned to DC j at node n in period t under scenario s.

${\mathit{ETW}}_{\mathit{rts}}$

Earliness in pharmacy r in period t under scenario s.

${\mathit{LTW}}_{\mathit{rts}}$

Tardiness in pharmacy r in period t under scenario s.

Considering above notations, the research problem is formulated as follows:

Objective functions

$$\begin{array}{cc}& \mathrm{Max}\sum _S\left(\left(\left(\sum _{m=1}^M,\sum _{p=1}^P,\sum _{r=1}^R,\sum _{k=1}^t,\sum _{t=k}^T,V_{\mathit{pmrs}}^{\ast },\times ,{\mathit{SP}}_{\mathit{pmrkts}},+,\sum _{m=1}^M,\sum _{p=1}^P,\sum _{r=1}^R,\sum _{k=1}^t,\sum _{t=k}^T,{\mathit{ISEX}}_p,\times ,{\mathit{REX}}_{\mathit{pmrkts}},\times ,{\mathit{xz}}_p\right)\right)\right)\hfill \\ \hfill & \left(\left(,-,\left(\sum _{c=1}^C,{\mathit{CRM}}_c,\times ,H_{\mathit{cs}},+,\sum _{d=1}^D,{\mathit{CD}}_d,\times ,Z_{\mathit{ds}},+,\sum _{m=1}^M,\sum _{j=1}^J,\sum _{t=1}^T,\sum _{g=1}^G,{\mathit{FTC}}_g,\times ,{\mathit{DS}}_{\mathit{mj}},\times ,{\mathit{NVM}}_{\mathit{gmjts}}\right)\right)\right)\hfill \\ \hfill & \left(\left(\left(,+,\sum _{j=1}^J,\sum _{r=1}^R,\sum _{d=1}^D,\sum _{c=1}^C,\sum _{t=1}^T,{\mathit{FTC}}_g,\times ,{\mathit{DS}}_{n{n}^{\prime }},\times ,{\mathit{NVJ}}_{\mathit{gjts}},+,\sum _{j=1}^J,\sum _{m=1}^M,\sum _{t=1}^T,\sum _{p=1}^P,{\mathit{IDC}}_{\mathit{jt}},\times ,{\mathit{ID}}_{\mathit{pmjts}}\right)\right)\right)\hfill \\ \hfill & \left(\left(\left(,+,,\sum _{m=1}^M,\sum _{r=1}^R,\sum _{t=1}^T,\sum _{p=1}^P,{\mathit{IRC}}_{\mathit{rt}},\times ,{\mathit{IR}}_{\mathit{pmrts}},+,\sum _{m=1}^M,\sum _{r=1}^R,\sum _{t=1}^T,\sum _{p=1}^P,{\mathit{SHC}}_{\mathit{pmrt}},\times ,{\mathit{LS}}_{\mathit{pmrts}}\right)\right)\right)\hfill \\ \hfill & \left(\left(\left(,+,\sum _{r=1}^R,\sum _{t=1}^T,\left({\mathit{ETW}}_{\mathit{rts}},+,{\mathit{LTW}}_{\mathit{rts}}\right),\times ,{\mathit{CTW}}_r,+,\sum _{m=1}^M,\sum _{p=1}^P,\sum _{r=1}^R,\sum _{k=1}^t,\sum _{t=k}^T,{\mathit{EXC}}_{\mathit{pmt}},\times ,{\mathit{REX}}_{\mathit{pmrkts}}\right)\right)\right)\hfill \\ \hfill & \left(\left(\left(+,\sum _{m=1}^M,\sum _{p=1}^P,\sum _{r=1}^R,\sum _{k=1}^t,\sum _{t=k}^T,{\mathit{DCE}}_{\mathit{pm}},\times ,{\mathit{REX}}_{\mathit{pmrkts}}\right)\right)\right)\hfill \\ \hfill & \left(\left(\left(,\times ,,{\mathit{xy}}_p,+,\sum _{m=1}^M,\sum _{p=1}^P,\sum _{r=1}^R,\sum _{k=1}^t,\sum _{t=k}^T,{\mathit{RMCE}}_{\mathit{pm}},\times ,{\mathit{REX}}_{\mathit{pmrkts}},\times ,{\mathit{yz}}_p\right)\right),\times ,P_S\right).\hfill \end{array}$$ 1

The first objective function (1) maximizes the expected value of the total PSC profit calculated from average revenues minus costs. The revenues consist of selling medicines to customers and recycled products to secondary markets. The costs include opening cost of remanufacturers and disposal centers, transportation costs of products and expired products, inventory costs, the penalty of unsatisfied demand, time-window violation costs, expiration costs, and costs of disposing and remanufacturing of outdated products.

$$\begin{array}{cc}& \mathrm{Min}\sum _S\left(\left(\sum _{m=1}^M,\sum _{j=1}^J,\sum _{t=1}^T,\sum _{g=1}^G,{\mathit{CEV}}_g,\times ,{\mathit{DS}}_{\mathit{mj}},\times ,{\mathit{NVM}}_{\mathit{gmjts}},+,\sum _{j=1}^J,\sum _{r=1}^R,\sum _{d=1}^D,\sum _{c=1}^C,\sum _{t=1}^T,{\mathit{CEV}}_g,\times ,{\mathit{DS}}_{n{n}^{\prime }},\times ,{\mathit{NVJ}}_{\mathit{gjts}}\right)\right)\hfill \\ \hfill & \left(\left(,+,\sum _{j=1}^J,\sum _{m=1}^M,\sum _{p=1}^P,\sum _{i_p=1}^{{\mathit{SL}}_p},\sum _{t=1}^T,{\mathit{CEM}}_{\mathit{mp}},\times ,{\mathit{FPM}}_{\mathit{pmjts}}^{i_p}\right)\right)\hfill \\ \hfill & \left(\left(,+,\sum _{m=1}^M,\sum _{p=1}^P,\sum _{d=1}^D,\sum _{r=1}^R,\sum _{k=1}^t,\sum _{t=k}^T,{(CED}_{\mathit{dp}},-,{\mathit{EBD}}_p,)\times ,{\mathit{xy}}_p,\times ,{\mathit{REX}}_{\mathit{pmrkts}}\right)\right)\hfill \\ \hfill & \left(\left(,+,\sum _{m=1}^M,\sum _{p=1}^P,\sum _{c=1}^C,\sum _{r=1}^R,\sum _{k=1}^t,\sum _{t=k}^T,{(CERM}_{\mathit{cp}},-,{\mathit{EBRM}}_p,)\times ,{\mathit{xz}}_p,\times ,{\mathit{REX}}_{\mathit{pmrkts}}\right),\times ,P_S\right).\hfill \end{array}$$ 2

The second objective function (2) minimizes the expected value of the environmental impacts of the PSC. The first to third terms indicate carbon emissions due to the transportation and manufacturing of pharmaceutical products. Besides, the fourth and fifth terms outline the environmental impacts of disposal and remanufacturing of medicines, expressed as the difference between carbon emission and environmental benefits.

$$\begin{array}{cc}& \mathrm{Max}\sum _S\left(\left(\sum _{m=1}^M,\sum _{p=1}^P,\sum _{r=1}^R,\sum _{k=1}^t,\sum _{t=k}^T,{\mathit{JO}}_d,\times ,Z_{\mathit{ds}}\right)\right)\hfill \\ \hfill & \left(\left(,+,,\sum _{m=1}^M,\sum _{p=1}^P,\sum _{r=1}^R,\sum _{k=1}^t,\sum _{t=k}^T,{\mathit{JO}}_c,\times ,H_{\mathit{cs}}\right)\right)\hfill \\ \hfill & \left(\left(,+,\sum _{m=1}^M,\sum _{p=1}^P,\sum _{c=1}^C,\sum _{r=1}^R,\sum _{k=1}^t,\sum _{t=k}^T,{\mathit{VJO}}_c,\times ,{\mathit{xz}}_p,\times ,{\mathit{REX}}_{\mathit{pmrkts}}\right)\right)\hfill \\ \hfill & \left(\left(,+,\sum _{m=1}^M,\sum _{p=1}^P,\sum _{d=1}^D,\sum _{r=1}^R,\sum _{k=1}^t,\sum _{t=k}^T,{\mathit{VJO}}_d,\times ,{\mathit{xy}}_p,\times ,{\mathit{REX}}_{\mathit{pmrkts}}\right),\times ,P_S\right).\hfill \end{array}$$ 3

The third objective function (3) states the social goal, which maximizes the expected value of job opportunities resulting from the opening of disposal centers and remanufacturers.

Constraints

$$\sum _{p=1}^P{\mathit{FPM}}_{\mathit{pmjts}}^{i_p={\mathit{SL}}_p}\le \sum _{g=1}^G{\mathit{NVM}}_{\mathit{gmjts}}\times {\mathit{VC}}_g\forall m,j,t,s$$ 4

$${\mathit{FPM}}_{\mathit{pmjks}}^{i_p={\mathit{SL}}_p}+{\mathit{FPRM}}_{\mathit{pmcjks}}^{i_p={\mathit{SL}}_p}=\sum _{r=1}^R\sum _{t=k}^{{\mathit{SL}}_p+k-1}{\mathit{FPR}}_{\mathit{pmjrkts}}^{i_p={\mathit{SL}}_p-t+k}\forall p,m,j,k,s$$ 5

$$\sum _{r=1}^R\sum _{g=1}^G{Y}_{\mathit{jjrgts}}\ge 1\forall j,t,s$$ 6

$$\sum _{n=1}^N\sum _{\begin{array}{c}{j}^{\prime }=1\\ j^{\prime }\ne j\end{array}}^J{Y}_{jn{j}^{\prime }ts}=0\forall j,t,s$$ 7

$$\sum _{g=1}^G{Y}_{\mathit{jnngts}}=0\forall j,n,t,s$$ 8

$$\sum _{n=1}^N{Y}_{jn{n}^{\prime }ts}=\sum _{n=1}^N{Y}_{j{n}^{\prime }nts}\forall j,n^{\prime },t,s$$ 9

$$\sum _{j=1}^J\sum _{g=1}^G{Y}_{\mathit{jjrgts}}\le 1\forall r,t,s$$ 10

$$\sum _{g=1}^G{Y}_{\mathit{jjngts}}=0\forall \mathrm{j},n\in \left\{d,,,c,,,j^{\prime }\right\},t,s$$ 11

$$\sum _{r=1}^R\sum _{g=1}^G{Y}_{\mathit{jnrgts}}=0\forall \mathrm{j},n\in \left\{d,,,c\right\},t,s$$ 12

$$\sum _{m=1}^M\sum _{p=1}^p\sum _{k=1}^t{\mathit{FPR}}_{\mathit{pmjrkts}}^{i_p={\mathit{SL}}_p-t+k}\le L\times \sum _{n=1}^N\sum _{g=1}^G{Y}_{\mathit{jnrgts}}\forall j,r,t,s$$ 13

$${\mathit{REX}}_{\mathit{pmrkts}}=\sum _{j=1}^J\sum _{b=1}^k{\mathit{FPR}}_{\mathit{pmjrbks}}^{i_p=t-k}-\sum _{b=k}^t{\mathit{SP}}_{\mathit{pmrkbs}}\forall p,m,r,t,k\le t,s$$ 14

$$\sum _{m=1}^M{I}_{\mathit{pmjts}}=\sum _{m=1}^M{I}_{pmjt-1s}+\sum _{m=1}^M{\mathit{FPM}}_{\mathit{pmjts}}^{i_p={\mathit{SL}}_p}-\sum _{r=1}^R\sum _{m=1}^M\sum _{k=1}^t{\mathit{FPR}}_{\mathit{pmjrkts}}^{i_p={\mathit{SL}}_p-t+k}\forall p,j,t,s$$ 15

$$\sum _{m=1}^M{I}_{\mathit{pmrts}}=\sum _{m=1}^M{I}_{pmrt-1s}+\sum _{m=1}^M\sum _{k=1}^t{\mathit{FPR}}_{\mathit{pmjrkts}}^{i_p={\mathit{SL}}_p-t+k}-\sum _{m=1}^M\sum _{k=1}^t{\mathit{SP}}_{\mathit{pmrkts}}-\sum _{m=1}^M\sum _{k=1}^t{\mathit{REX}}_{\mathit{pmrkts}}\forall p,r,t,s$$ 16

$$\sum _{p=1}^P\sum _{m=1}^M{I}_{\mathit{pmets}}\le I_n^{\mathit{max}}\forall n\in \left\{r,,,j\right\},t,s$$ 17

$$D_{\mathit{pmrts}}^{\ast }-\sum _{k=1}^t{\mathit{SP}}_{\mathit{pmrkts}}={\mathit{LS}}_{\mathit{pmrts}}\forall p,m,r,t,s$$ 18

$${\mathit{AT}}_{r^{\prime }ts}\ge {\mathit{AT}}_{\mathit{rts}}+{\mathit{Tt}}_{r{r}^{\prime }}-L\times \left(1,-,\sum _{j=1}^J,Y_{jr{r}^{\prime }gts}\right)\forall r,r^{\prime },t,s$$ 19

$${\mathit{AT}}_{r^{\prime }ts}\le {\mathit{AT}}_{\mathit{rts}}+{\mathit{Tt}}_{r{r}^{\prime }}+L\times \left(1,-,\sum _{j=1}^J,Y_{jr{r}^{\prime }gts}\right)\forall r,r^{\prime },t,s$$ 20

$${\mathit{AT}}_{\mathit{rts}}\ge {\mathit{Tt}}_{\mathit{jr}}-L\times \left(1,-,\sum _{j^{\prime }=1}^J,Y_{j^{\prime }jrgts}\right)\forall j,r,t,s$$ 21

$${\mathit{AT}}_{\mathit{rts}}\le {\mathit{Tt}}_{\mathit{jr}}+L\times \left(1,-,\sum _{j^{\prime }=1}^J,Y_{j^{\prime }jrgts}\right)\forall j,r,t,s$$ 22

$${\mathit{AT}}_{\mathit{rts}}+{\mathit{ETW}}_{\mathit{rts}}\ge {\mathit{LW}}_r\forall r,s$$ 23

$${\mathit{AT}}_{\mathit{rts}}-{\mathit{LTW}}_{\mathit{rts}}\le {\mathit{UW}}_r\forall r,s$$ 24

$$Q_{\mathit{jjts}}=\sum _{m=1}^M\sum _{p=1}^P\sum _{r=1}^R\sum _{k=1}^t{\mathit{FPR}}_{\mathit{pmjrkts}}^{i_p}\forall j,t,s$$ 25

$$Q_{{\mathit{jr}}^{\prime }ts}\ge Q_{\mathit{jnts}}-\sum _{m=1}^M\sum _{p=1}^P\sum _{k=1}^t{\mathit{FPR}}_{pmj{r}^{\prime }kts}^{i_p}+\sum _{m=1}^M\sum _{p=1}^P\sum _{k=1}^{t-1}{\mathit{REX}}_{pm{r}^{\prime }kt-1s}-M\times \left(1,-,Y_{jn{r}^{\prime }gts}\right)\forall j,n,r\in \left\{j,,,r\right\},t,s$$ 26

$$Q_{\mathit{jnts}}\le \sum _{g=1}^G{\mathit{NVJ}}_{\mathit{gjts}}\times {\mathit{VC}}_g\forall j,n\in \left\{j,,,r\right\},t,s$$ 27

$$\sum _{r=1}^R\sum _{j=1}^J\sum _{g=1}^G{Y}_{\mathit{jrdgts}}\le Z_{\mathit{ds}}\forall d,s,t$$ 28

$$\sum _{n\in \left\{r,,,d\right\}}\sum _{j=1}^J\sum _{g=1}^G{Y}_{\mathit{jncgts}}\le H_{\mathit{cs}}\forall d,s,t$$ 29

$$\sum _{m=1}^M\sum _{p=1}^P\sum _{r=1}^R\sum _{k=1}^{t-1}{(REX}_{pmrkt-1s}\times {\mathit{xy}}_p)\le L\times \sum _{r=1}^R\sum _{j=1}^J\sum _{g=1}^G{Y}_{\mathit{jrdgts}}\forall d,t,s$$ 30

$$\sum _{m=1}^M\sum _{p=1}^P\sum _{r=1}^R\left(\left(\sum _{k=1}^{t-1},{\mathit{REX}}_{pmrkt-1s},+,\sum _{k=1}^{t-2},{\mathit{REX}}_{pmrkt-2s}\right),\times ,{\mathit{yz}}_p\right)\le L\times \sum _{j=1}^J\sum _{n\in \left\{r,,,d\right\}}\sum _{g=1}^G{Y}_{\mathit{jncgts}}\forall c,t,s$$ 31

$${\mathit{FPRM}}_{\mathit{pmcjts}}^{i_p={\mathit{SL}}_p}\ge \sum _{r=1}^R{\mathit{REX}}_{pmrkt-2s}\times {\mathit{yz}}_p-M\times \left(1,-,\sum _{n\in \left\{r,,,d\right\}},\sum _{g=1}^G,Y_{\mathit{jncgts}}\right)\forall p,m,c,j,t,s$$ 32

$${\mathit{FPRM}}_{\mathit{pmcjts}}^{i_p={\mathit{SL}}_p}\le \sum _{r=1}^R{\mathit{REX}}_{pmrkt-2s}\times {\mathit{yz}}_p+M\times \left(1,-,\sum _{n\in \left\{r,,,d\right\}},\sum _{g=1}^G,Y_{\mathit{jncgts}}\right)\forall p,m,c,j,t,s$$ 33

$$\begin{array}{cc}& Y_{jn{n}^{\prime }gts},Z_{\mathit{ds}},H_{\mathit{cs}}\in \left\{0,1\right\}and\hfill \\ \hfill & {\mathit{FPM}}_{\mathit{pmjts}}^{i_p},{\mathit{FPR}}_{\mathit{pmjrkts}}^{i_p},{\mathit{NVM}}_{\mathit{gmjts}},{\mathit{NVJ}}_{\mathit{gjts}},{\mathit{ID}}_{\mathit{pmjts}},{\mathit{IR}}_{\mathit{pmrts}},\hfill \\ \hfill & {\mathit{AT}}_{\mathit{rts}},{\mathit{LS}}_{\mathit{pmrts}},{\mathit{REX}}_{\mathit{pmrkts}},{\mathit{SP}}_{\mathit{pmrkts}},Q_{\mathit{jnts}},{\mathit{ETW}}_{\mathit{rts}},{\mathit{LTW}}_{\mathit{rts}}\ge 0\forall m,t,i,j,k,s.\hfill \end{array}$$ 34

Constraint (4) states vehicles capacity limitation. Constraint (5) addresses the relation between input and output flows to DCs. Constraints (6) and (7) ensure that a route starts from a DC and returns to it too. Constraints (7–9) confirm a tour construction for DCs. Since the starting and ending point of each tour is one DC, there is no flow from each node to itself, and each vehicle enters a node, should go out as well. Constraint (10) grantees that each pharmacy is allocated exactly to one DC. Constraint (11) bans direct movements from DCs to disposal centers, remanufacturers, and other DCs. Constraint (12) prohibits movements from disposal centers or remanufacturers to pharmacies. Constraint (13) indicates that the pharmacy needs to be visited if there is a flow in a given period. Constraint (14) shows the expiration of products in pharmacies. Constraints (15) and (16) express inventory balance equations in DCs and pharmacies respectively. Constraint (17) acknowledges that the inventory amount cannot exceed the maximum possible inventory level. Constraint (18) calculates the number of lost sales. Constraints (19–22) represent the product’s arrival time to each pharmacy. Constraints (23) and (24) demonstrate time-window violations. Constraints (25) and (26) state total vehicle load after visiting each node. Constraint (27) guarantees that the whole load does not exceed the vehicle capacity. Constraint (28) shows that the flow to disposal centers can be established if they are opened. Constraint (29) is similarly defined for remanufacturers. Constraint (30) acknowledges that perishable products should be transferred to disposal centers if they are dangerous. Constraint (31) assures that remanufacturer should be visited either there are reproducible products in a given period or there are products that were remanufactured in the previous period. Constraints (32) and (33) show the number of reproducible products that return to the PSC. Finally, Constraint (34) displays the type of decision variables.

Demands based on a scenario-based game theory

The demand for a specific medicine is usually a function of utility that customers perceive based on its price and quality. Among various brands of manufacturers, customers choose the one which brings them the most utility. A pharmacy must carefully consider their customers’ requirements to properly meet their demands and subsequently maximize its profit. In this study, competition on price and quality among members of the PSC is considered to estimate the demand of each brand.

It is assumed that pharmacy r supplies product p from two types of manufacturers; high-quality manufacturers ($H$) with quality level ${\alpha }_{\mathit{pH}}$, and low-quality manufacturers ($L$) with quality level ${\alpha }_{\mathit{pL}},$ where $0<{\alpha }_{\mathit{pL}}<{\alpha }_{\mathit{pH}}<1$. In this structure, manufacturer $m$ incurs unit production cost $C_{\mathit{pm}}$ and sets wholesale price $W_{\mathit{pm}}$. Then, the pharmacy r sets retail price $V_{\mathit{pmr}}$ for product p of manufacturer $m$, where $m=H,L$ and $C_{\mathit{pH}}>C_{\mathit{pL}}$. The demand functions for each brand are therefore as follows:

$$D_{\mathit{pHr}}=a_{\mathit{pr}}-b_{\mathit{vr}}(V_{\mathit{pHr}}-s_{\mathit{vr}}{V}_{\mathit{pLr}})+b_{\alpha r}({\alpha }_{\mathit{pH}}-s_{\alpha r}{\alpha }_{\mathit{pL}})$$ 35

$${\mathrm{D}}_{\mathrm{pLr}}={\mathrm{a}}_{\mathrm{pr}}-{\mathrm{b}}_{\mathrm{vr}}({\mathrm{V}}_{\mathrm{pLr}}-{\mathrm{s}}_{\mathrm{vr}}{\mathrm{V}}_{\mathrm{pHr}})+{\mathrm{b}}_{\alpha \mathrm{r}}({\alpha }_{\mathrm{pL}}-{\mathrm{s}}_{\alpha \mathrm{r}}{\alpha }_{\mathrm{pH}})$$ 36

where $a_{\mathit{pr}}$ is the market potential of pharmacy r for product p. In the customer zone where pharmacy r is located, $b_{\mathit{vr}}$ and $b_{\alpha r}$ are demand sensitivity coefficients for price and quality respectively. $s_{\mathit{vr}}$($s_{\alpha r})$ is the substitutability coefficient related to the price (quality) of pharmacy rs competitors. This way, the profit functions of manufacturers and pharmacies are respectively as follows:

$${\pi }_{\mathit{pm}}=\left(W_{\mathit{pm}},-,C_{\mathit{pm}}\right)\sum _{r=1}^R{D}_{\mathit{pmr}}\forall p,m=H,L$$ 37

$${\pi }_{\mathit{pr}}=\sum _{m=1}^M\left(V_{\mathit{pmr}},-,W_{\mathit{pm}}\right)D_{\mathit{pmr}}\forall p,m=H,L.$$ 38

To apply the scenario-based game theory approach, a bi-level programming model is provided which includes two sub-models; upper and lower-level problems. The upper-level problem consists of objectives and decisions of upper-level decision-makers (DMs) that are leaders of the SC. The lower-level problem consists of decisions of lower-level DMs or followers. This way, leaders first make their decisions according to their goals and conditions. Then, followers make their decisions in response to the top level. Consequently, the variables of the two sub-models depend on each other. Since PSCs’ manufacturers mostly have a more prevailing position and market power than downstream members, they are the leaders and pharmacies are the followers. So, to obtain the equilibrium solution, using the backward deduction method, we first should solve the lower-level problem (Eq. 38) and find the optimal retail prices. Then, the results are applied to solve the upper-level problem (Eq. 37) and derive optimal wholesale prices. As a result, optimal prices for each manufacturer can be calculated from the following equations:

$$W_{\mathit{pm}}^{\ast }=\frac{{\sum }_{r=1}^R{a}_{\mathit{pr}}\left(2,+,s_{\mathit{vr}}\right)+b_{\alpha r}{s}_{\mathit{vr}}\left({\alpha }_{p{m}^{\prime }},-,s_{\alpha r},{\alpha }_{\mathit{pm}}\right)+2b_{\alpha r}\left({\alpha }_{\mathit{pm}},-,s_{\alpha r},{\alpha }_{p{m}^{\prime }}\right)+b_{\mathit{vr}}(2C_{\mathit{pm}}+s_{\mathit{vr}}{C}_{p{m}^{\prime }})}{{\sum }_{r=1}^R{b}_{\mathit{vr}}(4-s_{\mathit{vr}}^2)}$$ 39

$$V_{\mathit{pmr}}^{\ast }=\frac{a_{\mathit{pr}}\left(1,+,s_{\mathit{vr}}\right)+b_{\alpha r}{s}_{\mathit{vr}}\left({\alpha }_{p{m}^{\prime }},-,s_{\alpha r},{\alpha }_{\mathit{pm}}\right)+b_{\alpha r}\left({\alpha }_{\mathit{pm}},-,s_{\alpha r},{\alpha }_{p{m}^{\prime }}\right)+b_{\mathit{vr}}{W}_{\mathit{pm}}^{\ast }(1-s_{\mathit{vr}}^2)}{2b_{\mathit{vr}}(1-s_{\mathit{vr}}^2)}.$$ 40

After obtaining optimal prices, demands for each brand can be derived as follows:

$$D_{\mathit{pmr}}^{\ast }=a_{\mathit{pr}}-b_{\mathit{vr}}\left(V_{\mathit{pmr}}^{\ast },-,s_{\mathit{vr}},V_{p{m}^{\prime }r}^{\ast }\right)+b_{\alpha r}\left({\alpha }_{\mathit{pm}},-,s_{\alpha r},{\alpha }_{p{m}^{\prime }}\right)\forall m\ne m^{\prime }.$$ 41

Customer’s needs are constantly changing and their tendencies may not remain fixed over time. Therefore, the precise determination of parameters (e.g., customer’s sensitivity to price and quality) is not possible. To deal with this challenge, the competition takes place under three scenarios; optimistic, most likely and pessimistic. In the optimistic scenario, the coefficients of demand sensitivity are low and substitutability coefficients are high. Consequently, customers pay less attention to the brand, quality, and price and buy a specific medicine from any brand that is available at a pharmacy. In the most likely scenario, the coefficients take probable values. Under the pessimistic scenario, sensitivity to price and quality is very high and substitutability coefficients are low. Hence, the slightest mismatch between the price/quality of medicines and the taste of customers makes customers refuse to buy. This way, the optimal demand under scenario s is obtained as follows:

$$D_{\mathit{pmrs}}^{\ast }=a_{\mathit{pr}}-b_{\mathit{vrs}}\left(V_{\mathit{pmrs}}^{\ast },-,s_{\mathit{vrs}},V_{p{m}^{\prime }rs}^{\ast }\right)+b_{\alpha rs}\left({\alpha }_{\mathit{pm}},-,s_{\alpha rs},{\alpha }_{p{m}^{\prime }}\right)\forall m,m^{\prime }=H,L.$$ 42

Solution approach

The mathematical model developed to design the proposed sustainable CLPSC is a multi-objective programming model with three conflicting objective functions. Different approaches have been developed to solve the multi-objective programming models including priori, interactive and posteriori ones (Sazvar et al. 2014). One of the most used approaches is the LP-metrics method, which is more perceptible for executives compared to other methods, and in many cases of using this method such as Manopiniwes and Irohara (2017) and Abdelaziz et al. (2018), acceptable results have been provided.

Based on Dethloff (2001), the VRPSPD is an NP-hard problem. Since our problem is extended form of the VRPSPD (the integration of sustainable CLPSC and the VRPSPD), the proposed model is NP-Hard, too. This way, a two-phase hybrid approach is provided to solve the proposed MOMILP model especially in large scales. In the first phase, the multi-objective model is converted to a single-objective model using the LP-metrics method. Then, in the second phase, a heuristic approach is suggested to be able to obtain optimal/near-optimal solutions.

Given the first and third objective functions are maximization and the second is minimization, the LP-metrics objective function is formulated as follows:

$$Z_{\mathit{total}}=\frac{{w_1.({\mathrm{Z}}_1^{\mathit{max}}-Z}_1)}{{\mathrm{Z}}_1^{\mathit{max}}-{\mathrm{Z}}_1^{\mathit{min}}}+\frac{{w_2.(Z}_2-{\mathrm{Z}}_2^{\mathit{min}})}{{\mathrm{Z}}_2^{\mathit{max}}-{\mathrm{Z}}_2^{\mathit{min}}}+\frac{{w_3.({\mathrm{Z}}_3^{\mathit{max}}-Z}_3)}{{\mathrm{Z}}_3^{\mathit{max}}-{\mathrm{Z}}_3^{\mathit{min}}}$$ 43

where $w_i$ denotes the weight of the ith objective function (Z_i), which is determined based on DMs’ opinion. ${\mathrm{Z}}_i^{\mathit{max}}$ and ${\mathrm{Z}}_i^{\mathit{min}}$ respectively show the maximum and minimum values of the ith objective function. The steps of the heuristic algorithm applied are as follows (Kaur and Singh 2018):

First step

Consider the relaxed MILP model in which the binary variables $Y_{jn{n}^{\prime }gt}$ are considered as continuous positive variables ($Y_{jn{n}^{\prime }gt}\ge 0$).

Second step:

Solve the relaxed model optimally.

Third step:

Record all non-zero quantities of $Y_{jn{n}^{\prime }gt}$ which are obtained by solving the relaxed MILP model.

Fourth step:

Equalize each non-zero quantity of $Y_{jn{n}^{\prime }gt}$ to 1, and set them as constraints to the main MILP model.

Fifth step:

Solve the created model optimally.

The efficiency of the proposed two-phase hybrid approach is reported in Supplementary material.

Computational experiment

Case study

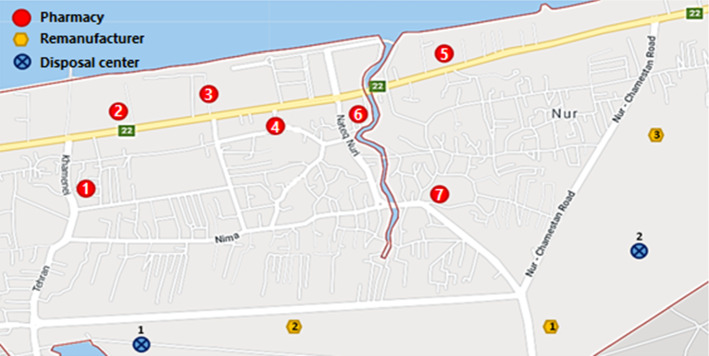
In this section, an Iranian medical SC is investigated as a real case study to validate the performance of the proposed MOMILP model. A PCS in Noor city, located in the north of Iran, is concentrated. This supply chain comprises 7 pharmacies (located in Noor city), a local DC (which is one of the branches of Darou Pakhsh Co., in Sari city) and a number of different brands of manufacturers. According to the expert’s suggestions, two potential locations for disposal sites and three potential remanufacturer centers are considered in the suburbs of the Noor city. The network configuration including pharmacies and potential points is shown in Fig. 4. Three high-consumption pharmaceutical products namely Tetracycline (1st product), Imatinib (2nd product), and Midazolam (3rd product) are taken into account. We suppose that medicines have six months’ lifetime. The expired antibiotic Tetracycline can be classified as one of the hazardous medicines. The toxicity is caused by tetracycline degradation products (epi-anhydrotetracycline or anhydrotetracycline), which can lead to a dangerous syndrome. Therefore, waste disposal of this product should follow the guidelines recommended by the ministry of health and the national environment agency (Beery et al. 2019; Toh and chew 2017). Imatinib is one of the medicines used to treat cancer, which can be remanufactured at a lower cost by extracting Active Pharmaceutical Ingredients (APIs) from expired Imatinib (Basha et al. 2015). We consider expired Midazolam recyclable, which can be sold to secondary markets. It can properly perform as an additive in Nickel electrodeposition from the Watts bath due to pure compounds in its pharmaceutical formulation (Duca et al. 2016).

Fig. 4.

Location of pharmacies, remanufacturers, and disposal centers in the Noor city

The demands of products for a four-year time horizon split into 24 periods (each period is two months) are brought for each pharmacy in detail. Customers in each particular region have different welfare and cultural conditions. In this regard and according to the customer zones, the demand sensitivity coefficients for price and quality, for each pharmacy, are estimated. The data related to each brand and its quality as well as production costs are available too.

The three different fleet of vehicles is employed for transferring products. All the data required for the case study is reported in “Appendix” in detail. Also, it should be noted that based on the experts’ opinions, weights of the objective functions considered as follows: $w_1=0.4,w_2=0.3$ and $w_3=0.3$.

Experimental results

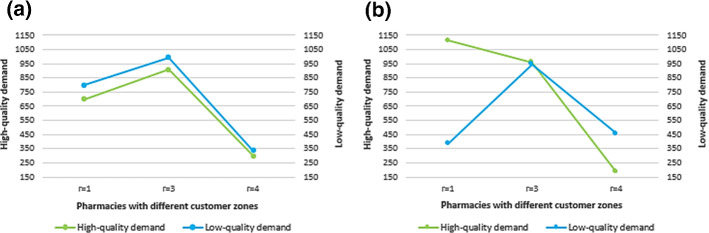
In this section, the obtained results of solving the proposed MOMILP problem for the aforementioned case study are discussed. The transferred flows from manufacturers to pharmacies in the first three periods are reported in Tables 2, 3 and 4. According to these tables, the competition on price and quality ensures that products of each brand are supplied to pharmacies according to their customers’ willingness to pay. As well, pharmacies stock products in a way that the desired products of their customers be available as much as possible. Regarding Table 7, the pharmacies whose customers are more price-sensitive (e.g., pharmacies 4, 5 and 6), receive a supply of pharmaceuticals, most of which includes economic low-quality alternative brands. While, the pharmacies with quality-sensitive customers (e.g., pharmacies 1, 2 and 7), receive a supply of pharmaceuticals, which mostly consist of high-quality international brands. However, in the absence of competition, products are transferred to pharmacies without any special regulation (Fig. 5).

Table 2.

Optimal flow of Tetracycline to pharmacies (t = 1, 2, 3)

Brand	Pharmacy	No competition			Competitive market
		Product flow in each period			Product flow in each period
		1	2	3	1	2	3
Plavix	1	540	700	–	845	1115	–
	2	400	510	–	535	640	–
	3	900	910	–	900	955	–
	4	350	300	310	200	185	175
	5	290	300	295	175	184	184
	6	210	210	210	180	185	180
	7	350	450	284	480	614	400
Osvah	1	530	800	–	225	385	–
	2	400	510	–	264	380	–
	3	905	995	–	905	950	–
	4	350	335	310	500	455	445
	5	290	295	300	405	415	415
	6	210	215	210	240	240	240
	7	335	500	300	197	335	184

Table 3.

Optimal flow of Imatinib to pharmacies (t = 1, 2, 3)

Brand	Pharmacy	No competition			Competitive market
		Product flow in each period			Product flow in each period
		1	2	3	1	2	3
Novartis	1	290	670	–	490	995	–
	2	500	660	–	670	784	–
	3	885	940	–	885	940	–
	4	340	320	350	185	212	205
	5	300	300	300	150	150	150
	6	195	195	195	170	165	170
	7	350	420	335	500	550	470
Soha	1	295	670	–	97	345	–
	2	500	660	–	330	536	–
	3	885	940	–	885	940	–
	4	330	315	350	485	426	495
	5	300	300	310	450	450	450
	6	200	195	200	228	225	228
	7	350	420	332	200	290	198

Table 4.

Optimal flow of Midazolam to pharmacies (t = 1, 2, 3)

Brand	Pharmacy	No competition			Competitive market
		Product flow in each period			Product flow in each period
		1	2	3	1	2	3
Actoverco	1	660	1100	–	965	1525	–
	2	725	1150	–	955	1440	–
	3	1155	1510	–	1155	1510	–
	4	445	895	450	250	747	250
	5	379	695	455	116	303	200
	6	395	800	390	342	685	342
	7	385	850	360	510	1170	505
Abidi	1	665	1110	–	360	685	–
	2	725	1140	–	495	850	–
	3	1155	1500	–	1155	1500	–
	4	445	895	450	640	1042	650
	5	380	695	460	642	1085	715
	6	400	795	400	456	914	456
	7	385	750	370	260	430	225

Table 7.

Factors related to customers’ preferences for each pharmacy

Pharmacy	Demand sensitivity to price $b_{\mathit{vrs}}$			Demand sensitivity to quality $b_{\alpha rs}$			Substitutability coefficient related to price $s_{\mathit{vr}}$			Substitutability coefficient related to quality $s_{\alpha r}$
	O	M	P	O	M	P	O	M	P	O	M	P
1	2	2	2	2	7	12	0.8	0.8	0.8	0.4	0.2	0.05
2	1	2	2	1	5	8	0.7	0.7	0.7	0.3	0.2	0.1
3	3	4	5	3	4	5	0.5	0.5	0.5	0.5	0.5	0.5
4	2	6	10	2	2	2	0.5	0.2	0.1	0.8	0.8	0.8
5	2	5	7	1	1	1	0.4	0.25	0.1	0.6	0.6	0.6
6	3	4	4	1	1	1	0.5	0.2	0.05	0.5	0.5	0.5
7	1	1	1	1	6	9	0.8	0.8	0.8	0.15	0.1	0.05

Fig. 5.

Demand of each brand a without competition; b with competition

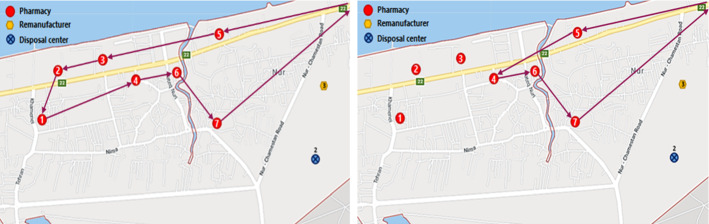
According to the results, disposal center 2 and remanufacturer 3 are selected for opening. The routes of transferring medicines (expired medicines) among pharmacies (disposal and remanufacturer centers) are outlined in Fig. 6 (Fig. 7).

Fig. 6.

Routes of transferring medicines among pharmacies

Fig. 7.

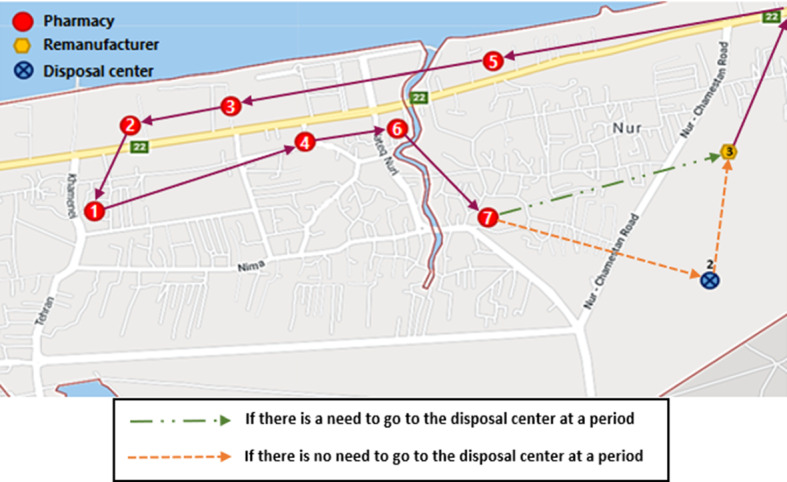
Routes of transferring expired medicines among centers

The waste flows of each product category are reported in Table 5. As can be seen, the proposed model makes it possible to collect expired medicines from pharmacies immediately after expiration. This prevents patients to access to the expired products which can have irreparable effects on patients' bodies and harm their health and life.

Table 5.

Collected expired medicines of each brand

Pharmacy	Waste flow
	Plavix	Osvah	Novartis	Soha	Actoverco	Abidi
1	245	354	287	294	255	390
2	294	186	295	206	212	336
3	430	359	452	339	358	400
4	396	169	398	279	385	315
5	368	160	390	209	360	306
6	344	–	346	180	263	337
7	275	242	326	262	242	392
Waste category	A	A	B	B	C	C
Total waste	3822		4263		4551

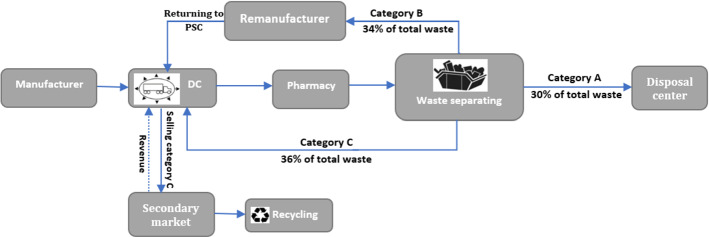
As Fig. 8 shows, 30% of the total collected waste is hazardous, that can cause serious environmental damages, and needs to be disposed of. This way, there is no need to dispose of other waste categories because they can be used for other purposes. If products were not classified, all waste flows would have to be disposed of. By categorizing wastes, the disposal costs have therefore been considerably saved. 36% of total waste is sold to secondary markets to be recycled and be used as raw materials in non-PSCs. It, therefore, causes to generate revenue through waste management. Finally, 34% of collected waste is remanufactured and returned to the PSC. This amount of return flow is equivalent to 12.88% of the total flow of Imatinib which is sent to pharmacies through the PSC. It leads to a considerable reduction in production and process times as well as raw materials usage.

Fig. 8.

Scheme of waste collection network

Sensitivity analysis

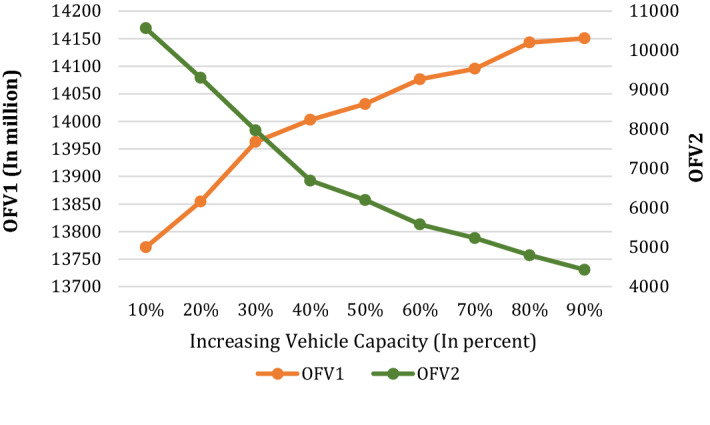
In this section, sensitivity analysis for the main parameters is done to verify the developed model and discover its applications. Figure 9 illustrates the fluctuation of the first Objective Function Value (OFV1) and OFV2 due to the variation of the vehicle’s capacity. A glance at this figure displays that both OFVs are getting better values by increasing the vehicle’s capacity. The OFVs initially have a significant improvement due to the reduction in the number of vehicles utilized. As Fig. 9 shows, when the vehicle’s capacity is increased by 30% from the base case, the OFV2 (amount of carbon emission) is decreased by 31.12%. While from some point onwards, the impact of capacity changes on the number of vehicles required, and subsequently the OFVs, is greatly reduced. For instance, whenever the vehicle’s capacity is increased by 80%, OFV2 is decreased by 57.75% (compared to the base case), indicating a decrease in the OFV2s slope.

Fig. 9.

OFV1 and OFV2 versus the vehicle’s capacity alteration

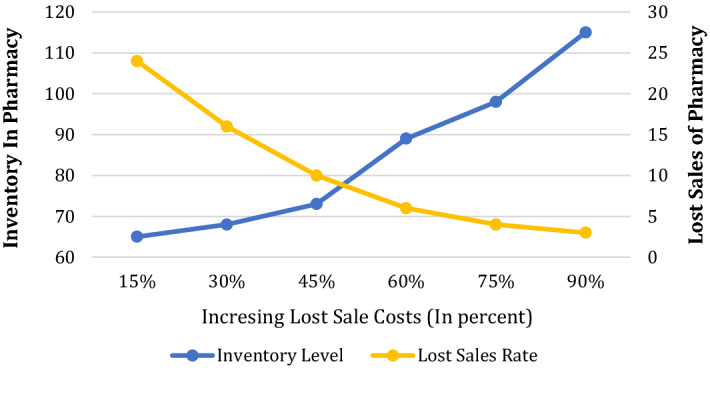
Figure 10 illustrates the impacts of lost sale cost (${\mathit{SHC}}_{\mathit{pmrt}}$) on inventory level and lost sale amounts in pharmacies. As can be seen, the total level of inventory grows by lost sale costs increasing. In other words, pharmacies prefer to consolidate their position in the competitive market by keeping higher levels of inventory. Also, as Fig. 10 shows, when the lost sale cost is increased by 30% and 75%, the inventory level is increased by 9.6% and 58%, respectively. So, the higher lost sale cost leads to a higher rate of increase in the inventory level. Besides, it is logical that increment in lost sale costs results in lost sales reduction. When the lost sale cost is increased by 60%, the lost sale amount is decreased by 82.35%.

Fig. 10.

Impact of the unit lost-sale cost on lost-sales and total inventory level (r = 4, t = 2)

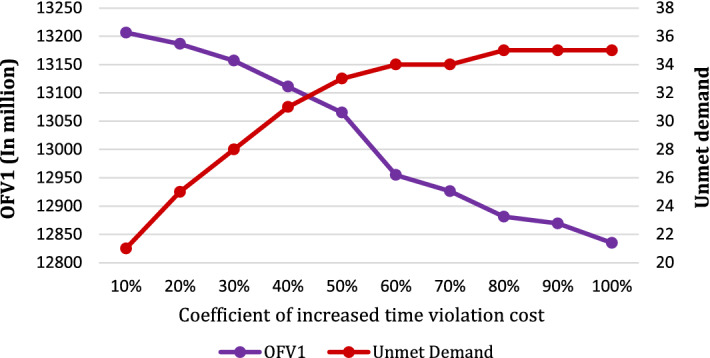
Figure 11 is devoted to an analysis of the time window violation cost (${\mathit{CTW}}_r$). The diagram demonstrates that with a constant lost-sale cost, the OFV1 decreases as the cost of time violation rises. In such a situation, the model may incur costs of routing, unmet demand, or even growth in vehicle numbers to satisfy demands in a predetermined time. Initially, to prevent the deviation from time windows, the amount of unmet demands is increased significantly. However, after a point (about 50% increase in cost), a sharp decline in the increasing rate of unsatisfied demand can be observed. For example, when the time violation cost is one and a half times the base case, the unmet demand is increased by 65%, while, when the violation cost doubles, the unmet demand is increased by 75%. The reason for these changes is that satisfying demands are more important than the response time for PSCs, even if it breaks the deadline.

Fig. 11.

OFV1 and unmet demand versus the time violation cost

Figure 12 represents OFV1 and OFV3 changes arising from the variation of the expiration cost (${\mathit{EXC}}_{\mathit{pmt}}$). As it is evident, both objective functions are getting worse values by increasing the expiration cost of the medicines. By an increase in expiration cost, the model seeks to reduce the number of expired medicines in all pharmacies. Accordingly, the less the expired product, the lower the number of variable occupations, and the value of OFV3 diminishes. Additionally, the negligible reduction in the OFV1 is probably caused by a decrease in revenue from expired medicines.

Fig. 12.

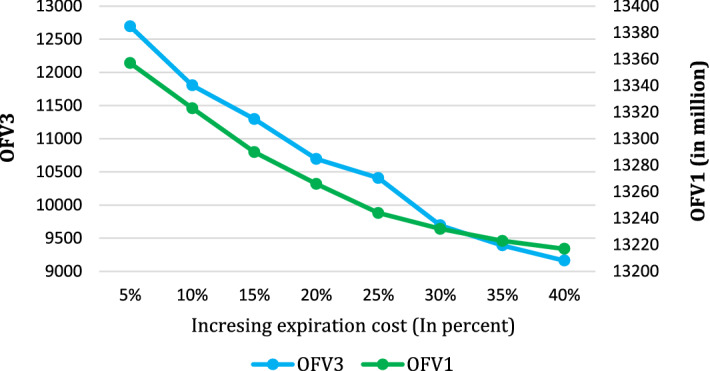
OFV1 and OFV3 versus the expiration cost

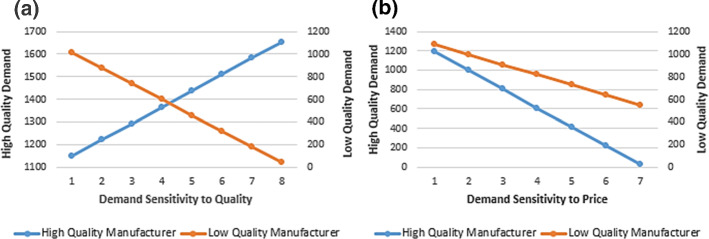
The change in customer’s demand for each brand against products’ price and quality is shown in Fig. 13. By keeping the price sensitivity constant, Fig. 13a demonstrates that high demand sensitivity to quality leads to a high level of demand for high-quality medicines. However, it causes a low demand for low-quality medicines. Regarding Fig. 13a, when the demand sensitivity to quality is increased from 1 to 6 the demand for high-quality brands is increased by 33%, whereas the demand for low-quality brands is decreased by 68.83%.

Fig. 13.

Each brand’s demand versus a demand sensitivity to the quality; b demand sensitivity to the price (P = 3, r = 3, t = 3)

By keeping the quality sensitivity parameter constant and according to Fig. 13b, the demand for both brands decreases when the price sensitivity increases. This is because of the inherent negative influence of price on the demand. Based on Fig. 13b, a sharp decline in the high-quality medicines’ demand can be observed, while low-quality products’ demand decreases with a gentle slope. For example, when the demand sensitivity to price is increased from 1 to 5, the demands for the high-quality and low-quality brands are decreased by 65.31% and 31.56% respectively.

Figure 14 indicates the transferred flow of medicines to pharmacies under different sets of game scenario’s probability. According to the diagram and given that the customers of pharmacy 7 pay more attention to quality, under the higher probability of a pessimistic scenario occurrence, the high-quality manufacturer will cover more market demand than the low-quality one. Hence, the pharmacy managers must properly replenish the inventory with customer’s favorable items. Because in the absence of required products, customers will refuse to buy from another brand. As the occurrence probability of the optimistic scenario increases, the flow of both brands grows, along with a decline in the difference of two brands flows. According to Fig. 14 the difference between the two brands' flows is decreased by 48.53% from pessimistic to the optimistic scenario. This situation can be desirable for pharmacy managers. Since in the absence of customers’ favorable brand, the possibility of buying medicines from another brand is enforced.

Fig. 14.

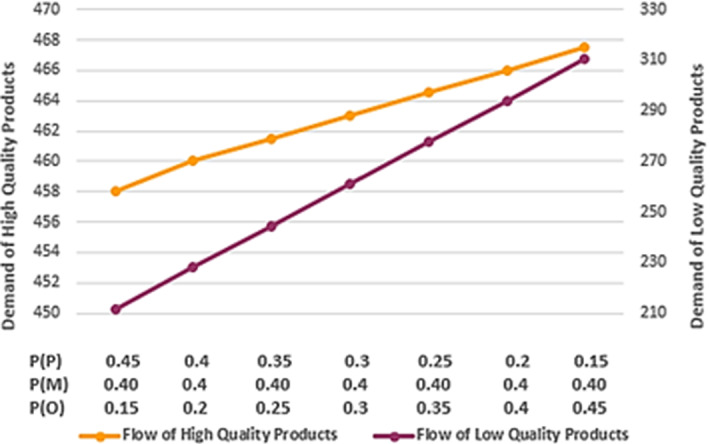
Transferred flow of medicines under different sets of game scenario’s probability (P = 3, r = 7, t = 3)

Managerial insights

An important obligation of a manager is to set goals, determine the path to achieve them, and make strategic, tactical and operational decisions. To accomplish this commitment, it is vital to have managerial insights. The presented model provides managerial perspectives for PSC managers through the following goals:

• Despite strategic decisions, tactical decisions related to PSC flows, especially replenishment of inventory, play a pivotal role in reducing costs as well as increasing customers’ satisfaction. Therefore, managers should appropriately plan PSCs to minimize their inventory costs. The proposed model increases knowledge of pharmacy managers to adopt proper replenishment policies, to keep their market shares by enhancing customers’ loyalty.

• The proposed scenario-based game theory approach provides an efficient way of determining customers’ demands in a competitive market. This way, it can help inventory holders and DC managers in making decisions on transferring optimal flows of each brand’s products to pharmacies.

• Market conditions are not always monotonous. Factors such as introducing a new product, changes in raw material prices or customers’ tastes can dramatically change the demand rate for a particular brand. Hence, managers should forecast sales under different scenarios to cope with market shocks and avoid from lost-sale or unwanted inventories.

• As can be seen from Fig. 11, price sensitivity is an inherently negative factor on demand. If the price sensitivity in a customer zone is high, which leads to a low demand rate for a particular brand, it is recommended to apply some incentive policies such as price mark-down to reduce perished products.

• Green policies, corporate social responsibility and environmentally-friendly performance are important factors in attracting customers. The suggested CLPSC can help managers to achieve these factors by coping with unauthorized dumping of pharmaceutical wastes, properly managing expired products and adopting a green transport system based on the SPD concept.

Theoretical insights and contributions

In this study, a scenario-based MOMILP model is developed to design a sustainable CLPSC network in a competitive market under the demand uncertainty, which aims at maximizing profit and social aspects, in addition to minimizing environmental harms. However, in spite of the fact that our study highlights PSC, the proposed methodologies are not case-specific and can be applied to any supply chain in various fields and industries. Accordingly, based on the current investigation, some theoretical contributions are extracted to enrich the literature of supply chain management as follows:

• This study establishes a benchmark model for supply chain administrators to successfully conduct and manage CLSC initiatives along with sustainable targets in any industrial sector. In the literature, many requirements of waste management have been overlooked in multi-product CLSC models. This research contributes to the closed-loop supply chain literature by specifying backward flows based on products’ specifications.

• Our study directly addresses integrated environmental approaches by designing a CLSC network along with VRPSPD, which is a critical dialogue in research on environmental management. To clarify, unlike other models, in this research for approaching the real-world conditions, almost all diverse environmental hazards arising from industrial and transportation activities are covered. It means that different environmental attributes of the proposed model can be used for a multitude number of studies discussing the environmental impacts of supply chain processes.

• The present study accomplishes the goal of creating an appropriate balance between overcoming demand uncertainty and increasing overall profitability by connecting game theory outcomes with the supply chain’s multi-objective framework. It should be noted that the proposed scenario-based game theory and its combination with the CLSC model are absolutely new in the area of supply chain management. The applied methods are convenient to perceive and implement. Due to their extreme flexibility, these procedures can yield to develop new models which are able to further extend this field, as well.

• As a novel idea, the presented scenario-based game theory is suitable and practical for any brand-differentiated supply chain, which enriches the supply chain context and provides a significant improvement in customer orientation activities, especially for urban areas with a broad spectrum of desires. The game scenarios can be evaluated and determined by subject matter experts, and applied to predict the demand, based on the products price and the quality levels under different situations.

• Finally, although the efficient proposed hybrid algorithm is only evaluated under CLSC cases with SPD, it can be simply utilized to deal with other complex VRPs as well as other optimization issues in the class of NP-Hard problems.

Conclusion

The current study focused on the integration of the sustainable CLPSC network design and VRPSPD in a competitive market. The model consisted of some manufacturers, DCs, pharmacies and potential locations for disposal centers and remanufacturers. Products, from different brands, were considered with specific lifetimes. The uncertainty in each brand’s demand was handled by a scenario-based game theory approach. The products were collected after their lifespan and managed in three ways according to their characteristics; disposing of, remanufacturing and recycling. To solve the proposed model, a hybrid solution approach was provided by incorporating the LP-metrics method with a heuristic algorithm. Furthermore, a real case study in Iran was applied to evaluate the applicability of the presented model.

According to the obtained results, classifying pharmaceutical wastes, in addition to a considerable improvement in the negative environmental effects of the PSC (due to proper disposal), could save costs and production times (through the remanufacturing process) and/or generate additional revenue (through selling some expired products to secondary markets). Also, considering the competition in designing the CLPSC could optimally affect major decision variables (e.g., the flow of each brand’s products to pharmacies and/or their inventory levels). If the competitive condition of real markets is not considered in designing a CLPSC, it may cause high lost-sales along with a huge inventory cost in some periods. Because pharmacies’ inventories may include some brands of products with negligible demand that consequently results in a high level of perished and non-perished inventories as well as customer loss.

The future extensions may include (1) improving the developed model by integrating resiliency and sustainability requirements, (2) considering the possibility of transferring excess inventories of an unwanted brand from one pharmacy to another one where there is a demand for that brand and, (3) Examining the application of the developed model for other real cases especially medical SCs involving with managing wastes generated due to COVID-19.

Supplementary Information

Below is the link to the electronic supplementary material.

Appendix: A detailed explanation on the case study’s data

See Tables 6, 7, 8, 9 and 10.

Table 6.

Demands of products for 6 periods of each year

Product	Pharmacy	Market potential of pharmacy ($a_{\mathit{pr}}$) in each time period
		1	2	3	4	5	6
$P1$	1	750	1200	800	1000	700	1300
	2	550	800	500	890	500	850
	3	1180	1280	1250	1220	1000	1350
	4	700	640	620	710	650	750
	5	580	600	600	600	630	550
	6	500	550	500	510	520	550
	7	780	1010	650	650	1090	1000
$P2$	1	400	1150	370	1170	400	1300
	2	650	970	700	1000	700	1000
	3	1170	1280	1200	1220	1200	1350
	4	670	640	700	650	700	650
	5	580	600	600	600	550	650
	6	500	480	500	450	520	500
	7	780	1030	750	1050	790	1100
$P3$	1	900	1800	850	2000	900	1800
	2	950	1800	1000	1900	1020	1650
	3	1400	2300	1430	2550	1380	2500
	4	890	1800	900	1800	850	1900
	5	860	1700	900	2000	830	2000
	6	900	1700	900	1800	800	1850
	7	850	1700	800	1750	900	1800

Table 8.

Data on the brand, cost, and quality of each product

Product	P1		P2		P3
Brand	Plavix	Osvah	Novartis	Soha	Actoverco	Abidi
Quality	0.95	0.5	0.95	0.35	0.7	0.4
Production cost (Rials)	578,000	285,000	260,000	91,000	75,000	45,000

Table 9.

Capacity and carbon emission of each type of vehicles

Vehicle	Capacity	Carbon emission (g ${\mathrm{CO}}_2/\mathrm{Km}$)
1	12,000	900
2	8000	600
3	5000	250

Table 10.

Number of labors required for each potential center

Centers	Disposal centers		Remanufacturers
Potential nodes	1	2	1	2	3
Number of labors	30	50	150	200	120