Skip to main content
PMC home page
Cerebral Cortex (New York, NY) logoLink to Cerebral Cortex (New York, NY)
. 2020 Nov 4;31(3):1478–1488. doi: 10.1093/cercor/bhaa290

Individual Differences in Cognitive Performance Are Better Predicted by Global Rather Than Localized BOLD Activity Patterns Across the Cortex

Weiqi Zhao 1, Clare E Palmer 2, Wesley K Thompson 3, Bader Chaarani 4, Hugh P Garavan 5, B J Casey 6, Terry L Jernigan 7,8,9,10, Anders M Dale 11,12,13,14, Chun Chieh Fan 15,16,✉
PMCID: PMC7869101  PMID: 33145600

Abstract

Despite its central role in revealing the neurobiological mechanisms of behavior, neuroimaging research faces the challenge of producing reliable biomarkers for cognitive processes and clinical outcomes. Statistically significant brain regions, identified by mass univariate statistical models commonly used in neuroimaging studies, explain minimal phenotypic variation, limiting the translational utility of neuroimaging phenotypes. This is potentially due to the observation that behavioral traits are influenced by variations in neuroimaging phenotypes that are globally distributed across the cortex and are therefore not captured by thresholded, statistical parametric maps commonly reported in neuroimaging studies. Here, we developed a novel multivariate prediction method, the Bayesian polyvertex score, that turns a unthresholded statistical parametric map into a summary score that aggregates the many but small effects across the cortex for behavioral prediction. By explicitly assuming a globally distributed effect size pattern and operating on the mass univariate summary statistics, it was able to achieve higher out-of-sample variance explained than mass univariate and popular multivariate methods while still preserving the interpretability of a generative model. Our findings suggest that similar to the polygenicity observed in the field of genetics, the neural basis of complex behaviors may rest in the global patterning of effect size variation of neuroimaging phenotypes, rather than in localized, candidate brain regions and networks.

Keywords: behavioral prediction, cognition, distributed effect sizes, individual differences, neuroimaging

Introduction

Neuroimaging is central to the search for neurobiological mechanisms of cognitive processes and psychopathology. However, by far, neuroimaging studies that aim to reveal the biological correlates of phenotypic variations have limited success in the identification of reliable biomarkers for clinical diagnoses or cognitive functions. One of many reasons for this challenge is the reliance on statistical thresholds and mass univariate statistical models for many neuroimaging studies. In traditional neuroimaging analyses, the association between an imaging phenotype and phenotypic variation is assessed with mass univariate statistical models where the associative effect is estimated independently at each measured unit of the brain data, for example, vertex, voxel, or region of interest. The magnitude of the generalizable brain-behavior association is usually inferred from the effect size estimates of “only the most significant” vertices/regions of interests (ROIs) using the mass univariate estimators. Such an approach assumes that the underlying true association is sparse and localized in the cortex, and hence that clusters of vertices/ROIs with minimum P values (min-P) form the basis of generalizable signals. Although study designs and covariates are controlled for in mass univariate statistical models used to detect brain-behavior associations, the resulting regions only explain minimal variation in behavior (Poldrack et al. 2017; Stanfield et al. 2008). With a sample size of more than 14 000 participants, Smith and Nichols (2018) demonstrated that a statistically significant imaging composite measure, surviving Bonferroni correction of 14 million tests, explained less than 1% of the variance in behavior.

In reaction to the difficulty in finding reproducible, localized brain-behavior associations using mass univariate models, neuroimaging researchers have turned to multivariate machine learning methods that utilize all available imaging features for behavioral prediction, where the most predictive imaging features are interpreted post hoc (Dosenbach et al. 2010; Lebedev et al. 2014; Niu et al. 2020). This multivariate machine learning approach has shown success at capturing generalizable brain-behavior associations (Kragel et al. 2018; Sui et al. 2020), including applications in understanding individual variability in brain maturation (Brown et al. 2012), intelligence (Finn et al. 2015), emotional processing (Chang et al. 2015), and symptoms of psychiatric disorder (Rosenberg et al. 2016), to name a few. However, many machine learning models rely on the raw imaging phenotype (Smith et al. 2015; Sripada et al. 2019; Hong et al. 2020), which prevents cross-study applications of mass univariate statistics. Some multivariate statistical methods also lack one important benefit of the statistical parametric brain mapping approach, that is, the unbiased estimation and interpretation of a brain-behavior association with proper control for confounds. The concern of black-box applications of multivariate prediction methods has arisen (Davatzikos 2019; Efron 2020) due to the data-driven approach, and the lack of hypothesis-driven, generative models. Cautious interpretation of predictive models is needed since the predictive features can be ephemeral rather than important and generalizable (Scheinost et al. 2019; Efron 2020).

Inspired by the success of the field of genetics in implementing generative models to identify generalizable genotype–phenotype mapping (Visscher et al. 2017; Efron 2020), we introduce a novel multivariate prediction method, the polyvertex score (PVS), that captures the many generalizable effect sizes across all vertices. It has several innovations. First, the PVS is a generative model that explicitly takes a global prior such that all vertices contribute to the observed brain-behavior association. No statistical threshold or dimension reduction of the imaging phenotype is necessary for the calculation of the PVS. Second, the PVS can be thresholded to reflect the user’s hypothesis on the underlying signal sparsity of a brain-behavior association of interest. Comparing the predictive performance of PVSs of varying statistical thresholds yields empirical insights into the true sparseness of a brain-behavior association. Last but not least, the PVS can be applied directly to statistical parametric maps derived from mass univariate analysis, setting it apart from existing multivariate statistical methods. It can be deployed in smaller sample studies to boost predictive power when the mass univariate summary statistics can be obtained from large neuroimaging consortiums.

For comparison purpose, two versions of the PVS were developed. The mass univariate PVS (PVSU) is a summary measure of all the mass univariate effect sizes across the cortex, which is readily available for most neuroimaging analyses. The Bayesian PVS, on the other hand, is a multivariate extension of the PVSU that accounts for correlation across vertices as well as the nonsparseness of the brain signal on behavior. Previous research have shown that ignoring the correlation structure among vertices results in biased estimation of the parameter of interest (Thompson et al. 2015), limiting the ability of mass-univariate approaches to localize effects and to make accurate predictions. The Bayesian PVS (PVSB) (Fig. 1) incorporates the covariance structure of the imaging phenotype during parameter estimation. Leveraging the unprecedented large sample size of the Adolescent Brain Cognitive Development (ABCD) Study, we demonstrated the utility of the PVSB as a reliable multivariate method with great out-of-sample prediction performance, by comparing it to the PVSU, the min-P, and popular multivariate methods, including lasso regression, random forest, and support vector regression (SVR) with linear kernel. In addition to its good predictive performance, the property of the PVSB enables us to demonstrate that the generalizable brain-behavior association is distributed in the global patterning of effect sizes across the cortex.

Figure 1.

Figure 1

Open in a new tab

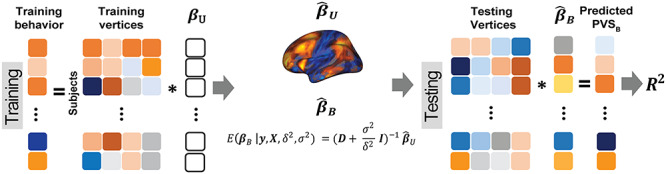
Overview of the PVSB and the PVSU algorithms. Ten-fold cross-validation was performed to obtain a PVSB for each individual. For each fold, mass univariate summary statistics, 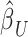Inline graphic, were obtained from the training set which contained 90% of the complete sample. Posterior mean effect sizes at each vertex, 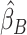Inline graphic, were approximated by multiplying the mass univariate beta estimates, 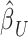Inline graphic, by the inverse of the correlation structure of the brain, D, and a shrinkage factor that accounts for the number of vertices, V, and the total signal of the brain-behavior association. The PVSB was subsequently calculated for the test set participants by multiplying their imaging phenotype with the 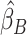Inline graphic. Simulations were conducted at three levels of total explainable signal, six levels of study sample size, and four levels of proportion of non-null vertices, yielding 60 instantiations of simulation conditions with 100 iterations per condition.

Materials and Methods

Mass-Univariate Parameter Estimation

We assume the relationship between a behavioral phenotype of interest and the imaging phenotype is captured by a general linear model. Specifically, let 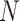Inline graphic denote the number of participants and let 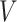Inline graphic denote the number of vertices. Then

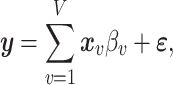graphic file with name M7.gif (1)

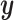where Inline graphic is a standardized 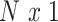Inline graphic vector of behavioral phenotypes, 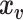Inline graphic is standardized 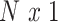Inline graphic vector of imaging data, and 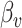Inline graphic is the association parameter for the 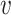Inline graphicth voxel, 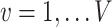Inline graphic. More generally, the regression model (1) will also include covariates of no interest, which we omit here for simplicity of exposition.

It is often not possible to estimate model (1) directly, as there are a greater number of vertices than participants, 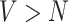Inline graphic, and the desired associations with the behavioral phenotype is instead usually estimated using a mass-univariate regression approach across individual voxels. The mass-univariate regression model is given by

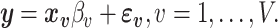graphic file with name M16.gif (2)

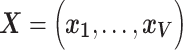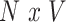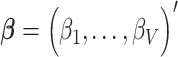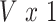Let Inline graphic denote the Inline graphic matrix of standardized imaging phenotypes and Inline graphic the Inline graphic vector of association parameters of interest. The mass-univariate brain mapping model (2) omits information contained in the correlation across columns of 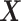Inline graphic when estimating 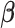Inline graphic. 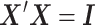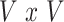In a least-squares framework, this is equivalent to assuming that the sample correlation matrix of the brain phenotype, Inline graphic, the Inline graphicidentity matrix. The least-squares estimates of 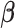Inline graphic based on mass-univariate model (2) thus take the form

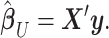graphic file with name M26.gif (3)

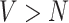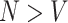Independent estimation of the parameter estimate at each vertex allows for estimation when Inline graphic and otherwise reduces the computational demand and produces more stable estimates when the voxels are highly correlated with each other (when Inline graphic).

Recent debates on reproducibility and small effect sizes in neuroimaging research are based on such mass-univariate estimates from the brain mapping framework. However, ignoring the correlation structure among vertices results in biased estimation of 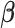Inline graphic as described in Thompson et al. (2015), limiting the ability of mass-univariate approaches to localize effects and to make accurate predictions. Moreover, the magnitude of the generalizable brain-behavior association is usually inferred from the effect size estimates of “only the most significant” vertices/ROIs using the mass univariate estimators (3). Such an approach assumes that the underlying true association is sparse and localized in the cortex, and hence that clusters of vertices/ROIs with min-P form the basis of generalizable signals. However, emerging evidence from large consortia such as the ABCD indicates that the explanatory power of the brain on behavior is nonsparse, and thus cannot be captured solely by the most significant vertices/ROIs. In order to generalize the effect sizes of the whole brain phenotype, we need a prediction framework that accounts for correlation across voxels as well as the nonsparseness of the brain signal on behavior. Rooted in this brain mapping approach, we propose the PVSB estimation and prediction framework.

Empirical Bayes Estimation of Parameter of Interest

To tackle the correlated signal of the imaging phenotype at each vertex, we developed a Bayesian approach where the correlation information across vertices is incorporated into the parameter estimation process. Similar frameworks have been proposed in the field of genetics (Vilhjálmsson et al. 2015). 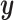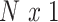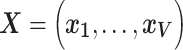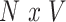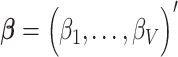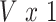Let Inline graphic denotes standardized Inline graphic vector of behavioral phenotypes, Inline graphic denotes the Inline graphic matrix of standardized imaging phenotypes and Inline graphic is a Inline graphic vector of association parameters of interest. The intuition behind the formulation of the PVSB is to estimate the posterior expectation of the multivariate linear regression coefficients 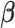Inline graphic from model (1) utilizing the mass-univariate estimator 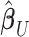Inline graphic from (3) and a regularized estimator of its 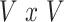Inline graphic correlation matrix.

To do so, we assume that the residuals 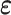Inline graphic are independent and normally distributed with constant variance, 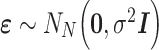Inline graphic, and give an independent normal prior with constant variance for the regression coefficients, 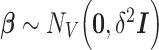Inline graphic. It is easy to show that the posterior distribution of 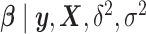Inline graphic is again multivariate normal with expectation

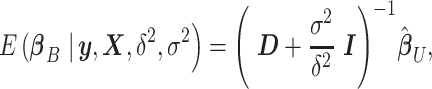graphic file with name M43.gif (4)

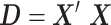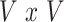where Inline graphic is the Inline graphic correlation matrix of 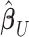Inline graphic. We can thus express the vertexwise posterior mean effect sizes of the brain phenotype under model (1) by weighting the mass univariate beta estimates 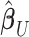Inline graphic with a factor that accounts for the observed correlation structure of the cortex 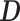Inline graphic and the per-vertex variance explained 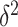Inline graphic. 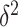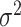Since we do not know Inline graphic and Inline graphica priori, we use plug-in estimators based on the summary statistics from the mass univariate model. We accomplish this using a method-of-moments estimator of the variance explained per vertex (Schwartzman et al. 2019):

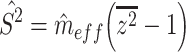graphic file with name M52.gif (5)

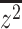where Inline graphicis the mean of the squared z-statistics of the mass univariate regressions across vertices, and the 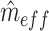Inline graphicis the estimated effective number of vertices: 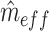Inline graphicis calculated as the number of vertices,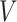Inline graphicdivided by the second spectral moment of the correlation matrix 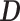Inline graphic. Then the estimated per-vertex variance explained is given by 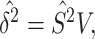Inline graphic and the estimated residual variance is given by 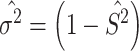Inline graphic. Thus, our Empirical Bayes estimator for 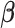Inline graphic is given by

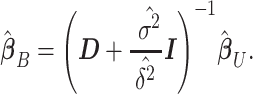graphic file with name M61.gif (6)

The benefits of implementing this Empirical Bayes parameter estimation are 2-fold: (i) the procedure takes into account the correlation of the brain phenotype across vertices, and (ii) the total estimated signal of the brain-behavior relationship is incorporated as a data-driven regularization parameter.

Behavioral Prediction

Polyvertex Scores

Motivated by the success of polygenic risk scores (PRS), a PVS can be calculated from neuroimaging data by aggregating the predictive power of all vertices on a given behavioral phenotype. We implemented two types of PVS that utilize the mass univariate and Empirical Bayes parameter estimates, respectively. A mass PVSU, based on the mass univariate parameter estimates, was computed as the brain phenotype at each vertex for an individual multiplied by the mass univariate parameter estimates acquired from an independent sample:

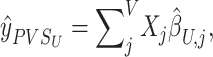graphic file with name M62.gif (7)

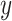where Inline graphic is a standardized 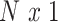Inline graphic vector of behavioral phenotypes, 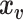Inline graphic is standardized 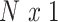Inline graphic vector of imaging data, and 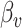Inline graphic is the association parameter for the 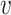Inline graphicth voxel, 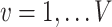Inline graphic. The PVSU summarizes the effect size at all vertices on individual variability in behavior, with the assumption of independence at each vertex.

Similarly, PVSB (Figure 1) was calculated using the Empirical Bayes parameter estimates:

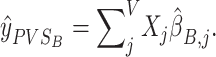graphic file with name M70.gif (8)

The PVSB is hypothesized to harness the multivariate effect of an imaging phenotype on behavior by accounting for the correlation structure and the total explainable signal of the brain phenotype and should therefore yield a superior predictive performance over the PVSU.

Thresholding Based on Statistical Significance

To address the possibility that the explanatory power on behaviors is sparse and localized in the brain, a canonical assumption of mass univariate statistical models, we tested whether thresholding the number of vertices based on statistical significance would improve the prediction performance of the PVSB. The thresholding procedure was performed as follows: we ranked the absolute effect sizes for all vertices and removed those ranked lower than a threshold proportion. Three levels of thresholding were implemented such that the top 50%, 10%, and 1% of vertices were retained for the PVSB.

To link our predictive methods with the canonical statistical inference approach where a brain and behavior relationship is established when any single vertex shows a significant association with the behavior, we compared our methods with the predictive performance of the vertex with the most significant mass univariate z-score, which we have referred to as the min-P model. A total of six prediction models were examined, namely, the PVSU, the PVSB, PVSB 50%, PVSB 10%, PVSB 1%, and min-P.

Out-of-sample variance explained 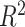Inline graphic was used to evaluate the predictive accuracy of each method. Simulations were performed to assess the predictive performance of the above-mentioned six methods. The simulation procedure, cross-validation scheme, and simulation results were shown in the Supplementary Material.

Empirical Data

We examined whether functional neuroimaging phenotypes could predict complex behaviors with greater predictive power by (i) aggregating over all unthresholded effects across the cortex and (2) incorporating the covariance structure of the imaging phenotype. The PVSB and its thresholded variants, the PVSU, and min-P model were implemented to assess the predictive power of two functional magnetic resonance imaging (fMRI) contrasts on two different cognitive tasks using the baseline data of the ABCD Study.

Sample

The ABCD Study is a population-based longitudinal study across 21 data acquisition sites in the United States of America following 11 875 demographically diverse children starting at 9 and 10 years old (Garavan et al. 2018). Participants were recruited through a probability sampling procedure at the school level within the defined catchment area of the study’s nationally distributed set of 21 recruitment sites. The ABCD sample also included a large twin cohort and many siblings. Family relatedness was documented and controlled for in the analyses in this paper such that twins and siblings from the same family were grouped into the same training or testing set. Study inclusion criteria were detailed in Casey et al. (2018) and Hagler et al. (2019). Additional data quality control was applied to the complete baseline data of the ABCD Study, yielding a final sample of over 6000 participants. Quality control criteria and the descriptive characteristics of the final sample were presented in the Supplementary Material.

With the complete baseline data of the ABCD study, we estimated the predictive performance of the vertex-wise “2 back versus 0 back” contrast from the Emotional N-back fMRI task (nBack; Casey et al. 2018) and the “correct stop versus correct go” contrast from the Stop Signal Task (SST; Logan 1994) on the “Total Composite (TC) Score” from the NIH Toolbox Cognition Battery (NTCB) ages 7–17 ( Gershon et al. 2013) and the “Stop Signal Reaction Time” (SSRT) from the SST task, respectively. NBack-SSRT and SST-TC associations were assessed to examine the specificity of prediction. Four brain-behavior associations of interest were examined: nBack predicting TC, nBack predicting SSRT, SST predicting TC, and SST predicting SSRT. To account for the potential contribution of subcortical ROIs on behavioral variability, a whole brain imaging phenotype was created by combining the BOLD activity of the FreeSurfer subcortical ROIs (excluding ventricles; Fischl et al. 2002) with the vertexwise fMRI data. The predictive performance of these whole brain phenotypes on the above-mentioned four associations was also estimated.

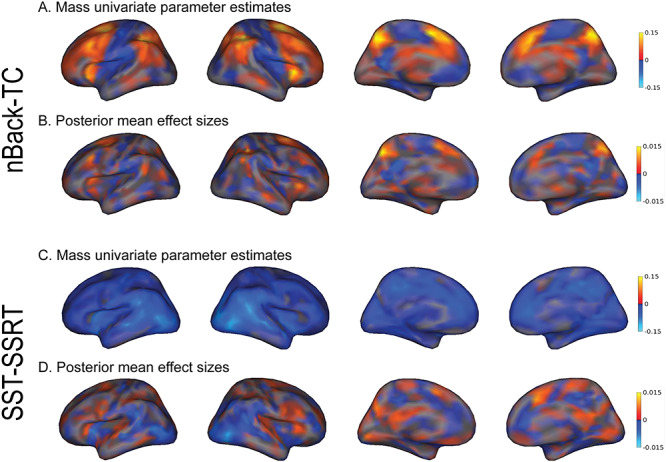
Ten-fold cross-validation was performed for each association. Variance explained 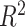Inline graphic, the squared Pearson correlation between the observed and predicted behavioral phenotypes, was calculated for each association. Rigorous covariate control was applied to the data to ensure that the identified brain-behavior associations were not attributable to demographic and socioeconomical confounds known to influence brain or behavioral variation. Failing to control for these confounds may result in inflated prediction performance for multivariate methods (Scheinost et al. 2019). Both brain and behavioral phenotypes were preresidualized for age, sex, race, ethnicity, household income, parental education, household marital status, and scanner ID independently within each training and testing set.

FMRI Tasks and Processing Steps

The nBack task incorporated facial and emotional processing to the traditional N-back task to assess memory and emotional regulation processes. The nBack task consisted of two runs. Within each run, participants were shown a series of stimuli and were instructed to indicate if a stimulus was the same as or different from the stimulus they saw N items earlier for each stimulus. There were two conditions for the nBack task: a 2-back versus fixation condition and a 0-back versus fixation condition which served as baseline. The “2 back versus 0 back” contrast was used in this analysis.

The SST was used to assess the BOLD activity during inhibitory control. Participants were instructed to indicate the direction of a left or right arrow as quickly and accurately as possible, but were instructed not to respond when a left or right arrow was followed by an upward arrow. The full details of the fMRI tasks used in the ABCD Study were documented in Casey et al. (2018).

Structural and task-based functional magnetic resonance imaging (MRI) data acquisition were conducted with 3T scanners, with multiband echo planar imaging with fast integrated distortion correction and were harmonized across scanner vendors. Preprocessing steps included head motion correction, B0 distortion correction, resampling with cubic interpolation, between-scan motion correction, and automated registration. General linear models implemented in AFNI’s 3dDeconvolve were used to estimate task-related activation strength at the individual subject level, with hemodynamic response functions modeled using a gamma variate basis function plus its temporal derivative. Averaged beta coefficients per participant across two runs were calculated by weighting each run with the nominal degrees of freedom of that run and were used in this analysis. Detailed imaging processing and analysis pipelines were described in Hagler et al. (2019).

Behavioral Measures

The NTCB ages 7–17 is a comprehensive suite of neurobehavioral measurements. NTCB consists of seven subtests: the Flanker Inhibitory Control and Attention Test, the Picture Sequence Memory Test, the List Sorting Working Memory Test, Picture Vocabulary Test, Oral Reading Recognition Test, Dimensional Change Card Sorting Test, and Pattern Comparison Processing Speed Test. The TC score, the average of all 7 subtests, is a composite index of general cognitive ability and was used in this study.

The SSRT was derived from the behavioral performance measures acquired during the SST. It was computed by subtracting the median stop signal delay of all successful stop trials from the nth percentile go reaction time, where n represents the percentage of successful inhibitions.

Multivariate Method Comparisons

To assess the predictive performance of the PVSB relative existing multivariate models, we submitted the above-mentioned empirical data to three additional multivariate methods: LASSO, random forest, and SVR with linear kernel, and compared their predictive performance with that of the PVSB. These methods were chosen to complement PVSB’s statistical emphasis. Although LASSO is a parametric regression-based method similar to the PVSB, its sparsity assumption sets it aside from the PVSB, which assumes a global prior. SVR and random forest, on the other hand, are popular nonparametric methods that capture nonlinear effects for better prediction. Matlab implementation of these multivariate methods was described in the Supplementary Material. To make our results compatible with previous multivariate analyses of differing covariates treatments (Finn et al. 2015; Sripada et al. 2019; Cui et al. 2020), we repeated these analyses with two additional covariate control schemes. Out-of-sample variance explained for all multivariate methods after controlling for (1) age, sex, and scanner ID, and (2) age, sex, scanner ID, race, and ethnicity, was estimated.

Results

Simulation Results: the PVSB Demonstrated Superiority at Capturing Global, Distributed Brain-Behavior Association Patterns

The reliability of the predictive performance of the PVS framework was established across a suite of simulated conditions (Fig. 2 and Supplementary Material). The PVSB better captured the variance explained in behavior than the PVSU and the min-P (most significant vertex) across varying conditions of magnitude (total explainable signal; Fig. 2A), sample size (Fig. 2B), and nonsparseness of the true signal across the cortex (proportion of non-null vertices; Fig. 2C). This shows the benefit of accounting for the correlation structure of the brain for behavioral prediction. The PVSB also outperformed its thresholded variants when the signal structure was global (Fig. 2D,E). When the true signal structure was sparse, thresholding PVSB at the corresponding threshold yielded better performance (Fig. 2F), demonstrating the sensitivity of the PVSB to the underlying true signal structure.

Figure 2.

Figure 2

Open in a new tab

The PVSB demonstrated superior predictive performance compared with the PVSU, and min-P (A–C) as well as its thresholded variants (D–F) across various simulated conditions. Figure 2 showed the mean and 1.96 standard deviation confidence interval of the proportion of total variance explained by each method. The advantage of the PVSB over the PVSU and the min-P was most prominent at higher levels of total explainable signal (A), larger sample size (B), and with increased proportion of non-null vertices (C). When the true signal structure was nonsparse, (10, 50, and 100% of non-null vertices; C), the advantage in prediction accuracy of the PVSB was prominent, manifested by its superior, prediction performance compared with the PVSU and min-P. Superior predictive performance was established for the PVSB compared with its thresholded variants (D, E). When the true signal structure was global, the PVSB outperformed its thresholded variants across levels of total explainable signals (D) and across sample sizes (E). Sensitivity to the underlying signal structure of the PVSB was estimated with varying simulated levels of signal sparsity (F): when the true signal structure was sparse, that is, the proportion of non-null vertices was small, the thresholded PVSB at the corresponding level of statistical threshold outperformed the unthresholded PVSB, highlighting the sensitivity of the PVSB to the underlying signal structure of the simulated brain-behavior association. The complete simulation results were reported in Supplementary Material.

Empirical Results: Behavioral Variability was Better Predicted by the Unthresholded Task Activation Pattern Captured by the PVSB

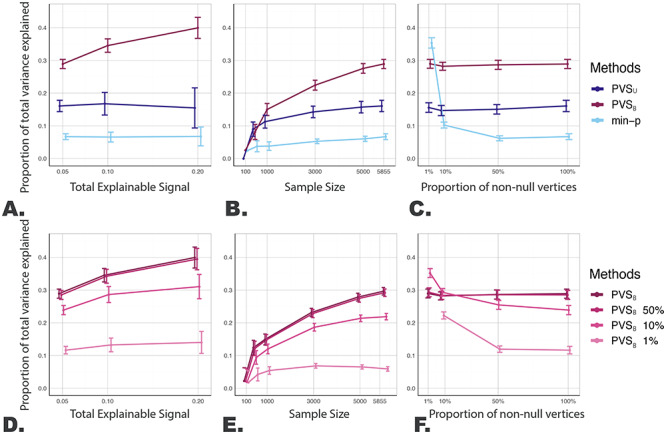
After establishing the efficacy of the PVSB at capturing global brain-behavior associations using simulation, we explored whether individual differences in cognitive processes can be better predicted by whole brain rather than thresholded task activation patterns using the baseline data from the ABCD Study (Fig. 3). For the nBack-TC association, the PVSB outperformed the PVSU and min-P, capturing 12.6% compared with 6.9% and 3.5% of the variance in the n-Back-TC association. Similar improvement in prediction accuracy was also observed for the SST-SSRT association. The PVSB was able to explain 11.7% of the variance in SSRT using the vertex-wise BOLD variation of the correct stop versus correct go contrast from the SST, compared with 1.7% and 1.5% for the PVSU and the min-P, respectively. The increased predictive performance of the PVSB highlights the importance of accounting for the correlation structure of the imaging phenotype when measuring the generalizable signal between brain and behavior. Interestingly, the imaging contrasts only showed associations with the behaviors that used similar underlying cognitive constructs to the fMRI tasks: no associations were found between the nBack contrast and SSRT and between the SST contrast and TC. Such specificity has been found in other fMRI studies (Rosenberg et al. 2020) and further highlights the benefit of the PVSB at capturing effective association patterns without overfitting.

Figure 3.

Figure 3

Open in a new tab

Decreased predictive performance was associated with more stringently thresholded models for the empirical brain-behavior associations. Variance explained, R2, for four brain-behavior associations (nBack predicting TC, SST predicting SSRT, nBack predicting SSRT, SST predicting TC) were examined using the PVSU, PVSB, thresholded variants of the PVSB, and min-P. Significant associations were identified for the nBack-TC and SST-SSRT, but not for the nBack-SSRT and SST-TC associations. For the two significant associations, the best prediction performance was achieved by the PVSB where all vertices where included in the model. Predictive performance decreased as more stringent thresholds were applied. All brain and behavioral variables were preresidualized for age and categorical variables including sex, parent marital status, highest level of parental education, household income, self-reported race and ethnicity, and MRI scanner ID.

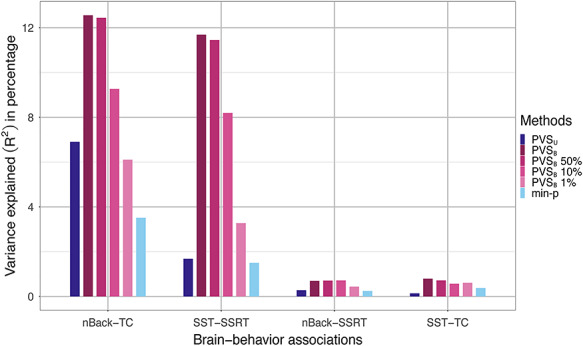
Thresholding the PVSB at varying statistical thresholds, on the other hand, did not confer any advantage for prediction accuracy. For both significant associations, the predictive performance of the PVSB decreased as more stringent statistical thresholds were applied. Specifically, for the nBack-TC association, decreased predictive performance was found for the PVSB 50% (R2 = 12.4%) and PVSB 10% (R2 = 9.2%) compared with the PVSB (R2 = 12.6%). A similar drop in predictive accuracy was found for the SST-SSRT association (PVSB: R2 = 11.7%, PVSB 50%: R2 = 11.5%; PVSB 10%: R2 = 8.2%). Thresholding based on the vertex-wise P values resulted in decreased prediction accuracy, suggesting that vertices with subthresholded P values were still informative for behavioral prediction. The visualization of the distributed pattern of mass univariate statistics (Fig. 4A,C) and the posterior mean effect sizes (Fig. 4B,D) across the cortex, further corroborated our hypothesis that the predictive effect of the brain on complex behavior was indeed global and distributed across the cortex. No improvement was observed by including subcortical ROIs for prediction, as shown by the comparable predictive performance of the cortical imaging phenotype relative to that of the whole brain imaging phenotypes (Supplementary Material Table 2).

Figure 4.

Figure 4

Open in a new tab

Distributed pattern of effects across the cortex for the nBack-TC and SST-SSRT associations. Unthresholded vertexwise mass univariate standardized parameter estimates and posterior mean effect sizes were displayed for the nBack-TC and SST-SSRT associations. The unthresholded mass univariate parameter estimates were used to calculate the PVSU and the posterior mean effect sizes were used to calculate the PVSB for each association. For the nBack-TC association, both mass univariate (A) and posterior mean effect size maps (B) showed distributed patterns of association across the cortex, suggesting that the association between imaging and behavioral phenotypes were global, spanning the whole cortex. Similar distributed patterns were found for the SST-SSRT association. Compared with the mass univariate statistical map (C), the posterior mean effect size map (D) of the SST-SSRT association showed greater variation in the relative weighting of brain regions on behavioral prediction, potentially contributing to the greater prediction accuracy for the PVSB compared with the PVSU for this association. The interpretation of the posterior mean effect size maps should be attempted with caution as the validity of these effect sizes rests upon the assumption of the global prior such that all vertices contribute to brain-behavior associations.

Multivariate Method Comparisons

The PVSB demonstrated comparable if not superior predictive performance compared to other multivariate methods (Table 1). All methods except the SVR with linear kernel explained at least 10% of the variance explained of the nBack-TC association after controlling for demographic variables. For the SST-SSRT association, the PVSB explained more than 10% of the out-of-sample variance in behavior, whereas random forest and LASSO achieved only 8% and 8.7% variance explained, respectively. Such difference in prediction accuracy may be due to overfitting of the random forest and LASSO to the noisier SST imaging phenotype, highlighting the importance of having high quality imaging data in multivariate statistical analysis. More stringent covariate control, on the other hand, reduced the predictive performance of all methods on the nBack-TC but not the SST-SSRT association (Supplementary Material Table 2), suggesting that insufficient covariates control would inflate the magnitude of association detected by multivariate statistical methods and that such inflation may be specific to the association of interest.

Table 1.

The PVSB demonstrated comparable if not superior generalization performance relative to other multivariate methods. The out-of-sample variance explained, R2, of each multivariate method was shown for each empirical brain-behavior association. Although the PVSB, random forest, and LASSO showed comparable predictive performance for the nBack-TC association, the PVSB outperformed other multivariate methods for the SST-SSRT association. Minimal association was again found for the nBack-SSRT and SST-TC contrasts

Associations PVSB Random Forest LASSO SVR
nBack-TC 11.58 10.88 10.42 2.25
nBack-SSRT 0.76 0.12 0.13 0.07
SST-TC 0.46 0.38 0.00 0.08
SST-SSRT 10.64 8.03 8.70 3.45
Open in a new tab

Discussion

In this study, we presented the empirical utility of a new multivariate prediction method, the PVSB, and showed that greater out-of-sample behavioral prediction of imaging phenotypes could be achieved by explicitly modeling the globally distributed brain-behavioral associations across the cortex. The PVSB captures the unthresholded, generalizable predictive effect of an imaging phenotype on behavior by calibrating the mass univariate summary statistics with the estimated covariance structure of the imaging phenotype and a global prior of effect sizes. Using the Emotional N-back and the SST fMRI contrasts from the ABCD Study, we demonstrated that greatest predictive performance of fMRI phenotypes on complex behaviors can be achieved using the unthresholded multivariate effect size pattern captured by the PVSB. Our findings suggested that the predictive power of imaging phenotypes on complex behaviors was distributed rather than localized across the cortex, and such global effect needs to be explicitly modeled in the statistical methods used by neuroimaging studies in order to holistically understand the neural bases of psychiatric disorders and cognitive functions.

Traditional methods used to analyze brain-behavior relationships aim to detect individual brain regions or localized clusters significantly associated with phenotypic variation. Rooted in signal detection theory, this brain mapping approach has been fruitful in characterizing the explanatory effect of brain regions on behavior, but has demonstrated suboptimal replicability (Ihnen et al. 2009; King et al. 2019) and therefore limited translational utility for psychopathology. When predicting individual differences in phenotypic variation, sparse and focal association patterns, captured by statistical thresholding based on P values, did not confer any advantage over the unthresholded association pattern captured by the PVSB. Along with other neuroimaging studies that have reported similar distributed association patterns (Gonzalez-Castillo et al. 2012; Poldrack et al. 2017; Bruin et al. 2019; Dubois et al. 2018; Sripada et al. 2019), our findings suggest that the power for predicting individual variability in complex cognitive behaviors is globally distributed in an imaging phenotype, above and beyond a localized and sparse region or network. Although lower level visual motor processes and specialized cognitive behaviors may be more accurately captured by localized association patterns (Sereno et al. 1995; Tsao et al. 2003), complex cognitive processes and risk for psychiatric disorders may be more accurately predicted by distributed, global patterns of BOLD activation across the cortex.

Our results further demonstrate the importance of moving beyond mass univariate statistical models in neuroimaging research (Reddan et al. 2017; Smith and Nichols 2018; Kragel et al. 2018). Common fMRI practice assumes that BOLD activity has a localized correlation structure. However, long-range correlations in BOLD activity across the cortex have been well documented by resting-state fMRI research and have demonstrated important behavioral implications. Here, we found that including the covariance structure of the imaging phenotype during parameter estimation greatly improved the predictive performance of functional imaging phenotypes. Similar improvement of predictive accuracy of regional cortical morphology on cognitive outcomes was shown in children (Palmer et al. 2020). Predictive performance is of great importance to the utility of biomarkers on clinical disorders or cognitive processes. As a result, neuroimaging studies that aim to generate potential biomarkers using functional neuroimaging phenotypes should adopt and develop new statistical methods that estimate the multivariate, distributed associative effects between brain and behavior.

Our results echoed the solution of the small effect size issue adopted by the field of genetics. Similar to traditional neuroimaging studies, mass univariate statistical models and statistical thresholding are used in genome-wide association studies (GWAS) to localize genetic loci that are significantly associated with psychiatric disorders and cognitive processes. With thousands of participants and unprecedented statistical power, GWAS-based significant genetic loci only account for a fraction of the variance in complex human phenotypes. To resolve this issue, PRS (Purcell et al. 2009) were subsequently developed from GWAS to aggregate the small effect sizes across the whole genome, including those nonsignificant loci (Yang et al. 2010; Davies et al. 2011; Le Hellard and Steen 2014; Torkamani et al. 2018). By pulling together the effects of many informative but not necessarily statistically significant genetic variants, PRS greatly improved the predictive performance of genetic data on stratifying psychiatric risk based on the polygenic burden of common variants (Purcell et al. 2009; Dudbridge 2013), fueling the discovery that complex behaviors are polygenic (Visscher et al. 2017; Gibson 2018). Given the similarity of observed small effect sizes of neuroimaging and genetics research, individual variability in complex behavior may be attributable to the structural and functional differences across the whole brain. Indeed, as our results indicated, complex behaviors are polyvertex, with each vertex contributing only minimally to the variance explained in behavior and thus not surviving statistical thresholding. To capture the distributed, small predictive effects of the brain on behavior, multivariate methods (Chang et al. 2015; Finn et al. 2015; Bruin et al. 2019) are essential, and a multivariate method that captures the subthreshold effect sizes of the imaging data is needed.

The PVSB is one of many multivariate statistical methods available for neuroimaging analyses. Although the predictive advantage of various multivariate models is dependent on the sample size, imaging features, the magnitude of the effect sizes and other sample characteristics (Jollans et al. 2019), our results showed that the predictive accuracy was comparable across multivariate methods, with slightly greater performance of the PVSB on the SST-SSRT contrast. In addition to its good prediction accuracy, the PVSB confers other advantages. First, following the brain mapping approach, the PVSB maps the effect sizes at every vertex without reducing the dimensionality of the imaging phenotype, providing the scientific interpretability unavailable to nonparametric multivariate methods, making it a useful tool for the neuroimaging community. Second, the PVSB offers empirical insights into the underlying signal structure of a brain-behavior association of interest. Last, mass univariate summary statistics from large neuroimaging dataset can be supplied to the PVSB for prediction in a small independent sample, which makes the PVSB a useful tool to harvest the statistical power of large neuroimaging consortiums for smaller imaging studies.

In summary, results from this study suggest that in order for neuroimaging studies to identify possible biomarkers for cognitive and clinical outcomes, greater predictive power of the functional neuroimaging phenotypes needs to established, which can be achieved through the statistical modeling of global, distributed effects using multivariate statistical methods, one of which being the PVSB. Using a large sample from the ABCD study, we have demonstrated the utility of employing multivariate parameter estimation and aggregating the effect across a functional neuroimaging phenotype for greater predictive power for behavior. With an increasing interest in the predictive utility of imaging phenotypes as biomarkers for health and disease, this novel work will pave the way for improving our ability to reach this goal.

Notes

Conflict of Interest: The authors declared no conflict of interest.

Funding

National Institutes of Health and additional federal partners (U01DA041022, U01DA041028, U01DA041048, U01DA041089, U01DA041106, U01DA041117, U01DA041120, U01DA041134, U01DA041148, U01DA041156, U01DA041174, U24DA041123, U24DA041147, U01DA041093, U01DA041025). This research is partially supported by National Institute of Mental Health grant (R01MH122688).

Declaration

Data used in the preparation of this article were obtained from the Adolescent Brain Cognitive Development (ABCD) Study (https://abcdstudy.org), held in the NIMH Data Archive (NDA). The ABCD Study is a multisite, longitudinal study designed to recruit more than 10 000 children age 9–10 and follow them over 10 years into early adulthood. A full list of supporters is available at https://abcdstudy.org/federal-partners.html. A listing of participating sites and a complete listing of the study investigators can be found at https://abcdstudy.org/Consortium_Members.pdf. ABCD consortium investigators designed and implemented the study and/or provided data but did not all necessarily participate in analysis or writing of this report. This manuscript reflects the views of the authors and may not reflect the opinions or views of the NIH or ABCD consortium investigators. The ABCD data repository grows and changes over time.

Supplementary Material

PVSB_CC_SI_Final_bhaa290
Click here for additional data file. (7.4MB, docx)

Contributor Information

Weiqi Zhao, Department of Cognitive Science, University of California, La Jolla, CA 92093, USA.

Clare E Palmer, Center for Human Development, University of California, La Jolla, CA 92161, USA.

Wesley K Thompson, Division of Biostatistics, Department of Family Medicine and Public Health, University of California, San Diego, La Jolla, CA, USA.

Bader Chaarani, Department of Psychiatry, University of Vermont, Burlington, Vermont, 05405, USA.

Hugh P Garavan, Department of Psychiatry, University of Vermont, Burlington, Vermont, 05405, USA.

B J Casey, Department of Psychology, Yale University, New Haven, Connecticut, 06520, USA.

Terry L Jernigan, Department of Cognitive Science, University of California, La Jolla, CA 92093, USA; Center for Human Development, University of California, La Jolla, CA 92161, USA; Department of Radiology, University of California, San Diego School of Medicine, La Jolla, CA 92037, USA; Department of Psychiatry, University of California, San Diego School of Medicine, La Jolla, CA 92037, USA.

Anders M Dale, Department of Radiology, University of California, San Diego School of Medicine, La Jolla, CA 92037, USA; Department of Psychiatry, University of California, San Diego School of Medicine, La Jolla, CA 92037, USA; Department of Neuroscience, University of California, San Diego School of Medicine, La Jolla, CA 92037, USA; Center for Multimodal Imaging and Genetics, University of California, San Diego School of Medicine, La Jolla, CA 92037, USA.

Chun Chieh Fan, Center for Human Development, University of California, La Jolla, CA 92161, USA; Center for Multimodal Imaging and Genetics, University of California, San Diego School of Medicine, La Jolla, CA 92037, USA.

References

  1. Brown  TT, Kuperman  JM, Chung  Y, Erhart  M, McCabe  C, Hagler  DJ  Jr, Venkatraman  VK, Akshoomoff  N, Amaral  DG, Bloss  CS  et al.  2012. Neuroanatomical assessment of biological maturity. Curr Biol. 22:1693–1698. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bruin  W, Denys  D, van  Wingen  G. 2019. Diagnostic neuroimaging markers of obsessive-compulsive disorder: initial evidence from structural and functional MRI studies. Prog Neuropsychopharmacol Biol Psychiatry. 91:49–59. [DOI] [PubMed] [Google Scholar]
  3. Casey  BJ, Cannonier  T, Conley  MI, Cohen  AO, Barch  DM, Heitzeg  MM, Soules  ME, Teslovich  T, Dellarco  DV, Garavan  H  et al.  2018. The adolescent brain cognitive development (ABCD) study: imaging acquisition across 21 sites. Dev Cogn Neurosci. 32:43–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Chang  LJ, Gianaros  PJ, Manuck  SB, Krishnan  A, Wager  TD. 2015. A sensitive and specific neural signature for picture-induced negative affect. PLoS Biol. 13:e1002180. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Cui  Z, Li  H, Xia  CH, Larsen  B, Adebimpe  A, Baum  GL, Cieslak  M, Gur  RE, Gur  RC, Moore  TM  et al.  2020. Individual variation in functional topography of association networks in youth. Neuron. 106:340–353.e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Davatzikos  C 2019. Machine learning in neuroimaging: progress and challenges. Neuroimage. 197:652–656. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Davies  G, Tenesa  A, Payton  A, Yang  J, Harris  SE, Liewald  D, Ke  X, Le Hellard  S, Christoforou  A, Luciano  M  et al.  2011. Genome-wide association studies establish that human intelligence is highly heritable and polygenic. Mol Psychiatry. 16:996–1005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Dosenbach  NUF, Nardos  B, Cohen  AL, Fair  DA, Power  JD, Church  JA, Nelson  SM, Wig  GS, Vogel  AC, Lessov-Schlaggar  CN  et al.  2010. Prediction of individual brain maturity using fMRI. Science. 329:1358–1361. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Dubois  J, Galdi  P, Paul  LK, Adolphs  R. 2018. A distributed brain network predicts general intelligence from resting-state human neuroimaging data. Philos Trans R Soc Lond B Biol Sci. 373:20170284. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Dudbridge  F 2013. Power and predictive accuracy of polygenic risk scores. PLoS Genet. 9:e1003348. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Efron  B 2020. Prediction, estimation, and attribution. J Am Stat Assoc. 115:636–655. [Google Scholar]
  12. Finn  ES, Shen  X, Scheinost  D, Rosenberg  MD, Huang  J, Chun  MM, Papademetris  X, Constable  RT. 2015. Functional connectome fingerprinting: identifying individuals using patterns of brain connectivity. Nat Neurosci. 18:1664–1671. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Fischl  B, Salat  DH, Busa  E, Albert  M, Dieterich  M, Haselgrove  C, van der  Kouwe  A, Killiany  R, Kennedy  D, Klaveness  S  et al.  2002. Whole brain segmentation: neurotechnique automated labeling of neuroanatomical structures in the human brain. Neuron. 33:341–355. [DOI] [PubMed] [Google Scholar]
  14. Garavan  H, Bartsch  H, Conway  K, Decastro  A, Goldstein  RZ, Heeringa  S, Jernigan  T, Potter  A, Thompson  W, Zahs  D. 2018. Recruiting the ABCD sample: design considerations and procedures. Dev Cogn Neurosci. 32:16–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Gershon  RC, Wagster  MV, Hendrie  HC, Fox  NA, Cook  KF, Nowinski  CJ. 2013. NIH toolbox for assessment of neurological and behavioral function. Neurology. 80:S2–S6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Gibson  G 2018. Population genetics and GWAS: a primer. PLoS Biol. 16:e2005485. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Gonzalez-Castillo  J, Saad  ZS, Handwerker  DA, Inati  SJ, Brenowitz  N, Bandettini  PA. 2012. Whole-brain, time-locked activation with simple tasks revealed using massive averaging and model-free analysis. Proc Natl Acad Sci U S A. 109:5487–5492. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Hagler  DJ, Hatton  SN, Makowski  C, Daniela Cornejo  M, Fair  DA, Dick  AS, Sutherland  MT, Casey  BJ, Barch  DM  et al.  2019. Image processing and analysis methods for the adolescent brain cognitive development study. Neuroimage. 202:116091. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hong  S-J, Sisk  L, Caballero  C, Mekhanik  A, Roy  AK, Milham  MP, Gee  DG. 2020. Decomposing complex links between the childhood environment and brain structure in school-aged youth. bioRxiv 2020.04.28.063461. [DOI] [PMC free article] [PubMed]
  20. Ihnen  SKZ, Church  JA, Petersen  SE, Schlaggar  BL. 2009. Lack of generalizability of sex differences in the fMRI BOLD activity associated with language processing in adults. Neuroimage. 45:1020–1032. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. International Schizophrenia Consortium, Purcell  SM, Wray  NR, Stone  JL, Visscher  PM, O’Donovan  MC, Sullivan  PF, Sklar  P. 2009. Common polygenic variation contributes to risk of schizophrenia and bipolar disorder. Nature. 460:748–752. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Jollans  L, Boyle  R, Artiges  E, Banaschewski  T, Desrivières  S, Grigis  A, Martinot  J-L, Paus  T, Smolka  MN, Walter  H  et al.  2019. Quantifying performance of machine learning methods for neuroimaging data. Neuroimage. 199:351–365. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. King  JB, Prigge  MBD, King  CK, Morgan  J, Weathersby  F, Fox  JC, Dean  DC 3rd, Freeman  A, Villaruz  JAM, Kane  KL  et al.  2019. Generalizability and reproducibility of functional connectivity in autism. Mol Autism. 10:27. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kragel  PA, Koban  L, Barrett  LF, Wager  TD. 2018. Representation, pattern information, and brain signatures: from neurons to neuroimaging. Neuron. 99:257–273. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Le Hellard  S, Steen  VM. 2014. Genetic architecture of cognitive traits. Scand J Psychol. 55:255–262. [DOI] [PubMed] [Google Scholar]
  26. Lebedev  AV, Westman  E, Van Westen  GJP, Kramberger  MG, Lundervold  A, Aarsland  D, Soininen  H, Kłoszewska  I, Mecocci  P, Tsolaki  M  et al.  2014. Random Forest ensembles for detection and prediction of Alzheimer’s disease with a good between-cohort robustness. Neuroimage Clin. 6:115–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Logan  GD 1994. On the ability to inhibit thought and action: a users’ guide to the stop signal paradigm In: Dagenbach  D, editor. Inhibitory processes in attention, memory, and language. Vol xiv San Diego, CA, US: Academic Press, pp. 189–239. [Google Scholar]
  28. Niu  X, Zhang  F, Kounios  J, Liang  H. 2020. Improved prediction of brain age using multimodal neuroimaging data. Hum Brain Mapp. 41:1626–1643. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Palmer  CE, Zhao  W, Loughnan  R, Zou  J, Fan  CC, Thompson  WK, Jernigan  TL, Dale  AM. 2020. Determining the association between regionalisation of cortical morphology and cognition in 10,145 children. bioRxiv. doi: 10.1101/816025. [DOI]
  30. Poldrack RA, Baker CI, Durnez J, Gorgolewski KJ, Matthews PM, Munafò MR, Nichols TE, Poline J-B, Vul E, Yarkoni T.  2017. Scanning the horizon: towards transparent and reproducible neuroimaging research. Nat Rev Neurosci. 18:115–126. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Reddan  MC, Lindquist  MA, Wager  TD. 2017. Effect size estimation in neuroimaging. JAMA Psychiat. 74:207–208. [DOI] [PubMed] [Google Scholar]
  32. Rosenberg  MD, Finn  ES, Scheinost  D, Papademetris  X, Shen  X, Constable  RT, Chun  MM. 2016. A neuromarker of sustained attention from whole-brain functional connectivity. Nat Neurosci. 19:165–171. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Rosenberg MD, Martinez SA, Rapuano KM, Conley MI, Cohen AO, Daniela Cornejo M, Hagler DJ, Anderson KM, Wager TD, Feczko E, Earl E, Fair DA, Barch DM, Watts R, Casey BJ.  2020. Behavioral and neural signatures of working memory in childhood. J Neurosci. 40:5090–5104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Scheinost  D, Noble  S, Horien  C, Greene  AS, Lake  EM, Salehi  M, Gao  S, Shen  X, O’Connor  D, Barron  DS  et al.  2019. Ten simple rules for predictive modeling of individual differences in neuroimaging. Neuroimage. 193:35–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Schwartzman  A, Schork  AJ, Zablocki  R, Thompson  WK. 2019. A simple, consistent estimator of heritability for genome-wide association studies. The Ann Appl Stat. 13:2509–2538. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Sereno  MI, Dale  AM, Reppas  JB, Kwong  KK, Belliveau  JW, Brady  TJ, Rosen  BR, Tootell  RB. 1995. Borders of multiple visual areas in humans revealed by functional magnetic resonance imaging. Science. 268:889–893. [DOI] [PubMed] [Google Scholar]
  37. Smith  SM, Nichols  TE. 2018. Statistical challenges in “big data” human neuroimaging. Neuron. 97:263–268. [DOI] [PubMed] [Google Scholar]
  38. Smith  SM, Nichols  TE, Vidaurre  D, Winkler  AM, Behrens  TEJ, Glasser  MF, Ugurbil  K, Barch  DM, Van Essen  DC, Miller  KL. 2015. A positive-negative mode of population covariation links brain connectivity, demographics and behavior. Nat Neurosci. 18:1565–1567. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Sripada  C, Rutherford  S, Angstadt  M, Thompson  WK, Luciana  M, Weigard  A, Hyde  LH, Heitzeg  M. 2019. Prediction of neurocognition in youth from resting state fMRI. Mol Psychiatry. 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Stanfield  AC, McIntosh  AM, Spencer  MD, Philip  R, Gaur  S, Lawrie  SM. 2008. Towards a neuroanatomy of autism: a systematic review and meta-analysis of structural magnetic resonance imaging studies. Eur Psychiatry. 23:289–299. [DOI] [PubMed] [Google Scholar]
  41. Sui  J, Jiang  R, Bustillo  J, Calhoun  V. Forthcoming 2020. Neuroimaging-based individualized prediction of cognition and behavior for mental disorders and health: methods and promises. Biol Psychiatry. doi: 10.1016/j.biopsych.2020.02.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Thompson  WK, Wang  Y, Schork  AJ, Witoelar  A, Zuber  V, Xu  S, Werge  T, Holland  D, Schizophrenia Working Group of the Psychiatric Genomics Consortium, Andreassen  OA  et al.  2015. An empirical Bayes mixture model for effect size distributions in genome-wide association studies. PLoS Genet. 11:e1005717. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Torkamani  A, Wineinger  NE, Topol  EJ. 2018. The personal and clinical utility of polygenic risk scores. Nat Rev Genet. 19:581–590. [DOI] [PubMed] [Google Scholar]
  44. Tsao  DY, Freiwald  WA, Knutsen  TA, Mandeville  JB, Tootell  RBH. 2003. Faces and objects in macaque cerebral cortex. Nat Neurosci. 6:989–995. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Vilhjálmsson  BJ, Yang  J, Finucane  HK, Gusev  A, Lindström  S, Ripke  S, Genovese  G, Loh  P-R, Bhatia  G, Do  R  et al.  2015. Modeling linkage disequilibrium increases accuracy of polygenic risk scores. Am J Hum Genet. 97:576–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Visscher  PM, Wray  NR, Zhang  Q, Sklar  P, McCarthy  MI, Brown  MA, Yang  J. 2017. 10 years of GWAS discovery: biology, function, and translation. Am J Hum Genet. 101:5–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Yang  J, Benyamin  B, McEvoy  BP, Gordon  S, Henders  AK, Nyholt  DR, Madden  PA, Heath  AC, Martin  NG, Montgomery  GW  et al.  2010. Common SNPs explain a large proportion of the heritability for human height. Nat Genet. 42:565–569. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

PVSB_CC_SI_Final_bhaa290
Click here for additional data file. (7.4MB, docx)

Articles from Cerebral Cortex (New York, NY) are provided here courtesy of Oxford University Press

RESOURCES