Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Jan 28;12(4):1360–1366. doi: 10.1021/acs.jpclett.0c03171

Effective Negative Diffusion of Singlet Excitons in Organic Semiconductors

Anton Matthijs Berghuis †,*, T V Raziman †, Alexei Halpin †, Shaojun Wang †,‡, Alberto G Curto †, Jaime Gómez Rivas †,¶,*
PMCID: PMC7869104  PMID: 33507078

Abstract

graphic file with name jz0c03171_0005.jpg

Using diffraction-limited ultrafast imaging techniques, we investigate the propagation of singlet and triplet excitons in single-crystal tetracene. Instead of an expected broadening, the distribution of singlet excitons narrows on a nanosecond time scale after photoexcitation. This narrowing results in an effective negative diffusion in which singlet excitons migrate toward the high-density region, eventually leading to a singlet exciton distribution that is smaller than the laser excitation spot. Modeling the excited-state dynamics demonstrates that the origin of the anomalous diffusion is rooted in nonlinear triplet–triplet annihilation (TTA). We anticipate that this is a general phenomenon that can be used to study exciton diffusion and nonlinear TTA rates in semiconductors relevant for organic optoelectronics.

The efficiency of silicon (Si) solar cells is limited by the Shockley–Queisser Limit (SQL). A promising technique to overcome the SQL is to add a singlet fission (SF) layer to the Si solar cell to reduce the losses associated with the thermalization of charge carriers created by high-energy photons.1−8 During SF, a singlet exciton is converted into two triplet excitons with energies roughly half that of the singlet energy. These triplets may then be transferred to a low-band-gap semiconductor, increasing the photogenerated current and the PV quantum efficiency.9 Tetracene is a suitable candidate as a SF material since its triplet energy is slightly larger than the band gap of Si, allowing for the transfer of triplet excitons.2,4 The transfer of triplet excitons in tetracene to a Si solar cell has recently been shown, but the overall efficiency is still below those of commercial Si solar cells.8 The dominant loss in SF cells is singlet transfer from tetracene to Si, which competes with the transfer of two triplet excitons and leads to a lower yield.8 A fundamental understanding of the combined excited-state dynamics and the diffusion of singlet and triplet excitons is required to facilitate the design of SF cells that enhance the fraction of triplet states reaching the interface while limiting the number of transferred singlet states. Studying triplet and singlet excitons independently is challenging as different techniques are required and singlets and triplets convert into each other through the processes of SF and triplet–triplet annihilation (TTA).

In this Letter, we combine two microscopy techniques, transient absorption microscopy (TAM) and transient fluorescence microscopy (TFM), to image the diffusion of singlet and triplet excitons on time scales from 200 fs to 2 μs. These techniques enable us to distinguish different regimes of transport and are sensitive to different types of excitons, radiative singlet excitons and dark triplet excitons. Our measurements show a paradoxical diffusion of singlet and triplet states on intermediate time scales (200 ps to 20 ns). During this interval, we observe that the spatial distribution of singlet excitons narrows, while the triplet distribution keeps expanding. Most interestingly, this negative diffusion leads to singlet distributions that are narrower than the size of the laser spot, enabling the generation of a singlet cloud with subdiffraction dimensions. We have constructed a model of the tetracene excited-state dynamics and exciton diffusion to explain the negative effective diffusion and the different behaviors of singlet and triplet excitons by the nonlinear triplet–triplet annihilation.

In most cases, exciton diffusion is studied by indirect techniques10−14 that give only the average value of the exciton diffusion length. Transient microscopy techniques may be used to probe exciton diffusion in space and time.15 These techniques generate excited states in a small region of the sample by a focused laser pulse and measure how these excited states expand over time by diffusion. TFM is sensitive to bright singlet states,16−22 while TAM probes the diffusion of both singlets and triplets as this technique allows the probing of ground state bleach, photoinduced absorption, or stimulated emission.23−30 In these measurements, the diffusion constant can be obtained in the linear regime by fitting the excited area with a Gaussian profile and extracting the variance as a function of time.31 This diffusion constant is given by

graphic file with name jz0c03171_m001.jpg 1

where t is the time after excitation and σ is the variance of the Gaussian profile.

In the literature, transient techniques have been used to study the exciton diffusion in tetracene crystals on short time scales (140 fs to 7 ns) with TAM25,28 and on long time scales (100 ns to 7 μs) with TFM,18 giving contradicting results. While the TAM measurements show a broadening of the spatial profile by 105 nm2 in less than 2 ns,25 the same broadening is seen after more than 200 ns when measured with TFM.18 We present TAM and TFM measurements, unify the different regimes of exciton diffusion in tetracene, and reconcile the discrepancies by demonstrating the important role of nonlinear triplet–triplet annihilation in exciton transport (see Table 1 and the Supporting Information (SI) 1–7 for a detailed description of the microscopes).32,33 Our results emphasize that the extensively used eq 1 should be avoided for the quantitative interpretation of transient measurements where nonlinear contributions can be significant.

Table 1. Characteristics of the Transient Absorption Microscope (TAM) and Transient Fluorescence Microscope (TFM).

  TAM TFM
measurement parameter change in absorption (singlets and triplets) fluorescence (singlets)
temporal resolution 200 fs 50 ps
temporal range 2 ns 2 μs
spatial sensitivity 30 nm 10 nm
excitation density >2 · 1018 cm–3 >5 · 1016 cm–3
Open in a new tab

Tetracene crystals were prepared by dropcasting a saturated solution of tetracene (99.99% Sigma Aldrich) in toluene in a nitrogen glovebox (SI 8). This resulted in thin crystals (50–200 nm) with relatively large lateral dimensions (up to 500 μm). The anisotropic fluorescence and extinction spectra are shown in SI 8. As confirmed with X-ray diffraction measurements, the long axis of the molecule lies in the out-of-plane direction.34

The spatial evolution of the fluorescence emerging from singlet excitons and measured with TFM is shown in Figure 1a. The images at 200 and 600 ns after excitation clearly show the anisotropic diffusion along the fast and slow axes, respectively, in the tetracene crystal, as reported before by Akselrod et al.18 (for a complete analysis, see SI 9). More interesting is the process underlying the rapid expansion of the fluorescence, followed by the contraction depicted during the first nanoseconds after excitation, which will be the focus of the rest of this letter. The cross sections along the fast axis, shown in Figure 1b, illustrate the expansion of the fluorescence spot from 0 (pink) to 2 ns (red), followed by a reduction at 5 ns (dark red) to a size smaller than that of the excitation spot. Each of these cross sections can be fitted with a Gaussian to extract the full-width at half-maximum (fwhm) from the variance (see SI 10). Figure 1c shows the evolution of the fwhm during the first 20 ns along the fast (light blue crosses) and low (dark blue crosses) tetracene axes. In contrast to exciton diffusion,18,25,35 the evolution is isotropic along both axis, indicating that the dominant process behind this spatial evolution is a different mechanism. Both profiles show a quick expansion from 570 to 650 nm followed by a negative effective diffusion, resulting in a spot size with a fwhm of 530 nm. The quick and rapid expansion can be explained by a combination of singlet–singlet annihilation and singlet diffusion, while the negative diffusion requires additional consideration.

Figure 1.

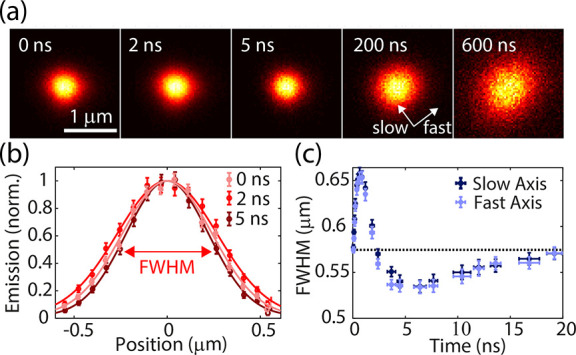
Figure 1

Open in a new tab

(a) The evolution of the spatial distribution of the (normalized) fluorescence from singlet excitons for an initial excitation density of 1018 cm–3. (b) Cross sections illustrating the expansion of the fluorescence spot from 0 (pink) to 2 ns (red), followed by a reduction at 5 ns (dark red) to a size smaller than the excitation spot. (c) The isotopic evolution of the fwhm during the first 20 ns.

Partial negative effective exciton diffusion has been shown in quantum wells36 and two-dimensional semiconductors (TMDs).22 However, in these cases the distribution of excited states always remained broader than the laser spot. The reason is that the underlying mechanism in those cases is fundamentally different than that for the organic semiconductor investigated here, where delayed singlets can be generated via nonlinear triplet–triplet annihilation. As we show next, a distribution of excitons narrower than the laser spot can be generated due to this nonlinear mechanism.

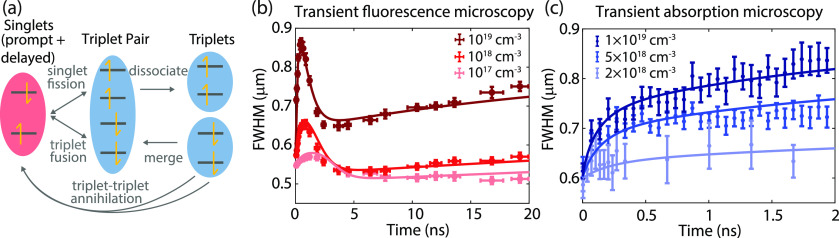
A model incorporating the tetracene excited-state dynamics is required to understand the spatial distribution and time evolution of the tetracene fluorescence. The excited singlet energy level in tetracene is close to twice the triplet exciton energy, which results in an efficient fission of singlet excitons into a pair of triplet states that can eventually dissociate into free triplets.2,37−39 These triplet states are relatively long-lived and can repopulate the singlet excited state via the opposite mechanism, i.e., triplet fusion or triplet–triplet annihilation.

We have simplified the excited state dynamics further (as illustrated in Figure 2a) to understand the observed negative diffusion. The kinetic model consists of the following three distinct excited states: prompt singlets that are excited at t = 0, triplet states that are created through singlet fission, and delayed singlets created from triplet–triplet annihilation. Although delayed and prompt singlets are indistinguishable in our measurements, it is possible to differentiate between them in the model. This distinction will clarify the observed effective negative diffusion.

Figure 2.

Figure 2

Open in a new tab

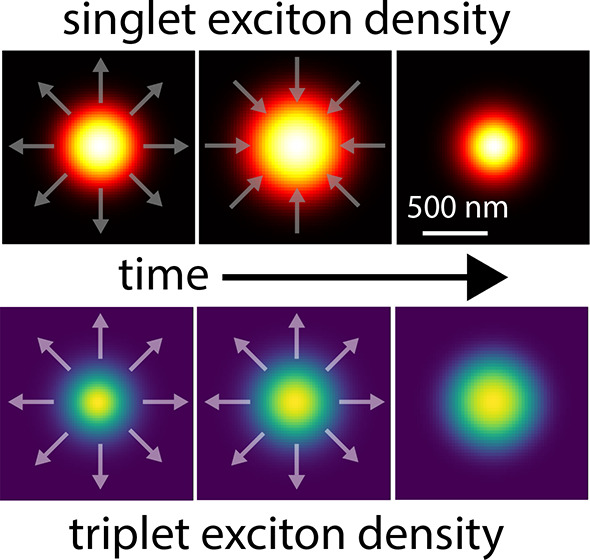
(a) Schematic representation of the model. (b) Time evolution of the excited-state population per exciton type. (c) Simulated fwhm of the different exciton distributions. (d–g) Cross sections of the distributions. (d) The initial distribution of the singlets after laser excitation. (e) The singlets split into triplet states. (f) Nonlinear triplet–triplet annihilation results in a delayed singlet distribution that is significantly narrower than both the triplet distribution and the prompt singlet distribution. (g) Practically all prompt singlets have either decayed to the ground state or split into triplets, leading to a total singlet distribution that is narrower than the laser excitation spot.

The different processes involved among these excited states are the radiative decay from singlet excited states to the ground state (at a rate kS), singlet–singlet annihilation (kSSA), singlet fission (kfis), and triplet–triplet annihilation (kTTA), which has a nonlinear dependence on the triplet concentration since it involves two triplet excitons. The diffusion of excitons in tetracene crystals is described by the 2D diffusion equation, assuming that the excitation density is constant along the out-of-plane direction. The diffusion model and excited state dynamics lead to the following three differential equations:

graphic file with name jz0c03171_m002.jpg 2
graphic file with name jz0c03171_m003.jpg 3
graphic file with name jz0c03171_m004.jpg 4

where NSp, NSd and NT are the prompt, delayed singlet, and triplet populations, respectively, and 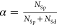Inline graphic is the fraction of prompt singlets. DS and DT are the diffusion tensors defining the diffusion constants of singlet and triplet excitons, respectively, along the fast and slow axes. The factor of 2 multiplying the fission and triplet–triplet annihilation rates in eq 3 indicates that two triplet excitons are generated or removed by singlet fission and triplet–triplet annihilation, respectively.

Since eqs 2–4 cannot be solved analytically, we modeled the excited state dynamics and diffusion numerically. The simulation was performed for a 31 × 31 grid with a Gaussian excitation profile at t = 0 and a time-step size of 1 ps. We fit all the parameters, except for the radiative decay rate, to the spatial evolution of the fluorescence profile for excitation densities of 1017, 1018, and 1019 cm–3. Also, we assumed isotropic diffusion, resulting in a single scalar value for the diffusion tensors. The resulting values and fits are given in Table 2. The populations of the different excited states over time are shown in Figure 2b. The prompt singlets (dark-green dashed curve) excited at t = 0 quickly convert to triplet states (solid blue curve) and subsequently populate the delayed singlets (light-green dotted curve). The total singlet population (solid-red curve) is the sum of the prompt and delayed singlets. While all of the populations (prompt and delayed singlets and triplets) show a positive diffusion, the total singlet population (red curve) has a negative effective exciton diffusion, with a decrease in the fwhm between 0.8 and 3 ns that was also observed in the experiment (Figure 2c). The processes that lead to the negative diffusion are explained in more detail in Figure 2d–g. The prompt singlet distribution is shown immediately after the excitation in Figure 2d (dark-green area). In the following hundreds of picoseconds (Figure 2e), the singlets split into triplets (blue area), leading to a fast decay of the singlets and a growth of the triplet population. Simultaneously, the singlet population broadens due to singlet diffusion and, more importantly, singlet–singlet annihilation, which leads to a faster decay of singlets at the center of the Gaussian profile. After 1.4 ns (Figure 2f), the triplet population reaches a maximum and decays by triplet–triplet annihilation (TTA) into singlet states. Since the TTA rate depends quadratically on the density of the triplet states, TTA is more efficient at the center of the Gaussian profile than at the edges, resulting in a delayed singlet distribution that is narrower than both the triplet and the prompt singlet distribution (Figure 2g). The quadratic relationship between the triplet concentration and number of generated singlets defines the theoretical minimum size that the singlet exciton cloud can reach as being 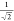Inline graphic of the fwhm of the Gaussian excitation profile in an ideal TTA material (see SI S11).

Table 2. Simulation Parameters Used in the Kinetic Model of Figure 2.

variable meaning value
kS radiative decay 0.08 ns–1
kSSA singlet–singlet annihilation 2 · 10–18 cm3 ns–1
kfis fission 1.5 ns–1
kTTA triplet–triplet annihilation 1.5 · 10–19cm3 ns–1
DS singlet diffusion 3 · 10–2 cm2 s–1
DT triplet diffusion 8 · 10–4 cm2 s–1
Open in a new tab

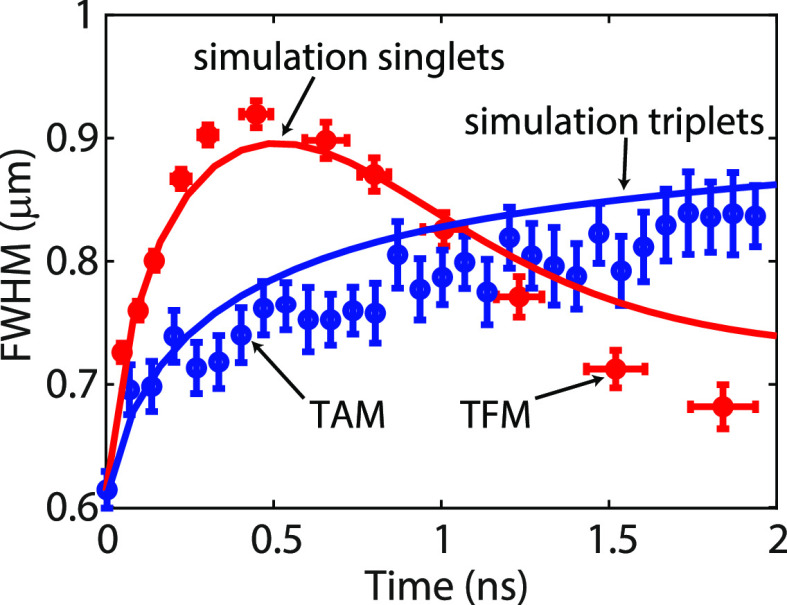
From the simulations in Figure 2c, we expect the negative exciton diffusion only for the singlet states and not for the triplet states. To verify this result, we performed TAM measurements on the tetracene crystal with the probe at λ = 820 nm. At this wavelength, the measurements are mainly sensitive to triplet photoinduced absorption.25,40 The evolution of the spatial distribution measured by TAM is shown with the blue circles in Figure 3 for an excitation density of 1019 cm–3 (full results in SI 12). The measured signal coincides almost perfectly with the simulated evolution plotted with the solid-blue curve in Figure 3. The rates used for this simulation are the same as those in Figure 2 (see Table 2), with an initial excitation density of 1019 cm–3.

Figure 3.

Figure 3

Open in a new tab

An opposite effective diffusion was measured for singlet excitons by TFM (red dots) and triplet excitons by TAM (blue dots), both of which were measured for an excitation density of 1019 cm–3. The time evolution of the fwhm of the exciton clouds was fitted by simulations of the diffusion of singlet (red curve) and triple states (blue curve) using the model described in Figure 2 and parameters given in Table 2 with N0 = 1019 cm–3.

To compare the diffusion of the singlet and the triplet states, we also performed TFM measurements for the same excitation density and plotted the result in Figure 3 with the red circles. The red curve in this figure is the result of the simulation with the same parameters as those for the triplet evolution. We see that the singlet expansion in the first nanoseconds is faster than the triplet expansion. However, the fwhm of the singlet distribution starts to decrease after 500 ps because of the nonlinear TTA, resulting in a singlet distribution that is narrower than the triplet distribution.

The model depicted in Figure 2a helped us to understand the physical process behind the negative diffusion but is not able to quantitatively capture the power dependence of the spatial evolution with the same set of parameters (see SI 13). To simulate the power-dependent results, we developed a more realistic model.2,41−44 The extended model is shown schematically in Figure 4a, illustrating the fission and fusion rates between the singlet state and the triplet pair, which are both independent of the concentration. The triplet pair can dissociate into long-lived triplets that can either follow a linear (called merge) or nonlinear (TTA) recombination to the singlet state, as indicated by the arrows in Figure 4a.45 The corresponding coupled differential equations are given in the Supporting Information (SI 14). With this three-state model, we can simulate the observed time evolution of the different excited states.

Figure 4.

Figure 4

Open in a new tab

(a) Schematic representation of the model. (b) Evolution of the width of the exciton distribution for initial densities 1017, 1018, and 1019 cm–3 represented by pink, red, and dark red crosses, respectively, as measured by TFM. The solid curves are the simulations for the corresponding singlet exciton densities. (c) fwhm of the excitons probed by TAM for increasing excitation densities for the initial densities of 1019 (dark blue circles) and 5 × 1018 cm–3 (blue circles). The solid curves are the simulations of the total number of triplet states (triplet pairs + free triplets).

The results of the simulations for the different initial excitation densities are convolved with the point-spread function of our microscope (SI Figures S2 and S6) and plotted along with the experimental results for different laser intensities in Figure 4b and c. These measurements show the time evolution of the fwhm of the profiles measured with TFM and TAM, respectively. The excellent agreement shows that we can simultaneously fit the triplet and singlet state diffusion with the same parameters for intensities spanning two orders of magnitude while also capturing the fluorescence decay dynamics (SI 15). The parameters used for the simulations are listed in the SI 14 and were obtained by fitting all rates to the evolution of both the triplet and singlet spatial profiles for the different excitation densities. These parameters are within the range of values reported in the literature.25,38,44,46−49

The diffusion profiles of Figures 4b and c can be understood as follows: the time evolution of the fwhm of the profiles measured with TFM for excitation densities of 1017, 1018, and 1019 cm–3 (pink, red, and dark red circles in Figure 4b, respectively) show an initial expansion, followed by a fwhm reduction and a slower expansion at longer times. The initial expansion for the two highest excitation densities is dominated by singlet–singlet annihilation, while the initial expansion for the lower excitation power originates from diffusion. The negative diffusion (fwhm reduction) is more prominent and faster for higher excitation powers because the difference between the fwhm of the triplet and singlet distributions is larger in this case and because the TTA rate increases nonlinearly with the concentration of the triplet states. The power-dependent time evolution of the fwhm measured with TAM is plotted in Figure 4c. The minimum excitation density for reliable measurements was ∼2 × 1018 cm–3; therefore, the measurements are presented for excitation densities of 2 × 1018 (light blue circles), 5 × 1018 (blue circles), and 1019 cm–3 (dark blue circles). Since the singlet fission rate is fast (3 ns–1), the triplet population follows the singlet population at short time scales, and the TAM measurements have a similar power-dependent broadening as the TFM measurements during the first 500 ps. Measurements at lower excitation densities would require much longer integration times or an investigation of thicker crystals. Additionally, the detection of triplet excitons by adding a phosphorescent emitter to the crystal has been suggested as a sensitive method to probe triplet excitons50

Using transient fluorescence microscopy, we have experimentally shown a negative singlet exciton diffusion in tetracene crystals, leading to exciton distributions that are narrower than the excitation beam size. We developed a kinetic model to explain the negative effective diffusion as a result of nonlinear triplet–triplet annihilation. The anomalous broadening and narrowing of the singlet distribution shows that caution is required when extracting diffusion constants from these direct microscopy techniques even at low excitation densities as other processes besides diffusion can influence the shape of the distribution. On the other hand, when interpreted correctly, these measurements give insight into more processes than just diffusion, such as singlet–singlet annihilation and the rate of nonlinear triplet–triplet annihilation. Furthermore, the excitation spot generated with far-field excitation followed by singlet fission and triplet–triplet annihilation could theoretically approach 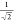Inline graphic of the diffraction limit a few nanoseconds after excitation. The negative effective diffusion is a universal property of triplet–triplet annihilation materials and is therefore also expected in other organic compounds relevant for photovoltaics and OLEDs, such as acene derivatives and TTA-UC systems.

Acknowledgments

We wish to acknowledge financial support from the Innovational Research Incentives Scheme of the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO) (Vici Grant 680-47-628) and the Gravitation Grant “Research Centre for Integrated Nanophotonics” (Grant 024.002.033). S.W. was partly supported by a Starting Grant from Soochow University (Q415900120) and the Priority Academic Program Development (PAPD) from Jiangsu Higher Education Institutions.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.0c03171.

  • Detailed characterization of the microscopes, fabrication of the crystal, analysis of triplet diffusion on long time scales, additional data of TAM on tetracene, additional simulations corresponding to TFM measurements, and fitting parameters and the analysis of the theoretical minimum spot size (PDF)

The authors declare no competing financial interest.

Supplementary Material

jz0c03171_si_001.pdf (1.7MB, pdf)

References

  1. Hanna M. C.; Nozik A. J. Solar Conversion Efficiency of Photovoltaic and Photoelectrolysis Cells with Carrier Multiplication Absorbers. J. Appl. Phys. 2006, 100, 074510. 10.1063/1.2356795. [DOI] [Google Scholar]
  2. Smith M.; Michl J. Singlet Fission. Chem. Rev. 2010, 110, 6891–6936. 10.1021/cr1002613. [DOI] [PubMed] [Google Scholar]
  3. Lee J.; Jadhav P.; Reusswig P. D.; Yost S. R.; Thompson N. J.; Congreve D. N.; Hontz E.; Van Voorhis T.; Baldo M. A. Singlet Exciton Fission Photovoltaics. Acc. Chem. Res. 2013, 46, 1300–1311. 10.1021/ar300288e. [DOI] [PubMed] [Google Scholar]
  4. Wu T. C.; Thompson N. J.; Congreve D. N.; Hontz E.; Yost S. R.; Van Voorhis T.; Baldo M. A. Singlet Fission Efficiency in Tetracene-Based Organic Solar Cells. Appl. Phys. Lett. 2014, 104, 193901. 10.1063/1.4876600. [DOI] [Google Scholar]
  5. Pazos-Outón L. M.; Lee J. M.; Futscher M. H.; Kirch A.; Tabachnyk M.; Friend R. H.; Ehrler B. A Silicon-Singlet Fission Tandem Solar Cell Exceeding 100% External Quantum Efficiency with High Spectral Stability. ACS Energy Letters 2017, 2, 476–480. 10.1021/acsenergylett.6b00678. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Rao A.; Friend R. H. Harnessing Singlet Exciton Fission to Break the Shockley-Queisser Limit. Nature Reviews Materials 2017, 2, 17063. 10.1038/natrevmats.2017.63. [DOI] [Google Scholar]
  7. Willems R. E.; Meskers S. C.; Wienk M. M.; Janssen R. A. Effect of Charge-Transfer State Energy on Charge Generation Efficiency via Singlet Fission in Pentacene-Fullerene Solar Cells. J. Phys. Chem. C 2019, 123, 10253–10261. 10.1021/acs.jpcc.9b00568. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Einzinger M.; Wu T.; Kompalla J. F.; Smith H. L.; Perkinson C. F.; Nienhaus L.; Wieghold S.; Congreve D. N.; Kahn A.; Bawendi M. G.; et al. Sensitization of Silicon by Singlet Exciton Fission in Tetracene. Nature 2019, 571, 90–94. 10.1038/s41586-019-1339-4. [DOI] [PubMed] [Google Scholar]
  9. Futscher M. H.; Rao A.; Ehrler B. The Potential of Singlet Fission Photon Multipliers as an Alternative to Silicon-Based Tandem Solar Cells. ACS Energy Letters 2018, 3, 2587–2592. 10.1021/acsenergylett.8b01322. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Kroeze J. E.; Savenije T. J.; Vermeulen M. J.; Warman J. M. Contactless Determination of the Photoconductivity Action Spectrum, Exciton Diffusion Length, and Charge Separation Efficiency in Polythiophene-Sensitized TiO2 Bilayers. J. Phys. Chem. B 2003, 107, 7696–7705. 10.1021/jp0217738. [DOI] [Google Scholar]
  11. Shaw P. E.; Ruseckas A.; Samuel I. D. Exciton Diffusion Measurements in Poly(3-hexylthiophene). Adv. Mater. 2008, 20, 3516–3520. 10.1002/adma.200800982. [DOI] [Google Scholar]
  12. Mikhnenko O. V.; Ruiter R.; Blom P. W.; Loi M. A. Direct Measurement of the Triplet Exciton Diffusion Length in Organic Semiconductors. Phys. Rev. Lett. 2012, 108, 137401. 10.1103/PhysRevLett.108.137401. [DOI] [PubMed] [Google Scholar]
  13. Mikhnenko O. V.; Blom P. W. M.; Nguyen T.-Q. Exciton Diffusion in Organic Semiconductors. Energy Environ. Sci. 2015, 8, 1867–1888. 10.1039/C5EE00925A. [DOI] [Google Scholar]
  14. Lin J. D.; Mikhnenko O. V.; Chen J.; Masri Z.; Ruseckas A.; Mikhailovsky A.; Raab R. P.; Liu J.; Blom P. W.; Loi M. A.; et al. Systematic Study of Exciton Diffusion Length in Organic Semiconductors by Six Experimental Methods. Mater. Horiz. 2014, 1, 280–285. 10.1039/C3MH00089C. [DOI] [Google Scholar]
  15. Ginsberg N. S.; Tisdale W. A. Spatially Resolved Exciton and Charge Transport in Emerging Semiconductors. Annu. Rev. Phys. Chem. 2020, 71, 1–30. 10.1146/annurev-physchem-052516-050703. [DOI] [PubMed] [Google Scholar]
  16. Zhao H.; Dal Don B.; Moehl S.; Kalt H.; Ohkawa K.; Hommel D. Spatiotemporal Dynamics of Quantum-Well Excitons. Phys. Rev. B: Condens. Matter Mater. Phys. 2003, 67, 035306. 10.1103/PhysRevB.67.035306. [DOI] [Google Scholar]
  17. Müller A. M.; Bardeen C. J. Using a Streak Camera to Resolve the Motion of Molecular Excited States with Picosecond Time Resolution and 150 nm Spatial Resolution. J. Phys. Chem. C 2007, 111, 12483–12489. 10.1021/jp072902t. [DOI] [Google Scholar]
  18. Akselrod G. M.; Deotare P. B.; Thompson N. J.; Lee J.; Tisdale W. A.; Baldo M. A.; Menon V. M.; Bulovic V. Visualization of Exciton Transport in Ordered and Disordered Molecular Solids. Nat. Commun. 2014, 5, 3646. 10.1038/ncomms4646. [DOI] [PubMed] [Google Scholar]
  19. Kulig M.; Zipfel J.; Nagler P.; Blanter S.; Schüller C.; Korn T.; Paradiso N.; Glazov M. M.; Chernikov A. Exciton Diffusion and Halo Effects in Monolayer Semiconductors. Phys. Rev. Lett. 2018, 120, 207401. 10.1103/PhysRevLett.120.207401. [DOI] [PubMed] [Google Scholar]
  20. Perea-Causín R.; Brem S.; Rosati R.; Jago R.; Kulig M.; Ziegler J. D.; Zipfel J.; Chernikov A.; Malic E. Exciton Propagation and Halo Formation in Two-Dimensional Materials. Nano Lett. 2019, 19, 7317–7323. 10.1021/acs.nanolett.9b02948. [DOI] [PubMed] [Google Scholar]
  21. Zipfel J.; Kulig M.; Perea-Causín R.; Brem S.; Ziegler J. D.; Rosati R.; Taniguchi T.; Watanabe K.; Glazov M. M.; Malic E.; et al. Exciton Diffusion in Monolayer Semiconductors with Suppressed Disorder. Phys. Rev. B: Condens. Matter Mater. Phys. 2020, 101, 115430. 10.1103/PhysRevB.101.115430. [DOI] [Google Scholar]
  22. Rosati R.; Perea-Causín R.; Brem S.; Malic E. Negative Effective Excitonic Diffusion in Monolayer Transition Metal Dichalcogenides. Nanoscale 2020, 12, 356–363. 10.1039/C9NR07056G. [DOI] [PubMed] [Google Scholar]
  23. Lo S. S.; Shi H. Y.; Huang L.; Hartland G. V. Imaging the Extent of Plasmon Excitation in Au Nanowires Using Pump-Probe Microscopy. Opt. Lett. 2013, 38, 1265–1267. 10.1364/OL.38.001265. [DOI] [PubMed] [Google Scholar]
  24. Grumstrup E. M.; Gabriel M. M.; Cating E. M.; Pinion C. W.; Christesen J. D.; Kirschbrown J. R.; Vallorz E. L.; Cahoon J. F.; Papanikolas J. M. Ultrafast Carrier Dynamics in Individual Silicon Nanowires: Characterization of Diameter-Dependent Carrier Lifetime and Surface Recombination with Pump-Probe Microscopy. J. Phys. Chem. C 2014, 118, 8634–8640. 10.1021/jp502737e. [DOI] [Google Scholar]
  25. Wan Y.; Guo Z.; Zhu T.; Yan S.; Johnson J.; Huang L. Cooperative Singlet and Triplet Exciton Transport in Tetracene Crystals Visualized by Ultrafast Microscopy. Nat. Chem. 2015, 7, 785–792. 10.1038/nchem.2348. [DOI] [PubMed] [Google Scholar]
  26. Grumstrup E. M.; Gabriel M. M.; Cating E. E. M.; Van Goethem E. M.; Papanikolas J. M. Pump-Probe Microscopy: Visualization and Spectroscopy of Ultrafast Dynamics at the Nanoscale. Chem. Phys. 2015, 458, 30–40. 10.1016/j.chemphys.2015.07.006. [DOI] [Google Scholar]
  27. Guo Z.; Wan Y.; Yang M.; Snaider J.; Zhu K.; Huang L. Long-Range Hot-Carrier Transport in Hybrid Perovskites Visualized by Ultrafast Microscopy. Science 2017, 356, 59–62. 10.1126/science.aam7744. [DOI] [PubMed] [Google Scholar]
  28. Zhu T.; Huang L. Exciton Transport in Singlet Fission Materials: A New Hare and Tortoise Story. J. Phys. Chem. Lett. 2018, 9, 6502–6510. 10.1021/acs.jpclett.8b02181. [DOI] [PubMed] [Google Scholar]
  29. Rozenman G. G.; Akulov K.; Golombek A.; Schwartz T. Long-Range Transport of Organic Exciton-Polaritons Revealed by Ultrafast Microscopy. ACS Photonics 2018, 5, 105–110. 10.1021/acsphotonics.7b01332. [DOI] [Google Scholar]
  30. Schnedermann C.; Sung J.; Pandya R.; Verma S. D.; Chen R. Y.; Gauriot N.; Bretscher H. M.; Kukura P.; Rao A. Ultrafast Tracking of Exciton and Charge Carrier Transport in Optoelectronic Materials on the Nanometer Scale. J. Phys. Chem. Lett. 2019, 10, 6727–6733. 10.1021/acs.jpclett.9b02437. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Havlin S.; Ben-Avraham D. Diffusion in Disordered Media. Adv. Phys. 1987, 36, 695–798. 10.1080/00018738700101072. [DOI] [Google Scholar]
  32. Werley C. A.; Teo S. M.; Nelson K. A. Pulsed Laser Noise Analysis and Pump-Probe Signal Detection with a Data Acquisition Card. Rev. Sci. Instrum. 2011, 82, 123108. 10.1063/1.3669783. [DOI] [PubMed] [Google Scholar]
  33. Saad N. A.; Rao D. N.; Naraharisetty S. R. G.; Sethupathy M.; Sahoo C. Ultrafast Pump-Probe Signal Detection Using a Data Acquisition Card. J. Instrum. 2018, 13, P10027. 10.1088/1748-0221/13/10/P10027. [DOI] [Google Scholar]
  34. Berghuis A. M.; Halpin A.; Le-Van Q.; Ramezani M.; Wang S.; Murai S.; Gómez Rivas J. Enhanced Delayed Fluorescence in Tetracene Crystals by Strong Light-Matter Coupling. Adv. Funct. Mater. 2019, 29 (36), 1901317. 10.1002/adfm.201901317. [DOI] [Google Scholar]
  35. Xie X.; Ma H. Opposite Anisotropy Effects of Singlet and Triplet Exciton Diffusion in Tetracene Crystal. ChemistryOpen 2016, 5, 201–205. 10.1002/open.201500214. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Zhao H.; Dal Don B.; Schwartz G.; Kalt H. Ultrafast Breathinglike Oscillation in the Exciton Density of ZnSe Quantum Wells. Phys. Rev. Lett. 2005, 94, 137402. 10.1103/PhysRevLett.94.137402. [DOI] [PubMed] [Google Scholar]
  37. Stern H. L.; Musser A. J.; Gelinas S.; Parkinson P.; Herz L. M.; Bruzek M. J.; Anthony J.; Friend R. H.; Walker B. J. Identification of a Triplet Pair Intermediate in Singlet Exciton Fission in Solution. Proc. Natl. Acad. Sci. U. S. A. 2015, 112, 7656–7661. 10.1073/pnas.1503471112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Burdett J. J.; Gosztola D.; Bardeen C. J. The Dependence of Singlet Exciton Relaxation on Excitation Density and Temperature in Polycrystalline Tetracene Thin Films: Kinetic Evidence For a Dark Intermediate State and Implications for Singlet Fission. J. Chem. Phys. 2011, 135, 214508. 10.1063/1.3664630. [DOI] [PubMed] [Google Scholar]
  39. Chan W. L.; Ligges M.; Zhu X. Y. The Energy Barrier in Singlet Fission Can Be Overcome Through Coherent Coupling and Entropic Gain. Nat. Chem. 2012, 4, 840–845. 10.1038/nchem.1436. [DOI] [PubMed] [Google Scholar]
  40. Zhang B.; Zhang C.; Xu Y.; Wang R.; He B.; Liu Y.; Zhang S.; Wang X.; Xiao M. Polarization-Dependent Exciton Dynamics in Tetracene Single Crystals. J. Chem. Phys. 2014, 141, 244303. 10.1063/1.4904385. [DOI] [PubMed] [Google Scholar]
  41. Pensack R. D.; Ostroumov E. E.; Tilley A. J.; Mazza S.; Grieco C.; Thorley K. J.; Asbury J. B.; Seferos D. S.; Anthony J. E.; Scholes G. D. Observation of Two Triplet-Pair Intermediates in Singlet Exciton Fission. J. Phys. Chem. Lett. 2016, 7, 2370–2375. 10.1021/acs.jpclett.6b00947. [DOI] [PubMed] [Google Scholar]
  42. Weiss L. R.; Bayliss S. L.; Kraffert F.; Thorley K. J.; Anthony J. E.; Bittl R.; Friend R. H.; Rao A.; Greenham N. C.; Behrends J. Strongly Exchange-Coupled Triplet Pairs in an Organic Semiconductor. Nat. Phys. 2017, 13, 176–181. 10.1038/nphys3908. [DOI] [Google Scholar]
  43. Tayebjee M. J.; Sanders S. N.; Kumarasamy E.; Campos L. M.; Sfeir M. Y.; McCamey D. R. Quintet Multiexciton Dynamics in Singlet Fission. Nat. Phys. 2017, 13, 182–188. 10.1038/nphys3909. [DOI] [Google Scholar]
  44. Yong C. K.; Musser A. J.; Bayliss S. L.; Lukman S.; Tamura H.; Bubnova O.; Hallani R. K.; Meneau A.; Resel R.; Maruyama M.; et al. The Entangled Triplet Pair State in Acene and Heteroacene Materials. Nat. Commun. 2017, 8, 15953. 10.1038/ncomms15953. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Bayliss S. L.; Chepelianskii A. D.; Sepe A.; Walker B. J.; Ehrler B.; Bruzek M. J.; Anthony J. E.; Greenham N. C. Geminate and Nongeminate Recombination of Triplet Excitons Formed by Singlet Fission. Phys. Rev. Lett. 2014, 112, 238701. 10.1103/PhysRevLett.112.238701. [DOI] [PubMed] [Google Scholar]
  46. Yost S. R.; Hontz E.; Yeganeh S.; Van Voorhis T. Triplet vs Singlet Energy Transfer in Organic Semiconductors: The Tortoise and the Hare. J. Phys. Chem. C 2012, 116, 17369–17377. 10.1021/jp304433t. [DOI] [Google Scholar]
  47. Wilson M. W.; Rao A.; Johnson K.; Gélinas S.; Di Pietro R.; Clark J.; Friend R. H. Temperature-Independent Singlet Exciton Fission in Tetracene. J. Am. Chem. Soc. 2013, 135, 16680–16688. 10.1021/ja408854u. [DOI] [PubMed] [Google Scholar]
  48. Burdett J. J.; Bardeen C. J. The Dynamics of Singlet Fission in Crystalline Tetracene and Covalent Analogs. Acc. Chem. Res. 2013, 46, 1312–1320. 10.1021/ar300191w. [DOI] [PubMed] [Google Scholar]
  49. Piland G. B.; Bardeen C. J. How Morphology Affects Singlet Fission in Crystalline Tetracene. J. Phys. Chem. Lett. 2015, 6, 1841–1846. 10.1021/acs.jpclett.5b00569. [DOI] [PubMed] [Google Scholar]
  50. Mikhnenko O. V.; Blom P. W.; Loi M. A. Sensitive Triplet Exciton Detection in Polyfluorene Using Pd-Coordinated Porphyrin. Phys. Chem. Chem. Phys. 2011, 13, 14453–14456. 10.1039/c1cp21146c. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz0c03171_si_001.pdf (1.7MB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES