Trajectories of scientific reasoning: A microgenetic study on children’s inquiry functioning

Abstract

From the literature, we know that young children engage in inquiry as an organized activity aimed either at confirming or refuting the relevance of certain ideas. The current study provides a characterization of changes in inquiry using a multiple case study of four 5-year old children. Three computer-based tasks were presented to the children as multivariable problem solving situations concerning moving objects. A description of the temporal unfolding of real-time action on a short-term time scale and long-term time scale of learning and development is provided. The results indicated that the development of inquiry did not follow linear growth but included advances and relapses, exploratory states and transitions. The data were compatible with the view that the child's thinking and acting form a complex dynamic system.

Introduction

Imagine a 5-year-old boy playing with toy cars using a wooden plank as a ramp. He lets his cars roll down while imagining an exciting race. He uses different kinds of toy cars, some of them heavier, some of them lighter. He sets different angles and distances for his ramp and discovers how far his cars go. He plays around with the physical properties of the objects and might reason about the relations between them. This boy – as most other children his age – is probably able to formulate hypotheses, propose causes and their effects on complex physical phenomena. In this paper, we address the scientific thinking of young children and aim to characterize the development of inquiry functioning on the short-term time scale of the activity and the long-term time scale of learning and development, using a microgenetic design with a multivariable problem solving task concerning moving objects.

Children's scientific reasoning has been a productive area of study for psychologists and educators (Zimmerman, 2007). In fact, many studies have proven that preschool children already use scientific reasoning in problem-solving tasks (e.g., Piekny & Maehler, 2013; Puche-Navarro, Colinvaux, & Dibar, 2001; Wilkening & Sodian, 2005). Scientific reasoning involves the use of scientific principles when problem solving (Zimmerman, 2007). This kind of thinking demands that children generate, evaluate and revise theories, and if the skills are highly developed, that they are aware of the change of knowledge (Koslowski, 1996; Kuhn, & Franklin, 2006; Metz, 2011; Zimmerman, 2007).

In this context, inquiry is defined as a set of cognitive processes for understanding phenomena, based on evidence, variable incidence and causal relationships. Inquiry allows the children to identify causal and non-causal relations within a system, to understand evidence and to recognize patterns within the evidence when interacting with the system (Kuhn, Pease, Iordanou & Wirkala, 2009). It can also lead to the coordination of multiple variables and the comprehension of the nature of the probabilities that constrain the system´s interactions. Children may use inquiry to propose hypotheses, suggest causes and effects, and coordinate theory-evidence and control variables (Kuhn, 2010; Kuhn & Pease, 2008). This is especially relevant in a problem-solving context, because such a context implies reaching a goal when faced with a situation with unknown elements (Jonassen, 1997). In this sense, inquiry implies an organized activity to answer a question posed by a problem situation through the coordination of multiple variables, generation of predictions, and reaching justified conclusions even on a rudimentary level (Kuhn & Pease, 2008; Kuhn, Pease, Iordanou & Wirkala, 2009).

The framework of complex dynamic systems offers a general theory for the study of developmental processes, which is also applicable to the development of a child's inquiry in a concrete problem solving context, and the development of the child's scientific thinking over the course of months or years. Based on a review of the literature, van Geert (2008) defined a complex dynamic system as any collection of components – such as various internal mental activities – that interact with one another and that change each other's properties as a result of that interaction. Complex dynamic systems are likely to have a number of properties, such as self-organization, the emergence of attractor states, soft assembly, differentiation into mutually interacting time scales, and discontinuous change (see Smith & Thelen, 1993; van Geert, 1991, 2008). Using the example above of the child with toy cars on a plank, a particular problem – “how can I get the car to arrive at a particular place” – is solved in a more or less systematic way, making particular choices about the information to use, doing particular things that reflect some sort of logic or systematic pattern.

A typical non-dynamic (or static) explanation of the child's problem solving would be that the child possesses an internal model of the problem at hand, for instance a mental model of the relationship between the speed of an object and the angle of the ramp it is rolling off, and that there is an internal computational process determining the most likely angle of the ramp. This then acts as an internal instruction to the child's motor system to position the ramp at the intended angle. If the result is not as expected, for instance the car does not reach the intended location, the child is likely to change his or her internal model or to redo the internal computation with different internal parameters, leading to another action. This is what Barsalou, Breazeal, and Smith (2007) called the ‘sense-think-act model’, with cognition referring to the ‘think’ part (see also Bickhard, 2009; 2012 for criticism).

In a complex dynamic systems approach, the child's positioning of the ramp is not the result of internal instruction based on internal computation combining external information with an internal mental model, but is an activity that emerges on the spot as a result of a multitude of local interactions between elements such as perceptions, actions in a particular context, memory trace activations, social referencing, and transient emotions, all without the necessity of an internal model of the task. In fact, knowledge is constructed on the time scale of an actual perception-action process including all that goes on in the form of covert, internal processes, and on the basis of processes such as perception, emotion, social cues, and the action affordances of the objects present. This construction process, which takes place on the short-term time scale of the real-time activity, is also referred to as a process of ‘soft assembly’ (Kloos & van Orden, 2009), in that it creates patterns that are both stable and flexible, that can be repeated and meanwhile undergo long-term development. Soft assembly means that understanding in scientific reasoning is something that it is not ‘inside the mind’ of the child, but that is a product of the interaction of the child´s knowledge with the settings and constraints of the task that he or she is actively trying to solve (Kloos & van Orden, 2009).

Children’s performance often shows a lot of intra-individual variability, in the sense that it fluctuates across measurement occasions. Though variability can exist at all time scales, the term is most often used for fluctuations on a relatively short time frame (Van Dijk & van Geert, 2015). The most common interpretation of this type of variability is that it is caused by changes in context and/or measurement error. For instance, the variations in performance of a child who is working on a problem-solving task may be caused in changes in alertness, distractibility, and motivation. The core assumption is thus that variability is externally ‘added’ to an underlying psychological process. However, according to the complex dynamic systems framework, variability should be seen as an intrinsic property of performance and development (Thelen & Smith, 1994; van Geert; 1994). The individual is not a passive recipient of changes in the context, but an agent who creates his own variability. From this point of view, intra-individual variability can be a driving force of development and a precursor of a new behavioral repertoire (Thelen, 1985).

This theoretical position was also applied to the domain of cognitive development in childhood by Siegler (1996, 2006), who argued that variability is one of the core mechanisms that causes the evolution of new strategies in children’s problem solving behavior. Intra-individual variability is the expression of an increased degree of exploration, which offers the possibility for differential reinforcement of successful strategies (many examples are reviewed in Siegler, 2006). Although an unlimited number of different patterns of variability can exist, three typical patterns have been distinguished in the literature (Van Dijk & van Geert, 2015). These patterns are a global decrease of variability, a global increase of variability, or a cyclical pattern (or peak pattern).

The plausibility of the complex dynamic systems approach for the study of cognitive problem-solving in an activity context has been shown for a variety of problem contexts (examples are Fischer & Bidell, 2006; Mercer, 2011; Schöner & Thelen, 2006; Smith, 2005; Smith & Thelen, 1993; Son, Smith, & Goldstone, 2011; Steenbeek, Jansen, & van Geert, 2012; Street, James, Jones, & Smith, 2011). In the present study, we sought to investigate whether inquiry processes have a number of properties that are characteristic of complex dynamic systems. We expect to find non-linear growth patterns and patterns of intra-individual variability. Also, inquiry is very context sensitive since it involves an interaction of the child’s knowledge and the specific task constraints within which they act (for instance Kloos & van Orden, 2009; Meindertsma, van Dijk, Steenbeek, & van Geert, 2014). It is expected that these properties and interactions strongly affect children’s performance. For this reason, we study the temporal trajectories of the actual problem solving activities as they unfold in children over the short-term time span of an actual problem solving situation and the long-term time span of eventual changes in the general pattern properties of the problem-solving activities, as suggested by Molenaar and Campbell (2009). This requires an observational, individual and time serial research design and corresponds to a microgenetic perspective.

The microgenetic perspective is considered to be a process-oriented approach aimed at studying development and learning (Granott & Parziale, 2002). Microdevelop-mental research focuses on the analysis of processes, which occur within specific task contexts, while people solve problems, perform tasks, or make discoveries. For instance, according to Miller and Coyle (1999) and Siegler, Adolph, and Lemaire (1996), researchers interested in micro-development analyze the process of change, identify its attributes and patterns, and look for the processes that underlie quantitative and qualitative change. This is in line with Thelen and Corbetta (2002) who stated that micro-development should be focused on the processes of change and not only on its endpoints.

Microgenetic studies aim to track changes in children’s performance by measuring them at multiple points in time. These measurements reveal a pattern of change, and provide compelling descriptions of change processes of individuals (van Geert & van Dijk, 2002). From an idiographic point of view, the systematic description of single cases using a microgenetic approach can lead to generalized knowledge if an abstract model is built through the continuous abstraction of the main interactions, process and components of the system (Molenaar & Valsiner, 2009).

Children’s inquiry: its nature and development

As a result of organized and self-directed cognitive activities toward their environment, children can reach an early, relatively coherent and stable understanding of the world around them (e.g., Zimmerman, 2000; 2007). The general picture that emerges from the literature is that although this kind of activity is inherently self-directed, its nature and development is strongly dependent on specific, well-structured educational conditions and guidance. For instance, young children can achieve high levels of self-directed scientific reasoning, including the child's reflection on his or her own reasoning and explanatory activities but this occurs only under specific educational conditions (Metz, 2011). The literature on constructivist science learning, emphasizes the importance of the child's own activity and experiences in the construction of children's scientific knowledge and reasoning skills. In this sense, demonstrations of scientifically described phenomena are not enough to foster the development of scientific thinking. It is necessary that inquiry is driven by questions and problems that the children are motivated to answer and solve (Kuhn & Pease, 2008). Therefore, educational scaf-folding of the self-directed process is of prime importance for the success of the developmental and learning outcomes (Alfieri, Brooks, Aldrich, & Tenenbaum, 2010; Gelman, 2009; Klahr & Nigam, 2004; Lehrer, Schauble, & Lucas, 2008; Mayer, 2004; Metz, 2011; Patrick, Mantzicopoulos, & Samarapungayan, 2009; Sarama & Clements, 2009).

Inquiry is considered to be an important process that explains how cognitive structures and processes become actions (Puche-Navarro, 2005) and how they organize the activity to evaluate the hypothesis or its alternatives (Zimmerman, 2000). In this sense, inquiry can be aimed either at confirming or refuting the relevance of certain ideas or hypotheses related to the facts, or to validate criteria for particular situations.

There have been different approaches to the properties of scientific inquiry in young children. Some approaches emphasize the representational aspect of scientific inquiry, the "what" and the content; others focus on the strategic aspect, the "how", and still others focus on the motivational and interest aspects. In the first approach, we find notions such as beliefs, mental models, misconceptions, belief revision, mental model transformation and categorical and ontological shifts in the basic features of a person's beliefs or knowledge about the nature of reality (see for instance Chi, & Brem, 2009; Hewson & Hewson, 1984; Tyson, Venville, Harrison, & Treagust, 1997; Vosniadou, 2009). In the second type of approach we find notions such as causal reasoning (see for instance Gopnik & Tenenbaum, 2007; McClelland & Thompson, 2007), control of variables strategy (CVS; see for instance Chen & Klahr, 1999; 2008; Kuhn, 2007), evidence evaluation and epistemic understanding (Chin & Brewer, 2001; Kuhn, Cheney, & Weinstock, 2000), and argumentation (e.g., Kuhn, 2010).

When reviewing the literature, it stands out that most studies on inquiry treat the content and the strategic aspects of scientific reasoning would as independent variables that contribute to the short-term dependent variables ‘level of science reasoning’, ‘structure of inquiry’ and the long-term dependent variables ‘development of science reasoning and of inquiry’ in young children. For instance, Piekny and Mahler (2013) explored the development of scientific reasoning based on the Dual Search Model of Scientific reasoning (Klahr, 2000, 2005; Klahr & Dunbar, 1988) across childhood. The authors demonstrated that the three general domain components, such as hypothesis generation, experimentation, and evidence evaluation, required by inquiry process developed asynchronously at different points in time. The literature also describes a global increase in inquiry skills (e.g., Piekny, Grube, Maehler, 2014; Tytler & Peterson, 2005). In general, many of these studies tended to focus on differences by age or by age-behavior-ability relationships between age groups (Puche-Navarro & Marti, 2011), thus describing possible general developmental trajectories of the children’s inquiry. However, a comparison between age groups or general longitudinal descriptions would only lead to a statistical model predicting group distributions of the dependent variable, and could not be confounded with a description of the process of ‘inquiry’ which focusses on intra-individual differences (for a general account see Molenaar & Campbell, 2009). There is a lack of studies with longitudinal designs and/or many repeated measures, which could lead to a description of the long-term trajectories of developmental change as well as the short-term micro-developmental changes that take place on the time scale of real-time problem situations.

If a process of situated inquiry complies with the general properties of a complex dynamic system, it is likely that it also inherits other general properties of complex dynamic systems such as self-organization, the emergence of temporarily stable patterns, short-term processes and long-term transitions. Based on these ideas, we expect that the development of scientific reasoning in individuals will show non-linear patterns and specific patterns of variability. The patterns we expect would be similar to complex growth patterns such as scalloping as stated by Fischer (Fischer & Yan, 2002; Fischer & Bidell, 2006). Scalloping implies regressing back to a lower level of functioning when the person faces some change in the context or state of the problem he or she is solving. In addition, because the perceived task properties are intrinsic to the self-organizing process, performance is expected to be very context- and content-sensitive.

In this person-oriented process study on problem-solving behavior in children, we asked ourselves the question: what does a real-time particular problem-solving process look like? By particular we mean: in particular children, for a particular occasion and with a particular type of question. It is a question of which do not know the answer yet. In the literature, it is very hard to find studies that describe the details of a particular problem-solving situation as a real-time process. Hence, a descriptive study of a particular problem-solving situation is therefore a first step towards a better understanding of the real-time nature of this type of process as it unfolds in a particular situation.

Research Questions

This study aimed to describe the development of inquiry within a microgenetic research design, with a combination of short-term events within each problem-solving session and long-term event analysis over the course of six months. We focused on young children’s performance in problem solving situations that involve the comprehension of object movement systems in a computer-based task. We explored several dynamic aspects of inquiry, such as non-linearity, trail-by-trail and session-by-session variability, and context dependency.

The research questions were:

1. Is there an increase/growth in the problem-solving behavior over time in terms of inquiry functioning? If so, what pattern does it follow?

2. Is there a changing pattern of variability in the inquiry functioning of the children on the problem-solving task? If so, what pattern does it follow?

Method

Participants

Four pre-school children from the city of Cali, in the country of Colombia participated in this study. They belonged to medium-high socio-economical level families, based on the geographical location of where they lived in the city. The sample consisted of three boys we will refer to as Jerónimo, Samuel, and Juan (aged 5.2, 5,6 and 5.6), and a girl we will refer to as Mariana (aged 5.6 years) (the names are pseudonyms). All the children attended the same school and were in transition grade which is comparable to elementary school/ kindergarten in the US system. All the children had access to computers in their homes and schools and used them to play on a regular basis. They are also familiar with video games with a similar game play as used in these tasks (using arrows and spacebar to move objects around).

Measures

Children were repeatedly confronted with a computer game in which they had to manipulate three types of variables in order to figure out their influence on a physical system. The three problem-solving situations involved manipulating variables in order to reach a specific objective, which in each case was a ball reaching a target. The tasks involved the use of inclined planes to move a ball (task A), collision of an object with the ball (task B) and a catapult to throw the ball (task C). The tasks were similar in structure and implied the manipulation of three physical variables, changing the objects or positions involved in the problem on a screen with the computer keyboard. Two of the variables in each task had three possible values and the other one had two possible values. Changing the values of the variable allowed the children to modify the outcome distance. The children had to choose the value of the three variables in order to reach one of six possible targets in a plane with a ball. The targets were identified with different colors.

The tasks were (See Figure 1 and Table 1):

Figure 1.

Frames from the actual digital tasks (task A, B and C) (2-column).

Table 1.

Variable values for the tasks

Inclined planes			Collision			Catapult
Mass of counterweight	Location of counterweight	Mass of projectile	Striking object	Angle of strike	Type of ball	Height	Length	Typof bal
1	Long	1	High	90	1	High	Long	1
2	Short	2	Medium	45	2	Medium	Short	2
3		3	Low		3	Low		3

1. Inclined Planes. For this task, children must manipulate the height of the ramp, the type of ball and the length it has to travel over the ramp in order to achieve the required distance.

2. Collision. In this task, the children must use a mobile impulse generator (a baseball bat, a racket, or a golf club) in two different possible angles in order to push one of three different balls to a certain point on the horizontal scale.

3. Parabolic Movement. In this task, the children must manipulate a catapult device, setting three different possible projectiles, with three different possible counterweights, in two different possible positions in order to throw the three different balls towards a target point.

Procedure

After receiving approval from their caregivers, the children were tested 12 times (intervals of roughly 2 weeks among sessions during a period of five months and thirty days). The children completed one task per session, and they faced each task four times. The tasks were presented in the same order for the four children (A, B, C, A, B, C and so on). None of the participants had previously received information on the content of the tasks. For all tasks and in each session a familiarization story was presented and the children were allowed to freely manipulate the elements of the tasks. This condition was intended to give the researcher assurance about the children's understanding of the assignment and their comprehension of the variables involved in the construction of each of the three tasks. During the experiment, an experimenter was always present, introducing the task and setting the targets. The experimenter did not interfere or help the children to reach the targets. The tasks took place in the children’s homes in a separated room. For every task the children had to reach 6 different distances to the target, and were given a maximum number of 10 attempts to reach each target. Here, ‘attempt’ refers to every time the child set the values of the variables in the movement system and threw the object to try reach a target. After the children reached the target or after 10 attempts were made for each target, the next target was presented. The order in which the target distances were presented was determined by the combinations of variable values that were needed to reach the target. This order was counter-balanced among sessions.

The data were collected using software that registered the setting of the system for every attempt. This software was developed in the programming language Python and the database was designed using PostgreSQL. Each attempt was scored during a coding session using an Excel work-sheet programmed to score the attempts in terms of the levels of performance.

Analyses

In this study, we focused on two measures as indicators of the performance in each session. These were: 1) levels of inquiry, and 2) error index. With regard to the first measure, the child’s performance was scored based on the adjustments made by the children on the moving object in order to reach a target. Every attempt (every time the child specifies the values of the variables in the movement system and throws the object to reach a target) was scored on a 9-point scale, and this score was established on the basis of the changes the child made in comparison to the previous attempt (changes in the choices of the values). This scale described how systematic the child’s attempt to change the previous outcome was. It considers whether the child simply repeats the previous attempt, makes counter-productive adjustments, or makes well-organized controlled changes in the values. For every attempt, four dimensions were considered: the use of the task feedback, variable coordination, variable isolation and success reaching the target.

The use of task feedback refers to making changes related to the distance reached versus target distance. The use of task feedback is the case when a child reduces the distance reached when he or she observed to have over-passed on the previous attempt or when he or she increases the distance after falling short on the previous attempt. Variable coordination implies the synchronization of the direction of the adjustments. For example, if one variable is increased in its value and another one is decreased, this would cancel out the net result, which would be not be coordination of variables. On the other hand, if all the selected variables are either increased or decreased, there would be variable coordination. Variable isolation refers to the use of the minimum number of possible variables. When a child concentrates on only one or two variables, he or she is having more control over the task through variable isolation. Finally, reaching the target or not was also taken in consideration to determine each level, because this was the goal of the game. See Table 2 for a description of the resulting inquiry levels. All inquiry levels were automatically generated within the software of the game.

Table 2.

Levels of inquiry functioning that describe the performance on each individual attempt

	Level	Use of task feedback	Variable coordination	Variable isolation	Succes
1	Reiteration of magnitudes between attempts (Repeating same conditions from last attempt)	No	No	No	No
2	Basic adjustment without magnitude coordination nor previous information coordination.	No	No	No	No
3	Basic adjustment with magnitude but without coordination with previous information coordination.	No	Yes	No	No
4	Basic adjustment isolating variables but with-out previous information coordination.	No	Yes	Yes	No
5	Adjustments without magnitude coordination but coordinated with previous information.	Yes	No	Yes	No
6	Adjustment with multiple variables with magnitude and previous information coordination and partially attuned with the goal.	Yes	Yes	No	No
7	Systematic adjustment isolating variables and with previous information coordination and partially attuned with the goal.	Yes	Yes	Yes	No
8	Adjustments with multiple variables and with magnitude and previous feedback coordination attuned with the goal.	Yes	Yes	No	Yes
9	Adjustment with variable isolation and with previous information coordination. Goal reached.	Yes	Yes	Yes	Yes

In order to understand the application of the inquiry levels, consider the following example. In the first attempt, the moving object did not reach the target but moved beyond it. In the second attempt, the child made an adjustment with two variables (ball –1; angle +1) (no variable isolation). He did not coordinate the magnitude of these adjustments (no variable coordination), and did not coordinate his procedures using previous information in order to reduce the distance previously reached (no task feedback). The result is still overpassing the target. This attempt was scored at level 2 according to Table 2. In a third attempt, the child coordinated previous information by reducing the distance (task feedback) and isolating only one variable (ball -2) (variable isolation), also coordinating the magnitude of his adjustment (variable coordination). However, the ball overpassed the target. This attempt was scored at level 7 accordingly.

The second measure in the analysis was the ‘error index’, which was computed as the sum of absolute distances between the target and the result achieved for all attempts on the same target. There were 6 error indexes per session and 72 for the whole series of repeated tasks. Consider the following example: imagine that for the first attempt, the target was located at a distance of 5, and the moving object reached a distance of 3, leading to a difference of 2. For the second attempt, the target was still 5 and the result was 4, which results in an absolute difference of 1. For the third attempt the child reached the target (the difference was 0). The total error index for this target would be calculated as the sum of the absolute differences, which in this case would be equal to 3 (2+1+0). The error index was also automatically generated by an algorithm within the database.

Each target could be reached by specific combinations of values from the three variables. However, the number of unique combination was not the same for each target position. In total, there were eighteen combinations of values (3*3*2). Targets 3 and 4 were reached for five of these combinations (each), targets 2 and 5 were reached for three of these combinations (each), and targets 1 and 6 were reached with one unique combination (each). This means that if a child selects a random combination of values, he or she has a high probability of reaching target 3 and 4 (roughly .28 each), a lower probability of reaching targets 2 and 5 (roughly .17 each), and very low probability of reaching targets 1 and 6 (roughly .06 each). However, since all positions were offered in each session (in the same order), we do not expect this to influence the sessions performance or the developmental trajectories of the performance over time.

The analyses were predominantly based on the description of individual developmental trajectories. First, in order to answer RQ1, the average inquiry level for every session was presented showing general trajectories. These were followed by the raw data, plotted in combination with Loess smoothing, in order to capture the local tendencies and to obtain an impression of the local variability at the same time. Note that in those series that contained less than 15 data points, a moving average with a window of three data points was used instead of a Loess smoothing. After this, the error index trajectories are described, in combination with their pattern of intra-individual variability, in order to answer RQ2. For this purpose, we use a so-called minmax graph: a graphical representation of the lower and upper extremes in the data that uses a moving window (for a more elaborate description, see van Geert & van Dijk, 2002).

Finally, in order to answer RQ3 and test task differences, a Monte Carlo analysis was performed on the individual time series. The analysis was based on a random permutation technique, which is a statistical procedure based on estimating probabilities by randomly drawing samples from a dataset based on the null hypothesis, and comparing the empirically found values with the result from a resampling procedure. If the probability of finding the observed value in the resampling procedure is very low (in this case below 5%), the result is considered to differ significantly from the null hypothesis model. The analysis was performed in Poptools (Hood, 2004; also see Todman & Dugard, 2001).

In the current data, the Monte Carlo procedure was used to test whether there was a difference in difficulty of the six possible target positions. We did this by comparing the sum of all error indices of the different positions and the mean of the inquiry level for each position. It is important to note that this analysis was based on the null hypothesis that there was a symmetrical distribution in the difficulty of the six positions. This null hypothesis is solely based on the a-priori chances of reaching the target with a random combination of values at the three variables. Under this null hypothesis, position 3 and 4 were equally difficult (a priori chance of reaching the target was roughly 0.28 each, because for each of these targets 5 out of 18 combinations lead to reaching this result). The same applied for positions 2 and 5 (a priori chance was 0.17, because 3 out of 18 combination lead to reaching this target) and 1 and 6 (a priori chance was 0.06, because 1 out of 18 combinations lead to reaching this target). Following this assumption, we computed the ratio of the performance at position 1 over 6, 2 over 5, and 3 over 4 (1 divided by 6, 2 divided by 5, and 3 divided by 4). If these ratios were equal or close to 1, the performance was roughly symmetrical. For error index, values smaller than 1 suggest better performance closer to the starting position of the ball (fewer errors), whereas for the mean inquiry level, values below 1 suggest worse performance for positions closer to the starting position (higher inquiry levels). If the values differed significantly from 1, it was asymmetric. In the Monte Carlo analysis, we reshuffled the data without replacement across positions and compared the results of this with the empirical error indices of the six positions. After reshuffling the data 5000 times we calculated the frequency that the empirical values were replicated by the resampled data and transformed this into a p-value.

Results

Individual trajectories

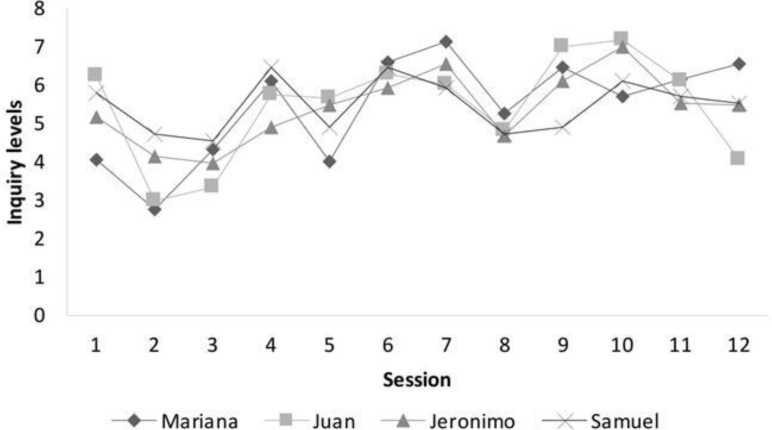
Three out of four children showed a general increase in the mean inquiry level per session in combination with a slight oscillatory pattern (see Figure 2). There were several relapses that indicated individual and inter-task differences, for example, Mariana’s decline in the last session with task A, Jerónimo’s irregular performance in task B at the 8^th session, Juan’s marked decrease for the 11^th and 12^th sessions. In general, the three children’s trajectories seem to be quite similar when describing averages per session. In contrast, Samuel’s mean does not show a general increase and has a relatively low performance in the 5^th, 8^th and 9^th sessions.

Figure 2.

Inquiry level mean for each session.

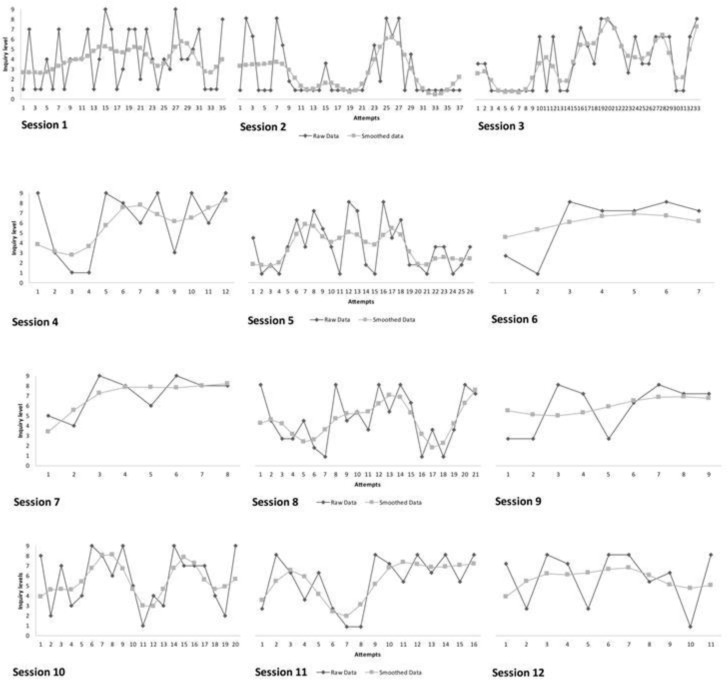
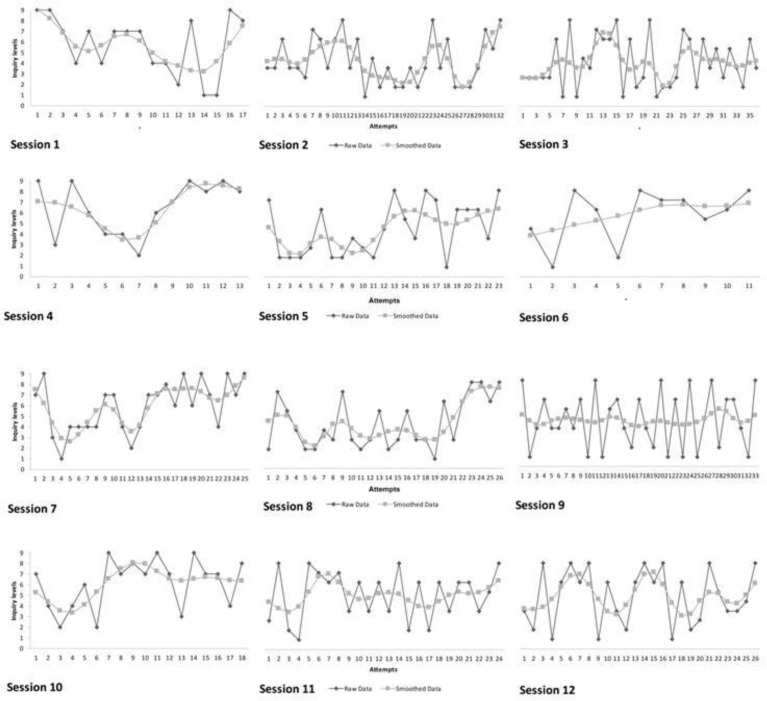
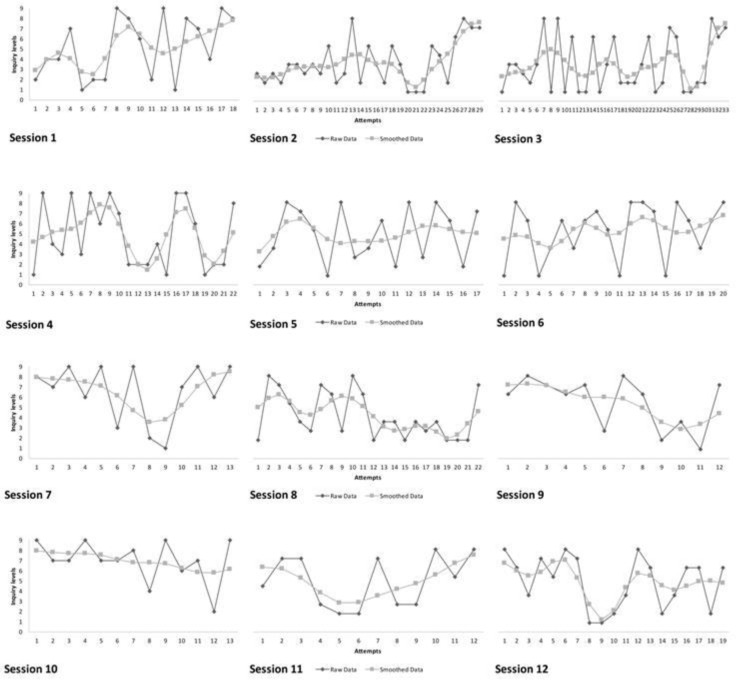
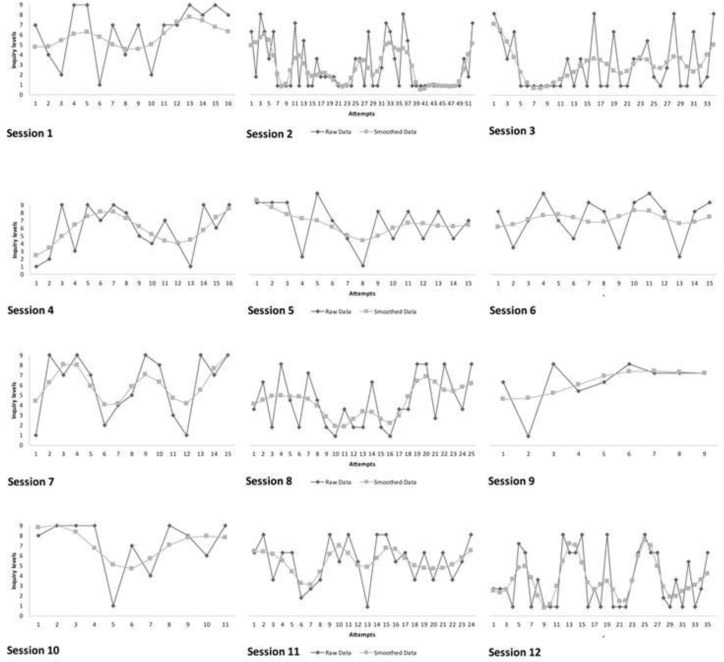
Figures 3 to 6 show the general trajectories of the raw data and a Loess trend line of the real-time inquiry levels of the four individual children across the entire measurement period. Each figure shows a combination of graphs, one graph for each session in which the performance (inquiry level) for each of the child’s attempts is depicted. Visual inspection shows a large degree of variability between the individual attempts within and across all sessions. Recall that ‘attempt’ refers to every time the child set the values of the variables in the movement system and threw the object to try reach a target. Depending on the performance of the child, the number of attempts could be different (a new target was presented after the child either reached the target or after 10 attempts maximum, which implies that a session can be between 6 and 60 attempts long). Some sessions seem to show a global increase in performance (for instance, Mariana’s 3rd and Jerónimo’s 1st session) but others do not. Although there is a global reduction of low level inquiry over the sessions, it is remarkable that all children show some attempts with a low inquiry level even in the final sessions.

Figure 3.

General trajectories of the inquiry level for each attempt within each session (Mariana).

Figure 6.

General trajectories of the inquiry level for each attempt within each session (Samuel).

Figure 4.

General trajectories of the inquiry level for each attempt within each session (Jeronimo).

Figure 5.

General trajectories of the inquiry level for each attempt within each session (Juan)

Though some global similarities in the mean inquiry levels per session exist (see Figure 2), we observed a lot of variability when zooming in at a microscopic time scale (Figures 3 to 6). Overall, a general pattern of variability can be described in terms of a tendency of the trajectories to concentrate in higher levels, but also with low levels of performance which remain to be part of the children’s behavioral repertoire.

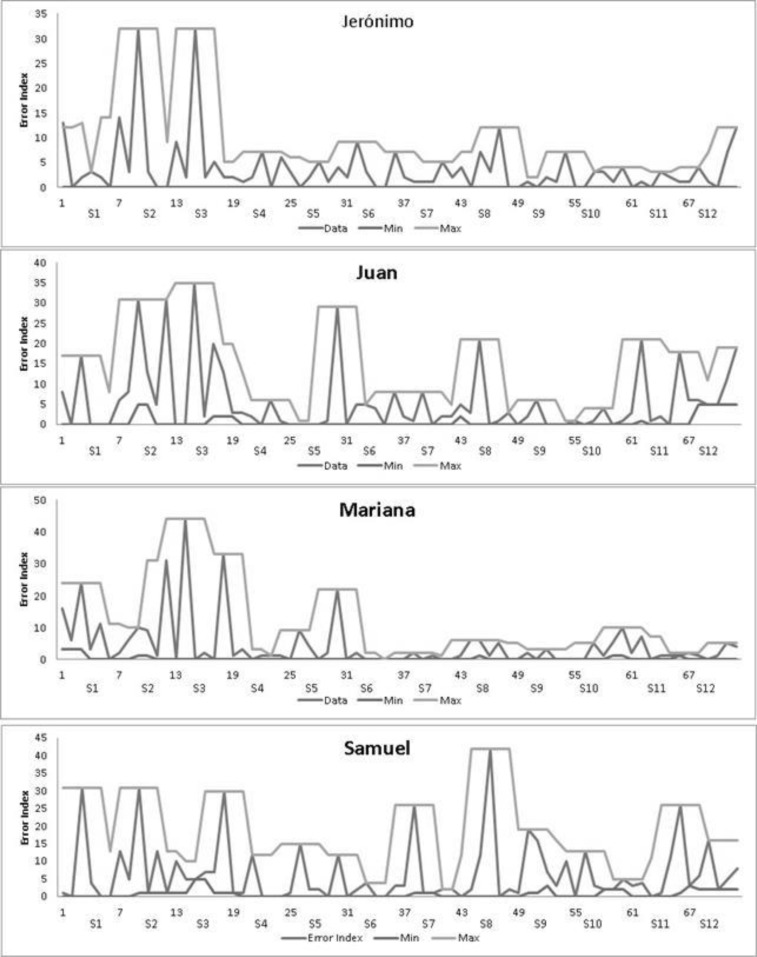
Some general patterns can also be observed when inspecting the development of the error index. For both Mariana and Jerónimo (see Figure 7), a clear decrease in the general level and variability range can be identified after sessions 4 and 5. For Juan, there is also a clear reduction of variability, but the bandwidth of performance remains to be larger than the other two children.

Figure 7.

Variability range of the error index for each target, for all sessions.

For Samuel’s error index trajectory, no clear trend can be described. The variability remained large for the entire trajectory with peaks and valleys on his performance all along the trajectory. In summary, these results showed that three out of four children showed a decrease in the variability of the error index, indicating that their performance became more regulated and stable. However, in all children, smaller or larger bursts of variability remained present along the entire trajectory.

Relation between target position and performance

When considering the performance for the different target positions, in three out of four children (Samuel, Juan, and Jerónimo) the distribution of errors was clearly skewed (i.e., the performance for position 6 was generally better than for position 1). This was surprising, since, given the task structure, a symmetrical distribution was expected. In Mariana’s case the distribution was generally more symmetrical. We tested this observation with a Monte Carlo analysis by taking the ratio of the ‘mirror targets’ as a criterion (performance on target 1divided by target 6, and 2 by 5 and 3 by 4 respectively). The results (see table 3) showed that for error index, three children (Juan, Jerónimo and Samuel) showed a significant difference between position 1 and 6 and only for Jerónimo between 3 and 4 (position 3 being less optimal than 4). For the inquiry level average, two children (Samuel and Juan) showed a significant difference between position 1 and 6, one child between 2 and 5 (Jerónimo) and one between position 3 and 4 (Samuel). It is noteworthy that in all these significant cases the targets that were on the on the “left tail” of the task (that is far from the ramp, bat, catapult) were consistently performed better (fewer errors and higher inquiry level) than on the “right tail” (that is close to the ramp, bat or catapult).

Table 3.

Results of the Monte Carlo analyses concerning the differences between target positions using mean inquiry levels and error index(p-values between parentheses)

		Inquiry level			Error index
		1 against 6	2 against 5	3 against 4	1 over 6	2 over 5	3 over 4
Mariana	ratio p-value	1.009 (0.156)	1.009 (0.406)	1.008 (0.308)	1.05 (0.407)	1.04 (0.158)	0.01 (0.532)
Jerónimo	ratio p-value	1.008 (0.337)	1.006 (0.013)	1.009 (0.582)	0.73 (0.004)	0.84 (0.090)	0.79 (0.049)
Samuel	ratio p-value	1.112 (0.012)	1.005 (0.304)	1.098 (0.029)	0.88 (0.009)	0.81 (0.355)	1.35 (0.102)
Juan	ratio p-value	1.007 (0.011)	1.006 (0.257)	1.009 (0.172)	0.85 (0.031)	0.90 (0.131)	1.35 (0.342)

Note: The ratio was calculated as the value at position 1, 2, and 3 (respectively) divided by the value at position 6, 5, and 4 respectively.

Discussion

When overall trajectories were considered, two prominent observations stood out. First, when we look at each session’s average performance a robust trend towards a higher performance was observed in three out of four participating children. Patterns varied from a stepwise or global increase as were seen in Mariana and Jerónimo, to oscillating trajectories characterized by relapses as seen in Juan and Samuel. Secondly, there was a great degree of variability in the performance of the four children. Children clearly did not gradually improve their problem-solving performance across time but showed large moment-to-moment fluctuations, even after many repeated administrations of the same task. This means that after repeated exposure to the same problem-solving task, children tended to regulate their strategies maintaining a high degree of exploration, whereas at the same time, they had a tendency to show an increase in their efficiency in arriving at the solution. This phenomenon could be related to the emergence of new forms of cognitive functioning throughout the inquiry process. The findings indicated that the development of inquiry in this task does not follow a linear growth but includes advances and relapses, exploratory states and transitions. It is characterized by a high degree of performance variability – which was most prominent shortly after the task introduction and showed a reduction over time-and individual differences.

The observed real-time variability can be understood as an expression of the flexibility required for the system to change over time and to find new and more stable forms of organization. In addition, the presence of variability suggests a coexistence of basic and advanced forms of reasoning during the unfolding of the process. This is also observed in a process called ‘scalloping’ as described by Fischer (Fischer & Yan, 2002; Fischer & Bidell, 2006), where a learner regresses back to a lower level of functioning when he or she faces some change in the context. The combination of simultaneous low-level and high-level functioning allows the flexibility that is required to attain the kind of complex and recursive cognitive functioning demanded by inquiry. This fragility does not allow the inquiry functioning to be easily generalized across tasks, and minor changes in the situation itself cause the system to fall to lower levels and to constantly reconstruct itself (Fischer & Bidell, 2006). This phenomenon follows the idea of Kloos and van Orden (2009) regarding the strong context dependence of the cognitive activity and its ‘soft assembly’ nature.

In addition, when we examined the within-task differences, there was a clear asymmetry in performance suggesting that children perceive the targets differently. In five out of eight comparisons, the performance on position 1 was significantly worse than in position 6. Though the same trend was visible between other target comparisons, the results were less robust. However, in all cases, the targets that were on the far end of the start position had a better performance (fewer errors, higher inquiry levels) than targets that were closer to the starting position. It should be noted that the analysis was based on a-priori chances of reaching the target based on a random combination of values. Of course children do not adjust the values on a random basis but do this purposely, as the other results have already indicated. There is no intrinsic reason in the game why targets closer to the base would be more difficult than targets on the far end, though the performance indicates that they are. However, the results show that in many cases the performance was worse for targets closer to the base and that the null hypothesis was rejected. This trend was also corroborated by the observations during the task administration that some children often responded as being more ‘worried’ when presented with target 1, for instance by saying “no, not the difficult one again!”. A possible explanation might be that the task demanded a high inhibition load on the children, something they had difficulty coping with. It is possible that the children anticipated target 1 as harder to reach because of a perceived demand of being ‘extra cautious’ about passing over the target. Instead, target 6 could be perceived as a ‘get as far as you can’ goal.

This observation coincides with Thelen and Smith’s (1994) view that cognitive processing emerges in the form of context-embedded perception-action loops, and that they are in that sense soft-assembled and intrinsically variable (see also Bickhard, 2009, 2012). The presence of variability does not necessarily imply self-organizing dynamics operating along the developmental trajectories. An alternative explanation could have to do with lack of consolidation of a general domain component, such as hypothesis generation, experimentation, and evidence evaluation (Piekny & Mahler, 2013). These would arise in a stable form at different moments of development, acting as the mechanism that generates the observed behavior of the child. On the other hand, a dynamic system approach could prove to be a plausible alternative to explain the emergent and soft-assembled nature of these processes. This kind of description is compatible with the non-linear development we observed. Also, the soft-assembled nature of inquiry revealed by the fragility of the performance could account for the coexistence of its components with a probabilistic nature within the children’s performance.

It is important to note that inquiry also has a clear social component, which should be included in further research. Several studies have focused on the influence of a supporting adult on the performance of the child during a scientific task (e.g. Peterson, & French, 2008; Rappolt-Schlichtmann, Tenenbaum, Koepke, & Fischer, 2007). However, in the present study, we have limited ourselves to problem solving in a self-regulatory context, that is, the emergence of problem solving in the sole interaction between a child and a task. Although self-regulation is an extensive topic in itself that exceeds the scope of this paper, it should be noted that several authors (such as Boekaerts & Cascallar, 2006) have pointed at emergent aspects of self-regulation.

The results of this study are based on a multiple case study of four individuals. It may be argued that further study is needed aimed at collecting a more extensive database of subjects that allows for the comparison between a larger set of (types) of trajectories. However, this does not mean that the study of a small set of individuals by definition leads to limited knowledge. Maybe it could be argued that only knowledge about universals, that is, universal processes of problem-solving in children, is valid scientific knowledge, and knowledge about particular individuals is less scientifically valid. However, if scientific research is a way of answering questions about things we still do not know, then the detailed study of a particular problem-solving process, is also a valid scientific activity, based on a valid scientific question. If it were indeed so that we knew already a lot about how particular problem-solving processes in young children look like, how they evolve over time and so forth, then doing yet another detailed analysis of a particular problem-solving process would probably add very little to our scientific knowledge, unless this study were aimed at answering questions that resulted from the previous person oriented studies. However, the point is that we know very little about the particulars and the detailed time-dependent structure of children’s problem solving behavior when repeatedly faced with a task situation.

The question may be asked as to whether the knowledge about a few particular cases is generalizable. The answer to this question depends on the definition of generalizability. In the standard account, generalizability is a statistical property of a particular finding based on a sample of independent cases, which basically amounts to the probability that the finding is true (or within which limits it is true) of another sample of independent cases that represent the same general category, namely the set of all possible cases representing that category (which is customarily called the population). The category in question can be any general natural category, for instance the category of 5-year-old children, or it can be any combination of such general natural categories for instance the combination of the category of 5-year-old children with the category of physics problems. In a person-oriented account, generalization itself is a process, rather than a given statistical property of the finding based on a particular sample. Generalization is a process of belief revision, based on existing and newly acquired evidence. It is part of an epistemic process going both ways, namely the way of particularization (answering the question of how a general model of certain phenomena and processes works out if it is carried out on the level of actual, real-time, particular processes) and the way of generalization (answering the question of how a model based on particulars works out of it is linked with general theoretical principles and empirical findings on other particulars). Generalization in the case of a few specific person-oriented process studies begins with trying to establish the differences and similarities between the cases, and trying to connect the findings with general theoretical principles (such as those regarding the importance of variability, self-organization etc.).

In person-oriented research, generalization is often not an immediate result of a single study, but is very often a long and very tedious process that requires chains of connected studies. Hence, the question to be answered is not so much whether the findings generalize, for example to the general population of a particular category, or to other tasks or general classes of tasks, but rather whether a particular empirical study makes a relevant contribution to the long and laborious process of generalization, and if so, what is contribution might be.

In the current study, we have tried to make a contribution towards understanding inquiry functioning and its development in children, by providing a detailed description of the temporal unfolding of such processes on the short-term time scale of the child's actual solving of the problems and the long-term time scale of learning and development, which in this particular study covered the changes occurring over a period of five months. We believe that such detailed process descriptions are the necessary first steps towards a better understanding of the complex dynamic nature of inquiry processes in young children.

Authors' contributions

This work is a product of the intellectual environment of the four authors; all authors have contributed in various degrees to the analytical methods used, to the research concept, to the study’s design and to the resulting manuscript. JM collected all data, carried out most statistical analyses and wrote the first versions of the manuscript. MVD carried out part of the statistical analyses and revised the manuscript. RP designed the study and supervised the study as a whole. PVG provided theoretical and methodological advice and was actively involved in writing the first and final version of the manuscript. All authors approved submission of the final manuscript.