Image-Based Elastography of Heterochromatin and Euchromatin Domains in the Deforming Cell Nucleus

Abstract

Chromatin of the eukaryotic cell nucleus comprises of microscopically dense heterochromatin and loose euchromatin domains, each with distinct transcriptional ability and roles in cellular mechanotransduction. While recent methods have been developed to characterize the mechanics of nucleus, measurement of intranuclear mechanics remains largely unknown. Here, we describe the development of nuclear elastography, which combines microscopic imaging and computational modeling to quantify the relative elasticity of the heterochromatin and euchromatin domains. Using contracting murine embryonic cardiomyocytes, nuclear elastography reveals that the heterochromatin is almost four times stiffer than the euchromatin at peak deformation. The relative elasticity between the two domains changes rapidly during the active deformation of the cardiomyocyte in the normal physiological condition but progresses more slowly in cells cultured in a mechanically stiff environment, although the relative stiffness at peak deformation does not change. Further, we found that the disruption of the KASH domain of the LINC complex compromises the intranuclear elasticity distribution resulting in elastically similar heterochromatin and euchromatin. These results provide insight into the elastography dynamics of heterochromatin and euchromatin domains and provide a non-invasive framework to further investigate the mechanobiological function of subcellular and subnuclear domains limited only by the spatiotemporal resolution of the acquired images.

Graphical Abstract

Optical microscopy, image analysis, and computational modeling are used in combination to investigate the intranuclear elastography. Relative stiffness of euchromatin and heterochromatin domains are quantified non-invasively. Compared to a soft mechanical environment, on a stiff substrate the dynamics of nuclear elastography is altered. Nuclear envelope protein disruption affects the relative stiffness of the intranuclear space.

1. Introduction

The eukaryotic cell nucleus contains thousands of genes and long non-coding regions in the chromatin. The chromatin is compacted to fit inside a small nuclear volume through hierarchical condensation mechanisms resulting in a complex architecture ^[1–3]. The condensation is non-random and follows a sophisticated pattern for the efficient transcription of the necessary genes. When stained using a DNA binding chemical such as DAPI, the interphase chromatin shows two distinctive regions – the heterochromatin and the euchromatin ^[4]. Several studies suggest that the heavily stained, brighter region is the heterochromatin. It is the dense and tightly packed form of DNA, is transcriptionally inactive, and plays a critical role in maintaining structural integrity of the nucleus ^[5,6]. The lightly stained, less bright euchromatin is the loosely packed form of DNA and they are thought to be the transcriptionally active regions in the nucleus ^[7]. In stem cells, the two chromatin regions are not distinct but in most differentiated tissue specific cells, the two regions are distinctively separated ^[8]. Although the functions of these two regions are presently explained from the transcriptional perspective, the detailed functional difference between the two regions still remain elusive.

In the recent years, probing the mechanical properties of the heterochromatin and the euchromatin has gained significant interest because of the discovery of potential mechanisms that transduce mechanical forces into biological signals inside the cell nucleus – resulting into the emerging field of nuclear mechanobiology ^[9–11]. Mechanotransduction inside the nucleus is known to play critical roles in development, physiology, homeostasis and diseases ^[12,13]. Clear experimental results have been presented to show that the deformation and force in the nuclear microenvironment is directly related to the gene transcription ^[14–16]. To quantify and further understand the deformation characteristics of the nucleus, nuclear mechanics have been investigated for a significant time ^[17,18]. Traditionally, the bulk nuclear deformation quantification and bulk mechanical properties of nuclei such as elastic modulus have been primary probed by research groups ^[19–23] without delving into the detailed intranuclear mechanical characterization – mostly due to technical limitations. Recently, new technologies ^[24] have enabled us to calculate spatiotemporal displacements and generate high-resolution deformation maps in the nucleus from optical microscopy image data which enables our ability to ask and answer in depth questions regarding nuclear mechanobiology. However, as of now, no study exists that attempted to quantify intranuclear mechanical properties such as elastic modulus distribution although having this information will expand the predictive ability to quantify cell deformation by analytical and computational models. The significant effort in this line have been pursued by the intranuclear rheology^[25,26] which tracks the passive movement of fiduciary markers such as beads but such approach has a few limitations – (1) the characterization of the mechanical properties under active mechanical loading is limited, (2) inserting beads in the nucleus is technically difficult, specifically in several primary cells and for cells in situ or in vivo, (3) bead insertion can be a highly invasive method which compromises the cell viability. Atomic force microscopy (AFM) can also potentially probe the nuclear elasticity distribution ^[27–30], but that is also technically challenging specifically because – (1) the insertion of AFM probe inside the nucleus after crossing cell and tissue barrier is difficult, (2) this technique is invasive for the cell, and therefore it can significantly disrupt the cell physiology.

Optical microscopy-based ^[31–33] elastography has the potential to reveal the intranuclear distribution of mechanical property in a non-invasive way. Elastography is used to solve many engineering problems where the mechanical property needs to be quantified in a minimally invasive manner. For biological problems elastography is used in different organs at the tissue scale with multiple modalities and variations such as ultrasound and magnetic resonance imaging, proving their translational/ clinical potential ^[34–36] but such modalities do not have the spatial resolution to image the intranuclear details. The basic paradigm of elastography is to use the known displacement of the domain of interest and the appropriate combination of force and/ or displacement boundary condition to inversely estimate the most probable elasticity parameters in the domain of interest. There are several technological challenges toward achieving a reliable, high resolution spatial elastography including divergence of the solution and ill-posed problem. However, simplification of the elastography problem can be achieved by discretizing the domain of interest into localized individual subdomains where the intra-subdomain elasticity can be assumed to be uniform. Using this approach, it is possible to quantify the elastic properties of two separate domains such as heterochromatin and euchromatin in the nucleus. In this paper, we report the execution of this objective of quantifying the heterochromatin and euchromatin elastic modulus using an optical microscopy-based approach. Although the ideal elastography solution could address the mechanical properties of chromatin at highest possible resolution, a two-domain elastography is the natural first step before achieving the high resolution elastography.

In the present study, we establish, validate and demonstrate the application of ‘nuclear elastography’, a technique to quantify the elasticity of the heterochromatin and the euchromatin domains of a deforming nucleus through an elaborate microscopic image analysis-based workflow. To accomplish this multi-step process, we first quantified the displacement map in the nucleus using our previously established technique ‘deformation microscopy’ ^[24]. Next, we executed an inverse problem solution framework to iteratively calculate the elasticity of the chromatin domains by using the already computed intranuclear displacement field, and the boundary displacement information as the boundary condition. As the model system we applied the technique on the nucleus of murine embryonic cardiomyocytes cultured on a PDMS substrate thus exploiting the inherent deformation behavior of beating cardiomyocytes in vitro. Besides, being a highly differentiated cell, when stained, the cardiomyocyte nucleus shows distinctive regions of heterochromatin and euchromatin. To rigorously validate the nuclear elastography technique, we applied known elastic moduli to heterochromatin as well as euchromatin and under this circumstance, we deformed the nucleus using experimentally similar deformation situation such as applying same displacement boundary condition on the nuclear periphery. Then, we used the baseline known elasticity values to reproduce the inversely calculated elasticity values obtained by nuclear elastography technique. After validation, we focused on applying the nuclear elastography in several physiological and pathological conditions, thus revealing new biological insights into nuclear mechanics. We showed that the dynamics of intranuclear elasticity was altered in cardiomyocytes cultured on pathologically stiff substrates compared to cardiomyocytes cultured on soft substrates that resemble native cardiac mechanical properties. Further, we showed that the intranuclear elasticity distribution was significantly compromised after global disruption of LINC complex by compromising the KASH domain, but not the nesprin-3 alone, in the nuclear envelope. Our data shows that the mechanical properties of the chromatin domains are optimized to enable physiological cell function and such optimization is disrupted in the pathological condition.

2. Results and Discussion

2.1. Nuclear elastography provides the relative elastic modulus of the chromatin domains

Nuclear elastography workflow starts with the time-lapse high-resolution imaging of a deforming nucleus inside a live cell. The spatial image texture in the image frames is first utilized to quantify a high-resolution spatial displacement map inside the nucleus via deformation microscopy ^[24] which uses image registration by hyperelastic warping ^[37–39]. The displacement map serves two purposes – they are used to execute the optimization algorithm by minimization of an objective function computed as the sum of root mean square error in the displacement, and also, they serve as the boundary condition in the domain of interest – the nucleus. Next, the workflow requires the creation of an in silico model of the nucleus for further finite element analysis in the open source software suite FEBio ^[40] (Figure 1). During this step, we discretized the nucleus into two domains – euchromatin and heterochromatin using a Hill’s function formulation. Further, we applied an inverse problem solution framework to characterize the mechanical property of the two chromatin domains – euchromatin and heterochromatin by using the minimization of the displacement data based objective function and the displacement boundary condition. The results of two-domain elastography presented in this work is obtained using MATLAB and several open-source software packages such as FEBio ^[40], GibbonCode and TetGen using only a desktop computer, where each run takes around 20 minutes. Therefore, this technique is scalable to broader use in the academic research settings.

Figure 1.

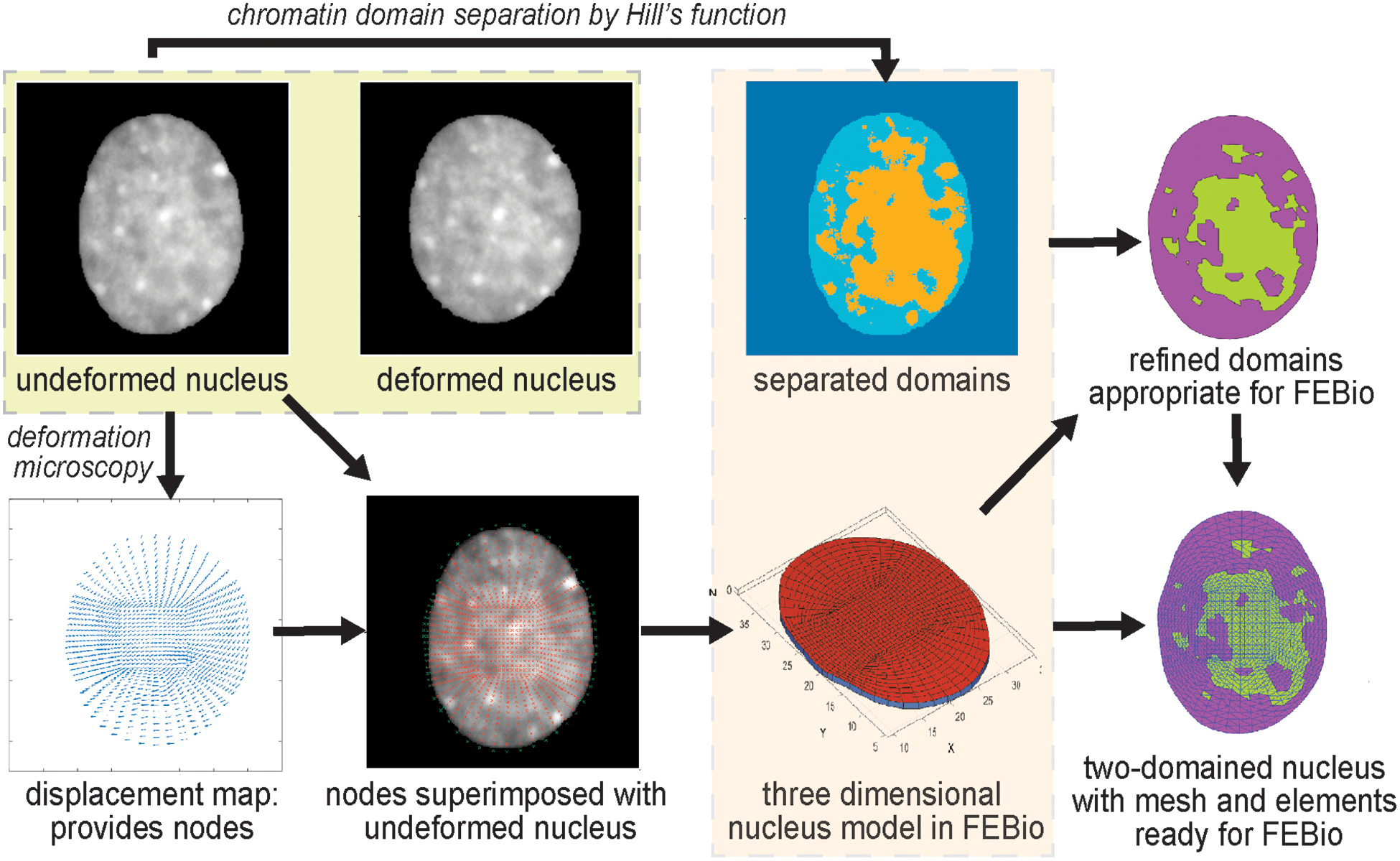
Workflow of the two-domain nuclear elastography. An undeformed image and a deformed image of the same nucleus are used to compute the relative elasticity of the heterochromatin (dense chromatin) and the euchromatin (loose chromatin) domains. First, the displacement map is obtained through deformation microscopy ^[24]. It is to be noted that the displacement fields are computed for thousands of nodes ^[24] and all of them are subsequently used for elastography. For visualization purpose the displacement fields are shown for a few nodes only. The heterochromatin and euchromatin domains are separated through a Hill function formulation (Figure S1 and Methods). The distribution of the nodes and their detailed information (location and connectivity) from the displacement map is used to create a three-dimensional ‘FEBio preprocessor’ model of the nucleus. Based on the separated domain map and the distribution of the nodes, the elements of the in silico nucleus are assigned to either the heterochromatin domain or the euchromatin domain. Further, the domains are refined to match the elements in the model nucleus, which is finally used through the FEBio interface for execution and postprocessing.

This workflow enables us to apply any material model in the inverse problem solution such as hyperelastic or linear elastic material model. Because the elastic modulus is the most generic characterization of elasticity, we used material models which involves the elastic modulus. For the hyperelastic inverse solution we used the neo-Hookean model which involves the elastic modulus (E). For the linear elastic model, we used the Hooke’s law which also quantifies the elastic modulus (E), traditionally called the Young’s modulus. In either scenario, after the complete procedure we obtained the elastic modulus of the heterochromatin (E_h) and the euchromatin (E_e) domains. In this paper we report the ratio of E_h / E_e, and not the absolute values of E_h and E_e separately because with a displacement boundary condition we can only obtain the relative values. Therefore, all the results in this work only determines the relative measure of the elasticities of the heterochromatin vs euchromatin and should be interpreted accordingly. Such approach of finding relative elastography from displacement boundary conditions is common in the elastography ^[41–43]. The extension and implication of the same framework with a force or stress boundary condition is discussed later.

2.2. Validation studies reveal the capability and limitations of nuclear elastography

The real experimental displacement data that we have used in this study is generated from our previous technique deformation microscopy ^[24], which utilizes a new-Hookean hyperelastic material model. It should be noted that for the calculation of displacement field, the deformation microscopy is applied on the whole intranuclear space irrespective of the demarcation of the euchromatin and heterochromatin domains. For the inverse solution to quantify the Elastic modulus, any material model could be incorporated. Given that we could use either hyperelastic neo-Hookean model or linear elastic Hookean model, we validated this technique for all possible scenarios such as forward hyperelastic model – inverse hyperelastic model, forward hyperelastic model – inverse elastic model, and forward elastic model – inverse elastic model. The specific results for a forward hyperelastic material model and the inverse elastic material model results are summarized in Table 1. For different ratios of E_hf and E_ef (f denotes the forward problem), we obtain the inversely calculated ratio of E_h and E_e. We calculate the error in the inverse estimation as. $100*\left(\raisebox{1ex}{$E_h$}\!\left/ \!\raisebox{-1ex}{$E_e$}\right.-\raisebox{1ex}{$E_{hf}$}\!\left/ \!\raisebox{-1ex}{$E_{ef}$}\right.\right)/\left(\raisebox{1ex}{$E_{hf}$}\!\left/ \!\raisebox{-1ex}{$E_{ef}$}\right.\right)$ It can be noted from Table 1 that for E_hf /E_ef = 1, we obtain only an error of 0.41%. At a different ratio such as E_hf /E_ef = 0.1, we obtain an error of 9.30%. Heterochromatin is denser than euchromatin, so it is expected that heterochromatin is stiffer than euchromatin. Therefore E_hf /E_ef = 0.1 is probably not a physically realistic case. However, for the case E_hf /E_ef = 10 we obtain an error of 12.37%. For all the cases we found the inversely calculated displacement almost perfectly matches with the forward simulation displacement as denoted by R² values close to 1 (Figure 2a, 2b, 2c). Even for the cases of E_hf /E_ef = 0.1 and E_hf /E_ef = 10 we obtained R² values close to 1. This result suggests that although the optimization algorithm matches the displacement efficiently, an error occurs in the E_h /E_e. To understand the reason, we continued the validation study with the cases for the forward elastic material model and the inverse elastic material model (Table S1) as well as for the forward hyperelastic material model and the inverse hyperelastic material model (Table S2). In all cases, we found the error almost approaches to 0% even for extreme ratios such as E_hf /E_ef = 0.1 and E_hf /E_ef = 10. As expected, in these cases as well, the displacement from forward simulation and the inverse problem solution closely matches (Figure 2e, 2f, Figure S2). This data confirms that the error incurred in the inverse estimation as elaborated in the Table 1 is caused by the discrepancy in the material model used in the forward simulation (hyperelastic) vs inverse solution (elastic).

Table 1.

Summary of the validation of two-domain nuclear elastography for the forward hyperelastic material model and the inverse elastic material model for a range of elasticity ratios.

Forward problem			Inverse solution			Error
Ehf	Eef	Ehf /Eef	Eh	Ee	Eh/Ee
1000	1000	1	991	987	1.004	0.41%
1000	10000	0.1	276	2525	0.109	9.30%
10000	1000	10	2550	291	8.763	12.37%

Figure 2.

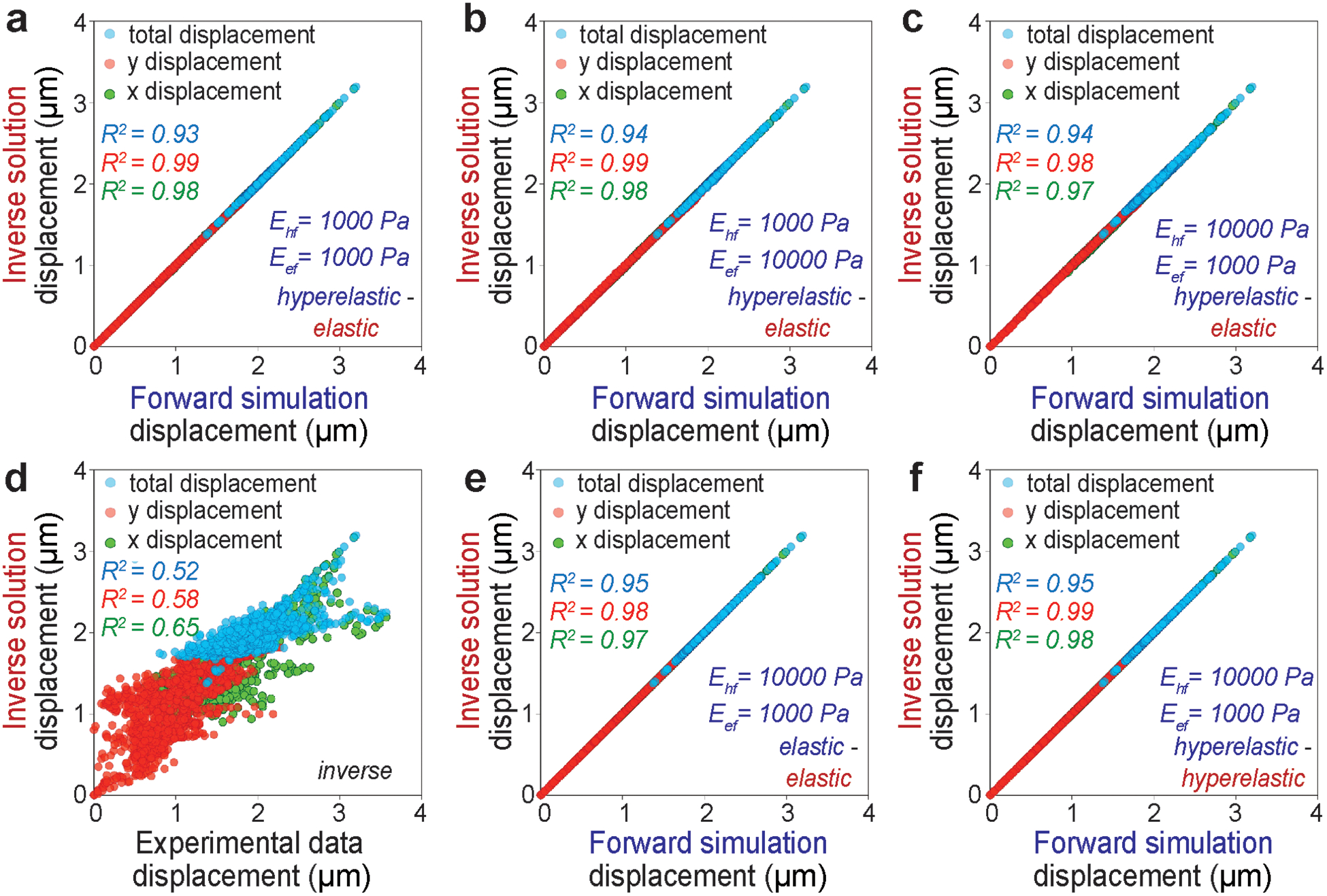
Displacement in x direction, displacement in y direction and total displacement in the xy plane is used as the measure of the accuracy of the two-domain nuclear elastography. The upper row shows the displacements from the forward hyperelastic material model and the inverse elastic material model for a range of elasticity ratios - (a) E_hf/E_ef = 1:1, (b) E_hf/E_ef = 1:10, (c) E_hf/E_ef = 10:1. Displacement data from the inverse problem solution is plotted against the actual displacement data fed to the inverse problem - in (d). The displacement from the forward elastic material model and the inverse elastic material model is plotted in (e) for a physically realistic value of E_hf/E_ef = 10:1. The displacements from the forward hyperelastic material model and the inverse hyperelastic material model is plotted in (f) for a physically realistic value of E_hf/E_ef = 10:1.

For the real experimental data, the displacement values after the completion of the inverse problem solution do not perfectly match with the input experimental displacement (Figure 2d), which will most likely cause an error in the calculation of E_h /E_e. To understand the reason behind this and potential impact of this error in the workflow, we continued with the next level of validation studies to assess our degree of confidence in the E_h /E_e value for real experimental data. We reveal that the large displacement is one of the responsible factors behind the mismatch between displacement calculation and resulting error in the elasticity ratio calculation (Figure 3a, 3b, 3c). Even for E_hf /E_ef = 10, at smaller displacement factors such as 0.05 and 0.1, which represent a small deformation, the error is almost zero (Table S3) and we obtain E_h /E_e = 10. With a displacement factor of 0.5, the error increases to 5.96%, and at a displacement factor = 1, we reach an error of 12.37% (Table 1). At even higher but experimentally unrealistic displacement factors such as 1.5, 2 and 3 the error magnifies drastically (Table S3). This data suggests that for large deformations, which might be the case in real experimental data in some parts of the nucleus, the technique becomes less robust. From Figure 2d it can be noted that we reached a maximum displacement of 4.5 μm (as an estimate based on maximum × displacement of 3 μm and maximum × displacement of 3 μm) for the cardiomyocyte beating induced nuclear deformation experiments. Most of the net displacement vector magnitudes lie between 0.8 to 3 μm. Cardiomyocyte beating is a physiological scenario where the nuclear deformation is the largest. For other realistic physiological loading such as osmotic loading of chondrocytes in cartilage ^[24] or active mechanical loading induced chondrocyte deformation in cartilage ^[38], the nuclear deformation is significantly smaller. Therefore, our demonstration of nuclear elastography shows the highest possible error in the relative elasticity of heterochromatin and euchromatin because of the choice of our problem. The extreme displacement factors such as 1.5 and higher are used only for the understanding and demonstrating the source of error, and they are not realistic values.

Figure 3.

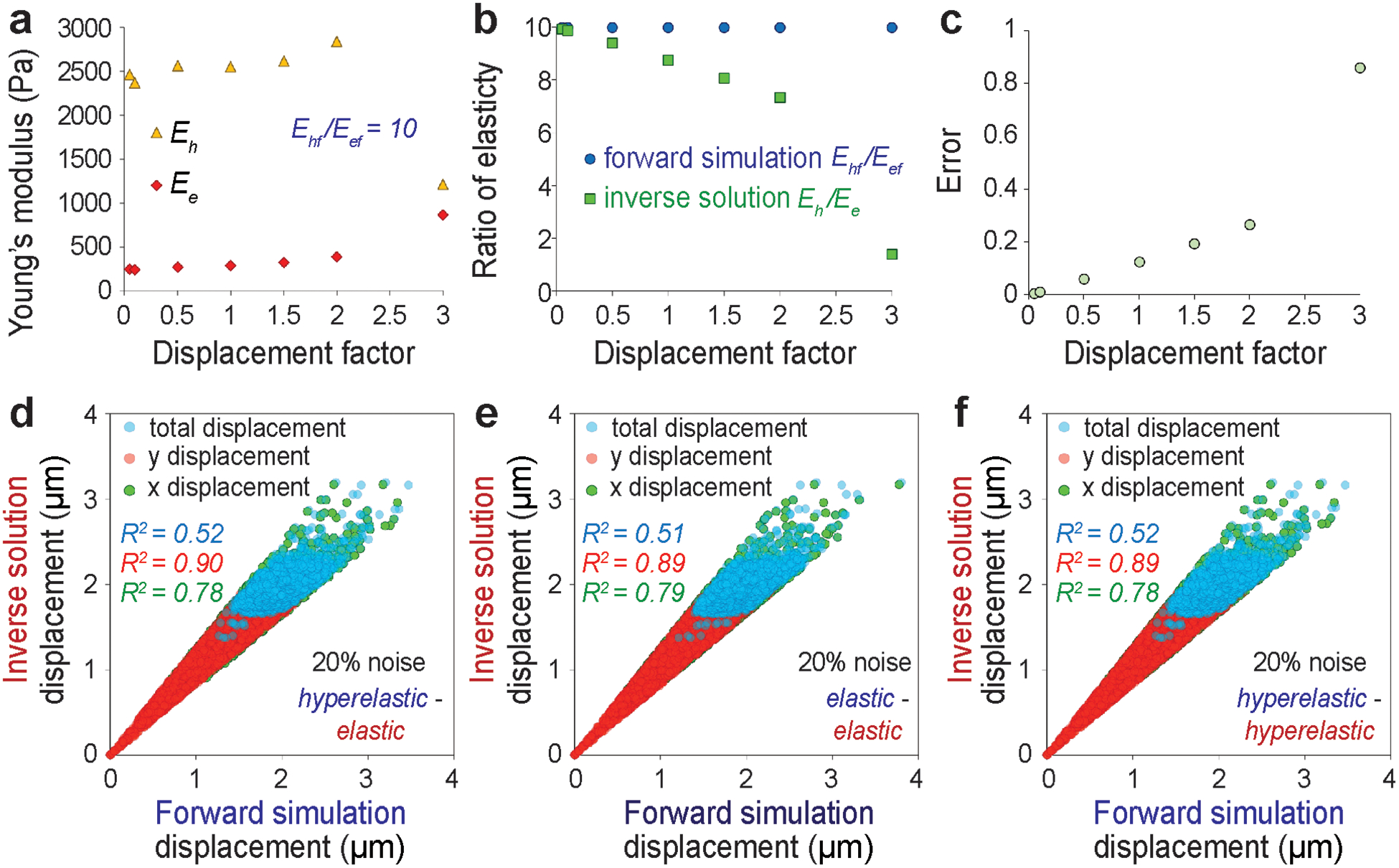
Effect of large displacement and noise on the accuracy of the elastography. For predetermined forward elasticity values of E_hf = 2500 Pa and E_ef = 250 Pa, at different displacement factors (see Methods), the E_h and the E_e values are inversely computed (a), their ratio is presented (b) and the error in such calculation is shown (c). Effect of 20% noise in the displacement data is investigated and the displacements are plotted for different combinations of forward model and inverse solution – (d) forward hyperelastic material model and the inverse elastic material model, (e) forward elastic material model and the inverse elastic material model, (f) forward hyperelastic material model and the inverse hyperelastic material model.

Another contributing factor that introduces error in the E_h /E_e calculation is the noise in the displacement data, which might be created by the inherent noise in the digital image or the error created by the displacement calculation. For every combination of forward and inverse material model it can be noted that the displacement mismatch is magnified by the noise, especially at a larger displacement (Figure 3d, 3e, 3f). Accordingly, the error in the E_h /E_e is incurred as computed (Table S4) – for E_hf /E_ef = 10, we get an error of 14.54% at the noise level of 20% for the forward hyperelastic material model and inverse elastic material model. However, it was further revealed that if we use the same material model for forward and inverse simulation (Table S5, Table S6), the error drastically drops even at 20% of noise. At E_hf /E_ef = 10, the error drops to 2.85% for the forward elastic material model and the inverse elastic material model; and the error drops to 3.03% for the forward hyperelastic material model and the inverse hyperelastic material model. Therefore, we can conclude that for this technique to be applied in the present form in order to reveal difference between experimental groups, the observed value of E_h /E_e should be drastically different between the groups – which is a limitation of the present study. However, for the same reason stated above, performing a high-quality microscopy to achieve higher signal to noise ratio will abruptly improve the reliability of the elastography.

2.3. Pathological condition alters the dynamics of beating cardiomyocyte nuclear mechanics

Cardiomyocytes are known to modulate their beating behavior in vitro based on the microenvironment stiffness. Physiological beating properties are observed on substrates that resemble native cardiac stiffness (~12 kPa), while microenvironments with increased stiffness led to a decline in the contractility ^[44]. The stiffening of cardiac environment is associated with various pathological conditions including cardiac hypertrophy, cardiac infarction and cardiac fibrosis ^[45,46]. Since a decline in cardiomyocyte contractility is associated with an abrogated nuclear strain transfer ^[24], with possible downstream nuclear mechanobiological implications, we aimed to understand how the altered microenvironment mechanics affects the dynamics of intranuclear mechanics specifically the relative elasticity of the two chromatin domains.

On implementation of nuclear elastography we found that under physiological condition, where cardiomyocytes were cultured on soft substrate resembling the native heart stiffness, the nucleus deforms by a large extent and over this timeframe of large deformation at peak cardiomyocyte contraction (t₁ and t₂), the E_h/E_e value is between 2.5 and 3 (Figure 4). It should also be noted that during this timeframe, the strain values of the euchromatin region (the less stiff region) is significantly higher than the strain in the stiffer heterochromatin region (Figure S3). At later timepoints (t₃ and t₄) of post peak-deformation, when the nucleus comes back to its resting post-systolic state, the E_h /E_e value drastically increases by more than three times attaining a value of at least 8.5. Also, the nuclear strain in the post peak-contraction timepoints significantly decreases in accordance with a lower nuclear deformation (Figure S3). The sudden change in stiffness ratio is attained rapidly only over a single timepoint change (t₂ = 312 ms to t₃= 468 ms). It might be possible that the stiffness difference between the heterochromatin and the euchromatin regions needs to be diminished during peak nuclear deformation to accommodate a large nuclear strain. From the baseline resting state of E_h /E_e, when the cell deforms more, therefore undergoing through higher strain, the quantity E_h /E_e decreases. This can either mean that the euchromatin stiffens more compared to heterochromatin or it can mean heterochromatin softens more compared to the euchromatin. However, it is not possible to specifically determine which one is the more likely situation. Quantification of absolute values of E_h and E_e using stress boundary condition can elucidate more details, which is not the focus of the present work.

Figure 4.

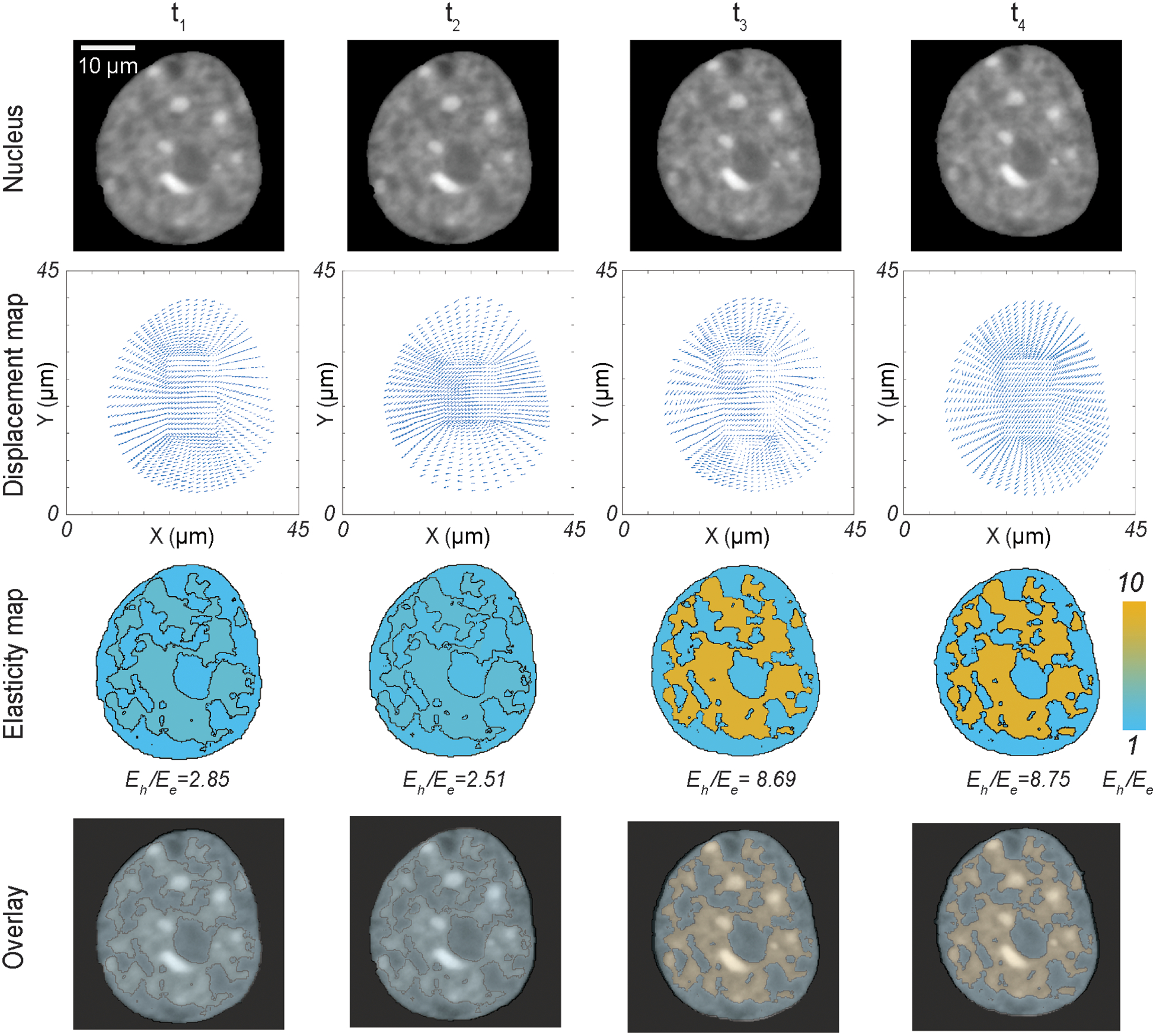
Dynamics of the relative elasticity of the heterochromatin domain and the euchromatin domain on a beating cardiomyocyte in physiological condition - with raw nuclear image, displacement map from deformation microscopy, elasticity map from two-domain elastography and the overlay of raw image + elasticity map. Timepoints for imaging and analysis are as follows: t₁ = 156 ms, t₂ = 312 ms (peak contraction), t₃ = 468 ms, t₄ = 624 ms.

For a stiff environment (434 kPa) which resembles the pathological cardiac condition, again we noticed a dynamic change in the E_h /E_e (Figure 5), however the dynamics of nuclear mechanics significantly changes from that of the soft substrate (Figure 4). The E_h /E_e attains a value of 5.03, when the nucleus is most deformed (Figure S4) at peak cardiomyocyte contraction. However, at a less deformed configuration (t₁), the E_h /E_e value is 1.49, and at the later timepoints, where the nucleus slowly comes back to its resting state, the E_h/E_e value slowly adapts to 6.29 and 7.83. In essence, on stiff substrate we observe a gradual change of E_h /E_e over time. This observation is in stark contrast with the nucleus on soft substrate, where we observed mostly two mechanical states of E_h /E_e. There is a possibility that for nuclei in stiff environments, the required mechanism of abrupt change in E_h /E_e is compromised, which leads to an altered lower strain value (Figure S4), eventually having possible downstream mechanobiological implications.

Figure 5.

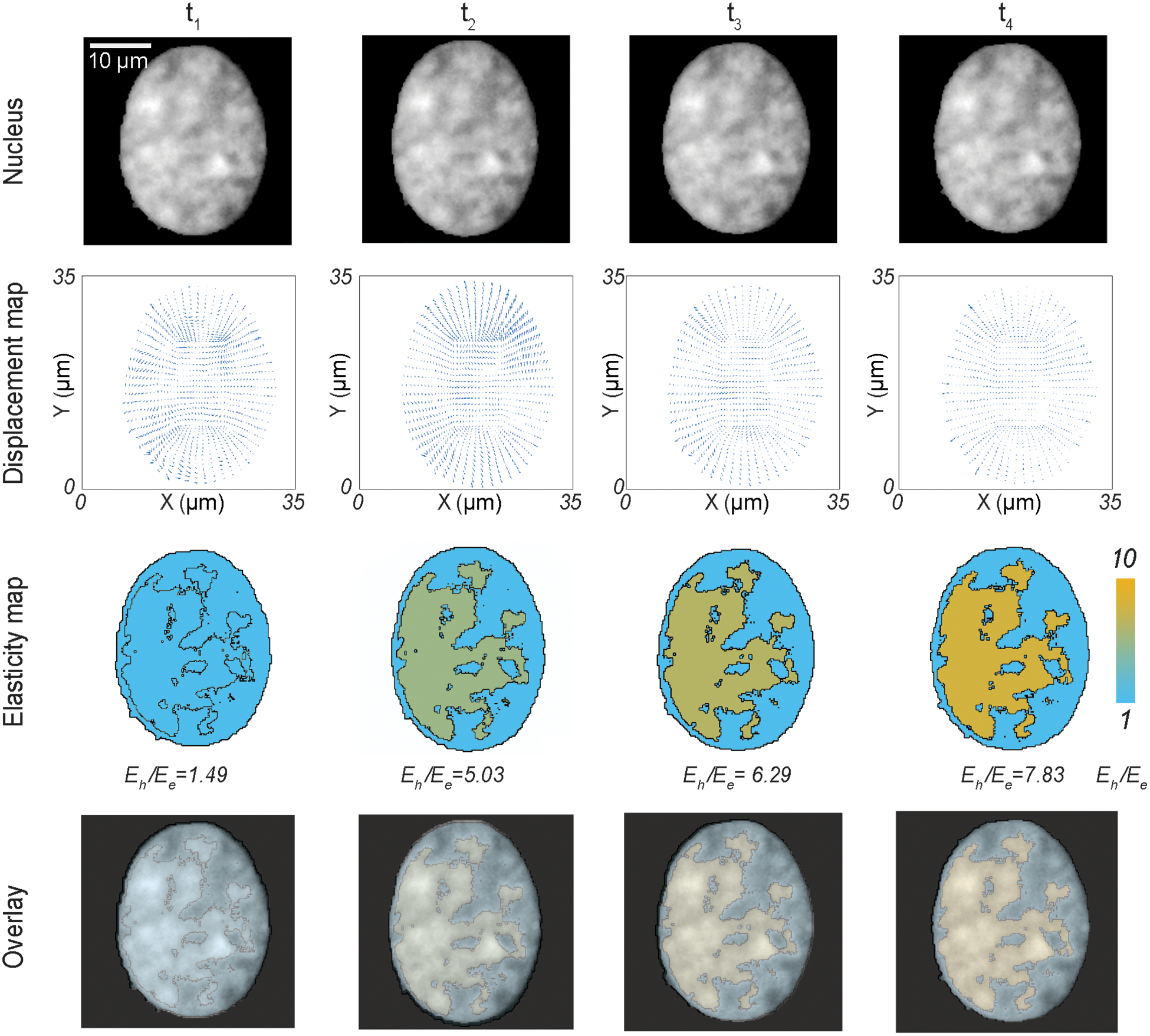
Dynamics of the relative elasticity of the heterochromatin domain and the euchromatin domain on a beating cardiomyocyte in pathological condition (stiff substrate) - with raw nuclear image, displacement map from deformation microscopy, elasticity map from two-domain elastography and the overlay of raw image + elasticity map. Timepoints for imaging and analysis are as follows: t₁ = 156 ms, t₂ = 312 ms (peak contraction), t₃ = 468 ms, t₄ = 624 ms.

It should be noted that such drastic change in the stiffness ratio over time (Figure 4 and Figure 5) in the two chromatin domains cannot be explained from any known biological process, to the best of our knowledge. The change in E_h /E_e over time suggests that the two different domains have a separate time-dependent mechanical behavior, suggesting a more complex viscoelastic phenomenon which can be explored in future studies. However, at a given timepoint the situation is more likely quasi-static, or a dynamic (cyclic) equilibrium of the contracting cells as reported before ^[47]. Therefore, the elasticity ratio calculation by inverse problem is still valid at a given timepoint.

2.4. KASH disruption, but not nesprin-3 knock-down, affects the relative chromatin stiffness

The intranuclear chromatin is connected with the cytoskeletal structure through the LINC complexes. The cytoskeletal proteins actin filaments, intermediate filaments and microtubules are respectively connected with nesprin-1 and 2, nesprin-3 and nesprin-4^[12]. All nesprins are connected with the KASH domain of the LINC complex located between the inner nuclear membrane and the outer nuclear membrane. The KASH domains are in turn connected with the SUN domain of the LINC complex, which protrude beyond the inner nuclear membrane to connect with the chromatin architecture. Because of such connectivity between the cytoskeletal and the intranuclear space, force can transduce through these structures to deform the chromatin architecture. Mutations in the LINC complexes are linked to pathological conditions ^[48,49]. In cardiomyocytes, desmin is a prominent intermediate filament ^[50] and therefore, nesprin-3 is a prominent structural component. From our previous studies we found that nesprin-3 disruption causes lower intranuclear tensile strain in cardiomyocytes ^[24]. Therefore, we were particularly interested in understanding the role of nesprin-3 disruption in the intranuclear elasticity. As a second application of nuclear elastography in a cell physiology relevant problem, we hypothesized that during cardiomyocyte contraction intranuclear mechanics is compromised after knock-down of nesprin-3 or overall disruption of the LINC complex. To test this hypothesis, cardiomyocytes were transduced with vectors to knock-down nesprin-3 (shSyne3) or that overexpress a dominant-negative KASH construct (TmKash3) which displaces native nesprins via the KASH domain but lacks the cytoskeletal binding domains. After either type of disruption, the amplitude of cardiomyocyte beating decreases, more prominently after the KASH disruption. This can be visualized by the magnitude of the displacement and strain inside the nuclei (Figure 6 and Figure S5).

Figure 6.

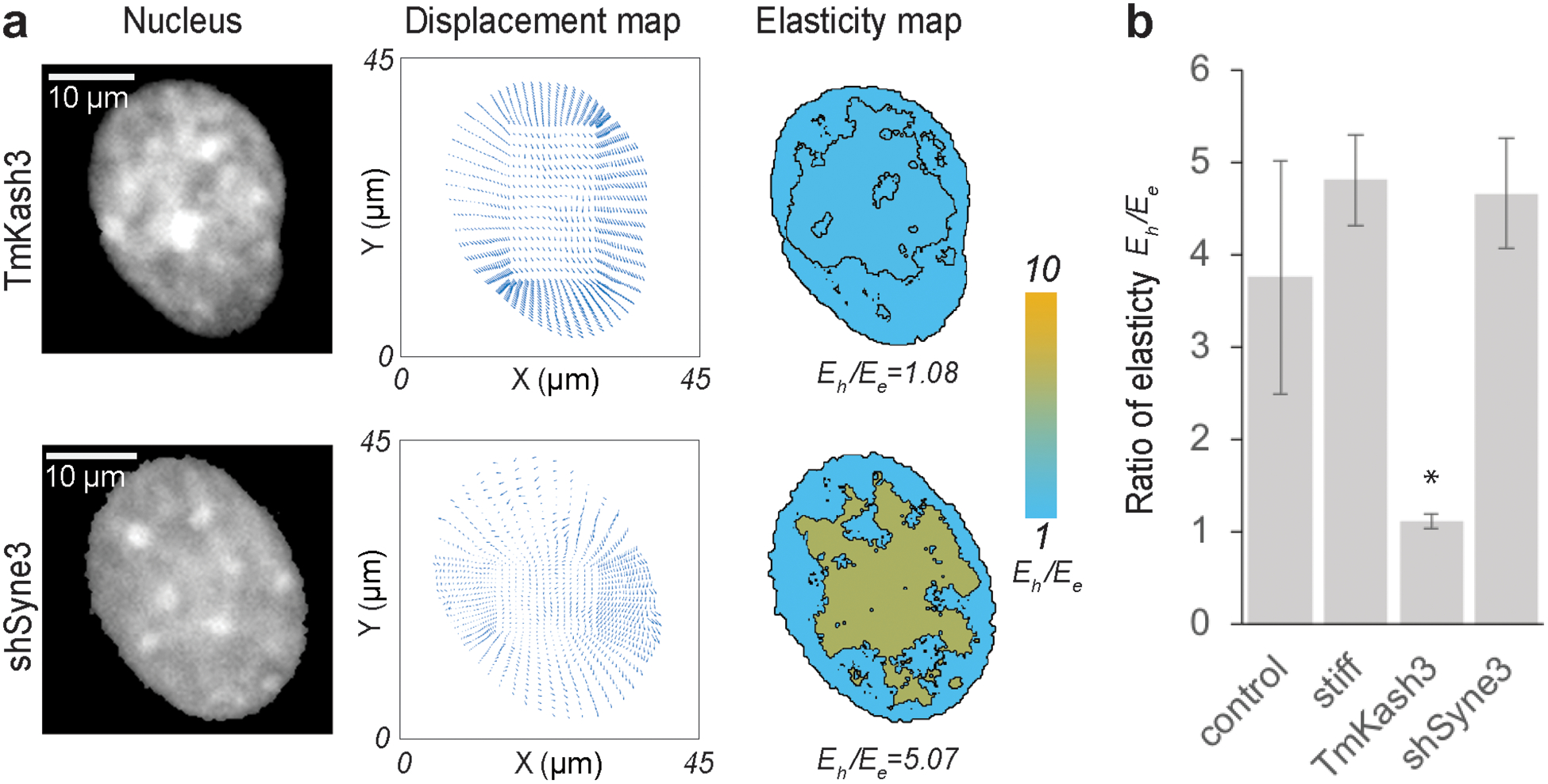
(a) Raw image of the nucleus, displacement map from deformation microscopy and elasticity map for KASH domain disrupted and nesprin-3 disrupted nuclei of beating cardiomyocytes. (b) The ratio of heterochromatin elasticity and euchromatin elasticity is shown for cardiomyocytes on soft substrates (physiological condition), stiff substrates (pathological condition), LINC complex disruption via TmKash3 and nesprin-3 knock down via shRNA interference (n ≥ 4, *p < 0.01) for a timepoint where the deformation of the nucleus was highest in each individual case (peak contraction).

As a result of these treatments, we found that at peak nuclear deformation, the KASH disruption led to a E_h /E_e value close to 1, but the knock-down of nesprin-3 led to a value of E_h /E_e = 5.07 (Figure 6a). Interestingly, the overall intranuclear strain decreases for both LINC complex manipulations compared to untreated cardiomyocytes ^[24,51] (Figure S5). However, while a significant change in the E_h /E_e value occurs after LINC disruption via TmKash3, knock down of nesprin-3 alone did not change the E_h/E_e value significantly at the peak nuclear deformation (Figure 6b). The stiffened microenvironments also did not significantly change the E_h /E_e value at peak nuclear deformation. These results suggest that the effect of nesprin-3 in determining the relative heterochromatin vs euchromatin mechanical stiffness is not significant, whereas overall LINC disruption has significantly abrupt effect on the intranuclear mechanics. After the disruption of nesprin-3, there are three types of nesprin remain mostly intact to maintain the integrity of the chromatin architecture but a complete disruption of the KASH domain should disrupt the integrity of chromatin architecture. We could further observe that after LINC disruption the intranuclear strain distribution is more random irrespective of the euchromatin or heterochromatin location, whereas nesprin-3 knock down showed that the higher strain is still associated with the euchromatin region, similar to untreated cells on soft substrates (Figure S5). Because the chromatin architecture is connected to the nuclear envelope and through several linker molecules ^[12,52], a complete disruption of KASH domain most likely isolates the chromatin architecture significantly from the nuclear envelope, thus diminishing the structural difference between euchromatin and heterochromatin, hence poising them to be mechanically similar. Such disruption and change in chromatin mechanics can cause abrupt change in the gene expression profile of the nucleus. In our previous work ^[51] we found that KASH domain disruption causes an overall enrichment of both repressive epigenetic markers H3K9me3 and H3K27me3 marked chromatin in cardiomyocytes, suggesting a global repression of the genes in the nucleus. It should be noted that out of many inner nuclear membrane and outer nuclear membrane proteins we only disrupted two structural entities namely nesprin-3 and KASH. There are many other proteins which need to be systematically disrupted to fully appreciate their potential impact on the stiffness of intranuclear space. It is possible that some of these proteins transduce force from cytoskeleton to nucleus, like nesprin-3, but do not significantly affect the elasticity of intranuclear space.

2.5. Nuclear elastography can be generalized and depends on image acquisition parameters

In this paper, we demonstrated that the relative elasticity of the heterochromatin and the euchromatin can be quantified in a non-invasive manner solely based on the images of a deforming nucleus. Previous studies indicated the possibility that heterochromatin might be stiffer than euchromatin by treating nucleus with histone methylase inhibitors which increased heterochromatin level and overall nuclear stiffness ^[53], but direct proof of such possibility has not been reported so far. To the best of our knowledge the present study is the first report which mechanically delineates the euchromatin and heterochromatin using an experimental approach. The basic requirement to apply this technique is to distinguish the euchromatin and the heterochromatin from spatial image intensity, as well as obtaining a reliable intranuclear displacement map – both aspects improve with higher resolution in the microscopy images. With the rapid advent in the microscopy technology, it is possible to apply this technique in other mechanobiological problems where the intranuclear mechanics needs to be probed. Although we applied the technique in nuclei that has an endogenous green fluorescent tag, this technique can be also applied to other live nuclear imaging modalities such as Hoechst and DRAQ5^[24]. Besides, the workflow used in this study is applicable for both 2D and 3D imaging data. In this work the euchromatin and the heterochromatin delineation was assumed to be identical on both surfaces of the 3D nucleus model, because we used a 2D projection of the 3D image stack to obtain the displacement data. This approach is reasonable because for the cardiomyocyte cultured on a 2D substrate, the axial dimension of the nucleus is much smaller compared to the planar dimensions ^[24]. However, a true 3D elastography of the complexly connected heterochromatin and euchromatin domains is still possible with the same workflow even though the euchromatin and heterochromatin cannot be assumed uniform in the axial direction, which will be explored in future studies.

One key limitation of this technique lies in the assumption that the euchromatin and the heterochromatin regions are distinguished solely based on the image pixel intensity, which is likely an oversimplification. Although the traditional biological definition of heterochromatin and euchromatin relies on the image pixel intensity in the stained nucleus, debates still exist about distinguishing the euchromatin and heterochromatin using such a simplified methodology ^[4]. Also, some of the low intensity pixels might be attributed to other specific nuclear bodies such as nucleolus and lamina, and not euchromatin. Besides, the elasticity values we obtain from each domain is an average of the corresponding domain. Technically, it is possible to live stain specific regions in the nucleus such as the lamina and the nucleolus with different colors to delineate those regions from euchromatin. Subsequently, a multi- (e.g., four-) domain elastography with euchromatin, heterochromatin, nucleolus and lamina is executable with the same elastography workflow. Moreover, a more computationally demanding elastography method including the calculation of stiffness at each pixel/voxel can offset such assumptions and limitations, in addition to the acquisition of images with improved (e.g., super) resolution in spatial and temporal domains. Such aspects are important to understand the mechanics of the nucleus and can be addressed in a future work.

2.6. Implementation of force boundary conditions in the nuclear elastography

In this work we implemented displacement boundary condition which can only provide the relative elasticity of the domains of interest such as the euchromatin and heterochromatin. Calculation of the absolute values of E_h and E_e require a known force or stress boundary condition. However, depending on the experimental measurements available, our elastography framework can be used to solve force or displacement boundary conditions, or a hybrid of both. In future embodiments, inclusion of force boundary conditions can enable calculation of absolute stiffness through the material interior. However, the measurement of force boundary conditions is challenging at the nuclear envelope, and may require new and creative experimental approaches, or hybrid modeling methods. For example, traction force microscopy may provide cell surface force estimates, but then additional information regarding the mechanics of cytoplasm is required to estimate how these mechanical signals propagate through the cytoskeletal network to impact the nuclear envelope. Alternatively, FRET based LINC-specific microscopy measurements ^[54] may enable direct estimates of force or stress at the nuclear envelope, but they are technically more challenging to implement. In future studies, we envision making estimates of force or stress boundary conditions at the nuclear envelope, which would enable quantification of absolute values of stiffness within the nuclear interior. Such estimates may be possible through a hybrid of experimental or modeling approaches, e.g., using LINC-specific FRET-based sensors ^[54], which would further elucidate how intranuclear stiffness changes with increases in cell deformation.

3. Experimental section/ Methods

3.1. Cell culture:

We obtained B6.Cg-Tg(HIST1H2BB/EGFP)1Pa/J mice from Jackson Laboratory (#006069). All animal procedures were performed following Institutional Animal Care & Use Committee (IACUC) approved protocols at University of Colorado Boulder (Protocol number: 1507 and 2628). Nuclei of the cells from homozygous mice bred from this colony display a strong fluorescence at 488 nm caused by the green fluorescence tag attached to its histone H2B. Because histone H2B is ubiquitous in all nucleosomes in the chromatin, fluorescence intensity of H2B linearly correlates with the chromatin density in the nucleus. The fluorescent labeling of chromatin through this green fluorescent tag is routinely used in labs ^[55] to study chromatin dynamics in live cells and we showed that the use of this tag is equivalent to other live chromatin stains such as Hoechst or DRAQ5 for the visualization of chromatin ^[24]. Cardiomyocytes were isolated from embryonic mice hearts 18.5 days post conception by incubation of the tissue in 0.125% trypsin/EDTA overnight followed by 10 min digestion in residual trypsin under the application of medium maintained at 37°C. After isolation, cells were cultured on PDMS substrates. Cardiomyocytes were cultured in Advanced DMEM/F12 containing 10% FBS at 37°C with 5% CO₂ until the imaging experiment was carried out.

3.2. Soft and stiff substrate:

To mimic the physiological (soft) and pathological (stiff) conditions, Polydimethylsiloxane (PDMS) substrates with different formulations were used. For making soft substrate, we used Sylgard®527 ratio 1:1 (E=11.7 ± 5.4 kPa) and for making stiff substrate, we used Sylgard®184 (Dow Corning) ratio 1:10 (E=434.3 ± 54.4 kPa). Mechanical properties of the substrates were characterized as reported in our previous work ^[24]. For live cell imaging with 100× objective, thin (~80 μm) PDMS films were deposited on glass slides, degassed under vacuum for 30 min, cured for 2h at 100°C, and mounted on custom made cell culture dishes. Further, PDMS was ozone-treated and coated with Matrigel (Geltrex, ThermoFisher) for 1h at 37°C.

3.3. Disruption of LINC complex:

Cardiomyocytes were transduced with vectors to knock down nesprin-3 (shSyne3) or express a dominant negative KASH construct (TmKash3) that displaces native nesprins via the KASH-domain but lacks cytoskeleton binding domains. The transduction was thoroughly validated as reported in our previous publication ^[24] which includes the use of a control construct that was identical to TmKash3 but lacked the KASH domain to compete with nesprins for SUN connections. For the nesprin-3 disruption validation we used scrambled control and validated the disruption by showing that the nesprin-3 gene expression decreases to almost zero after the shRNA treatment.^[24]

3.4. Imaging of deforming cells:

Image stacks of cardiomyocyte nuclei during contractions were captured using an inverted epi-fluorescence microscope (Nikon Ti-Eclipse) with a 100× objective and an EMCCD camera (Andor). Images were captured at 6.4 frames per second over a period of 10 s to visualize the entire contraction cycle of cardiomyocytes. For each nucleus, one contraction cycle was selected from the image stack to perform nuclear deformation analysis. Images of the nuclei in a post-diastolic resting state were selected as undeformed reference image. All the subsequent images in the same beating cycle were used as target, undeformed images. We calculated the displacement and strain map in the nucleus for all the target images. Subsequently, the nucleus with the highest average absolute spatial strain magnitude was designated as the timeframe corresponding to the peak cardiomyocyte contraction ^[24].

3.5. Displacement mapping:

From the undeformed reference image and the deformed image, the displacement map was generated using our already established technique – ‘deformation microscopy’ ^[24,39,56]. Briefly, in this technique, the undeformed image is hyperelastically warped ^[37] to register with the deformed image. Deformation microscopy provides the nodal coordinate information (x, y) and the displacement map d(x, y) at each node that was further used for elastography and the strain calculations where relevant. The strains calculated were $E_{xx}=\frac{\partial u}{\partial x}$ and $E_{yy}=\frac{\partial v}{\partial y}$, where u and v are the x and y components of the displacement d(x, y). Further, hydrostatic strain is defined as the average of the E_xx and E_yy: $E_{hyd}=\frac{1}{2}\left(E_{xx}+E_{yy}\right)$. It should be noted that such strain calculations have never been used in this work for the elastography. The elastography is based only on the displacement data. The strain values are only used to qualitatively visualize the strain distribution as well as the deformation in the nucleus.

3.6. Two-domain elastography:

The primary focus of this paper is to establish and apply the two-domain elastography to quantify the relative elasticity between the euchromatin and the heterochromatin domains of the nucleus. Therefore, this section is reported in detail. The endpoint goal of this workflow is to obtain the ratio of the heterochromatin elastic modulus (E_h) and the euchromatin elastic modulus (E_e).

3.6.1. Separation of chromatin domains:

Segmentation of intranuclear space has been demonstrated previously to quantify chromatin condensation ^[57,58]. For the present study, which is instead motivated by the need to distinguish the heterochromatin and the euchromatin domains in a consistent and automated manner, we applied the Hill equation ^[59], a commonly used technique in biochemistry to study the binding kinetics of ligand and receptor. The rationale behind this approach is that when the pixel grayscale intensity from a raw image of nucleus is plotted after sorting by value which can range from 0 to 255, it resembles the Hill equation sigmoidal plot (Fig. S1). A sigmoidal curve was fit to the pixel grayscale intensity according to the Hill equation. The sigmoidal curve provides an inflexion point which is decided as the cut-off pixel intensity. Any pixel intensity higher than the cut-off intensity value was assigned to the heterochromatin domain, and any pixel intensity lower than the cut-off intensity value was assigned to the euchromatin domain. Therefore, a binary measure of the heterochromatin domain and the euchromatin domain was obtained. It is noteworthy that such approach provides an unbiased, user independent cut-off intensity to distinguish the two chromatin domains.

3.6.2. Generation of nuclear model for finite element analysis framework:

Using the known coordinates of the nodes obtained from the deformation microscopy, we created a two-dimensional connectivity network. The 2D connectivity network was further transferred to a MATLAB- based open-source Toolbox GibbonCode, which can be interfaced with the open-source Finite Element Analysis package FEBio 2.6. From the 2D connectivity network, we created a 3D model consisting tetrahedral mesh using another open-source code TetGen. The 3D model is created to exploit the FEBio software, the 3D nucleus is of prismatic shape, and only one element thick. The two opposite surfaces of the 3D model nucleus had identical x-y displacement values.

3.6.3. Inverse solution for elasticity calculation:

To estimate the Young’s modulus of the heterochromatin (E_h) and the euchromatin (E_e) regions, we created an inverse problem solution framework. Briefly, we assigned two guess values (random numbers) of E_h and E_e in the model, applied the displacement boundary condition d(x, y), which is found from the experimental data, and executed the FEBio run to compute the displacement d’(x,y) at each node. Then, we computed the sum of root mean square error in the displacement defined as $SE={\sum }_{i=1}^n{\left[d^{\prime }\left(x,y\right)-d\left(x,y\right)\right]}^2$, where n is the number of nodes. After that, we used an optimization algorithm to iteratively calculate the value of E_h and E_e by minimizing the objective function SE. For solving the optimization problem, we used our in-house code based on the MATLAB function fminsearch. The lower and upper bounds in the function was chosen to be 100 and 2×10¹⁰ to accommodate a wide range of values for E_h and E_e. A plane stress condition was used in the 3D finite element model because the cell and hence the nucleus has much smaller dimension in the z direction (< 5%) compared to its x and y dimensions. Besides, the contractile force is applied on the nucleus in the xy plane, thus further validating the plane stress assumption. Poisson’s ratio was assumed to be 0.35 for all cases because biological materials show a Poisson’s ratio in the range of 0.3 to 0.5, although all our results are independent of a large range of Poisson’s ratio.

3.6.4. Validation of elastography:

To validate the elastography technique that was eventually applied to experimental data, we applied known material properties E_hf and E_ef for the two chromatin domains and executed the forward FEBio run to determine the displacement data at the nodes. Further, we used the forward run displacement data as the input d(x, y) to execute the inverse problem, and therefore to find the E_h and E_e values. We used different combinations of material model for the forward simulation and the inverse solution – (1) hyperelastic material forward model, elastic material inverse solution, (2) elastic material forward model, elastic material inverse solution, (3) hyperelastic material forward model, elastic material inverse solution. For all cases, Poisson’s ratio was assumed to be 0.35. The hyperelastic material model utilizes the neo-Hookean model which has the parameters elastic modulus (E) and the Poisson’s ratio (ν). It employs the hyperelastic strain energy density function ^[60] $W=\frac{\mu }{2}\left(I_1-3\right)-\mu \text{ln}J+\frac{\lambda }{2}{\left(\text{ln}J\right)}^2$, where I₁ is the first invariant of the right Cauchy-Green deformation tensor and J is the determinant of the deformation gradient tensor. μ and λ are the Lame constants defined as $\frac{E}{2\left(1+v\right)}$ and $\frac{Ev}{2\left(1+v\right)\left(1-2v\right)}$ respectively. The linear elastic material model employs the Hookean model which also has the parameters elastic modulus (E) and the Poisson’s ratio (ν). However, it employs a different strain energy function $W=\frac{1}{2}E{\epsilon }^2$, where ε is the strain.

3.6.4.1. Effect of large displacement:

The nuclear deformation might be associated with larger displacements. Therefore, we estimated the effect of larger displacement on accuracy of the inverse problem solution. To do this, we modified the displacement solution from the forward simulation by computing n* d(x,y), where n is a constant displacement factor uniformly applied to all nodes. Higher the value of n is, it represents a larger displacement. We applied a range of displacement factors such as 0.05, 0.1, 0.5, 1.5, 2 and 3. The values 1.5, 2 and 3 accommodate 50%, 100%, and 200% added displacement to the baseline displacement d(x,y).

3.6.4.2. Effect of noise:

We also estimated the effect of noise, which is inherent to the experimental data, on the accuracy of the inverse solution. For this study, artificial noise was added to the forward run displacement data as follows: d(x,y)+d”(x,y), where d(x,y) is the mean data and d”(x,y) is the noise added. The noise was simulated using a uniformly distributed pseudorandom number generator and its magnitude was varied as ±5%, ±10% and ±20% of the local mean value. These magnitudes were determined from the experimental results of the present study.

3.7. Statistics:

One-way Analysis of Variance (ANOVA), followed by post hoc Tukey’s test was used to test for statistically significant differences between treatment groups. The coefficient of determination (R²) was calculated using linear regression. Error margins are reported as standard deviation (SD) about the mean, as indicated in the figure captions.