Segmented Regression in an Interrupted Time Series Study Design

KEY POINT:

Segmented regression can be used in an interrupted time series study design to analyze trends in an outcome of interest before and after implementing a well-defined intervention.

In this issue of Anesthesia & Analgesia, Drzymalski et al¹ study the implementation of the “no pain labor & delivery-global health initiative” in a Chinese hospital. The authors used segmented regression to assess how the proportion of live births by cesarean delivery, as well as other secondary outcomes, changed after as compared to before the noted implementation.

When a health care initiative, guideline, education program, or policy change is implemented, researchers are often interested in the effect of this intervention on patient- or system-level outcomes, such as complication rates or costs. Because such interventions are commonly implemented throughout a hospital or perhaps even an entire region or nation, the random assignment of individual patients to either the intervention or a control group is not possible. Random assignment of patient clusters (eg, by hospital units/wards or entire hospitals) may be an option but is often also not feasible. In the absence of a control group, researchers then commonly instead estimate the effect of the intervention by comparing the outcome of interest before versus after the intervention.

A common approach to data analysis in such “before-and-after” studies is (a) to compare mean values or proportions of the outcome between the pre- and postintervention periods using simple hypothesis tests like a t test or χ² test and (b) to conclude that the intervention had an effect when a significant difference is observed. However, this approach is flawed, mainly because there may already have been a trend toward better outcomes in the preintervention period that continues into the postintervention period.² Such trends are not uncommon because many subtle changes, which are unrelated to the intervention of interest, but instead to general advances in patient care, effects of continuing education and training, reading journals, increasing experience of health care staff over time, as well as many other factors, may change outcomes over time. Therefore, any simple comparison that fails to account for such an underlying trend will overestimate the effect of the intervention or will suggest a spurious effect when there is actually no true effect (Figure A).

Time series data—a chronologically ordered series of repetitive observations in a population of interest—that have been “interrupted” at a clearly defined time point by a clearly defined event can often be appropriately analyzed with segmented regression.² Segmented regression basically models the trend of the outcome over time, and in its simplest form, is specified such that it fits 2 separate lines to the data, 1 before the intervention and 1 after the intervention.³

Depending on the outcome of interest, the segmented regression model can be a linear (continuous outcome), logistic (binary outcome), Poisson (count data), or other regression model.³ The regression coefficients estimate the slope of the regression line in the preintervention period (the trend before the intervention), the shift in the level of the outcome at the beginning of the postintervention period as compared to the end of the preintervention period, as well as the change in the slope after the intervention of interest.

Either a significant shift of the level of the outcome after the intervention (Figure B), or a significant change in the slope (Figure C), suggests a true rather than spurious association between the intervention and the outcome (Figure). Note, however, that testing of 2 null hypotheses increases the risk of a type I error when rejection of either null hypothesis leads to a conclusion of an association. Therefore, researchers should either (a) apply a multiplicity adjustment⁴ or (b) have a clear a priori hypothesis as to whether the intervention would be expected to change the level of the outcome or the slope of the trend. It is also important to consider whether a change is expected immediately after the intervention or only after a time lag, as the model can be modified accordingly.

Figure.

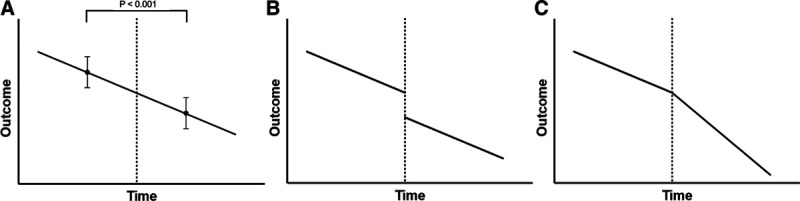
The change of an outcome over time. The time point of the intervention of interest is marked by the dotted line. When there is a trend in the preintervention period that continues into the postintervention period, a simple “before-and-after” comparison of mean values or proportions may misleadingly suggest an effect of the intervention when there is, in fact, none (A). Segmented regression fits 2 separate lines, 1 for the pre- and 1 for the postintervention period. An abrupt change in the outcome after the intervention (B) or a change in the slope (C) suggests a valid association between the intervention and the outcome.

To obtain valid inferences from a segmented regression analysis, the assumptions of the underlying linear, logistic, or other regression techniques must be met. Moreover, the pre- and postintervention observation periods should have sufficient duration, preferably, 1 calendar year.⁵ This reduces the risk that seasonal trends; random variation of the outcome around its mean value (regression to the mean); or a transient improvement in outcomes after the intervention because subjects are aware that they are being observed (Hawthorne effect), markedly bias the results. As with other nonrandomized study designs, confounders can seriously distort the estimated relationship between the intervention and the outcome, and they should accordingly be adjusted for in the analysis.⁶