Modeling the Degradation Effects of Autophagosome Tethering Compounds

Dear Editor,

The selective degradation of specific pathogenic proteins provides exciting strategies for drug discovery. Emerging new concepts such as proteolysis-targeting chimeras and autophagosome-tethering compounds (ATTECs) are based on the design of “molecular glues” or bifunctional chimeric compounds that tether the target protein (protein of interest, POI) to a specific component of the protein-degradation machinery (PDM) [1–3]. The formed trimer (POI–compound–PDM) then accelerates degradation of the POI, leading its selective reduction. Interestingly, the dose-dependence curves of the POI-compound relationship are U-shaped, with an optimal compound concentration for maximum lowering of the POI and “hook” effects at higher compound concentrations [1], different from traditional Boltzmann dose-dependent curves [4]. This is explained by the logic that when the compound concentration is too high, each molecule may interact with the POI and PDM separately, without tethering them together. Meanwhile, there has been a lack of mathematic modeling describing such effects. While modeling of the trimer formation has been published in a top-tier journal [5], the degradation of the POI was not considered at all. Such modeling has been challenging, because incorporating the degradation greatly increases the modeling calculation. In addition, most of the existing degrader technologies are based on ubiquitination [1], which is a complicated enzymatic reaction that is highly challenging to model [6].

We have proposed and demonstrated a new degrader technology by harnessing autophagy for selective degradation using ATTECs [2]. We demonstrated that compounds that interact with both the POI and the autophagosome protein LC3 tether POI to autophagosomes for subsequent autophagic degradation [2]. Since ATTECs tether POI directly to the PDM without involving complicated enzymatic reactions, they may provide an ideal scenario for mathematical modeling of the degrader’s effects [2]. Here, we describe a simplified model of the degradation effects of an ATTEC, providing possible insights for understanding the dose-dependence data and potential clues for inventing better compounds.

Many parameters may influence the degradation kinetics and the dose-dependence effects [7, 8], and considering all of them as variables may make the model highly complicated and difficult to resolve. Thus, we focused on the relationship between the degradation of the POI and the ATTEC’s affinity to the POI or LC3, and considered them as the only variables. Meanwhile, we estimated the values of all other parameters and considered them as constants to simplify the model as much as possible. Based on these assumptions, we performed the modeling based on the kinetic and steady-state equations of all the relevant chemical reactions (see Modeling Methods in Supplementary Materials).

Kinetic Modeling of Each Species Involved in an ATTEC

We first solved kinetic equations [Eq. (5) to Eq. (10) in Modeling Methods of the Supplementary Materials] using codes written with MatLab and simulated the kinetic changes of different species in the system. With the indicated kinetic parameters, the kinetic changes of each species were calculated (Fig. S1). The kinetic parameters were estimated based on our previous experimental measurements on the GW5074 compound [2].

Based on the kinetic simulation, the free mutant HTT protein (mHTT, the POI) and free LC3 protein had the fastest decay rates and reached steady-state within a few hours (Fig. S1, mHTT and LC3 panels) due to the rapid formation of the ATTEC·mHTT and ATTEC·LC3 binary complexes, respectively. The free ATTEC molecule had a rapid decay but bounced back a little at a much slower rate (Fig. S1, ATTEC panel). The first decay phase was also due to the rapid formation of the ATTEC·LC3 and ATTEC·mHTT binary complexes. The bounce-back illustrated the recycling of ATTEC after degradation of the mHTT·ATTEC·LC3 proteins. The LC3·ATTEC complex increased rapidly due to the formation of this binary complex (Fig. S1, LC3·ATTEC panel). Both the ATTEC·mHTT binary complex and the mHTT·ATTEC·LC3 ternary complex increased rapidly and then decayed slowly to reach a steady-state level (Fig. S1, ATTEC·mHTT and mHTT·ATTEC·LC3 panels). The phase of rapid increase was due to the formation of these complexes, and the slow decay phase of ATTEC·mHTT was due to the degradation of this complex as well as its consumption due to the formation of the ternary complex. The slow decay phase of the mHTT·ATTEC·LC3 complex was due to the degradation of this complex, and was balanced by its formation.

The major purpose of the model was to understand the kinetics of the total mHTT level, which is the sum of free mHTT, the binary ATTEC·mHTT complex, and the ternary mHTT·ATTEC·LC3 complex. Thus, we calculated the sum of the levels of these three species, and simulated the kinetic curves of total mHTT (Fig. S2). The total mHTT level decayed over time, reaching a steady-state after ~30 to ~150 h depending on the kinetic parameters (Fig. S2). We then investigated how the kinetic parameters influence the kinetic curve of the total mHTT level. The K_on1 and K_off1 values determined the kinetics of the formation of the ATTEC·LC3 and mHTT·ATTEC·LC3 complexes. A larger K_on1 or smaller K_off1 led to faster ATTEC·LC3 and mHTT·ATTEC·LC3 formation. Consistent with this, the total mHTT level decayed faster and reached a lower steady-state level with a larger K_on1 and smaller K_off1 (Fig. S2). Notably, these curves were more sensitive to K_on1 changes in a lower value range [between 0.000223 and 0.00223 (h·nmol/L)^-1] and to K_off1 changes in a higher value range [between 10.4 and 1.04 (h)^-1]. Similar findings were obtained on the influences of K_on2 and K_off2, which determine the kinetics of the formation of the ATTEC·mHTT and mHTT·ATTEC·LC3 complexes (Fig. S2). Under all conditions, the total mHTT level at 48 h was very close to the steady-state level, suggesting that this compound treatment time used in previously published experiments is reasonable [2].

Modeling of the Dose-Dependent Curves for ATTEC

We then solved the steady-state equations [Eq. (11) to Eq. (16) in Modeling Methods of the Supplementary Materials] and simulated the dose-dependence curves of ATTEC. All the ATTEC curves were U-shaped (Fig. S3), consistent with the autophagosome-tethering mechanism in which a sufficient concentration of ATTEC is needed, whereas excessively high concentrations may lead to separate binding of ATTEC to LC3 and mHTT, without tethering the two together. Since at the same K_d values (K_dH for the equilibrium dissociation constant of the ATTEC to mHTT, and K_dL for the equilibrium dissociation constant of the ATTEC to LC3), the dose-dependence curves changed very little with K_on and K_off varying two orders of magnitude (Fig. S3), we focused on analyzing the effect of K_d on the degradation efficiency of the ATTEC.

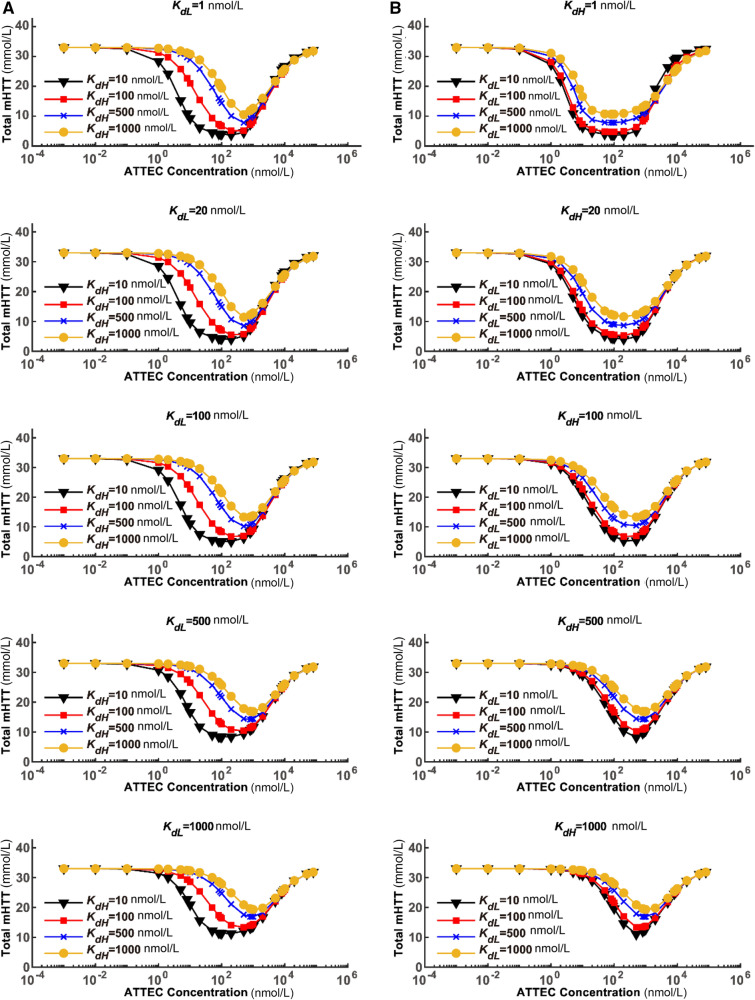
We simulated the dose-dependence curves with different sets of compound–protein affinity parameters (Fig. 1). The shape of the dose-dependence curve closely resembled the experimental data that we published previously [2]. The target protein mHTT was only lowered to a certain degree; the extent of lowering is referred to as maximum degradation (D_max). D_max was reached only at optimal concentrations of the ATTEC. It was clear that both D_max and the optimal concentrations for degradation were influenced by the K_d values (Fig. 1), which are further analyzed below.

Fig. 1.

Modeling of the dose-dependence curves for the ATTEC with varying K_d values. The relationship between the steady-state concentrations of total mHTT and the concentrations of ATTEC molecules are shown. A The ATTEC dose-dependence curves with a set of K_dH values and a fixed K_dL in each panel. B Similar to A, but with a set of K_dL values and a fixed K_dH in each panel. The K_dL and K_dH values are set to a series of representative numbers that are easy for calculation and covering the range of our previously-discovered ATTECs.

Relationship Between Affinity (K_d) and Maximum Degradation (D_max)

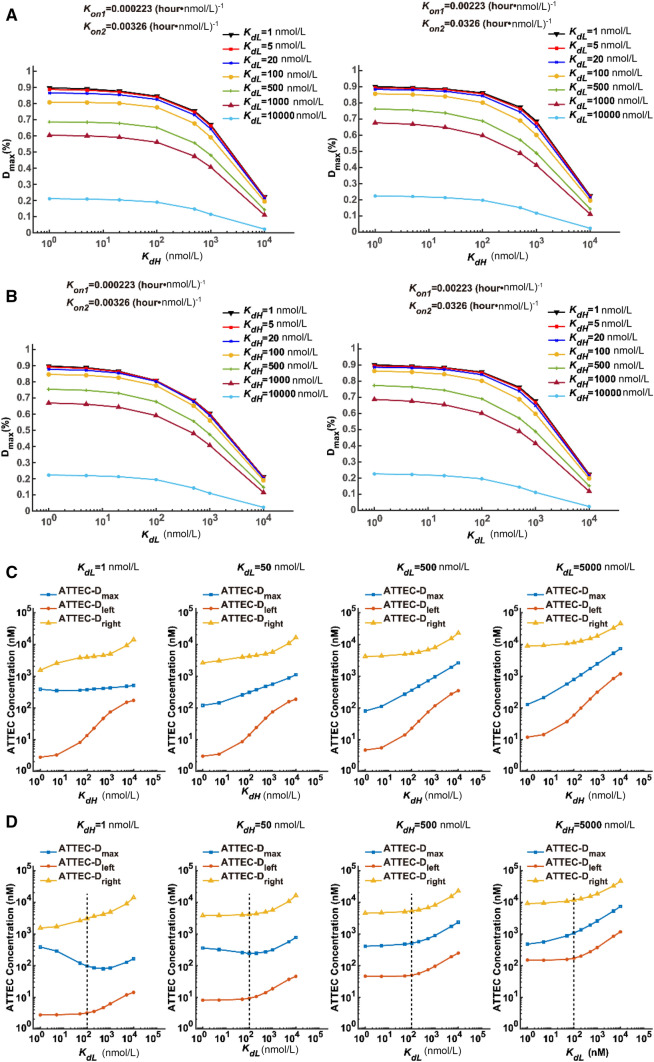
In order to visualize the relationship between D_max and K_d values, we plotted the D_max–K_dH relationship assuming several different K_dL values (Fig. 2A). Since a K_on change between 0.00023 and 0.0023 (hour·nmol/L)^-1 led to subtle differences in D_max (Fig. S3), we simulated based on both of these K_on values and obtained very similar results (Fig. 2A). A K_dH increase led to decreased D_max values, consistent with the prediction that lowering affinity (higher K_d) to the POI leads to less efficient degradation. Meanwhile, the curves were relatively flat within the range 1–100 nmol/L K_dH, and dropped rapidly within the range 100–10000 nmol/L K_dH (Fig. 2A), suggesting that D_max is sensitive to K_dH only in the low-affinity range (high K_dH values at 100–10000 nmol/L). The D_max–K_dL relationship was very similar to the D_max–K_dH relationship (Fig. 2B), suggesting that D_max is also sensitive to K_dL only in the low-affinity range. Thus, while a relatively high affinity of ATTEC to POI (mHTT) and LC3 is desired to achieve a higher D_max, it may not be necessary to make huge efforts to achieve extremely high affinity (such as ~1 nmol/L K_d), because K_d values within 1–100 nmol/L lead to a similar D_max.

Fig. 2.

The relationship between the degradation effect (D_max and the effective concentration range) and the compound–protein affinity (K_dL and K_dH). A Simulated D_max–K_dH relationship assuming the indicated K_dL values. B Simulated D_max–K_dL relationship assuming the indicated K_dH values. C, D Plots of concentrations needed to achieve maximum degradation ATTEC–D_max or half-maximum degradation ATTEC–D_left and ATTEC–D_right at different sets of K_dL and K_dH values. C ATTEC–D_max, ATTEC–D_left, and ATTEC–D_right concentrations assuming different K_dH values at a fixed K_dL in each panel. D Similar to C, but assuming different K_dL values at a fixed K_dH in each panel. Dashed lines indicate 100 nmol/L, below which K_dL has little influence on the effective concentration range. The K_dL and K_dH values were set to a series of representative numbers that are easy for calculation and covering the range of our previously-discovered ATTECs.

Relationship Between Affinity (K_d) and Effective Compound Concentrations

As noted above, the dose-dependence curve of the ATTEC is unlike the common Boltzmann curves that fit most chemical responses. Instead, the ATTEC curve was U-shaped, and an optimal concentration range is desired for efficient degradation. This optimal range could be influenced by the ATTEC’s affinity for both the POI and LC3, as illustrated by our modeling data assuming several different sets of K_d values (Fig. 1). Resolving the relationship between the optimal concentration range and the K_d values may guide compound optimization.

In order to visualize this relationship, we plotted three different ATTEC concentrations against the K_d values. The ATTEC–D_max value indicates the ATTEC concentration needed to reach the maximum degradation effect. The ATTEC–D_left and ATTEC–D_right indicate the lower and higher concentrations needed to reach half of the maximum degradation effect, respectively.

We first plotted these concentrations against K_dH, assuming several different K_dL values (Fig. 2C). The general trend was that ATTEC–D_max, ATTEC–D_left, and ATTEC–D_right all increased with K_dH (Fig. 2C), suggesting that higher ATTEC concentrations are needed to achieve efficient degradation when the affinity of the ATTEC for mHTT decreases, represented by increased K_dH values. In addition, the size of the effective concentration window (Fig. 2C, distance between yellow and red curves, log scale) also decreased as K_dH increased, especially at a larger K_dH range, suggesting that the effective concentration range is larger when the affinity of the ATTEC for the POI is high. Finally, the ATTEC–D_left curves generally had a larger slope, suggesting that the lower concentration required to achieve half of the maximum degradation effect is more sensitive to the affinity of the ATTEC for the POI.

We then plotted ATTEC–D_max, ATTEC–D_left, and ATTEC–D_right against K_dL. Interestingly, the curves differed from those plotted against K_dH. The major difference was that the size of the effective concentration window (Fig. 2D, distance between yellow and red curves) was insensitive to K_dL values, suggesting that the ATTEC’s affinity for LC3 is not a major factor contributing to the size of the effective concentration range. Second, the ATTEC–D_max curve (Fig. 2D, blue) did not always increase monotonically, and an optimal K_dL between 100 and 1000 nmol/L was required to reach the lowest ATTEC–D_max, at least when K_dH is low (Fig. 2D, K_dH = 1 nmol/L or 50 nmol/L). Thus, it seems that a high affinity of ATTEC for LC3 is not always desired to reach maximum degradation effects at low ATTEC concentrations. Finally, for K_dL <100 nmol/L (Fig. 2D, left to the dashed lines in each panel), the ATTEC–D_left and ATTEC–D_right were largely unaffected, whereas they did increase when K_dL was >100 nmol/L. Thus, in order to induce efficient degradation at lower ATTEC concentrations, a higher affinity for LC3 (lower K_dL) is desired only when K_dL is >100 nmol/L. Further increasing the affinity for LC3 may not be necessary, at least in the conditions assumed in our modeling.

In this study, we presented the first simplified model of ATTEC-induced lowering of mHTT. Although we used mHTT for our simulation, the modeling is applicable to other POIs. While the model was over-simplified, the shape of the dose-dependence curves largely fit the experimental data [2]. We further studied the influence of ATTEC’s affinity for the POI and LC3, and found some interesting properties. In general, the D_max was negatively correlated with both K_dH and K_dL, but was not so sensitive when the K_d values were <100 nmol/L (Fig. 2A, B). Lower K_dH values were also required to achieve the desired effective concentration range (Fig. 2C), but lower K_dL values may not be necessary, especially when K_dL is <100 nmol/L (Fig. 2D). Thus, optimizing the compounds to reach a higher affinity for the POI is more important, and an attempt to reach extremely high affinity for LC3 (<100 nmol/L) may not be necessary. As we chose mHTT as the POI, it is worth mentioning that the ATTECs that we discovered in a previous study have been confirmed to interact specifically with an expanded stretch of polyQ, without influencing other polyQ protein levels, based on proteomics analysis [2]. These predictions are based on many assumptions, including the estimation of the starting concentrations of the mHTT and LC3 proteins, and certainly need further confirmation by experiments. For example, the starting concentration may be different for other POIs, and this may influence the dose-dependence curve, especially in the lower concentration range (Fig. S4). Meanwhile, as the first model for ATTEC-induced degradation, and even for ternary complex-induced degradation, it may still provide insights into the properties of such degradation and possible factors to consider for compound optimization. Besides neurodegeneration, many other neurological diseases are also associated with protein abnormalities in the brain [9, 10]. ATTEC molecules may selectively degrade these pathogenic proteins and provide entry points to treat these diseases. Understanding how it works by mathematical modeling may provide insights into optimizing such compounds, and thus benefit drug discovery for neurodegeneration and other neurological diseases.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Conflict of interest

The authors declare that they have no conflict of interest.