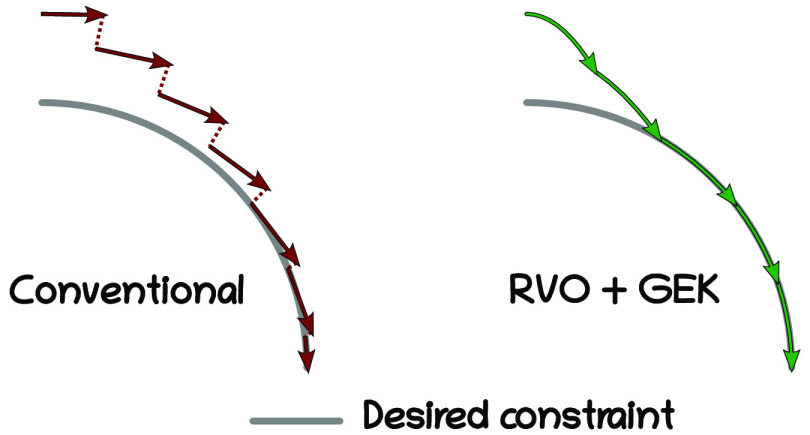
Abstract
Gaussian process regression has recently been explored as an alternative to standard surrogate models in molecular equilibrium geometry optimization. In particular, the gradient-enhanced Kriging approach in association with internal coordinates, restricted-variance optimization, and an efficient and fast estimate of hyperparameters has demonstrated performance on par or better than standard methods. In this report, we extend the approach to constrained optimizations and transition states and benchmark it for a set of reactions. We compare the performance of the newly developed method with the standard techniques in the location of transition states and in constrained optimizations, both isolated and in the context of reaction path computation. The results show that the method outperforms the current standard in efficiency as well as in robustness.
I. Introduction
The ability of ab initio methods to accurately and efficiently predict molecular structures such as equilibrium structures and transition states, or series of structures, as in reaction pathways, is of fundamental importance as we use more and more sophisticated computer hardware and theoretical methods through computer simulations, to understand and categorize, for example, chemical reactions, decay processes, or molecular reorganization as an effect of exposure to electromagnetic radiation–X-ray or optical. In this endeavor, efficient and robust molecular geometry optimization methods are required and of essence.
The standard optimization paradigm is a surrogate model based on second-order Taylor expansion approximations combined with step restriction,1−3 approximate Hessians,4 and Hessian-update methods.5−14 This standard surrogate model has, however, several limitations. For example, the model has almost no flexibility beyond a pure harmonic shape of the energy hypersurface, i.e., it will never describe the parent model correctly. The model only strictly interpolates correctly for the last two data points and can only describe a single stationary point. Recently an alternative surrogate model–the Kriging model,15,16 in particular, the gradient-enhanced Kriging (GEK)17−19 −has been proposed and explored by a number of research groups for geometry optimizations of equilibrium and transition state structures and explorations of reactions paths.20−28 These studies have demonstrated the potential of the Kriging procedure as a competitive alternative to the standard. However, these studies have also shown that in order to excel, as compared with commonly used algorithms, a GEK-based method not only should be based on internal coordinates27 but also be able to make use of the empirical and practical knowledge accumulated through decades of use and improvement of second-order methods. Raggi and co-workers28 have recently demonstrated how the use of Hessian model functions4 eliminated the required optimization through likelihood maximization of the characteristic lengths–hyperparameters of the GEK model. Moreover, the same study proposed a new type of optimization–restricted-variance optimization (RVO)–in which the explicit variance of the surrogate model is used in an efficient way as the optimization explores the multidimensional energy functional. This, in combination with the use internal coordinates29 that are invariant to translations and rotations, demonstrated superior convergence behavior for three different benchmark test suites for the case of finding molecular equilibrium structures.
In this report, we will investigate the ability of RVO to contribute to optimizations of transition states, minimum energy paths–as experienced, for example, in photoinitiated decay–or whole thermal reaction paths. A key ingredient in these tasks is the ability to perform geometry optimizations with geometrical constraints. Let us briefly set the stage by summarizing the state of the art in association with constrained molecular optimizations and transition state optimizations in combination with Gaussian process regression (GPR)–as Kriging is also known–methods. On the issue of transition state (TS) optimizations, two investigations stick out. First, Denzel and Kästner explored the projected rational-function optimization (P-RFO) of Baker30 in combination with the GPR Hessian in optimizing TS structures.22 Starting structures were generated by the image dependent pair potential (IDPP) of Smidstrup and co-workers,31 which employs only start and final structures and does not include any energy calculations. The IDPP is generated based on pairwise distances and subsequently investigated by the nudged elastic band method (NEB).32−36 Using the GPR technique developed for equilibrium structure optimizations–Cartesian coordinates, multilevel GPR, a universal characteristic length–Denzel and Kästner could demonstrate superior behavior (convergence rate and robustness) as compared to those of conventional methods. Second, Koistinen et al.26 explored GPR methods in optimizing TS stuctures starting from a single structure using a minimum mode following method, in which the so-called dimer method37−40 generated the minimum modes. The particular implementation of GPR, to support these optimizations, used a covariance function based on inverted interatomic distances, to which the authors attribute the robustness and success of the implementation. For the case of constrained optimization in combination with GPR, we would like to mention four studies on the use of the nudged elastic band method.20,24,25,41 In all studies, the use of GPR significantly reduced the number of evaluations of the energy and gradient of the parent model. It is also worth mentioning that Koistinen and co-workers41 propose the use of the variance to identify parts of the reaction path which might need further improvement.
In the present study, the RVO method will be explored in connection with TS and constrained optimizations. For the TS optimization, we will explore the image RFO (I-RFO) approach.42 We will, in particular, investigate the ability of the GEK to produce reasonable Hessians, which will guide the partition of the variable space into the subspace for minimization and maximization, respectively. Moreover, we emphasize the use of the restricted variance to make the approach robust. For the constrained optimization, we will combine RVO techniques with the restricted-step projected constrained optimization (RS-PCO) method.43,44 This will, in particular, be studied in connection with a) a conventional constrained optimization where a minimum energy structure is searched, subject to some arbitrary geometrical constraints, b) a hierarchical TS finder initially using constraints to find the quadratic region of the TS structure followed by an uphill-trust-region approach14,45 to locate the stationary point,46,47 and c) a method for reaction path evaluation based on sequential constrained optimizations.48 Performance will be assessed by benchmark calculations in which the standard surrogate model is contrasted against the GEK alternative. It is our perceived notion that the inherent advantages of the GEK surrogate model will manifest themselves by superior optimization characteristics.
The rest of this report will be organized as follows. First, we will present a theory section outlining GEK-supported RVO in combination with standard methods for TS, constrained, and reaction pathway optimization. This will be followed by a description of the simulations, which will document performance characteristics and the computational details. Third, the results will be presented and discussed. Finally, a summary and conclusion section will end this report.
II. Theory
The GEK-supported restricted-variance optimization is a multilayer optimization method–alternated evaluations on the expensive parent and the cheap surrogate model in a computationally optimal way. Here the optimization on the surrogate model, defined by a fixed number of sample points, is usually explored to convergence–the microiterations. Subsequently, the updated coordinate is evaluated on the parent model and included to describe an updated surrogate model–the macroiteration. Much of the success of the Kriging approach is that the surrogate model to a large extent is very accurate and that microiterations can be performed virtually free of computational cost. This is an excellent recipe for accelerated convergence.
Below, a brief presentation is given of the gradient-enhanced Kriging surrogate model, the selection of the associated characteristic lengths, and restricted-variance optimization as implemented in our previous work.28 This approach is the main engine behind the surrogate model that is used in this study for TS structure optimizations and for performing constrained geometry optimizations. The initial presentation will be followed by brief reviews of the specific methods used for the benchmark calculations. These presentations will pay special attention to aspects which are relevant to the use of GEK and RVO.
In what follows here, bold lower- and uppercase symbols represent column vectors and matrices, respectively.
II.A. Gradient-Enhanced Kriging
The gradient-enhanced Kriging method has been presented in detail elsewhere.17−19 Thus, we will here just briefly present the approach as implemented and used in this study. This will be followed by a short description of how the characteristic lengths of the GEK are selected and how the variance estimate associated with GEK is used in connection with step-restricted optimization.
Typically, ab initio simulations provide energies and gradients as functions of the molecular structure. In this respect, the most efficient surrogate models use all this information; one such method is the gradient-enhanced Kriging. In our implementation, we have used the so-called direct approach in which the gradient information is used as additional data to the energy values. This results in a surrogate model which mathematically is expressed, for a system with K dimensions and n sample points, as
| 1 |
where μ is known as
the trend function, and  and
and  are the sets of weights associated with
the energies and gradients, respectively. The covariance function
are the sets of weights associated with
the energies and gradients, respectively. The covariance function 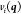 contains the
correlation between the coordinates
of the prediction point
contains the
correlation between the coordinates
of the prediction point 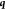 and the ith sample point.
and the ith sample point.
The exact form of the covariance function is at the core of the method. First we express the generalized distances, dij, between sample points i and j of the GEK as
| 2 |
where K is the number of degrees of freedom of the molecular system (K = 3N – 6 for a nonlinear system with N nuclei and no external fields), and lk is a scale parameter that influences the width of the covariance function–the characteristic length–in the kth dimension. In our implementation, we have used the Matérn-5/2 covariance function, given as
| 3 |
a choice we share with other implementations due to the characteristics of the function, being three times differentiable with respect to qi,k and allowing an adequate modeling of chemical systems.21,25
Once the covariance function is defined, the weights  and
and  are obtained to ensure that the predicted
energy and gradient at the sample points exactly reproduces the sample
data.
are obtained to ensure that the predicted
energy and gradient at the sample points exactly reproduces the sample
data.
II.A.1. Selection of Characteristic Lengths
The characteristic lengths, lk, are of fundamental importance to the approach–failure or success is closely related to the selected values of this parameter. One approach, selected by many, is to tune them to maximize the likelihood of the surrogate model.49 This step is, however, a potential performance and time bottleneck of the approach—it could render the generation of the surrogate model as expensive as the parent model it was called in to replace. This is usually overcome by two simplifications. First, rather than using individual lk values, a single value is used. This is a decision that reduces the parameter space in which the maximization is performed, at the expense of the inherent potential of the method. Second, the l value is not optimized on the fly but is rather selected empirically by optimizing the overall performance using a large test/training set of data.
We have, however, selected a different route. In this approach, we view the inclusion of additional data points as a process similar to the Hessian update associated with standard quasi-Newton optimization methods. Thus, we select the lk values such that the surrogate model reproduces our initial approximation of the parent model through the empirical Hessian information. In that sense, we first select the coordinates that will define the GEK as those which diagonalize the Hessian-model-function (HMF) Hessian.4 Second, we select the lk values from the analytic expression
| 4 |
where lk is the characteristic length of coordinate k, Hkk is the
corresponding eigenvalue of the approximate Hessian (in the HMF approach
these are always positive), and 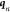 is
the latest, or current, sample point.
Moreover, to avoid too long characteristic lengths, Hkk is set to be no smaller than a threshold
set to 0.025 Eh/[a0,rad].2 This expression arises
from the curvature of a surrogate model built with a single sample
point, evaluated at the sample point, which for a Matérn-5/2
covariance function, eq 3, is
is
the latest, or current, sample point.
Moreover, to avoid too long characteristic lengths, Hkk is set to be no smaller than a threshold
set to 0.025 Eh/[a0,rad].2 This expression arises
from the curvature of a surrogate model built with a single sample
point, evaluated at the sample point, which for a Matérn-5/2
covariance function, eq 3, is 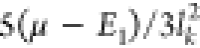 for each k coordinate,
with E1 being the energy at the sample
point. This therefore guarantees that, when the GEK model is constructed
with a single sample point, the curvature at that point will exactly
match the one suggested by the HMF Hessian. The inclusion of further
samples plays a similar role to that of the Hessian update. Thus,
this selection of the lk values will ensure a reasonable description of the local curvature
of the surrogate model, which will improve as more sample points are
included.
for each k coordinate,
with E1 being the energy at the sample
point. This therefore guarantees that, when the GEK model is constructed
with a single sample point, the curvature at that point will exactly
match the one suggested by the HMF Hessian. The inclusion of further
samples plays a similar role to that of the Hessian update. Thus,
this selection of the lk values will ensure a reasonable description of the local curvature
of the surrogate model, which will improve as more sample points are
included.
II.B. Restricted-Variance Optimization
Step size restrictions adapted to second-order optimization procedures have been instrumental to efficient and robust optimization procedures.1,50 The success of the restriction is that it should tether the optimization to the part of the surrogate model for which the approach is expected to be a good approximation–the quadratic region. However, a simple measure of this has escaped the quantum chemists, and ad hoc procedures and equations have been used to dynamically select the so-called trust radius during the optimization. For a GEK-based surrogate model, there is, however, an explicit analytical expression to measure the quality of the fit between the parent and surrogate model. This estimated quality, as measured by the expected variance, is expressed as51
| 5 |
where 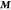 is the covariance matrix between all the
sample points,
is the covariance matrix between all the
sample points, 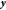 is the column vector of function values
(energies and gradients), and
is the column vector of function values
(energies and gradients), and 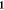 is
a column vector with elements equal
to 1 where they correspond to energies in
is
a column vector with elements equal
to 1 where they correspond to energies in 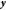 and to 0 where they correspond to gradients.
In the equation, the first factor accounts for the variance of the
sample points, while the second measures the distance of
and to 0 where they correspond to gradients.
In the equation, the first factor accounts for the variance of the
sample points, while the second measures the distance of 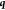 to the sample points and will give zero
whenever
to the sample points and will give zero
whenever 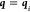 . Assuming a Gaussian variance, the actual
energy can thus be estimated, with a 95% confidence, to lie in the
interval
. Assuming a Gaussian variance, the actual
energy can thus be estimated, with a 95% confidence, to lie in the
interval 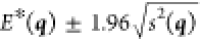 .
.
The restricted-variance optimization (RVO) method is designed such that the optimization is restricted to the subspace of the surrogate model for which the 95% confidence interval is within the specified threshold, σRVO, i.e.,
| 6 |
If the variance restriction is invoked, the microiterations are terminated, and a new macroiteration is executed.
In our implementation, we extensively use the restricted-step rational-function optimization (RS-RFO)1 when exploring the surrogate model. However, rather than to apply an ad hoc geometrically defined step-restriction we will exclusively use RVO.28
II.C. Transition State Optimization
Transition
state optimization is the search for a first-order saddle point on
a potential energy surface: it is a mixed minimization and maximization
problem–one maximizes the energy in the subspace spanned by
the reaction vector and minimizes the energy in the complementary
subspace. For the TS optimization, we will explore the restricted-step
image RFO (RS-I-RFO) approach.42,52 The I-RFO method of
Helgaker uses the presumed reaction vector,  , and the corresponding eigenvalue, ω,
to modify the full Hessian and gradients if ω is negative–the
image function technique of Smith52
, and the corresponding eigenvalue, ω,
to modify the full Hessian and gradients if ω is negative–the
image function technique of Smith52
| 7 |
and
| 8 |
such that the maximization effectively becomes a minimization using the Hessian and gradient of the image function. The subsequent minimizations are done jointly. While the use of an analytic Hessian is optimal, an empirical Hessian in combination with the MSP Hessian-update method12−14 or other methods to predict the reaction vector can be sufficient. The present study will explore the extent to which the Hessian of the surrogate model, as its quality improves with an increasing number of sample points, can be a realistic and efficient substitute.
In the context of the RVO method, the RS-I-RFO is applied to the microiterations, while the macroiterations are unchanged; i.e., each macroiteration consists of building the GEK surrogate model and searching for a stationary point on it (a minimum with RS-RFO or a saddle point with RS-I-RFO).
II.D. Constrained Optimization
For the constrained optimization, we will use the projected constrained optimization method (PCO).43,44 Below, the PCO approach will be outlined. This will be followed by two examples: first, on how this technique can be used to identify regions close to a transition state, and second, how to follow reaction paths in which the energy decreases–as in a reaction path between two minima through a TS or the preferred decay path of a molecule raised to an excited state by the absorption of a quantum of electromagnetic radiation.
II.D.1. Projected Constrained Optimization
The main machinery is a standard Lagrange multiplier approach, that is, the use of a Lagrangian function of the form
| 9 |
where 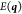 is the energy,
is the energy, 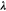 are the Lagrangian multipliers, and
are the Lagrangian multipliers, and 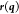 –a column vector with the elements
–a column vector with the elements 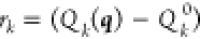 –are the equations of the constraints.
–are the equations of the constraints.
Here 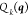 is a constraint,
a function of the coordinates,
and
is a constraint,
a function of the coordinates,
and 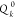 is the desired value, a constant, of that
particular function. At convergence
is the desired value, a constant, of that
particular function. At convergence 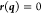 , that is, the Lagrangian
function and the
energy have the same value:
, that is, the Lagrangian
function and the
energy have the same value: 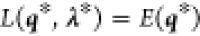 . To find the optimal
coordinates,
. To find the optimal
coordinates, 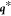 , the expression above is Taylor-expanded
to second order around the present coordinates,
, the expression above is Taylor-expanded
to second order around the present coordinates, 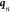 and
and 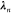
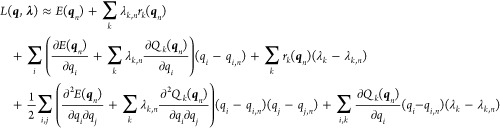 |
10 |
Discarding third-order terms, we recast this equation to (correct to second order)
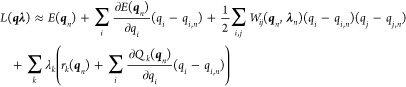 |
11 |
where we have defined an
effective Hessian, 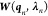 , as
, as
| 12 |
This has to be used in an iterative way for finding the optimal
parameters. At convergence, we note that, since 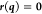 , we have the condition
, we have the condition
| 13 |
where 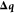 is a column vector of coordinate
displacements,
and the notation
is a column vector of coordinate
displacements,
and the notation 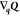 indicates a matrix with the Qk derivatives–with dimensions nq × nQ:
indicates a matrix with the Qk derivatives–with dimensions nq × nQ:
| 14 |
This allows us to
approximately define a unitary transformation, 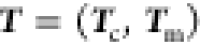 , of the coordinates into two subspaces–one
for the minimization (m) and one to fulfill the constraints (c), with
the associated vector
, of the coordinates into two subspaces–one
for the minimization (m) and one to fulfill the constraints (c), with
the associated vector 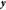 with dimension of the numbers of constraints
and the complementary vector
with dimension of the numbers of constraints
and the complementary vector  with dimension of the total number of degrees
of freedom minus the number of constraints, respectively. That is,
with dimension of the total number of degrees
of freedom minus the number of constraints, respectively. That is,
| 15 |
The unitary matrix has two required properties
| 16 |
| 17 |
sufficient conditions for the definition of the matrix through a Gram–Schmidt orthonormalization. With this on hand, we can approximately separate the Lagrangian into one equation to fulfill the constraints, namely,
| 18 |
and the complementary equation
for the minimization in a reduced space, now completely expressed
in terms of 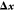 and
and 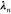 .
.
In terms of an RVO implementation, we proceed as follows:
while
the first step (computing 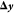 and
and 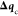 ) is performed completely independent of
the minimization, the latter (computing
) is performed completely independent of
the minimization, the latter (computing 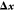 and
and 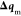 ) is performed in the presence of the former
displacement. The global variance restriction σRVO is defined as in the standard RVO,28 but
if
) is performed in the presence of the former
displacement. The global variance restriction σRVO is defined as in the standard RVO,28 but
if 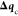 were allowed to use this whole variance,
there would be no further room for minimization. Therefore, we apply
a reduced threshold for the computation of
were allowed to use this whole variance,
there would be no further room for minimization. Therefore, we apply
a reduced threshold for the computation of 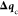 , by multiplying σRVO by
a factor that depends on the maximum gradient of any of the constraints
, by multiplying σRVO by
a factor that depends on the maximum gradient of any of the constraints
| 19 |
In addition, we note that the evaluation of the constraints and the associated gradients usually requires the Cartesian coordinates of the system. While in an unconstrained RVO the microiterations can be carried out completely in internal coordinates; the incorporation of the constraints means that the internal coordinates must be converted to Cartesian at every microiteration. This has the benefit that inconsistencies in the internal coordinates (e.g., negative bond lengths) can be detected and the microiterations can be interrupted. As for the unconstrained RVO, microiterations are also interrupted if the maximum allowed variance is reached, or if a stationary point is found on the surrogate model. In either case, a new sample point is then evaluated at the level of the parent model.
II.D.2. Transition State Finding Procedure
The transition state optimization method described in section IIC is not guaranteed to converge or to converge to the desired saddle point. In fact, it will typically only converge to a saddle point when starting within the region where the PES has the right curvature–one and only one negative Hessian eigenvalue. Thus, for effectively locating transition states, it is crucial to be able to guide the search toward this region. Several methods exist for this task that require more or less input from the user. In this investigation, we will use the option that in OpenMolcas is activated by using the “FindTS” keyword, and which we will therefore call FindTS. This is an opportunistic approach relying heavily on the computational chemist’s ability to guess the main feature of the transition state structure. The initial part of the procedure is a constrained optimization using constraints the user believes to be important coordinates of the transition state structure. The purpose of this initial step is to lead the optimization on the PES such that either the Hessian-update method or the GEK picks up a negative curvature–something which sometimes fails. Once a negative curvature is found, the constraints are eliminated, and the optimization proceeds as a normal transition state optimization.
II.D.3. Reaction Path Optimization
Reaction paths, understood as the trajectory in nuclear geometry space that a system follows during a reaction or other chemical process, are properly approached through molecular dynamics simulation, either quantum or semiclassical. However, as part of a static PES analysis, it is useful to obtain optimal paths that link different distinguished structures or points on the surface, such as a saddle point and a minimum, or two minima, or a Franck–Condon (FC) point and a crossing point, or a FC point and a minimum, etc. The most commonly explored type of path is the steepest descent path (SDP), which is defined as the path that, from its initial point, is always tangent to the local gradient and proceeds downhill. Unlike stationary points, an SDP is not invariant to coordinate choice; when mass-weighted coordinates are used, the SDP corresponds to an infinitely damped MD trajectory with zero kinetic energy. If every point of a path has positive curvature along the directions orthogonal to the path, the path can be seen as proceeding along a “valley” of the PES and is then known as minimum energy path (MEP), but there is no guarantee an SDP will satisfy this condition, although the terms are sometimes used interchangeably.53−56 For an SDP starting at a saddle point, where the gradient is zero, the path is taken as tangent to the Hessian eigenvector with negative curvature at the initial point; if this is done in mass-weighted coordinates, the displacement along this path–and by extension the path itself–is known as intrinsic reaction coordinate (IRC).
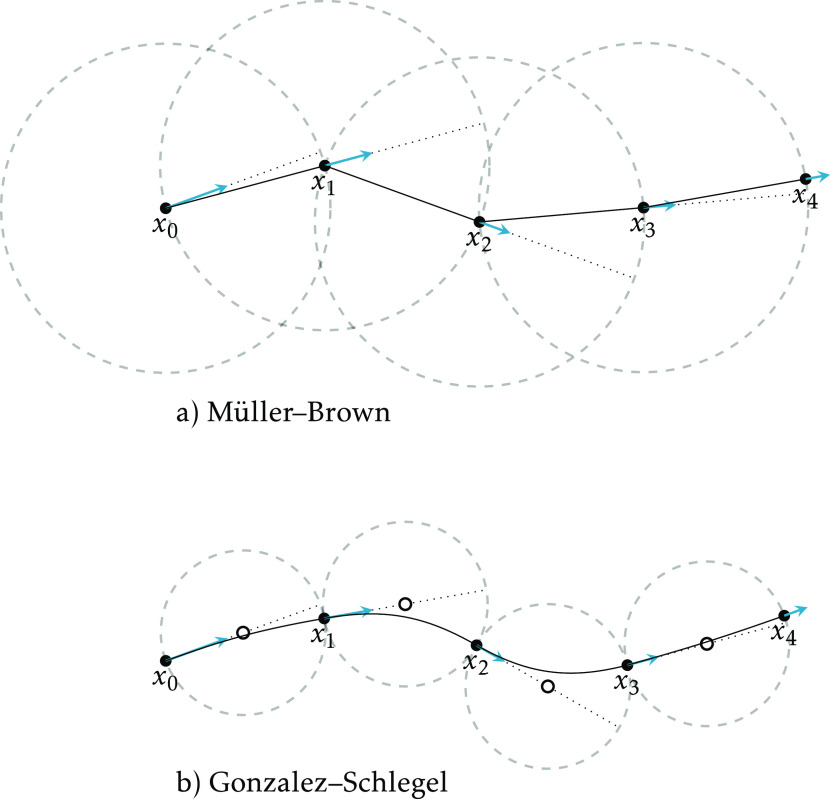
There are two main strategies for optimizing a reaction path: sequential and collective. In a sequential optimization, successive points on the path are optimized one by one; once a point is found, it is not modified, and the next point is searched. In a collective optimization, all (sampled) points on the path are optimized simultaneously. The NEB34 and string57 methods are examples of collective approaches. In this work, we use a sequential method based on successive constrained optimizations. Initially,44 the algorithm implemented in Molcas was that of Müller and Brown,58 where each point is constrained to lie on the surface of a hypersphere centered on the previous point. In current OpenMolcas versions, the algorithm of Gonzalez and Schlegel48 is preferred, the difference is that the hypersphere is now centered a “half step” away from the previous point, in the negative gradient direction (see Figure 1).
Figure 1.
Two algorithms for computing an SDP as a series of constrained optimizations. The points x0...x4 represent the optimized points, and the arrows represent the force (negative gradient) at those points. In a), each point is optimized on a hypersphere (dashed) centered on the previous point, and the distance between points is exactly the radius. In b), the centers of the hyperspheres (small circles) are located along the line defined by the previous point and its gradient (dotted). The distance between points is only approximately the diameter; but by construction all the gradients are perpendicular to two hyperspheres, and the path can be described as a chain of circular arcs.
The constraints applied during the optimization can be expressed as
| 20 |
where 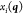 is the ith Cartesian coordinate
corresponding to the geometry described by
is the ith Cartesian coordinate
corresponding to the geometry described by 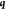 ,
, 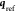 is
the reference geometry (the center of
the hypersphere), and wi is the weight assigned to the ith coordinate. If
all weights are equal to 1, this is just the Euclidean distance, and
if the weights are the masses of the corresponding atoms, it is the
distance in mass-weighted coordinates, as required for an IRC calculation.
Since the Cartesian coordinates
is
the reference geometry (the center of
the hypersphere), and wi is the weight assigned to the ith coordinate. If
all weights are equal to 1, this is just the Euclidean distance, and
if the weights are the masses of the corresponding atoms, it is the
distance in mass-weighted coordinates, as required for an IRC calculation.
Since the Cartesian coordinates 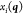 are, in general, not unique, they are translated
and rotated to minimize the value of
are, in general, not unique, they are translated
and rotated to minimize the value of 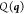 .
.
So, the procedure, according to the Gonzalez–Schlegel algorithm, is as follows. From the initial point, a new reference geometry is obtained by displacing the geometry along the direction given by the gradient, a distance half the desired path resolution. A new starting geometry is generated by further displacing the reference geometry by the same amount in the same direction. From this starting geometry, a constrained optimization is performed, with the constraint described above. On convergence, the optimized point is saved, and a new reference geometry is generated as above. This is repeated until termination, which occurs when the total gradient at an optimized constrained structure is below a threshold, when the geometry difference between two optimized structures is too small, when a maximum number of steps is reached, or when the energy of an optimized point increases with respect to the energy of the previous optimized point. The sequence of optimized points is an approximated sample of the path.
There is a small difference when the initial point of the path is a saddle point. In this case, the first constrained optimization takes the initial point as reference, with no displacement, and the starting geometry is generated by displacing it half the path resolution distance along the direction given by an input “reaction vector”. Ideally, this vector should be the Hessian eigenvector with negative eigenvalue at the initial point, but almost any approximate vector that is not orthogonal to the true reaction vector works in practice, and the procedure can be initiated without computing the full Hessian. Once the path in this “forward” direction is concluded, a new “backward” path is computed from the same initial saddle point, but now the first starting geometry is displaced in the opposite direction.
III. Computational Details
Benchmark calculations are performed to compare the performance of a standard second-order optimization technique in combination with a Hessian-update method (RS-RFO and BFGS) and the method proposed in this work (GEK-supported RVO), applied to the optimization of transition state structures and other constrained geometry optimizations.
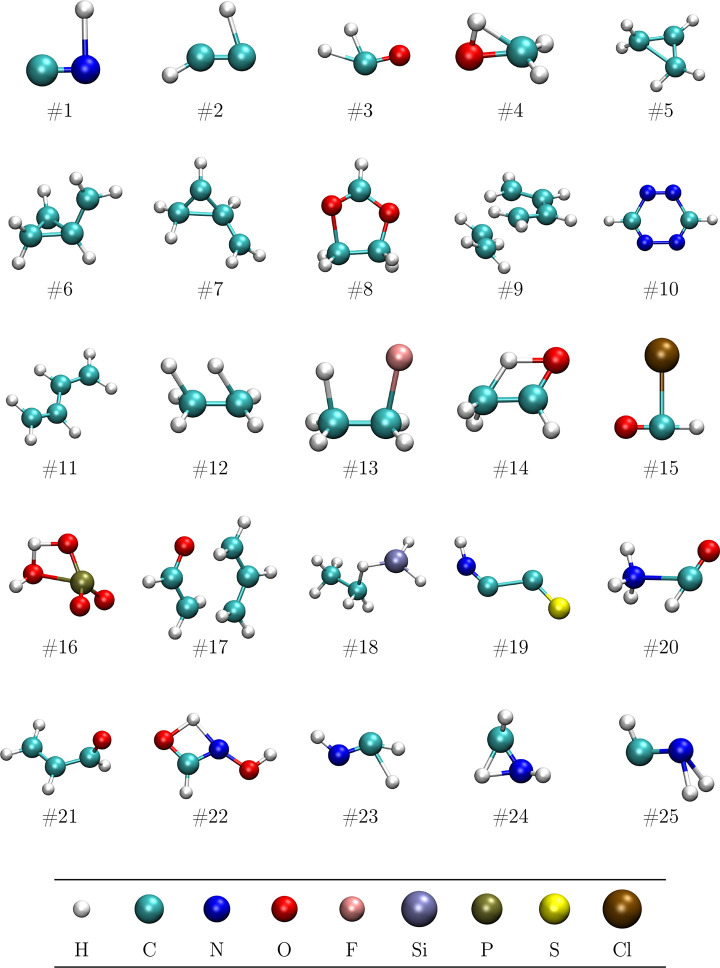
All the benchmarks are based on the Baker-TS test suite,59 for which the initial structures are displayed in Figure 2, but we will test different features of the optimization approach. First, starting from the Baker-TS initial structures, a saddle-point optimization is performed using the FindTS option with suitable guiding constraints. Our expectation here is that the GEK surrogate model will eliminate the need of a special Hessian-update procedure and in a stable way provide a realistic approximation of the surface around the saddle point. Second, a constrained optimization is carried out with the same initial structures and constraint definitions, but aiming for a constrained minimum instead of an unconstrained saddle point. In this case, we expect the RVO method to enable a faster achievement of the constraints without sacrificing the quality of the energy minimization. Third, starting from the optimized saddle-point structures, we will perform an IRC optimization, computing the backward and forward reaction paths. This entails a series of constrained optimizations, and we hope that the information from the previously optimized structures will contribute to a significant performance enhancement in RVO with respect to RS-RFO.
Figure 2.
Starting structures for the Baker-TS test suite. The bottom row of spheres shows the color code.
The new optimization procedure has been implemented in a development (public) branch of the Slapaf module of the open-source OpenMolcas quantum chemistry program package60 and will be incorporated into the main release shortly.
Energies and gradients were computed at the DFT level of approximation, using the B3LYP functional and def2-SVP61 basis set, with unrestricted SCF for the open-shell cases: #4, #5, and #8. Two-electron integrals were computed with atomic compact Cholesky decomposition (acCD)62 with default threshold (10–4 Eh). To reduce the influence of numerical noise in the comparisons, the accuracy of the computed energies and gradients was increased 2–3 orders of magnitude from the default.
Unless explicitly stated, the defaults in OpenMolcas were used for geometry optimizations. This includes the definition of nonredundant internal coordinates from force-constant-weighted redundant coordinates, and the approximate Hessian was expressed through the Hessian Model Function (HMF);4,29 Hessian updates with BFGS over the last 5 iterations; a restricted-step rational-function optimization (RS-RFO) procedure with a step restriction of 0.3 au; convergence criteria: gradient root-mean-square (rms) and maximum component below 3 × 10–4 Eh a0–1 and 4.5 × 10–4 Eh a0–1, respectively; and displacement rms and maximum component below 1.2 × 10–3 a0 and 1.8 × 10–3 a0. For saddle-point optimizations, the default method is the “image” variant (RS-I-RFO),1 with MSP Hessian updates over the last 10 iterations. No symmetry was enforced in any of the calculations.
In the case of RVO, the defaults are as given in our previous work:28 using at most 10 previous samples (energies and gradients) for building the GEK surrogate model; a baseline or trend function 10.0 Eh above the maximum energy of the samples; a Matérn-5/2 covariance function; and a maximum variance 0.3 a0 times the largest Cartesian gradient at the last iteration. For saddle-point optimizations, the maximum number of samples is increased to 20, and only during the initial constrained phase of a FindTS optimization, the maximum variance factor is decreased to 0.1 a0.
The IRC calculations were done with the Gonzalez–Schlegel algorithm, with a step size of 0.1 a0 in normalized mass-weighted Cartesian coordinates, so the constraint corresponds to a hypersphere of 0.05 a0 radius. The starting structure was the saddle point optimized with RS-I-RFO in all cases. After every step of the path, the previous optimized structure is displaced along the direction of the gradient to provide an initial structure for the next optimization. In some circumstances, the SDP can pass through a valley–ridge transition point,63 continue on a ridge, and end at a saddle point. This happens, for instance, when the initial structure has some symmetry that is reduced along the path, as in reactions #12 and #13, which would end at the eclipsed conformation of CH3CH3 and CH3CH2F, respectively. Although this is in accordance with the SDP definition, it is an undesirable occurrence, since the resulting path is unstable with respect to numerical noise and it does not directly connect the saddle point and a minimum. In order to avoid this situation, a small random displacement is added to each initial structure along the path to break a possible symmetry. The reaction paths were computed for a maximum of 15 steps on either side. The step size was reduced to half the above value in some cases where a finer resolution seemed desirable, especially where the reaction involves mainly the movement of hydrogen atoms: #2, #4, #8, #22, #23, #24, and #25. For the IRC calculations of #9, the default geometry convergence criteria were increased by a factor of 20 to reduce the total number of iterations, as it was the slowest case in the benchmarks.
For the first two benchmark calculations (saddle-point optimization and constrained optimization), we established specific constraints for each system. The goal of these constraints is only to initially guide the TS optimization toward a saddle point, until a negative curvature is found on the PES, at which point the constraint is discarded and a normal saddle-point optimization proceeds. These constraints therefore imply some arbitrariness and chemical knowledge from the user. They were designed in a simple way such that the optimization proceeds smoothly with RFO, but they were not further optimized to minimize the iteration count, and the same constraints were used for RVO without change. The specific constraints are described in Table 1.
Table 1. Description of the Constraints Used As a Guide for Saddle-Point Optimization and for the Constrained Optimizations of the Baker-TS Set.
| system | constraint(s) |
|---|---|
| #1 | C–N–H angle: 45° |
| #2 | C–H bond that forms: 1.3 Å |
| #3 | H–H bond: 1.3 Å |
| #4 | C–O–H angle (with migrating H): 50° |
| #5 | C–C bond that breaks: 1.5 Å |
| #6 | C2–C4 bond (product numbering): 1.85 Å |
| #7 | C1–C3 bond (product numbering): 1.4 Å |
| #8 | C–O bonds that break/form: 1.6 Å |
| #9 | C–C bonds that form: 1.8 Å |
| #10 | C–N and N–N bonds that break: 1.7 Å |
| #11 | C–C–C–C dihedral: 90° |
| #12 | H–H bond: 1.0 Å; C–H bond that breaks (outer one at the initial structure): 1.6 Å |
| #13 | F–H bond: 1.0 Å; C–F and C–H bonds that break: 2.0 Å |
| #14 | O–H bond: 1.0 Å; C–C–O--H dihedral (with migrating H): 5° |
| #15 | Cl–H bond: 1.8 Å |
| #16 | sum of P–O1 and O2–H bonds (both forming) equal to sum of P–O2 and O1–H bonds (the latter breaking) |
| #17 | C–O bond that breaks: 1.8 Å; C–C bond that forms: 2.2 Å |
| #18 | C–Si bond that forms: 2.0 Å |
| #19 | C–C bond: 1.8 Å |
| #20 | N–H bond that forms: 1.8 Å; H–N–C–H (with migrating H): –15° |
| #21 | C–C–C-O dihedral: 70° |
| #22 | O–H bond that forms: 1.5 Å; C–N–O–H (with spectator OH): 160° |
| #23 | H–H bond: 1.2 Å |
| #24 | N–H bond that forms: 1.4 Å |
| #25 | N–H bonds that break: 1.4 Å |
IV. Results and Discussion
The first set of calculations consisted in the optimization of saddle-point structures, starting from the structures in the Baker-TS set and providing the initial constraints specified in Table 1 for the FindTS method.
The optimizations converged with no major issues with both the conventional RS-I-RFO method and the new RVO method. A comparison of the performance of both methods is displayed in Figure 3, where it is evident that, in general, RVO outperforms RS-I-RFO. In most cases, the constraints are only active for 1–5 iterations, and a saddle point is found in 10–20 iterations. The root-mean-square displacement (rmsd) between the optimized structures with both methods is smaller than around 10–3 Å, except for a handful of cases commented below; this confirms that RVO provides a faster route from starting to optimized structure, using the same initial information. The total number of iterations was reduced from 400 to 294, a 26.5% decrease. The number of iterations with active constraints is actually larger with RVO (74 vs 63), and the main improvement comes in the saddle-point optimization itself, where RVO is able to explore the PES more efficiently.
Figure 3.
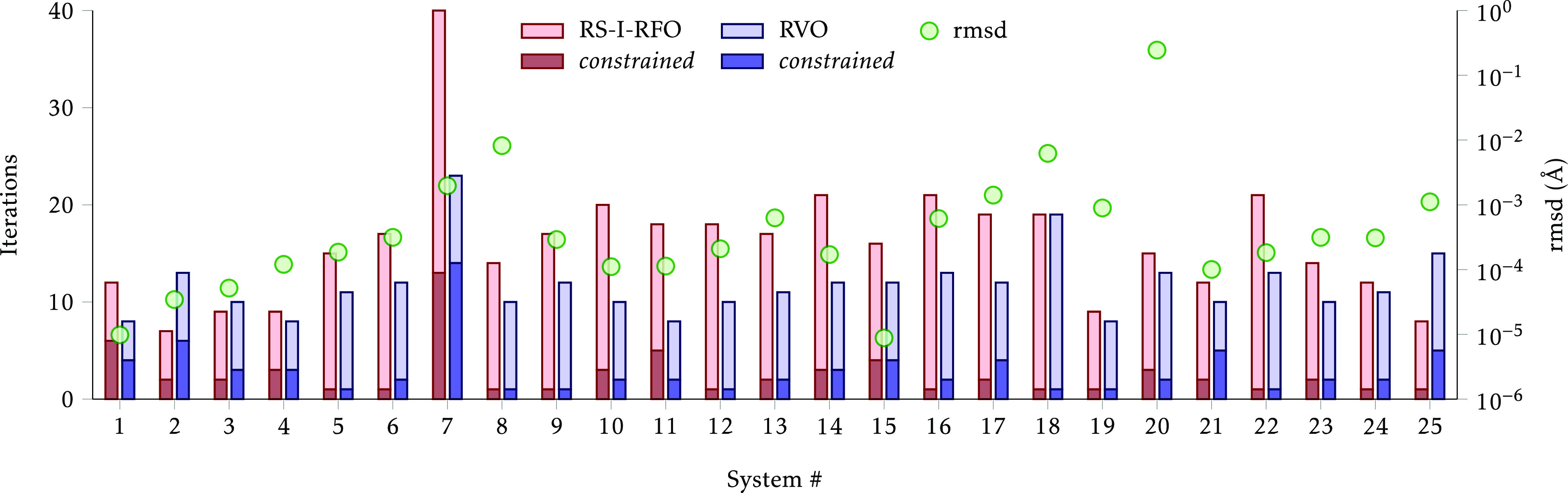
Number of iterations to converge the Baker-TS structures to a saddle point. The darker color in the bars indicates the iterations with active constraints. The circles represent the root-mean-square displacement between the converged structures.
The system with the largest number of iterations and the largest differences is #7, ring opening of bicyclo[1.1.0]butane (TS 2). According to the original source for the starting structure,14 the ring-opening reaction proceeds in two steps at the AM1 level, which is why there are two TS structures in #6 and #7. However, at our B3LYP/def2-SVP level, we could not find an intermediate, and it seems the reaction occurs in a single step. Nevertheless, it was possible to locate a saddle point distinct from the one found for #6. The apparent discrepancy between the AM1 and B3LYP PESs is probably the reason for the large number of iterations required, especially with active constraints.
System #20, 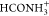
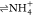 + CO, yielded the
largest rmsd between
the two methods, almost 0.25 Å. The converged structure
contains well-separated CHO and NH3 fragments; the H–N–C–H
dihedral specified in the constraints is −43° with RS-I-RFO,
while it is −4° with RFO. A calculation of the harmonic
frequencies indicated that the RS-I-RFO structure is a second-order
saddle point with a lowest imaginary frequency of 24i cm–1, and the RVO structure is a first-order saddle point
with a lowest real frequency of 31 cm–1 and
about 0.025 kcal/mol lower in energy than the RS-I-RFO structure.
In all other systems, the frequencies confirmed both structures as
first-order saddle points.
+ CO, yielded the
largest rmsd between
the two methods, almost 0.25 Å. The converged structure
contains well-separated CHO and NH3 fragments; the H–N–C–H
dihedral specified in the constraints is −43° with RS-I-RFO,
while it is −4° with RFO. A calculation of the harmonic
frequencies indicated that the RS-I-RFO structure is a second-order
saddle point with a lowest imaginary frequency of 24i cm–1, and the RVO structure is a first-order saddle point
with a lowest real frequency of 31 cm–1 and
about 0.025 kcal/mol lower in energy than the RS-I-RFO structure.
In all other systems, the frequencies confirmed both structures as
first-order saddle points.
The other two systems with relatively large rmsd are #8 and #18 (8 × 10–3 Å and 6 × 10–3 Å, respectively). In these cases, the differences are hardly appreciably even after superimposing both structures and are probably due to a somewhat flat PES. The RVO structures are, respectively, 5 × 10–3 kcal/mol and 2 × 10–4 kcal/mol lower than the RS-I-RFO structures. For #13, the RVO structure is 3 × 10–4 kcal/mol lower, and for #25 it is 2 × 10–4 kcal/mol lower; for all other systems, the difference is smaller than 10–4 kcal/mol.
After verifying the good behavior of the RVO method for optimizing saddle points, we check its performance for the optimization of constrained minima. First we carried out constrained optimizations using the same constraints as in Table 1, i.e., the same as in the first benchmark, but where the constraints are never turned off. The results are shown in Figure 4. Since the optimization now searches for a minimum, the “conventional” method is RS-RFO and not RS-I-RFO.
Figure 4.
Number of iterations to converge the Baker-TS structures to a constrained minimium. The circles represent the root-mean-square displacement between the converged structures.
We note at once that five systems–#8, #9, #12, #16, and #20–failed to converge with the RS-RFO method (in the maximum number of iterations allowed, which was 100). In all these cases, the imposed constraints are quickly satisfied and the gradient is reduced, but the geometry starts to oscillate close to convergence. In contrast, the RVO method achieves convergence in all the test systems and always with fewer or, at most, the same number of iterations as the RS-RFO method. The rmsd between the converged structures is in all cases smaller than 2 × 10–3 Å, except for #3, H2CO ⇌ H2 + CO (0.1 Å). The optimized structure with RVO consists of an almost linear arrangement of H2 (elongated) and CO, while with RS-RFO the H–C–O angle is 168° and the energy is 8 × 10–3 kcal/mol higher. The total number of iterations, excluding the systems that did not converge with RS-RFO, is reduced from 321 with RS-RFO to 233 with RVO (a 27.4% saving).
Our final benchmark is the computation of the reaction path passing through the optimized transition states, also known as intrinsic reaction coordinate (IRC). This implies a series of constrained optimization where each optimization involves a constraint that is expressed as a distance in (3N–6)-dimensional space from a previous reference structure. We expected that the gains of RVO would be especially important in this benchmark, due to its use of the previous points for building the surrogate model; on the other hand, with RS-RFO, the previous points can only influence the guessed Hessian.
The results, summarized in Figure 5, show that indeed RVO affords a significant reduction in the number of iterations required to compute the IRC paths. The total number was 3730 with RS-RFO and 1893 with RVO, representing almost a 50% decrease. We observe a reduction in all systems but very particularly in #16, #20, and #25.
Figure 5.
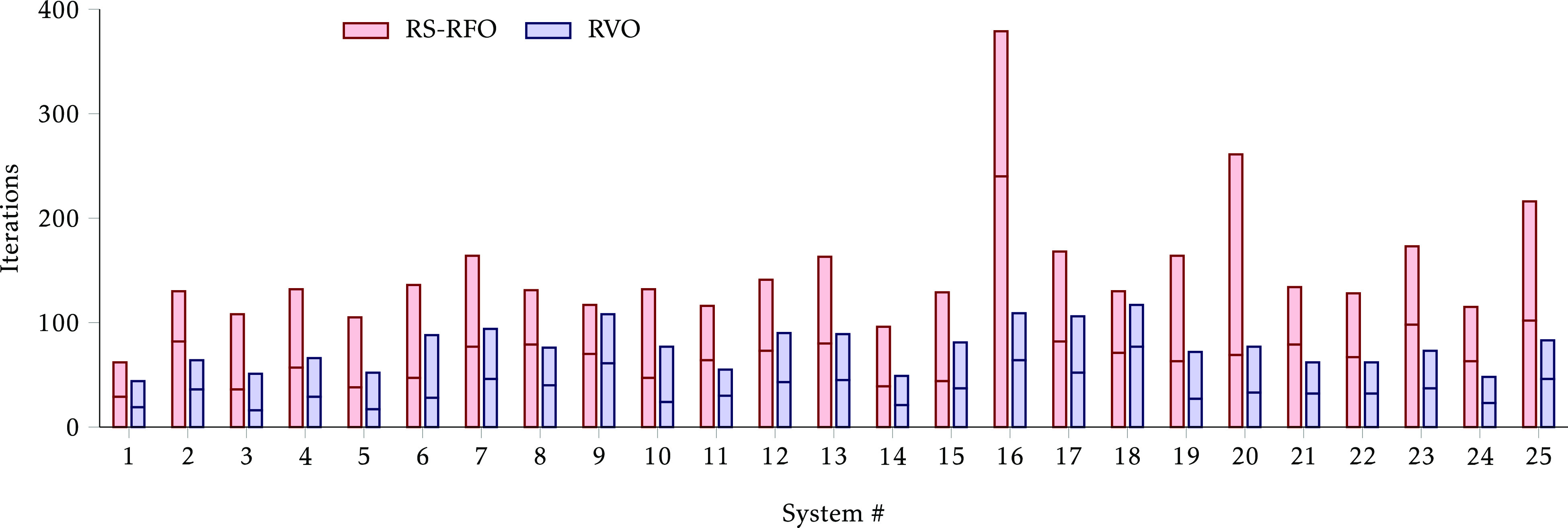
Number of iterations to converge the IRC optimization from the saddle point. The horizontal division in each bar separates the iterations toward reactants (below) and products (above).
It is not straightforward to provide a single measure of the similarity between the paths computed with the two methods, but as an illustration we show in Figure 6 a more detailed comparison of the paths for system #22, HCONHOH ⇌ HCOHNOH, which is quite typical. Each constrained optimization takes 4–8 iterations with RS-RFO and only 2–4 iterations with RVO. The rmsd between the two methods tends to be smaller close to the initial saddle point, which is logical as differences accumulate, but does not grow beyond 2 × 10–3 Å, indicating that the computed paths are essentially identical. Similar figures for the other systems are provided in the Supporting Information.
Figure 6.
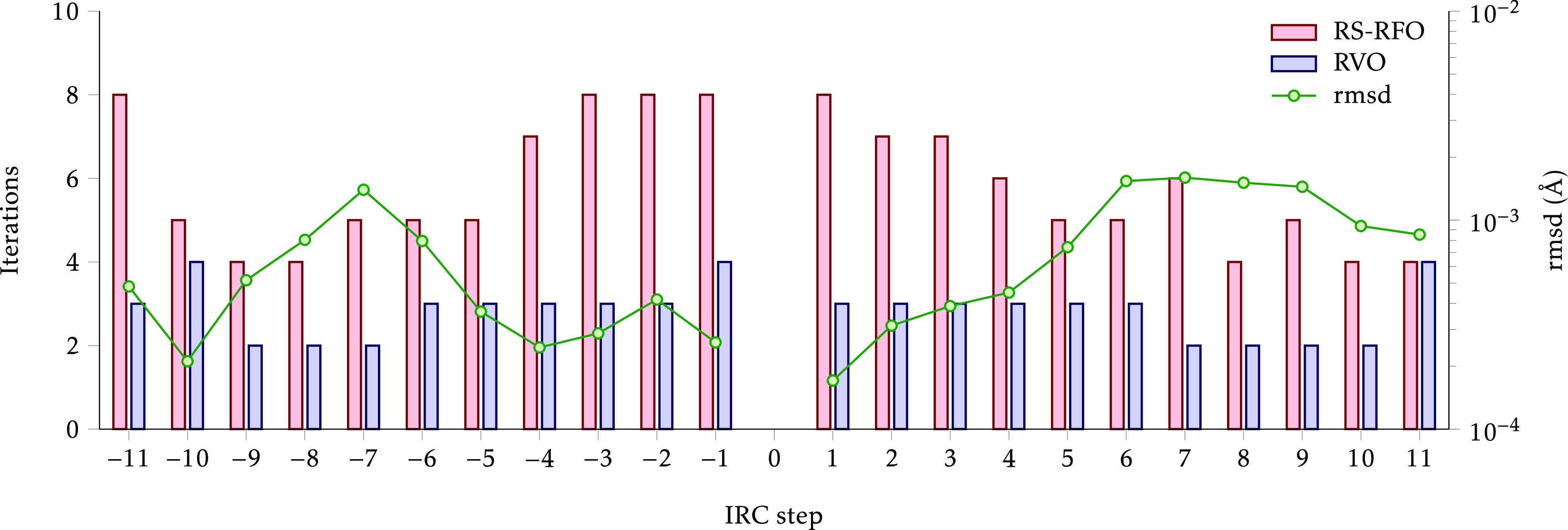
Comparison of performance for the IRC optimization of reaction #22. The bars show the number of iterations needed for optimizing each step of the path (0 is the initial saddle point, negative steps go toward reactants). The circles represent the root-mean-square displacement between the corresponding optimized structures.
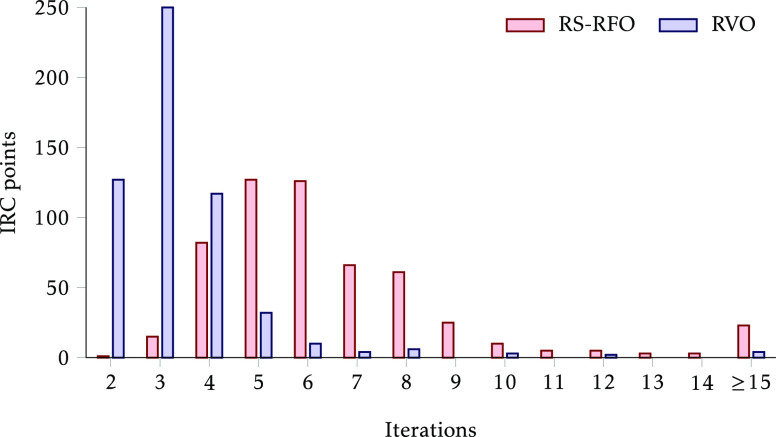
A clear advantage of RVO with respect to RS-RFO in constrained optimizations is that it can use the microiterations to converge the constraints as much as needed, within the limits of the maximum allowed variance. This means that when a system is close to convergence but still far from satisfying the constraints, with RS-RFO several expensive iterations are still necessary, especially when the step size is limited; with RVO, however, the fulfillment of the constraints can be ensured with the very cheap microiterations, and the number of macroiterations required can be greatly reduced. If, in addition, the surrogate model is accurate enough, the energy (or, in fact, gradient) minimization can effectively be done at the same time, and the fulfillment of the constraints will not degrade the energy convergence. We see signs of this in the IRC optimizations, where very often RVO takes only 2–3 iterations per point (the practical minimum is 2, since the first iteration is always setting up the initial structure), while RS-RFO more typically takes 4–6 iterations. This is reflected in Figure 6, and also in Figure 7, which displays the frequency at which each number of iterations required occurs. It is evident that the number of iterations necessary to optimize each point is significantly lower with RVO than with RS-RFO.
Figure 7.
Histogram of the number of iterations needed for optimizing each IRC point. The tallest bar, for example, means that 250 points converged on 3 iterations with RVO.
V. Summary
We have extended the restricted-variance optimization method, based on a gradient-enhanced Kriging surrogate model,28 to work with arbitrary geometrical constraints. The resulting method combines the projected constrained optimization43 and the RVO. This also allows a straightforward application of the algorithm to the location of saddle points on potential energy surfaces.
We have tested this development on a common set of 25 transition state structures. The calculations included the optimization of saddle points, of constrained minima structures, and the computation of reaction paths by performing a series of constrained optimizations. In all cases, we observed that the new RVO method outperforms a state-of-the-art conventional second-order method, as implemented in the OpenMolcas quantum chemistry package,60 reducing the total number of iterations by 25% to 50%. It is also observed that the RVO method seems to be more robust and less susceptible to convergence problems.
This work complements our previous one, proving that the GEK surrogate model built from very limited hard data (previous optimization iterations) and empirical “chemical knowledge” (embedded in the use of internal coordinates and in the HMF that defines the characteristic lengths) can be superior to the commonly employed second-order expansions for applications not limited to the location of minimum energy points. The GEK surrogate model can easily describe a saddle point on the potential energy surface, and this already occurs after a reduced number of macroiterations. On the other hand, the very fast microiterations on the surrogate model make it possible to ensure that geometrical constraints are satisfied, without the unnecessary evaluation of the parent energy and gradient, which comes with a high cost.
Finally, we note that it is possible to define constraints that are not of a strictly geometrical nature. For instance, for the location of conical intersections, an energy difference constraint is used,64 or one could desire to constrain the value of some other property, like the dipole moment or NMR chemical shifts. The PCO method can still be used as long as the derivatives of the constraints with respect to the geometry can be computed or obtained. However, the RVO as implemented here requires the computation of the constraints (and their gradients) during the microiterations, where no quantum-chemical calculation is done, and this is currently not implemented for nongeometrical constraints. Possible approximations could be assuming that the constraint does not change during the microiterations or using an auxiliary surrogate model for the constraints. These approaches are under investigation in our group.
Acknowledgments
Funding from the Swedish Research Council (grant 2016-03398) and the Olle Engkvist foundation (grant 18-2006) is recognized. Part of the computations were enabled by resources provided by the Swedish National Infrastructure for Computing (SNIC) at the Uppsala Multidisciplinary Center for Advanced Computational Science (UPPMAX) and the National Supercomputer Centre (NSC), partially funded by the Swedish Research Council (grant 2018-05973).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.0c01163.
The authors declare no competing financial interest.
Supplementary Material
References
- Besalú E.; Bofill J. M. On the automatic restricted-step rational-function-optimization method. Theor. Chem. Acc. 1998, 100, 265–274. 10.1007/s002140050387. [DOI] [Google Scholar]
- Schlegel H. B. Geometry optimization. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2011, 1, 790–809. 10.1002/wcms.34. [DOI] [Google Scholar]
- Thøgersen L.; Olsen J.; Yeager D.; Jørgensen P.; Sałek P.; Helgaker T. The trust-region self-consistent field method: Towards a black-box optimization in Hartree–Fock and Kohn–Sham theories. J. Chem. Phys. 2004, 121, 16. 10.1063/1.1755673. [DOI] [PubMed] [Google Scholar]
- Lindh R.; Bernhardsson A.; Karlström G.; Malmqvist P.-Å. On the use of a Hessian model function in molecular geometry optimizations. Chem. Phys. Lett. 1995, 241, 423–428. 10.1016/0009-2614(95)00646-L. [DOI] [Google Scholar]
- Broyden C. G. The Convergence of a Class of Double-rank Minimization Algorithms 1. General Considerations. IMA J. Appl. Math. 1970, 6, 76–90. 10.1093/imamat/6.1.76. [DOI] [Google Scholar]
- Goldfarb D. A family of variable-metric methods derived by variational means. Math. Comput. 1970, 24, 23–23. 10.1090/S0025-5718-1970-0258249-6. [DOI] [Google Scholar]
- Fletcher R. A new approach to variable metric algorithms. Comput. J. 1970, 13, 317–322. 10.1093/comjnl/13.3.317. [DOI] [Google Scholar]
- Shanno D. F. Conditioning of quasi-Newton methods for function minimization. Math. Comput. 1970, 24, 647–647. 10.1090/S0025-5718-1970-0274029-X. [DOI] [Google Scholar]
- Fletcher R.Practical Methods of Optimization; John Wiley & Sons, Ltd.: 2000; 10.1002/9781118723203. [DOI] [Google Scholar]
- Nocedal J. Updating quasi-Newton matrices with limited storage. Math. Comput. 1980, 35, 773–773. 10.1090/S0025-5718-1980-0572855-7. [DOI] [Google Scholar]
- Liu D. C.; Nocedal J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. 10.1007/BF01589116. [DOI] [Google Scholar]
- Murtagh B. A. Computational experience with quadratically convergent minimisation methods. Comput. J. 1970, 13, 185–194. 10.1093/comjnl/13.2.185. [DOI] [Google Scholar]
- Powell M. J. D. Recent advances in unconstrained optimization. Math. Program. 1971, 1, 26–57. 10.1007/BF01584071. [DOI] [Google Scholar]
- Bofill J. M. Updated Hessian matrix and the restricted step method for locating transition structures. J. Comput. Chem. 1994, 15, 1–11. 10.1002/jcc.540150102. [DOI] [Google Scholar]
- Krige D. G. A statistical approach to some basic mine valuation problems on the Witwatersrand. J. South. Afr. Inst. Min. Metall. 1951, 52, 119–139. [Google Scholar]
- Matheron G. Principles of geostatistics. Econ. Geol. Bull. Soc. Econ. Geol. 1963, 58, 1246–1266. 10.2113/gsecongeo.58.8.1246. [DOI] [Google Scholar]
- Liu W.; Batill S.. Gradient-Enhanced Response Surface Approximations Using Kriging Models. 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization; 2002; p 5456, 10.2514/6.2002-5456. [DOI] [Google Scholar]
- Han Z.-H.; Görtz S.; Zimmermann R. Improving variable-fidelity surrogate modeling via gradient-enhanced kriging and a generalized hybrid bridge function. Aerosp. Sci. Technol. 2013, 25, 177–189. 10.1016/j.ast.2012.01.006. [DOI] [Google Scholar]
- Ulaganathan S.; Couckuyt I.; Ferranti F.; Laermans E.; Dhaene T. Performance study of multi-fidelity gradient enhanced kriging. Struct. Multidiscip. Optim. 2015, 51, 1017–1033. 10.1007/s00158-014-1192-x. [DOI] [Google Scholar]
- Koistinen O.-P.; Maras E.; Vehtari A.; Jónsson H. Minimum energy path calculations with Gaussian process regression. Nanosyst.: Phys., Chem., Math. 2016, 7, 925–935. 10.17586/2220-8054-2016-7-6-925-935. [DOI] [Google Scholar]
- Denzel A.; Kästner J. Gaussian process regression for geometry optimization. J. Chem. Phys. 2018, 148, 094114. 10.1063/1.5017103. [DOI] [Google Scholar]
- Denzel A.; Kästner J. Gaussian Process Regression for Transition State Search. J. Chem. Theory Comput. 2018, 14, 5777–5786. 10.1021/acs.jctc.8b00708. [DOI] [PubMed] [Google Scholar]
- Garijo del Río E.; Mortensen J. J.; Jacobsen K. W. Local Bayesian optimizer for atomic structures. Phys. Rev. B: Condens. Matter Mater. Phys. 2019, 100, 104103. 10.1103/PhysRevB.100.104103. [DOI] [Google Scholar]
- Garrido Torres J. A.; Jennings P. C.; Hansen M. H.; Boes J. R.; Bligaard T. Low-Scaling Algorithm for Nudged Elastic Band Calculations Using a Surrogate Machine Learning Model. Phys. Rev. Lett. 2019, 122, 156001. 10.1103/PhysRevLett.122.156001. [DOI] [PubMed] [Google Scholar]
- Koistinen O.-P.; Ásgeirsson V.; Vehtari A.; Jónsson H. Nudged Elastic Band Calculations Accelerated with Gaussian Process Regression Based on Inverse Interatomic Distances. J. Chem. Theory Comput. 2019, 15, 6738–6751. 10.1021/acs.jctc.9b00692. [DOI] [PubMed] [Google Scholar]
- Koistinen O.-P.; Ásgeirsson V.; Vehtari A.; Jónsson H. Minimum Mode Saddle Point Searches Using Gaussian Process Regression with Inverse-Distance Covariance Function. J. Chem. Theory Comput. 2020, 16, 499–509. 10.1021/acs.jctc.9b01038. [DOI] [PubMed] [Google Scholar]
- Meyer R.; Hauser A. W. Geometry optimization using Gaussian process regression in internal coordinate systems. J. Chem. Phys. 2020, 152, 084112. 10.1063/1.5144603. [DOI] [PubMed] [Google Scholar]
- Raggi G.; Fdez. Galván I.; Ritterhoff C. L.; Vacher M.; Lindh R. Restricted-Variance Molecular Geometry Optimization Based on Gradient-Enhanced Kriging. J. Chem. Theory Comput. 2020, 16, 3989–4001. 10.1021/acs.jctc.0c00257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindh R.; Bernhardsson A.; Schütz M. Force-constant weighted redundant coordinates in molecular geometry optimizations. Chem. Phys. Lett. 1999, 303, 567–575. 10.1016/S0009-2614(99)00247-X. [DOI] [Google Scholar]
- Baker J. An algorithm for the location of transition states. J. Comput. Chem. 1986, 7, 385–395. 10.1002/jcc.540070402. [DOI] [Google Scholar]
- Smidstrup S.; Pedersen A.; Stokbro K.; Jónsson H. Improved initial guess for minimum energy path calculations. J. Chem. Phys. 2014, 140, 214106. 10.1063/1.4878664. [DOI] [PubMed] [Google Scholar]
- Mills G.; Jónsson H. Quantum and thermal effects in H2 dissociative adsorption: Evaluation of free energy barriers in multidimensional quantum systems. Phys. Rev. Lett. 1994, 72, 1124–1127. 10.1103/PhysRevLett.72.1124. [DOI] [PubMed] [Google Scholar]
- Mills G.; Jónsson H.; Schenter G. K. Reversible work transition state theory: Application to dissociative adsorption of hydrogen. Surf. Sci. 1995, 324, 305–337. 10.1016/0039-6028(94)00731-4. [DOI] [Google Scholar]
- Jónsson H.; Mills G.; Jacobsen K. W.. Nudged elastic band method for finding minimum energy paths of transitions. In Classical and Quantum Dynamics in Condensed Phase Simulations; Berne B. J., Ciccotti G., Coker D. F., Eds.; World Scientific: 1998; Chapter 16, pp 385–403, 10.1142/9789812839664_0016. [DOI] [Google Scholar]
- Henkelman G.; Jónsson H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys. 2000, 113, 9978–9985. 10.1063/1.1323224. [DOI] [Google Scholar]
- Henkelman G.; Uberuaga B. P.; Jónsson H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. 10.1063/1.1329672. [DOI] [Google Scholar]
- Henkelman G.; Jónsson H. A dimer method for finding saddle points on high dimensional potential surfaces using only first derivatives. J. Chem. Phys. 1999, 111, 7010–7022. 10.1063/1.480097. [DOI] [Google Scholar]
- Olsen R. A.; Kroes G. J.; Henkelman G.; Arnaldsson A.; Jónsson H. Comparison of methods for finding saddle points without knowledge of the final states. J. Chem. Phys. 2004, 121, 9776–9792. 10.1063/1.1809574. [DOI] [PubMed] [Google Scholar]
- Heyden A.; Bell A. T.; Keil F. J. Efficient methods for finding transition states in chemical reactions: Comparison of improved dimer method and partitioned rational function optimization method. J. Chem. Phys. 2005, 123, 224101. 10.1063/1.2104507. [DOI] [PubMed] [Google Scholar]
- Kästner J.; Sherwood P. Superlinearly converging dimer method for transition state search. J. Chem. Phys. 2008, 128, 014106. 10.1063/1.2815812. [DOI] [PubMed] [Google Scholar]
- Koistinen O.-P.; Dagbjartsdóttir F. B.; Ásgeirsson V.; Vehtari A.; Jónsson H. Nudged elastic band calculations accelerated with Gaussian process regression. J. Chem. Phys. 2017, 147, 152720. 10.1063/1.4986787. [DOI] [PubMed] [Google Scholar]
- Helgaker T. Transition-state optimizations by trust-region image minimization. Chem. Phys. Lett. 1991, 182, 503–510. 10.1016/0009-2614(91)90115-P. [DOI] [Google Scholar]
- Anglada J. M.; Bofill J. M. A reduced-restricted-quasi-Newton–Raphson method for locating and optimizing energy crossing points between two potential energy surfaces. J. Comput. Chem. 1997, 18, 992–1003. . [DOI] [Google Scholar]
- De Vico L.; Olivucci M.; Lindh R. New General Tools for Constrained Geometry Optimizations. J. Chem. Theory Comput. 2005, 1, 1029–1037. 10.1021/ct0500949. [DOI] [PubMed] [Google Scholar]
- Culot P.; Dive G.; Nguyen V. H.; Ghuysen J. M. A quasi-Newton algorithm for first-order saddle-point location. Theor. Chim. Acta 1992, 82, 189–205. 10.1007/BF01113251. [DOI] [Google Scholar]
- Cerjan C. J.; Miller W. H. On finding transition states. J. Chem. Phys. 1981, 75, 2800–2806. 10.1063/1.442352. [DOI] [Google Scholar]
- del Campo J. M.; Köster A. M. A hierarchical transition state search algorithm. J. Chem. Phys. 2008, 129, 024107. 10.1063/1.2950083. [DOI] [PubMed] [Google Scholar]
- Gonzalez C.; Schlegel H. B. An improved algorithm for reaction path following. J. Chem. Phys. 1989, 90, 2154–2161. 10.1063/1.456010. [DOI] [Google Scholar]
- Huang D.; Allen T. T.; Notz W. I.; Miller R. A. Sequential kriging optimization using multiple-fidelity evaluations. Struct. Multidiscip. Optim. 2006, 32, 369–382. 10.1007/s00158-005-0587-0. [DOI] [Google Scholar]
- Bakken V.; Helgaker T. The efficient optimization of molecular geometries using redundant internal coordinates. J. Chem. Phys. 2002, 117, 9160–9174. 10.1063/1.1515483. [DOI] [Google Scholar]
- Jones D. R. A Taxonomy of Global Optimization Methods Based on Response Surfaces. J. Global Optim. 2001, 21, 345–383. 10.1023/A:1012771025575. [DOI] [Google Scholar]
- Smith C. M. How to find a saddle point. Int. J. Quantum Chem. 1990, 37, 773–783. 10.1002/qua.560370606. [DOI] [Google Scholar]
- Hirsch M.; Quapp W. Reaction Pathways and Convexity of the Potential Energy Surface: Application of Newton Trajectories. J. Math. Chem. 2004, 36, 307–340. 10.1023/B:JOMC.0000044520.03226.5f. [DOI] [Google Scholar]
- Bofill J. M.; Quapp W. The variational nature of the gentlest ascent dynamics and the relation of a variational minimum of a curve and the minimum energy path. Theor. Chem. Acc. 2016, 135, 11. 10.1007/s00214-015-1767-7. [DOI] [Google Scholar]
- Quapp W. Comment on “Analyses of bifurcation of reaction pathways on a global reaction route map: A case study of gold cluster Au5” [J. Chem. Phys. 143, 014301 (2015)]. J. Chem. Phys. 2015, 143, 177101. 10.1063/1.4935181. [DOI] [PubMed] [Google Scholar]
- Leines G. D.; Rogal J. Comparison of minimum-action and steepest-descent paths in gradient systems. Phys. Rev. E 2016, 93, 022307. 10.1103/PhysRevE.93.022307. [DOI] [PubMed] [Google Scholar]
- E W.; Ren W.; Vanden-Eijnden E. String method for the study of rare events. Phys. Rev. B: Condens. Matter Mater. Phys. 2002, 66, 052301. 10.1103/PhysRevB.66.052301. [DOI] [Google Scholar]
- Müller K.; Brown L. D. Location of saddle points and minimum energy paths by a constrained simplex optimization procedure. Theor. Chim. Acta 1979, 53, 75–93. 10.1007/BF00547608. [DOI] [Google Scholar]
- Baker J.; Chan F. The location of transition states: A comparison of Cartesian, Z-matrix, and natural internal coordinates. J. Comput. Chem. 1996, 17, 888–904. . [DOI] [Google Scholar]
- Fdez. Galván I.; Vacher M.; Alavi A.; Angeli C.; Aquilante F.; Autschbach J.; Bao J. J.; Bokarev S. I.; Bogdanov N. A.; Carlson R. K.; Chibotaru L. F.; Creutzberg J.; Dattani N.; Delcey M. G.; Dong S. S.; Dreuw A.; Freitag L.; Frutos L. M.; Gagliardi L.; Gendron F.; Giussani A.; González L.; Grell G.; Guo M.; Hoyer C. E.; Johansson M.; Keller S.; Knecht S.; Kovačević G.; Källman E.; Li Manni G.; Lundberg M.; Ma Y.; Mai S.; Malhado J. P.; Malmqvist P. Å.; Marquetand P.; Mewes S. A.; Norell J.; Olivucci M.; Oppel M.; Phung Q. M.; Pierloot K.; Plasser F.; Reiher M.; Sand A. M.; Schapiro I.; Sharma P.; Stein C. J.; Sørensen L. K.; Truhlar D. G.; Ugandi M.; Ungur L.; Valentini A.; Vancoillie S.; Veryazov V.; Weser O.; Wesołowski T. A.; Widmark P.-O.; Wouters S.; Zech A.; Zobel J. P.; Lindh R. OpenMolcas: From Source Code to Insight. J. Chem. Theory Comput. 2019, 15, 5925–5964. 10.1021/acs.jctc.9b00532. [DOI] [PubMed] [Google Scholar]
- Weigend F.; Ahlrichs R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
- Aquilante F.; Gagliardi L.; Pedersen T. B.; Lindh R. Atomic Cholesky decompositions: A route to unbiased auxiliary basis sets for density fitting approximation with tunable accuracy and efficiency. J. Chem. Phys. 2009, 130, 154107. 10.1063/1.3116784. [DOI] [PubMed] [Google Scholar]
- Bofill J. M.; Quapp W. Analysis of the Valley–Ridge inflection points through the partitioning technique of the Hessian eigenvalue equation. J. Math. Chem. 2013, 51, 1099–1115. 10.1007/s10910-012-0134-3. [DOI] [Google Scholar]
- Fdez. Galván I.; Delcey M. G.; Pedersen T. B.; Aquilante F.; Lindh R. Analytical State-Average Complete-Active-Space Self-Consistent Field Nonadiabatic Coupling Vectors: Implementation with Density-Fitted Two-Electron Integrals and Application to Conical Intersections. J. Chem. Theory Comput. 2016, 12, 3636–3653. 10.1021/acs.jctc.6b00384. [DOI] [PubMed] [Google Scholar]
- Schaftenaar G.; Noordik J. H. Molden: A pre- and post-processing program for molecular and electronic structures. J. Comput.-Aided Mol. Des. 2000, 14, 123–134. 10.1023/A:1008193805436. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.