Spectral Characterization of Mid-Infrared Bloch Surface Waves Excited on a Truncated 1D Photonic Crystal

Abstract

The many fundamental roto-vibrational resonances of chemical compounds result in strong absorption lines in the mid-infrared region (λ ∼ 2–20 μm). For this reason, mid-infrared spectroscopy plays a key role in label-free sensing, in particular, for chemical recognition, but often lacks the required sensitivity to probe small numbers of molecules. In this work, we propose a vibrational sensing scheme based on Bloch surface waves (BSWs) on 1D photonic crystals to increase the sensitivity of mid-infrared sensors. We report on the design and deposition of CaF₂/ZnS 1D photonic crystals. Moreover, we theoretically and experimentally demonstrate the possibility to sustain narrow σ-polarized BSW modes together with broader π-polarized modes in the range of 3–8 μm by means of a customized Fourier transform infrared spectroscopy setup. The multilayer stacks are deposited directly on CaF₂ prisms, reducing the number of unnecessary interfaces when exciting in the Kretschmann–Raether configuration. Finally, we compare the performance of mid-IR sensors based on surface plasmon polaritons with the BSW-based sensor. The figures of merit found for BSWs in terms of confinement of the electromagnetic field and propagation length puts them as forefrontrunners for label-free and polarization-dependent sensing devices.

The label-free chemical identification of molecular biolayers is of crucial importance for the study of the interaction among cells, for antibody testing, and for determining the binding affinity in protein–protein interactions in general.

In the visible range, one of the most widely spread label-free sensors of molecular monolayers is based on functionalized Au surfaces sustaining surface plasmon polaritons (SPPs), that is, propagating plasmons at the interface between a metal and a dielectric material.¹⁻³ SPPs provide electromagnetic fields evanescently decaying in both the metal and the dielectric half space with decay lengths of a few tens of nanometers, which results in an enhanced sensitivity to very thin molecular layers. In the mid-infrared (λ ∼ 2–20 μm, mid-IR), where vibrational absorption provides unique insights into protein orientation and conformation,⁴ the SPP approach proves to be less effective given the poor confinement that inherently comes with longer wavelengths and with metals behaving closer to perfect conductors. Proposed strategies to obtain stronger field confinement at a surface in the mid-IR range have made use of SPPs supported by doped semiconductors instead of metals⁵⁻⁸ or by non-neutral graphene,^9,10 or have exploited different hybrid polaritonic modes instead of SPPs, such as phonon polaritons in hexagonal boron nitride (hBN) and in silicon carbide (SiC).¹¹⁻¹³ Approaches alternative to surface wave sensing are based on surface-enhanced infrared absorption (SEIRA) in resonant metal nanoantennas.^14,15 Compared to surface-wave approaches, nanoantennas display higher field confinement and enhancement in the mid-IR, but have difficulties in placing the analyte in the hotspot.^16,17

Alongside with metal–dielectric interfaces and hybrid polaritonic modes, it is also possible to engineer and shape mode profiles at the nanoscale by means of either natural or artificial photonic crystals.¹⁸ Photonic crystals, which also have been mainly developed in the visible spectral range,¹⁹ are low-loss dielectric systems characterized by a periodic modulation of the refractive index along one or more spatial dimensions.²⁰ The refractive index modulation defines a lattice in which the discrete states of the electromagnetic field (modes) result from an effective periodic potential and thus present local profiles that are impossible to obtain in conventional quasi-homogeneous media.²¹ Photonic crystals can be tailored, by changing either the geometry or the refractive index contrast, to generate photonic bandgaps (PBGs), in which the propagation of specific wavelengths inside the photonic crystals along specific directions is prohibited. It has been shown that, in the PBG, photonic crystals can be described as metal-like composite metamaterials with a negative value of the real part of the effective dielectric function, a condition that enables photonic crystals sustaining surface electromagnetic waves at certain frequencies within the PBG.²²

Among all PBG structures, truncated 1D photonic crystals (1DPCs) sustain surface electromagnetic waves at the boundary with a homogeneous external medium. Such propagating surface modes, which are usually named Bloch surface waves (BSWs), are characterized by dispersion curves located within the PBG of the 1DPC, below the light line of the external medium.^20,23 These modes present an exponential decay of the field envelope both inside the 1DPC and in the homogeneous external medium (EF in Figure 1a). It is, therefore, natural to compare BSWs on dielectric 1DPCs to surface plasmon polaritons (SPP) on thin metal films, since they share the same exponential decay behavior.²⁴ BSWs have proven particularly effective for optical sensing in the visible range,^25,26 since they show lower absorption losses than their SPP counterpart. Moreover, BSWs have similar properties if compared to SPPs, also offering some advantages: (i) as for SPPs, the dispersion of BSWs can be designed at almost any wavelength by properly choosing the refractive index and thickness of the layers constituting the 1DPC;²⁷ (ii) given the lower intrinsic losses of dielectrics with respect to metals in the visible/near-infrared range, their resonances appear much narrower than those of SPPs;²⁴ (iii) by properly choosing the dielectric materials with thermo-optic coefficients compensating that of the external medium, one can reduce the effect of temperature on the sensor.²⁸ By a careful selection of the materials, the concept of truncated 1DPC can be fully translated to the mid-IR;²⁹ therefore, BSW sensors could become among the best choices for mid-IR applications.

Figure 1.

(a) Pictorial sketch of the CaF₂ prism with the 1DPC deposited on its surface (bottom surface in the figure). The electromagnetic field impinges on the photonic crystal in a total internal reflection scheme, with an incidence angle θ. Parallel (β) and perpendicular (k_x) components of the wavevector k with respect to the 1DPC interfaces are also indicated. The electric field (EF) exponentially decays into the external medium. (b) Pictorial sketch of the optical setup used to spectrally characterize BSWs: the incoming radiation is reflected by a focusing mirror (FM), narrowed by an iris (I) to produce a quasi-collimated beam, and linearly polarized by a wire-grid polarizer (P) (the two electric field components E_σ and E_π are indicated in the figure). The radiation excites the BSWs in a Kretschmann–Raether configuration (KR), and the incidence angle can be controlled remotely with the use of a rotational motorized stage (MS). Two plane mirrors (PM) are used to collect the reflected radiation that is then focused onto a MCT photovoltaic detector.

Notably, 1DPC can be designed to sustain both σ- (or s, transverse electric) and π- (or p, transverse magnetic) polarized BSWs (σ-BSW and π-BSW, respectively) in the same spectral range, while SPPs can support only π-polarized surface waves. This allows designing sensors that are capable of probing the mid-IR absorption and refractive index of biomolecules oriented along different directions, a feature of particular interest in the study of single biomolecular layers as it enables the study in real time of conformational changes in biomolecules under different external stimuli.

In this work, we report on the design, fabrication, and characterization of CaF₂/ZnS 1DPCs that were optimized to sustain both σ-BSW and π-BSW modes at wavelengths around λ₀ = 5.6 μm, close to the relevant absorption features of proteins. At variance with one previous attempt to excite BSW in the mid-IR,²⁹ our multilayer stacks were grown directly on CaF₂ prisms, allowing us to reduce the number of unnecessary interfaces when exciting in the Kretschmann–Raether configuration. Moreover, our multilayer structure has been optimized to maximize the BSW bandwidth up to the maximum value achievable for a 1DPC on a CaF₂ substrate. We thoroughly characterized the 1DPC in the mid-IR by means of Fourier-transform infrared spectroscopy (FTIR). The BSWs spectral features, and those of guided modes (GMs), were measured under total internal reflection conditions with a custom variable-incidence angle setup built into the FTIR sample compartment (see Figure 1b). Based on the experimental results, we finally discuss the performances of our 1DPCs, benchmarking them against the standard figures of merit (FOMs) used for SPPs in metals and in doped semiconductors.^30,31

Experimental Results

For the fabrication of the 1DPC sustaining BSWs in the mid-IR range, we chose CaF₂ and ZnS as the low-index and high-index materials for the stack layers, respectively. Commercial crystalline CaF₂ is among the best choices as a substrate material;^29,32 it is highly transparent up to λ = 10 μm and it has a low value of the refractive index (n ≃ 1.39 at λ₀).³³ Also, it is almost insoluble in water, and large crystals are available for shaping them into prisms. CaF₂ appears, therefore, to be the most sensible choice for the low index layers of the stack in order to have the largest possible bandgap, as already discussed in ref (29). Most notably, thermal deposition of CaF₂ results in a columnar growth,³⁴ where voids are found in the grown layers. We could thus exploit the presence of the voids to further reduce the effective index of the evaporated layers³⁵ below 1.39, yielding an even broader bandgap for our 1DPC.

As the high index material, we use ZnS (n ≃ 2.24 at λ₀)³⁶ that offers excellent transparency up to λ = 12 μm and is not soluble in water. With these two materials, we designed a 1DPC sustaining BSWs in the mid-IR with two ZnS/CaF₂ pairs and a thin ZnS surface “defect” layer on top (see the Supporting Information).

Deposition and Characterization of Materials

We deposited CaF₂ and ZnS by means of thermal evaporation³⁷ in the same high vacuum chamber. One of the main issues in the deposition of multilayers is the strain accumulation that, for large thicknesses of the deposited layers (see Figure 2a), can lead to adhesion loss and consequent delamination. In particular, we found an extremely poor adhesion between the evaporated ZnS film and the CaF₂ crystalline substrates/prisms. In order to reduce this issue, we have deposited a 20 nm thick CaF₂ adhesion layer onto the CaF₂ substrate before the deposition of the first ZnS layer.

Figure 2.

(a) SEM image of a multilayer, single layers corresponding to different materials are labeled in the figure. (b) Reflectance measurements performed with unpolarized IR radiation at near-normal incidence (9° ± 7° incidence angle) on such multilayer compared with the fitting curve obtained with a simple multilayer model (see Supporting Information for more details).

Morphological characterization of the multilayer inner structure was investigated via focus ion beam (FIB) milling followed by cross-sectional electron microscopy analysis in a dual-beam apparatus. In Figure 2a, we report the SEM image corresponding to the measured multilayer (see Methods and Supporting Information for more details). In the CaF₂ films of the multilayer section, it is possible to identify needle-like features showing dark-pixel contrast with the bright CaF₂ material. These features can be identified as voids, thus, pointing to a lamellar arrangement of the deposited material, further organized into columns oriented along the growth direction. It is possible to recognize distinct columnar regions or domains in which the interlamellar voids are stacked with similar orientation. These findings are in agreement with the AFM images showing columnar triangular arrangement of the surface features of the deposited material (see Supporting Information). As a consequence of the spatial heterogeneity of the deposited CaF₂, an effective refractive index of the film lower than the nominal value is expected. In order to verify this hypothesis, we measured the mid-IR reflectance of the 1DPC at near-normal incidence (i.e., 9° ± 7° from the 1DPC surface normal) for wavelengths ranging between 2 and 10 μm (see Figure 2b) and retrieved the refractive indices of ZnS and CaF₂ with a simplified Fresnel multilayer model, neglecting losses and assuming homogeneous materials with perfectly flat interfaces. To fit the reflectance data, we used the mean value of the layer thicknesses, as measured by electron microscopy (as indicated in Figure 2). We note that the layers show a clear corrugation mostly due to the CaF₂ growth yielding a surface roughness R_q equal to ∼30 nm for the multilayer stack (see Figures S1 and S2). Notably, we get n = 1.20 ± 0.05 and 2.20 ± 0.02 for CaF₂ and ZnS, respectively, for all the deposited multilayers (see Supporting Information). It is worth noticing that, while the refractive index found for ZnS is close to that expected for the ideal crystalline material, the index found for CaF₂ is significantly lower than 1.39. This is indeed due to the coexistence of the CaF₂ with the voids: by using Maxwell-Garnett mixing rule, it is possible to estimate the fraction of the voids around 40% of the volume, a value that can slightly vary depending on the assumptions made on the shape of the inclusions.^38,39 A similar filling fraction was found also by SEM imaging of the multilayers cross-section (see Supporting Information).

One-Dimensional Photonic Crystal Design

The final 1DPC geometry was designed and optimized to sustain σ-BSW modes at λ₀, starting from the experimental values found for the real part of the refractive indices of the CaF₂ and ZnS layers. As far as concerns the imaginary part of the refractive indices, we assumed 10^–4 and 10^–6 for CaF₂ and ZnS, respectively. The periodic 1DPC defines the photonic properties of the multilayer, whereas the additional top “defect” layer is used to fine-tune the BSW dispersion. The 1DPC was tailored to sustain BSWs in the wavelength range between 3.3 μm (3000 cm^–1) and 8 μm (1250 cm^–1) when the external medium is vacuum. In Figure 1a, a sketch of the CaF₂ prism with the 1DPC and the reference system used for the simulations is shown. Light in the prism propagates with a wavevector k that can be decomposed into its parallel (β) and perpendicular (k_x) components with respect to the 1DPC interfaces.

The design maximizes the resonant BSW field at the 1DPC/external medium interface and the BSW bandwidth, covering the entire range from 3.3 to 8 μm, for the σ polarization, by optimizing the layer thicknesses d_ZnS, d_CaF2, and the defect cap layer thickness d_ZnS,CL (see Figure 2 and Methods). Moreover, the 1DPC can also sustain a π-polarized BSW.

Figure 3a,b shows the square modulus of the electric and of the magnetic field inside the 1DPC structure when the σ-polarized BSW (a) and the π-polarized (b) BSW are excited in the Kretschmann–Raether configuration (in the inset of Figure 3, the σ and the π component of the electric field are highlighted). They are excited at λ_BSW^σ = λ₀ = 5.6 μm and at λ_BSW = 4.47 μm at the respective resonant angles, θ_BSW^σ = 55.13° and θ_BSW = 52.41°. In addition, from the inverse of the imaginary part of the perpendicular component of the BSW wavevector, we retrieve the penetration distance of the electric field into the external medium, which we found equal to l_d^σ ≃ 810 nm and l_d ≃ 690 nm, an improvement of about 1 order of magnitude compared with SPPs supported by noble metals in the mid-IR, whose evanescent tails extend by several micrometers. Finally, we evaluate the field enhancement (fe) as the ratio between the electromagnetic field intensity in the external medium with (|E_surf^σ|² or |H_surf|²) and without (|E₀|² or |H₀|²) the 1DPC in total internal reflection conditions. From the plots in Figure 3a,b, we find fe^σ ∼ 90 and fe^π ∼ 1.5 for σ- and π-polarization, respectively.

Figure 3.

Square modulus of the electric field (a) and of the magnetic field (b) along the direction x perpendicular to the surface, when a σ- and a π-polarized BSW is excited at λ_BSW^σ = λ₀ = 5.6 μm and λ_BSW = 4.47 μm, respectively. In the two panels, the refractive index profile of the 1D photonic crystal is also reported (dashed red lines). σ (c) and π (d) photonic band structure (PBS) for the 1DPC used into our experiments. The plots show only the portion of PBS included between the air and the CaF₂ prism light lines (blue and red solid lines, respectively). The permitted photonic bands are gray filled, whereas the white area indicates the forbidden bands where the BSWs can be excited. The BSW (orange) and the GMs (green) theoretical (solid lines) and experimental (points) dispersions are reported. The dotted horizontal line highlights λ₀. The red area in the PBS plots is the (β,ω) window accessed in the measurements in this work. The inset schematically shows the σ and π electric field directions.

In Figure 3c,d, we plot the photonic band structure (PBS, more details are provided in the Methods section) in the (β̃,ω̃) plane, where we use the 1DPC periodicity Λ = 3.20 μm to define 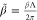as the normalized parallel component of the wavevector (as defined in Figure 1a) and ω̃ = Λ/λ as the normalized angular frequency. The PBSs were calculated for an infinite 1DPC with d_ZnS and d_CaF2 averaged between the two values of thickness of the fabricated structure reported in Figure 2a. Such diagrams are invariant with respect to the periodicity Λ = d_ZnS + d_CaF2, provided the ratio d_ZnS/d_CaF2 is kept constant. In Figure 3c,d, we report only the portion of PBS included between the air light line (blue) and the CaF₂ light line (red). This portion of the (β̃,ω̃) plane is the only region of the dispersion plot where the BSWs can be excited. The black solid lines fix the edge of the PBS and the permitted bands are gray filled. The white area represents the PBG in which the electromagnetic radiation does not propagate neither inside the 1DPC nor in the external medium. BSW and GMs dispersion curves are also plotted in the diagrams, showing that the BSW dispersions for both polarizations lay within the first PBG of the 1DPC. The corresponding normalized angular frequency at the chosen λ₀ is marked with a horizontal dotted line.

Broadband Infrared Study of BSWs and Guided Modes and Comparison with Simulations

A custom optical setup has been built to measure the mid-IR spectra of our 1DPCs excited in the Kretschmann–Raether configuration (Figure 1). The linearly polarized IR input beam (either σ- or π-polarized) passes through an iris with a diameter of 1.5 mm, in order to readily produce a quasi-collimated beam with diameter smaller than the size of the prism facet. The reflected signal is collected by plane (PM) and focusing mirrors (FM), and the reflection from a clean CaF₂ prism is used as a reference. Measurements were performed in the wavelength range between 1.6 and 10 μm, for all the accessible incidence angles θ and for both σ and π electric field polarizations. A selection of the collected reflectance curves is reported in Figure 4a.

Figure 4.

(a) FTIR reflectance in Kretschmann-Raether configuration between 1300 and 5500 cm^–1 for three representative incidence angles. Data below 1300 cm^–1 are not shown due to the absorption of the tail of the strong phonon mode of the CaF₂ prism substrate. Data measured in π-polarization are shifted vertically for sake of clarity. Absorption dips related to BSWs are highlighted in blue, while those related to GMs in violet. Asterisks mark the absorption peaks due to impurities within the CaF₂ layers and on the sample surface. (b, c) Close-up of frequency shifts for σ-BSWs and π-BSWs for several incidence angles, as indicated in the figure. Selected absorption peaks are indicated with narrow arrows, so to identify their center frequency, the broad arrow highlights the spectral shift in the resonances as a function of increasing the incidence angle of the incoming light.

In Figure 4b, for the σ-polarized spectra, we observe a narrow reflectance dip red-shifting in frequency between ν = 1500 and 2000 cm^–1 as θ is decreased. We ascribe this spectral feature to the σ polarized BSW whose depth and width result from the combined effect of radiation losses, related to the 1DPC number of periods, and absorption losses in the 1DPC.⁴⁰ Around ν = 3000 cm^–1 we observe further reflectance dips superimposed to the vibrational absorption of C–H stretching lines typical of organic compounds accidentally present on the 1DPC surface and in the CaF₂ voids. Around 5000 cm^–1, a third broader and less intense dip is observed. As before, by decreasing θ, we observe a red-shift of the dip frequencies. We assign the dips around ν = 3000 cm^–1 and 5000 cm^–1 to a pair of distinct GMs sustained by the 1DPC (defined as GM1 and GM2, respectively). Note that the field of the GM modes is mostly confined inside the 1DPC and not at its surface, so they are of marginal interest for sensing applications.

The reflection spectra for π-polarized radiation in Figure 4a also show dips in their profiles. Contrary to the σ case, due to the poor mode confinement, very broad dips are observed. They are assigned to the π-BSW, whose frequency range is indeed calculated between ν = 2000 and 3000 cm^–1 for the probed θ range. Again, the dip red-shifts with decreasing θ (Figure 4c). We note that, for large enough θ, the BSW partly overlaps with the C–H absorption peaks. Hence, the BSW dip appears deeper due to the local increase of the material losses introduced by the C–H bonds present inside the dielectric stack. Therefore, the effective center frequency of the BSW resonance dip is partially masked by the C–H absorption peaks. Finally, in Figure 4a, between ν = 3500 and 4500 cm^–1 and between ν = 5000 and 5700 cm^–1, we observed two additional series of reflectance dips that we associate to π-polarized GMs.

Noticeably, the measure of the π-polarized reflectance also allows us to identify several sharp absorption peaks below 1600 cm^–1 that we assign to impurities within the multilayer structure (in particular, separate analysis of the FTIR transmittance of CaF₂ and ZnS monolayers reveals that the absorption takes place in the nominally pure CaF₂ layers that indeed contain oxide impurities). The absorption peaks due to impurities are almost negligible with σ polarization, thanks to the different distribution of the electric field in the 1DPC, that is more confined on the surface. Indeed, the σ-BSW modes in Figure 4a are found to be extremely robust against the presence of impurities within the layers and also against the interface roughness.

In Figure 5a,b, we perform a direct comparison of our experimental results (red map) with the numerical model (blue map). While for the σ-BSW mode a single Lorentzian peak captures the correct line shape, multiple Lorentzian peaks are used to extract the center frequency of π-BSW modes and GMs. The angular positions of the BSWs and of the GMs are reported as dots, demonstrating an excellent agreement in terms of slope of the curves. The small discrepancy of about 1.5° in the absolute value of the incidence angle stems from both an uncertainty in the definition of the normal incidence angle on the prism facet (∼0.5°) and from the error in the evaluation of the material refractive indices used for modeling. The latter error can be ascribed to the errors in the measurement of the absolute reflectance of our multilayer, and on the used simple Fresnel fitting model that does not account for the incidence angle nor for the distribution of incidence angles of the light focused on the multilayer surface. The (θ,λ) coordinates are also converted into (β̃,ω̃) coordinates and data points are placed into the PBS of Figure 3c,d. The BSWs and the GMs are reported by orange and green dots, respectively. A summary of the comparison between the theoretical and the experimental results is reported in Table 1 for θ = 55.7°.

Figure 5.

Experimental dispersion of BSWs (black dots) and GMs (blue dots) for both σ (a) and π (b) polarizations with the respective error bars obtained via a Lorentz fitting of the spectra in Figure 4. The simulated reflectivity map is superimposed in blue while the red map in (a) is the experimental reflectivity of the 1DPC.

Table 1. Summary of the Theoretical and of the Experimental Center Energy for the 1DPC Modes Obtained for θ = 55.7°.

		theo (cm–1/μm)	exp (cm–1/μm)
σ	BSW	1830/5.45	1730/5.77
	GM1	3130/3.20	2970/3.37
	GM2	5650/1.77	5260/1.90
π	BSW	2810/3.56	2550/3.92
	GM1	4170/2.40	3650/2.74
	GM2	5750/1.74	5240/1.91

The aim of introducing a high-index cap layer is to optimize the BSW mode position as close as possible to the PBG center (therefore the cap layer is also called a “defect” layer in analogy with in-gap defect states in real crystals), which can be achieved by properly tuning its thickness. Considering the BSW dispersions, we can calculate the BSW mode position in the PBG at λ₀ through the following relation:

1

where ω̃_dw and ω̃_up are the lower and upper normalized frequency edges of the PBG for the given normalized wavevector k̃_BSW, respectively. We obtain a BSW mode position in the PBG, %ω_σ, equal to 55.6% (the center being %ω = 50.0%) for a bandwidth (ω̃_up – ω̃_dw) of 0.223 (corresponding to a PBG equal to Δλ = 2.4 μm if considered in wavelengths) for the σ polarization. This ensures a strong mode localization at the truncation interface, that is, a narrower resonance,⁴¹ as demonstrated by the experiments. On the contrary, for the π polarization, a BSW is observed at λ = 4.47 μm for θ = 54.3°. Here, a BSW mode position %ω_π equal to 91.2%, very close to the upper band edge, and a bandwidth of 0.093 (Δλ = 0.65 μm), are obtained. This explains the low localization of the surface mode and the very broad experimental absorption peak when the π-BSW is excited. The σ-BSW is much more localized at the interface, which accounts for the higher fe^σ factor, whereas the π-BSW extends into the substrate, justifying the very low fe^π factor (Figure 3b). Both BSW modes are leaky into the substrate but with a coupling coefficient that is smaller for the σ polarization. Such a coupling coefficient corresponds to radiation losses of the surface wave’s energy.⁴² Certainly, the 1DPC structure can be optimized for π-BSW, while achievement of simultaneous optimization of both σ- and π-BSW⁴³ is yet to be demonstrated in the mid-IR.

Evaluation of BSWs against SPPs and PhPs

As the last step, we take advantage of a recently proposed analysis tool^30,31 to assess the trade-off between losses and field confinement in surface waves. We apply this approach to benchmark BSWs against SPPs (in both Au and heavily doped semiconductors, with different carrier concentrations and effective masses^8,44,45) and other polaritonic excitations such as phonon polaritons in SiC.^12,46 In the following discussion, the comparison among the different surface modes is made for the σ-BSWs.

In order to extract the proposed figures of merit for confinement and propagation for our BSWs, we evaluate the nominal propagation length of the surface modes, l_m, by the following relation:⁴⁷

2

where Δθ is the angular full width at half-maximum (fwhm) of the BSW dip and n_p is the prism refractive index. As suggested by Dastmalchi et al.,³⁰ we can evaluate the figure of merit for the field propagation as

3

and the figure of merit for the field confinement as

4

where l_d is determined by the exponential decay of the fields outside the 1DPC, which is highlighted in Figure 3a. We calculated the figures of merit for the BSWs excited on our fabricated 1DPC at several different target wavelengths. Hence, we compared them to those obtained (at 6 μm) for the SPPs sustained by a noble metal (Au) and a doped Ge semiconductor with plasma wavelength around 5.6 μm.³¹ More recently, also hybrid polaritonic modes such as phonon polaritons have attracted attention, and a sensing scheme was also proposed.¹¹ These excitations, sustained by strongly polar materials within their Reststrahlen bands, show indeed remarkably high propagation lengths and low losses in the mid-IR region but present obviously poor frequency tuning. For this reason, the figures of merit of the material of choice for this benchmarking (SiC) are calculated at a wavelength of 11.1 μm,⁴⁶ within the narrow spectral range in which it sustains phonon polaritons.

The analysis confirms that 1DPCs represent an excellent alternative to all the other materials currently under consideration in the mid-IR. Indeed, BSWs outperform the extreme confinement properties of nonmetal polaritonic systems, such as doped semiconductors below the plasma frequency and polar materials within their Reststrahlen bands, and combine it with the advantage of a large spectral tunability. Moreover, they display longer propagation lengths with respect to SPPs in doped semiconductors, even if they are still shorter than SPPs in metals. However, we recall that the quasi-perfect conductor behavior of metals in this spectral range prevents their actual use for surface wave sensing, as shown by the extremely poor FOM_conf in Figure 6.

Figure 6.

Figure of merit FOM_conf for the confinement of the evanescent field in the external medium plotted versus the figure of merit FOM_prop for the propagation length. Data for SPPs, relative to a noble metal or a doped semiconductor (ref (44)) and phonon polaritons (ref (45)), are reported for a single wavelength. Data for σ-BSWs are instead shown for a broader energy range (color code bar on the side).

Conclusion

We have shown that it is possible to grow 1DPCs that sustain both σ- and π-polarized BSWs in the mid-IR directly on CaF₂ prisms. By leveraging the columnar growth of CaF₂ deposited thermally, we obtain a very low effective refractive index of CaF₂ layers of about 1.2, allowing for an increase of the bandwidth with respect to what expected with tabulated values of crystalline materials for the mid-IR. We have spectrally characterized our mid-IR 1DPCs, finding them extremely robust against geometrical imperfections such as interface roughness. Clear signatures of σ- and π-polarized BSWs have been identified in the spectra and a surface field enhancement of 90 has been calculated for σ-BSWs. We have quantitatively benchmarked the BSWs in the mid-IR against surface plasmon polaritons and phonon polaritons in similar frequency ranges. The outstanding figures of merit found for BSWs in terms of both confinement of the electromagnetic field and propagation lengths put them as forefrontrunners for label-free polarization-dependent sensing devices.

Methods

Sample Preparation

Custom-designed CaF₂ prisms (quoted in Figure 1a), with the basis angle equal to 55°, were bought from Korth Kristalle. The thermal evaporation was performed in a high-vacuum chamber, with limiting pressure of 5 × 10^–7 Torr, equipped with two evaporation sources and a shutter. CaF₂ and ZnS layers are deposited without breaking the vacuum from granulate materials (UMICORE, purity 99.99%) using molybdenum boats. The samples were characterized by atomic force microscopy (AFM), dual-beam focus ion beam (FIB) milling cross sectional analysis, scanning electron microscopy (SEM), and near-normal incidence reflectance. The multilayers were deposited on CaF₂ prisms and on additional flat CaF₂ substrates placed close-by in the vacuum chamber to be used for characterization and tests.

Numerical Methods

Design and numerical simulations were carried out by means of the transfer matrix method (TMM) implemented by a custom-made MATLAB code.⁴⁰ The numerical simulations refer to the same Kretschmann–Raether configuration used to experimentally excite the BSW of the 1DPC (Figure 1a). It is well-known that BSW can be excited only in a total internal reflection configuration from the substrate side, which must provide a refractive index larger than that of the external medium.²⁰ Our procedure provides the optimal thicknesses of the layers of the stack: d_ZnS = 950 (±100) nm, d_CaF2 = 2250 (±150) nm, and d_ZnS,CL = 190 (±40) nm; the values in the brackets mark the BSW existence conditions. The thicknesses measured by SEM (Figure 2a) reported above appear in the range of existence of the BSW provided by simulations. Numerical simulations were then performed again with the exact deposited thicknesses. For sake of simplicity all numerical results reported in the paper are obtained for the deposited 1DPC.

The PBS for the σ- and π-polarization are calculated through an iterative plane wave Eigen–Solver method implemented by the MPB free open source code distributed through GNU General Public License by MIT.⁴⁸ The PBSs are calculated for an infinite 1DPC with d_ZnS and d_CaF2 averaged between the two thickness values for the fabricated structure reported in Figure 2.

FTIR Measurements

Infrared measurements were carried out in a Bruker Vertex 70v interferometer. A globar source was used in conjunction with a broadband beamsplitter and a N₂-cooled MCT detector from Infrared Associates Inc. The interferometer was operated in low vacuum to eliminate IR absorption from the atmospheric water vapor and CO₂. Both the polarizer and the rotational stage in Figure 1 were remotely controlled, in order to perform several measurements without the need of breaking the vacuum in the interferometer. The prism alignment was performed by backtracing the reflected beam to the aperture wheel of the interferometer with the light beam impinging at normal incidence on the lateral facet of the prism. This condition guarantees an initial incidence angle θ equal to the prism cut angle of 55.00°. The motorized rotational stage employed to vary the incidence angle during the experiment has a precision of 0.25°.

Glossary

Abbreviations

SEIRA

surface enhanced infrared absorption

FTIR

Fourier transform infrared spectroscopy

AFM

atomic force microscopy

SEM

scanning electron microscopy

FIB

focused ion beam

1DPC

1D photonic crystal

BSW

Bloch surface wave

PBS

photonic band structure

PBG

photonic band gap

GMs

guided modes

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsphotonics.0c01657.

• 1DPC fabrication and materials characterization; 1DPC design optimization: numerical methods details; FoM calculation (PDF)

Author Contributions

^# These authors contributed equally (A.O., M.P., and R.P.). The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The research leading to these results has received funding from the Italian Ministry of Education, University, and Research (MIUR), PRIN project “Plasmon-enhanced vibrational circular dichroism”, ID 2015FSHNCB. F.M., M.O., A.O., A.S., R.P., and L.B. acknowledge funding from Sapienza University through H2020Project Program. A.O, F.M, and A.S. acknowledge funding from Regione Lazio (Italy; ID 85–2017–14945, “TurnOff”) and from the Italian MIUR Ministry (ID ARS01_00769, “NeoN”). R.P. acknowledges support from the Ph.D. program Modelli Matematici per l’Ingegneria, l’Elettromagnetismo e Nanoscienze of Sapienza, University of Rome, Italy.

The authors declare no competing financial interest.