Midline Shift vs. Mid-Surface Shift: Correlation with Outcome of Traumatic Brain Injuries

Abstract

Traumatic brain injury (TBI) is a major health and socioeconomic problem globally that is associated with a high level of mortality. Early and accurate diagnosis and prognosis of TBI is important in patient management and preventing any secondary injuries. Computer tomography (CT) imaging assists physicians in diagnosing injury and guiding treatment. One of the clinical parameters extracted from CT images is midline shift, a measure of linear displacement in brain structure, which is correlated with TBI patient outcomes. However, only a tiny fraction of the overall tissue displacement is quantified through this parameter. In this paper, a novel measurement of overall mid-surface shift is proposed that quantifies the total volume of brain tissue shifted across the midline. When compared to traditional midline shift, mid-surface shift has a stronger correlation with TBI patient outcomes.

I. Introduction

Traumatic Brain Injury (TBI) is a major cause of death and disability, with an estimated sixty-nine million individuals worldwide diagnosed with TBI each year [1]. Computed tomography (CT) imaging is the gold standard method to rapidly diagnose traumatic brain injury and guide initial management decisions in the “golden hours” of treatment. Emergent treatment decisions are typically based on the combination of clinical status, concisely summarized by the Glasgow Coma Scale (GCS), and CT scan information. For example, it is recommended that intracranial pressure (ICP) monitors be placed in TBI patients with an abnormal head CT and GCS of 8 or less [2]. Concurrent decisions regarding the urgent medical management of elevated intracranial pressure and the need for craniotomy or craniectomy similarly depend on CT scan data. In recognition of this reality, current guidelines for the pre-hospital management of TBI call for emergency medical providers to screen for TBI by assessing the GCS, along with pupillary size and reactivity, and to rapidly transport individuals with suspected severe TBI to the nearest facility with an immediately available CT scanner [3].

Outcome prediction for TBI patients is of importance for planning rehabilitation goals, providing informed expectations to relatives, and evaluation of treatment effectiveness [4], [5]. It has been shown that midline shift (MLS) is strongly associated with outcome in moderate and severe traumatic brain injury [6]. MLS, the maximum amount of horizontal brain shift, is correlated with increased ICP, and it is one of the parameters clinicians use to estimate the severity of TBI. As it signifies tissue compression and risk of herniation, the presence of MLS is widely used in clinical decisionmaking and CT severity rating scales, such as the Marshall and Rotterdam scores [7]. However, clinicians typically measure MLS at a single arbitrary level, most typically at the narrow boundary between the two lateral ventricles, known as the septum pellucidum. By measuring MLS in just a single slice, only a tiny fraction of the overall tissue displacement is quantified. Furthermore, MLS measurements are subject to inherent inaccuracy on account of head rotation in the CT scanner.

The goal of this study is to develop a novel measurement of mid-surface shift (MSS), and calculate its correlation with TBI patient outcomes. Section II describes how the MLS and MSS are measured and provides a review of state-of-the-art methods for measuring MLS. In Section III, the results of several statistical analyses comparing MLS and MSS in terms of their correlations with different TBI patient outcomes are described. Section IV compares MLS and MSS by applying logistic regression on patient clinical and demographic information and finally we provide concluding remarks in Section V.

II. Midline and Mid-surface shifts

Physicians typically determine MLS by measuring the distance between the ideal midline, identified by the attachment of the falx cerebri to the skull, and to an arbitrary point that corresponds to the actual midline (i.e., a line that lies between the left and right lateral ventricles or through the third ventricle). Usually the thin band of tissue that separates the lateral ventricles, called the septum pellucidum (SP), is used for this purpose. This manual measurement of MLS is prone to human error as well as inherent inaccuracies created by rotation of the head in the coronal plane. To make the process of calculating the MLS automated, a number of methods have been proposed that detect the linear displacement of MLS using CT images. State-of-the-art methods for detecting MLS are described below.

A. Automated Midline Shift (MLS) Detection

Liao et al. [8] classified MLS algorithms to symmetry-based methods and landmark-based models. In the symmetry-based algorithms such as [9], a curve that connects all deformed and displaced structures is calculated, with MLS determined by the position of the central control point after detecting the deformed midline. The landmark-based methods such as [10], [11] often use lateral ventricles as one of the landmarks to calculate the amount of shift. Hooshmand et al. [10] developed landmark-based methods to measure the MLS. The method proposed in [10] first selects CT slices using Digital Imaging and Communications in Medicine (DICOM) metadata such as image type and window center. To compute MLS, the algorithm first detects the ideal midline using anatomic features of the skull, after which the actual midline is determined by analyzing ventricle placement detected through segmentation, with MLS ultimately calculated as the mean distance between the ideal and actual midlines on all selected CT slices.

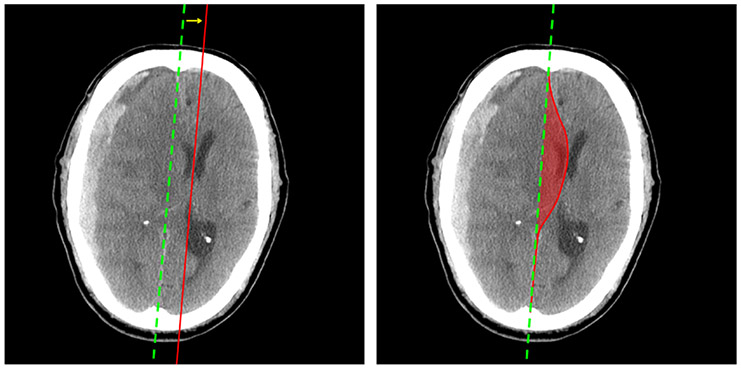
A limitation of these aforementioned methods is that by quantifying MLS as a linear displacement, other potentially clinically relevant information related to the brain injury, such as location, shape, and volume of the brain shift, are ignored. Figure 1 provides a comparison of MLS (left image) and MSS (right image) measurements in a patient CT image. As shown in the right figure, the area between the ideal midline and the deformed line can be calculated in each slice, from which the MSS can be measured.

Fig. 1:

Examples of MLS and MSS on one CT image. In each image, the green (dotted) line is the ideal midline (i.e. brain midline without an injury). In the left image, the red line is the actual midline. In the right image, the voxels enclosed by the ideal midline and the annotated curve contribute to the MSS.

B. Mid-Surface Shift (MSS) Measurement

MSS is a proposed volumetric measurement to evaluate the deformation of brain structure. Determining the mid-surface and measuring its shift can potentially provide more accurate information about the effects of TBI. Here, MSS is defined as the ratio between the mid-surface volume and the brain volume as calculated from selected CT slices. To ensure consistency across patients, an automated CT image series and slice selection method was developed.

1). Automated Series Selection:

Each patient can have multiple series of CT scans within a DICOM file, which may include bone and scout images that are unsuitable for analysis. The series is selected based on the following criteria using metadata tags embedded in the DICOM file:

• the series should contain only axial images;

• the default window level should be between 25 Hounsfield unit (HU) and 100 HU; and

• slice thickness should be the closest to 5 mm.

2). Automated Brain Mask Segmentation:

The skull is segmented and removed from the CT images as it is only necessary to compute the brain area on each slice in order to estimate brain volume. As the skull might be fractured and therefore not a closed surface, 3D Chan-Vese segmentation [12] is used on the contrast-adjusted CT images to account for these issues. The active contour algorithm iteratively evolves the boundary of initial segmentation by minimizing an energy function based on intensity and contour smoothness. To segment the brain mask, normalized CT images are replicated and stacked according to the ratio of the slice thickness to pixel spacing, in order to account for vertical spacing. The active contour algorithm is initialized with the largest component of the pixel-wise exclusive or (XOR) between skull and non-zero regions of the CT image. After performing active contour, the duplicated slices are combined using the center slice.

3). Slice Selection:

Slices in a series are selected by filtering out those with brain area smaller than 90% of the slice with the maximum area. Slices that are disconnected from the longest consecutive slices are excluded.

4). Manual Annotation:

The mid-surface was annotated manually using biomarkers in the brain. Annotation starts at the center of the anterior of each slice, and follows the falx cerebri and the middle of the ventricle. Once the posterior of the brain is reached, the annotations are again guided by the falx cerebri. To calculate the volume of shift, the ideal midline is first identified as the line formed by the intersections of the annotated mid-surface curve and the inner edge of the skull. Finally, the ratio between the volume of shift and brain volume is calculated. Let A_enclosed,i be the number of voxels enclosed by the annotated mid-surface and the ideal midline on the i^th slice, and A_brain,i be the brain mask area on the i^th slice. Let m and n be the first and last selected slices as described in section II-B3, respectively, then the MSS is

$$\text{MSS}=\frac{{\sum }_{i=n}^m{A}_{\text{enclosed},i}}{{\sum }_{i=n}^m{A}_{\text{brain},i}}.$$ (1)

III. Statistical Analysis

In the following series of experiments, three methods for measuring a shift in brain structure are compared with respect to TBI patient outcomes: MLS as calculated by a physician via manual annotation (“MLS by annotation”), MLS as calculated using the algorithm of Hooshmand et al. [10] as described in Section II (“MLS by algorithm”), and MSS as calculated by a physician via manual annotation (“MSS by annotation”).

A. Patient Characteristics

A previously described database [13] of consecutive patients with subdural hematoma who were admitted to the Michigan Medicine neurological ICU at some point during their primary hospitalization was used in this study. Patient characteristics of the cohort are described in Table I. Glasgow Coma Score (GCS) on admission showed that the majority of patients were classified as mild TBI (GCS 13-15). MLS was measured manually at the level of the septum pellucidum by a single study author (Craig Williamson). Based on these measurements, 19 (40 percent) patients had a MLS of at least 5 mm.

TABLE I:

Patient characteristics

Characteristics	Values, No.(%) or mean (SD) N = 48
Age, years	70.3 (13.7)
Male	27 (56%)
GCS on admission	13.8 (2.6)
Mild (GCS 13-15)	42 (88%)
Moderate (GCS 9-12)	2 (4%)
Severe (GCS 3-8)	4 (8%)
Charlson Comorbidity Index	2.2 (2.0)
Hematoma width, mm	13.0 (6.3)
MLS, mm	4.8 (4.8)
≥ 5 mm	19 (40%)
< 5 mm	29 (60%)

B. Correlation with Outcome at Discharge

The Glasgow Outcome Score (GOS) is widely accepted as a standard method for describing the disability or recovery outcome in TBI patients. GOS categorizes patients into five groups. A higher score indicates a better outcome for the TBI patient. A brief description of each GOS rating is shown in Table II. Using these definitions, the dataset contains 25 patients with a favorable outcome and 23 with an unfavorable outcome.

TABLE II:

Glasgow Outcome Score (GOS)

GOS	Description	Classification
1	Death	Unfavorable
2	Persistent vegetative state	Unfavorable
3	Severe disability	Unfavorable
4	Moderate disability	Favorable
5	Low disability	Favorable

The Kendall’s tau correlation coefficient (τ) was calculated between each measurement and 5 GOS groups. Since a larger number of MLS or MSS indicates a more severe TBI case, a negative correlation between the MLS/MSS and the GOS is expected. These coefficients and their 95% confidence intervals (CI) are shown in Table III. As expected, a negative correlation between each measurement and the ordered GOS outcome was observed. The proposed MSS annotation not only shows the strongest correlation with the GOS rating at hospital discharge but is also significant at level of 0.05. It should be mentioned that neither MLS by algorithm nor MLS by physician’s manual annotation has significant correlation with outcome.

TABLE III:

Correlation between each measurement and the five GOS groups

Measurement	τ	95% CI
MLS by annotation	−0.14	[−0.341, 0.067]
MLS by algorithm	−0.17	[−0.346, 0.013]
MSS by annotation	−0.26	[−0.445, −0.073]

The point-biserial correlation coefficient (r_pb) was calculated to examine the correlation between each measurement and the dichotomized GOS outcome (favorable versus unfavorable). The correlation coefficients and 95% CI are shown in Table IV. The MLS measurement by annotation shows less correlation with the outcome.

TABLE IV:

Correlation between each measurement and dichotomized GOS groups

Measurement	rpb	95% CI
MLS by annotation	−0.24	[−0.488, 0.051]
MLS by algorithm	−0.32	[−0.555, −0.042]
MSS by annotation	−0.31	[−0.542, −0.023]

In TBI severity rating scales, 5 mm is a typical threshold for assessing severity of MLS. According to neurosurgical guidelines, a MLS greater than 5 mm is an indication for the evacuation of an acute subdural hematoma [14]. It is hypothesized that there is an appropriate threshold for the proposed MSS, which will potentially help with clinical decision making. Hence, potential thresholds were explored, with Fisher’s exact test being used to examine the association between dichotomized MSS and its correlation with dichotomized GOS groups. The MSS threshold used, the odds ratio, and p-values obtained from Fisher’s exact tests are shown in Table V. Given the MSS range (0.007-0.087 percent) in the dataset, a sequence of thresholds ranging from 0.01 to 0.08, in 0.01 increments, were evaluated. The only significant result was at a threshold of 0.02, corresponding to 2% of the brain volume. In this experiment, 26 patients with MSS greater than 0.02 were identified, with 22 patients having an MSS less than 0.02. An odds ratio less than 1 indicates that patients with MSS greater than the threshold are less likely to have a favorable outcome. However, the association between the dichotomized MSS and the outcome may not be significant. The significance level using p-values are shown in Table V. The odds of patients with MSS greater than or equal to 0.02 having a favorable outcome is 0.30 times of that of patients with MSS less than 0.02. In other words, patients with MSS greater than or equal to 0.02 have significantly higher odds of having an unfavorable outcome compared to those with MSS less than 0.02.

TABLE V:

Fisher’s exact test between dichotomized MSS using different thresholds and dichotomized GOS groups (1-3 versus 4-5) using all subjects

MSS threshold (≥)	Odds ratio	p-value
0.01	0.39	0.29
0.02	0.30	0.05*
0.03	0.33	0.12
0.04	0.21	0.07
0.05	0.59	0.66
0.06	0.28	0.34
0.07	0	0.48
0.08	0	0.48

The odds ratios and p-values of the Fisher’s exact tests are shown in Table VI. We used 0.02 as the threshold to dichotomize MSS values and assumed that 5 mm is the best threshold to dichotomize MLS values. 19 patients had MLS ≥ 5 mm according to the manual annotation, but 17 patients with MLS ≥ 5 mm were identified using the automated MLS algorithm. The odds ratios of the three measurements show the same trend. Patients with MLS/MSS measured above the threshold are less likely to have a favorable outcome. The MSS annotation is the only measurement among the three to have a significant association with favorable/unfavorable outcome. It is noteworthy that the threshold on MSS (0.02) is calculated and so optimized based on all samples used to generate odd ratio for MSS in table VI.

TABLE VI:

Fisher’s exact test between dichotomized measurement and dichotomized GOS (1-3 versus 4-5)

Measurement	Odds ratio	p-value
MLS by annotation	0.36	0.14
MLS by algorithm	0.35	0.13
MSS by annotation	0.30	0.05*

IV. Logistic Regression Analysis

Age and Glasgow Coma Scale (GCS) on admission are known to be accurate and important predictors of TBI outcome [15]. In this analysis, logistic regression was performed using age and GcS on admission, plus each of the three non-dichotomized values, respectively. 14 (30%) patients were held out as a test set. For the remaining 34 patients in the training set, three-fold cross-validation was performed. The performance of each logistic regression model on test set is shown in below Table VII.

TABLE VII:

Logistic regression performance on the test set

Model	Sens.	Spec.	AUC	Acc.	Prec.	F1
+ MLS by annotation	0.71	0.57	0.65	0.64	0.63	0.67
+ MLS by algorithm	0.86	0.43	0.69	0.64	0.60	0.71
+ MSS by annotation	0.86	0.71	0.71	0.79	0.75	0.80

The model using the MSS annotation has the best sensitivity, specificity, AUC, accuracy, precision and F1 score.

V. Conclusion

In this paper, two brain structure shift measurements related to TBI were discussed: midline shift (MLS) and mid-surface shift (MSS). Two methods were used to calculate MLS - manual annotation by a physician and automated MLS measurement. CT images in our dataset were manually annotated for MSS and correlation analysis between each measurement and patient outcomes (as measured by GOS) was performed. MSS correlation with patient outcomes was consistently stronger than the MLS manual annotation, irrespective of whether the outcomes were dichotomized into favorable/unfavorable. Compard to automated MLS, MSS correlation was stronger with respect to non-dichotomized outcomes and was comparable when outcomes were dichotomized. A key observation is that only MSS correlation was found to be significant in both cases. Consequently, MSS has a stronger correlation with TBI patient outcomes as compared to MLS. In addition, a significant and promising threshold for MSS measurement was determined (.02) that may assist in clinical decision making in the future.

Based on this work, we propose that MSS is a new and more significant measurement of brain structure shift. However, more data from different centers are required to further validate the results.