Scalable generalized linear mixed model for region-based association tests in large biobanks and cohorts

Abstract

With very large sample sizes, biobanks provide an exciting opportunity to identify genetic components of complex traits. To analyze rare variants, region-based multiple variant aggregate tests are commonly used to increase power for association tests. However, due to the substantial computation cost, existing region-based tests cannot analyze hundreds of thousands of samples while accounting for confounders, such as population stratification and sample relatedness. Here we propose a scalable generalized mixed model region-based association test, SAIGE-GENE, which is applicable to exome-wide and genome-wide region-based analysis for hundreds of thousands of samples and can account for unbalanced case-control ratios for binary traits. Through the extensive simulation studies and analysis of the HUNT study with 69,716 Norwegian samples and the UK Biobank data with 408,910 White British samples, we show that SAIGE-GENE can efficiently analyze large sample data (N > 400,000) with type I error rates well controlled.

Introduction

In recent years, large cohort studies and biobanks, such as Trans-Omics for Precision Medicine (TOPMed) study¹ and UK Biobank², have sequenced or genotyped hundreds of thousands of samples, which are invaluable resources to identify genetic components of complex traits, including rare variants (minor allele frequency (MAF) < 1%). It is well known that single variant tests are underpowered to identify trait-associated rare variants³. Gene- or region-based tests, such as Burden test, SKAT⁴ and SKAT-O⁵, can be more powerful by grouping rare variants into functional units, i.e. genes. To adjust for both population structure and sample relatedness, gene-based tests have been extended to mixed models⁶. For example, EmmaX⁷ based SKAT⁴ approaches (EmmaX-SKAT) have been implemented and used for many rare variant association studies including TOPMed^1,8. The generalized linear mixed model gene-based test, SMMAT, has been recently developed⁶. However, these approaches require O(N³) computation time and O(N²) memory usages, where N is the sample size, which are not scalable to large datasets.

Here, we propose a novel method called SAIGE-GENE for region-based association analysis that is capable of handling very large samples (> 400,000 individuals), while inferring and accounting for sample relatedness. SAIGE-GENE is an extension of the previously developed single variant association method, SAIGE⁹, with a modification suitable to rare variants. Same as SAIGE, it utilizes state-of-the-art optimization strategies to reduce computation cost for fitting null mixed models. To ensure computation efficiency while improving test accuracy for rare variants, SAIGE-GENE approximates the variance of score statistics calculated with the full genetic relationship matrix (GRM) using the variance calculated with a sparse GRM and the ratios of these two variances estimated from a subset of genetic markers. Because the sparse GRM, which is constructed by thresholding small values in the full GRM, preserves close family structures, this approach provides a more accurate variance estimation for very rare variants (minor allele count (MAC) < 20) than the original approach in SAIGE⁹. By combining single variant score statistics, SAIGE-GENE can perform Burden, SKAT and SKAT-O type gene-based tests. We have also developed conditional analysis to perform association tests conditioning on a single variant or multiple variants to identify independent rare variant association signals. Furthermore, SAIGE-GENE can account for unbalanced case-control ratios of binary traits by adopting a robust adjustment based on saddlepoint approximation^10–12 (SPA) and efficient resampling¹³ (ER). The robust adjustment was previously developed for independent samples¹⁴ and we have extended it for related samples in SAIGE-GENE.

We have demonstrated that SAIGE-GENE controls for type I error rates in related samples for both quantitative and binary traits through extensive simulations as well as real data analysis, including the Nord Trøndelag Health Study (HUNT) study for 69,716 Norwegian samples^15,16 and the UK Biobank for 408,910 White British samples². By evaluating the computation performance, we have shown its feasibility for large-scale genome-wide analysis. To perform exome-wide gene-based tests on 400,000 samples with on average 50 markers per gene, SAIGE-GENE requires 2,238 CPU hours and less than 36 Gb memory, while current methods will cost more than > 10 Tb in memory. We have further applied SAIGE-GENE to 53 quantitative traits and 10 binary traits in the UK Biobank and identified several significantly associated genes.

RESULTS

Overview of Methods

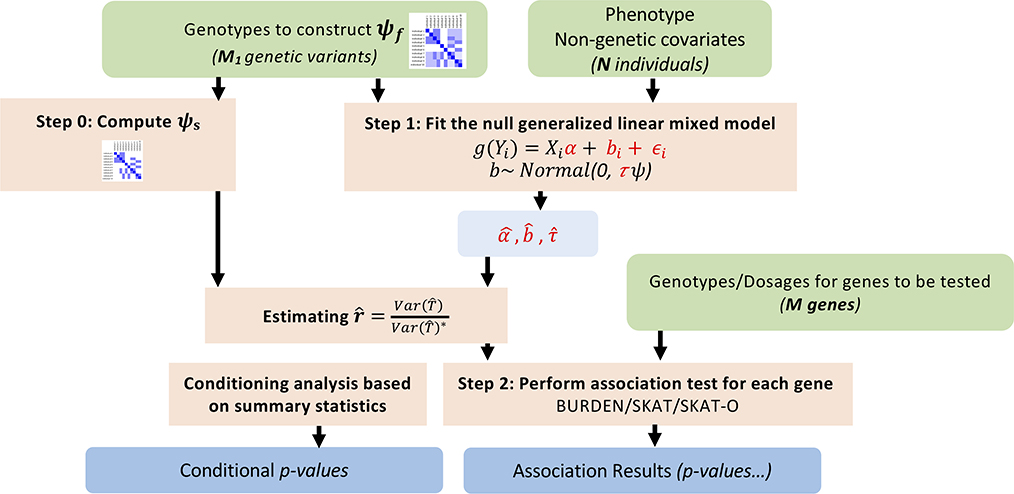
SAIGE-GENE consists of two main steps: 1. Fitting the null generalized linear mixed model (GLMM) to estimate variance components and other model parameters. 2. Testing for association between each genetic variant set, such as a gene or a region, and the phenotype. Three different association tests: Burden, SKAT, and SKAT-O have been implemented in SAIGE-GENE. The workflow is shown in the Extended Data Fig. 1.

SAIGE-GENE uses similar optimization strategies as utilized in the original SAIGE to fit the null GLMM in Step 1. In particular, the spectral decomposition has been replaced by the preconditioning conjugate gradient (PCG) to solve linear systems without calculating and inverting the N × N GRM. To reduce the memory usage, raw genotypes are stored in a binary vector and elements of GRM are calculated when needed rather than being stored.

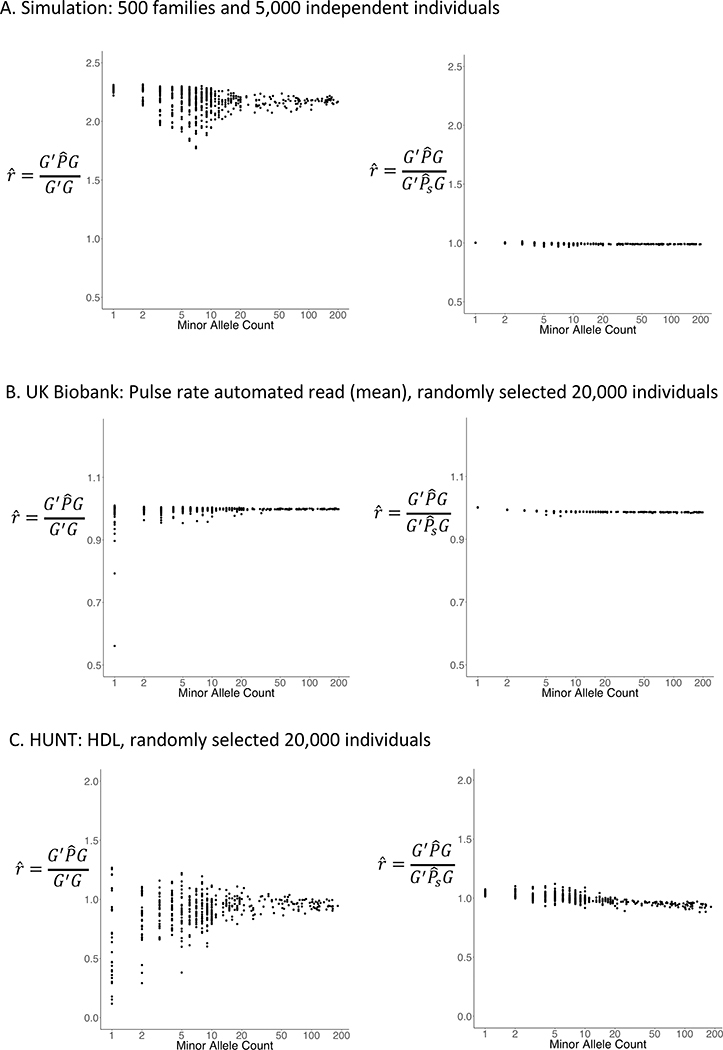
One of the most time-consuming part in association tests is to calculate variance of single variant score statistic, which requires O(N²) computation. To reduce computation cost, existing approaches, such as SAIGE⁹, BOLT-LMM¹⁷, and GRAMMA-Gamma¹⁸, approximate the variance of single variant score statistics with the full GRM using the variance estimate without a GRM and the ratio of these two variances. The ratio, which is assumed to be constant, is estimated using a subset of randomly selected genetic markers. However, for very rare variants with MAC below 20, the constant ratio assumption is not satisfied (Extended Data Fig. 2, left panel). This is because rare variants are more susceptible to close family structures. Thus, to better approximate the variance, SAIGE-GENE incorporates close family structures through a sparse GRM, in which GRM elements below a user-specified relatedness coefficient are zeroed out and close family structures are preserved. The ratio between the variance with the full GRM and with the sparse GRM is much less variable (Extended Data Fig. 2, right panel). To construct a sparse GRM, a small subset of randomly selected genetic markers, i.e. 2,000, are firstly used to quickly estimate which sample pairs pass the user-specified coefficient of relatedness cutoff, e.g. ≥0.125 for up to 3^rd degree relatives. Then the coefficients of relatedness for those related pairs are further estimated using the full set of genetic markers, which equal to values in the full GRM. Given that estimated values for variance ratios vary by MAC for the extremely rare variants (Extended Data Fig. 2, left panel), such as singletons and doubletons, the variance ratios need to be estimated separately for different MAC categories. By default, MAC categories are set to be MAC equals to 1, 2, 3, 4, 5, 6 to 10, 11 to 20, and > 20.

In Step 2, gene-based tests are conducted using single variant score statistics and their covariance estimates, which are approximated as the product of the covariance with the sparse GRM and the pre-estimated ratio. SAIGE-GENE can carry out Burden, SKAT, and SKAT-O approaches. Since SKAT-O is a combined test of Burden and SKAT, and hence provides a robust power, SAIGE-GENE performs SKAT-O by default.

If a gene or a region is significantly associated with the phenotype of interest, it is necessary to test if the signal is from rare variants or just a shadow of common variants in the same locus. We have developed conditional analysis using linkage disequilibrium (LD) information between conditioning markers and the tested gene¹⁹. Details are described in the Online Methods section.

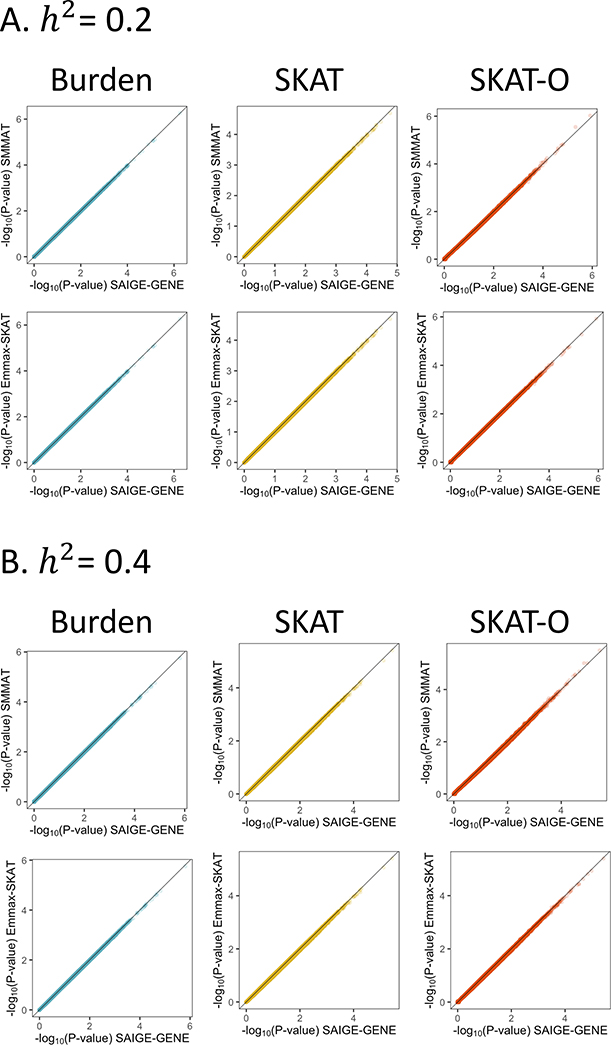
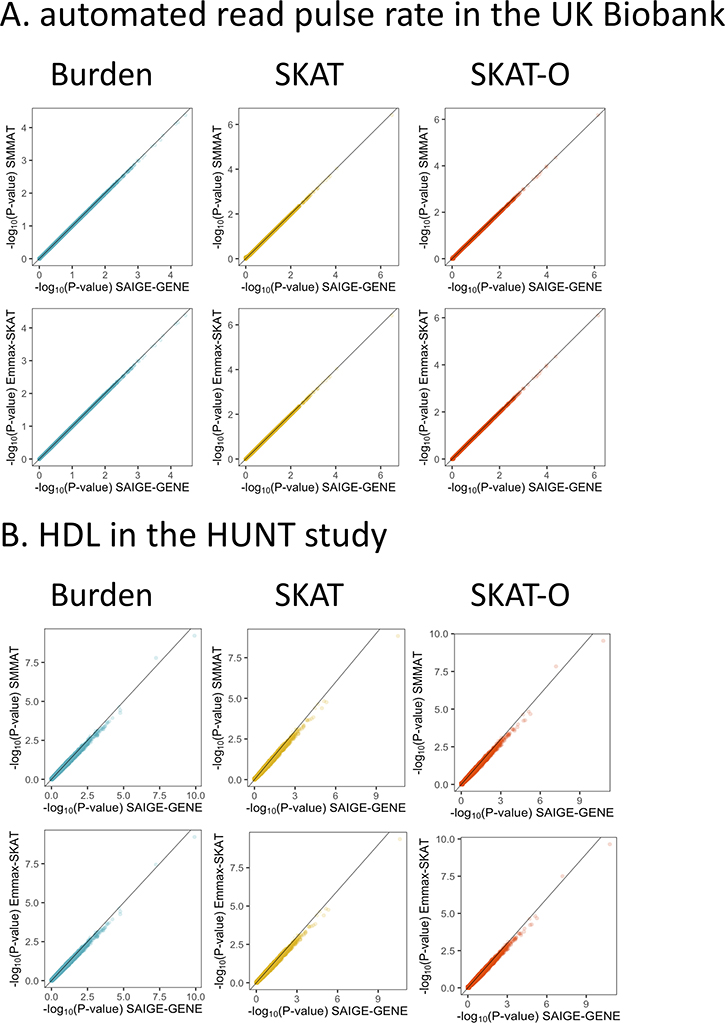
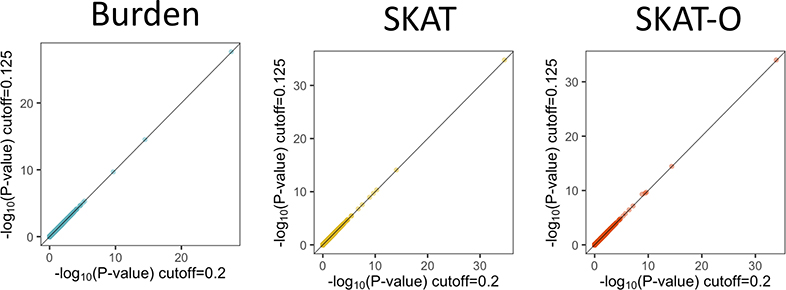
SAIGE-GENE uses the same generalized linear mixed model as in SMMAT, while SMMAT calculates the variances of the score statistics for all tested genes using the full GRM directly and hence can be thought of as the “exact” method. When the trait is quantitative, GLMM used by SAIGE-GENE and SMMAT is equivalent to the linear mixed model (LMM) of EmmaX-SKAT. We have further shown that SAIGE-GENE provides consistent association p-values to the two “exact” methods, EmmaX-SKAT and SMMAT (r² of −log₁₀ p-values > 0.99), using both simulation studies (Extended Data Fig. 3) and real data analysis for down-sampled UK Biobank and HUNT (Extended Data Fig. 4), but with much smaller computation and memory cost (Figure 1). We have also shown that SAIGE-GENE with different coefficient of relatedness cutoffs (0.125 and 0.2) produced nearly identical association p-values for automated read pulse rates in UK Biobank (Extended Data Fig. 5).

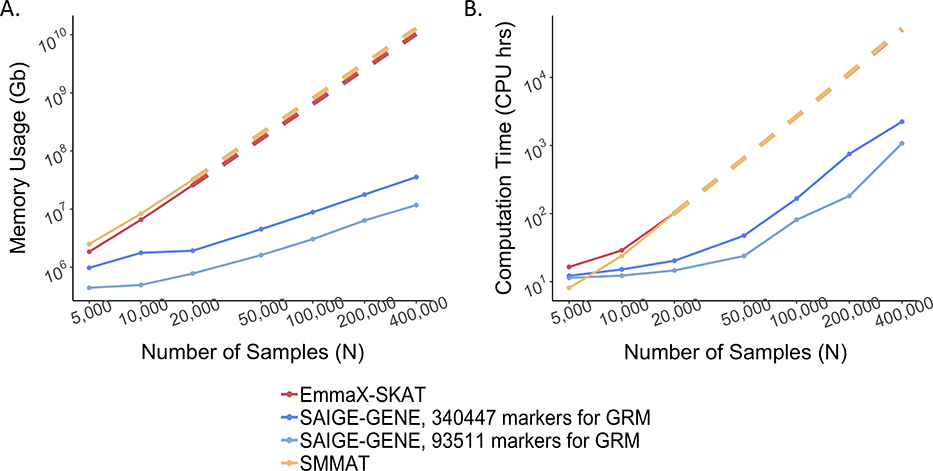
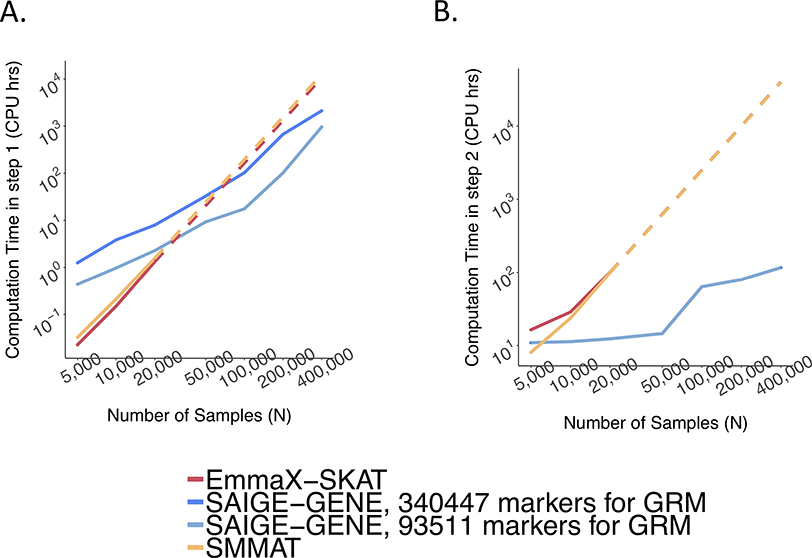
Figure 1.

Estimated and projected computation cost by sample sizes (N) for gene-based tests for 15,342 genes, each containing 50 rare variants.

Benchmarking was performed on randomly sub-sampled UK Biobank data with 408,144 White British participants for waist-to-hip ratio. The reported run times and memory are medians of five runs with samples randomly selected from the full sample set using different sampling seeds. The reported computation time and memory for EmmaX-SKAT and SMMAT is the projected computation time when N > 20,000. A. Log-log plots of the memory usage as a function of sample size (N) B. Log-log plots of the run time as a function of sample size (N). Numerical data are provided in Supplementary Table 1.

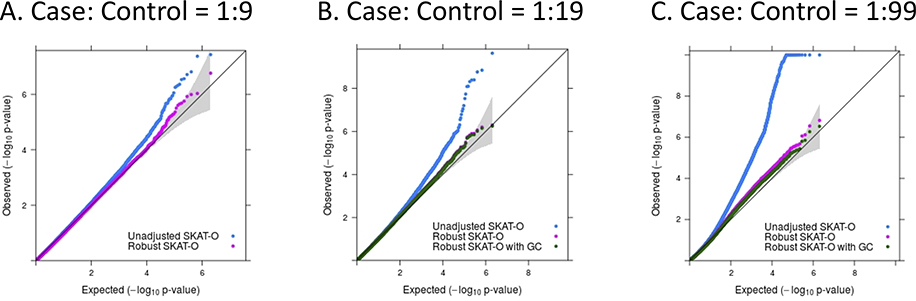
For binary phenotypes with unbalanced case-control ratios, single variant score statistics do not follow the normal distribution, leading to inflated type I error rates for region-based test¹³. To address this problem, we have recently developed an adjustment for independent samples¹⁴. The approach uses saddlepoint approximation^10–12 (SPA) and efficient resampling¹³ (ER) to calibrate the variance of single variant score statistics. We have extended this approach to GLMM for SAIGE-GENE, which provides greatly improved type I error control than the unadjusted approach of assuming normality (Extended Data Fig. 6). Details can be found in Supplementary Note 1.3.3.

Computation and Memory Cost

To evaluate the computation performance of SAIGE-GENE, we randomly sampled subsets of the 408,144 UK Biobank participants with the White British ancestry and non-missing measurements for waist hip ratio². We benchmarked SAIGE-GENE, EmmaX-SKAT, and SMMAT for exome-wide gene-based SKAT-O tests, in which 15,342 genes were tested with assuming that each has 50 rare variants.

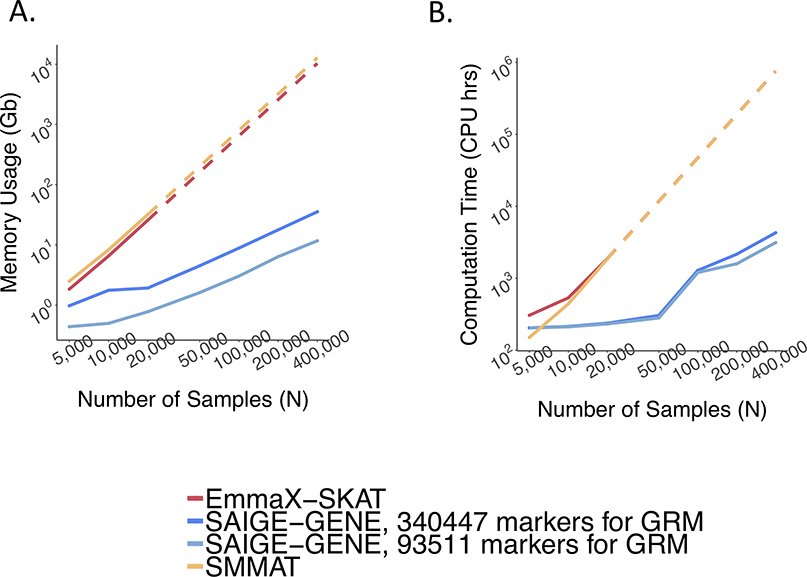
Memory usage is plotted in Figure 1A. The memory cost of SAIGE-GENE is linear to the number of markers, M₁, used for kinship estimation, but using too few markers may not be sufficient to account for subtle sample relatedness, leading to inflated type I error rates^9,20. SAIGE-GENE uses 11.74 Gb with M₁ = 93,511 and 35.59 Gb when M₁ = 340,447 when the sample size N is 400,000, making it feasible for large sample data. In contrast, with N = 400,000 the memory usages in EmmaX-SKAT and SMMAT are projected to be nearly 10Tb.

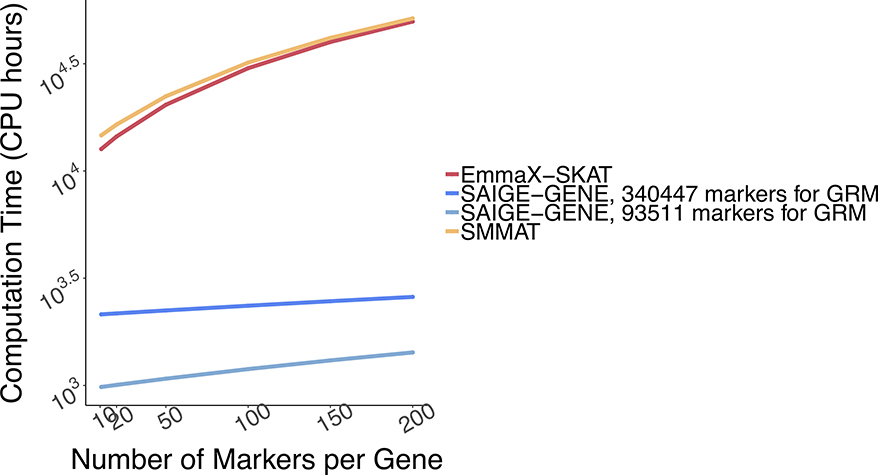
Total computation time for exome-wide gene-based tests is plotted in Figure 1B. Computation time for Step 1 and Step 2 are plotted separately in Extended Data Fig. 7 with numbers presented in Supplementary Table 1. The computation time for Step 1 in SAIGE-GENE is approximately O(M₁N^1.5) and in SMMAT and EmmaX-SKAT is O(N³). In Step 2, the association test for each gene costs O(qK) in SAIGE-GENE, where q is the number of markers in the gene and K is the number of non-zero elements in the sparse GRM. Compared to O(qN²) in Step 2 of SMMAT and EmmaX-SKAT, SAIGE-GENE decreases the computation time dramatically. For example, in the UK Biobank (N =408,910) with the relatedness coefficient ≥ 0.125 (corresponding to preserving 3^rd degree or closer relatives in the GRM), K = 493,536, which is the same order of magnitude of N, and hence O(qK) is greatly smaller than O(qN²). As the computation time in Step 2 is approximately linear to q, the number of markers in each variant set, the total computation time for exome-wide gene-based tests was projected by different q and plotted in Extended Data Fig. 8. In addition, we plotted the projected computation time for genome-wide region-based tests in Extended Data Fig. 9, in which 286,000 chunks with 50 markers per chunk were assumed to be tested, corresponding to 14.3 million markers in HRC-imputed UK Biobank data with MAF ≤ 1% and imputation info score ≥ 0.8.

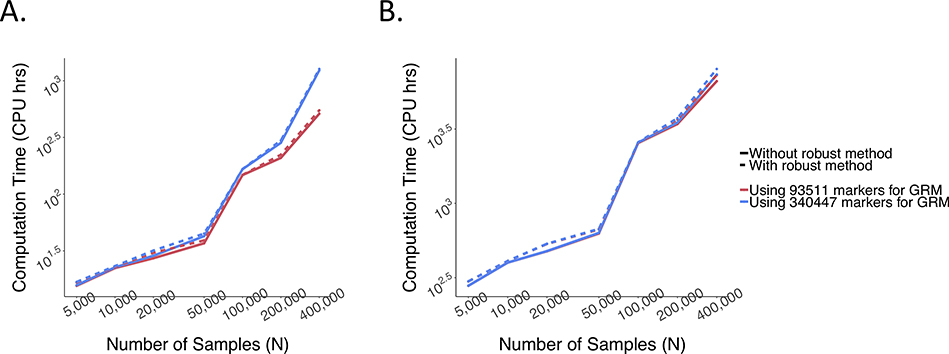
With M₁ = 340,447 and N = 400,000, it takes SAIGE-GENE 2,238 CPU hours for the exome-wide analysis and 3,919 CPU hours for the genome-wide analysis for waist hip ratio. Compared to EmmaX-SKAT and SMMAT, SAIGE-GENE is 25 times faster for the exome-wide analysis and 161 times faster for the genome-wide analysis. More details are presented in Supplementary Table 1. Additional steps in the robust adjustment for binary traits only slightly increases the computation cost (1,269 vs 1,232 CPU hours for exome-wide analysis with M₁ = 93,511) compared to the unadjusted approach (Supplementary Table 2 and Extended Data Fig. 10). Details are described in Supplementary Note 1.4

The computation time for constructing the sparse GRM is O($M_1^{*}{N}^2$ + M₁K), where $M_1^{*}$ is the number of a small set of markers used for initial determination of related sample pairs, which by default is set to be 2,000. The construction of the sparse GRM is needed for each data set once and then it will be re-used for all phenotypes. For example, for the UK Biobank with N = 408,910, M₁= 340,447, $M_1^{*}$ = 2000, K = 493,536 with the relationship coefficient ≥ 0.125, corresponding to up to 3^rd degree relatives, it took 312 CPU hours to create the sparse GRM.

Gene-based association analysis of quantitative traits in HUNT and UK Biobank

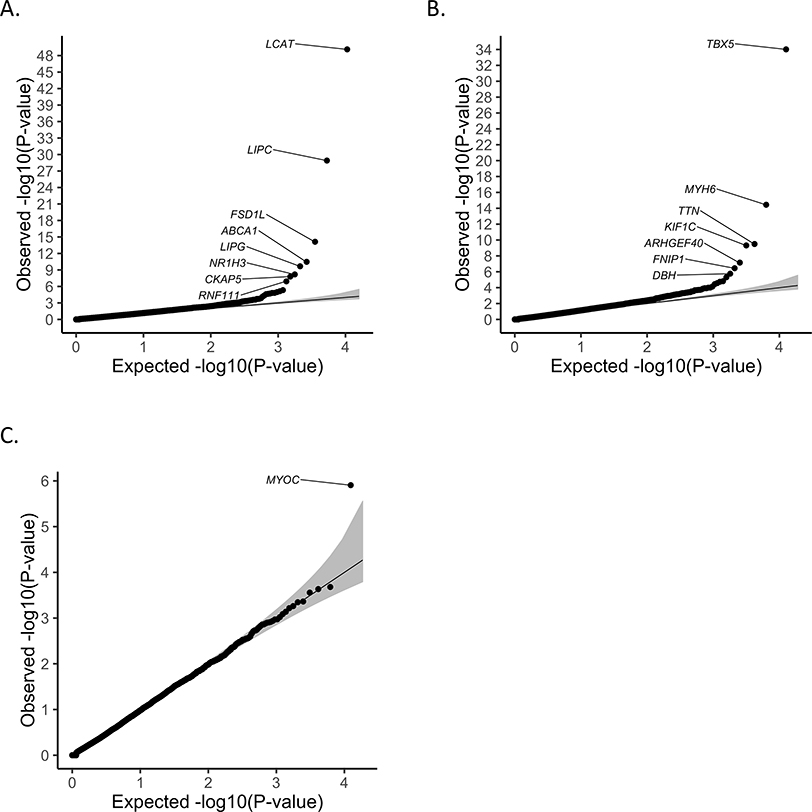
We applied SAIGE-GENE to analyze 13,416 genes, with at least two rare (MAF ≤ 1%) missense and stop-gain variants that were directly genotyped or imputed from HRC for high-density lipoprotein (HDL) in 69,716 Norwegian samples from the HUNT study⁹, which has substantial sample relatedness. The quantile-quantile (QQ) plot for the p-values of SKAT-O tests from SAIGE-GENE for HDL in HUNT is shown Figure 2A. As Table 1 shows, eight genes reached the exome-wide significant threshold (p-value ≤ 2.5×10⁻⁶) and all of them are located in the previously reported GWAS loci for HDL^21,22. After conditioning on the most significant nearby variants from single-variant association tests (500 kilobases upstream and downstream), all genes, except for FSD1L, remained significant, suggesting that SAIGE-GENE has identified associations of rare coding variants that are independent from the nearby association signals, pointing to candidate causal genes at those loci.

Figure 2.

Quantile-quantile plots of exome-wide gene-based association results.

A. Results for high-density lipoprotein (HDL) in the HUNT study (N = 69,214). SKAT-O test in SAIGE-GENE was performed for 13,416 genes with stop-gain and missense variants with MAF ≤ 1%, of which 10,600 having at least two variants are plotted. B. Results for automated read pulse rate in the UK Biobank (N = 385,365). The SKAT-O test in SAIGE-GENE was performed for 15,338 genes with stop-gain and missense variants with MAF ≤ 1%, of which 12,636 having at least two variants are plotting. C. Results for glaucoma in the UK Biobank (N cases = 4,462; N controls = 397,761). SKAT-O approach in SAIGE-GENE was performed for 15,338 genes with stop-gain and missense variants with MAF ≤ 1%, of which 12,638 having at least two variants are plotting. N: sample size.

Table 1.

Genes that are significantly associated with automated read pulse rate (N = 385,365) and glaucoma (N cases = 4,462; N controls = 397,761) in the UK Biobank and high-density lipoprotein (HDL) in the HUNT study (N = 69,214) with SKAT-O p-values < 2.5×10⁻⁶ from SAIGE-GENE. Conditional analysis was performed when the top hit in the locus (+/− 500kb of the start and end positions of the gene) is not included in the gene-based test. The p-value of conditional analysis is NA when the top hit is a rare missense or stop gain variant included in the gene-based test. N: sample size.

	Gene	Number of Markers	SAIGE-GENE SKAT-O Test		Top Hit in the Locus
			p-value	p-value Conditional	Variant (GRCh37/hg19)	p-value	MAF
Pulse Rate (UK Biobank)	TBX5	4	9.69E-35	NA	12:114837349_C/A	7.73E-35	0.0049
	MYH6	14	3.61E-15	2.56E-13	14:23861811_A/G	1.04E-168	0.3698
	TTN	368	3.18E-10	3.41E-06	2:179721046_G/A	8.73E-100	0.0885
	KIF1C	12	4.78E-10	NA	17:4925475_C/T	3.18E-10	0.0063
	ARHGEF40	7	7.02E-08	2.57E-10	14:21542766_A/G	3.30E-52	0.1688
	FNIP1	8	3.58E-07	4.31E-02	5:131107733_C/T	1.22E-08	0.0027
	DBH	12	1.74E-06	1.74E-06	9:136149399_G/A	3.46E-06	0.1870
HDL (HUNT)	LCAT	3	7.34E-50	NA	16:67974303_A/T	1.78E-48	0.0008
	LIPC	4	1.25E-29	6.63E-31	15:58723939_G/A	7.50E-89	0.1889
	FSD1L	3	7.40E-15	1	9:107793713_T/C	1.45E-20	0.0021
	ABCA1	14	3.32E-11	1.28E-11	9:107620797_A/G	3.64E-48	0.0055
	LIPG	3	2.15E-10	2.41E-10	18:47156926_C/A	5.92E-40	0.2348
	NR1H3	2	6.53E-09	1.69E-09	11:47246397_G/A	3.66E-13	0.3220
	CKAP5	7	1.62E-08	1.21E-09	11:47246397_G/A	3.66E-13	0.3220
	RNF111	11	1.18E-07	1.37E-09	15:58856899_C/G	2.82E-24	0.0047
Glaucoma (UK Biobank)	MYOC	6	1.23E-06	NA	1:171605478_G/A	9.13E-16	0.0014

We also applied SAIGE-GENE to analyze 15,342 genes for 53 quantitative traits using 408,910 UK Biobank participants with White British ancestry². Heritability estimates based on the full GRM are presented in Supplementary Table 3A. Supplementary Table 4A presents all genes with p-values reaching the exome-wide significant threshold (p-value ≤ 2.5×10⁻⁶). The same MAF cutoff ≤ 1%, for missense and stop-gain variants were applied. Figure 2B shows the QQ plot for automated read pulse rate as an exemplary phenotype. MYH6, ARHGEF40 and DBH remain significant after conditioning on the most significant nearby variants (Table 1). Gene TBX5, MYH6, TTN, and ARHGEF40 are known genes for heart rates by previous GWAS^23–26. To our knowledge, KIF1C and DBH have not been reported by association studies for heart rates, but Dbh(−/−) mice have decreased heart rates compared to their littermate controls Dbh(+/−) mice²⁷. For DBH, no single variant reaches the genome-wide significance (the most significant variant is 9:136149399 (GRCh37) with MAF = 18.7% and p-value =3.46×10⁻⁶). Fifteen genes that were exome-wide significant have no genome-side significant single variants (Supplementary Table 5). After conditioning on the most significant nearby variants, total 64 genes for 12 traits remained exome-wide significant (Supplementary Table 6A). SAIGE-GENE has identified several potentially novel gene-phenotype associations, such as DBH for automated read pulse rate (p-value_SKAT-O =1.74×10⁻⁶), and also replicated several previous findings, such as the association between ADAMTS3 and height²⁸. Details have been described in Supplementary Note 2.1. These results have demonstrated the value of gene-based tests for identifying genetic factors for complex traits.

Gene-based association analysis of binary traits in UK Biobank

We applied SAIGE-GENE to ten binary phenotypes with various case-control ratios in the UK Biobank. The heritability estimates in a liability scale are presented in Supplementary Table 3B. Nine genes for six binary phenotypes reached the exome-wide significant threshold (p-value < 2.5×10⁻⁶) (Supplementary Table 4B), all of which have been identified by both SAIGE-GENE and single variant tests, including the gene MYOC, known for glaucoma²⁹ (Figure 2C). Six genes for six binary phenotypes remained exome-wide significant after conditioning on top variants (Supplementary Table 6B).

Simulation Studies

We investigated the type I error rates and power of SAIGE-GENE by simulating genotypes and phenotypes for 10,000 samples in two settings. One had 500 families and 5,000 unrelated samples and the other had 1,000 families. Each family had 10 members based on the pedigree shown in Supplementary Figure 1.

Type I error rates

The type I error rates of SAIGE-GENE, EmmaX-SKAT, and SMMAT were evaluated from 10⁷ simulated gene-phenotype combinations, each with 20 genetic variants with MAF ≤ 1% on average. A sparse GRM with a cutoff 0.2 for the coefficient of relatedness was used in SAIGE-GENE. Two different values of the variance component parameter corresponding to the heritability h² = 0.2 and 0.4 were considered for quantitative traits (see ONLINE METHODS). The empirical type I error rates at the α = 0.05, 10⁻⁴ and 2.5×10⁻⁶ are shown in the Supplementary Table 7. Our simulation results suggest that SAIGE-GENE relatively well controls type I error rates, while the type I error rates are slightly inflated when heritability is relatively high (h² = 0.4). Similar results have been observed on a larger sample size with 1,000 families and 10,000 unrelated samples (Supplementary Note 2.2 and Supplementary Table 8). Adjusting the test statistics using the genomic control (GC) inflation factor has addressed the inflation (Supplementary Note 1.3.4).

Further simulations were conducted to evaluate type I error rates of SAIGE-GENE, EmmaX-SKAT, and SMMAT for skewed distributed phenotypes, which are common in real data (Supplementary Figure 2A). All three methods had inflated type I error rates for phenotypes with skewed distributions (Supplementary Table 9). With inverse normal transformation on phenotypes (Supplementary Figure 2B), the inflation has been reduced but slight inflation was still observed (Supplementary Table 9). A potential reason is that inverse normal transformation disrupts sample relatedness in raw phenotypes, leading to poor fitting for the null GLMM. We then conducted a three-step phenotype transformation procedure as described in Supplementary Note 2.3, which maintains sample relatedness in raw phenotype, and observed well controlled type I error rates by all three methods (Supplementary Table 10). Further simulation studies using real genotype data from the UK Biobank have shown that SAIGE-GENE well controlled type I error rates in the presence of subtle population structure or non-negligible cryptic relatedness between families (Supplementary Table 11 and 12). Details have been described in Supplementary Note 2.4 and 2.5.

We also evaluated the type I error rates of SAIGE-GENE for binary traits with various case-control ratios. Similar with quantitative traits, a sparse GRM with a cutoff 0.2 was used. The variance component parameter τ = 1 was assumed, corresponding to liability-scale heritability 0.23. As expected, when case-control ratios were balanced or moderately unbalanced (e.g. 1:1 and 1:9), type I error rates were well controlled even without the robust adjustment, while when the ratios were extremely unbalanced (e.g. 1:19 and 1:99), inflation was observed (Supplementary Table 13A and Extended Data Fig. 6). With the robust adjustment, type I error rates were relatively well controlled for the unbalanced case-control ratios (Supplementary Table 13B and Extended Data Fig. 6). However, for phenotypes with case-control ratio=1:99, slight inflation was still observed, although the inflation has been dramatically alleviated compared to the unadjusted method. Then the genomic control adjustment can be used to further control the type I error rates (Supplementary Table 13B). We also evaluated empirical type I error rates of SAIGE-GENE for binary traits under case-control sampling with case-control ratios 1:1 and 1:9 based on a disease prevalence 1% in the population (Supplementary Note 2.6) and observed well-controlled type I error rates (Supplementary Table 14).

Power

We evaluated empirical power of SAIGE-GENE and EmmaX-SKAT for quantitative traits. Two different settings of proportions of causal variants were used: 10% and 40%. In each setting, among causal variants, 80% and 100% had negative effect sizes. The absolute effect sizes for causal variants were set to be |0.3log₁₀(MAF)| and |log₁₀(MAF)|, respectively, when the proportions of causal variants are 0.4 and 0.1. Supplementary Table 15 shows that the power of both methods is nearly identical for all simulation settings for Burden, SKAT and SKAT-O tests.

We also evaluated empirical power of SAIGE-GENE for binary traits using two different study designs: cohort study with various disease prevalence (0.01–0.5); and case-control sampling with different case-control ratios (1:1–1:19) based on a disease prevalence 1% in the population. In each setting, 40% variants were causal variants. Among them, 80% were risk-increasing variants and 20% were risk-decreasing. The absolute effect sizes of causal variants were set to be |0.55log₁₀(MAF)| and |0.35log₁₀(MAF)| for cohort study and case-control sampling, respectively. Supplementary Table 16 shows the empirical power of SKAT-O in both simulation studies. SAIGE-GENE had similar empirical power as unadjusted SAIGE-GENE in balanced case-control ratios and higher power in unbalanced scenarios. The power is small when case: control ratio is 1:99 due to the limited number of cases (100 cases), which can be alleviated with larger sample size.

DISCUSSION

In summary, we have presented a method, SAIGE-GENE, to perform gene- or region-based association tests in large cohorts or biobanks in the presence of sample relatedness. Similar to SAIGE⁹, which was previously developed for single-variant association tests, SAIGE-GENE uses GLMM to account for sample relatedness, scalable computational approaches for large sample sizes, and the robust adjustment¹⁴ to account for unbalanced case-control ratios of binary traits.

SAIGE-GENE uses several optimization strategies that are similar to those used in SAIGE to make fitting the null GLMM feasible for large sample sizes. For example, instead of storing the GRM in the memory, SAIGE-GENE stores genotypes in a binary vector and computes the elements of the GRM as needed. PCG is used to solve linear systems instead of inverting a matrix. However, some optimization approaches are specifically applied in the gene-based tests in regard of rare variants. As estimating the variances of score statistics for rare variants are more sensible to family structures, we use a sparse GRM to preserve close family structures rather than ignoring all sample relatedness. In addition, the variance ratios are estimated for different MAC categories, especially for those extremely rare variants with MAC lower than or equal to 20.

For binary phenotypes, SAIGE-GENE uses the robust adjustment, thereby also relatively well controls the type I error rates for both balanced and unbalanced case-control phenotypes. However, slight inflation is still observed in extremely unbalanced phenotypes (≤1:99). To address this, we suggest using the genomic control to further control type I error.

In numerical optimization, using good initial values can improve the model convergence. In the analysis of 24 quantitative traits in the UK Biobank with sample size (N) ≥ 100,000, we note that the models with the full GRM and the sparse GRM produced different variance component estimates, but they are relatively concordant (Pearson’s correlation R² = 0.66, Supplementary Figure 3). This indicates that the parameter estimates from the sparse GRM can be used as initial values to facilitate the model fitting. We implemented this approach in SAIGE-GENE.

SAIGE-GENE has some limitations. First, similar to SAIGE and other mixed-model methods, the time for algorithm convergence may vary among phenotypes and study samples given different heritability levels and sample relatedness. Second, similar to SAIGE⁹ and SMMAT⁶, SAIGE-GENE uses penalized quasi-likelihood (PQL)³⁰ for binary traits to estimate the variance component which is known to be biased. However, as shown in simulation studies in SAIGE⁹ and SMMAT⁶, PQL-based approaches work well to adjust for sample relatedness.

Overall, we have shown that SAIGE-GENE can account for sample relatedness while maintaining test power through simulation studies. By applying SAIGE-GENE to HUNT⁹ and UK Biobank², we have demonstrated that SAIGE-GENE can identify potentially novel association signals. Currently, our method is the only available mixed effect model approach for gene- or region-based rare variant tests for large sample data, while accounting for unbalanced case-control ratios for binary traits. By providing a scalable solution to the current largest and future even larger datasets, our method will contribute to identifying trait-susceptibility rare variants and genetic architecture of complex traits.

METHODS

Generalized linear mixed model

In a study with sample size N, we denote the phenotype of the ith individual using y_i for both quantitative and binary traits. Let the 1 × (p + 1) vector X_i represent p covariates including the intercept, the N × q matrix G_i represent the allele counts (0, 1 or 2) for q variants in the gene to test. The generalized linear mixed model can be written as

$${g(\mu }_i)=X_i\alpha +G_i\beta +b_i,$$

where μ_i is the mean of phenotype, b_i is the random effect, which is assumed to be distributed as N(0, τ ψ), where ψ is an N × N genetic relationship matrix (GRM) and τ is the additive genetic variance parameter. The link function g is the identity function for quantitative traits with an error term ε~N(0,ϕI) and logistic function for binary traits. The parameter α is a (p + 1) × 1 coefficient vector of fixed effects and β is a q × 1 coefficient vector of the genetic effect.

Estimate variance component and other model parameters (Step 1)

Same as in the original SAIGE⁹ and GMMAT³¹, to fit the null GLMM in SAIGE-GENE, penalized quasi-likelihood (PQL) method^30,32 and the computational efficient average information restricted maximum likelihood (AI-REML) algorithm^31,33 are used to iteratively estimate ($\hat{\tau },\hat{\alpha },\hat{b}$) under the null hypothesis of β = 0. At iteration k, let (${\hat{\tau }}^{\left(k\right)},{\hat{\alpha }}^{\left(k\right)},{\hat{b}}^{\left(k\right)}$) be estimated $(\hat{\tau },\hat{\alpha },\hat{b}),{\hat{\mu }}_i^{\left(k\right)}$ be the estimated mean of y_i and ${\hat{\mathrm{\Sigma }}}^{\left(k\right)}={\{{\hat{W}}^{(k)}\}}^{-1}+{\hat{\tau }}^{\left(k\right)}\psi$ be an N × N matrix of the variance of working vector ${\tilde{y}}_i$, in which ψ is the N × N GRM. For quantitative traits, ${\hat{W}}^{\left(k\right)}={\hat{\varphi }}^{-1}I$ and ${\tilde{y}}_i=X_i{\alpha }^{\left(k\right)}+b_i^{\left(k\right)}.$ For binary traits, ${\hat{W}}^{\left(k\right)}=diag[{\hat{\mu }}_i^{(k)}({1-\hat{\mu }}_i^{(k)})]$ and ${\tilde{y}}_i=X_i{\alpha }^{\left(k\right)}+b_i^{\left(k\right)}+(y_i-{\hat{\mu }}_i^{\left(k\right)})/\left\{{\hat{\mu }}_i^{(k)}\left({1-\hat{\mu }}_i^{(k)}\right)\right\}$. To obtain the log quasi-likelihood and average information at each iteration, SAIGE and SAIGE-GENE use the preconditioned conjugate gradient approach (PCG)^31,32 to obtain the product of inverse of ${\hat{\mathrm{\Sigma }}}^{(k)}$ and any other vector by iteratively solving a linear system with ${\hat{\mathrm{\Sigma }}}^{(k)}$. This approach is more computationally efficient than using Cholesky decomposition to obtain ${\{{\hat{\mathrm{\Sigma }}}^{(k)}\}}^{-1}$. The numerical accuracy of PCG has been evaluated in the SAIGE paper⁹.

Gene-based association tests (Step 2)

Test statistics of the Burden, SKAT and SKAT-O tests for a gene can be constructed based on score statistics from the marginal model for individual variants in the gene. Suppose there are q variants in the region or gene to test. The score statistic for variant j (j=1,..,q) under H₀: β_j = 0 is $T_j={g_j}^T(Y-\hat{\mu })$ where g_j and Y are N × 1 genotype and phenotype vectors, respectively, and $\hat{\mu }$ is the estimated mean of Y under the null hypothesis.

Let u_j denote a threshold indicator or weight for variant j and U = diag(u₁,…,u_q) be a diagonal matrix with u_j as the jth element. Similar to the original SKAT and SKAT-O papers^4,5, to upweight rare variants, the default setting in SAIGE-GENE is u_j = Beta(MAF_j, 1, 25), which upweight rarer variants. The Burden test statistics can be written as $Q_{Burden}={({\sum }_{j=1}^q{u}_j{T}_j)}^2$. Suppose $\tilde{G}=G-X{(X^T\hat{W}X)}^{-1}{X}^T\hat{W}G$ is the covariate adjusted genotype matrix, where G = (g₁,…,g_q) is the N × q genotype matrix of the q genetic variants, and $\hat{P}={\hat{\Sigma }}^{-1}-{\hat{\Sigma }}^{-1}X{(X^T{\hat{\Sigma }}^{-1}X)}^{-1}{X}^T{\hat{\Sigma }}^{-1}$ with $\hat{\Sigma }={\hat{W}}^{-1}+\hat{\tau }\psi .$ Under the null hypothesis of no genetic effects, Q_Burden followed ${\lambda }_B{\chi }_1^2$, where ${\lambda }_B=J^T\mathrm{U}{\tilde{G}}^T\hat{P}\tilde{G}\mathrm{U}J,J$ is a q × 1 vector with all elements being unity and ${\chi }_1^2$ is a chi-squared distribution with 1 degree of freedom³. The SKAT test⁴ can be written as $Q_{SKAT}={\sum }_{j=1}^q{u}_j^2{T}_j^2$, which follows a mixture of chi-square distribution ${\sum }_{j=1}^q{{\lambda }_{Sj}\chi }_1^2$, where λ_Sj are the eigenvalues of $U{\tilde{G}}^T\hat{P}\tilde{G}U$. The SKAT-O test⁵ uses a linear combination of the Burden and SKAT tests statistics $Q_{SKATO}=(1-\rho )Q_{SKAT}+\rho Q_{Burden},0\le \rho \le 1$. To conduct the test, the minimum p-value from grid of ρ is calculated and the p-value of the minimum p-value is estimated through numerical integration. Following the suggestion in Lee et al³⁴, we use a grid of eight values of $\rho =(0,{0.1}^2,{0.2}^2,{0.3}^2,{0.4}^2,{0.5}^2,0.5,1)$ to find the minimum p-value.

Approximate ${\tilde{\mathit{G}}}^{\mathit{T}}\hat{\mathit{P}}\tilde{\mathit{G}}$

For each gene, given $\hat{P}$, the calculation of ${\tilde{G}}^T\hat{P}\tilde{G}$ requires applying PCG for each variant in the gene, which can be computationally very expensive. Suppose $\tilde{g}$ represents a covariate adjusted single variant genotype vector. To reduce computation cost, an approximation approach has been used in SAIGE, BOLT-LMM¹⁷ and GRAMMAR-GAMMAR¹⁸, in which the ratio between ${\tilde{g}}^T\hat{P}\tilde{g}$ and ${\tilde{g}}^T\tilde{g}$ is estimated by a small subset of randomly selected genetic markers. The ratio has been shown to be approximately constant for all variants. Given the estimated ratio $\hat{r}={\tilde{g}}^T\hat{P}\tilde{g}/{\tilde{g}}^T\tilde{g},{\tilde{g}}^T\hat{P}\tilde{g}$ for all other variants can be obtained as $\hat{r}{\tilde{g}}^T\tilde{g}$. However, the variations of the estimated $\hat{r}$ for extremely rare variants are large and including some closely related samples in the denominator helps reduce the variation of $\hat{r}$ as shown in Supplementary Figure 2. Let ψ_S denote a sparse GRM that preserves close family structure and ψ_f denote a full GRM. We estimate the ratio ${\hat{r}}_s={\tilde{g}}^T\hat{P}\tilde{g}/{\tilde{g}}^T{\hat{P}}_s\tilde{g}$, where ${\hat{P}}_s={{\hat{\Sigma }}_s}^{-1}-{{\hat{\Sigma }}_s}^{-1}X{(X^T{{\hat{\Sigma }}_s}^{-1}X)}^{-1}{X}^T{{\hat{\Sigma }}_s}^{-1}$ and ${\hat{\Sigma }}_s={\hat{W}}^{-1}+\hat{\tau }{\psi }_s$.

In ψ_s, elements below a user-specified relatedness coefficient cutoff, i.e. > 3^rd degree relatedness, are zeroed out with only close family structures being preserved. To construct ψ_s, a subset of randomly selected genetic markers, i.e. 2,000, is firstly used to quickly estimate which related samples pass the user-specified cutoff. Then the relatedness coefficients for those samples are further estimated using the full set of genetic markers, which equal to corresponding values in the ψ_f. In the model fitting using ψ_s, ${{\hat{\Sigma }}_s}^{-1}X$ and ${{\hat{\Sigma }}_s}^{-1}\tilde{g}$ need to be calculated. For this we use a sparse-LU based solve method³⁵ implemented in R. The constructed ψ_s is also used for approximating the variance of score statistics with ψ_f. For a biobank or a data set, ψ_s only needs to be constructed once and can be re-used for any phenotypes in the same date set.

SAIGE-GENE estimates variance ratios for different MAC categories. By default, MAC categories are set to be MAC equals to 1, 2, 3, 4, 5, 6 to 10, 11 to 20, and is greater than 20. Once the MAC categorical variance ratios are estimated, for each genetic marker in tested genes or regions, ${\hat{r}}_s$ can be obtained according to its MAC. Let ${\hat{R}}_s$ be a q × q diagonal matrix whose jth diagonal element is the ratio ${\hat{r}}_s$ for the jth marker in the gene (i.e. ${{\tilde{g}}_j}^T\hat{P}{\tilde{g}}_j/{{\tilde{g}}_j}^T{\hat{P}}_s{\tilde{g}}_j$). For the tested gene with q markers, ${\tilde{G}}^T\hat{P}\tilde{G}$ can be approximated as ${\hat{R}}_s^{\frac{1}{2}}{\tilde{G}}^T{\hat{P}}_s\tilde{G}{\hat{R}}_s^{\frac{1}{2}}$ (See Supplementary Note for more details).

Robust adjustment for ${\hat{R}}_s^{\frac{1}{2}}{\tilde{G}}^T{\hat{P}}_s\tilde{G}{\hat{R}}_s^{\frac{1}{2}}$ to account for unbalanced case-control ratios

To account for unbalanced case-control ratios of binary traits in region- or gene-based tests, we recently developed a robust adjustment for independent samples¹⁴. The approach first obtains well-calibrated p-values of single variant score statistics using SPA^10–12 and ER¹³. SPA is a method to calculate p-values by inverting the cumulant generating function (CGF). Since CGF completely specifies the distribution, SPA can be far more accurate than using the normal distribution. However, since SPA is still an asymptotic based approach, it does not work well when variants are very rare (ex. MAC ≤10). For those variants, we use ER, which resamples the case-control status of only individuals carrying a minor allele and is extremely fast for very rare variants. To account for the fact that individuals can have different non-genetic risk of diseases (due to covariates), the resampling was done with the estimated disease risk μ_i. Next, variances of single variant score statistics are obtained by inverting those p-values, which are then used to calibrate the variances of region- or gene-based test statistics. We have extended the approach for related samples in SAIGE-GENE. For variants with MAC > 10, single-variant p-values are obtained by SAIGE, which basically applies SPA to GLMM. For variants with MAC ≤10, we use ER with GLMM estimated $\widehat{{\mu }_i}$, which includes the random effect to maintain the correlation structure among samples. After calculating p-values of T_j for j=1,…,q, the variance of T_j is calibrated by inverting the corresponding p-value. Then the calibrated variance is applied to ${\hat{R}}_s^{\frac{1}{2}}{\tilde{G}}^T{\hat{P}}_s\tilde{G}{\hat{R}}_s^{\frac{1}{2}}$ to compute robust p-value for the region- or gene-based test. The details can be found in Supplementary Note.

Conditional analysis

In SAIGE-GENE, we have implemented the conditional analysis to perform gene-based tests conditioning on a given markers using the summary statistics from the unconditional gene-based tests and the linkage disequilibrium r² between testing and conditioning markers¹⁹. Let G be the genotypes for a gene to be tested for association, which contains q markers, and G₂ be the genotypes for the conditioning markers, which contains q₂ markers. Let β denote a q × 1 coefficient vector of the genetic effect for the gene to be tested and β₂ be a q₂ × 1 coefficient vector of the genetic effect for the conditioning markers. The genotype matrix with the non-genetic covariates projected out $\tilde{G}=G-X{\left(X^T\hat{W}X\right)}^{-1}{X}^T\hat{W}G$ and ${\tilde{G}}_2=G_2-X{\left(X^T\hat{W}X\right)}^{-1}{X}^T\hat{W}{G}_2$. In the unconditioned association tests, the test statistics $T={\tilde{G}}^T(Y-\hat{\mu })$ and $T_2={{\tilde{G}}_2}^T(Y-\hat{\mu })$. In conditional analysis, under the null hypothesis, E(T) = $\mathrm{E}({\tilde{G}}^{T}P({\tilde{G}}_2{\beta }_2\left)\right)={\tilde{G}}^T\hat{P}{\tilde{G}}_2{\beta }_2$ and E(T₂) = $\mathrm{E}\left({\tilde{G}}_2^{T}P\right({\tilde{G}}_2{\beta }_2\left)\right)={\tilde{G}}_2^T{{\hat{P}}_s\tilde{G}}_2{\beta }_2$. T and T₂ jointly follow the multivariate normal with mean (E(T), E(T₂)) and variance $S=\left[\begin{array}{cc}{\tilde{G}}^T\hat{P}\tilde{G}& {\tilde{G}}^T\hat{P}{\tilde{G}}_2\\ {\tilde{G}}_2^T\hat{P}\tilde{G}& {\tilde{G}}_2^T\hat{P}{\tilde{G}}_2\end{array}\right]$.

Thus under the null hypothesis of no association of T, i.e. H₀: β = 0, the T|T₂ follows the conditional normal distribution with $\mathrm{E}(T|T_2)={\tilde{G}}^T\hat{P}{\tilde{G}}_2{({\tilde{G}}_2^T\hat{P}{\tilde{G}}_2)}^{-1}T2$ and $\mathrm{var}(T|T_2)={\tilde{G}}^T\hat{P}\tilde{G}-{\tilde{G}}^T{\hat{P}\tilde{G}}_2{({\tilde{G}}_2^T{\hat{P}\tilde{G}}_2)}^{-1}{\tilde{G}}_2^T\hat{P}\tilde{G}$, and p-values can be calculated from the conditional distribution.

Data simulation

We carried out a series of simulations to evaluate and compare the performance of SAIGE-GENE, EmmaX-SKAT^5,7 and SMMAT⁶. We used the sequence data from 10,000 European ancestry chromosomes over 1Mb regions that was generated using the calibrated coalescent model in the SKAT R package⁵. We randomly selected 10,000 regions with 3Kb from the sequence data, followed by the gene-dropping simulation³⁶ using these sequences as founder haplotypes that were propagated through the pedigree of 10 family members shown in Supplementary Figure 11. Only variants with MAF ≤ 1% were used for simulation studies. Quantitative phenotypes were generated from the following linear mixed model $y_i=X_1+X_2+G_i\beta +b_i+{\epsilon }_i$, where G_i is the genotype value, β is the genetic effect sizes, b_i is the random effect simulated from $N(0,\mathrm{\tau }\psi )$, and ε_i is the error term simulated from $N(0,(1-\mathrm{\tau }\left)I\right)$. Two covariates, X₁ and X₂, were simulated from Bernoulli(0.5) and N(0,1), respectively. Binary phenotypes were generated from the logistic mixed model $logit({\pi }_{i0})={\alpha }_0+b_i+X_1+X_2+G_i\beta$, where β is the genetic log odds ratio, b_i is the random effect simulated from N(0, τ ψ) with τ = 1. The intercept α₀ was determined by the disease prevalence (i.e. case-control ratios). Given τ = 1, the liability scale heritability is 0.23³⁷.

To evaluate the type I error rates at exome-wide α=2.5×10⁻⁶, we first simulated 10,000 regions, and then simulated 1000 sets of quantitative phenotypes for each simulated region with different random seeds under the null hypothesis with β = 0. Gene-based association tests were performed using SAIGE-GENE, EmmaX-SKAT, and SMMAT therefore in total 10⁷ tests for each of Burden, SKAT, and SKAT-O tests were carried out. Two different settings for τ were evaluated: 0.2 and 0.4 and two different sample relatedness settings were used: one has 500 families and 5,000 independent samples and other one has 1,000 families, each with 10 family members. We also simulated 1,000 sets of binary phenotypes for case-control ratios 1:99, 1:19, 1:9, 1:4, and 1:1 for 500 families and 5,000 independent samples. Burden, SKAT, and SKAT-O tests were performed on the 10,000 genome regions using SAIGE-GENE, in total 10⁷ tests for each method for each case-control ratio.

For the power simulation, phenotypes were generated under the alternative hypothesis β ≠ 0. Two different settings for proportions of causal variants are used: 10% and 40%, corresponding to |β| = |log10(MAF)| and |β| = |0.3log10(MAF)|, respectively. In each setting, 80% and 100% had negative effect sizes. We simulated 1,000 datasets in each simulation, and power was evaluated at test-specific empirical α, which yields nominal α=2.5×10^-6. The empirical α was estimated from the type I error simulations. Similarly, 1,000 sets of binary traits were generated for 10,000 samples (500 families and 5,000 independent samples) under the alternative hypothesis β ≠ 0 using two different settings: cohort study with various disease prevalence (0.01, 0.05, 0.1, and 0.5); and case-control sampling with three different case-control ratios (1:19, 1:9, and 1:1) based on a disease prevalence 1% in the population (Supplementary Note 2.5). 40% variants are simulated as causal variants, among which 80% are risk-increasing variants and 20% are risk-decreasing. The absolute effect sizes of causal variants are set to be |0.55log₁₀(MAF)| and |0.35log₁₀(MAF)| for cohort study and case-control sampling, respectively.

HUNT and UK Biobank data analysis

We applied SAIGE-GENE to the high-density lipoprotein (HDL) levels in 69,500 Norwegian samples from a population-based HUNT study^15,16. About 70,000 HUNT participants were genotyped using Illumina HumanCoreExome v1.0 and 1.1 and imputed using Minimac3³⁸ with a merged reference panel of Haplotype Reference Consortium (HRC)³⁹ and whole genome sequencing data (WGS) for 2,201 HUNT samples. Variants with imputation r² < 0.8 were excluded from further analysis. Participation in the HUNT Study is based on informed consent, and the study has been approved by the Data Inspectorate and the Regional Ethics Committee for Medical Research in Norway. Total 13,416 genes with at least two rare (MAF ≤ 1%) missense and/or stop-gain variants with imputation r² ≥ 0.8 were tested. Variants were annotated using Seattle Seq Annotations (http://snp.gs.washington.edu/SeattleSeqAnnotation138/). We used 249,749 pruned genotyped markers to estimate relatedness coefficients in the full GRM for Step 1 and used the relative coefficient cutoff ≥ 0.125 for the sparse GRM.

We have also analyzed 53 quantitative traits and 10 binary traits using SAIGE-GENE in the UK Biobank for 408,910 participants with White British ancestry². UK Biobank protocols were approved by the National Research Ethics Service Committee and participants signed written informed consent. Markers that were imputed by the HRC³⁹ panel with imputation info score ≥ 0.8 were used in the analysis. Total 15,342 genes with at least two rare (MAF ≤ 1%) missense and stop-gain variants that were directly genotyped or successfully imputed from HRC (imputation score ≥ 0.8) were tested. We used 340,447 pruned markers, which were pruned from the directly genotyped markers using the following parameters, were used to construct GRM: window size of 500 base pairs (bp), step-size of 50 bp, and pairwise r² < 0.2. We used the relative coefficient cutoff ≥ 0.125 for the sparse GRM.

DATA AVAILABILITY STATEMENT

SAIGE-GENE is implemented as an open-source R package available at https://github.com/weizhouUMICH/SAIGE/master.

The summary statistics and QQ plots for 53 quantitative phenotypes and 10 binary phenotypes in UK Biobank by SAIGE-GENE are currently available for public download at https://www.leelabsg.org/resources.

Genome build

All genomic coordinates are given in NCBI Build 37/UCSC hg19.

Statistical analysis

We performed gene-based Burden, SKAT and SKAT-O tests using SAIGE-GENE on 15,342 genes for 53 quantitative traits and 10 binary traits in 408,910 UK Biobank participants with White British ancestry, who passed the quality control in the UK Biobank². In the linear mixed model for quantitative traits, the first four genetic principal components (PCs), gender and age when attended assessment center were included as the non-genetic covariates. In the logistic mixed model for binary traits, the first four genetic principal components, gender and birth year were included as the non-genetic covariates. We also performed the same gene-based tests 13,416 genes for HDL levels in 69,500 Norwegian samples from the HUNT study^15,16. In the linear mixed model for HDL, age, sex, genotyping batch, and first four PCs were included as non-genetic covariates. The numbers of samples used for analysis are included in the legend of each figure.

Life Sciences Reporting Summary

Further information on study design is available in the Nature Research Reporting Summary linked to this article.

Extended Data

Extended Data Fig. 1. Workflow of SAIGE-GENE.

SAIGE-GENE consists of two steps: (1) Fitting the null generalized linear mixed model (GLMM) to estimate variance components and other model parameters; (2) Testing for association between each genetic variant set, such as a gene or a region, and the phenotype.

Extended Data Fig. 2. Plots of the variance ratio of the score statistics by MAC for rare variants with and without the full GRM for sample relatedness (left) and with the full GRM and a sparse GRM for closely related samples (right).

a, Genotypes were simulated for 500 families and 5,000 independent individuals based on the pedigree structure shown in Supplementary Fig. 1 and the null model was fitted for the simulated quantitative trait with h² = 0.2. The sparse GRM was constructed using a coefficient of relatedness cutoff 0.2. b, 20,000 samples with White British ancestry were randomly selected from the UK Biobank and the null model was fitted for the automated read pulse rate. The sparse GRM was constructed using a coefficient of relatedness cutoff 0.125. c, 20,000 samples were randomly selected form the HUNT study and the null model was fitted for HDL. The sparse GRM was constructed using a coefficient of relatedness cutoff 0.125.

Extended Data Fig. 3. Scatter plots of association P-values from SAIGE-GENE versus SMMAT and EmmaX-SKAT for the Burden, SKAT, and SKAT-O tests based on simulation data on the −log₁₀ scale.

1,000,000 genes were tested with 1,000 families, each having 10 members, as shown in the Supplementary Fig. 1. The Pearson’s correlation coefficients r² > 0.99 for −log₁₀(P-values) between SAIGE and SMMAT and between SAIGE and EmmaX-SKAT. a, h² = 0.2. b, h² = 0.4.

Extended Data Fig. 4. Scatter plots of association P-values from SAIGE-GENE versus SMMAT and EmmaX-SKAT for the Burden, SKAT, and SKAT-O tests based on real data analysis on the −log₁₀ scale.

a,b, 12,000 genes were tested for automated read pulse rate on 20,000 randomly selected white British samples in the HRC-imputed UK Biobank (a) and for HDL on 20,000 randomly selected samples in HUNT (b). Missense and stop-gain variants with MAF ≤ 1% were included. The Pearson’s correlation coefficients r² > 0.99 for −log₁₀(P-values) between SAIGE and SMMAT and between SAIGE and EmmaX-SKAT.

Extended Data Fig. 5. Scatter plots of association P-values on the −log10 scale from SAIGE-GENE with two sample relatedness cutoffs for the sparse GRM, 0.125 and 0.2. 15,338 genes were tested for automated read pulse rate in white British samples in the HRC-imputed UK Biobank (N = 385,365).

N, sample size. Missense and stop-gain variants with MAF ≤ 1% were included. a, Burden. b, SKAT. c, SKAT-O.

Extended Data Fig. 6. Quantile-quantile plots of association P-values for 10 million variant sets from the simulation study for phenotypes with various case-control ratios (N = 100,000).

a, Case:Control = 1:9. b, Case:Control = 1:19. c, Case:Control = 1:99. N, sample size.

Extended Data Fig. 7. Empirical computation time.

a,b, Step 1 for fitting a null mixed model (a) and Step 2 for association tests (b), respectively, by sample sizes (N) for gene-based tests for 15,342 genes, each containing 50 rare variants. Benchmarking was performed on randomly sub-sampled UK Biobank data with 408,144 White British participants for waist-to-hip ratio. The reported run time was median of five runs with samples randomly selected from the full sample set using different sampling seeds. The reported computation time for EmmaX-SKAT and SMMAT was projected when N > 20,000. As the number of tested markers varies by sample sizes, the computation time was projected for 50 markers per gene for plotting. Numerical data are provided in Supplementary Table 1.

Extended Data Fig. 8. Log-log plot of the estimated run time as a function of number of markers per gene.

Benchmarking was performed on randomly sub-sampled 400,000 UK Biobank data with 408,144 white British participants for waist-to-hip ratio on 15,342 genes. The plotted run time was median of five runs with samples randomly selected from the full sample set using different sampling seeds. The computation time for other different number of markers per gene was projected based on the benchmarked time.

Extended Data Fig. 9. Log-log plots of the estimated run time and memory usage as a function of sample size (N) for genome-wide tests for 286,000 chunks.

a, Run time. b, Memory usage. Each chunk contains 50 variants on average, given that there are 14.3 million markers in the HRC-imputed UK Biobank with MAF ≤ 1% and imputation info score ≥ 0.8. Numerical data are provided in Supplementary Table 1. Benchmarking was performed on randomly sub-sampled UK Biobank data with 408,144 white British participants for waist-to-hip ratio. The plotted run time and memory were medians of five runs with samples randomly selected from the full sample set using different sampling seeds.

Extended Data Fig. 10. Log-log plots of the estimated run time for as a function of sample size (N) for SAIGE-GENE with and without using the robust adjustment.

a, Exome-wide gene-based tests for 15,871 genes. b, Genome-wide tests for 286,000 chunks. Each gene or chunk contains 50 variants on average. Benchmarking was performed on randomly sub-sampled UK Biobank data with 402,163 white British participants tested for glaucoma (PheCode: 365, 4,462 cases and 397,701 controls). The case-control ratio remained the same in subsampled data sets. The reported run time was median of five runs with samples randomly selected from the full sample set using different sampling seeds. As the number of tested markers varies by sample sizes, the computation time was projected for 50 markers per gene for plotting. Numerical data are provided in Supplementary Table 2.