Abstract
Evaluation of airborne infection risk with spatial and temporal resolutions is indispensable for the design of proper interventions fighting infectious respiratory diseases (e.g., COVID-19), because the distribution of aerosol contagions is both spatially and temporally non-uniform. However, the well-recognized Wells-Riley model and modified Wells-Riley model (i.e., the rebreathed-fraction model) are limited to the well-mixed condition and unable to evaluate airborne infection risk spatially and temporally, which could result in overestimation or underestimation of airborne infection risk. This study proposes a dilution-based evaluation method for airborne infection risk. The method proposed is benchmarked by the Wells-Riley model and modified Wells-Riley model, which indicates that the method proposed is a thorough expansion of the Wells-Riley model for evaluation of airborne infection risk with both spatial and temporal resolutions. Experiments in a mock hospital ward also demonstrate that the method proposed effectively evaluates the airborne infection risk both spatially and temporally. The proposed method is convenient to implement for the development of healthy built environments.
Keywords: Infectious respiratory disease, Airborne infection risk, Dilution, Spatial and temporal, Wells-riley model
1. Introduction
Infectious respiratory diseases (e.g., tuberculosis, influenza, and aspergillosis) are severe threats to people's health and economic development [1]. Particularly, the global pandemic of COVID-19 results in substantial loss of human lives and jeopardizes human development (social, economic, etc.). Airborne infection due to the inhalation of pathogen-laden aerosols is one major transmission pathway of infectious respiratory diseases [2]. Infectors' coughing, sneezing, talking, and breathing generate tens of thousands of infectious droplets, and most of the generated infectious droplets evaporate into the air as infectious droplet nuclei [3,4]. A COVID-19 infector can yield infectious droplets with 100,000 virions every minute of speaking [4,5]. The airborne transmission of the infectious droplet nuclei can occur over a long distance, causing cross infections. For example, Yu et al. [6] found that SARS airborne infections occurred between different rooms and between adjacent buildings. Liu et al. [7] measured the concentration of airborne COVID-19 RNA in isolation wards and ventilated patient rooms, and suggested that COVID-19 could be transmitted via aerosols. More and more evidence reveals the airborne infection risk of COVID-19 [8,9].
Evaluation of airborne infection risk should take into account the spatially and temporally non-uniform distribution of pathogen-laden aerosols [1]. The spread of pathogen-laden aerosols is significantly affected by the complicated and transient interactions among the respiratory flows and thermal plumes of occupants, and ventilation flow, which results in the spatially and temporally non-uniform distribution of pathogen-laden aerosols [10]. Since occupants generally spend more than 90% time conducting indoor activities, indoor ventilation is one of the most effective engineering solutions for reducing airborne transmission by diluting the pathogen-laden aerosols with pathogen-free air [11,12]. Airflow patterns of advanced ventilation with non-uniform aerosol distribution can more effectively reduce airborne transmission risk. For example, displacement ventilation and stratum ventilation target diluting the airborne contaminants in the breathing zone rather than the entire room, thus improve the contaminant removal efficiency of the breathing zone by up to 50% [13].
However, it is challenging to evaluate the airborne infection risk with spatial and temporal resolutions in practice. The dose-response model and Wells-Riley model are two methods for quantitative evaluation of the airborne infection risk [14]. Since the dose-response model requires the information which is costly to obtain during experimental and on-site studies, e.g., the particle sizes and infectivity (involving medical and microbiological sciences), the dose-response model is less frequently used than the Wells-Riley model [1,10,15]. The Wells-Riley model is a simple and quick evaluation method of the airborne infection risk, because it uses the concept of quantum to implicitly consider the infectivity, infectious source strength, biological decay of pathogens, etc. [14]. As a result, the Wells-Riley model has been widely used in the studies of infectious respiratory diseases [1,10,15]. However, the Wells-Riley model is based on the well-mixed and steady assumption that the distribution of pathogen-laden aerosols is spatially and temporally uniform. With this assumption, the airborne infection risk could be underestimated by the Wells-Riley model, and the interventions for reducing airborne infection risk suggested by the Wells-Riley model could be improper [1,10,16]. For example, the Wells-Riley model suggests a larger ventilation flow rate. However, increasing the ventilate rate might deteriorate indoor air quality due to the potential negative effects of the increased ventilation flow rate on the contaminant removal efficiency of non-uniform airflow pattern [17].
Rudnick and Milton [18] proposed the concept of rebreathed fraction, and used it to modify the Wells-Riley model for the transient condition. The rebreathed fraction is calculated from the difference between indoor and outdoor CO2 concentrations [18]. The rebreathed-fraction model has been well recognized for the airborne infection risk with a temporal resolution [10,19,20]. However, the rebreathed-fraction model is also based on the well-mixed assumption, and thus cannot evaluate the airborne infection risk spatially [18]. Numerical simulations (e.g., computational fluid dynamics) have been used to provide the spatial quantum concentration of airborne pathogens for the Wells-Riley model to evaluate the airborne infection risk spatially [22,23]. However, this method is inapplicable to physical experiments because it is impossible to measure the quantum concentration of airborne pathogens for experimental and on-site studies [1,10,18]. Although numerical simulations are powerful in epidemical studies, physical experiments are indispensable for reliable results [10]. Thus, there is an urgent need for an evaluation method of airborne infection risk with spatial and temporal resolutions for practical applications.
This study will provide a dilution-based evaluation method of the airborne infection risk for both spatial and temporal resolutions. The proposed model is illustrated in Section 2, and benchmarked by the Wells-Riley model under the well-mixed and steady condition in Section 3, and by the rebreathed-fraction model under the well-mixed and transient condition in Section 4. Experiments of a mock hospital ward served by displacement ventilation are conducted in Section 5 to demonstrate the applicability of the method proposed to evaluate airborne infection risk spatially and temporally. Further improvements of the proposed method are discussed in Section 6.
2. Dilution-based airborne infection risk estimation proposed
The concept of dilution is diluting the airborne contaminants with clean air so that the concentration of airborne contaminants is reduced. Dilution is the mechanism of ventilation in reducing airborne infection risk [1]. According to the concept of dilution, the dilution ratio is defined as the ratio between the source concentration to the contaminant concentration at the target position (Equation (1)). The dilution ratio can vary among different positions relative to the contaminant source transiently. The dilution ratio can be calculated from the measured concentration of tracer gas in field studies or from the predicted pollutant distribution by CFD simulations. With the dilution ratio, the quantum concentration of airborne pathogens at the target position is calculated with Equation (2), which is the quantum concentration exhaled by the infector diluted at the target position. The quantum is an infectious dose unit [24], and one quantum is the quantity of pathogens required to cause an infection risk of 63.2% (i.e., 1-e−1) [19]. For example, the quantum generate rate of a Tuberculosis infector as suggested by Andrews et al. [25] is 1.25 quanta/h, and that of an asymptomatic infector COVID-19 could be 142 quanta/h [26]. The quantum generation rate is generally inversely calculated by the (modified) Wells-Riley model with epidemical data [18,27], and can also be calculated from the basic reproduction number with epidemical data [28] or by the method requiring detailed information of biological properties of pathogens [26]. It is noted that the penetration factor of mask in Equation (2) () is used to account for the effects of facial masks [29,30] in reducing the airborne infection risk [14].
| (1) |
| (2) |
where C source and C target are the airborne contaminant concentrations at the source and target position respectively (ppm); C quantum is the airborne quantum concentration at the target position (quanta/m3); D is the dilution ratio at the target position; p infector is the breathing rate of the infector (m3/s); q is the quantum generation rate (quanta/s); is the penetration factor of mask.
With the quantum concentration at the target position, the quanta inhaled by a susceptible at the target position over a given exposure period is calculated by Equation (3). With the inhaled quanta, the airborne infection risk of a susceptible at the target position over that exposure period is estimated based on Poisson distribution (Equation (4)). The pathogens are discrete matters and distribute in a medium randomly following Poisson distribution [14,18,20,32]. The airborne infection risk is the probability of that susceptible to be infected because of the inhaled airborne pathogens. The dilution-based airborne infection risk proposed is obtained as Equation (5) by combining Equations (2), (3), (4)).
| (3) |
| (4) |
| (5) |
where C quantum(t) and D(t) are the quantum concentration (quanta/m3) and dilution ratio at the target position at time t during a given exposure period of T respectively; N quantum is the inhaled quanta by a susceptible at the target position during the given exposure period; P D is the airborne infection risk at the target position during the given exposure period estimated by the dilution-based estimation method proposed; p susceptible is the breathing rate of the susceptible (m3/s), which can be different from that of the infector because the infector and susceptible have different health conditions and might have different activity levels [26].
Since the method proposed employs the concept of the quantum, it has the merit as the Wells-Riley model of implicitly considering the biological complexities of the infectivity, infectious source strength, biological decay of pathogens, etc., which makes the evaluation of the airborne infection risk by the method proposed simple and quick [14]. Moreover, compared with the Wells-Riley model, the method proposed has two advantages. First, the method proposed can estimate the airborne infection risk for any target position during any exposure period (Equation (5)), i.e., the method proposed evaluates the airborne infection risk for both spatial and temporal resolutions. Second, the method proposed is more convenient for practical applications. The Wells-Riley model (Equation (6)) requires knowing the numbers of infectors, but the method proposed does not. The information on the numbers of infectors is not always available, particularly when asymptomatic infectors present. It was reported that the asymptomatic infectors were responsible for 79% of COVID-19 infections in Wuhan [4,33]. When using the proposed dilution-based evaluation of airborne infection risk, firstly the dilution ratio is calculated according to Equation (1) with the measured/simulated pollutant concentrations at the source and the target position, and then the airborne infection risk is calculated with the dilution ratio according to Equation (5). Since neither Equation (1) nor Equation (5) requires the numbers of infectors, the proposed dilution-based evaluation does not require knowing the numbers of infectors. The mechanism of the dilution-based evaluation not requiring knowing the numbers of infectors is that the dilution ratio implicitly includes the information of the numbers of infectors, which will be revealed in Section 3. Besides, the Wells-Riley model (Equation (6)) requires the input of the ventilation flow rate which is inconvenient to measure in practice [18]. For example, Wu et al. [34] measured on-site tracer gas concentration in a residential building, and approximated the ventilation flow rate from the measured tracer gas concentration for the Wells-Riley model to evaluate the airborne infection risk. The approximation of the ventilation flow rate from the tracer gas concentration increases the evaluation complexity and decreases the evaluation reliability. In contrast, the dilution ratio can be conveniently and reliably obtained from the tracer gas concentration (Equation (1)) for the method proposed to evaluate the airborne infection risk, which will be further demonstrated in Section 5.
| (6) |
where I is the number of infectors; P WR is the airborne infection risk estimated by the Wells-Riley model; p is the breathing rate of a typical person (m3/s); Q is the ventilation flow rate (m3/s); t is the time length of the exposure period (s).
3. Benchmark with Wells-Riley model under well-mixed and steady condition
As introduced in Section 1, the Wells-Riley model has been well recognized to provide a reliable evaluation of the airborne infection risk under the well-mixed and steady condition. Since the method proposed evaluates the airborne infection risk for both spatial and temporal resolutions, the well-mixed and steady condition is one of the special cases. When the method proposed applies to the well-mixed and steady condition, it should produce identical or similar results to those from the Wells-Riley model. This is proofed as follows. According to the mass conservation law, the variation of contaminants in the space is the generated contaminants in the space minus the contaminants removed from the space by ventilation, which is described by Equation (7) when contaminants are well mixed in the space air [20,34]. When the contaminants refer to the exhaled air by the infectors (Equation (8)) and the contaminants in the ventilation air supply is zero (clean air), the contaminant concentration in the exhaled air is unity and the dilution ratio is the reciprocal of the contaminant concentration in the space air (Equation (9)). For the steady condition, the variation of the contaminant concentration in the space air is zero (Equation (10)). From Equations (8), (9), (10)), the dilution ratio under the well-mixed and steady condition is obtained as the function of the ventilation flow rate, numbers of infectors, and breathing rate of infectors (Equation (11)), implying that the dilution ratio implicitly takes into account the ventilation flow rate, numbers of infectors, and breathing rate of infectors, which makes the implementation of the method proposed convenient in practice as discussed in Section 2. Combing Equations (5), (11)), the method proposed for the well-mixed and steady condition is obtained as Equation (12). In Equation (12), the breathing rate by the susceptible can be the same as that of a typical person and the penetration factor of mask can be unity as assumed by the Wells-Riley model (i.e., wearing no masks). As a result, the proposed model for the well-mixed and steady condition (Equation (12)) produces the same airborne infection risk as the Wells-Riley model (Equation (6)). This indicates that the method proposed is an expansion of the Wells-Riley model for the evaluation of airborne infection risk with both spatial and temporal resolutions.
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
where C in and C o are the contaminant concentrations (i.e., the concentrations of exhaled air by the infectors) in the space air and ventilation supply air respectively (ppm); D ms is the dilution ratio under the well-mixed and steady condition; G is the contaminant generation rate in the space (i.e., exhaled air by the infectors which can be represented by exhaled CO2 or other tracer gases) (m3/s) [18,20,21]; P D,ms is the airborne infection risk estimated by the dilution-based estimation method proposed under the well-mixed and steady condition; V is the volume of the space (m3).
4. Benchmark with rebreathed-fraction model under well-mixed and dynamic condition
The rebreathed-fraction model (Equations (13), (14))) is a modified Wells-Riley model for a reliable evaluation of the airborne infection risk under the well-mixed and transient condition [10,[18], [19], [20]]. Since the method proposed can evaluate the airborne infection risk for both spatial and temporal resolutions, the well-mixed and transient condition is one of the special cases. When the method proposed applies to the well-mixed and transient condition, it should produce identical or similar results to those from the rebreathed-fraction model. This is proofed as follows. By integrating Equation (7), the transient contaminant concentration in the space air is obtained as Equation (15) [18,20]. When the contaminants refer to the exhaled air by infectors, the dilution ratio under the well-mixed and transient condition is obtained as Equation (16) from Equations (8), (9), (15) with the contaminant concentrations in the exhaled air and the ventilation air supply of unity and zero respectively. When the contaminant is CO2, the contaminant generation rate in the space is the CO2 generated by all occupants (Equation (17)), and Equation (15) is transferred to be Equation (18). According to the definition of the rebreathed fraction (Equation (14)) [18] and Equation (18), the rebreathed fraction is expressed as Equation (19). From Equations (16), (19)), the relationship between the dilution ratio and rebreathed fraction under the well-mixed and transient condition is obtained as Equation (20). With Equation (20) to replace the dilution ratio in Equation (5), the method proposed under the well-mixed and transient condition is expressed as Equation (21). In Equation (21), the breathing rate by the susceptible can be the same as that of a typical person and the penetration factor of mask can be unity as assumed by the rebreathed-fraction model (i.e., wearing no masks). As a result, the proposed model for the well-mixed and transient condition (Equation (21)) produces the same airborne infection risk as the rebreathed-fraction model (Equation (13)). This indicates that while the rebreathed-fraction model is a limited expansion of the Wells-Riley model with a temporal resolution of airborne infection risk, the method proposed is a thorough expansion of the Wells-Riley model with both spatial and temporal resolutions of airborne infection risk.
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
where , and are the CO2 concentrations in the exhaled air, space air and ventilation air supply respectively (ppm); D mt is the dilution ratio under the well-mixed and transient condition; f is the rebreathed faction;
is the CO2 generation rate by the occupants in the space (m3/s); n is the number of occupants in the space; P RF are P D,ms are the airborne infection risks under the well-mixed and transient condition estimated by the rebreathed-fraction model and the dilution-based estimation method proposed respectively.
5. Demonstration of applicability of method proposed for both spatial and temporal resolutions
Experiments are conducted to demonstrate the effectiveness of the method proposed for the evaluation of airborne infection risk for both spatial and temporal resolutions. The environmental chamber, with dimensions of 8.8 m (length) × 6.1 m (width) × 2.4 m (height), is configured as a mock hospital ward with multiple beds (Fig. 1 ). The ward is served with displacement ventilation that the conditioned air is supplied near the floor level (S1–S14) (with the supply air temperature around 20 °C and supply airflow rate around 12 ACH) and exhausted from the ceiling (E1- E3). Displacement ventilation has an airflow pattern with high contaminant removal efficiency at the breathing level [13]. SF6 (released from the mouth of the infector in Fig. 1) is used as the tracer gas to represent the airborne contaminants. Gas has been justified and used as a reasonable surrogate for virus-laden aerosols [18,20,[34], [35], [36], [37], [38]]. Three target positions (L1-L3) with the standing susceptible occupants are concerned, and the tracer gas concentrations at the three target positions are measured at the breathing level (i.e., at the height of 1.5 m above the floor). INNOVA 1412i is used to measure the concentration of SF6 with a measurement accuracy of 0.06 ppm.
Fig. 1.
Experimental setup of mock hospital ward with multiple beds served with displacement ventilation.
Note: S1–S14 are the air supply terminals; E1- E3 are the exits; L1-L3 are sampling points at the height of 1.5 m above the floor.
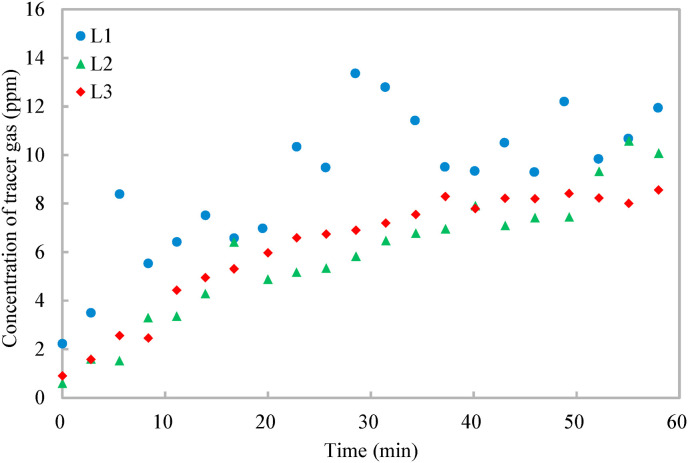
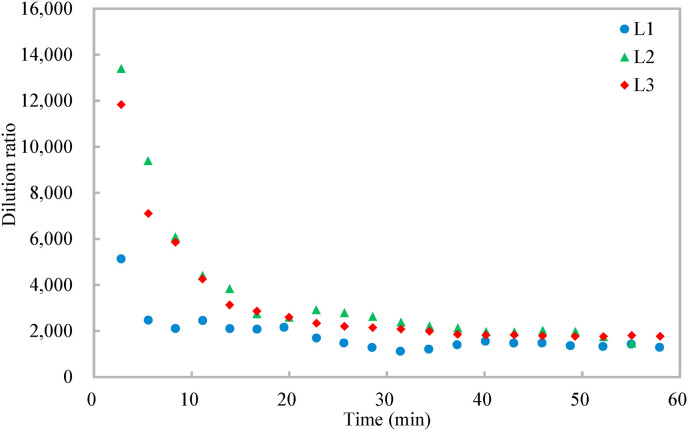
Fig. 2 shows that the tracer gas distribution is both spatially and temporally non-uniform. The concentration of the tracer gas generally increases first and then tends to be steady, but fluctuates slightly due to the randomness induced by air turbulence [14]. The tracer gas concentration at the target position of L1 is higher than those at the other two target positions because it is the closest to the infector. From the tracer gas distribution, the dilution ratio is calculated (Equation (1)). The dose rate of the tracer gas is 2 ml/s and the breathing rate of the resting infector is 0.49 m3/h [26], resulting in a contaminant concentration of the source around 14,700 ppm for the calculation of the dilution ratio (Equation (1)). Fig. 3 shows that the dilution ratio also has spatial and temporal resolutions, varying from around 2000 to 14,000. The dilution ratios at the three target positions decrease first and then tend to be steady, and the dilution ratio of the target position (L1) closest to the infector is the smallest.
Fig. 2.
Variations of tracer gas concentrations at different target positions with time.
Fig. 3.
Variations of dilution ratio at different target positions with time.
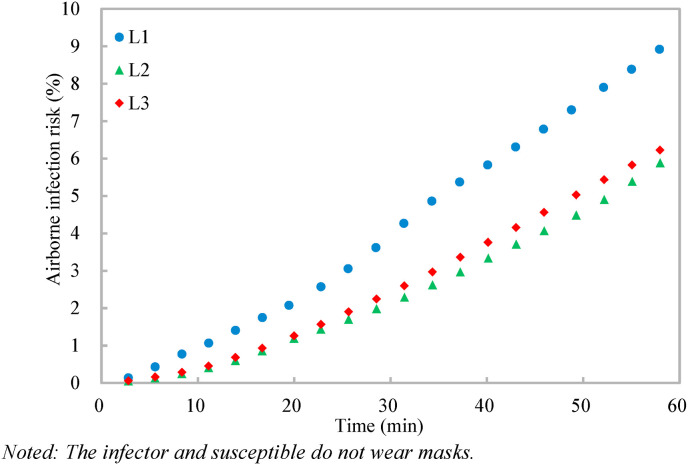
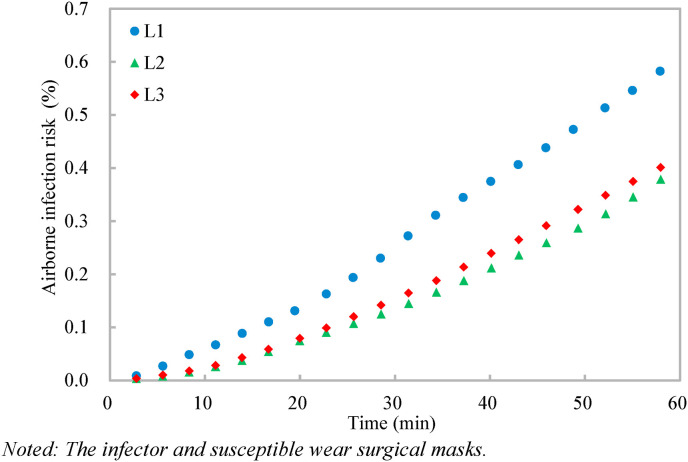
With the dilution ratio, the airborne infection risks at the three target positions are calculated (Equation (5)) (Fig. 4, Fig. 5 ). The quantum generation rate of a COVID-19 infector is assigned to be 142 quanta/h and the breathing rate of a standing susceptible is 0.54 m3/h [26]. It should be noted that the quantum generation rate of COVID-19 varies when the activity level and viral load of the infector vary [26], and the quantum generation rate of 142 quanta/h is used as a specific case [21] for the application demonstration of the proposed dilution-based evaluation of airborne infection risk. Two scenarios are considered, one with no masks and the other with surgical masks for both the infector and susceptible. Under Scenario 1 with no masks (i.e., with the penetration factor of mask of unity) (Fig. 4), the airborne infection risks at the three target positions increase with time, and the airborne infection risks at the target positions over the given exposure period (1 h) of L1-L3 are 9.5%, 5.9%, and 6.7% respectively. The large variations of the airborne infection risk indicate that the airborne infection risk should be evaluated both spatially and temporally. Otherwise, the infection airborne risk could be overestimated (e.g., for the target position far away from the source, such as L2 and L3) or underestimated (e.g., for the target position close to the source, such as L1). When surgical masks with an efficiency of 75% [12] are used by both the infector and susceptible under Scenario 2 (Fig. 5), the penetration factor of mask is 0.0625 (i.e., (1–0.75)2), and the airborne infection risks of all the three target positions are largely reduced to be below 0.7%, indicating that the surgical masks are effective in reducing the cross infections [4]. These results demonstrate the effectiveness of the method proposed in evaluating the airborne infection risk both spatially and temporally.
Fig. 4.
Variations of airborne infection risks at different target positions with time.
Noted: The infector and susceptible do not wear masks.
Fig. 5.
Variations of airborne infection risks at different target positions with time.
Noted: The infector and susceptible wear surgical masks.
6. Discussion
The indoor airborne infection risk control is particularly important since people spend around 90% of their time indoors. However, the current practice of indoor environments generally controls the aerosol pollutant concentration (e.g., the exhaled CO2 by CFD simulations or experimental measurements) for indoor air quality [13,17,39]. This is ineffective for the airborne infection risk control of infectious respiratory diseases, because the current aerosol pollutant control does not consider the biological properties of pathogens (e.g., the viral load and infectivity) [13,17,39]. It is challenging to obtain the biological properties of pathogens [14]. The biological properties of pathogens differ among infectious respiratory diseases [28]. Even for the same infectious respiratory disease, the biological properties of the pathogen are variable [26]. The well-recognized Wells-Riley model and its modification (the rebreathed-fraction model) estimate the airborne infection risk with the infector's quantum generation rate, considering the biological properties of pathogens implicitly [14]. However, the Wells-Riley model has no spatial and temporal resolutions and the rebreathed-fraction model has no temporal resolution, resulting in overestimation/underestimation of airborne infection risk [14,18,21]. The proposed dilution-based evaluation of airborne infection risk, as a thorough expansion of the Wells-Riley model, has both spatial and temporal resolutions (Sections 2, 5).
Moreover, both the Wells-Riley model (Equation (6)) and the rebreathed-fraction model (Equation (13)) cannot take into account the effects of different values of quantum generation rates when there are multiple infectors in an indoor environment [18]. Infectors of the same respiratory disease can have different quantum generation rates, e.g., caused by different infection stages, activity levels, etc., which could significantly affect the airborne infection risk [26]. When the quantum generation rates of infectors in an indoor environment are different, the dilution ratios of infectors with different quantum generation rates should be calculated separately at a target position (Equation (22)). To obtain the dilution ratio of each infector, the exhaled pollutants by infectors should be differentiated, e.g., obtaining C source,k and C target,k in Equation (22) with different tracer gases or CFD simulations. Each infector's dilution ratio can also be calculated by the linear superposition theory of fixed airflow field with the accessibility index [40] or the contribution ratio [41], which will be further developed and calibrated in future studies. Then, based on each infector's dilution ratio and quantum generation rate, the airborne infection risk at the target position is calculated by Equation (23) (modified from Equation (5)).
| (22) |
| (23) |
where Subscript k indicates the kth infector, for example, C target,k is the contaminant concentration at the target position caused by the kth infector.
It should be noted that there are other modifications of the Wells-Riley model [26,27], which also have the potential to be applied to the proposed dilution-based evaluation of airborne infection risk. For example, besides ventilation, other factors could also affect the removal of infectious viruses, e.g., masks, ultraviolet irradiation, and filters. The proposed dilution-based evaluation of airborne infection risk in Equation (5) only accounts for the effect of masks with the penetration factor of mask [14]. To take into account the factors related to the infectious virus removal (i.e., the ventilation, particle deposition on surfaces, and viral inactivation), the Wells-Riley model has been modified to be Equation (24) with the help of the infectious virus removal rate [26]. Similarly, the proposed dilution-based evaluation of airborne infection risk (Equation (5)) can be modified to Equation (25) to account for the factors related to infectious virus removal. It should be noted that the modified infectious virus removal rate in Equation (25) does not explain the effect of the ventilation because the effect of the ventilation has already been implicitly explained by the dilution ratio (Equation (11)). Moreover, the modified infectious virus removal rates for different target positions can be different, e.g., with local filters or viral inactivation devices, which will be further investigated in future studies.
| (24) |
| (25) |
where P MWR and are the modified Wells-Riley model and the modified dilution-based evaluation of airborne infection risk which take the factors related to infectious virus removal into account; N o is the initial quantum number in the indoor environment (quanta); is the initial quantum concentration at the target position (quanta/m3); IVRR is the infectious virus removal rate which is the sum of the contributions of the ventilation, particle deposition on surfaces, and viral inactivation (s−1); is the modified infectious virus removal rate which is the sum of the contributions of the particle deposition on surfaces and viral inactivation (s−1).
It should also be noted that the proposed dilution-based evaluation of airborne infection risk is particularly useful for the field of built environments. During the design and operation of buildings, it is impractical to measure the virus to evaluate and control airborne infection risk. The proposed method employs the concept of dilution, which measures/simulates the tracer gas instead of measuring the virus. At present, the common practice is to support the design of an indoor environment with full-scale laboratory measurements. An example of how the proposed method can be used in a hospital ward with multiple beds is demonstrated in Section 5. Measurements of tracer gas, released at the location of one infected patient, are performed. Similarly, different tracer gasses (N2O, SF6, Freon, etc.) can be released at several locations simultaneously. Thus, without increasing the measurement time, the importance of the infected person's location can be studied. The proposed method can be used to assess the performance of different designs easily. The development and use of a large number of cheap wireless sensors will allow for quick and detailed spatial and temporal assessment of airborne infection risk with the proposed method. Thus, the proposed method is convenient for practical applications in the field of built environments.
7. Conclusions
This study proposes an evaluation method for the airborne infection risk based on the concept of dilution. The dilution ratio is used to calculate the inhaled quanta of airborne pathogens with which the airborne infection risk is calculated according to Poisson distribution. The method proposed is benchmarked by the Wells-Riley model under the well-mixed and steady condition, and by a modified Wells-Riley model (i.e., rebreathed-fraction model) under the well-mixed and transient condition, which indicates that the method proposed is a thorough expansion of the Wells-Riley model. Compared with the Wells-Riley model, the method proposed has two advantages of 1) evaluation of airborne infection risk for both spatial and temporal resolutions, and 2) convenience in practical applications. Experiments in a mock hospital ward with multiple beds served with displacement ventilation demonstrate that the method proposed effectively evaluates airborne infection risk both spatially and temporally. The method proposed contributes to the reliable evaluation of airborne infection risk and developing effective interventions for reducing cross infections of infectious respiratory diseases (e.g., COVID-19).
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
The work described in this paper is supported by the National Natural Science Foundation of China (Project No. 51878585). The help of Ms. Yalin Lu in the experiments is highly appreciated.
References
- 1.Aliabadi A.A., Rogak S.N., Bartlett K.H., Green S.I. Preventing airborne disease transmission: review of methods for ventilation design in health care facilities. Advances in Preventive Medicine. 2011 doi: 10.4061/2011/124064. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Li Y., Leung G.M., Tang J.W., Yang X., Chao C.Y., Lin J.Z., Lu J.W., Nielsen P.V., Niu J., Qian H., Sleigh A.C., Su H.J.J., Sundell J., Wong T.W., Yuen P.L. Role of ventilation in airborne transmission of infectious agents in the built environment-a multidisciplinary systematic review. Indoor Air. 2007;17(1):2–18. doi: 10.1111/j.1600-0668.2006.00445.x. [DOI] [PubMed] [Google Scholar]
- 3.Nicas M., Nazaroff W.W., Hubbard A. Toward understanding the risk of secondary airborne infection: emission of respirable pathogens. J. Occup. Environ. Hyg. 2005;2(3):143–154. doi: 10.1080/15459620590918466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Prather K.A., Wang C.C., Schooley R.T. Reducing transmission of SARS-CoV-2. Science. 2020 doi: 10.1126/science.abc6197. [DOI] [PubMed] [Google Scholar]
- 5.Stadnytskyi V., Bax C.E., Bax A., Anfinrud P. The airborne lifetime of small speech droplets and their potential importance in SARS-CoV-2 transmission. Proc. Natl. Acad. Sci. Unit. States Am. 2020;117(22):11875–11877. doi: 10.1073/pnas.2006874117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yu I.T., Li Y., Wong T.W., Tam W., Chan A.T., Lee J.H., Leung D.Y., Ho T. Evidence of airborne transmission of the severe acute respiratory syndrome virus. N. Engl. J. Med. 2004;350(17):1731–1739. doi: 10.1056/NEJMoa032867. [DOI] [PubMed] [Google Scholar]
- 7.Liu Y., Ning Z., Chen Y., Guo M., Liu Y., Gali N.K., Sun L., Duan Y., Cai J., Westerdahl D., Liu X., Xu K., Ho K., Kan H., Fu Q., Lan K. Aerodynamic analysis of SARS-CoV-2 in two Wuhan hospitals. Nature. 2020;582(7813):557–560. doi: 10.1038/s41586-020-2271-3. [DOI] [PubMed] [Google Scholar]
- 8.Allen J.G., Marr L.C. Recognizing and controlling airborne transmission of SARS-CoV-2 in indoor environments. Indoor Air. 2020;30(4):557. doi: 10.1111/ina.12697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Morawska L., Cao J. Airborne transmission of SARS-CoV-2: the world should face the reality. Environ. Int. 2020;139:105730. doi: 10.1016/j.envint.2020.105730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ai Z.T., Melikov A.K. Airborne spread of expiratory droplet nuclei between the occupants of indoor environments: a review. Indoor Air. 2018;28(4):500–524. doi: 10.1111/ina.12465. [DOI] [PubMed] [Google Scholar]
- 11.Ashrae Position document on airborne infectious diseases. 2020. https://www.ashrae.org/file%20library/about/position%20documents/airborne-infectiousdiseases
- 12.Zhang J. Integrating IAQ control strategies to reduce the risk of asymptomatic SARS CoV-2 infections in classrooms and open plan offices. Science and Technology for the Built Environment. 2020;26:1013–1018. [Google Scholar]
- 13.Yang B., Melikov A.K., Kabanshi A., Zhang C., Bauman F.S., Cao G., Awbi H., Wigo H., Niu J., Cheong K.W.D., Tham K.W., Sandberg M., Nielsen P.V., Kosonen R., Yao R., Kato S., Sekhar S.C., Schiavon S., Karimipanah T., Li X., Lin Z. A review of advanced air distribution methods-theory, practice, limitations and solutions. Energy Build. 2019 109359. [Google Scholar]
- 14.Sze To G.N., Chao C.Y.H. Review and comparison between the Wells–Riley and dose‐response approaches to risk assessment of infectious respiratory diseases. Indoor Air. 2010;20(1):2–16. doi: 10.1111/j.1600-0668.2009.00621.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Qian H., Zheng X. Ventilation control for airborne transmission of human exhaled bio-aerosols in buildings. J. Thorac. Dis. 2018;10:S2295. doi: 10.21037/jtd.2018.01.24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Asadi S., Bouvier N., Wexler A.S., Ristenpart W.D. The coronavirus pandemic and aerosols: does COVID-19 transmit via expiratory particles? Aerosol. Sci. Technol. 2020;54(6):635–638. doi: 10.1080/02786826.2020.1749229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cheng Y., Zhang S., Huan C., Oladokun M.O., Lin Z. Optimization on fresh outdoor air ratio of air conditioning system with stratum ventilation for both targeted indoor air quality and maximal energy saving. Build. Environ. 2019;147:11–22. [Google Scholar]
- 18.Rudnick S.N., Milton D.K. Risk of indoor airborne infection transmission estimated from carbon dioxide concentration. Indoor Air. 2003;13(3):237–245. doi: 10.1034/j.1600-0668.2003.00189.x. [DOI] [PubMed] [Google Scholar]
- 19.Hella J., Morrow C., Mhimbira F., Ginsberg S., Chitnis N., Gagneux S., Mutayoba B., Wood R., Fenner L. Tuberculosis transmission in public locations in Tanzania: a novel approach to studying airborne disease transmission. J. Infect. 2017;75(3):191–197. doi: 10.1016/j.jinf.2017.06.009. [DOI] [PubMed] [Google Scholar]
- 20.Issarow C.M., Mulder N., Wood R. Modelling the risk of airborne infectious disease using exhaled air. J. Theor. Biol. 2015;372:100–106. doi: 10.1016/j.jtbi.2015.02.010. [DOI] [PubMed] [Google Scholar]
- 21.Zhang S., Ai Z., Lin Z. Occupancy-aided ventilation for both airborne infection risk control and work productivity. Build. Environ. 2021;188:107506. doi: 10.1016/j.buildenv.2020.107506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Qian H., Li Y., Nielsen P.V., Huang X. Spatial distribution of infection risk of SARS transmission in a hospital ward. Build. Environ. 2009;44(8):1651–1658. [Google Scholar]
- 23.Zhu S., Srebric J., Spengler J.D., Demokritou P. An advanced numerical model for the assessment of airborne transmission of influenza in bus microenvironments. Build. Environ. 2012;47:67–75. doi: 10.1016/j.buildenv.2011.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wells W.F. Cambridge University Press; Cambridge MA: 1955. Airborne Contagion and Air Hygiene; pp. 117–122. [Google Scholar]
- 25.Andrews J.R., Morrow C., Wood R. Modeling the role of public transportation in sustaining tuberculosis transmission in South Africa. Am. J. Epidemiol. 2013;177(6):556–561. doi: 10.1093/aje/kws331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Buonanno G., Stabile L., Morawska L. Estimation of airborne viral emission: quanta emission rate of SARS-CoV-2 for infection risk assessment. Environ. Int. 2020;141:105794. doi: 10.1016/j.envint.2020.105794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sun C., Zhai Z. The efficacy of social distance and ventilation effectiveness in preventing COVID-19 transmission. Sustainable Cities and Society. 2020;62:102390. doi: 10.1016/j.scs.2020.102390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Dai H., Zhao B. Association of the infection probability of COVID-19 with ventilation rates in confined spaces. Building Simulation. 2020;13(6):1321–1327. doi: 10.1007/s12273-020-0703-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Leung N.H., Chu D.K., Shiu E.Y., Chan K.H., McDevitt J.J., Hau B.J., Yen H., Li Y., Ip D., Malik Peiris J., Seto W.H., Leung G., Milton D., Cowling B. Respiratory virus shedding in exhaled breath and efficacy of face masks. Nat. Med. 2020;26(5):676–680. doi: 10.1038/s41591-020-0843-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zhai J. Facial mask: a necessity to beat COVID-19. Build. Environ. 2020;175:106827. doi: 10.1016/j.buildenv.2020.106827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Riley E.C., Murphy G., Riley R.L. Airborne spread of measles in a suburban elementary school. Am. J. Epidemiol. 1978;107(5):421–432. doi: 10.1093/oxfordjournals.aje.a112560. [DOI] [PubMed] [Google Scholar]
- 33.Li R., Pei S., Chen B., Song Y., Zhang T., Yang W., Shaman J. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2) Science. 2020;368(6490):489–493. doi: 10.1126/science.abb3221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wu Y., Tung T.C., Niu J.L. On-site measurement of tracer gas transmission between horizontal adjacent flats in residential building and cross-infection risk assessment. Build. Environ. 2016;99:13–21. doi: 10.1016/j.buildenv.2016.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ai Z., Mak C.M., Gao N., Niu J. Tracer gas is a suitable surrogate of exhaled droplet nuclei for studying airborne transmission in the built environment. Building Simulation. 2020;13:489–496. doi: 10.1007/s12273-020-0614-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Liu L., Li Y., Nielsen P.V., Wei J., Jensen R.L. Short-range airborne transmission of expiratory droplets between two people. Indoor Air. 2017;27:452–462. doi: 10.1111/ina.12314. [DOI] [PubMed] [Google Scholar]
- 37.Kang M., Wei J., Yuan J., Guo J., Zhang Y., Hang J., Qu Y., Qian H., Zhuang Y., Chen X., Peng X., Shi T., Wang J., Wu J., He J., Li Y., Zhong N. Probable evidence of fecal aerosol transmission of SARS-CoV-2 in a high-rise building. Ann. Intern. Med. 2020 doi: 10.7326/M20-0928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Yu I.T., Li Y., Wong T.W., Tam W., Chan A.T., Lee J.H., Leung D.Y., Ho T. Evidence of airborne transmission of the severe acute respiratory syndrome virus. N. Engl. J. Med. 2004;350(17):1731–1739. doi: 10.1056/NEJMoa032867. [DOI] [PubMed] [Google Scholar]
- 39.Tian X., Zhang S., Awbi H.B., Liao C., Cheng Y., Lin Z. Multi-indicator evaluation on ventilation effectiveness of three ventilation methods: an experimental study. Build. Environ. 2020;180:107015. [Google Scholar]
- 40.Shao X., Liang S., Li X., Liang C., Yan S. Quantitative effects of supply air and contaminant sources on steady contaminant distribution in ventilated space with air recirculation. Build. Environ. 2020;171:106672. [Google Scholar]
- 41.Zhang W., Hiyama K., Kato S., Ishida Y. Building energy simulation considering spatial temperature distribution for nonuniform indoor environment. Build. Environ. 2013;63:89–96. [Google Scholar]