Computational Investigation of Protein Photoinactivation by Molecular Hyperthermia

Abstract

To precisely control protein activity in a living system is a challenging yet long-pursued objective in biomedical sciences. Recently, we have developed a new approach named molecular hyperthermia (MH) to photoinactivate protein activity of interest without genetic modification. MH utilizes nanosecond laser pulse to create nanoscale heating around plasmonic nanoparticles to inactivate adjacent protein in live cells. Here we use a numerical model to study important parameters and conditions for MH to efficiently inactivate proteins in nanoscale. To quantify the protein inactivation process, the impact zone is defined as the range where proteins are inactivated by the nanoparticle localized heating. Factors that reduce the MH impact zone include the laser pulse duration, temperature-dependent thermal conductivity (versus constant properties), and nonspherical nanoparticle geometry. In contrast, the impact zone is insensitive to temperature-dependent material density and specific heat, as well as thermal interface resistance based on reported data in the literature. The low thermal conductivity of cytoplasm increases the impact zone. Different proteins with various Arrhenius kinetic parameters have significantly different impact zones. This study provides guidelines to design the protein inactivation process by MH.

Introduction

Light offers advantages in spatiotemporal resolution to selectively and remotely control biological functions in living systems [1]. Various approaches have been developed during the last decade, such as optogenetics [2] and synthetic photoswitches [3,4]. Optogenetics utilizes photosensitive molecules to genetically modify proteins of interest and enables light manipulation in targeted cells. This revolutionary technique has allowed understanding how specific cell types contribute to complex neural circuits and brain functions. While optogenetics is undoubtedly powerful, the requirement of genetic modification still limits its clinical and translational value for human. Another emerging approach for light control of protein activity is by synthetic photoswitches. However, there are limited numbers of photoswitches (mostly based on azobenzene) available, thus narrow options of wavelength window. To overcome these drawbacks, nanoparticles provide promising opportunities in this area [5–8]. One attractive candidate is plasmonic nanoparticles [9]. Plasmonic nanoparticles are discrete metallic nanoparticles whose free electrons can strongly oscillate with electromagnetic fields, known as localized surface plasmon resonance (LSPR). Due to these strong light-matter interactions, plasmonic nanoparticles have unique optical properties, such as strong light absorption or scattering. Among different plasmonic nanoparticles, gold nanoparticles have good chemical stability and have been used to optically control tissue and cellular behaviors, including photothermal therapy of tumor treatment [10], neuron firing [11–13], heat shock protein expression [14], and optoporation [15,16].

Upon light irradiation, gold nanoparticles convert electromagnetic wave energy into thermal energy and heat up surrounding medium, known as plasmonic heating [17,18]. The plasmonic heating process can be engineered on different time and length scales by controlling light energy input [19,20]. This is because the heat diffusion is highly dependent on time. A long duration of energy input (such as seconds to minutes) allows heat to dissipate away from individual particles and to interact with each other. Thus, a large-scale heating can be achieved by applying a long duration energy input to a system with multiple particles, known as collective heating [21–24]. The collective heating effect can lead to a global temperature rise in the macroscopic scale and various biomedical applications, such as the thermal therapy for cancer treatment (Fig. 1) [25]. On the other hand, the localized heating can be achieved by applying an intense energy input with a short duration (such as a nanosecond laser pulse). In this scenario, the short pulse duration locally heats up the nanoparticle and surrounding medium but is insufficient to heat up the entire system. Hence, highly localized heating can be achieved around individual particles. By tuning the laser pulse duration, the localized heating area can be in the nanoscale (Fig. 1). The nanoscale plasmonic heating provides new approaches to trigger cellular or even subcellular thermal responses [19,26–28].

Fig. 1.

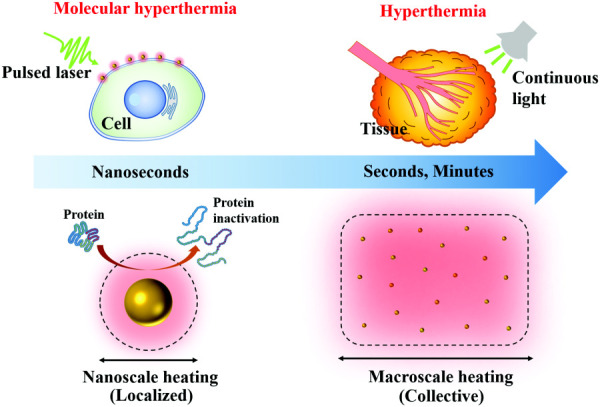
Comparison between molecular hyperthermia and hyperthermia. Molecular hyperthermia utilizes a nanosecond laser pulse to generate nanoscale heating (localized heating) and inactivate proteins without killing cells. On the other hand, hyperthermia uses macroscale heating (collective heating) of plasmonic nanoparticles induced by continuous irradiation (seconds to minutes) to kill tumor tissue.

Recently, we developed a method called molecular hyperthermia (MH) to photoinactivate protein activity [29,30] by taking advantage of nanoscale plasmonic heating. MH utilizes nanosecond laser pulses to excite plasmonic nanoparticle, for example, gold nanosphere (AuNS), as a nanoheater to thermally inactivate proteins adjacent to the nanoparticle. MH selectively inactivates enzymes targeted by AuNS and leaves untargeted enzymes intact, demonstrating the spatial selectivity of MH [29,31]. We further showed that MH can be used to inactivate cell membrane proteins in live cells without compromising cell viability [30]. Therefore, MH is a promising method to manipulate protein activity and cellular behavior selectively and remotely. Compared with other methods such as optogenetics, MH does not require genetic modification and can be adapted for disease treatment. However, MH is a complicated process, and involves not only heat transfer but also temperature-dependent chemical reactions (thermal inactivation of proteins). So far, most models of nanoparticle plasmonic heating focused only on heat transfer process [27,32,33]. To better understand the MH, a numerical model is needed to allow quantitative description of protein inactivation induced by nanosecond laser plasmonic heating.

In this work, we developed a numerical model that can quantitatively describe the confined nanoscale heating of gold nanoparticle and protein inactivation during MH. With this model, we investigated important parameters for MH, such as laser pulse shape and duration, temperature-dependent material properties, and nanoparticle shape. This work provides a better understanding of the protein inactivation response due to the nanoscale plasmonic heating, and design guidelines for biomedical applications of MH.

Methods

Heat Transfer Model and Analytical Solution.

The model is a spherical nanoparticle as a heat source immersed in aqueous medium. The heat generation is homogeneous inside the nanoparticle, and two-temperature effect is negligible in this study. The reason is that the electron-electron interaction time (femtoseconds) and electron–phonon thermalization time (picoseconds) are very short compared with laser pulse duration (nanoseconds) [34]. The analytical solution for this problem was used as a benchmark for numerical solution. We neglect the interfacial thermal resistance in the analytical solution, and we will discuss the effect of the thermal interfacial resistance in the numerical solution.

The governing equations for one-dimensional transient heat transfer in spherical coordinate system are given by

$$\frac{1}{{\alpha }_{Au}}\frac{\partial T_{Au}(r,t)}{\partial t}=\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial T_{Au}}{\partial r}\right)+\frac{Q_v}{k_{Au}}$$ (1)

$$\frac{1}{{\alpha }_m}\frac{\partial T_m(r,t)}{\partial t}=\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial T_m}{\partial r}\right)$$ (2)

where T is the temperature, k is the thermal conductivity, and α is the thermal diffusivity. The subscripts m and Au indicate medium and gold, respectively. Upon laser irradiation, the light energy is first absorbed by electrons at the surface of the particle and the thermal equilibrium of electron gas in the whole nanoparticle will be soon reached due to the electron–electron scattering. Next, energy is transferred from electron gas into gold lattice. Because the electron–electron interaction is much faster (in femtosecond (fs) range) than the lattice heating (in picosecond (ps) range), the energy transfer to lattice is uniform in the nanoparticle and can be considered as a uniform volumetric heating (Q_v). The volumetric heat source of nanoparticle excited by rectangular pulse was expressed by the following equation:

$$Q_v=\frac{C_{\mathrm{abs}}F}{V_{NP}2\mu }\left[u\left(t\right)-u(t-2\mu )\right],\hspace{0.17em}\mathrm{where}\hspace{0.17em}\hspace{0.17em}u\left(t-t_0\right)=\left\{\begin{array}{c}0,\hspace{0.17em}\mathrm{for}\hspace{0.17em}\hspace{0.17em}t<t_0\\ 1,\hspace{0.17em}\mathrm{for}\hspace{0.17em}\hspace{0.17em}t\ge t_0\end{array}\right.$$ (3)

where u(t) is the Heaviside unit step function, $\mu$ is the central time of pulse (5 ns), $2\mu$ is the pulse duration (10 ns), F is the laser fluence (260.9 J m⁻²), and V_NP is the volume of AuNS. C_abs is the absorption cross section of AuNS for laser wavelength of 532 nm (1.38 × 10⁻¹⁵ m²), as calculated by the Mie theory [35].

The boundary conditions and the initial condition are given by the following equations:

$${\frac{\partial T}{\partial r}|}_{r=0}=0$$ (4)

$${\left.T\right|}_{r=\infty }=T_{\mathrm{ref}}=300.0\hspace{0.17em}K$$ (5)

$${\left.T\right|}_{t=0}=T_{\mathrm{ref}}=300.0\hspace{0.17em}K$$ (6)

We neglected the interfacial thermal resistance at the interface of gold and medium. The continuous interfacial conditions are described by the following equation:

$${\left.T_{\mathrm{Au}}\right|}_{r=R_{\mathrm{NP}}}={\left.T_m\right|}_{r=R_{\mathrm{NP}}}$$ (7)

$${k_{\mathrm{Au}}\frac{\partial T_{\mathrm{Au}}}{\partial r}|}_{r=R_{\mathrm{NP}}}={k_m\frac{\partial T_m}{\partial r}|}_{r=R_{\mathrm{NP}}}$$ (8)

where R_NP is the nanoparticle radius (15 nm).

The analytical solution was in part modified from the transient one-dimensional heat transfer problem that Goldenberg and Tranter studied [36]. Goldenberg and Tranter considered a sphere embedded in an infinite medium domain and a uniform volumetric heat generation was introduced to the sphere with a constant value for time larger than 0. In our case, we considered not only the heating process but also the cooling process. Therefore, the heat source term is multiplied by Heaviside unit step functions as described in Eq. (3).

To find the analytical solution, first, we changed the variable as ${V_1=T}_{\mathrm{Au}}-T_{\mathrm{ref}}$ and ${V_2=T}_m-T_{\mathrm{ref}}$. Second, we introduced Laplace transform $\ell \left[V\left(t\right)\right]\left(s\right)=\overline{V}\left(s\right)$ to Eqs. (1)–(8)

$$\frac{d^2}{d{r}^2}\left(r\overline{V_1}\right)-r{q_1}^2\overline{V_1}=-\frac{rA}{k_{\mathrm{Au}}s}\left(1-e^{-2\mu s}\right),\hspace{0.17em}\mathrm{where}\hspace{0.17em}\hspace{0.17em}A=\frac{C_{\mathrm{abs}}F}{V_{NP}2\mu }$$ (9)

$$\frac{d^2}{d{r}^2}\left(r\overline{V_2}\right)-r{q_2}^2\overline{V_2}=0$$ (10)

$${\frac{d\overline{V_1}}{dr}|}_{r=0}=0$$ (11)

$${\left.\overline{V_2}\right|}_{r=\infty }=0$$ (12)

$${\left.\overline{V_1}\right|}_{r=R_{\mathrm{NP}}}={\left.\overline{V_2}\right|}_{r=R_{\mathrm{NP}}}$$ (13)

$$k_{\mathrm{Au}}{\frac{d\overline{V_1}}{dr}|}_{r=R_{\mathrm{NP}}}=k_m{|}_{r=R_{\mathrm{NP}}}$$ (14)

where ${q_1}^2=s/{\alpha }_{\mathrm{Au}}$ and ${q_2}^2=s/{\alpha }_m$.

Third, the solution for Eqs. (9)–(14) is derived from Goldenberg and Tranter

$$\overline{V_1}=\frac{{\alpha }_{\mathrm{Au}}A}{k_{\mathrm{Au}}{s}^2}\left[1+\frac{k_m}{k_{\mathrm{gold}}}\frac{R_{\mathrm{NP}}\mathrm{s}\mathrm{in}h{q}_{1}r}{rD\left(s\right)}\right](1-e^{-2\mu s})$$ (15)

$$\overline{V_2}=\frac{{\alpha }_{\mathrm{Au}}A}{k_{\mathrm{Au}}{s}^2}\frac{R_{\mathrm{NP}}}{r}\frac{\left[\text{sin}h{q}_1{R}_{\mathrm{NP}}-q_1{R}_{\mathrm{NP}}\mathrm{c}\mathrm{os}h{q_{1}R}_{\mathrm{NP}}\right]e^{-q_2(r-R_{\mathrm{NP}})}}{\left(1+q_2{R}_{\mathrm{NP}}\right)D\left(s\right)}(1-e^{-2\mu s})$$ (16)

where $D\left(s\right)=\frac{\text{sin}h{q}_1{R}_{\mathrm{NP}}-q_1{R}_{\mathrm{NP}}\mathrm{c}\mathrm{os}h{q_{1}R}_{\mathrm{NP}}}{1+q_2{R}_{\mathrm{NP}}}-\frac{k_m}{k_{Au}}\mathrm{s}\mathrm{in}h{q}_1{R}_{\mathrm{NP}}$. We define $\overline{V_h}=\overline{V}/(1-e^{-2\mu s})$ as the solution of the heating process in the Laplace domain. The subscript h indicates the heating process.

Next, we found the inverse Laplace transform for Eqs. (15) and (16). For the heating process, the inverse Laplace transform of $\overline{V_h}$ has been given by Goldenberg and Tranter [36] ($V_h$). The cooling process was calculated by adding the term $-{\overline{V_h}e}^{-2\mu s}$ to the heating process solution $\overline{V_h}$. Following the t-translation rule of Laplace transform, the inverse Laplace transform of $-{\overline{V_h}e}^{-2\mu s}$ is $-V_h$ with a shift in time (with a distance of $2\mu$). Therefore, the NP and medium temperatures with both heating and cooling processes are given by Eqs. (17) and (18), respectively,

$$T_{\mathrm{Au}}={V_{1h}\left(t\right)-V}_{1h}\left(t-2\mu \right)u\left(t-2\mu \right)+T_{\mathrm{ref}}$$ (17)

$$T_m={V_{2h}\left(t\right)-V}_{2h}\left(t-2\mu \right)u\left(t-2\mu \right)+T_{\mathrm{ref}}$$ (18)

When t is smaller than $2\mu$, the system is under heating process. The expression of T is equal to $V_h\left(t\right)+T_{\mathrm{ref}}$. When t is larger than $2\mu$, the system is under cooling process. T is equal to ${V_h\left(t\right)-V}_h\left(t-2\mu \right)+T_{\mathrm{ref}}$. The complete forms of analytical solutions (Eqs. (17)–(18)) were organized in Table 1.

Table 1.

Analytical solution of single gold nanosphere heated by a rectangular pulse

Heating process	$${\left.T_{\mathrm{Au}}(r,t)\right|}_{t<2\mu }=T_{\mathrm{ref}}+\frac{{R_{\mathrm{NP}}}^2}{k_{\mathrm{Au}}}\frac{C_{\mathrm{abs}}F}{V_{\mathrm{NP}}2\mu }\left\{\frac{1}{3}\frac{k_{Au}}{k_m}+\frac{1}{6}\left(1-\frac{r^2}{{R_{\mathrm{NP}}}^2}\right)-\frac{2R_{\mathrm{NP}}b}{r\pi }{\int }_0^{\infty }\frac{\exp (-\frac{y^{2}t}{{\gamma }_1})}{y^2}\frac{\left(\text{sin}y-y\text{cos}y\right)\text{sin}(\frac{ry}{R_{NP}})}{[{\left(c\text{sin}y-y\text{cos}y\right)}^2+b^2{y}^2{\text{sin}}^{2}y]}dy\right\}$$ (19)
		$${\left.T_{\mathrm{Au}}(r=0,t)\right|}_{t<2\mu }=T_{\mathrm{ref}}+\frac{{R_{\mathrm{NP}}}^2}{k_{\mathrm{Au}}}\frac{C_{\mathrm{abs}}F}{V_{\mathrm{NP}}2\mu }\left\{\frac{1}{3}\frac{k_{\mathrm{Au}}}{k_m}+\frac{1}{6}-\frac{2b}{\pi }{\int }_0^{\infty }\frac{\exp (-\frac{y^{2}t}{{\gamma }_1})}{y}\frac{\left(\text{sin}y-y\text{cos}y\right)}{[{\left(c\text{sin}y-y\text{cos}y\right)}^2+b^2{y}^2{\text{sin}}^{2}y]}dy\right\}$$ (20)
	$${\left.T_{\mathrm{water}}(r,t)\right|}_{t<2\mu }=T_{\mathrm{ref}}+\frac{{R_{\mathrm{NP}}}^3}{r{k}_{\mathrm{Au}}}\frac{C_{\mathrm{abs}}F}{V_{\mathrm{NP}}2\mu }\left\{\begin{array}{c}\frac{1}{3}\frac{k_{Au}}{k_m}-\frac{2}{\pi }{\int }_0^{\infty }\frac{\exp \left(-\frac{y^{2}t}{{\gamma }_1}\right)}{y^3}\\ \frac{\left(\text{sin}y-y\text{cos}y\right)\left[by\text{sin}y\text{cos}\sigma y-\left(c\text{sin}y-y\text{cos}y\right)\text{sin}\sigma y\right]}{[{\left(c\text{sin}y-y\text{cos}y\right)}^2+b^2{y}^2{\text{sin}}^{2}y]}dy\end{array}\right\}$$ (21)
Cooling process	$${\left.T_{\mathrm{Au}}\left(r,t\right)\right|}_{t\ge 2\mu }=T_{\mathrm{ref}}+\frac{2{R_{\mathrm{NP}}}^{3}b}{r\pi k_{\mathrm{Au}}}\frac{C_{\mathrm{abs}}F}{V_{\mathrm{NP}}2\mu }{\int }_0^{\infty }\frac{\exp \left[-\frac{y^2\left(t-2\mu \right)}{{\gamma }_1}\right]-\exp \left(\frac{-y^{2}t}{{\gamma }_1}\right)}{y^2}\frac{\left(\text{sin}y-y\text{cos}y\right)\text{sin}(\frac{ry}{R_{\mathrm{NP}}})}{[{\left(c\text{sin}y-y\text{cos}y\right)}^2+b^2{y}^2{\text{sin}}^{2}y]}dy\hspace{0.17em}$$ (22)
	$${\left.T_{\mathrm{Au}}\left(r=0,t\right)\right|}_{t\ge 2\mu }=T_{\mathrm{ref}}+\frac{2{R_{\mathrm{NP}}}^{2}b}{\pi k_{\mathrm{Au}}}\frac{C_{\mathrm{abs}}F}{V_{\mathrm{NP}}2\mu }{\int }_0^{\infty }\frac{\exp \left[-\frac{y^2\left(t-2\mu \right)}{{\gamma }_1}\right]-\exp \left(\frac{{-y}^{2}t}{{\gamma }_1}\right)}{y}\frac{\left(\text{sin}y-y\text{cos}y\right)}{[{\left(c\text{sin}y-y\text{cos}y\right)}^2+b^2{y}^2\hspace{0.17em}{\text{sin}}^{2}y]}dy$$ (23)
	$${\left.T_m(r,t)\right|}_{t\ge 2\mu }=T_{\mathrm{ref}}+\frac{{R_{\mathrm{NP}}}^3}{r{k}_{\mathrm{Au}}}\frac{C_{\mathrm{abs}}F}{V_{\mathrm{NP}}2\mu }\left\{\begin{array}{c}\frac{1}{3}\frac{k_{\mathrm{Au}}}{k_m}-\frac{2}{\pi }{\int }_0^{\infty }\frac{\exp \left[-\frac{y^2\left(t-2\mu \right)}{{\gamma }_1}\right]-\exp \left(\frac{y^{2}t}{{\gamma }_1}\right)}{y^3}\\ \frac{\left(\text{sin}y-y\text{cos}y\right)\left[by\text{sin}y\text{cos}\sigma y-\left(c\text{sin}y-y\text{cos}y\right)\text{sin}\sigma y\right]}{[{\left(c\text{sin}y-y\text{cos}y\right)}^2+b^2{y}^2\hspace{0.17em}{\text{sin}}^{2}y]}dy\end{array}\right\}$$ (24)
	$$b=\frac{k_m}{k_{Au}}\sqrt{\frac{{\alpha }_{\mathrm{Au}}}{{\alpha }_m}},\hspace{0.17em}c=1-\frac{k_m}{k_{\mathrm{Au}}},\hspace{0.17em}{\gamma }_1=\frac{{R_{\mathrm{NP}}}^2}{{\alpha }_{\mathrm{Au}}},\hspace{0.17em}\sigma =\left(\frac{r}{R_{\mathrm{NP}}}-1\right)\sqrt{\frac{{\alpha }_{\mathrm{Au}}}{{\alpha }_m}}$$ (25)

Finite Element Simulation.

All finite element simulations were conducted in comsol 5.3 software. The governing equations, boundary and initial conditions were described in the previous section. Taking thermal interfacial resistance into account, the boundary condition at the interface of gold and water is described by the following equation:

$$-k_{\mathrm{Au}}{\frac{\partial T_{\mathrm{Au}}}{\partial r}|}_{r=R_{\mathrm{NP}}}=-k_m{\frac{\partial T_m}{\partial r}|}_{r=R_{\mathrm{NP}}}={\frac{1}{R}\hspace{0.17em}\left.(T_{\mathrm{Au}}-T_m)\right|}_{r=R_{\mathrm{NP}}}$$ (26)

The volumetric heat generation by a Gaussian pulse with a full duration of 2$\mu$ is defined by the following equation:

$$Q_v=\frac{C_{\mathrm{abs}}F}{V_{\mathrm{NP}}}\frac{3}{\mu \sqrt{2\pi }}{e}^{-\frac{{9\left(t-\mu \right)}^2}{2{\mu }^2}}$$ (27)

The medium domain is 10 times larger than the nanoparticle. The nanoparticle is located at the center of the medium domain. For gold nanorods (AuNRs), there are two important dimensions: axial dimension (z) and radial dimension (r). The origins of z and r are at the center of the nanorod.

The model was built in comsol 5.3 with 2D axisymmetric to decrease the computational time. The number of elements of the domain was in the range of 13,461–21,517 depending on the shape of the nanoparticle. The maximum size was determined by mesh independence test and was set to be 1.5 nm (see Fig. S2 available in the Supplemental Materials on the ASME Digital Collection). The time-step was 0.1 ns and the total simulation time is 50 ns.

Absorption Cross-Section (C_abs) Calculation for AuNRs.

The absorption cross section (C_abs) of AuNRs was calculated by MNPBEM tool box in matlab [37]. Because C_abs of AuNRs is highly dependent on incident light orientation, we calculated the average C_abs by varying the propagation and the polarization direction of incident light. The refractive index of water was constant 1.33, and dielectric function of gold was obtained from Johnson and Christy [38].

Protein Inactivation Calculated by Arrhenius Model.

We assumed that protein inactivation is a two-state, first-order kinetic model with native (N) and inactivated (I) states

$$N\stackrel{k\left(T\right)}{\to }I$$ (28)

The temperature-dependence of reaction rate can be described by Arrhenius model in the following equation:

$$k\left(T\right)=A_0{e}^{-\frac{E_a}{RT}}$$ (29)

And the protein inactivation can be estimated by the following equation:

$$s\left(r\right)=\hspace{0.17em}{e}^{-\int k\left(T\right)dt}$$ (30)

In this study, we first selected α-chymotrypsin as the model protein since our previous experiments have demonstrated the feasibility of α-chymotrypsin photoinactivation by MH [29]. The pre-exponential factor (A₀) of protein inactivation is 9.75 × 10³⁸ s⁻¹ and activation energy (E_a) is 244 kJ mol⁻¹ for α-chymotrypsin (see Fig. S3 available in the Supplemental Materials on the ASME Digital Collection) [19,39,40]. For other proteins, the Arrhenius kinetic parameters were derived from the literature [41–47].

Temperature-Dependence of Material Properties.

Table 2 shows material properties used in the numerical and analytical solutions. Constant material properties were calculated from polynomial formulas at T_ref = 300.0 K.

Table 2.

Temperature-dependent material properties

Parameters	Expression	Temperature-dependent value [48]	Constant [48] Tref = 300.0 K
Specific heat of gold	CAu (J kg−1 K−1)	3.9935 × 105·T−2 + 1.1490 × 102 + 3.2288 × 10−2·T	1.290 × 102
Specific heat of water	Cm (J kg−1 K−1)	1.2010 × 104−8.0407 × 102·T + 3.0987 × 10−1·T2−5.3819 × 10−4·T3+3.6254 × 10−7·T4	4.182 × 103
Thermal conductivity of gold	kAu (W m−1 K−1)	3.3064 × 102−2.5367 × 10−2·T−8.1914 × 10−5·T2+6.7929 × 10−8·T3−2.1536 × 10−11·T4	3.173 × 102
Thermal conductivity of water	km (W m−1 K−1)	−8.6908 × 10−1+8.9488 × 10−3·T−1.5837 × 10−5·T2+7.9754 × 10−9·T3	6.056 × 10−1
Gold density	ρAu (kg m−3)	1.9501 × 104+6.9338 × 10−1·T−2.0419 × 10−4·T2+4.2980 × 10−8·T3	1.928 × 104
Water density	ρm (kg m−3)	8.3847 × 102−1.4005·T−3.0112 × 10−3·T2+3.7182 × 10−7·T3	9.976 × 102

Results

Localized Heating Versus Collective Heating.

We developed a dimensionless parameter to differentiate localized heating versus collective heating, for MH and hyperthermia, respectively. The effective thermal diffusion length in the medium can be written as the following equation [49]:

$$L_d=\sqrt{{\alpha }_m\tau }$$ (31)

where ${\alpha }_m$ is thermal diffusivity of the medium and $\tau$ is the heating duration. In a colloidal solution system, the mean interparticle distance is given by the following equation [50]:

$$\overline{d}\approx 0.554n^{-1/3}$$ (32)

where n is the particle density (m⁻³). The ratio of L_d and $\overline{d}/2$ gives a dimensionless parameter $\xi$

$$\xi =\frac{L_d}{\overline{d}/2}=\frac{2\sqrt{{\alpha }_m\tau }}{0.554n^{-1/3}}\approx 3.6n^{1/3}\sqrt{{\alpha }_m\tau }$$ (33)

The dimensionless parameter $\xi$ characterizes whether the heat from individual particles overlaps. When $\xi$ is much smaller than 1 ($\xi$< 0.1), the thermal diffusion length is much smaller than interparticle distance. Hence, heat is localized around individual nanoparticles without overlap, namely, localized heating (Fig. 2(a)). The localized heating occurs when energy input duration is short and particle density is low. When $\xi$ is close to 1, the heat diffusion length is close to interparticle distance so that heat from neighboring particles starts to overlap (Fig. 2(b)). With a continuous energy input, heat overlap between particles will further develop and raises the temperature in a collective manner. This multiple particle heating can cause global tissue heating when $\xi$ is much larger than 1 (typically when $\xi$>10), known as collective heating (Fig. 2(c)) [21–24]. With nanoparticle density of 10¹⁵ NP m⁻³, hyperthermia requires a relatively long laser irradiation (longer than 0.1 s) to generate collective heating between particles and increases temperature of the whole tissue [51]. On the other hand, MH uses the nanosecond laser pulse to generate localized heating around particles and inactivates proteins ($\xi <0.01$, Fig. 2(d)). Therefore, the protein inactivation by MH falls well within a localized heating scenario.

Fig. 2.

Dimensionless parameter to define conditions for localized and collective heating. (a)–(c) Schematic of localized heating versus collective heating. (d) Dimensionless parameter $\xi$ to differentiate localized heating and collective heating. Τ is the energy input duration and n is the nanoparticle density. The solid line indicates $\xi$ = 1, while the dashed lines indicate $\xi$ = 10 and 0.1, respectively. MH: molecular hyperthermia.

Numerical Model Validation.

We confirmed the accuracy of the numerical model by comparing the numerical solution with the analytical solution. Figures 3(a) and 3(b) illustrates the geometry and laser profile for the model. An AuNS with diameter of 30 nm (D_NP = 30 nm) is in the center of a spherical medium domain. The size of medium domain is 300 nm (D_m = 300, Fig. 3(a)). The boundary temperature of the medium domain is set to 300 K (first-type boundary condition). For analytical solution, the AuNS is immersed in an infinite domain of water, which initial temperature was 300 K. The single rectangular laser pulse (10 ns, laser intensity is 26.09 × 10⁹ W m⁻²) is used to heat the AuNS (Fig. 3(b)). Temperature profiles at three different positions from numerical simulation are compared with analytical solution (Fig. 3(c)). For both cases, the temperature rises quickly and returns to initial temperature (300 K) after 40 ns. These results demonstrate that the simulation time (50 ns) is sufficient for single particle to cool down. We also compared the numerical and analytical solution of temperature distribution at three different time points (Fig. 3(d)). Because the thermal conductivity of gold is significantly larger than that of water, the temperature distribution in AuNS is nearly uniform. The temperature difference between numerical solution and analytical solution is negligible. This suggests that the medium domain is large enough, and the first-type boundary condition (constant temperature) is satisfactory for this numerical simulation. The MH induced protein inactivation was calculated by the Arrhenius model. We assumed that the protein distribution is homogeneous around the AuNSs. The protein inactivation profile was calculated along the radial direction after the single pulse irradiation at 50 ns (Fig. 3(e)). The inactivation of proteins is localized around the AuNS and the border of inactivation zone is quite sharp. We defined the impact zone as the distance from particle surface to where 50% of protein stays intact (Fig. 3(e)). Both numerical and analytical solutions give the same impact zone (–10.5 nm, Fig. 3(f)). These results confirmed the accuracy of the numerical method.

Fig. 3.

Numerical model validation. (a) The model geometry for numerical simulation. D_NP is diameter of gold nanosphere (AuNS). D_m is diameter of medium domain and is set to be 10 times D_NP. (b) Rectangular laser intensity profile in both numerical and analytical solutions. (c) Temperature profile of three different positions (illustrated by insert picture) by numerical and analytical solutions. (d) Temperature distribution of three different time points by numerical and analytical solutions. (e) Protein inactivation profile in the radial direction after laser irradiation. (f) Impact zone was predicted by the numerical method and analytical method.

Effects of Pulse Shape and Duration.

We investigated the effect of pulse shape and pulse duration on MH. Here, we compared two pulse shapes, i.e., rectangular and Gaussian (bell). Also, we compared different durations of the Gaussian pulses. All laser pulses share the same fluence (260.9 J m⁻², Fig. 4(a)). All Gaussian pulses start at 0 ns time point, and their peak position vary from 5 ns to 20 ns depending on the pulse durations. Figure 4(b) shows that the temperature response of AuNS varies according to pulse shapes and durations. The peak temperature of AuNS decreases when the pulse duration is stretched. For the rectangular shape pulse, the peak temperature of AuNS appears at the end of the pulse (10 ns). The protein activity distribution is calculated based on the temperature profile (Fig. 4(c)). Although all pulse energy is the same, pulses with longer duration inactivate less proteins than the pulses with shorter duration. This is due to the nonlinear temperature-dependence of protein inactivation in the Arrhenius model. Pulses with shorter duration generate greater temperature rise and accelerate protein inactivation. Interestingly, the impact zone of the rectangular pulse (10 ns duration) is same as that of the Gaussian pulse with peak position at 10 ns (μ = 10 ns, Fig. 4(d)).

Fig. 4.

Effect of laser pulse shape and duration on molecular hyperthermia. (a) The laser profiles with different shapes (Gaussian and rectangular) and different pulse durations. μ is the center of Gaussian pulse. All laser pulses shared the same laser fluence (260.9 J m⁻²). (b) Temperature profile of the gold nanosphere (AuNS) for different pulses. (c) Protein activity distribution after different laser pulse. (d) Effect of pulse duration on the impact zone. The dash line indicates the impact zone of 10 ns rectangular pulse.

Effect of Temperature-Dependent Material Properties.

We studied the effect of temperature-dependent material properties (k, C_p and ρ in water medium and AuNS) on the localized heating and the protein inactivation. Figure 5(a) shows that no obvious difference is observed for the temperature-dependent density and the specific heat. However, the temperature-dependent thermal conductivity significantly decreases the temperature profiles in both gold and medium. Consequently, the impact zone decreases by 1.3 nm, or 12% lower than the case with constant properties (Fig. 5(b)). If we considered the temperature-dependences for all material properties (labeled as [k, ρ, C_p] (T)), the result is same as the temperature-dependent thermal conductivity (labeled as k(T)). These results demonstrate that the change of the thermal conductivity has a significant effect on MH. When applying MH on real biological environment such as cytoplasm, due to the high protein content in cells, the thermal conductivity of cytoplasm differs from that of pure water. The thermal conductivity of single live cells was measured to be 0.56–0.58 Wm⁻¹K⁻¹ [52]. The protein concentration in the cytoplasm is about 100 mg mL⁻¹ and this gives an estimated thermal conductivity of 0.57 W m⁻¹ K⁻¹ [53,54]. The impact zone increases slightly using cytoplasm thermal conductivity (11.2 nm) compared with using water properties (10.5 nm). Therefore, the MH can work more efficiently in cytoplasm than in pure water.

Fig. 5.

Effect of temperature-dependent material properties. (a) Comparison of temperature profile in different points for constant and temperature-dependent material properties. Point 1 indicates the center of the nanoparticle. Point 2 indicates the location in medium that 15 nm from the surface of the particle. (b) Comparison of impact zones for constant and temperature-dependent material properties and the cytoplasm. The “constant properties” indicates results with constant water properties. Specifically, for cytoplasm as medium, the thermal conductivity of medium (k_m) is 0.57 W m⁻¹K⁻¹, while other material properties are same as constant water properties. K(T), ρ(T), and Cp(T) indicate that thermal conductivity, density, and specific heat of materials are temperature dependent, respectively. The last group indicates results with temperature-dependences for all material properties ([k, ρ, Cp] (T)).

Effect of Interfacial Thermal Resistance.

Next, we study the effect of interfacial thermal resistance (or Kapitza resistance, R_K) at gold-medium interface on MH. R_K originates from the mismatch of phonon transport at the gold-medium interface, which can be significantly tuned by surface chemical modifications (Fig. 6(a)). In MH, the surface of AuNS was modified with polyethylene glycol (PEG) and antibodies. Thus, it is important to estimate the effect of R_K on MH in a wide range. In this study, we considered a large range of R_K (1 × 10⁻¹⁰ K m² W⁻¹ to 1 × 10⁻⁵ K m² W⁻¹) to cover data reported previously (Table 3). Figure 6(b) shows that R_k increases the temperature in the AuNS significantly. In contrast, medium temperature does not change significantly with changing R_K. The medium temperature has a slight drop only when R_K is larger than 1 × 10⁻⁷ K m² W⁻¹ (Fig. 6(b)). The small drop in medium temperature is due to the heat flux decrease through the gold-medium interface (Fig. 6(c)). Consequently, the impact zone is smaller when R_K exceeds 1 × 10⁻⁷Km² W⁻¹(Fig. 6(d)). However, when comparing our results with the R_K values reported by previous studies (marked by gray shade), the thermal interfacial resistance has a negligible effect on MH.

Fig. 6.

Effect of thermal interfacial resistance between gold and medium on protein inactivation. (a) Schematic of the interfacial resistance between AuNS and medium. (b) Temperature profile for different Kapitza resistances at t = 9 ns. Insert figures shows the temperature profile of medium at 30 nm from the nanoparticle center. (c) Heat flux at the gold-medium interface for different Kapitza resistance. (d) Impact zone for different Kapitza resistances. The interfacial thermal conductance (g) is the reciprocal of Kapitza resistance.

Table 3.

Summary of Kapitza thermal resistance of nanostructures from previous reports

Material	Nanostructure	Solvent	Interfacial modification	Kapitza resistance (RK, ×10−8 Km−2 W−1)	Methods	Reference
Pt	Nanoparticle	Water	No	1.61	DMM	[55]
		Toluene	Citrate	0.77	TA
AuPt	Nanoparticle, 10 nm	Toluene	Alkanethiol	20
	Nanoparticle, 3–5 nm	Water/alcohol	Tiopronin	0.50–1.11		[56]
		Water/alcohol	Thioalkylated ethylene glycol	0.29–0.63
Au-core/AuPt-shell	Nanoparticle, 22 nm	Water/alcohol	CTAB	0.36–0.56
Al	Flat surface	Water	PEG-silane	0.48–0.67	TDTR	[57]
	Flat surface	Water	OTS	1.54–1.82
Au	Nanoparticle	Toluene	No	8.33	DMM	[55]
		Water	Citrate	0.83–1.11	SAXS	[58]
	Flat surface	Water	C18	1.82–2.22	TDTR	[57]
			C11OH	0.83–1.25
	Nanorod	Water	CTAB	0.22–0.77	TA	[59]
			PEG-COOH	–0 (underestimated)
	Nanoparticle	Toluene	No	1–2	LJ model	[60]
		Water		0.59–0.67
	Flat surface	No	Dodecyltriethoxysilane	2.78	TDTR	[61]
			11-mercapto-undecyltrimethoxysilane	1.54
			11-amino-undecyltrietdoxysilane	2.12
			11-bromo-undecyltrimethoxysilane	2.56
			Dodecyl-dimethyl-monochlorosilane	2.94
	Nanorod	Methanol	CTAB	2.5–3.13	TA	[62]
		Ethanol		2.63–3.85
		Toluene		2.86–4.00
		Hexane		3.45–4.76
	Flat surface	Water	n-undecanethiol (n = 11–18)	1.43–1.67	TDTR	[63]
			Methyl 3-mercaptopropionate	0.65–0.80
			11-(1H-pyrrol-1-yl) undecane-1-thiol	0.65–0.80
			11-Mercapto-1-undecanol	0.45–0.63
			11-Mercapto-undecanoic acid	0.45–0.63
	Nanorod	Water	CTAB	1.2	TA	[64]
			PEG	0.44
	Flat surface	Hexylamine	SAMs	0.48–1.82	EMD	[65]
Carbon	Nanotube	D2O	Polystyrene sulfonate surfactant	8.33	TA	[66]

Effects of Nanoparticle Shape: Nanosphere Versus Nanorods.

Next, we investigated the effect of nanoparticle shape on MH. Gold nanorod (AuNR) is another type of nanoparticle commonly used in biomedical applications. Biological tissue significantly absorbs and scatters visible light and is more transparent to near infrared light. AuNRs response to light in near-infrared range and offer a better light penetration depth for the biological tissue. To estimate the AuNR performance for MH, AuNRs with different aspect ratios were studied here (Fig. 7(a)). We kept two factors the same for all particles: particle volume (V_NP) and volumetric heating rate (Q_v). These conditions ensure that the same amount of heat is generated among nanoparticles with different shapes. Figure 7 suggests that gold nanosphere (AuNS) has the highest temperature increase and nanoparticle temperature decreases with the aspect ratio. Compared with AuNSs, AuNRs have higher surface area and therefore enhance the heat dissipation to the surrounding medium, resulting in a lower nanoparticle temperature.

Fig. 7.

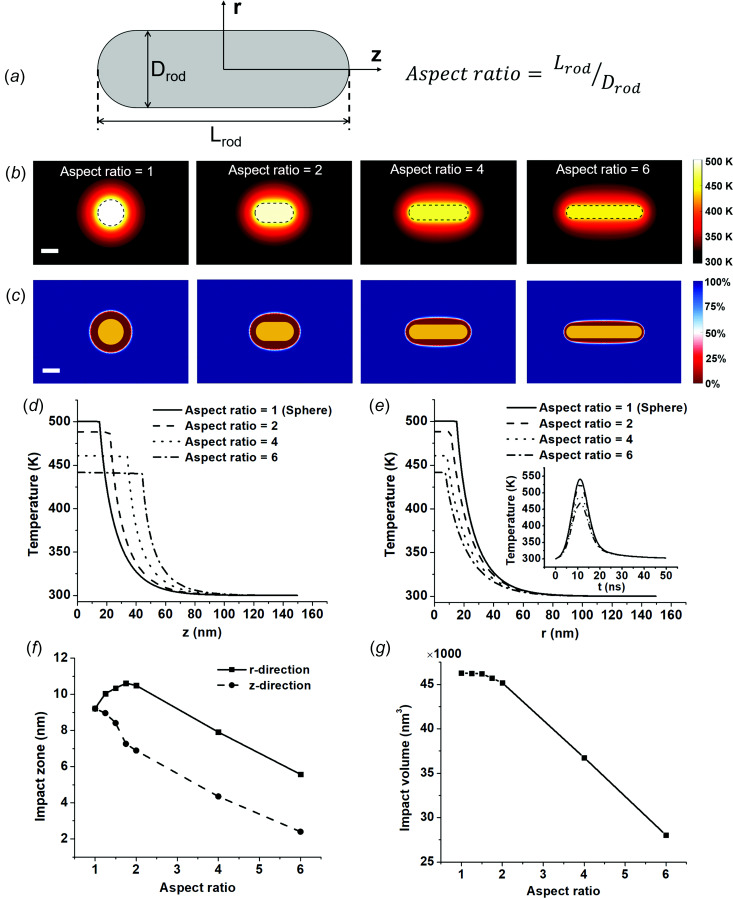
Effect of particle shape on molecular hyperthermia. (a) Geometry of gold nanorod (AuNR). Aspect ratio is defined as the ratio between length and radius of rod. All AuNRs in this study have the same volume. (b) Temperature distribution around AuNRs with different aspect ratios. (c) Protein activity distribution around AuNRs. 100% indicates all proteins are intact and 0% indicates all proteins are inactivated, the boundary of impact zone (50%) is shown in white color. (d) Temperature distribution in the axial direction for AuNRs with different aspect ratios. (e) Temperature distribution in the radial direction for AuNRs with different aspect ratios. Insert is gold temperature profile as a function of time. (f) Impact zone changes with aspect ratio in the axial and radial directions. (g) Impact volume for AuNRs with different aspect ratios.

We further investigated the protein inactivation for different shapes of gold nanoparticles (Figs. 7(c), (f), and (g)). The impact zone in the axial direction (z-direction) decreases with higher aspect ratio. It is interesting that the impact zone in the radial direction (r-direction) first increases for nanorod with aspect ratio of 2 compared with spherical particle, but then decreases with aspect ratio from 2 to 6 (Fig. 7(f)). The impact zone in the r-direction reaches maximum value when aspect ratio was around 1.75. We further compared the impact volume for particle with different shapes, which is defined as the volume where proteins are inactivated by the localized heating. The impact volume decreases with increasing aspect ratio for AuNRs because of higher surface-to-volume ratio and heat dissipation rate than spherical nanoparticle (Fig. 7(g)). It is worth noting that we only considered constant volumetric heating generation in these comparisons. AuNRs have two plasmonic peak, corresponding to LSPR from longitudinal and transverse modes. By adjusting the aspect ratio of AuNRs from 2 to 6, the longitudinal peak can be tuned from 600 nm to more than 1000 nm. Also, the longitudinal peak absorption is significantly higher than transverse peak (see Fig. S1 available in the Supplemental Materials on the ASME Digital Collection). Thus, by applying laser at longitudinal peak, AuNR would generate more heat than AuNS.

Effect of Arrhenius Kinetic Parameters on Protein Thermal Denaturation.

We investigated different proteins using their respective kinetic parameters for thermal denaturation, i.e., the activation energy (E_a) and the pre-exponential factor (A₀). Here, we listed E_a and A₀ of 19 different proteins in Table 4 from the literature. Impact zones were calculated with the same condition in Fig. 5 (30 nm AuNS and temperature dependent material properties).

Table 4.

Kinetic parameters and impact zones of different proteins

Protein	Ea (kJ mol−1)	A0 (s−1)	Impact zone (nm)	Reference
Amylase (malt)	171.13	6.6 × 1023	<1.0	[41,67]
Hemoglobin	313.38	5.4 × 1045	6.7	[41,67]
Rennin	371.54	6.4 × 1057	13.2	[41,67]
Egg albumin	549.78	2.0 × 1081	12.9	[41,67]
Peroxidase (milk)	772.37	1.6 × 10114	15.6	[41,67]
Hemolysin	825.92	3.9 × 10129	23.0	[41,67]
Invertase (yeast)	216.73	7.6 × 1030	1.7	[41,67]
	459.40	5.9 × 1052	<1.0	[41,67]
	358.57	4.9 × 1069	>135.0 nm	[41,67]
	308.36	4.6 × 1045	7.4	[41,67]
Opsin	311.02	1.1 × 1049	12.0	[42]
Isorhodopsin	386.18	6.9 × 1057	11.0	[42]
Rhodopsin	415.59	1.7 × 1062	11.3	[42]
G actin	231.67	2.8 × 1033	2.9	[43]
β-trypsin	275.55	7.9 × 1041	7.7	[44]
Horseradish peroxidase	159.78	5.3 × 1024	1.4	[45]
Catalase	254.78	2.1 × 1038	6.1	[46]
α-chymotrypsin	244	9.75 × 1038	9.3	[19,40]
P-glycoprotein	161.25	1.8 × 1023	<1.0	[47]

Kinetic parameters of the Arrhenius model were obtained from experimental measurements in the literature. The simulation was conducted with condition of 30 nm AuNS and temperature dependent material properties.

Most of the proteins in our study can be inactivated by MH with an impact zone from 1 to 20 nm. Some proteins in the list are interesting in the context of biomedical engineering and sciences. For example, opsin is a G-protein coupled receptor (GPCR) and plays an important role in sensory neurons for vision. GPCRs are a large protein family and contain many potential drug targeting sites for disease treatments. In our previous study, we have investigated protease-activated receptor 2 (PAR2), which is also a GPCR [30]. Although kinetic parameters vary from protein to protein, impact zones of opsin and related receptors suggest MH can be a useful method to inactivate GPCRs. On the other hand, the activity of some proteins could be insensitive to MH. For example, P-glycoprotein (P-gp) can be overexpressed by cancer cells and is related to multidrug resistance in cancer chemotherapies. Many researches tried to inhibit activity of P-gp in cancer cells as a method to overcome the tumor multidrug resistance. However, we observed that the impact zone of P-gp is below 1 nm, meaning that they cannot be inactivated under current condition of MH. This may be due to that higher temperature is required, or the measured Arrhenius parameters need further validation.

Since different proteins were characterized by different Arrhenius parameters, we then systemically investigated a range of Arrhenius parameters on MH (Fig. 8). There are two interesting findings. First, localized protein inactivation only occurs when the protein's kinetic parameters are in the triangle shaded area shown in Fig. 8(a). We plotted all protein kinetic parameters from Table 4 in Fig. 8(a) and most were localized in the “triangle area.” Previous studies reported correlation between E_a and A₀ and were also displayed in Fig. 8(a) [67,68]. Above the triangle area, the impact zone is very large, and all proteins get inactivated even at the boundary of the computational domain (which is held at constant temperature, 300 K). This shows that the combination of E_a and A₀ gives a thermally unstable situation. Below the triangle area, the combination of E_a and A₀ does not lead to any protein inactivation since the impact zone is less than 1 nm. Second, we observed that the impact zone seems to correlate with the activation energy E_a (Fig. 8(b)). Proteins with E_a smaller than 200 kJ mol⁻¹ have a very small impact zone. The impact zone increases when E_a is larger than 200 kJ mol⁻¹. The results also demonstrate that the protein inactivation by MH was highly localized around the nanoparticle as the impact zone hardly exceeded 20 nm.

Fig. 8.

Impact zones for different proteins. (a) Contour plot of impact zone as a function of E_a and A₀. The shaded region suggests that molecular hyperthermia can inactivate proteins effectively. The open dots are experimental measurements of E_a and A₀ for different proteins from Table 4. The solid line indicates the empirical correlation between E_a and A₀ [68]. (b) Impact zones calculated based on the E_a–A₀ correlation (solid line) and real protein kinetic parameters (open dots). The thermally unstable proteins are not plotted on the figure since they have unrealistic impact zones.

Discussion

In this study, we built a computational model to study the protein inactivation behavior during MH. We studied important factors that affect the protein inactivation in MH including laser pulse shape, duration, temperature-dependent material properties, thermal interfacial resistance, nanoparticle shape, and protein target. The results provided a guideline in designing and applying MH for various biomedical applications. There were several interesting aspects that have emerged from our studies.

Material Properties in the Nanoscale.

The material properties utilized here were all obtained from bulk materials. However, the physical properties of material may vary in the nanoscale. For example, the melting temperature of AuNS drops significantly compared with bulk gold when the particle size is smaller than 10 nm [69]. Since we used 30 nm AuNS in our study, the melting point of particles in our study can be considered the same as bulk gold (1337 K). Also, we limited our laser energy to ensure the nanoparticle temperature below gold melting point. Therefore, we did not consider the phase change effects in this study. However, AuNS could undergo phase change process at high laser fluence and possibly reshaping and fragmentation. Besides melting temperature, the thermal conductivity was also reported to be highly dependent on material size when it comes to nanoscale. Chen et al. estimated the thermal conductivity for 3 nm AuNS to be 24.14 W m⁻¹K⁻¹, an order magnitude lower than bulk gold [70]. In our previous study, we compared finite element model and molecular dynamics model to investigate the material properties of both gold and medium in the nanoscale [29]. We found an obvious mismatch between two models when we use bulk material properties in FEM. This indicated that the size dependence of material properties should be considered in computational methods. However, a lot remains unknown in this area, and further experimental and numerical studies are required to elucidate the heat transfer process in the nanoscale.

Protein Inactivation in a Wide Temperature Range.

In this study, we adopted a conventional Arrhenius model for protein inactivation process in which both pre-exponential factor (A₀) and activation energy (E_a) are independent of temperature. This hypothesis is valid for low temperature range. However, in a wider temperature range, the activation energy and pre-exponential factor both vary with temperature as demonstrated by our previous study [31]. Also, the protein inactivation process was assumed to a first-order, irreversible process in this study. The thermal inactivation of protein is a much more complicated process and is highly dependent on the protein structure [71].

Conclusions

In this study, we numerically investigated protein photoinactivation during MH by combining the heat transfer model with the chemical reaction model. Impact zone was defined to quantify the protein inactivation efficiency. First, we studied the effect of pulse shape and duration and found that stretching the laser pulse duration reduces impact zone with the same laser energy. Second, we demonstrated that temperature-dependent material density and specific heat have very small effect on MH, while temperature-dependent thermal conductivity decreases the impact zone and the low thermal conductivity of cytoplasm increases the impact zone. Third, thermal interface resistance has a limited impact on MH below 1 × 10⁻⁷Km² W⁻¹, a value larger than reported values for interface resistance. Fourth, the nanosphere has larger impact volume than nanorods with the same heat generation. Finally, the protein Arrhenius parameters have significant influence on the impact zone. In summary, this work provides an analytical interpretation of protein photoinactivation by MH and offers a clear guideline to design MH for biomedical applications.

Supplementary Material

Supplementary Material

Supplementary Word & Figures

Funding Data

• •National Institute of General Medical Sciences (NIGMS) of the National Institutes of Health (Award No. R35GM133653; Funder ID: 10.13039/100000057).
• •Collaborative Sciences Award from American Heart Association (Award No. 19CSLOI34770004; Funder ID: 10.13039/100000968).
• •High-Impact/High-Risk Research Award from Cancer Prevention and Research Institute of Texas (Award No. RP180846; Funder ID: 10.13039/100004917).

Nomenclature

A₀ =

pre-exponential factor in Arrhenius model

AuNR =

gold nanorod

AuNS =

gold nanosphere

C_abs =

absorption cross section area, m²

C_p =

specific heat, J kg⁻¹ K⁻¹

Cht =

α-chymotrypsin

CTAB =

cetyl trimethylammonium bromide

$\overline{d}=$ =

interparticle distance, m

D_m =

diameter of medium domain, 2R_m, m

D_NP =

diameter of nanoparticle, 2R_NP, m

D_rod =

diameter of rod

DMM =

diffuse-mismatch model

E₀ =

activation energy in Arrhenius model

EMD =

equilibrium molecular dynamics

F =

laser fluence, J m⁻²

G =

interfacial thermal conductance, W K⁻¹ m⁻²

GPCR =

G-protein coupled receptor

k =

chemical reaction rate constant, s⁻¹

k_Au =

thermal conductivity of gold, W m⁻¹ K⁻¹

km =

thermal conductivity of medium, W m⁻¹ K⁻¹

L_d =

thermal diffusion length, M

L_rod =

length of rod

LJ =

Lennard-Jones

LSPR =

localized surface plasmon resonance

MH =

molecular hyperthermia

OTS =

octadecyltrichlorosilane

P-gp =

P-glycoprotein

PEG =

polyethylene glycol

Q_v =

volumetric heating rate, W m⁻³

R =

the gas constant, 8.314 J K⁻¹ mol⁻¹

R_K =

Kapitza resistance, Km² W⁻¹

s =

survival fraction of protein

SAM =

self-assembly monolayer

SAXS =

small angle X-ray scattering

T =

temperature, K

t₀ =

laser duration, s

TA =

transient absorption measurement

TDTR =

time-domain thermoreflectance

u(t) =

Heaviside unit step function

V_NP =

nanoparticle volume, m³

α =

thermal diffusivity, m² s⁻¹

μ =

center position of the pulse, s

ξ =

dimensionless parameter, $\frac{L_d}{\frac{\overline{d}}{2}}$

2μ =

pulse duration, s