Two decades of research with the GreenLab model in agronomy

Abstract

Background

With up to 200 published contributions, the GreenLab mathematical model of plant growth, developed since 2000 under Sino-French co-operation for agronomic applications, is descended from the structural models developed in the AMAP unit that characterize the development of plants and encompass them in a conceptual mathematical framework. The model also incorporates widely recognized crop model concepts (thermal time, light use efficiency and light interception), adapting them to the level of the individual plant.

Scope

Such long-term research work calls for an overview at some point. That is the objective of this review paper, which retraces the main history of the model’s development and its current status, highlighting three aspects. (1) What are the key features of the GreenLab model? (2) How can the model be a guide for defining relevant measurement strategies and experimental protocols? (3) What kind of applications can such a model address? This last question is answered using case studies as illustrations, and through the Discussion.

Conclusions

The results obtained over several decades illustrate a key feature of the GreenLab model: owing to its concise mathematical formulation based on the factorization of plant structure, it comes along with dedicated methods and experimental protocols for its parameter estimation, in the deterministic or stochastic cases, at single-plant or population levels. Besides providing a reliable statistical framework, this intense and long-term research effort has provided new insights into the internal trophic regulations of many plant species and new guidelines for genetic improvement or optimization of crop systems.

INTRODUCTION

We present an overview of two decades of developing the GreenLab model and its applications in agronomy. This model inherits both from architectural models, designed to address botany issues, and from crop models, designed to address agronomy issues.

The architectural models of trees (Halle et al., 1978) identify the basic components of tree development. Architectural models and their reiterations rely on a few key notions such as axis types, with monopodial or sympodial ramifications, and axial or terminal flowering. A fundamental model assumption is that the same types of axes are duplicated in the plant at different development stages. This enabled efficient sampling strategies for measurements, paving the way for the calibration and evaluation of models representing the stochastic functioning of meristems.

GreenLab is also affiliated to crop models such as STICS (Brisson et al., 1998), APSIM (Keating et al., 2003), Tomsim (Heuvelink, 1998), Pilote (Maillol et al., 2011), EcoMeristem (Luquet et al., 2006) and SUNFLO (Casadebaig et al., 2011). Some of these models have shown good performances for yield prediction. Most of them share a common set of assumptions: (1) they use stand-level data, such as the leaf area or biomass per organ compartments; (2) Beer–Lambert’s law models light interception by foliage as a function of the leaf area index (LAI); (3) a harvest index, the percentage of biomass allocated to the organ of interest, characterizes the plant or stand yield; and (4) they may incorporate (sub-)models, especially for the photosynthesis process, respiration or for the effect of irrigation, nitrogen, etc. In contrast, crop models have limitations related to the fact that organs are not individualized but pooled into compartments: (1) the initial effect of the seed reserves cannot be represented; (2) LAI is not easily simulated; (3) planting density is often ignored; (4) mortality during development is difficult to integrate; (5) different modules of crop models do not synchronize easily, and their interactions are difficult to model; (6) variability within the stand is ignored; (7) for woody plants, girth growth is ignored; and (8) 3-D plant representation is not simulated.

Functional–structural plant models (FSPMs) combine both structural and functional approaches. FSPMs seek to accurately simulate the physiological functioning associated with plant growth and architecture in relation to environmental parameters. Different formalisms have been proposed for the development modules: object-oriented formalisms (Eschenbach, 2005), or the most widespread formalisms which are language based using L-system grammar (Prusinkiewicz et al., 1988) and its extensions such as XL (Kniemeyer et al., 2004; Henke et al., 2016) or L-Py (Boudon et al., 2012). The organs play a functional role as source and sink, as shown in Lignum (Perttunen et al., 1998), Vica (Wernecke et al., 2000), L-peach (Allen et al., 2005) and L-Kiwi (Cieslak et al., 2011). They provide interesting insights into plant functioning and a way of integrating the existing biological knowledge of a given plant species (Guo et al., 2011). However, the simulations are computationally costly, and their complexity raises difficulties for a rigorous application of statistical methods for parameter estimation and model evaluation based on experimental measurements. Above all, FSPMs concern individual plants: unlike crop models, they do not readily extend to stand scale. In the following, we show that a different modelling strategy can be adopted, as is the case for the GreenLab model, addressing the scientific problem as follows. Can we find a concise mathematical representation for metabolic processes with phytomer-level structures to generically describe plant growth and development at an individual level up to a stand scale?

We recall here the choices that have governed the selection of equations and formalisms in the GreenLab model, and we summarize two decades of research with GreenLab in plant architecture development and production. The characteristics of GreenLab are given below.

(a) The GreenLab model is an FSPM (Sievänen et al., 2014) integrating both functional and structural descriptions for metabolic (or physiological) processes with phytomer-level structures. It enables studies from the organ level up to the macroscopic scale. The plant types studied cover a broad spectrum from herbaceous plants to trees. The model benefits from the ecophysiological concepts assumed in crop models [thermal time, light use efficiency (LUE), water use efficiency (WUE) or a common pool]. The restrictions mentioned for FSPMs also apply for GreenLab; the studied stand must be composed of a fixed genotype (clone, variety), with plants of the same age, cultivated in an isotropic environment (e.g. no asymmetric gravitropism or phototropism). Many cultivated plants meet these requirements.

(b) GreenLab is a stochastic, discrete, dynamic mathematical model with a voluntarily limited set of variables and physically interpretable parameters, allowing: (1) parameter estimation (strategy of protocols for data acquisition and inverse methods); (2) model analysis (stability, trajectories, sensibility and uncertainty analysis, etc.); (3) model evaluation on cultivated plants (for plant breeding); and (4) optimization and control of farming systems.

(c) The plant structure development formalism is based on a stochastic dual-scale automaton (Zhao et al., 2003). The 3-D shape is not detailed, but the number of organs can be expressed by recursive equations.

(d) GreenLab formalism is deployed under various environments and programming languages; we developed stand-alone simulation and calibration tools (Kang et al., 2009; Hua et al., 2011; Wang et al., 2013; De Reffye et al., 2016; Ribeyre et al., 2018). Simple deterministic simulation was also plugged in platforms (Smoleňová et al., 2012; Griffon and de Coligny, 2014) and in a knowledge-and-data-driven model (KDDM) (Fan et al., 2015).

In this research in context review, the manuscript is organized as follows. (1) The overall model is first simply introduced. (2) The botanical and mathematical knowledge necessary for the analysis, modelling and simulation is gradually recalled. Then, the focus is on ecophysiological concepts and their modelling. (3) Two case studies are then presented. We refer to the bibliography for more details in an ePub format (De Reffye et al., 2016) or eLearning web media (Jaeger et al., 2015). (4) An example of model behaviour is proposed. (5) The Discussion points out several benefits of the GreenLab approach before concluding.

GreenLab approach at a glance

As in many FSPMs and crop models, GreenLab equations take the form of a discrete dynamic system:

$${\displaystyle \begin{array}{l}{\displaystyle [X\left(t\right),Y\left(t\right)]=greenlab\mathrm{\_}function(E\left(t\right),X(t-1),Y(t-1),\psi )}\end{array}}$$ (1)

where ψ stands for the parameter set, t for the simulation cycle, X(t) stands for the plant structure component in cycle t, Y(t) stands for the organ biomass allocated to each organ cohort in cycle t and E(t) reflects the environmental conditions during cycle t.

Table 1 gives the list of variables and parameters with their respective units.

Table 1.

Alphabetically sorted terms of GreenLab model entities, parameters and variables

Ba o	No unit	Organ o sink strength variation Beta law first parameter
Bb o	No unit	Organ o sink strength variation Beta law second parameter
CD	No unit	Cycle of development
GU	CD	Growth unit
a	No unit	Branching rate (probability), aφ is indexed to physiological age φ
b	No unit	Development rate (probability), possibly indexed to physiological age φ
c	No unit	Viability, possibly indexed to physiological age φ
D(t)	No unit	Plant demand at cycle t
I	MJ cm−2	Radiant energy received per surface unit during one cycle
N φ o(u)	No unit	Number of organs o of physiological age φ of u cycles
maxφ	No unit	Maximum physiological age
o	No unit	Generic organ (o = a, leaf; o = i, internode; o = p, petiole; o = f, female fruit; o = m, male fruit)
P o	No unit	Organ o sink strength function
Q(t)	g	Biomass produced at plant level during cycle t
Q0	g	Seed biomass, stands for Q(0)
q φ o(t)	g	Biomass of one organ o of physiological age φ produced in cycle t
Sf(t)	cm2	Leaf area functioning in cycle t
Sp	cm2	Plant production surface area
Sd	cm2	Available surface area per plant (= cultivated area/number of plants)
t	CD	Current cycle of development, depending on thermal time
TQ(t)	g	Total biomass produced at plant level from cycles 1 to t
w	No unit	Rhythm ratio
ε	cm	Leaf thickness
φ	No unit	Current physiological age
Λ	g MJ–1	Light use efficiency

CD, GU and o are entity definitions standing, respectively, for the cycle of development defined by thermal time, the growth unit, expressed as a successive list of CDs, and for organ generic notation (o is to be replaced in context with leaf, petiole, internode, etc.). The variable t stands for the current CD. All variables are normalized to one CD so the time unit ‘per CD’ is omitted, for the sake of clarity.

Concerning plant development, the number of physiological ages is maxφ, standing for the number of different axis typologies in the modelled plant; a, b, c and w define the development parameters, respectively standing for the branching, development, viability and rhythm ratio rates. They are defined from statistics based on plant axis phytomer distributions. From these, development simulation defines the organ cohorts N^φ_o(u), i.e. the number of organs o of age u and physiological age φ, in each growth cycle t (i.e. appearing in cycle t – u).

Concerning now production, the model parameters to be fitted using a target file filled with sparse organ weight measurements are those related to organ o sink strengths, P_o, Ba_o and Bb_o respectively, standing for the sink strength value (P_o) and its variation during organ expansion (Ba_o and Bb_o define the variation shape) and those related to biomass production at plant level, Q0, the seed biomass, Sp, the production surface area and Λ, light use efficiency. These parameters define plant demand D(t) and production Q(t) in each cycle t, computing the functional leaf area Sf(t) from the various leaf cohorts and leaf thickness ε.

Modelling plant structure and development

Botanical components of plant structure.

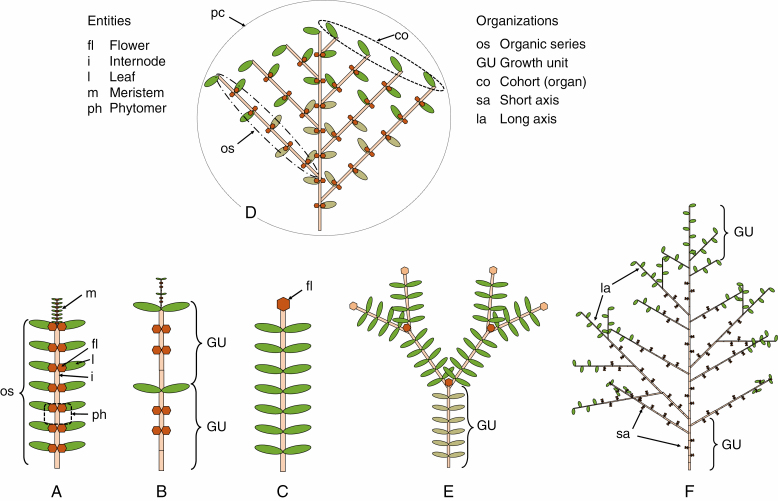
The architectural models of the botanist Francis Hallé provide qualitative descriptions of plant structure and development (Hallé et al., 1978). They serve as a frame to more quantitative information regarding meristem activity over time for axis development by continuous or rhythmic phytomer production. In the latter case, the axis is made up of modules called growth units (GUs). A phytomer is a structure comprising an internode that ends in a node on which organs (leaves, fruits and axillary meristems) are attached. Flowering can be axial or terminal. Axial flowering does not stop the functioning of apical meristems and produces branched monopodial systems. Terminal flowering stops axis development, producing sympodial branched systems (Fig. 1). Some important notions must be defined:

Fig. 1.

Botanical entities in the GreenLab model. (A) The leafy axis representing a plant with continuous development, defining the organic series. (B) A leafy axis with rhythmic development. (C) A leafy axis module with terminal flowering. (D) Monopodial structure with continuous development. (E) Modular structure with sympodial development. (F) Monopodial structure with rhythmic development.

• 1.The organic series (Buis and Barthou, 1984) is defined as ‘all organs of the same morphological nature (leaves, internodes, fruits) generated by the same primary meristem during the development of a leafy axiFs and on which the same morphogenetic characteristic is considered’.
• 2.A cohort is a set of organs of the same nature, created at the same time by the parallel functioning of meristems. The development outcome is expressed numerically in terms of chronological cohort sequences.
• 3.A plant crown is the combination of primary bearing axes and secondary ramified axes, on which the number of phytomers produced per axis is counted. A tree includes a large number of main and secondary plant crowns. From the top to the bottom of the main stem, it is normally the same ramified branch that grows until it stops due to the abortion of the terminal meristem.

In our model, the root system is considered as a single simple compartment; its underlying structure is ignored.

Cycle of development, chronological age.

In our model, the average duration, in thermal time, required to place a new phytomer at the end of the plant main stem is called the cycle of development (CD), expressed in degree days. The CD is chosen as a reference time step. The plant chronological age, t, is therefore expressed in terms of CD.

The concept of physiological age.

In most branched plants, different sorts of leafy axes coexist in their structure, each with specific features. For example, in coffee trees, the stem is orthotropic and the branches are plagiotropic. Botanists are used to sorting these different axes into categories whose spatial and temporal combinations allow a description of the structural patterns of trees (Barthélémy and Caraglio, 2007). In GreenLab, an index, φ, is assigned to the types of axes and called ‘physiological age’ (Rivals, 1965). Axillary meristems may have the same physiological age as the meristem of the stem (the case of a reiteration) or an older age (the case of a branch). A meristem may undergo a physiological age transition during axis development and transform into a flower (e.g. sunflower). In a tree, long shoots have a young physiological age that corresponds to a long development time, and short shoots that bear fruits correspond to an old physiological age with a short life span.

Each tree species has a particular organization of physiological ages of axillary meristems borne by a GU: as the plant develops, this organization gives rise to the ‘architectural unit’ (Barthélémy and Caraglio, 2007). For instance, in many species such as poplar, cherry or elm, the physiological ages of the axillary buds increase top-down inside the GU, a phenomenon called ‘acrotony’.

A botanical automaton to simulate the development.

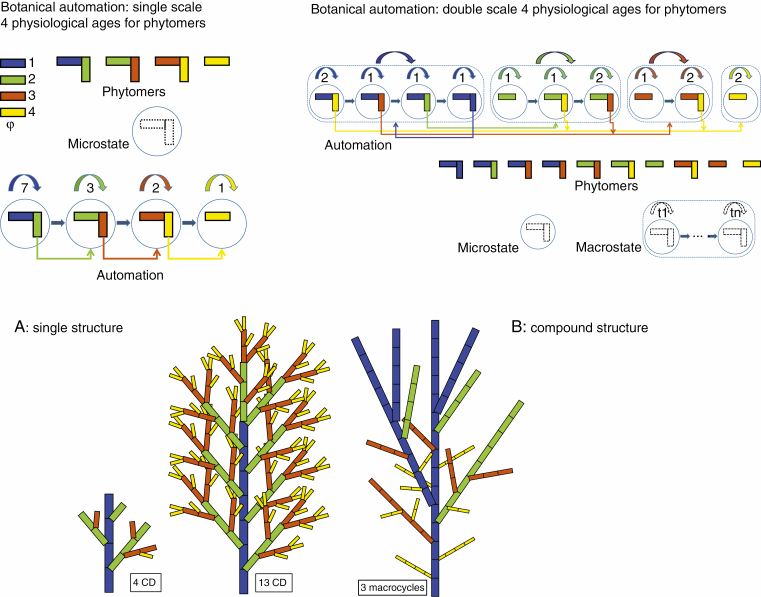
To simulate the development of a botanical structure, it is sufficient to describe the rules governing the physiological age value of any newly produced phytomer. To this end, we developed a dual-scale automaton approach using graph-based notations (Zhao et al., 2003), as shown in Fig. 2.

Fig. 2.

The development of a botanical structure, driven by the operation of a single (A) or double scale (B) botanical automaton. The colours correspond to the physiological ages of the axes; blue for the stem and reiterations, green for the branches, brown for the branchlets and yellow for the twigs. In both automatons, transitions in physiological ages are indicated by arrows, carrying the number of transitions (tk). In the double scale automaton, growth units are modelled by macro-states, composed of several micro-state transitions (standing for list of phytomers).

The structures can be simple or compound, depending on whether the meristems have continuous or rhythmic functioning. In the latter case (mainly trees), the automaton is on a double scale, with the meristems setting up the GUs and with two time scales being considered. The microcycle (the basic CD) stands for the phytomer, while the macrocycle stands for GU construction. Figure 2 shows such a rhythmic development of a compound structure with three macrocycles and ten microcycles. The portions of axes (derived from the automaton) that remain in the same physiological age are called ‘development axes’. A leafy axis whose apical meristem has undergone several transitions is therefore made up of a succession of development axes.

Given the list of physiological ages and their transitions, it is recursively possible to formally express the number of phytomers produced in a given cycle without iteratively simulating them (Yan et al., 2003). This so-called structural factorization is very efficient to provide a faster means of either designing, understanding or simulating the architecture model of plants (Yan et al., 2003). This formalism extends straightforwardly to the stochastic case, assigning probabilities to transition occurrences.

Stochastic version of the development model.

Most plants have their development and architecture disrupted by hazards that affect bud functioning. The random events that we consider in our model correspond to the appearance, or not, of a phytomer at a given position in the plant structure as defined by the deterministic application of the automaton transition rules, as detailed in the following paragraphs.

Axis development.

Axis development can be seen as a random alternation of phytomers in proportion b (development rate) and void entities in proportion (1 – b) corresponding to pauses in the meristem’s functioning. Then, the distribution of the number of phytomers per axis resulting from a Bernoulli process for N cycles with a parameter b follows a binomial law B(N,b). Note that N and b can be retrieved from the distribution of developed phytomers thanks to the mean–variance relationship in binomial laws [mean = N b and variance = mean (1 – b)]. The first validation of the modelling of leafy axis development was carried out on coffee trees (De Reffye, 1981a, b).

Within the same architecture, the axes may have different average development speeds. For instance, coffee and cotton branches generally grow more slowly on average than stems. This can be modelled with a ‘rhythm ratio’ w = X/N, which is the ratio of the number X of phytomers produced for N CDs of development (De Reffye, 1981a).

Meristem viability.

The viability of a meristem at age t CD is defined by the survival rate c. In the general case, the viability c is variable and the mortality rate of the branches evolves according to a sigmoid form, described by a function of two parameters, which can be estimated by the inverse method (e.g. De Reffye, 1981b for coffee tree, or Diao et al., 2012 for eucalyptus).

Branching.

Variability in plant architecture is also due to the branching process. In the immediate branching case, the axillary meristem produces a branch with probability a immediately or remains dormant forever. The parameter a may be variable, especially at young ages. Branch groupings can be modelled through a Markov chain using a coupling parameter r between branched and unbranched (see De Reffye, 1982, or Guédon et al., 2007 for more complex patterns).

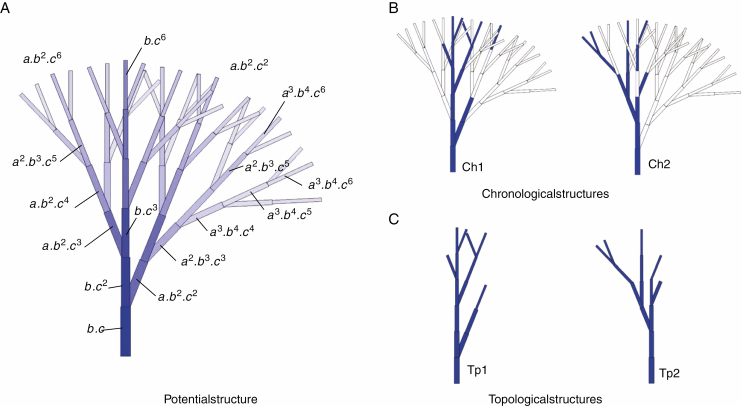
Chronological, topological and potential structures.

Using GreenLab’s botanical automaton, plant development simulations may generate three kinds of structure representations: chronological, topological or potential structures (Fig. 3).

Fig. 3.

Potential, chronological and topological structures. The potential structure (A) contains all the chronological simulations. The colour gradient illustrates the decrease in the existence rates of phytomers due to their positions in the structure. Some of these rates are displayed depending on the branching rate (a), development probability (b) and viability (c). In (B) two random chronological simulations Ch1 and Ch2 are reproduced as well as their corresponding topological representations Tp1 and Tp2, where void entities are removed (C).

The chronological structure expresses the botanical structure in which the creation of both phytomers and pauses is represented. Pauses are visualized as void entities. Stochastic simulations of the same plant generate a very large number of possible chronological structures. This spatio-temporal representation has a high pedagogical interest since meristem functioning can be followed step by step.

The topological structure is a representation of the botanical structure in which only the created phytomers are represented (the pauses are not visible). This is the structure that corresponds to observations on plants.

The potential structure, planar, contains the totality of all the chronological structures that can be obtained by stochastic simulation: it corresponds to the application of the associated deterministic automaton. An existence (occurrence) rate can be assigned to each element of the potential structure. The sum of the rates of existence for the entities of the potential structure gives the average number of phytomers produced by the plant.

Visualization of plant architecture.

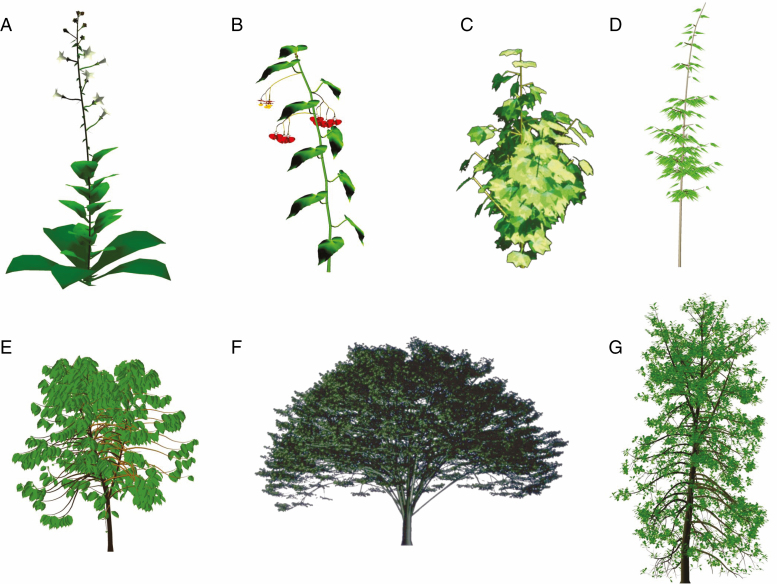
In addition to a graph of phytomer organization generated by the botanical automaton, geometric functions defining organ dimensions and the angles of phyllotaxis, branching and bending of the axes enable simulations of plant architecture. The result may remains purely geometric (photosynthesis is ignored), but such models can be used in computer graphics to simulate landscapes, or in agronomy to calculate, for example, the interception of light. Such a stochastic approach was first applied with the AMAP model (De Reffye et al., 1988b; Jaeger and de Reffye, 1992), and applied to numerous species (Fig. 4) from which GreenLab’s geometric instantiation and representation of structure are inherited.

Fig. 4.

Plant architectures generated from AMAP structural model implementations. (A) Tobacco (Poisson and Rey, 1997), (B) begonia (Lecoustre et al., 1992), (C) cotton (De Reffye et al., 1988a), (D) bamboo (Dabadie et al., 1991), (E) coffee (De Reffye et al., 1981b), (F) elm (De Reffye et al., 1991b), (G) cherry (De Reffye, 1981b).

Biomass production and partitioning

Ecophysiological variables.

Ecophysiology considers, on the one hand, the sugars produced by the leaves (photosynthesis) and used for the functioning of the plant (respiration) and, on the other hand, those used for the production of biomass (cellulose) that gives rise to organ growth. The latter is the carbon fixed on the architecture and is the result of net photosynthesis. Under normal conditions, the proportion of fixed sugars is considered constant.

More or less precise functioning processes may be considered by the model user: for example, organ composition costs or respiration can be taken into account as well (e.g. the cost of sugars is about twice as high for producing oil as for producing cellulose for the same weight).

The source–sink concept.

In our approach, once the functioning of meristems is known, the cohorts of organs produced with the botanical automaton for each development cycle defines the number of differentiated organ clusters. Some, such as leaves, are source organs. All organs, including leaves, are attractive sinks for the biomass produced. The growth process is also discretized in CD in order to synchronize with development. The growth loop is initiated by the reserves from the seed (Ma et al., 2006).

GreenLab, like several crop models, uses the notion of a common pool that stores synthesized biomass and distributes it to organ compartments. This notion is relevant for herbaceous plants, but is less realistic for woody trees, although it can be adapted, for instance concerning girth growth (see below).

Source organs.

Leaves are the source organs of the plant. Crop models consider that dry matter production is proportional to the intercepted light. The proportionality factor is called the LUE. Under standard conditions, it can be considered as constant. In the field, dry matter production is found to be proportional to plant transpiration, which is the main limiting factor. The proportionality factor then becomes the WUE.

Sink organs.

The biomass attributed to every organ, distributed from the common pool, is set proportional to its sink strength. Sink strength varies during the duration of organ expansion tx, following the same form of sink function for all organs of the same type o (o = leaf, internode, fruit, etc.) in a cohort. The function expression is empirically determined; it must adjust to the evolution of the numerical values of the sink strength during organ expansion. In GreenLab, the roots are considered as a single organ with a long duration of expansion. Secondary growth is deduced from Pressler’s law (Pressler, 1865): for each CD, each active leaf produces a ring element (virtual organ) with a constant sink.

The sink strength of an organ of expansion duration tx_o is modelled by the function:

$${\displaystyle \begin{array}{l}{\displaystyle P_o^{\phi }\left(t\right)=p_o^{\phi }\cdot F_o\left(\frac{t}{t{x}_o}\right)}\end{array}}$$ (2)

Where the parameter $p_o^{\phi }$ is the strength of the organ sink, t is its chronological age, φ is its physiological age and o characterizes its type (o = a for the leaf, o = i for the internode, o = f for the fruit). $F_o\left(\frac{t}{t{x}_o}\right)$ is the variation function of the sink related to its maturation where tx_o is the domain of t for the chronological age of the organ expressed in cycles (tx_o ≥ 1 and 0 ≤ t ≤ tx_o).

The GreenLab model defines the sink function according to a discretized beta law function:

$${\displaystyle \begin{array}{l}{\displaystyle F_o\left(\frac{t}{t{x}_o}\right)=\frac{1}{M}\cdot {\left(\frac{t}{t{x}_o}\right)}^{a-1}\cdot {(1-\frac{t}{t{x}_o})}^{b-1},0\le t\le t{x}_o}\end{array}}$$ (3)

where parameters a and b, verifying the constraint a ≥ 1 and b ≥ 1, drive the curve shape; M is a normalization factor.

Plant demand.

The plant demand D(t) at a given age t is the sum of the active sink organs. Thanks to the notion of cohorts, the demand can be factorized. The number of phytomers produced by the botanical automaton gives the number of leaves, internodes and fruits produced in each cycle. In the eqn (4), organs of type o, physiological age φ and aged u cycles have a sink function $P_o^{\phi }\left(u\right)$ defined from eqn (2). They appeared in cycle $t-u+1$ and are in number $N_o^{\phi }(t-u+1)$. Demand expression D(t) is obtained by a convolution as follows:

$${\displaystyle \begin{array}{l}{\displaystyle D\left(t\right)={\displaystyle \sum _{o,\phi }}({\displaystyle \underset{u=1}{{\displaystyle \sum ^t}}}{N}_o^{\phi }(t-u+1)\cdot P_o^{\phi }\left(u\right))}\end{array}}$$ (4)

Calculation of biomass production by the plant.

Starting from the seed, the calculation of biomass production and biomass partitioning requires the biomass supply Q in cycle t – 1 and demand D in cycle t.

Most crop models use Beer–Lambert’s law to calculate biomass production per unit of cultivated area and per unit of time:

$${\displaystyle \begin{array}{l}{\displaystyle Q=\mathit{\Lambda }\cdot \mathit{I}\cdot \mathit{S}\mathit{p}\cdot (1\mathit{-}\mathrm{e}\mathrm{x}\mathrm{p}(\mathit{-}\mathit{k}\cdot \mathrm{L}\mathrm{A}\mathrm{I}))}\end{array}}$$ (5)

where Λ is the LUE, I the radiant energy received per surface unit and Sc the cultivated area. LAI is the ‘leaf area index’ (ratio of the leaf area to the cultivated area Sc) and k a coefficient that depends on the average inclination of the leaves. LAI can be measured in the field by an instrument, for instance the Plant Canopy Analyzer (PCA) LAI-2000 (LI-Cor Inc., Lincoln, NE, USA), and the expression 1 – exp (–k · LAI) estimates the rate of leaf overlapping intercepting light.

The GreenLab model adapts eqn (5), which is transformed into:

$${\displaystyle \begin{array}{l}{\displaystyle Q\left(t\right)=\mathrm{\Lambda }\cdot I\cdot Sp\cdot (1-\exp (-k\cdot \frac{Sf\left(t\right)}{Sp}))}\end{array}}$$ (6)

In this expression, Q(t) is the amount of biomass synthesized by the plant in cycle t, and Sf(t) is the total plant leaf surface area. The variable Sp is called the ‘production surface area’ of the plant and should be interpreted as an empirical parameter, adjusted to relate to the measured weight of the plant $TQ\left(t\right)=\underset{u=0}{\sum ^t}Q\left(u\right)$ and its leaf surface area Sf(t).

Computation of organ biomass increment.

Plant demand D(t) is calculated in each development cycle t using eqn (4). Similarly, the biomass supply Q(t) is calculated by recurrence using eqn (6).

The biomass growth of an o-type organ depends on the value of its sink and the ratio of the ratio supply synthesized to the previous cycle Q(t – 1) by the current demand D(t). The expansion of the organ of type o appearing in cycle u when the plant is at cycle t (t > u) is written:

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{\Delta }{q}_o^{\phi }(u,t)=P_o^{\phi }(t-u+1)\cdot \frac{Q(t-1)}{D\left(t\right)}}\end{array}}$$ (7)

The weight of the organ (sum of expansions) that appeared in cycle u when the plant was at cycle t is then:

$${\displaystyle \begin{array}{l}{\displaystyle q_o^{\phi }(u,t)={\displaystyle \underset{j=u}{{\displaystyle \sum ^t}}}{P}_o^{\phi }(j-u+1)\cdot \frac{Q(j-1)}{D\left(j\right)}}\end{array}}$$ (8)

Note that organ o with physiological age φ and appearing at cycle t – u + 1 is represented $N_o^{\phi }(t-u+1)$ times as a cohort in the plant structure.

The series $q_o^{\phi }(1,t),\dots ,q_o^{\phi }(t,t)$ defines the organic series describing the organ o biomass profile along a leafy axis according to the rank of its phytomer.

Allometric relationships define the geometric shape of an organ according to its volume v, which depends on its weight q and density δ, according to the expression: v = q/δ. The total functional leaf area can then be calculated as:

$${\displaystyle \begin{array}{l}{\displaystyle Sf\left(t\right)=\frac{1}{\epsilon }\cdot d_a\cdot {\displaystyle \underset{\phi =1}{{\displaystyle \sum ^{mx\phi }}}}{\displaystyle \underset{u=(t-ta)+1}{{\displaystyle \sum ^{max(t,ta)}}}}{N}_a^{\phi }\left(u\right)\cdot q_a^{\phi }(u,t)}\end{array}}$$ (9)

where ta is the duration of leaf functional activity, assumed here to be equal to its expansion duration tx. The index φ denotes physiological age (from 1 to mxφ), d_a the leaf mass density and ε leaf thickness (assumed constant here). Within a cohort of leaves appearing at chronological age u, the number of leaves $N_a^{\phi }\left(u\right)$ is recorded, with their individual biomass $q_a^{\phi }(u,t)$.

Equation of plant growth recurrence.

Lastly, by expressing the leaf surface areas as a function of the previous Q/D ratios, we get the generic recurrence equation that characterizes the individual growth of a computational plant according to the GreenLab model:

$${\displaystyle \begin{array}{ll}{\displaystyle Q\left(t\right)=}& \mathrm{\Lambda }\cdot I\cdot Sp\cdot (1-\exp (-\frac{k}{\epsilon \cdot Sp}\cdot {\displaystyle \underset{\phi =1}{{\displaystyle \sum ^{mx\phi }}}}{\displaystyle \underset{u=(t-ta)+1}{{\displaystyle \sum ^{max(t,ta)}}}}{N}_a^{\phi }\left(u\right)\cdot \\ & {\displaystyle \underset{j=u}{{\displaystyle \sum ^t}}}{p}_a^{\phi }(j-u+1)\cdot \frac{Q(j-1)}{D\left(j\right)}\left)\right)\end{array}}$$ (10)

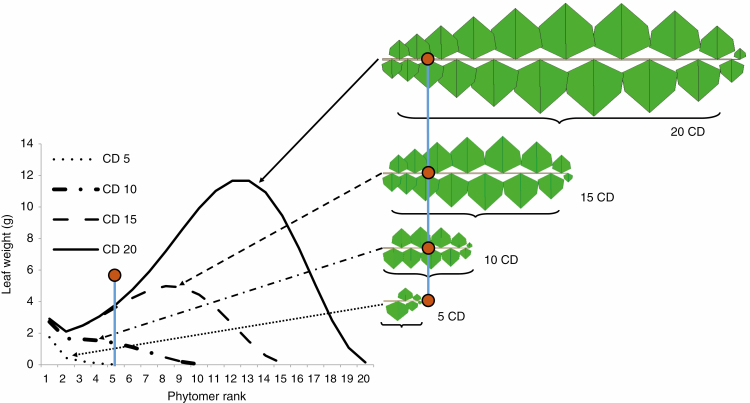
The plant can therefore be broken down as individual parts into a small number of categories of axes, which in turn are broken down into organic series, the description of which gathers all the necessary information contained in development and growth. Through adapted sampling among the organic series, it is possible to define very effective targets for calibration of the sink–source model based on the experimental data. Organic series are built by sampling within the plant architecture. Measurements can be taken over several growth stages (Fig. 5).

Fig. 5.

Simulation of the growth of a leafy axis over four development stages (at 5, 10, 15 and 20 CDs), building four organic series. The organs of the organic series grow until the end of their expansion. Right: the four curves of leaf weights according to their rank within the organic series. The brown dot corresponds to the fifth rank in each series. Left: a graphical representation of the four organic series.

Application of plant architecture to agronomy: two case studies

Calibration and evaluation of the GreenLab model.

Evaluation of the model is here based on its ability to correctly fit organic series, by finding the optimum values of the sink–source parameters using an inverse method. Organic series are outputs of the model and contain the history of growth. The non-linear least squares method is used for this purpose (Guo et al., 2006). Other heuristic methods have also been used, such as particle swarm optimization (Qi et al., 2010) and neural networks (Fan et al., 2015).

We illustrate here the parameter estimations on maize and coffee. Data and sources codes are available as Supplementary Data S1. These are also available from the following link http://greenlab.cirad.fr/StemGL/AoB_19945R_Codes.zip.

These case studies are somewhat iconic. The study of maize is interesting as it has a simple non-branched deterministic structure but complex organ expansions, due to their duration and sink strength variation. The fruits are not numerous, but their biomass is significant due to their high sink strength. Thus, this example applies to numerous crop plants, such as rice, wheat, tomato, sunflower, etc. Conversely, the coffee tree is a stochastic branched structure. Despite its relatively simple structure with only two physiological ages, the establishment of the structure displays a different speed of axis development (the rhythm ratio between trunk and branches is close to 3/4), stochastic development both on the trunk and branches, and stochastic ramification with a coupling effect. However, organ expansions are almost immediate and the fruit sink strength is comparable with that of other organs. This example applies for other branched crops, such as cotton, and also for trees in general. Applications of the GreenLab model were also successfully used on temperate and tropical rhythmic species: pine (Wang et al., 2011), maple (Taugourdeau et al., 2019) and teak (Tondjo et al., 2018).

Study of a deterministic example: the case of maize.

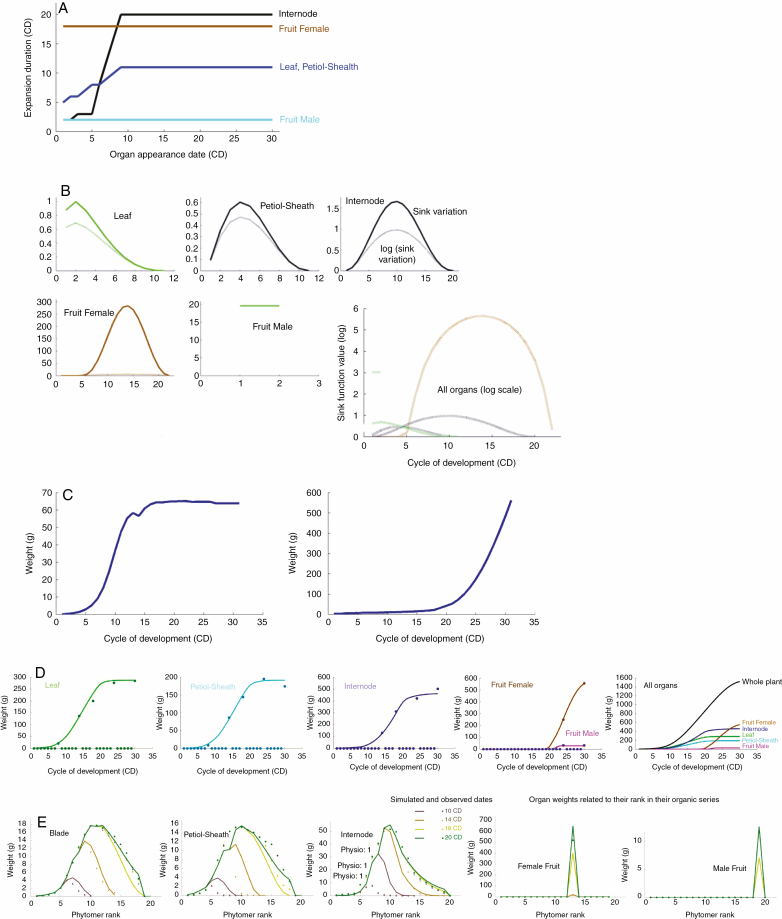
A maize experiment was carried out in France (Feng et al., 2014). The planting density was d = 7.5 plants m^–2, corresponding to the available average surface area per plant Sd = 1333 cm² per plant. The thermal time–development cycle relationship was established. Maize stops developing above 21 phytomers, but growth continues. The weights of organ compartments and organic series were measured on plants over five growth stages (CDs 10, 14, 19, 27 and 31). For the compartments, each mean and variance on a date corresponded to a sample of five plants. For organic series, the average per organ and per rank in the series was taken into account. There were 249 items (organs and compartments) to be adjusted together by the model, and 13 source–sink parameters to be estimated using the inverse method. The expansion time tx of leaf, sheath and internode increased from the base of the stem and stabilized at the tenth phytomer. This variation could be measured or estimated by optimizing the fit of the organic series. Organ expansion durations usually vary significantly (Fig. 6A). The expansion time of the cob was estimated at 30 CDs and that of the tassel at 2 CDs. The leaf thickness parameter was measured as ɛ = 0.024

Fig. 6.

The maize study case. (A) Organ expansion durations. The curves show the variations in expansion times bottom up along the stem, by type of organ (black for the internode, brown for the cob, blue for leaves and cyan for the tassel. The duration of organ expansion varies until stabilization. (B) Organ sink function shapes, computed by the inverse method from the organic series; they explain the organ weight profiles along the organic series. The dotted curves stand for the log organ sink functions; they are used here for graphical comparison, illustrating the high sink value of the cob (in brown). (C) Global plant curves, from CD 1 to the final stage (CD 30). Left: total cumulated plant biomass; the sigmoid shape comes from the effect of Sp. Right: demand per cycle; the demand from the cob hides the effect of the other organs. (D) Adjustment of the evolution of organ weights in organic series over five growth stages (plain curves are the simulated weights to be compared with the dots corresponding to the field measures). (E) Adjustment of the evolution of organ weights in organic series over four growth stages (10, 14, 18 and 20 CDs)

The parameters to be estimated by the inverse method were: Q0, reserve provided by the seed; Λ, LUE parameter; Sp, plant production area; sSp, standard deviation of the production area; P_a, Ba_a, parameters of the blade sink function (P_a = 1); P_p, Ba_p, parameters of the sheath sink function; P_i, Ba_i, parameters of the internode sink function; P_f, Ba_f, parameters of the cob sink function; and P_m, parameters of the tassel sink function. Secondary sink shape parameters Bb_b, Bb_p, Bb_f, and tassel sink shape parameters Ba_m and Bb_m were experimentally defined since Ba_b, Ba_p and Ba_f, assess the shape of the curves for the blade, petiole and fruit, while the short expansion time minimizes the shape effect on the tassel.

The numerical results are presented in Table 2 and Fig. 6C–E. The calculated parameters ensured a good fit of the compartments and organic series at the five growth stages (Fig. 6D, E), meaning that they could be considered as invariant during maize growth.

Table 2.

Model parameter values

Q0 (g)	1.1
Λ (g MJ–1)	0.056
Sp (cm2)	1200
sSp (cm2)	160
P a (No unit)	1
Ba a (No unit)	2.7
P p (No unit)	0.91
Ba p (No unit)	2.2
P i (No unit)	2.5
Ba i (No unit)	4.1
P f (No unit)	2400
Ba f (No unit)	7.3
P m (No unit)	4.2
Bb a (No unit)	3.8
Bb p (No unit)	3.8
Bb f (No unit)	4.8
Ba m (No unit)	1
Bb m (No unit)	2

Parameters Bb_a to Bb_m relative to organ sink strength variation were empirically estimated; parameters Q0 to P_m were then calculated by the least squares method. Λ, light use efficiency; Sp, production surface area; sSp, Sp variation; P_a, leaf sink strength; Ba_a, leaf sink strength variation parameter 1; P_p, petiole sink strength; Ba_p, petiole sink strength variation parameter 1; P_i, internode sink strength; Ba_i, internode sink strength variation parameter 1; P_f, cob sink strength; Ba_f, cob sink strength variation parameter 1; P_m, tassel sink strength; Bb_a, leaf sink strength variation parameter 2; Bb_p, petiole sink strength variation parameter 1; Bb_f, cob sink strength variation parameter 2; Ba_m, tassel sink strength variation parameter 1; Bb_m, tassel sink strength variation parameter 2.

The method calculated the seed reserve Q0, and a good approximation of Sd = 1333 plants m^–2, with Sp = 1200 plants m^–2, which validated the model. The estimated standard deviation of the production area sSp made it possible to correctly estimate the evolution of the standard deviation of the compartments. The sink of the cob was very high (P_f = 2400): the cob captured almost all of the synthesized biomass during its growth. The variations of the sink strengths are shown in Fig. 6B.

Using Table 2 providing the parameters used to simulate plant growth, and adding the positions, orientations and the organ shapes, completed the set of parameters necessary to build the plant 3-D structure.

Study of a stochastic example: the case of Coffea.

A Coffea pseudozanguebarie growth study was undertaken in Ivory Coast with fourteen 2-year-old trees. At this stage, no mortality or flowering was observed. We noted the stochastic aspect of the branch sizes from the development, as well as the gradual implementation of branching from the base of the trunk. The absence or presence of branches on the trunk, and their positions, were noted; the organic series measured on trunks and branches from the top were recorded, and the organs were weighed in terms of dry matter.

Results of the organic series analysis.

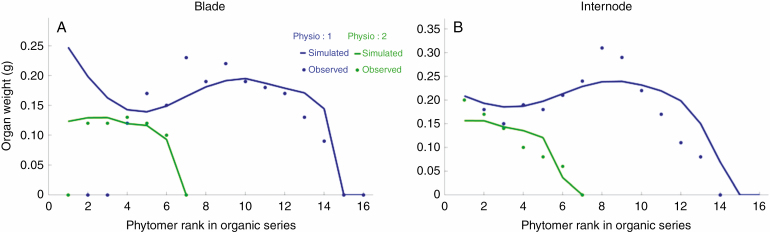
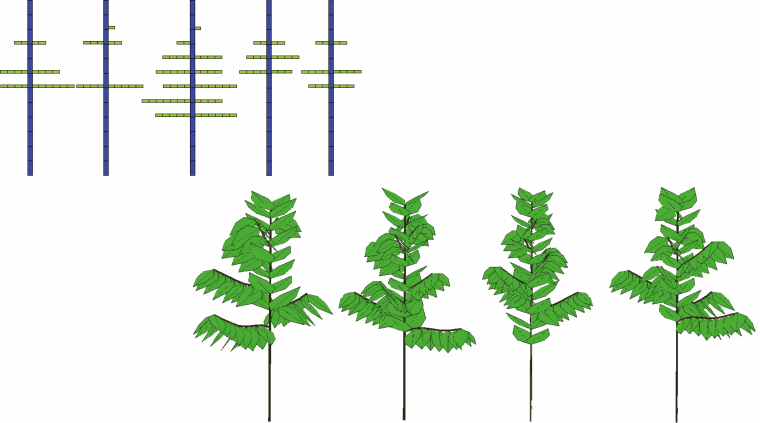
The analysis of the organic series then retrieved the source–sink parameters of coffee tree growth. This stochastic case required transformation of the data using the negative binomial law (Kang et al., 2018). The organic series fitting the results (Fig. 7) showed that the GreenLab model was correctly calibrated on this plant. The bottom row of Fig. 8 illustrates four 3-D simulations using the estimated parameters with additional geometrical parameters (branching angles and phyllotaxy).

Fig. 7.

Blade (A) and internode (B) organic series fitting on Coffea pseudozanguebarie trunks (physiological age 1 in blue) and branches (physiological age 2 in green). Note that the older leaves of the trunk (blue dots in A) are missing because they have fallen.

Fig. 8.

Top row: description of five observed Coffea pseudozangebarie crowns. Bottom row: four Coffea canephora stochastic simulations at the age of 16 CD.

Results of the crown analysis.

The top row of Fig. 8 illustrates four observations of crowns in the study. The crown analysis method (Kang et al., 2018) was used to calculate the development parameters of the trunk (b1 = 0.8), the branches (b2 = 0.9) and the rhythm ratio (w = 0.75).

Comments on the model principles and its emergent behaviour

The concept of the production surface area introduced in eqn (6) is designed to enable the GreenLab model to build the link between the plant on an individual scale (i.e. without light competition) and the stand level. Analysing model behaviour [eqn (6)] helps in understanding this concept. At the beginning of growth, the leaf surface area per production surface area (the ratio Sf/Sp) is small. The expression [eqn (6)] then becomes:

$${\displaystyle \begin{array}{l}{\displaystyle Q\left(t\right)\approx \mathit{\Lambda }\cdot \mathit{I}\cdot \mathit{k}\cdot \mathit{S}\mathit{f}\left(\mathit{t}\right)}\end{array}}$$ (11)

Growth is proportional to the leaf surface area, meaning that all the leaves separately intercept light: this is then called ‘free’ growth. At this stage, growth is exponential.

After some time, in the case of a high planting density, the foliage covers the entire ground and the ratio k · Sf/Sp is higher. The expression [eqn (6)] then becomes:

$${\displaystyle \begin{array}{l}{\displaystyle Q\left(t\right)\approx \mathit{\Lambda }\mathit{·}\cdot \mathit{I}\cdot \mathit{S}\mathit{p}}\end{array}}$$ (12)

Once the competition effect between plants is reached, growth is said to be ‘limited’, and becomes constant and proportional to the surface area available on the ground for the plant in competition with its neighbours. Biomass production evolves according to a sigmoid form. Once the effect of competition is reached, Sp must logically approach the available average surface area per plant Sd, according to the planting density: Sd = Sc/d, where Sc is the cultivated area and d is the planting density. So the relationship Sp ≈ Sd should be observed. The validity of Sp = Sd equality in the case of high planting densities has been confirmed on several species for different densities: on maize (Ma et al., 2007), on beetroot (Lemaire et al., 2009) and on tomato (Zhang et al., 2009).

DISCUSSION

Compared with FSPM and crop models, GreenLab’s positioning falls somewhat ‘in between’. What are the benefits of this approach for agronomy, seen as a voluntarily simplified model from an ecophysiological point of view and from a structural (geometrical) point of view?

Validation of the GreenLab model on crop plants and its positioning

The GreenLab approach shows genericity of the model when applied to crop plants, even when faced with various plant architectures. In our studies, architectural variability was wide, covering continuous growth to rhythmic growth, on both temperate and tropical species, potentially modelling the stochastic effects of phytomer development, branching and viability. Indeed, for about 20 crop plants (grasses, shrubs and trees), parameters were satisfactorily estimated for the GreenLab model (Fig. 9). The development and growth parameters, using the crown and organic series analysis, were computed successfully and fitted the data well. They validated the model application and illustrated its genericity. Moreover, on these plants, the set of estimated parameters showed good stability under various climatic conditions, and most could be considered as invariant (Ma et al., 2007; Kang et al., 2012). Thus, GreenLab positions itself as a generic model that capture the key development and functional feature of plants with minimal equations.

Fig. 9.

Various plants calibrated and simulated with the GreenLab model (De Reffye et al., 2018a). (A) Beetroot (ITB – Institut Technique de la Betterave, France), (B) arabidopsis (Ensam, – Ecole Nationale Supérieure des Arts et Métiers, France), (C) maize (CAU – Chinese Agricultural University), (D) chrysanthemum (University of Wageningen), (E) sunflower (Ensam), (F) tomato (CAU), (G) buddleia (Cirad), (H) coffea (University of Daloa, Ivory Coast), (I) pine (CAF – Chinese Academy of Forestry), (J) teak (University of Lomé, Togo).

The GreenLab model is a ‘source–sink solver’, i.e. a tool for finding the source–sink dynamics of a plant during its past growth. A very important point when using models in agronomy is the measurement sampling strategy. The GreenLab model uses the different axis types (physiological ages) and their grouping into crowns and organic series. These entities, which are generic and adapted to all architectural models, support the calibration of the model, using efficient inverse methods for parameter estimation. Moreover, missing data due to organ abortion are no longer a drawback. From a correctly collected sample, we can reconstruct the history of demand and biomass supply for each development cycle, using crown and organic series analyses.

In plant breeding, the growth parameters of the GreenLab model can be considered, as a first approximation, as invariant, because the source–sink relationships are relatively independent of the environmental parameters. The establishment of relationships between these parameters and quantitative trait loci (QTLs) should lead to effective selection in the search for ideotypes (Letort et al., 2008).

In the context of phenotyping, where FSPMs are beginning to be used (Luquet et al., 2012), the GreenLab model provides an effective framework for streamlining trait measurements and their analysis according to organic series.

Switch from individual plant to stand

Introducing the notion of plant architecture in agronomy in its botanical component is relevant from an ecological point of view (De Reffye et al., 2009); compared with crop models that generally consider a stand scale, GreenLab seeks a better representation of plant growth and stand production by using the concept of plant architecture as a support for plant functioning. GreenLab’s approach has relatively few parameters (usually a few dozen to simultaneously fit individual organ mass at several stages of plant growth), compared with most other FSPMs. Biomass computation from the production surface area and functioning leaf area is efficient (Beer–Lambert’s law and not computation of explicit light interception with organ geometries) as shown in the comparison with photon ray tracing used by Wang et al. (2012). The GreenLab model and its approach at plant level is fully ecophysiogically compatible with crop models that use only compartments. Crop models can be considered as a projection of the GreenLab model, which uses either phytomers or compartments. Thus, the GreenLab model enables a switch from the functioning of the individual plant to that of the stand, with the use of production area parameter Sp, related to planting density. As shown by Baey et al. (2014), compared with crop models such as Stics, Ceres, Pilot, etc., GreenLab shows a comparable performance working in compartment mode. Taking into account planting density, germination times and the calculated variance of Sp makes the calculated LAI and production similar to those calculated by a crop model (Feng et al., 2014).

CONCLUSION

GreenLab’s approach reflects a macroscopic approach, relating to the phytomer level. It does not provide an understanding of fine physiological processes. However, the approach is of particular interest in terms of genericity, complexity and computational performance, and its ability to estimate source–sink relations. Its formalism also allows the switch from the individual plant scale to the crop/stand level.

GreenLab’s approach has helped to take up the challenge of reproducing the growth dynamics of all organs with a very limited set of parameters. Development of the GreenLab model has always paid careful attention to the parameter estimation methodology. The organic series, i.e. the sequence of organs along the axis, defines the core key for defining relevant measurement strategies and experimental protocols allowing a wide range of applications.

This approach retains a degree of rigidity; it assumes that the development of the potential structure follows invariant kinetics according to thermal time. In other words, feedback (other than external interactions) between growth and development is ignored. However, promising studies have been undertaken to overcome these difficulties. The kinetic approach dependency to the thermal time of the sinks can be replaced by the supply to demand ratio (Q/D), giving equivalent adjustments (Zhang et al., 2009). Similarly, the numerical values of development, mortality and branching rates found by the crown method can be linked to functions depending on Q/D (De Reffye et al., 2018b). Thus, we are currently upgrading the model with the feedback effect of the internal trophic competition, represented by the ratio of biomass supply to demand, contributing to a new way to understandplant structural plasticity.

SUPPLEMENTARY DATA

Supplementary data are available online at https://academic.oup.com/aob and consist of Data S1: data and source codes.