Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Dec 24;125(1):65–73. doi: 10.1021/acs.jpca.0c08283

On the Accuracy of the Direct Method to Calculate pKa from Electronic Structure Calculations

Felipe Ribeiro Dutra †, Cleuton de Souza Silva ‡, Rogério Custodio †,*
PMCID: PMC7872415  PMID: 33356255

Abstract

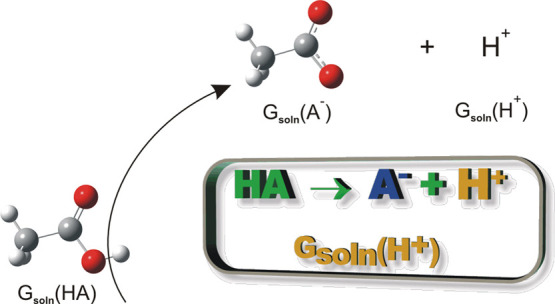
graphic file with name jp0c08283_0002.jpg

The direct method (HA(soln) ⇌ A(soln)– + H(soln)+) for calculating pKa of monoprotic acids is as efficient as thermodynamic cycles. A selective adjustment of proton free energy in solution was used with experimental pKa data. The procedure was analyzed at different levels of theory. The solvent was described by the solvation model density (SMD) model, including or not explicit water molecules, and three training sets were tested. The best performance under any condition was obtained by the G4CEP method with a mean absolute error close to 0.5 units of pKa and an uncertainty around ±1 unit of pKa for any training set including or excluding explicit solvent molecules. PM6 and AM1 performed very well with average absolute errors below 0.75 units of pKa but with uncertainties up to ±2 units of pKa, using only the SMD solvent model. Density functional theory (DFT) results were highly dependent on the basis functions and explicit water molecules. The best performance was observed for the local spin density approximation (LSDA) functional in almost all calculations and under certain conditions, as high as those obtained by G4CEP. Basis set complexity and explicit solvent molecules were important factors to control DFT calculations. The training set molecules should consider the diversity of compounds.

1. Introduction

The pKa of an acid can be accurately determined experimentally by different techniques, such as capillary electrophoresis, spectrophotometry, and high-performance liquid chromatography.1−3 Theoretically, the simplest way to estimate the pKa of an acid in solution using quantum methods is based on the calculation of the equilibrium reaction Gibbs energy: HA(soln) ⇌ A(soln)– + H(soln)+. This calculation process is known as a direct method, and its application is rarely found in the literature.4−6 Usually, significant errors are produced in determining free energies of these three chemical species in solution. One of the most difficult terms to estimate theoretically is the free energy of the solvated proton.7 Some have attempted using experimental values or theoretical approaches to achieve acceptable values of ΔGsolv(H+),8−11 which are normally between −252.6 and −271.7 kcal mol–1.12 Currently, the most used value is −265.6 ± 1 kcal mol–1; however, the use of this value is questioned because the error is considered significant.13−16

One of the most common procedures for minimizing calculation errors uses thermodynamic cycles involving deprotonation reactions in the gas phase, combined with the same reaction in solution for the acid of interest.17−21 The calculation of Gibbs energies in the gas phase is usually performed by ab initio or density functional theory (DFT) calculations. In solution, different implicit solvation models are used (conductor-like polarizable continuum model (C-PCM),22 conductor-like screening model (COSMO),23 and solvation models (SM-X)8), whether or not they explicitly include solvent molecules. Explicit inclusion of solvent molecules can assist in modeling solute–solvent interactions. There are problems related to the number of solvent molecules, as well as the best position of each solvent molecule around the solute.21,24 Even with these uncertainties regarding the inclusion of explicit molecules, the method works reasonably well for compounds with low and, in some cases, intermediate complexity.25−28 However, this approach is not efficient for flexible molecules due to conformational changes in solution with respect to the gas phase, especially when the acid has a high degree of freedom and can assume several conformations in solution, requiring the use of other methodologies.29,30

To simplify the calculation steps and improve the performance of theoretical methods for calculating pKa, in addition to eliminating the gas phase dependency, another common procedure uses isodesmic reactions. The method considers proton competition between two acids. One is a reference acid, and pKa is determined from the second acid. In other words, the free energy of the reaction is estimated according to the reaction HA(soln) + Ref(soln)– ⇌ A(soln)– + HRef(soln).25,31−33

The isodesmic method is considerably simple and provides satisfactory results for several compounds. Another advantage is that the use of doubtful energies with respect to the proton are not required. The method depends directly on the choice of the reference substance. The usual recommendation is to use reference molecules with similar chemical structures and pKa values to the molecule of interest.31,34−37

In addition to these two strategies, there are others that follow the same patterns, by determinations related to a reference molecule, more complex thermodynamic cycles, or descriptions through empirical equations correlating some molecular properties to the pKa itself.38−40 Regardless of the adopted methodology, errors or significant uncertainties always arise with respect to experimental values used, choice of references, or conformational differences between aqueous and gaseous phases, in addition to error by the implicit solvation model or inclusion of explicit solvent molecules.41,42

The direct method is the simplest alternative, depending on the Gibbs energy of the acid, its conjugated base, and the proton in solution. As mentioned previously, one of the main difficulties is the determination of the free energy of the solvated proton. Many papers have estimated the best free energy based on cluster models or least-squares methods or combination of theoretical and experimental data.14,43−45 The general tendency of the literature also suggests that the use of a specific parameter for the free energy of the solvated proton is satisfactory for high-level calculations.28,34,35 It seems convenient to have a simple procedure to estimate pKa using the Gibbs energy of the solvated proton compatible with the level of theory and calculation conditions. Therefore, the objective of this work is to evaluate the performance of the pKa calculation using the direct method, considering the energy of the solvated proton as an adjustable parameter. The pKa calculation is evaluated at different levels of theory, such as Hartree–Fock (HF), semiempirical, DFT, and composite methods. Assessment of the solvent effect is carried out using a continuous solvation model and the role of explicit solvent molecules.

2. Computational Method

Gibbs energy of the direct deprotonation reaction (HA(aq) ⇌ A(aq)– + H(aq)+) can be calculated by the equation

2. 1

where R is the gas constant and T is the temperature. Gaq(A–), Gaq(HA), and Gaq(H+) are the respective Gibbs energies of the conjugate base (A–), protonated acid (HA), and the proton (H+) in solution.46Gaq(H+) cannot be calculated accurately by solvation models. Therefore, the present work proposes to determine it by rearranging eq 1 as

2. 2

Thus, one can estimate the average value of Gaq(H+), 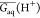Inline graphic, for a training set from the experimental pKa(exp) values and theoretical values of Gibbs energies of the acid and its conjugate base at any level of theory. This average Gibbs energy of the solvated proton can then be used to determine the pKa of acids at the same level of theory from eq 3

2. 3

In the present work, the free energies for Gaq(HA) and Gaq(A–) were performed using the Gaussian16 program47 at the temperature of 298.15 K using the solvation model density (SMD).8 SMD has been recommended by Gaussian16 for continuous representation of solvent effect. Calculations of all acids and the respective conjugate bases were performed at the following theory levels according to Gaussian definition: AM1,48 PM6,49 HF,50 local spin density approximation (LSDA), PBE0,51 M06-2X,52 B3LYP,53,54 CAM-B3LYP,55 WB97XD,56 B2PLYP,57 and the G4CEP composite method.58 LSDA is a combination of Slater exchange potential and Vosko–Wilk–Nusair59 correlation functional. HF and DFT calculations were performed with aug-cc-pVDZ and aug-cc-pVTZ basis functions.

The use of AM1 and PM6 semiempirical methods in predicting pKa is generally associated with chemometric methods, quantitative structure–activity relationship (QSAR) or quantitative structure–property relationship (QSPR).60−62 However, the literature indicates that it is possible to achieve a certain accuracy in the calculation of pKa.63 HF calculations were considered because of the absence of electronic correlation effects. The criterion for choosing DFT methods ranges from its simplicity and use in the literature, such as LSDA, PBE0,51 and B3LYP,53,54 to more recent and sophisticated hybrid functionals, such as M06-2X,52 CAM-B3LYP,55 WB97XD,56 and B2PLYP.57 The G4CEP composite method was chosen because it includes extrapolation of the basis function, reduction of the computational cost using pseudopotential, and additional corrections related to deficiencies of the basis functions and electronic correlation.58 It is important to mention that the G4CEP method was used to calculate pKas using thermodynamic cycle with excellent performance.28

In addition to the use of implicit solvation, the presence of explicit water molecules was also analyzed.33 The orientation and position of the water molecules in these systems are extremely important and were initially placed close to the oxygens from two carboxyl groups. To identify the most stable molecular geometries, a preoptimization was performed at the B3LYP/aug-cc-pVDZ level for the DFT calculations and later the structures were reoptimized at the respective level of theory. This procedure was used for calculations including or not the explicit water molecules.

3. Results and Discussion

3.1. Assessing the Training Set

To assess the dependence of the pKa calculation with a set of reference molecules, a set of 22 monoprotic acids, previously used by de Souza Silva and Custodio,28 were employed. The average proton solvation energy was determined from three distinct training sets: (a) training set 1—the entire set of 22 acids, (b) training set 2—three very simple reference acids (acetic, propanoic, and butanoic acids), and (c) training set 3—three acids chosen arbitrarily from the 22 (pentanoic, 2-chlorobutanoic, and 2-methylbutanoic acids). The use of these three sets indicates sensitivity of the average energy of the solvated proton with the number and type of reference molecules. Training set 1 was the first set analyzed. It is representative of all molecules, and in principle, the solvated proton energy should provide the smallest error for this set of molecules. It is expected that for a transferable free energy of the solvated proton, a small training set must provide an equivalent result obtained by the full set of molecules. This hypothesis will be analyzed comparing the results from the three training sets.

Table 1 shows the 22 acids studied, the respective experimental pKa values, and the differences between the experimental and calculated values for each level of theory, in addition to the mean absolute error (MAE), standard deviation (std. dev.), and the largest positive and negative deviation with respect to the experimental data for each theoretical method. These are the simplest calculations using aug-cc-pVDZ basis functions for the Hartree–Fock and DFT methods. The solvent effect was represented using only the SMD model for all calculations. The literature suggests that calculated pKa values are considered acceptable if they have a mean absolute error below one pKa unit.64Table 1 shows that six of the 11 levels satisfy the criterion. The lowest mean absolute errors were obtained by the PM6 (0.57), G4CEP (0.63), AM1 (0.73), HF (0.95), and B2PLYP (0.96) methods, with standard deviations of 0.66, 0.42, 0.81, 0.89, and 0.94, respectively, in units of pKa. Standard deviations multiplied by 2 provide an uncertainty estimate with 95% confidence. The maximum positive and negative deviations show that some results present significant errors. However, Table 1 indicates that unusual deviations are usually related to a few specific acids that produce inadequate results for almost all methods, such as trichloroacetic and hexanoic acids. Surprisingly, the computationally most expensive method, G4CEP, and the semiempirical ones, PM6 and AM1, showed the best performances. PM6 was previously tested in the literature using the isodesmic method with an average error similar to the present work.63 If computational cost is considered, the semiempirical methods are more advantageous than G4CEP. Although the latter presents a lower uncertainty, which can be verified both by the standard deviation multiplied by 2 and the most positive and negative deviations with respect to the experimental data. Importantly, the results obtained with the direct method using G4CEP are a little better than using a thermodynamic cycle.28 The seven functionals tested yielded inadequate performance. Six of the seven showed mean absolute errors just above one pKa unit, and the best results were close to one.

Table 1. Experimental pKa Values and Differences between Experimental and Calculated Values for Different Levels of Theory, in Addition to the Mean Absolute Error, Standard Deviation, and the Largest Positive and Negative Deviationsa.

acids pKab (exp) G4CEP AM1 PM6 HF LSDA PBE B3LYP CAM B3LYP WB97XD M062X B2PLYP
acetic 4.76 0.12 –0.53 0.04 –0.73 –1.32 –0.59 –1.45 –1.46 –0.53 –0.67 –1.31
propanoic 4.88 –0.77 –0.77 0.75 –0.47 –1.37 –1.47 –1.32 –1.29 –1.48 –1.27 –1.32
butanoic 4.82 0.27 0.55 –1.20 –0.89 –1.49 –1.28 –0.97 –0.80 –1.09 –1.24 –0.86
pentanoic 4.82 –0.32 –0.64 0.11 –1.67 –0.92 –1.61 –1.44 –1.36 –1.56 –1.07 –1.39
hexanoic 4.85 –1.61 0.64 0.20 –1.69 –1.12 –2.16 –2.50 –1.50 –1.01 –1.75 –1.60
chloroacetic 2.86 0.79 0.19 –0.38 0.98 1.13 1.23 0.08 –0.07 1.26 0.99 0.07
bromoacetic 2.90 0.21 –0.61 –0.42 0.68 1.22 0.71 0.81 0.68 0.58 0.50 0.67
trichloroacetic 0.70 1.04 3.52 2.66 4.52 4.34 5.03 5.07 4.63 4.78 4.63 4.79
2-chlorobutanoic 2.83 0.78 1.17 0.01 0.76 0.45 0.71 1.17 0.68 0.61 0.40 1.27
3-chlorobutanoic 3.98 –0.43 0.00 0.52 –0.28 –0.20 –0.32 –0.06 –0.17 –0.17 –0.31 –0.11
4-chlorobutanoic 4.52 –0.52 –0.37 0.81 –0.27 –0.62 –0.18 –0.01 0.23 0.19 0.64 –0.15
3-butenoic 4.35 –0.07 0.25 –0.27 0.01 –0.26 –0.29 –0.09 –1.07 –0.27 –1.14 –0.16
2-methylpropanoic 4.84 –0.17 –0.09 0.72 –0.96 0.05 –0.01 –1.15 –0.78 –0.83 –1.13 –0.80
2.2-dimethylpropanoic 5.03 –0.64 0.20 –0.34 –1.02 –1.16 –0.92 –0.73 –0.82 –0.93 –0.77 –0.76
3-methylbutanoic 4.77 –1.29 0.09 0.25 –0.89 –1.09 –1.17 –0.95 –0.75 –1.81 –0.90 –0.99
2-methylbutanoic 4.80 –0.87 –0.24 0.01 –1.18 –1.45 –1.01 –0.90 –0.79 –1.15 –1.11 –0.78
2-butynoic 2.62 1.17 1.45 –0.28 1.13 1.30 0.75 1.59 1.75 1.17 1.36 0.77
2-chloropropanoic 2.83 0.82 –0.19 –0.06 1.01 0.75 0.72 1.29 1.15 0.92 0.36 1.07
3-bromopropanoic 4.00 1.01 –0.81 0.21 0.00 0.96 1.24 0.41 0.35 –0.04 1.18 0.35
3-chloropropanoic 3.98 0.05 –0.59 –0.51 0.57 0.91 0.39 0.53 0.56 1.25 1.20 0.51
trans-crotonic 4.69 –0.22 –0.75 –0.64 –0.44 –1.02 –0.79 –0.57 –0.36 –0.92 –0.60 –0.31
formic 3.75 0.64 –2.46 –2.20 0.82 0.93 1.01 1.21 1.19 1.03 0.70 1.05
MAE   0.63 0.73 0.57 0.95 1.09 1.07 1.11 1.02 1.07 1.09 0.96
std   0.42 0.81 0.66 0.89 0.81 1.00 1.04 0.91 0.93 0.85 0.94
max   1.17 3.52 2.66 4.52 4.34 5.03 5.07 4.63 4.78 4.63 4.79
min   –1.61 –2.46 –2.20 –1.69 –1.49 –2.16 –2.50 –1.50 –1.81 –1.75 –1.60
Open in a new tab
a

HF and DFT calculations used aug-cc-pVDZ basis functions. All calculations were performed with solvent represented by SMD and free energies of the solvated proton obtained with training set 1.

b

Data from refs (72) and (73).

In general, error in the pKa calculation produced by the direct method may result from sensitivity to the training set. Table 2 shows the mean absolute errors, standard deviations, and the largest positive and negative deviations for each theoretical method using training sets 2 and 3, which use only three acids to determine the average energy of the solvated proton. The calculated pKa values are available as Supporting Information in Tables S1 and S2.

Table 2. Mean Absolute Error (MAE), Standard Deviation (Std. Dev.), and the Largest Positive (Max) and Negative (Min) Deviations at Different Levels of Theorya.

Training Set 2
  G4CEP AM1 PM6 HF LSDA PBE B3LYP CAM B3LYP WB97XD M062X B2PLYP
MAE 0.63 0.73 0.59 1.01 1.41 1.30 1.41 1.26 1.21 1.18 1.25
std. dev. 0.43 0.85 0.66 1.08 1.35 1.29 1.38 1.29 1.27 1.28 1.27
max 1.30 3.77 2.80 5.22 5.73 6.14 6.32 5.81 5.81 5.69 5.95
min –1.49 –2.21 –2.06 –0.99 –0.10 –1.05 –1.25 –0.32 –0.78 –0.69 –0.43
Training Set 3
  G4CEP AM1 PM6 HF LSDA PBE B3LYP CAM B3LYP WB97XD M062X B2PLYP
MAE 0.63 0.75 0.57 1.01 1.11 1.12 1.13 1.01 1.11 1.06 0.95
std. dev. 0.43 0.80 0.66 1.08 1.01 1.14 1.09 1.04 1.13 1.07 1.00
max 1.31 3.43 2.62 5.22 4.98 5.67 5.46 5.12 5.49 5.23 5.09
min –1.48 –2.55 –2.24 –0.99 –0.85 –1.52 –2.11 –1.01 –1.11 –1.15 –1.30
Open in a new tab
a

HF and DFT calculations used aug-cc-pVDZ basis functions. All calculations were performed with the SMD model and training sets 2 and 3.

Table 2 shows that mean absolute errors below one pKa unit continue in the increasing sequence: PM6, G4CEP, and AM1. Almost all functionals maintained error above one pKa unit, and the errors did not present a well-defined trend. Compared with Table 1, the mean absolute error produced by training set 3 is closer to set 1 than set 2 for DFT calculations. The mean absolute errors for the G4CEP, PM6, and AM1 methods are not particularly sensitive with the chosen reference acids. In the case of DFT calculations, training set 2 reached a maximum mean absolute error of 1.41 units of pKa while training set 3 achieved a value of 1.13 pKa units. The worst performance of training set 2 is certainly associated with the similarity of the reference acids, the diversity in the set of 22 acids, and the exchange and correlation effects of the functionals. The more diversified electronic environments of training set 3 certainly provided a better representation of the substances for calculation of the 22 acids.

3.2. Basis Set Dependency

The Hartree–Fock and DFT methods depended on the choice of basis function. The best alternative for a quantum calculation is to consider a complete basis set or the extrapolation of properties with increasing complexity of a basis function.25,65−67 Calculations applicable to medium or large molecules are made with modest basis functions, like the one used in the previous chapter. However, it is necessary to assess whether enlargement of the basis function is significant in determining pKa using the direct method. Therefore, the Hartree–Fock and DFT calculations were also performed with aug-cc-pVTZ basis functions.

Table 3 summarizes the mean absolute errors for all levels tested, standard deviations, and the largest positive and negative deviations for each method. Details of the pKa deviations for all acids and the three training sets are available as Supporting Information in Tables S3–S5. Table 3 shows that there are important consequences in increasing the basis function. Almost all DFT calculations improve with mean absolute errors below 1.1 pKa units. The only exception is the WB97XD method for the second training set, which shows a significant increase in the average error. On the other hand, calculations employing the LSDA, M062X, and B2PLYP functionals provided mean errors below one unit of pKa. Training sets 1 and 3 produce results similar to each other and near the average errors using the aug-cc-pVDZ basis function. Calculations for training set 2 are significantly improved with aug-cc-pVTZ compared to aug-cc-pVDZ. These changes are, in part, a consequence of the nature of the energies produced by the methods themselves and small changes in the optimized molecular geometries. The structures are optimized initially at the B3LYP/aug-cc-pVDZ level and, later, at the corresponding level of calculation. Thus, the exceedingly small mean absolute error, standard deviation, and the largest positive and negative deviation from the LSDA results are surprising for any training set with aug-cc-pVTZ basis functions. These data surpass the performance verified by the semiempirical and G4CEP methods. Tables S3–S5 show that the pKa deviations calculated with LSDA, with respect to the experimental data, are usually lower than 0.5 units of pKa with few exceptions. A final aspect of Table 3 is that, although almost all functionals improved with the size of the basis function, the largest positive deviations persist. Analysis of Tables S3–S5 indicates that trichloroacetic acid is persistent in the deviation of pKa for almost all functionals tested. The remaining deviations are within the estimated uncertainty.

Table 3. Experimental pKa, Mean Absolute Error (MAE), Standard Deviations (Std. Dev.), and the Largest Positive (Max) and Negative (Min) Deviation at HF and DFT Levelsa.

Training Set 1
  HF LSDA PBE B3LYP CAM B3LYP WB97XD M062X B2PLYP
MAE 1.10 0.39 1.04 1.07 1.06 1.07 0.82 0.93
std. dev. 0.88 0.33 1.00 0.86 0.87 0.86 0.74 0.90
max 4.37 1.43 5.04 4.42 4.30 4.33 3.85 4.50
min –2.04 –1.12 –1.96 –1.58 –1.79 –1.72 –1.17 –1.70
Training Set 2
  HF LSDA PBE B3LYP CAM B3LYP WB97XD M062X B2PLYP
MAE 1.10 0.39 1.15 1.23 1.17 1.43 0.96 1.07
std. dev. 1.15 0.34 1.23 1.27 1.16 1.32 1.05 1.13
max 5.10 1.48 5.91 5.53 5.21 5.71 4.76 5.36
min –1.30 –1.07 –1.09 –0.47 –0.87 –0.34 –0.27 –0.83
Training Set 3
  HF LSDA PBE B3LYP CAM B3LYP WB97XD M062X B2PLYP
MAE 1.08 0.49 1.09 1.04 1.09 1.13 0.85 0.93
std. dev. 0.97 0.38 1.17 0.96 1.01 1.11 0.92 0.97
max 4.71 1.07 5.73 4.77 4.86 5.11 4.45 4.87
min –1.69 –1.47 –1.27 –1.22 –1.22 –0.94 –0.58 –1.32
Open in a new tab
a

All calculations were carried out with the SMD model, aug-cc-pVTZ basis set, and training sets 1, 2, and 3.

In general, results with the larger basis sets improve performance of the DFT calculations. Although the computational cost increases, the deviation with respect to the experimental data for part of the tested functionals is significant. The LSDA functional with aug-cc-pVTZ functions produced exceptional results at a considerably reduced computational cost, which qualifies it as the best alternative associated with direct determination of pKa.

3.3. Explicit Solvent

In thermodynamic cycles, the literature frequently indicates that, in addition to the reaction field, the inclusion of explicit solvent molecules improves the pKa estimate. Table 4 presents the mean absolute error and standard deviations of pKa regarding experimental data using the SMD model and one explicit water molecule. The position of the water molecule can change the value of the pKa, and the optimized molecular geometry should characterize the global minimum of energy and not a local one. Data related to the deviation of each pKa with respect to experimental results for the three training sets and including one water molecule are found in Tables S6–S11.

Table 4. Mean Absolute Error (MAE) and Standard Deviations (Std. Dev.) at Different Levels of Theory Using the SMD Model and One Explicit Water Molecule with Training Sets 1, 2, and 3a.

Training Set 1 + SMD + H2O
  G4CEP AM1 PM6 HF LSDA PBE B3LYP CAM B3LYP WB97XD M062X B2PLYP
aug-cc-pVDZ
MAE 0.50 0.72 0.89 1.12 0.49 0.91 0.84 0.79 0.77 0.59 0.78
std. dev. 0.29 0.74 0.85 0.87 0.34 0.60 0.60 0.57 0.67 0.61 0.61
aug-cc-pVTZ
MAE       1.01 0.47 0.65 0.71 0.73 0.72 0.63 0.68
std. dev.       0.81 0.33 0.54 0.54 0.48 0.65 0.47 0.61
Training Set 2 + SMD + H2O
  G4CEP AM1 PM6 HF LSDA PBE B3LYP CAM B3LYP WB97XD M062X B2PLYP
aug-cc-pVDZ
MAE 0.70 0.85 0.88 1.51 0.51 1.41 0.90 1.01 1.01 0.89 0.85
std. dev. 0.54 0.74 0.85 1.24 0.53 0.91 0.82 0.76 0.87 0.77 0.74
aug-cc-pVTZ
MAE       1.33 0.46 0.91 0.72 0.76 0.78 0.72 0.99
std. dev.       1.04 0.37 0.63 0.54 0.54 0.76 0.52 0.75
Training Set 3 + SMD + H2O
  G4CEP AM1 PM6 HF LSDA PBE B3LYP CAM B3LYP WB97XD M062X B2PLYP
aug-cc-pVDZ
MAE 0.51 0.73 0.88 1.14 0.48 1.06 0.96 0.87 0.92 0.57 0.87
std. dev. 0.28 0.74 0.86 1.09 0.46 0.72 0.85 0.68 0.83 0.68 0.76
aug-cc-pVTZ
MAE       1.30 0.77 0.73 0.93 1.15 0.92 0.90 0.70
std. dev.       1.03 0.50 0.57 0.61 0.81 0.83 0.75 0.66
Open in a new tab
a

The aug-cc-pVTZ and aug-cc-pVTZ basis sets were used for HF and DFT calculations.

Table 4 shows that the G4CEP method maintains the same regularity with excellent performance for training sets 1 and 3 with mean errors around 0.5 units of pKa and uncertainties less than ±0.6. The mean error increases for training set 2 but is still an excellent option since the average error is 0.70 units of pKa with an uncertainty around ±1 pKa unit.

The AM1 and PM6 semiempirical methods performed worse with the inclusion of one water molecule, even for training sets 1 and 3. The PM6 results show a mean absolute error around 0.72 units of pKa. In contrast, for AM1, this error is significantly larger and about 1.13 units of pKa for training sets 1 and 3. Uncertainties also increase to approximately ±1.5 and ±2 units of pKa for PM6 and AM1, respectively. For training set 2, the mean absolute error and uncertainties increase for both methods, though more significantly for AM1. The inclusion of a second water molecule in semiempirical calculations keeps the errors in the same order of magnitude but favoring the AM1 method instead of PM6 (data not shown).

The Hartree–Fock results improve accuracy and achieve a mean absolute error lower than one unit of pKa with the aug-cc-pVDZ basis function but worsen the results with aug-cc-pVTZ. HF calculations tend to favor bonded states by reducing bond lengths with larger basis functions, which affects geometry, cancellation of errors, and the quality of calculated results. On the other hand, DFT results improve significantly with the inclusion of one water molecule. Training sets 1 and 2 improve with aug-cc-pVTZ, while with training set 3, this association is not evident. Almost all functionals tested present mean absolute errors lower than 1 unit of pKa. The worst performances are related to PBE/aug-cc-pVDZ calculations and training set 2. These results and analyses of all previous data indicate that the largest deviations occurred with acids containing halogens. The inclusion of halogenated compounds in the training set provides average free energies of the solvated proton suitable to the acids tested in this article. This information shows that the training set must be representative of acids in the validation set. However, one of the most remarkable aspects is, once again, the excellent performance of the LSDA functional. The mean absolute error and standard deviation are usually below 0.5 pKa units, except for aug-cc-pVTZ and training set 3. Due to its simplicity, LSDA is not recommended for the calculation of chemical properties. However, the use of this functional with empirically adjusted solvated proton free energy yields an efficient cancellation of errors. Additionally, by increasing to two explicit water molecules, the mean absolute errors are reduced even further for LSDA and almost all other functionals, producing uncertainties below ±1 unit of pKa for both aug-cc-pVDZ and aug-cc-pVTZ calculations.

3.4. Gibbs Energy of the Solvated Proton

The literature presents a set of possibilities for free energy of the solvated proton with values between −252.6 and −271.7 kcal mol–1.12 Many studies use the value of −265.6 ±1 kcal mol–1, due to reduced experimental uncertainty and quality of the pKa estimates. As an example, Zhan and Dixon68 performed high-level ab initio calculations in the supermolecule/continuous approach and obtained a value of −264.3 kcal mol–1, and when corrected to the standard condition of 1 M, it became −265.63 ± 0.22 kcal mol–1.69

However, calculations in the present work demonstrate that the adjustment of this energy is essential and can significantly reduce the pKa error. As a consequence, the direct method is extremely attractive, economical, and simple for the determination of pKa values. Table 5 shows all Gibbs energies of proton solvation used in this work. There is a significant difference between the values obtained with the AM1 and PM6 semiempirical methods from those obtained from ab initio and DFT calculations. This difference arises because AM1 and PM6 produce enthalpies of formation at 298 K, rather than molecular electronic energies. Therefore, programs that use AM1 and PM6 energies to estimate thermochemical quantities are working with the free energy of formation and not free molecular energy. Regardless of how the free-energy calculation is conducted, the pKa results are quite promising and follow a relatively accurate trend, especially without the inclusion of explicit solvent molecules.

Table 5. Average Gibbs Energies of the Solvated Proton Calculated at Different Levels of Theory with the aug-cc-pVDZ and aug-cc-pVTZ Basis Functions with Training Sets 1, 2, and 3 and Solvent Effect Represented by SMD and with and without One Explicit Water Molecule. Data in kcal mol−1.

SMD
  G4CEP AM1 PM6 HF LSDA PBE B3LYP CAM B3LYP WB97XD M062X B2PLYP
aug-cc-pVDZ
train. 1 –266.91 104.93 120.86 –277.22 –267.22 –271.97 –273.07 –271.88 –274.71 –273.14 –272.12
train. 2 –267.08 104.59 120.67 –278.17 –269.12 –273.49 –274.78 –273.49 –276.12 –274.59 –273.71
train. 3 –267.09 105.06 120.92 –278.17 –268.09 –272.84 –273.61 –272.55 –275.67 –273.95 –272.53
aug-cc-pVTZ
train. 1       –279.02 –271.67 –273.43 –273.95 –272.84 –276.11 –272.65 –273.18
train. 2       –271.74 –274.62 –275.46 –274.09 –277.98 –273.87 –274.37 –271.74
train. 3       –279.49 –271.19 –274.37 –274.43 –273.61 –277.17 –273.46 –273.69
SMD + H2O
  G4CEP AM1 PM6 HF LSDA PBE B3LYP CAM B3LYP WB97XD M062X B2PLYP
aug-cc-pVDZ
train. 1 –265.71 104.11 123.30 –277.31 –268.66 –271.72 –272.39 –271.30 –274.34 –272.67 –271.42
train. 2 –264.80 104.72 123.37 –279.14 –269.25 –273.46 –273.26 –272.40 –275.50 –273.79 –272.16
train. 3 –265.83 104.20 123.39 –278.24 –269.04 –272.63 –273.43 –272.01 –275.30 –273.01 –272.24
aug-cc-pVTZ
train. 1       –279.24 –269.13 –272.90 –273.92 –272.74 –275.84 –272.33 –272.77
train. 2       –270.11 –273.40 –274.83 –274.24 –276.89 –273.53 –273.16 –270.11
train. 3       –280.72 –269.33 –273.86 –274.15 –273.16 –276.53 –272.92 –273.93
Open in a new tab

On the other hand, we noted that the ab initio and DFT data of the free energies of the solvated proton are relatively close to the interval given by the literature. Tests involving the solvent effect, considering only the SMD model, change in the basis functions, or the inclusion of explicit solvent molecules indicates a greater similarity in the mean absolute errors and standard deviations for training sets 1 and 3 due to greater diversity of the acids present in training. Table 5 shows a greater similarity between the free energies of the solvated proton involving these two training sets than data obtained with set 2. In general, each theoretical method presents a specific Gibbs energy of the solvated proton that corrects a systematic error in obtaining pKa. The G4CEP method produced extremely reliable results with reduced standard deviations in all tests performed and presented a free energy for the solvated proton close to the most used value of −265 kcal mol–1. On the other hand, DFT calculations presented values close to −270 kcal mol–1. The best results produced with LSDA also showed Gibbs energies of the solvated proton around this value. Note that the lack of electronic correlation in the HF method significantly increases the energy value of the solvated proton. It is important to remember that when performing a frequency calculation in SMD, the standard state is 1 atm, and not 1 mol L–1. Therefore, the Gibbs energies of all species require a correction of 1.9 kcal mol–1, as shown in the literature.44,70,71 This correction is just an additive constant and its effect is being canceled between the acid and the respective conjugated basis. On the other hand, to define the free energy of the solvated proton, it must be considered. Since the main objective of the paper is to find an empirical transferable parameter to be used by each method, the formal energies of the solvated proton shown in Table 5 were not corrected by this constant.

4. Conclusions

The direct method (HA(soln) ⇌ A(soln)– + H(soln)+) for the pKa calculation of monoprotic acids seems to be as efficient as thermodynamic cycles. The results of direct calculation are sensitive to the level of calculation and Gibbs energy of the solvated proton. The procedure was analyzed at different levels of theory: two semiempirical levels (AM1 and PM6), one composite method (G4CEP), seven functionals (LSDA, PBE0, B3LYP, M06-2X, CAM-B3LYP, WB97XD, and B2PLYP), and Hartree–Fock (HF). Two basis functions were tested for HF and DFT: aug-cc-pVDZ and aug-cc-pVTZ. The solvent was described by the SMD model, including and excluding explicit water molecules. The Gibbs energy of the solvated proton was determined using three training sets chosen from 22 monoprotic carboxylic acids: (a) training set 1, which included the entire set of 22 acids; (b) training set 2, which contained three very simple reference acids (acetic, propanoic, and butanoic acids); and (c) training set 3, which consisted of three acids chosen arbitrarily from the 22 (pentanoic, 2-chlorobutanoic, and 2-methylbutanoic acids). Evaluation of the results involving all of the mentioned conditions allowed specific and general conclusions to be drawn.

Acceptable pKa results were considered to have mean absolute errors less than 1 pKa unit. In this sense, the best performance in any condition was obtained by the G4CEP method. The mean absolute errors were close to 0.5 units of pKa with a standard deviation usually below this quantity, leading to an uncertainty around ±1 unit of pKa for any training set with or without explicit solvent. This performance is better than the thermodynamic cycles with the same set of acids. Another important aspect is the proximity of the optimized Gibbs energy of the solvated proton, which is close to the most used value of −265.6 kcal mol–1.

The PM6 and AM1 methods perform very well with average absolute errors below 0.75 units of pKa and uncertainties of less than ±2 units of pKa using the SMD solvent model without explicit solvent molecules. The Gibbs energies of the solvated proton adjusted with the semiempirical methods have no correlation with the experimental data since the electronic energies of these methods reproduce enthalpies of formation and not absolute molecular enthalpy.

The Hartree–Fock and DFT results showed a worse performance using aug-cc-pVDZ basis functions and SMD compared to the semiempirical and G4CEP methods. On the other hand, the use of aug-cc-pVTZ basis functions and explicit water molecules significantly reduced the mean absolute error and pKa uncertainty, making them attractive due to the computational cost and accuracy. The best result was achieved by the LSDA functional under almost all calculation conditions. The performance of this functional is exceptional, mainly at the aug-cc-pVTZ level. The errors and uncertainties are as good as those obtained by the G4CEP method, i.e., around 0.5 units and ±1 unit of pKa, respectively. The values of free energies of the solvated proton for almost all functional ones were generally higher than −270 kcal mol–1. The only functional that had a value below −270 kcal mol–1 was LSDA.

Hartree–Fock calculations performed worse than semiempirical calculations in any condition. Obviously, the absence of electronic correlation is mandatory for an acceptable pKa result, and empirical adjustment is not sufficient. The Gibbs energy values of the solvated proton were the furthest from the most used value compared with experimental data.

In general, the addition of solvent molecules tends to improve results, except for semiempirical levels. An increase in the complexity of the basis functions is an important factor to be controlled, especially for DFT calculations. Regarding the training sets, better results are obtained using selected molecules representing the chemical diversity of all species to be calculated.

Acknowledgments

The authors acknowledge financial support from Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP—Center for Computational Engineering and Sciences, grants 2013/08293-7 and 2017/11485-6) and Fundo de Apoio ao Ensino, à Pesquisa e à Extensão da UNICAMP (FAEPEX-UNICAMP). This study was also financed, in part, by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES)—finance code 001. The National Center of High-Performance Computing in São Paulo (CENAPAD—SP) and National Center of High-Performance Computing in Ceará (CENAPAD-UFC) are acknowledged for access to their computational facilities.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.0c08283.

  • Experimental pKa and results from calculations combining different levels of theory, basis sets, and solvent representation with three different training sets to determine the Gibbs energy of the proton in solution (Tables S1–S11) (PDF)

The authors declare no competing financial interest.

Supplementary Material

jp0c08283_si_001.pdf (169.9KB, pdf)

References

  1. Reijenga J.; van Hoof A.; van Loon A.; Teunissen B. Development of Methods for the Determination of PKa Values. Anal. Chem. Insights 2013, 8, 53–70. 10.4137/ACI.S12304. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Dubey S. K.; Singhvi G.; Tyagi A.; Agarwal H.; Krishna K. V. Spectrophotometric Determination of PKa and Log P of Risperidone. J. Appl. Pharm. Sci. 2017, 7, 155–158. 10.7324/JAPS.2017.71123. [DOI] [Google Scholar]
  3. Manderscheid M.; Eichinger T. Determination of PKa Values by Liquid Chromatography. J. Chromatogr. Sci. 2003, 41, 323–326. 10.1093/chromsci/41.6.323. [DOI] [PubMed] [Google Scholar]
  4. Lopez X.; Schaefer M.; Dejaegere A.; Karplus M. Theoretical Evaluation of p K a in Phosphoranes: Implications for Phosphate Ester Hydrolysis. J. Am. Chem. Soc. 2002, 124, 5010–5018. 10.1021/ja011373i. [DOI] [PubMed] [Google Scholar]
  5. Brown T. N.; Mora-Diez N. Computational Determination of Aqueous Pka Values of Protonated Benzimidazoles (Part 1). J. Phys. Chem. B 2006, 110, 9270–9279. 10.1021/jp055084i. [DOI] [PubMed] [Google Scholar]
  6. Brown T. N.; Mora-Diez N. Computational Determination of Aqueous PKa Values of Protonated Benzimidazoles (Part 2). J. Phys. Chem. B 2006, 110, 20546–20554. 10.1021/jp0639501. [DOI] [PubMed] [Google Scholar]
  7. Shields G. C.; Seybold P. G.. Computational Approaches for the Prediction of pKa Values, 1st ed.; CRC Press: Boca Raton, 2013. [Google Scholar]
  8. Marenich A. V.; Cramer C. J.; Truhlar D. G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. 10.1021/jp810292n. [DOI] [PubMed] [Google Scholar]
  9. Barone V.; Cossi M.; Tomasi J. A New Definition of Cavities for the Computation of Solvation Free Energies by the Polarizable Continuum Model. J. Chem. Phys. 1997, 107, 3210–3221. 10.1063/1.474671. [DOI] [Google Scholar]
  10. Marenich A. V.; Olson R. M.; Kelly C. P.; Cramer C. J.; Truhlar D. G. Self-Consistent Reaction Field Model for Aqueous and Nonaqueous Solutions Based on Accurate Polarized Partial Charges. J. Chem. Theory Comput. 2007, 3, 2011–2033. 10.1021/ct7001418. [DOI] [PubMed] [Google Scholar]
  11. Hofer T. S.; Hünenberger P. H. Absolute Proton Hydration Free Energy, Surface Potential of Water, and Redox Potential of the Hydrogen Electrode from First Principles: QM/MM MD Free-Energy Simulations of Sodium and Potassium Hydration. J. Chem. Phys. 2018, 148, 222814 10.1063/1.5000799. [DOI] [PubMed] [Google Scholar]
  12. Takano Y.; Houk K. N. Benchmarking the Conductor-like Polarizable Continuum Model (CPCM) for Aqueous Solvation Free Energies of Neutral and Ionic Organic Molecules. J. Chem. Theory Comput. 2005, 1, 70–77. 10.1021/ct049977a. [DOI] [PubMed] [Google Scholar]
  13. Alongi K. S.; Shields G. C.. Theoretical Calculations of Acid Dissociation Constants: A Review Article. Annual Reports in Computational Chemistry; Elsevier Masson SAS: Paris, 2010; Vol. 6, pp 113–138. [Google Scholar]
  14. Tissandier M. D.; Cowen K. A.; Feng W. Y.; Gundlach E.; Cohen M. H.; Earhart A. D.; Coe J. V.; Tuttle T. R. The Proton’s Absolute Aqueous Enthalpy and Gibbs Free Energy of Solvation from Cluster-Ion Solvation Data. J. Phys. Chem. A 1998, 102, 7787–7794. 10.1021/jp982638r. [DOI] [Google Scholar]
  15. Camaioni D. M.; Schwerdtfeger C. A. Comment on “Accurate Experimental Values for the Free Energies of Hydration of H+, OH-, and H3O+.”. J. Phys. Chem. A 2005, 109, 10795–10797. 10.1021/jp054088k. [DOI] [PubMed] [Google Scholar]
  16. Donald W. A.; Williams E. R. An Improved Cluster Pair Correlation Method for Obtaining the Absolute Proton Hydration Energy and Enthalpy Evaluated with an Expanded Data Set. J. Phys. Chem. B 2010, 114, 13189–13200. 10.1021/jp1068945. [DOI] [PubMed] [Google Scholar]
  17. Ho J.; Coote M. L. First-Principles Prediction of Acidities in the Gas and Solution Phase. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2011, 1, 649–660. 10.1002/wcms.43. [DOI] [Google Scholar]
  18. Pliego J. R.; Riveros J. M. Theoretical Calculation of PKa Using the Cluster-Continuum Model. J. Phys. Chem. A 2002, 106, 7434–7439. 10.1021/jp025928n. [DOI] [Google Scholar]
  19. da Silva C. O.; da Silva E. C.; Nascimento M. A. C. Ab Initio Calculations of Absolute PKa Values in Aqueous Solution I. Carboxylic Acids. J. Phys. Chem. A 1999, 103, 11194–11199. 10.1021/jp9836473. [DOI] [Google Scholar]
  20. Pliego J. R. Thermodynamic Cycles and the Calculation of PKa. Chem. Phys. Lett. 2003, 367, 145–149. 10.1016/S0009-2614(02)01686-X. [DOI] [Google Scholar]
  21. Kelly C. P.; Cramer C. J.; Truhlar D. G. Adding Explicit Solvent Molecules to Continuum Solvent Calculations for the Calculation of Aqueous Acid Dissociation Constants. J. Phys. Chem. A 2006, 110, 2493–2499. 10.1021/jp055336f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Cossi M.; Rega N.; Scalmani G.; Barone V. Energies, Structures, and Electronic Properties of Molecules in Solution with the C-PCM Solvation Model. J. Comput. Chem. 2003, 24, 669–681. 10.1002/jcc.10189. [DOI] [PubMed] [Google Scholar]
  23. Klamt A.; Schüürmann G. COSMO: A New Approach to Dielectric Screening in Solvents with Explicit Expressions for the Screening Energy and Its Gradient. J. Chem. Soc., Perkin Trans. 2 1993, 5, 799–805. 10.1039/P29930000799. [DOI] [Google Scholar]
  24. Jia Z.-k.; Du D.-m.; Zhou Z.-y.; Zhang A.-g.; Hou R.-y. Accurate PKa Determinations for Some Organic Acids Using an Extended Cluster Method. Chem. Phys. Lett. 2007, 439, 374–380. 10.1016/j.cplett.2007.03.092. [DOI] [Google Scholar]
  25. Toth A. M.; Liptak M. D.; Phillips D. L.; Shields G. C. Accurate Relative PKa Calculations for Carboxylic Acids Using Complete Basis Set and Gaussian-n Models Combined with Continuum Solvation Methods. J. Chem. Phys. 2001, 114, 4595–4606. 10.1063/1.1337862. [DOI] [PubMed] [Google Scholar]
  26. Namazian M.; Halvani S. Calculations of PKa Values of Carboxylic Acids in Aqueous Solution Using Density Functional Theory. J. Chem. Thermodyn. 2006, 38, 1495–1502. 10.1016/j.jct.2006.05.002. [DOI] [Google Scholar]
  27. Caballero N. A.; Melendez F. J.; Muñoz-Caro C.; Niño A. Theoretical Prediction of Relative and Absolute PKa Values of Aminopyridines. Biophys. Chem. 2006, 124, 155–160. 10.1016/j.bpc.2006.06.007. [DOI] [PubMed] [Google Scholar]
  28. Silva C. S.; Custodio R. Assessment of PKa Determination for Monocarboxylic Acids with an Accurate Theoretical Composite Method: G4CEP. J. Phys. Chem. A 2019, 123, 8314–8320. 10.1021/acs.jpca.9b05380. [DOI] [PubMed] [Google Scholar]
  29. Philipp D. M.; Watson M. A.; Yu H. S.; Steinbrecher T. B.; Bochevarov A. D. Quantum Chemical PKa Prediction for Complex Organic Molecules. Int. J. Quantum Chem. 2018, 118, e25561 10.1002/qua.25561. [DOI] [Google Scholar]
  30. Bochevarov A. D.; Watson M. A.; Greenwood J. R.; Philipp D. M. Multiconformation, Density Functional Theory-Based PKa Prediction in Application to Large, Flexible Organic Molecules with Diverse Functional Groups. J. Chem. Theory Comput. 2016, 12, 6001–6019. 10.1021/acs.jctc.6b00805. [DOI] [PubMed] [Google Scholar]
  31. Sastre S.; Casasnovas R.; Muñoz F.; Frau J. Isodesmic Reaction for PKa Calculations of Common Organic Molecules. Theor. Chem. Acc. 2013, 132, 1310–1318. 10.1007/s00214-012-1310-z. [DOI] [Google Scholar]
  32. Jorgensen W. L.; Briggs J. M.; Gao J. A Priori Calculations of PKa’s for Organic Compounds in Water. The PKa of Ethane. J. Am. Chem. Soc. 1987, 109, 6857–6858. 10.1021/ja00256a053. [DOI] [Google Scholar]
  33. Ho J.; Coote M. L. A Universal Approach for Continuum Solvent PKa Calculations: Are We There Yet?. Theor. Chem. Acc. 2010, 125, 3–21. 10.1007/s00214-009-0667-0. [DOI] [Google Scholar]
  34. Casasnovas R.; Fernández D.; Ortega-Castro J.; Frau J.; Donoso J.; Muñoz F. Avoiding Gas-Phase Calculations in Theoretical PKa Predictions. Theor. Chem. Acc. 2011, 130, 1–13. 10.1007/s00214-011-0945-5. [DOI] [Google Scholar]
  35. Casasnovas R.; Ortega-Castro J.; Frau J.; Donoso J.; Muñoz F. Theoretical PKa Calculations with Continuum Model Solvents, Alternative Protocols to Thermodynamic Cycles. Int. J. Quantum Chem. 2014, 114, 1350–1363. 10.1002/qua.24699. [DOI] [Google Scholar]
  36. Sastre S.; Casasnovas R.; Muñoz F.; Frau J. Isodesmic Reaction for Accurate Theoretical PKa Calculations of Amino Acids and Peptides. Phys. Chem. Chem. Phys. 2016, 18, 11202–11212. 10.1039/C5CP07053H. [DOI] [PubMed] [Google Scholar]
  37. Govender K. K.; Cukrowski I. Density Functional Theory in Prediction of Four Stepwise Protonation Constants for Nitrilotripropanoic Acid (NTPA). J. Phys. Chem. A 2009, 113, 3639–3647. 10.1021/jp811044b. [DOI] [PubMed] [Google Scholar]
  38. Sutton C. C. R.; Franks G. V.; da Silva G. First Principles PKa Calculations on Carboxylic Acids Using the SMD Solvation Model: Effect of Thermodynamic Cycle, Model Chemistry, and Explicit Solvent Molecules. J. Phys. Chem. B 2012, 116, 11999–12006. 10.1021/jp305876r. [DOI] [PubMed] [Google Scholar]
  39. Ho J. Predicting PKa in Implicit Solvents: Current Status and Future Directions. Aust. J. Chem. 2014, 67, 1441–1460. 10.1071/CH14040. [DOI] [Google Scholar]
  40. Alexov E.; Mehler E. L.; Baker N.; M. Baptista A.; Huang Y.; Milletti F.; Erik Nielsen J.; Farrell D.; Carstensen T.; Olsson M. H. M.; et al. Progress in the Prediction of p K a Values in Proteins. Proteins: Struct., Funct., Bioinf. 2011, 79, 3260–3275. 10.1002/prot.23189. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Lee A. C.; Crippen G. M. Predicting PKa. J. Chem. Inf. Model. 2009, 49, 2013–2033. 10.1021/ci900209w. [DOI] [PubMed] [Google Scholar]
  42. Rupp M.; Korner R.; Tetko V. I. Predicting the PKa of Small Molecules. Comb. Chem. High Throughput Screening 2011, 14, 307–327. 10.2174/138620711795508403. [DOI] [PubMed] [Google Scholar]
  43. Malloum A.; Fifen J. J.; Conradie J. Solvation Energies of the Proton in Methanol Revisited and Temperature Effects. Phys. Chem. Chem. Phys. 2018, 20, 29184–29206. 10.1039/C8CP05823G. [DOI] [PubMed] [Google Scholar]
  44. Kelly C. P.; Cramer C. J.; Truhlar D. G. Aqueous Solvation Free Energies of Ions and Ion–Water Clusters Based on an Accurate Value for the Absolute Aqueous Solvation Free Energy of the Proton. J. Phys. Chem. B 2006, 110, 16066–16081. 10.1021/jp063552y. [DOI] [PubMed] [Google Scholar]
  45. Lian P.; Johnston R. C.; Parks J. M.; Smith J. C. Quantum Chemical Calculation of p K a s of Environmentally Relevant Functional Groups: Carboxylic Acids, Amines, and Thiols in Aqueous Solution. J. Phys. Chem. A 2018, 122, 4366–4374. 10.1021/acs.jpca.8b01751. [DOI] [PubMed] [Google Scholar]
  46. Liptak M. D.; Shields G. C. Accurate p K a Calculations for Carboxylic Acids Using Complete Basis Set and Gaussian-n Models Combined with CPCM Continuum Solvation Methods. J. Am. Chem. Soc. 2001, 123, 7314–7319. 10.1021/ja010534f. [DOI] [PubMed] [Google Scholar]
  47. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.. et al. Gaussian 16; Revision B.01; Wallingford Center: New Haven, 2016. [Google Scholar]
  48. Dewar M. J. S.; Zoebisch E. G.; Healy E. F.; Stewart J. J. P. AM1: A New General Purpose Quantum Mechanical Molecular Model1. J. Am. Chem. Soc. 1985, 107, 3902–3909. 10.1021/ja00299a024. [DOI] [Google Scholar]
  49. Stewart J. J. P. Optimization of Parameters for Semiempirical Methods V: Modification of NDDO Approximations and Application to 70 Elements. J. Mol. Model. 2007, 13, 1173–1213. 10.1007/s00894-007-0233-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Roothaan C. New Developments in Molecular Orbital Theory. Rev. Mod. Phys. 1951, 23, 69–89. 10.1103/RevModPhys.23.69. [DOI] [Google Scholar]
  51. Adamo C.; Barone V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. 10.1063/1.478522. [DOI] [Google Scholar]
  52. Zhao Y.; Truhlar D. G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Function. Theor. Chem. Acc. 2008, 120, 215–241. 10.1007/s00214-007-0310-x. [DOI] [Google Scholar]
  53. Becke A. D. Density-functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
  54. Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  55. Yanai T.; Tew D. P.; Handy N. C. A New Hybrid Exchange-Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. 10.1016/j.cplett.2004.06.011. [DOI] [Google Scholar]
  56. Chai J.-D.; Head-Gordon M. Long-Range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. 10.1039/b810189b. [DOI] [PubMed] [Google Scholar]
  57. Grimme S. Semiempirical Hybrid Density Functional with Perturbative Second-Order Correlation. J. Chem. Phys. 2006, 124, 034108 10.1063/1.2148954. [DOI] [PubMed] [Google Scholar]
  58. Silva C. S.; Pereira D. H.; Custodio R. G4CEP: A G4 Theory Modification by Including Pseudopotential for Molecules Containing First-, Second- and Third-Row Representative Elements. J. Chem. Phys. 2016, 144, 204118 10.1063/1.4952427. [DOI] [PubMed] [Google Scholar]
  59. Vosko S. H.; Wilk L.; Nusair M. Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis. Can. J. Phys. 1980, 58, 1200–1211. 10.1139/p80-159. [DOI] [Google Scholar]
  60. Citra M. J. Estimating the PKa of Phenols, Carboxylic Acids and Alcohols from Semi-Empirical Quantum Chemical Methods. Chemosphere 1999, 38, 191–206. 10.1016/S0045-6535(98)00172-6. [DOI] [PubMed] [Google Scholar]
  61. Soriano E.; Cerdán S.; Ballesteros P. Computational Determination of PK a Values. A Comparison of Different Theoretical Approaches and a Novel Procedure. J. Mol. Struct.: THEOCHEM 2004, 684, 121–128. 10.1016/j.theochem.2004.06.041. [DOI] [Google Scholar]
  62. Tehan B. G.; Lloyd E. J.; Wong M. G.; Pitt W. R.; Montana J. G.; Manallack D. T.; Gancia E. Estimation of PKa Using Semiempirical Molecular Orbital Methods. Part 1: Application to Phenols and Carboxylic Acids. Quant. Struct. Relat. 2002, 21, 457–472. . [DOI] [Google Scholar]
  63. Kromann J. C.; Larsen F.; Moustafa H.; Jensen J. H. Prediction of PKa Values Using the PM6 Semiempirical Method. PeerJ 2016, 4, e2335 10.7717/peerj.2335. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Manallack D. T. The pKa Distribution of Drugs: Application to Drug Discovery. Perspect. Med. Chem. 2007, 1, 25–38. 10.1177/1177391X0700100003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Petersson G. A.; Al-Laham M. A. A Complete Basis Set Model Chemistry. II. Open-shell Systems and the Total Energies of the First-row Atoms. J. Chem. Phys. 1991, 94, 6081–6090. 10.1063/1.460447. [DOI] [Google Scholar]
  66. Montgomery J. A.; Ochterski J. W.; Petersson G. A. A Complete Basis Set Model Chemistry. IV. An Improved Atomic Pair Natural Orbital Method. J. Chem. Phys. 1994, 101, 5900–5909. 10.1063/1.467306. [DOI] [Google Scholar]
  67. Montgomery J. A.; Frisch M. J.; Ochterski J. W.; Petersson G. A. A Complete Basis Set Model Chemistry. VI. Use of Density Functional Geometries and Frequencies. J. Chem. Phys. 1999, 110, 2822–2827. 10.1063/1.477924. [DOI] [Google Scholar]
  68. Zhan C. G.; Dixon D. A. Absolute Hydration Free Energy of the Proton from First-Principles Electronic Structure Calculations. J. Phys. Chem. A 2001, 105, 11534–11540. 10.1021/jp012536s. [DOI] [Google Scholar]
  69. Bryantsev V. S.; Diallo M. S.; Goddard W. A. III Calculation of Solvation Free Energies of Charged Solutes Using Mixed Cluster/Continuum Models. J. Phys. Chem. B 2008, 112, 9709–9719. 10.1021/jp802665d. [DOI] [PubMed] [Google Scholar]
  70. Ho J. Are Thermodynamic Cycles Necessary for Continuum Solvent Calculation of PK a s and Reduction Potentials?. Phys. Chem. Chem. Phys. 2015, 17, 2859–2868. 10.1039/C4CP04538F. [DOI] [PubMed] [Google Scholar]
  71. Ho J.; Ertem M. Z. Calculating Free Energy Changes in Continuum Solvation Models. J. Phys. Chem. B 2016, 120, 1319–1329. 10.1021/acs.jpcb.6b00164. [DOI] [PubMed] [Google Scholar]
  72. Haynes W. M., Ed. CRC Handbook of Chemistry and Physics, 96th ed.; CRC Press: Boca Raton, 2016. [Google Scholar]
  73. Dobos D.Electrochemical Data: A Handbook for Electrochemists in Industry and Universities; Elsevier Scientific Pub. Co.: Amsterdam, 1975. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp0c08283_si_001.pdf (169.9KB, pdf)

Articles from The Journal of Physical Chemistry. a are provided here courtesy of American Chemical Society

RESOURCES