Abstract
We report on a comparison between two optical detection techniques, one based on a Quartz-Enhanced Photoacoustic Spectroscopy (QEPAS) detection module, where a quartz tuning fork is acoustically coupled with a pair of millimeter-sized resonator tubes; and the other one based on a Photothermal Spectroscopy (PTS) module where a Fabry-Perot interferometer acts as transducer to probe refractive index variations. When resonant optical absorption of modulated light occurs in a gas sample, QEPAS directly detects acoustic waves while PTS probes refractive index variations caused by local heating. Compact QEPAS and PTS detection modules were realized and integrated in a gas sensor system for detection of carbon monoxide (CO), targeting the fundamental band at 4.6 μm by using a distributed-feedback quantum cascade laser. Performance was compared and ultimate detection limits up to ∼ 6 part-per-billion (ppb) and ∼15 ppb were reached for QEPAS and the PTS module, respectively, using 100 s integration time and 40 mW of laser power.
Keywords: Laser spectroscopy, Quartz tuning fork, Fabry-Perot interferometer, Gas sensing, Carbon monoxide
1. Introduction
Gas sensing plays a major role in a wide range of applications. Environmental monitoring of species in atmosphere such as chlorofluorocarbons (CFC) compounds and greenhouse gases (GHG), landfill emissions, human breath diagnostic for the detection of biomarkers or leakage of hydrocarbons in pipelines transport systems are only few of many examples in which gas sensors are employed. Among toxic species, carbon monoxide (CO) is responsible for over 35.000 deaths per year [1]. Carbon monoxide is a colourless, odourless and tasteless flammable gas released during incomplete combustion of organic compounds. The exhaust emissions in poorly ventilated environments can lead to CO concentrations reaching lethal levels. Carbon monoxide binds selectively with haemoglobin (Hb) forming carboxyhaemoglobin (COHb), which impairs the oxygen carrying capacity of the blood. The effects on human health cause cardiac and pulmonary disorders, central nervous system involvement and movement and vision disorders, headache, fatigue, coma, breathlessness and even death [2]. Deaths by CO poisoning are still very frequent and even small concentrations can be dangerous for long exposure times [3]: the World Health Organization (WHO) issued a maximum concentration of 8.7 ppm for an exposure time of 8 h [4]. CO detection requires highly sensitive and selective techniques, with fast response time and suitable for outdoor operation. Tunable diode laser absorption spectroscopy (TDLAS) techniques can accomplish these requirements. In TDLAS the emission of a narrow bandwidth laser is scanned over an optical absorption line of the gas of interest. In most cases, this is done by ramping the injection current of the laser across the absorption line and the transmitted light is retrieved by a photodetector. However, the sensitivity of TDLAS depends on the interaction length. Longer optical paths in small volumes can be obtained by using multipass cells, which increase the effective pathlength by several orders of magnitude [5,6]. However, the alignment is critical to preserve the multiple reflections pattern between the mirrors composing the multipass cell. Alternative techniques to TDLAS are based on indirect detection of light absorption. The most representative techniques are based on photoacoustic spectroscopy (PAS) and photothermal spectroscopy (PTS), which probe pressure waves and density variations, respectively, produced in the gas sample as a consequence of light absorption. Quartz-enhanced PAS (QEPAS) employs a quartz tuning fork (QTF) to detect pressure waves exploiting the piezoelectric effect occurring when prongs are put in vibration at one of the natural frequencies of QTF flexural modes. QEPAS proved to be an extremely sensitive [7,8] and compact [9] technique, capable of reaching even the part-per-trillion concentration range [10,11]. As an alternative to QTF, membrane and capacitive microphones [12], as well as cantilevers [13,14] have been successfully employed as sound wave detector. Optical microphones (OMs) are devices in which the transduction mechanism of acoustical waves is based on light detection. OMs have been used to measure the refractive index changes induced by pressure waves [15]. A classification of OMs has been proposed by Bilaniuk in [16]. Phase-modulated interferometric transduction probing thermal waves proved to be extremely sensitive for gas sensing. Mach-Zender as well as Fabry-Pérot configurations have been already employed for this purpose [[17], [18], [19], [20], [21]]: the latter is well suited for transducer miniaturization.
In this work, we developed a gas sensor for carbon monoxide detection exploiting a continuous-wave distributed-feedback quantum cascade laser (CW-DFB-QCL) and two interchangeable compact detection modules. The first is a QEPAS spectrophone formed by a QTF and a pair of microresonator tubes to detect pressure waves; the second is based on a commercial optical microphone (Xarion-ETA250 Ultra) used as interferometric-PTS transducer to probe refractive index changes. Both modules were tested and compared in terms of sensitivity and long-term stability for CO trace gas detection in nitrogen.
2. Generation of the photoacoustic and photothermal waves
The photoacoustic and photothermal effects arise from the absorption of modulated light in a gas sample. The process of photon absorption from a molecule involves transitions from the ground level to an excited state. The molecules release the excess energy via radiative or non-radiative pathways. In the near- and mid-infrared spectral region, non-radiative pathways overcome radiative deactivation, with typical relaxation time of sec [22]. Non-radiative relaxations occur via energy transfer processes in which the excited molecules collide with neighbourhood ones. By means of these collisions, the vibrational energy is converted into kinetic energy, i.e. heat. If the gas molecules absorb light emitted from a modulated source, modulated gas heating with the same periodicity and intensity proportional to the number of the absorbing molecules will occur. However, the latter relationship holds only if the following conditions are satisfied: (i) the light source modulation frequency () is much lower than the relaxation rate of the gas molecule, ; (ii) small optical absorptions to avoid absorption saturation. The periodic heat release causes a local change in density, involving the generation of thermal and acoustic photo-induced effects. Photo-induced effects are treated as small perturbations upon the equilibrium state of the thermodynamic quantities. The temperature rise involves gas expansion, producing two effects: (i) the generation of a diffusive thermal localized wave, which decays exponentially from the excitation region and (ii) the generation of acoustic modes, which can propagate far from the excitation area. The hydrodynamic relaxation of the gas can be modelled by solving a set of coupled differential equations, namely the continuity equation, the laws of momentum and energy conservation and the ideal gas law, in the form of Navier-Stokes equations. Berne and Pecora in [23] obtained the generalized solutions of the hydrodynamic response. A simpler solution is given for the one-dimensional relaxation case, which highlights the main differences between the two hydrodynamic relaxation modes. This simplified model is often employed to describe the effects that occur on thin membranes as a result of light absorption. Let us assume to excite along the z-direction an infinite-extended sample in the x–y plane with a single-pulse excitation and a Gaussian intensity distribution (in the x–y plane) with a beam waist w. The hydrodynamic solution in terms of density perturbation δρ can be retrieved in the form of [24]:
| (1) |
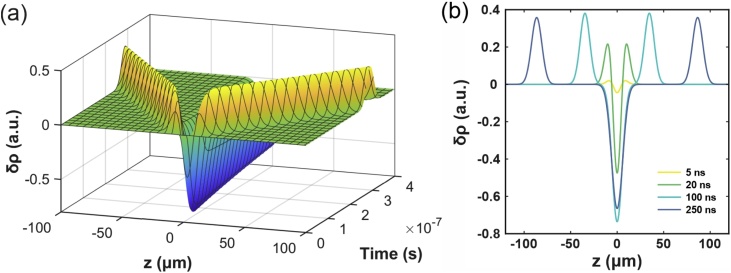
The first term in Eq. 1 describes the propagation of the acoustic wave along z at the speed of sound c, with an acoustic attenuation constant Γ (m2s−1). The second term represents the thermal wave with a thermal diffusivity (m2s-1). A simulation of the density perturbation as a function of both the distance z from the heat source and time is represented in Fig. 1(a), while Fig. 1(b) shows the evolution of density perturbation at four different time frames. In the simulation, thermodynamic constants for air at normal ambient temperature and pressure have been used.
Fig. 1.
Gas density perturbation for one-dimensional hydrodynamic relaxation of a sample excited from a Gaussian intensity distribution single-pulse obtained by using Eq. 1. The density decrease at corresponds to the diffusive thermal mode, while the ‘wings’ represent the propagating acoustic mode. For the simulation, the following parameters have been used: beam waist, μm; acoustic attenuation constant, ; thermal diffusivity, ; speed of sound, . (b) Density perturbation at four different times (5, 20, 100 and 250 ns).
The two hydrodynamic relaxation modes are well distinguishable: the thermal wave exhibits a negative maximum fixed at the heat source () because of gas thermal expansion. Such perturbation is localized in the excitation region and broadens in space over time, reducing its peak value. The positive perturbation, instead, corresponds to the acoustic propagating mode. Typically, sound waves experience low propagation losses in low-viscous media such as air, in the order of fraction of percent per kilometre. Hence, pressure waves can travel far from the excitation source and can be detected at much greater distance. It is worth noticing that, while photothermal effects does not interfere with the detection of acoustic effects, the opposite is not always true: photoacoustic effects may affect the photothermal signal. In conclusion, the scenario depicted here illustrates the response of a thin film to a single-excitation event, which is far from the complex case of a continuous excitation within a gas sample investigated in this work. Nevertheless, these results are significant and can be generalized through the convolution of the single-excitation response function with the time-dependent heat source. Both photoacoustic and photothermal spectroscopy rely on the same signal generation process but differ in terms of detection. In both cases, the photo-induced signal can be expressed as [17,25]:
| (2) |
where P is the optical power of the light source, f is the modulation frequency, is the absorption coefficient of the gas molecules and V the interaction volume. In QEPAS, the modulation frequency of the excitation laser has to be fixed at half of the QTF resonance frequency in order to operate in wavelength modulation spectroscopy and 2f detection. For PTS, such a restriction is not required and the modulation frequency can be freely tuned to achieve the highest signal-to-noise ratio. Gas pressure can contribute to the optimization of the signal. Usually, non-radiative collisional deactivation is more efficient at higher pressures since the excited molecules have a larger number of neighbored collisional partners. However, pressure may affect other parameters that take part in signal generation - e.g. the Q-factor of the QTF (for QEPAS) as explained in Sect. 4.1, or thermal properties of the gas buffer for PTS. Since the optimal pressure is hard to be estimated in advance, it is usually experimentally determined by varying the gas pressure within the detection module while keeping fixed all other parameters. The beam waist size plays an important role in QEPAS: the laser beam must be focused between QTF prongs as it passes through tubes, without touching both elements, otherwise a resonant background noise deteriorates the QEPAS sensor performance. For such a reason, the development of QTF with large prong spacings (up to 1.5 mm) has been beneficial to reduce the noise down the Johnson noise of the QTF [26]. Similarly, in PTS the excitation beam must be focused between interferometer mirrors, without touching them, to avoid mirrors heating which would increase the background noise and to avoid losses in the optical power delivered to the sample gas.
3. Experimental setup
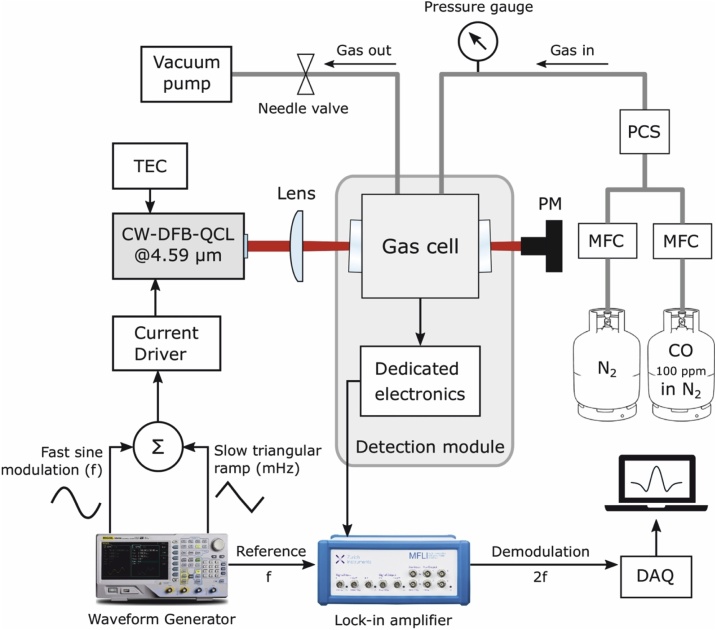
A schematic of the experimental setup for the investigated gas sensor system is shown in Fig. 2.
Fig. 2.
Schematic of the gas sensor system for CO detection. DAQ: data acquisition card; MFC: mass flow controller; PCS: pressure control system; PM: power meter; TEC: thermoelectric cooler. The sensor system can easily accommodate QEPAS or PTS detection module.
A continuous-wave (CW) distributed-feedback (DFB) quantum cascade laser (QCL) (AdTech Optics HHL-14-15) emitting at a wavelength of μm was used as the excitation source. The laser targets the R(9) CO absorption line of the fundamental band falling at . The linestrength of the transition was retrieved by HITRAN database [27] and results . The laser beam was focused by a 50 mm focal length convex-plane CaF2 lens in the gas cell. The estimated beam waist in the focus spot was ∼90 μm. Two temperature controllers (Wavelength Electronics, PTC2.5K-CH) were connected to thermoelectric cooler (TEC) Peltier elements to stabilize the QCL temperature: one to fix the laser chip temperature to 14.55 °C, while the second one to stabilize the housing temperature to 25 °C, with a fan-assisted heat sink. An offset current of 240 mA was injected into the laser to tune its emission to the CO absorption line. An emitted optical power of 40 mW was measured with the power meter. A low frequency (2 mHz) voltage ramp was applied to the external modulation input of the QCL current supply (Wavelength Electronics, QCL OEM 300) to scan the laser wavelength. A sinusoidal dither was added to the low-frequency voltage ramp for a fast-optical frequency modulation. Both voltage signals were generated by a two-channel waveform generator (Rigol, DG4162). The waveform generator also provided the reference TTL signal at the dither frequency for the lock-in amplifier (Zurich Instruments, MFLI). The setup allows to easily interchange the QEPAS and PTS detection modules, which will be discussed in detail in the next section. Both modules were included in gas cells mounted on a 5-axis compact rotation-translation stage (Thorlabs, PY005/M) to guarantee a correct alignment of the laser beam within the gas cell. The gas was inserted within the cell by using a gas line. For both detection modules, the signal was sent to the lock-in amplifier and demodulated at the 2nd harmonic. The integration time was set to 1 s with a 4th order low-pass filter. The lock-in amplifier was connected to a DAQ card (National Instruments, DAQ-6363) and the signal was recorded by a personal computer. The gas line started from two gas cylinders, one containing pure N2 used as carrier gas, and the other containing CO in a certified concentration of 100 ppm in N2. Both gas flows were regulated by using two mass flow controllers (Vögtlin Instruments, red-y), also used to perform dilutions, while the total flow was kept constant. Constant gas replenishment prevented cumulative heating within the cell. The gas mixture was fluxed through the gas cell by means of a valve system, a pressure controller and a rotary pump. The pressure controller stabilized the pressure within the gas cell.
4. Detection modules
4.1. QEPAS module
The QTF is an electro-mechanical oscillator which can be modelled both as an RLC circuit (Butterworth–Van Dyke model) and a mechanical damped oscillator. The resonance frequencies of piezoelectrically active, anti-symmetrical flexural modes are defined by Eq. 3:
| (3) |
where is the component of the quartz Young’s modulus in the vibration plane, is the density of quartz, while w and L are respectively the width and length of the QTF’s prong in the vibration plane. The number n defines the mode of vibration and its value is for the fundamental mode. Thus, the resonance frequency can be chosen by properly designing the prong geometry. An important parameter which defines the quality of a resonance mode is the Q-factor, expressed as the ratio between the resonance frequency () and the full width at half maximum (FWHM) of the resonance profile. Several works [26,28] proved the dependency of the Q-factor upon QTF geometry, surrounding gas properties and intrinsic losses due to thermoelastic effects and support losses. Typical Q-factor values range between in vacuum down to at ambient pressure due to air damping effects. Standard tuning forks have several limitations related to their geometry and properties. A fundamental resonance frequency as high as ∼32.7 kHz has two negative consequences for QEPAS: (i) the photoacoustic signal is smaller when using higher modulation frequencies, according to Eq. 2; (ii) it may be unsuitable for spectroscopic applications involving gases with slow relaxation times (τ), such as carbon monoxide [29]. Moreover, the prong spacing is only 300 μm, with the consequence of a difficult optical alignment of the laser beam and often requiring the use of spatial filters, which ultimately reduce the optical power delivered to the gas sample. To overcome these limitations, a custom QTF, labelled in this work as S15, has been used. In Table 1, a comparison between the geometrical properties of the standard QTF and the S15 is reported.
Table 1.
Comparison between standard and S15 QTF’s parameters. The geometrical parameters are referred to prong’s dimensions: L, length; w, width; T, crystal thickness; g, prongs’ spacing; f0, fundamental resonance frequency.
| QTF | L (mm) | w (mm) | T (mm) | g (mm) | f0 (kHz) |
|---|---|---|---|---|---|
| Standard | 3.0 | 0.34 | 0.33 | 0.30 | 32.7 |
| S15 | 9.4 | 2.0 | 0.25 | 1.5 | 15.8 |
In S15 QTF, the prongs’ spacing has been increased by five times to 1.5 mm and the prong geometry has been designed in order to reduce the fundamental frequency below 20 kHz, without affecting the Q-factor, as demonstrated in Ref. [21]. The S15 QTF was coupled with millimeter-sized resonator (mR) tubes, in a dual-tube on-beam configuration, i.e. with the laser beam passing through mR-tubes and QTF prongs (see Fig. 3(a)). The mR-tubes act as an organ pipe acoustic resonator and can enhance the intensity of the acoustic field between the QTF prongs up to 60 times [21]. The QTF coupled with mR-tubes is referred to as QEPAS spectrophone. For a selected QTF, the geometric parameters influencing the enhancement factor are the tubes length (l) and internal diameter (ID). The optimal tube length can be estimated by considering the open-end correction [30,31] as:
| (4) |
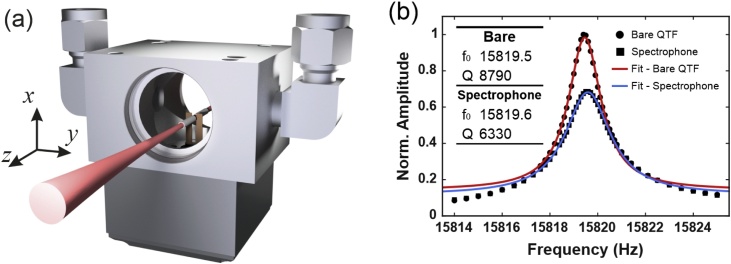
A tube length of l=9.4 mm and internal diameter of ID = 1.41 mm were chosen, assuming the speed of sound in air at ambient pressure and . In [30], a description of the optimal tube positioning with respect to the QTF is provided. The tubes were placed upon a V-groove cylinder, and were held in position using a resin at a distance of ∼250 μm from the prong surface (along z-direction, see Fig. 3(a)) and 1 mm distance from the top of the QTF (along x-direction)
Fig. 3.
(a) Sketch of the QEPAS spectrophone inside of the gas cell. (b) Resonance profile of QTF-S15 at ambient pressure, as bare (circles) and with mR-tubes (squares). Lorentzian fit of bare S15 (red solid line) and spectrophone (blue solid line) have been performed to retrieve the resonance frequency and the Q-factor.
The frequency response of the QTF was acquired by applying a 10 mV peak-to-peak sinusoidal voltage to the QTF in a frequency range nearby the calculated resonance frequency, by varying the excitation frequency step-by-step. The laser was turned off and pure N2 was flowed through the gas cell at atmospheric pressure. The electric excitation results in a piezoelectric charge displacement on its prongs via the inverse piezoelectric effect. The collected charges are converted to a voltage signal by means of a low-noise trans-impedance amplifier. The lock-in amplifier demodulates the voltage signal at the same frequency of the excitation source. In Fig. 3(b) the resonance profiles for the bare QTF-S15 and QEPAS spectrophone are shown.
The comparison between the bare QTF and the spectrophone resonance curve clearly shows the effects of acoustic coupling. The resonance profile broadens as a consequence of the acoustic coupling between the QTF and low Q-factor resonator tubes while the peak value is only slightly shifted. For the spectrophone, a resonance frequency of ∼15819.6 Hz was measured together with a Q-factor of ∼6330 at atmospheric pressure.
4.2. PTS module
Thermal perturbations within a sample can be efficiently detected by probing its refractive index changes. Compared to acoustic waves that can propagate far from the generation source, thermal waves are heavily damped and can only be detected nearby the excitation region. The refractive index perturbation () as a function of temperature variation () can be expressed for a gas in the Clausius-Mossotti approximation [19], as:
| (5) |
where n is the refractive index and is the temperature of the gas sample. Optical interferometry can be used to detect the refractive index change in the gas sample with high sensitivity. The refractive index change induces a phase shift () in the electromagnetic wave that can be measured by an interferometer:
| (6) |
where L is the interaction length and λ the wavelength of the probe beam. Compact and sensitive detection can be realized by using a Fabry-Pérot interferometer (FPI) with mm-sized interferometer spacing [20,21]. The advantage of an FPI compared to single-passage interferometers is the enhancement factor of the effective optical length provided by the finesse () of the interferometer. The reflected intensity can be expressed with the Airy formula as [32]:
| (7) |
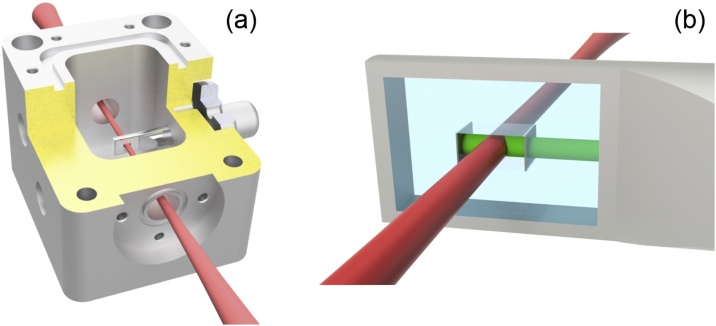
where is the optical phase shift for a cavity round-trip with a mirror spacing d, θ is the angle of incidence, while IR and I0 are the reflected and incident intensities, respectively. A perturbation in the wave phase results in a change in IR. The transducer used in this work is based on a Fabry-Perot interferometer. The commercial instrument comes as a box, containing the electronics and the probe NIR laser fibre-guided to the interferometer head. The head includes the interferometer, which consists of a pair of mirrors aligned to the probe beam, having a spacing of 2 mm, a length (along excitation beam direction) of 1.3 mm and a height of 1 mm. The reflected light is coupled back to the fibre and is monitored. The beams travelling to and coming from the sensor head within the common fibre are split using an optical circulator. The probe laser wavelength is stabilized to the Fabry-Perot resonance profile by the use of an electrical feedback current [33]. The highest sensitivity to reflected intensity changes is achieved when the laser is locked to the inflection point of the FPI’s resonance profile. The instrument provides four levels of frequency cut-off (10 Hz, 10 kHz, 100 kHz, 200 kHz) and three levels of gain (-12, 0, +20 dB). In this work, a cut-off frequency of 10 Hz and a gain level of +20 dB were set. A stainless-steel airtight gas cell was designed to accommodate the interferometer head. A CAD model of the gas cell is given in Fig. 4(a) and a zoomed view of the interferometer head is provided in Fig. 4(b).
Fig. 4.
(a) Sectioned view of the gas cell with the optical transducer. Top lid and windows not shown for clarity. (b) Enlarged view of the transducer head containing the interferometer: the probe beam (green) overlaps with the excitation beam (red) between the interferometer mirrors.
The excitation beam was focused through the interferometer, without touching its optical components. An optical coupling efficiency > 98 % was achieved. The frequency response was tested by generating a photothermal signal within the gas. For this purpose, a certified mixture of 100 ppm of CO:N2 was fluxed through the gas cell at a pressure of 600 Torr. The excitation laser current was tuned to the CO absorption peak and modulated with a sinusoidal dither with frequencies spanning from 15 to 2000 Hz and the acquired signal demodulated at the 2nd harmonic by the lock-in amplifier. The integration time was set to 1 s. For each excitation frequency, the modulation amplitude was properly adjusted in order to maximize the 2f-peak value.
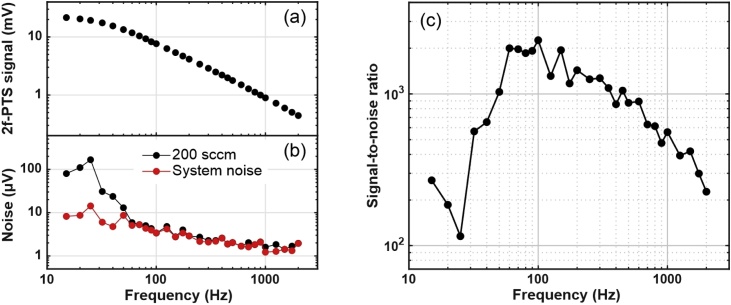
In Fig. 5(a) the signal amplitude as a function of the modulation frequency is represented on a bi-logarithmic scale. As expected for a photothermal source, the signal depends on the modulation frequency according to Eq. 2. The linearity holds true for Hz and the signal rapidly decreases as the frequency increases with a reduction factor of −20 dB/decade. Below 50 Hz, a deviation from linearity is observed, which can be explained by the cut-off frequency set on the instrument (10 Hz). For each frequency value, the noise level was measured as the standard deviation (1-σ) of a two-minutes-long acquisition of the PTS signal with a gas flow of 200 standard cubic centimetre (sccm) and the excitation laser turned on.
Fig. 5.
(a) PTS signal demodulated at the 2nd harmonic as a function of the excitation source’s modulation frequency; (b) Noise level measured in 200 sccm gas flow (black) and in static conditions without excitation laser (red); (c) Signal-to-noise ratio calculated by ratio of the black curves in (a) and (b).
The obtained data points are reported in Fig. 5(b) as black circles. The noise level of the system was also measured with the same procedure when the excitation laser was switched off and no gas was flowing through the cell: it is referred to as system noise in Fig. 5(b) (red circles). The noise level with gas flow approaches the noise level without gas flow at high frequencies (> 60 Hz), but it is significantly higher at lower frequencies. In particular, in the range 15−30 Hz, the noise level for a gas flow in the cell is almost one order of magnitude higher than the noise level without gas flow. The signal-to-noise ratio (SNR) is represented in Fig. 5(c) and it was obtained by dividing the interferometer signal (data points in Fig. 5(a)) with the noise level measured at the operating conditions (black circles in (b)). The best performances were achieved for a modulation frequency of 100 Hz.
5. Calibration curve, sensitivity and limits of detection
5.1. QEPAS sensor
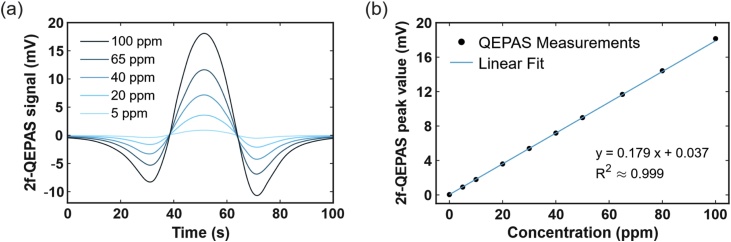
As previously argued, the optimal pressure is hard to be predicted in advance because it depends both on gas properties and on the detection module characteristics. However, when both modules operate at pressures close to the atmospheric one, the pressure dependence of the PTS and QEPAS signal is extremely weak (few percent of signal variations upon changes of 50 Torr). The optimal gas pressure maximizing the QEPAS signal was 760 Torr. A modulation frequency of 7909.8 Hz, corresponding to half of the fundamental resonance of the S15 QTF, was used. Starting from the certified concentration of 100 ppm of CO:N2, different CO concentrations ranging from 5 ppm up to 80 ppm were obtained by using a gas mixer. For each concentration, several spectral scans of the CO absorption line were recorded. Representative 2f-QEPAS scans are reported in Fig. 6(a). The averaged peak signals values were plotted as function of the CO concentration. The dataset together with the best linear fit, representing the calibration curve of the CO sensor, are shown in Fig. 6(b).
Fig. 6.
(a) 2f-QEPAS signal for 100 ppm, 65 ppm, 40 ppm, 20 ppm and 5 ppm CO concentrations in N2 when the sensor operates in spectral scan acquisition mode. (b) QEPAS peak signals plotted as a function of the CO concentration (datapoints) together with the best linear fit (solid line).
The asymmetry of the negative lobes in Fig. 6(a) is due to the residual amplitude modulation [34], arising from the intensity modulation of the laser. The peak value scales linearly with the concentration of the gas target as proved by the coefficient of determination . The sensitivity of the calibration curve results in μV/ppm with a background signal (from pure N2) of μV and 1σ noise of μV. A noise equivalent concentration (NEC) of 22 ppb with 1 s integration time (with a bandwidth of 78 mHz) was calculated.
5.2. PTS sensor
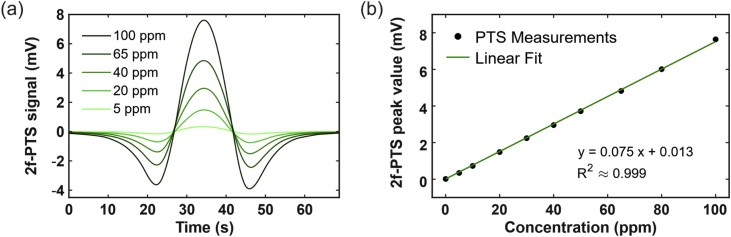
PTS measurements were carried out by using the related module. The optimal gas pressure in this case was found to be 600 Torr. A modulation frequency of 100 Hz was used, as described in Sect. 4.2. As before, a range of CO concentrations between 5 ppm and 100 ppm was investigated by flowing a mixture of CO and N2 through the cell. In Fig. 7(a) representative spectral scans are shown.
Fig. 7.
(a) 2f-PTS signal as a function of time in the spectral scan acquisition mode for different CO concentrations in N2. (b) PTS peak signals at different CO concentrations (datapoints) and the related best linear fit (solid line).
In Fig. 7(b) the peak values, averaged over several scans, are plotted as a function of the CO concentration and the best linear fit provided a sensitivity of with a background signal of 13 μV and 1-σ noise of 4 μV. A noise equivalent concentration of 53 ppb was calculated with 1 s integration time.
6. Long-term stability
With regard to the sensitivity expressed in terms of NEC, the QEPAS-module can reach a performance ∼2.5 times higher than the PTS-module. Together with NEC, the minimum absorption coefficient () and the normalized noise equivalent absorption (NNEA) were also estimated and listed in Table 2.
Table 2.
Comparison of the main figures of merit for the two detection modules. The values given were obtained for an optical power of 40 mW and an integration time of 1 s (corresponding to 78 mHz bandwidth).
| Detection module | NEC (ppb) | NNEA | |
|---|---|---|---|
| QEPAS | 22 | ||
| PTS | 53 |
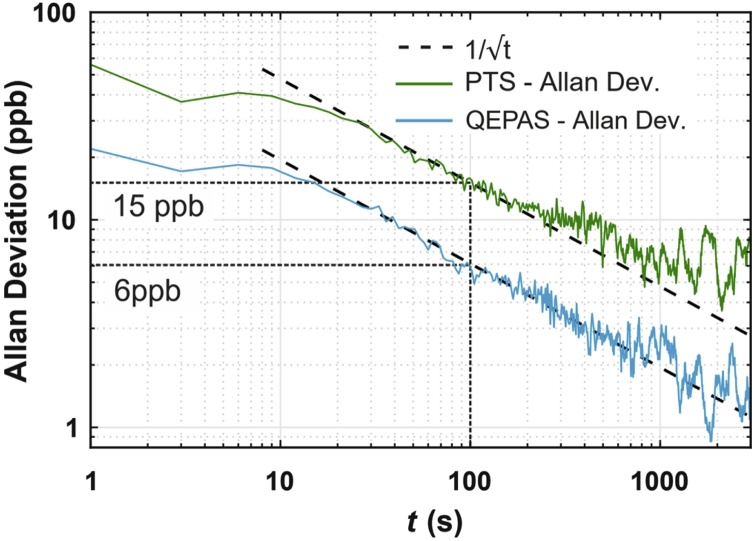
While the NNEA describes the sensor performances on a short time-scale, other measurements are required to characterize long-term drifts and establish the signal averaging limits. The most common approach consists in performing the Allan variance of time sequences of measurements in order to determine how the minimum detection limit (MDL) varies as a function of the signal integration time [35]. Real systems are stable only for a limited time and their stability can be affected by thermal drifts of the laser source, moving fringes or mechanical instabilities. The Allan variance analysis was performed by tuning the laser emission to the CO absorption peak while N2 was fluxed through the gas cell at the same operative conditions used for the calibration of the sensors. The signal was acquired with an integration time sec for approximately 3 h, while a sampling frequency of 1 datapoint every 3 s was used to un-correlate the measurements. The measurements were elaborated by a Matlab-based code [36] and the results are shown in Fig. 8 for both QEPAS- and PTS-module.
Fig. 8.
Allan deviations (in ppb) for QEPAS and PTS sensors, both calculated starting from a 3 -h noise acquisition where the laser was turned ON and tuned to the absorption peak with pure N2 within the gas cell. Dashed line represents the trend. Dotted black line represents MDL at 100 s.
The calculated Allan deviations (), expressed in ppb unit, are represented for both the QEPAS and PTS sensors by the solid lines. The initial drop behaviour is typical of low-pass filtering of a signal [37], which can be related to the lock-in amplifier settings used in this work. This is proven by the fact that this behaviour is common for both curves. The dashed line represents the trend: when the white noise () dominates the measurements, the standard deviation decreases by a factor of 10 as the integration time is 100-fold increased. Starting from integration time of 20 s, the QEPAS Allan deviation follows the trend, indicating that the main noise source is the thermal Johnson noise of the quartz tuning fork, up to two thousands seconds [35]. On the other hand, the noise of the PTS transducer deviates from the trend for integration times longer than 300 seconds, indicating the contribution of different noise sources. For both sensors, the MDL was estimated for 100 s integration time, leading to 6 ppb and 15 ppb for QEPAS and PTS sensors, respectively.
7. Conclusions
In this work, we developed a QCL-based sensor for trace gas detection of carbon monoxide, using two interchangeable modules for detection of the optical absorption. Pressure waves have been detected by means of a QEPAS spectrophone, composed by a custom quartz tuning fork with a resonance frequency of kHz and mR tubes having a length of 9.4 mm and an internal diameter of 1.41 mm. An MDL of 6 ppb was achieved with a lock-in integration time of 100 s and laser power of 40 mW. Thermal-induced effects were probed by measuring refractive index changes, using an interferometric technique based on a rugged Fabry-Perot interferometer. From the calibration curve, an MDL of 15 ppb was achieved with the same operative conditions used for the QEPAS module.
A comparison between the two detection modules showed that QEPAS is capable of reaching an MDL ∼2.5 times lower than the commercial optical system. On the other hand, the latter is less sensitive to optical misalignment. In both cases, a high compactness can be achieved by reducing the gas cell dimension down to transducer sizes. The QEPAS sensitivity can be further increased by working in humidified environment, since water vapor molecules can efficiently improve the CO vibrational − translational (V—T) relaxation processes within the gas mixture and by using a grooved-QTF as reported in [38], reaching a NNEA as low as .
Funding
D.P. acknowledges the financial support from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie project OPTAPHI, grant No. 860808. All authors acknowledge financial support received from the Austrian FFG under the scope of the research project MIRCAVS (Project No. 856914). The authors from Dipartimento Interateneo di Fisica di Bari acknowledge the financial support from THORLABS GmbH within the joint-research laboratory.
Declaration of Competing Interest
No conflict of interest
Biographies

Davide Pinto obtained his M.Sc. Degree (cum laude) in Materials Science and Technology in 2020 from the University of Bari. On the same year, he won a European Joint Doctorate inside the OPTAPHI Project (Horizon 2020) at the Vienna University of Technology (TUW) and Université de Montpellier (UM). His current research activity is focused on the development of trace gas sensors based on photoacoustic and photothermal spectroscopy and PTS detection for BTEX with long wavelength QCLs.

Harald Moser completed his studies in Technical Chemistry at the Graz University of Technology with a focus on process engineering. After his M.S. Degree, he completed his dissertation on the subject of industrial application of laser spectroscopy at the Vienna University of Technology (TUW). Within a Post Doc position, he currently supports leading companies in the field of petrochemistry, process sensor technology and paper / pulp production in the research and development of online measurement systems and process analysis.

Johannes P. Waclawek received his PhD degree in Technical sciences on the subject of laser based photoacoustic and photothermal trace gas sensing from the Vienna University of Technology, Austria, after he graduated in Physical Engineering and Chemistry. In his current Post-Doc position, he focuses on the development of compact laser based photothermal sensor platforms enabling highly sensitive as well as robust spectroscopic measurements for industrial, environmental and medical applications.

Stefano Dello Russo obtained his M.S. degree (cum laude) in Physics in 2018 from the University of Bari. From the same year, he is a PhD student at the Physics Department of the University of Bari, developing his research work at PolySense Lab, joint-research laboratory between Technical University of Bari and THORLABS GmbH. Currently, his research activities are focused on the development of custom tuning forks for Quartz-Enhanced Photoacoustic Spectroscopy and on the study of vibrational-translational dynamics of molecules in gaseous mixtures.

Pietro Patimisco obtained the Master degree in Physics (cum laude) in 2009 and the PhD Degree in Physics in 2013 from the University of Bari. Since 2018, he is Assistant professor at the Technical University of Bari. He was a visiting scientist in the Laser Science Group at Rice University in 2013 and 2014. Dr. Patimisco’s scientific activity addressed both micro-probe optical characterization of semiconductor optoelectronic devices and optoacoustic gas sensors. Recently, his research activities included the study and applications of trace-gas sensors, such as quartz-enhanced photoacoustic spectroscopy and cavity enhanced absorption spectroscopy in the mid infrared and terahertz spectral region, leading to several publications, including a cover paper in Applied Physics Letter of the July 2013 issue.

Vincenzo Spagnolo obtained the PhD in physics in 1994 from University of Bari. From 1997–1999, he was researcher of the National Institute of the Physics of Matter. Since 2004, he works at the Technical University of Bari, formerly as assistant and associate professor and, starting from 2018, as full Professor of Physics. Since 2019, he is vice-rector of the Technical University of Bari, deputy to technology transfer. He is the director of the joint-research lab PolySense between Technical University of Bari and THORLABS GmbH, fellow member of SPIE and senior member of OSA. His research interests include optoacoustic gas sensing and spectroscopic techniques for real-time monitoring. His research activity is documented by more than 220 publications and two filed patents. He has given more than 50 invited presentations at international conferences and workshops.

Prof. Dr. Bernhard Lendl received his PhD degree in Technical Chemistry from Technische Universität Wien (TUW) in 1996. In 2001 he became associate professor at TUW. In 2008 he founded the TUW spin-off company QuantaRed Technologies GmbH. Since 2011 he heads the research division on environmental and process analytical chemistry at TU Wien where he was also appointed full professor for Vibrational Spectroscopy in 2016. His research focuses on advancing analytical sciences through the development of novel analytical techniques and instrumentation based on infrared and Raman spectroscopy and their application to environmental and process analytical chemistry, material characterization as well as bio-medical diagnostics. His scientific work is documented in more than 270 papers published in international journals, 14 book chapters and several patents (11AT, 1DE, 3 EU, 4 US, 1JP, 1 RU). Lendl is recipient of the Anton Paar Research Award (2018), the Robert Kellner Lecture DAC (EuCheMS) in 2015, the FACSS Innovation Award in 2011 and the Dr. Wolfgang Houska Award (B&C foundation) in 2008.
References
- 1.Mattiuzzi C., Lippi G. Worldwide epidemiology of carbon monoxide poisoning. Hum. Exp. Toxicol. 2020;39:387–392. doi: 10.1177/0960327119891214. [DOI] [PubMed] [Google Scholar]
- 2.Lambrini K., Christos I., Petros O., Alexandros M. Dangerous gases and poisoning: a literature review. J. Healthc. Commun. 2018;03 doi: 10.4172/2472-1654.100136. [DOI] [Google Scholar]
- 3.Townsend C.L. Effects on health of prolonged exposure to low concentrations of carbon monoxide. Occup. Environ. Med. 2002;59:708–711. doi: 10.1136/oem.59.10.708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Raub J. World Health Organization; Geneva: 1999. International Programme on Chemical Safety, eds., Carbon Monoxide, 2. Ed. [Google Scholar]
- 5.Herriott D., Kogelnik H., Kompfner R. Off-axis paths in spherical mirror interferometers. Appl. Opt. 1964;3:523. doi: 10.1364/AO.3.000523. [DOI] [Google Scholar]
- 6.White J.U. Long optical paths of large aperture. J. Opt. Soc. Am. 1942;32:285. doi: 10.1364/JOSA.32.000285. [DOI] [Google Scholar]
- 7.Dong L., Lewicki R., Liu K., Buerki P.R., Weida M.J., Tittel F.K. Ultra-sensitive carbon monoxide detection by using EC-QCL based quartz-enhanced photoacoustic spectroscopy. Appl. Phys. B. 2012;107:275–283. doi: 10.1007/s00340-012-4949-1. [DOI] [Google Scholar]
- 8.Sampaolo A., Patimisco P., Giglio M., Chieco L., Scamarcio G., Tittel F.K., Spagnolo V. Highly sensitive gas leak detector based on a quartz-enhanced photoacoustic SF6 sensor. Opt. Express. 2016;24:15872–15881. doi: 10.1364/OE.24.015872. [DOI] [PubMed] [Google Scholar]
- 9.Sampaolo A., Csutak S., Patimisco P., Giglio M., Menduni G., Passaro V., Tittel F.K., Deffenbaugh M., Spagnolo V. Methane, ethane and propane detection using a compact quartz enhanced photoacoustic sensor and a single interband cascade laser. Sens. Actuators B Chem. 2019;282:952–960. doi: 10.1016/j.snb.2018.11.132. [DOI] [Google Scholar]
- 10.Spagnolo V., Patimisco P., Borri S., Scamarcio G., Bernacki B.E., Kriesel J. Part-per-trillion level SF_6 detection using a quartz enhanced photoacoustic spectroscopy-based sensor with single-mode fiber-coupled quantum cascade laser excitation. Opt. Lett. 2012;37:4461. doi: 10.1364/OL.37.004461. [DOI] [PubMed] [Google Scholar]
- 11.He Y., Ma Y., Tong Y., Yu X., Tittel F. HCN ppt-level detection based on a QEPAS sensor with amplified laser and a miniaturized 3D-printed photoacoustic detection channel. Opt. Express. 2018;26:9666. doi: 10.1364/OE.26.009666. [DOI] [PubMed] [Google Scholar]
- 12.Wilcken K., Kauppinen J. Optimization of a microphone for photoacoustic spectroscopy. Appl. Spectrosc. 2003;57:1087–1092. doi: 10.1366/00037020360695946. [DOI] [PubMed] [Google Scholar]
- 13.Tomberg T., Vainio M., Hieta T., Halonen L. Sub-parts-per-trillion level sensitivity in trace gas detection by cantilever-enhanced photo-acoustic spectroscopy. Sci. Rep. 2018;8:1848. doi: 10.1038/s41598-018-20087-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kuusela T., Kauppinen J. Photoacoustic gas analysis using interferometric cantilever microphone. Appl. Spectrosc. Rev. 2007;42:443–474. doi: 10.1080/00102200701421755. [DOI] [Google Scholar]
- 15.Bonilla-Manrique O.E., Posada-Roman J.E., Garcia-Souto J.A., Ruiz-Llata M. Sub-ppm-Level Ammonia detection using photoacoustic spectroscopy with an optical microphone based on a phase interferometer. Sensors. 2019;19:2890. doi: 10.3390/s19132890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bilaniuk N. Optical microphone transduction techniques. Appl. Acoust. 1997;50:35–63. doi: 10.1016/S0003-682X(96)00034-5. [DOI] [Google Scholar]
- 17.Davis C.C., Petuchowski S.J. Phase fluctuation optical heterodyne spectroscopy of gases. Appl. Opt. 1981;20:2539. doi: 10.1364/AO.20.002539. [DOI] [PubMed] [Google Scholar]
- 18.Davis C.C. Trace detection in gases using phase fluctuation optical heterodyne spectroscopy. Appl. Phys. Lett. 1980;36:515–518. doi: 10.1063/1.91590. [DOI] [Google Scholar]
- 19.Campillo A.J., Petuchowski S.J., Davis C.C., Lin H. Fabry–Perot photothermal trace detection. Appl. Phys. Lett. 1982;41:327–329. doi: 10.1063/1.93524. [DOI] [Google Scholar]
- 20.Waclawek J.P., Bauer V.C., Moser H., Lendl B. 2f-wavelength modulation Fabry-Perot photothermal interferometry. Opt. Express. 2016;24 doi: 10.1364/OE.24.028958. [DOI] [PubMed] [Google Scholar]
- 21.Waclawek J.P., Kristament C., Moser H., Lendl B. Balanced-detection interferometric cavity-assisted photothermal spectroscopy. Opt. Express. 2019;27 doi: 10.1364/OE.27.012183. [DOI] [PubMed] [Google Scholar]
- 22.Flygare W.H. Molecular relaxation. Acc. Chem. Res. 1968;1:121–127. doi: 10.1021/ar50004a004. [DOI] [Google Scholar]
- 23.Berne B.J., Pecora R. Wiley; New York, NY: 1976. Dynamic Light Scattering. [Google Scholar]
- 24.Bialkowski S.E. John Wiley & Sons; 1996. Photothermal Spectroscopy Methods for Chemical Analysis. [Google Scholar]
- 25.Sigrist M.W. Laser generation of acoustic waves in liquids and gases. J. Appl. Phys. 1986;60:R83–R122. doi: 10.1063/1.337089. [DOI] [Google Scholar]
- 26.Patimisco P., Sampaolo A., Giglio M., dello Russo S., Mackowiak V., Rossmadl H., Cable A., Tittel F.K., Spagnolo V. Tuning forks with optimized geometries for quartz-enhanced photoacoustic spectroscopy. Opt. Express. 2019;27:1401–1415. doi: 10.1364/OE.27.001401. [DOI] [PubMed] [Google Scholar]
- 27.Gordon I.E., Rothman L.S., Hill C., Kochanov R.V., Tan Y., Bernath P.F., Birk M., Boudon V., Campargue A., Chance K.V., Drouin B.J., Flaud J.-M., Gamache R.R., Hodges J.T., Jacquemart D., Perevalov V.I., Perrin A., Shine K.P., Smith M.-A.H., Tennyson J., Toon G.C., Tran H., Tyuterev V.G., Barbe A., Császár A.G., Devi V.M., Furtenbacher T., Harrison J.J., Hartmann J.-M., Jolly A., Johnson T.J., Karman T., Kleiner I., Kyuberis A.A., Loos J., Lyulin O.M., Massie S.T., Mikhailenko S.N., Moazzen-Ahmadi N., Müller H.S.P., Naumenko O.V., Nikitin A.V., Polyansky O.L., Rey M., Rotger M., Sharpe S.W., Sung K., Starikova E., Tashkun S.A., Auwera J.V., Wagner G., Wilzewski J., Wcisło P., Yu S., Zak E.J. The HITRAN2016 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2017;203:3–69. doi: 10.1016/j.jqsrt.2017.06.038. [DOI] [Google Scholar]
- 28.Patimisco P., Sampaolo A., Mackowiak V., Rossmadl H., Cable A., Tittel F.K., Spagnolo V. Loss mechanisms determining the quality factors in quartz tuning forks vibrating at the fundamental and first overtone modes. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2018;65:1951–1957. doi: 10.1109/TUFFC.2018.2853404. [DOI] [PubMed] [Google Scholar]
- 29.Patimisco P., Sampaolo A., Dong L., Tittel F.K., Spagnolo V. Recent advances in quartz enhanced photoacoustic sensing. Appl. Phys. Rev. 2018;5 doi: 10.1063/1.5013612. [DOI] [Google Scholar]
- 30.Ogawa N., Kaneko F. Open end correction for a flanged circular tube using the diffusion process. Eur. J. Phys. 2013;34:1159–1165. doi: 10.1088/0143-0807/34/5/1159. [DOI] [Google Scholar]
- 31.Dello Russo S., Giglio M., Sampaolo A., Patimisco P., Menduni G., Wu H., Dong L., Passaro V.M.N., Spagnolo V. Acoustic coupling between resonator tubes in quartz-enhanced photoacoustic spectrophones employing a large prong spacing tuning fork. Sensors. 2019;19:4109. doi: 10.3390/s19194109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hodgson N., Weber H. 2. ed. Springer; New York, NY: 2005. Laser Resonators and Beam Propagation: Fundamentals, Advanced Concepts and Applications. [Google Scholar]
- 33.Fischer B. Optical microphone hears ultrasound. Nat. Photonics. 2016;10:356–358. doi: 10.1038/nphoton.2016.95. [DOI] [Google Scholar]
- 34.Patimisco P., Sampaolo A., Bidaux Y., Bismuto A., Scott M., Jiang J., Muller A., Faist J., Tittel F.K., Spagnolo V. Purely wavelength- and amplitude-modulated quartz-enhanced photoacoustic spectroscopy. Opt. Express. 2016;24 doi: 10.1364/OE.24.025943. [DOI] [PubMed] [Google Scholar]
- 35.Giglio M., Patimisco P., Sampaolo A., Scamarcio G., Tittel F.K., Spagnolo V. Allan Deviation Plot as a tool for quartz-enhanced photoacoustic sensors noise analysis, IEEE trans. Ultrason. Ferroelectr. Freq. Control. 2016;63:555–560. doi: 10.1109/TUFFC.2015.2495013. [DOI] [PubMed] [Google Scholar]
- 36.Hopcroft M.A. 2020. allan, MATLAB Cent. File Exch.https://www.mathworks.com/matlabcentral/fileexchange/13246-allan [Google Scholar]
- 37.Werle P. Accuracy and precision of laser spectrometers for trace gas sensing in the presence of optical fringes and atmospheric turbulence. Appl. Phys. B. 2011;102:313–329. doi: 10.1007/s00340-010-4165-9. [DOI] [Google Scholar]
- 38.Li S., Dong L., Wu H., Sampaolo A., Patimisco P., Spagnolo V., Tittel F.K. Ppb-level quartz-enhanced photoacoustic detection of carbon monoxide exploiting a surface grooved tuning fork. Anal. Chem. 2019;91:5834–5840. doi: 10.1021/acs.analchem.9b00182. [DOI] [PubMed] [Google Scholar]