Integrating Three Characteristics of Executive Function in Non-Demented Aging: Trajectories, Classification, and Biomarker Predictors

Abstract

Objective

With longitudinal executive function (EF) data from the Victoria Longitudinal Study, we investigated three research goals pertaining to key characteristics of EF in non-demented aging: (a) examining variability in EF longitudinal trajectories, (b) establishing trajectory classes, and (c) identifying biomarker predictors discriminating these classes.

Method

We used a trajectory analyses sample (n = 781; M age = 71.42) for the first and second goals and a prediction analyses sample (n = 570; M age = 70.10) for the third goal. Eight neuropsychological EF measures were used as indicators of three EF dimensions: inhibition, updating, and shifting. Data-driven classification analyses were applied to the full trajectory distribution. Machine learning prediction analyses tested fifteen predictors from genetic, functional, lifestyle, mobility, and demographic risk domains.

Results

First, we observed: (a) significant variability in EF trajectories over a 40-year band of aging and (b) significantly variable patterns of EF decline. Second, a four-class EF trajectory model was observed, characterized with classes differentiated by an algorithm of level and slope information. Third, the highest group class was discriminated from lowest by several prediction factors: more education, more novel cognitive activity, lower pulse pressure, younger age, faster gait, lower body mass index, and better balance.

Conclusion

First, with longitudinal variability in EF aging, the data-driven approach showed that long-term trajectories can be differentiated into separable classes. Second, prediction analyses discriminated class membership by a combination of multiple biomarkers from demographic, lifestyle, functional, and mobility domains of risk for brain and cognitive aging decline.

Executive function (EF) refers to mental control processes, associated with neuroanatomical integrity of the brain, that monitor aspects of action and cognition in humans (Luszcz, 2011; Miyake & Friedman, 2012). Much empirical and theoretical work has examined EF performance and structure based on three dimensions: shifting (switching flexibly between tasks or mental sets), updating (monitoring and adding/deleting working memory representations), and inhibition (inhibit dominant or prepotent responses; Miyake et al., 2000; Miyake & Friedman, 2012). According to the de/differentiation theory, consolidation of EFs into a single dimension is likely to occur in aging. In general, EFs undergo changes across the lifespan from EF differentiation (multidimensional structure) in older children and young adults (Miyake et al., 2000; Wiebe & Karbach, 2017) to EF dedifferentiation (unidimensional structure) in non-demented and impaired aging (Adrover-Roig, Sesé, Barceló, & Palmer, 2012; de Frias, Dixon, & Strauss, 2006, 2009; Li, Vadaga, Bruce, & Lai, 2017). However, other studies have reported retention of EF differentiation in older adults (Hedden & Yoon, 2006; Hull et al., 2008; Kievit et al., 2014). For the current study, we conducted the analyses to test whether we would observe a unidimensional or multidimensional model of EF in non-demented aging.

In adulthood, these dimensions show a pattern described as “unity and diversity”—the dimensions are moderately correlated with one another, but are clearly separable and contribute differentially to overall EF performance (Friedman & Miyake, 2017). Evidence of the unity and diversity of EFs in older adults has been replicated in multiple studies (Fisk & Sharp, 2004; Hedden & Yoon, 2006; Hull, Martin, Beier, Lane, & Hamilton, 2008; Vaughan & Giovanello, 2010). The unity/diversity model (Friedman & Miyake, 2017) assumes that each EF process is controlled by multiple brain regions. The major clusters of EF abilities (i.e., switching, interference control, monitoring) can be performed at varying levels by cognitively normal individuals. However, across life, individualized accumulation of various risk and protective factors can lead to substantial individual differences in level and trajectories of performance. For instance, in the field of EF, research has demonstrated considerable variability of normative EF aging (e.g., de Frias et al., 2009; Goh et al., 2012; McFall et al., 2016; Sapkota et al., 2017). Organizing this variability according to both level and slope will enhance our understanding of the range of normal of EF aging, but also lead to the early detection of individuals or classes who may be at elevated risk for exacerbated or impaired cognitive decline.

In the course of recent EF research, multiple predictors have been linked to decline and, occasionally, stable patterns of aging (Anstey, Cherbuin, Budge, & Young, 2011; Bento-Torres et al., 2017; Erickson, Leckie, & Weinstein, 2014; Roberts & Mapel, 2012; Sapkota, Vergote, Westaway, Jhamandas, & Dixon, 2015; Sternäng et al., 2015; Thibeau, McFall, Camicioli, & Dixon, 2017; Watson et al., 2010; Wisdom, Callahan, & Hawkins, 2011; Zaninotto, Batty, Allerhand, & Deary, 2018). Examining multiple factors simultaneously that may differ depending on the characteristics of individualized trajectory patterns can lead to novel insights about the risk-elevating and protective-enhancing factors that most contribute to differential EF change. In addition, some novel clinical implications may be noted. For instance, the identification of operative factors can lead to precision strategies for promoting healthier EF by targeting factors that reduce risk and enhance protection (McFall et al., 2019).

A methodological limitation of previous studies is the use of single measures or average composite scores. Latent variables provide an alternative and enhanced estimation of a construct. The use of structural equation modeling of latent variables, comprised of multiple indicators, account for unreliability within the construct and provide an accurate estimation of the relationships in conditional growth models (Little, 2013). Furthermore, this approach provides a way to conduct factor analysis and test the dimensionality of EFs, reducing error and the risk that single measures influence the estimate of EF. Our methods also improve on previous research by incorporating latent class growth analyses (LCGA) and random forest analysis (RFA). The advantage of LCGA is that it identifies subgroups of individuals with similar patterns of change over time on a latent variable (see Andruff, Carraro, Thompson, Gaudreau, & Louvet, 2009). Each individual has a unique developmental course; however, the distribution of individual differences is specified by a finite set of polynomial functions corresponding to a discrete trajectory. This is a data-driven technique that uses level and slope algorithms in order to estimate trajectory classes and account for the magnitude and direction of change. The advantage of RFA is that predictors from multiple domains (previously studied independently or in small combinations) can be examined simultaneously in a competitive computational context in order to identify those that best discriminate EF class membership.

The purpose of the present study was to examine trajectories and predictors of EF performance (level) and longitudinal change (slope) in a cognitively normal aging group. Accordingly, three research goals guided this study. The first goal was to examine the distribution of individualized trajectories of EF performance over a 40-year band of aging. We expected to find significant variability in EF performance (level) and rate (slope) of decline (McFall et al., 2014). The second goal was to apply data-driven LCGA to the trajectory distribution in order to establish objectively separable classes of EF change trajectories. With the LCGA approach, we expected to objectively separate neighboring (but statistically distinguishable) classes of EF trajectories based on an algorithm including individualized level and slope values. The third goal was to identify the biomarker risk predictors from genetic, functional, lifestyle, mobility, and demographic domains that best discriminated these classes. By using the random forest approach, we expected factors from multiple domains to predict trajectory class membership (as has been observed with memory; McFall, McDermott, & Dixon, 2019; Sapkota et al., 2018).

Method

Participants

Characteristics

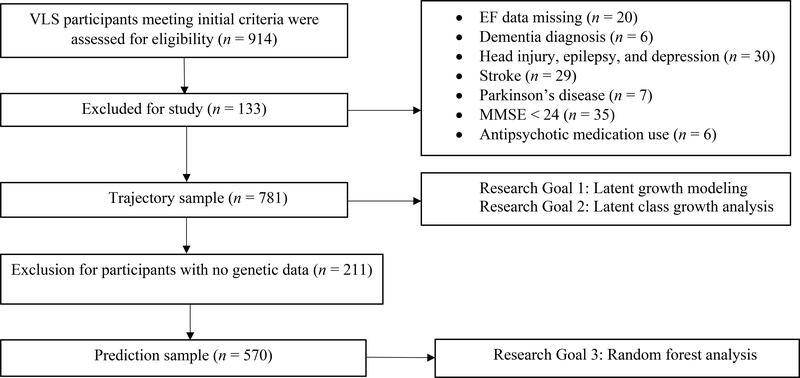
Participants were volunteer community-dwelling adults from the Victoria Longitudinal Study (VLS). The VLS is an ongoing large-scale, multi-cohort, longitudinal sequential study of cognitive, neuropsychological, genetic, metabolic, biomedical, and lifestyle aspects of human aging (Dixon & de Frias, 2004). Participants were originally recruited by using advertisements through the public media and requests from community groups. All participants provided written informed consent and were offered nominal fees for their participation. Data collection procedures were in full and certified compliance with the University of Alberta Human Research Ethics Board. Using standard procedures (i.e., Dixon, Small, MacDonald, & McArdle, 2012; McFall et al., 2014), we assembled and merged corresponding three-wave VLS samples collected in the same era (2000 – 2016). All participants started at wave 1 (W1); no new participants were recruited at wave 2 (W2) or wave 3 (W3). As part of the VLS design, each cohort sample is comprised of adults (initially aged 55–85 years, 98% Caucasian), and re-tested at approximately 4-year intervals. Accordingly, the initial source sample included 914 persons (baseline M age = 71.91, SD = 9.18, range = 53.24 – 100.16, 66.2% female, M years of education = 15.09). Multiple exclusionary criteria were applied at baseline. Participants were excluded if they had (a) EF data missing from all three waves (n = 20), (b) a diagnosis of mild to very serious Alzheimer’s disease or other forms of impairment and dementia (n = 6), (c) history of very serious head injury, epilepsy, and depression (n = 30), (d) moderately-to-very serious stroke (n = 29), (e) moderately-to-severe Parkinson’s disease (n = 7), (f) Mini-Mental Status Examination (MMSE) score less than 24 (n = 35), and (g) anti-psychotic medication use (n = 6). All participants remained non-demented for the duration of the study. We established a trajectory sample comprised of 781 participants (baseline M age = 71.42, SD = 9.07, range = 53.24 – 95.25, 66.6% female; see Table 1). The mean longitudinal intervals (in years) were as follows: W1-W2 M = 4.4 (SD = .58), W2-W3 M = 4.6 (SD = .76), and W1-W3 M = 9.1 (SD = .84). The wave-to-wave retention rates were as follows: (a) W1-W2 = 69% and (b) W2-W3 = 75%. For the subset of participants who contributed genetic data during collection occurring from 2009 – 2011, we established a prediction sample comprised of 570 participants (baseline M age = 70.10, SD = 8.50, range = 53.24 – 95.25, 66.5% female; see Table 2). We used the trajectory sample for the first and second research goals and the prediction sample for the third goal. For a consort diagram, see Figure 1.

Table 1.

Descriptive Statistics for the Trajectory Sample by Longitudinal Wave

	W1	W2	W3
n	778	541	407
Age	71.42 (9.07; 53.24 – 95.25)	74.94 (8.70; 57.27 – 94.53)	78.12 (8.19; 62.44 – 97.26)
Gender (% Female)	66.6	66.0	67.6
HAY	5.43 (1.50; 1 – 10)	5.43 (1.48; 1 – 9)	5.50 (1.40; 1 – 10)
STRPb	1.28 (.75; −.73 – 6.14)	1.39 (1.10; .03 – 10.53)	1.36 (.90; −.02 – 7.52)
Color trails b	98.01 (33.87; 46.67 – 266.22)	101.56 (38.62; 43.77 – 331.99)	110.24 (46.10; 53.01 – 345.27)
Brixton	4.72 (2.18; 1 – 10)	5.32(2.01; 1 – 10)	5.35 (2.04; 1 – 10)
LSER	11.33 (4.44; 0 – 20)	11.19 (4.38; 0 – 20)	10.97(4.29; 0 – 20)
LSET	8.36(2.89; 0 – 18)	8.34 (2.95; 0 – 14)	8.26 (3.00; 0 – 14)
CSPAN	3.05 (1.27; 0 – 7)	2.97(1.27; 0 – 7)	2.88 (1.15; 0 – 7)
RSPAN	2.88(1.02; 0 – 6)	2.74 (.99; 0 – 5)	2.63 (1.03; 0 – 5)

Note. Results presented as Mean (Standard Deviation) and Range unless otherwise stated. HAY = Hayling; STRP = Stroop; LSER = Letter Series; LSET = Letter Sets; CSPAN = Computational Span; RSPAN = Reading Span; W1 = Wave 1; W2 = Wave 2; W3 = Wave 3

^bLower scores indicate better performance

Table 2.

Baseline Descriptive Statistics for the Prediction Sample

	W1
n	570
Age	70.10 (8.50; 53.24 – 95.25)
Gender (% Female)	66.5
Education (Years)	15.32 (2.96; 5 – 24)
BDNF (% Met+)	34.9
IDE (% G−)	13.3
APOE (% ɛ4+)	23.0
COMT (% Val+)	77.4
Pulse Pressure	52.06(10.30; 32.13 – 99.25)
Body Mass Index	26.91 (4.17; 14.95 – 48.61)
Gait	6.33 (1.64; 3.38 – 20.66)
Balance	2.78 (1.01; .78 – 11.65)
Peak Expiratory Flow	426.02 (119.06; 0 – 770)
Grip Strength	29.63 (9.44; 12.25 – 59.25)
Everyday Physical Activity	15.95 (5.15; 0 – 31)
Everyday Novel Cognitive Activity	75.81 (16.78; 20 – 130)

Note. Results presented as Mean (Standard Deviation; Range) unless otherwise stated; W1 = Wave 1; BDNF = Brain Derived Neurotrophic Factor; IDE = Insulin Degrading Enzyme; APOE = Apolipoprotein E; COMT = Catechol-O-Methyl Transferase; Met+ = risk allele combinations; G− = risk allele combination; ɛ4+ = risk allele combinations. Val+ = risk allele combinations.

Figure 1.

Consort diagram. Participants from the VLS were first assessed for three initial criteria [age = 53–95; members of longitudinal sample (2002-forward); neuropsychological battery]. The trajectory sample served Research Goals 1 and 2. The prediction sample served Research Goal 3.

Executive function measures

For the first and second research goals, eight standard neuropsychological measures were used as indicators of three common dimensions of EF: two each for inhibition (Hayling, Stroop) and updating (Computational Span, Reading Span) and four for shifting (Brixton, Color Trails, Letter Series, Letter Sets). These measures have been tested in multiple studies and their psychometric properties have been reported in both clinical and healthy populations (i.e., Bielak, Mansueti, Strauss, & Dixon, 2006; de Frias & Dixon, 2014; McFall et al., 2013, 2014; Sapkota et al., 2015; Quereshi & Seitz, 1993). See Supplementary Material for descriptions of all EF measures.

Fifteen biomarker risk factor predictors

For the third research goal, a total of 15 biomarker risk factor predictors were used to discriminate classes of EF trajectories. Baseline (W1) predictors were selected from multiple domains: genetic [apolipoprotein E (APOE), brain-derived neurotrophic factor (BDNF), insulin degrading enzyme (IDE), catechol-O-methyltransferase (COMT)], functional [pulse pressure (PP), body mass index (BMI), peak expiratory flow, grip strength], lifestyle (everyday physical activity, everyday novel cognitive activity), mobility (balance, gait), and demographic (age, education, sex). We note that some of the predictors were from demographic and lifestyle domains and are not typically considered biomarkers. However, our assumption is that their observed influence on brain and cognitive aging changes operate indirectly through biological mechanisms. Therefore, as we use it, the term biomarker reflects this assumption. See Supplementary Material for more information about each predictor, including DNA extraction and genotyping.

Statistical Analyses

We used Mplus 7 (Muthén & Muthén, 2010) and data from the trajectory sample for preliminary analyses and the first and second research goals. We used R 3.3.2 (R Development Core Team, 2015) and data from the prediction sample for the third goal. The statistical analyses are summarized below; details are provided in the Supplementary Material.

Two sets of preliminary statistical analyses were performed. Using confirmatory factor analysis (CFA) and eight EF indicators, we established the best fitting EF latent variable by testing one-, two-, and three-factor models. The second analysis involved testing the measurement invariance of the EF latent variable model across three waves. In subsequent growth models, we used continuous age (centered at age 75 years) as the metric of longitudinal change. This was done in order to give the initial time point a meaningful occasion of measurement. By doing so, we were able to interpret baseline differences as performance level at age 75 (midpoint of the age range).

Research Goal 1: Examining Variability in EF Longitudinal Trajectories

Latent growth modeling was used to establish an EF latent growth. Following previous protocols and guidelines (Little, 2013; McFall et al., 2014; Thibeau et al., 2017), we established the best fitting model by testing (a) fixed intercept model (no interindividual or intraindividual variability in EF level), (b) random intercept model (interindividual but no intraindividual variability in EF level), (c) random intercept fixed slope model (interindividual variability in EF level but no interindividual variability in change), and (d) random intercept random slope model (interindividual variability in both EF level and change).

Research Goal 2: Establishing Latent Classes of EF Trajectories

LCGA was used to analyze individualized EF latent variable trajectory data. For each class model tested, we used a random intercept, random slope growth model fully constrained (intercept and slope constrained to be equal) within each class to determine group differences (Jung & Wickrama, 2008). Specifically, the variance of the intercept and the slope were fixed to zero within classes. In contrast, the variances were allowed to vary across classes. Since there is no within class variability, there are fewer parameters to estimate and there is no covariance between the intercept and slope (Berlin, Parra, Williams, 2013).

In order to compare class models based on their relative fit, we used recommended fit indices: AIC, BIC, − 2LL, and entropy. Following earlier methodological developments (Andruff et al., 2009; Jung & Wickrama, 2008; Ram and Grimm, 2009) and previous longitudinal aging analyses comparing classes (McDermott et al., 2017; McFall et al., 2019; Han et al., 2013), we identified the best model with a combination of five considerations: (a) lowest AIC, BIC, and −2LL (absolute value), (b) high entropy value (>.80), and (c) classes with substantial (>10%) membership numbers. Regarding the latter characteristic, the 10% criterion was expected to yield about 100 participants to accommodate further statistical analyses. We used class membership in subsequent prediction analyses.

Research Goal 3: Biomarker Risk Predictors Discriminating Classes of EF Trajectories

RFA (Kuhn & Johnson, 2013) was used to determine the most important predictors discriminating classes of EF trajectories. RFA determines a ranking of predictors in terms of importance, as identified by the algorithm in a competitive computational context. Notably, RFA produces a conservative estimate of its predictive ability (out-of-bag error rate) and copes with large number of predictor variables, restricting the number of variables used in each ntree, which can show important predictors that could have been overshadowed by a stronger competitor (Strobl, Malley, & Tutz, 2009). We used the “Party” package for variable importance and missForest for missing data imputation. For the party package, we specifically used the permutation accuracy importance or mean decrease in accuracy to assess relative level of importance with the cforest function (Hothorn, Bühlmann, Dudoit, Molinaro, & van der Laan, 2006). For the missforest package, the algorithm works as a nonparametric imputation method, fitting a random forest on the observed data and then predicting the missing data for each variable (Stekhoven, 2011). The prediction sample had the following missing data characteristics: M percentage = 1.2% (range = 0.4% – 4%). Model strength was assessed as the area under the receiver operation characteristic curve (C- statistic), with values closer to 1 indicating better model strength (see Hajian-Tilaki, 2013). The number of ntrees used was 5000, sufficient for good model stability, and mtry was set at 4 ($\sqrt{\#ofpredictors}$), for an optimal number of predictors at each potential split (Genuer, Poggi, & Tuleau-Malot, 2010).

Results

The one-factor EF model fit the longitudinal data well, χ² (219, N = 781) = 360.644, p <.001, RMSEA = .029, CFI = .978, SRMR = .039 (Table 3). This model was selected over the two-factor [χ² (225, N = 781) = 874.380, p <.001, RMSEA = .061, CFI = .897, SRMR = .159] and three-factor [χ² (210, N = 781) = 770.907, p <.001, RMSEA = .058, CFI = .911, SRMR = .160] models because it represented the best fitting model for this aging sample. Therefore, we used the one-factor model in subsequent analyses. Table 4 shows the standardized coefficients for each factor loading on the one-factor model. In SEM, these parameter estimates are equivalent to standardized measures of effect size based on the covariance matrix (Kelley & Preacher, 2012). We then conducted measurement invariance testing (Table 3). Based on criteria to evaluate model fit and selection (Chen, 2007; Rutkowski and Svetina, 2014), the results supported metric invariance. Model fit criteria were not met for scalar invariance and thus we proceeded to test a model with partial scalar invariance. A partial scalar model with intercepts constrained to be equal across time for Hayling and Stroop resulted in the optimal model and showed good fit indices, χ² (237, N = 781) = 464.543, p <.001, RMSEA = .035, CFI = .964, SRMR = .066. Overall, these results indicated two important points about the EF model: (a) it measured the same construct at each wave and (b) the same indicator variables marked EF at each wave. Partial scalar results allowed comparison of latent variable means.

Table 3.

Goodness of Fit Indices for Executive Function Confirmatory Factor Analysis One-Factor Model and Measurement Invariance Testing

Model	χ2	df	p	RMSEA	CFI	SRMR
One-factor EF (Wl)	23.708	18	.165	.020 (.000–.040)	.995	.020
One-factor EF (W2)	30.044	18	.037	.035 (.009–.057)	.987	.025
One-factor EF (W3)	23.532	18	.171	.027 (.000–.055)	.992	.030
One-factor EF	360.644	219	<.001	.029 (.023–.034)	.978	.039
(W1.W2.W3)
Metric	422.058	233	<.001	.032 (.027–.037)	.970	.056
Scalar	793.263	249	<.001	.053 (.049–.057)	.914	.091
Partial Scalara	464.543	237	<.001	.035 (.030–.040)	.964	.066

Note. RMSEA = Root Mean Square Error of Approximation; CFI = Comparative Fit Index; SRMR = Standardized Root Mean Square Residual; Change from configural to metric: Δχ² = 61.414, Δdf = 14, p <.001, ΔRMSEA = .003, ΔCFI = .008, ΔSRMR = .017); Change from metric to scalar: Δχ² = 371.205, Δdf = 16, p <.001, ΔRMSEA = .021, ΔCFI = .056, ΔSRMR = .035; Change with partial scalar model: Δχ² = 42.485, Δdf =4, p <.001, ΔRMSEA = .003, ΔCFI = .006, ΔSRMR = .01. EF = Executive Function; W1 = Wave 1; W2 = Wave 2; W3 = Wave 3

^aPreferred model.

Table 4.

Standardized Coefficients for Factor Loadings on the One-Factor Model

Indicator	W1	W2	W3
HAY	.36 (.03)	.40 (.03)	.60 (.03)
	[.29 – .42)	[.32 – .47]	[.52 – .67]
STRP	.42 (.03)	.44 (.03)	.51 (.04)
	[.36 – .48]	[.37 – .51]	[.43 – .59]
Color trails	.64 (.02)	.72 (.02)	.71 (.02)
	[.60 – .69]	[.67 – .76]	[.65 – .75]
Brixton	.44 (.03)	.38 (.04)	.43 (.05)
	[.37 – .50]	[.30 – .46]	[.33 – .53]
LSER	.80 (.01)	.84 (.01)	.89 (.01)
	[.77 – .84]	[.81 – .87]	[.86 – .92]
LSET	.71 (.02)	.77 (.02)	.84 (.02)
	[.66 – .75]	[.73 – .81]	[.79 – .88]
CSPAN	.58 (.02)	.64 (.02)	.71 (.03)
	[.53 – .63]	[.58 – .69]	[.64 – .77]
RSPAN	.59 (.02)	.67 (.02)	.69 (.03)
	[.54 – .64]	[.62 – .72]	[.62 – .74]

Note. Results presented as Beta Coefficients (Standard Error) and [ 95% Confidence Intervals]. HAY = Hayling; STRP = Stroop; LSER = Letter Series; LSET = Letter Sets; CSPAN = Computational Span; RSPAN = Reading Span; W1 = Wave 1; W2 = Wave 2; W3 = Wave 3.

Research Goal 1: Examining Variability in EF Longitudinal Trajectories

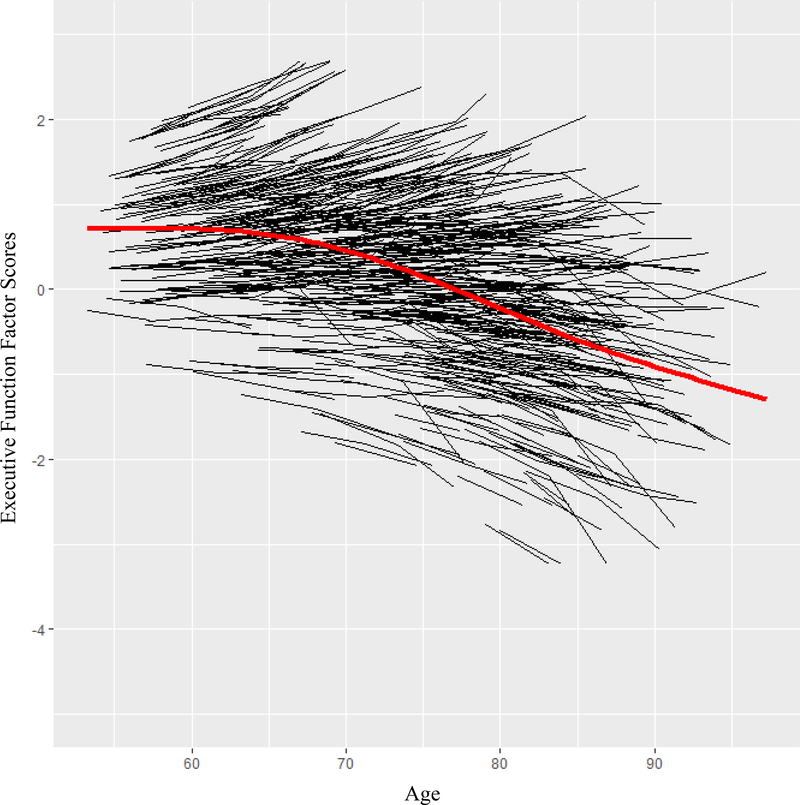
The best-fitting unconditional growth model was established as a random intercept, random slope (unstructured covariance; see Table 5 for model goodness of fit indexes). The model indicated significant (a) variability in EF performance at age 75 (b = 1.084, p < .001), (b) EF decline with greater age (M = −.003, p = .02); and (c) variable patterns of decline across individuals (b = .001, p < .001). Figure 2 shows the individualized trajectories and the group-level mean growth curve for overall EF change.

Table 5.

Absolute Fit Indices for Executive Function Latent Growth Models

Model	−2LL	AIC	BIC	D	Δdf
Fixed intercept	2472.391	4952.782	4971.424	−	−
Random intercept	933.360	1876.719	1900.022	1539.0	1*
Random intercept	918.817	1849.634	1877.597	14.5	1*
fixed slope
Random intercept	364.757	745.514	782.798	554.0	2*
random slope a

Note. −2LL = −2 log likelihood; AIC = Akaike information criterion; BIC = Bayesian information criterion; D = deviance statistic; df = degrees of freedom

^aPreferred model.

^*p<.001

Figure 2.

Executive function trajectory distribution. The black lines show the individualized trajectories and the red line show the group-level mean of individualized trajectories based on factor scores from latent growth model. Significant variability was found in (a) level of EF at the centering age (b = 1.084, p < .001) and (b) rate of decline for EF (b= .001, p < .001). Individuals declined in EF with greater age (M = −.003, p = .02).

Research Goal 2: Establishing Latent Classes of EF Trajectories

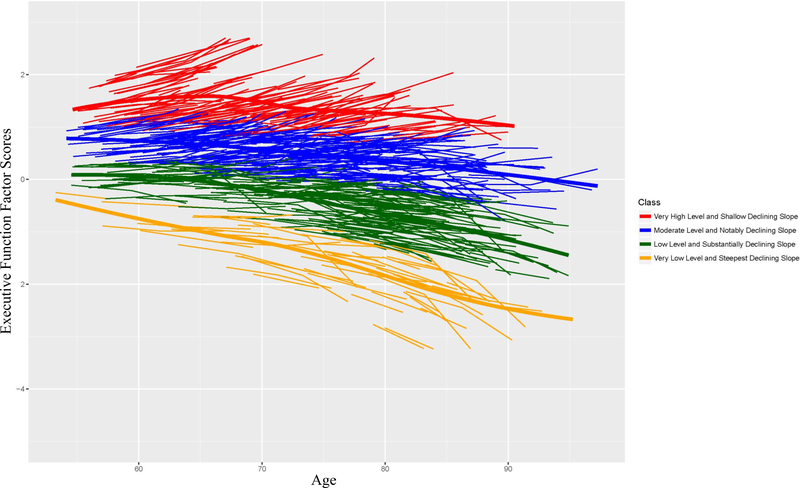
With a combined consideration of intercept and slope, the LCGA results identified a four-class model as the best-fitting solution (Table 6). The model had a very good entropy value (0.83) and each class had more than 10% of the sample. The specific characteristics of each class were as follows: (a) very high level (intercept) and shallow declining slope (n = 119 [15.2%; M age = 66.25 (7.40)], intercept = 1.286 [SE =.025; 95% CI: 1.237 – 1.336], slope = −.014 [SE =.003; 95% CI: −.019 – −.009]); (b) moderate level and notably declining slope (n = 278 [35.5%; M age = 69.84 (8.27)], intercept = .420 [SE =.015; 95% CI: .391 – .449], slope = −.020 [SE =.002; 95% CI: −.024 – −.016]); (c) low level (i.e., factor scores below 0) and substantially declining slope (n = 290 [37.1%; M age = 73.69 (8.99)], intercept = −.464 [SE =.015; 95% CI: −.493 – −.435], slope = −.042 [SE =.002; 95% CI: −.046 – −.038]; and (d) very low level and steepest declining slope (n = 94 [12.0%; M age = 75.65 (9.48)], intercept = −1.543 [SE =.021; 95% CI: −1.583 – −1.503], slope = −.059 [SE =.003; 95% CI: −.064 – −.054]). Figure 3 shows the trajectory distribution of each class. Five- and six-class models resulted in a class with proportion <10% and therefore were not considered further. The highest performing class (class a) was represented as highest-level-and-stable and the lowest (class d) as lowest-level-and-declining. Arguably, these two trajectory classes would represent the most separation of dynamic EF performance patterns and produce the strongest and most interpretable results. In addition, this approach would permit us to discover the risk biomarkers most predictive of each of these extreme secondary phenotypes.

Table 6.

Fit Indices and Entropy for Estimated Latent Class Growth Models

Model	Los Likelihood	AIC	BIC	Entropy
One-class	−2213.383	4436.767	4460.070	−
Two-class	−1859.812	3735.624	3772.908	.733
Three-class	−1614.991	3251.981	3303.248	.821
Four-class a	−1458.333	2944.666	3009.914	.834
Five-class	−1297.685	2629.369	2708.599	.863
Six-class	−1297.685	2635.369	2728.581	.877

Note. AIC = Akaike information criterion; BIC = Bayesian information criterion

^aPreferred model.

Figure 3.

Classification of executive function based on the four-class model. The data-driven approach characterized four classes based on level and slope information. Color coded lines represent individualized performance. Thick lines represent mean class change.

Research Goal 3: Biomarker Risk Predictors Discriminating Classes of EF Trajectories

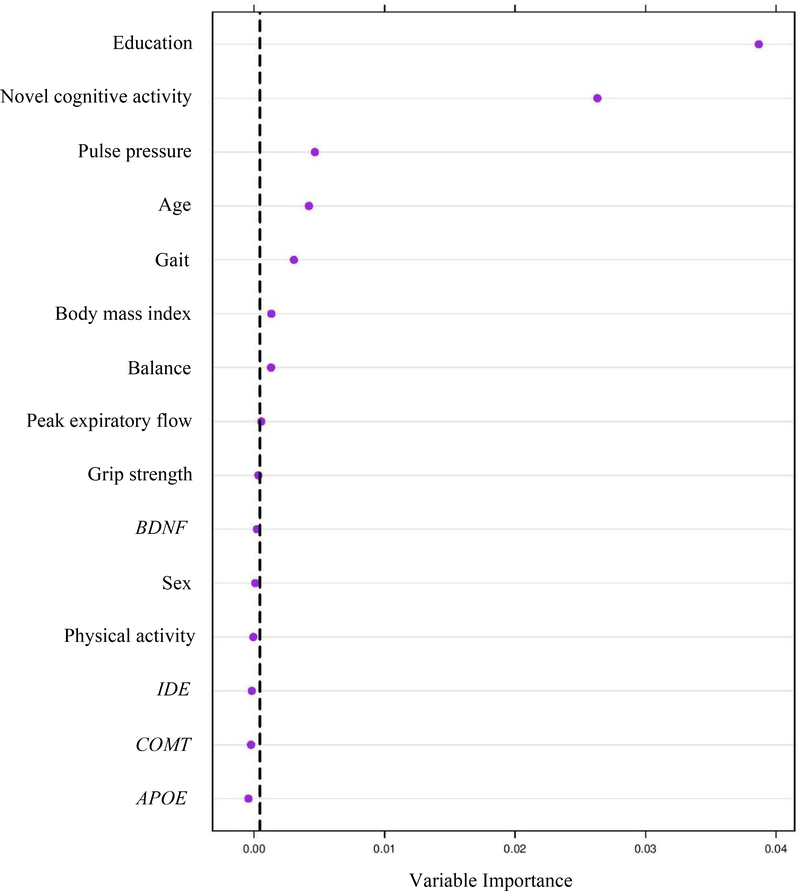
The relative predictive importance of 15 risk and protective markers was first computed for these trajectory classes: highest-level-and-stable and lowest-level-and-declining. Seven predictors represented demographic (education, age), lifestyle (everyday novel cognitive activity), functional (PP, BMI), and mobility (gait, balance) domains (C = 0.84; 95% CI [.77 – .91]). Figure 4 shows the predictors in order of importance, those to the right of the vertical line having the best permutation accuracy importance. We found membership in the highest-level-and-stable class was predicted by more education, more novel cognitive activity, lower PP, younger age, faster gait, lower BMI, and better balance.

Figure 4.

Relative importance of predictors discriminating highest-level-and-stable versus lowest-level-and-declining classes of executive function trajectories. Variable importance was calculated based on the mean decrease in accuracy, which quantifies the importance of a variable by measuring prediction changes in accuracy.

To further examine predictive patterns, we computed parallel analyses for the two neighboring classes: moderate level and notably declining (class b) and low level and substantially declining (class c). RFA results showed five important predictors representing lifestyle (novel cognitive activity, physical activity), demographic (education, age), and mobility (gait) domains (C = 0.63; 95% CI [.58 – .68]). Membership in class b was predicted, in order of importance, by more novel cognitive activity, more education, younger age, more physical activity, and faster gait.

To include the whole sample for prediction analysis, we merged neighboring and phenotypically similar classes from the four-class model based on level and slope information: top two classes (class a and class b) and bottom two classes (class c and class d). RFA results did not differ substantially. Specifically, four predictors discriminated these classes and represented demographic (education, age), genetic (BDNF), and lifestyle (novel cognitive activity) domains (C = 0.70; 95% CI [.66 – .74]).]). Membership in the top two classes was predicted, in order of importance, by more education, BDNF Met- (non-risk), more novel cognitive activity, and younger age. See Table 1 of the Supplementary Material for more follow-up analyses.

Discussion

We investigated three research goals relating to key characteristics of EF in non-demented aging: (a) examining variability in EF longitudinal trajectories, (b) establishing trajectory classes, and (c) biomarker risk predictors discriminating classes of EF trajectories. We included a trajectory sample for the first and second goals and a prediction sample for the third goal. Our results showed that the best fit was provided by the one-factor model. This provides support for the theory (Adrover-Roig et al., 2012;Miyake et al., 2000; Wiebe & Karbach, 2017; de Frias et al., 2009) that, with normal lifespan development and aging, EF abilities that emerge in earlier life (older children and younger adults) as multidimensional (typically two or three factors) become less differentiated in older adulthood, as indicated by a unidimensional (one-factor) structure. We note, however, that although our data provide strong support for this theory in the last 40 years of the lifespan, they do not speak directly to the early adulthood and midlife periods.

For our first research goal (examining variability in EF longitudinal trajectories), we demonstrated significant individual variability in level and slope of EF performance (Figure 2). This means that although there was significant longitudinal decline with increasing age, older adults showed variable patterns in EF level and change. In other words, the change-related variability and the general trajectory of decline demonstrate substantial variability in the aging of EF over a 40-year period. Because we have represented a broader construct of EF (in our latent variable), we can characterize the variability in level and slope of non-demented EF aging with more confidence (than we could have with a single measure). As can be seen in Figure 2, EF aging included notable individualized and distribution-wide variability in both level and change. This carries both theoretical and clinical interest, as it underscores the importance of examining not just mean level between-subject differences (or within-group changes) but also within-person level and variability within a distribution of trajectories and across subgroups (or classes) of trajectories. In accordance with the unity/diversity model and other studies (Friedman & Miyake, 2017; Goh, An, & Resnick, 2012; Lin, Wang, Wu, Rebok, & Chapman, 2017), these results demonstrate that the longitudinal cognitive aging of EFs is not characterized by a uniform but rather heterogeneous process. The observed individual variability in level and slope of EF allowed us to explore our next research goal: establishing classes of EF trajectories.

For the second research goal (establishing latent classes of EF trajectories), the full-sample distribution of individualized EF trajectories empirically discriminated four classes of aging. These classes were distinguished by both level and slope information for each individual and characterized by (a) very high level and shallow declining slope, (b) moderate level and notably declining slope, (c) low level and substantially declining slope, and (d) very low level and steepest declining slope. We characterized the highest class as highest-level-and-stable and the lowest class as lowest-level-and-declining. From a data-driven perspective, the results of this analysis established that the broad distribution of EF trajectories could be objectively classified into four discriminable classes. Conceptually, these patterns may represent different types of aging individuals. For instance, the upper (higher) classes may be more suggestive of “typical” non-demented aging. In contrast, the profiles of the lower two classes, where there is more EF decline, may represent a signal emerging from neurodegenerative pathology that is likely to transition into a form of mild cognitive impairment. Each of the trajectory classes is quantitatively differentiated from the others. Accordingly, they vary (as classes) in both level and slope. Because we used these two components in the classification algorithm, it is possible to see (from Figure 3) that some individual trajectories associated with one class may appear to overlap with some of the trajectories in a neighboring class. This phenomenon is a product of the simultaneous consideration of more than one criterion component and emphasizes the dynamic and variable nature of actual EF trajectories over a 40-year band of aging. Of both theoretical and clinical interest is the determination of the specific factors that are associated with this variability and change. Specifically, it is useful to know that aging individuals’ EF change patterns may be affected in particular by other attributes (e.g., lifestyle, functional, mobility) that interact to produce specific trajectories that may lead toward or away from impairment. This approach and these results could advance our ability to identify and use early and more personalized clinical interventions for a non-demented aging population. Some of these risk predictors may be modifiable and could therefore serve as immediate targets for risk reduction or protection enhancement (see also McFall et al., 2019).

For the third research goal (biomarker risk predictors discriminating classes of EF trajectories), we first conducted RFA on the highest-level-and-stable versus lowest-level-and-declining classes. We observed that a substantial number of factors predicted the former from the latter class. Specifically, the predictors were, in order of importance: more education, more novel cognitive activity, lower PP, younger age, faster gait, lower BMI, and better balance. Second, for the two neighboring classes (moderate level and notably declining slope and low level and substantially declining slope) membership in the former class was predicted by more novel cognitive activity, more education, younger age, more physical activity, and gait. Third, for the top two classes (class a and class b) and bottom two classes (class c and class d) membership in the top two classes was predicted by more education, BDNF Met- (non-risk), more novel cognitive activity, and younger age. Why might these cognitive aging and dementia risk factors discriminate these patterns of EF aging?

Research has suggested that there may be some delay in cognitive impairment when there is greater cognitive brain reserve capacity (Stern, 2003). Therefore, education may be a factor that helps maintain cognitive reserve capacity and protect against age-related detrimental changes in the brain. Recent research has also found that early childhood education may promote developmental changes that are essential to protect against cognitive decline in late-life (Zahodne et al., 2015). Common affected age-related functions in EF include inhibition, shifting, updating, abstraction, mental flexibility, and concept formation (Bielak et al., 2006; Bopp & Verhaeghen, 2005; Harada et al., 2013; Wasylyshyn, Verhaeghen, & Sliwinski, 2011). The mechanism behind this impairment may be related to age-related cortical thinning and volumetric loss, in regions such as the prefrontal cortex, which disrupt the response of cognitive activity in the brain (Li et al., 2017; Yuan & Raz, 2014).

Engagement in cognitive activity has been shown to protect against cognitive impairment leading to dementia by enhancing cognitive reserve or plasticity (i.e., Blasko et al., 2014; Lachman, Agrigoroaei, Murphy, & Tun, 2010; Mitchell et al., 2012; Runge, Small, McFall, & Dixon, 2014; Valenzuela & Sachdev, 2009; Wang, Karp, Winblad, & Fratiglioni, 2002; Wilson, Scherr, Schneider, Tang, & Bennett, 2007). Cognitive reserve may work to improve cerebral blood flow, stimulate neurogenesis, and potentiate synaptic strength (Barulli & Stern, 2013; Blasko et al., 2014; Esiri & Chance, 2012; Whalley, Deary, Appleton, & Starr, 2004). Increases in brain volume in response to cognitive training may be due to increased neural activity and the ability of the brain to develop neural scaffolding (Park & Bischof, 2013).

PP is commonly used as a proxy for arterial stiffness (systolic minus diastolic blood pressure). Lower values of PP, which indicate better vascular health, may be beneficial for EF by preventing mini-infarcts or cerebrovascular vascular damage and reducing pathophysiology related to neurodegenerative processes (Nation et al., 2013; Warsch & Wright, 2010). Elevated BMI poses a risk for impaired insulin regulation, systemic inflammation, and pathophysiological changes in vascular health (i.e., Anstey et al., 2011; Taki et al., 2008). Therefore, it may be beneficial for EF to maintain lower BMI levels as opposed to higher in this age group. Research has shown that worse PP (i.e., 72 mmHG; McFall et al., 2014) and BMI > 25 (Gunstad et al., 2007) produces poorer EF performance and greater EF decline in non-demented aging adults.

Studies have hypothesized that cognitive decline affects mobility, especially when there is impairment in EF (i.e., Ble et al., 2005). Evidence suggests that this occurs because numerous EF components are needed when particular mobility tasks are performed in everyday environments. For instance, response inhibition is needed to allow an individual to focus on gait when walking in an environment with numerous distractors (Mirelman et al., 2012). EF deficits also contribute to poor locomotion and difficulties performing a turn (i.e., Kearney et al., 2013). Therefore, mobility markers may be important for overall EF performance and change in non-demented aging.

The BDNF polymorphism was the only genetic marker that contributed substantial importance to the RFA models. BNDF is a molecule present in the prefrontal cortex and helps modulate brain plasticity (Komulainen et al., 2008). Furthermore, it supports the health and functioning of glutamatergic neurons, which are major projection neurons that connect cognitive brain regions. Research indicates that BDNF concentration declines in adulthood (Cotman & Engesser-Cesar, 2002; Erickson et al., 2010). However, secretion of BDNF is higher in Val homozygotes than in Met carriers, which places the Met homozygotes at greater risk of selective cognitive deficits (Nagel et al., 2008; Sapkota et al., 2015). Substitution of Val to Met may result in disruption of neuronal trafficking and processing (Egan et al., 2003; Liu et al., 2014). As such, BDNF has been shown to interact with other brain aging genetic risk factors in affecting EF performance (Sapkota & Dixon, 2018).

Overall, RFA showed that multiple predictors discriminated data-driven classes of EF trajectories. That these predictors emerged in the competitive context of other previously observed EF predictors in aging is novel information. Conceptually, this means that in non-demented aging sustained levels of EF performance into late life are supported by relative unique risk-reducing or protective factors. Among previously identified predictors of EF performance and change, our results suggest that some are more influential than others. That these operative factors for secondary phenotypes are representative of multiple domains of influence emphasize the important theoretical point that EF change in normal aging is broadly and multiply-determined. Moreover, the RFA produced a rank ordering of the significant predictors, a result that will be useful for further clinical research. We infer that the substantial number and variety of predictors discriminating the distinct upper and lower classes is reasonable because the distinct patterns of level and slope represented in these classes are at the extremes of non-demented EF aging. We note that age is among the important factors discriminating these classes. However, it is not the only predictive factor nor is it the most important one according to the permutation importance. The implication of the RFA results involve identification of a set of factors influencing EF aging as well as promising targets for promoting healthy EF aging. Such interventions may be more powerful in that they target an empirically determined subset of the roster of previously identified predictors. In addition, they imply the potential benefit of precision multi-modal interventions that include representatives of several domains (i.e., demographic, lifestyle, mobility, functional). Notably, our results indicated that sex was not an important predictor, thus implying that these targets may not vary for males and females.

There are several limitations associated with this study. First, by design the participants were relatively healthy, predominantly Caucasian (98% white, non-Hispanic), and non-demented. As a group, they may not represent the broader population of aging adults. Conceivably, prediction patterns could vary across a broader range of aging adults, including impaired and diverse groups. Nonetheless, our sample reflects a portion of older adults in western or developed countries where there is rapid older population growth. Second, although the comparison classes are similar in age range, some age imbalance was observed in that the lower-class members were more likely to be in the oldest decade and had a higher mean age. This could have influenced the significant results of some aging-related predictors. However, age was not the leading, or sole, predictor in the RFA models, indicating age was not driving the effect. Third, our trajectory analyses were based on a distribution spread across a 40-year band of aging, but each individualized trajectory included a maximum of three time points. Several factors may limit generalizability of the four-class model, including (a) longer (or shorter) time frames, (b) alternative algorithms, and (c) more (or fewer) time points per participant. Fourth, although the classes were identified based on trajectory differences, the predictors were taken from baseline performance. The predictive importance of a predictor may vary if tested at different time points. Therefore, testing time-varying predictors may yield interesting results. However, this reflects a different research question and a different approach to the analyses. Specifically, the goal of the alternative approach would be interesting but would be aimed at predicting actual performance changes and whether they are coupled with predictor changes. In this study, our aim was to examine prediction of EF change classes as rendered across multiple waves of data. Fifth, some risk factors were available in the VLS data set (i.e., smoking, alcohol) but were not used here due to low frequency or non-normality issues. In addition, other factors that could be related to overall cognitive function (including EF) such as fish consumption or cholesterol level were not available in the VLS battery. Future research should implement RFA models with additional predictors in order to assess their impact on EF level, structure, and change in aging.

Among strengths, we first note the use of a relatively large, well-characterized sample. This was important in order to (a) capture the substantial variability we found in the EF level and change data and (b) provide multiple domains of predictors relevant to EF aging. Second, using age as the metric of change in the growth models allowed us to examine EF trajectories over a 40-year band of aging. This accelerated longitudinal approach was essential because it enabled us to cover a wide age range of interest in a shorter period of time, which would not be possible with a single cohort longitudinal design (Galbraith, Bowden, & Mander, 2017). Third, we established classes based on individualized level and slope information with a large distribution of EF trajectories. Precise trajectory information is a contributing factor to objective group classification that offers advantages to single-wave or single-measure classification systems. Fourth, we used machine learning (RFA) for our prediction analyses. This relatively novel approach has great performance and prediction accuracy (i.e., Couronné, Probst, & Boulesteix, 2018; McFall et al., 2019; Sapkota & Dixon, 2018), which enabled us to obtain a precise order of predictors according to their importance on EF trajectory data.

In sum, in our first two sets of analyses we found (a) significant variability in EF level and slope and (b) dynamic variability differences leading to four data-driven trajectory classes. Using RFA, we identified multiple predictors that discriminated between the trajectories. These results emphasize that distributions of individualized trajectories can be analyzed with data-driven technologies to reveal underlying latent classes of EF aging change. In addition, such classes, when properly validated, may serve as secondary phenotypes representing detectably different patterns of asymptomatic cognitive aging. That there were multiple predictors of both higher and lower EF change classes shows that among previously associated predictors, only selected predictors emerge in this analytic context. A clinical implication of these results is that the promotion of healthier EF can be potentially influenced by targeting factors that selectively reduce risk and factors that enhance protection. These factors differ depending on the precise characteristics of the individual’s trajectory patterns. Finally, from a research methods perspective, this research illustrates the potential contributions of a dynamic and data-driven approach to EF performance and change. Although mean level between-subject differences are useful for identifying single candidate predictors, research designs and analytic strategies that incorporate within-subject level and change variability, as well as multiple predictors, can lead to novel outcomes.