Cumulative dietary risk assessment of chronic acetylcholinesterase inhibition by residues of pesticides

Abstract

A retrospective cumulative risk assessment of dietary exposure to pesticide residues was conducted for chronic inhibition of acetylcholinesterase. The pesticides considered in this assessment were identified and characterised in a previous scientific report on the establishment of cumulative assessment groups of pesticides for their effects on the nervous system. The exposure assessments used monitoring data collected by Member States under their official pesticide monitoring programmes in 2016, 2017 and 2018, and individual food consumption data from 10 populations of consumers from different countries and from different age groups. Exposure estimates were obtained by means of a two‐dimensional probabilistic model, which was implemented in SAS ^® software. The characterisation of cumulative risk was supported by an uncertainty analysis based on expert knowledge elicitation. For each of the 10 populations, it is concluded with varying degrees of certainty that cumulative exposure to pesticides contributing to the chronic inhibition of acetylcholinesterase does not exceed the threshold for regulatory consideration established by risk managers.

Summary

A retrospective cumulative risk assessment (CRA) of dietary exposure to pesticide residues in 2016, 2017 and 2018 was conducted for chronic erythrocyte acetylcholinesterase (AChE) inhibition.

The first step of the process was to establish a cumulative assessment group (CAG) of pesticides causing this effect. This was reported in an EFSA scientific report on the establishment of CAGs for their effects on the nervous system published in 2019. More than 400 active substances were considered for inclusion in a CAG for brain and/or erythrocyte AChE inhibition. In total, 47 active substances were included, of which 11 are N‐methyl carbamate (NMC) insecticides and 36 are organophosphorus (OP) pesticides. All active substances were characterised by no observed adverse effect levels (NOAELs) for short‐ and long‐term cumulative exposure/risk assessment, derived from the most sensitive indicator, using all available information across studies, species and sexes. Sources of uncertainty associated with the methods used to collect and assess toxicological data and resulting from the limitations in the available data and scientific knowledge were identified for appropriate consideration during the CRA.

In a second step, cumulative exposure calculations were performed using monitoring data collected by Member States under their official monitoring programmes in 2016, 2017 and 2018 and individual food consumption data from 10 populations of consumers from different European countries and from different age groups. Regarding the selection of relevant food commodities, the assessment included water, foods for infants and young children and 35 raw primary commodities of plant origin that are widely consumed within Europe.

Exposure estimates were obtained with SAS^® software using a two‐dimensional probabilistic method, which is composed of an inner loop execution and an outer loop execution. Variability within the population was modelled through the inner loop execution and was expressed as a percentile of the exposure distribution. The outer loop execution was used to derive 95% confidence intervals around those percentiles (reflecting the sampling uncertainty of the input data). The SAS programme had been validated beforehand against the Monte Carlo Risk Assessment (MCRA) software, version 8.3.

As agreed by risk managers in the Standing Committee on Plants, Animals, Food and Feed (SC PAFF), calculations were carried out according to a tiered approach. While the first‐tier calculations (Tier I) use very conservative assumptions for an efficient screening of the exposure with low risk for underestimation, the second‐tier assessment (Tier II) includes assumptions that are more refined but still intended to be conservative. For each scenario, exposure estimates were obtained for different percentiles of the exposure distribution and the total margin of exposure (MOET, the ratio of the toxicological reference dose to the estimated exposure) was calculated at each percentile. In accordance with the threshold agreed at the SC PAFF, further regulatory consideration would be required when the MOET calculated at the 99.9th percentile of the exposure distribution is below 100.

According to the Tier II scenario, median estimates of the MOET at the 50th percentile of the exposure distribution were all well above 100. From the 95th percentile, MOET estimates below 100 were observed for two out of the 10 population groups and at the 99.9th percentile, estimates were below 100 for eight of the 10 population groups. The lowest MOETs were estimated for the populations of Italian adults and French children. In all populations, the high exposure estimates were predominantly driven by a few substance‐commodity combinations (occurrence of omethoate and dimethoate in olives for oil production, pirimiphos‐methyl in wheat, chlorpyrifos in oranges, and, to a lesser extent, worst‐case assumptions regarding the occurrence of monocrotophos and dichlorvos in drinking water).

As indicated above, the exposure calculations were conducted with conservative assumptions likely to overestimate the exposure, even in the more refined Tier II scenario. To assess the impact of the assumptions, several sensitivity analyses were conducted. These showed that assuming, when processing factors are missing, that all residues in the raw primary commodity reach the end consumer without any loss in the processed commodities contributed the most to the conservatism of the calculations.

The third and last step of the assessment was the cumulative risk characterisation. This was based on the outcome of the first two steps and included an uncertainty analysis, performed following the guidance of the EFSA Scientific Committee in order to take account of the limitations in scientific knowledge and data and of the assumptions used in all steps of the assessment. Thirty‐five sources of uncertainty affecting the input data, model assumptions and the assessment methodology were identified by a Working Group of six toxicologists and six exposure experts. The impact of the uncertainties was assessed in a sequential approach using expert knowledge elicitation (EKE) techniques and 1‐D Monte Carlo simulations. First, the impact of each source of uncertainty on the MOETs at the 99.9th percentile of exposure was quantified for the Italian adult population, which was selected as reference population as it showed the lowest estimated MOET. This showed that uncertainties had variable effects, with some tending to overestimate the MOET (e.g. in some cases, the metabolites were not considered in the assessment) and others tending to underestimate it (e.g. limited availability of processing factors). The combined impact of the sources of uncertainties was subsequently quantified for the Italian adult population. Finally, dependencies between sources of uncertainty and differences between populations were assessed.

As a result of this process, the MOETs at the 99.9th percentile and their confidence intervals, as derived from the cumulative exposure calculations, were adjusted to take account of the overall impact of uncertainties and the probability for the MOET at the 99.9th percentile of the exposure distribution being below 100 was assessed for all 10 populations.

Taking account of all uncertainties identified by the experts, for chronic inhibition of erythrocyte AChE, it was concluded that, with varying degrees of certainty, cumulative exposure does not exceed the threshold for regulatory consideration for any of the population groups considered. This certainty exceeds 90% for two adult populations and 85% for the other adult populations and is in the range from 67% to 90% for two child and two toddler populations, from 60% to 90% for Danish toddlers and from 50% to 90% for French children.

It was not possible to address the relevance and contribution of oxidative stress by substances other than OPs and NMCs as a cause of inactivation of AChE in this assessment. Recommendations of reducing the impact of identified uncertainties in this CRA are provided in the end of this report.

1. Introduction

Cumulative risk assessment (CRA) has been defined as the analysis, characterisation and possible quantification of the combined risks to health or the environment from multiple agents or stressors (US Environmental Protection Agency, 2003). It differs from most assessments which consider the effects of one agent or stressor in isolation.

In order to comply with provisions of Regulation (EC) No 396/2005 on Maximum Residue Levels (MRLs) of pesticides in or on food and feed regarding cumulative and synergistic effects of pesticides, EFSA and the Panel on plant protection products and their residues (PPR panel) started in 2007 the development of the necessary methodologies to carry out CRA of pesticide residues. This methodological development included a tiered approach for the assessment of cumulative risks of pesticides residues (EFSA PPR Panel, 2008), a guidance on the use of probabilistic methodology for modelling dietary exposure to pesticide residues (EFSA PPR Panel, 2012) and a procedure to establish cumulative assessment groups (CAGs) of pesticides on the basis of their toxicological profile (EFSA PPR Panel, 2013a).

In April 2020, EFSA completed a pilot project and issued the first two reports on retrospective cumulative risk assessments of dietary exposure to pesticide residues (EFSA, 2020a,b). These reports concerned two acute effects on the nervous system and two chronic effects on the thyroid gland.

1.1. Background and Terms of Reference

The Pesticides Residues unit is requested by EFSA to prepare a scientific report on the CRA of chronic acetylcholinesterase (AChE) inhibition by residues of pesticides. The legal background of this request is the article 32 of Regulation (EC) No 396/2005, which provides that EFSA draws up annual reports on pesticide residues taking account of the results of official control of pesticide residues in food commodities carried out by Member States and including an analysis of the risks to the health of consumers. The present report is therefore delivering a retrospective assessment of chronic cumulative risks resulting from the actual exposure to acetylcholinesterase inhibitors.

The precise assessment question addressed by the present report is defined as follows: What was the chronic cumulative risk of erythrocyte AChE inhibition for European consumers resulting from dietary exposure to pesticide residues from 2016 to 2018?

The central nervous system (CNS) as well as the peripheral nervous system (PNS) are well‐known targets of the effects from AChE inhibition, e.g. by pesticide classes such as organophosphates (OPs) and N‐methyl carbamates (NMCs). In particular, AChE inhibition by OPs or NMCs could result in rapid accumulation of acetylcholine (ACh), consequently triggering an overstimulation of nicotinic and muscarinic ACh receptors of autonomic organs and skeletal muscles in the PNS and cholinergic receptors of the CNS (Thompson and Richardson, 2003).

However, the assessment question for this CRA focusses on the AChE inhibition in erythrocytes (rather than in the brain) in order to provide a conservative assessment of neurotoxic effects of AChE inhibitors for the consumers. Measurement of erythrocyte AChE activity is considered as a suitable surrogate of the effects on AChE in neural tissues for several reasons. Inhibition of AChE is generally more sensitive in erythrocytes than in brain (about one order of magnitude), because, toxicokinetically, AChE inhibitors would first be absorbed into the blood before being circulated to the other target organs, e.g. CNS and PNS. Furthermore, the blood‐brain barrier can restrict the entry of chemicals from the blood into the CNS. Last, but not least, there are generally more data from experimental animal (as well as human) studies on AChE inhibition in erythrocytes than in CNS and PNS (US‐EPA 2000).

Non‐dietary routes of exposure to pesticides and chemicals other than residues of pesticides are not considered in the assessment.

The present assessment is unrelated to developmental neurotoxicity (DNT). When CAGs were established for the effects of pesticides on the nervous system, DNT was not considered because, at that time, data were lacking in regulatory dossiers (EFSA, 2019a). It is known, however, that, compared to adults, infants (as well as children) have less mature metabolic pathways and are still undergoing critical periods of neurodevelopment (EFSA Scientific Committee, 2017a). Exposure to pesticides during early life might result in longer retention of chemicals in the body and, subsequently, higher risk of developing diseases occurring later in life (WHO and EEA, 2002). In particular, one study in children reported that lower AChE activity in erythrocytes was associated with certain neurodevelopmental deficits (e.g. in attention, inhibition and memory) in boys but not in girls (Suarez‐Lopez et al., 2013). A CRA regarding DNT risk would require the establishment of a dedicated CAG and the characterisation of substances included in such CAG specifically for DNT.

1.2. Input from risk managers and threshold for regulatory consideration

During the Standing Committee on Plants, Animals, Food and Feed of 11–12 June 2015 (European Commission, 2015), Member States agreed on the use of the combined margin of exposure (MOET, also known as Total Margin of Exposure) concept as the mode of calculation and expression of cumulative risks.

Furthermore, during the Standing Committee on Plants, Animals, Food and Feed of 18–19 September 2018 (European Commission, 2018), Member States agreed on an MOET of 100 at 99.9th percentile of exposure at whole population level as the threshold for regulatory consideration and as an indicative target of safety by analogy to the safety margin currently used for establishing toxicological reference values (a factor 10 for inter‐species variability and a factor of 10 for intra‐species variability).

The uniform principles for evaluation and authorisation of plant protection products further specify that in interpreting the results of evaluations, Member States shall take into consideration possible elements of uncertainty in order to ensure that the chances of failing to detect adverse effects or of underestimating their importance are reduced to a minimum. In addition, Article 1 of Regulation (EC) No 1107/2009 states that Member States shall not be prevented from applying the precautionary principle where there is scientific uncertainty. Estimates of cumulative risk are necessarily subject to a degree of scientific uncertainty, due to limitations in the data and to assumptions used to address those limitations. In this context, the Standing Committee on Plants, Animals, Food and Feed stated that the MOET of 100 at 99.9th percentile of exposure would be acceptable provided that the assumptions are sufficiently conservative (European Commission, 2018). This assessment therefore includes a rigorous analysis of the assumptions and uncertainties involved, leading to a quantitative assessment of the degree of certainty that the MOET at the 99.9th percentile of exposure is above 100. This provides a measure of the degree to which the assumptions in the assessment are conservative.

2. Data and methodologies

2.1. Cumulative assessment groups (CAGs)

In 2019, EFSA established cumulative assessment groups (CAGs) of pesticides for five effects on the nervous system: brain and/or erythrocyte acetylcholinesterase inhibition, functional alterations of the motor, sensory and autonomic divisions and histological neuropathological changes in neural tissue (e.g. axonal degeneration and demyelination) (EFSA, 2019a). A CAG was established for each of the five specific effects and 422 active substances were screened for potential inclusion in these CAGs.

As a rule, an active substance is included in a CAG if it has a known mode of action capable to induce directly the specific effect or if at least one of the indicators of the effect was observed at a statistically significant and/or biologically relevant level in at least one toxicological study with this active substance and the study was assessed as ‘acceptable’ in the Draft Assessment Report (DAR), Renewal Assessment Report (RAR) or equivalent document, unless:

• This observation was age‐related or occurred at or above the maximum tolerated dose, or,

• Consideration of the dose–response relationship showed that the observation was not treatment‐related.

In the specific case of the CAGs for brain and/or erythrocyte AChE inhibition (CAG‐NCN),1 all active substances from the chemical classes of NMCs and OPs were systematically included considering the relationship of the chemical structure and the mechanism of action. In total, 47 active substances were included in the CAG for brain and/or erythrocyte AChE inhibition, of which 11 were NMCs and 36 OPs.

All these substances were characterised by no observed adverse effect levels (NOAELs) in view of short‐ and long‐term cumulative risk assessment, derived from the most sensitive indicator (either brain or erythrocyte AChE inhibition), using all available information across studies, species and sexes. The toxicological characterisation for long‐term cumulative risk assessment is reported in Table 1. Brain and/or erythrocyte AChE inhibition was considered adverse when it reached a statistically significant (p < 0.05) decrease of 20% or more compared to concurrent control groups. Data collection spreadsheets elaborated by EFSA's contractors (RIVM, ICPS, ANSES, 2013, 2016) were used to the purpose of the toxicological characterisation. Only studies assessed as ‘acceptable’ in the final DAR or RAR were considered. Where appropriate, in case two or more studies of similar design within the same species were available, they were combined to derive the NOAEL based on the whole information. In one case (thiodicarb), no NOAEL could be set, and a default NOAEL was determined from the LOAEL by applying an additional uncertainty factor (UF) of 10 by default, rather than based on a case assessment as recommended by the guidance of EFSA on default values to be used in the absence of measured data (EFSA Scientific Committee, 2012). Human studies reported in the spreadsheets were never used for the establishment of CAGs, as the provisions of Commission Regulation (EU) No 283/2013 authorising their use (scientific validity, ethical generation and leading to lower regulatory limit values compared to animal studies) were never met.

Table 1.

CAG on brain and/or erythrocyte AChE inhibition toxicological characterisation of the active substances for chronic risk assessment

Active substance	Indicator of specific effect	NO(A)EL mg/kg bw	LO(A)EL mg/kg bw	Study (as referenced in the source)	Source
Acephate	AChE inhibition (brain, erythrocytes)	0.25	2.5	2‐year rat (■■■■■, 1981) Administration via diet	JMPR 2002
Aldicarb	AChE inhibition (erythrocytes)	0.05	0.1	Acute neurotoxicity rat (■■■■■, 1994b) Administration via gavage	DAR 1996
Azinphos‐ethyl	AChE inhibition (erythrocyte)	0.0125	0.025	90‐day dog (■■■■■, 1963) Administration via diet	JMPR 1973
Azinphos‐methyl	AChE inhibition (erythrocytes)	0.16	0.74	1‐year dog (■■■■■, 1990) Administration via diet	DAR 1996, Addendum 6, 2000 (neurotox)
Benfuracarb	AChE inhibition (erythrocytes)	1.81	9.4	28‐day neurotoxicity rat (■■■■■, 2003) Administration via diet	DAR 2004
Cadusafos	AChE inhibition (erythrocytes)	0.045	0.22	2‐year rat (■■■■■, 1986) Administration via diet	DAR 2004
Carbaryl	AChE inhibition (brain, erythrocytes)	1	10	90‐day neurotoxicity rat (■■■■■, 1990) Administration via gavage	DAR 2004
Carbofuran	AChE inhibition (brain)	0.015	0.03	Acute neurotoxicity rat (■■■■■, 2007c) Administration via gavage	Revised DAR 2008
Carbosulfan	AChE inhibition (brain, erythrocytes)	0.5	5	Acute neurotoxicity rat (■■■■■, 1996, 1982b) Administration via gavage	Revised DAR 2009
Chlorfenvinphos	AChE inhibition (brain, erythrocytes)	0.15	15	2‐year rat (author not reported, JMPR 1994) Administration via diet	JMPR 1994
Chlorpyrifos	AChE inhibition (erythrocytes)	0.1	1	2‐year rat (■■■■■, 1988) Administration via diet	Addenda to the original Assessment Report 2013
Chlorpyrifos‐methyl	AChE inhibition (brain, erythrocytes)	1	50	2‐year rat (■■■■■ 1991) Administration via diet	DAR 1997 EC review report 2005
Diazinon	AChE inhibition (brain, erythrocytes)	0.02	5.6	90‐day dog (■■■■■, 1988) Administration via diet	EFSA conclusion 2006
Dichlorvos	AChE inhibition (erythrocytes)	0.008	0.08	2‐year dog (■■■■■, 1967)	DAR 2003
Dimethoate	AChE inhibition (brain, erythrocytes)	0.1	0.2	2‐year rat (■■■■■, 1986) Administration via diet	DAR 2004
Ethephon	AChE inhibition (erythrocytes)	6	14	28‐day cholinesterase inhibition study in dogs (■■■■■, 2006) Administration via diet	DAR 2004
Ethion	AChE inhibition (brain)	0.06	0.71	90‐day dog (■■■■■, 1988) Administration via diet	JMPR 1990
Ethoprophos	AChE inhibition (brain)	0.04	2.4	2‐year rat (■■■■■, 1992a/b) Administration via diet	DAR 2004
Fenamiphos	AChE inhibition (brain, erythrocytes)	0.083	0.35	1‐year dog (■■■■■, 1991) Administration via diet	DAR 2003
Fenitrothion	AChE inhibition (brain, erythrocytes)	0.5	1.5	2‐year rat (■■■■■, 1974) Administration via diet	DAR 2003
Fenthion	AChE inhibition (erythrocytes)	0.05	0.23	1‐year dog (■■■■■, 1990 Administration via diet	DAR 1996
Fonofos	AChE inhibition (erythrocytes)	0.2	1	1‐year dog (■■■■■, 1995) Administration via capsule	EPA 1999
Formetanate	AChE inhibition (erythrocytes)	0.37	1.75	1‐year dog (■■■■■, 1986) Administration via diet	DAR 2004 EFSA 2006
Fosthiazate	AChE inhibition (brain)	0.42	2.36	2‐year rat (■■■■■, 1990)	DAR 1998 EC review report 2003
Malathion	AChE inhibition (erythrocyte)	17	35	2‐year rat (■■■■■, 1996a) and 2‐year rat (■■■■■, 1980) combined Administration via diet	DAR 2003
Methamidophos	AChE inhibition (brain, erythrocytes)	0.1	0.22	2‐year rat (■■■■■, 1984b) Administration via diet	DAR 2000 EC review report 2006
Methidathion	AChE inhibition (brain, erythrocytes)	0.16	0.8	2‐year rat (■■■■■, 1986) Administration via diet	JMPR 1992
Methiocarb	AChE inhibition (erythrocytes)	1.32	6.46	90‐day dog (■■■■■, 2000) Administration via diet	DAR 2004
Methomyl	AChE inhibition (brain, erythrocytes)	0.25	0.5	Acute neurotoxicity rat (■■■■■, 1998a) Administration via gavage	DAR 2004
Monocrotophos	AChE inhibition (brain, erythrocytes)	0.005	0.05	2‐year rat (■■■■■, 1983) Administration via diet	JMPR 1991
Omethoate	AChE inhibition (erythrocytes)	0.027	0.04	2‐year rat (■■■■■, 1995); supplementary 32‐week rat (■■■■■, 1994)	DAR 2004 (dimethoate)
Oxamyl	AChE inhibition (brain, erythrocytes)	0.1	0.75	Acute neurotoxicity rat (■■■■■, 1997) Administration via gavage	DAR 2003
Oxydemeton‐methyl	AChE inhibition (brain, erythrocytes)	0.027	0.224	2‐year rat (■■■■■, 1984) Administration via diet	DAR 2004
Parathion	AChE inhibition (brain)	0.25	2.5	2‐year rat (■■■■■, 1984) Administration via diet	JMPR 1995
Parathion‐methyl	AChE inhibition (erythrocytes)	0.25	2.5	2‐year rat (■■■■■, 1983) Administration via diet	DAR 2001
Phenthoate	AChE inhibition (erythrocytes)	0.29	0.87	2‐year dog (■■■■■, 1972) Administration via diet	JMPR 1980
Phosalone	AChE inhibition (erythrocytes)	0.17	0.9	1‐year dog (■■■■■, 1992) Administration via diet	DAR 2004
Phosmet	AChE inhibition (brain)	1.1	1.8	2‐year rat (■■■■■, 1991) Administration via diet	DAR 2004
Phoxim	AChE inhibition (erythrocytes)	0.1	0.38	2‐year dog (■■■■■, 1977) Administration via diet	JECFA 1999
Pirimicarb	AChE inhibition (brain, erythrocytes)	10	25	1‐year dog (■■■■■, 1998) Administration via capsule	DAR 2003
Pirimiphos‐methyl	AChE inhibition (brain)	0.4	2.1	2‐year rat (■■■■■, 1974) Administration via diet	DAR 2003
Profenofos	AChE inhibition (erythrocytes)	0.017	0.56	2‐year rat (■■■■■, 1981a) Administration via diet	JMPR 2007
Pyrazophos	AChE inhibition (erythrocytes)	0.05	0.125	2‐year dog (■■■■■, 1976) Administration via diet	JMPR 1992
Thiodicarb	AChE inhibition (brain, erythrocytes)	0.5a	5	Acute neurotoxicity rat (■■■■■, 2000d) Administration via gavage	DAR 2003
Tolclofos‐methyl	AChE inhibition (brain, erythrocytes)	6.9	34	2‐year mouse (■■■■■, 1983) Administration via diet	DAR 2003
Triazophos	AChE inhibition (erythrocytes)	0.012	0.13	1‐year dog (■■■■■, 1989) Administration via diet	JMPR 2002
Trichlorfon	AChE inhibition (brain)	4.5	13.3	2‐year rat (■■■■■, 1989) Administration via diet	DAR 2004

^aNOAEL derived from the LOAEL with an UF of 10.

EFSA conclusions on the pesticide risk assessment in the context of Regulation (EC) No 1107/2009 finalised until end 2018 and dealing with active substances included in the CAG were considered to retrieve any element of expert judgement and to ensure consistency of the NOAELs set for AChE inhibition with the acceptable daily intake (ADI) and acute reference dose (ARfD) of the active substances. For active substances not reviewed by EFSA, the scientific evaluations conducted by the body constituting the main source of the data collection were also considered (e.g. JMPR evaluations).

2.2. Cumulative exposure assessments using SAS^® software

2.2.1. General principles

Cumulative exposure to pesticide residues was assessed in accordance with the guidance on probabilistic modelling of dietary exposure to pesticide residues (EFSA PPR Panel, 2012) and in analogy to the pilot phase (EFSA, 2019b). Exposure estimates were obtained using a two‐dimensional method where variability was modelled by means of an inner loop execution and uncertainty was modelled through an outer loop execution (see Figure 1).

Figure 1.

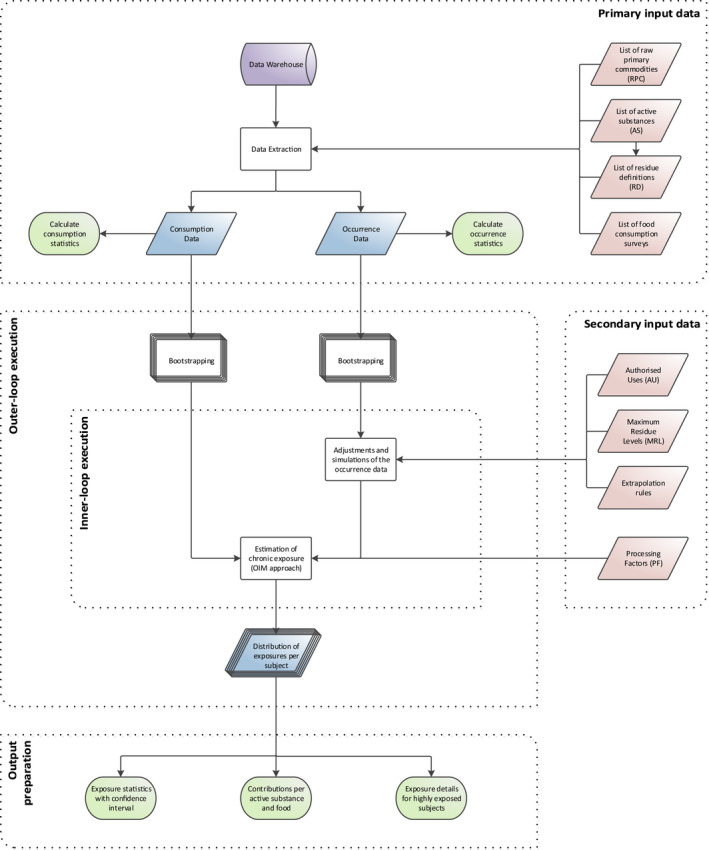
General process for calculating chronic cumulative exposure to pesticides

To start this two‐dimensional simulation, occurrence data (i.e. the amounts of pesticide residue that are reported to be present in/on foods) and food consumption data (i.e. the types and amounts of those food consumed in a person's diet) are used as primary input data. Whenever exposure calculations start, the occurrence and food consumption data for the relevant food commodities, active substances and dietary surveys, are extracted. These data are taken from the data stored in EFSA Data Warehouse.

Within the inner loop execution, occurrence data are subject to several simulations and imputations. These adjustments are intended to account for inaccuracies and missing information in the occurrence data set (e.g. unspecific measurements, measurements below the analytical limit of quantification, etc.). The consumption data and adjusted occurrence data are then used to estimate chronic dietary exposures using an empirical approach, referred to as the observed individual means (OIM) approach. This results in a distribution that represents the variability of chronic exposures within the population.

The different simulations performed during the inner loop execution require the use of additional data, referred to as secondary input data. This includes various types of data which can be used either for the adjustment of the occurrence data (e.g. authorisation status of the active substance) or for improvement of the exposure estimates (e.g. processing factors).

In order to quantify the uncertainties, the model uses an outer loop execution where the inner loop execution is repeated several times. Prior to each execution, the original consumption and occurrence data sets are modified by means of bootstrapping: a random resampling technique for quantifying sampling uncertainty. By repeating the inner loop execution multiple times (i.e. 100), the model produces multiple exposure distributions. The differences among those distributions reflect the sampling uncertainty around the estimated exposure distribution.

During the output preparation, summary statistics (i.e. percentiles of exposure) are generated for the multiple distributions, resulting in multiple estimates for each percentile of exposure. From these multiple estimates, confidence intervals around each percentile are produced. Subsequently, in order to identify risk drivers, details on the highly exposed consumers are extracted (i.e. consumers Primary input data with exposure exceeding the 99th percentile) and average contributions per food commodity and active substance are calculated.

According to the risk management principles agreed among Member States (European Commission, 2018), the methodology described above is applied in a tiered approach. While the first‐tier calculation (Tier I) uses very conservative assumptions, the second‐tier assessment (Tier II) includes assumptions that are more refined although still intended to be conservative. Furthermore, in order to better understand the impact related to some of the assumptions and uncertainties, several sensitivity analyses were carried out.

Annex A presents the input data used for the cumulative exposure calculations to CAG‐NCN.

All extractions, simulations, imputations and calculations described in the subsequent sections were programmed with SAS^® Studio 3.8 (Enterprise Edition).

2.2.2. Primary input data

2.2.2.1. Raw primary commodities

EFSA selected 35 raw primary commodities (RPCs) of plant origin that are widely consumed in Europe (EFSA, 2015a). Water and foods specifically intended for infants and young children were integrated in the exposure assessment based on their importance in (certain) diets. The full list of the included food commodities is provided in Annex A – Table A.02. In Table 2 of the present report the variables contained in the list of food commodities are provided.

Table 2.

Description of the variables contained in the list of RPC

Name	Label	Description
prodCode	RPC code	Code of the raw primary commodity as defined by EFSA's harmonised terminology for scientific research (MATRIX catalogue; EFSA, 2019c).
prodName	RPC name	Name of the raw primary commodity as defined by EFSA's harmonised terminology for scientific research (MATRIX catalogue; EFSA, 2019c).

For the dietary surveys used in this assessment (see Section 2.2.2.5), the average contribution of the 35 RPCs to the total consumption of plant commodities (excluding sugar plants) ranges from 75% to 88%. Sugar plants and commodities of animal origin were not considered. As the occurrence of pesticide residues in these commodities is less frequent and at lower levels, their contribution to the dietary exposure is expected to be much lower than the contribution of plant commodities (EFSA, 2020a,b).

2.2.2.2. Active substances

The CAG under analysis in the present report includes 47 pesticide active substances associated with the brain and/or erythrocyte acetylcholinesterase inhibition (CAG‐NCN, see Section 2.1).

The list of active substances, which incorporates the key input data for cumulative exposure assessment, is presented in Annex A – Table A.01. The variables contained in the list of active substances are described in Table 3.

Table 3.

Description of the variables contained in the list of active substances

Name	Label	Description
paramCode_AS	Substance code	Code of the active substance as defined by EFSA's harmonised terminology for scientific research (PARAM catalogue; EFSA, 2019c).
paramName_AS	Substance name	Name of the active substance as defined by EFSA's harmonised terminology for scientific research (PARAM catalogue; EFSA, 2019c).
NOAEL	NOAEL	No observed adverse effect level (NOAEL) of the active substance (EFSA, 2019a).
Mechanism	Mechanism of action	Short reference to the mechanism of action or to the mode of action, where available (EFSA, 2019a).
Study_type	Study type	Type of regulatory toxicity study required by Regulation (EC) No 1107/2009 from which the NOAEL has been derived (EFSA, 2019a).

The toxicity of the active substances within the CAG is defined by means of the no observed adverse effect level (NOAEL) for AChE inhibition in brain and/or erythrocytes. It is worth mentioning that when an index compound is identified for the CAG, toxicity may also be expressed as a relative potency factor, i.e. the ratio of the NOAEL to that of the index compound (EFSA PPR Panel, 2012). This allows for the expression of exposure estimates in equivalents of the index compound. In this assessment, however, exposure estimates were normalised to a dimensionless number, referred to as the normalised exposure (see Section 2.2.4.2), without any impact of the results and their reliability (as demonstrated mathematically in EFSA (2020a,b)). Index compounds and relative potency factors were therefore no longer considered.

2.2.2.3. Residue definitions

While the CAG is defined at the level of the pesticide active substances, the occurrence data reported to EFSA refer to a residue definition for enforcement purposes (see Section 2.2.2.4). As the residue definitions, defined by Regulation (EC) No 396/2005, may change over time, single active substances may be associated with multiple residue definitions throughout the reference period. EFSA therefore collected all the residue definitions that were applicable to the selected food commodities and active substances during the reference period 2016–2018. The residue definitions collected for CAG‐NCN are presented in Annex A – Table A.03.

Depending on the metabolism and availability of analytical methods, the residue definitions may either be equal to the active substance, may include additional metabolites, or even incorporate multiple active substances. When the residue definition includes additional metabolites that are specific to the active substance (i.e. complex residue definition), the residue definition is assigned to the active substance assuming that the metabolites will have the same toxicological potency as the parent compound (e.g. sum of aldicarb, its sulfoxide and its sulfone, expressed as aldicarb). When the residue definition includes multiple active substances, however, the active substances may have different toxicological potencies (e.g. methomyl/thiodicarb). The latter are referred to as unspecific residue definitions.

When active substances are associated with an unspecific residue definition (e.g. sum of dimethoate and omethoate, expressed as dimethoate), further distinction is made between exclusive and non‐exclusive associations.

• Supposing that omethoate would be applied to the field, omethoate cannot be metabolised into dimethoate and the measured residue would be attributed to omethoate only. In this case, the association is considered exclusive.

• Supposing that dimethoate would be applied to the field, dimethoate would partially metabolise into omethoate. In this case, only a proportion of the measured residue would be attributed to dimethoate and the remaining part would be attributed to omethoate. Hence, the association is not exclusive.

Data on the proportions, however, were not readily available to EFSA. Therefore, a default proportion of 0.5 (≈ 50%) was assumed for all associations that are not exclusive.

In order to allow for the correct allocation of active substances to the measured residues (see Section 2.2.4.1), this information was integrated in the list of residue definitions. Table 4 provides an overview of all relevant variables.

Table 4.

Description of the variables contained in the list of residue definitions

Name	Label	Description
paramCode_RD	Residue code	Code of the residue definition as defined by EFSA's harmonised terminology for scientific research (PARAM catalogue; EFSA, 2019c).
paramName_RD	Residue name	Name of the residue definition as defined by EFSA's harmonised terminology for scientific research (PARAM catalogue; EFSA, 2019c).
paramCode_AS	Substance code	Code of the associated active substance(s) as defined by EFSA's harmonised terminology for scientific research (PARAM catalogue; EFSA, 2019c).
paramName_AS	Substance name	Name of the associated active substance(s) as defined by EFSA's harmonised terminology for scientific research (PARAM catalogue; EFSA, 2019c).
MW_factor	MW conversion factor	Multiplication factor used to convert the amount of measured residue into active substance. This factor is derived from the molecular weights (MW) of both compounds.
Is_exclusive	Exclusive	Indicates whether the association between active substance and residue definition is exclusive.
Proportion	Proportion	Estimated proportion of the active substance within the associated residue definition, only applicable when the association is not exclusive.

2.2.2.4. Occurrence data

The occurrence data collected under Article 31 of Regulation (EC) No 396/2005 are the most appropriate data available to EFSA for performing a retrospective exposure assessment to pesticide residues. These data are obtained from the official control activities carried out in the EU Member States, Iceland, Norway and EU pre‐accession countries. These data are reported to EFSA using the Standard Sample Description (SSD) (EFSA, 2010, 2013a,b). Although the occurrence data are collected at the level of individual measurements, the SSD allows identification of measurements associated with a single food sample (e.g. samples analysed for multiple pesticide residues). After validation by EFSA, the collected data are integrated in the EFSA Data Warehouse.

All occurrence data referring to the relevant food commodities (see Section 2.2.2.1) and residue definitions (see Section 2.2.2.3) were extracted from the Data Warehouse. Only measurements validated under the 2016, 2017 and 2018 EU reports on pesticide residues in food were included (EFSA, 2018a, 2019d, 2020c).

According to the risk management principles agreed among Member States (European Commission, 2018), the following additional criteria were applied to the extracted data.

• Only samples resulting from the EU‐coordinated control programme (EUCP), national control programmes or a combination of those were selected (SSD codes K005A, K009A and K018A). Samples associated with increased control programmes or any other type of programme were excluded as they were not considered to be representative of the market.

• Only samples obtained through selective or objective sampling were retained (SSD codes ST10A and ST20A). Samples obtained through suspect sampling or any other type of sampling were not considered to be representative of the market and therefore excluded.

• As the food consumption data are translated into RPCs, samples for processed commodities were excluded from the assessment, except for foods for infants and young children. This means that for the 35 RPCs, only samples with a product treatment specified as ‘unprocessed’ or ‘freezing’ were selected (SSD codes T998A and T999A). Regarding foods for infants and young children, the product treatment ‘processed’ was considered implicit (SSD code T100A).

• Only measurements reported as a numerical (i.e. quantifiable) value or as a non‐quantified value were considered useful for the assessment (SSD codes VAL and limit of quantification (LOQ)). Other result types were not considered valid and therefore excluded.

• Only measurements reported for the enforcement residue definition that was applicable at the time of sampling, or for the most complete subset of that enforcement residue definition were used (SSD codes P004A and P005A). Measurements referring to parts of the residue definition were excluded from the assessment.

• When the LOQ value for a measurement could not be reported by the Member States (i.e. for residue definitions composed of multiple components), the median LOQ of all measurements referring to the same residue definition/commodity combination was assumed.

• When several measurements with overlapping residue definitions were reported for the same sample, only the measurement referring to the most recent enforcement residue definition was retained for assessment.

Occurrence data from all EU Member States, Iceland, Norway and EU pre‐accession countries were pooled into one single data set for the CAG. The key variables retained in the occurrence data set are summarised in Table 5.

Table 5.

Description of the variables contained in the occurrence data set

Name	Label	Description
labSampCode	Sample code	Alphanumeric code of the analysed sample.
prodCode	RPC code	Code of the raw primary commodity as defined by EFSA's harmonised terminology for scientific research (MATRIX catalogue; EFSA, 2019c).
prodName	RPC name	Name of the raw primary commodity as defined by EFSA's harmonised terminology for scientific research (MATRIX catalogue; EFSA, 2019c).
paramCode	Residue code	Code of the residue definition as defined by EFSA's harmonised terminology for scientific research (PARAM catalogue; EFSA, 2019c).
paramName	Residue name	Name of the residue definition as defined by EFSA's harmonised terminology for scientific research (PARAM catalogue; EFSA, 2019c).
resLOQ	Limit of quantification	The lowest quantifiable amount (in mg/kg) detectable by the laboratory's analytical system.
resVal	Result value	Concentration of the measured residue (in mg/kg) within the analysed sample.
resType	Result type	Indicates the type of result, whether it could be quantified/determined or not.

Considering the size of the occurrence data sets, only the summary statistics per residue definition and food commodity are reported (see Annex A – Table A.09). Occurrence data for drinking water were not available to EFSA and were therefore imputed according to the assumptions elaborated in Section 2.2.4.1.

2.2.2.5. Consumption data

The EFSA Comprehensive European Food Consumption Database (Comprehensive Database) provides a compilation of existing national information on food consumption at individual level. It was first built in 2010 (EFSA, 2011; Huybrechts et al., 2011; Merten et al., 2011). Details on how the Comprehensive Database is used are published in the Guidance of EFSA (EFSA, 2011). Data reported in the Comprehensive Database may either refer to raw primary commodities (RPCs), RPC derivatives (i.e. single‐component foods altered by processing) or composite foods (i.e. multicomponent). Consumption data for RPC derivatives and composite foods, however, cannot be used in exposure assessments when the occurrence data are reported for the RPCs.

To address the above issue, EFSA transformed the Comprehensive Database into a new RPC Consumption Database by means of the RPC model (EFSA, 2019e). This model converts the consumption data for composite foods or RPC derivatives into their equivalent quantities of RPCs, except foods for infants and young children.2 The RPC model was applied to the Comprehensive Database as of 31 March 2018, when it contained results from 51 different dietary surveys carried out in 23 different Member States covering 94,523 individuals.

In view of the present project, the food consumption data extracted from the RPC Consumption Database were limited to the population classes and countries listed below, covering multiple European regions and age groups:

• Toddlers3: Denmark, The Netherlands and The United Kingdom

• Other children4: Bulgaria, France and The Netherlands

• Adults5: Belgium, Czechia, Italy and Germany

An overview of the selected dietary surveys is provided in Annex A – Table A.04.

For chronic exposure assessment, individuals who participated for only 1 day of the dietary survey were excluded because at least two survey days per individual are normally required to assess repeated exposure (EFSA, 2011). As a result, 65 individuals were excluded from the assessment, i.e. 64 from the Belgian survey and one from the Bulgarian survey.

Using the extraction criteria described above, a single consumption data set was obtained for chronic exposure assessment of the CAG‐NCN. The key variables retained in the consumption data set are summarised in Table 6. Summary statistics on the quantities of RPC consumed per country, survey and population class are reported (see Annex A – Table A.10).

Table 6.

Description of the variables contained in the food consumption data set

Name	Label	Description
Country	Country	Country where the dietary survey took place as defined by EFSA's harmonised terminology for scientific research (COUNTRY catalogue; EFSA, 2019c).
Survey	Survey	Acronym of the dietary survey
PopClass	Population class	Participant's population class, based on age, as defined by EFSA's harmonised terminology for scientific research (AGECLS catalogue; EFSA, 2019c).
ORSUBID	Subject ID	A pseudonymised subject ID number generated by EFSA upon receipt of the data
Weight	Body weight	Bodyweight of the subject (in kg)
ndays	Number of survey days	Number of days on which the participant's consumption was surveyed
day	Survey day	Ordinal number of the day on which the participant's consumption was surveyed
prodCode	RPC code	Code of the raw primary commodity as defined by EFSA's harmonised terminology for scientific research (MATRIX catalogue; EFSA, 2019c).
prodName	RPC name	Name of the raw primary commodity as defined by EFSA's harmonised terminology for scientific research (MATRIX catalogue; EFSA, 2019c).
FoodEx2_Facets	Processing code	FoodEx2 facet code describing the processing technique, including additional descriptors such as qualitative information, part consumed or the nature of the food (EFSA, 2015b).
RPCD_amount	RPCD amount	Amount of raw primary commodity derivative (in grams)
RPC_amount	RPC amount	Amount of raw primary commodity (in grams)

2.2.3. Secondary input data

2.2.3.1. Maximum residue levels

Certain assumptions on the extrapolation of occurrence data (see Section 2.2.4.1) require information on the maximum residue levels (MRLs). An MRL is the upper legal level of a concentration for a pesticide residue in or on food or feed set in accordance with Regulation (EC) No 396/2005. This regulation also defines a procedure for the setting and modification of MRLs. MRLs may therefore have been modified throughout the 2016–2018 reference period. In order to obtain a single list of MRLs, EFSA decided to use the MRLs as of 31 December 2018 (i.e. the end of the current reference period). Hence it was assumed that those MRLs were applicable during the entire reference period, regardless whether the MRL or residue definition may have changed during that period.

MRLs for the relevant food commodities (see Section 2.2.2.1) and enforcement residue definitions (see Section 2.2.2.3) were extracted from the EU Pesticides Database6 and organised in a data format that can be used directly for exposure assessment (see Annex A – Table A.05). Table 7 describes the variables that were part of this data format.

Table 7.

Description of the variables contained in the list of maximum residue levels

Name	Label	Description
paramCode_RD	Residue code	Code of the residue definition as defined by EFSA's harmonised terminology for scientific research (PARAM catalogue; EFSA, 2019c).
paramName_RD	Residue name	Name of the residue definition as defined by EFSA's harmonised terminology for scientific research (PARAM catalogue; EFSA, 2019c).
prodCode	RPC code	Code of the raw primary commodity as defined by EFSA's harmonised terminology for scientific research (MATRIX catalogue; EFSA, 2019c).
prodName	RPC name	Name of the raw primary commodity as defined by EFSA's harmonised terminology for scientific research (MATRIX catalogue; EFSA, 2019c).
MRL	MRL (mg/kg)	Numerical value of the maximum residue level (MRL) as defined by Regulation (EC) No 396/2005, expressed in mg/kg.
atLOQ	MRL at LOQ	Indicates whether the maximum residue level (MRL) is set at the analytical limit of quantification (LOQ). Under Regulation (EC) No 396/2005 such MRLs are marked with an asterisk (*).

2.2.3.2. Authorised uses

In some cases, the imputations and simulations performed on the occurrence data rely on the authorisations for use of the active substance(s) (see Section 2.2.4.1). While the approval status of an active substance under Regulation (EC) No 1107/2009 is regulated at EU level, the authorisations for plant protections products (PPP, i.e. formulated products containing the active substances) are delivered at national level within the EU Member States. A centralised database compiling these national authorisations is not yet available at EU level.

National authorisations can be reported to EFSA under Regulation (EC) No 396/2005, either for an MRL application under Article 10, or for an MRL review under Article 12. There is, however, no legal obligation to systematically report all national authorisations and the MRL review programme is still in progress. A comprehensive overview of all PPP authorisations within the EU is therefore also not available to EFSA. Meanwhile, a tentative list of authorised uses was elaborated according to the following principles.

• When the MRL for a given combination of active substance and RPC was not set at the LOQ (see Section 2.2.3.1), the active substance was assumed to be authorised for use on that specific commodity. This assumption also accounts for uses authorised outside the EU and for which treated products may be placed on the EU market.

• For the remaining combinations of active substance and RPC (i.e. where the MRL was set at LOQ), EFSA screened the relevant reasoned opinions issued under Article 12 of Regulation (EC) No 396/2005 and the subsequent reasoned opinions issued under Article 10. Any authorised use reported in those reasoned opinions was recorded.

• When the MRL was set at LOQ and a review under Article 12 of Regulation (EC) No 396/2005 had not been issued, it was assumed that the use was not authorised.

The authorised uses collected by EFSA were integrated in a data format that can be readily used for exposure assessment (see Annex A – Table A.06). Table 8 describes the variables of this data format.

Table 8.

Description of the variables contained in the list of authorised uses

Name	Label	Description
paramCode_AS	Substance code	Code of the active substance as defined by EFSA's harmonised terminology for scientific research (PARAM catalogue; EFSA, 2019c).
paramName_AS	Substance name	Name of the active substance as defined by EFSA's harmonised terminology for scientific research (PARAM catalogue; EFSA, 2019c).
prodCode	RPC code	Code of the raw primary commodity as defined by EFSA's harmonised terminology for scientific research (MATRIX catalogue; EFSA, 2019c).
prodName	RPC name	Name of the raw primary commodity as defined by EFSA's harmonised terminology for scientific research (MATRIX catalogue; EFSA, 2019c).
Source	Source	Indicates the source of the information (i.e. MRL legislation, MRL review or MRL application).
Reference	Reference	EFSA Journal reference to the relevant reasoned opinion (i.e. when the information was retrieved from an MRL review or application).

2.2.3.3. Extrapolation rules

The extrapolation of occurrence data described in Section 2.2.4.1 is carried out in compliance with the guidelines on comparability, extrapolation, group tolerances and data requirements for setting MRLs (European Commission, 2017). These extrapolation rules depend on when the active substance is applied to the plant.

For the current assessment, available occurrence data do not provide any information on when the plant commodity was treated. Therefore, the most conservative extrapolation rules were applied, i.e. for treatments after formation of the edible plant parts. These extrapolation rules were integrated in a data format that can be readily used for exposure assessment (see Annex A – Table A.07). Table 9 describes the variables of this data format.

Table 9.

Description of the variables contained in the list of extrapolation rules

Name	Label	Description
prodCode_from	RPC code (from)	Code of the raw primary commodity from which the extrapolated measurements are taken (i.e. source commodity). This code is compliant with EFSA's harmonised terminology for scientific research (MATRIX catalogue; EFSA, 2019c).
prodName_from	RPC name (from)	Name of the raw primary commodity from which the extrapolated measurements are taken (i.e. source commodity). This code is compliant with EFSA's harmonised terminology for scientific research (MATRIX catalogue; EFSA, 2019c).
prodCode_to	RPC code (to)	Code of the raw primary commodity to which the measurements are extrapolated (i.e. target commodity). This code is compliant with EFSA's harmonised terminology for scientific research (MATRIX catalogue; EFSA, 2019c).
prodName_to	RPC name (to)	Name of the raw primary commodity to which the measurements are extrapolated (i.e. target commodity). This code is compliant with EFSA's harmonised terminology for scientific research (MATRIX catalogue; EFSA, 2019c).

2.2.3.4. Processing factors

Occurrence data for pesticide residues are collected at the level of the RPC (see Section 2.2.2.4). Food consumption data may be collected at the level of RPC, RPC derivative or composite food, but for the purpose of this assessment, all consumption data for composite foods and RPC derivatives were converted into their equivalent quantities of RPCs (see Section 2.2.2.5). Combining occurrence and consumption data at RPC level implies that all residues present in the RPC will reach the end consumer. This assumption, however, is conservative. In reality, residue concentrations will most likely change due to processing, such as peeling, washing, cooking etc.

The effect of processing is usually addressed by means of processing factors. A processing factor accounts for the change in residue concentrations and is specific to each RPC, processing type and active substance. Processing factors are quantified by dividing the residue concentration in the processed commodity by the residue concentration in the raw commodity.

The European database on processing factors is the most recent and the most comprehensive compilation of processing factors currently available at EU level (Scholz et al., 2018a). Processing factors for the active substances and RPCs under assessment were extracted from the database according to the following criteria:

• For each active substance, RPC and processing technique only the median processing factor was extracted.

• Only the processing factors indicated as reliable or indicative were extracted. Processing factors indicated as unreliable were excluded from the assessment (e.g. a processing factor for pirimiphos‐methyl in flour was not used as it was rated as non reliable in Scholz et al. (2018a)).

Processing techniques reported in the processing factor database were then compared to the processing techniques reported in the RPC consumption data set. The processing techniques from both databases were matched according to the following principles:

• When a generic processing technique was reported in the RPC consumption database (e.g. juice) while more specific processing techniques were reported in the processing factor database (e.g. pasteurised juice and unpasteurised juice), the specific processing technique with the highest processing factor was selected.

• When a specific processing technique was reported in the RPC consumption database (e.g. mashed potato) while a more generic processing technique was reported in the processing factor database (e.g. boiled potato), the generic processing factor was applied to the specific processing techniques.

• Processing factors were extrapolated between raw primary commodities with similar properties (i.e. oranges and mandarins, apples and pears, table and wine grapes, wheat and rye grain).

• Processing factors for peeling were applied to the corresponding fruit with inedible peel, even when the processing technique was not specified in the RPC consumption database (i.e. oranges, mandarins, bananas and melons).

Although the European database on processing factors is the most comprehensive compilation of processing factors currently available at EU level, this compilation is limited to all processing factors that have been evaluated by EFSA until 30 June 2016. Meanwhile, additional processing factors were assessed by EFSA in the framework of Regulation (EC) No 396/2005 and Regulation (EC) No 1107/2009. Additional processing factors evaluated by EFSA until 31 December 2019 were therefore also integrated in the current assessment.

By following these principles, lists of processing factors were obtained for the assessment of CAG‐NCN (see Annex A – Table A.08). Table 10 describes the variables contained in the list of processing factors.

Table 10.

Description of the variables contained in the list of processing factors

Name	Label	Description
paramCode_AS	Substance code	Code of the active substance as defined by EFSA's harmonised terminology for scientific research (PARAM catalogue; EFSA, 2019c).
paramName_AS	Substance name	Name of the active substance as defined by EFSA's harmonised terminology for scientific research (PARAM catalogue; EFSA, 2019c).
prodCode	RPC code	Code of the raw primary commodity as defined by EFSA's harmonised terminology for scientific research (MATRIX catalogue; EFSA, 2019c).
prodName	RPC name	Name of the raw primary commodity as defined by EFSA's harmonised terminology for scientific research (MATRIX catalogue; EFSA, 2019c).
facetCode	Processing code	FoodEx2 facet code describing the processing technique, including additional descriptors such as qualitative information, part consumed or the nature of the food (EFSA, 2015b).
facetDesc	Processing description	Description of the processing code.
procFac	Processing factor	Numerical value representing the expected residue concentration in the processed commodity divided by the residue concentration in the raw commodity.
Source	Source	Indicates the source of the information (i.e. type of report).
Reference	Reference	Journal reference to the relevant report.
Comment_PF	Comment	Indicates whether the processing factor relies on any type of assumption or extrapolation.

2.2.4. Inner loop execution

2.2.4.1. Adjustments and simulations on the occurrence data

2.2.4.1.1. Allocation of active substances to the occurrence data

While the cumulative assessment groups are defined at the level of the pesticide active substances, the occurrence data reported to EFSA refer to enforcement residue definitions (see Section 2.2.2.4). Hence, the original occurrence data set obtained from the EFSA Data Warehouse is converted into a new intermediate data set where measurements are assigned to active substances instead of residue definitions.

Some of these residue definitions however, referred to as unspecific residue definitions, may be associated with multiple active substances (see Section 2.2.2.3). Allocation of active substances to these unspecific residue definitions is performed in accordance with the risk management principles agreed among Member States (European Commission, 2018).

Under the Tier I assumptions, measurements for unspecific residue definitions are always assigned to the most potent active substance (i.e. the substance with the lowest NOAEL), regardless of its authorisation status. This approach is expected to overestimate the exposure because a PPP containing a less potent active substance may have been used. This overestimation may be even more substantial when PPPs containing the most potent active substance are not authorised for use on the relevant commodity.

A more likely scenario would be the use of a combination of more potent and less potent substances. Therefore, for the Tier II calculations, each measurement is randomly assigned to one of the active substances with PPP authorisation on that commodity, regardless of whether the active substance is part of the CAG or not. If PPPs are not authorised for any of the active substances associated to the unspecific residue definition, an active substance is selected at random. Furthermore, special consideration is given to the active substances that may metabolise into another active substance, the non‐exclusive substances (see Section 2.2.2.3). If the measurement is assigned to a non‐exclusive substance (e.g. dimethoate), the model assumes that the measurement is partially composed of the assigned active substance while the remaining fraction is attributed to the active substance into which it metabolises (e.g. omethoate), the exclusive substance.

A more detailed description of the methodologies used to allocate active substances to the occurrence data is provided in Appendix A.

Although the Tier II assumptions are expected to better reflect reality, some uncertainties related to this approach were still identified. Under ideal circumstances, the probability to select an active substance should be based on market share data for those active substances. Similarly, the proportion of the non‐exclusive substance should be derived from the available metabolism data. Both market share data and metabolism data were not readily available. In the absence of these data, assumptions on equal probability and equal proportion are applied instead. It should be noted that these assumptions may either underestimate or overestimate the actual exposure.

An additional uncertainty derives from the assumption that measurements for unspecific residue definitions result from the use of single active substances. This assumption implies that other active substances associated with that unspecific residue definition are not present (i.e. implicit zero measurements). Although it is unlikely that substances covered by the same enforcement residue definition are used simultaneously, this possibility cannot be excluded.

2.2.4.1.2. Extrapolation of occurrence data

For some active substances and food commodities, the number of measurements may be limited. Furthermore, data may even be missing completely for certain combinations. In order to address the uncertainties related to those limited or missing data, extrapolation rules are integrated in the exposure model.

The extrapolations are carried out in compliance with the guidelines on comparability, extrapolation, group tolerances and data requirements for setting MRLs (European Commission, Directorate General for health and food safety, 2017). These extrapolation rules were developed and validated in view of extrapolating occurrence data from ‘data rich’ commodities (e.g. apples) to ‘data poor’ commodities (e.g. pears). However, there is currently no clear guidance on the number of measurements needed to perform a reliable probabilistic calculation. In the framework of this assessment, a minimum of 10 measurements per active substance and commodity is considered sufficient to perform a reliable probabilistic assessment.

Hence, combinations of food commodities and active substances with less than 10 measurements are identified in the data set (i.e. the target combination). Measurements for the same active substance but a different commodity (i.e. source commodity) are then extrapolated to the target commodity provided that:

• the extrapolation is compliant with the extrapolation rules reported in Section 2.2.3.3,

• the MRLs are the same in both the source and target commodity,

• the use of the active substance is authorised in both the source and target commodity and

• the number of measurements for the source commodity is higher than or equal to 10.

The extrapolated measurements are randomly assigned to the available target commodity samples, excluding samples where the active substance was already measured. The number of extrapolated measurements is reported in the final output (see Section 2.2.6).

The methodology used for extrapolation of occurrence data is independent of the Tier I or Tier II scenarios. A more detailed description is provided in Appendix B.

2.2.4.1.3. Imputation of left‐censored occurrence data

Over 95% of the occurrence data used for the current exposure assessment are left censored (see Section 2.2.2.4). Left‐censored data are measurements reported below the limit of quantification (LOQ) and for which an accurate value is not available. Some of these results may be low positive residues while others will be true zeroes (no‐residue situation).

In order to address the uncertainties resulting from the high proportion of left‐censored data, measurements below the LOQ were imputed in compliance with the risk management principles agreed among Member States (European Commission, 2018).

Under Tier I assumptions, left‐censored measurements were imputed with 1/2 LOQ when at least one positive result (i.e. above LOQ) was reported for a given substance‐commodity combination. Measurements for all remaining combinations were imputed with a zero (i.e. assuming a no‐residue situation).

For the Tier II assessment, use frequencies are estimated for each pesticide and each commodity, assuming that all samples were treated according to at least one agricultural use pattern (AUP).7 An AUP is the combination of pesticide uses applied to a single commodity or crop. The estimated use frequencies are then used to calculate a proportion of true zeros, and the corresponding number of left‐censored measurements is then selected at random from the data set. While the selected measurements are imputed with zero, the remaining left‐censored measurements are imputed with 1/2 LOQ. A more detailed description of the methodology is provided in Appendix C.

As for the allocation of active substances, the Tier II assumption is expected to be more refined compared to the Tier I assumption, which is a very conservative assumption. These Tier II calculations would be even more accurate if actual data on the use frequency of pesticides would be made available. In particular, for pesticides with unquantifiable residues, the estimated use frequency will be 0% which is most likely an underestimation of the real use frequency. On the other hand, this scenario also assumes that the total AUP frequency is 100%, meaning that all commodities were treated according to at least one AUP. This tends to overestimate the exposure.

2.2.4.1.4. Imputation of occurrence data for drinking water

Occurrence data for water are not available to EFSA (see Section 2.2.2.4). According to the risk management principles agreed among Member States (European Commission, 2018), occurrence data for water are imputed for the five most potent active substances within the CAG.

For this purpose, the five substances with the lowest NOAEL are extracted from the list of active substances (i.e. monocrotophos, dichlorvos, triazophos, azinphos‐ethyl and carbofuran; see also Section 2.2.2.2) and a measurement in water is added to the occurrence data set for each of these substances. These measurements are associated with a single fictitious sample code. While under the Tier I assessment, a result value of 0.001 mg/kg is assigned to each measurement, a result value of 0.0005 mg/kg is assigned under Tier II. These assumptions are also expected to overestimate the exposure, since none of these active substances were approved and used in the EU during the period 2016–2018.

2.2.4.1.5. Calculation of mean occurrence values

Although individual residue measurements are required to enable bootstrapping and quantify the impact of sampling uncertainty, short‐term variability of residues between samples is not relevant when modelling chronic exposure (EFSA PPR Panel, 2012). Chronic exposure is therefore estimated using the average concentration for each active substance and commodity.

Hence, the occurrence data set obtained after imputation of the occurrence data for drinking water (see Section 2.2.4.1.4) is used to calculate the average concentrations per active substance and food commodity. Under Tier II assumptions, the average concentrations also account for the implicit zero measurements resulting from the assignment of active substances to unspecific residue definitions (see Section 2.2.4.1.1).

2.2.4.2. Chronic exposure distribution

Chronic dietary exposure is modelled by means of an empirical approach, referred to as the Observed Individual Means (OIM) approach (EFSA PPR Panel, 2012). This method uses the mean consumption over the survey days of each individual to estimate the individuals’ long‐term consumption. Using the individuals’ bodyweight and the mean occurrence values obtained from Section 2.2.4.1.5, the individuals’ chronic exposures resulting from each food commodity and active substance are calculated. It should be noted, however, that due to the limited duration of the dietary surveys, the OIM approach tends to overestimate upper tail exposures in chronic assessments.

In order to combine the different substances in a total chronic exposure estimate, the toxicity of each substance also needs to be accounted for. The use of relative potency factors has previously been suggested by EFSA (EFSA PPR Panel, 2012), but this method requires identification of an index compound for each CAG. Alternatively, the exposure estimates for the different active substances are divided by the corresponding NOAEL. These potency‐adjusted estimates can then be combined to obtain a total normalised exposure (NET) for each individual.

Combining occurrence and consumption data at RPC level also implies that all residues present in the RPC will reach the end consumer, while alteration of residues is expected to occur when the RPCs are processed prior to consumption. This uncertainty, which is generally expected to overestimate exposure, is addressed by integrating processing factors where available (see Section 2.2.3.4). Considering however that processing factors account for both the chemical alteration of the substance and weight change of the food, occurrence values need to be combined with the consumed amount of processed food (i.e. RPC derivative) instead of the consumed amount of RPC. Furthermore, as the consumed amounts are expressed in g and occurrence data are expressed in mg/kg, a correction factor of 1000 needs to be considered.

Based on the considerations above, the NET is calculated for each individual according to the equations reported below.

$${\text{NET}}_{\mathrm{i}}=\sum _{\mathrm{d}}^{\mathrm{Days}}\sum _{\mathrm{c}}^{\mathrm{Commodities}}\sum _{\mathrm{p}}^{\mathrm{processes}}\sum _{\mathrm{s}}^{\mathrm{Substances}}\left\{\begin{array}{c}{\displaystyle \frac{({\text{RPC}}_{\mathrm{idcp}}·{10}^{-3})·{\overline{\mathrm{X}}}_{\mathrm{cs}}}{{\text{BW}}_{\mathrm{i}}·{\text{Days}}_{\mathrm{i}}·{\text{NOAEL}}_{\mathrm{s}}}}\text{if}{\text{PF}}_{\mathrm{cps}}\text{unspcified}\\ {\displaystyle \frac{({\mathrm{RPCD}}_{\mathrm{idcp}}·{10}^{-3})·{\overline{\mathrm{X}}}_{\mathrm{cs}}·{\mathrm{PF}}_{\mathrm{cps}}}{{\mathrm{BW}}_{\mathrm{i}}·{\mathrm{Days}}_{\mathrm{i}}·{\mathrm{NOAEL}}_{\mathrm{s}}}}\mathrm{if}{\mathrm{PF}}_{\mathrm{cps}}\mathrm{unspcified}\end{array}\right.$$

where NET_i is the total normalised exposure of individual i;

RPC_idcp is the amount of commodity c with processing type p consumed by individual i on day d, expressed in kg of raw primary commodity per day;

RPCD_idcp is the amount of commodity c with processing type p consumed by individual i on day d, expressed in kg of raw primary commodity derivative per day;

BW_i is the body weight of individual i, expressed in kg;

Day_i is the number of survey days of individual i;

${\overline{X}}_{\mathit{cs}}$ is the average concentration of substance s in commodity c, expressed in mg/kg;

PF_cps is the processing factor for substance s in commodity c with processing type p;

NOAEL_s is the no observed adverse effect level for substance s, expressed in mg/kg bodyweight per day.

After having calculated the NET for each individual, empirical distributions of individual NETs are obtained. The distributions represent the variability of exposure within the different population groups.

The methodology used to derive the chronic exposure distribution is independent of the Tier I or Tier II scenarios, and a more detailed description is provided in Appendix D

2.2.5. Outer loop execution

The consumption data used for this assessment are subject to sampling uncertainty and will not represent perfectly the true diets within the population. Likewise, the occurrence data will not perfectly reflect the true distribution of residue concentrations in food. These sampling uncertainties are addressed by repeating the inner loop execution multiple times, each time replacing the consumption and occurrence data sets with bootstrap data sets (EFSA PPR Panel, 2012). Bootstrap data sets are obtained by resampling with replacement the same number of observations from the original data sets. Each time the inner loop is executed with bootstrap data sets, a bootstrap distribution of NETs will be obtained. This shows how the distribution of NETs may have looked like if random sampling from the population would have generated different samples than those actually observed (Efron and Tibshirani, 1993).

It should be noted that both consumption and occurrence data incorporate several multivariate patterns (e.g. association of foods and individuals’ characteristics, co‐occurrence of residues etc.). These patterns need to be preserved in the bootstrap data sets.

Consumption data are therefore resampled at the individual level, i.e. selecting all consumption events and all survey days of the resampled individual. Hence, for each dietary survey, the bootstrap data sets contain the same number of individuals as the original data set.

Occurrence data, on the other hand, are resampled at the level of the laboratory sample i.e. selecting all measurements obtained. Hence, the bootstrap data sets contain for each food commodity the same number of laboratory samples as the original data set.

In the current exposure model, the inner loop execution is repeated 100 times. The first execution also referred to as the nominal run, is performed with the original data sets. The remaining executions are performed with bootstrap data sets.

Although the outer loop execution is primarily intended to address the sampling uncertainty of the consumption and occurrence data, it also addresses uncertainty resulting from the probabilities applied in the model. This is particularly true for the Tier II scenarios where several simulations and imputations rely on the random selection of measurements (see Section 2.2.4.1).

2.2.6. Output preparation

Through the inner and outer loop executions, multiple NET distributions are generated (i.e. 100 bootstrap distributions per dietary survey). To describe each bootstrap distribution, the following parameters are derived:

• mean of the NET,

• standard deviation of the NET,

• percentiles of the NET (P2.5, P5, P10, P25, P50, P75, P90, P95, P97.5, P99, P99.9 and P99.99).

According to the risk management principles agreed among Member States (European Commission, 2018), the parameters of the exposure distribution are expressed in total margin of exposure (MOET). The margin of exposure is normally calculated as the ratio of a toxicological reference dose (i.e. NOAEL) to the estimated exposure. Considering that the exposure is already normalised (see Section 2.2.4.2), the MOET is in this case the reciprocal value of the NET.

As a result, 100 MOET estimates are obtained for each parameter of the exposure distributions. These 100 estimates reflect the uncertainty distribution around the true value of those parameters. From these uncertainty distributions, a 95% confidence interval is calculated for each parameter. The median of the uncertainty distribution is selected as the central estimate for the confidence interval.

To better understand the factors that influence the lowest MOETs (or the highest NETs), individuals with an MOET lower than the MOET calculated at the 99th percentile of the exposure distribution are extracted for each dietary survey and bootstrap distribution. The relevant information associated with those individuals is also retrieved (i.e. amounts of foods consumed and concentrations of active substances). Based on the individuals’ information, average contributions are calculated per dietary survey, active substance and food commodity.

Additional information is gathered throughout the calculation process to support the identification of missing information. These intermediate outputs mainly refer to the missing occurrence data and possible extrapolations (see Section 2.2.4.1.2). For the Tier II scenario, the estimated use frequencies are also reported (see Section 2.2.4.1.3).

The above‐reported percentiles were calculated using SAS^® software, which provides five validated options for the definition of percentiles.8 For the purpose of this assessment, the following percentile definition was selected. Let n be the number of non‐missing values for a variable, let x₁, x₂, …, x_n represent the ordered values of the variable and set p = t/100. Then, the tth percentile is calculated as follows.

$$\mathrm{y}=(1-g)x_j+g{x}_{j+1}$$

where y is the tth percentile;

j is the integer part of np;

g is the fractional part of np.

This definition was considered to be the most appropriate because it allows for the differentiation of percentiles, even when p > (n − 1)/n. This is particularly useful for the dietary surveys with toddlers and children where a 99.9th percentile needs to be calculated even though the number of individuals is lower than 1,000. This method still contains an important bias because the calculated percentile will always be lower than or equal to the highest observation. For dietary surveys with a low number of individuals, it is not unlikely that the true percentile will be higher than the highest observation in the empirical distribution. However, estimation of percentiles beyond the highest observation would require parametric modelling of the exposure distribution which needs to be further investigated before being implemented in cumulative exposure assessment.

2.2.7. Tiers and sensitivity analyses

According to the risk management principles agreed among Member States (European Commission, 2018), the exposure calculations are performed in a tiered approach:

• The first‐tier calculations (Tier I) use very conservative assumptions that are less resourceful regarding data and computational capacity. This allows for an efficient screening of the exposure with low risk for underestimation of the real exposure to pesticide residues.

• The second‐tier assessment (Tier II), which is more resourceful, includes more refined assumptions but it is still intended to be conservative.

Table 11 summarises the main assumptions and methodologies applied in the exposure model. The key differences between Tier I and Tier II are also highlighted.

Table 11.

Overview of the main assumptions and methodological approaches used for assessing chronic cumulative exposure to pesticide residues

	Description
Consumption data
Number of surveys	10
Population classes	Adults (Belgium, Czechia, Germany and Italy) Other children (Bulgaria, France and Netherlands) Toddlers (Denmark, Netherlands and United Kingdom)
Food commodities	35 raw primary commodities (includes conversion from foods as eaten) + 4 categories of foods for infants and young children + drinking water
Other criteria	Individuals who participated only 1 day in the dietary survey were excluded
Occurrence data (extraction)
Reference period	2016–2018 (latest available three‐year cycle)
Food commodities	35 raw primary commodities (unprocessed or frozen) + 4 categories of foods for infants and young children
Residue definitions	All residue definitions associated with CAG‐NCN during the reference period (excl. overlapping residue definitions at sample level)
Sampling framework	EU‐coordinated or national control programmes
Sampling type	Objective or selective sampling only
Occurrence data (simulations and imputations)
Unspecific residue definitions	Tier I: Most potent active substance is allocated to each sample	Tier II: Random allocation of authorised active substances to each sample*
Extrapolations	Extrapolation of measurements per active substance and commodity in accordance with guidance document SANCO 7525/VI/95 (European Commission, Directorate General for health and food safety, 2017), when MRL is equal and substance is authorised in both source (N ≥ 10) and target (N < 10) commodities.
Left‐censored data	Tier I: Imputed at ½ LOQ for food‐substance combinations with quantifiable findings	Tier II: Imputed at 1/2 LOQ based on estimated use frequencies (assuming 100% crop treatment)
Drinking water	Tier I: Imputed at 0.1 μg/L for the five most potent active substances	Tier II: Imputed at 0.05 μg/L for the five most potent active substances
Exposure calculations
Exposure model	Observed Individual Means approach (inner loop execution)
Uncertainty model	Empirical bootstrapping (outer loop execution, n = 100)
Processed foods	Processing factors obtained or extrapolated from the European database on processing factors for pesticides in food (Scholz et al., 2018a)

^*Accounts for substances that are not part of the CAG and for residue definitions that are not exclusive (see Section 2.2.4.1.1).

Although the methods and assumptions applied in the model were selected with the view of minimising the uncertainties, resources may sometimes be insufficient to allow for a more accurate assessment (e.g. information on use frequencies and processing factors). In order to assess how these additional data or improvement might impact on the exposure estimates, the following sensitivity analyses were applied to the Tier II scenario:

• Sensitivity analysis A assumes that left‐censored data are imputed at 1/2 LOQ when the use of the active substance is authorised.

• Sensitivity analysis B assumes that all left‐censored data are imputed at zero.

• Sensitivity analysis C assumes that residues will not be present in any processed food.

• Sensitivity analysis D excludes all foods for infants and young children.

• Sensitivity analysis E excludes the sample with the highest measurement for the sum of dimethoate and omethoate in olives for oil production.

• Sensitivity analysis F excludes pesticides belonging to the N‐methyl carbamates group.

• Sensitivity analysis G excludes samples obtained through a selective sampling strategy.

• Sensitivity analysis H assumes that a pesticide is authorised for use in a commodity when the percentage of positive findings in that commodity exceeds one percent.

• Sensitivity analysis I excludes drinking water.

• Sensitivity analysis J excluding sampling uncertainty (i.e. outer loop execution without resampling of the occurrence data and food consumption data).

• Sensitivity analysis K assumes that omethoate is not authorised for use on olives for oil production.

• Sensitivity analysis L excludes samples reported by pre‐accession countries.

For these sensitivity analyses, only the impact on the 99.9th percentile of the exposure distribution (expressed in MOET) was reported. Detailed results were in this case not provided.

2.3. Uncertainty analysis

There are several limitations in the available knowledge and data that affect the capacity of risk assessors to provide a precise answer to the assessment question mentioned in Section 1. Therefore, an uncertainty analysis was conducted in order to provide an answer to the following:

If all the uncertainties in the model, 9 exposure assessment, hazard identification and characterisation and their dependencies could be quantified and included in the calculation, what would be the probability that the MOET for the 99.9th percentile of exposure in 2016–2018 is below 100? This question was considered separately for each of the 10 consumer populations addressed in the probabilistic modelling.

This uncertainty analysis was conducted following the guidance of the EFSA Scientific Committee on uncertainty analysis in scientific assessments for case‐specific assessments (EFSA Scientific Committee, 2018a).10

2.3.1. Model and process for characterising the overall uncertainty

The approach developed for characterising overall uncertainty in this assessment is summarised graphically in Figure 1. The whole approach is based upon taking the output of the probabilistic modelling – specifically the uncertainty distribution produced by the modelling for the MOET at the 99.9th percentile of exposure, represented diagrammatically at the top left of Figure 1 – as the starting point for the uncertainty analysis. The uncertainty analysis was carried out using a combination of expert knowledge elicitation (EKE) and probabilistic calculations. Expert judgements were elicited from a group of 12 experts, as follows:

Toxicology experts: Judy Choi, Tamara Coja, Antonio Hernandez‐Jerez, Alfonso Lostia (for EKE Q1 only), Kyriaky Machera, Iris Mangas.

Exposure experts: Bruno Dujardin, Samira Jarrah, Alexandra Mienne, Luc Mohimont, Marloes Schepens, Anneli Widenfalk.

In the first step of the analysis, the experts considered systematically each part of the cumulative assessment to identify sources of uncertainty that might influence the outcome. This was followed by five further key steps, listed on the right‐hand side of Figure 1, as follows:

Expert Knowledge Elicitation Question 1 (EKE Q1): This was the first of three steps where the impact of uncertainties on the assessment was quantified by expert judgement. EKE Q1 required the toxicology or exposure experts to consider separately each source of uncertainty related to their respective area of expertise (i.e. toxicology or exposure) and quantify its impact on the assessment in terms of how much the median estimate of the MOET at the 99.9th percentile of exposure calculated by the probabilistic model for the Italian adult population would change if that source of uncertainty was resolved (e.g. by obtaining perfect information on the input or assumption affected by the uncertainty). Focussing on a single population avoided repeating the assessment for each population, which would take 10 times as long and be more vulnerable to biases in judgement due to progressive expert fatigue. Italian adults were chosen as the focus because this was the population with the lowest median estimate of the MOET at the 99.9th percentile of exposure.11 The experts expressed their judgements as multiplicative factors, e.g. a factor of 1 would represent no change in the MOET at the 99.9th percentile of exposure, factors greater than 1 represent an increase, factors less than 1 represent a decrease. The scale and methods used for this step are described in Section 2.3.3 and the results are reported in Section 3.2.2 and Appendix F.

EKE Question 2 (EKE Q2): For this question, the experts were asked to consider all the sources of uncertainty relating to exposure or toxicology (according to their expertise), and quantify their combined impact on the assessment in terms of how much the median estimate of the MOET at the 99.9th percentile of exposure calculated by the probabilistic model for the Italian adult population would change if all those sources of uncertainty were resolved. This focussed on Italian adults for the same reason as EKE Q1 (see above) and the degree of change was again expressed as a multiplicative factor. When answering EKE Q2, the experts took account of their evaluations of the individual uncertainties, as assessed in EKE Q1, and combined them by expert judgement. The experts’ uncertainty about the combined impact was elicited in the form of a distribution for the multiplicative factor. The methods used for this step are described in Section 2.3.4 and the results are reported in Section 3.2.3 and Appendices G and H.

Combine distributions using Monte Carlo simulations: In this step, the distributions for the multiplicative factors quantifying the exposure and toxicology uncertainties, elicited in EKE Q2, were combined by multiplication with the uncertainty distribution for the MOET at the 99.9th percentile of exposure produced by the probabilistic model. Since each of the distributions from EKE Q2 is for a multiplicative adjustment to the MOET at the 99.9th percentile of exposure, multiplying the three distributions together results in a new distribution for the MOET at the 99.9th percentile of exposure which incorporates the experts’ assessment of the impact of the exposure and toxicology uncertainties. This was repeated for each of the 10 modelled populations (see Section 2.3.5).

EKE Question 3 (EKE Q3): For reasons of practicality, the preceding steps involved two important simplifications. In EKE Q1 and Q2, the uncertainties were assessed with reference to only one of the 10 modelled populations (Italian adults). Then, in the Monte Carlo simulations, the distributions elicited for Italian adults were applied to all 10 populations, and it was that assumed that the model distributions and the distributions for exposure and toxicology uncertainties are independent of one another. These simplifications introduce additional uncertainties into the assessment. Therefore, EKE Q3 asked the experts to consider the calculated probability of the MOET at the 99.9th percentile of exposure being less than 100 (derived from the distribution produced by the Monte Carlo simulation for each population) and judge how that probability would change if it was adjusted for any dependencies between the exposure and toxicology uncertainties, for differences in uncertainty between Italian adults and each of the other populations, and also for any other remaining uncertainties. In recognition of the difficulty of this judgement, the experts’ response to this question was elicited as an approximate probability (range of probabilities) for each population. The method used for this step is described in Section 2.3.6 and the results are reported in Section 3.2.4 and Appendix I.

Extrapolation to EFSA PRIMo populations: The recommendation of European Commission and Member States that the MOET at the 99.9th percentile of exposure should be assessed for each of the consumer populations included in the EFSA PRIMo model is addressed in Section 4.2, where the implications of the results for the PRIMo populations are discussed.

Note that different sources of uncertainty were combined by expert judgement in EKE Q2, whereas the two distributions resulting from that (one for exposure and the other for toxicology) were combined by Monte Carlo simulation. This combination of methods for combining uncertainties was considered more practical than combining all the individual uncertainties by Monte Carlo simulation, which would have required eliciting distributions for each of them in EKE Q1 and specification of a suitable model to combine them. It was also considered more rigorous and reliable than combining all the uncertainties in a single expert judgement since that would have required simultaneous consideration of both the exposure and toxicology uncertainties while each expert was specialised in either exposure or toxicology.

Figure 2.

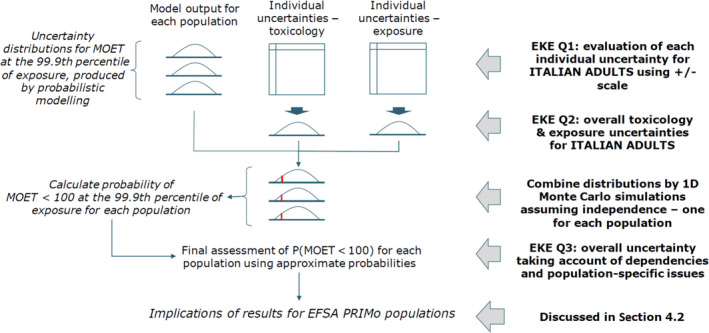
Overview of the approach to characterising overall uncertainty in the CRA

2.3.2. Identification of sources of uncertainty affecting the assessment

Sources of uncertainty affecting the assessment were identified as recommended by EFSA Scientific Committee (2018a,b).

The sources of uncertainty were first identified by expert discussion using a systematic approach, reviewing each part of the assessment for potential sources of uncertainty. Specifically, the experts examined each type of input data (e.g. occurrence date, processing factors…) and each part of the assessment model (e.g. Dose‐Addition model as assumption of the mode of combined toxicity, OIM model for the calculation of long‐term exposure…) and considered whether it was affected by any types of uncertainty, including those listed in Table 1 of the EFSA Scientific Committee (2018a,b) (e.g. ambiguity, accuracy, sampling uncertainty, missing data, missing studies, assumptions, excluded factors, use of fixed values, etc.). All sources of uncertainty identified in the CRA on chronic effects on the thyroid (EFSA, 2020a,b) were critically reviewed for their applicability to the present assessment.

Afterwards, the identified uncertainties were further discussed and precisely defined/described in such a way that they were unambiguously understood by the experts participating to the uncertainty analysis and overlapping with each other to the smallest possible extent. For instance, three distinct sources of uncertainty were identified regarding the handling of left‐censored measurements of residues, corresponding to three associated assumptions: assumption of the authorisation status for pesticide/commodity combinations, assumption of the use frequency for authorised pesticide/commodity combinations and assumption of the residue level (1/2 LOQ) to be imputed to the commodity when it was treated.

All the identified sources of uncertainty were listed in tables, which are presented in Section 3.2.1. The experts then collected and appraised further information that would be helpful to evaluate their impact. The results of these discussions and investigations were then summarised in a series of notes, which are included in Appendix E and cross‐referenced to the list of uncertainties.

The identified sources of uncertainty were subsequently divided into two groups: those relating to exposure and those relating to toxicology. In subsequent steps of the uncertainty analysis (EKE Questions 1 and 2, see Sections 2.3.3 and 2.3.4), the uncertainties relating to exposure were evaluated by the exposure experts in the Working Group and the uncertainties relating to toxicology were evaluated by the toxicology experts.

2.3.3. Evaluation of individual sources of uncertainty (EKE Question 1)

EKE Question 1 comprised two subquestions, both of which were addressed for each of the sources of uncertainty identified by the Working Group. The subquestions were specified as follows:

EKE Q1A: If this source of uncertainty was fully resolved (e.g. by obtaining perfect information on the issue involved) and addressed in the modelling, by what multiplicative factor would this change the median estimate of the MOET for CAG‐NCN at the 99.9th percentile of exposure in the Italian adult population at Tier II?

EKE Q1B: Is the impact of this source of uncertainty the same for the other populations that were assessed? If not, list those populations for which the impact would be smaller, and those for which it would be larger.

The role of these questions in the uncertainty analysis (depicted in Figure 1) and the detailed wording of the questions was explained to and discussed with the experts to ensure a common understanding. Examples were provided to illustrate the meaning of a source of uncertainty being ‘fully resolved’: e.g. if the cause of a source of uncertainty is that there are very few data available for one of the model inputs, or that the data are biased or unreliable, then EKE Q1A asks the experts to consider how the estimated MOET would change if the current data were replaced with a very large sample of perfectly reliable data, such that this source of uncertainty was removed. It was also explained that when assessing the impact of an uncertainty, the experts needed to consider the extent to which the active substances affected by it are risk drivers, as indicated by outputs from the Tier II calculations.

The meaning of ‘multiplicative factor’ was carefully explained to the experts, and they were asked to assess the factor using the scale shown in Figure 3. They were asked to express their uncertainty by giving a range of factors that they judged has at least a 90% probability of containing the true factor (i.e. the change in estimated MOET that would actually occur if the uncertainty was really resolved). For example: ‘‐ ‐ ‐/•’ means at least a 90% chance the true factor is between x1/10 and +20%; ‘++/++’ means ≥ 90% chance between 2x and 5x etc.

Figure 3.

Scale used by the experts when assessing EKE Question 1

It was explained to the experts that some sources of uncertainty were already quantified to some extent in the probabilistic modelling: specifically, sampling variability for occurrence and consumption data was quantified by bootstrapping. For these, the experts were asked to identify and assess any remaining uncertainty not addressed in the modelling.

When making their assessments, the experts were provided with the agreed description/definition of each of the uncertainties, the detailed notes summarising the information collected to support the assessment (Appendix E) and information on risk drivers (Section 3.1.2 and Annex C, Figure C.03).

Twelve experts participated in answering EKE Q1: six exposure experts and six toxicology experts. The questions were first addressed separately by each expert, working individually and remotely. Each expert was asked to answer both questions (Q1A and Q1B) for each of the uncertainties that related to their area of expertise (exposure or toxicology). The answers provided by the experts were then collated and differences between different experts were discussed in two MS teams meetings (one dedicated to exposure uncertainties and one dedicated to toxicology uncertainties) to arrive at a consensus judgement. The final judgements for EKE Q1A and Q1B for each source of uncertainty are reported in Section 3.2.2 and Appendix F.

2.3.4. Evaluation of combined impact of uncertainties relating to exposure and toxicology (EKE Question 2)

The EKE Q2 was specified as follows: If all the identified sources of uncertainty relating to [exposure/hazard identification and characterisation] were fully resolved (e.g. by obtaining perfect information on the issues involved) and addressed in the modelling, by what multiplicative factor would this change the median estimate for the MOET at the 99.9th percentile of exposure for CAG‐NCN in the Italian adult population at Tier II?

This question was addressed twice: once for the uncertainties relating to exposure and once for those relating to toxicology. As for EKE Q1, the experts’ assessment of the impact of the uncertainties was elicited as a multiplicative factor relative to median estimate of the MOET at the 99.9th percentile of exposure for Italian adults.

Before answering the question, the meaning of ‘perfect information’ in the EKE question was discussed and defined as ‘perfect information on actual consumption, occurrence, processing methods, and processing factors, perfect fit of the OIM model with the toxicokinetic and toxicodynamic processes, lowest BMDL20s for erythrocyte AChE inhibition from a perfect set of toxicity studies and perfect knowledge of CAG membership and how substances combine’.

The elicitation was conducted in two stages. In the first stage, 11 experts (the same experts as for EKE Q1 with the exception of one toxicology expert) worked separately to make individual judgements.

The experts’ uncertainty about the multiplicative factor required by the question was elicited in the form of a probability distribution using the ‘Sheffield’ protocol12 described in EFSA's guidance document on expert knowledge elicitation (EFSA, 2014a). Application of this to EKE Q2 was guided and facilitated by a member of the Working Group who has extensive experience with the Sheffield protocol. The facilitator also provided training to the experts in each step of the process, including how to make probability judgements and interpret fitted distributions, before they applied it to the present assessment.

The individual judgements were elicited using the quartile method (EFSA, 2014a): experts were asked first for their lower and upper plausible bounds for the multiplicative factor, then for their median estimate and finally for their lower and upper quartile estimates. The individual judgements were elicited in this order to mitigate psychological biases known to affect expert judgement, especially anchoring and adjustment, and overconfidence (EFSA, 2014a). Since the individual judgements were made remotely by experts working on their own, they were asked to enter them in the MATCH software13 (Morris et al., 2014), view the best fitting distribution and feedback statistics (33rd and 66th percentiles) provided by MATCH, and adjust their judgements until they were satisfied that the final distribution appropriately represented their judgement.

The experts were asked to take account of the following evidence when making their judgements, together with any other relevant information they were aware of: the evaluations of the individual uncertainties from EKE Q1 (Section 3.2.2 and Appendix F) and detailed supporting notes on them (Appendix E); the results of the cumulative exposure assessments, information on risk drivers and sensitivity analyses (Sections 3.1.2 and 3.1.3); detailed graphics and tables on the model outputs and contributions of risk drivers (Annex C, Figure C.03); tabulated data for the simulated individuals in the 99–100th percentile of total normalised exposure, showing the extent to which they were comprised of one or multiple substances and commodities (Annex C, Table C.03); and the EFSA Scientific report on the establishment of CAGs of pesticides for their effects on the nervous system (EFSA, 2019a).

The experts were provided with a template document in which to record their judgements, reasoning and final distribution. These were then used by the facilitator to produce one graph in which the distributions provided by all the experts for the question on toxicology uncertainties were plotted together and a second graph, showing the distributions for the question on exposure uncertainties.

In the second stage, the experts met by two MS teams meetings (one dedicated to exposure uncertainties and one dedicated to toxicology uncertainties) and worked together to develop consensus judgements.

The consensus judgements were elicited following the guidance for facilitation of consensus judgements in the Sheffield protocol provided by EFSA (2014a,b,c) and in the SHELF framework.14 The facilitator explained the form of consensus judgement required by the Sheffield method: not an average or compromise between the individual judgements, but the experts’ collective assessment of what a rational impartial observer would judge (‘RIO’ concept), having seen the evidence, the list of uncertainties and the individual judgements and having heard the experts’ discussion (EFSA, 2014a,b,c; Oakley and O'Hagan, 2016).

The consensus judgements were developed by facilitated discussion between the experts. First, the experts discussed the distributions fitted to their individual judgements and the evidence and reasoning that their judgements were based on. Next, the experts worked towards agreement on shared judgements, which they considered to be a consensus in the sense defined by the RIO concept (see above). The experts were first asked for their consensus judgement for the plausible range for the multiplicative factor. Then, three further consensus judgements were elicited using the probability method, to reduce the tendency of experts to anchor on their individual judgements for medians and quartiles (Oakley and O'Hagan, 2016). In the probability method (described in EFSA (2014a,b,c) as the fixed interval method), the experts are asked to judge the probability that the quantity of interest lies above (or below) some specified value. For this purpose, the facilitator chose three values in different parts of the plausible range, favouring regions where differences between the individual distributions were most marked. The experts’ consensus judgements for these three values, together with their consensus for the plausible range, were entered into the SHELF Shiny app for eliciting a single distribution15 and the best‐fitting distribution provided by the app was displayed for review by the experts.

A series of checks were then made and discussed with the experts: first, how closely the resulting distribution fitted the consensus judgements, then the values of the median, tertiles and 95% probability interval for that distribution. If any of these, or the visual shape of the distribution, were not judged by the experts as appropriate to represent their consensus, then alternative distributions fitted by the app were considered or, if necessary, the experts made adjustments to one or more of their judgements, until they were satisfied with the final distribution. For exposure uncertainties, this process was completed within the web meeting. For toxicology uncertainties, the process was completed by email using an approach based on the EFSA ‘Delphi’ EKE method (EFSA, 2014a,b,c), in which the facilitator conducted three rounds of email consultation with the experts to arrive at a final consensus distribution. A second distribution, which was also considered reasonable by all the experts but received fewer preferences, was also taken forward to the next step in order to assess the impact of the final choice on the combined uncertainty (see next section).

2.3.5. 1‐D Monte Carlo simulation to combine distributions quantifying uncertainties related to exposure and toxicology

In this step, the two consensus EKE Q2 distributions elicited to quantify uncertainties relating to exposure and toxicology, respectively, were combined by Monte Carlo simulation with an uncertainty distribution for the MOET at the 99.9th percentile of exposure generated by the model. The latter distribution comprised, for each modelled population, the 100 estimates of the MOET at the 99.9th percentile of exposure generated in the 100 outer loops (see Section 2.2.5). A computer programme to carry out this calculation was prepared in advance using the R software, assuming independence between the three distributions, and this programme was then run for each of the 10 consumer populations. This was done after the consensus EKE Q2 distributions became available, so that the results could be used as the starting point for EKE Q3.

Specifically, the following process was followed:

• Draw a sample of 10⁵ values from the experts’ exposure‐factor distribution.

• Draw a sample of 10⁵ values from the experts’ toxicity‐factor distribution.

• Multiply corresponding pairs of exposure‐factor and toxicity‐factor values to produce a sample of 10⁵ values for the combined toxicity and exposure factor.

For each consumer group:

• Multiply each of the 100 values for the estimates of the MOET at 99.9th percentile of exposure generated by the model by each of the 10⁵ values from the previous bullet. This results in 10⁷ values for the MOET at 99.9th percentile of exposure, adjusted for combined uncertainties (MOET adjusted for uncertainties).

• From these 10⁷ values, the MOETs at 2.5th, 25th, 50th, 75th and 97.5th percentiles of the exposure as well as the probability of the MOET at the 99.9th percentile of exposure being less than 100 were calculated for graphical presentation and tabulation (Figure 6, Table 21).

Figure 6.

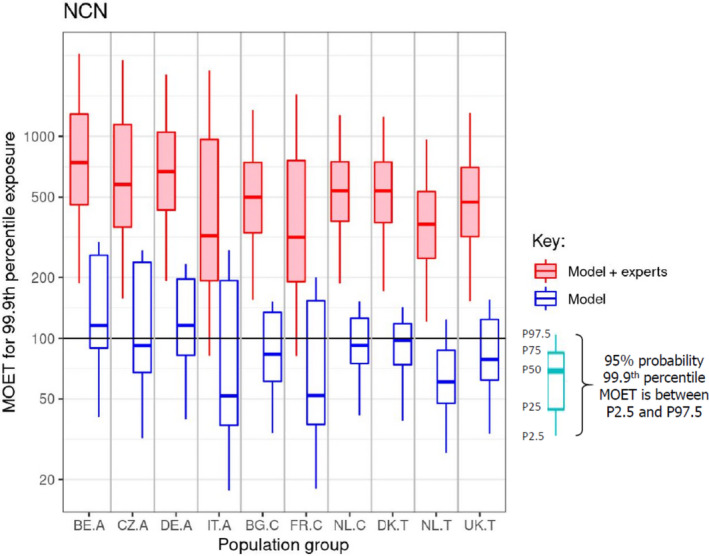
CAG‐NCN: ‘Model’ boxplots show the output of the Tier II model for the MOET at the 99.9th percentile of exposure in each consumer population in 2016–2018. ‘Model+experts’ boxplots show the result of combining the output of the Tier II model with the elicited distributions quantifying additional sources of uncertainty related to toxicology and exposure, assuming perfect independence between them. Note that the vertical axis is plotted on a logarithmic scale; the values plotted for ‘model+experts’ are shown numerically in Table 21. A key to the populations and explanation of the boxplots are provided in the footnote below the graph

• Keys: Population groups: BE.A (Belgian adults), CZ.A (Czech Republic adults), DE.A (German adults), IT.A (Italian adults), BG.C (Bulgarian children), FR.C (French children), NL.C (Dutch children), DK.T (Danish toddlers), NL.T (Dutch toddlers), UK.T (United Kingdom toddlers). The lower and upper edges of each boxplot represent the quartiles (P25 and P75) of the uncertainty distribution for each estimate, the horizontal line in the middle of the box represents the median (P50) and the ‘whiskers’ above and below the box show the 95% probability interval (P2.5 and P97.5).

Table 21.

CAG‐NCN Statistics for the MOET at the 99.9th percentile of exposure in each consumer population in 2016–2018, calculated by combining the elicited distributions for uncertainties related to exposure and toxicology with the output of the Tier II model. P2.5, P25 etc. refer to the percentiles plotted in the ‘model+experts’ boxplots in Figure 6

Population group	MOET at the 99.9th percentile of exposure distribution combining model and elicited uncertainties related to toxicology and exposure (from ‘model+expert’ boxplots in Figure 6)					Probability of 99.9%ile MOET < 100 (%)*
	P2.5	P25	P50	P75	P97.5
Belgian adults	187	456	742	1,286	2,558	0.13 (0.15)
Czech Rep. adults	157	354	578	1,143	2,374	0.30 (0.35)
German adults	192	430	670	1,048	2,016	0.10 (0.11)
Italian adults	82	193	321	965	2,115	4.91 (5.46)
Bulgarian children	155	332	499	743	1,344	0.30 (0.36)
French children	82	191	316	758	1,608	4.96 (5.51)
Dutch children	187	378	538	747	1,273	0.09 (0.11)
Danish toddlers	171	373	537	745	1,248	0.24 (0.28)
Dutch toddlers	121	248	365	553	965	1.05 (1.22)
United Kingdom toddlers	153	318	472	702	1,301	0.31 (0.37)

^*Figures given between brackets were obtained with the sensitivity analysis using the alternative distribution for uncertainties related to toxicology, instead of the consensus distribution (see Table 19). They show that the choice of the consensus distribution has a minor impact on the results.

These computations were conducted twice to explore the impact of the final choice of the consensus distribution for toxicology uncertainties: once with the preferred distribution and once with the alternative distribution, which was also considered to be reasonable by all the toxicology experts.

The results of the Monte Carlo simulations were presented in two forms: first, boxplots showing the median, quartiles and 95% probability interval for the quantified uncertainty of the MOET at the 99.9th percentile of exposure for each of the 10 consumer populations in each CAG; and second, tables containing the numerical values used in the boxplots plus, for each CAG and population, the calculated probability of the MOET at the 99.9th percentile of exposure being less than 100. The latter probabilities were then used as the starting point for judgements on EKE Q3 (see below).

In addition, the Monte Carlo simulations described above were extended to explore the impact of different degrees of dependence between the uncertainties relating to exposure and toxicology (specifically, rank correlations (rho) of –1, –0.75, –0.5, –0.25, 0.25, 0.5, 0.75 and 1).

2.3.6. Accounting for dependencies, differences between populations and other uncertainties (EKE Question 3)

Two versions of EKE Question 3 were defined, one for the Italian adults and one for the other populations. This was necessary because the aim of EKE Q3 was to take account of all remaining uncertainties. For the Italian population, this comprised mainly the potential impact of dependencies between the distributions combined in the Monte Carlo simulations (described in the preceding section) while, for the other populations, EKE Q3 also assessed the additional uncertainty due to using the toxicology and exposure uncertainty distributions elicited for Italian adults also in the computations for the other nine consumer populations.

For Italian adults, EKE Q3 was specified as follows: If all the uncertainties in the model, exposure assessment, hazard identification and characterisation and their dependencies were fully resolved (e.g. by obtaining perfect information on the issues involved) and addressed in the modelling, what is your probability that this would result in the estimated MOET at 99.9th percentile of exposure for the Italian adult population in 2016–2018 being below 100?

For the other nine consumer populations, EKE Q3 was specified as follows: If all the uncertainties in the model, exposure assessment, hazard identification and characterisation and their dependencies, and differences in these between populations, were fully resolved (e.g. by obtaining perfect information on the issues involved) and addressed in the modelling, what is your probability that this would result in the estimated MOET at 99.9th percentile of exposure for [name of population] in 2016–2018 being below 100?

For both versions of the question, it was agreed that ‘perfect information’ had the same meaning as that defined for EKE Q2 (Section 2.3.4).

Before eliciting EKE Q3, the Working Group reviewed the issues to be considered. The facilitator explained that a dependency would exist between the toxicology and exposure uncertainty distributions if having perfect information on toxicology would alter the experts’ assessment of the uncertainties on exposure, or vice versa. The experts considered that dependencies could be expected if resolving some uncertainties led to a change in the risk drivers, which might alter their assessment of the remaining uncertainties. The facilitator also explained that any additional uncertainties, which the experts considered had not been fully accounted for earlier, including any arising from the EKE process itself, should also be taken into account when making judgements for EKE Q3.

The facilitator asked the experts to consider, as their starting point for answering Q3 for each population, the calculated probability of the MOET at the 99.9th percentile of exposure being less than 100 provided by the Monte Carlo simulations in the preceding step. In addition, the experts were advised to consider the following evidence:

• The information on the calculated MOET distribution for each population contained in the boxplots and tables reflecting the Monte Carlo simulations described in the preceding section;

• The results of the additional simulations exploring the impact of different degrees of dependence between the uncertainties relating to exposure and toxicology;

• Considerations about possible dependencies between the uncertainties relating to exposure and toxicology;

• Considerations identified in the group discussion of population differences for individual sources of uncertainty (outcome of the EKE Q1B in the Section 3.2.2 and Appendix F);

• And their personal knowledge and reasoning about the issues involved.

Judgements for EKE Q3 were elicited using the Approximate Probability Scale (Table 12), which is recommended in EFSA's guidance on uncertainty analysis for harmonised use in EFSA assessments (EFSA Scientific Committee, 2018a). The experts were advised to focus on the numeric probability ranges, not the verbal terms, and to consider which range (or, if appropriate, set of ranges) described their judgement on EKE Q3 for each population.

Table 12.

Approximate Probability Scale for harmonised use in EFSA

Probability term	Subjective probability range
Almost certain	99–100%
Extremely likely	95–99%
Very likely	90–95%
Likely	66–90%
About as likely as not	33–66%
Unlikely	10–33%
Very unlikely	5–10%
Extremely unlikely	1–5%
Almost impossible	0–1%

Elicitation for EKE Q3 was conducted in two stages.

In the first stage, the 11 experts (the same experts as for EKE Q2) worked remotely and separately to make individual judgements. They were asked to record their individual judgements in spreadsheet templates provided by the facilitator. The completed templates were collected, and the judgements were collated in a table, showing the number of experts who selected each probability range for each population.

While the individual judgements were being made, it was noted by one of the exposure experts that the sensitivity analyses showed that alternative assumptions for missing processing factors and excluding a specific sample of occurrence data had a much larger impact on results for the Italian adults than for the other populations. This implied that the impact of these sources of uncertainty on the assessment would be less for the other populations than for Italian adults, which would need to be taken into account by the experts when considering EKE Q3. To help the experts make judgements about this, new calculations were performed, showing how shifting the probability distribution for the MOET at the 99.9th percentile up or down (to take account of differences in uncertainty compared to the Italian population) would change the % probability that the MOET at the 99.9th percentile would be 100 for each population. This was repeated for different values of rho, to help the experts take account of dependency between the toxicology and exposure uncertainties. The results of these calculations were made available to the experts as additional evidence to support their assessment of EKE Q3. It was explained to the experts that the calculations assumed the whole of the distribution for the MOET at the 99.9th percentile is shifted up or down by the same amount and that the shape and width of the distribution are unchanged.

In a second stage, the experts met by MS Teams and the table compiling their judgements were displayed on screens for review by the group. The facilitator then led a discussion to develop consensus judgements (applying the RIO concept, see Section 3.2.4). This was done first for the Italian population, and subsequently for all other nine populations. The agreed numeric probability ranges for each population and the associated rationale was displayed by the facilitator for review by the experts.

3. Results

Section 3.1 summarises the chronic cumulative exposure estimates obtained from the calculations. Exposure estimates are presented for CAG‐NCN, two different scenarios (Tier I and Tier II) and 10 different dietary surveys. More detailed results (including graphs and charts) are provided in the annexes.

• Annex B presents the results of the Tier I cumulative exposure calculations to CAG‐NCN.

• Annex C presents the results of the Tier II cumulative exposure calculations to CAG‐NCN.

All exposure estimates are expressed in total margin of exposure (MOET), which is the ratio of a toxicological reference dose (i.e. NOAEL) to the estimated exposure (see Section 2.2.6). Hence, an MOET below 1 implies that the estimated exposure exceeds the NOAEL. Likewise, an MOET of 100 means that the estimated exposure is 100 times lower than the NOAEL. The threshold for regulatory consideration agreed among Member States is an MOET of 100 at the 99.9th percentile of the exposure distribution (European Commission, 2018). MOETs below this threshold may therefore trigger risk management decision by the European Commission and Member States.

It should be emphasised that results presented are exposure estimates based on the methods and assumptions listed in Section 2 and do not account for all possible uncertainties. A complete analysis of all identified uncertainties is therefore performed in Section 3.2 as preliminary step to the overall risk characterisation (see Section 4).

3.1. Cumulative exposure assessments using SAS^® software

3.1.1. Tier I

The results in Table 13 were obtained using the Tier I calculations. The largest margins of exposure were observed for adults, where MOET estimates at the 99.9th percentile ranged from 21.9 (Czechia) to 16.8 (Italy). The margins of exposure for toddlers and other children were smaller. MOET estimates for these age classes ranged from 5.24 (Dutch toddlers) to 11.6 (French children).

Table 13.

Estimates of the total margin of exposure (MOET) and their corresponding 95% confidence intervals at the 50th, 95th, 99th and 99.9th percentiles of the exposure distribution for the Tier I scenario of CAG‐NCN

Country	Population class	50th Percentile	95th Percentile	99th Percentile	99.9th Percentile
Belgium	Adults	82.7 [67.4–95.4]	42 [31.6–46.3]	31.2 [24.7–35.5]	21.1 [15.2–27.2]
Czechia	Adults	85.5 [61.7–102.8]	43.9 [29.6–52.7]	33 [21.2–39.8]	21.9 [16.3–26.8]
Germany	Adults	81 [71.7–86.4]	34.7 [30.7–36.8]	24.9 [22.1–26.6]	17.2 [14.7–18.2]
Italy	Adults	47 [24.8–69.7]	29.6 [15.7–41.8]	23.6 [12–33.5]	16.8 [9.52–25.3]
Bulgaria	Other children	28.7 [26.7–30.3]	15 [12.9–15.9]	9.69 [7.85–11.5]	7.84 [7.52–8.85]
France	Other children	37.8 [30.6–43.1]	19.5 [12.8–22.8]	15.4 [10.2–18.7]	11.6 [8.99–15]
Netherlands	Other children	35.7 [31.6–38.2]	16.6 [15.3–18.3]	13 [11.3–14.5]	9.83 [8.58–11.8]
Denmark	Toddlers	31 [28.7–32.4]	16.9 [15.7–18.1]	12.6 [10.2–13.4]	7.23 [5.04–10.8]
Netherlands	Toddlers	27 [24.3–29.1]	12.8 [11.1–14.5]	9.61 [6.17–11.4]	5.24 [4.42–8.99]
United Kingdom	Toddlers	38.6 [35.1–41.1]	20 [17.3–21.7]	14.4 [12–16.6]	9.54 [6.89–12.1]

The main contributors were identified for the upper percentile of the distribution (see Annex B, Figure B.03 and Table B.02). Omethoate made the greatest contribution to the upper tail exposure (17–40%) followed by azinphos‐ethyl (6.4–34.4%), diazinon (4.9–31.1%), profenofos (7.7–22.5%), dichlorvos (7.3–12.8%) and carbofuran (4.5–8.2%). Most of the contribution for omethoate came from olives for oil production (up to 28.9%), oranges (up to 9.2%) and apples (up to 8%). Other substances only played a minor role in overall exposure (not more than 5%).

Although MOET estimates below 100 were observed for all populations, the Tier I calculations are by nature very conservative. This is clearly evidenced by the contributions of azinphos‐ethyl, diazinon, profenofos, dichlorvos and carbofuran, where occurrence data below the LOQ represent between 99 and 100% for these pesticides (see Annex A – Table A.09). Under the Tier I assumptions, the majority of these occurrence data were assumed to be 1/2 LOQ, which may not be representative considering that authorisations for these six pesticides are very limited (see Annex A – Table A.06). The authorisation status is accounted for under the Tier II assumptions.

3.1.2. Tier II

The results from the Tier II calculations are displayed in Table 14. As with the Tier I result, the largest margins of exposure at the 99.9th percentile were observed for adults; adult MOETs ranged from 51.6 (Italy) to 116 (Germany). The difference between the margins of exposure for other children and toddlers compared to adults, however, was much smaller than in the Tier I calculations; the MOETs for other children ranged from 51.8 (France) to 91 (Netherlands) whilst the MOETs for toddlers ranged from 60.3 (Netherlands) to 97.4 (Denmark).

Table 14.

Estimates of the total margin of exposure (MOET) and their corresponding 95% confidence intervals at the 50th, 95th, 99th and 99.9th percentiles of the exposure distribution for the Tier II scenario of CAG‐NCN

Country	Population class	50th Percentile	95th Percentile	99th Percentile	99.9th Percentile
Belgium	Adults	442 [235–701]	204 [77.6–440]	159 [52.2–369]	115 [40.2–289]
Czechia	Adults	371 [175–702]	173 [61–420]	133 [45.2–340]	91 [31.5–271]
Germany	Adults	539 [410–682]	257 [113–411]	178 [69.7–327]	116 [39.5–232]
Italy	Adults	150 [48–650]	90.6 [27.5–404]	70.3 [21.6–329]	51.6 [16.5–266]
Bulgaria	Other children	287 [256–328]	147 [82–199]	105 [54.4–164]	82.9 [32.7–151]
France	Other children	259 [139–432]	83.6 [33.5–266]	63.4 [20.6–215]	51.8 [16.6–191]
Netherlands	Other children	286 [178–401]	154 [69.1–244]	118 [52–192]	91 [41.3–149]
Denmark	Toddlers	286 [205–362]	173 [115–222]	123 [75.9–165]	97.4 [38.6–143]
Netherlands	Toddlers	235 [154–324]	122 [60.5–186]	82.6 [35.9–146]	60.3 [26.8–120]
United Kingdom	Toddlers	290 [219–364]	147 [71.4–216]	104 [46.2–175]	78.1 [33.1–153]

The main contributors for the exposures exceeding the 99th percentile were different from the Tier I calculations (see Annex C, Figure C.03 and Table C.02). Omethoate and dichlorvos remained major contributors to the exposure (35.6–81.4% and 2.9–6.0%, respectively), whilst pirimiphos‐methyl (8.8–20.9%), chlorpyrifos (7.3–36.7%), monocrotophos (3–12.5%) and dimethoate (4.2–10%) were new major contributors. Other substances contributed for less than 5% of exposure. Pesticide/commodity combinations contributing, in Tier II, at least 5% of the cumulative exposures exceeding the 99th percentile estimate are reported for each of the 10 populations in Table 15.

Table 15.

Pesticide/commodity combinations contributing, in Tier II, at least 5% of the cumulative exposures exceeding the 99th percentile estimate in the assessed populations

Pesticide	Commodity	Contribution to the cumulative exposure (%)
		Adults				Other children			Toddlers
		BE	CZ	DE	IT	BG	FR	NL	DK	NL	UK
Omethoate	Olives for oil production	47	49	42	57	36	53	35	31	35	38
Pirimiphos‐methyl	Wheat	12	11	10	13	12	10	20	11	8	15
Chlorpyrifos	Oranges	< 5	< 5	7	< 5	< 5	< 5	5	9	5	< 5
Monocrotophos	Drinking water	7	7	6	< 5	6	5	7	8	< 5	7
Dimethoate	Olives for oil production	6	6	5	7	< 5	7	< 5	< 5	< 5	< 5
Dichlorvos	Drinking water	5	< 5	< 5	< 5	< 5	< 5	< 5	5	< 5	5

The change in the main contributors is likely due to the different assumptions made in the Tier II calculations. Under this scenario, left‐censored data are imputed with ½ LOQ based on estimated use frequencies. In Tier I, even when only one quantifiable finding was identified, all left‐censored data are imputed with ½ LOQ. The different treatment of left‐censored data caused the MOETs to increase approximately fivefold from Tier I to Tier II.

3.1.3. Sensitivity analyses

Although Tier II calculations are expected to reflect a more refined scenario, this scenario was still subject to uncertainties. Some of these uncertainties were addressed through sensitivity analyses. A comparison between the MOETs obtained at the 99.9th percentile from the Tier II calculations and their corresponding sensitivity analyses is made in Table 16.

Table 16.

Estimates of the total margin of exposure (MOET) and their corresponding 95% confidence intervals at the 99.9th percentiles of the exposure distribution for the Tier II scenario of CAG‐NCN and several sensitivity analyses

Country	Population class	Tier II	Sensitivity analysis Aa	Sensitivity analysis Bb	Sensitivity analysis Cc	Sensitivity analysis Dd	Sensitivity analysis Ee	Sensitivity analysis Ff	Sensitivity analysis Gg	Sensitivity analysis Hh	Sensitivity analysis Ii	Sensitivity analysis Jj	Sensitivity analysis Kk	Sensitivity analysis Ll
Belgium	Adults	115 [40.2–289]	66.3 [30.5–81.2]	119 [41.2–307]	373 [303–488]	147 [38.4–314]	269 [234–311]	118 [35.2–290]	101 [28.8–288]	113 [39.8–303]	120 [37.6–467]	112 [111–156]	151 [49.6–324]	140 [39.6–297]
Czechia	Adults	91 [31.5–271]	52.8 [25.1–87.6]	96.1 [31.3–339]	444 [419–471]	112 [31–282]	256 [202–293]	88 [26–261]	74.7 [20–265]	86.7 [35.9–289]	106 [30.5–432]	84.3 [83.8–119]	118 [37.3–294]	103 [31–284]
Germany	Adults	116 [39.5–232]	53.9 [29.4–69.1]	121 [39–257]	363 [323–399]	128 [38.4–238]	211 [163–243]	104 [35.8–218]	93.6 [28–226]	105 [42.7–232]	118 [41.8–277]	106 [105–138]	133 [49.4–240]	121 [36.3–239]
Italy	Adults	51.6 [16.5–266]	30.9 [12.6–75.1]	58.3 [15.9–341]	503 [389–558]	59.1 [14.8–264]	212 [155–296]	46.8 [14.2–227]	40.2 [10.1–213]	51.9 [18.1–260]	49.3 [15.8–310]	44.5 [44.2–65.1]	64.6 [18.2–296]	57.1 [15.5–274]
Bulgaria	Other children	82.9 [32.7–151]	35.3 [21.6–39.5]	93.3 [33–172]	232 [214–274]	92.6 [29.9–150]	140 [127–155]	77.9 [29.2–141]	67.9 [19.6–145]	81 [36.4–153]	91.5 [33–203]	75.5 [75–98.3]	94.7 [34–154]	85.9 [31.2–152]
France	Other children	51.8 [16.6–191]	32.2 [12.9–57.1]	55.3 [16.1–212]	263 [227–348]	60.6 [14.7–188]	164 [143–196]	46.4 [13.6–165]	39.7 [10.7–165]	51.5 [19.7–173]	51.6 [14.9–252]	43.5 [43.2–62]	66 [19.8–200]	55.7 [14.5–187]
Netherlands	Other children	91 [41.3–149]	38.2 [24.8–47]	96.4 [39.3–166]	222 [165–305]	103 [37.9–160]	130 [110–167]	86.2 [33.6–132]	77.8 [28.1–131]	89.1 [42.7–138]	103 [38.1–212]	88.5 [87.9–115]	108 [44.9–146]	99.1 [37.4–150]
Denmark	Toddlers	97.4 [38.6–143]	33.3 [26.5–42.6]	101 [28.7–163]	233 [191–263]	105 [38.2–140]	130 [106–145]	96.3 [38.2–131]	88.3 [28.5–132]	100 [38.2–139]	112 [41–187]	93.4 [93.1–114]	107 [40.2–142]	102 [36.3–143]
Netherlands	Toddlers	60.3 [26.8–120]	26.7 [16.9–36.1]	66.7 [26.3–137]	235 [229–309]	64.4 [24.4–123]	92.7 [80.1–126]	62.8 [25–106]	48.9 [17.8–108]	59.5 [28.1–114]	68.8 [26.5–132]	56.3 [55.8–68.8]	75.8 [30–123]	63.6 [25.1–119]
United Kingdom	Toddlers	78.1 [33.1–153]	29 [19.9–39.7]	88.1 [32–172]	260 [244–276]	88.1 [30.3–154]	132 [110–154]	72.4 [28.7–139]	65.8 [22.2–143]	75.3 [34.9–153]	85.5 [32.8–218]	74.6 [73.9–94.4]	90.4 [39.5–157]	81.9 [31.5–158]

^aSensitivity analysis assuming that left‐censored data are at 1/2 LOQ when the use of the active substance is authorised.

^bSensitivity analysis assuming that all left‐censored data are at zero.

^cSensitivity analysis assuming that residues will not be present in any processed food.

^dSensitivity analysis excluding foods for infants and young children.

^eSensitivity analysis excluding the sample with the highest measurement for the sum of dimethoate and omethoate in olives for oil production.

^fSensitivity analysis excluding pesticides belonging to the N‐methyl carbamates group.

^gSensitivity analysis excluding samples obtained through a selective sampling strategy.

^hSensitivity analysis assuming that a pesticide is authorised for use in a commodity when the percentage of positive findings in that commodity exceeds 1%.

ⁱSensitivity analysis excluding drinking water.

^jSensitivity analysis excluding sampling uncertainty (i.e. outer loop execution without resampling of the occurrence data and food consumption data).

^kSensitivity analysis assuming that omethoate is not authorised for use on olives for oil production.

^lSensitivity analysis excluding samples reported by pre‐accession countries.

Sensitivity analyses A and B tested the uncertainty of imputing left‐censored data with 1/2 LOQ based on use frequencies. Sensitivity analysis A imputes all left‐censored data with 1/2 LOQ based on authorisation rather than use frequency. This is over‐conservative, as the commodities are not expected to be treated with all authorised substances at the same time. On the other hand, sensitivity analysis B imputes all left‐censored data with zero. This is not sufficiently conservative, as not all left‐censored data would be true zeros. In sensitivity analysis A, the MOETs dropped by 1.61–2.69 times. In sensitivity analysis B, the MOETs rose 1.03–1.13 times. Although the results from the Tier II calculations were in between the results from sensitivity analyses A and B, the margins of exposure obtained from Tier II were closer to those of sensitivity analysis B. This indicates that imputation of left‐censored data based on use frequency resulted primarily in zero values.

Sensitivity analysis C investigated the effect missing processing factors might have on the margins of exposure. When no residues were assumed to be present in processed foods, the MOETs rose by a factor of 2.39–9.74. This change indicates that processing factors were not available for most of the major contributors to exposure (see Annex A – Table A.03). Although including additional processing factors would likely not increase the margins of exposure to the extent suggested in sensitivity analysis C, more information on processing factors could substantially reduce the uncertainty.

Sensitivity analysis D investigated the effect of excluding foods for infants and young children in CAG‐NCN. There were no substantial changes in the margins of exposure when this assumption was made. This confirms previous findings of EFSA that exposure of toddlers to pesticide residues mainly comes from conventional foods (EFSA PPR Panel, 2018). This is due to the default MRL of 0.01 mg/kg, which applies to pesticide residues in foods for infants and young children.

Furthermore, results for the Tier II scenario are characterised by large confidence intervals compared to results previously obtained for the dietary exposure assessment to pesticides affecting the thyroid (EFSA, 2019b). These large confidence intervals are caused by the limited number of measurements for dimethoate and omethoate in olives for oil production (see Annex A – Table A.09). Out of 79 olive samples, 57 were analysed for the sum of dimethoate and omethoate. None of these measurements exceeded 0.08 mg/kg, except for one measurement of 4.9 mg/kg. This data set generates a high variability in the estimated occurrence of omethoate in olives, which is subsequently reflected in the (sampling) uncertainty interval of the exposure estimates.

An additional sensitivity analysis E was therefore performed to assess the impact of excluding this highest measurement in olives. When this sample is excluded a twofold increase of the MOET is observed in average and the width of the confidence interval is reduced by a factor of five. This provides an indication of how the outcome of this exposure assessment might be impacted if the sampling uncertainty for this commodity were to be resolved, i.e. if more samples were obtained to estimate more accurately how frequently such high values actually occur in olives.

In order to investigate the robustness of the results for Tier II, additional sensitivity analyses were carried out. Sensitivity analysis F investigated the effect of excluding pesticides belonging to the group of N‐methyl carbamates (i.e. aldicarb, benfuracarb, carbaryl, carbofuran, carbosulfan, formetanate, methiocarb, methomyl, oxamyl, pirimicarb and thiodicarb). This exclusion led to mostly decreases of MOETs by a factor of 1.01–1.12 (except for Belgium Adults and Dutch Toddlers). Sensitivity analysis G tested the effect of excluding samples obtained through a selective sampling strategy and resulted in a 1.1‐ to 1.3‐fold decrease of the MOETs. Sensitivity analysis H investigated the assumption that a pesticide would be authorised for use in a commodity when the percentage of positive findings in that commodity exceeds one percent. This analysis resulted in a minor decrease for MOETs by a factor of 1.01–1.1 (except for Danish Toddlers). Sensitivity analysis I was conducted in order to examine the effect of excluding the exposure via drinking water. This assumption caused some increase in the MOETs, ranging from 1.02 to 1.16 times. Sensitivity analysis J investigated the effect of removing sampling variability, meaning that the outer loop executions were performed without resampling (or bootstrapping) the occurrence and food consumption data. This resulted in a slight decrease of MOETs (1.03‐ to 1.19‐fold) but, more importantly, the width of the confidence intervals was reduced by an approximate factor of 10. Sensitivity analysis K investigated the assumption that omethoate would not be authorised for use on olives, which resulted in a 1.1‐ to 1.3‐fold increase of the estimated MOETs. Lastly, sensitivity analysis L investigated the effect of excluding samples from pre‐accession countries (Albania, Bosnia and Herzegovina, Kosovo, Montenegro, Republic of North Macedonia, Serbia and Turkey). Results revealed that this assumption leads to an increase of MOETs by 1.04–1.22 times.

3.2. Uncertainty analysis

3.2.1. Sources of uncertainty

Thirty‐two sources of uncertainty related to the assessment inputs were identified as affecting the CRA (Table 17).

Table 17.

Sources of uncertainty concerning the input data and affecting the CRA of chronic erythrocyte AChE inhibition (CAG‐NCN)

Assessment input	Type of uncertainty	Uncertainty number	Description	Area of expertise
Consumption data	Excluded data	U1	Consumption data of animal commodities and plant commodities not in the list of the 35 selected commodities and their processed derivatives have not been considered in the assessment.	Exposure
	Ambiguity	U2	The consumption data do not always discriminate between different commodities of a same group as defined in part B of annex I to Regulation (EC) No 396/2005 (e.g. tomatoes and cherry tomatoes are considered as tomatoes).	Exposure
	Accuracy	U3	The accuracy of the reported amount of food consumed in surveys may be affected by methodological limitations or psychological factors.	Exposure
	Sampling variability	U4	The reliability of risk estimates at the 99.9th percentile of exposure in the 10 populations under consideration is affected by the sample size (number of consumers) of the respective surveys.	Exposure
	Sampling bias	U5	Selection bias of consumers in food consumption surveys affects the representativeness of consumption data of the respective populations.	Exposure
	Use of fixed values	U6	In the RPC model, one invariable recipe and conversion factor are used to convert the amount of food consumed into the respective amount of raw primary commodity.	Exposure
Occurrence data	Missing data	U7	The contribution of active substance/commodity combinations, for which occurrence data are missing and extrapolation from another commodity is not possible, was not accounted in the assessment.	Exposure
	Excluded data	U8	The contribution to the risk of metabolites and degradation products not included in the residue definition for monitoring has not been considered.	Exposure
	Ambiguity	U9	The occurrence data do not always discriminate between different commodities of a same group as defined in part B of annex I to Regulation (EC) No 396/2005 (e.g. tomatoes and cherry tomatoes are considered as tomatoes).	Exposure
	Accuracy	U10	The accuracy of the quantification of residue levels above the LOQ is affected by the laboratory analytical uncertainty.	Exposure
	Sampling variability	U11	The reliability of risk estimates at the 99.9th percentile of exposure in the 10 populations under consideration is affected by the sample size (number of occurrence data) for each pesticide/commodity combination.	Exposure
	Sampling bias	U12	Selection bias of lots of commodities to be controlled in official monitoring programmes affects the representativeness of occurrence data. See Section 2.2.2.4 on the extraction criteria applied to the monitoring data.	Exposure
	Extrapolation uncertainty	U13	In case of extrapolation of occurrence data between 2 commodities, it is uncertain that the residue profiles in the 2 commodities are actually identical. See Sections 2.2.3.3 and 2.2.4.1.3 regarding the extrapolation rules.	Exposure
	Other uncertainty	U14	It is uncertain whether the use of pooled occurrence data from all EU Member states is representative of the actual residue levels to which the 10 populations under consideration are actually exposed to.	Exposure
	Assumption	U15	The assumption used to assign occurrence data to active substances in case of unspecific residue definition for monitoring (see Sections 2.2.2.3 and 2.2.4.1.1) is subject to uncertainty.	Exposure
	Assumption	U16	In the handling of left‐censored data, the assumption about the authorisation status of the pesticide/commodity combinations under consideration (see Section 2.2.3.2) is subject to uncertainty.	Exposure
	Assumption	U17	In the handling of left‐censored data, the assumption about the use frequency for authorised pesticide/commodity combinations (see Section 2.2.4.1.3) is subject to uncertainty.	Exposure
	Assumption	U18	In the handling of left‐censored data, the assumption about the residue level (1/2 LOQ as imputed value) when an active substance is used, and its residues are below the LOQ, is subject to uncertainty.	Exposure
	Assumption	U19	The assumption about the occurrence of residues in drinking water (see Section 2.2.4.1.4) is subject to uncertainty.	Exposure
Processing factors	Assumption	U20	The assumption that pesticide residues are transferred without any loss to processed commodities when processing factors are not available is subject to uncertainty.	Exposure
	Ambiguity	U21	The assignment of processing factors, derived from a limited number of standardised studies, to food items of the EFSA food classification and description system (FoodEx) resulting from multiple processing techniques of the EFSA RPC‐model, is subject to uncertainty. See Section 2.2.3.4 for the principles of assignment of processing factors.	Exposure
	Accuracy	U22	In processing studies, the accuracy of the quantification of residue levels above the LOQ in raw and processed commodities is affected by the laboratory analytical uncertainty.	Exposure
	Accuracy	U23	Processing factors are overestimated when residue levels in the processed commodity are below the LOQ.	Exposure
	Use of fixed values	U24	The value of processing factors used in the calculations is the median value of a limited number of independent trials.	Exposure
	Excluded data	U25	Some processing factors are not considered in the assessment (e.g. peeling and washing of commodities with edible peel).	Exposure
NOAELs	Adequacy of the CAG	U26	It is uncertain whether the CAG contains all the OPs and NMC insecticides causing the effect.	Toxicology
	Adequacy of the CAG	U27	There is uncertainty about the contribution of pesticides other than OPs and NMCs to erythrocyte AChE inactivation through oxidative stress and further inhibition of enzyme activity.	Toxicology
	Adequacy of the CAG	U28	It is uncertain whether the CAG contains only the active substances causing the effect.	Toxicology
	Accuracy	U29	The accuracy of the NOAEL‐setting is affected by the original studies/data quality (e.g. study conducted under Good Laboratory Practice GLP or not, guidelines referred to or not, statistical analysis performed or not, overall quality of reporting).	Toxicology
	Accuracy	U30	The accuracy of the NOAEL‐setting is affected by the data collection methodology (interpretation of raw data by the assessors, transfer of information from original studies to source documents, and from source documents to working documents (excel spreadsheets).	Toxicology
	Accuracy	U31	The accuracy of the NOAEL‐setting is affected by the assessment methodology and principles (i.e. how the available information was assessed to derive NOAELs for erythrocyte AChE inhibition).	Toxicology
	Accuracy	U32	The accuracy of the NOAEL‐setting is affected by the study design of the critical study (e.g. dose selection and spacing, study duration, route of administration, analytical methods…).	Toxicology

Three additional sources of uncertainty were found to be associated with the assessment methodology and are listed in Table 18.

Table 18.

Sources of uncertainty concerning the assessment methodology and affecting the CRA of chronic erythrocyte AChE inhibition

Element of the assessment methodology	Uncertainty number	Description	Area of expertise
Dose‐addition	U33	It is uncertain how well dose‐addition represents the actual mode of combined toxicity	Toxicology
OIM model	U34	It is uncertain how well the chronic exposure calculation model (OIM) fits to the human toxicokinetic and toxicodynamic processes involved in the effect	Exposure and toxicology
UF for intraspecies variability	U35	It is uncertain if the default UF for intraspecies variability covers the sensitivity to AChE inhibition of the elderly and infants below 16 weeks of age.	Toxicology

Out of these 35 sources of uncertainty,16 34 are retained for the elicitation of their impact in Section 3.2.2. It was decided to exclude the source of uncertainty U27 from the next step of the process, due to specific difficulties which are described below.

3.2.1.1. Exclusion of U27 (contribution of substances acting through oxidative stress) from the next steps of the uncertainty analysis

Oxidative stress has been reported to play an important role in the toxicity of various pesticides in both human and animal studies. Different pesticides classes have been involved, including OPs (Ranjbar et al., 2002; Lee et al., 2007; Possamai et al., 2007; Deeba et al., 2017), NMCs (Mansour et al., 2009), organochlorines (Stevenson et al., 1995; Pal et al., 2009), pyrethroids (Deeba et al., 2017; Kale et al., 1999; Raina et al., 2009), neonicotinoids (El‐Gendy et al., 2010), triazines (Singh et al., 2010), dithiocarbamates and paraquat (Ahmad et al., 2010). Oxidative stress is usually evidenced by increased concentration of plasma and red blood cell thiobarbituric acid reactive substances, changes in antioxidant status and altered activities of cellular enzymes (Prakasam et al., 2001).

There have been studies published to indicate that other pesticide classes besides OPs and NMCs, such as pyrethroids and azoles, can also inhibit AChE in erythrocytes and/or the CNS (Abd‐Elhakim et al., 2020; Ansari et al., 2012; El‐Demerdash, 2007; Kale et al., 1999; Ncir et al., 2018; Noshy et al., 2018; Yousef et al., 2006). Instead of direct inhibition of AChE, these other pesticide classes are reported to induce oxidative stress, which might contribute to AChE inactivation in erythrocytes.

Pesticides can disturb oxidative homoeostasis through direct or indirect pathways, including the overproduction of free radicals, lipid peroxidation and alteration in antioxidant defence mechanisms, including detoxification and scavenging enzymes (Singh et al., 2007; Mostafalou and Abdollahi, 2013). The generation and accumulation of free radicals inside erythrocytes result in lipid peroxidation of cell membranes (Banerjee et al., 1999; Panemangalore et al., 1999) and further interference with membranes‐dependent processes, including enzyme activities and the functionality of receptors and channels located at the plasma membrane level (El‐Demerdash, 2011). For instance, pyrethroids have demonstrated to cause a decrease in erythrocyte and brain AChE which was referred to the increase in lipid peroxidation (El‐Demerdash, 2007). In the study of Hernández et al. (2005), sprayers utilising OP presented significantly lower levels of AChE than sprayers that did not use these compounds. However, the latter group also presented significant decrease (9%) of enzyme activity compared to controls. In a further study of the same group, greenhouse workers exposed to insecticides other than OPs had significant decrease of AChE activity (35%) as compared to controls (García‐García et al., 2016), and this decrease was attributed to oxidative stress. Overall, the decline in AChE activity might be used as a surrogate marker of oxidative stress in the biomonitoring of workers exposed to pesticides in general (Hernández et al., 2013).

The decrease in AChE activity under oxidative stress results from the irreversible inactivation of the enzyme (e.g. by shifting to a partially unfolded state, observed as cleavage of peptide bonds in electrophoresis), which entails loss of its catalytic activity (Weiner et al., 1994). It consists in an indirect effect occurring when the cell's antioxidant defences are overwhelmed, and therefore, the mechanism of action of the other pesticide classes inducing oxidative stress leading to AChE inhibition is entirely different from the direct interaction of the enzyme by the active substance through covalent (OPs) or non‐covalent binding (NMCs).

There is currently a scarcity of data or studies that demonstrates a causal relationship of oxidative stress from pesticides leading to AChE inhibition, e.g. oxidative stress and AChE inhibition often measured at the same time. It is infrequent to measure AChE activity in regulatory toxicological studies with substances other than OPs and NMCs, and it is therefore very difficult to evaluate the contribution of substances leading to AChE inhibition as a result of oxidative stress.

A data collection on toxicological effects of pesticides (Nielsen et al., 2012), covering active substances approved until May 2009, reported a limited number of cases of AChE inhibition caused by substances other than OPs and NMCs (chlorpropham, desmedipham, dimoxystrobin, fenpropidin, fenpropimorph, monilate, propamocarb, prosulfocarb, thiram and ziram). Generally, AChE inhibition was observed at levels at least one order of magnitude higher than the critical effect triggering the ADI.

With respect to oxidative stress itself, measurements of indicators such as increased reactive oxygen species, free radicals or malondialdehyde (a marker lipid peroxidation) and/or a decreased level of the antioxidants glutathione, glutathione peroxidase, superoxide dismutase or catalase are also very infrequent in regulatory toxicological studies (Nielsen et al., 2012).

Lastly, it should be mentioned that oxidative stress, sufficient to exceed the antioxidant defence mechanisms, can come from multiple causes, including dietary exposure to pesticides and other classes of chemicals (e.g. heavy metals, alcohol) and non‐dietary sources such as occupational exposure, air pollution or smoking (Aseervatham et al., 2013). These other sources leading to oxidative stress hinder clear risk characterisation of dietary exposure to pesticides leading to oxidative stress and AChE inhibition in human observational studies.

In view of the above, considering that:

• AChE activity is not systematically measured in toxicological studies of pesticides other than OPs and NMCs, which prevents a reliable and consistent toxicological characterisation of all pesticides for the inhibition of AChE activity;

• AChE inhibition caused by pesticides other than OPs and NMCs is mainly due to oxidative stress and occurs when the protective cellular mechanisms are overwhelmed;

• A level of oxidative stress sufficient to exceed the repair mechanisms can result from multiple causes other than dietary exposure to pesticides, that cannot be considered as the assessment question under consideration focuses on pesticides residues and the dietary route,

this source of uncertainty was not considered in the subsequent steps of the uncertainty analysis, and the contribution of oxidative stress caused by substances other than OPs and NMCs to the inactivation of AChE was not included in the present assessment.

3.2.2. Impact of individual sources of uncertainty

The elicitation questions to be addressed here for each source of uncertainty were expressed as follows:

EKE Q1A: ‘If this source of uncertainty was fully resolved (e.g. by obtaining perfect information on the issue involved) and addressed in the modelling, by what multiplicative factor would this change the median estimate of the MOET for chronic AChE inhibition for the 99.9th percentile of the Italian adults population at Tier II?’

EKE Q1B: ‘Is the impact of this source of uncertainty the same for the other populations that were assessed? If not, list those populations for which the impact would be smaller, and those for which it would be larger.’

The 34 sources of uncertainty retained for the elicitation process were divided into two groups according to the area of expertise they are related to (exposure and toxicology) as indicated in Tables 17 and 18. The sources of uncertainty concerning consumption data, occurrence data, processing factors and the OIM model (after advice of the experts in toxicology on human toxicokinetic and toxicodynamic processes) were evaluated by six experts in exposure as described in Section 2.3.3. The sources of uncertainty concerning the NOAELs, dose addition and the UF for intra‐species variability were evaluated by six experts in toxicology.

EKE Q1A was addressed using the notes compiled in Appendix E and the resulting assessments (ranges of multiplicative factors of MOET at 99.9th percentile of exposure distribution at Tier II) are reported in Appendix F.

3.2.2.1. Italian adult population

The experts judged that U20 (missing processing factors) is by far the source of uncertainty with the highest impact. Perfect information leading to the establishment of processing factors for all relevant processing operations would multiply the MOET estimate at 99.9th percentile of the Italian adult population by a factor between 2 and 10, based on the sensitivity analysis C reported in Table 16. Resolving source of uncertainty U11 (sampling variability of occurrence data), U15 (unspecific residue definitions), U29 (Uncertainties related to original studies/data quality) or U34 (adequacy of the OIM model) would also lead to an increase of the MOET by a multiplicative factor possibly exceeding 1.2 (i.e. 20% increase) but remaining below 2. Minor increases of the MOET (not exceeding factors of 1.2) are also expected if perfect information would solve the source of uncertainty U17 (left‐censored data: assumption about the use frequency), U19 (assumption about pesticides in drinking water) or U25 (processing factors not considered, i.e. peeling of commodities with edible peel and washing).

In the opposite direction, resolving source of uncertainty U1 (omitted commodities), U4 (sampling variability of consumption data) or U8 (metabolites not accounted) would lead to a decrease of the MOET by a multiplicative factor below 1, possibly lower than 0.8 (i.e. 20% decrease) but remaining higher than 0.5. The source of uncertainty U26 (OPs and NMCs not included in the CAG) was judged to have a similar impact by some but not all experts. Minor decreases of the MOET (by a multiplicative factor not lower than 0.8) are also expected if source of uncertainty U5 (Representativeness of the consumption data) or U31 (Uncertainty related to the NOAEL‐setting principles) was fully resolved.

Solving the source of uncertainty U32 (Uncertainty related to the study design of the critical study) would result in either increase or decrease of the MOET by a multiplicative factor possibly ranging from 0.5 to 2.

For all other sources of uncertainty, the experts judged that perfect information could either increase or decrease the MOET but by a low multiplicative factor between 0.8 and 1.2.

3.2.2.2. Other populations

Perfect information resolving the uncertainty may have higher or lower impacts in the other nine populations in case of sources of uncertainty U1 (omitted commodities), U4 (sampling variability of consumption data), U11 (sampling variability of occurrence data), U15 (unspecific residue definitions), U19 (assumption about pesticides in drinking water), U20 (missing processing factors) and U34 (adequacy of the OIM model). In each case, the difference with the Italian population was not sufficient to lead to a different range of multiplicative factors.

3.2.2.3. Exclusion of U35 (adequacy of the UF for intraspecies variability) from the next steps of the uncertainty analysis

Out of these 34 sources of uncertainty, 33 are retained for the next step of the elicitation process. It was decided to exclude the source of uncertainty U35 from the next step of the process. This source of uncertainty was found of marginal relevance for all 10 populations subject to the uncertainty analysis, because these populations only include consumers from 1 to 65 years of age, for whom the default UF of 10 for intraspecies variability is adequate.

The adequacy of the default UF for intraspecies variability is questionable for both infants of less than 16 weeks of age and the elderly population (i.e. adults older than 65 years old). The EFSA Scientific Committee (2017a) views this period of 16 weeks of age or less, when the metabolic and excretory capacities of infants are still immature, as the time which health‐based guidance values for the general population cannot be applied without further considerations. In addition, the elderly population might exhibit higher sensitivity to AChE inhibitors.

The sensitivity of infants and the elderly population to chronic AChE inhibition is considered further in Section 4.3.

3.2.3. Combined impact of uncertainties relating to toxicology and exposure in the Italian adult population

The combined impact of individual uncertainties was evaluated as described in Section 2.3.4, addressing the following elicitation question:

EKE Q2: ‘If all the identified sources of uncertainty relating to [exposure/toxicology] were fully resolved (e.g. by obtaining perfect information on the issues involved) and addressed in the modelling, by what multiplicative factor would this change the median estimate for the MOET at the 99.9th percentile of exposure for chronic inhibition of erythrocyte AChE in the Italian adult population at Tier II?’

The elicitation took place in October 2020 by MS Teams meetings and the elicitation records can be found in appendices G (combined impact of toxicology uncertainties) and H (combined impact of exposure uncertainties). Only a summary is provided in the following two sections.

3.2.3.1. Combined impact of uncertainties related to toxicology

After the EKE Q1 session, none of the sources of uncertainty pertaining to toxicology was found to lead, if resolved, to multiplicative factors higher than 2 or lower than 0.5.

Following discussion, the experts identified the major contributors to the combined uncertainty related to toxicology as follows17:

• U29: Uncertainties on the original studies/data quality (+, see Note 27)

• U32: Uncertainty related to the study design of the key study (+/–, see Note 30, the most influential components of this source of uncertainty being related to the difference between NOAELs and precise BMDL20s, the measurement of AChE activity and the actual concentration of dichlorvos in the animal diet from the key study for that substance)

Possible dependencies between these uncertainties were considered. Although study guidelines and GLP (U29) do not give specific directions on the dose selection and spacing, study duration, route of administration or analytical methods (U32), they do support a good study design. Therefore, if it is known that an appropriate guideline and GLP were followed in a study (U29), uncertainties relating to study design may be reduced (U32). However, it was agreed that if there was a dependency between the impacts of these sources of uncertainty, it would be minor.

Minor contributors to the combined uncertainty included:

• U26: NMCs and OPs not included in CAG‐NCN and not accounted in the model exposure estimates (–, see Note 25)

• U31: Uncertainty related to the NOAEL‐setting principles (–, see Note 29, the most influential component of this source of uncertainty being the NOAEL set for dimethoate and used for the CRA calculations)

Overall, the experts judged that there would be little change affecting the MOET at the 99.9th percentile of exposure in the Italian adult population if all the uncertainties affecting toxicology were resolved. This is because perfect information on some sources of uncertainty would tend to increase the MOET while for other sources of uncertainty, it would decrease the MOET. To some degree, these effects would tend to cancel each other out. The experts agreed that resolving all uncertainties affecting toxicology would most likely slightly increase the MOET. Their results of the consensus process are summarised in Table 19. The experts made judgements for the plausible limits and probabilities for three values of the multiplicative factor f and reviewed and discussed alternative distributions fitted to those judgements. Consensus on a final distribution was not reached in the MS Teams meeting, so the process was completed by email using an approach based on the EFSA ‘Delphi’ EKE method (EFSA, 2014a,b,c). The facilitator sent the experts a summary of the discussion and judgements in the web meeting, asked them to assess which of distributions obtained in the web meeting they felt best represented their consensus judgement and gave them the option of proposing alternative distributions. The facilitator collated the experts’ responses in a second summary and conducted a second round of email consultation in which experts were asked to choose between the most preferred distribution from the first round, alternative distributions proposed by three of the experts and a further distribution, in which the facilitator attempted to reflect the range of the other four distributions by adjusting the alpha and beta parameters of one of them. This adjusted distribution was considered reasonable by all the experts and received the most preferences and was agreed by the experts as the final consensus distribution to be used as the basis in the subsequent steps of the uncertainty analysis. An alternative distribution, which was also considered reasonable by all the experts but received fewer preferences, was also taken forward for use in a sensitivity analysis to assess the impact of the distribution choice on the combined uncertainty. The parameters for this alternative distribution and the final consensus distribution are shown in Table 19, and the final consensus distribution is also shown in Figure 4.

Table 19.

CAG‐NCN Consensus judgements and distribution of the experts for the combined impact of the quantified uncertainties affecting toxicology (if resolved) on the MOET at the 99.9th percentile of exposure for the Italian adult population in 2016–2018. The impact is expressed as a multiplicative factor f to be applied to the Tier II median estimate (shown in Table 14). The bottom rows of the table give the parameters for the consensus distribution, which is shown graphically in Figure 4, and also for an alternative distribution for use in sensitivity analysis to check the impact of distribution choice

	Experts’ toxicology multiplicative factor (f)
Lower plausible bound	f = 0.5 (experts judged there to be < 1% probability that f would be < 0.5)
Upper plausible bound	f = 2 (experts judged there to be < 1% probability that f would be > 2)
Probability 1	p(f < 0.8) = 10% (experts’ probability that f would be less than 0.8)
Probability 2	p(f > 1.2) = 30% (experts’ probability that f would be more than 1.2)
Probability 3	p(f < 1) = 45% (experts’ probability that f would be less than 1)
Fitted distribution (retained as an alternative to the final consensus)	Beta distribution with parameters alpha = 3.39 and beta = 5.60, scaled to the interval from 0.5 to 2 (the experts’ plausible bounds)
Final consensus distribution (obtained by adjusting the parameters alpha and beta)	Beta distribution with parameters alpha = 3.15 and beta = 4.60, scaled to the interval from 0.5 to 2 (the experts’ plausible bounds)

Figure 4.

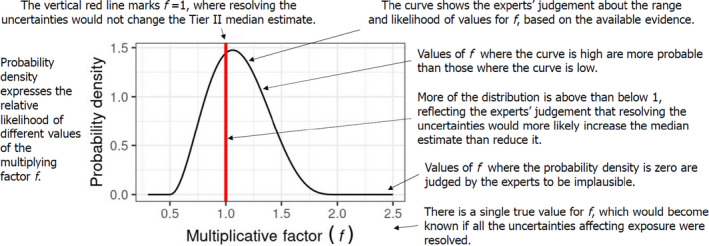
CAG‐NCN: Consensus distribution of the experts for the combined impact of the quantified uncertainties affecting toxicology (if resolved) on the MOET at the 99.9th percentile of exposure for the Italian adult population in 2016–2018, expressed as a multiplicative factor f to be applied to the Tier II median estimate shown in Table 14. The probability distribution is shown by the curve, which represents the probability density (relative likelihood) for different values of the multiplicative factor f. Distribution parameters are shown in Table 19

3.2.3.2. Combined impact of uncertainties related to exposure

After the EKE Q1 session, one of the sources of uncertainty pertaining to exposure was found to lead, if resolved, to a multiplicative factor between 2 and 10. Following discussion, this source of uncertainty (U20: missing processing factors) was considered as the only major contributor to the combined uncertainty related to exposure (+, see Note 20).17

Minor contributors to the combined uncertainty included:

• U1: contribution of plant and animal commodities not accounted in the assessment (–, see Notes 1, 2 and 3)

• U4: Sampling variability of consumption data (–, see Note 7)

• U8: contribution of metabolites and degradation products not accounted in the assessment (–, see Note 11)

• U11: Sampling variability of occurrence data (+, see Note 7)

• U15: Uncertainty resulting from unspecific residue definitions (+, see Note 16)

• U17: Assumption on the use frequency (+, see Note 18)

• U19: Assumption of residues in drinking water (+, see Note 19)

• U34: Uncertainty about the adequacy of the OIM model (+, see Note 32)

The experts identified negative dependencies between U15 on unspecific residue definition and U20 on missing processing factors18 and between U11 on occurrence data variability and U20.19

Overall, the experts judged that the MOET at the 99.9th percentile of exposure in the Italian adult population would be multiplied by a factor ranging from 1.5 to 10, and most likely between 5 and 6 if all the uncertainties affecting exposure were resolved. The experts’ judgement that the MOET cannot be reduced by multiplicative factors lower than 1 is due to the dominant impact of U20 (missing processing factors). The width of the distribution results from the rather large number of other sources of uncertainty and because solving them may possibly result in multiplicative factors either at the lower or upper ends of the range of plausible values for 2 of them at the same time. The consensus judgement is shown in Table 20 together with the parameters for their final consensus distribution, which is also presented in Figure 5.

Table 20.

CAG‐NCN Consensus judgements and distribution of the experts for the combined impact of the quantified uncertainties affecting exposure (if resolved) on the MOET at the 99.9th percentile of exposure for the Italian adult population in 2016–2018. The impact is expressed as a multiplicative factor f to be applied to the Tier II median estimate (shown in Table 14). The bottom row of the table gives the parameters for the consensus distribution, which is shown graphically in Figure 5. For more explanation, see Table 19

	Experts’ exposure multiplicative factor (f)
Lower plausible bound	f = 1.5
Upper plausible bound	f = 10
Probability 1	P (f < 4) = 20%
Probability 2	P (f < 6) = 55%
Probability 3	P (f > 7) = 10%
Consensus distribution	Beta distribution with parameters alpha = 3.51 and beta = 3.91, scaled to the interval from 1.5 to 10 (the experts’ plausible bounds)

Figure 5.

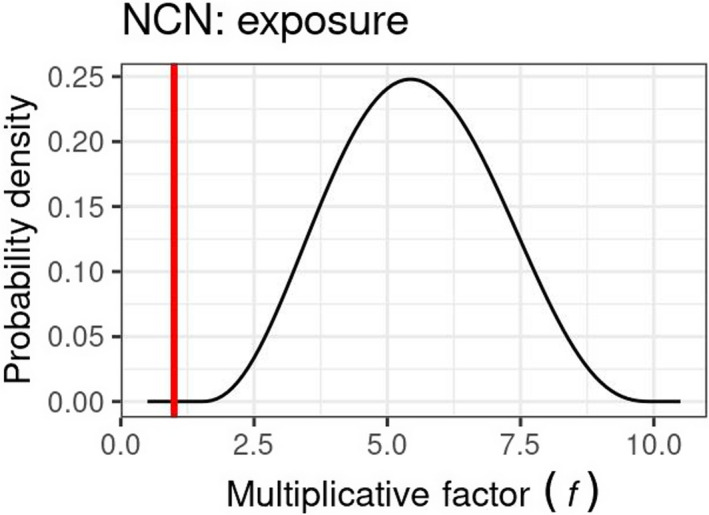
CAG‐NCN: Consensus distribution of the experts for the combined impact of the quantified uncertainties affecting exposure (if resolved) on the MOET at the 99.9th percentile of exposure for the Italian adult population in 2016‐2018, expressed as a multiplicative factor f to be applied to the Tier II median estimate shown in Table 14. Distribution parameters are shown in Table 20. Graph content is explained in Figure 4

3.2.3.3. Combined impact of uncertainties related to exposure and toxicology

The elicited distributions for the uncertainties related to toxicology and exposure regarding the Italian adult population were combined with the output of the Tier II model for the MOET at the 99.9th percentile of exposure in each consumer population (see Section 3.1.2), using the Monte Carlo calculation described in Section 2.3.5. These calculations were conducted assuming perfect independence between the elicited distributions for uncertainties affecting exposure and toxicology. The results are shown in Figure 6.

It can be seen in Figure 6 that the median estimates for ‘model+experts’ are markedly higher than those for ‘model’. This is to be expected, because the uncertainties quantified in the expert elicitation include the impact of assumptions in the model that make it intentionally conservative (over‐estimating exposure and hence under‐estimating MOETs). However, the 95% probability intervals for the MOET at the 99.9th percentile of exposure still extend below 100 for two populations (Italian adults and French other children).

The boxplots for ‘model+experts’ in Figure 6 are not much wider than those for ‘model’, contrasting with results in previous assessments where the boxplots for ‘model+experts’ were much wider than those for ‘model’ (EFSA, 2020a,b). This is due to the relative contribution of sampling uncertainty for occurrence data, which is quantified in the model, being larger in the present assessment.

Statistics associated with the ‘model+experts’ boxplots as well as calculated probabilities for the MOET at the 99.9th percentile of exposure being below 100 in each population group are shown in Table 21. Note that they do not take account of dependencies and population differences in uncertainty, which are addressed in EKE Q3 (see below).

3.2.4. Accounting for dependencies, population differences and additional uncertainties

EKE was used to evaluate how much the calculated probabilities for the MOETs at the 99.9th percentile of exposure should be adjusted to take account of a) dependencies between the elicited distributions for exposure and toxicology and the uncertainties quantified in the model (which were assumed in the calculation to be independent), b) differences between the uncertainties affecting exposure and toxicology for the Italian adult population (which were quantified by the elicited distributions) and the uncertainties for other population groups (which were assumed in the ‘model + experts’ calculation to be the same as for Italian adults) and c) any other uncertainties which were not yet accounted for.

These factors were addressed by considering the following elicitation question (EKE Q3):

For the Italian adult population: ‘If all the uncertainties in the model, exposure assessment, hazard identification and characterisation and their dependencies were fully resolved (e.g. by obtaining perfect information on the issues involved) and addressed in the modelling, what is your probability that this would result in the MOET for the 99.9th percentile of exposure for the Italian adult population in 2016–2018 being below 100?’

For each of the other nine modelled populations: ‘If all the uncertainties in the model, exposure assessment, hazard identification and characterisation and their dependencies, and differences in these between populations, were fully resolved (e.g. by obtaining perfect information on the issues involved) and addressed in the modelling, what is your probability that this would result in the MOET for the 99.9th percentile of exposure for the [name of the population] in 2016–2018 being below 100?’

As indicated in Section 2.3.6, the assessment of dependencies between uncertainties in the exposure and hazard assessments was facilitated by additional simulations exploring the impact of different degrees of dependence between them. This quantified the range of possible effects resulting from either perfect positive or perfect negative dependency, by providing upper and lower bounds, respectively, for the probability for the MOET being below 100. In practice, the real level of dependency would be between these two extremes (Table 22).

Table 22.

Effect of dependencies on the probability (expressed as a percentage) that the MOET for the 99th percentile of exposure for each population in 2016–2018 is below 100 assuming no dependence (column 2) or varying degrees of dependence (columns 3–8) between the experts’ assessments of uncertainties relating to exposure and toxicology, i.e. between the distributions in Figures 4 and 5 above. The degree of dependency is shown as a correlation coefficient (rho)

Population	Q2 probability assuming independence – rho = 0 (%)	Q2 probability with negative dependency (%)				Q2 probability with positive dependency (%)
		rho = –1	rho = –0.75	rho = –0.5	rho = –0.25	rho = +0.25	rho = +0.5	rho = +0.75	rho = +1
Belgian adults	0.13	0.00	0.00	0.02	0.06	0.22	0.33	0.47	0.61
Czech Rep. adults	0.30	0.00	0.01	0.06	0.16	0.48	0.68	0.93	1.19
German adults	0.10	0.00	0.00	0.01	0.04	0.18	0.28	0.41	0.55
Italian adults	4.91	2.43	2.88	3.55	4.23	5.63	6.29	6.98	7.62
Bulgarian children	0.30	0.00	0.01	0.06	0.16	0.50	0.72	0.99	1.27
French children	4.96	2.35	2.85	3.55	4.25	5.70	6.39	7.09	7.74
Dutch children	0.09	0.00	0.00	0.01	0.04	0.18	0.29	0.44	0.61
Danish toddlers	0.24	0.00	0.02	0.07	0.14	0.36	0.51	0.69	0.88
Dutch toddlers	1.05	0.01	0.10	0.33	0.65	1.53	2.02	2.58	3.14
UK toddlers	0.31	0.00	0.01	0.06	0.16	0.52	0.76	1.06	1.38

Eleven experts participated to these assessments and provided independent replies. Later, they considered differences in their judgements and developed a consensus assessment of the probability of the MOET for the 99.9th percentile of exposure in 2016–2018 being below 100 in each of the 10 populations under consideration. The consensus elicitation process was conducted as described in Section 2.3.6 and took place in November 2020.

The elicitation record can be found in Appendix I. Only a summary is provided in the following two sections.

3.2.4.1. Italian adult population

For the Italian adult population, only the dependencies between the toxicology and exposure uncertainty distributions were considered when addressing EKE Question 3, since EKE Question 2 refers specifically to the Italian adult population.

The experts identified mainly negative dependencies between exposure and toxicological uncertainties.20 Overall, the level of dependencies identified is low because they concern only a fraction of all uncertainties. Based on these dependencies and assuming that some others might not have been identified, rho is estimated to lie between –0.25 and +0.25, with a higher plausibility of negative values, as the majority of the identified dependencies are negative. Considering the calculations conducted for different degrees of dependency between toxicology and exposure uncertainties (Table 22), the probability of the estimated 99.9th percentile of the MOET distribution for the Italian adult population being below 100 if all the uncertainties in the model, exposure assessment, hazard identification and characterisation and their dependencies were fully resolved and addressed in the modelling was judged by the experts to lie within the range 1–10%.

3.2.4.2. Other populations

For the other nine consumer populations, EKE Question 3 requires considering, in addition, how the uncertainties relating to exposure and toxicology differ between them and the Italian adult population.

The dependencies between the toxicology and exposure uncertainties identified for the Italian adult population are expected to be of generic nature and therefore apply equally to all the other populations. Additionally, no evidence suggesting a different degree of dependency between exposure and toxicological uncertainties in the different populations was identified, and therefore the experts judged that the estimated range of values for rho (–0.25 to +0.25) for the Italian population applies also for the other populations.

Under EKE Q1, for the other populations, the following sources of uncertainty were identified to have an impact differing from the Italian population (Appendix F): U1 on excluded commodities (larger impact for the other populations) (–/.), U4 on the consumption data sampling variability (larger or smaller impact in other populations, depending on the number of subjects in the survey) (–/.), U11 on the occurrence data sampling variability (smaller impact for populations with lower olive oil consumption) (./+), U15 on unspecific residue definition (smaller impact for populations with lower olive oil consumption) (./+), U19 on the assumption about pesticides in drinking water (larger impact in most of the other populations) (./.), U20 on missing processing factors (smaller impact in all other populations) (++/+++) and U34 on OIM model (larger or smaller impact in other populations, depending on the number of days in the dietary survey) (./+).

The source of uncertainty responsible of the largest part of differences between populations is U20, because this is the source of uncertainty with the largest absolute impact (see sensitivity analysis C Table 16), and there is a large difference in the ratios shown in Table I.1 of Appendix I between the Italian adult population and all the other populations. The next largest ratios in Table I.1 of Appendix I are for sensitivity analysis E, showing the impact of removing the olive sample with exceptionally high levels of dimethoate/omethoate residues (4.9 mg/kg). However, the experts judged that the impact of this olive sample is already covered by sensitivity analysis C (impact of missing processing factors, e.g. olives for oil production) and would be accounted twice if the impact suggested by sensitivity analysis E was added to that of sensitivity analysis C in their assessment. This is because the assumption that no residue is transferred to processed commodities (linked to sensitivity analysis C) has the same effect as assuming that only raw commodities free of residues are used to prepare processed food (meaning that the sample under consideration in sensitivity analysis E would be disregarded). Based on the above, experts did not consider sensitivity analysis E further in their judgements on EKE Q3.

Table I.1.

Median MOET estimates at the 99.9th percentiles of the exposure distribution for the Tier II scenario and several sensitivity analyses. Ratios of the median MOET of the sensitivity analyses to the respective median MOET in the Tier II scenario are shown in italics

	BE.A	CZ.A	DE.A	IT.A	BG.C	FR.C	NL.C	DK.T	NL.T	UK.T
Median MOET tier II	115	91	116	51,6	82,9	51,8	91	97,4	60,3	78,1
Sensitivity analysis C (Missing processing factors): median MOET (ratio to MOET tier II)	373 3.2	444 4.9	363 3.1	503 9.8	232 2.8	263 5.1	222 2.4	233 2.4	235 3.9	260 3.3
Sensitivity analysis E (Exclusion of the olive sample with residues of the sum of dimethoate and omethoate at 4.9 mg/kg considered a potential outlier): median MOET (ratio to MOET tier II)	269 2.3	256 2.8	211 1.8	212 4.1	140 1.7	164 3.2	130 1.4	130 1.3	92.7 1.5	132 1.7
Sensitivity analysis I (Contribution of pesticides in drinking water excluded): median MOET (ratio to MOET tier II)	120 1.0	106 1.2	118 1.0	49,3 1.0	91,5 1.1	51,6 1.0	103 1.1	112 1.2	68,8 1.1	85,5 1.1
Sensitivity analysis K (assuming that omethoate is not authorised in olives for oil production): median MOET (ratio to MOET tier II)	1511.3	1181.3	1331.1	64.61.3	97.41.1	661.3	1081.2	1071.1	75.81.3	90.41.2
Sensitivity analysis C, E, I and K are those related to sources of uncertainty which matter in terms of population differences. They relate to U20 (missing processing factors), U11 (occurrence data sampling variability), U19 (assumption of pesticides in drinking water) and U15 (unspecific residue definitions), respectively. It must be noted that sensitivity analyses E can be considered as superseded by sensitivity analysis C (dependencies between these uncertainties were established when resolving the EKE Q2). Therefore, only sensitivity analyses C, K and I (drinking water) remain informative for the assessment of population differences. In addition, with respect to sensitivity analyses K and I, the differences observed between the ratios for the different populations are difficult to interpret as these differences are small and might be due to the known instability of MOET median estimates (see Note 7).

Sources of uncertainty U4 (sampling variability of consumption data) and U34 (adequacy of the OIM model) were considered as contributing to a lesser extent to differences between populations, depending on the number of subjects (U4) and recorded days in the surveys (U34).

The differences between populations identified in response to EKE Q1b for other sources of uncertainty were not further considered due to the small magnitude of the individual impacts of these sources of uncertainty, and the lack of consistency in the direction of these impacts.

The experts assessed the combined impact of these differences in three steps, which were repeated for each population. In the first step, the experts considered how different was the impact of U20 (missing processing factors) compared to the Italian population, based on sensitivity analysis C in Table 16. Based on this comparison, they discussed by what approximate factor the ‘model+experts’ boxplots shown in Figure 6 would shift if the distribution for exposure uncertainties was elicited taking account of the impact of missing processing factors in the considered population, instead of the Italian population. For example, Table I.1 in Appendix I shows that the impact of sensitivity analysis C on the P99.9 MOET for French children was about half as large as its impact on Italian adults. This suggests that the model+experts distribution for French children in Figure 6 would shift downwards (towards lower MOETs) by a factor of about 0.5 if the exposure uncertainty distribution had been elicited considering the impact of U20 for French children rather than Italian adults.

In a second step, the experts considered the potential impact of the approximate shift factor on the % probability of the MOET being below 100 for the considered population. This was assessed with the help of calculations showing how shifting the ‘model+experts’ distribution up or down by different factors affects the % probability of the MOET being below 100 for each population and different degrees of dependency (rho). For French children, a shift factor of 0.5 combined with the expected degree of dependency (rho of –0.25 to +0.25) would increase the probability of the P99.9 MOET being below 100 from about 5% to about 27% (see Table I.2 in appendix I). This provides an indication of the differing impact of uncertainty about missing processing factors (U20) on the assessment for French children.

Table I.2.

Shifting of the MOET distribution for the French children population assuming different degrees of dependency

rho	Group	×0.1	×0.2	×0.33	×0.5	×0.66	=	×1.5	×2	×33	×5	×10
–1	FR.C	87.6%	66.0%	50.1%	22.5%	13.2%	2.3%	0.1%	0.0%	0.0%	0.0%	0.0%
–0.75	FR.C	85.8%	65.9%	51.1%	25.2%	12.4%	2.8%	0.3%	0.0%	0.0%	0.0%	0.0%
–0.5	FR.C	84.9%	65.7%	49.7%	26.2%	13.3%	3.5%	0.5%	0.1%	0.0%	0.0%	0.0%
–0.25	FR.C	84.4%	65.5%	48.6%	26.9%	14.3%	4.2%	0.8%	0.2%	0.0%	0.0%	0.0%
0	FR.C	84.1%	65.5%	47.6%	27.3%	15.2%	5.0%	1.1%	0.3%	0.0%	0.0%	0.0%
0.25	FR.C	83.7%	65.4%	46.8%	27.6%	16.0%	5.7%	1.5%	0.4%	0.1%	0.0%	0.0%
0.5	FR.C	83.5%	65.2%	46.2%	27.8%	16.7%	6.4%	1.8%	0.6%	0.1%	0.0%	0.0%
0.75	FR.C	83.3%	65.0%	45.7%	28.0%	17.3%	7.1%	2.2%	0.8%	0.1%	0.0%	0.0%
1	FR.C	83.1%	64.8%	45.2%	28.1%	17.8%	7.7%	2.6%	1.0%	0.2%	0.0%	0.0%

In the third and final step, the experts discussed the additional impact of differences in uncertainties U4 and/or U34 in the considered population, when compared with the Italian adult population. For example, the experts noted that the dietary survey for French children had fewer subjects (482 vs. 2,313 for the Italian adults, U4), which would tend to decrease the shift factor indicated by the previous step, and a longer survey duration (7 day vs. 3 day for the Italian adults), which would also tend to decrease the shift factor. Taking into account their uncertainty about the relative magnitudes of these impacts and how they would combine, the experts agreed a consensus range of 10–50% for the probability of the estimated 99.9th percentile of the MOET distribution for the French children population being below 100 if all the uncertainties in the model, exposure assessment, hazard identification and characterisation and their dependencies were fully resolved and addressed in the modelling.

These three steps were repeated for all the remaining populations, taking into account the specific considerations relevant to each one. The results for all the populations are summarised in Table 23.

Table 23.

Estimated probability of the MOET at the 99.9th percentile of the exposure distribution in Tier II scenario being below 100 for the non‐Italian populations, impact of dependencies and population differences

Population	Median estimate of the MOET at 99.9th percentile of exposure distribution and 95% CI after adjustment for exposure and toxicology uncertainties quantified for the Italian population	Probability of 99.9%ile MOET < 100, assuming no difference between populations and full independence between exposure and toxicology uncertainties	Estimated shift factor resulting from differences in the effect of uncertainty U20 (processing factors) compared to the Italian population	Probability of 99.9%ile MOET < 100, taking account of dependencies and additional differences in uncertainties compared to the Italian population
Belgian adults	742 [187–2,558]	0.13%	0.33	5–15%
Czech Rep. adults	578 [157–2,374]	0.30%	0.5	1–10%
German adults	670 [192–2,016]	0.10%	0.33	5–15%
Bulgarian children	499 [155–1,344]	0.30%	0.3	10–33%
French children	316 [82–1,608]	4.96%	0.5	10–50%
Dutch children	538 [187–1,273]	0.09%	0.25	10–33%
Danish toddlers	537 [171–1,248]	0.24%	0.25	10–40%
Dutch toddlers	365 [121–965]	1.05%	0.4	10–33%
UK toddlers	472 [153–1,301]	0.31%	0.33	10–33%

As can be seen by comparing the third and fifth columns of Table 23, accounting for dependencies and differences with the Italian adult population increases drastically the probability of the MOET at the 99.9th percentile of the exposure distribution being below 100. This is due mainly to the impact of U20 (missing processing factors) which is markedly larger in the Italian adult population than in any other population, as shown by sensitivity analysis C of Table 16. This indicates that, if perfect information on the effect of processing was available for all pesticide/commodity/processing type combinations, the increase of the MOET in the nine other populations would be two to four times smaller than in the Italian population (shift factors of 0.5–0.25).

4. Risk characterisation

4.1. Risks for the assessed populations

Based on the above finding and analyses, the cumulative risks for chronic AChE inhibition can be summarised as follows:

1. The probabilistic modelling of cumulative exposure showed 8 of the 10 populations with median estimate of the MOET below 100 at 99.9th percentile of the exposure (Table 14, second column of Table 24), which has been identified by the European Commission and Member States as a threshold for regulatory consideration. The populations with the lowest estimates were Italian adults and French children. Rather wide confidence intervals were obtained. This was due to one very high measurement for the sum of dimethoate and omethoate in olives for oil production (4.9 mg/kg) out of a rather small total number of samples (n = 57).

2. Uncertainties in the hazard identification and characterisation and exposure assessment, as well as model uncertainties were quantified for the Italian population by a formal process of expert judgement and were combined with the model results by calculation for all 10 populations. For all population groups, this increased the median estimate of the MOET at the 99.9th percentile of exposure by about a factor of six (Table 21, third column of Table 24), reflecting the effect of purposely conservative assumptions in the assessment, as called for by the legislation (see Section 1.2).

3. After this adjustment, calculated probabilities for the MOET at the 99.9th percentile of exposure being below the threshold for regulatory consideration were about 5% for the Italian adult and French children populations, about 1% for the population of Dutch toddlers and below 0.5% for all other populations (right hand column of Table 21).

4. Finally, the experts considered the impact of dependencies between the toxicology and exposure uncertainties and differences in the uncertainties between populations. Low levels of dependency were identified between the toxicology and exposure uncertainties, but important differences between populations were observed, mainly with respect to U20 (missing processing factors) and, to a lesser extent, U4 (sampling variability of consumption data) and U34 (adequacy of the OIM model). This resulted in the overall expert assessment shown in fourth column of Table 24. For the adult populations, the probability of the MOET at the 99.9th percentile of exposure being below the threshold for regulatory consideration was assessed to range between 1 and 10% (CZ and IT) or 5 and 15% (BE and DE). This probability ranged from 10% to 33% for Bulgarian children, Dutch children and toddlers and for UK toddlers and was the largest for Danish toddlers (10–40%) and French children (10–50%).

5. EFSA's guidance on communicating uncertainty (EFSA, 2019f) recommends that for the purpose of communication, probabilities quantifying uncertainty should be expressed as ‘percentage certainty’ of the more probable outcome (in this case, that the MOET at the 99.9th percentile of exposure in 2016–2018 is equal or greater than 100, rather than less). This advice is applied in the right‐hand column of Table 24. Also shown in the same column are verbal probability terms associated with the assessed range of percent certainty, based on the approximate probability scale recommended for harmonised use in EFSA assessments (EFSA, 2018a)

Table 24.

CAG‐NCN: Outcome of the CRA of chronic erythrocyte AChE inhibition resulting from dietary exposure to pesticides for each population in 2016–2018

Population	MOET at the 99.9th percentile of exposure
	Median and 95% CI following model	Median and 95% CI after adjustment for uncertainties quantified for the Italian population	Probability for MOET < 100 taking account of dependencies and population differences	Corresponding percent certainty that the MOET is equal to or greater than 100, and associated probability term
Belgian adults	115 [40.2–289]	742 [187–2,558]	5–15%	85–95% (likely to very likely)
Czech Rep. adults	91 [31.5–271]	578 [157–2,374]	1–10%	90–99% (very likely to extremely likely)
German adults	116 [39.5–232]	670 [192–2,016]	5–15%	85–95% (likely to very likely)
Italian adults	51.6 [16.5–266]	321 [82–2,115]	1–10%	90–99% (very likely to extremely likely)
Bulgarian children	82.9 [32.7–151]	499 [155–1,344]	10–33%	67–90% (likely)
French children	51.8 [16.6–191]	316 [82–1,608]	10–50%	50–90% (about as likely as not to likely)
Dutch children	91 [41.3–149]	538 [187–1,273]	10–33%	67–90% (likely)
Danish toddlers	97.4 [38.6–143]	537 [171–1,248]	10–40%	60–90% (likely)
Dutch toddlers	60.3 [26.8–120]	365 [121–965]	10–33%	67–90% (likely)
UK toddlers	78.1 [33.1–153]	472 [153–1,301]	10–33%	67–90% (likely)

As explained in Section 3.2.1.1, the outcome of the assessments summarised above did not consider the contribution of pesticide residues causing AChE inhibition through oxidative stress. The data currently available did not allow the evaluation of this contribution. It is therefore not possible to quantify the amount by which the probabilities for the MOETs being below 100 would increase if the impact of oxidative stress would be considered.

4.2. Risks for the other European populations

During the Standing Committee on Plants, Animals, Food and Feed of 18–19 September 2018 (European Commission, 2018), Member States recommended considering, in CRA, all population subgroups of consumers included in the EFSA PRIMo model (EFSA, 2018b).

In total, 30 Member State diets for chronic exposure assessments are incorporated in the PRIMo model. However, for reasons of resources, calculations were restricted to 10 population groups only, which, in addition, do not necessarily correspond to diets of the PRIMo model. This is because these population groups were extracted from different food consumption surveys (e.g. a more recent food consumption survey was used for UK toddlers), or from diets which are not considered by the PRIMo model (e.g. Belgian, Bulgarian and Czech surveys).

Nevertheless, considering the long‐term average consumption of plant commodities in population groups of the EFSA PRIMo Model reported in Appendix E Note 34, population groups with the highest vulnerability in terms of dietary exposure potential are toddlers and children, especially from Germany, France, Denmark, Netherlands and United Kingdom. As most of these populations are part of the 10 selected populations, it is reasonable to consider the assessed populations cover the populations of the PRIMo model anticipated to be at the highest risk.

4.3. Other considerations

As a threshold for regulatory considerations, risk managers established a target MOET of at least 100 by analogy with safety margin currently used for establishing the toxicological reference values, which includes a factor of 10 for inter‐species variability and a factor of 10 for intra‐species variability, but the risk managers recognised that a higher or lower MOET might be appropriate in certain circumstances (European Commission, 2018).

As discussed in Section 3.2.2.3, the 10 populations used for this CRA cover consumers aged 1–65 years. Populations that might be more susceptible to health effects from dietary exposure to pesticides, such as elderly adults older than 65 years old and infants below the age of 16 weeks, were not included in this CRA.

The elderly population may exhibit higher sensitivity to AChE inhibition due to pre‐existing medical conditions (e.g. diabetes, cancer, heart disease, etc.), weaker immune system, age‐related decline in metabolism, lower detoxification capacity and recovery in the brain, lower AChE activity and lesser adaptive regulation of acetylcholine release as well as increased oxidative stress due to their longer exposure to chemicals through dietary and non‐dietary routes. Evidence in the decline of AChE activity with age is available from ageing studies in rats (Pope, 2010). This is more relevant for OPs, as NMCs do not cross the blood–brain barrier and the effects in the brain induced by NMCs are much lower than that induced by OPs (Jokanović, 2009). As indicated in Section 3.2.2.3, the uncertainty about the adequacy of the uncertainty factor of 10 to reflect the intra‐species variability in toxicological sensitivity to AChE inhibition of aged persons has marginal relevance, because none of the populations under consideration includes consumers over the age of 65. It is therefore uncertain if the conclusions derived from the assessments performed for the 10 population groups sufficiently cover and protect from the risk of the elderly population. Additional data (e.g. health status of the elderly population) and evaluations (exposure assessment) would be required for a better understanding of aged‐related differences in toxicokinetics of pesticides and the impact of dietary exposure to pesticides (in this case, OPs and NMCs leading to AChE inhibition) on the health status of the elderly population.

The reasons of the higher sensitivity of infants of less than 16 weeks of age to chemical substances in their food have been described by the EFSA Scientific Committee (2017a) and a decision tree approach for an adequate risk assessment was proposed. Infants below 16 weeks of age are however expected to be exclusively fed on breast milk and/or infant formula, for which a legal limit of 0.01 mg/kg is set for pesticides residues by Commission Directives 2006/125/EC21 and 2006/141/EC.22 It was concluded by the PPR Panel (2018) that this default MRL of 0.01 mg/kg for infant formulae does not result in an unacceptable exposure to infants for all compounds, to which a HBGV of 0.0026 mg/kg bw per day or higher applies after application of the guidance on risk assessment of substances in food for infants (EFSA Scientific Committee, 2017a). The setting of lower MRLs was, however, recommended for active substances with HBGV for infants below 0.0026 mg/kg bw per day.

On the other hand, for infants above 16 weeks of age and young children, the established approach for setting HBGVs is considered appropriate (EFSA PPR Panel, 2018). Between the age of 16 weeks and 1 year, infants are progressively fed with conventional food and are exposed to increasing levels of pesticide residues. In its scientific opinion on pesticides in foods for infants and young children (EFSA PPR Panel, 2018), the PPR panel has shown, through five case studies, that the acute and chronic exposure to pesticide residues in post‐marketing scenario of infants between 16 weeks and 1 year, despite their higher consumption rate per kg body weight, was similar to the exposure of toddlers aged of 12–36 months.

5. Conclusions

EFSA conducted a cumulative risk assessment of chronic AChE inhibition for 10 European populations of consumers, covering different countries and different age groups. To this end, cumulative exposure calculations were performed by probabilistic modelling using monitoring data collected by Members States in 2016, 2017 and 2018. Based on a rigorous uncertainty analysis, considering all uncertainties identified by the experts, their dependencies and differences between populations, it was concluded, with varying degrees of certainty, that cumulative exposure does not exceed the threshold for regulatory consideration for any of the population groups considered. This certainty exceeds 90% for two adult populations and 85% for the other adult populations and is in the range from 67% to 90% for two child and two toddler populations, from 60% to 90% for Danish toddlers and from 50% to 90% for French children.

It was not possible to address the relevance and contribution of oxidative stress by substances other than OPs and NMCs as a cause of inactivation of AChE.

6. Recommendations

Despite the considerable amount of data used to perform it, CRA is subject to important uncertainties. To reduce the impact of these uncertainties, it is recommended to:

With respect to the toxicological assessment:

• Use BMD modelling to characterise the active substances included in the CAG;

• Systematically measure erythrocyte and brain AChE activity in toxicological studies of pesticides of other chemical classes than OPs and NMCs.;

• Consider other recommendations listed in the scientific report on the establishment of CAGs of pesticides for their effects on the nervous system (EFSA, 2019a), regarding developmental neurotoxicity and the regular update of the CAGs.

With respect to the exposure assessment:

• Consolidate the list of processing factors available for CRAs;

• Include the available monitoring data for processed commodities in cumulative exposure calculations and upgrade the probabilistic modelling software tools as appropriate to make this possible;

• Collect information from competent organisations on national authorisations, use statistics of plant protection products and pesticide residues in drinking water, on risk‐based criteria;

• Assess the contribution of metabolites to the effects under consideration, through the application of the guidance of the PPR Panel on the establishment of the residue definition for dietary risk assessment (EFSA PPR Panel, 2016);

• Develop a guidance in order to ensure a consistent use of the code ST20A (Selective sampling) in the context of Regulation (EC) No 396/2005 by data providers.

It is furthermore recommended to consider performing a cumulative risk assessment for a population of aged consumers (above 65 years of age).

Abbreviations

ACh

Acetylcholine

AChE

Acetylcholinesterase

ADI

Acceptable Daily Intake

ARfD

Acute Reference Dose

AUP

Agricultural Use Pattern

BMD

Benchmark Dose

BMDL

Lower confidence limit of the benchmark dose

BW

Body Weight

CAG

Cumulative Assessment Group

CAG‐NCN

Cumulative Assessment Group for the chronic assessment of brain and/or erythrocyte AChE inhibition

CNS

Central Nervous system

CRA

Cumulative Risk Assessment

DAR

Draft Assessment Report

EKE

Expert Knowledge Elicitation

EUCP

European Coordinated Programme

GLP

Good Laboratory Practice

JMPR

Joint Meeting on Pesticide Residues

LOAEL

Lowest Observed Adverse Effect Level

LOQ

Limit of Quantification

MCRA

Monte Carlo Risk Assessment (software)

MoA

Mode of Action

MOE

Margin of Exposure

MOET

Combined Margin of Exposure

MRL

Maximum Residue Level

NCM

N‐Methyl Carbamate

NET

Total Normalised Exposure

NOAEL

No Observed Adverse Effect Level

OIM

Observed Individual Mean (model)

OP

Organophosphorus

PNS

Peripheral Nervous System

PPP

Plant Protection Product

RAR

Renewal Assessment Report

RPC

Raw Primary Commodity

RIO

Rational Impartial Observer (concept)

SSD

Standard Sample Description

UF

Uncertainty Factor

Appendix A – Procedure for the allocation of active substances to the measurements

1.

• 1Select distinct combinations of raw primary commodity (RPC) and residue definition reported in the occurrence data set.
• 2Identify the possible combinations of RPC, residue definition and active substance (by joining the information of the residue definitions table). Retain information on the MW conversion factor, on whether this combination is exclusive or not, and on the proportion for the non‐exclusive combinations.
• 3Add the relevant NOAEL to each combination (join information from the active substance table using the active substance as the key).
• 4Identify the authorisation status for each combination (join information from the authorisations table using the RPC and active substance as the keys).

Tier I

• 5There may now be combinations of RPC, residue definition and active substance (AS) which refer to the same RPC and residue definition. Data are sorted by RPC, residue definition and NOAEL (ascending) and for each combination of RPC and residue definition, the first combination of RPC, residue definition and AS is retained, i.e. the one with the lowest NOAEL (most toxic AS).
• 6For each measurement in the occurrence data set, the AS is assigned on the basis of the combinations derived at step 5 (using the RPC and the residue definition as keys).

Tier II

• 7There may now be combinations of RPC, residue definition and active substance (AS) which refer to the same RPC and residue definition. For each RPC and residue definition, only the combinations with authorised uses are retained. If none are authorised, all combinations are retained.
• 8For each measurement in the occurrence data set, the AS is assigned on the basis of the combinations derived at step 5 (using the RPC and the residue definition as keys). If for a given measurement more than one AS could be assigned, only one AS is selected randomly using equal probability (regardless whether the AS is part of the cumulative assessment group).
• 9For each measurement, it is verified whether the combination RPC, residue definition and AS assigned is exclusive or not. If it is not exclusive:

  1. The residue value and the LOQ value are multiplied by the proportion specified in the residue definition table.

  2. The exclusive active substance of that residue definition is identified (from the residue definitions table)

  3. A new measurement is generated for the same sample but for the exclusive active substance identified above. The residue value and the LOQ value are also multiplied by a factor equal to (1 – proportion of the non‐exclusive substance).

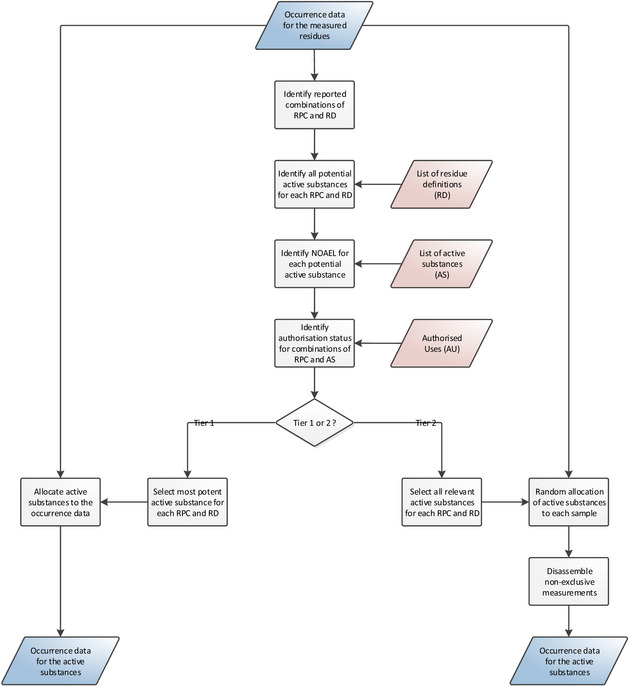
Flowchart for the allocation of active substances to the measurements

Appendix B – Procedure for the extrapolation of measurements

1.

1. Within the occurrence data set, count the number of observations per combination of active substance (AS) and raw primary commodity (RPC).

2. From the raw primary commodities table and the active substances table, create a full matrix with all possible combinations of AS and RPC. Join this table with table created at step 1 to derive a complete list of missing and observed combination (using RPC and AS as keys).

3. Identify the MRL and the authorisation status of each of these combinations (using RPC and AS as keys). Since MRLs are defined at residue definition level, a preliminary step joins MRL table and residue definition table to associate MRL information to the active substances.

4. Identify for each combination all valid extrapolations on the basis of the extrapolation rule table. Extrapolations for a given AS and RPC are considered valid only when:

   1. the number of observations for the FromFood is equal or above 10.

   2. the number of observations for the ToFood is below 10.

   3. MRL for FromFood and ToFood is equal.

   4. Both FromFood and ToFood are authorised.

5. For each AS and for each valid extrapolation, the measurements in the FromFood are listed (can be positive or left‐censored).

6. For each AS and for each valid extrapolation, the samples of the ToFood that were not analysed for the AS are listed (i.e. the missing values). This implies indeed that no extrapolation will be done if there are no samples at all for a given food.

7. Random measurements (identified at step 7) are combined with random samples (identified at step 6). This is repeated until all the FromFood measurements or all the ToFood samples are assigned. Hence, if there are insufficient measurements in the FromFood, missing values in the ToFood will remain. If there are insufficient samples in the ToFood, some measurements in the FromFood will not be assigned.

8. Newly extrapolated values are added to the occurrence data set.

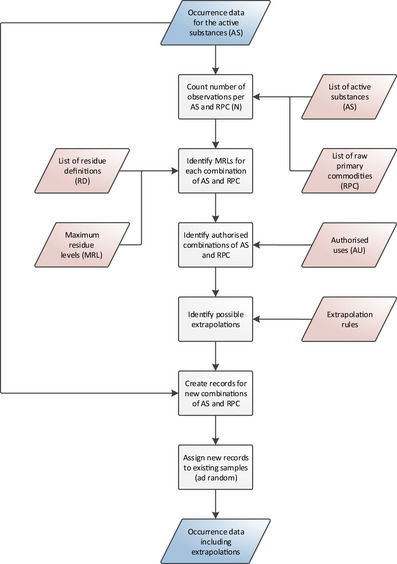
Flowchart for extrapolation of the occurrence data

Appendix C – Procedure for the imputation of left‐censored measurements

1.

Tier I

1. Retrieve from the occurrence data set all records which refer to a quantifiable result and identify distinct combinations of raw primary commodity (RPC) and active substance (AS). This results in a list of RPC/active substance combinations where the non‐quantifiable results will be assumed to be at ½ LOQ.

2. Identify in the occurrence data set all left‐censored records that refer to any of the combinations listed at step 1 (using RPC and AS as keys). Assign ½ LOQ as a result for those records.

3. Assign zero to all remaining left‐censored records in the occurrence data set.

Tier II

• 1Define the list of agricultural use patterns (AUPs) observed in the data set. An AUP is the combination of active substances (AS) quantified within a raw primary commodity (RPC). The list is derived as follows:

  1. Retrieve from the occurrence data set all samples which have at least one quantifiable result.

  2. Identify for each of the previous samples the AUP by concatenating the active substances quantified in each sample.

  3. Select all the distinct AUPs and assign an identifier to each AUP.

Example : Among all apple samples, substances X, Y and Z were measured, and the following combinations were quantified within single samples: (X), (X‐Y-Z), (Y), (X‐Y) and (Y‐Z). These combinations are now identified as AUP1, AUP2, AUP3, AUP4 and AUP5, respectively.

• 2Count the number of samples for each AUP, i.e. the number of times that the AUP appears in the data set.

Example : Number of apple samples where AUP1 was observed is 200; number of apple samples where AUP2 was observed is 23; etc.

• 3Identify the analytical scope of each sample and, for each AUP, identify the number of samples where the AUP is covered by the analytical scope:
  • aFrom the occurrence data set, identify for each sample the analytical scope by concatenating the active substances measured in each sample.

Example : Samples were measured either for substance Y only (Scope1), for substances X and Y (Scope2), for substances X, Y and Z (Scope3) or for substances Y and Z (Scope4).

• bCount the number of samples for each analytical scope.

Example : Number of samples where Scope1 was measured is 500; number of samples where Scope2 was measured is 250; number of samples where Scope3 was measured is 1,250; Number of samples where Scope4 was measured is 2000.

• cFor each AUP, identify the analytical scopes that include all ASs of that AUP.

Example : AUP1 is covered by Scope2 and Scope3 only.

• dFor each AUP, sum the number of samples for all analytical scopes identified at step 3c.

Example : The number of samples where Scope2 and Scope3 were measured is 250 and 1,250. Hence the total number of samples where AUP1 is covered by the analytical scope is 1,500.

• 4Calculate frequency for each AUP (N samples AUP/N samples analytical scope).

Example : Number of apple samples where AUP1 was observed is 200 (calculated at step 2). Number of apple samples where AUP1 is covered by the analytical scope is 1500 (calculated at step 3). Hence, the frequency of AUP1 in apples is 13.3%.

• 5Adjust frequencies for authorised AUPs (i.e. when all substances in the AUP are authorised) to obtain a total AUP frequency of 100% per RPC. This assumes that each sample in the occurrence data set was treated according to one AUP.

Example : 5 AUPs were observed in apples and frequencies for each AUP were calculated: AUP1 (13.3%), AUP2 (2.3%), AUP3 (9.8%), AUP4 (1.2%) and AUP5 (0.2%). However, only AUP1, AUP3 and AUP4 include substances that are all authorised. Therefore, only these AUPs are adjusted to obtain a total number AUP frequency of 100%. Frequencies of AUP2 and AUP5 remain unchanged and the following adjusted frequencies are obtained: AUP1 (53.4%), AUP2 (2.3%), AUP3 (39.3%), AUP4 (4.8%) and AUP5 (0.2%).

• 6Calculate use frequency for each combination of RPC and AS and identify the corresponding number of measurements that should be set to 1/2 LOQ:
  • aFor each combination of RPC and AS, calculate the use frequency by summing the AUP frequencies of all AUPs that contain the AS.

Example : 5 AUPs were observed in apples and the following adjusted frequencies are obtained: AUP1 (53.4%), AUP2 (2.3%), AUP3 (39.3%), AUP4 (4.8%) and AUP5 (0.2%). Only AUP1, AUP2 and AUP4 include the use of substance X. Therefore, the estimated use frequency of substance X in apples is 60.5%.

• bFor each combination of RPC and AS, calculate the percentage of true zeros (i.e. 100 – use frequency calculated at step 6.a)

Example: If the estimated use frequency of is 60.5%, the expected percentage of true zeros is 39.5%.

• cFor each combination of RPC and AS, calculate the number of true zeros by multiplying the percentage of true zeros (calculated at step 6.b) with number of measurements for that active substance and RPC and divide by 100.

Example: For substance X in apples, if the expected percentage of true zeros is 39.5% and the total number of measurements is 3562, the estimated number of true zero measurements is 1407.

• dFor each combination of AS and RPC, count the total number of measurements. Subtract from this value the number of samples that already have a measured value and the number of true zeroes calculated at step 6c. This is the number of samples that should be set to 1/2 LOQ. If a negative number is obtained, set to 0.

Example: For substance X in apples, if the total number of measurements is 3562, the number of quantifiable measurements is 126 and the estimated number of true zero measurements is 1407, the number of measurements to be imputed at 1/2 LOQ is 2029.

• 7From the left‐censored data reported in the occurrence data set, randomly select for each RPC and AS the number of samples (as calculated above). Assign a residue value of 1/2 LOQ.
• 8Assign zero to all remaining left‐censored records in the occurrence data set.

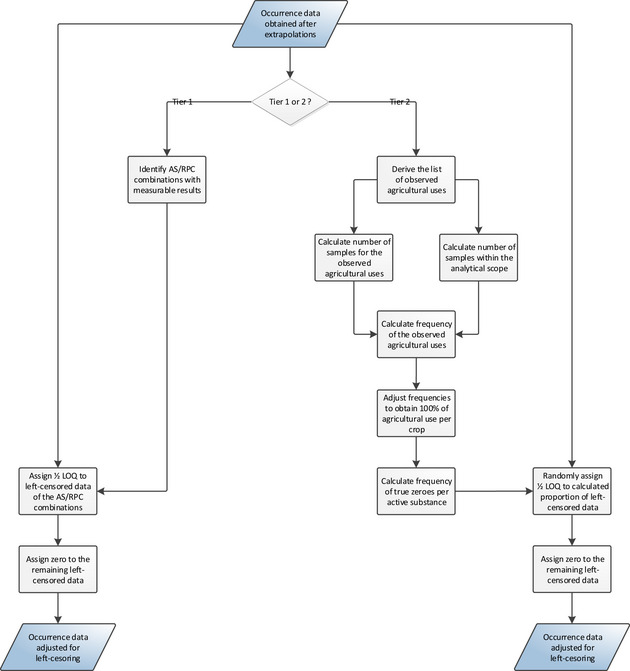
Flowchart for the imputation of left‐censored measurements

Appendix D – Procedure for deriving the chronic exposure distribution

1.

1. Calculate average concentrations for each active substance and raw primary commodity (RPC). Under Tier II assumptions, the average concentrations also account for the implicit zero measurements resulting from the assignment of active substances to unspecific residue definitions. Assign to each consumption record mean occurrence value of active substances in RPC by joining consumption data with occurrence data (using the RPC as key).

2. Assign processing factors (PF) to the relevant records of data set created at step 1 by joining information from the processing factors table (using the RPC, active substance and foodEx2 facet as the keys). If no processing factor is available for a specific combination, then a missing value is assigned to the PF.

3. Calculate normalised exposure (NE) for each record using formula described in Section 2.2.4.2 to obtain NE per subject, RPC and active substance.

4. Sum all normalised exposures of RPCs and active substances per subject to obtain a total normalised exposure (NET) for each subject.

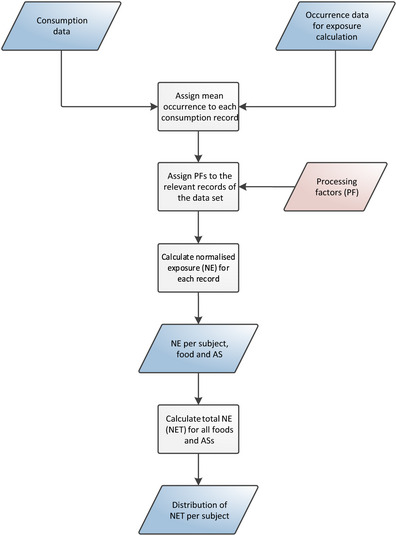
Flowchart for the calculation of chronic exposure

Appendix E – Technical notes supporting the EKE process

1.

Note 1 (Contribution of the selected 35 commodities to the overall diet of plant origin) – U1

The contribution of the 35 commodities selected (see annex A, Table A.02) for the assessment to the overall long‐term diet of plant origin has been calculated for the 10 populations assessed, based on the respective consumption survey data and using the RPC model (EFSA, 2019e) to convert the amounts food as consumed into the respective amounts of raw primary commodities. Sugar plants were excluded from these calculations as residues in sugar are very unlikely due to the extensive processing that is applied to sugar plants.

The calculations reported in Table E.1 show that this contribution ranges, in average, from 75% (Bulgarian children) to 88% (Italian adults), with standard deviations ranging from 6% to 13%.

Table E.1.

Contribution (in % of the total weight) of the selected 35 commodities to the overall diet of plant origin in the population groups considered in the assessment

Country	Population class	survey	No. of subjects	Mean proportion (%)	Standard deviation (%)
Belgium	Adults	DIET NATIONAL 2004	1,292	79.7	11.4
Czechia	Adults	SISP04	1,666	79.9	12.0
Germany	Adults	NATIONAL NUTRITION SURVEY II	10,419	79.6	12.4
Italy	Adults	INRAN SCAI 2005‐06	2,313	88.4	7.6
Bulgaria	Other children	NUTRICHILD	433	74.6	13.3
France	Other children	INCA2	482	83.7	7.4
Netherlands	Other children	VCP KIDS	957	81.5	8.4
Denmark	Toddlers	IAT 2006‐07	917	84.2	6.0
Netherlands	Toddlers	VCP KIDS	322	82.8	8.3
United Kingdom	Toddlers	DNSIYC 2011	1,314	86.5	8.6

Note 2 (Contribution of animal commodities to the pesticide residues intake) – U1

Food from animal origin represents a major part of human diet. Its omission from the exposure calculations leads, therefore, to an underestimation of the risks.

The EFSA annual European Union reports on pesticide residues in food contain detailed information on pesticide residues in animal products in dedicated sections (EFSA, 2018a, 2019d, 2020c).

In 2016, 8,351 samples of products of animal origin were analysed, of which 17% contained residues at or above the LOQ of 49 different pesticides. The most frequently quantified were copper, DDT, hexachlorobenzene (HCB), thiacloprid, chlordane, HCH‐beta, chlorate, benzalkonium chloride (BAC), didecyldimethylammonium chloride (DDAC), hexachlorocyclohexane (HCH)‐alpha and dieldrin. In 2017, 9,682 samples were analysed, of which 13% contained quantifiable residues of 48 different pesticides. The most frequently quantified were copper, HCB, DDT, chlordecone, thiacloprid, fipronil and BAC. In 2018, 11,549 samples were analysed, of which 12% contained quantifiable residues of 48 pesticides. The most frequently quantified were chlordecone, DDT, HCB, copper, thiacloprid, fipronil, BAC, chlorates, amitraz, DDAC, acetamiprid, chlorpyrifos, dimoxystrobin, mercury and HCH (beta). Chlorpyrifos was reported mainly in terrestrial invertebrate animals.

Most of the compounds found in animal commodities are banned or no longer used as pesticides in Europe, but they are still present in the food chain due to their persistence in the environment. The presence of residues of OPs in animal products is infrequent and residues of NMCs are not found.

Each year, some animal commodities are selected under the EUCP for a targeted risk assessment. Over the EUCP 3‐year cycle considered in the present assessment, six animal products were selected: cow's milk, swine fat, poultry fat, sheep fat, bovine fat and chicken eggs. Short‐term risk assessments have been conducted when any of the substances included in the EUCP was found in at least one sample of these commodities at quantifiable levels. This has been the case for three OPs: chlorpyrifos‐methyl, diazinon and pirimiphos‐methyl. The short‐term exposure calculations using the highest measured residue concentration in the respective commodity are reported in Table E.2. They indicate that the acute exposures are at least three orders of magnitude below the respective ARfDs.

Table E.2.

Short‐term dietary exposure assessment for OPs found in animal products under the EUCP of 2016, 2017 and 2018

Substance	Commodity	No. of samples < LOQ	No. of samples ≥ LOQ	Short‐term exposure (% of the ARfD)a
Chlorpyrifos‐methyl	Swine meat	914	2	0.005
Pirimiphos‐methyl	Swine meat	881	3	0.01
Diazinon	Sheep meat	411	2	0.03
Diazinon	Bovine fat	810	1	0.1

^aThe result corresponds to the sample containing the highest residue concentration for the respective substance/commodity combination (most conservative estimate).

The contribution of animal commodities to the chronic intake of pesticide residues is difficult to determine precisely because the vast majority of occurrence data for animal commodities are left‐censored and, therefore, calculations largely depend on the assumptions for handling results below the LOQ. Therefore, such calculations were not performed. However, the calculations reported in Note 3 inform about the overall impact of all omitted commodities, including those from animal origin.

Note 3 (Contribution of the selected 35 commodities to the overall intake of pesticide residues) – U1

Based on the occurrence data collected during the 3‐year cycle of the EUCP under consideration, long‐term dietary exposures to substances of the CAG included in the EUCP were calculated deterministically with the PRIMo model version 3.1 (EFSA, 2018b, 2019g) using either the full diet or only the 35 commodities of plant origin selected to perform the present CRA. These calculations used samples taken by selective or objective sampling strategies only (i.e. sample strategies ST10A and ST20A as defined in EFSA, 2013a – see also Note 13). Suspect sampling23 was not considered. They were performed with two alternative assumptions for measurements reported below the LOQ (upper and lower bound approaches). In the upper bound approach, a level equal to the LOQ was assumed for all samples reported below the LOQ, if at least one sample of the respective substance/commodity combination had quantifiable residues. In contrast, when all samples of a substance/commodity combination were reported to be below the LOQ, the contribution of this combination to the total dietary intake was considered as being nil. In the lower bound approach, the assumption was that residues in samples reported to be below the LOQ were in all cases true zeros.

The calculations were conducted for all populations included in the PRIMo model and the results for the population with the highest intake can be found in Table E.3.

Table E.3.

Contribution of the selected 35 commodities of plant origin to total long‐term exposure to residues of substances included in CAG‐NCNa

Active substance	Total Long‐term exposure (% of ADI)		Long‐term exposure related to selected commodities (% of ADI)		Contribution of selected commodities to total long‐term exposure (%)
	Lower bound	Upper bound	Lower bound	Upper bound	Lower bound	Upper bound
Acephate	0.01	0.19	< 0.01	0.17	22	93
Azinphos‐methyl	< 0.01	1.94	< 0.01	1.93	100	100
Carbaryl	0.04	1.00	< 0.01	0.94	3	94
Carbofuran	0.45	20.00	0.04	19.05	9	95
Chlorpyrifos	10.25	52.49	9.55	46.82	93	89
Chlorpyrifos‐methyl	0.57	4.85	0.54	3.75	95	77
Diazinon	0.64	44.43	0.02	42.03	3	95
Dichlorvos	0.85	58.17	0.82	58.16	96	100
Dimethoate	5.46	31.29	5.29	29.19	97	93
Ethephon	0.74	2.82	0.13	2.53	18	90
Ethion	0.03	0.45	< 0.01	0.36	3	80
Fenamiphos	0.03	6.29	0.03	6.23	97	99
Fenitrothion	0.01	3.91	0.01	3.89	100	99
Fenthion	< 0.01	0.62	< 0.01	0.53	100	85
Formetanate	0.07	1.77	0.07	1.74	100	98
Fosthiazate	0.03	2.52	0.03	2.51	100	100
Malathion	0.02	0.60	0.02	0.47	94	78
Methamidophos	0.07	3.69	0.02	3.53	26	96
Methidathion	0.04	14.48	0.04	14.32	97	99
Methiocarb	0.01	0.77	0.01	0.74	50	97
Methomyl	0.17	2.04	0.02	1.95	14	95
Monocrotophos	0.02	0.95	0.02	0.90	100	95
Omethoate	16.83	96.62	16.36	91.80	97	95
Oxamyl	0.23	4.09	0.01	3.95	6	96
Oxydemeton‐methyl	< 0.01	0.03	0.00	0.00	0	0
Parathion	0.01	3.16	0.01	3.16	100	100
Parathion‐methyl	< 0.01	1.10	< 0.01	1.10	100	100
Phosmet	0.46	3.30	0.44	3.16	95	96
Pirimicarb	0.10	0.70	0.09	0.66	93	94
Pirimiphos‐methyl	9.12	13.22	8.77	12.39	96	94
Profenofos	0.07	0.24	< 0.01	0.21	3	88
Thiodicarb	< 0.01	0.11	< 0.01	0.010	100	87
Tolclofos‐methyl	0.07	0.001	0.07	0.001	100	100
Triazophos	0.10	2.29	0.10	2.09	99	91

^aSome of the substances included in the CAG are not covered by the EUCP, and for these substances, the contribution of the selected commodities to the total exposure was not calculated: azinphos‐ethyl, benfuracarb, cadusaphos, carbosulfan, chlorfenvinphos, ethoprophos, fonofos, phenthoate, phosalone, phoxim, pyrazophos and trichlorfon. All these substances have been withdrawn form the EU market and their occurrence in commodities is rare (see Table E.10). Aldicarb is not reported because this substance has not been found in any sample during the reference period.

The contribution of the selected 35 commodities to the total long‐term exposure is better reflected by the lower bound calculations as these calculations rely on quantified residues only. The table shows that the contribution of the selected 35 commodities exceeds 80% of the total intake for about 65% of the active substances (rows highlighted in green). For the 35% of substances for which this is not the case, the total long‐term exposure never exceeds 1% of the ADI, as can be seen in the second column of the table.

In the upper bound approach, the contribution of selected 35 commodities to the total long‐term exposure exceeds 80% in most cases.

Note 4 (Ambiguity of consumption and occurrence data) – U2 and U9

Part B of annex I to Regulation (EC) No 396/2005 defines groups of commodities containing a main product (e.g. tomatoes) and other similar products to which the same MRL applies (e.g. ground cherries, cape gooseberries, cherry tomatoes etc.). Each group has a code number.

The EFSA Standard Sample Description (SSD) (EFSA, 2014b) defines a matrix code ProdCode, derived from the group code number of the Regulation, and requires this code to be used for the sample description in the reporting of occurrence data. For the monitoring data from 2016 to 2018, a mechanism to differentiate commodities within each group listed in part B of Annex I was not in place, and therefore, the occurrence data of all commodities of the group were merged and reported under the same code.

The EFSA comprehensive food consumption database contains similar ambiguities and is built on a similar level of aggregation of RPCs as for occurrence data. The consequence is that probabilistic modelling combines indiscriminately occurrence and consumption data for different commodities of a same group, although the residue profiles and consumption level may differ between these commodities.

The proportion of occurrence data that are allocated to one of the 35 RPCs in the scope of this CRA, but which are in fact different commodities, is expected to be low (less than 5%, based on rough estimation), but precise information about the exact cases and proportions is not available.

In chronic exposure assessment, as both the occurrence and consumption data are averaged, this source of uncertainty is not expected to have a significant effect.

Note 5 (methodological characteristics of food consumption surveys, quality check of consumption data) – U3

Basic information (survey method and number of days in the survey) on the nine dietary surveys from which the 10 population groups were extracted to perform the present CRAs is provided in Annex A Table A.04.

Additional methodological features (e.g. days between non‐consecutive days, interview administration, portion size estimation, dietary software and related databases, additional food information (brand, household processing, packaging), evaluation of under‐reporting) characterising six of these surveys (Belgium (Diet National 2004), Bulgaria (NUTRICHILD), Czech Republic (SISP04), Germany (German National Nutrition Survey II), France (INCA2) and Italy (INRAN‐SCAI 2005–06)) were described and critically discussed by EFSA (2011) and Merten et al. (2011). This information is important to evaluate the level of accuracy of food consumption data and to compare results of exposure calculations performed with consumption data collected in these surveys.

After collection, food consumption data provided to EFSA are subject to a validation process upon reception (EFSA, 2011). First, the food classification is compared to the food descriptions reported by the data provider. Any inconsistency identified is reported to the data provider for confirmation or correction. Furthermore, the amounts of food reported are validated against several maximum limits, which are derived from the food consumption data already available to EFSA. These limits are defined for each food category per eating occasion and per day. If one of these limits is exceeded, the data provider is requested to provide a justification or to correct the amount reported if necessary.

Note 6 (psychological factors in consumption surveys) – U3

In its guidance on the EU Menu methodology, EFSA collected information on the magnitude, nature and determinants of misreporting (EFSA, 2014c), including both under‐ and over‐reporting. This information suggests that over‐reporting occurs much less often than under‐reporting, and that the importance of under‐ and over‐reporting varies between population subgroups and commodities (tendency to under‐report foods with high content of fat or sugar). It was estimated that when a food consumption database is used to assess dietary exposure, the presence of under‐reporting may lead to the under‐estimation of mean dietary exposure in the population, and to the under‐estimation of the percentage of consumers of some foods high in fat or in sugar. Under‐reporting is however likely to have little effect on the assessment of high percentiles of dietary exposure per kilogram body weight.

For six of the surveys used in the present assessment (Belgium (Diet National 2004), Bulgaria (NUTRICHILD), Czech Republic (SISP04), Germany (German National Nutrition Survey II), France (INCA2) and Italy (INRAN‐SCAI 2005–06)), information available about the identification of under‐reporters, cut‐off values and percentage of under‐reporters was reported by Merten et al. (2011).

Note 7 (Population size and sampling variability – Consumption and occurrence data) – U4 and U11

With respect to consumption data, the number of subjects in the 10 populations used to perform CRA ranges from 322 (NL, toddlers, 2 years old) to 10,419 (Germany, adults). The Guidance on the use of the comprehensive food consumption database contains a section on the reliability of high percentiles in food consumption. The minimum number of subjects in a population needed to achieve a 95% confidence interval (significance level (α) at 0.05) increases with the percentile to be computed. This is achieved for n ≥ 59 and n ≥ 298 for the 95th or 99th percentiles, respectively (EFSA, 2011). The number of subjects needed to achieve similar statistical robustness at the 99.9th percentile is approximately 3000.

Furthermore, it is known that sampling of skewed distributions (like the populations of consumers) may underestimate high percentiles, because there is a high probability that values from the upper tail of the distribution will not be sampled. To illustrate the problem, a simulation starting from a skewed parametric distribution (in this case a lognormal distribution with a true 99.9th percentile of 646.9, see Figure E.1) was performed. From this distribution 1,000 values were sampled at random and the observed 99.9th percentile of the sample was computed. This process was repeated 1,000 times and the 99.9th percentile for the 1000 samples were plotted and compared to the true 99.9th percentile of this distribution (see Figure E.2). It turned out that by selecting 1,000 values from the distribution, the observed 99.9th percentile will be underestimated in around 75% of the cases and this underestimation may be by a factor up to 2. Although this is only a theoretical simulation, it clearly shows that the 99.9th percentile of the exposure distribution, which is skewed, is likely to be underestimated.

Figure E.1.

Density plot for a skewed distribution (lognormal)

Figure E.2.

Density plot of the observed 99.9th percentile of 1,000 simulated samples (each with a sample size of 1,000 values)

With respect to occurrence data, the number of data (measurements) for each pesticide/commodity combination in the scope of the conducted CRAs varies widely, from zero to several thousands. The precise number of measurements available for each combination can be found in Annex A Table A.09. Table E.4 gives an overview of these numbers.

Table E.4.

Number of measurements available for pesticide/commodity combinations under the scope of the present assessmenta

Number of measurements	Number of pesticide/commodity combinations	Comment
Less than 100	74	Mainly pesticide/commodity combinations involving olives for oil production
At least 100 and less than 300	90	Pesticides commodity combinations involving oats, wine grapes, omethoate and dimethoates measured separately and ethephon
At least 300 and less than 1,000	355	–
At least 1,000 and less than 3,000	846	–
More than 3,000	517	Includes pirimiphos‐methyl/wheat, chlorpyrifos/oranges

^aFood intended for infants and young children are excluded from this table as a legal limit of 0.01 mg/kg applies for pesticides residues in these commodities (Commission Directives 2006/125/EC and 2006/141/EC). Pesticide/commodity combinations for which no measurements are available are also excluded from the table. For specific information about these combinations, see Note 10.

The overall sampling variability associated with consumption and occurrence data was quantified by outer loop execution and the resulting confidence intervals can be found in Section 3.1.2. It is acknowledged that bootstrapping performs less well for small data sets (EFSA Scientific Committee, 2018a,b, annex B.11), especially when the focus is on the tail of the variability distribution as is the case here (99.9th percentile). Therefore, to address the additional uncertainty associated with the use of the bootstrap method, given the sample sizes involved in the exposure assessment, EFSA (2020a,b) compared model outputs for the 10 populations, in similar CRAs, for any indication of influence of sample size on the estimates obtained. It was noted that:

• Boxplots of 99.9th percentiles from MCRA24 bootstrap samples for the different consumer groups shows no sign of instability for the groups having smaller numbers of participants in consumption surveys (Figure E.3).

• Boxplots of the ratio of the 99.9th percentile to the 50th percentile from MCRA bootstrap samples for the different consumer groups also shows no sign of instability for the groups having smaller numbers of participants in consumption surveys (Figure E.4).

Figure E.3.

Boxplots of 99.9th percentiles from MCRA bootstrap samples for the different consumer groups. NAM, NAN, TCF and TCP refer to CAG‐NAM, CAG‐NAN, CAG‐TCF and CAG‐TCP,25 respectively

Figure E.4.

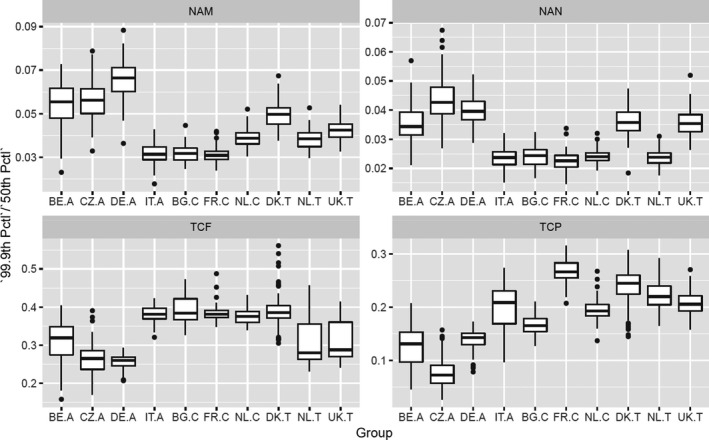
Boxplots of the ratio of the 99.9th percentile to the 50th percentile from MCRA bootstrap samples for the different consumer groups. NAM, NAN, TCF and TCP refer to CAG‐NAM, CAG‐NAN, CAG‐TCF and CAG‐TCP, respectively

Overall, this supported that estimating the 99.9th percentile was not particularly problematic.

In the present assessment, an instability of the median estimate of the 99.9th percentile was however noticed when repeating the Tier II calculations (see Table E.5). This instability is consistent across the different population groups, meaning that if the median estimate is higher in one set of runs for Italian adults it is higher for all the other population groups too. This seems to suggest that this instability arises from the bootstrap resampling of residues.

Table E.5.

Comparison of multiple runs of the Tier II calculations, all performed with 100 bootstrap samples

Country	Population class	Tier II (original run)	Tier II (run 2)	Tier II (run 3)
Belgium	Adults	115 [40.2–289]	130 [35.2–301]	138 [44.4–330]
Czechia	Adults	91 [31.5–271]	102 [28.4–282]	107 [32.6–289]
Germany	Adults	116 [39.5–232]	116 [38.5–231]	123 [40–235]
Italy	Adults	51.6 [16.5–266]	54.3 [16.3–276]	57.9 [17.8–272]
Bulgaria	Other children	82.9 [32.7–151]	84.1 [34.7–152]	91.5 [35.3–153]
France	Other children	51.8 [16.6–191]	53 [14.9–190]	56.1 [18.7–194]
Netherlands	Other children	91 [41.3–149]	100 [40.3–143]	102 [39.6–147]
Denmark	Toddlers	97.4 [38.6–143]	100 [38.6–140]	104 [37.5–142]
Netherlands	Toddlers	60.3 [26.8–120]	62.7 [25.6–115]	64.4 [27.5–124]
United Kingdom	Toddlers	78.1 [33.1–153]	78.4 [31.7–151]	82.3 [33.3–155]

An additional calculation was therefore performed using 500 bootstrap executions instead of 100 (see Table E.6). As can be seen from the results, the instability mainly impacts on the median value of the confidence intervals, while the lower and upper are less affected.

Table E.6.

Comparison of the Tier II calculations performed with 100 bootstraps vs. 500 bootstraps

Country	Population class	Tier II (original run – 100 bootstraps)	Tier II (500 bootstraps)
Belgium	Adults	115 [40.2–289]	134 [40.7–312]
Czechia	Adults	91 [31.5–271]	99.8 [31.3–275]
Germany	Adults	116 [39.5–232]	119 [36.6–233]
Italy	Adults	51.6 [16.5–266]	55.9 [15.6–271]
Bulgaria	Other children	82.9 [32.7–151]	87.1 [31.4–151]
France	Other children	51.8 [16.6–191]	55.1 [15.4–193]
Netherlands	Other children	91 [41.3–149]	96.8 [39.8–148]
Denmark	Toddlers	97.4 [38.6–143]	103 [27.7–142]
Netherlands	Toddlers	60.3 [26.8–120]	61.6 [25.3–122]
United Kingdom	Toddlers	78.1 [33.1–153]	81.9 [31.1–149]

However, even with 500 bootstraps, the median of the confidence intervals is still not completely stable. The reason for this instability is the bimodality of the confidence intervals, which is well visualised with the violin plots in Figure E.5, which are alternative representations of boxplots showing the density of observations of MOET estimates.

Figure E.5.

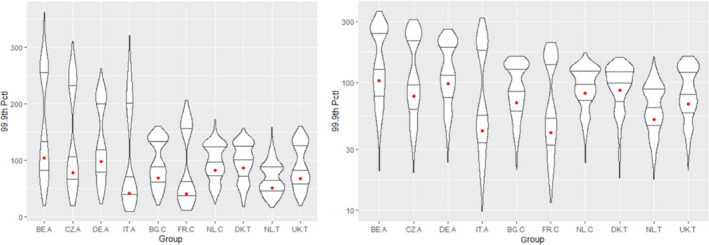
Violin plots for the confidence intervals of the MOET at the 99.9th percentile of the exposure distributions presented by population (500 bootstraps). The horizontal lines are at quartiles and median, i.e. the ends of the box and the median line in normal boxplots. The width of violin is proportional to density of observation for each value of the MOET at the 99.9th percentile of the exposure distribution. The first version has a linear axis and the second a logarithmic axis. Roughly 3/8 of the samples are in the upper cluster (for all populations where there is clear separation). The nominal run is indicated by a red point and is consistently below the median

Sensitivity analysis J (see Table 16 in Section 3.1.3) also demonstrated that the width of the confidence intervals is almost entirely driven by the sampling uncertainty. The reason for this width and bimodality of the confidence intervals is caused by two different factors:

There are 79 samples only for olives for oil production. Only two of these contained quantifiable residues for the sum of dimethoate and omethoate (0.08 and 4.9 mg/kg). As the bootstrap analysis proceeds with sampling with replacement, it can be predicted that the sample with 4.9 mg/kg will not be part of around 36% of the bootstrap samples, will be sampled once in around 37% of the bootstrap samples and it will be sampled twice or thrice in about 26% of the samples. As explained in Note 16, this sample, where a concentration of 4.9 mg/kg was measured, has a large contribution to the MOET at 99.9th percentile of the distribution. Therefore, its absence in 36% of the bootstrap samples will result in a dramatic downwards impact on the average concentration of omethoate in olives for oil production, and in a much higher MOET, consequently creating the upper cluster of the bimodal confidence intervals.

To check the impact of this single sample on the MOET estimates at the 99.9th percentile of the exposure distribution, a sensitivity analysis was performed, with exclusion of this sample from the calculations. This sensitivity analysis is reported as sensitivity analysis E in Table 16 of Section 3.1.3.

In addition, occurrence data for the sum of dimethoate and omethoate in olives for oil production in 2014, 2015, 2016, 2017 and 2018 were consulted. In total, 104 samples were analysed, and quantifiable residues were found in 11 of them. The values found were 0.01, 0.02 (× 3), 0.03, 0.05, 0.06, 0.08, 0.18, 0.35 and 4.9 mg/kg. These data suggest that the value of 4.9 mg/kg is an exceptional finding and that the actual probability to encounter such a concentration is likely to be smaller than 1 out of 79.

Note 8 (Representativeness of consumption data) – U5

Biases can arise from a survey sample that does not represent the population group at national level.

For six surveys (Belgium (Diet National 2004), Bulgaria (NUTRICHILD), Czech Republic (SISP04), Germany (German National Nutrition Survey II), France (INCA2) and Italy (INRAN‐SCAI 2005–06)), information about the sampling strategy has been reported by EFSA (2011) and Merten et al. (2011). The information includes the sampling design (sampling method, sampling frame), response rate, sample stratification variables (gender, age, geographical areas, day of the week and season, others (education level, urban vs urban residence, ethnicity), excluded groups (e.g. institutionalised persons, pregnant or breastfeeding women) and subjects’ long‐term dietary pattern (e.g. vegetarian, health related or slimming). With respect to ethnicity, details were not available to the experts about the representativeness of the consumption data for this criterion.

Another factor affecting the representativeness of consumption data is the temporal gap between the period of the surveys and the reference period of the assessment (2016–2018). Depending on the survey, the consumption data used in this CRA were collected from 2001 to 2007. Possible changes in food consumption practices over a period of more than 10 years need to be considered. In the Netherlands, the evolution in food consumption was reported by RIVM by comparing the results of surveys conducted from 2007 to 2010 and from 2010 to 2016.26 Over this period of about 5 years, the consumption of cereal products and vegetables (increase of 3%) was rather stable, while a slight increase of the fruit consumption, including nuts and olives (increase of 9%) were noted. Decrease in the consumption of potatoes, milk products and meat products was also noted. These observations are supported by the observation of an overall positive trend in the prevalence of daily fruit and vegetable consumption between 2002 and 2010 by adolescents in 33 countries (Vereecken et al., 2015).

Note 9 (RPC model) – U6

In order to perform cumulative exposure assessments, the EFSA RPC model (EFSA, 2019e) was used to convert the consumption data for composite foods (i.e. foods consisting of multiple components, e.g. apple strudel) and RPC derivatives (i.e. single‐component foods which have been physically changed by processing, e.g. apple juice) into the equivalent quantities of RPCs (i.e. single‐component foods which are unprocessed or whose nature has not been changed by processing, e.g. apples).

The main sources of uncertainty of the RPC model result from the following:

• The RPC model still relies on the FoodEx coding system, which is less accurate than the more recent FoodEx2 coding system. Although the FoodEx classification system has been expanded to include intermediate codes, the specificity of the RPC model is still limited by the FoodEx classification system applied in the comprehensive European food consumption database at the time of the model's development. Food consumption data in the comprehensive database have since been updated to include dietary surveys coded with the revised FoodEx2 system (EFSA, 2015b). Meanwhile, RPC consumption data resulting from composite foods that could not be assigned with a more accurate classification code may either be over‐ or underestimated.

• When a food code reported in the comprehensive database was not sufficiently detailed for disaggregation, more specific foods and food components were assigned using probabilities. This probabilistic assignment introduces an element of uncertainty. Although foods are selected based on the reported consumption records in the food consumption database, a food which is not representative of what was actually consumed may be selected. Some sensitivity tests demonstrated that results obtained through the RPC model may be very variable when low probabilities are considered. This instability was addressed by excluding foods and food components that had probabilities below 10%. This approach increased the reliability of the RPC model. However, the exclusion of certain foods also implies that consumption data for frequently consumed RPCs (e.g. apples) may be slightly overestimated. Likewise, RPCs that are not frequently consumed (e.g. cherries) are likely to be underestimated. In practice, in the present case, as only 35 major commodities are considered, the exclusion or rare food components results in possible overestimation of the actual consumption of these commodities.

• The RPC model does not consider inter‐country variation, consumer habits, personal preferences, and product or recipe variation. Furthermore, differences between commercial products and household prepared foods are not accounted for. This may lead to either over‐ or underestimations of the RPC consumption.

• In the final step of the RPC conversion, amounts of RPC derivatives are converted to corresponding amounts of RPC, using reverse yield factors. There is currently no harmonised list of reverse yield factors available on either European or worldwide level and reverse yield factors sourced in the conversion table of the model may not be accurate. Furthermore, the RPC model uses one single factor for each processing technique. In reality, yields vary among households and industrial manufacturers. This uncertainty is not expected to have a major impact on average consumption/exposure, but it is expected to underestimate upper tail consumption/exposure.

Consumers with the highest consumption of RPC derivatives and composite foods are the most sensitive to this source of uncertainty.

Note 10 (Missing occurrence data) – U7

Occurrence data are missing for only one (out of 240) authorised pesticide/commodity combination: ethephon/olives for oil production. For this combination, it was not possible to extrapolate occurrence data from any other commodities. Therefore, its contribution to the cumulative risk has not been accounted for.

Note 11 (Contribution of metabolites) – U8

In order to evaluate the risk from dietary intake of pesticide residues, it is needed to take account of all metabolites and degradation products which contribute significantly to the risk under consideration. This is done by defining a residue definition for risk assessment. This residue definition may not be the same as the enforcement residue definition which is pursuing another purpose.

When the residue definition for risk assessment includes more compounds than the enforcement residue definition, and when enough data are available, a conversion factor is determined to translate residue concentrations expressed following the residue definition for monitoring into their counterpart for risk assessment.

In the present exercise, the occurrence data were used without any correction by conversion factors for reason of resources, and because the existing residue definition for risk assessment established with respect to the critical effect (e.g. leading to the ADI) is not necessarily valid for acetyl cholinesterase inhibition, although for OPs and NMCs AChE inhibition is in many cases the critical effect.

The residue definition for risk assessment of all substances of CAG‐NCN established by EFSA or the JMPR were collected and compared to the respective enforcement residue definitions in Table E.7.

Table E.7.

Residue definition for enforcement and risk assessment in plant commodities of substances included in CAG‐NCN

Substance	Residue definition for enforcement applied to occurrence data collected during the reference period	Residue definition for risk assessment (plant commodities)	Conversion factor	Comment
Acephate	Acephate	Acephate	–	Methamidophos is monitored separately
Aldicarb	Aldicarb (sum of aldicarb, its sulfoxide and its sulfone, expressed as aldicarb)	Aldicarb (sum of aldicarb, its sulfoxide and its sulfone, expressed as aldicarb)	–	EFSA scientific opinion 2006
Azinphos‐ethyl	Azinphos‐ethyl	Not available	Not available	The residue following application of azinphos‐ethyl consisted partly of the P = 0 metabolite presumably owing to its higher chemical stability. After 14 days approximately 10% of the residue could be determined by TLC and GLC as the P = 0 analogue.a
Azinphos‐methyl	Azinphos‐methyl	Azinphos‐methyl	–	Provisional, apples and pears only. EFSA reasoned opinion 2014
Benfuracarb	Sum of carbofuran (including any carbofuran generated from carbosulfan, benfuracarb or furathiocarb) and 3‐OH carbofuran expressed as carbofuran	Sum of carbofuran and 3‐hydroxy carbofuran, both free and conjugated expressed as carbofuran	Not available	EFSA conclusion 2009
Cadusafos	Cadusafos	Cadusafos	–	EFSA conclusion 2009
Carbaryl	Carbaryl	Sum of carbaryl, 4‐hydroxycarbaryl and 5‐hydroxycarbaryl expressed as carbaryl	Available data not sufficient	EFSA conclusion 2006
Carbofuran	Sum of carbofuran (including any carbofuran generated from carbosulfan, benfuracarb or furathiocarb) and 3‐OH carbofuran expressed as carbofuran	Sum of carbofuran and 3‐hydroxy carbofuran, both free and conjugated expressed as carbofuran	Not available	EFSA conclusion 2009
Carbosulfan	Carbofuran (sum of carbofuran (including any carbofuran generated from carbosulfan, benfuracarb or furathiocarb) and 3‐OH carbofuran expressed as carbofuran)	Sum of carbofuran and 3‐hydroxy carbofuran, both free and conjugated expressed as carbofuran	Not available	EFSA conclusion 2009
Chlorfenvinphos	Chlorfenvinphos	Chlorfenvinphos, sum of (E)‐ and (Z)‐ isomers	–	JMPR, 1996b
Chlorpyrifos	Chlorpyrifos	RD‐risk assessment 1: Raw commodities: chlorpyrifos Processed commodities: sum of chlorpyrifos and its desethyl metabolite, expressed as chlorpyrifos (tentative)	–	EFSA MRL review 2017 RD‐risk assessment 2 (not relevant): All crops: sum of 3,5,6‐trichloropyridinol (3,5,6‐ TCP) and its conjugates, expressed as 3,5,6‐TCP
Chlorpyrifos‐methyl	Chlorpyrifos‐methyl	RD‐risk assessment 1: Fruit crops, root crops and pulses/oilseeds: chlorpyrifos‐methyl Processed commodities: sum of chlorpyrifos‐methyl and desmethyl chlorpyrifos‐methyl, expressed as chlorpyrifos‐methyl (tentative)	–	EFSA MRL review 2017 RD‐risk assessment 2 (not relevant): All crops: sum of 3,5,6‐trichloropyridinol (3,5,6‐ TCP) and its conjugates, expressed as 3,5,6‐TCP
Chlorpyrifos‐methyl	Cereals only: sum of chlorpyrifos‐methyl and desmethyl chlorpyrifos‐methyl, expressed as chlorpyrifos‐methyl	Cereals only: sum of chlorpyrifos‐methyl and desmethyl chlorpyrifos‐methyl, expressed as chlorpyrifos‐methyl (tentative)	–	EFSA MRL review 2017
Diazinon	Diazinon	Raw commodities: Diazinon Processed commodities: sum of diazinon and desethyl diazinon	–	EFSA conclusion 2006
Dichlorvos	Dichlorvos	Not available	Not available	EFSA conclusion 2006: Not sufficient information to derive a RD
Dimethoate	Dimethoate	Dimethoate	–	EFSA conclusion 2018 Omethoate monitored separately
Dimethoate	Sum of dimethoate and omethoate expressed as dimethoate	See Dimethoate and Omethoate
Ethephon	Ethephon	Ethephon	–	– Modification of existing MRL for ethephon in persimmons (EFSA reasoned opinion 2017) – EFSA MRL review 2009
Ethion	Ethion	Ethion	–	JMPR, 1994c
Ethoprophos	Ethoprophos	Residue definition in primary crops: ethoprophos and M5, expressed as ethoprophos Residue definition in rotational crops: ethoprophos, EPPA and M5, expressed as ethoprophos	Not available	EFSA conclusion 2018 M5: Ethyl‐phosphate, O‐ethyl phosphoric acid EPPA: (M31), M1M, M1, O‐ethyl Spropyl phosphorothioate
Fenamiphos	Sum of fenamiphos and its sulfoxide and sulfone expressed as fenamiphos	Sum of fenamiphos and its sulfoxide and sulfone expressed as fenamiphos	–	EFSA conclusion 2019
Fenitrothion	Fenitrothion	Fenitrothion (Note: the toxicological relevance of desmethylfenitrothion and dimethylphosphorothioic acid is unknown. Therefore, this definition could be reconsidered in the future)	–	EFSA conclusion 2006
Fenthion	Sum of fenthion and its oxygen analogue, their sulfoxides and sulfone expressed as fenthion	Sum of fenthion, its oxon and their sulfoxides and sulfones, expressed as fenthion	–	JMPR, 1995, p. 109d
Fonofos	Fonofos	Not available	Not available
Formetanate	Sum of formetanate and its salts expressed as formetanate (hydrochloride)	Formetanate Sum of formetanate and its salts expressed as formetanate (hydrochloride)	–	EFSA MRL review 2010
Fosthiazate	Fosthiazate	Not available	Not available
Malathion	Malathion (sum of malathion and malaoxon expressed as malathion)	Malathion and its metabolites malaoxon, desmethyl‐malathion, malathion monocarboxylic acid and malathion dicarboxcylic acid expressed as malathion toxic equivalents	Pending, further consideration necessary	EFSA conclusion 2009
Methamidophos	Methamidophos	Methamidophos	–	Scientific support for preparing an EU position in the 44th Session of the Codex Committee on Pesticide Residues (CCPR) (EFSA scientific report 2012)
Methidathion	Methidathion	Methidathion	–	Consumer safety assessment of the EU MRLs established for methidathion (EFSA reasoned opinion 2010)
Methiocarb	Sum of methiocarb and methiocarb sulfoxide and sulfone, expressed as methiocarb	Provisionally proposed as: 1) Methiocarb 2) M01 (a potency factor of 3 can be established to consider the sum of parent methiocarb and M01, if any genotoxicity potential can be ruled out for M01) 3) Sum of M03, M04 and M05, free and conjugated.	Not available	EFSA conclusion 2018 M01: methiocarb sulfoxide M03: methiocarb phenol M04: methiocarb sulfoxide phenol M05: methiocarb sulfone phenol
Methomyl	Methomyl	Methomyl (for fruit crops only; tentative for other crops)	–	EFSA MRL review 2015
Methomyl	Sum of methomyl and thiodicarb expressed as methomyl (applicable until May 2017)	See methomyl and thiodicarb
Monocrotophos	Monocrotophos	Not available	Not available	New studies were carried out on the metabolism of monocrotophos in plants and its degradation in soil. The degradation products previously found were O‐desmethylmonocrotophos, dimethyl phosphate and N‐hydroxymethylmonocrotophos. Maize grains and fodder were analysed for trimethyl phosphate at various intervals after treatment but residues of this compound were not detectable. Residues of Nhydroxymethyl‐monocrotophos, which occurs as a glycoside in crops, were determined in maize and sugar cane. Residues in the edible parts of crops were not detectable but were present in foliage and fodder (FAO, 1991).e
Omethoate	Sum of dimethoate and omethoate expressed as dimethoate	See Dimethoate and Omethoate
Omethoate	Omethoate	Omethoate	–	EFSA conclusion 2018
Oxamyl	Oxamyl	Oxamyl	–	EFSA MRL review 2010
Oxydemeton‐methyl	Sum of oxydemeton‐methyl and demeton‐S‐methylsulfone expressed as oxydemeton‐methyl	Sum of oxydemeton‐methyl, demeton‐S‐methylsulfon (M01), metabolite M06 and metabolite M07 expressed as oxydemeton‐methyl	Not available	EFSA conclusions 2006
Parathion	Parathion	Not available	Not available	In a plant metabolism study parathion was the major component of the residue (62% of the 14C) in wheat grain harvested 7 days after the second application of ring‐labelled parathion to the plant. Paraoxon was not detected in the grain and 4‐nitrophenol comprised 7.4% of the 14C. Parathion, paraoxon and 4‐nitrophenol accounted for 37%, 1.2% and 13% of the 14C in the wheat straw, respectively. In the straw and grain 72% and 82%, respectively, of the 14C was extractable with aqueous methanol (JMPR, 1995).d
Parathion‐methyl	Sum of Parathion‐methyl and paraoxon‐methyl expressed as Parathion‐methyl	Not available	Not available
Phenthoate	Phenthoate	Not available	Not available	Info on metabolism in plants and animal commodities in FAO, 1980f
Phosalone	Phosalone	Phosalone and oxophosalone	Data not sufficient to derive a CF	EFSA conclusion 2006
Phosmet	Phosmet	Phosmet (phosmet and phosmet oxon expressed as phosmet)	Not available	EFSA conclusion 2011 Residue definition for RA is provisional, pending the results study aimed to compare the relative potency of phosmet oxon and parent phosmet
Phosmet	Phosmet (phosmet and phosmet oxon expressed as phosmet)	Phosmet (phosmet and phosmet oxon expressed as phosmet)	–	EFSA conclusion 2011 Residue definition for RA is provisional, pending the results study aimed to compare the relative potency of phosmet oxon and parent phosmet
Phoxim	Phoxim	Not available	Not available	Only info found on residues (FAO, 1984)g
Pirimicarb	Pirimicarb	Pirimicarb (sum of pirimicarb, desmethyl pirimicarb and desmethyl formamido pirimicarb, expressed as pirimicarb)	1.3 for fruits and spices (fruits and berries), 1.4 for fruiting vegetables, spices (seeds) and for pulses and oilseeds, 1.7 for stem vegetables and fresh legume vegetables, 1 for root and tuber vegetables, 2.8 for lettuces, brassica and herbs.	EFSA MRL review 2014
Pirimicarb	Pirimicarb (sum of Pirimicarb and Desmethyl pirimicarb expressed as Pirimicarb)	Pirimicarb (sum of pirimicarb, desmethyl pirimicarb and desmethyl formamido pirimicarb, expressed as pirimicarb)	Not available
Pirimiphos‐methyl	Pirimiphos‐methyl	Pirimiphos‐methyl	–	EFSA MRL review 2015
Profenofos	Profenofos	Profenofos	–	Scientific support for preparing an EU position in the 44th Session of the Codex Committee on Pesticide Residues (CCPR) (EFSA scientific report 2012)
Pyrazophos	Pyrazophos	Not available	Not available
Thiodicarb	Methomyl and Thiodicarb (sum of methomyl and thiodicarb expressed as methomyl)	See methomyl and thodicarb	–	EFSA conclusion 2006
Thiodicarb	Thiodicarb	Thiodicarb	–	EFSA conclusion 2006
Tolclofos‐methyl	Tolclofos‐methyl	– For leafy crops (lettuce) and soil treatment: tolclofos‐methyl and the metabolites TM‐CH2OH conjugate and metabolite ph‐CH3-conjugate expressed as tolclofos‐methyl (preliminary pending on toxicological information and/or field trials). – For root and tuber (potato): tolclofos‐methyl and metabolite DM‐TM-CH2OH expressed as tolclofos‐methyl. – For processing: tolclofos‐methyl and TM‐DM (provisional).	Not available	EFSA conclusion 2018
Triazophos	Triazophos	Triazophos	–	Scientific support for preparing an EU position in the 46th Session of the Codex Committee on Pesticide Residues (CCPR) (EFSA scientific report 2014).
Trichlorfon	Trichlorfon	Not available	Not available	Additional info on residues (FAO, 1971)h

^a http://www.inchem.org/documents/jmpr/jmpmono/v073pr02.htm

^b http://www.fao.org/fileadmin/templates/agphome/documents/Pests_Pesticides/JMPR/Evaluation96/chlorfen.pdf

^c http://www.fao.org/fileadmin/templates/agphome/documents/Pests_Pesticides/JMPR/Evaluation94/ethion.pdf

^d http://www.fao.org/fileadmin/templates/agphome/documents/Pests_Pesticides/JMPR/Reports_1991-2006/Report1995.pdf

^e http://www.fao.org/fileadmin/templates/agphome/documents/Pests_Pesticides/JMPR/Reports_1991-2006/REPORT1991.pdf

^f http://www.inchem.org/documents/jmpr/jmpmono/v080pr31.htm

^g http://www.inchem.org/documents/jmpr/jmpmono/v84pr38.htm

^h http://www.inchem.org/documents/jmpr/jmpmono/v071pr09.htm

Note 12 (laboratory analytical uncertainty) – U10

In accordance with Article 37 of Regulation (EU) 2017/625,27 laboratories designated for official control of pesticide residues must be accredited to ISO/IEC 17025.28

The guidance on the use of the EFSA Standard Sample Description (EFSA, 2014b) provides official laboratories in Member States with a standardised model for the reporting of harmonised data on analytical measurements of chemical substances occurring in food, feed and water. It provides that laboratories have to always analyse and quantify pesticide residue according to the harmonised EU residue definitions, as provided by annexes II and III of Regulation (EC) No 396/2005. In reporting the results, and for the sake of comparability of data, the analytical uncertainty shall not be taken into account. However, the sample is reported to be compliant or not (considering the analytical uncertainty) under a dedicated field of the reporting model.

Furthermore, the Guidance document of the European Commission on analytical quality control and method validation procedures for pesticide residues and analysis in food and feed proposes a default measurement uncertainty of 50% (corresponding to a 95% confidence level and a coverage factor of 2), calculated from EU proficiency tests (European Commission, 2019) for multiresidues analytical method. In general, this 50% value covers the interlaboratory variability between the European laboratories and is recommended to be used by regulatory authorities in cases of enforcement decisions (MRL exceedances).

Note 13 (sampling strategy and representativeness of occurrence data) – U12

Various sampling strategies are used by Member States (objective sampling, selective sampling, suspect sampling, convenient sampling and census). These types of sampling are described in the Guidance on the use of the EFSA Standard Sample Description (EFSA, 2013a). To perform the CRAs reported in the present document, EFSA used samples collected under the official monitoring programmes of Member States in 2016, 2107 and 2018 and coded following sampling strategies ST10A or ST20A. The sampling strategies corresponding to these codes are defined as follows:

• ST10A (objective sampling): Strategy based on the selection of a random sample from a population on which the data are reported. Random sample is a sample which is taken under statistical consideration to provide representative data.

• ST20A (selective sampling): Strategy based on the selection of a random sample from a subpopulation (or more frequently from subpopulations) of a population on which the data are reported. The subpopulations may or may not be determined on a risk basis. The sampling from each subpopulation may not be proportional: the sample size is proportionally bigger for instance in subpopulations considered at high risk.

Under the selective sampling strategy, it is common that some food products, production methods, producers or countries are more targeted than others, and this affects the overall representativeness of the monitoring data. There are however inconsistencies in the interpretation of the term ‘selective sampling’ at member‐state level, as indicated by large differences in the proportion of samples coded ST20A between countries.

Although a representative sampling of occurrence data includes lots of commodities pertaining to various distribution channels (e.g. products for local consumption, grocery stores, specialised in foods imported from third countries) or produced following various method, including organic farming and a representative survey of consumption data includes consumers adhering to the respective distribution channels or methods of production, occurrence and consumption data are randomly associated by the model. The existing relationships between preferential consumption practices and the associated residue patterns are therefore lost. This was considered and it was concluded that this has a very minor impact at overall population level, especially at the percentile of interest of the cumulative exposure distribution.

To quantify the impact of samples belonging to the selective sampling strategy, a sensitivity analysis was performed, from which these samples were excluded (see uncertainty analysis G in Table 16 of Section 3.1.3).

It must also be noted that monitoring data from pre‐accessing countries were merged to the pool of monitoring data submitted by Member States. To check the impact of these data from non‐EU countries, a sensitivity analysis was conducted in which monitoring data from Member States only were used. This uncertainty analysis is reported as sensitivity analysis L in Table 16 of Section 3.1.3.

Note 14 (extrapolation of occurrence data between crops) – U13

Crop to crop extrapolation of occurrence data was envisaged between specific pairs of commodities as foreseen in guidance document SANCO 7525/VI/95 (European Commission, Directorate General for health and food safety, 2017), for cases where the last application of the pesticide takes place after forming of the edible part of the crop, when the number of occurrence data for the ‘data poor’ commodity was less than 10. The precise modalities governing these extrapolations are given in Section 2.2.3.3.

However, for the present assessment, this did not apply to any pesticide/commodity combination.

Note 15 (Pooling of occurrence data from all EU Member States) – U14

Occurrence data from all countries were pooled into one single data set that was used to calculate the cumulative risk for the 10 populations. This was done to increase the statistical robustness of the outcomes. Although this leads to losing the country specificity of the residue concentrations in commodities, this is not considered to be a major issue since most of the EU population is purchasing and consuming a mixture of local and imported commodities that is drawn from, and similar to, the mixture that is represented by the single data set with pooled occurrence data (‘common market’).

It should be noted that samples analysed and reported in national monitoring programmes are not only taken from lots intended for the internal market, but also from lots which are in transit or intended for export. This makes very difficult to make national risk assessments based on occurrence data reflecting exactly the residue level in commodities consumed in this country. Such assessments would require a specific data extraction based on information provided about the sampling point.

Note 16 (Unspecific residue definitions for enforcement) – U15

In tier II, in the absence of information related to the use frequency of pesticides, occurrence data for unspecific residue definition for enforcement were randomly allocated to one of the active substances included in the residue definition and authorised to be used on the respective commodity. All details of the implementing procedure are given in Section 2.2.2.3.

With respect to the active substances included in CAG‐NCN, 3 residue definitions are unspecific because they include more than one active substance (Table A.03 of Annex A):

• Sum of carbofuran (including any carbofuran generated from carbosulfan, benfuracarb or furathiocarb) and 3‐OH carbofuran expressed as carbofuran. Residues analysed for this residue definition may result from the use of carbofuran, carbosulfan, benfuracarb or furathiocarb. During the reference period, none of these substances had authorised uses and residues above the LOQ were found in 19 samples. They were randomly assigned to the use of carbofuran, carbosulfan or benfuracarb. When assigned to the use of carbosulfan or benfuracarb, 50% of the measured residue was accounted as carbofuran, resulting from the metabolism of the applied substance.

• Sum of methomyl and thiodicarb expressed as methomyl. Residues analysed for this residue definition may result from the use of methomyl or thiodicarb. During the reference period, methomyl was assumed to be authorised on 22 commodities. Residues above the LOQ were found in 32 samples in total. When found in any of the 22 authorised commodities, these residues were entirely assigned to methomyl.

• Sum of dimethoate and omethoate expressed as dimethoate. Residues analysed for this residue definition may result from the use of dimethoate or omethoate. During the reference period, only dimethoate was approved in EU and was assumed to be authorised on carrots, olives for oil production, rye and wheat. Although not approved in the reference period, omethoate was also (wrongly) assumed to be authorised on carrots and olives, because individual MRLs for this substance were established in 2018. In 2016, 2017 and 2018, 82,928 samples were analysed for the sum of dimethoate and omethoate, and samples contained residues at levels exceeding the LOQ. When found in rye or wheat, these residues were entirely assigned to the use of dimethoate, and 50% of the measured residue was accounted as omethoate, resulting from the metabolism of dimethoate. When found in any other commodity, including olives from oil production and carrots, the residues were randomly assigned to the use of either dimethoate or omethoate. When assigned to the use of dimethoate, 50% of the measured residue was accounted as omethoate resulting from the metabolism. When assigned to the use of omethoate, the measured residues were considered as consisting of omethoate only. In the course of 2018, specific residue definitions were established for omethoate and dimethoate and therefore they were analysed and reported separately. In order to quantify the impact of the wrong assumption that omethoate is authorised on olives for oil production, a sensitivity analysis was conducted (sensitivity analysis K in Table 16 of Section 3.1.3).

In the present exercise, this source of uncertainty has an important impact because the contribution of omethoate and dimethoate in olives for oil production to the cumulative exposure of the Italian adult population above the 99th percentile amount to 57% and 7%, respectively. This contribution is essentially due to a sample containing a residue of 4.9 mg/kg, analysed according to the unspecific residue definition.

In order to support the evaluation of the impact of this source of uncertainty, decay curves of residues in olives were collected from supervised residue trials available to EFSA (Table E.8) to follow the evolution of the omethoate/dimethoate ratios from the normal PHI (28 days) until 42 days after treatment.

Table E.8.

Supervised residue trials on olives (GAP/SEU Foliar appl. 2 × 480 g active substance/ha, PHI 28 days)a

Trial/country/year	Days after last application	Dimethoate (mg/kg)	Omethoate (mg/kg)	Omethoate/dimethoate
1/ES/2008	0	4.054	0.228	0.06
	7	2.365	0.356	0.15
	14	2.435	0.44	0.18
	21	2.216	0.485	0.22
	28	1.687	0.504	0.30
	35	1.358	0.483	0.36
	42	0.758	0.426	0.56
2/ES/2008	0	3.864	0.294	0.08
	7	1.972	0.348	0.18
	14	0.877	0.268	0.31
	21	0.766	0.402	0.52
	28	0.544	0.463	0.85
	35	0.405	0.375	0.93
	42	0.253	0.286	1.13
3/ES/2008	0	5.934	0.916	0.15
	7	1.853	1.055	0.57
	14	0.466	1.241	2.7
	21	0.167	1.221	7.3
	28	0.071	0.854	12
	35	0.079	0.48	6.1
	42	0.011	0.298	27
4/ES/2009	0	3.45	0.816	0.24
	7	1.493	0.991	0.66
	14	0.122	0.485	4.0
	21	0.371	0.548	1.5
	28	0.116	0.439	3.8
	35	0.022	0.187	8.5
	42	0.033	0.307	9.3
5/ES/2008	0	0.67	< 0.01	< 0.01
	7	0.154	0.016	0.10
	14	0.138	0.013	0.09
	21	0.036	< 0.01	< 0.28
	28	0.012	< 0.01	< 0.83
	35	0.016	< 0.01	< 0.63
	42	0.012	< 0.01	< 0.83
6/GR/2009	0	2.15	0.042	0.02
	28	0.116	0.321	2.8
	35	0.035	0.187	5.38
	42	0.011	0.142	13
7/GR/2009	0	2.035	0.47	0.23
	28	0.122	0.331	2.7
	35	0.021	0.182	8.7
	42	0.016	0.141	8.8
8/GR/2010	0	1.2	0.37	0.31
	28	< 0.01	0.29	> 29
	35	< 0.01	0.13	> 13
	42	< 0.01	0.1	> 10
9/IT/2008	0	6.244	0.31	0.05
	7	2.563	0.381	0.15
	14	2.062	0.49	0.24
	21	1.371	0.343	0.25
	28	0.944	0.297	0.31
	35	0.836	0.331	0.40
	42	0.643	0.269	0.42
10/FR/2009	0	2.309	0.076	0.03
	28	0.55	0.24	0.44
	35	0.493	0.23	0.47
	42	0.392	0.205	0.52
11/FR/2010	0	1.9	0.19	0.1
	7	0.02	0.15	7.5
	14	< 0.01	0.11	> 11
	21	0.01	0.08	8
	28	0.04	0.22	5.5
	35	0.01	0.17	17
	42	0.02	0.13	6.5
12/FR/2011	0	3.4	0.53	0.16
	7	< 0.01	0.21	> 21
	14	< 0.01	0.14	> 14
	21	< 0.01	0.09	> 9
	28	< 0.01	0.27	> 27
	35	< 0.01	0.19	> 19
	42	< 0.01	0.12	> 12
13/IT/2012	0	2.01	0.34	0.17
	28	0.06	0.22	3.7
	35	< 0.01	0.2	> 20
	42	< 0.01	0.11	> 11
14/IT/2012	0	0.93	0.12	0.13
	28	0.12	0.07	0.58
	35	0.01	0.01	1
	42	0.04	0.04	1
15/GR/2012	0	3.4	0.41	0.12
	28	0.16	0.28	1.8
	35	0.22	0.24	1.1
	42	0.02	0.23	12
16/GR/2012	0	3.51	0.48	0.14
	28	0.74	0.78	1.1
	35	0.43	0.33	0.77
	42	0.17	0.33	1.9
17/ES/2012	0	3.7	0.31	0.08
	28	0.34	0.5	1.5
	35	0.07	0.33	4.7
	42	0.06	0.27	4.5
18/ES/2012	0	3.69	0.15	0.04
	28	0.76	0.26	0.34
	35	0.58	0.23	0.40
	42	0.55	0.27	0.49
19/ES/2012	0	4.83	0.31	0.06
	28	1.46	0.36	0.25
	35	1.1	0.34	0.31
	42	0.25	0.26	1.0
20/ES/2012	0	6.34	0.32	0.05
	28	1.5	0.88	0.59
	35	0.85	0.75	0.88
	42	0.26	0.35	1.3

^aEFSA reasoned opinion 2016 (http://www.efsa.europa.eu/en/efsajournal/pub/4647 and background documents on http://registerofquestions.efsa.europa.eu/roqFrontend/outputLoader?output=ON-4647).

This table shows wide variations of the omethoate/dimethoate ratio, generally from 0.25 to 5 at the PHI of 28 days. Higher values are sometimes found, but in most cases due to very low amounts of dimethoate. There is one exception with an omethoate/dimethoate ratio of 12 found in a residue trial in Spain, with still a sum for omethoate and dimethoate residues close to 1 mg/kg. At longer PHIs, the omethoate/dimethoate ratio is increasing, but the omethoate levels is found to be stable or decreasing.

An additional uncertainty derives from the assumption that measurements for unspecific residue definitions result from the use of one active substance only. This assumption implies that other active substances associated to that unspecific residue definition are not present (i.e. implicit zero measurements). Although it is unlikely that substances with similar pesticidal activity are used on the same crop, this possibility cannot be excluded.

Note 17 (Assumption of the authorisation status of pesticide/commodity combinations) – U16

In the absence of country‐specific information on authorised uses of pesticides, it was assumed that an authorisation exists in all EU countries for an active substance/commodity combination when the MRL in place on 31 December 2018 was above the LOQ. When the MRL was set at the LOQ but a use had been reported to EFSA in the context of article 12 and/or subsequent article 10 reasoned opinions, authorisation was also assumed. The full description of the assumption process is given in Appendix C. The full list of the assumed authorised uses is given in Annex A, Table A.06.

This source of uncertainty is related to the first of three assumptions affecting the treatment of occurrence data below the LOQ. The assumption of the authorisation status determines the list of pesticide/commodity combinations for which samples with results below the LOQ might have been treated and therefore are assigned with non‐zero values. For all pesticide/commodity combinations with no authorised use, all results reported below the LOQ are considered as zero.

On one hand, the assumption on authorisations, as described above, leads to an overestimation of the risk because authorisations for any active substance/commodity combination are not necessary granted in all Member States, but more often in certain Member States only.

On the other hand, it also leads to an underestimation of the risk when an authorisation does not result in an MRL above the LOQ, or even in the absence of authorisation, in case of uptake of residues in soil by the plant.

The magnitude of the over‐ or underestimation is however depending on the toxicological potency of the active substance: if a child with a body weight of 20 kg consumes 200 g/day of a commodity containing 0.01 mg/kg (common LOQ level) of a substance with an NOAEL of 0.1 mg/kg bw per d, the MOE associated with the intake of this substance would be 1000. As indicated in Table 1, 21 substances in CAG‐NCN have a NOAEL for AChE inhibition ≤ 0.1 mg/kg bw per d (aldicarb, azinphos‐ethyl, cadusafos, carbofuran, chlorpyrifos, diazion, dichlorvos, dimethoate, ethion, ethoprophos, fenamiphos, fenthion, methamidophos, monocrotophos, omethoate, oxamyl, oxydemeton‐methyl, phoxim, profenofos, pyrazophos and triazophos). Nine of these substances have authorised used for 2 to 29 of the 35 commodities selected for the present assessment (Annex A, Table A.06).

Table 16 in Section 3.1.3 reports a sensitivity analysis (sensitivity analysis H) in which all pesticide/commodity combinations with a percentage of positive findings (i.e. above the LOQ) exceeding 1% are considered authorised.

Note 18 (Assumption of the use frequency of pesticides and on the residue level (1/2 LOQ as imputed value)) – U17 and U18

Statistics on the use frequency of pesticides in crops are not available to EFSA.

Therefore, a second assumption affecting the treatment of left‐censored data concerns the frequency of application of pesticides on the crop for which an authorisation for use has been granted. The European Commission and Member States have defined the assumptions to be made in tiers I and II of probabilistic modelling (European Commission, 2018). All details of the implementing procedure are given in Appendix C. The scenario applicable to Tier II assumes that the total AUP frequency is 100%, meaning that all commodities are treated according to at least one AUP, or, in other words by one or several substances of CAG‐NCN.

When the implementing procedure referred to in the previous paragraph has been applied to the data set, a non‐zero value equal to ½ LOQ is assigned to each left‐censored data associated to an AUP. In reality, the actual residue level may take any value comprised between zero and the LOQ. This is a third assumption affecting the treatment of left censored data.

The impact of the assumptions of the use frequency was quantified in the sensitivity analyses A and B reported in Table 16 of Section 3.1.3.

Note 19 (Residues in drinking water) – U19

With respect to pesticides in drinking water, assumptions were used, which are based on Council Directive 98/83/EC of 3 November 1998 on the quality of water intended for human consumption. This Directive sets an MRL of 0.1 μg/L to each individual pesticide, and of 0.5 μg/L to the sum of all individual pesticides detected and quantified. In tier I, it was assumed that the five most potent pesticides of the CAG (monocrotophos, dichlorvos, triazophos, azinphos‐ethyl and carbofuran) were at a level of 0.1 μg/L. This corresponds to the worst possible exposure complying with the legal provisions. In tier II, it was assumed that the same pesticides were at 50% of the allowed level (0.05 μg/L). Based on these assumptions, water contributes to about 8% (Italian adult) to 20% (Belgian adult) of the exposure above 99th percentile in tier II (Annex C, Table C.02).

In order to quantify the impact of the contribution of drinking water on the MOET estimate at 99.9th percentile of the exposure distribution, a sensitivity analysis has been conducted (sensitivity analysis I in Table 16). It must be noted that the pesticides on which the assumption is based are not approved in EU, and their presence in drinking water of European consumers is very unlikely.

The assumptions described above were made because EFSA does not have access to detailed monitoring data on pesticides in drinking water. Member States are however obliged under the Drinking Water Directive to monitor on a regular basis the quality of the drinking water that is supplied to consumers and to report triennially the results to the Commission, which produces a synthesis report.29

The last available report of the drinking water quality in EU Member States covers the 2011–2013 period. This report states that Member States monitor a considerable number of pesticides and metabolites (degradation and reaction products) in drinking water that are chosen at national level and are thus specific for each Member State. However, only those pesticides that are likely to be present in a given supply need to be monitored. For reporting purposes, a short list of 13 pesticides was agreed between European Commission and Member States. This list is composed exclusively of herbicides, which, due their physico‐chemical properties, are the most prone to be present in water. For these, monitoring frequency and information on non‐compliance were reported for 2011–2013. Even though the reporting of pesticides’ short list is a harmonised approach and comparable, it does not show the full picture of all pesticides and all relevant metabolites occurring in a country. Nevertheless, the reported compliance rates are consistently high (total of more than 99.9%).

Note 20 (Missing information about the effect of processing) – U20

To perform calculations, a processing factor for a pesticide/commodity/processing technique combination has been used if:

• A reliable median value was available in the database of processing techniques and processing factors compatible with the EFSA food classification and description system FoodEx 2 (Scholz et al., 2018a) or in EFSA outputs published after June 2016. To be reliable, the PF had to be based on three or more acceptable individual PF values or on two acceptable individual PF values with a variation of less than 50%.

• The processing techniques reported in the processing factor database was matching the processing techniques reported in the RPC consumption data set. The processing techniques from both databases were matched according to principles described in Section 2.2.3.4.

In the absence of processing factors, it was assumed in the model that all residues in the raw commodity are quantitatively transferred to the processed commodity and reach the consumer.

The list of processing factors used to perform the calculations are given in Annex A Table A.8.

With respect to risk drivers, processing factors reflecting peeling and juicing were used for chlorpyrifos in oranges. No processing factors have however been used for the pesticide/commodity combinations omethoate/olives for oil production, dimethoate/olives for oil production and pirimiphos‐methyl/wheat. For these combinations, indicative processing factors are reported in Table E.9.

Table E.9.

Indicative processing factors for substance/commodity combinations identified as risk drivers for CGA‐NCN, not used in the cumulative exposure calculations

Active substance	Commodity	Contribution to the MOET	Processed commodity	Processing factor	Source/comments
Omethoate	Olives	31–57%	Olives for oil production, crude oil	Median PF: 0.01 Number of studies: 5	EFSA reasoned opinion 2016 Not included in Scholz et al. (2018a), because not covered by the scope Omethoate: Log Pow = –0.9 at 20°C (pH 7)
			Table olives, 6 months canned olives	Median PF: 0.08 Number of studies: 5	EFSA reasoned opinion 2016 Not included in Scholz et al. (2018a), because not covered by the scope
Dimethoate	olives	5–7%	Olives for oil production, crude oil	Median PF: 0.33 Number of studies: 5	EFSA reasoned opinion 2016 Not included in Scholz et al. (2018a), because not covered by the scope Dimethoate: Log Pow = 0.75 at 20°C (pH 7)
			Table olives, 6 months canned olives	Median PF: 0.28 Number of studies: 3	EFSA reasoned opinion 2016 Not included in Scholz et al. (2018a), because not covered by the scope
Pirimiphos‐methyl	wheat	8–20	Bran	Median PF: 3.1 Number of studies: 1	Scholz et al. (2018a). Study acceptable but PF not included because not considered as reliable (1 study only).
			Flour, whole meal	Median PF: 0.76 Number of studies: 1	Scholz et al. (2018a). Study acceptable but PF not included because not considered as reliable (1 study only).
			Flour, white	Median PF: 0.18 Number of studies: 1	Scholz et al. (2018a). Study acceptable but PF not included because not considered as reliable (1 study only).

The impact of this source of uncertainty was quantified by a sensitivity analysis (sensitivity analysis C in Table 16 of Section 3.1.3).

Although not related to the effect of processing, it is known that residue levels decline between the market distribution and the time of consumption. Therefore, the consumer might be exposed to residue level lower than those measured and reported by official laboratories. Not taking account of this decline leads to an overestimation of the risk, which was considered and estimated to be minor compared to the effect of missing information on the effect of processing and to the effect of washing and peeling (Note 24). There are theoretical reasons to this: this decline is governed by photolysis, volatilisation and to some extent to chemical degradation, but these processes start directly after treatment in field, and not only after marketing or purchase of the commodity by the consumer. When they are major degradation/dissipation routes (e.g. volatility of dichlorvos), residues decline shortly after harvest and are low at any other point of the distribution channel and later at point of consumption. When the substance is more stable, these processes are expected to play a minor role and to be much less efficient than industrial or household processing with hydrolysing conditions or physical treatments such as fractionation of commodities, peeling or washing. Collecting factual information on the degradation of residues after retail store would be cumbersome, due to the complexity of this phenomenon, its substance specificity and the multiple influencing factors.

Note 21 (Applicability of processing factors in the EFSA food classification and description system (FoodEx)) – U21

The database of validated processing factors developed by Scholz et al. (2018a) has been developed to be compatible with the EFSA food classification and description system FoodEx 2.

In the first part of the project, a compendium of representative processing techniques was elaborated based on the standard protocols used in regulatory processing studies (Scholz et al., 2018b). The original study reports of a representative set of processing studies covering the most important processes in food processing, with respect to importance in both consumption and production were reviewed to identify the main processes relevant in food processing (cooking in water, steaming, canning of fruits and vegetables (including jam/jelly/marmalade production as well as purée and paste production), dehydration/drying of fruits, vegetables, herbs and spices, frying and deep frying, baking and roasting, microwaving, production of fruit and vegetable juices, wine manufacturing, fermentation and pickling, oil production including essential oils, soya milk and tofu production, beer brewing, milling processes, starch production, cocoa powder production, sugar production).

For each process, a typical set of processing conditions was provided based on published literature and/or inquiry in the food processing industry. Detailed descriptions of processing conditions were given and the processes were visualised in flowcharts.

In a second step of the project, the food/feed items and processes as described in the compendium were coded using the FoodEx2 coding system (van Donkersgoed et al., 2018), and therefore linked with each other. Additionally, a key facet was added in order to be able to link food and feed items to the EFSA RPC‐model.

The sources used to code the foods, feeds and processes are described, as well as the coding decisions. The results of the coding are listed as Appendix A to Scholz et al. (2018b).

Linking processing techniques investigated in regulatory studies with processing techniques of the EFSA RPC‐model, includes uncertainties, first from the fact that processing factors derived from processing studies conducted according to a limited number of standardised protocols are assigned to food as consumed which may have been processed following conditions diverging to varying extent from the these standard conditions. A second source of uncertainty is associated to extrapolations of PFs derived for commodities investigated in processing studies to other commodities.

To perform the present assessment, processing techniques reported in the processing factor database were matched with the processing techniques reported in the RPC consumption data set according to the principles described in Section 2.2.3.4.

Note 22 (Accuracy of processing factors) – U23

Processing factors are calculated as the ratio between the residue concentrations in the processed commodity and in the RPC.

In case of residue levels below the LOQ either in the processed or raw commodity, Scholz et al. (2018a) proceeded as follows:

• When residues in the processed commodity were below the LOQ, the calculation assumed as worst case that the actual residue concentration in the processed commodity was equal to the LOQ and in this case the calculated processing factor represented a maximum value. In the present assessment, this concerned the following RPC/processed commodity combinations: carbofuran/grapefruit juice, carbofuran/orange juice, chlorpyrifos/orange juice, chlorpyrifos‐methyl/orange (canned fruit), malathion/orange juice (pasteurised) and phosmet/orange pulp.

• When residues in the raw commodity were below the LOQ, the calculation assumed as best‐case scenario that the actual residue concentration in the raw commodity was equal to the LOQ and in this case the calculated processing factor represents a minimum value. In such case, the processing factor was not considered reliable in the processing factor database and, therefore, not used in the calculations.

Note 23 (Use of a fixed value of processing factors) – U24

Only one value of processing factor is used for each pesticide/commodity/processing type, corresponding to the median of the distribution of values derived from the available processing studies considered as reliable or indicative by Scholz et al. (2018a). Information on the number of independent trials performed to determine processing factors and individual results can be found in Scholz et al. (2018a).

With respect to risk drivers, processing factors reflecting peeling and juicing were used for chlorpyrifos in oranges, which were medians from four and six individual values, respectively.

Note 24 (Effect of washing and peeling of commodities with edible peel) – U25

The effect of peeling and washing on pesticide residue levels for fruits and vegetables with edible peel and which are consumed raw is not normally considered in deterministic risk assessments because the default worst‐case assumption used is that these commodities may also be consumed unwashed including the peel. Consequently, the available processing factors for peeling and washing of commodities with edible peel are not included in the standard regulatory data set of processing factors (Scholz et al., 2018a).

In the absence of these processing factors, the cumulative exposure calculations assumed in all cases that all residues in the raw commodity were present in the commodity as eaten, even if it is washed or peeled. This assumption leads to an overestimation of the intake levels of pesticide residue. For fruits and vegetables which are mainly consumed cooked, the effect of washing is however covered by the available processing factors for cooking techniques.

Information on the effects of washing of fruits and vegetables on pesticide residue levels from published literature was combined and analysed in a meta‐analysis review (Keikotlhaile et al., 2010); however, the analysis did not distinguish different types of active substances or different commodity types and therefore only a general conclusion can be drawn. It was reported that overall, washing leads to a combined reduction of pesticide residue levels by a weighted mean response ratio of 0.68.

Information from published literature on the effects of washing and peeling was recently reviewed for specific identified pesticide/commodity combinations (Chung, 2018). A correlation between water solubility of the active substance and pesticide decrease after washing could not be observed. The reduced effect of washing on residue levels for some pesticide/commodity combinations was reported to be attributed to penetration of active substances into the waxy surface of some fruits or translocation of the active substance into plant tissues. It was reported that the partition coefficient (Kow) of active substances may be an indicative factor of the residues partitioning into the waxy surface of some fruits, although a correlation with pesticide decrease after washing was not demonstrated. The time after pesticide spray application was reported to be a contributing factor for a variety of crops, with the decline in time in the proportion of residues reduced by washing being attributed to translocation of residues deeper into the crop surface. The mode of action in terms of whether an active substance is systemic or non‐systemic (contact) was one of several factors used to explain the differences in processing factors for various household processing conditions, including washing and peeling, for various pesticide/commodity combinations.

Information on the frequency of peeling and washing of commodities with edible peel which are consumed raw is not available to EFSA.

None of the risk drivers identified by the calculations is concerned by this source of uncertainty.

Note 25 (Organophosphorous and N‐methyl carbamates missing from the CAGs) – U26

If the CAG does not contain active substances contributing to the risk, the outcome of the risk assessment might be underestimated.

Four hundred and twenty‐two active substances were considered for inclusion in CAG‐NCN. The full list can be found in Appendix A to EFSA (2019a). These were all the substances approved until 31 May 2013 and additional non‐approved substances present in the EU consumer's diet as evidenced by the 2011 annual report on the Rapid Alert System for Food and Feed (European Commission, 2012) and/or the 2010 annual report on pesticide residues in food (EFSA, 2013b).

However, from one year to the other, different non‐approved substances are found by the EU control laboratories. Therefore, monitoring data of the reference period (2016, 2017 and 2018) were consulted to retrieve the number of occurrences of OPs and NMC insecticides not included in CAG‐NCN at quantifiable levels in at least one sample of any of the selected 35 commodities (Table E.10). When an ADI was available, long‐term lower‐ and upper‐bound exposures related to the 35 selected commodities were calculated following the same modalities as the calculations reported in columns 4 and 5 of Table E.3 in Note 3 for substances included in the CAG. All calculated lower bound exposures were very low, not exceeding 0.02% of the respective ADIs and at least two orders of magnitude below those reported for risk drivers: Lower bound estimates for omethoate, dimethoate, pirimiphos‐methyl, chlorpyrifos were 16.8, 5.5, 9.1 and 10.3% of their respective ADIs. Upper bound estimates are less reliable indications of the actual contribution to the risk because they are much depending on the assumption applied to left‐censored data.

Table E.10.

Occurrence of/Exposure (calculated with PRIMo v3.1) to OPs and NMCs not included in CAG‐NCN in the 35 selected raw agricultural commodities, based on the 2016, 2017 and 2018 monitoring data corresponding to sampling strategies ST10A and ST20A

Active substance	Chemical class	ADI (mg/kg bw per day, EU Pesticides database)		No of quantifications > LOQ in any of the selected commodities	Long‐term exposure related to selected commodities (% of ADI)
		ADI	Source		Lower bound	Upper bound
Bendiocarb	NMC	0.004	JMPR 1984	5	< 0.01	0.2
Bromophos‐ethyl	OP	0.003	JMPR 1975	1	< 0.01	0.5
Dioxacarb	NMC	–	–	2
Fenobucarb	NMC	–	–	12
Isocarbophos	OP	–	–	8
Isoprocarb	NMC	–	–	1
Mecarbam	OP	0.002	JMPR 1986	1	< 0.01	0.4
Methacrifos	OP	0.006	JMPR 1990	1	< 0.01	0.1
Pirimiphos‐ethyl	OP	–	–	1
Phorate	OP	0.0007	JMPR 2005	47	0.02	11
Phosphamidon	OP	0.0005	JMPR 1986	1	< 0.01	2
Promecarb	NMC	–	–	4
Propoxur	NMC	0.02	JMPR 1989	26	0.01	0.4
Prothiofos	OP	–	–	6
Quinalphos	OP	–	–	4
Terbufos	OP	–	–	1
Total number of quantifications:				121

In the absence of an available ADI, calculations could not be conducted for nine substances. However, their average levels in the commodities where they were found were, in all cases, below 0.0005 mg/kg, i.e. more than two orders of magnitude below the average residues of dimethoate in olives for oil production. This implies that it is very unlikely that the few samples of commodities where one of these compounds was quantified could significantly change the MOET estimations if they were included in the calculations. This would require extremely low ADIs for these compounds.

For additional element of comparison, the number of occurrences above the LOQ of substances included in CAG‐NCN is given in Table E.11. This shows that substances included in the CAGs are found in quantifiable levels about 100 times more frequently than the omitted OPs and NMCs.

Table E.11.

Number of quantifications above the LOQ of substances included in CAG‐NCN in the 35 selected commodities, based on the 2016, 2017 and 2018 monitoring data corresponding to sampling strategies ST10A and ST20A

Active substance	Number of quantifications > LOQ in any of the selected 35 commodities	Active substance	Number of quantifications > LOQ in any of the selected 35 commodities
Acephate	67	Malathion	185
Aldicarb	0	Methamidophos	54
Azinphos‐ethyl	12	Methidathion	37
Azinphos‐methyl	8	Methiocarb	85
Benfuracarb	19	Methomyl	61
Cadusafos	1	Monocrotophos	4
Carbaryl	15	Omethoate	347
Carbofuran	19	Oxamyl	17
Carbosulfan	19	Oxydemeton‐methyl	0
Chlorfenvinphos	5	Parathion	3
Chorpyriphos	5,118	Parathion‐methyl	3
Chlorpyrifos‐methyl	1,844	Phenthoate	4
Diazinon	16	Phosalone	0
Dichlorvos	9	Phosmet	750
Dimethoate	336	Phoxim	1
Ethephon	548	Pirimicarb	1,149
Ethion	5	Pirimiphos‐methyl	781
Ethoprophos	10	Profenofos	65
fenamiphos	28	Pyrazophos	1
Fenitrothion	16	Thiodicarb	37
Fenthion	5	Tolclophos‐methyl	82
Fonofos	0	Triazophos	34
Formetanate	82	Trichlorfon	4
Fosthiazate	71
Total number of quantifications:			11,957

Note 26 (Active substances wrongly assigned to CAGs) – U28

If an active substance, not causing the effect, is included in the CAG, the outcome of the risk assessment might be overestimated.

For the CAG‐NCN, the Scientific report on CAGs for the effects of pesticides on the nervous system concluded that the possibility of including substances not contributing to the risk was virtually non‐existent (EFSA, 2019a) because all active substances but two are OPs or NMC insecticides acting biologically via AChE inhibition. The two exceptions are tolclofos‐methyl and ethephon, which have other biological actions, but have shown weaker, but however significant, inhibition of AChE in toxicological studies.

It should be discussed that NMCs and OPs are two chemical classes of AChE inhibitors that act by the same mechanism at biochemical level, i.e. binding to the hydroxyl group of the amino acid serine in the catalytic centre of the enzyme, but have important differences at molecular and tissue levels. While the phosphorylation by OPs on the serine residue of AChE may undergo the so‐called ‘ageing’ reaction, ultimately leading to an irreversible inhibition of AChE, carbamylation of such residue by NMCs is quickly reversible, thus allowing the spontaneous recovery of the catalytic activity of the enzyme.

In addition, the capacity of NMCs to cross the blood–brain barrier and enter the brain is weak, which subsequently results in fewer brain effects and generally with lower severity observed with NMCs than with OPs (Rosman et al., 2009). Thus, cholinergic effects from NMC exposure are mostly consequences from AChE inhibition in the peripheral autonomous system and neuromuscular junction. On the other hand, when erythrocyte AChE is irreversibly inhibited by OPs, the recovery of catalytic activity depends on de novo synthesis of new erythrocytes, which are released from the bone marrow to the bloodstream. For most OPs, the recovery rate of erythrocyte AChE is about 1%/day, which is slightly over 3 months but somewhat shorter than the lifespan of erythrocytes (Mason, 2000). Conversely, the half‐life of AChE resynthesis in the nervous system is estimated to be 5–7 days; therefore, the enzyme is restored in brain more rapidly than in erythrocytes (Lotti, 1995).

Considering the toxicokinetic differences from OPs (e.g. their effects do not cumulate along time), the contribution of NMCs to the chronic inhibition of AChE was investigated by a sensitivity analysis, in which they were omitted from the calculations. The results are given in Table 16 of Section 3.1.3 (sensitivity analysis F). From these results, it appears that NMCs do not contribute significantly to the cumulative risk of chronic AChE inhibition. When they are excluded from the calculations, the MOET estimates at the 99.9th percentile of the exposure are even lowered. This counterintuitive result might be explained by the side effect their exclusion has on the handling process of left‐censored occurrence data, which tends to increase the frequency of use of pesticides with lower NOAELs.

Note 27 (Uncertainties related to original data quality) – U29

The robustness of the hazard characterisation process and, in fine, the chance that the selected NOAELs reflect at best the actual BMDL20s for erythrocyte AChE inhibition depend on multiple factors, which, for the sake of the uncertainty analysis, have been grouped under four main types: factors related to the quality of data, factors related to the data collection methodology, factors related to the principles used to assess the data and factors related to the design of the key toxicological study.

In Table E.12, information was collected regarding these different factors.

Table E.12.

CAG‐NCN: Information about the hazard characterisation of substances included in CAG‐NCN

Active substance (chemical class)	AChE inhibition	NO(A)EL mg/kg bwa	LO(A)EL mg/kg bw	Key study	Mode of administration	GLP	Statistical analysis	Guidelines and other information
Acephate (OP)	Brain, erythrocytes	0.25	2.5	2‐year rat (■■■■■, 1981)	Diet	Yes	Yes	Guidelines not specified
Aldicarb (NMC)	Erythrocytes	0.05	0.1	Acute neurotoxicity rat (■■■■■, 1994b)	Gavage	Not reported	Yes	FIFRA Guideline 81‐8
	Brain	0.1	0.5	Acute neurotoxicity rat (■■■■■, 1994b)	Gavage	Not reported	Yes	FIFRA Guideline 81‐8
	Erythrocyte	0.5	1.5	2‐year rats (■■■■■, 1993)	Diet	No	No reported	Guidelines not reported Brain AChE depressed by 12% at LOAEL
Azinphos‐ethyl (OP)	Erythrocytes	0.0125	0.025	90‐day dog (■■■■■, 1963)	Diet	No	Not reported	Study poorly reported
Azinphos‐methyl (OP)	Erythrocytes	0.16	0.74	1‐year dog (■■■■■, 1990)	Diet	Yes	Yes	Guidelines not specified
	Brain	0.74	4.09	1‐year dog (■■■■■, 1990)	Diet	Yes	Yes	Guidelines not specified
Benfuracarb (NMC)	Erythrocytes	1.81	9.4	28‐day neurotoxicity rat (■■■■■, 2003)	Diet	Yes	Yes	Guidelines no: OECD 424
	Brain	9.4	45.8	28‐day neurotoxicity rat (■■■■■, 2003)	Diet	Yes	Yes
Cadusafos (OP)	Erythrocytes	0.045	0.22	2‐year rat (■■■■■, 1986)	Diet	Yes	Yes	Guidelines: EU B32
	Brain		>0.22	2‐year rat (■■■■■, 1986)	Diet	Yes	Yes	Guidelines: EU B32
Carbaryl (NMC)	Brain, erythrocytes	1	10	90‐day neurotoxicity rat (■■■■■, 1990)	Gavage	Yes	Yes	Guidelines: US‐EPA 82.7
	Brain, erythrocytes	10		2‐year rat (■■■■■ 1993)	Diet	Yes	Yes
Carbofuran (NMC)	Brain	0.015	0.03	Acute neurotoxicity rat (■■■■■, 2007c)	Gavage	Yes	Yes	Overall NOAEL: 0.03 mg/kg bw based on AChE effects in brain and RBC in males and females at 0.1 mg/kg bw for adult rats and NOEL of 0.015 mg/kg bw for pups based on AChE effects in brain at 0.03 mg/kg bw.
	Erythrocytes	0.03	0.1	Acute neurotoxicity rat (■■■■■, 2007c)	Gavage	Yes	Yes
	Brain, erythrocytes	0.91	4.92	2‐year rat (■■■■■, 1991)	Diet	Yes	Yes	Guidelines n°: OECD 453
Carbosulfan (NMC)	Brain, erythrocytes	0.5	5	Acute neurotoxicity rat (■■■■■, 1996, 1982b)	Gavage	Yes	Yes	Guidelines n°: OECD 424
	Brain, erythrocytes	1	26.8	2‐year rat (■■■■■, 1982 a)	Diet	Yes	Yes	Guidelines n°: OECD 453
Chlorfenvinphos (OP)	Brain, erythrocytes	0.15	15	2‐year rat (author not reported, JMPR 1994)	Diet	Not reported	Yes	Guideline not reported
Chlorpyrifos (OP)	Erythrocytes	0.1	1	2‐year rat (■■■■■, 1988)	Diet	Yes	Yes	Commission Directive 88/302/EEC
	Brain	1	10	2‐year rat (■■■■■, 1988)	Diet	Yes	Yes
Chlorpyrifos‐methyl (OP)	Brain, erythrocytes	1	50	2‐year rat (■■■■■, 1991)	Diet	Yes	Yes	OECD Guideline 453
Diazinon (OP)	Brain, erythrocytes	0.02	5.6	90‐day dog (■■■■■, 1988)	Diet	Yes	Yes	Guidelines n°: OECD 409
Dichlorvos (OP)	Erythrocytes	0.008	0.08	2‐year dog (■■■■■, 1967)	Diet	No	Not reported	Tentative NOAEL based on a supplemental study not according to any guideline and with limited results
	Erythrocytes	0.23	2.3	2‐year rat (■■■■■, 1967)	Diet	No	Not reported
	Brain	2.3	11.7	2‐year rat (■■■■■, 1967)	Diet	No	Not reported
Dimethoate (OP)	Brain, erythrocytes	0.1			Diet			EFSA conclusion 2013: ADI was based on an overall NOAEL, combining reproduction, neurotoxicity and developmental neurotoxicity studies.
	The long‐term NOAELs for brain and erythrocyte AChE inhibition are 0.06 and 0.04 mg/kg, respectively, observed in the 90‐day interim and terminal sacrifice in the 2‐year study in rat (■■■■■, 1986). This study was conducted under GLP and results were statistically significant. The respective LOAELs for brain and erythrocyte inhibition are 0.3 and 0.2, respectively.
Ethephon (OP)	Erythrocytes	6	14	28‐day cholinesterase inhibition study in dogs (■■■■■, 2006)	Diet	Yes	Yes	No guideline applicable
	Brain		> 14	28‐day cholinesterase inhibition study in dogs (■■■■■, 2006)	Diet	Yes	Yes
Ethion (OP)	Brain	0.06	0.71	90‐day dog (■■■■■, 1988)	Diet	No	Yes	95% reduction in erythrocyte acetylcholinesterase activity at 6.9 mg/kg bw.
Ethoprophos (OP)	Brain, erythrocytes	0.04	2.4	2‐year rat (■■■■■, 1992a/b)	Diet	Yes	Yes	US EPA 40 CFR 160
Fenamiphos (OP)	Erythrocytes	0.083	0.35	1‐year dog (■■■■■, 1991)	Diet	Yes	Yes	OECD TG 452
	Brain		> 0.35	1‐year dog (■■■■■, 1991)	Diet	Yes	Yes
Fenitrothion (OP)	Brain, erythrocytes	0.5	1.5	2‐year rat (■■■■■, 1974)	Diet	No	Yes	Comparable to OECD 451
Fenthion (OP)	Erythrocytes	0.05	0.23	1‐year dog (■■■■■, 1990)	Diet	Not reported	Not reported	Guidelines not reported. Very concise summary in DAR. No information on brain AChE inh.
	Brain, erythrocytes	0.25	1	2‐year rat (■■■■■, 1990)	Diet	Not reported	Not reported	Guidelines not reported. Very concise summary in DAR
Fonofos (OP)	Erythrocytes	0.2	1	1‐year dog (■■■■■, 1995)	Capsule	Not reported	Not reported	Guidelines n°: 83‐1b
	Brain	1	1.75	1‐year dog (■■■■■, 1995)	Capsule	Not reported	Not reported
Formetanate (NMC)	Erythrocytes	0.37	1.75	1‐year dog (■■■■■, 1986)	Diet	Yes	Yes	Similar to OECD guideline 409
	Brain		> 8.45	1‐year dog (■■■■■, 1986)	Diet	Yes	Yes
Fosthiazate (OP)	Brain	0.42	2.36	2‐year rat (■■■■■, 1990)	Diet	Not available	Not available	Not available
	Erythrocytes	0.48	0.97	28‐day rat (■■■■■, 1989)	Diet	Not available	Not available	Not available
Malathion (OP)	Erythrocyte	17 (Rucci, 1980)	35 (Daly, 1996)	2‐year rat (■■■■■, 1996) and 2‐year rat (■■■■■, 1980) combined	Diet	No (■■■■■, 1980) Yes (■■■■■, 1996)	Yes (■■■■■, 1980) Yes (■■■■■, 1996)	Guidelines not reported (■■■■■, 1980). OECD guideline 453 (■■■■■, 1996)
	Brain	Not measured (■■■■■, 1980); NOAEL 29 mg/kg bw per d (■■■■■, 1996)
Methamidophos (OP)	Brain, erythrocytes	0.1	0.29	2‐year rat (■■■■■, 1984b)	Diet	Yes	Yes	Guidelines n°: OECD 453
Methidathion (OP)	Brain, erythrocytes	0.16	1.72	2‐year rat (■■■■■, 1986)	Diet	Not reported	Not reported	Guidelines not reported
Methiocarb (NMC)	Erythrocytes	1.32	6.46	90‐day dog (■■■■■, 2000)	Diet	Yes	Yes	OECD guideline 409
	Brain		> 5.91	90‐day dog (■■■■■, 2000)	Diet	Yes	Yes
Methomyl (NMC)	Brain, erythrocytes	0.25	0.5	Acute neurotoxicity rat (■■■■■, 1998a)	Gavage	Yes	Yes	USEPA 81‐8
	Brain, erythrocytes		> 95	90‐day neurotoxicity rat (■■■■■, 1998b)	Diet	Yes	Yes	USEPA 81‐7
Monocrotophos (OP)	Brain, erythrocytes	0.005	0.05	2‐year rat (■■■■■, 1983)	Diet	Not reported	Not reported	Guidelines not reported
Omethoate (OP)	Erythrocytes	0.027	0.04	2‐year rat (■■■■■, 1995); supplementary 32‐week rat (■■■■■, 1994)	Diet	Yes	Yes	OECD 453 (main study)
	Brain	0.04	0.32	2‐year rat (■■■■■, 1995); supplementary 32‐week rat (■■■■■, 1994)	Diet	Yes	Yes
Oxamyl (NMC)	Brain, erythrocytes	0.1	0.75	Acute neurotoxicity rat (■■■■■, 1997)	Gavage	Yes	Yes	USEPA
	Brain, erythrocytes	1.69	15.3	90‐day neurotoxicity rat (■■■■■, 1997)	Diet	Yes	Yes	US EPA
Oxydemeton‐methyl (OP)	Brain, erythrocytes	0.027	0.224	2‐year rat (■■■■■, 1984)	Diet	Yes	Not reported	Guidelines n°: EEC method B.33
Parathion (OP)	Brain	0.25	2.5	2‐year rat (■■■■■, 1984)	Diet	No	Not reported	Guidelines n°: OECD 452
	Erythrocytes	0.1	0.4	2‐year rat (■■■■■, 1987)	Diet	Yes	Not reported	Guidelines n°: FIFRA 83‐5 guidelines
	Brain	0.4	1.6	2‐year rat (■■■■■, 1987)	Diet	Yes	Not reported
Parathion‐methyl (OP)	Erythrocytes	0.25	2.5	2‐year rat (■■■■■, 1983)	Diet	No	Not reported	Guidelines n°: OECD 452
	Brain, erythrocytes	0.1	0.5	2‐year rat (■■■■■, 1981)	Diet	No	Not reported	Guidelines n°: OECD 453
Phenthoate (OP)	Erythrocytes	0.29	0.87	2‐year dog (■■■■■, 1972)	Diet	No	Not reported	Guidelines not reported No information on acceptability and limitation of studies
Phosalone (OP)	Erythrocytes	0.17	0.9	1‐year dog (■■■■■, 1992)	Diet	Yes	Yes	US EPA Guidelines, FIFRA 83‐1
	Brain	0.9	11	1‐year dog (■■■■■, 1992)	Diet	Yes	Yes
Phosmet (OP)	Erythrocytes	1.1	1.8	2‐year rat (■■■■■, 1991)	Diet	Yes	Yes	EPA‐FIFRA Guideline No. 83‐5
	Brain	1.8	9.4	2‐year rat (■■■■■, 1991)	Diet	Yes	Yes
Phoxim (OP)	Erythrocytes	0.1	0.38	2‐year dog (■■■■■ 1977)	Diet	No	Not reported	Guidelines not reported. Acceptability of the studies not reported
	Brain	0.38	19	2‐year dog (■■■■■, 1977)	Diet	No	Not reported
Pirimicarb (NMC)	Brain, erythrocytes	10	25	1‐year dog (■■■■■, 1998)	Capsule	Yes	Yes	67/548/EEC B.30
Pirimiphos‐methyl (OP)	Brain	0.4 b	2.1	2‐year rat (■■■■■, 1974)	Diet	No	Not reported	Level of detail in the report not to current standards
	Erythrocytes	2.1	12.6	2‐year rat (■■■■■, 1974)	Diet	No	Not reported
	Brain, erythrocytes	0.4	4	90‐day rat (■■■■■, 1970)	Diet	No	Not reported
Profenofos (OP)	Erythrocytes	0.017	0.56	2‐year rat (■■■■■, 1981a)	Diet	Not reported	Yes	Guidelines not reported. No information on brain AChE inh.
	Erythrocytes	< 1.7	1.7	90‐day neurotoxicity rat (■■■■■, 1994b)	Diet	Yes	Yes	Guidelines no: US EPA FIFRA
	Brain	1.7	38	90‐day neurotoxicity rat (■■■■■, 1994b)	Diet	Yes	Yes
Pyrazophos (OP)	Erythrocytes	0.05	0.125	2‐year dog (■■■■■, 1976)	Diet	No	Not reported	Guidelines not reported. No information on brain AChE inh.
	Erythrocytes	0.1	4	2‐year rat (■■■■■, 1991a)	Diet	Yes	Yes	Guidelines no: OECD 453
	Brain	4.8	19	2‐year rat (■■■■■, 1991a)	Diet	Yes	Yes
Thiodicarb (NMC)	Brain, erythrocytes	0.5	5	Acute neurotoxicity rat (■■■■■, 2000d)	Gavage	Yes	Not reported	Guidelines not reported. NOAEL derived from the LOAEL with an UF of 10.
	Erythrocytes	15	80	2‐year rat (■■■■■ 1994b; ■■■■■, 1995a)	Diet	Yes	Yes	Guidelines not reported
Tolclofos‐methyl (OP)	Erythrocytes	6.4	32.2	2‐year mouse (■■■■■, 1983)	Diet	No	Yes	in accordance with 88/302/EEC, Part B
	Brain	32	134	2‐year mouse (■■■■■, 1983)	Diet	No	Yes
Triazophos (OP)	Erythrocytes	0.012	0.13	1‐year dog (■■■■■, 1989)	Diet	Yes	Yes	Guidelines not reported. No information on brain AChE inh
	Erythrocytes	0.15	1.3	2‐year rat (■■■■■, 1990)	Diet	Yes	Yes	EPA guidelines
	Brain	1.6	15	2‐year rat (■■■■■, 1990)	Diet	Yes	Yes
Trichlorfon (OP)	Brain	4.5	13.3	2‐year rat (■■■■■, 1989)	Diet	Yes	Yes	OECD 453
	Erythrocytes	13.3	52.7	2‐year rat (■■■■■, 1989)	Diet	Yes	Yes

^aValues in bold were extracted from the EFSA scientific report on CAGs and were used for the calculations.

^bSee also the Note 27.

The present note deals with the uncertainty resulting from eventual shortcomings related to the quality of key data. In this respect, GLP conditions, statistical analysis and reference to test guidelines were considered as positive indicators of the quality of the study used to set the NOAEL of substances included in CAG‐NCN. This information, and eventual other relevant observations were collected and reported in columns 7, 8 and 9 of Table E.12).

Most of the key studies used for the setting of NOAELs were performed under GLP conditions and were supported by statistical analysis. Nevertheless, for three risk drivers (pirimiphos‐methyl, monocrotophos and dichlorvos), critical studies had shortcomings regarding either GLPs, statistical analysis or test guidelines. There is a general tendency that in case of low‐quality studies, assessors derive conservative NOAELs.

With respect to monocrotophos, the NOAEL is the lowest (0.005 mg/kg bw per d) of all substances included in CAG‐NCN. It is, therefore, unlikely that with perfect information, the NOAEL would go even lower. An NOAEL of 0.006 mg/kg, corresponding to the highest tested dose, was observed in humans after a treatment of 28 days. This suggests that the MOET is likely to be higher with perfect information.

With respect to dichlorvos, the NOAEL of 0.008 mg/kg bw per day is the second lowest of all substances in CAG‐NCN. It is derived from a 2‐year dog study and used as tentative basis of the ADI due to the uncertainties of the genotoxic and carcinogenic properties of dichlorvos as well as the overall poor quality of the dossier (EFSA conclusion, 200630). A 2‐year rat study with a NOAEL of 0.23 mg/kg bw per day suggests that it is likely that, with perfect information, the NOAEL would be higher.

With respect to pirimiphos‐methyl, the poor data quality raises questions about the accuracy of the NOAELs, especially as the NOAEL is based on AChE inhibition in the brain. In the 2017 DAR of the Rapporteur Member State, the following is quoted about the 2‐year rat study (■■■■■ 1974): ‘Inhibition of brain and erythrocyte cholinesterase activity was seen at 300 ppm (2.1 mg/kg bw/d) and to a smaller and less consistent extent at 50 ppm (0.4 mg/kg bw/d) …; the degree of inhibition did not increase with duration of dosing. There was evidence of recovery in males, after 4 weeks; in females, erythrocyte activity normalised, but brain activity remained depressed. The fluctuations in the cholinesterase data, for example the apparent recovery of activity in brains of top dose males at 52 weeks, cast doubts on the reliability of the assay results, suggesting a potential for false negative results. For this reason, the sporadic findings of brain acetylcholinesterase inhibition of > 20% at 50 ppm are considered treatment related’’. In addition:

• In the 90‐day rat study, NOAELs for both the brain and erythrocyte AChE inhibition were 0.4 mg/kg bw per day.

• A 28‐day study and a 56‐day study in humans suggest an NOAEL of 0.25 mg/kg bw per day for erythrocyte AChE inhibition (see EFSA conclusion, 200531), which is close to the NOAEL of 0.4 mg/kg.

Therefore, the NOAEL of 0.4 mg/kg bw per d used in the calculation was found appropriately reflecting erythrocyte AChE inhibition of pirimiphos‐methyl, based on a combined assessment of all relevant available information.

Note 28 (Uncertainties related to the data collection methodology) – U30

The second factor affecting the hazard characterisation process concerns the method used to collect information. The first‐hand information consists in the original experimental results. The management of this information proceeds through the following steps:

• Interpretation and analysis of raw data of toxicological studies by the laboratory and/or regulatory assessors/bodies;

• Transfer of information from the original toxicological studies to the source documents (DARs, JMPR evaluations) by evaluating bodies;

• Transfer of information from the source documents to the working documents (excel spreadsheets) that were used for the characterisation on substances included in CAG‐NCN. This transfer of information was performed by EFSA contractors. The methodology to collect and report the information is precisely described in 2 external scientific reports (RIVM, ICPS, ANSES, 2013, 2016).

In each step, information can in theory be lost and there is some probability that active substances causing AChE inhibition might have not been identified during the review of the 422 active substances in the scope of the data collection procedure to establish the CAG. This is however extremely unlikely for the first two steps described above as AChE inhibition is a critical effect of OPs and NMC insecticides.

Mistakes in the transcription of data from source documents to the excel spreadsheets by the EFSA contractors cannot be excluded considering the huge amount of data involved in the exercise. The risk of such mistakes is, however, mitigated by procedures prevailing in the EU approval process of substances (e.g. circulation of the dossier to all Member States, peer‐review procedure). In addition, after assessment of this information and elaboration of CAG‐NCN, the existing EFSA conclusions or JMPR evaluations dealing with the included substances were cross‐checked to identify studies eventually omitted in the data management process and to ensure the consistency of the evaluation of AChE inhibition with theses outputs.

It was noted that the original study report of the key study used for the setting of the NOAEL of monocrotophos, one of the risk drivers, was never submitted for evaluation in the EU. This NOAEL (0.005 mg/kg bw per day) relies on the assessment by the JMPR. The absence of a cross‐check with an evaluation by EFSA was compensated by the fact that the studies were peer‐reviewed and considered reliable by JMPR experts. Additionally, the NOAEL of 0.005 mg/kg bw per day derived from a 2‐year study in rats (JMPR, 199132) was comparable with the NOAEL of 0.006 mg/kg bw per d derived from a human study on six male human volunteers (JMPR, 199333).

Note 29 (Uncertainty related to the Hazard characterisation principles) – U31

The third factor creating uncertainty in the hazard characterisation process concerns the principles and expert judgement used in the NOAEL setting for AChE inhibition. These are described in detail by the EFSA scientific report dealing with the establishment of CAGs for the nervous system (EFSA, 2019a). In summary, as the effect was defined as ‘brain and/or erythrocyte AChE inhibition’, brain and erythrocytes AChE inhibitions were considered as equally appropriate indicators for NOAEL setting. NOAELs were therefore derived for each AS from the most sensitive of these two indicators, using all available information across studies, species and sexes. AChE inhibition was considered relevant only when a statistically significant (p < 0.05) decrease of the AChE activity of 20% or more was observed with respect to concurrent control groups.

As indicated in the interpretation of the ToRs of the present assessment, it was however decided to evaluate the risk with respect to erythrocyte AChE inhibition in order to ensure an optimal protection of consumers. For this reason, the EKE question 1a was drafted as follows: ‘If this source of uncertainty was fully resolved (e.g. by obtaining perfect information on the issue involved) and addressed in the modelling, by what multiplicative factor would this change the median estimate of the MOET for chronic erythrocyte AChE inhibition for the 99.9th percentile of the [critical population] at Tier 2?’ Information allowing the comparison between levels causing brain and erythrocyte AChE was collected for each substance of CAG‐NCN and reported in Table E.12. This confirms that overall, erythrocytes are more sensitive to AChE inhibition than brain. For six substances (carbofuran, ethion, fosthiazate, parathion, pirimiphos‐methyl and trichorfon), however, the NOAELs were set with reference to brain AChE inhibition. In most cases, data related to erythrocyte AChE inhibition in Table E.12 indicate that the use of the NOAEL for brain AChE inhibition do not constitute an overestimation NOAEL for AChE inhibition in erythrocytes. The only exception is parathion, for which the assessment of AChE was aligned on the JMPR evaluation, which disregarded erythrocyte AChE inhibition. If the NOAEL would be based on erythrocyte AChE inhibition, it would decrease from 0.25 mg/kg to 0.1 mg/kg. This would have an extremely low impact on the cumulative exposure considering the long‐term exposure to parathion (Table 3) and the low rate of its occurrence in commodities (Table E.11).

In addition, for dimethoate, an NOAEL of 0.1 mg/kg bw per day was used for consistency with the EFSA conclusions from 2013. This value corresponds to a combined assessment of data from reproduction, neurotoxicity and developmental neurotoxicity studies. This NOAEL does, however, not reflect erythrocyte AChE inhibition as it was reported to be 2.5 times lower (0.04 mg/kg bw per day) in a 2‐year chronic toxicity study in rats (EFSA conclusions 2018).

Note 30 (Uncertainty related to the study design of the critical study) – U32

The last factor affecting the hazard characterisation process concerns the design of the key study used to derive the NOAEL. Relevant elements of the study design include the study duration, route of administration, dose spacing between NOAEL and LOAEL (columns 3–6 of Table E.12, respectively), as well as any other aspect of technical nature (such as the method applied for the measurement of AChE activity). It results from these multiple factors that this source of uncertainty is complex, especially because these factors act with opposite effects on the multiplicative factor on the MOET.

For OPs, the study duration needs to be sufficient to ensure that AChE inhibition reaches its maximum. Studies of too short duration could result into overestimated values for the NOAELs and, therefore, contribute to an overestimation of the MOET. The study duration was, however, sufficient in the vast majority of cases. Indeed, most substances were characterised on the basis of 2‐year rat, 1‐year dog or 2‐year dog studies. Azinphos‐ethyl, diazinon and ethion were characterised based on 90‐day dog studies and etephon based on a 28‐day rat study (column 5 of Table E.12).

For NMCs, the study duration is not a critical factor because the inhibition of AChE is quickly reversible and is not expected to increase over time in case of repeated exposure. However, for this class of substances, the route of administration of the substance in the key study is important, as gavage leads to a fast absorption and peak systemic concentrations which are not necessarily representative of the actual absorption rate and systemic concentrations when the substance is present in food. Gavage was the route of administration for carbofuran, carbosulfan, methomyl, oxamyl and thiodicarb (column 6 of Table E.12). For these substances, the NOAEL may have been set at values lower than they should be to reflect the practical conditions, what may contribute to an underestimation of the MOET.

A major point of the study design contributing to the uncertainty is the dose spacing between the NOAEL and the LOAEL. This results from the definition of ‘perfect information on the issue involved’ which refers to ‘the lowest BMDL20 from a perfect set of toxicity studies’ (see Section 2.3.4). The fact of using NOAELs for the toxicological characterisation of pesticides, instead of deriving BMDL20s from these studies, contributes to the uncertainty of the hazard characterisation. As the NOAELs are based on one single experimental dose, if the dose spacing in a study increases, the likelihood of the observed NOAEL being substantially lower than the actual dose that would cause a 20% AChE inhibition increases. In a generic context, the EFSA Scientific Committee (2017b) compared NOAELs and BMDL5s based on observations related to other substances and effects, so the derived conclusions might differ for an AChE inhibition of 20% by pesticides. It was further noted that NOAELs are by definition set at a level of AChE inhibition below 20% and therefore, that it is therefore likely that these NOAELs would generally be lower, rather than higher, than the respective BMDL20s, so that resolving this uncertainty would be more likely to increase the MOET than decrease it. Information about the dose spacing can be drawn from Table E.12 by comparing columns 3 and 4, corresponding to NOEALs and LOAELs, respectively. In the case of monocrotophos and dichlorvos, the NOAELs and LOAELs differ by a factor of 10.

In the key study for dichlorvos, a marked loss of dichlorvos from the diet (up to 70% of the nominal concentration) was observed (■■■■■ 1967), due to the high vapour pressure of dichlorvos (2.1 Pa at 25°C (EFSA conclusions, 2006)). This contributes to a potential overestimation of the MOET.

There is some uncertainty about the sensitivity of the analytical methods used in the measurement of erythrocyte AChE activity. The reported methods as described in the key study of the six risk drivers were the following

• Omethoate: Method citing Okabe (1977) only briefly described

• Dimethoate: Method citing Augustinsson (1978)

• Chlorpyrifos: Photometric method from Boehringer Mannheim (1981); specific detail to the method unclear

• Dichlorvos: Electrometric method from Michel (1949) with modifications; only cited

• Monocrotophos: Method unknown due to lack of original study

• Pirimiphos‐methyl: No method of ChE inhibition mentioned

The lack of a common assay among the measurements of AChE activity of these risk drivers contributes to the uncertainty in an undefined direction.

A last uncertainty inherent to the design of toxicological studies is the fact that the substance is administered at constant daily dose levels, while actual daily exposures to individual substances vary significantly around the average concentration used in the assessment of chronic risks.

Note 31 (Adequacy of the dose addition model) – U33

The rationale behind the use of dose addition when performing cumulative risk assessment has been given by the PPR panel in its opinions on the establishment of CAGs (EFSA PPR Panel, 2013a) and on the relevance of dissimilar modes of action (EFSA PPR Panel, 2013b).

Adequacy of the dose addition model as the default assumption was, amongst other aspect of CRA, recently investigated in the EuroMix collaborative EU research project.34 Although neurotoxicity was not addressed specifically, the results of a range of bioassays for steatosis and craniofacial malformations were in agreement with the dose addition model (Lichtenstein et al., 2020; van Oostrom et al., 2020; Zoupa et al., 2020). This applies to test mixtures containing substances eliciting the common adverse effect through both, similar and dissimilar modes of action. Confidence intervals of the dose–response curves for the mixtures overlapped with those of the single substances when all were scaled to the IC using relative potency factors.

Moreover, the calculations performed for the present assessment show that the risk is essentially driven by OPs. The parallelism observed by Bosgra et al. (2009) in dose–response curves of 15 OPs (including chlorpyrifos, dichlorvos, dimethoate and pirimiphos‐methyl) further supports the adequacy of the dose‐addition model. The dose additivity of OPs is also discussed in an EPA report on OPs CRA (U.S. Environmental Protection Agency, 2006). It was shown that the model can be applied to test mixtures containing substances eliciting the common adverse effect through both similar and dissimilar modes of action.

There is uncertainty regarding the slope and the shape of the dose–response curves for the substances included in the assessment, which is not addressed in the present assessment. This is because the dose addition model assumes that, when the dose–response curves are normalised for potency, they are all identical, with the same shape and slope (this assumption is sometimes expressed as requiring that the dose–response curves are parallel, e.g. EFSA PPR Panel, 2008). In the calculations performed for the current assessment, the normalisation for potency occurs when the individual MOE for each substance is calculated, by dividing the NOAEL for that substance by the exposure to that substance, before the individual MOEs are combined to calculate the MOET (Section 2.1). Since this assumption is required for the dose addition model, uncertainty about the slope of the shape of the dose–response curve is implicitly part of the uncertainty regarding the adequacy of the dose addition model for the present assessment. To the extent that available evidence supports the dose addition model for CAG‐NCN, it also implies that, if there are deviations from identicality of the normalised dose–response curves (what, from the first part of this note, is unlikely), they are a minor source of uncertainty in the present assessment.

Uncertainty about the slope and shape of dose–response curves does not affect the cumulative assessment in any other way. Although the estimated exposures for individual substances are generally a small fraction of the corresponding NOAELs, the cumulative assessment makes no assumption about the magnitude of effect (AChE inhibition). Instead, the assessment sums the exposures as proportions of their respective NOAELs (i.e. after normalisation for potency, see above) and the result is used only to assess the MOET, which expresses how close the combined exposure is to the level that corresponds to the critical effect size (20% for AChE inhibition). Similarly, the conclusion of the assessment concerns only how close the cumulative exposure is to the threshold for regulatory concern. At no stage in the assessment is there any assumption, assessment or conclusion regarding the magnitude of effects at the MOET.

Note 32 (Adequacy of the OIM model) – U34

The long‐term exposure distributions were calculated with the OIM model. In this simple model, for each individual of the population, the daily consumption of each food commodity, averaged over the number of days of the survey, is multiplied by the mean concentration of each substance in the food commodity. As the duration of food consumption surveys is relatively short in all cases (2–7 days), the calculated exposure for each individual may significantly differ from the real long‐term exposure, e.g. over years or a lifetime. For this reason, it is acknowledged that the exposures calculated with this method are about right in the middle of the exposure distribution but are expected to overestimate the upper tail and underestimate the lower tail of real long‐term exposures (EFSA PPR Panel, 2012; Goedhart et al., 2012, RIVM letter report 2015‐0191, 2015).

As the threshold for regulatory consideration is established at the 99.9th percentile of the exposure distribution, the use of the OIM model is consequently per se a source of overestimation of the exposure (and of underestimation of the MOET) if an effect requires more than 2–7 days to reach the maximum of its magnitude. To assess the impact of this source of uncertainty in the present assessment, one needs to consider how long the dietary exposure to pesticides needs to be to reach the maximum AChE inhibition.

Due to the irreversible nature of AChE inhibition by OPs, it is estimated that the time needed under continuous exposure to OPs to reach the highest level of AChE inhibition would be consistent with the rate of restoring AChE activity (about 1% daily) by the continuous release of erythrocytes in blood from the bone marrow, compensating their limited lifetime of 4 months at most. This was supported by findings from the key studies of the 6 risk drivers regarding the time needed to reach maximum AChE inhibition in erythrocytes, which consistently ranged from 1 to 6 months.

This source of uncertainty is particularly complex in case of cumulative risk assessment because not a single commodity, but multiple commodities contribute to the total exposure of one individual. It results that an overestimated intake during the survey period resulting from a larger than usual consumption of a certain commodity may be mitigated to a certain extent by a lower than usual consumption of another commodity during the same survey period. These mitigating effects are expected to depend upon the number of commodities, which, through the residue they contain, participate significantly to the risk. Also, the nature of the commodities driving the risk is important to consider, as some commodities constituting the basis of the diet (e.g. bread) are consumed on a much more regular basis than seasonal commodities (e.g. strawberries). Hence, the average consumption derived from a short survey period is expected to reflect the long‐term consumption of the subject with higher accuracy for basic commodities than for commodities consumed periodically.

In order to evaluate the magnitude of the overestimation of the risk resulting from the use of the OIM model, it might be interesting to consider the ratio between MOET estimates at 50th and 99.9th percentiles of the exposure distribution. A large ratio might be indicative of an important overestimation at the 99.9th percentile. In Table E.13, such ratios were calculated for each population covered by the present assessment and, for the sake of comparison, those conducted earlier by EFSA for hypothyroidism and C‐cell hypertrophy, hyperplasia and neoplasia (EFSA, 2020a,b).

Table E.13.

Ratios between MOET estimates at 50th and 99.9th of the cumulative exposure distribution for chronic AChE inhibition, hypothyroidism and C‐cell hypertrophy, hyperplasia and neoplasia

Ratios between MOET estimates at 50th and 99.9th
3.8	4.1	4.6	2.9	3.5	5.0	3.1	2.9	3.9	3.7	Chronic AChE inhibition Number of substances in the CAG: 47 Commodities driving the risk (4): olive for oil production, wheat, orange, drinking water
3.2	3.9	3.9	2.6	2.6	2.6	2.6	2.6	3.5	3.4	Hypothyroidism Number of substances in the CAG: 128 Commodities driving the risk (9): wheat, oats, tomatoes, rye, rice, oranges, wine grapes, apples, potatoes
7.9	14.3	7.0	5.0	6.0	3.7	5.1	4.0	4.5	4.9	C‐cell hypertrophy, hyperplasia, neoplasia Number of substances in the CAG: 17 Commodities driving the risk (7): apples, wine grapes, strawberries, peaches, pears, table grapes, lettuce
2	2	2	3	2	7	2	7	2	4	Number of days in the survey
BE	CZ	DE	IT	BG	FR	NL	DK	NL	UK	Populations No. of Subjects
1356	1666	10419	2313	434	482	957	917	322	1314
Adults				Other children			Toddlers

Note 33 (Assessment factor for intraspecies variability) – U35

To take account of a potential sensitivity of particular groups of consumers to a toxicological effect exceeding the usual factor of 10 for intraspecies variability, it is part of normal practice to apply an extra UF in the establishment of ADIs or ARfDs of active substances. Because the setting of an MOET of 100 as threshold for regulatory consideration by risk managers does not consider this possibility, accounting for such additional sensitivity could consist in dividing the NOAEL by an appropriate factor before running the calculations for the populations concerned by the issue.

For AChE inhibition, the adequacy of the factor of 10 for intraspecies variability could be questioned for infants of less than 16 weeks (e.g. due to immature metabolic capacities and still under critical periods of development) and the elderly population (due to worsened health conditions due to existing diseases, age‐related decline in metabolism, lower detoxification capacity).

As mentioned in Section 4.3, infants less than 16 weeks of age are expected to be exclusively fed on breast milk and/or infant formula, for which a legal limit of 0.01 mg/kg is set for pesticides residues by Commission Directives 2006/125/EC and 2006/141/EC.²² Furthermore, it was concluded by the EFSA PPR Panel (2018) that this default MRL of 0.01 mg/kg for infant formulae does not result in an unacceptable exposure to infants for all compounds, to which a HBGV of 0.0026 mg/kg bw per day or higher applies after application of the guidance on risk assessment of substances in food for infants (EFSA Scientific Committee, 2017a).

Uncertainty about the intraspecies variability for the elderly populations results from potential ageing‐related factors such as their longer exposure to chemicals, pre‐existing medical conditions (e.g. diabetes, cancer, heart disease, etc.), weaker immune system, declined metabolism, lower detoxification capacity and recovery in the brain, lower AChE activity and lesser adaptative regulation of acetylcholine release. Evidence in the decline of AChE activity with age is available from ageing studies in rats (Pope, 2010) and is more relevant for OPs as NMCs do not cross the blood–brain barrier and the effects in the brain induced by NMCs are much lower than that induced by OPs (Jokanović, 2009).

It was, however, not envisaged to use an additional safety factor in the setting of NOAELs in the present exercise because none of the populations for which calculations were performed included consumers belonging to the anticipated more vulnerable groups. Indeed, consumers forming the populations used in the present exercise were all aged from 1 to 65 years and it is mainly outside this age range that particular sensitivity to AChE can be envisaged.

Note 34 (Information on PRIMo chronic diets) – Section  4.2

Table E.14.

Long‐term average consumption of plant commodities in population groups of the EFSA PRIMo Model

Long‐term diet	Subgroup of population/age group	Mean body weight (kg)	Total average consumption of plant commodities (g/kg bw per day)
DE child	Children between 2 and 5 years	16.2	38.26
DE general	General population	76.4	18.87
DE women 14–50 years	Women of child‐bearing age	67.5	19.96
DK adult	15–74 years	75.1	8.71
DK child	4–6 years	21.8	23.08
ES adult	Adults > 17 years	68.5	12.19
ES child	7–12 years	34.5	17.77
FI adult	Adults	77.1	12.59
FI child 3 years	Children up to 3 years	15.2	16.73
FI child 6 years	Children up to 6 years	22.4	13.08
FR infant	7–18 months	9.1	11.06
FR toddler 2–3 years	25–36 months	13.6	20.87
FR child 3 to < 15 years	Children from 3 to less than 15 years	18.9	24.88
FR adult	Adults > 15 years	66.4	12.48
IE adult	Adults 18–64 years	75.2	25.60
IE child	5–12 years	20.0	3.61
IT adult	18–64 years	66.5	12.12
IT toddler	1–17 years	41.6	16.42
LT adult	19–64 years	70.0	10.20
NL child	2–6 years	18.4	37.27
NL general	General population, 1–97 years	65.8	17.31
NL toddler	8 to 20 months	10.2	60.61
PL general	General population, 1–96 years	62.8	9.71
PT general	General population	60.0(a)	20.84
RO general	General population	60.0(a)	23.13
SE general	General population, 1–74 years	60.0(a)	19.65
UK infant	6 months–1 year	8.7	18.58
UK toddler	18 months–4 years	14.6	21.04
UK adult	19–64 years	76.0	8.97
UK vegetarian	No information	66.7	10.80

Appendix F – Uncertainty analysis – EKE Q1: Outcome of the impact assessment of individual sources of uncertainty affecting the CRA for CAG‐NCN

1.

The ranges for the values of multiplicative factors that would adjust the median estimate of the MOET for CAG‐NCN at the 99.9th percentile of exposure in Tier II were estimated for each source of uncertainty identified in Section 3.2.1 (first column of Table F.1), assuming that it was fully resolved and addressed in the modelling.

These judgements were first conducted for the Italian adult population (EKE Q1A), based on information specific to the cumulative exposure of this population (Sections 3.1.2 and 3.1.3). The scale and methods used for this estimation are described in Section 2.3.2. For example: ‘– – –/●’ means at least a 90% chance the true factor is between ×1/10 and +20%; ‘++/++’ means ≥ 90% chance between 2× and 5× etc. It was secondly assessed whether the same multiplicative factor would apply to the other nine populations for which the cumulative exposure was modelled (EKE Q1B). The outcome of these judgements and the respective rationales are given in the second and third columns of Table F.1.

In the last column of Table F.1, reference is given to notes in Appendix E which summarise information used to address EKE Q1A and Q1B.

Source of uncertainty	Consensus judgement	Consensus rationale	Information notes
U1 (omitted commodities)	–/●	a) Inclusion of the omitted commodities in the assessment would be expected to reduce the MOET possibly by more than 20% in the Italian adult population, but by less than a factor of 2. The key points, which in combination, support this judgement are (i) the mean contribution (and the associated standard deviation) of the 35 plant commodities to the overall diet of plant origin (see Table E.1, Note 1) and (ii) the contribution of the 35 selected commodities to the total long‐term exposure, which is weak to some substances (e.g. carbofuran, diazinon, methomyl, oxamyl), as best reflected by the lower bound calculations reported in Table E.3, Note 3). No increase of the MOET is anticipated, i.e. the multiplicative factor can only be below 1. b) The multiplicative factor can be lower for other populations, mainly adult populations as children and toddlers are closer to the Italian adult population regarding the contribution of the 35 plant commodities to the overall plant diet. Nevertheless, consensus judgement still remains within the same range (–/●).	Notes 1, 2 and 3.
U2 (ambiguity in consumption data)	●/●	a) Perfect information can change the MOET in both directions, but the change would be small and would not exceed 20% because (i) the model combines average consumptions and average concentrations for each commodity, and (ii) the pesticide/commodity combinations driving the risk are unaffected by this source of uncertainty. b) No differences are expected between populations.	Note 4
U3 (accuracy of consumption data	●/●	a) Perfect information can change the MOET in both directions, but the change would be small and would not exceed 20%. No significant methodological limitation was identified in the consumption surveys. The effect of under reporting was considered as limited because it is unlikely to affect fruit and vegetables, which are the commodities of importance for exposure to pesticide residues. The effect of over‐reporting was also considered limited based on detailed records of consumption data for subjects with exposures exceeding the 99th percentile (Annex C, Table C.03). b) No differences are expected between populations.	Note 5 and 6
U4 (sampling variability of consumption data)	–/●	a) Perfect number of consumers in the survey (i.e. number high enough to ensure reliability at the 99.9th percentile of exposure) would result in a decrease of the MOET due to the high probability that consumers in the upper tail of the exposure distribution will not be sampled (highly exposed consumers). b) As the number of subjects varies considerably between populations, differences are expected between the different populations, especially the ones with lower number of subjects for which the underestimation of the exposure at P99.9 would be expected to be larger (e.g. 322 subjects for the Dutch survey).	Note 7
U5 (Representativeness of the consumption data)	●/●	a) Perfect information can change the MOET in both directions. A decrease is more plausible than an increase due to the recent increase in fruit and vegetable consumption by a few percents, not captured yet by recent surveys. The change would however be small and would not exceed 20%. Additionally, apart from oranges, being one of the risk drivers, the positive trend in fruit and vegetable consumption does not concern commodities identified as risk drivers. Despite the lack of information on whether ethnical differences are well accounted in surveys, the 35 commodities selected are basic commodities which are most likely consumed by all populations. b) No differences are expected between populations.	Note 8
U6 (use of invariable recipes and conversion factors by the RPC model)	●/●	a) Perfect information can change the MOET in both directions. The change would be small and within 20% as over‐ and under‐estimations resulting from variations in recipes tend to cancel out in the long term. b) No differences are expected between populations.	Note 9
U7 (pesticide/commodity combinations without occurrence data)	●/●	a) Solving this uncertainty can only decrease the MOET. However, the impact would be extremely low because only one substance/commodity combination is affected by this issue. b) No differences are expected between populations.	Note 10
U8 (metabolites not accounted)	–/●	a) Solving this uncertainty can only decrease the MOET. The MOET could be decreased possibly by more than 20% but less than a factor of 2, considering the cases where a residue definition for risk assessment differs from the residue definition for monitoring and cases where information on the residue definition for risk assessment is missing. b) No differences are expected between populations.	Note 11
U9 (ambiguity of occurrence data)	●/●	a) Perfect information can change the MOET in both directions, but the change would be small and would not exceed 20% because the model combines average consumptions and average concentrations for each commodity. b) No differences are expected between populations.	Note 4
U10 (analytical uncertainty for occurrence data)	●/●	a) Perfect information would have a very limited impact on the MOET since the total number of measurements is high and analytical uncertainties are expected to average out. b) No differences are expected between populations.	Note 12
U11 (sampling variability of occurrence data)	●/+	a) Perfect information on sampling variability regarding occurrence data will only be expected to increase the MOET by a factor up to 2. The key points driving this consensus are the following: (i) the median estimate of the MOET at the 99.9th percentile resulting from the Tier II calculations is unstable and the value used as model output for the uncertainty analysis is likely to underestimate the real one; (ii) based on the monitoring data from 2014 to 2018, the probability to encounter a concentration of 4.9 mg/kg (which was observed for the sum of omethoate and dimethoate in one olive sample only) is expected to be smaller than 1 out of 79 (total number of determinations), and the sensitivity analysis E (i.e. excluding the residue concentration of 4.9 mg/kg) suggests that the 99.9th percentile of the exposure distribution may be overestimated by a factor up to 2. b) The overestimation may be smaller for populations that have a smaller contribution of omethoate and dimethoate in olives for oil production to the cumulative exposure (German adults, United Kingdom toddlers, Bulgarian children, Dutch toddlers, Dutch children, Danish toddlers).	Note 7
U12 (representativeness of the occurrence data)	●/●	a) Perfect information can change the MOET in both directions, but the change would be small and would not exceed 20%. Sensitivity analysis G did not confirm the theoretical expectation that samples coded as ‘selective sampling’ lead to an underestimation of the MOET. The impact of this source of uncertainty is however difficult to evaluate due to inconsistencies in the interpretation of the term ‘selective sampling’ at member‐state level. b) No differences are expected between populations.	Note 13
U13 (extrapolation of occurrence data)	●/●	The impact of this source of uncertainty is nil because this type of extrapolation was not needed in the present assessment.	Note 14
U14 (pooling of occurrence data from all Member States)	●/●	a) Perfect information could change the MOET in both directions, depending on the country and pesticide/commodity combination. Considering the large number of pesticide/commodity combinations, the overall impact of this source of uncertainty on the MOET is expected to be low due to an averaging effect. Moreover, populations usually consume a mixture of imported and locally grown commodities. b) No differences are expected between populations.	Note 15
U15 (unspecific residue definitions)	●/+	a) This source of uncertainty affects the risk drivers omethoate and dimethoate on olives for oil production. Omethoate and dimethoate differ in potency by a factor 4. Perfect information on the exact ratio between the two compounds is expected to increase the MOET by a factor up to 2. This is based on information about the evolution of the omethoate/dimethoate ratio on olives after harvest (high ratios are unlikely to be associated to high levels of the sum of the two compounds) and the results from sensitivity analysis K where omethoate was assumed to not be authorised as this is the case. b) This uncertainty would be expected to have smaller impact in populations consuming less olive oil	Note 16
U16 (left‐censored data: assumption of the authorisation status of pesticide/commodity combinations)	●/●	a) There was a general agreement that this type of uncertainty would not impact the MOET by more than 20% towards both directions, because it is subject to two factors acting in opposite directions. This is supported by the sensitivity analysis H in which all pesticide/commodity combinations with detection rates exceeding 1% were considered as authorised. b) No differences are expected between populations.	Note 17
U17 (left‐censored data: assumption about the use frequency)	●/●	a) Perfect information would tend to increase the MOET because the assumption that all samples were treated with at least one active substance (assigned an authorised use) is considered conservative (e.g. organic farming is not considered, information on percentage of quantifiable measurements in Annex C, Table A.09). However, sensitivity analysis B shows that the magnitude of the impact is below 20%. b) No differences are expected between populations.	Note 18
U18 (left‐censored data: assumption on the residue level)	●/●	a) Perfect information would have a limited impact on the MOET based on the results of sensitivity analysis B, and assuming a similar finding in the opposite direction if left censored data were imputed to the level of LOQ instead of 1/2 LOQ. b) No differences are expected between populations	Note 18
U19 (assumption about pesticides in drinking water)	●/●	a) Perfect information would increase the MOET, based on the fact that the five most potent substances of the CAG assumed to be present at 0.05 μg/L in drinking water are not approved in the EU and on quantitative information about the contribution of drinking water in Annex C, Table C.02. The impact is however lower than 20%, as suggested by sensitivity analysis I. b) Differences between populations are suggested by sensitivity analysis I (to be discussed/addressed under EKE Q3).	Note 19
U20 (missing processing factors)	++/+++	a) Perfect information would increase the MOET based on indicative information about PFs related to pesticide/commodity combinations driving the risk, and sensitivity analysis C. b) This sensitivity analysis suggests smaller impacts in all the other populations (in some populations, the judgement would be ++/++) which can be considered in EKE Q3.	Note 20
U21 (Use of processing factors in the EFSA food classification and description system (FoodEx))	●/●	a) Perfect information could change the MOET in both directions, depending on the food consumed and the actual recipe/processing. Considering the large number of recipes and processing types in a long‐term assessment, contrasting effects are expected and would tend to average out across foods. In addition, as this source of uncertainty does not concern most risk drivers the overall impact is expected to be limited. b) No differences are expected between populations.	Note 21
U22 (analytical uncertainty for processing factors)	●/●	a) Perfect information would have a very limited impact on the MOET considering the number of measurements and the fact that analytical uncertainties are expected to average out. b) No differences are expected between populations.	‐
U23 (accuracy of processing factors)	●/●	a) Perfect information on the actual levels in processed commodities would only further decrease the processing factor, and therefore the multiplicative factor can only be above 1. The magnitude of the impact is however very low considering the small number of processing factors concerned by this source of uncertainty and the low values of these PFs. b) No differences are expected between populations	Note 22
U24 (use of fixed values of processing factors)	●/●	a) Only one risk driver is concerned (chlorpyrifos/orange), for which two PFs were used (peeling and juicing) and, in this case, they were median values of four and six independent trials. b) No differences are expected between populations.	Note 23
U25 (processing factors not considered (peeling of commodities with edible peel and washing)	●/●	a) Perfect information on peeling and washing can only result in multiplicative factors above 1. However, the impact is minor because none of the risk drivers is concerned by this source of uncertainty. b) No differences are expected between populations.	Note 24
U26 (OPs and NMCs not included in the CAG)	–/● or ●/●	a) Perfect information on the omitted substances and their inclusion in the CAG can only decrease the MOET. The overall quantification rate of the substances not included in the CAG (16 non‐approved OPs and NMCs) is about 1% of the quantification rate of substances included in the CAG. Results from deterministic exposure calculations in PRIMo for the 7 substances with known ADIs (especially lower bound estimates which are better indicators of risk drivers than upper bound estimates) suggest that their contribution to the cumulative exposure would be minor. On the other hand, regarding the 9 substances for which ADIs are missing, despite the very low quantification rate, account is taken of the fact that one single sample may significantly alter the MOET at the percentile of interest (see sensitivity analysis E in Table 16 in Section 3.1.3), depending on the residue level and the potency of the substance. The experts did not agree on a consensus range for the impact of this source of uncertainty and 2 consensus judgements were retained. However, those experts supporting the judgement (−/.) agreed that the decrease of the MOET was unlikely to be much larger than 20%. b) No differences are expected between populations.	Note 25
U27 (contribution of substances acting through oxidative stress)		Not assessed (see Section 3.2.1)
U28 (substances included in the CAG not causing the effect)	●/●	a) There is a high level of certainty that all substances in the CAG contribute to chronic AChE inhibition. b) No differences are expected between populations.	Note 26
U29 (Uncertainties related to original studies/data quality)	●/+	a) Perfect data quality could either increase or decrease the MOET. The former is judged more plausible because the NOAELs of 2 risk drivers with low data quality (monocrotophos and dichlorvos) used for the CRA calculations were particularly low (0.005 mg/kg bw per d and 0.008 mg/kg bw per d, respectively) compared to all other substances of the CAG and would likely increase if information from studies of perfect quality were available. In general, in case of low‐quality studies and/or lack of statistical analysis, the assessors tend to derive lower NOAELs. b) No differences are expected between populations.	Note 27
U30 (Uncertainties related to the data collection methodology)	●/●	a) Perfect information could either increase or decrease the MOET. The impact would be low (less than 20%) considering that the information in source documents has been checked during the EFSA peer review process or JMPR evaluations, and that the working documents (excel spreadsheets) were checked against EFSA conclusions. b) No differences are expected between populations.	Note 28
U31 (Uncertainty related to the NOAEL‐setting principles)	●/●	a) Using perfect NOAELs for erythrocyte AChE inhibition would most probably decrease the MOET because a NOAEL of 0.04 mg/kg bw per d for dimethoate (a risk driver) would be used instead of the NOAEL of 0.1 mg/kg bw per d. The change would, however, not exceed 20%, considering the contribution of dimethoate to the risk. b) No differences are expected between populations.	Note 29
U32 (Uncertainty related to the study design of the critical study)	–/+	a) Perfect study design such that the NOAELs would precisely reflect BMDL20s could change the MOET by a factor ranging from 1/2 to 2. There are several factors in interplay and with opposing effects, the main ones being the dose spacing and the methods/assays used to measure AChE activity, which are old and differ between substances. This is a major source of uncertainty, as suggested by the differences observed by the EFSA Scientific Committee between NOAELs and BMDs (EFSA Scientific Committee, 2017a,b). b) No differences are expected between populations.	Note 30
U33 (adequacy of the dose‐addition model)	●/●	a) Perfect information would be expected to have minor impact on the MOET as OPs and NMCs have a similar mode of action b) No differences are expected between populations	Note 31
U34 (adequacy of the OIM model)	●/+	a) Perfect information could increase the MOET due to the inherent limitations of the OIM model in the tails of the exposure distribution. The increase could be larger than 20%, although unlikely much larger. The key elements which support this judgement are the following: (i) Most of the commodities driving the risk (i.e. olive oil, wheat and drinking water) are consumed with relatively moderate daily fluctuations and for such commodities the OIM model is expected to produce better long‐term exposure estimates at extreme percentiles (ii) The ratio between the MOET estimates at P50 and P99.9 of the exposure distribution for the Italian adult population is 3, excluding an impact exceeding a factor of 2. b) Differences are expected between populations depending on the number of days in the respective consumption surveys.	Note 32
U35 (adequacy of the UF for intraspecies variability)	●/●	a) Source of uncertainty of marginal relevance as the Italian adult population includes individuals from 18 to 65 years old. b) No differences are expected between populations as none of the 10 populations under consideration includes infants of less than 16 weeks or elderly people.	Note 33

Appendix G – Record of judgements and reasoning for EKE Q2 on uncertainties related to toxicology

1.

Record during the expert MS Teams meeting on 30 September 2020

The text of EKE Q2 is shown in the footnote for reference.35

The facilitator explained the concept of consensus used in the Sheffield method for EKE (EFSA, 2014a,b,c): although their personal opinions may differ, the experts are asked to agree on what it would be reasonable for a rational impartial observer (‘RIO’) to think, having seen the evidence and individual judgements and heard the discussion. To develop such a consensus for EKE Q2 on exposure, the experts discussed the relative magnitudes of the individual uncertainties and how they would combine, taking into account the identified dependencies between them, i.e. positively, negatively dependent or independent uncertainties.

None of the sources of uncertainty pertaining to toxicology was found to have an impact exceeding a factor of 2 in either direction on the MOET during the EKE Q1 session.

The sources of uncertainty most impacting the upper end of the distribution were U29 on the quality of the original studies and data quality and U32 on the study design of the critical study. U29 was assessed in EKE Q1 as (./+) and U32 as (–/+). Under U32, the most influential component was the possible difference between the NOAELs and the precise BMDL20s. The experts noted the differences observed by the EFSA Scientific Committee between NOAELs and BMDL5s (EFSA Scientific Committee, 2017a,b) while also taking into account that those observations related to other substances and effects, so the relationship between NOAELs and BMDL20s might differ for AChE inhibition by pesticides. It was further noted that NOAELs are always set at a level of AChE inhibition below 20%. Therefore, it was likely that these NOAELs would generally rather be lower than the respective BMDL20s and resolving this uncertainty would be more likely to increase the MOET than decrease it.

The experts discussed whether there is a dependency between uncertainties U29 and U32. Although study guidelines and GLP (considered in U29) do not give specific directions on the dose selection and spacing, study duration, route of administration or analytical methods (considered in U32), they do support a good study design. Therefore, if it is known that an appropriate guideline and GLP were followed in a study (U29), uncertainties relating to study design may be reduced (U32). However, it was agreed that if there was a dependency in the impacts of these sources of uncertainty, it would be minor. Based on these considerations, the experts concluded that the combined impact of the toxicology uncertainties on the MOET could not be higher than a factor of 2 and, therefore, concluded for an upper plausible bound of 2.

The source of uncertainty most impacting the lower end of the distribution was U32 on the study design of the critical study (assessed in EKE Q1 as –/+). As discussed in the EKE Q1 session, U32 involves several factors with opposing effects on the MOET, e.g. dose selection and spacing, study duration, route of administration and test methods used. The most important aspects under U32 were considered to be related to the methods of measuring AChE activity, the vaporisation of dichlorvos in the key study and the use of NOAELs, rather than the derivation of BMDL20s, to characterise the substances. However, the last of these, resolving the uncertainty regarding the relationship between NOAELs and BMDL20s, was considered more likely to increase the MOET than decrease it for the reasons explained above.

Uncertainty U26, on the OPs and NMCs not included in the CAG, although expected to result in a decrease of the MOET due to missing information on the contribution of nine non‐approved substances for which no TRVs (e.g. ADI) were available, was considered unlikely to cause a decrease of more than 20% (assessed in EKE Q1 as./. or –/.). This was supported by data from lower bound exposure estimates in PRIMo suggesting that the contributions for the substances not included in the CAG would not be expected to exceed the 0.02% of their respective ADIs (highest result for phorate). Therefore, this uncertainty was not considered to have a major impact on the overall MOET.

Uncertainty U31, related to the hazard characterisation (NOAEL‐setting) principles, is mainly driven by the NOAEL of 0.1 mg/kg bw per day for dimethoate used for ADI derivation and MOET calculation (overall NOAEL set for reproduction, neurotoxicity and developmental neurotoxicity), instead of 0.04 mg/kg bw per day for erythrocyte AChE inhibition as reported in the key study (see table under Technical Note 28). However, this was considered to have a minor impact and would not be expected to decrease the MOET by more than 20% (assessed in EKE Q1 as./.) due to the limited contribution of dimethoate to the risk (see Annex C, Figure C.03).

Based on these considerations, the experts concluded that the combined effect of the toxicology uncertainties could not reduce the MOET by more than a factor of 2 and, therefore, agreed on a lower plausible bound of 0.5 for the multiplicative factor required by EKE Q2.

Further judgements were elicited using the probability method (Oakley and O'Hagan, 2016), which is described in EFSA (2014a,b,c) as the fixed interval method. In this method, the experts are asked to judge the probability that the quantity of interest lies between a specified value and the lower or upper bound. For this purpose, the facilitator chose three values in different parts of the plausible range, favouring regions where differences between the individual distributions were most marked. Specifically, the experts were asked the three questions shown below. For each question, a range of answers was discussed, and a provisional consensus was agreed. Distributions were fitted to the provisional consensus probabilities using the MATCH tool and displayed for review by the experts.

What is the probability for the true value to be lower than 0.8?

Provisional consensus: 10%

What is the probability for the true value to be higher than 1.2?

Provisional consensus: 25%

What is the probability for the true value to be lower than 1?

Provisional consensus: 45%

The experts agreed that the sources of uncertainty impacting the upper and lower ends of the distribution were nearly of the same strength, with a slight predominance of those impacting the upper end. The tendency towards the upper end was based on uncertainty U32 (major contributor) and particularly the effect of using NOAELs instead of BMDL20s and U26 (albeit with minor impact), as explained above.

The best fitting of the distributions available in MATCH for these provisional judgements was the Scaled Beta, with a 95% probability interval of 0.69 to 1.48 and a median of 1.04. This distribution is shown in Figure G.1.

Figure G.1.

First provisional consensus distribution. Scaled Beta with median of 1.04 and 95% probability interval of 0.69–1.48

The experts were asked whether they considered this distribution appropriate to represent their consensus judgement on EKE Q2, i.e. what it would be reasonable for a rational impartial observer to think, having seen the evidence and individual judgements and heard the discussion. In the course of discussing this, two additional MATCH distributions were considered. The first alternative distribution was also a Scaled Beta, showing the effect of changing the probability for the true value being between 1.2 and 2 from 25% to 30% (see Figure G.2). The second alternative also used this revised probability judgement but fitted a Log Student‐t distribution instead of a Scaled Beta (shown in Figure G.3, truncated to the experts’ plausible bounds of 0.5 and 2).

Figure G.2.

Second provisional consensus distribution. Scaled Beta with median of 1.05 and 95% probability interval of 0.67–1.54

Figure G.3.

Third provisional consensus distribution. This is a Log Student‐t distribution truncated at 0.5 and 2. Considering only the part of the distribution which is shown in this figure, the median is 1.05 and 95% probability interval of 0.63–1.69. See Figure G.4 for the non‐truncated version of this distribution

The alternative distributions are plotted together in Figure G.4 for comparison. The main difference is in the lower and upper tails, where the third distribution (Log Student‐t) has more probability than the first and second (Beta distributions). The full Log Student‐t distribution also extends beyond the experts’ plausible bounds of 0.5 and 2, as can be seen in Figure G.4.

Figure G.4.

Comparison of the three provisional consensus distributions. Consensus #1, #2 and #3 correspond to the distributions shown in Figures G.1, G.2 and G.3, respectively. Note that distribution #3 is truncated at the consensus plausible bounds of 0.5 and 2 in Figure G.3, but actually extends beyond those bounds at both ends as can be seen here. The non‐truncated version of consensus distribution #3 has a median of 1.04 and 95% probability interval of 0.56–1.97

Continuation of the consensus discussion by email after the meeting

The facilitator sent the draft record of the consensus discussion at the meeting to all the experts on 2 October and asked them to review it and send any additions or corrections by email by 6 October. In the same email, the experts were asked to look carefully at the three alternative distributions in Figures G.1–G.3 and also the untruncated version of distribution #3 that is shown in Figure G.4, paying particular attention to the differences between them, and answer three questions, which are reported below together with the responses of the experts.

Question 1 (answered separately for each of the four distributions in Table G.1, below): Do you consider that it would be reasonable or unreasonable for a rational impartial observer to take this distribution as their judgement for EKE Q2, having seen the evidence and individual judgements and heard the discussion? Please note that you are not restricted to choosing one distribution as ‘reasonable’. If you think 2 or more distributions are similar enough that they could all be reasonable choices for the rational impartial observer, you should enter them all as ‘reasonable’. Enter ‘unreasonable’ for any distributions you think it would be unreasonable for the rational impartial observer to choose, and briefly summarise your reasons for that.

Table G.1.

Responses of the experts to Question 1 in the first round of email discussion of the consensus judgements Do you consider that it would be reasonable or unreasonable for a rational impartial observer to take this distribution as their judgement for EKE Q2, having seen the evidence and individual judgements and heard the discussion? Expert F did not have time to respond in this round of consultation

Distribution	Enter ‘Reasonable’ or ‘Unreasonable’	If unreasonable, please indicate what aspects of the distribution seem unreasonable to you?
Consensus #1 (shown in Figures G.1 and G.4)	A: Reasonable C: Unreasonable D: Reasonable E: Unreasonable	C: No probability is given to multiplicative factor (MF) values above 1.7 but this does not reflect the consensus judgement on upper bound of 2. E: Upper bound ends at 1.65; this seems unreasonable since we discussed that the plausible bond is up to 2.
Consensus #2 (shown in Figures G.2 and G.4)	A: Reasonable C: Unreasonable D: Reasonable E: Reasonable	C: No probability is given to MF values above 1.7 but this does not reflect the consensus judgement on upper bound of 2. (E explanation for ‘reasonable’: Probability for the true value being between 1.2. and 2 is 30%. Upper bound ends at 1.8 which seems reasonable. It is considered very similar to Figure G.3.)
Truncated version of Consensus #3 (shown in Figure G.3)	A: Reasonable C: Unreasonable D: Unreasonable E: Reasonable	C: The distribution exceeds the lower plausible bound of 0.5 and upper plausible bound of 2, both bounds agreed in the meeting. D: The 95% probability interval (especially with the upper bound) is not reasonable. If U32 (namely a lower NOAEL than BMDL20) is the primary cause for the shift of the distribution towards the upper end, it is my scientific opinion that it is highly unlikely that the upper 95% probability would exceed 1.5. (E explanation for ‘reasonable’: Lower and upper tails are the discussed plausible bounds of 0.5 and 2. This is preferred since end at 2 and also the 95% is wider (0.63–1.69), but it is considered very similar to Figure G.2.)
Untruncated version of Consensus #3 (shown in Figure G.4)	A: Reasonable C: Unreasonable D: Unreasonable E: Unreasonable	C: The distribution exceeds the lower plausible bound of 0.5 and upper plausible bound of 2, both bounds agreed in the meeting. Additionally, the probability of MF of MOET to be > 2 would be lower than the probability of MF to be below 0.5, which is opposite to expert judgement concluded in the meeting. D: See rationale above for truncated version of consensus #3, which applies here for this version as well. The upper bound in this version is even higher than the truncated version and therefore is also unreasonable. E: It extends in the lower and upper tails beyond the discussed plausible bounds of 0.5 and 2, this seems unreasonable.

Question 2: Which of the four distributions do you think it would be most reasonable for the rational impartial observer to choose? Please tick only one of the 4 options.

Question 3 (optional): If you would like to propose a different distribution for the consensus, you can produce this with the MATCH tool by copying all the entries that were made for consensus distribution #1 (circled in red in the screenshot below), and then changing the probabilities (enter revised probabilities in the boxes and press enter, or you can just drag the coloured bars) and/or the choice of distribution (click buttons) to view alternative distributions. If you produce an alternative distribution that you would like to propose to the other experts as a consensus (what a rational impartial observer would think), please paste a screen‐shot of your whole MATCH screen (including your judgements and the plotted distribution) at the end of this document.

The responses provided by the experts to Questions 1 and 2 are shown in Tables G.1 and G.2 below, followed by alternative distributions which were suggested by 3 experts in response to Question 3.

Table G.2.

Responses of the experts to Question 2 in the first round of email discussion of the consensus judgements Which of the four distributions do you think it would be most reasonable for the rational impartial observer to choose? Expert F did not have time to respond in this round of consultation

	Tick one
Consensus #1 (shown in Figures G.1 and G.4)	D
Consensus #2 (shown in Figures G.2 and G.4)	C, E
Truncated version of Consensus #3 (shown in Figure G.3)
Untruncated version of Consensus #3 (shown in Figure G.4)	A

Expert A proposal for alternative consensus distribution

‘In my opinion, the sources of uncertainty should have a slight predominance towards the upper end. A gamma distribution also contributes to avoid an abrupt lower end relative to the beta distribution. It is important not to go beyond the limits agreed (0.5 and 2.0)’.

Expert C proposal for alternative consensus distribution:

‘In order to account for the multiplicative factor being more than 1.7, more probability has been now given to multiplicative factor values towards upper bound (2)’.

Expert D proposal for alternative consensus distribution:

‘I do not fully agree that the overall impact of the uncertainties tends to the upper bound. The influence of U26 was not fully discussed, and it is my opinion that this could also play a role in the MOET calculation although the influence of this uncertainty is minor.’

‘With this said, I would prefer if the probability for the true value to be less than 1 is set at 50% instead of 45% (the other values remain the same). Assuming a scaled beta distribution, this would result in a median of 1.02 and 95% probability interval of 0.7–1.475’.

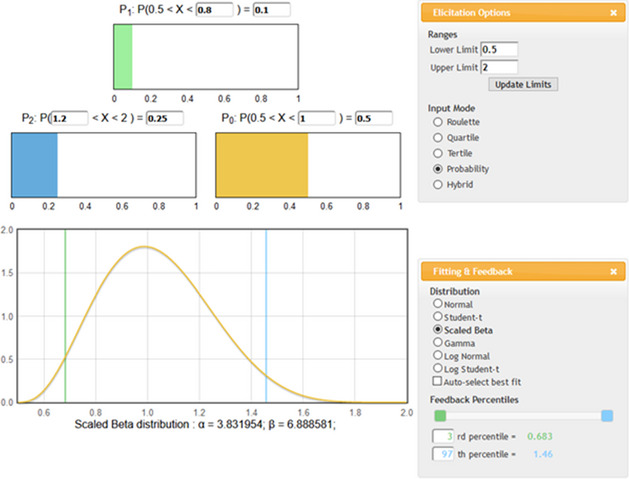
Second round of email consultation on Friday 9 October

In this round, experts were asked for responses to the alternative distributions proposed by experts A, C and D, plus the second distribution from the preceding round. The second distribution from the preceding round was included because it was more favourably assessed than the other 3 distributions in that round, and was also the preference of expert E who did not propose a new alternative, although one expert considered it unreasonable as a consensus distribution. This distribution is plotted together with the new proposals for comparison in Figure G.5.

Figure G.5.

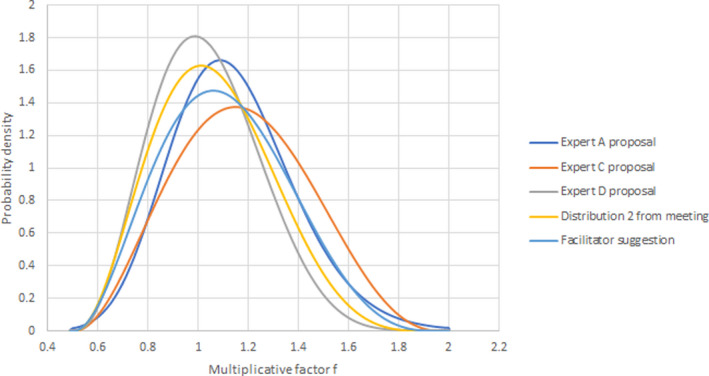
Alternative distributions proposed by experts A, C and D plus the second distribution from the preceding round of consultation and a suggestion from the Facilitator

Since there are still some differences between those four alternatives, a fifth distribution was added (also plotted in Figure 5G, in which the facilitator attempted to reflect the range of the other 4. This was done by taking the second distribution from the preceding round as a starting point and adjusting the distribution parameters (alpha and beta). In both the lower and upper tails, this additional distribution lies between the other four distributions (Figure G.5).

Median, 95% probability interval (which will be shown in the report of the CRA) and the probability that the multiplicative factor exceeds 1 are shown in Table G.3.

Table G.3.

Selected statistics for the five distributions in Figure G.5

Distribution	Median	95% probability interval			Prob. f > 1
Expert A proposal	1.123	0.713	–	1.668	70%
Expert C proposal	1.171	0.701	–	1.693	73%
Expert D proposal	1.022	0.673	–	1.475	54%
Distribution 2 from meeting	1.051	0.667	–	1.541	58%
Facilitator suggestion	1.097	0.673	–	1.615	64%

In this second round, the experts were asked to look carefully at the five alternative distributions, plotted together in Figure G.5 and the respective statistics in Table 3, and the explanations provided by Experts A, C and E for their proposals. They were asked to pay attention to the differences between the distributions and statistics and answer two further questions which are shown below. The facilitator requested that, when answering the questions, the experts try to stop thinking as an individual expert and think instead about what it would be reasonable for a rational impartial observer (e.g. the risk manager) to think, as this is the form of consensus that is sought in the Sheffield method for expert elicitation.

Question 1 (to be answered separately for each of the five distributions in the Table below): Do you consider that it would be reasonable or unreasonable for a rational impartial observer to take this distribution as their judgement for EKE Q2, having seen the evidence and individual judgements and heard the discussion? Please note that you are not restricted to choosing one distribution as ‘reasonable’. If you think two or more distributions are similar enough that they could all be reasonable choices for the rational impartial observer, you should enter them all as ‘reasonable’. Enter ‘unreasonable’ for any distributions you think it would be unreasonable for the rational impartial observer to choose, and briefly summarise your reasons for that.

Question 2: Which of the five distributions do you think it would be most reasonable for the rational impartial observer to choose? Please tick only one of the five options.

The facilitator informed the experts that, due to limitation of time, further alternative distributions were not being requested and, instead, a final consensus would be derived from the responses to these questions.

The responses provided by the experts to Questions 1 and 2 are shown in Tables G.4 and G.5 below.

Table G.4.

Responses of the experts to Question 1 in the second round of email discussion of the consensus judgements Do you consider that it would be reasonable or unreasonable for a rational impartial observer to take this distribution as their judgement for EKE Q2, having seen the evidence and individual judgements and heard the discussion?

Distribution	Enter ‘Reasonable’ or ‘Unreasonable’	If unreasonable, please indicate what aspects of the distribution seem unreasonable to you?
Expert A proposal	A: Reasonable C: Reasonable D: Unreasonable E: Unreasonable F: Unreasonable	D: Although I personally do not agree with the tendency of the true MOET value going towards the upper end, I can accept that the rational impartial observer might find this slight tendency plausible. However, I do not agree with the P0 value of 0.252 (i.e. 74.8% probability of the true value higher than 1). As my opinion for the consensus, the P0 value should be higher. E: Based on the discussion probability > 1 70% seems unreasonable. F: High probability towards values above 1,2
Expert C proposal	A: Reasonable C: Reasonable D: Unreasonable E: Unreasonable F: Unreasonable	D: It is not clear from the proposal of Expert C as to why higher probability for the upper bound of the multiplicative factor (MF) should be given. Also, I do not agree with the P0 value of 0.25 and P2 value of 0.45. This latter puts too much emphasis that the true MOET value is likely to be higher than 20%, which I do not agree as a consensus. E: Based on the discussion probability > 1 70% seems unreasonable. F: Even higher probability towards values above 1.2
Expert D proposal	A: Reasonable C: Reasonable D: Reasonable E: Unreasonable F: Unreasonable	E: 95% bound up to 1.475 seems unreasonable. F: Very high probability for values below 1
Distribution 2 from the meeting	A: Reasonable C: Reasonable D: Reasonable E: Reasonable F: Reasonable	E: I cannot find any strong reason to say this is unreasonable. To me is similar enough to the facilitator suggestion.
Facilitator suggestion	A: Reasonable C: Reasonable D: Reasonable E: Reasonable F: Reasonable	E: I cannot find any strong reason to say this is unreasonable. To me is similar enough to the above. This could be a bit ‘better’ because the upper bounds go a bit upper. F: Preferable than distribution 2 since the upper bound is getting closer to 2 (than in distribution 2) and the median is approximately 10% higher than 1 which is reasonable based on the considered uncertainties (mainly U32).

Table G.5.

Responses of the experts to Question 2 in the second round of email discussion of the consensus judgements Which of the five distributions do you think it would be most reasonable for the rational impartial observer to choose?

	Tick one*
Expert A proposal	A1
Expert C proposal	A3
Expert D proposal	A5, D
Consensus distribution 2 from the meeting	A4
Facilitator suggestion	A2, C, E, F

^*Expert A gave a rank order (1st to 5th), which is shown here as A1–A5.

Other comments provided by experts on Question 1:

Expert A: I don't find strong arguments against any of the 5 distributions, so I cannot say that any of them is unreasonable because in my view there are not significant differences among them. Considering the uncertainties affecting toxicology any of them might be correct with minor differences. The most reasonable option indicated below is based particularly on the median value and on the tailing where a less abrupt lower end may be more reasonable. The remaining distributions have an abrupt lower end and a lower median value with the exception of expert C.

Expert C: All distributions are considered very close. More than one significant figure after the point does not reflect the remaining uncertainties. The magnitude of remaining uncertainty is not reasonably quantifiable in very narrow range of given probabilities.

Third round of email discussion

The facilitator drafted the following text summarising the responses received and proposing a final consensus based on those responses:

Two distributions (Consensus distribution 2 from the meeting and Facilitator suggestion) were considered by all the experts to be ‘reasonable’ for a rational impartial observer to take as their judgement for EKE Q2, after seeing the evidence, individual judgements and discussion. The other three distributions in the final round were considered ‘unreasonable’ for a rational impartial observer by either two or three experts, and therefore are not suitable to be reported as consensus distributions.

The two distributions that were considered ‘reasonable’ by all experts could potentially be adopted as consensus distributions, since all experts considered them as reasonable choices for the rational impartial observer. Of these two distributions, the Facilitator suggestion was the first preference for three experts (and second preference for another), while the other was not the first preference for any expert.

It was therefore proposed to take the ‘Facilitator suggestion’ distribution as the consensus distribution for use in the next stage of the uncertainty analysis. If time permits, a sensitivity analysis will be conducted to check the difference between using the Facilitator suggestion or the Consensus distribution 2 from the meeting.

The facilitator sent the updated record including the responses to the second round of consultation and the draft summary and consensus proposal to the experts on 13 October together with the following final questions:

• If you are not content with the proposal to take the Facilitator suggestion as the consensus distribution for the next stage of the uncertainty analysis, please email the facilitator and include your alternative proposal.

• The facilitator recognises that it would have been better to refer to this as ‘Additional option’ rather than ‘Facilitator suggestion’. If any expert feels they would have given a different assessment if it had been referred to as ‘Additional option’, please edit your responses above in track changes and email to the facilitator.

Three experts (A, C and D) replied to these questions. All three were content that the ‘Facilitator suggestion’ distribution should be taken as the final consensus. None of them said they would have given a different assessment if this had been referred to as ‘Additional option’ rather than ‘Facilitator suggestion’. Expert A commented that when all the distributions are plotted together the differences are too small to be relevant and expected that sensitivity analysis would confirm this. Expert D commented that the ‘Facilitator suggestion’ is reasonable as a consensus because it covers the relatively narrow range of upper‐lower intervals from all of the experts and it was the ‘middle ground’ among the judgements discussed. Experts E and F did not reply, and it was concluded that they were content with the proposed conclusion on the consensus distribution.

Conclusion on consensus distribution for toxicology uncertainties

The experts accepted as their consensus the distribution shown in Figure G.6, which was considered reasonable by all of them (Table G.4) and received more preferences than the other distributions considered in the second round of email consultation (Table G.5). The distribution shown in Figure G.7 was also considered reasonable by all the experts but was less preferred. The next stage of the uncertainty analysis will therefore take the distribution in Figure G.6 as the primary basis for further assessment but will also include a sensitivity analysis to assess how different the results would be with the distribution in Figure G.7.

Figure G.6.

Consensus distribution for the multiplicative factor by which the median MOET at the 99.9th percentile of exposure for chronic inhibition of erythrocyte AChE in the Italian adult population at Tier II P99.9 would change if all the identified sources of uncertainty relating to toxicology were resolved. This is a Scaled beta distribution with alpha = 3.15, beta = 4.6 and limits of 0.5 and 2. The red line shows f = 1, i.e. no change in MOET

Figure G.7.

Alternative distribution, which was also considered reasonable by the experts, though less preferred than the distribution in Figure G.6 and will be used in sensitivity analysis. This is a Scaled beta distribution with alpha = 3.39 and beta 5.60, beta = 4.6 and limits of 0.5 and 2. The red line shows f = 1, i.e. no change in MOET

Appendix H – Record of judgements and reasoning for EKE Q2 on uncertainties related to exposure

1.

Record during the expert MS teams meeting on 29 September 2020

The text of EKE Q2 is shown in the footnote for reference.36

The facilitator explained the concept of consensus used in the Sheffield method for EKE (EFSA, 2014a,b,c): although their personal opinions may differ, the experts are asked to agree on what it would be reasonable for a rational impartial observer (‘RIO’) to think, having seen the evidence and individual judgements and heard the discussion. To develop such a consensus for EKE Q2 on exposure, the experts discussed the relative magnitudes of the individual uncertainties and how they would combine, taking into account the identified dependencies between them, i.e. positively, negatively dependent or independent uncertainties.

The experts considered that uncertainty U20 on missing processing factors has the highest impact on the MOET and, therefore, the most influence on the probability distribution for the multiplicative factor.

Experts agreed that it is almost impossible for more than two uncertainties to occur at the same time at the lower or upper end of the range of plausible values if they are independent.

It was expected that there would be a degree of negative dependency between U15 on unspecific residue definition and U20 on processing factor18 and between U11 on occurrence data variability and U20.37

Sources of uncertainties with consensus judgements (./.) not influencing the MOET in one direction only, would be expected to have a minor impact and cancel one another out.

The experts judged that the sources of uncertainty most impacting the upper end of the distribution were U20 on the missing processing factors (major contributor) and U34 on the adequacy of the OIM model (minor contributor). During the session on EKE Q1, U20 was the only uncertainty identified to have a multiplicative factor on the MOET exceeding 2 and possibly reaching 10 for the Italian adult population (sensitivity analysis C). Regarding U34, the experts judged it unlikely that the MOET would increase by much more than 20% if this source of uncertainty was resolved and assessed the impact of U34 as a multiplicative factor of approximately 1.5.

A value between 7 and 8 was assigned as a more plausible upper bound for U20; when this value (7–8) is combined with the impact of U34 (~ 1.5), a higher upper bound of 10 would seem reasonable although with a very low probability. The above consensus assumes that U20 and U15 are independent which explains why the combined impact of U20 and U34 was judged to be less than the product of their individual upper bounds (i.e. less than 7–8 × 1.5).

Uncertainties U15 on unspecific residue definition (./+) and U11 on occurrence data variability (./+) would not be expected to further increase the MOET due to the negative dependency of U15 and U11 with U20.

Uncertainties U17 (assumption on the use frequency) and U19 (assumption of residues in drinking water) with consensus judgements (./.) would rather impact the upper bound of the distribution but would not be expected to further increase the MOET due to their competing effect with sources of uncertainty with multiplicative factors below 1.

Based on these considerations, the experts judged that the combined impact of the exposure uncertainties may be expected to increase the MOET up to a maximum factor of 10 and concluded for an upper plausible bound of 10 but with a very low probability.

The experts judged that the sources of uncertainty most impacting the lower end of the distribution were U20 on missing processing factors (drives the distribution to the right, see discussion on U20 below), U1 on commodities not included in the assessment, U4 on consumption data sampling variability and U8 on the unaccounted contribution of metabolites and degradation products. The source of uncertainty U5 (representativeness of consumption data) also contributes towards the lower end, but to a lesser extent.

The consensus in the EKE Q1 session per source of uncertainty was that if U1, U4 or U8 were resolved, they would not decrease the MOET by much more than 20% each. Therefore, when combined, U1, U4 and U8 would be expected to decrease the MOET by no more than a multiplicative factor of 0.5, considering that no dependencies were identified between them.

As U20 on missing processing factors is the uncertainty with the highest impact on the MOET and, therefore, the one driving the whole distribution, the impact of U1, U4 and U8 on the MOET would be expected to be mitigated by U20. This triggered discussion on the most plausible value for the lower bound of the multiplicative factor assignable to U20 which was estimated to be 4. Multiplication of this lower bound for U20 with 0.5 for combined impact of U1, U4 and U8 resulted in an indicative lower bound of 2 for the probability distribution.

Based on these considerations and in order to cover virtually 100% probability, the experts agreed on an even lower plausible bound of 1.5 but with a very low probability.

Further judgements were elicited using the probability method (Oakley and O'Hagan, 2016), which is described in EFSA (2014a,b,c) as the fixed interval method. In this method, the experts are asked to judge the probability that the quantity of interest lies between a specified value and the lower or upper bound. For this purpose, the facilitator chose three values in different parts of the plausible range, favouring regions where differences between the individual distributions were most marked. Specifically, the experts were asked the three questions shown below. For each question, a range of answers was discussed, and a provisional consensus was agreed. Distributions were fitted to the provisional consensus probabilities using the MATCH tool and displayed for review by the experts.

• What is the probability for the true value to be lower than 2? Provisional consensus: 5%

• What is the probability for the true value to be lower than 4? Provisional consensus: 25%

• What is the probability for the true value to be higher than 7? Provisional consensus: 10%.

The best fitting of the distributions available in MATCH for these provisional judgements was the Normal, but the experts preferred the Scaled Beta, with a 90% probability interval of 2.81–7.54 and a median of 5.00. This distribution is shown in Figure H.1.

Figure H.1.

First provisional consensus distribution. Scaled Beta with median of 5.00 and 90% probability interval of 2.81–7.54

The experts were asked whether they considered this distribution appropriate to represent their consensus judgement on EKE Q2, i.e. what it would be reasonable for a rational impartial observer (RIO) to think, having seen the evidence and individual judgements and heard the discussion. There was a general agreement that the median value of the provisional distribution (Figure H.1) should move to the right to better reflect the large impact of processing. As the probability for values to be lower than 2 was found difficult to judge, the facilitator asked the experts to elicit judgements on other values. The probability for values to be lower than 4 was reconsidered and a lower percentage of 20% was still judged plausible. The probability for values to be lower than 6 was considered to be 55% with a probability of 10% for values to be between 7 and 10. Therefore, the following input values were inserted in the MATCH tool:

• Probability for the true value to be lower than 4: 20%;

• Probability for the true value to be lower than 6: 55%;

• Probability for the true value to be larger than 7: 10%.

The experts viewed the fitted distributions in MATCH and agreed on the Scaled Beta, which has a 90% probability interval of 3.15–7.97 and a median of 5.50.⁴ This distribution is shown in Figure H.2. The experts agreed that this graph reflects a reasonable distribution of RIO for the multiplicative factor by which the median MOET at the 99.9th percentile of exposure for chronic inhibition of erythrocyte AChE in the Italian adult population at Tier II P99.9 would change if all the identified sources of uncertainty relating to exposure were resolved.

Figure H.2.

Consensus distribution. Scaled Beta with median of 5.50 and 90% probability interval of 3.15–7.97

Appendix I – Record of judgements and reasoning on EKE Q3 on the impact of dependencies and population differences

1.

Record during the expert MS Teams meeting on 20 November 2020

The text of EKE Q3 is shown in the footnote for reference.38

The facilitator explained the concept of consensus used in the Sheffield method for EKE (EFSA, 2014a,b,c): although their personal opinions may differ, the experts are asked to agree on what would be reasonable for a rational impartial observer (‘RIO’) to think, having seen the evidence and individual judgements and heard the discussion. To elicit individual and consensus judgements on EKE Q3 for each population, the approximate probability scale (APS) (EFSA Scientific Committee, 2018a,b) was used.

In their judgements, the experts considered the following information:

• Boxplots for the P99.9 of the MOET distributions for the 10 populations as calculated by Monte Carlo simulations combining output from the Tier II exposure model with the probability distributions of the multiplicative factors for the exposure and toxicology uncertainties as derived under EKE Q2 for the Italian adults (Figure 6 and Table 21).

• The estimated probability that the P99.9 of the MOET per population is below the regulatory threshold of 100 assuming that all exposure and toxicological uncertainties are independent (rho = 0) and, in all populations, the same as for the Italian adult population (Table 21).

• The estimated probability that the P99.9 of the MOET per population is below 100 assuming different degrees of dependency between uncertainties on exposure and toxicology (rho = –1.00, –0.75, –0.50, ‐0.25, +0.25, +0.50, +0.75 and +1.00) (see Table 22).

For the assessment of differences between populations, the following additional information was also considered by the experts:

• The sources of uncertainty identified to have different impact between populations in response to EKE Q1b.

• The results from the sensitivity analyses concerning sources of uncertainty having varying impacts on populations. In these sensitivity analyses, the impact in the different populations is reflected by the intensity of change of the median estimate of the MOET (Table 16). To facilitate the comparison between populations, ratios of the median P99.9 of the MOET obtained in the sensitivity test to the respective median MOET in the Tier II calculation were also provided to the experts in a separate table (Table I.1).

• In addition, the experts considered results from calculations showing how shifting the MOET distributions (i.e. as obtained by combining the output of the Tier II exposure model with the probability distributions of the multiplicative factors of the MOET for the exposure and toxicology uncertainties derived under EKE Q2 for the Italian adults), up or down (to allow for differences in uncertainty compared to the Italian population) would affect the % probability of MOET < 100 for each population assuming different degrees of dependency. These calculations assume that the whole distribution is shifted up or down by the same amount and the width of the distribution remains unchanged (see Tables I.2–I.10 on ‘other populations’).

Table I.10.

Shifting of the MOET distribution for the UK toddler population assuming different degrees of dependency

rho	group	×0.1	×0.2	×0.33	×0.5	×0.66	=	×1.5	×2	×3	×5	×10
–1	UK.T	100.0%	59.1%	16.4%	2.8%	0.1%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.75	UK.T	96.2%	56.0%	18.0%	3.5%	0.5%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.5	UK.T	93.9%	54.9%	19.6%	4.7%	1.1%	0.1%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.25	UK.T	92.3%	54.3%	20.9%	5.8%	1.7%	0.2%	0.0%	0.0%	0.0%	0.0%	0.0%
0	UK.T	91.0%	53.9%	21.9%	6.9%	2.3%	0.3%	0.0%	0.0%	0.0%	0.0%	0.0%
0.25	UK.T	89.8%	53.5%	22.9%	8.0%	3.0%	0.5%	0.0%	0.0%	0.0%	0.0%	0.0%
0.5	UK.T	88.8%	53.1%	23.7%	9.0%	3.7%	0.8%	0.1%	0.0%	0.0%	0.0%	0.0%
0.75	UK.T	87.9%	52.7%	24.4%	10.0%	4.4%	1.1%	0.2%	0.0%	0.0%	0.0%	0.0%
1	UK.T	86.9%	52.3%	25.1%	10.9%	5.2%	1.4%	0.2%	0.0%	0.0%	0.0%	0.0%

I.1. Results and discussion

Italian adults

To reach consensus on EKE Q3 for the Italian adult population, i.e. on the probability for the MOET < 100 at Tier II for the P99.9, the facilitator asked the experts to:

• Review the range of individual judgements and what degrees of dependency they correspond to

• Share opinions about which uncertainties might be dependent and to what degree

• Share reasons for individual judgements in the lower, mid and upper ranges of responses provided

The consensus could be one or more ranges from the Approximate Probability Scale (APS) or a custom range of probabilities, comprising parts of one or more APS ranges.

Discussion and rationale for consensus:

For all levels of possible dependency (even for rho = +1 or –1) between exposure and toxicological uncertainties, the probability for the MOET < 100 at Tier II for the P99.9 remained within 1–10% (see Table 22). The experts identified mainly negative dependencies between exposure and toxicological uncertainties.39 This is because (in most cases) resolving the toxicological uncertainties on the NOAEL of specific risk drivers (e.g. uncertainties related to dimethoate, monocrotophos, dichlorvos) would decrease the impact of the exposure uncertainties involving these specific risk drivers whereas resolving the exposure uncertainties (e.g. demonstrating that processing decreases the levels of dimethoate in olive oil, and that monocrotophos and dichorvos do not occur in drinking water) would decrease the impact of the toxicological uncertainties (see rationale on dependencies in footnote).

Overall, the experts agreed that the identified dependencies have a minor impact (rho between ± 0.25), because they concern only a fraction of all uncertainties. They might result in a slightly lower probability for an MOET < 100 when compared to the probability for a rho of 0 as most of these dependencies are negative. It was concluded that, for Italian adults, the abovementioned dependencies and any additional non‐identified ones, including possibility of dependencies between the EKE and model distributions, would result in a probability for an MOET < 100 within the range 1–10%.

The experts agreed a consensus range of 1–10% for the probability that the estimated 99.9th percentile of the MOET distribution for the Italian adult population being below 100 if all the uncertainties in the model, exposure assessment, hazard identification and characterisation and their dependencies were fully resolved and addressed in the modelling.

Other populations

To reach consensus on EKE Q3 for the other populations, i.e. on the probability for the P99.9 of the MOET per population to be below 100 at Tier II, the facilitator asked the experts, for each population, to:

• Review the range of their individual judgements

• Share opinions about whether and why the degree of dependency might be different to Italian adults

• Share opinions about whether and how the impacts of the uncertainties differ between this population and Italian adults, based on the sources of uncertainty with different impact between populations

• Share reasons for individual judgements in the lower, mid and upper ranges of responses provided

The consensus could be one or more ranges from the APS or a custom range of probabilities, comprising parts of one or more APS ranges.

Degree of dependency between exposure and toxicological uncertainties per population group

The group agreed that the rationales supporting the dependencies identified for the Italian population are also applicable to the other populations considering that the risk drivers are the same at the percentile of the exposure distribution of interest in all populations. Additionally, no evidence suggesting a different degree of dependency between exposure and toxicological uncertainties in the different populations was identified. Therefore, the experts judged that the estimated range of values for rho (–0.25 to +0.25) for the Italian population applies also for the other populations.

Sources of uncertainty with different impact between populations

Under EKE Q1, the following sources of uncertainty were identified to have an impact differing from the Italian population: U1 on excluded commodities (larger impact for other populations) (–/.), U4 on the consumption data sampling variability (larger or lower impact in other populations, depending on the number of subjects) (–/.), U11 on the occurrence data sampling variability (lower impact for populations with lower olive oil consumption) (./+), U15 driven by the omethoate/dimethoate ratio in olives (lower impact for populations with lower olive oil consumption) (./+), U19 on the assumption about pesticides in drinking water (larger impact in most of the other populations) (./.), U20 on missing processing factors (smaller impact in all other populations) (++/+++) and U34 on OIM model (larger or lower impact in other populations, depending on the number of days in the dietary survey) (./+).

The source of uncertainty responsible of the largest part of differences between populations is U20, because this is the source of uncertainty with the largest absolute impact, and there is a large difference in the ratios shown in Table I.1 between the Italian populations and all other populations. The next largest ratios in Table I.1 of Appendix I are for sensitivity analysis E, showing the impact of removing the olive sample with exceptionally high levels of dimethoate/omethoate residues (4.9 mg/kg). However, the experts judged that the impact of the olive sample with exceptionally high levels of dimethoate/omethoate residues is already covered by sensitivity analysis C (impact of missing processing factors, e.g. olives for oil production) and would be accounted twice if the impact suggested by sensitivity analysis E was added to that of sensitivity analysis C in their assessment. This is because the assumption that no residue is transferred to processed commodities (linked to sensitivity analysis C) has the same effect as assuming that only raw commodities free of residues are used to prepare processed food (meaning that the sample under consideration in sensitivity analysis E would be disregarded). Based on the above, experts did not consider sensitivity analysis E further in their judgements on EKE Q3.

Sources of uncertainty U4 (sampling variability of consumption data) and U34 (adequacy of the OIM model) were also considered as contributing, albeit to a lesser extent, to differences between populations, depending on the number of subjects (U4) and recorded days in the surveys (U34).

The differences between populations identified in response to EKE Q1b for other sources of uncertainty were not further considered due to the small magnitude of the individual impacts of these sources of uncertainty, and the lack of consistency in the direction of these impacts.

In first instance, to make their judgements on the probability for the P99.9 of the MOET to be below 100 at Tier II for each population, the experts compared the ratios reported for sensitivity analysis C in Table I.1 with the ratio reported for the Italian population. Based on this comparison, they discussed by what approximate factor the ‘model+experts’ boxplots shown in Figure 6 would shift if the distribution for exposure uncertainties was elicited taking account of the impact of missing processing factors in the considered population, instead of the Italian population. For example, Table I.1 shows that the impact of sensitivity analysis C on the P99.9 MOET for French children is about half as large as its impact on Italian adults. This suggests that the model+experts distribution for French children in Figure 6 would shift downwards (towards lower MOETs) by a factor of about 0.5 if the exposure uncertainty distribution had been elicited considering the impact of U20 for French children rather than Italian adults.

In a second step, the experts considered the potential impact of the approximate shift factor on the % probability of the MOET being below 100 for the considered population. This was assessed with the help of calculations showing how shifting the ‘model+experts’ distribution up or down by different factors affects the % probability of the MOET being below 100 for each population and different degrees of dependency (rho). For French children, a shift factor of 0.5 combined with the expected degree of dependency (rho of –0.25 to +0.25) would increase the probability of the P99.9 MOET being below 100 from about 5% to about 27% (see Table I.2 in appendix I). This provides an indication of the differing impact of uncertainty about missing processing factors (U20) on the assessment for French children.

In the third and final step, the experts discussed the additional impact of differences in uncertainties U4 and/or U34 in the considered population, when compared with the Italian adult population. For example, the experts noted that the dietary survey for French children had fewer subjects (482 vs. 2,313 for the Italian adults, U4), which would tend to decrease the shift factor indicated by the previous step, and a longer survey duration (7 days vs. 3 days for the Italian adults), which would also tend to decrease the shift factor. Taking into account their uncertainty about the relative magnitudes of these impacts and how they would combine, the experts agreed a consensus range of 10‐50% for the probability of the estimated 99.9th percentile of the MOET distribution for the French children population being below 100 if all the uncertainties in the model, exposure assessment, hazard identification and characterisation and their dependencies were fully resolved and addressed in the modelling.

These three steps were repeated for all the remaining populations.

French children

Sensitivity analysis C (U20; Table I.1) suggests that the French children population is less sensitive than the Italian adult population to missing processing factors. Accounting this difference would shift the MOET distribution down by a factor of about 0.5 which, based on Table I.2, indicates a probability for the MOET to be lower than 100 of 27.3% (rho = 0) and within a range from 26.9%–27.7% (assuming that rho ranges between –0.25 and +0.25).

Considering in addition that:

• The French survey has less subjects (482) than the Italian one (2313). The impact of U4 is therefore larger for French children than for Italian adults, and accounting this difference would also tend to shift the MOET distribution towards lower values (because solving U4 decreases the MOET);

• The data set on the diet of French children is derived from a 7‐day survey vs. a 3‐day survey for Italian adults. The impact of U34 is therefore lower for French children than for Italian adults, and accounting this difference would also tend to shift the MOET distribution towards lower values (because solving U34 increases the MOET),

the experts agreed that for French children the impact of U20 combined with U4 and U34 would result in a probability range for a MOET < 100 between 10 and 50%. The upper bound of the probability is driven by the additional impact of differences in uncertainties U4 and U34.

The experts agreed a consensus range of 10–50% for the probability that the estimated 99.9th percentile of the MOET distribution for the French children population being below 100 if all the uncertainties in the model, exposure assessment, hazard identification and characterisation and their dependencies were fully resolved and addressed in the modelling.

Dutch toddlers

Sensitivity analysis C (U20; Table I.1) suggests that the Dutch toddler population is less sensitive than the Italian adult population to missing processing factors. Accounting this difference would shift the MOET distribution down by a factor of about 0.4 which, based on Table I.3, indicates a probability for the MOET to be lower than 100 between 14.5% and 36.6% (rho = 0).

Table I.3.

Shifting of the MOET distribution for the Dutch toddler population assuming different degrees of dependency

rho	group	×0.1	×0.2	×0.33	×0.5	×0.66	=	×1.5	×2	×3	×5	×10
–1	NL.T	100.0%	71.9%	35.4%	8.6%	1.7%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.75	NL.T	99.8%	73.3%	35.7%	10.2%	2.5%	0.1%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.5	NL.T	99.3%	72.9%	35.9%	11.8%	3.6%	0.3%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.25	NL.T	98.7%	72.1%	36.2%	13.3%	4.7%	0.6%	0.0%	0.0%	0.0%	0.0%	0.0%
0	NL.T	98.0%	71.2%	36.6%	14.5%	5.8%	1.0%	0.1%	0.0%	0.0%	0.0%	0.0%
0.25	NL.T	97.2%	70.2%	37.0%	15.8%	6.9%	1.5%	0.2%	0.0%	0.0%	0.0%	0.0%
0.5	NL.T	96.5%	69.3%	37.3%	16.8%	7.9%	2.0%	0.3%	0.1%	0.0%	0.0%	0.0%
0.75	NL.T	95.7%	68.4%	37.6%	17.8%	8.9%	2.6%	0.5%	0.1%	0.0%	0.0%	0.0%
1	NL.T	95.0%	67.5%	37.8%	18.7%	9.8%	3.1%	0.7%	0.2%	0.0%	0.0%	0.0%

Considering in addition that:

• The Dutch survey has less subjects (322) than the Italian one (2313). The impact of U4 is therefore larger for Dutch toddlers than for Italian adults, and accounting this difference would also tend to shift the MOET distribution towards lower values (because solving U4 decreases the MOET);

• The data set on the diet of Dutch toddlers is derived from a 2‐day survey vs. a 3‐day survey for Italian adults. The impact of U34 is therefore larger for Dutch toddlers than for Italian adults, and accounting this difference would tend to shift the MOET distribution, in this case, towards higher values (because solving U34 increases the MOET),

the experts agreed that for Dutch toddlers the impact of U20 combined with U4 and U34 would result in a probability range for a MOET < 100 between 10% and 33%. The highest probability would not be expected to exceed 33% despite the additional contribution of differences in uncertainty U4, because this contribution is mitigated by the differences in U34 and because toddlers are assumed to consume more or less the same types of food every day.

The experts agreed a consensus range of 10–33% for the probability that the estimated 99.9th percentile of the MOET distribution for the Dutch toddler population being below 100 if all the uncertainties in the model, exposure assessment, hazard identification and characterisation and their dependencies were fully resolved and addressed in the modelling.

German adults

Sensitivity analysis C (U20; Table I.1) suggests that the German adult population is less sensitive than the Italian adult population to missing processing factors. Accounting this difference would shift the MOET distribution down by a factor of about 0.33 which, based on Table I.4, indicates a probability for the MOET to be lower than 100 of 10.8% (rho = 0) and within a range from 9.9% to 11.7% (assuming that rho ranges between –0.25 and +0.25).

Table I.4.

Shifting of the MOET distribution for the German adult population assuming different degrees of dependency

rho	group	×0.1	×0.2	×0.33	×0.5	×0.66	=	×1.5	×2	×3	×5	×10
–1	DE.A	70.2%	28.4%	5.4%	0.4%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.75	DE.A	72.8%	30.9%	7.9%	1.1%	0.1%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.5	DE.A	73.4%	31.8%	8.9%	1.7%	0.3%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.25	DE.A	73.2%	32.4%	9.9%	2.3%	0.6%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
0	DE.A	72.7%	32.8%	10.8%	2.9%	0.9%	0.1%	0.0%	0.0%	0.0%	0.0%	0.0%
0.25	DE.A	72.0%	33.2%	11.7%	3.6%	1.2%	0.2%	0.0%	0.0%	0.0%	0.0%	0.0%
0.5	DE.A	71.4%	33.6%	12.6%	4.2%	1.6%	0.3%	0.0%	0.0%	0.0%	0.0%	0.0%
0.75	DE.A	70.7%	33.9%	13.4%	4.9%	2.0%	0.4%	0.1%	0.0%	0.0%	0.0%	0.0%
1	DE.A	70.0%	34.2%	14.2%	5.5%	2.4%	0.6%	0.1%	0.0%	0.0%	0.0%	0.0%

Considering in addition that:

• The German survey has more subjects (10,419) than the Italian one (2,313). The impact of U4 is therefore smaller for German adults than for Italian adults, and accounting this difference would therefore tend to shift the MOET distribution towards higher values (because solving U4 decreases the MOET);

• The data set on the diet of German adults is derived from a 2‐day survey vs. a 3‐day survey for Italian adults. The impact of U34 is therefore larger for German adults than for Italian adults, and accounting this difference would also tend to shift the MOET distribution towards higher values (because solving U34 increases the MOET),

the experts agreed that for German adults the impact of U20 combined with U4 and U34 would result in a probability range for a MOET < 100 between 5% and 15%. It was considered unlikely that this probability would be > 15%, and this is why the experts chose an upper range value of up to 15% instead of the 33% anticipated by the approximate probability scale.

The experts agreed a consensus range of 5–15% for the probability that the estimated 99.9th percentile of the MOET distribution for the German adult population being below 100 if all the uncertainties in the model, exposure assessment, hazard identification and characterisation and their dependencies were fully resolved and addressed in the modelling

Belgian adults

Sensitivity analysis C (U20; Table I.1) suggests that the Belgian adult population is less sensitive than the Italian adult population to missing processing factors. Accounting this difference would shift the MOET distribution down by a factor of about 0.33 which, based on Table I.5, indicates a probability for the MOET to be lower than 100 of 10.3% (rho = 0) and within a range from 9.6% to 11.1% (assuming that rho ranges between –0.25 and +0.25).

Table I.5.

Shifting of the MOET distribution for the Belgian adult population assuming different degrees of dependency

rho	group	×0.1	×0.2	×0.33	×0.5	×0.66	=	×1.5	×2	×3	×5	×10
–1	BE.A	66.1%	23.3%	8.4%	0.7%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.75	BE.A	64.9%	26.6%	8.5%	1.5%	0.2%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.5	BE.A	64.8%	28.0%	8.9%	2.1%	0.4%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.25	BE.A	64.7%	28.7%	9.6%	2.6%	0.7%	0.1%	0.0%	0.0%	0.0%	0.0%	0.0%
0	BE.A	64.5%	29.3%	10.3%	3.1%	1.0%	0.1%	0.0%	0.0%	0.0%	0.0%	0.0%
0.25	BE.A	64.3%	29.7%	11.1%	3.7%	1.4%	0.2%	0.0%	0.0%	0.0%	0.0%	0.0%
0.5	BE.A	63.9%	30.1%	11.8%	4.2%	1.7%	0.3%	0.0%	0.0%	0.0%	0.0%	0.0%
0.75	BE.A	63.5%	30.4%	12.5%	4.7%	2.0%	0.5%	0.1%	0.0%	0.0%	0.0%	0.0%
1	BE.A	63.1%	30.7%	13.1%	5.3%	2.4%	0.6%	0.1%	0.0%	0.0%	0.0%	0.0%

Considering in addition that:

• The Belgian survey has less subjects (1,356) than the Italian one (2,313). The impact of U4 is therefore larger for Belgian adults than for Italian adults, and accounting this difference would therefore also tend to shift the MOET distribution towards lower values (because solving U4 decreases the MOET);

• The data set on the diet of Belgian adults is derived from a 2‐day survey vs. a 3‐day survey for Italian adults. The impact of U34 is therefore larger for Belgian adults than for Italian adults, and accounting this difference would tend to shift the MOET distribution towards higher values in this case (because solving U34 increases the MOET),

the experts agreed that for Belgian adults the impact of U20 combined with U4 and U34 would result in a probability range for a MOET < 100 between 5% and 15%. It was considered unlikely that this probability would be > 15%, and this is why the experts chose an upper range value of up to 15% instead of the 33% anticipated by the approximate probability scale.

The experts agreed a consensus range of 5–15% for the probability that the estimated 99.9th percentile of the MOET distribution for the Belgian adult population being below 100 if all the uncertainties in the model, exposure assessment, hazard identification and characterisation and their dependencies were fully resolved and addressed in the modelling.

Czech adults

Sensitivity analysis C (U20; Table I.1) suggests that the Czech adult population is less sensitive than the Italian adult population to missing processing factors. Accounting this difference would shift the MOET distribution down by a factor of about 0.5 which, based on Table I.6, indicates a probability for the MOET to be lower than 100 of 5.9% (rho = 0) and within a range from 5.0% to 6.7% (assuming that rho ranges between –0.25 and +0.25).

Table I.6.

Shifting of the MOET distribution for the Czech adult population assuming different degrees of dependency

rho	group	×0.1	×0.2	×0.33	×0.5	×0.66	=	×1.5	×2	×3	×5	×10
–1	CZ.A	66.4%	45.8%	15.7%	3.2%	0.1%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.75	CZ.A	68.0%	44.7%	15.0%	3.3%	0.6%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.5	CZ.A	69.4%	43.9%	16.0%	4.2%	1.1%	0.1%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.25	CZ.A	70.3%	43.3%	16.9%	5.0%	1.5%	0.2%	0.0%	0.0%	0.0%	0.0%	0.0%
0	CZ.A	70.7%	42.7%	17.7%	5.9%	2.1%	0.3%	0.0%	0.0%	0.0%	0.0%	0.0%
0.25	CZ.A	71.0%	42.2%	18.5%	6.7%	2.6%	0.5%	0.1%	0.0%	0.0%	0.0%	0.0%
0.5	CZ.A	71.0%	41.9%	19.1%	7.5%	3.2%	0.7%	0.1%	0.0%	0.0%	0.0%	0.0%
0.75	CZ.A	70.9%	41.6%	19.6%	8.2%	3.7%	0.9%	0.2%	0.0%	0.0%	0.0%	0.0%
1	CZ.A	70.7%	41.4%	20.1%	8.9%	4.3%	1.2%	0.2%	0.0%	0.0%	0.0%	0.0%

Considering in addition that:

• The Czech survey has less subjects (1,666) than the Italian one (2,313). The impact of U4 is therefore larger for Czech adults than for Italian adults, and accounting this difference would therefore also tend to shift the MOET distribution towards lower values (because solving U4 decreases the MOET);

• The data set on the diet of Czech adults is derived from a 2‐day survey vs. a 3‐day survey for Italian adults. The impact of U34 is therefore larger for Czech adults than for Italian adults, and accounting this difference would tend to shift the MOET distribution towards higher values in this case (because solving U34 increases the MOET),

the experts agreed that for Czech adults the impact of U20 combined with U4 and U34 would result in a probability range for a MOET < 100 between 1 and 10%.

The experts agreed a consensus range of 1–10% for the probability that the estimated 99.9th percentile of the MOET distribution for the Czech adult population being below 100 if all the uncertainties in the model, exposure assessment, hazard identification and characterisation and their dependencies were fully resolved and addressed in the modelling.

Dutch children

Sensitivity analysis C (U20; Table I.1) suggests that the Dutch Children population is less sensitive than the Italian adult population to missing processing factors. Accounting this difference would shift the MOET distribution down by a factor of about 0.25 which, based on Table I.7, indicates a probability for the MOET to be lower than 100 of 13.5% (when MOET shifts by a factor of 0.33) to 44.3% (when MOET shifts by a factor of 0.2) (rho = 0).

Table I.7.

Shifting of the MOET distribution for the Dutch children population assuming different degrees of dependency

rho	group	×0.1	×0.2	×0.33	×0.5	×0.66	=	×1.5	×2	×3	×5	×10
–1	NL.C	99.5%	44.2%	5.6%	0.4%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.75	NL.C	97.1%	43.0%	8.6%	1.1%	0.1%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.5	NL.C	94.7%	43.6%	10.4%	1.7%	0.3%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.25	NL.C	92.7%	44.0%	12.0%	2.5%	0.6%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
0	NL.C	90.9%	44.3%	13.5%	3.3%	0.9%	0.1%	0.0%	0.0%	0.0%	0.0%	0.0%
0.25	NL.C	89.3%	44.5%	14.9%	4.2%	1.3%	0.2%	0.0%	0.0%	0.0%	0.0%	0.0%
0.5	NL.C	87.9%	44.6%	16.2%	5.1%	1.8%	0.3%	0.0%	0.0%	0.0%	0.0%	0.0%
0.75	NL.C	86.5%	44.6%	17.3%	6.0%	2.3%	0.4%	0.0%	0.0%	0.0%	0.0%	0.0%
1	NL.C	85.2%	44.6%	18.4%	6.9%	2.9%	0.6%	0.1%	0.0%	0.0%	0.0%	0.0%

Considering in addition that:

• The Dutch survey has less subjects (957) than the Italian one (2,313). The impact of U4 is therefore larger for Dutch children than for Italian adults, and accounting this difference would therefore also tend to shift the MOET distribution towards lower values (because solving U4 decreases the MOET);

• The data set on the diet of Dutch children is derived from a 2‐day survey vs. a 3‐day survey for Italian adults. The impact of U34 is therefore larger for Dutch children than for Italian adults, and accounting this difference would tend to shift the MOET distribution towards higher values in this case (because solving U34 increases the MOET),

the experts agreed that for Dutch children the impact of U20 combined with U4 and U34 would result in a probability range for a MOET < 100 between 10 and 33%.

The experts agreed a consensus range of 10–33% for the probability that the estimated 99.9th percentile of the MOET distribution for the Dutch children population being below 100 if all the uncertainties in the model, exposure assessment, hazard identification and characterisation and their dependencies were fully resolved and addressed in the modelling.

Bulgarian children

Sensitivity analysis C (U20; Table I.1) suggests that the Bulgarian children population is less sensitive than the Italian adult population to missing processing factors. Accounting this difference would shift the MOET distribution down by a factor of about 0.3 which, based on Table I.8, indicates a probability for the MOET to be lower than 100 of 20% (when MOET shifts by a factor of 0.33) to 50.1% (when MOET shifts by a factor of 0.2) (rho = 0).

Table I.8.

Shifting of the MOET distribution for the Bulgarian children population assuming different degrees of dependency

rho	group	×0.1	×0.2	×0.33	×0.5	×0.66	=	×1.5	×2	×3	×5	×10
–1	BG.C	100.0%	53.0%	14.0%	2.8%	0.1%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.75	BG.C	95.3%	50.8%	16.4%	3.4%	0.6%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.5	BG.C	92.6%	50.4%	17.8%	4.4%	1.1%	0.1%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.25	BG.C	90.9%	50.2%	19.0%	5.4%	1.6%	0.2%	0.0%	0.0%	0.0%	0.0%	0.0%
0	BG.C	89.4%	50.1%	20.0%	6.4%	2.2%	0.3%	0.0%	0.0%	0.0%	0.0%	0.0%
0.25	BG.C	88.1%	49.9%	20.9%	7.3%	2.8%	0.5%	0.1%	0.0%	0.0%	0.0%	0.0%
0.5	BG.C	87.0%	49.8%	21.8%	8.3%	3.4%	0.7%	0.1%	0.0%	0.0%	0.0%	0.0%
0.75	BG.C	86.0%	49.6%	22.5%	9.2%	4.1%	1.0%	0.2%	0.0%	0.0%	0.0%	0.0%
1	BG.C	85.0%	49.4%	23.3%	10.0%	4.7%	1.3%	0.2%	0.0%	0.0%	0.0%	0.0%

Considering in addition that:

• The Bulgarian survey has less subjects (434) than the Italian one (2,313). The impact of U4 is therefore larger for Bulgarian children than for Italian adults, and accounting this difference would therefore also tend to shift the MOET distribution towards lower values (because solving U4 decreases the MOET);

• The data set on the diet of Bulgarian children is derived from a 2‐day survey vs. a 3‐day survey for Italian adults. The impact of U34 is therefore larger for Bulgarian children than for Italian adults, and accounting this difference would tend to shift the MOET distribution towards higher values in this case (because solving U34 increases the MOET),

the experts agreed that for Bulgarian children the impact of U20 combined with U4 and U34 would result in a probability range for a MOET < 100 between 10 and 33%.

The experts agreed a consensus range of 10–33% for the probability that the estimated 99.9th percentile of the MOET distribution for the Bulgarian children population being below 100 if all the uncertainties in the model, exposure assessment, hazard identification and characterisation and their dependencies were fully resolved and addressed in the modelling.

Danish toddlers

Sensitivity analysis C (U20; Table I.1) suggests that the Danish toddler population is less sensitive than the Italian adult population to missing processing factors. Accounting this difference would shift the MOET distribution down by a factor of about 0.25 which, based on Table I.9, indicates a probability for the MOET to be lower than 100 of 14.7% (when MOET shifts by a factor of 0.33) to 44.5% (when MOET shifts by a factor of 0.2) (rho = 0).

Table I.9.

Shifting of the MOET distribution for the Danish toddler population assuming different degrees of dependency

rho	group	×0.1	×0.2	×0.33	×0.5	×0.66	=	×1.5	×2	×3	×5	×10
–1	DK.T	100.0%	38.9%	7.9%	1.4%	0.2%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.75	DK.T	97.7%	42.0%	10.5%	2.2%	0.5%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.5	DK.T	95.3%	43.3%	12.0%	2.9%	0.8%	0.1%	0.0%	0.0%	0.0%	0.0%	0.0%
–0.25	DK.T	93.2%	44.0%	13.4%	3.6%	1.1%	0.1%	0.0%	0.0%	0.0%	0.0%	0.0%
0	DK.T	91.4%	44.5%	14.7%	4.3%	1.5%	0.2%	0.0%	0.0%	0.0%	0.0%	0.0%
0.25	DK.T	89.7%	44.8%	16.0%	5.2%	1.9%	0.4%	0.0%	0.0%	0.0%	0.0%	0.0%
0.5	DK.T	88.1%	45.0%	17.2%	6.0%	2.4%	0.5%	0.1%	0.0%	0.0%	0.0%	0.0%
0.75	DK.T	86.7%	45.1%	18.3%	6.9%	2.9%	0.7%	0.1%	0.0%	0.0%	0.0%	0.0%
1	DK.T	85.3%	45.1%	19.3%	7.7%	3.4%	0.9%	0.2%	0.0%	0.0%	0.0%	0.0%

Considering in addition that:

• The Danish survey has less subjects (917) than the Italian one (2,313). The impact of U4 is therefore larger for Danish toddlers than for Italian adults, and accounting this difference would therefore also tend to shift the MOET distribution towards lower values (because solving U4 decreases the MOET);

• The data set on the diet of Danish toddlers is derived from a 7‐day survey vs. a 3‐day survey for Italian adults. The impact of U34 is therefore lower for Danish toddlers than for Italian adults, and accounting this difference would also tend to shift the MOET distribution towards lower values (because solving U34 increases the MOET),

the experts agreed that for Danish toddlers the impact of U20 combined with U4 and U34 would result in a probability range for a MOET < 100 between 10 and 40%.

The experts agreed a consensus range of 10–40% for the probability that the estimated 99.9th percentile of the MOET distribution for the Danish toddler population being below 100 if all the uncertainties in the model, exposure assessment, hazard identification and characterisation and their dependencies were fully resolved and addressed in the modelling.

UK toddlers

Sensitivity analysis C (U20; Table I.1) suggests that the UK toddler population is less sensitive than the Italian adult population to missing processing factors. Accounting this difference would shift the MOET distribution down by a factor of about 0.33 which, based on Table I10, indicates a probability for the MOET to be lower than 100 of 21.9% (rho = 0) and within a range from 20.9% to 22.9% (assuming that rho ranges between –0.25 and +0.25).

Considering in addition that:

• The UK survey has less subjects (1,314) than the Italian one (2,313). The impact of U4 is therefore larger for UK toddlers than for Italian adults, and accounting this difference would therefore also tend to shift the MOET distribution towards lower values (because solving U4 decreases the MOET);

• The data set on the diet of UK toddlers is derived from a 4‐day survey vs. a 3‐day survey for Italian adults. The impact of U34 is therefore slightly smaller for UK toddlers than for Italian adults, and accounting this difference would also tend to shift the MOET distribution towards lower values (because solving U34 increases the MOET),

the experts agreed that for UK toddlers the impact of U20 combined with U4 and U34 would result in a probability range for a MOET < 100 between 10% and 33%.

The experts agreed a consensus range of 10–33% for the probability that the estimated 99.9th percentile of the MOET distribution for the UK toddler population being below 100 if all the uncertainties in the model, exposure assessment, hazard identification and characterisation and their dependencies were fully resolved and addressed in the modelling.

Annex A – Input data for the exposure assessment of CAG‐NCN

1.

Annex A can be found online on EFSA's Knowledge Junction: https://doi.org/10.5281/zenodo.4436115

Annex B – Output data for the Tier I exposure assessment of CAG‐NCN

1.

Annex B can be found online on EFSA's Knowledge Junction: https://doi.org/10.5281/zenodo.4436115

Annex C – Output data for the Tier II exposure assessment of CAG‐NCN

1.

Annex C can be found online on EFSA's Knowledge Junction: https://doi.org/10.5281/zenodo.4436115

Suggested citation: EFSA (European Food Safety Authority) , Anastassiadou M, Choi J, Coja T, Dujardin B, Hart A, Hernandez‐Jerrez AF, Jarrah S, Lostia A, Machera K, Mangas I, Mienne A, Schepens M, Widenfalk A and Mohimont L, 2021. Scientific report on the cumulative dietary risk assessment of chronic acetylcholinesterase inhibition by residues of pesticides. EFSA Journal 2021;19(2):6392, 151 pp. 10.2903/j.efsa.2021.6392