Skip to main content
PMC home page
Systematic Biology logoLink to Systematic Biology
. 2020 Aug 4;70(2):307–321. doi: 10.1093/sysbio/syaa063

Genomic Characterization and Curation of UCEs Improves Species Tree Reconstruction

Matthew H Van Dam 1,2,✉, James B Henderson 2, Lauren Esposito 1,2, Michelle Trautwein 1,2
Editor: Brian Wiegmann
PMCID: PMC7875437  PMID: 32750133

Abstract

Ultraconserved genomic elements (UCEs) are generally treated as independent loci in phylogenetic analyses. The identification pipeline for UCE probes does not require prior knowledge of genetic identity, only selecting loci that are highly conserved, single copy, without repeats, and of a particular length. Here, we characterized UCEs from 11 phylogenomic studies across the animal tree of life, from birds to marine invertebrates. We found that within vertebrate lineages, UCEs are mostly intronic and intergenic, while in invertebrates, the majority are in exons. We then curated four different sets of UCE markers by genomic category from five different studies including: birds, mammals, fish, Hymenoptera (ants, wasps, and bees), and Coleoptera (beetles). Of genes captured by UCEs, we find that many are represented by two or more UCEs, corresponding to nonoverlapping segments of a single gene. We considered these UCEs to be nonindependent, merged all UCEs that belonged to a particular gene, constructed gene and species trees, and then evaluated the subsequent effect of merging cogenic UCEs on gene and species tree reconstruction. Average bootstrap support for merged UCE gene trees was significantly improved across all data sets apparently driven by the increase in loci length. Additionally, we conducted simulations and found that gene trees generated from merged UCEs were more accurate than those generated by unmerged UCEs. As loci length improves gene tree accuracy, this modest degree of UCE characterization and curation impacts downstream analyses and demonstrates the advantages of incorporating basic genomic characterizations into phylogenomic analyses. [Anchored hybrid enrichment; ants; ASTRAL; bait capture; carangimorph; Coleoptera; conserved nonexonic elements; exon capture; gene tree; Hymenoptera; mammal; phylogenomic markers; songbird; species tree; ultraconserved elements; weevils.]

Phylogenomic methods rely on sampling orthologous loci from the genomes of nonmodel organisms and then using these loci to estimate evolutionary relationships. Commonly used sampling strategies include ultraconserved genomic elements (UCEs) (sensu Faircloth et al. 2012), anchored hybrid enrichment (Lemmon et al. 2012), exon capture (Bi et al. 2013), transcriptome sequencing, along with homologous k-mer blocks (Sanderson et al. 2017), and conserved nonexonic elements (CNEEs; Edwards et al. 2017). While UCEs and anchored hybrid enrichment markers are generally identified without regard to what genomic class they fall into, transcriptome sequencing, exon capture (Bi et al. 2013), and CNEEs (Edwards et al. 2017) each select for a specific class of marker as their names entail.

UCEs are among the most widely used types of phylogenomic markers and have been used to resolve both higher level and population level phylogenetic relationships (McCormack et al. 2012; Winker et al. 2018). They are found throughout the animal tree of life, including Cnidaria, flat worms (Platyhelminthes), arachnids, insects, as well as in birds and mammals (Moyle et al. 2016; Esselstyn et al. 2017; Faircloth 2017; Locke et al. 2018; Quattrini et al. 2018; White and Braun 2019). UCEs are advantageous because of their ease of capture from nonmodel organisms, and they (and other probe-based approaches) can provide access to loci from degraded DNA of museum specimens (Bi et al. 2013; Blaimer et al. 2016; McCormack et al. 2016; Van Dam et al. 2017). The process of identifying UCEs is independent of knowing their genetic identity and instead simply selects loci that are highly conserved, single copy, lack repeats (and having a user-defined GC content), and are of a particular length (typically 160 bp) (Faircloth et al. 2012; Faircloth 2017).

Independent of phylogenetics, a large volume of research has been conducted to identify the function of UCEs in the genome and towards understanding why they are highly conserved over many millions of years (Dermitzakis et al. 2003; Bejerano et al. 2004; Sandelin et al. 2004; Woolfe et al. 2004; Vavouri et al. 2007; McCole et al. 2014, 2018; Kushawah and Mishra 2017). The sets of UCEs used in phylogenomics have not been formally categorized even at a fundamental level (intronic, exonic, and/or intergenic) (but see Jarvis et al. 2014). The genomic identity of phylogenetic markers affects how data is treated in analyses (e.g., models of nucleotide substitution rate based on codon position) as well as their potential phylogenetic informativeness (Gilbert et al. 2018). Generally, UCEs are considered primarily noncoding entities and are treated as such in phylogenetic analyses (but see Jarvis et al. 2014; Branstetter et al. 2017b; Bossert et al. 2018).

Like many different classes of phylogenomic markers, UCEs have been treated as anonymous, independent loci. A marker’s independence is relevant to subsequent analyses, particularly in multispecies coalescent tree estimation. Treating nonindependent samples as independent violates the assumption of statistical independence between samples which could bias results by giving more representation to particular gene tree topologies (see Szöllõsi et al. 2015).

Here, we examined 11 sets of UCEs that have been used for phylogenomic estimation across the tree of life and identified the genetic class of each UCE as intronic, exonic, or intergenic. We compared these characterizations between organismal classes using five previously published UCE studies from mammals, birds, fish, and insects (Hymenoptera: wasps, ants, and bees, and Coleoptera: beetles). Next, we examined the phylogenetic utility of intergenic and genic UCEs across taxa. Our data exploration revealed that many genes are actually represented by multiple nonoverlapping UCEs (referred to throughout as cogenic UCEs in accordance with Scornavacca and Galtier [2017]). We then concatenated (referred to herein as merged) all cogenic UCEs and reconstructed gene and species trees to examine how merging affected average bootstrap support (ABS) values. Finally, we performed a simulation study to test the effects of merging cogenic UCEs on phylogenetic accuracy of species trees.

Methods

Genomic Characterization of UCEs across the Tree of Life

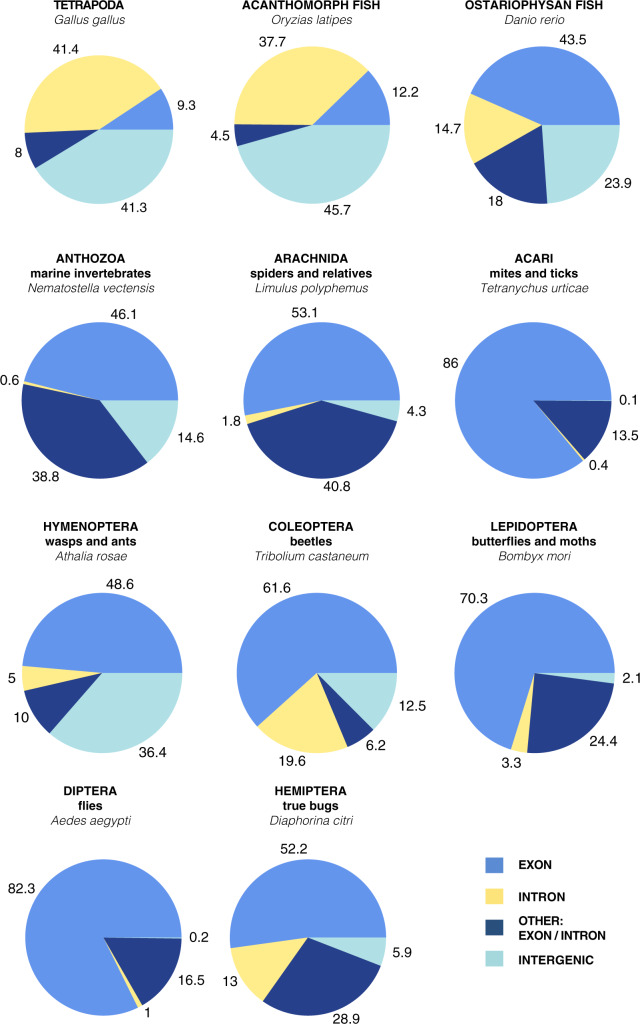
First, we characterized the genomic identity of 11 sets of UCEs representing diverse regions of the animal tree of life, from mammals and birds to marine invertebrates (Fig. 2) by using blastn (version 2.9.0, Camacho et al. 2008) to compare the base taxon’s probes of each taxon set back to their base genome. For the tetrapod and acanthomorph fish UCE sets, we used the genome from which the baits were designed (the source of the flanking DNA used to buffer the conserved regions to appropriate length). In these two cases, probes were identified by performing an all to all alignment (Faircloth et al. 2012). We used the “base” genome of the chicken (Gallus gallus) for tetrapods and medaka (Oryzias latipes) for the acanthomorph fish (Faircloth et al. 2012; Faircloth et al. 2013; Alfaro et al. 2018). For all 11 UCE sets, we downloaded each original probe set, identified and extracted the base-genome’s (or assigned base-genome’s) specific probes from the total probe fasta file and generated a new fasta containing only the base-genome’s probes. Using blastn, we aligned the probes against the base-genome using default settings (Camacho et al. 2008). The resulting m8 file from the blastn search was then filtered in Inline graphic (R Core Team 2019, for code see Supplementary Material.) for 100% matches over the 120 bp length of the probe.

Figure 2.

Figure 2.

Open in a new tab

Characterization of 11 UCE probe sets according to the annotated base genome for each set. UCEs are in four different categories: intergenic (not in a gene), exon, intron, and other. The “other” category includes UCEs that span an intron and exon or an exon and an intergenic region.

To identify a UCE’s position within a genome, we identified the UCE’s scaffold and/or chromosome and position from the m8 file. This information allowed us to search the base-genome’s GFF file to identify overlap between each UCE and particular gene features. The positions of UCEs that fell within introns were inferred from start and stop positions of exons within gene regions. The NCBI records for the specific genomes and GFF files are listed in Supplementary Material S1, file 8 available on dryad.

Focal Taxa UCE Characterization and Curation

Data acquisition and alignment

To examine how UCE characterization can affect phylogenetic inference, we used UCE data from five phylogenetic studies using four UCE bait sets representing: weevils (Coleoptera UCE baits: Faircloth 2017; Van Dam et al. 2017), ants (Hymenoptera UCE baits-V2: Branstetter et al. 2017b), mammals (Tetrapod 5K-UCE baits: Faircloth et al. 2012; Esselstyn et al. 2017), songbirds (Tetrapod 5K-UCE baits: Faircloth et al. 2012; Moyle et al. 2016), and carangimorph fish (acanthomorph fish UCE baits: Faircloth et al. 2013; Harrington et al. 2016; Alfaro et al. 2018), see file 11 for table of UCE counts by taxon. Using the original data from these studies, we followed their assembly and matrix construction procedures largely using the PHYLUCE pipeline (Faircloth et al. 2012; Faircloth 2016).

For three of the data sets (fish, ants, and weevils), aligned fasta sequences were already available. For birds and mammals, we downloaded raw reads and followed the procedures of the previous authors to create our aligned matrices. In the case of the mammal data set (Esselstyn et al. 2017), following the authors protocols, we extracted UCE loci from the genomes and combined these with the scaffolds made from raw reads.

For all alignments, we used the 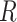Inline graphic package ips (Heibl 2008) and removed any ragged ends with the function “trimEnds” having a minimum of four taxa present in the alignment and filled any gap character “Inline graphic” with “n” before the first and last nonambiguous nucleotide.

Curation of Genic UCEs

After determining which UCEs were found within genes from our focal UCE sets, we then identified genes that contain multiple UCEs (cogenic UCEs) (Table 1). Cogenic UCEs were merged into a single alignment per gene using scripts we developed. We then curated two sets of UCEs for each taxon group: one that included all UCEs, called Unmerged, and another that included all merged cogenic UCEs 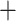Inline graphic all remaining UCEs called Merged.

Table 1.

Number of single and cogenic UCEs found in each data set

UCE set Single UCE per gene Co-genic UCEs
Coleoptera 528 497
Hymenoptera 1024 624
Tetrapods 736 2222
Fish 276 438
Open in a new tab

This count includes both exonic and intronic UCEs.

Calculation of Distance between UCEs for Gallus gallus

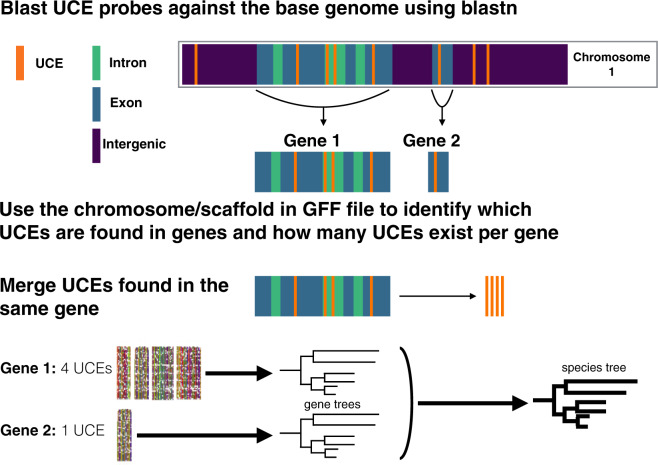
The distances between cogenic UCEs (e.g., Fig. 1, see “Gene 1”) were often found to be thousands to tens of thousands of base pairs long. Merging distant regions of the same gene (which naturally happens in the case of transcriptome sequencing, i.e., mRNA) increases the chance of merging regions with different recombination histories which may impact species tree analyses (but see Lanier and Knowles 2012). To understand more about where UCEs occur in a genome in relation to one another, we used the Gallus gallus genome (the base-genome of the tetrapod-5k-UCE probe set) and a custom R script to explore the distance (in base pairs) between cogenic UCEs as well as the distance to the nearest UCE upstream and downstream from a set of cogenic UCEs (referred to herein as nearest neighbor UCEs). For each set of cogenic UCEs, we used the results of the blastn analyses described above to identify where a particular UCE locus was found (position, gene, and scaffold/chromosome). We then calculated the distance between cogenic UCEs, the start of one to the start of the next. Because the m8 file (results from blastn) is already ordered by position along a particular chromosome/scaffold, to find the nearest neighbor distances we simply found the distance upstream and downstream from the UCEs that bookended a particular set of cogenic UCEs.

Figure 1.

Figure 1.

Open in a new tab

General workflow used to identify and merge cogenic UCEs for gene tree and species tree reconstruction.

Species Tree Analyses of Curated UCEs

Species tree analyses of Merged versus Unmerged UCEs

To evaluate the effects of merging cogenic UCEs, we reconstructed species trees based on Unmerged and Merged UCEs for weevils, ants, mammals, songbirds, and carangimorph fish. For clarity, our 1) Unmerged UCE set is based on standard protocols and considers each UCE locus as an independent unit (one UCE locus used to reconstruct a single gene tree) and 2) our Merged UCE set includes cogenic UCEs merged together to generate a single gene tree along with all remaining genic and intergenic UCEs each treated as a single locus.

For each Unmerged and Merged set of UCEs, we ran a maximum likelihood (ML) analysis in RAxML 8.2.11 (Stamatakis 2014) with the “–f a” options for a rapid bootstrap analysis (100 BS replicates) and search for best scoring tree. A General Time Reversible 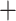Inline graphic gamma (GTRGAMMA) site rate substitution model was used for each locus. Next, we constructed two species trees per taxon group using ASTRAL-III (Zhang et al. 2018) with default parameters, first using the gene trees from all Unmerged UCE loci, and second, using the gene trees from the Merged data set. We ran ASTRAL with the default settings and performed multilocus bootstrapping (Seo 2008). In ASTRAL, we also calculated quartet support for each of our species trees, to measure the amount of gene tree conflict (Sayyari and Mirarab 2016).

Gene tree analyses of Genic versus Intergenic UCEs

As there are currently different maker types that target specific genomic classes, for example, CNEEs (Edwards et al. 2017), we examined whether there are differences in support for genic versus intergenic UCE loci. We reconstructed gene trees based on only Genic and only Intergenic UCEs for weevils, ants, mammals, songbirds, and carangimorph fish. Using 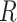Inline graphic/Unix scripts modified from Van Dam et al. (2017), we ran a maximum likelihood (ML) analysis in RAxML 8.2.11 (Stamatakis 2014) on each individual UCE locus with the “–f a” options for a rapid bootstrap analysis (100 bootstrap replicates [BS]) and the best-scoring tree. A General Time Reversible 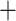Inline graphic gamma (GTRGAMMA) site rate substitution model was used for each locus.

Effects of Characterizing and Curating UCEs on Bootstrap Values and Topologies

ABS comparisons

To identify differences in bootstrap support between the gene trees generated from the Genic UCEs versus Intergenic UCEs and between the gene trees generated from the Unmerged cogenic UCEs versus the Merged cogenic UCEs, we calculated ABS values for each individual gene tree (see Supplementary Material available on Dryad for R and Python code). ABS ABS were calculated using a modified R script from (Borowiec et al. 2015). While nonparametric bootstrapping is not a measure of absolute of gene tree estimation error (GTEE), there is a loose correlation (Efron et al. 1996; Holmes 2003, 2005; Susko 2009; Molloy and Warnow 2018).

T-tests and GLM

We performed two-sample 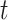Inline graphic-tests in 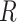Inline graphic (using the base-R 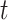Inline graphic-test function) between the means of the ABS from the Merged cogenic and the means of the ABS from the Unmerged cogenic gene tree sets for all taxa to determine if merging had a statistically significant effect on ABS values. We then calculated Cohen’s d statistic in 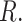Inline graphic We calculated the same summary statistics for the Genic versus Intergenic gene trees as well. Next, we investigated the effect of locus length, genomic categorization, and merged or unmerged status on ABS value using a generalized linear model (GLM). We used a GLM (Gaussian family) with AICc model selection to justify whether adding the extra interaction terms was warranted. All GLMs supported the inclusion of adding interactions between gene type and loci length.

Comparison of merged and unmerged topologies and shapes: species trees

To assess the impact of our curation on resulting species tree topologies, we used the 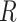Inline graphic package Phangorn (Schliep 2011) to calculate the Robinson–Foulds distance (RF-dist) (Robinson and Foulds 1981), a tree distance metric that relies on topology. In addition, we calculated the KF-distance (KF-dist) (Kuhner and Felsenstein 1994) which measures the sum of squares differences between individual branch lengths. The distances were calculated between the Merged and Unmerged species trees for each focal taxon.

Comparison of tree topologies and shapes: gene trees

For assessing differences between the gene trees from the Merged and Unmerged UCE sets, we used two different tree shape metrics from their Laplacian spectrum calculated in the R package RPANDA (Lewitus and Morlon 2015; Morlon et al. 2016). We selected the skewness (asymmetry) of the spectral density profile and the peakedness (peak height) the largest y-axis value of the spectral density profile (Morlon et al. 2016). Normalized, each of these metrics gives a separate description of tree shape: skewness detects the relative timing between branching events (lower values indicate more branching near the stem of the tree whereas higher values indicate more branching near the tips) and peakedness detects ladderization (lower peak height values indicate a more even tree shape, whereas higher values indicate a more ladderized tree shape). We also used RF-dist to compare tree to tree distance among our Merged and Unmerged UCE gene tree sets.

Assessing Species Tree Accuracy for Merged and Unmerged UCEs

We conducted a simulation study to determine whether merging cogenic UCEs improves the accuracy of inferred species trees. We outline below our procedures based on Mirarab and Warnow (2015) with slight modifications.

Simulation methods for gene trees and species trees

As in Mirarab and Warnow (2015) and Molloy and Warnow (2018), we used SimPhy (Mallo et al. 2016) to simulate 100 species trees and their constituent gene trees, each with 50 taxa, under three different levels of incomplete lineage sorting (see Supplementary Material S1 file 5 available on Dryad, for specific simulation parameters). For each species tree, we simulated 354 gene trees, or roughly the number of genes with cogenic UCEs that we identified in the Tetrapod UCE data set. Sequences were simulated from these gene trees using Indelible (Fletcher and Yang, 2009). 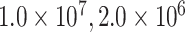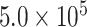We performed 100 replicates each with 354 genes, a speciation rate of 1e-07, with a tree depth of Inline graphic, and Inline graphic generations, and a global population size of 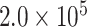Inline graphic, as in Mirarab and Warnow (2015). Sequence lengths were designated to reflect the lengths of genes harboring cogenic UCEs found in the chicken genome (the “base” genome for the Tetrapod UCE set). Specifically, lengths were drawn from lognormal distributions with the log mean controlled by drawing uniformly between 12.102 and 12.045, which corresponds to lengths between 170,270 and 180,262.4 bp.

After creating the 354 sets of loci for each of the 100 species trees, we subdivided each of these loci to represent our Unmerged data set. Here, we selected five subloci from each of the larger loci. These subloci were uniform in length, each 1000 bp, and were randomly sampled across the larger loci’s length. This resulted in 1770 total alignments per species tree. We then merged these subloci as in our Merged data set, resulting in 354 merged loci per species tree. Additionally, we investigated the effect of loci length by merging loci iteratively—for example, merge subloci 1–2, 1–3, 1–4, and 1–5 (see Supplementary Material S1, file 4 available on Dryad).

Along with testing the accuracy of species trees based on Merged and Unmerged loci, we also tested the effects of randomly merging loci. By building species trees based on randomly merging loci (Randomly Merged), we were able to examine whether species tree accuracy improvement based on the Merged loci set were simply due to longer loci or shared genealogy. To generate Randomly Merged loci sets, we randomly merged, without replacement, loci from the Unmerged data set such that each Randomly Merged set was composed of 5 different subloci from the 354 loci for a particular species tree (see Supplementary Material S1, file 6 available on Dryad).

Gene trees were reconstructed using RAxML under a GTRGAMMA site rate substitution model for each locus. To estimate species trees we used ASTRAL-MP (Yin et al. 2019) to take advantage of AVX2-CPU and GPU processors so that the analyses would finish in a timely manner. We then compared the resulting Robinson–Foulds tree distance between our Merged, Unmerged, and Randomly Merged species trees to their associated simulated “true” species trees.

Results

Genomic Characterization of UCEs across the Tree of Life

For the 11 UCE sets, roughly 51% 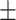Inline graphic 16.5 95%CI of UCEs were found within exonic regions of the genome (Fig. 2; Supplementary Material S1, file 10 available on Dryad for table of counts). The percentage of UCEs located within exons varied greatly between organismal classes; for the Insecta UCEs, 82.3% (Diptera) and 48.6% (Hymenoptera) were found in exons, whereas in Vertebrata, the exon percentage varied between 9.3% (Tetrapoda) and 43.5% (Ostariophysan fish). This large difference between invertebrate and vertebrate exonic UCEs may be due to differences in the UCE-pipelines (all-to-all vs. all-to-base-taxon alignment). The vertebrate sets tended to comprise mostly noncoding regions compared to the invertebrates. The percentages of UCEs found in intergenic regions of the genome varied between 0.1% (Acari: mites/ticks) and 45.7% (Acanthomorpha fish). There were some UCEs that could not be placed within an intron, exon, or an intergenic region alone and were found to span any two of these regions (Fig. 2). For some UCE sets, these loci were a relatively major component (see Anthozoa UCE set Fig. 2). Also, within the tetrapod UCE probe set, we found several probes that could not be recovered or that were duplicated in more recent genome assemblies. Though this affected only a few probes, it demonstrates that probe recovery may change as genomic assemblies are improved or updated.

Focal Taxa UCE Characterization and Curation

For weevils, ants, mammals, songbirds, and carangimorph fish, we filtered the UCEs from genic regions of the genome and identified the genes that each UCE represented. We found that within Insecta, between 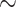Inline graphic52% (weevils) and 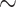Inline graphic62% (ants) of the UCEs are single UCEs in a gene (singleton UCEs) (Supplementary Material S1, file 9 available on Dryad). Almost as many UCEs belong to genes that are represented by more than one UCE (cogenic) (Supplementary Material S1, file 9 available on Dryad). For the tetrapod UCE set, there are roughly three times as many cogenic UCEs as there are singleton UCEs. Within the carangimorph fish UCE set, 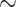Inline graphic63% of UCEs are singletons.

Calculation of Distance between UCEs for Gallus gallus

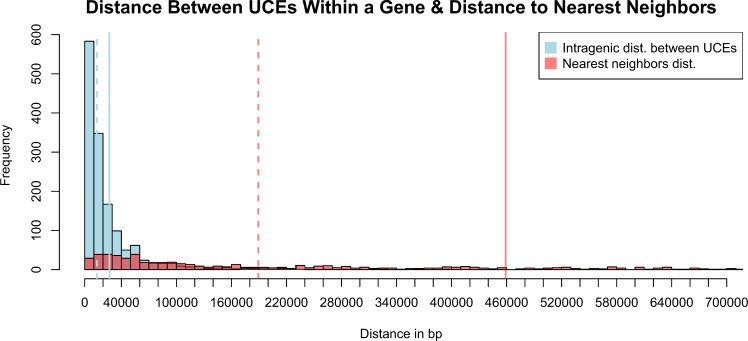
We found that the majority of UCEs within a gene were clumped rather than widely dispersed compared to their nearest neighbor distances (from the ends of one genic UCE set to the next outside of that gene) within 20 kb of one another, with an average of 27 kb, (median 13 kb). While some of the nearest neighbor UCEs were within 10 kb (see Fig. 3), most were much farther apart (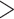Inline graphic100 kb with an average distance of 458 kb, median 189 kb).

Figure 3.

Figure 3.

Open in a new tab

Histogram of distances between UCEs in the 5k-Tetrapod UCE set. UCEs were mapped back to the chicken genome (blastn 100% matches of probe to base over 100% of the length of UCE probe). The distances between cogenic UCEs were then measured (light blue bars), followed by measuring the distance up and downstream from a genic set of UCEs to its nearest neighbor UCE (light red bars). Vertical solid lines indicate the mean distance between cogenic UCEs (blue) or mean distance to nearest neighboring UCE (red) for a cogenic set of UCEs, and dashed lines indicate the median. Both estimates are local to a UCE’s scaffold/chromosome.

Phylogenetic Analyses of Curated UCEs

Gene tree and species tree analyses of Merged cogenic UCEs versus Unmerged cogenic loci

Regarding gene tree analyses across all taxa for Merged cogenic versus their corresponding Unmerged cogenic UCEs, we found that the ABS per-gene tree was significantly higher for Merged cogenic UCEs than for their corresponding Unmerged cogenic UCEs (Table 2, Fig. 4) according to both the 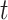Inline graphic-test and Cohen’s d. (Note: here we are comparing the merged cogenic UCEs and the same corresponding UCEs, yet unmerged.)

Table 2.

Merged cogenic and Unmerged cogenic gene tree support metrics

Mean ABS Mean ABS    
MERGED UNMERGED t-Test  
UCE set co-genic co-genic P value Cohen’s d
Weevils 54.54468 47.32786 0.0007544 0.6321575
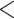Ants 57.67213 47.2517 Inline graphic2.2e–16 1.27434
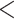Mammals 74.11935 55.07754 Inline graphic2.2e–16 1.748992
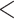Birds 46.13401 23.69862 Inline graphic2.2e–16 2.061103
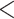Fish 46.30876 29.7862 Inline graphic2.2e–16 1.661292
Open in a new tab

Means of ABS values per-gene tree and 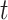Inline graphic-tests between gene trees that were merged when multiple UCEs were found within a single gene, and the same set of UCEs, unmerged and treated as single individual genes. Results show significant differences between Merged cogenic and Unmerged cogenic gene tree ABS values.

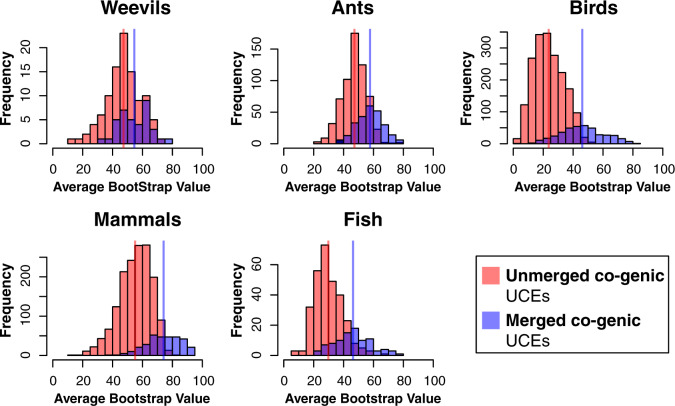
Figure 4.

Figure 4.

Open in a new tab

Histograms of ABS values of gene trees for Merged cogenic UCEs and corresponding Unmerged cogenic UCEs (excluding all intergenic and singleton UCEs). Red bars represent ABS values of gene trees for Unmerged cogenic UCEs, where each individual UCE provides a single gene tree estimate. The purple bars represent the ABS of gene trees generated by Merged cogenic UCEs, where all UCEs representing a particular gene were merged to estimate a single gene tree. Vertical lines represent the mean ABS of each UCE set. The distributions are significantly different between Unmerged cogenic and Merged cogenic treatments, with the distribution of Merged cogenic UCE gene tree ABS higher than Unmerged cogenic.

The species tree results from the analyses based on Merged UCEs (merged cogenic UCE gene trees + all remaining UCE gene trees) and from the analyses of the standard UCE treatment (Unmerged, one UCE locus - one gene tree) produced similar, but not identical, results in terms of ABS and topologies. ABS from the species tree analyses (Table 3) increase for the trees based on Merged UCEs (0.29–5.13 ABS support improvement) in all but the fish species tree which decreased by 0.38 ABS support. Average ASTRAL quartet support values, which measure the conflict between gene trees by node, improve in Merged species trees across all taxa. Regions where support was weak in the analyses based on standard UCE treatment remained weak with slight improvement in the Merged analyses; however, these two data treatments often resulted in different topologies. Comparisons of the topological differences of the remaining Unmerged versus Merged species trees can be found in Supplementary Material S1, file 3 available on Dryad.

Table 3.

Support for Unmerged and Merged species trees.

  ABS ABS Quartet Support Quartet Support
  UNMERGED MERGED UNMERGED MERGED
UCE set species tree species tree species tree species tree
Weevils 90.38 91.11 58.83 59.84
Ants 94.1 94.39 61.39 61.98
Mammals 93.65 96.23 69.29 71.05
Birds 86.1 91.23 50.56 52.65
Fish 89.73 89.35 55.4 56.62
Open in a new tab

Comparison between ASTRAL Unmerged and Merged UCE species trees, ABS and the average ASTRAL quartet support listed for the five focal taxa.

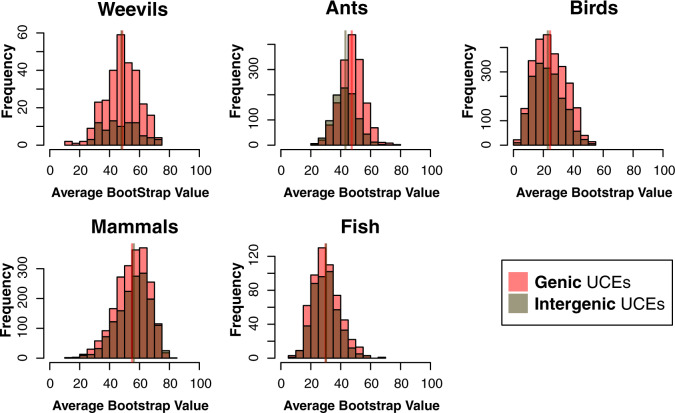
Gene Tree Analyses of Genic versus Intergenic UCEs

Our comparison of gene trees based on unmerged Genic UCE loci versus those found in the Intergenic regions shows little difference in ABS (Fig. 5; Table 4). In the weevil and fish data sets, there was no significant difference between the ABS of intergenic and unmerged genic gene trees, according to the 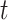Inline graphic-test and Cohen’s d. In the mammal set, there was significantly more support for the intergenic gene trees according to the 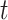Inline graphic-test but not Cohen’s d. There was significantly more support for the genic gene trees in the ant and bird data sets according to the 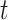Inline graphic-test (Table 4), but Cohen’s d indicates a small difference between the ant data sets and no difference in the bird data sets.

Figure 5.

Figure 5.

Open in a new tab

Histograms of ABS values for gene trees based on Intergenic UCEs and Genic UCEs. Vertical lines represent the mean of the ABS values for each set of gene trees (overlapping or adjacent in all but ants). Generally, the distribution of ABS values for gene trees based on Intergenic UCEs and Genic UCEs are largely similar.

Table 4.

Means of ABS values per-gene tree for intergenic and genic UCEs across taxa

  Mean ABS Mean ABS t-Test  
UCE set INTERGENIC GENIC P value Cohen’s d
Weevils 47.96106 48.45831 0.7336 0.1251066
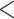Ants 43.17255 47.35368 Inline graphic2.2e–16 0.2306506
Mammals 56.19731 54.98488 0.0009687 0.0693968
Birds 22.98138 24.49267 8.02E–07 0.0304717
Fish 29.90741 30.18136 0.6196 0.0441318
Open in a new tab

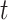Inline graphic-Tests indicate significant differences in the ant and bird data sets, yet Cohen’s d shows no differences in ant data sets and a weak difference in bird data sets.

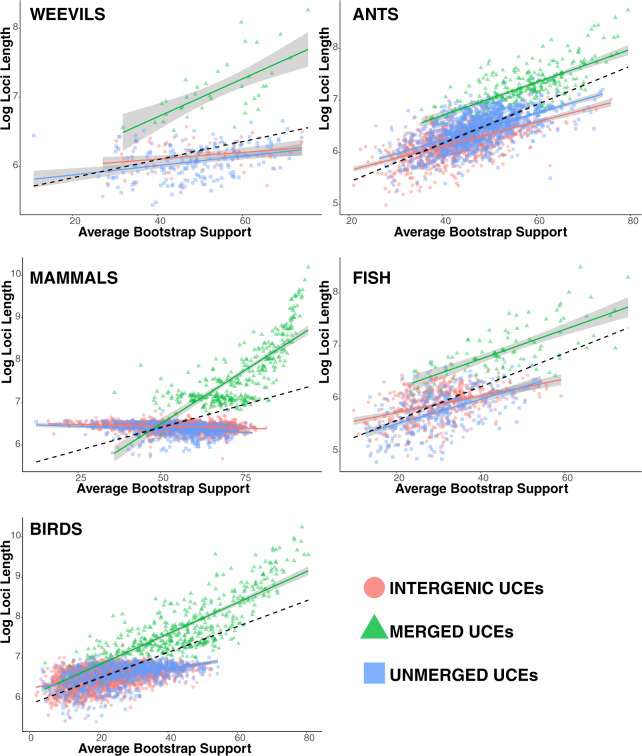
GLM

In general, ABS values were highly correlated with locus length (Fig. 6). Another factor influencing model fit of the GLM in all but the weevil data set was the merging of cogenic UCEs. In contrast, including unmerged UCEs as a category did not significantly improve model fit except in the ant dataset where it was slightly improved.

Figure 6.

Figure 6.

Open in a new tab

Linear regression of log UCE length versus ABS values of the corresponding gene tree. Categories include Intergenic (all UCEs from intergenic regions), Merged (all merged cogenic UCEs), and Unmerged (all remaining genic UCEs that were single representatives of single genes). The dashed line represents the correlation of ABS values versus log loci length for all gene trees. Gray regions around regression lines represent the 95% confidence interval. Generally, ABS values increase with increasing loci length.

Comparison of tree metrics

The RF-dist distances and KF-dist distances were computed for the Merged versus Unmerged species trees for all taxa (Supplementary Material S1, file 1 available on Dryad). For the Merged versus Unmerged species tree comparisons, RF-dist ranged from 0 (ants) to 20 (birds), and KF-dist ranged from 0.52 (fish) to 1.63 (birds).

Both the gene tree distributions of spectral density profiles and RF-dist show the same general pattern, the shape of the trees from the Merged data sets are less variable and more similar to one another than the shape of the trees from the more broadly distributed Unmerged data sets (Supplementary Material S1, file 1 available on Dryad). The pairwise RF-dist show that the gene trees from the Merged data sets tended to be only slightly more similar to one another than the gene trees from the Unmerged data sets. For the spectral density profiles, both skewness and peakedness (peak height) measures of gene tree shape show that on average the distribution of tree shape from the Merged data sets is less variable and the gene trees are more similar to one another, whereas their component Unmerged data set gene trees are more widely dispersed (Supplementary Material S1, file 1 available on Dryad). In addition, gene trees from the Merged versus the component Unmerged analyses occupy subtly different regions of tree shape—with most significantly shifted into another tree shape region (Supplementary Material S1, file 1 available on Dryad). These metrics largely indicate that the gene trees from the Merged analyses are converging on a narrower and slightly different region of tree shape.

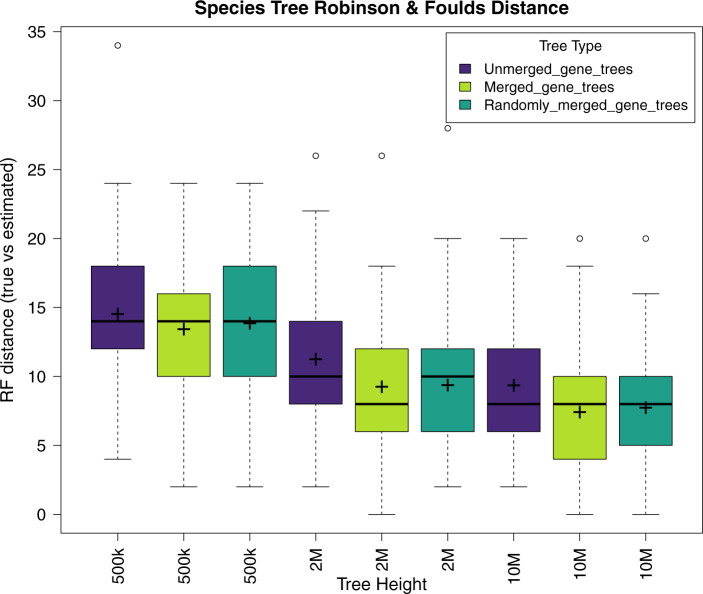
Assessing Species Tree Accuracy for Merged, Unmerged, and Randomly Merged loci

The simulation results favored the Merged loci over the Unmerged loci, for two of the three sets of simulations having significantly different RF-distances based on the 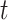Inline graphic-test (Table 5). The gene trees from the Merged loci and those from the Randomly Merged loci performed similarly, with the mean from the Merged data sets slightly closer to that of the true tree but this result was not statistically significant (Table 5, Fig. 7, see Supplementary Material S1, file 4 available on Dryad for individual trees). All data types performed better as tree height increased (Fig. 7).

Table 5.

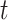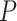Inline graphic-Test Inline graphic values of Robinson and Foulds distances from simulations

  t-Test P value t-Test P value t-Test P value
  RF-unmerged RF-merged versus RF-unmerged versus
Tree versus RF-randomly RF-randomly
height RF-merged merged merged
500k 0.1137 0.5376 0.3277
2M 0.0008226 0.8408 0.001885
10M 0.0007307 0.5542 0.005825
Open in a new tab

The RF-distance is produced by comparing the estimated tree to the true tree.

Figure 7.

Figure 7.

Open in a new tab

Box plot of Robinson and Foulds tree distance between the true species tree and the estimated species trees. The “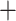Inline graphic” symbol represents the mean RF-distance, the black horizontal band represents the median.

Discussion

In the broad effort to resolve the tree of life, UCEs are increasingly used as phylogenomic markers across a wide range of organismal diversity. The affordability, bioinformatic accessibility, and phylogenetic utility of UCEs have brought them into common usage (Faircloth 2012). UCEs are generally treated as noncoding loci in phylogenomic analyses; however, here we characterized UCE sets from diverse organisms and we find that they belong to exonic, intronic, and intergenic regions. The identification of coding regions in UCEs has been mentioned in previous studies but not thoroughly explored (Jarvis et al. 2014; Branstetter et al. 2017b; Bossert and Danforth 2018).

It is important to note that our characterizations were based on recent annotations of the base genomes for each UCE set (see Supplementary Material S1, file 8 available on Dryad) and are largely dependent on the quality of these annotations. Our categorization of UCEs as exonic relied on gene annotations based on transcriptomes and, in many cases, algorithmic predictions. We expect that over time some of these UCE characterizations will change in accordance with updated annotations of the base genomes. In addition, as a gene’s isoforms are better documented, the category of both exonic and intronic UCEs will likely increase as well. The annotations for the base genomes for these UCE sets are in varying stages of completeness, yet in most cases they are more complete than the genome annotation for other taxa included in these studies. Because we assume UCE orthology between taxa within a single study, we expect that the genomic categorization of the base taxon’s UCEs also extends to the UCEs of other taxa (though equally complete and annotated genomes would be required to test this further).

UCEs were first described from the mouse and human genomes as noncoding regions (Dermitzakis et al. 2003), and thus this characterization has been carried over to all organisms, although it may be only partially true for vertebrates (Fig. 2). Interestingly, we find the genomic identity of UCEs appears to vary between invertebrates and vertebrates, with invertebrate UCEs being primarily coding and vertebrate UCEs being mostly noncoding (Fig. 2). An explanation for the contrast between the genomic characterization of vertebrate versus invertebrate UCEs is unclear. The taxa that the invertebrate and vertebrate UCE sets were designed across share common ancestry at a similar age of 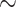Inline graphic300 Ma (Bethoux 2009; Smith and Marcot 2015), so the difference is not necessarily driven by the evolutionary age of the lineage. It is possible that the contrasting breakdown of invertebrate and vertebrate UCEs instead relates to the quality of the assembled genomes used in probe design, variation in the probe design pipeline used for vertebrate and invertebrate UCE sets (Faircloth et al. 2012; Faircloth 2017), or more interestingly, genome size and evolution.

Our results on the categorization of vertebrate UCEs are similar in composition to those reported from UCEs identified between mouse and human genomes (McCole et al. 2018). It has been suggested that UCEs play a role in genome stability because they are enriched in contact domains (McCole et al. 2018) and have been shown to exhibit elevated synteny (Dimitrieva and Bucher 2012). In mice and human genomes, boundary regions flanking contact domains, as well as loop anchors, are relatively depleted of UCEs; however, the UCEs that do occur in these regions are disproportionally exonic and may play a role in splicing (McCole et al. 2018). It is possible that invertebrate UCEs are more often pulled from boundary regions flanking contact domains and loop anchors and this could explain their high exonic content.

Genomic categorization is increasingly relevant in phylogenetic analyses. Studies based on coding regions often yield varying results based on how genes are analyzed (either as amino acids or by nucleotides or by only certain nucleotide positions) sometimes depending on the age of the radiation being assessed. UCEs have been treated as noncoding units even when combined with exons (but see Jarvis et al. 2014; Bossert et al. 2018). Yet, once coding regions from UCEs are characterized, subsequent analyses can consider how to perform analyses based on amino acids versus nucleotides and specific nucleotide positions.

When we considered genic UCEs, we not only found that many were exonic, but we also found that genic UCEs often occur in multiples within a single gene or are cogenic. Across taxa, cogenic UCEs were more numerous than UCEs that were single representatives of particular genes, except in the Hymenoptera UCE set. Although many UCEs are cogenic, they have been historically treated as independent loci in species tree analyses, thus over-representing particular gene trees in the summary species tree analysis. By merging all cogenic UCEs, we ameliorate the issue of nonindependence (at least in these obvious cases).

After analyzing the gene trees of the merged loci, we found that the ABS of Merged gene trees are significantly higher than these same loci Unmerged (treated as singletons) (Fig. 4; Table 2). Merged and Unmerged gene tree topologies varied as well, with the distribution of Merged gene tree topologies generally showing less variability and covering a narrower region of tree space according to spectral analyses that consider branch length and tree shape (evenness vs. ladderized) (Supplementary Material S1, file 1 available on Dryad). This suggests that the longer merged loci provide more decisive phylogenetic signal, a finding that is supported in phylogenetic literature (Faircloth et al. 2012; Portik et al. 2016; Branstetter et al. 2017b; Edwards et al. 2017; Van Dam et al. 2017; Karin et al. 2019). Also, the ABS of the Merged species trees improved across taxa (excluding the fish data set, Table 2), and topologies varied from species trees based on standard protocols (Supplementary Material S1, file 2 available on Dryad).

In general, we find that loci length is the predominate driver for the increased ABS based on merging UCEs by gene (Fig. 6). Given the relationship demonstrated between ABS and estimated gene tree accuracy (Liu et al. 2015; Molloy and Warnow 2018; Zhang et al. 2018), we expected that, broadly speaking, the merging of UCEs from the same genes into longer loci would result in more highly supported gene trees which would improve the accuracy of the resulting species tree. Our simulation results support this hypothesis. Our investigation of the accuracy between simulated sets of Merged (complete, long loci), Unmerged (subdivided loci, the length of standard UCEs), and Randomly Merged UCEs, favored the merged loci in terms of their ability to recover the correct species tree under varying levels of incomplete lineage sorting. However, the distributions between the Merged and Randomly Merged largely overlap (Fig. 7). Suggesting that perhaps the simulated species trees were not fully in the anomaly zone where multispecies coalescent methods are expected to outperform random concatenation. The simulations also indicate that the shared phylogenetic signal in the fewer Merged loci outperforms many more, shorter Unmerged loci, yet another instance of longer loci being more informative (Adams and Castoe 2019; Bayzid and Warnow 2013). Our simulation results suggest that using fewer long (more informative) loci is preferable to many shorter, less informative loci.

Our results are also in accord with other studies (Edwards et al. 2017; Adams and Castoe 2019) that identify that longer loci are preferable to shorter, less informative ones, despite that longer loci increase the probability of spanning recombination blocks. The effect of recombination on summary species tree methods has received recent attention (Lanier and Knowles 2012; Gatesy and Springer 2014; Edwards et al. 2016; Jennings 2017). A series of papers by Gatesy and Springer suggest that recombination misleads species tree methods (Gatesy and Springer 2014; Gatesy and Springer 2018), and thus the authors advocate for concatenation methods. Yet a simulation study by Lanier and Knowles (2012) found that recombination did not have an overtly negative influence on coalescent-based phylogenetic analyses under high levels of incomplete lineage sorting (although only relatively short loci were considered and see Gatesy and Springer 2018).

Another advocated approach to address the issue of recombination in species tree analyses has been to select loci that are separated by an intrachromosomal distance threshold (Jennings 2017) to satisfy the evolutionary independence assumption of coalescent-based phylogenetic methods (Arbogast et al. 2002). In some UCE studies, UCEs within 10 kb of each other were discarded to avoid physical linkage (Faircloth et al. 2013; Alfaro et al. 2018), a physical recombination distance estimated for fish. However, the accurate estimation of recombination blocks across diverse, nonmodel organisms is currently an unrealistic approach for phylogenomics considering that recombination rates, even across the genomes of individuals within species, show substantial heterogeneity (Comeron et al. 2012).

UCEs tend to be clustered in genes. For example, in the Gallus gallus genome, cogenic UCEs were generally clustered within a distance of 20 kb, while the distance between cogenic UCEs and their nearest neighbor outside of the gene were much longer (>400 kb on average). This clustering suggests that merging multiple sections of the same gene may not be problematic in regard to chromosomal distance as suggested by Springer and Gatesy (2018). Though 20 kb may be longer than some suggested recombination distances (Drosophila 12.5 kb: Jennings 2017), it is shorter than others (Tiger salamander 17 kb–1.7 Mb: Jennings 2017). Again, this highlights the ambiguity surrounding the determination of appropriate recombination distances and where they stop and start over potentially millions of years of evolution.

In addition, the “merging” of distinct and perhaps distant regions of a single gene naturally occurs in the production of a transcriptome, and coalescent-based phylogenetic analyses based on transcriptome data are widely used (Lin et al. 2014; Fernández et al. 2018; Wipfler et al. 2018). The combined effect of linkage, recombination, and selection on species tree accuracy remains unclear. In general, the interplay between recombination and selection (e.g., selective sweeps and recombination hotspots) has not been adequately addressed in regard to their effects on the accuracy of multispecies coalescent methods. As more chromosome-level genomes become available (Dudchenko et al. 2017), these more nuanced investigation can begin.

When multiple UCEs are found within a single gene, treating them as independent units in species tree analyses potentially over-represents a single gene (but see Scornavacca and Galtier 2017). The definition of a gene, however, is not universal. Here, we used the GFF files from well-annotated base genomes with predefined units termed genes. This process of identifying genes in a genome by default necessitates the importance of high-quality genome annotation and the criteria/methods used in the annotation (e.g., identifying genes from robust transcriptomes and/or algorithmically). The chicken genome, for example, was annotated through masking repetitive regions and then using transcripts (cDNA and ESTs) and RNA-Seq data to identify the potential genes, which were then filtered further using standard gene (codon) models (Warren et al. 2016). This high-quality annotation lessens human arbitration in gene definition, as defining genes is primarily based on biological evidence.

However, there are still several decisions one could make in determining what is genic or intergenic. For instance, the percent of UCEs found in genes will substantially decrease if we only consider the genes derived from transcriptome data and exclude those characterized through model predictions. This can be seen when looking at the chicken genome (base genome of the Tetrapod UCE data set Galgal5), if we filter by NCBI Dbxref GeneID “curated” versus “uncurated” genes, results in a far smaller subset. However, the number of NCBI “curated” genes is roughly less than one-third the total number protein coding genes that are generally considered to be in the chicken genome, see UniProt database (Hillier et al. 2004). Thus, only selecting UCEs that intersect with the “curated” set will result in far fewer genic UCEs. In addition, more detailed characterizations of where a UCE falls in a gene may also affect results. 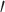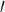For example, White and Braun (2019) examined the intersection of UCEs in Galgal5 and not only examined which ones were located in exons but whether they were located in 3Inline graphic or 5Inline graphic untranslated regions (UTRs) or in protein coding sequences (CDS) of the exon. The number found in protein coding regions of the exon by White and Braun (2019) was only 348, in contrast to our result of 467. Overall, the specifics of how one decides to annotate a UCEs’ basic identity could greatly change the downstream analyses.

Although we assume that genomic identities are shared across orthologous UCEs, it remains an open question. For example, do genic UCEs in a chicken remain genic in an anole lizard? One issue with attempting to document the conservation of a UCE’s genomic class is the thoroughness of gene annotation/prediction in a particular reference genome. Comparisons between poorly annotated genomes will likely underestimate the number of genic UCEs. Some differences (genic or not genic) between genomes are probably due to a mix of gene annotation and biology. For example, a genic UCE found in both the chicken and anole but not genic in the zebra finch (Taeniopygia guttata a nearer relative to the chicken), could be due to the gene not being algorithmically predicted in the zebra finch. However, a change in UCE function, for example, loss of function within a particular taxon, could contribute to differences in rates and affect branch length and topology estimates. Fortunately, methods developed to find outlier trees/taxa and prune these taxa from alignments (Mai and Mirarab 2018; Borowiec 2019) should buffer against extreme cases where a potential change in function has a dramatic effect on evolutionary rates.

UCEs are increasingly important and frequently used in phylogenomics due to their accessibility in specimens of varying quality, relatively low cost, and a user-friendly bioinformatics pipeline (Faircloth et al. 2012). However, amongst genomic subsampling methods, they return the second shortest loci on average (RADSeq being the shortest; Karin et al. 2019), and shorter loci tend to have fewer informative sites (Van Dam et al. 2017), impeding multispecies coalescent-based phylogenetic analyses (Molloy and Warnow 2018). Uninformative loci can also contribute to gene tree estimation error, which in turn hampers species tree inference. Our results suggest that when using species tree methods based on UCE data, merging cogenic UCEs may help reduce the negative impacts of uninformative and/or short loci, resulting in a more highly supported and potentially more accurate phylogenetic estimate.

Acknowledgments

The authors would like to thank Brian Simison and Joe Russack (California Academy of Sciences, CAS) for access to AWS servers. Sarah Crews for helping in the editing the manuscript. We would also like to thank the CAS Center for Comparative Genomics Reading Group for discussion of this paper. Thanks to the Doolin Foundation for Biodiversity and NSF 1754376, 1856402 for funding this research. We would also like to thank Brian Wiegmann, Adam Leaché, Brant Faircloth, and three anonymous reviewers for their useful comments that improved the quality of this manuscript.

Supplementary Material

Data available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.g79cnp5nd.

Code: https://github.com/matthewhvandam/integrating-functional-genomics-into-phylogenomics

References

  1. Adams R.H., Castoe T.A.. 2019. Statistical binning leads to profound model violation due to gene tree error incurred by trying to avoid gene tree error. Mol. Phylogenet. Evol. 134:164–171. [DOI] [PubMed] [Google Scholar]
  2. Alfaro M.E., Faircloth B.C., Harrington R.C., Sorenson L., Friedman M., Thacker C.E., Oliveros C.H., Èerný D., Near T.J.. 2018. Explosive diversification of marine fishes at the Cretaceous-Paleogene boundary. Nat. Ecol. Evol. 2:688–696. [DOI] [PubMed] [Google Scholar]
  3. Arbogast B., Edwards S.V., Wakeley J., Beerli P., Slowinski J.B.. 2002. Estimating divergence times from molecular data on phylogenetic and population genetic time scales. Annu. Rev. Ecol. Syst. 33:707–740. [Google Scholar]
  4. Bayzid M.S., Warnow T.. 2013. Naive binning improves phylogenomic analyses. Bioinformatics 29:2277–2284. [DOI] [PubMed] [Google Scholar]
  5. Bejerano G., Pheasant M., Makunin I., Stephen S., Kent W.J., Mattick J.S., Haussler D.. 2004. Ultraconserved elements in the human genome. Science 304:1321–1325. [DOI] [PubMed] [Google Scholar]
  6. Bethoux O. 2009. The earliest beetle identified. J. Paleontol. 83:931–937. [Google Scholar]
  7. Bi K., Linderoth T., Vanderpool D., Good J.M., Nielsen R., Moritz C.. 2013. Unlocking the vault: next-generation museum population genomics. Mol. Ecol. 22:6018–6032. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Blaimer B.B., Lloyd M.W., Guillory W.X., Brady S.G.. 2016. Sequence capture and phylogenetic utility of genomic ultraconserved elements obtained from pinned insect specimens. PLoS One 11:e0161531. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Borowiec M.L. 2019. Spruceup: fast and flexible identification, visualization, and removal of outliers from large multiple sequence alignments. J. Open Source Softw. 4:1635. [Google Scholar]
  10. Borowiec M.L., Lee E.K., Chiu J.C., Plachetzki D.C.. 2015. Extracting phylogenetic signal and accounting for bias in whole-genome data sets supports the Ctenophora as sister to remaining Metazoa. BMC Genomics 16:987. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Bossert S., Danforth B.N.. 2018. On the universality of target-enrichment baits for phylogenomic research. Methods Ecol. Evol. 9:1453–1460. [Google Scholar]
  12. Bossert S., Murray E.A., Almeida E.A.B., Brady S.G., Blaimer B.B., Danforth B.N.. 2018. Combining transcriptomes and ultraconserved elements to illuminate the phylogeny of Apidae. Mol. Phylogenet. Evol. 130:121–131. [DOI] [PubMed] [Google Scholar]
  13. Branstetter M.G., Danforth B.N., Pitts J.P., Faircloth B.C., Ward P.S., Buffington M.L., Gates M.W., Kula R.R., Brady S.G.. 2017a. Phylogenomic analysis of ants, bees and stinging wasps: improved taxon sampling enhances understanding of hymenopteran evolution. Curr. Biol. 27:1019–1025. [DOI] [PubMed] [Google Scholar]
  14. Branstetter M.G., Longino J.T., Ward P.S., Faircloth B.C.. 2017b. Enriching the ant tree of life: enhanced UCE bait set for genome-scale phylogenetics of ants and other Hymenoptera. Methods Ecol. Evol. 8:768–776. [Google Scholar]
  15. Camacho C., Coulouris G., Avagyan V., Ma N., Papadopoulos J., Bealer K., Madden T.L.. 2008. BLAST+: architecture and applications. BMC Bioinformatics 10:421. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Comeron, J.M., Ratnappan, R. and Bailin, S., 2012. The many landscapes of recombination in Drosophila melanogaster. PLoS Genetics 8:e1002905. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Dermitzakis E.T., Reymond A., Scamuffa N., Ucla C., Kirkness E., Rossier C., Antonarakis S.E.. 2003. Evolutionary discrimination of mammalian conserved non-genic sequences (CNGs). Science 302(5647):1033–1035. [DOI] [PubMed] [Google Scholar]
  18. Dimitrieva S., Bucher P.. 2012. Genomic context analysis reveals dense interaction network between vertebrate ultraconserved non-coding elements. Bioinformatics 28:395–401. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Dudchenko O., Batra S.S., Omer A.D., Nyquist S.K., Hoeger M., Durand N.C., Shamim M.S., Machol I., Lander E.S., Aiden A.P., Aiden, E.L., 2017. De novo assembly of the Aedes aegypti genome using Hi-C yields chromosome-length scaffolds. Science 356:92–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Edwards S.V., Xi Z., Janke A., Faircloth B.C., McCormack J.E., Glenn T.C., Zhong B., Wu S., Lemmon E.M., Lemmon A.R.. 2016. Implementing and testing the multispecies coalescent model: a valuable paradigm for phylogenomics. Mol. Phylogenet. Evol. 94:447–462. [DOI] [PubMed] [Google Scholar]
  21. Edwards S.V., Cloutier A., Baker A.J.. 2017. Conserved nonexonic elements: a novel class of marker for phylogenomics. Syst. Biol. 66:1028–1044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Efron B., Halloran E., Holmes S.. 1996. Bootstrap confidence levels for phylogenetic trees. Proc. Natl. Acad. Sci. USA. 93:13429–13429. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Esselstyn J.A., Oliveros C.H., Swanson M.T., Faircloth B.C.. 2017. Investigating difficult nodes in the placental mammal tree with expanded taxon sampling and thousands of ultraconserved elements. Genome Biol. Evol. 9:2308–2321. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Faircloth B.C. 2016. PHYLUCE is a software package for the analysis of conserved genomic loci. Bioinformatics 32:786–788. [DOI] [PubMed] [Google Scholar]
  25. Faircloth B.C. 2017. Identifying conserved genomic elements and designing universal bait sets to enrich them. Methods Ecol. Evol. 8:1103–1112. [Google Scholar]
  26. Faircloth B.C., Branstetter M.G., White N.D., Brady S.G.. 2015. Target enrichment of ultraconserved elements from arthropods provides a genomic perspective on relationships among Hymenoptera. Mol. Ecol. Resour. 15:489–501. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Faircloth B.C., McCormack J.E., Crawford N.G., Harvey M.G., Brumfield R.T., Glenn T.C.. 2012. Ultraconserved elements anchor thousands of genetic markers spanning multiple evolutionary timescales. Syst. Biol. 61:717–726. [DOI] [PubMed] [Google Scholar]
  28. Faircloth B.C., Sorenson L., Santini F., Alfaro M.E.. 2013. A phylogenomic perspective on the radiation of ray-finned fishes based upon targeted sequencing of ultraconserved elements (UCEs). PLoS One. 8:e65923. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Felsenstein J. 1985. Confidence limits on phylogenies: an approach using the bootstrap. Evolution 39:783–791. [DOI] [PubMed] [Google Scholar]
  30. Fernández R., Kallal R.J., Dimitrov D., Ballesteros J.A., Arnedo M.A., Giribet G., Hormiga G.. 2018. Phylogenomics, diversification dynamics, and comparative transcriptomics across the spider tree of life. Curr. Biol. 28:1489-1497. [DOI] [PubMed] [Google Scholar]
  31. Gatesy J., Springer M.S.. 2014. Phylogenetic analysis at deep timescales: unreliable gene trees, bypassed hidden support, and the coalescence/concatalescence conundrum. Mol. Phylogenet. Evol. 80:231–266. [DOI] [PubMed] [Google Scholar]
  32. Gilbert P.S., Wu J., Simon M.W., Sinsheimer J.S., Alfaro M.E.. 2018. Filtering nucleotide sites by phylogenetic signal to noise ratio increases confidence in the Neoaves phylogeny generated from ultraconserved elements. Mol. Phylogenet. Evol. 126:116–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Harrington R.C., Faircloth B.C., Eytan R.I., Smith W.L., Near T.J., Alfaro M.E., Friedman M.. 2016. Phylogenomic analysis of carangimorph fishes reveals flatfish asymmetry arose in a blink of the evolutionary eye. BMC Evol. Biol. 16:224. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Heibl C. PHYLOCH: R language tree plotting tools and interfaces to diverse phylogenetic software packages. Available from: http://www.christophheibl.de/Rpackages.html.
  35. Hillier L.W., Miller W., Birney E., Warren W., Hardison R.C., Ponting C.P., Bork P., Burt D.W., Groenen M.A.M., Delany M.E., Dodgson J.B., Chinwalla A.T., Cliften P.F., Clifton S.W., Delehaunty K.D., Fronick C., Fulton R.S., Graves T.A., Wilson R.K.. 2004. Sequence and comparative analysis of the chicken genome provide unique perspectives on vertebrate evolution. Nature 432:695–716. [DOI] [PubMed] [Google Scholar]
  36. Holmes S. 2003. Bootstrapping phylogenetic trees: theory and methods. Stat. Sci. 18:241–255. [Google Scholar]
  37. Holmes S. 2005. Statistical approach to tests involving phylogenies In: Gascuel O. editor. Mathematics of evolution and phylogeny. Oxford, UK: Oxford University Press; p. 91–120. [Google Scholar]
  38. Jennings W.B. 2017. On the independent gene trees assumption in phylogenomic studies. Mol. Ecol. 26:4862–4871. [DOI] [PubMed] [Google Scholar]
  39. Jarvis E.D., Mirarab S., Aberer A.J., Li B., Houde P., Li C., Ho S.Y.W., Faircloth B.C., Nabholz B., Howard J.T., Suh A., Weber C.C., da Fonseca R.R., Li J., Zhang F., Li H., Zhou L., Narula N., Liu L., Ganapathy G., Boussau B., Bayzid M.S., Zavidovych V., Subramanian S., Gabaldón T., Capella-Gutiérrez S., Huerta-Cepas J., Rekepalli B., Munch K., Schierup M., Lindow B., Warren W.C., Ray D., Green R.E., Bruford M.W., Zhan X., Dixon A., Li S., Li N., Huang Y., Derryberry E.P., Bertelsen M.F., Sheldon F.H., Brumfield R.T., Mello C. V., Lovell P. V., Wirthlin M., Schneider M.P.C., Prosdocimi F., Samaniego J.A., Velazquez A.M.V., Alfaro-Núñez A., Campos P.F., Petersen B., Sicheritz-Ponten T., Pas A., Bailey T., Scofield P., Bunce M., Lambert D.M., Zhou Q., Perelman P., Driskell A.C., Shapiro B., Xiong Z., Zeng Y., Liu S., Li Z., Liu B., Wu K., Xiao J., Yinqi X., Zheng Q., Zhang Y., Yang H., Wang J., Smeds L., Rheindt F.E., Braun M., Fjeldsa J., Orlando L., Barker F.K., Jønsson K.A., Johnson W., Koepfli K.-P., O’Brien S., Haussler D., Ryder O.A., Rahbek C., Willerslev E., Graves G.R., Glenn T.C., McCormack J., Burt D., Ellegren H., Alström P., Edwards S. V., Stamatakis A., Mindell D.P., Cracraft J., Braun E.L., Warnow T., Jun W., Gilbert M.T.P., Zhang G.. 2014. Whole-genome analyses resolve early branches in the tree of life of modern birds. Science (80) 346. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Karin B.R., Gamble T., Jackman T.R.. 2020. Optimizing Phylogenomics with Rapidly Evolving Long Exons: Comparison with Anchored Hybrid Enrichment and Ultraconserved Elements. Molecular Biology and Evolution. 37:904–922. 10.1093/molbev/msz263. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Kuhner M.K., Felsenstein J.. 1994. A simulation comparison of phylogeny algorithms under equal and unequal evolutionary rates. Mol. Biol. Evol. 11:459–468. [DOI] [PubMed] [Google Scholar]
  42. Kushawah G., Mishra R.K.. 2017. Ultraconserved sequences associated with HoxD cluster have strong repression activity. Genome Biol. Evol. 9:2134–2139. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Lanfear R., Calcott B., Ho S.Y.W., Guindon S.. 2012. PartitionFinder: combined selection of partitioning schemes and substitution models for phylogenetic analyses. Mol. Biol. Evol. 29:1695–1701. [DOI] [PubMed] [Google Scholar]
  44. Lanfear, R., Frandsen, P.B., Wright, A.M., Senfeld, T. & Calcott, B.. 2017. PartitionFinder 2: New Methods for Selecting Partitioned Models of Evolution for Molecular and Morphological Phylogenetic Analyses. Molecular Biology and Evolution. 34:772–773. 10.1093/molbev/msw260. [DOI] [PubMed] [Google Scholar]
  45. Lanier H.C., Knowles L.L.. 2012. Is recombination a problem for species-tree analyses? Syst. Biol. 61:691–701. [DOI] [PubMed] [Google Scholar]
  46. Lewitus E., Morlon H.. 2016. Characterizing and comparing phylogenies from their Laplacian spectrum. Syst. Biol. 65:495–507. [DOI] [PubMed] [Google Scholar]
  47. Lemmon A.R., Emme S.A., Lemmon E.M.. 2012. Anchored hybrid enrichment for massively high-throughput phylogenomics. Syst. Biol. 61:727–744. [DOI] [PubMed] [Google Scholar]
  48. Lin G.H., Wang K., Deng X.G., Nevo E., Zhao F., Su J.P., Guo S.C., Zhang T.Z., Zhao H.. 2014. Transcriptome sequencing and phylogenomic resolution within Spalacidae (Rodentia). BMC Genomics 15:32. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Liu L., Xi Z., Wu S., Davis C.C., Edwards S.V.. 2015. Estimating phylogenetic trees from genome-scale data. Ann. N. Y. Acad. Sci. 1360:36–53. [DOI] [PubMed] [Google Scholar]
  50. Locke S.A., Van Dam A.R., Caffara M., Pinto H.A., Lopez-Hernandez D., Blanar C.. 2018. Nuclear and mitochondrial phylogenomics of the Diplostomoidea and Diplostomida (Digenea, Platyhelminthes) bioRxiv 333518; doi: 10.1101/333518. [DOI] [PubMed] [Google Scholar]
  51. Mai, U., Mirarab, S.. 2018. TreeShrink: fast and accurate detection of outlier long branches in collections of phylogenetic trees. BMC Genomics 19(S5):272. doi: 10.1186/s12864-018-4620-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Mallo D., De Oliveira Martins L., Posada D.. 2016. SimPhy: phylogenomic simulation of gene, locus, and species trees. Syst. Biol. 65:334–344. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. McCole R.B., Erceg J., Saylor W., Wu C.. 2018. Ultraconserved elements occupy specific arenas of three-dimensional mammalian genome organization. Cell Rep. 24:479–488. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. McCole R.B., Fonseka C.Y., Koren A., Wu C. -tin. 2014. Abnormal dosage of ultraconserved elements is highly disfavored in healthy cells but not cancer cells. PLoS Genet. 10:e1004646. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. McCormack J.E., Faircloth B.C., Crawford N.G., Gowaty P.A., Brumfield R.T., Glenn T.C.. 2012. Ultraconserved elements are novel phylogenomic markers that resolve placental mammal phylogeny when combined with species tree analysis. Genome Res. 22:746–754. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Mirarab S., Warnow T.. 2015. ASTRAL-II: coalescent-based species tree estimation with many hundreds of taxa and thousands of genes, Bioinformatics 31: i44–i52. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Molloy E.K., Warnow T.. 2018. To include or not to include: the impact of gene filtering on species tree estimation methods. Syst. Biol. 67:285–303. [DOI] [PubMed] [Google Scholar]
  58. Morlon H, Lewitus E, Condamine F., Manceau M., Clavel J., Drury J., 2016. RPANDA: an R package for macroevolutionary analyses on phylogenetic trees. Methods Ecol. Evol., 7:589–597. [Google Scholar]
  59. Moyle R.G., Oliveros C.H., Andersen M.J., Hosner P.A., Benz B.W., Manthey J.D., Travers S.L., Brown R.M., Faircloth B.C.. 2016. Tectonic collision and uplift of Wallacea triggered the global songbird radiation. Nat. Commun. 7:12709. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Portik D.M., Smith L.L., Bi K.. 2016. An evaluation of transcriptome-based exon capture for frog phylogenomics across multiple scales of divergence (Class: Amphibia, Order: Anura). Mol. Ecol. Resour. 16:1069–1083. [DOI] [PubMed] [Google Scholar]
  61. Quattrini A.M., Faircloth B.C., Dueñas L.F., Bridge T.C.L., Brugler M.R., Calixto-Botía I.F., DeLeo D.M., Forêt S., Herrera S., Lee S.M.Y., Miller D.J., Prada C., Rádis-Baptista G., Ramírez-Portilla C., Sánchez J.A., Rodríguez E., McFadden C.S.. 2018. Universal target-enrichment baits for anthozoan (Cnidaria) phylogenomics: new approaches to long-standing problems. Mol. Ecol. Resour. 18:281–295. [DOI] [PubMed] [Google Scholar]
  62. R Core Team. 2019. R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; Available from: https://www.R-project.org/. [Google Scholar]
  63. Robinson D., Foulds L.. 1981. Comparison of phylogenetic trees. Math. Biosci. 53:131–147. [Google Scholar]
  64. Sandelin A., Bailey P., Bruce S., Engström P.G., Klos J.M., Wasserman W.W., Ericson J., Lenhard B.. 2004. Arrays of ultraconserved non-coding regions span the loci of key developmental genes in vertebrate genomes. BMC Genomics 5:99. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Sanderson M.J., Marius N., McMahon M.M.. 2017. Homology-aware phylogenomics at gigabase scales. Syst. Biol. 66:590–603. [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Sayyari, E. and Mirarab, S.. 2016. Fast coalescent-based computation of local branch support from quartet frequencies. Mol. Biol. Evol. 33:654–1668. [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Schliep K.P. 2011. phangorn: phylogenetic analysis in R. Bioinformatics 27:592–593. [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Scornavacca, C. and Galtier, N.. 2017. Incomplete lineage sorting in mammalian phylogenomics. Syst. Biol. 66:112–120. [DOI] [PubMed] [Google Scholar]
  69. Seo T. 2008. Calculating bootstrap probabilities of phylogeny using multilocus sequence data. Mol. Biol. Evol. 25:960–971. [DOI] [PubMed] [Google Scholar]
  70. Smith D.M., Marcot J.D.. 2015. The fossil record and macroevolutionary history of the beetles. Proc. R. Soc. Lond. B Biol. Sci. 282. [DOI] [PMC free article] [PubMed] [Google Scholar]
  71. Stamatakis A. 2014. RAxML version 8: a tool for phylogenetic analysis and post-analysis of large phylogenies. Bioinformatics 30: 1312–1313. [DOI] [PMC free article] [PubMed] [Google Scholar]
  72. Susko E. 2009. Bootstrap support is not first-order correct. Syst. Biol. 58:211–223. [DOI] [PubMed] [Google Scholar]
  73. Szöllõsi G.J., Tannier E., Daubin V., Boussau B.. 2015. The inference of gene trees with species trees. Syst. Biol. 64:42–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
  74. Van Dam M.H., Lam A.W., Sagata K., Gewa B., Laufa R., Balke M., Faircloth B.C., Riedel A.. 2017. Ultraconserved elements (UCEs) resolve the phylogeny of Australasian smurf-weevils. PLoS One 12:e0188044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  75. Van Dam M.H., Trautwein M., Spicer G.S., Esposito L.. 2018. Advancing mite phylogenomics: designing ultraconserved elements for Acari phylogeny. Mol. Ecol. Resour. 19:465–475 doi: 10.1111/1755-0998.12962. [DOI] [PubMed] [Google Scholar]
  76. Vavouri T., Walter K., Gilks W.R., Lehner B., Elgar G.. 2007. Parallel evolution of conserved non-coding elements that target a common set of developmental regulatory genes from worms to humans. Genome Biol. 8:R15. [DOI] [PMC free article] [PubMed] [Google Scholar]
  77. Warren W.C., Hillier L.W., Tomlinson C., Minx P., Kremitzki M., Graves T., Markovic C., Bouk N., Pruitt K.D., Thibaud-Nissen F., Schneider V., Mansour T.A., Brown C.T., Zimin A., Hawken R., Abrahamsen M., Pyrkosz A.B., Morisson M., Fillon V., Vignal A., Chow W., Howe K., Fulton J.E., Miller M.M., Lovell P., Mello C.V., Wirthlin M., Mason A.S., Kuo R., Burt D.W., Dodgson J.B., Cheng H.H.. 2016. A new chicken genome assembly provides insight into avian genome structure. G3 (Bethesda, Md.). 7:109–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  78. White N.D. and Braun M.J.. 2019. Extracting phylogenetic signal from phylogenomic data: higher-level relationships of the nightbirds (Strisores). Mol. Phylogenet. Evol., 141:106611. [DOI] [PubMed] [Google Scholar]
  79. Winker K., Glenn T.C., Faircloth B.C.. 2018. Ultraconserved elements (UCEs) illuminate the population genomics of a recent, high-latitude avian speciation event. PeerJ 6:e5735. [DOI] [PMC free article] [PubMed] [Google Scholar]
  80. Wipfler, B., Letsch, H., Frandsen, P.B., Kapli, P., Mayer, C., Bartel, D., Buckley, T.R., Donath, A., Edgerly-Rooks, J.S., Fujita, M. and Liu, S., 2019. Evolutionary history of Polyneoptera and its implications for our understanding of early winged insects. Proc. Natl. Acad. Sci. USA 116:3024–3029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  81. Woolfe A., Goodson M., Goode D.K., Snell P., McEwen G.K., Vavouri T., Smith S.F., North P., Callaway H., Kelly K., Walter K., Abnizova I., Gilks W., Edwards Y.J.K., Cooke J.E., Elgar G.. 2004. Highly conserved non-coding sequences are associated with vertebrate development. PLoS Biol. 3:e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  82. Yin J., Zhang C., Mirarab S.. 2019. ASTRAL-MP: scaling ASTRAL to very large datasets using randomization and parallelization. Bioinformatics. 35:3961–3969. doi: 10.1093/bioinformatics/btz211. [DOI] [PubMed] [Google Scholar]
  83. Zhang C., Rabiee M., Sayyari E., Mirarab S.. 2018. ASTRAL-III: polynomial time species tree reconstruction from partially resolved gene trees. BMC Bioinformatics 19:153. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Systematic Biology are provided here courtesy of Oxford University Press

RESOURCES