Morphological Characters Can Strongly Influence Early Animal Relationships Inferred from Phylogenomic Data Sets

Abstract

There are considerable phylogenetic incongruencies between morphological and phylogenomic data for the deep evolution of animals. This has contributed to a heated debate over the earliest-branching lineage of the animal kingdom: the sister to all other Metazoa (SOM). Here, we use published phylogenomic data sets (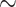45,000–400,000 characters in size with 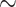15–100 taxa) that focus on early metazoan phylogeny to evaluate the impact of incorporating morphological data sets (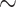15–275 characters). We additionally use small exemplar data sets to quantify how increased taxon sampling can help stabilize phylogenetic inferences. We apply a plethora of common methods, that is, likelihood models and their “equivalent” under parsimony: character weighting schemes. Our results are at odds with the typical view of phylogenomics, that is, that genomic-scale data sets will swamp out inferences from morphological data. Instead, weighting morphological data 2–10 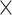in both likelihood and parsimony can in some cases “flip” which phylum is inferred to be the SOM. This typically results in the molecular hypothesis of Ctenophora as the SOM flipping to Porifera (or occasionally Placozoa). However, greater taxon sampling improves phylogenetic stability, with some of the larger molecular data sets (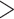200,000 characters and up to 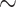100 taxa) showing node stability even with 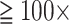upweighting of morphological data. Accordingly, our analyses have three strong messages. 1) The assumption that genomic data will automatically “swamp out” morphological data is not always true for the SOM question. Morphological data have a strong influence in our analyses of combined data sets, even when outnumbered thousands of times by molecular data. Morphology therefore should not be counted out a priori. 2) We here quantify for the first time how the stability of the SOM node improves for several genomic data sets when the taxon sampling is increased. 3) The patterns of “flipping points” (i.e., the weighting of morphological data it takes to change the inferred SOM) carry information about the phylogenetic stability of matrices. The weighting space is an innovative way to assess comparability of data sets that could be developed into a new sensitivity analysis tool. [Metazoa; Morphology; Phylogenomics; Weighting.]

As the first phylogenetic DNA sequence studies became available in the late 1980’s, integrating the new molecular data with the existing morphological data sets was highly debated (Hillis 1987; Kluge 1989). The comparison of the two types of data was not straightforward then (Baker et al. 1998; Zrzavý 1998; Lee 2001; Jenner 2003, 2004; Wortley and Scotland 2006) and remains elusive to the present (Scholtz 2010; Lee and Palci 2015; Pyron 2015; Wanninger 2015; Goloboff et al. 2019). Early studies empirically examined the relative contribution of molecular and morphological data to phylogenetic inference (Baker et al. 1998; Zrzavý 1998; Wortley and Scotland 2006; Cotton and Wilkinson 2008; Lee and Palci 2015); all found that morphology had an equal, if not stronger, impact when the number of characters for the two kinds of data were within an order of magnitude of each other. Prior to the phylogenomic revolution, the number of molecular characters was typically no more than 10 times the number of morphological characters. Giribet (2010) suggested that as more and more genomic level data are available, morphological data might become less dominant within combined data sets. And indeed, some systematists have expanded this thought, and explicitly conjectured that phylogenomic data will swamp inferences from morphology. This conjecture has since become a common assumption of phylogenomics (Lee and Palci 2015; Wanninger 2015). Most of the time, phylogenomicists simply ignore morphological characters. While there may be many reasons for this—including the mere difficulty of generating morphological data—this can oftentimes be attributed to the swamping assumption. The purpose of this article is to assess the interaction of genomic and morphological information and to test what we shall call “genomic swamping” in an important phylogenetic system. To our knowledge, this exploration has not been accomplished for any large phylogenomic data sets.

There are several ways we conceive of testing this hypothesis. First, and most intuitive, is to simply concatenate the existing morphological data with the largest phylogenomic data sets. This would result in combining data sets with differing numbers of taxa. Secondly, to increase comparability, exemplar approaches can be applied. This means that the larger matrices are subsampled to create data sets with consistently limited taxon numbers. Early publications using single or small numbers of genes came to conflicting conclusions about exemplar approaches (Rosenberg and Kumar 2001; Pollock et al. 2002; Zwickl and Hillis 2002; Rokas and Carroll 2005) and the more recent phylogenomic literature is also somewhat equivocal as to the impact of exemplar approaches (Nabhan and Sarkar 2012; Pyron 2015; Soares and Schrago 2015; Streicher et al. 2016; Bleidorn 2017; Shen et al. 2017; Folk et al. 2018; Tamashiro et al. 2019). The major problem with the exemplar approach is that it has the potential to enhance long-branch attraction, a well-known confounder of phylogenetic inference (Felsenstein 1978; Bergsten 2005; Philippe et al. 2005). However, one of the main themes of the more recent phylogenomic analyses relevant to taxon usage indicates that data type and data modeling are more important factors than taxon choice (Reddy et al. 2017; Dornburg et al. 2019). In addition to increased comparability, another benefit of the exemplar approach is that it allows us to quantify the well-known positive effect of improved taxon sampling—keeping in mind that even the largest data sets available are far from “complete.” Thus, we created exemplar data sets with the taxon numbers consistently limited to 6 and 11 for all data sets (see Materials and Methods section).

In this communication we use a well-studied, yet unresolved question in the tree of life to explore these important issues in phylogenomic analyses. We focus on the sister group of all other extant Metazoa (SOM), which has been hotly debated and intensively researched for well over a century. There are only five major lineages that could be considered the SOM: Bilateria, Cnidaria, Ctenophora, Placozoa, or Porifera, allowing for 105 possible bifurcating trees. As pointed out by Schierwater et al. (2009), a large number of these topologies have appeared in publications. The hypothesis of Porifera as the SOM has prevailed since early morphological studies and into the beginning of the DNA sequence era (Field et al. 1988; Schram 1991; Backeljau 1993; Zrzavý 1998; Philippe et al. 2009). With the advent of medium-sized phylogenetic molecular data in the first decade of the 21st Century, Placozoa gained momentum as being inferred as the most likely SOM (Dellaporta et al. 2006; Signorovitch et al. 2007). As phylogenomics came into play in the early 2000s, the hypotheses switched to primarily Porifera or Ctenophora inferred as the most probable SOM (Rokas et al. 2003; Rokas and Carroll 2005; Dunn et al. 2008; Srivastava et al. 2008; Pick et al. 2010; Nesnidal et al. 2013; Ryan et al. 2013; Moroz et al. 2014; Whelan et al. 2015; Shen et al. 2017; Laumer et al. 2018). The reasons for this disparity in hypotheses are surely varied and include sequence length differences, taxon sampling, and model application, among others.

Several studies have discussed the ramifications of both Porifera and Ctenophora inferred as the SOM, and it is clear that the evolution of some of the most fundamental morphological traits in animals is at stake—neural tissue, muscle cells, and mesoderm, to name a few (see Nielsen 2019 for a recent review). For instance, if ctenophores are inferred as the SOM, then the nervous tissue and neural systems most likely evolved twice, although an equally parsimonious scenario would involve two independent losses of a nervous system, one in Porifera and one in Placozoa. If Porifera is inferred as the SOM, then the neural tissue and the nervous system almost surely evolved only once. The latter hypothesis is more intuitive and parsimonious than the former. However, arguments as to the ease with which neural tissue and nervous systems can arise (i.e., from the neural genomic toolbox that the last common ancestor of all metazoans seems to have possessed) have also been proffered (Moroz et al. 2006; Moroz 2009, 2015). While these scenarios, which are based on one of the most complex and derived characters in animal architecture, seem to be very attractive, these might not be the most logical ones to discuss in the context of the first metazoan animals. The presence of very basic characters, like a basal membrane or an extracellular matrix, could be argued to be more relevant in terms of evolution. If such basic characters were examined, then Placozoa probably would be inferred as the SOM in most parsimony based scenarios (See Schierwater et al. 2009).

In the context of likelihood (and Bayesian) analyses, the choice of the applied models will often play a major role in methodological discussions (Yang et al. 1994; Lewis 2001a; Fan et al. 2011; Xie et al. 2011; Brown 2014; Duchêne et al. 2017; Oaks et al. 2019; Stamatakis 2019). It has recently been argued, though, that researchers can simply use the most parameter-rich model, that is, GTR+I+G (Abadi et al. 2019). Either way, discussions about integrating morphology and molecules in phylogenetic analysis often times boil down to character weighting of the two partitions, a subject that has been (Wheeler 1986; Goloboff 1993; Chippindale and Wiens 1994) and remains controversial (Goloboff et al. 2008; Simmons and Goloboff 2013; Mirande 2016; Schierwater et al. 2016; Mirande 2019). The only approach to “even out” a swamping effect that molecular characters might have over morphological characters in a combined analysis is weighting (Giribet 2010). Character weighting in simultaneous analysis of morphology and molecules is complicated by the methods that are used to collect the character information and also by the differences in the very nature of morphological versus sequence data.

It appears to us that systematists largely follow opposing trends: In molecular systematics, the data will often influence the way that characters are analyzed (through choosing appropriate models in likelihood and Bayesian approaches); whereas in morphological systematics, the method of analysis (parsimony) often seems to influence the scoring of characters. This seems to be related to fundamental differences in the two data types. Morphological characters are based on a researcher’s qualitative interpretation of complex phenotypic traits and on a subjective understanding of the morphology of the organisms being studied (Farris 1983). Molecular data, on the other hand—and phylogenomic data in particular—are to a higher extent a mixture of data with different characteristics: uninformative and informative sites, variant and invariant sites, and sites that are consistent and inconsistent with each other. Morphological data can also have these mixed features, but are typically highly curated. Our Tables 1 and 2 exemplify this trend: Even though the focus of most of the morphological data sets we used was not on the SOM question itself, the numbers of phylogenetically informative characters (those with at least two different character states on two sides of the SOM node) are generally very close to the total of characters in the data sets. On average, the molecular data sets include higher percentages of uninformative sites for this very deep evolutionary question than the morphological matrices (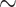30% for molecular and 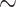10% for morphological matrices, see Tables 1 and 2).

Table 1.

Molecular data sets and individual analyses.

	#Taxa	#All Ch	#PI Ch	#PI Ch	#PI Ch	SOM	SOM	SOM	SOM
Study	“Full”	“Full”	“Full”	11 taxa	6 taxa	par6	ML6	par11	ML11	Original
Ch1	77	51,940	35,010	19,655	8681	CT	CT	CT	CT	CT
Ch2	77	51,940	23,144	10,871	5058	CT	CT	CT	CT	CT
Ch3	77	51,940	23,950	11,303	5228	CT	CT	CT	CT	CT
Ch4	77	51,940	26,353	12,935	6822	CT	CT	CT	CT	CT
RyE	61	88,384	52,793	31,988	13,168	CT	CT	CT	CT	CT
RyG	15	104,840	54,142	54,911	18,215	CT	CT	CT	CT	CT
Si1	90	102,464	89,636	39,775	16,776	CT	CT	CT	CT	PO
Si2	90	268,032	219,632	95,825	34,477	CT	CT	CT	CT	PO
Si3	97	401,632	310,886	144,147	47,803	CT	CT	CT	CT	PO
Wh1	70	46,542	36,525	17,247	4122	CT	CT	CT	CT	CT
Wh2	70	46,537	28,022	12,743	3615	CT	CT	CT	CT	CT
Wh3	70	46,542	30,598	13,661	4112	CT	CT	CT	CT	CT
Wh4	70	46,542	28,667	12,914	3626	CT	CT	CT	CT	CT

A list of the molecular studies used in the present communication, including data set sizes and phylogenetically informative characters. The three letter code in the “Study” column is used throughout the article to refer to these studies. Ry prefix Ryan et al. 2013; RyG Genomic, RyE EST, Si prefix Simion et al. 2017; Wh prefix Whelan et al. 2015; Ch prefix Chang et al. 2015. # Taxa “Full”, # All Ch “full”, # PI Ch represent the number of taxa in the original analysis and our “full” analyses, the total number of characters in the original analysis across the entire tree, and number of Phylogenetically Informative (PI) characters for the SOM node, respectively. SOM sister of all other Metazoa; PO Porifera inferred as the SOM; CT Ctenophora inferred as the SOM. Par “unweighted” parsimony, par6 and par11 refer to our parsimony analyses with and 11; ML maximum likelihood under WAG model, ML6 and ML11 refer to our likelihood analyses with 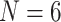and 11. Original refers to the results reported in the original publications for “full” taxon representation.

Table 2.

Morphological data sets and individual analyses.

	#Taxa	All Ch	PI Ch	PI Ch	PI Ch	SOM	SOM	SOM	SOM	Original	Original
Study	“Full”	“Full”	“Full”	11 taxa	6 taxa	par6	par11	ML6	ML11	Morpho	Com	Focus
Sch	9	17	13	17	13	PL	PL	PL	PL	PL	PL	A
Eer	40	138	130	33	21	PO	PO	PO	PO	PO	PO	B
Gle	58	94	94	24	14	PO	PO	PO	PO	PO	PO	C
Zrz	56	276	252	72	20	PO	PO	PO	PO	PO	PO	D
Bru	35	96	50	25	11	PO	PO	PO	PO	PO	NA	D
Bak	38	78	62	16	9	PL	PL	PL	PL	PL	NA	D
Com	11	62	61	61	52	PL	PL	PO	PL	NA	NA	NA
PO1	11	29	29	29	24	PO	PO	PO	PO	NA	NA	NA
PL1	11	27	27	27	22	PL	PL	PL	PL	NA	NA	NA

A list of the morphological studies used in the present communication, including data set sizes and phylogenetically informative characters. We also include three morphological matrices we constructed as described in the text (Com, PO1, and PL1). Abbreviated names for these data sets are as follows: Sch Schierwater et al. (2009); Eer Peterson and Eernisse (2001); Gle Glenner et al. (2004); Zrz Zrzavý (1998); Bru Brusca and Brusca (2003); Bak Backeljau (1993); Com combined morphological data; PO1 Porifera synapomorphies; PL1 Placozoa synapomorphies; # Taxa “Full”, # All Ch “Full”, # PI Ch represent the number of taxa in the original analysis and our “full” analyses, total number of characters in original analysis across the entire tree, and number of phylogenetically informative (PI) characters for the SOM node, respectively. SOM sister of all other Metazoa; PL Placozoa inferred as the SOM; PO Porifera inferred as the SOM. Par “unweighted” parsimony, par6 and par11 refer to our parsimony analyses with 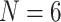and 11; ML maximum likelihood under Mk model, ML6 and ML11 refer to our likelihood analyses with 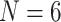and 11. Original Morpho refers to the results reported in the original publications and Original Com refers to combined molecular and morphological analyses as reported in the original publications. Focus refers to the phylogenetic question addressed in the original papers, where A direct test of the SOM, B overall metazoan analysis compared to 18S rDNA, C overall metazoan analysis using Bayesian methods, and D overall metazoan analysis to understand metazoan groupings. NA indicates that the category is not applicable to that data set.

Another obvious difference between morphology and molecular sequence data is that it is easier to visualize molecular characters as equivalent elements because of the nature of nucleic acid and amino acid sequences; one site equals one genetic character. Morphological traits, on the other hand, differ vastly in how much genetic information is needed for them to be expressed: Some morphological characters can be coded for by only a single locus or a few loci. For example, coat color in mice (Zahn 2019) and flower color (Bradley et al. 2017) describe very simple genetic architecture with one single genetic locus each, while other traits depend on interactions of tens or even hundreds of genes scattered throughout the genomes of the organisms being studied. For the example of human height, only 20% of the trait is explained by around 700 variants in over 400 loci, suggesting that even more loci are involved (Marouli et al. 2017). In a way, this makes weighting a bigger issue with morphology than with the more uniform molecular data, and ultimately renders comparisons between the two challenging. No objective reasoning for weighting has been given with respect to morphology versus molecules based on genetic architecture of the traits used, which is why methods such as implied weighting have been developed that apply weights a posteriori, based on features of the output of phylogenetic analysis (Farris 1969; Goloboff 1993; Goloboff et al. 2008; Goloboff 2014). While it somewhat depends on the taxonomic scope of a given study, it is safe to say that morphologists generally prefer complex traits over simple ones like flower color. Some degree of subjective weighting, then, has already been applied to the morphological character partitions.

In order to explore the impact of morphological data on overall phylogenetic hypotheses for the SOM, we examine the stability of phylogenomic hypotheses when combined with morphological data. We use differential weighting of morphological characters as a means to explore the morphology/molecular interaction space. We reason that the impact of morphology is significant in cases where relatively small weights applied to morphological characters can alter a phylogenetic hypothesis. If larger weights are needed to alter a phylogenetic hypothesis, then we interpret the genomic swamping phenomenon to be the dominant factor. The purpose of this study is not to determine what weights to use in combined analyses. Instead, we assess the relative influence of the two data types and aim to gain some perspective on the weighting space.

Materials and Methods

Molecular Data Matrices: Table 1 lists the 13 molecular data sets we analyzed and Supplementary File S1 available on Dryad at http://dx.doi.org/10.5061/dryad.prr4xgxhf contains all the molecular matrices we used. Table 1 shows the molecular data sets from four of the largest recent phylogenomic studies that address the SOM question directly (Ryan et al. 2013; Chang et al. 2015; Whelan et al. 2015; Simion et al. 2017). Each of these four studies presented multiple data sets for their analyses. We chose 13 matrices to span the four different studies, to cover a broad range of taxon numbers (from 15 to 97 for the “full” matrices), and to include a range of character set sizes (from 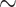40k to 400k molecular characters). Ryan et al. (2013) presented both a whole genome data set (RyG; 15 taxa, 20% missing data) and a partial genomic EST data set covering more taxa (RyE; 61 taxa, 65% missing data). Whelan et al. (2015) present over 20 data sets of which we use one (Wh1), along with three that were recorded in Feuda et al. (2017: Wh2, Wh3, and Wh4). All four of these matrices have the same taxon sampling of 70 taxa, and ca. 46,500 characters (See Supplementary File S1 available on Dryad). They differ in the way the amino acid positions were coded, using three common methods of reducing the amino acid states based on biochemical properties to optimize data sets for phylogenetics: the alphabet reduction methods Dayhoff-6 (Wh2; Dayhoff et al. 1978), S&R-6 (Wh4; Susko and Roger 2007), and KGB-6 (Wh3; Kosiol et al. 2004). Chang et al. (2015) also present multiple data sets of which we use one here (Ch1), as well as three recoded from Feuda et al. (2017). All four of these data sets have the same taxon representation (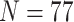), and the same number of characters (51,940), but also differ in the way the amino acids are coded: 20 amino acid code (Ch1), Dayhoff-6 (Ch2), S&R-6 (Ch3), and KGB-6 (Ch4). Simion et al. (2017) presented four data sets of which we use three in this study: Si1, Si2, and Si3. Si3 is the complete supermatrix of 401,632 amino acid positions for 97 species; Si1 and Si2 are both limited to 90 species to test the impact of removing poriferan clades. In addition, Si1 and Si3 include raw amino acid sequences while Si2 includes the amino acids recoded in the Dayhoff 6-states alphabet (Dayhoff et al. 1978). See the Readme.txt in Supplementary File S1 available on Dryad for the links the matrices were downloaded from.

Exemplar Approach for Phylogenomic Data Sets: The simplest way to evaluate the interaction between morphological and phylogenomic characters is to concatenate the available morphological and phylogenomic data. The published phylogenomic data sets tend to include more taxa (usually 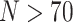with maximum 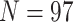) than the morphological matrices (minimum 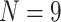, maximum 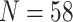). We explore the use of exemplar approaches to increase comparability. With five relevant ingroup taxa (Bilateria, Cnidaria, Ctenophora, Porifera, and Placozoa) and an outgroup (Choanoflagellata), this leads to the simplest exemplar approach having six taxa. Doubling this number where possible, we also created 11-taxon data sets with two representatives each for Porifera, Ctenophora, Cnidaria, Bilateria, and outgroups (one choanoflagellate and one fungus), and one placozoan representative (Placozoa for most published phylogenomic data sets before 2017 has a single representative). We were consistent about the taxa used; specifically, the six-taxon data sets are subsets of the 11-taxon data sets, and the 11-taxon data sets are subsets of the “full” data sets. In this way we generated 26 exemplar molecular data sets of the 13 from the literature, for a total of 39 molecular data sets for our analyses (Table 1).

Morphological Data Matrices: Table 2 shows the data sets from six morphological treatments of metazoan phylogeny that addressed the SOM question (Backeljau 1993; Zrzavý 1998; Peterson and Eernisse 2001; Brusca and Brusca 2003; Glenner et al. 2004; Schierwater et al. 2009—these data sets are reproduced in Supplementary File S2 available on Dryad). Only one of the morphological studies focused on addressing the SOM question directly (Schierwater et al. 2009). The focus of all six morphological data sets is listed in Table 2. Please note that almost all morphological and molecular data sets include characters that are not phylogenetically informative for the SOM node, where none of the five groups (Placozoa, Porifera, Ctenophora, Cnidaria, and Bilateria) are distinguishable from the others through the presence of a different state. Since the data sets have overlapping character information, we also created a combined morphological data matrix (Com) with 62 characters, where we removed redundant characters across the six studies (see collated character list in Supplementary File S2 available on Dryad). Focusing on the SOM node only, we then removed one of these characters that provides no phylogenetic information for the SOM node, the same way we did with all the data sets from the literature (see Tables 1 and 2). Some of the morphological data sets we used contradict each other in terms of the phylogeny they support. Therefore, we also wanted to explore the impact of matrices made up of only those characters that are diagnostic for the alternative hypotheses that place either Placozoa or Porifera as the inferred SOM. Of the 61 phylogenetically informative characters in the Com data matrix there are only two that unambiguously support the inference of Ctenophora as the SOM, 27 support the inference of Placozoa as the SOM and 29 support the inference of Porifera as the SOM (all with Consistency Indices [CI] of 1.0). We then used these characters to create PO1 for Porifera and PL1 for Placozoa (which share 21 characters), yet did not create a separate dataset for the two characters that support Ctenophora inferred as the SOM. So, we restructured the published morphological matrices in three novel ways: PL1 contains all morphological characters that support Placozoa as the inferred SOM, PO1 contains all morphological characters that support Porifera as the inferred SOM, and Com contains all nonredundant morphological characters that are phylogenetically informative for the SOM node in total. Supplementary File S2 available on Dryad also lists the morphological characters in these reduced partitions.

Exemplar Approach for Morphological Data Sets: As with the phylogenomic data, for morphology we created subdata sets with six taxa: one each for Porifera, Ctenophora, Cnidaria, Bilateria, and Placozoa, as well as an outgroup (Choanoflagellata). We also double the number of ingroup and outgroup representatives to increase the exemplar approach to 11 taxa with two representatives each for Porifera, Ctenophora, Cnidaria, Bilateria, and outgroups (one choanoflagellate and one fungus); a single representative was used for Placozoa. We were consistent about the taxa that represent the five ingroups and the outgroups; specifically, the six-taxon data sets are subsets of the 11-taxon data sets, and the 11-taxon data sets are subsets of the “full” data sets. In this way we generated 18 exemplar morphological data sets from the six in the literature and our three combined matrices, for a total of 27 morphological data sets for our analyses (Table 2).

Combined matrices: We analyzed all pairwise combinations of morphological matrices (Sch, Eer, Gle, Zrz, Bru, Bak, Com, PO1, and PL1) with molecular matrices (RyG, RyE, Si1, Si2, Si3, Wh1, Wh2, Wh3, Wh4, Ch1, Ch2, Ch3, and Ch4) for a total of 117 bipartitioned matrices. Unsurprisingly, not all species could be matched exactly across the different data sets from the literature. In those cases, we matched the taxon name in the morphology matrices with a representative from the molecular data sets at the lowest taxonomic rank possible (see Supplementary File S3 available on Dryad for details). In order to match the higher taxon numbers of the “full” molecular partitions, in some cases we had to replicate morphological character state information (Supplementary File S3 available on Dryad).

Phylogenetic Analysis: We performed both likelihood and parsimony analyses for all combinations of molecular and morphological data sets. PAUP (six and 11 taxa data sets; Swofford 2002) and TNT (“full” data sets; Goloboff et al. 2008) were used to accomplish the parsimony runs; IQ-TREE (six- and 11-taxon data sets) and RAxML (“full” data sets) were used to accomplish the likelihood runs (Stamatakis 2014; Nguyen et al. 2015). Parsimony searches were exhaustive for the six-taxon data sets, branch-and-bound for the 11-taxon data sets, and heuristic (100 random starting additions and TBR branch swapping) for the “full” data sets. For likelihood, we used default tree search settings. Bootstrap support values were obtained using the default settings of each program with 100 bootstrap replicates for each analysis.

Character weighting: A critical part of this study is character weighting of the morphological data. PAUP, RAxML, and TNT have weighting commands built-in that we used. For likelihood in IQ-TREE, we multiplied the morphological characters to achieve the same result. We initially explored the weighting space with weights of 1, 2, 4, 8, 16, 32, 64, and 128 in parsimony for the exemplar data sets. These unreported results indicated that we can halve the number of analyses while still covering the weighting space sufficiently by reducing the weights to the following: 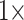(i.e., “unweighte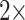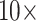d”), , , and 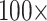. For instance, for the Sch matrix in likelihood, we assembled four matrices: 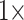= 17 characters (i.e., the original values), 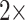= 34 characters, 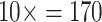characters, and 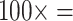1,700 characters. These weighted partitions were then combined with the various molecular partitions described above. For the molecular data, we applied the following five weighting matrices: PAM250, WAG, LGM2, and LGX2; and “unweighted” molecular data in parsimony. In all parsimony analyses, we thus applied four morphological weights (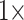, , 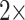, 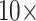and 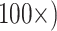to each of the nine morphological matrices by 13 molecular matrices, and used five different molecular weighting schemes for a total of 2,340 analyses for each of two different data set sizes (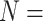6, 11), plus one analysis on the “full” data sets; this sums up to a grand total of 5,148 parsimony analyses.

In all of the likelihood analyses that included morphology, the Mk model was applied to the morphological characters only. The Mk model is the default k-state generalization of the Jukes–Cantor model (Lewis 2001b), as described in the IQ-TREE documentation (Nguyen et al. 2015). There are well-known problems and controversies surrounding likelihood models for morphology, and the Mk model in particular (Puttick et al. 2017; see Goloboff et al. 2019). Consequently, we chose the Mk model, because it is the simplest likelihood model for morphology, and it is implemented in the programs we used for our likelihood trees, IQ-TREE and RAxML. We applied four morphological weighting schemes (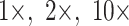, and 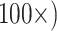for each of the nine morphological matrices by 13 molecular matrices. We also varied the amino acid model that was used in order to explore the impact of some of the more popular likelihood models on our inferences. The models we used are CAT, LG+CAT, WAG, and C10 for a total of 1872 analyses for each of the exemplar data sets ( 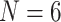and 11), and an additional 468 analyses using the “full” data sets under the C10 model. This resulted in a grand total 4212 likelihood analyses. We also explored the dynamics of rescored matrices from the Si (Si2), Ch (Ch2, Ch3, Ch4), and Wh (Wh2, Wh3, Wh4) data sets using Dayhoff-6, S&R-6, and KGB-6 rescoring approaches under maximum likelihood. For these rescored matrices, we used the profile mixture model C10 (Quang et al. 2008), which is not available for parsimony.

It is important to keep in mind that “unweighted” does not mean the same thing when applying a different optimality criterion. “Unweighted” parsimony applies the same weight to all of the characters. The same is not true for “unweighted” likelihood, as the calculations that add up all the site log likelihoods to retrieve the overall likelihood score are dependent on the model choice. Therefore, even in “unweighted” likelihood, different characters contribute to the overall result to varying degrees. All in all, we carried out 9360 tree search analyses for this study. These matrices were used as an attempt to examine as wide a range of weighting schemes as possible and as comparable as possible across likelihood and parsimony.

Results

Summary of Morphological and Genomic Analyses from the Literature: Four published genomic studies that directly address the SOM question were used in the present analyses (Table 1). The results obtained in the original papers are discussed briefly below and summarized in Tables 1 and 2. Ryan et al. (2013) analyzed both EST and genomic DNA sequence data sets using likelihood and inferred Ctenophora as the SOM with high bootstrap support (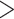95%) in both analyses. Chang et al. (2015) obtained Ctenophora as the hypothesized SOM with full bootstrap and Bayesian posterior support (100% and pp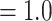). Ctenophora was also obtained as the hypothesized SOM in Whelan et al. (2015) using the Wh1 matrix listed in the present study with 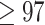% bootstrap and full Bayesian posterior support. Simion et al. (2017) used several matrices in their analysis of which we use three here: Si1, Si2, and Si3. These three matrices differ in taxonomic coverage, in the number of amino acid positions included in the matrices, and in how the amino acids were coded. All three matrices as analyzed by Simion et al. (2017) showed Porifera as the SOM with full bootstrap support for most likelihood models used in that paper—the only cases in Table 1 where Ctenophora is not inferred as the SOM. In their reassessment of Wh1 and Ch1, Feuda et al. (2017) rescored these previously published data sets to conform to different rescored amino acid rules (see Materials and Methods section). This recovered Porifera as the inferred SOM in most cases reported by Feuda et al. (2017)—we did not reproduce this result in our analyses of the exemplar matrices ( 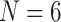and 11; see Table 1); however, we used a different model.

For morphology, four of the published data sets placed Porifera as the inferred SOM (Zrzavý 1998; Peterson and Eernisse 2001; Brusca and Brusca 2003; Glenner et al. 2004), while two studies (Backeljau 1993; Schierwater et al. 2009) posited Placozoa as the inferred SOM (Table 2). Four of the studies combined molecular information (always 18S rDNA) with morphology (Zrzavý 1998; Peterson and Eernisse 2001; Glenner et al. 2004; Schierwater et al. 2009), and all combined matrices produced the same result as the morphological matrices from each study (i.e. inference of Porifera as the SOM for Eer, Gle, and Zrz; and Placozoa as the SOM for Sch).

Individual Morphological and Phylogenomic Analyses: Reporting on our individual analyses, all of the molecular matrices in this study, regardless of the analysis type, always inferred Ctenophora as the SOM (Table 1), with high bootstrap proportions (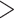95%) at the critical node. This pattern includes the three Si data sets, which in the original publication (Simion et al. 2017) resulted in Porifera inferred as the SOM. The reasons for this could be the difference in taxon sampling and the models we applied. In contrast, none of the morphological matrices inferred Ctenophora as the SOM, regardless of the analysis type. Instead, 21 of 36 individual analyses recovered Porifera, and 15 of 36 inferred Placozoa as the SOM with high bootstrap proportions of 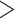95% (Table 2). This clear distinction between molecular and morphological data sets holds regardless of the number of taxa used in the analysis (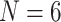, 11, or “full”). Evidently, there are strong and contrasting phylogenetic inferences derived from phylogenomic (Table 1) and morphological (Table 2) data.

Ratios of Phylogenomic to Morphological Characters: The ratios of informative molecular to morphological characters are reported in Supplementary File S4 available on Dryad. Even the smallest molecular data matrices (Wh2: 3615 informative characters for N6; Ch2: 10,871 informative characters for 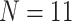; and Ch2: 23,144 informative characters for 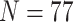/“full”) when compared to the largest morphological matrices (Com: 52 informative morphological characters for 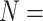6; Zrz: 72 informative characters for 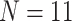; and Zrz: 252 informative characters for 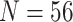/ “full”) give ratios of 70:1, 151:1, and 92:1, respectively.

The largest ratios result from combining the largest molecular matrix (always Si3 with 47,803 informative molecular characters for 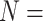6, 144,147 informative characters for 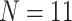, and 310,886 informative characters for 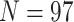/“full”) with the smallest morphological matrices (Bak = nine informative morphological characters for 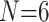, Bak = 16 informative characters for 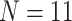, and Sch 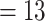informative characters for 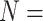9/“full”) and go up to 5311:1, 9009:1, and 23,914:1, respectively. In other words, each morphological character in our analyses is combined with 70 to 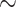24,000 molecular characters.

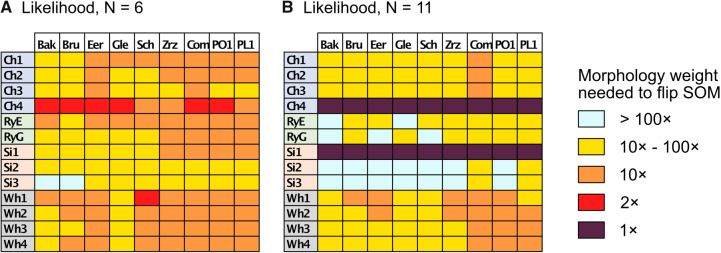
Combined Analyses of Small Exemplar Matrices (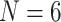 and 11): The results of the combined morphological/molecular analyses under likelihood using C10 are given in Figure 1. Likelihood analyses using other models (WAG, CAT, LG+CAT, WAG, and C10) are included in Supplementary Figure S1 available on Dryad. With some likelihood models and data set combinations, the inferred SOM is flipped from Ctenophora to Porifera or Placozoa at the lower morphological character weights applied in this study. Most matrices flip with morphological character weights of 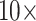, while some of the Ch and Wh matrices flip at morphological weights of 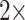for 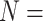6. For C10, 55.5% of the data set combinations flip by 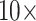morphological character weight, and the majority are flipped by 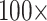weighting. The exceptions to this rule are the Si2 and Si3 (and in some cases RyE and RyG) phylogenomic data sets, which are mostly immune to flipping with weights up to .

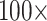Figure 1.

Molecular topology stability heat maps for the likelihood analyses using combined exemplar molecular (C10)/morphology (Mk) data sets for six (a, left) and 11 (b, right) taxa. The stability of the molecular topology is greater when the flip from Ctenophora to another SOM requires a higher weighting of morphological characters.

The results of the combined morphological/molecular analyses using the LGX2 amino acid weighting matrix under parsimony are shown in Figure 2. Parsimony analyses using other weighting matrices (PAM250, LGM2, or WAG) as well as analyses for “unweighted” molecular characters are included in Supplementary Figure S2 available on Dryad. For the LGX2 amino acid weighting matrix, flipping the inferred SOM from Ctenophora to Placozoa or Porifera in all data set combinations is accomplished with morphological weights less than 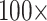, and the grand majority are flipped with weights less than 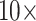. In general, then, it appears that Ctenophora is less stable as the inferred SOM using parsimony than likelihood, except when the PAM250 scoring matrix is used in parsimony (see Supplementary Fig. S2 available on Dryad). For instance, the Ch matrices get flipped to Porifera (or Placozoa in some cases) when combined with most morphological matrices under comparably low weighting (equal weight or 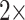weighting). But the two larger of the three Si matrices only flip at 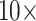weighting or 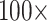weighting.

Figure 2.

Molecular topology stability heat maps for the parsimony analyses using combined exemplar molecular (LGX2)/morphology (no transformation) data sets for six (a, left) and 11 (b, right) taxa. The stability of the molecular topology is greater when the flip from Ctenophora to another SOM requires a higher weighting of morphological characters.

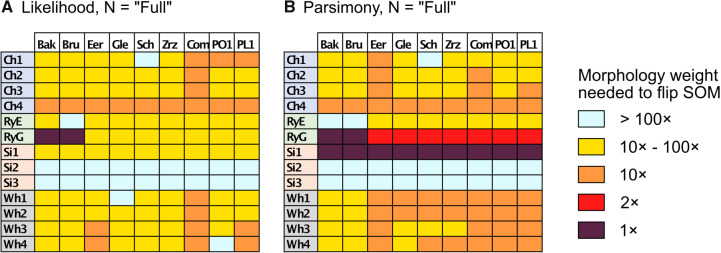
“Full” Data Matrices: The larger matrices (“full” taxon representation) in general show a greater topological stability than the exemplar data sets, and are only impacted by adding morphology between 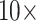and 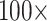character weighting under both parsimony and likelihood, in most cases. There are some exceptions, though, especially under parsimony. Figure 3 compares the results for the “full” matrices using likelihood (model C10) and parsimony (amino acid weighting matrix LGX2 scoring matrix). For both parsimony and likelihood, about 35% of the “full” matrices flip at morphological weights of 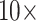or less (81 of 234), and 82% flip at morphological weights of 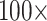or less (191 of 234; Fig. 3). Specifically, the Si2 and Si3 matrices, as well as the Si1, RyG, and RyE matrices in singular cases, do not flip until between 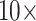and 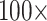morphological weights, or more. However, Si1 flips when only 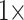weighting is applied to any morphological matrix with the “full” data sets, and the combined morphological matrix flips all of the Ch, Wh, and Ry molecular matrices regardless of optimality criterion. Overall in our “full” analyses, those molecular data sets with the highest degree of taxon sampling among them are more resistant to being flipped through the influence of adding morphological characters.

Figure 3.

Molecular topology stability heat maps comparing the weights at which the flip from Ctenophora to another SOM occurs for the “full” taxa data sets for the C10 model with Mk for morphology (a, left, likelihood) and the LGX2 transformation matrix with no transformation for morphology (b, right, parsimony). The stability of the molecular topology is greater when the flip requires a higher weighting of morphological characters.

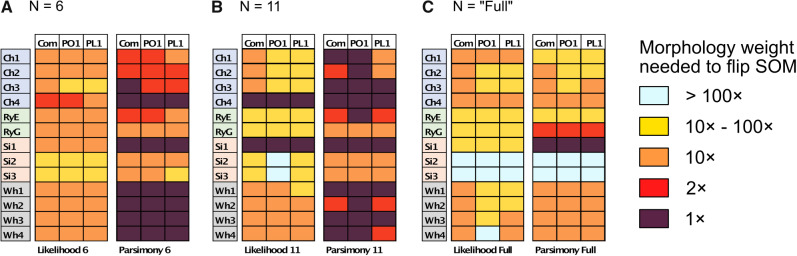
Combined Morphological Matrix: There are no reasons obvious for us to prefer any of the morphological characters used in one study over those of another. The individual studies from the literature more often show Porifera as the inferred SOM, but when we combine the morphological influence of all these studies, we infer Placozoa as the SOM in all cases except for the likelihood analysis of the six-taxon data set (see the Com results in Table 2). Our combined matrix of 61 phylogenetically informative characters changes the inference for all molecular matrices in almost all analyses with weighting below 100 (Fig. 4).

Figure 4.

Molecular topology stability heat maps comparing the weights at which the flip from Ctenophora to another SOM occurs when combined with our three curated morphological matrices Com (our combined matrix), PL1 containing only characters that support Placozoa as the SOM, and PO1 containing only characters that support Porifera as the SOM (see Materials and Methods section). Shown are our analyses for six taxa (a), 11 taxa (b), and “full” taxa (c), each for likelihood using the C10 model on the left, and for parsimony using the LGX2 amino acid transformation matrix on the right. The stability of the molecular topology is greater when the flip requires a higher weighting of morphological characters.

Discussion

Overview: This study gives an idea of how strong and how consistent the influence from genome-scale molecular and morphological data can be when combined. Our results suggest several important ideas about phylogenetic analysis of difficult to resolve nodes like the SOM node. First, morphological characters indeed can have an important role in influencing phylogenomic data sets, because, contrary to the prevailing genomic swamping assumption, they are not always readily overcome by genomic data for the SOM node. Second, the standard support measures for maximum parsimony, maximum likelihood, and Bayesian phylogenetic methods do not allow a satisfactory interpretation of the stability of phylogenomic inferences—simple addition of morphological data can “destabilize” inferred topologies with maximum support values, at least after upweighting. Third, taxon sampling is important in phylogenetic studies as our comparisons of 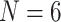, 11, and “full” matrices show. The more taxa in an analysis, the harder it is for morphological data to flip the molecular hypotheses. In this context, our data can also be seen as a quantification of how strongly the choices of optimality criterion, molecular model, and weighting scheme will influence the topological stability of molecular data sets when combined with morphology—or vice versa. Our results suggest that combined analyses may be highly sensible. Morphology can be added to molecular data quite easily with both likelihood and parsimony criteria and can have a huge impact even under low weighting schemes, which suggests that it should not be left out without consideration. Rather, we encourage phylogeneticists to study morphology in order to go beyond molecular sequence data but also novel morphological evidence.

Weighting Morphological and Phylogenomic Data: Weighting characters a priori is usually subjective. Indeed, many of the morphological characters in this study had been curated by the morphologists and exclude characters they may not see as homologous, so some degree of subjective weighting had already been applied to these partitions before our current analyses. We do not aim to lay claim to an objective weighting scheme in the present study. Instead, our study is the first exploration of the weighting space for the SOM question, and our results of when the inferred SOM “flips” from one taxon to another show informative patterns across the different data sets. Our analyses thus allow a new way of comparing the topological stability of these data sets: The “flipping” patterns show clear differences to the distribution of character ratios between morphological and molecular data, in both the “full” and exemplar analyses (Compare Figs. 1–3 with Supplementary File S4 available on Dyrad)—this means that the number of characters and the number of taxa are not all that define the topological stability. We are therefore tempted to interpret that those molecular data sets that are more resistant to flipping have fewer incongruencies than those that flip more readily—and, thinking in the other direction, those morphological data sets that flip the same molecular data set with minimal weight appear to be the most congruent.

Almost all of the molecular matrices—exemplar and “full”—can be flipped with morphological weighting between 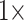and , under parsimony and likelihood. In some of our analyses, simple addition of “unweighted” morphology flips the inferred SOM from Ctenophora to Porifera or Placozoa. Some data sets, such as the Ch and Wh data sets, are particularly easy to flip. Others, such as the Si1, Si2, and Si3 data sets are more difficult to flip, but nevertheless they can be with 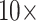weighting of some morphological matrices. In general, the molecular topologies are more stable under likelihood, but can sometimes also be flipped with less than 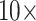weighting of morphology on the exemplar data sets ( 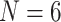and 11) and between 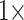and 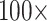weighting in the “full” data sets.

Ratios of Phylogenetically Informative Characters: We here aim to contextualize the weighting we carried out by comparing the ratios of molecular to morphological characters in our analyses, which seem to provide both a sense of the magnitude of the range in weighting schemes we apply here and an idea of how strong the influence of adding morphological characters might be. The ratios of phylogenetically informative molecular to morphological characters range from 70:1 to 23,914:1 (Supplementary File S4 available on Dryad). That is, each morphological character is outnumbered between 70 and 24,000 times by molecular characters in the combined analyses. This suggests that weighting morphological characters by , for example, may not be a drastic weighting scheme, particularly when considering the evolutionary significance and genetic complexity of morphological features. Even when the number of phylogenetically informative molecular characters is up to four orders of magnitude greater than that of morphological characters, we still see a flip to what the morphological data suggests after relatively little weighting. For example, Si3 has over 9000 molecular characters for each morphological character in Bak, yet weighting the latter 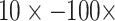will flip the topology in the exemplar parsimony analyses. Another example: Si1 has around 7000 molecular characters for each morphological one in Sch, but adding it with equal weighting ( 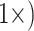flips the topology in the “full” parsimony analysis. In fact, almost all matrices flip at or below 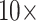for the exemplar parsimony approaches (Fig. 2).

In light of these results, we can update Giribet’s (2010) observation that the contribution of morphology can be strong when the ratio of morphological characters to molecular characters is within an order of magnitude: Morphological characters can retain strong phylogenetic influence in studies with molecular character numbers of even up to four orders of magnitude greater. Unlike the assertion of Giribet (2010), we only look at a single unstable node, though, and more stable molecular relationships still may swamp out conflicting morphologically supported relationships. However, most of the “important” open phylogenetic questions are unsolved because of node instability. Comparable additions of morphological data to phylogenomic assessments may prove similarly useful for other disputed relationships, such as those within the deuterostomes and the Trochozoa.

When thinking about the ratios presented here, it is also worth mentioning that recent methodological developments are enabling morphologists to assess many more characters than more traditional studies could (Heiss et al. 2013; Tessler et al. 2016; Heiss et al. 2018; Catalano et al. 2019). This implies that the morphological data sets used here may leave out characters that new methods could possibly retrieve in future publications. A subset of these could be phylogenetically informative regarding the SOM question and may thus lower the ratios in the future. Still, it appears certain that next generation sequencing will continue to provide molecular character numbers on a scale unreachable by even the most elaborate quantitative morphological methods.

It is also important to consider that the variability of morphological characters can be quite different from that of molecular characters. Morphologists have long discussed the differences between characters, for example, when dental characteristics inform a different tree topology than nondental morphology, which some researchers have attributed to selection pressures acting somewhat independently on the different 3D body parts (Gaubert et al. 2005; Kivell et al. 2013; Mounce et al. 2016). The way that we often think about a sequence of molecular characters, on the other hand, is arguably 1D. This makes them easy to work with computationally, and it suggests an equivalency. Yet, there are issues around variability that are unique to molecular characters. Different parts of the same sequence can evolve at diverse rates, and mutational saturation effects can cloud the search for true signal (Brown et al. 1979; Wilke et al. 2009). High among-site variation of substitution rates can similarly lead to a lower effective evolutionary signal in a given sequence (Gu et al. 1995; Sullivan et al. 1995; Hong-Wen and Yun-Xin 2000; Buckley et al. 2001).

When we reflect on the underlying reasons for molecular variability, where different functional parts (genes) are subject to quite different evolutionary pressures, we find that this somewhat mirrors the case of morphology. In the end, the patterns of molecular variability emerge from selection working on morphological phenotypes, and accordingly morphology influences molecules and vice versa (Zhang and Yang 2015; Echave et al. 2016). All this illustrates that to some extent, the ratios depend on what data sets one uses, and are not without bias. This being said, we find it significant that when a few dozen morphological characters are outnumbered by orders of magnitude, they can often flip even the most comprehensive genomic topologies in the current literature.

The Influence of Taxon Number and Optimality Criterion on Topological Stability: There is a strong impact of taxon sampling on these analyses, as the molecular inference of Ctenophora as SOM is more stable in the “full” matrices relative to the smaller exemplar matrices, and in the molecular data sets with the most taxa (the Si matrices). This corroborates the notion that greater taxon sampling will improve the topological stability of a phylogeny. It is important to note in this context that even the “full” matrices that we could access from the published literature addressing the SOM question by no means resemble a “complete” taxon sampling. For example, if these studies had included the million or more arthropod species rather than one, the numbers of phylogenetically informative characters might differ from what we find and report here.

Figure 4 shows the stability of tree topologies when the underlying molecular data sets are combined with our curated morphological matrices Com, PO1, and PL1. When these highly consistent morphological character matrices (PL1 and PO1) are combined with molecular data, most of the molecular matrices are flipped between 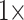and 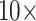weighting, whether parsimony or likelihood is used with the exemplar data sets, and in half of the “full” analyses. The results of our concatenation study show just how heavily the inferred answer to the SOM question depends on the optimality criterion applied, and on the level of taxon sampling. We interpret this to mean that we will need to improve taxon sampling further for both molecular and morphological characters in order to arrive at a more stable inference.

What is the SOM? The original studies using the Ryan et al. (2013), Chang et al. (2015), and Whelan et al. (2015) matrices hypothesized Ctenophora as the SOM. Feuda et al. (2017) and Simion et al. (2017) point out that if improved models of compositional and among-site heterogeneity are incorporated into the analysis of these data, then Porifera is inferred as the SOM instead. Specifically, they show that amino acid recoding (addressing compositional heterogeneity) and a specific model accommodating site-specific amino acid preferences (CAT-GTR+G) resulted in rejection of Ctenophora as the inferred SOM. We show here for small exemplar data sets (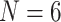 and 11) that the Whelan et al. (2015), Ryan et al. (2013), and Chang et al. (2015) data sets can all similarly be flipped to infer Porifera or Placozoa as the SOM by simply adding weighted morphological data—frequently with less than 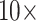morphological weight to molecular weight in both parsimony and likelihood analyses.

For parsimony, we note that a very simple transformation matrix (PAM250) does not flip Ctenophora from being inferred as the SOM very easily, but increasingly complex transformation matrices (WAG, LGM2, and LGX2), facilitate flipping to the morphological inference (Supplementary Fig. 2 available on Dryad). Interestingly, the molecular topological stability decreases when applying the simpler transformation matrices (PAM250 and WAG) when compared to “unweighted” parsimony (i.e., without accommodating for substitution saturation and rate heterogeneity). The more elaborate transformation matrices LGM2 and LGX2, on the other hand, lead to increased topological stability for the inference from molecular data. In general, the topological stability of the genomic data sets supporting Ctenophora is greater under likelihood than with parsimony for both exemplar data sets and the “full” data sets.

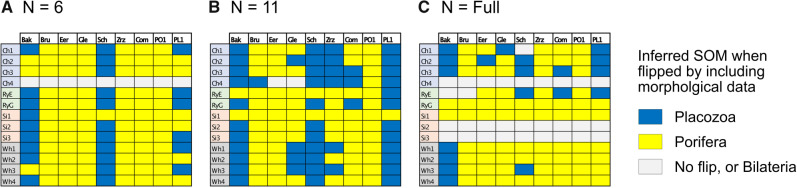
We thus report that the addition of morphological characters to phylogenomic data under certain weighting schemes infers Porifera as the SOM, shifting away from the recent preference for Ctenophora as the inferred SOM (Ryan et al. 2013; Chang et al. 2015; Whelan et al. 2015). Figure 5 shows the taxon inferred as the SOM in the LGX2 scoring matrix parsimony analyses. Under this weighting scheme, the SOM flips to Porifera in 217 out of 351, or 62%, of analyses (from 58% for 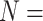“full” to 82% for 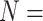6; Fig. 5). Approximately 27% of the analyses flipped to Placozoa as the inferred SOM (94 out of 351 analyses; most notably in the Bak, PL1, and Sch combinations with phylogenomic matrices). The rest either flipped to Bilateria, or did not flip away from Ctenophora even after 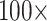weighting of morphology. It should be noted that the different data sets are not fully independent, but share varying numbers of characters. Accordingly, the percentages of analyses that flip should be taken with a grain of salt.

Figure 5.

The inferred SOM when flipped by combined parsimony analysis using the LGX2 amino acid transformation matrix and weighting morphology by 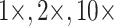, or 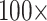. White indicates that no flip occurred (as in the Si2 and Si3 combined matrices) or that the flip was to Bilateria (as in the Ch4 matrix). Results for the exemplar taxon sets are shown in a (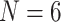) and b (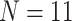), and the results for the “full” taxon data set are shown in c.

We are not aware of any way to test if the morphological data available for the SOM question carries “true” signal, or rather indifferent or even actively misleading noise. If we were to assume that the morphological traits in the data sets we used mostly carry high-quality phylogenetic signal, then we could consider them arbiters of the long standing SOM question. Then we might conclude that the addition of morphology pushes Ctenophora out of the inferred SOM position in the vast majority of weighting and modeling schemes applied to the matrices in this study, and mostly inserts Porifera (in 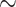62% of our analyses), or sometimes Placozoa (in 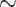27% of our analyses). If we assumed that the morphological influence mostly represents misleading noise, then our results would simply show that the molecular influence is surprisingly weak. Either way, these results are a reason to be cautious when solely relying on molecular data to answer the SOM question. Accordingly, until a proper weighting scheme is developed, more data are collected, and more refined analyses are done, this phylogenetic question remains unresolved.

Are Morphological Characters Worth Adding to Phylogenomic Data Sets? Conflicting inferences from different data types always have and will be an inevitability in phylogenetic analysis. Early conflicting systems in phylogenetics did not only include morphological versus molecular data, but for the most part conflict was drawn out of comparing different kinds of morphological data such as soft tissues versus fossilizable structures (Mounce et al. 2016). Indeed, the nature of phylogenetic analysis is that any individual character can be in conflict with any other character. Morphologists have given much thought to the problems involving phylogenetic data sets. Jenner (2003, 2004) suggested that morphological data sets needed to be expanded for questions involving Metazoa. His focus was on morphological characters as arbiters of phylogenetic accuracy, and he argued more or less for a separation of molecular and morphological data, and a larger focus on morphology for testing hypotheses about phylogenetic relationships.

More recently, Scholtz (2010) suggested that “if morphological and molecular results clash, there is no logical necessity to dismiss morphological data”, an idea that has been around since Kluge (1989) made his “total evidence” argument and Nixon and Carpenter (1996) expanded the idea into “simultaneous analysis”. However, this suggestion has been countered by Wanninger (2015) and Lee and Palci (2015) who state that the role of morphology in modern systematics, according to the former, is “to understand how phenotypic diversity evolved” and, according to the latter, is important in “time-scaling phylogenies.” Both of these publications imply that while morphological characters are important, they are somewhat irrelevant to the actual construction of phylogenetic trees for extant taxa. Their reasoning is based on the idea that the plentitude of phylogenomic molecular characters simply swamp the morphology, which we show here is not the case for at least one node of importance and could similarly prove not to be the case for other nodes that have weak support from molecular data. This leaves only one sound reason for excluding morphology from phylogenetics: If it could somehow be proven that the influence from morphology is in fact misleading from the true signal in a specific case. Testing this is typically impossible, as in the case of the SOM question, so why not include as much data as possible?

Our observation also means that “molecular morphology” (Rokas and Holland 2000; Ender and Schierwater 2003; Maeso et al. 2013) might be combinable with sequence data to sort out the inconsistencies in molecular data, as well. Molecular morphology characters include 3D stem and loop folding structures (Ender and Schierwater 2003; Edger et al. 2014; Desalle et al. 2017), near intron pairs (NIPs—Krauss et al. 2008), and overall chromosome or genome structure (Maeso et al. 2013; Eitel et al. 2018), among others.

Measures of Support and Flipping Hypotheses: Our results suggest that Bayesian, likelihood, and parsimony support measures often fail to adequately assess topological stability, even of phylogenies based on the largest current data sets. The Wh, Ch, Si, and Ry data sets all show high node support (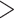95% bootstrap percentage and 1.0 Bayesian posterior probability) in their original publications and in our reanalyses for the SOM node. Yet, the addition of a small set of morphological characters (either equally or lightly up-weighted) can change the inferred SOM for many of these data sets. The suggestion that measures of support or stability based on bootstrap and Bayesian posteriors in phylogenomic data sets may be misleading has led to the suggestion that other support analyses are needed. Siddall (2010) developed the partition bootstrap method, and Narechania et al. (2012) presented the random concatenation approach (RADICAL), among others. These methods attempt to take into consideration the interaction of partitions in large molecular data sets and can be performed under parsimony and likelihood.

We note that the results of our weighting space analysis, the patterns of “flipping points,” carry a novel type of information about the phylogenetic stability of matrices. First, they show that the larger molecular data sets (both in number of taxa and informative characters) have greater topological stability. Second, when seen in combination with the ratios of phylogenetically informative characters (Supplementary File S4 available on Dryad), they allow a new way of identifying which data sets are more heavily influenced by the other datatype, suggesting a higher degree of incongruencies in the data. At the same time, this can allow us to identify the most stable morphological data sets. Third, we further imagine this to be a new way to assess the comparability of new data sets, free from some of the shortcomings of traditional support measures (e.g., bootstraps). Ultimately, a weighting space assessment could be developed into an interesting sensitivity analysis tool.

Conclusion

A lot is to be learned from quantifying the influence of different data types where they lead to conflicting hypotheses instead of a priori dismissing one of the data types. We here show the usefulness of exploring the weighting space for combined analyses of molecular and morphological data and suggest that this should become a more widely used procedure for testing the robustness of phylogenetic trees.

Exploring how one’s data set behaves in the weighting space compared to other data sets from the literature can provide a good measure of congruency and topological stability. Also performing differential weighting analysis to a lesser extent than this study may provide valuable information. Indeed, the solution to the SOM problem may not only lie in finding the model that best accommodates the different types of molecular heterogeneity (Feuda et al. 2017; Simion et al. 2017), but also in incorporating morphological data—the phylogenetic signal it contains may in turn help sort out the phylogenetic signal from the molecular data.

Supplementary Material

Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.prr4xgxhf.

Funding

US Department of Energy BER Award DE-SC0014377. The Korein Family Foundation Lewis and Dorothy Cullman Program in Molecular Systematics.