Abstract
Phylogeny estimation is a major step in many biological studies, and has many well known challenges. With the dropping cost of sequencing technologies, biologists now have increasingly large datasets available for use in phylogeny estimation. Here we address the challenge of estimating a tree given large datasets with a combination of full-length sequences and fragmentary sequences, which can arise due to a variety of reasons, including sample collection, sequencing technologies, and analytical pipelines. We compare two basic approaches: (1) computing an alignment on the full dataset and then computing a maximum likelihood tree on the alignment, or (2) constructing an alignment and tree on the full length sequences and then using phylogenetic placement to add the remaining sequences (which will generally be fragmentary) into the tree. We explore these two approaches on a range of simulated datasets, each with 1000 sequences and varying in rates of evolution, and two biological datasets. Our study shows some striking performance differences between methods, especially when there is substantial sequence length heterogeneity and high rates of evolution. We find in particular that using UPP to align sequences and RAxML to compute a tree on the alignment provides the best accuracy, substantially outperforming trees computed using phylogenetic placement methods. We also find that FastTree has poor accuracy on alignments containing fragmentary sequences. Overall, our study provides insights into the literature comparing different methods and pipelines for phylogenetic estimation, and suggests directions for future method development. [Phylogeny estimation, sequence length heterogeneity, phylogenetic placement.]
Phylogeny estimation is well known to have many computational and statistical challenges. One basic problem is estimating multiple sequence alignments, which is a standard precursor to a phylogeny estimation pipeline, and yet can have poor accuracy for large heterogeneous datasets. Progress on large-scale multiple sequence alignment over the last decade has resulted in many methods that are able to scale to very large datasets (e.g., with 10,000 or more sequences), including Clustal-Omega (Sievers et al., 2011), SATé (Liu et al., 2009; Liu et al., 2012), PASTA (Mirarab et al., 2015), Kalign3 (Lassmann, 2019), and a recent “regressive" method (Garriga et al., 2019). Once the alignment is estimated, the most accurate trees are often obtained using either heuristics for NP-hard optimization problems, such as maximum likelihood, or MCMC sampling of treespace, both of which result in substantial computational burdens when the number of sequences is large. Some very fast methods for maximum likelihood exist, such as the polynomial time method FastTree2 (Price et al., 2010) (now generally referred to just as FastTree), but FastTree is not as effective at the maximum likelihood optimization problem as other heuristics that make a significant attempt to search treespace, such as IQtree (Nguyen et al., 2015), PhyML (Guindon and Gascuel, 2003), and RAxML (Stamatakis, 2014).
Yet despite these advances in phylogeny estimation, there are still substantial challenges that remain, one of which is how to estimate a tree on a single gene when the sequence dataset contains substantial heterogeneity in sequence length. For example, Figure 1 shows the histograms of sequence length heterogeneity in four biological datasets, each of which has substantial sequence length heterogeneity, including many very short sequences.
Figure 1.
We present Figure 1 from Nguyen et al. (2015) (reprinted with permission under the Creative Commons Attribution (CC-BY) license), showing the histograms of sequence lengths for four biological datasets (two RNA datasets and two AA datasets).
In this paper we explore challenges in tree estimation when the datasets contain “fragmentary sequences" (i.e., sequences that are homologous only to a short region within the full-length alignment), as discussed in Sayyari et al. (2017) and Nguyen et al. (2015). Fragmentary sequences can result naturally from evolutionary processes that include loss of large genic regions, but other causes include choices made by the biologist for primer selection, and using reads or contigs for some taxa instead of fully assembled genes (due to assembly challenges or specific sequencing technologies).
To avoid possible confusion, we note an important distinction from other types of missing data. “Fragmentary” sequences, as explained above, are short, but contiguous sequences–data are assumed to be missing from around the fragment, but not from within it. By contrast, “sparse” or “gappy” sequences would be missing data throughout the sequence, not necessarily in continuous blocks. These two forms of missing data would have different effects on phylogenetic methods. In this paper, we concern ourselves specifically with the “fragmentary” case.
One approach is to estimate an alignment on the dataset and then compute a tree on the alignment, for example using maximum likelihood methods. However, as shown in Nguyen et al. (2015), standard approaches for aligning datasets with high levels of fragmentation have high error, requiring the use of different approaches that are better able to align datasets with fragmentary sequences (e.g., approaches that enable local alignment rather than global alignment). One such method is UPP (Nguyen et al., 2015), which combines PASTA (to align the full-length sequences) with a technique based on a hierarchical ensemble of profile Hidden Markov Models (Krogh et al., 1994; Durbin et al., 1998), to add the fragmentary sequences into the alignment of full-length sequences; this combination of local alignment (enabled through the use of profile Hidden Markov Models, i.e., pHMMs) and divide-and-conquer (to produce the ensemble) enables UPP to achieve high accuracy, even as the number of fragmentary sequences increases, and trees estimated on these alignments are consequently more accurate. However, getting a good alignment is not enough, as the second step of the tree estimation also presents challenges: a recent study (Sayyari et al., 2017) showed that FastTree, a fast maximum likelihood heuristic, can have poor accuracy on datasets that contain both fragmentary and full-length sequences, even when given the true alignment. Thus, this two-phase approach “first align, then compute a tree", which is commonplace in phylogenetics, presents additional complications for datasets with fragments.
Although phylogenetic placement, an approach designed for taxon identification and comparison of reads (Matsen et al., 2010; Matsen and Evans, 2013), was not developed for the purpose of estimating trees, here we investigate the accuracy of tree estimation methods that use phylogenetic placement, using the following protocol. Given a dataset containing full-length and fragmentary sequences, an alignment and a tree can be computed on the full-length sequences (subsequently called the “backbone alignment" and “backbone tree"), the fragmentary sequences can be added into the backbone alignment, and then a “phylogenetic placement" method, such as pplacer (Matsen et al., 2010), EPA-ng (Barbera et al., 2018), and APPLES (Balaban et al., 2020), can be used to add the fragmentary sequences into the backbone tree.
The technique for adding fragmentary sequences into backbone alignments impacts the final tree accuracy, and several techniques have been developed for this step. In particular, SEPP (Mirarab et al., 2012), which is a precursor to UPP, constructs a (relatively simple) ensemble of profile HMMs and provides improved accuracy compared to a single profile HMM. Once the extended alignment is computed, the fragmentary sequence can be added to the tree optimizing various criteria; for example, pplacer and EPA-ng use maximum likelihood to place the fragmentary sequences, while APPLES uses a distance-based criterion. Balaban et al. (2020) compared three phylogenetic placement methods, EPA-ng, pplacer, and APPLES, and found that the optimal choice of phylogenetic placement method depends on the number of leaves in the backbone tree (equivalently, the number of sequences in the backbone alignment). Specifically, when the backbone tree is not too large (e.g., below 5000 sequences) then pplacer has the best accuracy, but pplacer can fail on larger backbone trees (Linard et al. 2019; Balaban et al. 2020, both papers note “numerical issues” past about 5000 sequences), making it necessary to use alternative methods, such as APPLES. Furthermore, APPLES improved on EPA-ng, and is a very fast polynomial time method that enables phylogenetic placement into very large backbone trees. Hence, Balaban et al. (2020) found that two major competing phylogenetic placement methods are pplacer (which should only be used when the backbone tree is small enough) and APPLES (for larger backbone trees).
Thus, tree estimation from datasets containing a mixture of full-length and fragmentary sequences can be approached using two different protocols: the traditional MSA-ML approach (where an alignment is computed on the full dataset and then an ML tree is computed on the alignment) or phylogenetic placement-based approaches (where an alignment and tree are computed on the full-length sequences, and then the fragmentary sequences are added into the alignment and subsequently into the tree). Yet, to date, only one study (Janssen et al., 2018) has compared these two types of approaches to each other. The main purpose of Janssen et al. (2018) was to explore how phylogenetic placement using SEPP (to compute the alignment of amplicon reads) and pplacer (to place into a backbone tree) improved clinical discovery; however, they also provided a comparison of this placement-based approach (SEPP-pplacer) to a MSA-ML method they referred to as de novo. Their study showed that SEPP-pplacer produced more accurate trees than their de novo method, suggesting that placement-based methods should be considered for phylogeny estimation given unaligned fragmentary sequences. However, their study was limited to one model condition, and their de novo method used MAFFT for alignment of ultra-large datasets (10,000 fragments) and FastTree for tree estimation. Given that MAFFT is not as accurate on large datasets as PASTA and UPP (Mirarab et al., 2015; Nguyen et al., 2015) and FastTree is not as accurate as RAxML (especially given fragmentary sequences (Sayyari et al., 2017)), their study does not enable a full understanding of the relative performance of these two approaches. Addressing this question is the purpose of this study.
We evaluate different approaches to tree estimation on datasets with up to 1000 unaligned sequences, where all of the datasets are subjected to a process of fragmentation and contain some proportion of fragmentary sequences. Our study, which evaluates accuracy under a wide range of model conditions, shows clearly that pipelines that follow the two-phase paradigm “first align, then compute a tree on the alignment" have the best accuracy, but only if alignment and the tree estimation are performed using appropriate methods. In particular, we find that for datasets with fragmentary sequences, FastTree has poor accuracy compared to RAxML, thus supporting the findings in Sayyari et al. (2017), and that PASTA is not as accurate as some other methods, such as UPP. In particular, the most accurate method in our study computes an alignment using UPP and then a tree on the alignment using RAxML, and so is computationally intensive and may not be able to run on the ultra-large datasets being assembled. Therefore, we also provide a comparison of the best placement-based methods, as these are much less computationally intensive. Finally, our study suggests directions for future research.
Materials and Methods
Overview
We used nucleotide datasets from prior studies, which includes a combination of simulated and biological datasets, and made fragmentary versions of the datasets by randomly selecting some of the sequences and shortening them. For consistency, the same manual fragmentation procedures were applied to both the simulated and biological datasets; that is, we did not try identify or use fragments that might have been present in the biological data. We estimated alignments and trees on these modified datasets, each of which had at most 1000 sequences, using a variety of techniques (Tables 1 and 2). We evaluated the alignments and trees for accuracy by comparing them to the true alignments and trees for the simulated datasets and reference alignments and bootstrap trees for the biological datasets. Overall, we analyzed 120 simulated datasets from 6 model conditions (20 replicates per condition) and 2 biological datasets.
Table 1.
Base methods used in this study. Here, SEPP and UPP use ensembles of pHMMs (profiles of Hidden Markov Models) to compute extended multiple sequence alignments.
| Method | Type | Summary |
|---|---|---|
| PASTA | MSA/Tree co-estimation | Iterative divide-and-conquer MSA and tree co-estimation |
| UPP | MSA | Uses pHMMs to align sequences to a backbone alignment/tree |
| SEPP | MSA/ Placement | Uses pHMMs to align sequences to a backbone alignment/tree and pplacer for placement |
| RAxML | Tree estimation | A leading heuristic for ML tree estimation |
| FastTree | Tree estimation | A very fast but less accurate heuristic for ML tree estimation |
| pplacer | Phylogenetic placement | A leading phylogenetic placement method |
| APPLES | Phylogenetic placement | A fast and scalable distance-based placement method |
Table 2.
Pipelines used in this study. bb. = “backbone.”
| Pipeline | Type | Summary |
|---|---|---|
| PASTA-FastTree | MSA-ML | PASTA alignment on entire dataset  FastTree tree (PASTA default mode) FastTree tree (PASTA default mode) |
| PASTA-RAXML | MSA-ML | PASTA alignment on entire dataset  RAxML tree RAxML tree |
| UPP(F)-FastTree | MSA-ML | PASTA bb. alignment  FastTree bb. tree FastTree bb. tree  UPP alignment UPP alignment  FastTree tree FastTree tree |
| UPP(F)-RAXML | MSA-ML | PASTA bb. alignment  FastTree bb. tree FastTree bb. tree  UPP alignment UPP alignment  RAxML tree RAxML tree |
| UPP(R)-FastTree | MSA-ML | PASTA bb. alignment  RAxML bb. tree RAxML bb. tree  UPP alignment UPP alignment  FastTree tree FastTree tree |
| UPP(R)-RAXML | MSA-ML | PASTA bb. alignment  RAxML bb. tree RAxML bb. tree  UPP alignment UPP alignment  RAxML tree RAxML tree |
| UPP(F)-pplacer | Placement-based | PASTA bb. alignment  FastTree bb. tree FastTree bb. tree  UPP alignment UPP alignment  pplacer placement pplacer placement |
| SEPP(F)-pplacer | Placement-based | PASTA bb. alignment  FastTree bb. tree FastTree bb. tree  SEPP alignment SEPP alignment  pplacer placement pplacer placement |
| SEPP(F)-pplacer(c) | Placement-based | PASTA bb. alignment  FastTree bb. tree FastTree bb. tree  SEPP alignment and placement SEPP alignment and placement |
| UPP(F)-APPLES | Placement-based | PASTA bb. alignment  FastTree bb. tree FastTree bb. tree  UPP alignment UPP alignment  APPLES placement APPLES placement |
| UPP(R)-pplacer | Placement-based | PASTA bb. alignment  RAxML bb. tree RAxML bb. tree  UPP alignment UPP alignment  pplacer placement pplacer placement |
| SEPP(R)-pplacer | Placement-based | PASTA bb. alignment  RAxML bb. tree RAxML bb. tree  SEPP alignment SEPP alignment  pplacer placement pplacer placement |
| SEPP(R)-pplacer(c) | Placement-based | PASTA bb. alignment  RAxML bb. tree RAxML bb. tree  SEPP alignment and placement SEPP alignment and placement |
| UPP(R)-APPLES | Placement-based | PASTA bb. alignment  RAxML bb. tree RAxML bb. tree  UPP alignment UPP alignment  APPLES placement APPLES placement |
Datasets
We used sequence datasets from previous studies (Liu et al., 2011; Nguyen et al., 2015; Mirarab et al., 2015; Balaban et al., 2020); all datasets are available in public repositories associated with these prior publications. We limited the datasets to have at most 1000 sequences to enable us to run pplacer without concern for its failure on larger datasets (documented in Balaban et al. (2020) and Linard et al. (2019) and also to allow us to include RAxML analyses on these datsets.
We report empirical properties of the reference alignments for these datasets in Table 3. Specifically, for each dataset (or model condition), we report the number of sequences, average length of the unaligned sequences, average and maximum p-distances and percent gappiness in the reference alignment, and degree of resolution of the reference tree. The p-distance between two aligned sequences is the number of positions in which the two sequences are different and neither is gapped; we normalize these values by dividing by the number of total positions in which neither is gapped to produce a value between 0 and 1. The gappiness of an alignment is the percentage of the reference alignment that is occupied by gaps. Finally, the degree of resolution is the number of internal edges in the unrooted reference tree divided by the maximum possible (i.e.,  , where
, where 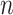 is the number of leaves).
is the number of leaves).
Table 3.
Dataset properties. Every statistic is computed per-replicate; statistics regarding fragments are obtained after making the alignments fragmentary (under the two fragmentation protocols), and the other statistics are based on the datasets before we introduce fragmentation for our experiments. The 1000M1–1000M4 and RNASim datasets are simulated, and we show results averaged over 20 replicates for each of these conditions. The last two columns indicate the number and average length of fragmentary sequences under low and high fragmentation conditions.
| Dataset | # Seqs. | Avg. p-distance | Max p-distance | % gaps | Avg. seq. length | Resolution | # Frags. (L/H) | Avg. frag. length (L/H) |
|---|---|---|---|---|---|---|---|---|
| 1000M1 | 1000 | 0.695 | 0.769 | 74.4 | 1011 | 99.6 | 250/500 | 505/252 |
| 1000M2 | 1000 | 0.684 | 0.762 | 74.2 | 1014 | 99.5 | 250/500 | 507/253 |
| 1000M3 | 1000 | 0.660 | 0.741 | 62.8 | 1008 | 99.4 | 250/500 | 504/252 |
| 1000M4 | 1000 | 0.495 | 0.606 | 60.5 | 1007 | 97.3 | 250/500 | 503/251 |
| RNASim | 1000 | 0.411 | 0.609 | 67.9 | 1555 | 100.0 | 250/500 | 777/388 |
| RNASim2 | 1000 | 0.378 | 0.455 | 64.4 | 1555 | 100.0 | 250/500 | 777/388 |
| 16S.M | 901 | 0.368 | 0.772 | 78.1 | 1036 | 46.9 | 225/450 | 518/259 |
| 23S.M | 278 | 0.397 | 0.703 | 83.7 | 1746 | 61.1 | 69/139 | 873/436 |
-
ROSE
The 1000M1, 1000M2, 1000M3, and 1000M4 model conditions are 1000-sequence nucleotide datasets that were simulated using ROSE (Stoye et al., 1998) for the SATé study (Liu et al., 2009). These datasets evolve with substitutions (under the GTRGAMMA model) and indels under varying rates of evolution; 1000M1 has the highest rate of evolution and 1000M4 the lowest rate. Each dataset has 20 replicates, and each replicate contains 1000 unaligned sequences each with approximately 1000 nucleotides. The reference trees are the “potentially inferrable model trees”, which are the model trees with the zero-event branches collapsed (i.e., these reference trees are not always binary). We obtained the resolution for 1000M1–1000M3 reference trees from Liu et al. (2009) (Table S7) and we calculated the resolution for the reference trees on the 1000M4 datasets (not provided in Liu et al. (2009)) to be 970/997=97.3%.
-
RNASim
We use the million-sequence RNASim dataset from Mirarab et al. (2015). Unlike the ROSE datasets, these were simulated under a non-standard model of evolution: the sites evolve under a non-homogeneous fitness model based on the energy of the RNA structure, and do not follow the standard phylogenetic model assumptions (e.g., that the sites evolve identically and independently down the tree, and that there is a single global substitution rate matrix applying to all the branches in the tree). We generated two datasets of 20 replicates each, with 1000 sequences per replicate. The first, “RNASim”, was compiled by just randomly sampling 1000 sequences from the full million-sequence set. The second, “RNASim2”, was built by randomly sampling 1000 sequences from two subsets of 500,000 taxa that form neighboring clades within the true tree. This produced dataets with lower average p-distance than the ROSE simulated datasets. The reference trees are computed by restricting the true tree to the taxon set of each replicate, and so are binary trees.
-
Biological Datasets
We use two biological datasets, 16S.M and 23S.M, from Cannone et al. (2002), which have reference alignments based on RNA structures. We use the cleaned reference alignments and bootstrap reference trees from Liu et al. (2009); the bootstrap reference trees were produced by running RAxML on the reference alignments and collapsing all edges with less than 75% bootstrap support (see the supplementary materials in Liu et al. (2009) for additional details).
We selected the ROSE nucleotide datasets to enable us to explore conditions with a range of overall evolutionary divergence (as measured using the average and maximum p-distance in the dataset), where sequence evolution is i.i.d., so that there is no model misspecification. The RNASim datasets enable us to explore conditions under more realistic model of sequence evolution than the ROSE datasets, and hence test methods under conditions with model misspecification. The biological datasets are included to provide additional insights into performance, but with the understanding that the true tree (and even the true alignment) are not known perfectly for these datasets. The two biological datasets have relatively high gappiness; this is particularly true for 23S.M, which is 78.1% gapped, making it (with respect to this property) the most challenging dataset we analyze.
It is well known that alignment and tree estimation are challenging on datasets that have large average p-distances (equivalently, low pairwise sequence identity) and this presents alignment challenges (e.g., see Sievers et al. (2011); Rost (1999)). The range in average p-distances for the simulated datasets we explore (i.e., 37.8–69.5%) is representative of the top 39% of the BRAliBASE dataset (Gardner et al., 2005), and enables us to explore how challenges in alignment estimation impact the choice of tree estimation strategy.
We made fragmentary sequence versions of these datasets, with two levels of fragmentation (low and high), reflecting the fraction of the sequences that are made fragmentary and the degree of fragmentation of these fragmentary sequences. Thus, we have two types of datasets, as follows:
Low fragmentation: 25% of the sequences are made fragmentary, average fragment length is 50% of the original median sequence length.
High fragmentation: 50% of the sequences are made fragmentary, average fragment length is 25% of the original median sequence length.
We followed the procedure used in Nguyen et al. (2015) to make the sequences fragmentary. The length of each fragment is drawn from a normal distribution with the desired mean and standard deviation 60. Given the fragment length distribution, the fragmented sequences are chosen at random, and each is cropped to a random substring of the desired length. The numbers and sizes of fragments in each dataset are indicated in Table 3. As noted before, for the purposes of all methods and evaluation that follows, the “fragmentary sequences” (or “fragments”) are specifically those that have been truncated by this procedure; they are not related to the “gappiness” measure in our dataset properties. We refer to the remaining sequences as “full-length” (or “backbone”) sequences.
Tree Estimation Methods
We computed trees on each dataset using one of two different protocols: one based on the standard two-phase approach (first align then compute a tree) and the other based on phylogenetic placement. We provide a concise glossary of each base method and protocol in Tables 1 and 2. A more detailed description of our protocols follows below.
Protocol 1: First align, then estimate an ML tree
The first protocol computes a multiple sequence alignment on the full dataset (including the fragments) and then runs a maximum likelihood heuristic on the multiple sequence alignment. For the multiple sequence alignment method, we use PASTA, SEPP, and UPP. PASTA is run in default mode, and so uses three iterations and returns the final alignment. SEPP and UPP use the following pipeline: first PASTA is run in default mode on the full-length sequences and a backbone tree is computed on the PASTA backbone alignment using an ML heuristic under GTRGAMMA (either FastTree or RAxML); this produces the backbone alignment and tree. Then, SEPP and UPP each builds an ensemble of profile HMMs using the backbone tree and alignment, and adds the fragmentary sequences into the backbone alignment. When the backbone tree is computed using FastTree, we will refer to this alignment estimation pipeline as SEPP(F) or UPP(F), and similarly when the backbone tree is computed using RAxML, we will refer to the pipeline as SEPP(R) or UPP(R).
For the final tree estimation method, we used FastTree and RAxML-NG (Kozlov et al., 2019) (henceforth referred to simply as RAxML) under the GTRGAMMA model, with the GTRGAMMA parameters estimated from the data. In all cases, the methods were run in default mode, with RAxML run with only one starting tree on the simulated replicates, and best-out-of-five on the biological datasets. We refer to each such pipeline with the pair “MSA-ML" where “MSA" refers to the multiple sequence alignment method and “ML" refers to the maximum likelihood heuristic.
For example, “PASTA-FastTree" refers to using PASTA to compute the multiple sequence alignment on the full dataset, followed by FastTree to compute a tree on the alignment, while “UPP(F)-RAxML" refers to using UPP(F) to compute the multiple sequence alignment on the full dataset followed by RAxML to compute a tree on the alignment. See Table 2 for a complete list of pipelines of this form.
Protocol 2: Placement-based methods
For the second protocol, we used PASTA (in default mode) to compute a backbone alignment and then a maximum likelihood heuristic to compute the backbone tree on the full-length sequences; we then computed an extended alignment for each fragmentary sequence and placed the fragmentary sequence into the backbone tree using a phylogenetic placement method. We refer to these collectively as “placement-based" methods. For the extended alignment estimation, we used SEPP and UPP, as described above, and for the phylogenetic placement method we used pplacer and APPLES. SEPP and UPP both use a backbone tree to produce the extended alignment, so the same backbone tree was used for the extended alignment and placement steps.
Analogously to our MSA-ML pipelines, we will refer to the placement-based methods with the pair “EA(B)-P”, where “EA” refers to the method for producing the extended alignment, “B” is the backbone tree estimation method, and “P” denotes the placement method. Thus, “UPP(F)-pplacer" refers to using UPP to compute the extended alignment with a FastTree backbone tree, followed by using pplacer to place the fragments into this backbone tree. We will refer to methods that use this protocol as “placement-based methods", since they use phylogenetic placement methods to compute the tree. Note that “UPP(F)” refers to exactly the same chain of program calls in both of our protocols; the extended alignment in the placement-based methods is the same as the MSA in the MSA-ML methods; the only difference is that in the placement-based methods, we retain the backbone tree as well.
Note that in a pipeline based on phylogenetic placement, two or more fragmentary sequences can be added into the same branch of the backbone tree; when this occurs, the resultant extended tree (which includes the fragmentary sequences as leaves) has a polytomy on that branch to which all the fragmentary sequences for that branch are attached. Thus, these pipelines can produce unresolved trees, and the potential to produce unresolved trees increases with the number of fragmentary sequences added to the backbone tree.
Evaluation
We evaluate the accuracy of each estimated tree 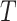 with respect to the reference tree
with respect to the reference tree 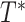 (i.e., either the model tree for simulated datasets or an estimated tree for the biological datasets) by using the FN (false negative) and FP (false positive) rates. The FN rate is given by
(i.e., either the model tree for simulated datasets or an estimated tree for the biological datasets) by using the FN (false negative) and FP (false positive) rates. The FN rate is given by 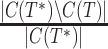 , where
, where  is the set of non-trivial bipartitions in tree
is the set of non-trivial bipartitions in tree  . Thus the FN rate is the fraction of non-trivial bipartitions in the true tree that the estimated tree fails to recover, with
. Thus the FN rate is the fraction of non-trivial bipartitions in the true tree that the estimated tree fails to recover, with  indicating complete recovery and
indicating complete recovery and 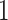 indicating complete failure. Similarly, the FP rate is given by
indicating complete failure. Similarly, the FP rate is given by 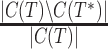 , and so is the fraction of incorrect bipartitions found in the estimated tree. When both the reference and estimated trees are fully resolved, then the FN and FP rates are identical, and both are equal to the well known Robinson-Foulds (RF) error rate (Robinson and Foulds, 1981). However, in our study the estimated trees are often incompletely resolved, which makes the use of the RF rate inappropriate (Rannala et al., 1998). We also had the additional challenge that the biological reference trees we used are far from fully resolved (Table 3). Thus, although there is clear appeal in having a single error metric for evaluating methods (for example, the FN and FP rates could be combined into a weighted sum, as suggested in Berry and Gascuel (1996)), we elected to continue with the use of two different metrics, FN and FP, noting that 1-FN corresponds to sensitivity and 1-FP corresponds to specificity. We also report the degree of resolution of the estimated trees.
, and so is the fraction of incorrect bipartitions found in the estimated tree. When both the reference and estimated trees are fully resolved, then the FN and FP rates are identical, and both are equal to the well known Robinson-Foulds (RF) error rate (Robinson and Foulds, 1981). However, in our study the estimated trees are often incompletely resolved, which makes the use of the RF rate inappropriate (Rannala et al., 1998). We also had the additional challenge that the biological reference trees we used are far from fully resolved (Table 3). Thus, although there is clear appeal in having a single error metric for evaluating methods (for example, the FN and FP rates could be combined into a weighted sum, as suggested in Berry and Gascuel (1996)), we elected to continue with the use of two different metrics, FN and FP, noting that 1-FN corresponds to sensitivity and 1-FP corresponds to specificity. We also report the degree of resolution of the estimated trees.
We evaluate the accuracy of the estimated alignments as follows. Every alignment can be described as a set of “homology pairs", which are the pairs of letters found in the same column of the alignment; the “homology" concept is fundamental in the MSA literature (Reeck et al., 1987; Morrison et al., 2015), and is used in several alignment methods, notably those that are based on “consistency", such as T-Coffee (Notredame et al., 2000). Thus, the true (or reference) alignment defines the true homology pairs, and the estimated alignment defines a set of estimated homology pairs. We compare two alignments by comparing the sets of homology pairs defined by the two alignments. We report SPFN (sum-of-pairs false negative, which is the fraction of the true homology pairs that are missing in the estimated alignment) and SPFP (sum-of-pairs false positive, which is the fraction of the homology pairs present in the estimated alignment that do not appear in the true alignment) rates, computed using FastSP (Mirarab and Warnow, 2011). For the simulated datasets the reference alignment is the true alignment, known to us because we perform the simulation; for biological datasets, we use the structurally-based alignment provided in Cannone et al. (2002).
Results
Alignment Error
Under low fragmentation (Supplementary Table 6 available on Dryad at http://dx.doi.org/10.5061/dryad.8pk0p2nj8), the trends are consistent across all datasets and for both SPFN and SPFP: the PASTA alignment has the highest error, while SEPP and UPP are very close, with a slight edge to UPP, and the choice of ML method to compute the backbone tree does not have much impact on SEPP or UPP. For all methods and both criteria, alignment error increases with the overall heterogeneity (e.g., on the ROSE datasets, the error rates are highest on 1000M1 and decrease as we move to 1000M4, and the error rates are higher for RNASim than RNASim2). Error rates on the RNASim and RNASim2 model conditions fall between those on 1000M2 and 1000M3, showing that these are harder model conditions than 1000M3 and 1000M4 and easier than 1000M1 and 1000M2. Alignment error rates on the two biological datasets are high, making them similar to 1000M1 and 1000M2. Results under high fragmentation (Supplementary Table 7 available on Dryad) show the same relative accuracy, but error rates are higher, and the differences between methods increase. Notably, under the high fragmentation conditions, PASTA increases in SPFN error, especially on the hardest model conditions, 1000M1 and 1000M2, where it has more than double the error rate of SEPP and UPP.
Tree Error
Because SEPP had slightly worse alignment accuracy than UPP, we omit it from the study for MSA-ML pipelines. However, we include SEPP in the study evaluating placement-based methods for the following reason: while SEPP has been tested for use with phylogenetic placement methods, UPP (which elaborates on SEPP) has not been.
For pipelines using pplacer, we consider the variant where we constrain the placement to the subtree selected by SEPP for aligning the query sequence, since this was how phylogenetic placement (based on SEPP and pplacer) was initially performed in Mirarab et al. (2012). We refer to this use of pplacer as “pplacer(c)", noting that otherwise pplacer allows the sequence to be placed anywhere in the backbone tree, and so is the unconstrained version.
Results for MSA-ML methods
Tree error rates are higher for the high fragmentation conditions than low fragmentation conditions, and for model conditions with high heterogeneity (i.e., high average p-distance), showing that the degree of fragmentation and rate of evolution impact error rates (see Supplementary Tables 8 and 9 available on Dryad). Furthermore, the differences between methods are highest for those conditions with high fragmentation and/or heterogeneity.
For each alignment method, using FastTree instead of RAxML increases the error rates, with large increases under high rates of evolution or high fragmentation. In general, the two pipelines with the highest FN error are PASTA-FastTree and UPP-FastTree, with PASTA-FastTree worse than UPP-FastTree for high rates of evolution and UPP-FastTree worse than PASTA-FastTree for low rates of evolution. Thus, FastTree produces trees with very high error rates for the high fragmentation condition. Finally, across all the simulated datasets and for both low and high fragmentation levels, the lowest FN rates are obtained by UPP-RAxML, for both ways of running UPP (i.e., with the RAxML backbone tree or the FastTree backbone tree), and the choice of backbone tree does not impact the resultant accuracy. Relative and absolute performance for FP rates are the same on the simulated data, which is consistent with the observation that the reference trees are nearly fully resolved.
We illustrate these trends by comparing the MSA-ML methods on the high fragmentation RNASim dataset (Fig. 2). The most accurate trees are obtained using UPP(F) or UPP(R) to estimate the alignment followed by RAxML to estimate the tree, and there is no detectable difference in accuracy between these two methods. The worst accuracy is obtained using FastTree on the UPP alignments, showing that FastTree degrades in the presence of fragmentation, compared to RaxML. Intermediate between these are the analyses using PASTA for the alignment, showing that PASTA is less accurate than FastTree in the presence of fragmentation.
Figure 2.
Tree error rates of MSA-ML methods on the RNASim dataset, under the high fragmentation condition. Errors indicate the false positive and false negative rates, and are averaged over 20 replicates. Error bars show standard error.
Because the biological reference trees have very low resolution (Table 3), FP rates are not helpful, and so we focus on the FN rates.
For both biological datasets and fragmentation conditions, RAxML produces more accurate trees than FastTree across all alignments. UPP-RAxML has a slight advantage over PASTA-RAxML on 16S.M (both fragmentation levels) and PASTA-RAxML has a slight advantage over UPP-RAxML on 23S.M (both fragmentation levels). Thus, the main trend here is that FastTree produces less accurate trees than RAxML on these data.
Results for placement-based methods
A comparison between placement-based methods shows a clear preference for MSA-ML pipelines, as illustrated in Figure 3 on the high fragmentation RNASim dataset (see Supplementary Tables 10 and 11 available on Dryad for the results on the full set of simulated model conditions and biological datasets, which show the same trends).
Figure 3.
Tree error rates of placement-based methods on the RNASim dataset, under the high fragmentation condition. Errors indicate the false positive and false negative rates, and are averaged over 20 replicates. Error bars show standard error.
The most noteworthy trend is that the pipelines that use APPLES for placing fragments have worse accuracy than the pipelines that use pplacer. Furthermore, the pipelines that use pplacer have fairly close accuracy for all simulated datasets, with an advantage to using UPP for the alignment estimation over using SEPP. Consistent with prior observations, the choice of ML heuristic for computing the backbone tree has little impact for the placement-based methods. SEPP-pplacer has an advantage over SEPP-pplacer(c), showing that constraining the placement (as is the default in Mirarab et al. (2012)) reduces accuracy.
As observed for the MSA-ML methods, error rates are higher on the RNASim datasets and 1000M1 conditions than on the other simulated datasets (and there are much larger differences between methods on these challenging datasets), and the lowest errors are obtained on the 1000M4 datasets.
Comparing MSA-ML and placement-based pipelines
We compare the different methods on the two biological datasets and a single (but representative) simulated model condition, the high fragmentation RNASim datasets (Fig. 4). The pipelines with FastTree backbones are nearly identical to results with the RAxML backbones, and are omitted from the figure. The pipelines with the best accuracy across all three datasets are UPP(R)-RAxML and PASTA-RAxML, with PASTA-FastTree also good on the biological datasets.
Figure 4.
Tree error rates of different methods on the RNASim (top), 16SM (middle), and 23SM (bottom) datasets, under the high fragmentation condition. FN indicates false negative rates, FP indicates false positive rates. Results for the RNASim datasets are averaged across 20 replicates, and error bars show standard error.
The least accurate method is UPP(R)-FastTree, showing that FastTree provides poor trees even on good alignments, a finding that is consistent with Sayyari et al. (2017). The placement-based methods are in between, with trees based on APPLES less accurate than trees based on pplacer.
A comparison of these for the three selected methods (UPP-RAxML, PASTA-RAxML, and PASTA-FastTree) on the full set of model conditions is provided in Table 4 (low fragmentation) and Table 5 (high fragmentation).
Table 4.
Tree error rates under low fragmentation for the best placement-based method and two MSA-ML methods. We show FN rates (top) and FP rates (bottom). We show results for the three best performing methods: the best placement-based pipeline (UPP(R)-pplacer), the best MSA-ML method (UPP(R)-RAxML), and a standard MSA-ML method (PASTA-RAxML). Each condition has 75% full-length sequences and 25% fragmentary sequences (which have an average 50% length). The best results for each model condition (within 1%) are shown in boldface. The error rates are averaged over 20 replicates for the simulated datasets.
| Method | 1000M1 | 1000M2 | 1000M3 | 1000M4 | RNASim | RNASim2 | 16S.M | 23S.M |
|---|---|---|---|---|---|---|---|---|
| FN Rate: | ||||||||
| PASTA-RAXML | 0.246 | 0.181 | 0.095 | 0.061 | 0.186 | 0.163 | 0.135 | 0.137 |
| UPP(R)-RAXML | 0.157 | 0.128 | 0.094 | 0.061 | 0.185 | 0.163 | 0.112 | 0.143 |
| UPP(R)-pplacer | 0.215 | 0.183 | 0.150 | 0.112 | 0.243 | 0.215 | 0.192 | 0.244 |
| FP Rate: | ||||||||
| PASTA-RAXML | 0.248 | 0.185 | 0.100 | 0.083 | 0.186 | 0.163 | 0.595 | 0.473 |
| UPP(R)-RAXML | 0.160 | 0.132 | 0.099 | 0.083 | 0.185 | 0.163 | 0.584 | 0.476 |
| UPP(R)-pplacer | 0.179 | 0.146 | 0.111 | 0.091 | 0.208 | 0.178 | 0.604 | 0.517 |
Table 5.
Tree error rates under high fragmentation for the best placement-based method and two MSA-ML methods. We show FN rates (top) and FP rates (bottom); We show results for the three most accurate methods: the best placement-based pipeline (UPP(R)-pplacer), the best MSA-ML method (UPP(R)-RAxML), and a standard MSA-ML method (PASTA-RAxML). Each condition has 50% full-length sequences and 50% fragmentary sequences with an average 25% length. The best results for each model condition (within 1%) are shown in boldface. The error rates are averaged over 20 replicates for the simulated datasets.
| Method | 1000M1 | 1000M2 | 1000M3 | 1000M4 | RNASim | RNASim2 | 16S.M | 23S.M |
|---|---|---|---|---|---|---|---|---|
| FN Rate: | ||||||||
| PASTA-RAXML | 0.765 | 0.616 | 0.355 | 0.164 | 0.436 | 0.362 | 0.409 | 0.321 |
| UPP(R)-RAXML | 0.370 | 0.304 | 0.237 | 0.167 | 0.377 | 0.338 | 0.340 | 0.363 |
| UPP(R)-pplacer | 0.488 | 0.437 | 0.380 | 0.320 | 0.507 | 0.477 | 0.496 | 0.458 |
| FP Rate: | ||||||||
| PASTA-RAXML | 0.766 | 0.618 | 0.359 | 0.184 | 0.436 | 0.362 | 0.723 | 0.585 |
| UPP(R)-RAXML | 0.372 | 0.307 | 0.241 | 0.187 | 0.377 | 0.338 | 0.690 | 0.611 |
| UPP(R)-pplacer | 0.370 | 0.307 | 0.234 | 0.170 | 0.397 | 0.362 | 0.712 | 0.613 |
Under all conditions, the best accuracy is obtained using the MSA-ML pipeline UPP(R)-RAxML. The differences between methods are largest under high fragmentation, but are also large under low fragmentation for high rates of evolution (e.g., 1000M1).
Runtime
Figure 5 shows the runtimes of each method, broken out by component and averaged over the 20 replicates of the 1000M2 model condition, where there are 500 full length sequences and 500 fragmentary sequences, each approximately 25% as long as the full-length sequences. The fastest methods are the placement-based methods, as well as PASTA-FastTree and UPP-FastTree; these took about 30 minutes with FastTree backbones, and about an extra 5 minutes when using RAxML backbones. The lion’s share of the runtime for these pipelines was spent computing the alignment; aligning the full dataset with PASTA was about as fast as aligning the backbone with PASTA and extending with UPP, with PASTA using most of the time in either case. By contrast, the FastTree, APPLES, and pplacer portions were insignificant. Although APPLES is much more scalable than pplacer, at 1000 sequences (with 500 fragmentary and 500 full-length), this dataset is not large enough for this difference to have a noteworthy impact.
Figure 5.
Method runtime on the 1000M2 dataset, under the high fragmentation condition. Results are averaged over 20 replicates.
The methods that compute RAxML trees on alignments (i.e., PASTA-RAxML and UPP-RAxML) are much slower, as RAxML takes about 40 minutes to an hour on these datasets. This brings the total to about 70-80 minutes for UPP-RAxML (plus or minus the RAxML backbone tree), and about 90 minutes for PASTA-RAxML.
Overall these results show that RAxML is the most computationally intensive part of the pipelines that compute ML trees on estimated alignments, while the most computationally intensive part of the placement-based methods is the calculation of the backbone alignment using PASTA. Using RAxML backbone trees adds an extra five minutes to the runtime, and so is not an issue on these datasets. Thus, the more accurate placement-based methods are faster than the more accurate ML-based methods, making the choice between them to some extent a trade-off between accuracy and running time.
Discussion
Although the study was limited to a small part of parameter space (i.e., trees with approximately 1000 leaves and mainly simulated datasets), the study reveals several trends regarding the relative accuracy of alignment and tree estimation methods given datasets that contain a mixture of full-length and fragmentary datasets. These trends also are helpful in understanding the design issues for phylogenetic placement methods, and in choosing between methods. We discuss these trends here, and compare our findings to prior work.
Importance of MSA Method
A main finding of this study is that when datasets have fragmentary sequences, the best is obtained using an MSA-ML protocol; however, not all MSA methods provide good accuracy. We examined two strategies for computing alignments: estimating the entire alignment in one stage with PASTA or using a two-stage approach where we use PASTA only to align the full-length sequences and then added the remaining fragmentary sequences into the backbone alignment using either UPP or SEPP. In this study, using the two-stage approach always matched or improved on the alignment accuracy (both SPFN and SPFP) compared to just using PASTA.
We also saw a slight advantage using UPP rather than SEPP to align the fragmentary sequences. Interestingly, we did not see any noteworthy differences between using FastTree or RAxML to compute the backbone tree, whether using UPP or SEPP. Overall, therefore, these results show that alignment estimation using a two-stage approach produces superior results over PASTA by itself, that the method used to compute the backbone tree on the full-length sequences does not have a significant impact, and that UPP has a slight advantage over SEPP.
These results are consistent with those shown in the paper introducing UPP (see Table 3 and Fig. 3 in Nguyen et al. (2015)), which showed that both alignment and tree error increased more rapidly for PASTA than for UPP as the degree of fragmentation increased. A comparison between SEPP(F) and UPP(F) is also provided in Nguyen et al. (2015) (see Additional File 1, Table S2.1), which also showed that UPP(F) had a small advantage over SEPP(F). Hence our study confirms prior results from Nguyen et al. (2015), and extends these observations to include the impact of how the backbone tree is calculated. Henceforth, when we refer to UPP, we mean either UPP(R) or UPP(F), since the two ways of computing alignments had indistinguishable accuracy.
RAxML vs. FastTree
One of the aspects of the study we performed is a comparison of FastTree and RAxML given alignments that contain fragmentary sequences. To the best of our knowledge, Sayyari et al. (2017) is the only other study that has evaluated RAxML and FastTree under simulation conditions where fragmentation was explicitly included. Sayyari et al. (2017) compared FastTree and RAxML on true alignments with 101 sequences that had fragmentary sequences, each obtained from a single model condition. Because their study was limited to one model condition and only explored true alignments, our study explores additional conditions that vary substantially in rate of evolution and sequence evolution model, in order to better evaluate the differences between these methods given alignments containing fragmentary sequences.
One of the consistent trends in this study is that for many model conditions with fragmentary sequences, FastTree produces less accurate trees than RAxML. This trend is less obvious when used with the PASTA alignment on the fragmentary datasets (which produces generally poorer alignments than the other alignments we tested, resulting in poor trees regardless of the tree estimation method used), but is very obvious when used with the better alignment methods we explored, especially under high fragmentation conditions. In particular, the degree of fragmentation and the rate of evolution impact the difference in FN rate between trees computed using FastTree or RAxML on the UPP alignment, with small differences (or no difference) when fragmentation and alignment error are both low, but increasing differences as fragmentation and alignment error increase. Thus, our study confirms the observation made by Sayyari et al. (2017) that FastTree is less accurate than RAxML given alignments containing fragmentary sequences.
In this context, it is worth recalling Janssen et al. (2018), which compared phylogenetic placement using SEPP-pplacer to their “de novo" method that used MAFFT to compute alignments and then computed trees using FastTree; although they found that SEPP-pplacer was more accurate than their de novo method, this is likely at least partly due to the use of MAFFT instead of UPP (or even PASTA), and the use of FastTree instead of RAxML, and is consistent with our findings.
One possible explanation for the difference in accuracy between FastTree and RAxML in the presence of fragmentary datasets is that they numerically treat gaps differently. Thus, although treating gaps are “missing data" theoretically should not change the guarantee of statistical consistency (Truszkowski and Goldman, 2016), it has the potential to impact accuracy on a given dataset, and the impact of gaps within sequence alignments on phylogeny estimation is a topic of significant and continued interest in the systematics community (see Lemmon et al. (2009); Wiens (2006); Truszkowski and Goldman (2016); Simmons (2014); Dobrin et al. (2018); Machado et al. (2019); Xia (2019) for an entry to this literature).
Comparing Phylogenetic Placement Methods
We explored pplacer with two different techniques to compute extended alignments (i.e., UPP and SEPP) and possibly constraining the placement to the alignment subset selected by the ensemble of profile Hidden Markov Models technique when used with SEPP. These results show that using pplacer with UPP improves accuracy compared to using pplacer with SEPP, and that the unconstrained use of pplacer is more accurate than the constrained version. The improvement we observed for the unconstrained version over the constrained version of pplacer, which only allows it to place fragments into the subtree of the backbone tree selected by SEPP during the alignment stage, is consistent with results shown in Figure 1 from Mirarab et al. (2012).
Our evaluation of APPLES was limited to its use with UPP, which had the best accuracy of all alignment methods. However, our study shows that pplacer was always more accurate than APPLES, given the same backbone tree and UPP alignment. The improvement of pplacer over APPLES was higher for the high fragmentation conditions than the low fragmentation conditions, and higher for the datasets that were difficult to align than the datasets where alignment error was generally low. However, even for the model conditions with low fragmentation, the differences could be large (e.g., the difference in accuracy on the two biological datasets with low fragmentation was in the 7-9% range). We conclude that pplacer is at least as accurate as APPLES for placing fragmentary sequences into backbone trees when the backbone trees are not too large (i.e., have at most 1000 leaves).
The only prior study that compared APPLES to pplacer is Balaban et al. (2020), which explored APPLES and pplacer for placing full-length sequences into backbones and used the true alignment rather than estimated alignments. One major finding in Balaban et al. (2020) is the propensity of pplacer to fail when the backbone tree was too large: in particular, they found that pplacer failed on many datasets where the backbone tree had 5000 leaves and always failed on backbone trees with 10,000 leaves. For this reason, our study did not compare APPLES and pplacer on such large backbone trees. When restricted to conditions where the backbone trees had at most 1000 leaves, Balaban et al. (2020) found that pplacer had better accuracy than APPLES, though they used a different criterion to evaluate accuracy than we did (specifically, they used “placement accuracy", which is the distance between the estimated placement for the fragment and the true placement, while we used the error in the final tree). Balaban et al. (2020) observed that pplacer was approximately 10% more accurate than APPLES for placement accuracy on 1000-taxon RNASim subsamples (see Table 3 and Fig. 3 in Balaban et al. (2020)), while we have a difference in FN rate of 14% and 20% on RNASim under low and high fragmentation, respectively. The relative performance observed between APPLES and pplacer is thus the same between the two studies (i.e., APPLES is less accurate than pplacer), but the criteria are different and the details of the study (fragmentary versus full-length sequences, true versus estimated alignments) are also different. Finally, although we restricted our study to datasets with backbone trees limited to at most 1000 sequences, we explored a wider range of model conditions than explored in Balaban et al. (2020), including both easier and harder model conditions than RNASim (which is the only source of datasets examined in Balaban et al. (2020)).
Impact of Dataset Properties on Performance
Because we observed that tree error was largely driven by alignment error (for both types of tree estimation methods, whether based on maximum likelihood on estimated alignments or using phylogenetic placement), the model conditions can be characterized as easy or difficult based on the alignment error rates we observed. With this context, the easiest model condition we explored was 1000M4, which is a simulated dataset generated under a modification of the GTRGAMMA model to allow for insertions and deletions, but with overall low rates of substitutions and indels. The other ROSE simulation conditions have higher rates of evolution than 1000M4, with 1000M1 having the highest rate (and being the hardest dataset in our collection). In terms of alignment error, RNASim and RNASim2 both fall in the middle of the ROSE conditions, despite each having a lower average p-distance than even 1000M4. Alignment error on the biological datasets 16S.M and 23S.M are high, placing them between 1000M1 and 1000M2 in terms of difficulty, even though they have even lower average p-distances than RNASim.
Since the evolutionary process operating on the ROSE datasets is much simpler than the evolutionary process used to generate the RNASim data, and of course the evolutionary processes under which the biological datasets evolved are also more complex than the ROSE simulation, an obvious explanation is that alignment error is higher on the RNASim and biological datasets because their sequence evolution is more complex than is modelled by ROSE. However, another possibility is that there is some other empirical property of the model condition that is making for alignment challenges. For example, it may be that the existence of very long branches in the tree may make alignment estimation difficult, which would be consistent with the observation that the biological datasets have low average p-distances but high maximum p-distances, and are difficult to align.
Model conditions that produce higher differences in alignment error also seem to produce larger differences in tree estimation error, but there were conditions with relatively small differences in alignment error that resulted in large differences in tree error. For example, the largest difference in alignment error for the low fragmentation conditions was on the 1000M1 condition (which had the highest alignment error rates), where the PASTA and UPP alignments differed in SPFN error by 4% and yet the RAxML trees on the PASTA and UPP alignments differed in FN error by 10%. Thus, while the relative accuracy of trees followed the relative accuracy of the alignments on which they were based, the degree of improvement depended on the actual condition, with larger differences in trees for conditions with high alignment error.
Conclusion
Based on our study, and considering evidence from other studies as well, we make the following concrete recommendations:
When the dataset contains fragmentary sequences, standard methods for aligning datasets (including PASTA) should not be used to align them all at once: this can produce very poor alignments, followed by very poor trees. Instead, we recommend that the full-length sequences first be aligned using a good method, such as PASTA, and then the fragmentary sequences should be added to this alignment with UPP using an estimated backbone tree computed on the full-length sequences (in fact, UPP has functionality that will do this process automatically). Thus, in particular we recommend examining the dataset for sequence length heterogeneity, and only using PASTA or other methods that align sequences all at once if nearly all the sequences are close to full-length.
After the sequences are aligned, the best accuracy is obtained by computing a tree on the multiple sequence alignment using a method that has been shown to have good accuracy even on alignments with many fragmentary sequences: RAxML clearly outperforms FastTree in this case (and we suggest not using FastTree on datasets with fragments), but other approaches, including other good maximum likelihood methods, may also provide good accuracy.
Challenges in analyzing very large datasets
When the total number of sequences is very large, the running time needed to use RAxML or other good maximum likelihood methods may be prohibitive, but adding fragments to the backbone tree with a placement method will have a tendency to produce trees that are very unresolved, requiring additional techniques to refine the resulting tree. Furthermore, not all phylogenetic placement methods can handle large backbones: as reported in Balaban et al. (2020), although APPLES can handle very large backbones and is very fast, pplacer fails on many backbones with 5,000 leaves and all backbones with 10,000 sequences. However, APPLES does not have the same accuracy as pplacer, and so these analyses may not provide adequate accuracy (though this will depend on the specific biological question being asked). Also, the computation of a backbone tree using RAxML can be prohibitively computationally expensive, when the number of full-length sequences is large. Although we did not find any reduction in accuracy when using FastTree instead of RAxML for the backbone tree estimation, it is not yet clear where it is safe to use FastTree instead of RAxML for tree estimation, and so caution should be applied in interpreting trees based on FastTree. Thus, large numbers of sequences (say, 10K or more sequences) present a challenge to the user for a combination of reasons that include the computational cost in running good maximum likelihood methods (such as RAxML) and accuracy degradations for the current phylogenetic placement methods, which this study does not explore.
Future work
In addition to the open questions mentioned above, much more still needs to be done to understand how to best estimate trees from alignments that have sequence length heterogeneity. Although we examined a range of model conditions, future work should explore additional conditions, especially those with very low rates of evolution (which can create challenges for tree estimation though not for alignment estimation) or those that evolve under models that violate standard GTRGAMMA model assumptions more significantly than RNASim. Our restriction to datasets with at most 1000 sequences allowed pplacer to complete analyses, and so additional study is needed to explore conditions with larger number of sequences (including those in which pplacer fails), in order to establish which methods provide good accuracy without being prohibitively computationally intensive. This study did not examine the challenges in computing alignments and trees when the input has other types of sequence length heterogeneity, including excessively long sequences (resulting, perhaps, from large insertions or many tandem duplications), or very high rates of deletions so that the sequences are short but not fragmentary. Hence, future work should examine such issues.
Closing remarks
Despite the cautionary advice, we close with optimistic statements. While estimating phylogenies from unaligned datasets is very difficult for ultra-large datasets, there has been substantial progress over the last few years that suggests that dataset size is not likely to remain a significant impediment in the long term. For example, there are divide-and-conquer strategies for improving scalability of phylogeny estimation methods (e.g., TreeMerge (Molloy and Warnow, 2019) and Guide Tree Merger (Smirnov and Warnow, 2020)) that do not require aligned sequence inputs and that could be used with any tree estimation method, including computationally intensive methods (e.g., Bayesian MCMC) or maximum likelihood estimation under complex models (e.g., the GHOST model (Crotty et al., 2020) available in IQtree). These and future advances may make it feasible to estimate highly accurate trees from ultra-large datasets of unaligned sequences without burdensome computational requirements. There has also been an increased attention to developing new phylogenetic placement methods that can scale to large datasets. Overall, we predict that over the near future, there will be new method development in multiple sequence alignment and phylogeny estimation, and some of these methods may well make highly accurate ultra-large phylogeny estimation feasible, even for these very challenging dataset conditions.
Acknowledgments
The authors acknowledge the support of the US National Science Foundation under grants ABI-1458652 and 1513629. We thank Olivier Gascuel, Erick Matsen, Erin Molloy, and the anonymous reviewers for their helpful feedback and suggestions, which led to improvements in the manuscript; we also thank Metin Balaban and Siavash Mirarab for advice on how to run APPLES.
Supplementary Material
Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.8pk0p2nj8.
References
- Balaban, M., Sarmashghi S., and Mirarab S.. 2020. APPLES: scalable distance-based phylogenetic placement with or without alignments. Systematic Biology 69:566–578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbera, P., Kozlov A. M., Czech L., Morel B., Darriba D., Flouri T., and Stamatakis A.. 2018. EPA-ng: massively parallel evolutionary placement of genetic sequences. Systematic biology 68:365–369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berry, V. and Gascuel O.. 1996. On the interpretation of bootstrap trees: appropriate threshold of clade selection and induced gain. Molecular Biology and Evolution 13:999–1011. [Google Scholar]
- Cannone, J., Subramanian S., Schnare M., Collett J., D’Souza L., Du Y., Feng B., Lin N., Madabusi L., Muller K., Pande N., Shang Z., Yu N., and Gutell R.. 2002. The Comparative RNA Web (CRW) site: an online database of comparative sequence and structure information for ribosomal, intron and other RNAs. BMC Bioinformatics 3http://www.rna.ccbb.utexas.edu. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crotty, S. M., Minh B. Q., Bean N. G., Holland B. R., Tuke J., Jermiin L. S., and Haeseler A. V.. 2020. GHOST: recovering historical signal from heterotachously evolved sequence alignments. Systematic Biology 69:249–264. [DOI] [PubMed] [Google Scholar]
- Dobrin, B. H., Zwickl D. J., and Sanderson M. J.. 2018. The prevalence of terraced treescapes in analyses of phylogenetic data sets. BMC evolutionary biology 18:46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durbin, R., Eddy S., Krogh A., and Mitchison G.. 1998. Biological Sequence Analysis. Cambridge University Press. [Google Scholar]
- Gardner, P. P., Wilm A., and Washietl S.. 2005. A benchmark of multiple sequence alignment programs upon structural RNAs. Nucleic Acids Research 33:2433–2439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garriga, E., Di Tommaso P., Magis C., Erb I., Mansouri L., Baltzis A., Laayouni H., Kondrashov F., Floden E., and Notredame C.. 2019. Large multiple sequence alignments with a root-to-leaf regressive method. Nature Biotechnology 37:1466–1470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guindon, S. and Gascuel O.. 2003. A simple, fast, and accurate algorithm to estimate large phylogenies by maximum likelihood. Syst Biol 52:696–704. [DOI] [PubMed] [Google Scholar]
- Janssen, S., McDonald D., Gonzalez A., Navas-Molina J. A., Jiang L., Xu Z. Z., Winker K., Kado D. M., Orwoll E., Manary M., Mirarab S., and Knight R.. 2018. Phylogenetic placement of exact amplicon sequences improves associations with clinical information. mSystems 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozlov, A. M., Darriba D., Flouri T., Morel B., and Stamatakis A.. 2019. RAxML-NG: a fast, scalable and user-friendly tool for maximum likelihood phylogenetic inference. Bioinformatics 35: 4453–4455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krogh, A., Brown M., Mian I. S., Sjölander K., and Haussler D.. 1994. Hidden Markov models in computational biology: applications to protein modeling. J. Mol. Biol. 235:1501–1531. [DOI] [PubMed] [Google Scholar]
- Lassmann, T. 2019. Kalign 3: multiple sequence alignment of large datasets. Bioinformatics 36:1928–1929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemmon, A. R., Brown J. M., Stanger-Hall K., and Lemmon E. M.. 2009. The effect of ambiguous data on phylogenetic estimates obtained by maximum likelihood and Bayesian inference. Systematic Biology 58:130–145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linard, B., Swenson K., and Pardi F.. 2019. Rapid alignment-free phylogenetic identification of metagenomic sequences. Bioinformatics 35:3303–3312. [DOI] [PubMed] [Google Scholar]
- Liu, K., Linder C. R., and Warnow T.. 2011. RAxML and FastTree: comparing two methods for large-scale maximum likelihood phylogeny estimation. PloS one 6:e27731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, K., Raghavan S., Nelesen S., Linder C. R., and Warnow T.. 2009. Rapid and accurate large-scale coestimation of sequence alignments and phylogenetic trees. Science 324:1561–1564. [DOI] [PubMed] [Google Scholar]
- Liu, K., Warnow T., Holder M. T., Nelesen S. M., Yu J., Stamatakis A. P., and Linder C. R.. 2012. SATé-II: very fast and accurate simultaneous estimation of multiple sequence alignments and phylogenetic trees. Syst Biol 61:90–106. [DOI] [PubMed] [Google Scholar]
- Machado, D. J., Castroviejo-Fisher S., and Grant T.. 2019. Evidence of absence treated as absence of evidence: The effects of variation in the number and distribution of gaps treated as missing data on the results of standard maximum likelihood analysis. bioRxiv Page 755009. [DOI] [PubMed] [Google Scholar]
- Matsen, F. A. and Evans S. N.. 2013. Edge principal components and squash clustering: using the special structure of phylogenetic placement data for sample comparison. PLOS One 8 doi:10.1371/journal.pone.0056859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsen, F. A., Kodner R. B., and Armbrust E. V.. 2010. pplacer: linear time maximum-likelihood and Bayesian phylogenetic placement of sequences onto a fixed reference tree. BMC bioinformatics 11:538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mirarab, S., Nguyen N., and Warnow T.. 2012. SEPP: SATé-enabled phylogenetic placement. Pages 247–258inBiocomputing 2012. World Scientific. [DOI] [PubMed] [Google Scholar]
- Mirarab, S., N.-p. Nguyen, L.-S. Wang, Guo S., Kim J., and Warnow T.. 2015. PASTA: ultra-large multiple sequence alignment of nucleotide and amino acid sequences. J. Computational Biology 22:377–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mirarab, S. and Warnow T.. 2011. FastSP: linear time calculation of alignment accuracy. Bioinformatics 27:3250–3258. [DOI] [PubMed] [Google Scholar]
- Molloy, E. K. and Warnow T.. 2019. TreeMerge: a new method for improving the scalability of species tree estimation methods. Bioinformatics 35:i417–i426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrison, D., Morgan M., and Kelchner S.. 2015. Molecular homology and multiple-sequence alignment: an analysis of concepts and practice. Australian Systematic Biology 28:46–62. [Google Scholar]
- Nguyen, L.-T., Schmidt H., von Haeseler A., and Minh B.. 2015a. IQ-TREE: a fast and effective stochastic algorithm for estimating maximum-likelihood phylogenies. Molecular Biology and Evolution 32:268–274 doi = 10.1093/molbev/msu300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen, N.-p. D.,Mirarab S., Kumar K., and Warnow T.. 2015b. Ultra-large alignments using phylogeny-aware profiles. Genome Biology 16:124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Notredame, C., Higgins D. G., and Heringa J.. 2000. T-Coffee: a novel method for fast and accurate multiple sequence alignment. Journal of Molecular Biology 302:205–217. [DOI] [PubMed] [Google Scholar]
- Price, M. N., Dehal P. S., and Arkin A. P.. 2010. FastTree 2 – approximately maximum-likelihood trees for large alignments. PLoS ONE 5:e9490. doi:10.1371/journal.pone.0009490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rannala, B., Huelsenbeck J. P., Yang Z., and Neilsen R.. 1998. Taxon sampling and the accuracy of large phylogenies. Syst. Biol. 47:702–710. [DOI] [PubMed] [Google Scholar]
- Reeck, G., de Haen C., Teller D., Doolitte R., Fitch W., Dickerson R., Chambon P., McLachlan A., Margoliash E., Jukes T., and Zuckerkandl E.. 1987. “homology" in proteins and nucleic acids: a terminology muddle and a way out of it. Cell 50:667. [DOI] [PubMed] [Google Scholar]
- Robinson, D. and Foulds L.. 1981. Comparison of phylogenetic trees. Mathematical Biosciences 53:131–147. [Google Scholar]
- Rost, B. 1999. Twilight zone of protein sequence alignments. Protein engineering 12:85–94. [DOI] [PubMed] [Google Scholar]
- Sayyari, E., Whitfield J. B., and Mirarab S.. 2017. Fragmentary gene sequences negatively impact gene tree and species tree reconstruction. Molecular Biology and Evolution 34:3279–3291. [DOI] [PubMed] [Google Scholar]
- Sievers, F., Wilm A., Dineen D., Gibson T. J., Karplus K., Li W., Lopez R., McWilliam H., Remmert M., Soding J., Thompson J. D., and Higgins D. G.. 2011. Fast, scalable generation of high-quality protein multiple sequence alignments using Clustal Omega. Mol. Syst. Biol. 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simmons, M. P. 2014. A confounding effect of missing data on character conflict in maximum likelihood and Bayesian MCMC phylogenetic analyses. Molecular phylogenetics and evolution 80:267–280. [DOI] [PubMed] [Google Scholar]
- Smirnov, V. and Warnow T.. 2020. Unblended disjoint tree merging using GTM improves species tree estimation. BMC Genomics 21:1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stamatakis, A. 2014. RAxML version 8: a tool for phylogenetic analysis and post-analysis of large phylogenies. Bioinformatics 30:1312–1313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stoye, J., Evers D., and Meyer F.. 1998. Rose: generating sequence families. Bioinf 14:157–163. [DOI] [PubMed] [Google Scholar]
- Truszkowski, J. and Goldman N.. 2016. Maximum likelihood phylogenetic inference is consistent on multiple sequence alignments, with or without gaps. Systematic biology 65: 328–333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiens, J. J. 2006. Missing data and the design of phylogenetic analyses. Journal of Biomedical Informatics 39:34–42. [DOI] [PubMed] [Google Scholar]
- Xia, X. 2019. A starless bias in the maximum likelihood phylogenetic methods (and other bias in parameter estimation). BioRxiv Page 435412. [Google Scholar]







