Fit to Burst: Toward Noninvasive Estimation of Achilles Tendon Load Using Burst Vibrations

Abstract

Objective:

Tendons are essential components of the musculoskeletal system and, as with any mechanical structure, can fail under load. Tendon injuries are common and can be debilitating, and research suggests that a better understanding of their loading conditions could help mitigate injury risk and improve rehabilitation. To that end, we present a novel method of noninvasively assessing parameters related to mechanical load in the Achilles tendon using burst vibrations.

Methods:

These vibrations, produced by a small vibration motor on the skin superficial to the tendon, are sensed by a skin-mounted accelerometer, which measures the tendon’s response to burst excitation under varying tensile load. In this study, twelve healthy subjects performed a variety of everyday tasks designed to expose the Achilles tendon to a range of loading conditions. To approximate the vibration motor-tendon system and provide an explanation for observed changes in tendon response, a 2-degree-of-freedom mechanical systems model was developed.

Results:

Reliable, characteristic changes in the burst response profile as a function of Achilles tendon tension were observed during all loading tasks. Using a machine learning-based approach, we developed a regression model capable of accurately estimating net ankle moment—which captures general trends in tendon tension—across a range of walking speeds and across subjects (R² = 0.85). Simulated results of the mechanical model accurately recreated behaviors observed in vivo. Finally, preliminary, proof-of-concept results from a fully wearable system demonstrated trends similar to those observed in experiments conducted using benchtop equipment.

Conclusion:

These findings suggest that an untethered, unobtrusive system can effectively assess tendon loading during activities of daily life.

Significance:

Access to such a system would have broad implications for injury recovery and prevention, athletic training, and the study of human movement.

I. Introduction

Tendons play a key role in the way we move about the world—serving not merely to transmit forces between muscle and bone, but also to amplify the power output of muscle [1], improve the efficiency of the muscle-tendon unit [2], [3], passively stabilize limbs [4], and buffer muscle from damage due to rapid lengthening [5], [6]. The Achilles tendon (AT) experiences the highest mechanical stress of any tendon in the human body [7]–[9] and is one of the most commonly injured tendons [10], [11]. Rupture of the AT, caused by excessive stress in the tissue, is a debilitating injury that can take months or even years to rehabilitate [12]–[15], with only a slim possibility of a full return to pre-injury performance levels [16], [17]. Research suggests that proper conditioning of the AT and a better understanding of its loading conditions during normal activities could reduce injury risk and/or accelerate recovery [18]–[20]. However, though in vivo assessment of tendon loading has been explored using invasive techniques [21]–[25], this task remains difficult to achieve noninvasively, with some proposing the use of elastography [26], laser Doppler vibrometry [27], and shear wave dispersion analysis [28].

More recent work has demonstrated that excitation of the AT by a skin-mounted piezoelectric tapping mechanism can provide insight into the tension state of the tendon by modeling the tendon as a Timoshenko beam and measuring shear wave velocity along it using a contact accelerometer [29]. In this prior study, the researchers demonstrated that micron-scale taps on the skin superficial to a tendon can propagate into the underlying tendinous tissue, suggesting that excitation of the tendon as a structure can be achieved noninvasively. High correlation between ankle torque—used as a proxy measure of AT force—and the square of shear wave velocity was reported for simple isometric calf exercises in a cohort of six healthy subjects. Representative results presented for walking and running gait also showed favorable trends between wave speed and ankle torque. In particular, the authors observed good temporal alignment between wave speed and torque waveforms and similar increases in peak torque with increasing walking speed. A subsequent study involving 12 healthy subjects walking at various speeds reported group coefficients of determination (R²) ranging from 0.80 to 0.84 between measured shear wave speed and AT stress estimated by inverse dynamics during the stance phase of gait [30]. While these results are promising and the methodology sound, some limitations do exist, particularly regarding translatability to an affordable, wearable system; specifically, challenges include the need for two accelerometers with a strict placement scheme, a voltage amplifier capable of delivering 150V excitation to a relatively expensive piezoelectric actuator, and subject-specific calibration exercise(s).

We envisioned that these limitations could be addressed by a novel system design, based on a single contact accelerometer to detect propagated vibrations produced by a small, cheap linear resonance actuator (LRA) on the skin superficial to the AT (Fig 1a). The LRA produces burst vibrations—intermittent sinusoidal excitations—which interact with the underlying tissue in a characteristic way based on the mechanical state of the tendon (i.e., its tension, stiffness, and damping) (Fig 1b). Thus, our system, like the aforementioned piezo-tapper technique [29], [30], measures local accelerations at the skin surface, though our approach differs in terms of how the tissue is mechanically excited and how the measured accelerations are interpreted. As detailed in [29], the authors “tap” the AT and measure the time delay between when the induced shear wave reaches two contact accelerometers in series; the AT is then assumed to behave like a Timoshenko beam, and the shear wave velocity is correlated to the axial force in the tissue, much as conventional elastography techniques relate wave velocity to mechanical properties like shear modulus. By contrast, our approach takes into account the entire transient response of the AT to a burst excitation, with the assumption that the AT responds to this input (i.e., absorbs and dissipates energy) differently based on the loading state of the tissue due to putative changes in the tissue’s mechanical properties. By describing the response of the tendon to these excitations at a variety of known loading states, we built a model with the aim of assessing tendon load noninvasively and potentially in real-time (Fig 1c). Access to such a tool could precipitate novel methods for injury prevention and rehabilitation, athletic training, patient-in-the-loop exoskeleton control, and the study of myriad neuromuscular and musculoskeletal disorders.

Fig 1.

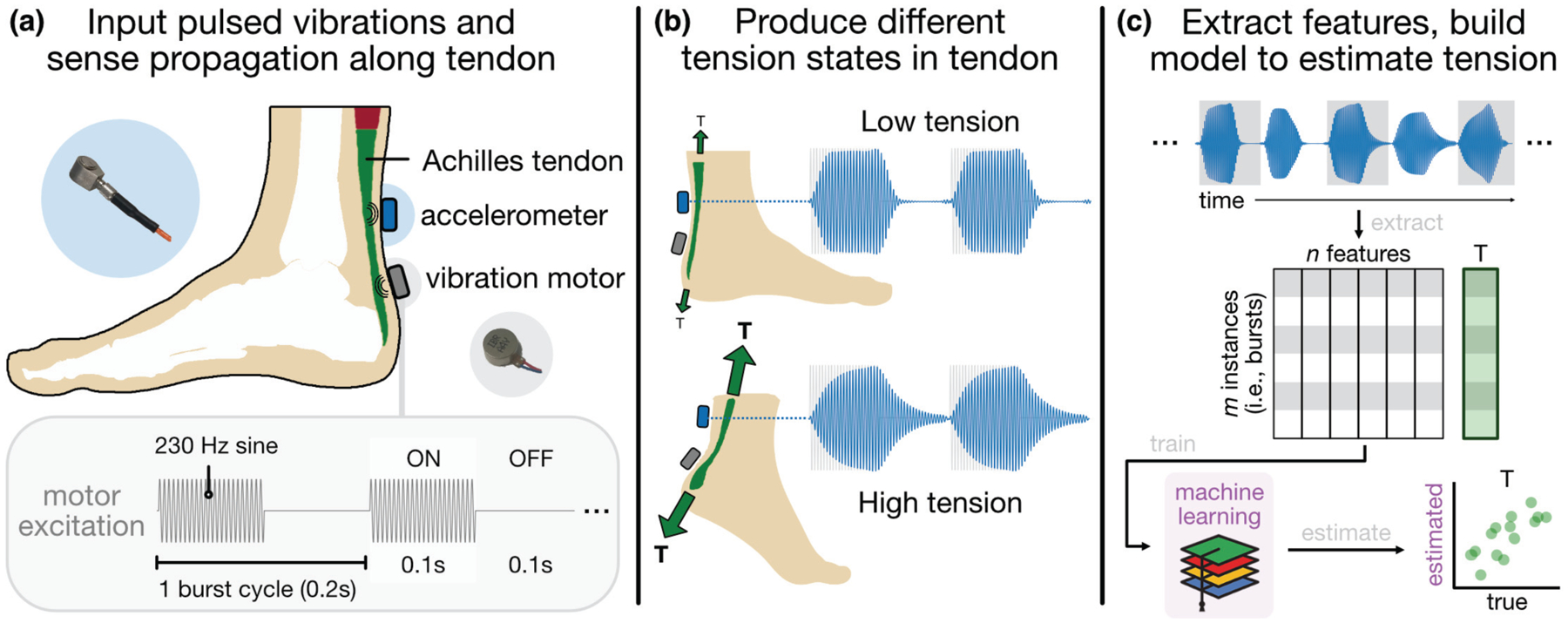
System architecture and approach, (a) A vibration motor and contact accelerometer are placed ~2 cm apart on the skin superficial to the AT. (b) Burst vibrations, the input waveform of which is depicted in the lower left, propagate along the tendon, which responds differently to the excitation based on its tension state, (c) Shape-based features are extracted from each burst response window and used to train a machine learning model for estimating tension in the tendon noninvasively.

In this work, we present results that demonstrate characteristic changes in tendon response as a function of AT tension across a battery of static and dynamic tasks performed by healthy subjects (N = 12). These changes are quantified as shape-based features extracted from accelerometer data, and a collection of these features are used to train a model for estimating a target variable related to AT tension (net ankle moment); this estimation model is evaluated on subject walking data to assess its performance. Simulation results from a 2-degree-of-freedom (DOF) mechanical systems analogy of the LRA-tendon unit are used to explain, in approximation, the tendon response observed in vivo. Finally, results of a proof-of-concept study (N = 1) using a fully wearable version of the tendon vibration hardware are presented.

II. Methods

A. Study participants

Twelve able-bodied subjects (8 male / 4 female, age: 25.3 ± 3.4 years, height: 172 ± 8.5 cm, mass: 70 ± 13 kg) participated in this study, which was conducted under approval from the Georgia Institute of Technology Institutional Review Board. Inclusion criteria included no history of major ankle injury.

B. Hardware and data acquisition

1). Tendon vibration

Tendon loading was assessed by way of a vibration motor and accelerometer placed ~2 cm apart from each other on the skin superficial to the AT, midway along the length of the free tendon and on the tendon’s midline in the mediolateral dimension (Fig 1a). The motor (i.e., the LRA) was placed distal to the accelerometer and thus proximal to the tendon’s insertion at the calcaneus. Both the motor and accelerometer were affixed to the skin using a double-sided adhesive foam pad (23-mm Stickie, Rycote, Gloucestershire, UK) and fabric tape (Kinesio Tex, Kinesio, Albuquerque, NM, USA).

The LRA (G0832012, Jinlong Manufacturing, China), which measures 8 mm in diameter and weighs 2 g, was driven by an AC voltage (amplitude: 3 V, max current: 90 mA) at its resonance frequency of 230 Hz. This 230-Hz sine wave was multiplied with a 5-Hz square wave (duty factor = 50%) to generate a continuous train of burst vibrations, the excitation signal of which was delivered to the motor by a benchtop function generator (33500 Series, Agilent Technologies, Santa Clara, CA, USA) (Fig 2a,b). Intermittence of excitation (“on-off” behavior) was important, as it was observed that rise and fall times changed characteristically with tendon tension (Fig 2c,d). The pulse rate (here, 5 Hz) was the effective data rate, as the loading state of the tendon was assessed once per burst period. The motor’s vibration amplitude was on the order of 1.5 g acceleration, and its axis of vibration was oriented orthogonal to the skin. Subjects reported only a mild “buzzing” sensation at the heel upon first application and, after only a few minutes, remarked on having forgotten that the motor was there.

Fig 2.

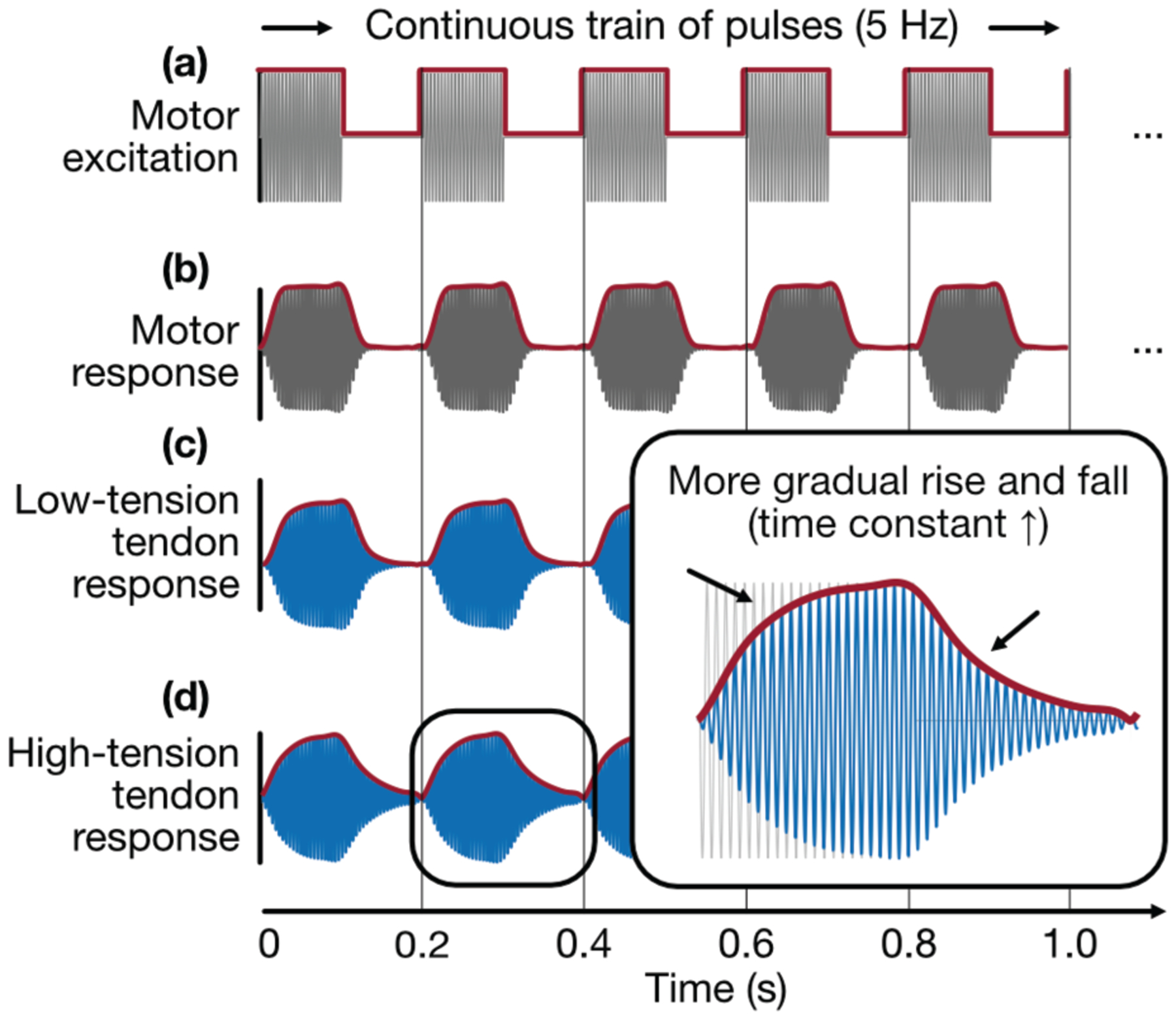
Vibration input and response, (a) A vibration motor is excited by a continuous train of bursts (230-Hz sine multiplied with 5-Hz square), (b) The motor exhibits its own (constant) rise and fall time due to internal stiffness and damping, (c) A tendon under low tension responds to burst vibration with a steeper rising and falling edge (faster energy absorption and dissipation), (d) A tendon under high tension responds to burst vibration with a more gradual rising and falling edge (slower energy absorption and dissipation).

The propagated vibrations were sensed on the skin by a miniature, high-bandwidth, uniaxial accelerometer (series 3225, Dytran Instruments, Inc., Chatsworth, CA, USA) (sensitivity =100 mV/g, frequency response ± 10% = 2 to 10,000 Hz). The accelerometer was oriented such that it was sensitive to vibrations orthogonal to the skin surface. The accelerometer was connected to a data acquisition unit (USB-4432, National Instruments, Austin, TX, USA)—itself connected to a laptop acquiring the data via MATLAB (MathWorks, Natick, MA, USA)—and was sampled at 25 kHz.

2). Conventional gait analysis instruments

All experiments were conducted in a fully equipped gait analysis lab (Fig 3a). Subjects’ lower bodies were instrumented with 16 retroreflective markers whose positions in space were tracked by a motion capture system (Vicon Motion Systems, Denver, CO, USA) comprised of 34 video cameras (sampling rate = 200 Hz). Arranged according to Vicon’s Plug-in-Gait lower body model [31], [32], these markers provided full 3D kinematics of subjects’ thigh, shank, and foot segments, and their trajectories were smoothed using a Woltring low-pass filter to remove noise [33]. All trials were performed on a split-belt treadmill instrumented with bilateral force plates (Bertec, Columbus, OH, USA) so as to capture ground reaction forces (GRF) and center of pressure underfoot (sampling rate = 1000 Hz). Using kinematic and kinetic information from the motion capture and force plate systems, joint angles (Fig 3c) and net moments (Fig 3d) at each joint were calculated by way of inverse dynamics [34] using the Plug-in-Gait solver within Vicon’s Nexus software package. This tool, which is an implementation of the Conventional Gait Model based on the Newington-Helen Hayes model [35], has been used extensively in gait studies and has been shown to provide reliable and clinically acceptable outputs of joint kinematics and kinetics, particularly in the sagittal plane, on which our analysis is focused [31], [32], [36], [37]. Ankle plantarflexor and dorsiflexor muscle activity—that of the medial and lateral gastrocnemius (MG, LG) and tibialis anterior (TA)—was acquired by three surface electromyography (EMG) sensors (SX230, Biometrics Ltd, Newport, UK) (sampling rate = 1000 Hz) (Fig 3e). These signals were rectified and digitally filtered using a Butterworth filter with a cutoff frequency of 6 Hz.

Fig 3.

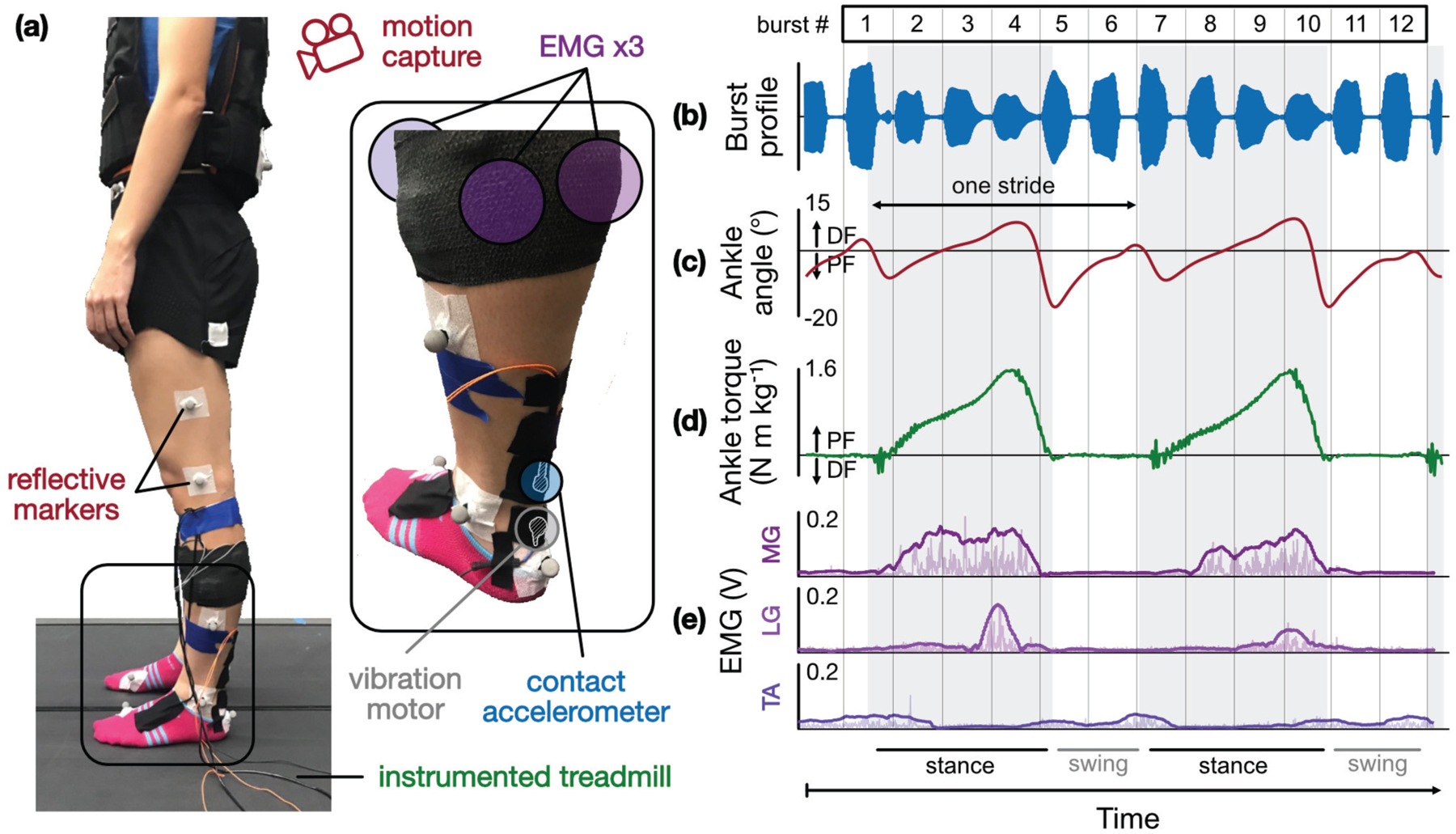
Subject instrumentation and sample biomechanics time series, (a) Each subject is instrumented with the tendon vibration hardware (motor and accelerometer) as well as a suite of sensors used in conventional gait analysis (motion capture, EMG, load cell-instrumented treadmill), (b) During each experiment, burst vibrations are delivered to the AT during any given task; (c) ankle angle (from inverse kinematics), (d) ankle torque (from inverse dynamics), and (e) EMG from the medial and lateral gastrocnemius (MG, LG) and tibialis anterior (TA) are acquired simultaneously.

C. Experimental procedure

After being instrumented, subjects were asked to perform a variety of tasks designed to impose a range of loading conditions upon the AT. These tasks included quiet standing (as a baseline), tiptoe standing (both two-legged and one-legged), calf raises at 2 s per cycle (both two-legged and one-legged), level treadmill walking at four speeds (1.0, 1.3, 1.6, and 1.8 m/s), and level treadmill running at three speeds (2.0, 2.3, and 2.6 m/s). To ensure that the burst response phenomena were not simply the result of a change in ankle angle, which might alter the distance between the motor and the accelerometer, or merely skin stretch, a subset of subjects performed a simple isometric calf contraction task in which the subject placed the foot on the floor in a slightly plantarflexed pose and isometrically contracted the calf muscle periodically, taking care not to change the joint angle or alter GRF. All tasks were performed for 60 s each, during which time data were collected continuously. Subjects were allowed to touch off on a support bar adjacent to the instrumented treadmill to aid in balance, though they were instructed not to bear any significant weight on the bar.

D. Data analysis

1). General analytical framework

The AT was mechanically stimulated using continuous trains of burst vibrations that propagate along the length of the tendon between a vibration motor (transmitter) and accelerometer (receiver). The accelerometer captured local accelerations of the underlying tissue, though its raw output contains information in frequency bands not relevant to our analyses (e.g., baseline wander caused by coarse limb motion, motion artifact, and interface noise) (Fig 4a). A digital bandpass filter (Kaiser-window finite impulse response filter, bandwidth: 215 to 245 Hz) was applied to mask frequency content outside of a narrow band around the stimulation (carrier) frequency of 230 Hz (Fig 4b).

Fig 4.

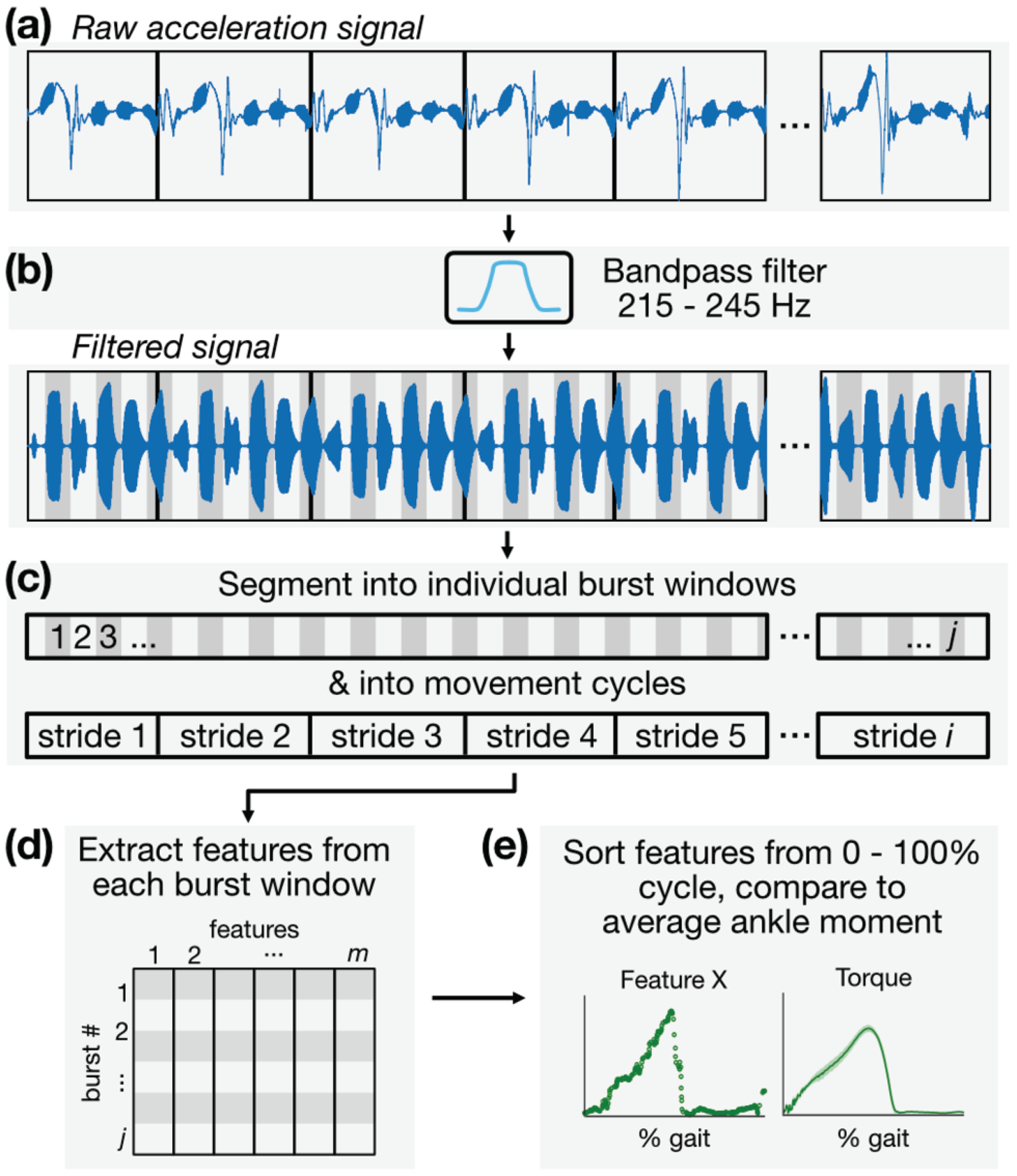
Signal processing and analytical framework, (a) The skin-mounted accelerometer captures not only local vibrations of the skin due to motor excitation but also coarse movement of the limb and other artifact, (b) The raw acceleration signal is bandpass filtered selectively around the motor excitation frequency of 230 Hz. (c) The signal is then segmented into individual burst windows and movement cycles, (d) Features are extracted from each burst window and stored in a feature matrix, (e) Features are plotted against their location in time within each movement cycle so that average behaviors across each cycle can be observed.

The filtered signal was then segmented into individual burst windows, each with a 200-ms period beginning at excitation onset (Fig 4c). For cyclical tasks such as calf raises and walking, the signal was also segmented into individual cycles of motion using GRF from the force plates as a timing reference. The beginning of each gait cycle (heel-strike) was defined as when GRF reached a nominal force threshold (25 N), and the transition to swing phase was signaled by GRF falling below this threshold. With both the onset time of each burst window and each motion cycle period known, the location (% cycle, defined simply as the fraction of the time between successive heel-strikes) of each burst within, for instance, the gait cycle was established; this was important for plotting variables of interest against % cycle, from which average behaviors can be observed. Individual burst windows were then treated as distinct data instances from which a set of features describing the shape of the response were extracted. The same segmentation process was performed for the time series of ankle torque, EMG, and other biomechanical variables that relate to tendon tension. Information extracted from each burst window—including that of the burst excitation response, torque, and others—was then arrayed in a table in which columns represented features and rows represented data instances (Fig 4d). This table of features was then used to train a machine learning model for estimating tendon loading states, the specifics of which are discussed below (Fig 4e).

2). Predictors: characterizing propagated vibrations

During pilot tests, it was observed that the shape of the tendon response—that is, the envelope of the burst vibration sensed at the accelerometer—changed distinctively in association with tendon tension. Characteristic shape changes included, mostly conspicuously, a more gradual rising and falling edge (increased rise and fall time constants in the analogy to a step response) of the burst envelope as AT tension increased (Fig 2 inset). A collection of 70 features that describe both temporal and amplitude-based attributes of the burst profile (e.g., rise/fall time, peak/median amplitude, other conventional statistics) was constructed (Table I, see Appendix) and used as predictors (inputs) for estimating a target variable related to AT tension. Candidate features were plotted against target variables to discern which might be suitable predictors.

3). Output: inverse dynamics

Since the purpose of this study is to estimate AT tension noninvasively, the ideal target (output) variable would be a direct measurement of tendon force / stress. However, ground-truth measurements—though theoretically possible through the use of implantable strain gauges, tendon buckles, or optical fibers [21]—are unfeasible for this study as they would require a sensor to be implanted in the body and affixed directly to the tendon. Therefore, we relied on proxy measures that are closely related to AT tension: net ankle joint moment and sum of calf EMG magnitude. The former can be calculated using inverse dynamics, given that limb kinematics (from motion capture) and endpoint kinetics (GRF from force plates) are known. Assuming minimal co-contraction of the ankle dorsiflexors, which is valid in the case of simple isometric exercises [38], [39] and during much of the stance phase of walking [40], [41], net ankle torque can be attributed predominantly to forces developed in the triceps surae, which are borne by the AT [42]. Therefore, ankle moment and AT tension are related by the moment arm distance between the tendon line-of-action and the joint center, which for our purposes is assumed to change minimally, though it may change by as much as 25% between heel-strike and push-off [43], [44]. (Limitations of this approach will be discussed at length in Section IV.) Thus, ankle torque derived from inverse dynamics was used as a target variable (ground truth) to estimate in the case of tasks with minimal co-contraction, including the stance phase of walking and running. During the swing phase of these tasks, joint torques are small due to the absence of GRF, and the assumption that net ankle torque is primarily attributable to forces in the calf is invalid, as activation of the ankle dorsiflexors is necessary to support the weight of the foot. For these reasons, net ankle torque was treated as the target variable only during stance. Non-negligible co-contraction was observed for certain tasks such as calf raises, likely because subjects required higher joint impedance to stabilize the limb and keep from falling. In these scenarios, sum of calf EMG (i.e., that ofMG and LG) was treated as the target variable.

4). Estimator: regression model

While a single feature extracted from the burst profile may bear a resemblance to the target variable, it was assumed that a fusion of multiple features would improve estimation performance by better accounting for complex relationships between variables and variation between subjects. To that end, we used sensor fusion paired with machine learning (ML) techniques to estimate AT loading during walking. The input to these ML models was the collection of 70 features (see above) extracted from 6770 burst windows during the stance phase of walking across all 12 subjects. Features were normalized to zero mean and unity variance to account for incongruous scaling between them. The output (label) was an 6770×1 vector containing the corresponding ankle torque at each burst instance. No bursts from swing phase (60 – 100 % gait) were used due to the presence of TA activity violating the assumption that net ankle moment was primarily associated with calf forces, as described above.

We trained regression models using a set of ML algorithms—including simple linear regression, regression trees, support vector machines with various kernel functions—on the feature table(s) described above and selected the candidate model that minimized root-mean-squared-error (RMSE) of a 10-fold cross-validation. By this selection criterion, an ensemble technique known as a bootstrap-aggregation (“bagging”) of regression trees [45] was chosen as the model type. Being an ensemble learner, this technique is inherently robust to overfitting [46]. Hyperparameters were similarly tuned by minimizing RMSE of a 10-fold cross-validation, whereby the final model was structured as a bag of 50 weak learners (trees), each with a minimum leaf size of 6 (no pruning nor early stopping was used). This eventual model was then evaluated on the 12-subject walking dataset using leave-one-subject-out cross-validation (LOSO-CV), in which 11 subjects’ data were used to train the model, while one subject’s data were left out as a test set; in this way, the model is presented with unseen data recurrently, simulating the inclusion of new subjects. This train-test split was performed in a round-robin manner such that all subjects’ data were tested upon once, and the estimation performance on each subject was averaged and expressed in terms of group R² and RMSE.

5). Mechanical system analogy

To supplement the more black-box, ML-based approach and develop a more mechanistic, intuitive understanding of why the AT’s response to burst excitation is modulated as we observed, we sought to model the motor-tendon structure as a mechanical system. As such, this simplified model was used as a framework to examine the effects of putative physiological changes in the tissue on a simulated burst excitation response. The system was approximated as a 2-degree of freedom (DOF), lumped parameter model with two mass-spring-dampers in series: one representing the vibration motor and the other representing the tendon to which it is attached. A schematic of the equivalent 2-DOF system is shown in Fig 5. The equation of motion (EOM) for such a system can be written as

$$m_T\stackrel{\mathrm{..}}{x_T}+c_T\stackrel{.}{x_T}-c_M\left(\stackrel{.}{x_M}+\stackrel{.}{x_T}\right)+k_T{x}_T-k_M\left(x_M-x_T\right)=0$$ (1)

$$m_M\stackrel{\mathrm{..}}{x_M}+c_M\left(\stackrel{.}{x_M}+\stackrel{.}{x_T}\right)+k_M\left(x_M-x_T\right)=F(t)$$ (2)

where, m is mass, c is damping coefficient, k is stiffness, F(t) is the external force applied by the motor, and subscripts T and M represent the tendon and motor, respectively.

Fig 5.

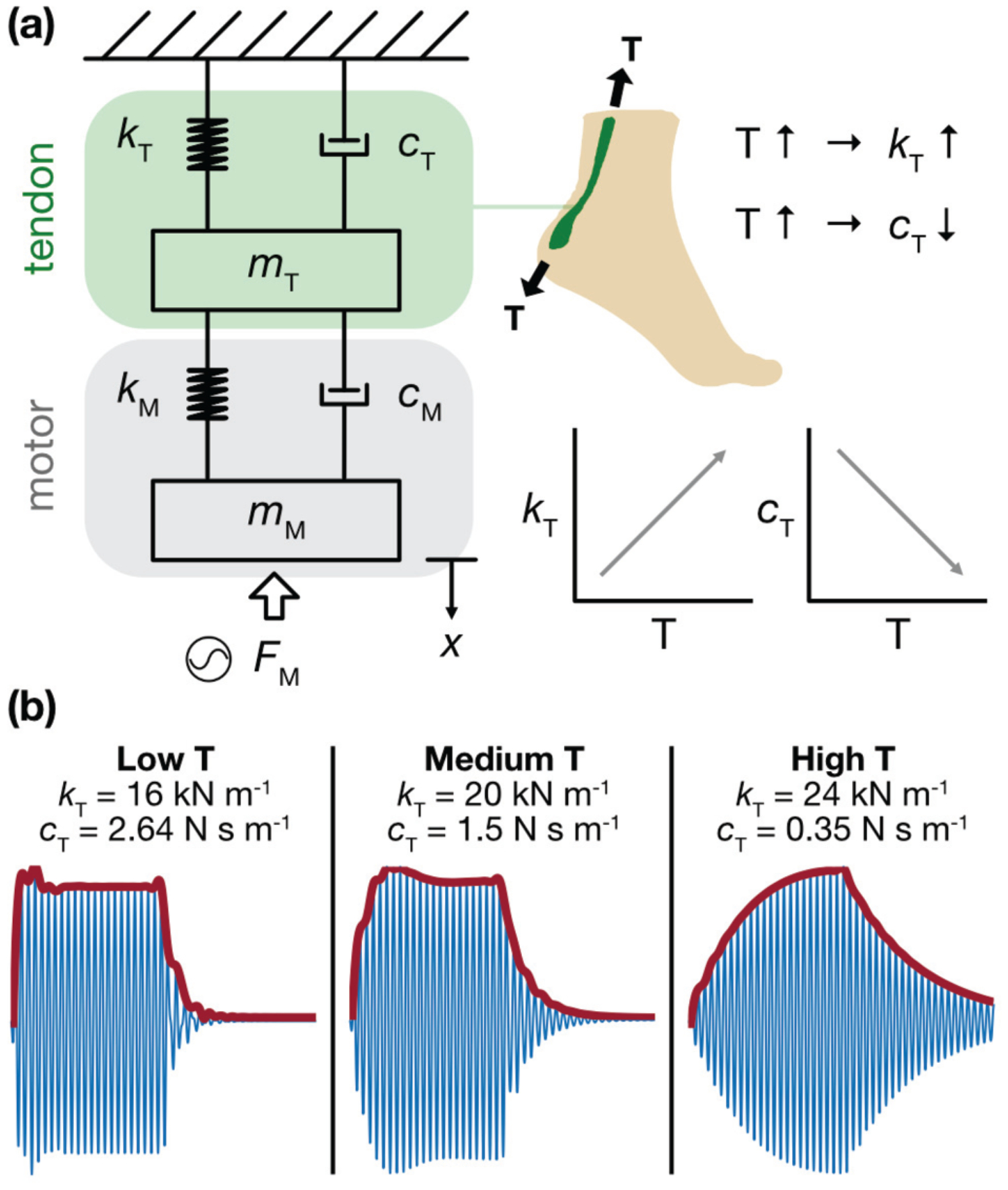
Simplified mechanical model of the LRA-tendon system, (a) The system is modeled as two mass-spring-dampers in series (2-DOF, lumped parameter) with motor excitation modeled as a sinusoidal input force. Based on observation and physiology, we assume that the tendon stiffness, k, is directly related to AT tension, T, and that tendon damping, c, is inversely related to T. (b) When the model simulates a low T (thus, low k and high c) state, the burst envelope exhibits a steep rise and fall; under midrange T(medium k and c), the rising and falling edges begin to take on a more gradual progression, as energy is stored and released more slowly; under high T (high k and low c), this behavior is even more pronounced. These results closely resemble the burst responses observed in vivo.

Approximating the AT as a Euler-Bemoulli beam, the transverse vibration EOM is given as

$$\frac{{\partial }^2}{\partial x^2}\left(EI\frac{{\partial }^{2}w}{\partial x^2}\right)-\frac{\partial }{\partial x}\left(T\frac{\partial w}{\partial x}\right)+\rho \text{A}\frac{{\partial }^{2}w}{\partial t^2}=f(x,t)$$ (3)

where, E is the modulus of elasticity, I is the second moment of area, w is the transverse displacement of the beam at location x, T is the external axial load, p is the density, A is the cross-sectional area, and f(x,t) is the external transverse force. Comparing equation (3) to a single DOF system $\text{EOM}(m\frac{{\partial }^{2}w}{\partial t^2}+c\frac{\partial w}{\partial t}+kw=f(x,t))$, the stiffness term, k_T, can be assumed to be proportional to the tendon tension (i.e., axial load). On the other hand, the tendon is a damping tissue that prevents damage to the muscles by dissipating a portion of the exerted forces [47]. It is shown that, as axial load increases, the damping ratio in a tendon unit decreases [48]. This can be due to the progressive extrusion of water from the tendon that potentially decreases the tissue’s viscoelastic damping [49], [50]. Thus, it can be assumed that the damping coefficient, c_T, is inversely proportional to the tendon tension, T. The equivalent stiffness and damping of the motor are determined experimentally by using a square excitation signal and measuring the transient free oscillation of the motor. The equivalent mass, stiffness, and damping of the tendon are then estimated heuristically to match the envelopes obtained from experimental tests.

E. A fully wearable system: proof-of-concept

All data previously reported in this manuscript were produced using a system that could not be considered truly wearable, as the accelerometer was tethered to a USB DAQ and laptop, and the motor was driven by a benchtop function generator. To maximize the utility of our approach, translation to an untethered system for use in activities of daily life is necessary. Thus, as a proof of concept, we developed a wearable, miniaturized system that replicated our experimental setup, giving us the ability to deliver excitation, capture the tendon response, and log data locally and independently of benchtop equipment (Fig 6).

Fig 6.

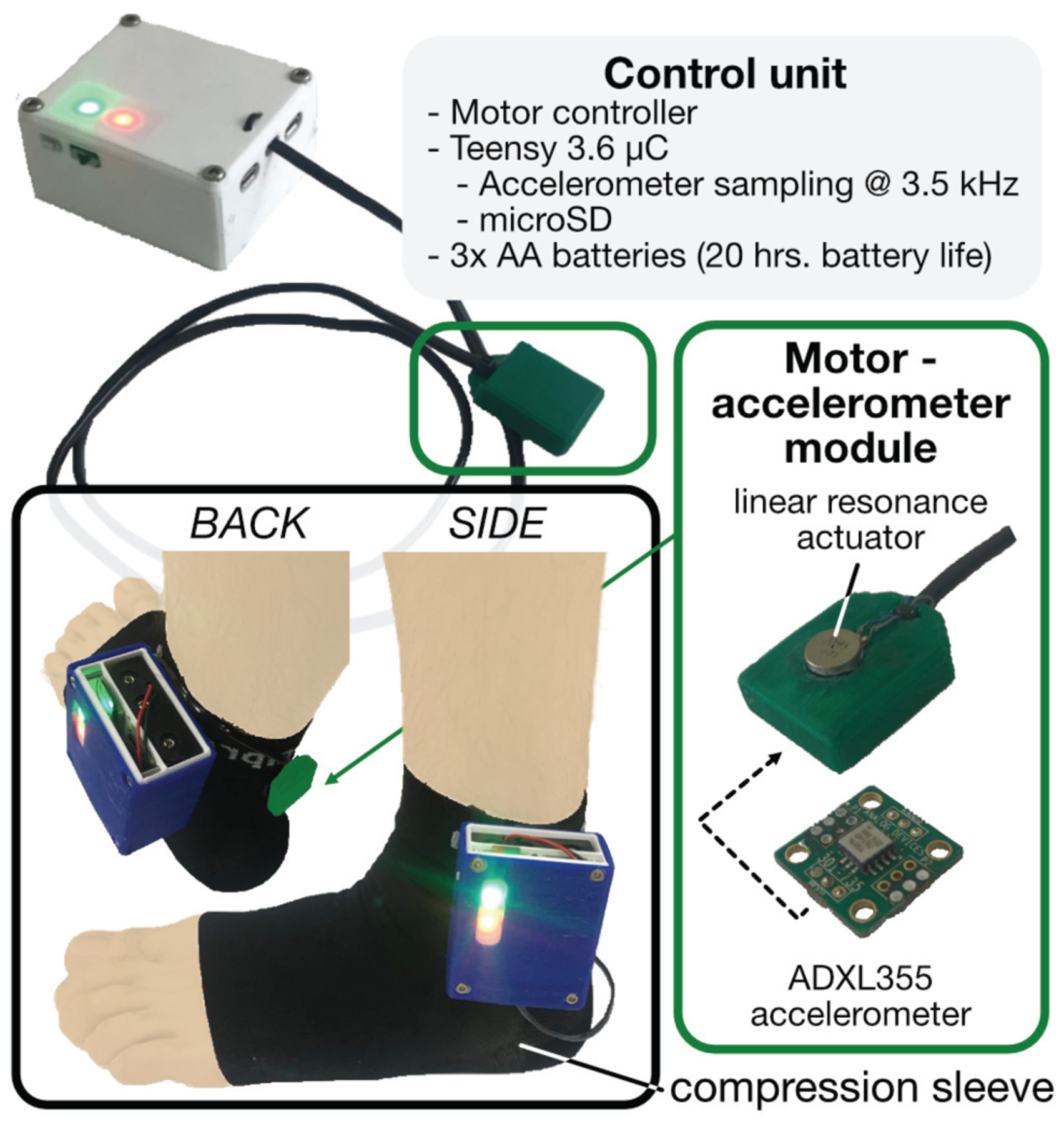
Fully wearable tendon vibration system. A battery-powered unit containing two microcontrollers—one for driving the LRA, the other for sampling and saving the accelerometer—is mounted on a compression sock. A single module housing the LRA and accelerometer is wired to the control unit, positioned on the skin above the AT, and held in place by the compression sock (pictured here outside the sock for better visualization).

The architecture of the wearable can be divided into actuation and sensing modalities. A microcontroller (Teensy 3.6, PRJC, Sherwood, OR, USA) generates the same excitation pattern used in the experimental setup (i.e., 230-Hz sine wave multiplied with a 5-Hz square wave). This waveform is then multiplied by a 7-kHz carrier wave, ultimately producing a pulse width-modulated (PWM) waveform. The PWM output then directly drives the same LRA as used above, which acts as an analog filter, effectively removing the 7-kHz PWM base frequency and vibrating at the same 230-Hz carrier, 5-Hz pulse train as above. A separate microcontroller interfaces with a digital MEMS accelerometer (full scale range = ±2 g, bandwidth = 1 to 1000 Hz) (ADXL355, Analog Devices, Norwood, MA, USA), sampling local skin acceleration over SPI at 20-bit resolution and at a sampling rate of 3.5 kHz. A custom control unit contains the batteries and the microcontrollers and is affixed to the lateral side of a compression sock. The LRA and accelerometer are packaged in a single, custom-designed module that is wired to the control unit and placed at a desired location along the Achilles tendon underneath the compression sock, creating a non-invasive and minimally obtrusive wearable system. Depressing a pushbutton on the control unit initiates excitation of the motor and sampling of the accelerometer, the output of which is written to an onboard SD card. Currently, 3 AA batteries power the device, which draws approximately 300mA during operation, yielding a battery life of roughly 20 hours, assuming continuous use.

The performance of the wearable was characterized in a proof-of-concept study (N=l) by conducting several of the same static and dynamic tasks: neutral standing, double- and single-limb tiptoe standing, and treadmill walking at 1.0 m/s.

III. Results and discussion

A. Representative subject: static and isometric tasks

Static tasks (baseline standing, 2-legged tiptoe, and 1-legged tiptoe) were performed to determine how burst responses changed at different levels of AT tension in the absence of joint motion. AT tension was nominal in the case of a neutral posture with no calf activation, with passive stretch of the tendon and small muscle activations to counteract sway making it non-negligible. By contrast, tiptoe standing produced high tension states in the tendon due to the contraction of the triceps surae pulling on the AT—with the 1-legged case demanding substantially more calf activity than the 2-legged case to support full body weight on a single limb.

Results from a representative subject, in which a candidate feature describing a burst profile attribute is plotted against the net ankle torque, demonstrate how each task stratifies AT force and produces a distinct change in the burst response (Fig 7a). The candidate feature, med_off_n, is defined as the median value of the “off” portion of the burst envelope (i.e., the free vibration stage when excitation is removed) normalized to the burst window’s maximum amplitude, whose units are immaterial. This feature reflects changes in the falling edge of the envelope and manifests physical changes in the tendon (i.e., the fact that the tendon is tauter and less damped) that allow the LRA-tendon system to “ring” for longer after forced excitation has ceased. This same candidate feature is used in Figs 7, 8, and 10, as, for the majority of subjects, it demonstrated strong correlation with target variables (e.g., group R² = 0.77 when comparing with ankle torque during walking). The relationship between med_off_n and net ankle moment appears more logarithmic than linear, suggesting that changes in the burst’s falling edge begin to saturate once the tendon is sufficiently taut. Regardless, good separation is achieved between the three tension states. On average, net ankle torque increased from 0.28 to 0.45 N m kg⁻¹ (62.8% increase) between neutral standing and two-legged tiptoe, and from 0.45 to 1.03 N m kg⁻¹ (128% increase) between two-legged tiptoe and 1-legged tiptoe; for these same transitions, the value of med_off_n increased from 0.1 to 0.25 (150% increase) and 0.25 to 0.34 (35% increase), respectively.

Fig 7.

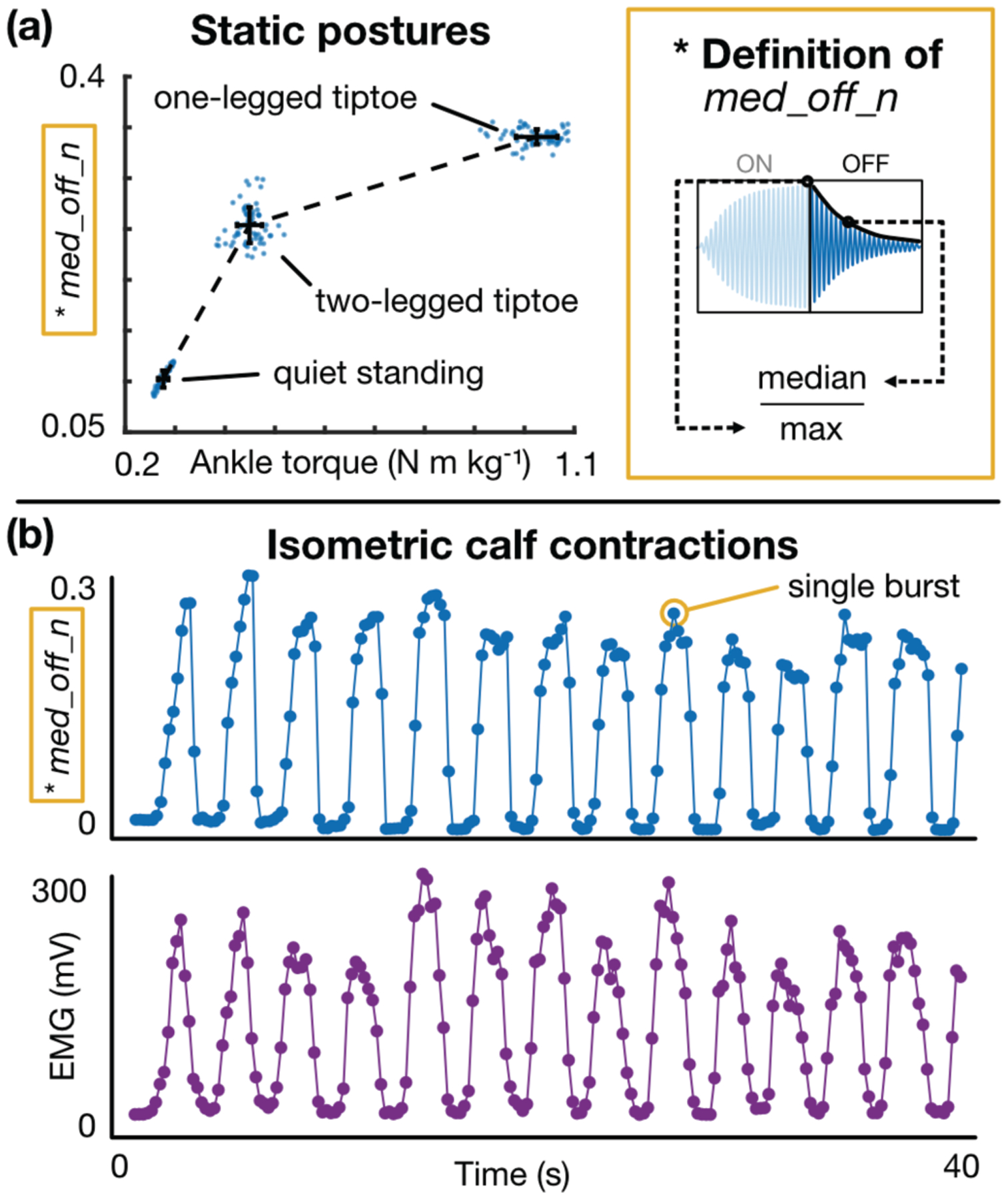
Static calf exercises: representative results, (a) A candidate feature (med_off_n) demonstrates how the burst response changes in response to a change in AT tension. Both med_off_n (y-axis) and net ankle torque (x-axis) increase as the subject switches from neutral standing (left cluster) to 2-legged tiptoe (middle cluster) to 1-legged tiptoe (right cluster). Each dot represents a single burst, and the error bars represent the standard deviation of each set of points, (b) med_off_n (top) and calf EMG (bottom) plotted against time for an isometric calf contraction task. These plots demonstrate that the tendon response changes regardless of joint angle or skin stretch.

Fig 8.

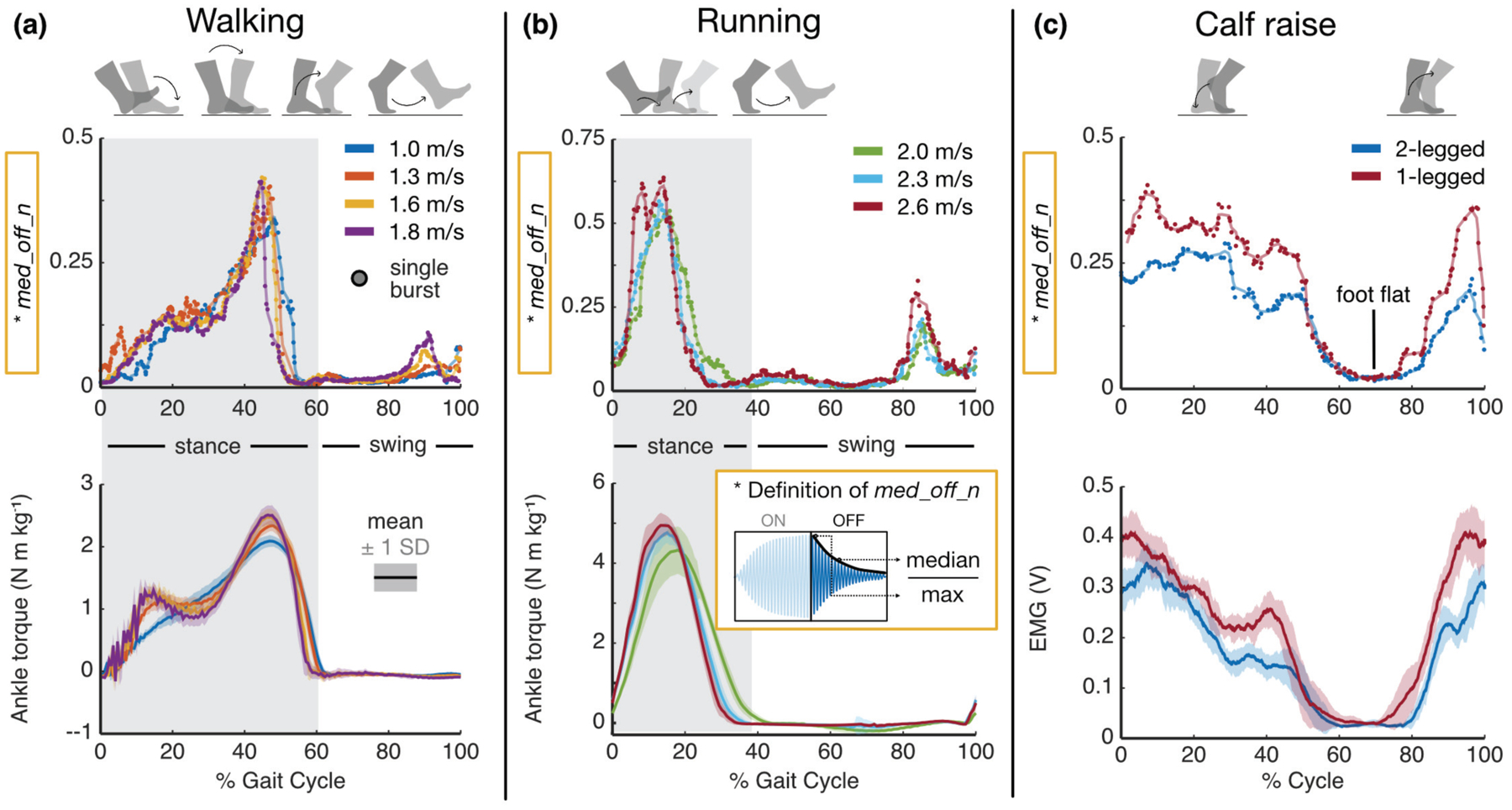
Dynamic exercises: representative results, (a) Burst response feature (top) and average ankle torque (bottom) against % cycle for a range of walking speeds. Each dot represents a single burst’s extracted feature. Note the strong temporal alignment, similar shape, and shared trend in peak values with increasing speed, suggesting that the burst response reflects changes in AT tension, (b) Same analysis and interpretation as before, though for running at a range of speeds, (c) Burst response feature (top) and average calf muscle activity (bottom) against % cycle for both 2-legged and 1-legged calf raises.

Fig 10.

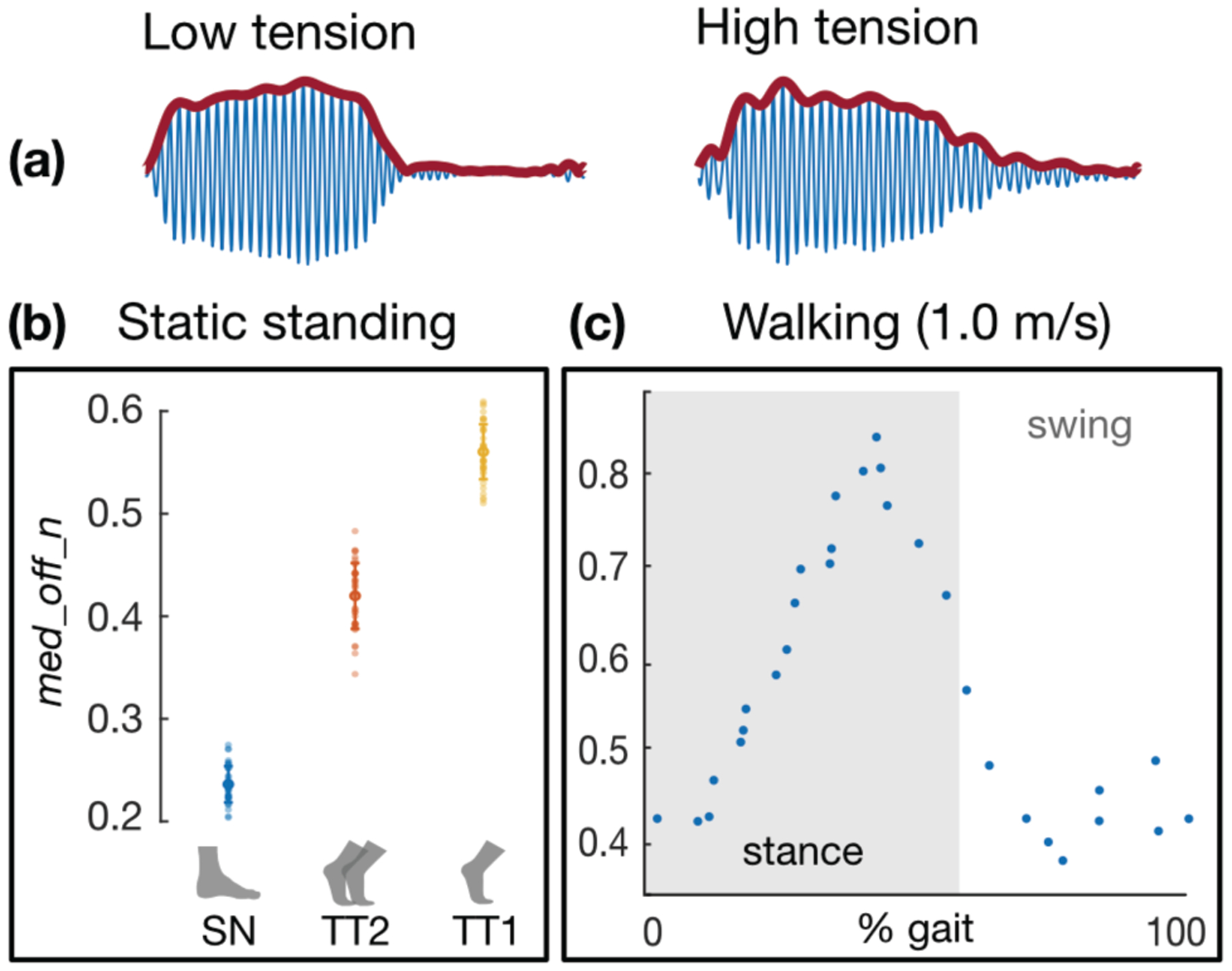
Wearable system: proof-of-concept results. (a) Sample acceleration data from the wearable system demonstrate similar trends in burst response as captured by benchtop equipment, (b) The candidate feature med_off_n again shows separation between low (“SN” = standing neutral), medium (“TT2” = 2-legged tiptoe), and high (“TT1” = 1-legged tiptoe) tension states during static exercises, much as in Fig 7a. (c) The candidate feature also resembles the classical ankle torque waveform during walking, much as in Fig 8a.

Results from the same representative subject performing the cyclic isometric calf contraction exercise over a 40-s interval are shown in Fig 7b, in which the value of med_off_n and calf muscle activation levels for each burst are plotted in parallel. EMG was chosen as the target variable here because, in asking subjects to maintain a constant ankle angle, significant co-contraction was observed, and thus inverse dynamics-derived joint torque did not provide a valid estimate of AT loading. These results indicate that, even at a constant joint angle, the burst profile evolves in response to changing AT tension. Further, this task demonstrates that our technique can still provide an estimate of an AT load corollate even in the presence of co-contraction, which is a limitation of the conventional inverse dynamics approach.

B. Representative subject: dynamic tasks

Though static postures and isometric tasks demonstrated encouraging results, we wanted to judge the true merit of our approach in the context of everyday tasks that involved motion. These tasks included calf raises under both double- and single-limb support, walking, and running. Variation in walking and running speeds was introduced to determine if trends in peak ankle moment, which increases with increasing speed, were able to be observed using the tendon vibration approach. Similar to Fig 7, results from a single, representative subject are illustrated in Fig 8, though similar behaviors were observed across subjects. Likewise, the feature med_off_n, extracted from each burst window, is plotted in parallel with the ensemble average of ankle torque (in the case of walking and running) and calf EMG (in the case of calf raises). As before, units for the y-axis values in the top row of plots are irrelevant as they merely describe an aspect of the shape of the burst envelope. Data were taken from 60-s trials for each exercise, so in the case of walking, the average torque waveforms represent the mean behavior across ~60 strides each, and the candidate feature plot superimposes the feature value of every burst in the minute-long trial (represented by each circular marker) against the percent of the gait cycle, which begins at heel-strike. The plots for running can be interpreted much the same, as can those for calf raise, though in the latter case, the movement cycle begins when the subject is at the apex of the calf raise cycle (i.e., on the tiptoes).

Fig 8a illustrates how even a single descriptor of the burst response (again, med_off_n) can closely track the shape of the ankle torque waveform during walking. Namely, the curves are squarely aligned in time, and even the modest increases in peak torque with increasing speed are evident in the burst feature (40 – 50 % gait). Furthermore, even finer details are reflected in the extracted feature plot: e.g., for the slowest walking speed (1.0 m/s), the torque curve increases monotonically during stance (0 – 60 % gait), while for higher speeds, the curve inflects during midstance (~15 – 30 % gait). Because the foot is no longer in contact with the force plate during swing (60 – 100 % gait), GRF is zero, and thus, inverse dynamics estimates low values of net ankle moment. The tendon vibration system continues to acquire information about the state of the AT throughout swing, which presents an advantage over the current standard of gait analysis techniques. Since our assumptions about AT tension’s relationship to net ankle torque break down during swing, it is difficult to judge the validity of our measurements during this phase of gait; however, experiments in which fiber optic cables are inserted into the AT [24] demonstrate similar trends to what we report here, as does the work done using the piezo-tapper / wave speed approach [29], [30]. The sudden rise in the burst feature waveform toward the end of swing (~ 90 % gait) is noteworthy, as it suggests that the AT is stretched either passively by momentum carrying the foot upward like a pendulum or actively by co-contraction of the dorsiflexors and plantarflexors, perhaps to return the ankle to a suitable position and stabilize the joint prior to heel-strike to minimize energy loss due to collision [51].

Fig 8b further demonstrates that the tendon vibration approach is capable of tracking AT tension-related states during an even more dynamic and high-energy task: running. Again, the shape of each candidate feature curve maps remarkably closely onto that of the net ankle torque curve, and both the peak feature values and the peak torques increase with running speed. For this particular subject, a “divot” is present in the peak of the burst feature waveform (~10 – 15 % gait) at the fastest running speed (2.6 m/s), which we attribute to motion artifact becoming more prevalent at faster speeds, or degradation in the adhesive holding the motor / accelerometer on the skin due to sweat, thus making the accelerometer more susceptible to motion artifact under high impact events such as during fast running. Temporal alignment remains precise, evidenced by the fact that the curves’ peaks occur in sequence, and the falling edges during stance (20 – 40 % gait) persist longer for slower running speeds. Again, a slight prominence in the feature value curve is evident in late swing, which we attribute to the same phenomenon as in walking.

Fig 8c compares the same candidate feature for the same representative subject to the ensemble average of calf EMG, which was used as a proxy for AT tension instead of net torque due to non-negligible co-contraction of the antagonist muscle (TA) during the exercise. Notably, the shapes of both sets of curves correspond favorably, as do the amplitude ratios between the 2-legged and 1-legged task.

Group correlations (i.e., across-subjects calculations of R²) between individual features and corresponding target variables for each movement task are demonstrated in Supplementary Figs 1 (walking), 2 (running), and 3 (calf raise).

C. Estimation of net ankle moment during walking

The results of Figs 7 and 8 demonstrate that even a single feature extracted from the burst envelope of a vibrated AT can closely track a proxy variable for AT tension—in the case of walking, net ankle moment—both in time and in amplitude. However, while this candidate feature appeared to be strongly linearly related to ankle torque for a number of subjects, its relationship was more complex for others. Therefore, by fusing a number of different features together, we hypothesized that we could build a more effective, robust model that could generalize across subjects, requiring the use of machine learning techniques.

Fig 9a illustrates the result of this regression model-based estimation of ankle torque, with an across-subjects R² of 0.85 ± 0.05 and RMSE of 0.34 ± 0.11 N m kg⁻¹. R² values for individual subjects are shown in Fig 9b, from which it is evident that the model performed consistently well across subjects. The group RMSE reported here is less than 25% of the typical ankle torque range at these walking speeds and is comparable to the estimation errors reported using the shear wave velocity technique, as is the across-subjects R² reported [30]. Model-based estimates of net ankle moment during running (R² = 0.82) can be found in Supplementary Fig 4.

Fig 9.

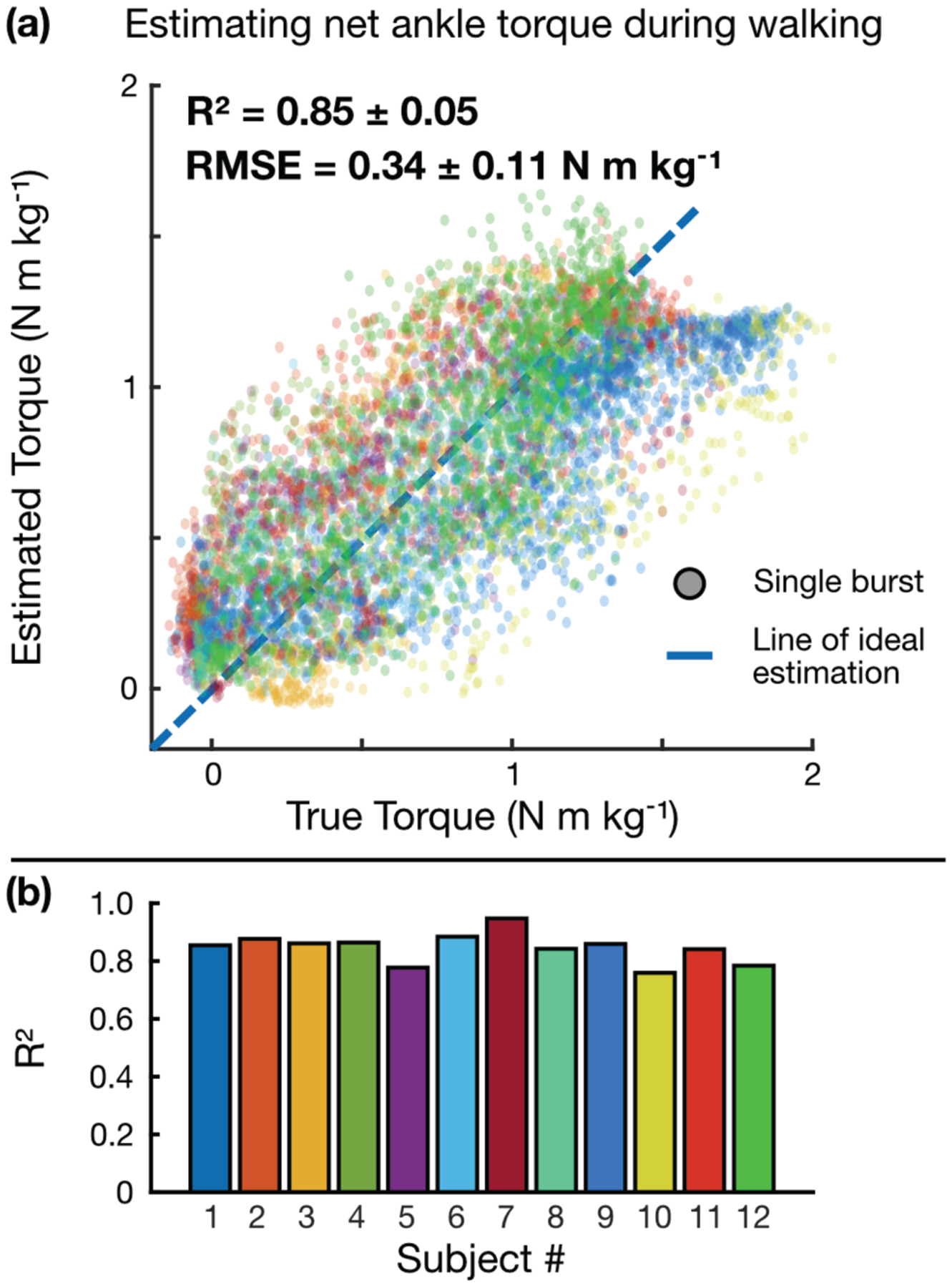
ML-based regression model for estimating ankle torque during walking, (a) Bagged regression tree model estimate of ankle torque vs. ankle torque calculated by inverse dynamics. Each dot represents a single burst, and each color represents a different subject, (b) Individual R² values for each subject, demonstrating consistent estimation performance across subjects.

D. 2-DOF mechanical model simulation

Estimated mechanical properties of the tendon and motor are substituted into equations (1) and (2) to qualitatively investigate the overall response of tendon-motor unit to a burst excitation for various quantities of tendon tension. By increasing the tendon axial load, the stiffness coefficient, k_T, increases, while the damping coefficient, c_T, decreases (Fig 5a). For reference, three arbitrary selected cases are shown in Fig 5b, in which the change in the calculated acceleration envelope is illustrated for three different tension levels. The obtained envelopes from the analytical model can be compared to those collected experimentally (e.g., Fig 2c,d) for low- to high-tension states. It is necessary to note that the 2-DOF model is utilized to show the potential of quantitative assessment of the tendon tension using analytical models and to gain an understanding of the physics of the tendon-motor system. Future research including measures of tendon dimensional and material properties can lead to a more realistic model capable of predicting the exact quantities of tendon tension at different states.

E. Proof-of-concept wearable results

Data acquired by the fully wearable system (Fig 6) are reported in Fig 10. For the sake of continuity, the same candidate feature reported above (med_off_n) is used to express these results. Importantly, similar changes in burst response observed in the above experiments (in particular, changes in rise and fall time constant) were preserved in the wearable setup, as shown in the sample waveforms in Fig 10a. In general, the signals appeared less “clean” than those obtained by the benchtop equipment, which we attribute to the microcontroller-derived excitation signal being sampled at a lower rate than was achieved with the benchtop function generator, as well as the digital accelerometer being more susceptible to artifact such as cable motion than its higher-sensitivity and -bandwidth counterpart used above. For the static trials, features of interest (particularly med_off_n, as shown) repeatably showed distinct separation between low (standing neutral), medium (2-legged tiptoe), and high (1-legged tiptoe) tension states, consistent with previous experimental results (Fig 10b). Notably, the trend observed during walking was also maintained in the wearable system, with the shape of the med_off_n curve resembling that of a classical ankle torque curve across gait both in time and amplitude (Fig 10c). While these results with the wearable system are only preliminary, they evince a similar potential for capturing tension-related states of the AT during both static and dynamic tasks, which holds promise for future experiments outside the laboratory or clinic.

IV. Limitations and Future work

A. Net ankle moment as a proxy for AT force

In this study we use net ankle moment, which is accessible through conventional gait analysis techniques and has been shown previously to correlate highly with AT force under certain conditions [42], [52], [53], to relate our directly measured state (surface accelerometry) to our desired state (AT load). However, the use of net ankle moment as a proxy for AT tension is a limitation in itself, primarily due to the fact that the AT moment arm varies with ankle angle and muscle load, either negligibly (<10%) [43], [54] or substantially (up to 25%) [44], [55] depending on the estimation method employed, for which there is no clear consensus [56], [57]. To address this limitation, future studies would require subject-specific estimations of AT moment arm—perhaps using an ultrasound-based method as in related studies [30]—or an EMG-informed musculoskeletal model. A wearable system might use empirical equations derived from radiography [58] to approximate AT moment arm as a function of measured ankle angle.

B. System hardware and methodology refinements

Though these preliminary findings are promising, room for improvement remains in the development of the device hardware, analysis techniques, and model system. In developing a more sophisticated mechanical model, we will gain a greater intuition and understanding of the phenomena observed in the burst response profile and how they relate to mechanical parameters of interest (tendon tension, stiffness, damping, etc.). In turn, these insights will enable us to extract more meaningful, accurate information from the data and perhaps extrapolate to new loading states.

Because our system uses a sensitive accelerometer coupled imperfectly to the skin, it was often susceptible to motion artifact, particularly during high-velocity, high-impact events such as heel-strike. Efforts to address this challenge include improvements in signal processing (e.g., rejection of signal portions heavily corrupted by artifact, development of a signal quality index for establishing data fidelity) and in hardware (e.g., ensuring better, more consistent sensor-to-skin contact).

In its present form, the effective data rate of our system is 5 Hz, which may suffice for certain applications, but to generate a faithful representation of AT tension across, say, the running cycle, a higher sampling rate will be required. Currently, this limitation is a consequence of the LRA; being a mass-spring-damper system itself, the motor exhibits a characteristic (constant) rise and fall time. Preliminary tests suggested that, when the motor was driven at a pulse rate greater than 10 Hz (at 50% duty), the oscillating mass was unable to return to a neutral position before the onset of the following excitation. This behavior caused the shape of the burst profile to saturate, at which point no additional information contained in the rising and falling edges of the envelope—which normally would evidence a change in tendon tension–was gained. Different excitation patterns—for instance, one with a lower duty factor, such that the free vibration stage (the “off” portion of the burst window) is maintained even at higher pulse rates—and other mechanical stimuli (e.g., an LRA with higher resonance / lower rise time, an actuator with higher bandwidth) may be explored.

Though general trends were observed, burst response did not vary with AT tension precisely the same across subjects. For example, changes in fall time constant might reach an asymptote at a lower tension state for one subject than for another. We attribute such inconsistencies to variation in subject anatomy and physiology (e.g., the tendon’s basal tension, modulus, length, and cross-sectional area, thickness of skin / fat / other surrounding soft tissues, body mass, pre-experiment activity level). Subject-specific calibration may help account for these variations and improve estimation performance.

Further development of the fully wearable system will focus on the addition of other useful signals such as joint angle (via inertial measurement unit) and EMG, miniaturization (at present, the AA batteries account for ~70% of the mass and volume and could be replaced by a lower-profile lithium-polymer battery), improved feature extraction techniques, and real-time feedback of tendon tension state to the user.

V. Conclusion

In this work, we have developed and evaluated a novel method of assessing aspects of ankle loading related to AT force noninvasively by analyzing the tendon’s response to burst vibrations on the skin surface. Results demonstrate strong spatiotemporal agreement between our system’s estimate of AT load-related parameters (i.e., net ankle moment and calf EMG) and those obtained from conventional gait analysis techniques. Using machine learning, we were able to accurately estimate ankle moment during walking across a range of speeds from features of the tendon’s burst response. Further, we developed a custom-designed, fully wearable system whose proof-of-concept results demonstrate similar trends to that of benchtop equipment experiments. These findings demonstrate that our approach holds promise as an effective means of tracking tendon loading over time across a variety of everyday tasks, which may provide invaluable information for injury risk mitigation, rehabilitation strategies, and the study of movement impairments. Our approach could potentially be applied to other tendons, such as the patellar or biceps tendon, both of which also exhibit a high incidence of injury, or even perhaps other tissues like the plantar fascia and muscle, to similarly assess loading conditions and mechanical properties such as stiffness. Armed with this knowledge, an orthopedist could provide better injury diagnoses and prognoses; a physical therapist could precisely track the course of an athlete’s recovery; an athlete could monitor the cumulative load on a particular muscle group; a physiatrist could peer deeper into movement disorders at the muscle-tendon unit level; and biomechanists could design better control strategies for robotic exoskeletons based on the mechanics of the underlying biology. As such, assessing tendon loading noninvasively could improve quality of life for countless individuals and put a spring back in their step.

VIII. Appendix

TABLE I.

Features Extracted from Burst Envelope

#	Feature	Description
1–3	max (& _on, _off)	Maximum amplitude
4–11	mean (& _n, _on, _on_n, _off, _off_n, _off_on, _off_n_max)	Mean amplitude
12–19	med (& _n, _on, _on_n, _off, _off_n, _off_on, _off_n_max)	Median amplitude
20–27	auc (& _n, _on, _on_n, _off, _off_n, _off_on, _off_n_max)	Area under the curve
28–35	std (& _n, _on, _on_n, _off, _off_n, _off_on, _off_n_max)	Standard deviation
36–41	meandiff (& _n, _on, _on_n, _off, _off_n)	Average slope
42–45	maxROC (_on, _on_n, _off, _off_n)	Maximum (absolute) slope
46–51	sr (& _n, _on, _on_n, _off, _off_n)	Slew rate (from reference levels 25% to 75% max amplitude)
52–54	C (& _on, _off)	Time index @ 50% total auc
55	tc	Time constant of exponential decay (slope of logarithmic fit line)
56	intercept	y-intercept of logarithmic fit line
57	i_min_log	Time index of minimum of logarithmic fit line
58	log_gof	Goodness of logarithmic fit line
59	symm_diff	Symmetry of burst envelope (folded in half, subtracted)
60	symm_diff_abs	Absolute value of residuals of the above
61	symm_ratio	Symmetry of burst envelope (folded in half, divided)
62	symm_pctdiff	Percent differences of the above
63–68	MX(& _n, _on, _on_n,_ off, _off_n)	Mobility parameter: ratio of std(X) to std(dX/dt)
69	MXX	2nd mobility parameter: ratio of std(dX/dt) to std(d2X/dt2)
70	FF	Form factor: ratio of MX to MXX

‘_on’ = specific to the “on” burst region; ‘_off’ = specific to the “off” burst region; ‘_offon’ = ratio of _off feature to _on feature; ‘_n’ = normalized to envelope max; ‘_n_max’ = normalized to envelope max²