Automatic segmentation, feature extraction and comparison of healthy and stroke cerebral vasculature

Highlights

• •Probabilistic filter with active contours to automate cerebrovascular segmentation.
• •Geometric features of vessel network to study cerebrovascular diseases.
• •Quantitative comparison of stroke and healthy cerebral vasculature.
• •Vascular changes with aging and cerebrovascular disease.
• •Comparison of CTA and MRA imaging modalities.

Abstract

Accurate segmentation of cerebral vasculature and a quantitative assessment of its morphology is critical to various diagnostic and therapeutic purposes and is pertinent to studying brain health and disease. However, this is still a challenging task due to the complexity of the vascular imaging data. We propose an automated method for cerebral vascular segmentation without the need of any manual intervention as well as a method to skeletonize the binary segmented map to extract vascular geometric features and characterize vessel structure. We combine a Hessian-based probabilistic vessel-enhancing filtering with an active-contour-based technique to segment magnetic resonance and computed tomography angiograms (MRA and CTA) and subsequently extract the vessel centerlines and diameters to calculate the geometrical properties of the vasculature. Our method was validated using a 3D phantom of the Circle-of-Willis region, demonstrating 84% mean Dice similarity coefficient (DSC) and 85% mean Pearson’s correlation coefficient (PCC) with minimal modified Hausdorff distance (MHD) error (3 surface pixels at most), and showed superior performance compared to existing segmentation algorithms upon quantitative comparison using DSC, PCC and MHD. We subsequently applied our algorithm to a dataset of 40 subjects, including 1) MRA scans of healthy subjects (n = 10, age = 30 ± 9), 2) MRA scans of stroke patients (n = 10, age = 51 ± 15), 3) CTA scans of healthy subjects (n = 10, age = 62 ± 12), and 4) CTA scans of stroke patients (n = 10, age = 68 ± 11), and obtained a quantitative comparison between the stroke and normal vasculature for both imaging modalities. The vascular network in stroke patients compared to age-adjusted healthy subjects was found to have a significantly (p < 0.05) higher tortuosity (3.24 ± 0.88 rad/cm vs. 7.17 ± 1.61 rad/cm for MRA, and 4.36 ± 1.32 rad/cm vs. 7.80 ± 0.92 rad/cm for CTA), higher fractal dimension (1.36 ± 0.28 vs. 1.71 ± 0.14 for MRA, and 1.56 ± 0.05 vs. 1.69 ± 0.20 for CTA), lower total length (3.46 ± 0.99 m vs. 2.20 ± 0.67 m for CTA), lower total volume (61.80 ± 18.79 ml vs. 34.43 ± 22.9 ml for CTA), lower average diameter (2.4 ± 0.21 mm vs. 2.18 ± 0.07 mm for CTA), and lower average branch length (4.81 ± 1.97 mm vs. 8.68 ± 2.03 mm for MRA), respectively. We additionally studied the change in vascular features with respect to aging and imaging modality. While we observed differences between features as a result of aging, statistical analysis did not show any significant differences, whereas we found that the number of branches were significantly different (p < 0.05) between the two imaging modalities (201 ± 73 for MRA vs. 189 ± 69 for CTA). Our segmentation and feature extraction algorithm can be applied on any imaging modality and can be used in the future to automatically obtain the 3D segmented vasculature for diagnosis and treatment planning as well as to study morphological changes due to stroke and other cerebrovascular diseases (CVD) in the clinic.

1. Introduction

Cerebrovascular diseases (CVD) are a leading cause of death and disability in the US and worldwide with stroke being a major contributor (Benjamin et al., 2019, Saxena et al., 2019). Assessing the structural changes in cerebral vasculature is pertinent to brain health and diagnosing and characterizing disease (Liu et al., 2018, Wright et al., 2013). Changes in vascular structure can indicate altered function and potential cerebral pathophysiology (Cassot et al., 2006, Gutierrez et al., 2015) and hence need to be characterized and quantified (Wright et al., 2013, Chen et al., 2018a), which in turn requires deep knowledge of the normal healthy vascular geometry and morphology (Mouches and Forkert, 2019). It has been shown in the literature that altered vascular properties such as the vessel diameters, tortuosity and the branching pattern are closely correlated with cerebrovascular diseases such as atherosclerosis and stroke (Kim et al., 2015, Lemasson et al., 2016). After an ischemic stroke, the reduced blood flow causes a series of changes leading to structural remodeling of the vasculature (Liu et al., 2014). Studying these acute and chronic changes in vascular structures is key to understanding the underlying physiological mechanism of disease and cerebral function. A well-segmented cerebral vasculature map is essential to visualize and quantify vessel occlusions, evaluate cerebral blood flow and perfusion, assess the extent of ischemia in stroke patients, and detect and assess other cerebral vascular malformations such as aneurysms (Saxena et al., 2019, Meijs et al., 2017, Steinman et al., 2003). Furthermore, in neurosurgical planning, choosing the appropriate endovascular procedure and determining the best surgical plan necessitates a 3D segmented map of the vasculature (kodoma, 1995, Murayama et al., 2019). For efficient diagnosis and treatment of stroke and other CVD, angiography imaging techniques such as Computed Tomography Angiography (CTA) and Magnetic Resonance Angiography (MRA) are routinely performed in the clinic as well as in acute hospital settings to visualize the blood vessels and flow of blood in the brain (Saxena et al., 2019, Quaday et al., 2014). These imaging techniques, however, only show 2D cross sectional slices which contain other anatomical structures as well as noise (Hsu et al., 2017). This potentially leads to error in diagnosis due to the partial information regarding vascular structure without a 3D volume available (Saxena et al., 2019).

Despite the clinical need, there is still a lack of a completely automated segmentation method of subject-specific 3D cerebral vasculature and subsequent feature extraction due to the various challenges posed by this problem. Cerebral vessel geometries vary greatly in length, diameter and tortuosity, making vessel tracking and segmentation a complex multi-scale problem (Luo and Zhong, 2005, Lesage et al., 2009, Zhao et al., 2018). Intensity inhomogeneities and inconsistent contrast exist due to flow velocity changes as well as varying imaging protocols (Zhao et al., 2018, Yu et al., 2016). An overlap of bony anatomical structures in CT and white/gray matter in MR can distort the vascular imagery due to a shadow effect (Luo and Zhong, 2005). Also, the smaller vessels whose diameters are at the scale of the image resolution are extremely hard to detect (Ajam et al., 2017). Due to all of these challenges, designing a robust segmentation method that works on all imaging modalities, remains the biggest challenge in visualization and assessment of 3D cerebral vasculature in the clinic (Ajam et al., 2017, Navab et al., 2015). In the past few years, there has been a significant effort towards solving the problem of segmentation and an increasing number of approaches have been proposed in the literature (Meijs et al., 2017, Kirbas and Quek, 2004). Most of these methods, however, have only been evaluated on a specific type of imaging data, such as either MRA or CTA (Wright et al., 2013, Meijs et al., 2017, Hsu et al., 2017, Kandil et al., 2019,, Livne et al., 2019). Clinically relevant segmentation algorithms need to cover a large range of image variability and need to be able to perform on different modalities.

Thresholding-based methods that utilize either global or local thresholds tend to lose vessel pixels, resulting in inaccurate segmentations (Kirbas and Quek, 2004, Passat et al., 2006). Other methods need varying forms of manual interventions at different stages (Chen et al., 2018a, Luo and Zhong, 2005). Also, many of the proposed methods in literature that use centerline tracking require some form of manual ‘seed points’ or initialization due to inconsistencies in intensity along the vessels in different slices (Meijs et al., 2017, Ajam et al., 2017, Kirbas and Quek, 2004). Furthermore, geometric feature extraction for characterization of cerebral vessels has been scarcely reported in the literature (Wright et al., 2013, Chen et al., 2018a, Mouches and Forkert, 2019). These methods require manual intervention in certain stages during segmentation and feature extraction. Most other 3D visualization and feature analysis tools in literature utilize only global geometric features such as length and volume (Slafer et al., 1994, Peng et al., 2010), even though local regional features provide more useful and targeted information on vasculopathies (Boussel et al., 2009, Bash et al., 2005). Some of the major contributions to cerebral vessel segmentation in the literature and their limitations are listed in Table 1, which comprises of various methods, ranging from established methods – which require manual intervention – to fully automated methods. We have tried to incorporate a comparison of different kinds of methods and highlight their validation, applications and limitations. The comparison table also includes several filter-based methods as well as machine learning approaches.

Table 1.

A summary of related work in the literature on cerebral vascular segmentation. The geometric feature extraction column indicates whether the paper presented any geometric features of the vasculature and the skeletonization column indicates whether this method obtains the centerline and diameter information needed for CFD and mesh reconstruction. The last two columns specify the corresponding validation protocol and the major limitations which we tried to address in our method.

Authors	Method	Modality		Skeletonization	Geometric Feature Extraction	Validation Protocol	Major Limitations
Flasque et al. (2001)	Centerline tracking and modeling	MRA	Manual or Semi-Automatic	✓	×	Phantom	Manual intervention required
Passat et al. (2006)	ATLAS registration with anatomical modeling and hit-or-miss transform	PC-MRA		✓	×	Manual	Manual intervention required
Chen et al. (2018b)	Semi-automated Open-Curve Active Contour Vessel Tracing	3D MRA		✓	✓	Manual	Some manual intervention required, only tested on patients with intracranial arterial stenosis
Gao et al. (2012)	Statistical model analysis and curve evaluation	MRA		×	×	Manual	Intensity based statistical analysis and local curve evaluation resulting in under-segmentation
Wright et al. (2013)	Neuron_Morpho plugin in ImageJ for segmentation (discontinued), morphometric analysis and feature extraction	MRA		✓	✓	NA	Insufficient Validation, performance accuracy unclear
Hsu et al.(2017)	Multiscale composite filter and mesh generation	MRA	Fully Automatic	✓	Limited	Manual, phantom	Not tested on CT data, limited feature extraction
Wang et al. (2015)	Otsu and Gumbel distribution-based threshold	MRA		×	×	Manual	Misclassification of skull pixels, under- segmentation of small vessels
Chen et al. (2018a)	Deep learning 3D U-Net architecture without manual annotation	MRA (CTA for training data)		×	×	Manual	Thresholding based filtering to generate training data, insufficient validation
Meijs et al. (2017)	Random forest classifier with local histogram features	4D CT		×	×	Manual	No geometrical information, manual validation
Zhao et al. (2018)	Weighted Symmetry Filter	MRA, Retinal images		×	×	Manual, phantom	No skeleton or geometrical information
Livne et al. (2019)	Deep learning-based U-net architecture	MRA		×	×	Manual	Poor inter-modal performance (monocentric data), no skeleton or geometrical information, no healthy dataset

Furthermore, to the best of our knowledge, there are no studies which quantitatively compare the differences in cerebral vascular structure and geometry in major vascular pathological conditions such as stroke with healthy subjects, which is an essential investigation for understanding brain health and disease (Wright et al., 2013, Hsu et al., 2017). Some studies have extracted vascular features of patients with intracranial arterial stenosis without a healthy control group (Chen et al., 2018b), or a healthy data set only (Wright et al., 2013), stating the importance of performing such a comparative analysis between healthy subjects and CVD patients (Wright et al., 2013, Hsu et al., 2017, Chen et al., 2018b). Another study compares the vessel tortuosity in healthy subjects versus patients with intracranial artery atherosclerosis (Kim et al., 2015) but performed this manually and visually using 2D slices of time of flight (TOF) MRA, lacking 3D segmentation or feature extraction, which could lead to miscalculation of the vascular features.

In this work, we propose an automated method for cerebral vascular segmentation that does not require initializing seed points or other manual intervention and can be applied to any imaging modality; we test our method on both MRA and CTA data. Our method accounts for the differences in intensity inhomogeneities and tissue/bone contrast between MR and CT data and includes extensive validation using a realistic 3D phantom of the Circle of Willis. By skeletonizing the segmented vasculature, we extract global and regional geometric features of the vessel network to characterize the structure of the vascular tree. Finally, we present a quantitative comparison of the geometric features of the cerebral vascular tree between healthy subjects and stroke patients for both MRA and CTA imaging modalities, to understand and quantify the structural differences in the vasculature caused by ischemic stroke, the most devastating cerebrovascular disease. It has been shown that Alzheimer’s disease, cerebral aneurysm, stroke and other CVD lead to or are preceded by changes in the vasculature (Kim et al., 2015, Govindpani et al., 2019, Arvanitakis et al., 2016, Kimmel et al., 1996, Horace, 1990), which could be quantified using our approach of analyzing the vascular features (Govindpani et al., 2019, Arvanitakis et al., 2016).

2. Materials and methods

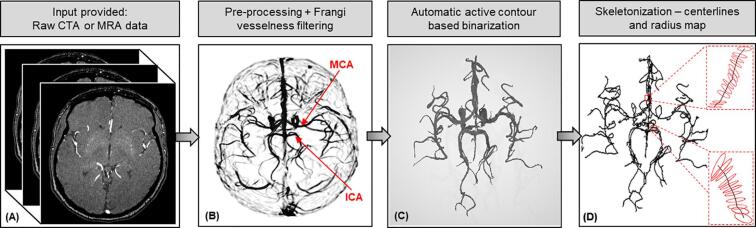
In this section, we first detail the steps in our automatic segmentation and feature extraction algorithm: 1) pre-processing, 2) vessel enhancement, 3) binarization, 4) skeletonization and 5) geometric feature extraction. We then present the validation of our algorithm on a 3D phantom of the Circle of Willis (CoW) region of the vasculature. Finally, we apply our proposed algorithm on four angiography datasets of CTA and MRA scans from healthy subjects and stroke patients to investigate the effect of disease, aging and imaging modality on vascular changes.

2.1. Pre-processing

We first performed skull-stripping using Hounsfield-unit thresholding and location-based segmentation for both MRA and CTA data to remove the bright skull regions that affect segmentation, especially in the CTA data (Muschelli et al., 2015). This step prevents non-vascular skull pixels from being falsely enhanced in the vessel enhancement step due to a tubular structure or higher intensity. Omitting the skull-stripping step would lead to mislabeling of non-vascular pixels. MRA data is less susceptible to this limitation than CTA since it uses time of flight (TOF) imaging which enhances contrast of the flowing blood due to varying magnetization whereas in CTA, bony structures are enhanced. For ‘skull-stripping’ the CTA data, we used the validated method (and algorithm) presented in Muschelli et al. (2015) for brain extraction from CT images using HU based thresholding and positional information. This method includes creating a brain mask and has successfully shown good performance on CT images acquired under different scanners and parameters (demonstrating high generalization) and robustness. For the ‘skull stripping’ on MR data, we chose the publicly available method called Brain Extraction Tool (BET) as presented in Smith (2002). After removing the skull, we chose the region of interest (ROI) by selecting slices only from the head region resulting in about 100 slices in the MRA and 150 slices in the CTA dataset (based on our datasets with 0.62 mm axial resolution in both CTA and MRA). This step involves excluding the additional slices below the head region and greatly improves computation speed and reduces noisy structures that reside outside the cerebral vasculature region of interest.

2.2. Vessel enhancement

The first step in the segmentation process is the vessel enhancement or ‘vesselness’ filtering, which is performed to suppress non-vascular structures and highlight the vessel pixels. We developed a custom multi-scale Frangi vesselness filter (Frangi et al., 1998) to obtain a probability map of the pixels belonging to the vascular network. After inputting raw MRA or CTA DICOM images, we apply a 2D Hessian based filter which enhances blood vessel contrast and eliminates other structures (Frangi et al., 1998). The Hessian filter can be described as a second-order partial derivative of the image intensity map, aimed at tracking the path of least curvature and preserving tubular structures (Refer to the Supplementary Materials). The eigenvalues of the Hessian matrix depend on the directional voxel spacing and provide information about the shape of the object in the image. Since vessels can be considered as 3D tubular structures at varying length scales, we assign a probability score of being on the vessel to every pixel with the center pixel having the highest probability and intensity. The pixels with a higher probability are more likely to belong on a vessel and retain a much higher intensity than the background, enhancing the vessel contrast. In the vessel-enhancement step, Gaussian smoothing is also performed along with the filtering to further reduce noise, since Gaussian smoothing reduces high frequency noise and results in the neighboring pixels being correlated (Cadena et al., 2017, Reddy, 2011). The variance of the Gaussian kernel used for filtering is chosen based on the expected diameters of the vessels, since it maximally suppresses the noise around the blood vessels in the second order directional derivatives obtained with the Hessian filter. The multi-scale nature of the filter allows us to set local as well as global parameters, with the capability of detecting vessels as small in diameter as the image resolution.

In our implementation, we use the following parameters for the vesselness and Gaussian filtering: Scale is defined as the standard deviation of the Gaussian kernel used for the analysis, which should be close to the expected radius of the vessel. Minimum (Maximum) Scale is the minimum (maximum) expected vessel radius in mm, at which the relevant structure is expected to be found, and Number of Scales (N) is an empirical parameter to set the range of radii detected. Since we are limited by the resolution of imaging, the Minimum Scale is the smallest ‘detectable’ radius and was set to half the size of a pixel, to detect vessels as thin in diameter as the pixel size. The Maximum scale was set to the largest possible vessel diameter. With this method, we can detect vessels with the diameter in the range of the image resolution (in our case, up to 0.23 mm, the finest resolution of the stroke MRA data). So, we set minimum value for human vasculature to one pixel by default and the maximum value to 10 mm (Reina-De La Torre et al., 1998). Step size between the minimum and maximum scale can be defined as small as needed (the algorithm will run longer for a larger number of steps) based on the size of the expectant structures. We set the default as 1 pixel (0.23 mm), attributing to the varying vessel scales in human vasculature.

The Gaussian filtering for noise reduction is performed for different variances (σ), close to the expected vessel diameter calculated as:$\sigma =(MaximumScale-MinimumScale)/(N-1)$. Auxiliary scalar function ‘c’ incorporates the grayscale range of the input data and its value at every pixel is normalized to the maximum intensity of the image and hence depends on the gray-scale range of the input images. Half the value of the maximum Hessian norm has proven to work in most cases, based on previous literature (Navab et al., 2015, Frangi et al., 1998). This is chosen based on the input image dataset and was set to 500 since the input grayscale images had 1024 intensity levels from 0 to 1. Additional information regarding the working principles of the Frangi vesselness filtering can be found in the Supplementary Materials.

2.3. Binarization

We segment the grayscale vessel probability map obtained using the vesselness filtering into a binary network of vessels using the ‘Chan-Vese’ Active Contours method (Chan and Vese, 2001). This method detects objects or regions of interest in an image based on parametric curve evolution and can iteratively detect objects without a gradient-defined boundary, using energy minimization. This segmentation technique, in combination with the pre-processing and multi-scale vesselness filtering provides a 3D binary mask of the vasculature to be used for vectorization and feature extraction. The default number of iterations of active contours was set to 750 and a binary mask specifying rectangular ROI boundaries around the brain was provided as input. The algorithm then moves the mask to locate the object from the vesselness probability maps based on the specified number of iterations, without the need of any manual initialization or seed points. The number of iterations was chosen based on the size of the images, since the contours move from the edges into the center of the image, tracing ROI boundaries. Based on most clinical imaging datasets of image size 512 × 512, we set the number of iterations to 1000. Due to the higher intensity of the vessel pixels and suppression of other structures in the preprocessing and vessel enhancement steps, the active contours automatically trace the vascular network, providing a binary volume. For additional noise reduction, we multiply the vesselness map with a binary elliptical 3D mask confined to the ROI, before binarizing, to eliminate any stray skull/edge pixels, as well as the superficial venous structures. Finally, to eliminate dangling structures or remnant noise from the segmentation, we perform an area opening operation (xxxx) to discard disconnected segments smaller than 10 mm long using 3D 26-point connectivity (Chris Solomon, 2020). The result of this step is a 3D connected binary network of the cerebral arteries.

2.4. Skeletonization

The binary vessel map was used to create a connected vascular network from which we extracted the geometric features corresponding to the entire vessel tree. We used medial axis thinning (Lee et al., 1994) to obtain the centerlines of the binary map and calculate the radii and angles at each point on the centerline. Having determined the 3D centerline representation and the corresponding voxel indices on the centerline, we used the connected segments to calculate the 3D angles (axial and sagittal) between these points. To obtain the radius at each point on the centerline, we calculated the geodesic distance map (Kimmel et al., 1996) between center pixels and the boundary pixels and take the shortest distance between them as the radius at that point. To perform this, we first traced the exterior boundaries of the objects in the ROI as well as the inner edges of any ‘holes’ present using the Moore neighborhood tracing method (Pradhan and Ghose, xxxx, Horace, 1990) and then calculated the distance from the center pixel using the geodesic distance method. This provides the radius of the vessel at every point on the centerline. Once we obtained the centerline network with precise radii at every point, we define a ‘branching node’ of the vascular tree as a point which is connected to three other points in 3D space, i.e., a bifurcation. After identifying all the branching nodes, we calculated the length of each vessel segment, defined as a series of connected points between two neighboring branching nodes. We then obtained quantifiable metrics of the vascular geometry in terms of these connected vessel segments. With this comprehensive information about the cerebral vascular tree, we can reconstruct the arterial vasculature using the centerlines, radius and angular information by constructing 3D circles along the vessel centerline to form a 3D volume.

2.5. Geometric feature extraction

With the information contained in the skeletonized segments about the measurements of diameter, centerline points, angles, bifurcation points and branching structure, we then calculated the global and local morphometric features of the complete vascular tree. The features calculated were as follows: 1) total length of the vessel network, calculated by summing the length of all the skeletal segments, 2) total number of branches, where a branch was defined as a sequence of points along the vessel starting at a bifurcation node and ending either at the next bifurcation or at the last point on the vessel (in the case of a terminating branch), 3) average and maximum branch length, defined as the mean and maximum geodesic length of all branches in the network, 4) average diameter of all points on the centerline, 5) total vessel volume, calculated by considering the vessels as cylinders with a varying diameter along the total length, 6) fractal dimension, determined using the box counting method based on the Minkowski-Bouligand dimension (Dubuc et al., 1989, Reishofer et al., 2012, Fernández and Jelinek, 2001), which provides a measure of morphological complexity in the cerebral vasculature, and 7) vessel tortuosity, defined using the sum of angles measurement (SOAM) (Bullitt et al., 2008), and calculated as the sum of all the angles between sets of 3 points on the centerline divided by the total length. These features have been linked to potential vascular pathology such as atherosclerosis and even brain tumor malignancy and can be used to study the changes in vessel structure in such cerebrovascular diseases (Kim et al., 2015, Zanto et al., 2011).

2.6. Validation

The accuracy of any vascular extraction method is determined by the precision of segmentation and the ability of the vessel enhancement and noise suppressing techniques. We extensively validated our method using a 3D vascular phantom of the Circle of Willis. This phantom establishes a physiologically realistic ground truth of the major arteries in the brain, against which the performance of our method was quantitatively evaluated since we know its geometrical properties. Using Somos® NeXt (Stratasys Ltd.), which is a commonly used standard in literature for medical phantoms (Liu et al., 2018, Filippou and Tsoumpas, 2018), we 3D printed and CT scanned the physical 3D phantom to replicate human CTA data and ran our segmentation algorithm on the scan (0.44 × 0.44 × 0.6 mm³, with 433 slices in total) acquired using a Siemens Somatom Definition Flash CT scanner at Banner University Medical Center (Tucson, AZ). Subsequently, we compared the reconstructed 3D geometry from the CT scan data with the ‘ground truth’ (original binary phantom STL) and performed error analysis to quantify the performance of the segmentation algorithm. The validation metrics used were Pearson’s correlation coefficient (Asuero et al., 2006), Dice similarity coefficient (Zou et al., 2004), modified Hausdorff distance (Dubuisson, 2002), and surface distance image registration error (Nanayakkara et al., 2009).

2.6.1. Performance with CT image acquisition noise and image resolution

Having validated our algorithm against the physical phantom, to investigate the effect of noise on our algorithm’s performance, we ran the algorithm on the same phantom STL with varying levels of added Poisson and Gaussian noise, to mimic the additional noise common in CT scans. Furthermore, we studied the performance of segmentation and reconstruction algorithms at different image resolutions. We down-sampled the phantom’s STL image resolution from 0.48 × 0.6 × 0.6 mm³ to 0.8 × 0.8 × 1.03 mm³ and then to 1.12 × 1.43 × 1.5 mm³ (64% down-sampled at each step) to replicate currently used varying MR and CT image resolutions. Subsequently, we performed the segmentation and reconstruction algorithms to assess the ideal or minimum resolution needed for efficient reconstruction of the vascular network.

2.6.2. Comparison with existing algorithms

For further validation, we quantitatively compared the results from our segmentation to the currently existing methods for vessel enhancement and extraction from existing image processing software such as ImageJ/FIJI (Schindelin et al., 2009). Some of the existing algorithms which can be used to enhance vessels and create a binary map are auto/manual local thresholding, such as Renyi Entropy based thresholding (Sahoo et al., 1997) and Phansalkar Thresholding (Phansalkar et al., 2011), Seeded Region Growing Segmentation (Adams and Bischof, 1994), and Trainable Weka Segmentation (Arganda-Carreras et al., 2017). We applied these methods to the 3D phantom in the FIJI environment, along with ImageJ’s implementation of Frangi Vesselness filtering and compared against our results. We chose these algorithms as they are open-source and widely used for segmentation.

2.7. Healthy vs. Stroke comparison

The geometric properties described in the previous section were obtained for the cerebral vasculature of four groups of data: 1) MRA scans of healthy subjects (n = 10, age = 30 ± 9), 2) MRA scans of stroke patients (n = 10, age = 51 ± 15) and 3) CTA scans of healthy subjects (n = 10, age = 62 ± 12), 4) CTA scans of stroke patients (n = 10, age = 68 ± 11). We included stroke and control groups for both modalities with a dataset comparatively large to similar studies in literature (Wright et al., 2013, Chen et al., 2018a, Chen et al., 2018b, Hsu et al., 2017). All groups include both male and female subjects in an approximately equal ratio (Table 4). For the healthy datasets, subjects with any history of hypertension, diabetes or any head trauma were excluded. The CTA stroke patient dataset consists of older adults within the same age range as the healthy CTA dataset and with major vessel occlusion in the M1 and M2 segments of the middle cerebral artery (MCA) or internal carotid artery (ICA) sites, which are the most common sites of vessel occlusion in an ischemic stroke (Blood Vessels of the Brain, 2020). Similarly, for the stroke MRA dataset, we chose age-adjusted patients with the healthy MRA dataset as much as possible, given that stroke occurs mostly in older populations. The average age of the subjects in the two groups falls within the same category (middle-aged) with mean ages 30 and 51 for healthy and stroke respectively. We further discuss the effects of different ages between groups in Section 4. The stroke MRA dataset also contains patients with M1, M2 or the ICA occluded.

Table 4.

A comparison of geometric features of the cerebral vascular tree of healthy subjects vs. stroke patients. Values are presented as average ± standard deviation of 10 subjects in each group with the bold font highlighting features that are significantly different between groups (p < 0.05).

	Healthy MRA	Stroke MRA	p - value	F-value	Healthy CTA	Stroke CTA	p-value	F-value
Number of subjects (female)	10 (6)	10 (5)			10 (4)	10 (4)
Age (years)	30 ± 9.3	51 ± 15.5	0.001		62 ± 12	65 ± 13.3	0.620
Total length (m)	3.05 ± 0.38	2.88 ± 0.86	0.45	0.571	3.46 ± 0.99	2.20 ± 0.67	0.006	9.441
Number of branches	139 ± 76	258 ± 63	0.001	14.952	171 ± 54.9	211 ± 75.69	0.209	1.695
Average branch length (mm)	14.81 ± 1.97	8.68 ± 2.03	<0.001	48.087	8.72 ± 1.72	9.89 ± 2.07	0.159	2.157
Maximum branch length (mm)	59.25 ± 10.78	88.72 ± 30.87	0.007	9.020	71.11 ± 10.9	59.38 ± 6.10	0.009	8.367
Average diameter (mm)	2.75 ± 0.37	2.27 ± 0.15	0.003	10.903	2.4 ± 0.21	2.18 ± 0.07	0.051	1.974
Total volume (ml)	67.07 ± 25.55	48.31 ± 18.92	0.07	3.482	61.80 ± 18.79	38.00 ± 21.83	0.017	6.823
Fractal dimension	1.36 ± 0.28	1.71 ± 0.14	0.004	10.619	1.56 ± 0.05	1.69 ± 0.20	0.049	4.434
Tortuosity (rad/cm)	3.24 ± 0.88	7.17 ± 1.61	<0.001	33.260	4.36 ± 1.32	5.80 ± 0.92	0.015	7.101

2.7.1. Medical imaging protocols

The CTA datasets from healthy subjects and stroke patients were both acquired at 0.43 × 0.43 × 0.62 mm³ resolution using the GE Lightspeed scanner at 100-120KV. All the CTA data were acquired after bolus injection of 90–120 ml contrast media with the injection rate of 4–5 ml/s (Omnipaque-350 mg/ml for stroke patients and Isovue-370 mg/ml for healthy subjects). The stroke CTA data was collected at the Centre Hospitalier Universitaire Vaudois, Lausanne, Switzerland and the healthy CTA data were collected at Stanford Healthcare, California, USA. From these datasets, CTA scans of 10 healthy subjects and 10 S patients were used for the comparative study. For the MRA study, we utilized data from 10 healthy subjects and 10 S patients as well. The MRA scans for healthy subjects were obtained from the MIDAS public database (Mouches and Forkert, 2019), wherein time of flight (TOF) MRA brain images from healthy volunteers were acquired at 0.5 × 0.5 × 0.8 mm³ and were collected and made available by the CASILab at The University of North Carolina at Chapel Hill and distributed by the MIDAS Data Server at Kitware, Inc. (Mouches and Forkert, 2019). The MRA scans of stroke patients were acquired using the Siemens 1.5T MR scanner with 0.23 × 0.23 × 0.62 mm³ resolution for two subjects, 0.35 × 0.35 × 0.62 mm³ resolution for one subject, and 0.41 × 0.41 × 0.62 mm³ resolution for the remaining subjects.

The data was not specifically obtained for the purpose of this study and is not currently public due to privacy issues of clinical data. Requests can be made to obtain the data via email to the corresponding author and will be shared upon obtaining the necessary permissions from the administering institution. The code for the segmentation and data analysis was developed in-house by the authors and will eventually be made public via a GitHub repository. Any requests for the code until the public release can be made via email to the corresponding author.

Having extracted the vascular features from healthy and stroke subjects, we compared the features between the healthy and stroke groups in each modality (CTA and MRA) using a one-way ANOVA. We also ran a three-factor ANOVA with age and imaging modality as the additional factors along with disease, to fit a least-squares regression model and assess the significance of aging and imaging modalities on our data using the JMP software by SAS. Along with the main effects, the JMP software was also used to analyze the interaction effects due to aging.

3. Results

3.1. Segmentation and feature extraction algorithms

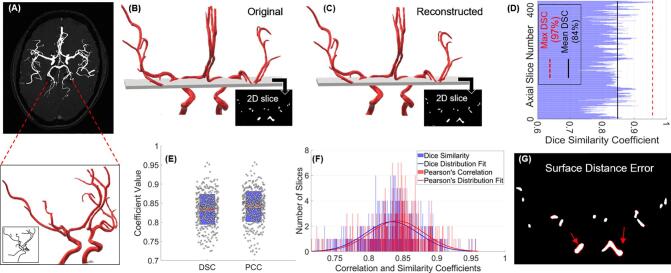
We observed accurate reconstruction of the phantom using our segmentation algorithm (Fig. 1A–C). Validation studies using the 3D phantom show that our algorithm detects vessels accurately with a slice-averaged Dice similarity coefficient (DSC) of 84.0%, Pearson’s correlation coefficient (PCC) of 83.4% and a modified Hausdorff distance of at most 3 pixels (Fig. 1D–F and Table 2). The surface distance error presents a visual representation of the false positive or false negative pixels overlapping (Fig. 1H) and quantitatively corresponds to the number of pixels mentioned in the Modified Hausdorff Distance (Table 2). We can see that the error between the original and reconstructed images is confined to the surface pixels of the vessels due to slight thinning but overall, the algorithm detects every vessel segment with high accuracy and allows for a complete reconstruction with the loss being restricted to 1–3 pixels confined to the surface (Fig. 1G–H). For the visualization of the error in a 2D cross-section, the slice shown in Fig. 1H was chosen specifically due to a large number of vessel cross-sections of various sizes being present as this could potentially lead to a larger error. This slice-overlay and error demonstrates the performance of our algorithm and a visual representation of the accuracy of reconstruction at varying vessel scales (Fig. 1G).

Fig. 1.

Validation of segmentation algorithm using a 3D phantom. (A) Extracted vasculature overlaid on TOF image of an axial slice of the brain and the 3D CoW phantom shown relative to the cerebral vasculature along with its extracted centerlines (embedded panel) for a visual representation, (B) original 3D phantom of the CoW with a 2D slice showing a cross section, (C) the 3D volume reconstructed using the CT scan of the 3D printed phantom with the corresponding 2D cross section shown for visual comparison of the 2D slices, (D) Dice similarity coefficient (DSC) per 2D axial slice corresponding to the reconstruction of the 3D phantoms on the left post CT scanning the 3D printed phantom, (E) box plots of the DSC and the Pearson correlation coefficient (PCC) showing the data points corresponding to each slice laid over a 95% confidence interval, along with (F) histogram of the DSC and PCC demonstrating the accuracy of the segmentation along with a distribution fit and, (G) corresponding 2D slices in B and C, showing an overlap of the original and segmented cross section, indicating the error for visualization (the ‘error pixels’ can be seen in red). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Table 2.

Validation and error analysis results for the 3D phantom as well as the quantification of performance with varying levels of added noise. Lastly, segmentation results using CT scan images of the 3D printed phantom to account for CT induced noise and comparison with ground truth data. Values are presented as the slice-average ± standard deviation.

	Dice similarity coefficient (%)	Pearson’s correlation (%)	Modified Hausdorff distance (pixels)
Phantom STL	84.3 ± 0.3	83.9 ± 0.3	3 ± 2
Phantom + 10% noise	84.7 ± 0.5	84.2 ± 0.4	3 ± 2
Phantom + 20% noise	83.7 ± 0.5	83.1 ± 0.4	3 ± 2
3D print + CT of phantom	84.6 ± 0.3	84.5 ± 0.3	2 ± 2

Furthermore, in our validation scheme, we demonstrate the impact of noise on our algorithm. The noise added phantom with varying levels (10%, 20%) of Poisson and Gaussian noise was also reconstructed with 83% DSC along with the CT scanned 3D printed phantom with inherent CT acquisition noise (Table 2), providing comparison against ground truth for data with CT noise. This establishes the accuracy of our method when used with existing noise induced by image acquisition and reconstruction. We observed a slight increase in DSC and PCC with added noise (Table 2) since Gaussian and Poisson noise add grayscale pixels randomly around the ROI, falsely appending a few pixels ‘missed’ in the segmented volume as the error is confined only to the pixels on the surface. We also studied the effects of image resolution in the vessel extraction and reconstruction, inferring that at worse resolutions below the standard CTA and MRA resolution (~0.5–0.6 mm), discontinuities appear in the segmented binary map, which leads to an over/under estimation of the radius at certain points and a decrease in the Dice similarity coefficient (Supplementary Materials). The quantitative comparison of results from ImageJ/FIJI using currently existing segmentation protocols against our method using the 3D phantom as the ground truth showed that our method of binarization combined with our implementation of the Frangi vesselness filtering outperforms the ImageJ/FIJI algorithms (Fig. 2 and Table 3).

Fig. 2.

The segmentation results from existing methods (implemented in ImageJ/FIJI) along with the current proposed method for visual comparison.

Table 3.

Performance comparison of segmentation results and subsequent error analysis using existing methods in ImageJ/FIJI. Results are reported in as slice average ± standard deviation.

Segmentation method	Dice Similarity Coefficient (%)	Pearson’s correlation (%)	Modified Hausdorff Distance (pixels)
Auto local thresholding	58 ± 13.1	57.6 ± 11.2	5 ± 4
Region growing	64.1 ± 15.6	63.3 ± 11.9	4 ± 3
Otsu/Renyi Entropy	65.2 ± 11.3	66.4 ± 10.3	4 ± 3
Proposed method	84.3 ± 0.3	83.9 ± 0.3	3 ± 2

3.2. Subject-specific vascular architectures

We applied our validated algorithms to four different image databases of MRA and CTA of healthy and stroke subjects. The results from the different steps of pre-processing, vessel enhancement, segmentation, and skeletonization of a representative MRA from a healthy subject are given in Fig. 3. We can see the vesselness map obtained by the vessel enhancement filtering after pre-processing and the subsequent anisotropic diffusion. It can be seen clearly that the MCA (middle cerebral artery) and the internal carotid arteries (ICA) have the highest probability value(s) in the vesselness map and hence appear the brightest. The smaller vessels such as the communicating arteries can be seen but are faint in comparison. Overall, we can clearly see the enhanced contrast in the vessels and the suppression of other structures. The binarized map obtained using the active contours segmentation shows how the automatic algorithm picks up the faint segments for better connectivity which thresholding-based algorithms tend to miss, without the need for manually placing seed points. As the last step, the 3D volume is reconstructed using the extracted centerline, diameter and angular information in the skeletonized visualization of the centerline trajectory and corresponding diameters.

Fig. 3.

Vessel segmentation and skeletonization: (A) raw stack of 2D MRA/CTA images, (B) vesselness probability map obtained after pre-processing and filtering, (C) binarized volume obtained using active contours segmentation, and (D) skeleton of the cerebral vasculature centerlines and surface cross-sections depicted by 3D circles and corresponding diameter values from segmentation.

We repeated this process on 40 healthy and stroke subjects including CTA and MRA scans (Table 4). Two healthy and two stroke subjects from the MRA dataset are represented in Fig. 4 for visual comparison. The segmented vasculature of the stroke subjects clearly shows the MCA M1 segment (left) and ICA (right) being cut off at the point marked by the arrow. Table 4 contains the quantitative information about the extracted geometrical features and a comparison between healthy and stroke vascular geometry. The total length, total number of branches, average diameter, average and maximum branch length, total volume, fractal dimension and vessel tortuosity are reported for the healthy and stroke subjects. The obtained values for the average diameter, length and branching of cerebral arterial trees agree with the values reported in literature (Hsu et al., 2017, Chen et al., 2018b). Many of the extracted geometrical features are significantly different in stroke patients as compared to healthy subjects for both imaging modalities based on the ANOVA test performed. Each ANOVA has 19 total degrees of freedom (1betweenand18withingroups). As hypothesized, the total length, volume and average diameter of cerebral vessels in stroke patients were lower whereas the fractal dimension, tortuosity was higher. The number of branches and branch length are higher in the stroke patients, although not statistically significant for either group. Certain features were only significantly different in either the MRA or the CTA groups and we hypothesize that this is due to the mean ages being significantly different in the healthy and stroke MRA groups. The CTA stroke and healthy groups were closely age-matched and consisted of older adults. This effect of aging is discussed in detail in Section 4.

Fig. 4.

A visual comparison of the vesselness map and corresponding binary volume of the cerebral vasculature: (A) two healthy subjects, and (B) two stroke patients. The red arrows on the stroke image data depicts the location of the occlusion. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

In order to investigate the potential differences in the vascular pattern between the four subject groups with CTA and MRA due to inherent differences in the imaging modalities as well as due to the different mean ages between the datasets, we performed a three-factor ANOVA test with disease, age, and imaging modality as the effect factors. While we observed differences between features as a result of aging, statistical analysis did not show any significant differences due to aging, given our sample size (Table 5). We saw a significant difference in the number of branches between the datasets from CTA compared to those from MRA (between modalities). However, we did not see significant differences in other features with respect to imaging modality (Table 5).

Table 5.

Results (p-values) from a three-factor ANOVA to test for significant differences in the features by accounting for age, imaging modality (CTA vs. MRA) and disease (healthy vs. stroke). The features which are significantly different have been highlighted in bold.

Effect Factor	Total length	Number of branches	Average branch length	Maximum branch length	Average diameter	Total volume	Fractal dimension	Tortuosity
Disease	0.154	0.030	0.039	0.048	0.055	0.261	0.006	<0.001
Age	0.618	0.432	0.283	0.869	0.424	0.781	0.118	0.461
Modality	0.112	0.038	0.069	0.209	0.966	0.723	0.905	0.223

4. Discussion

In this paper, we present a method to automatically segment and reconstruct cerebral vasculature, without the use of seed points or manual initialization, to obtain a connected network of the vessels. Though the vessel enhancement filtering (Frangi Filter) and contour-based segmentation has been in use for many years, we use efficient pre-processing, noise removal and combine these established methods to achieve accurate segmentation. This method overcomes the limitations of semi-automatic methods in literature which need manual intervention, with minimal pre-processing and no further post-processing required. We tested our method on MRA as well as CTA data, but it is extendable to other angiography modalities without being restricted to specific imaging protocols and can detect small vessels at the size of the image resolution without any manual initialization or intervention needed. We validated our method through extensive error analysis studies using a digital 3D phantom of the Circle of Willis and studied the effect of noise level in our algorithm. The physiologically realistic phantom utilized for validation served as a ground truth which allowed for quantification of the algorithm’s performance, using multiple standard evaluation metrics. Furthermore, we 3D printed the digital phantom to obtain a physical model of the CoW, perform CT imaging and further validate our method on those scans, comparing with absolute ground truth. Furthermore, we compared our results against other existing methods and showed superior performance visually as well as quantitatively (Fig. 2, Table 3). This demonstrates that other methods such as auto local thresholding, entropy or class-based segmentation and other methods such as region growing, which need seed points fail to achieve the segmentation accuracy of our method. An advantage of this method is that even in cases where the ‘vesselness’ map derived from Frangi filtering appears visually too faint (lower probability of those pixels than others due to thinner/low contrast vessels), the active contours is able to trace the vessel pixels and include them in the binary volume as the probability is higher than the background (Fig. 4). Hence, this combination algorithm overcomes the challenges of inconsistent intensity values over the length scales of various vessels and outperforms other methods. Recent advancements using machine learning-based methods using various kinds of neural networks (Livne et al., 2019) also show promise for future implementation. However, currently, there is a lack of robust and reliable inter-modality models that study geometrical features in healthy and pathological states.

We further developed the algorithm to include automatic feature extraction of the vessels to characterize patient-specific cerebral vasculature. This algorithm skeletonizes the vascular network and extracts regional geometric features including length, diameter, branching pattern, fractal dimension and tortuosity, which can be used to study the mechanism of vascular pathology and biometrics of structural changes in the cerebral vessels. Such analysis of vascular features has been very scarcely reported in literature with no other work presenting a comparison of healthy with pathological vasculature.

4.1. Effect of disease

Using this algorithm, we performed a comparative study of the vascular geometry in stroke patients and healthy subjects to quantify the structural changes in the cerebral vasculature induced by ischemic stroke, which is the largest contributor to death and disability due to cerebrovascular disease. Performing a three-factor ANOVA test, we expected to find the average diameter, volume and total length in stroke patients to be smaller due to a major vessel being occluded with a higher tortuosity and fractality since these have been shown to be indicators of vascular pathology (Gutierrez et al., 2015, Kim et al., 2015, Jiang et al., 2017). We also hypothesized that the number of branches would be smaller in the stroke data due to vessel occlusion but there is also contradictory information in literature regarding this as the vasculature tends to sprout additional smaller branches to compensate for the stroke (Liu et al., 2014, Shuaib et al., 2011). The results show that the vascular geometry differs significantly between the two groups for both the imaging modalities and to the best of our knowledge, this is the first study to present this quantitative comparison data using automated segmentation and skeletonization of vasculature.

As we hypothesized, compared to the healthy results, the stroke vasculature was found to have a lower volume (61.80 ± 18.79 ml vs. 34.43 ± 22.9 ml for CTA) and total length (3.46 ± 0.99 vs. 2.20 ± 0.67 for CTA and 3.05 ± 0.38 vs. 2.88 ± 0.86 for MRA) as well as smaller average diameter (2.75 ± 0.37 mm vs. 2.27 ± 0.15 mm for MRA and 2.4 ± 0.21 vs. 2.18 ± 0.07 for CTA); however, the vascular network of stroke patients possessed higher tortuosity (3.24 ± 0.88 vs. 7.17 ± 1.61 rad/cm for MRA and 4.36 ± 1.32 vs. 5.80 ± 0.92 rad/cm for CTA), fractality (1.36 ± 0.28 vs. 1.71 ± 0.14 for MRA and 1.56 ± 0.05 vs. 1.69 ± 0.20 for CTA) and varying branching pattern (Table 4). This is consistent with findings from literature, where higher complexity and tortuosity were observed in stroke patients along with additional smaller branches forming for collateral flow. We conclude that the volume and total length can still be lower because the newer collateral branches formed are smaller than the major vessel network missing in the segmented volume due to the occlusion. However, since the stroke MRA group has older subjects than the healthy MRA group, the volume is not significantly lower in them due to higher tortuosity and branching. In the CTA data, the healthy and stroke groups are more closely age-matched, and both consist of older adults, resulting in an overall higher tortuosity and other altered features. This brings up a very interesting discussion around the effects of aging on cerebral vasculature.

4.2. Effect of aging

It is important to note that aging has a significant impact on vascular impairment since the two groups presented in the MRA data have different age ranges (30 ± 9 years for healthy subjects and 51 ± 15 years for stroke patients). Multiple studies have noted that aging results in an increase in arterial stiffness, arteriolar tortuosity and endothelial molecular dysfunction, potentially leading to hypo-perfusion (Xu et al., 2017). These alterations in the vasculature, in turn lead to pathophysiological manifestations such as atherosclerotic vascular diseases, stroke, aneurysms, vascular inflammation, hypertension and hemorrhages (Ungvari et al., 2018, Donato et al., 2018). Hence these structural changes in the vasculature found in stroke patients, are also directly correlated with the aging process. This can be seen in the differences in the features between younger and older subjects even within the same group (for example, healthy subjects from the CTA group with an older mean age have higher tortuosity, fractality and number of branches than the healthy subjects from the MRA group with a younger mean age). in order to study the effect of aging, we performed a three-factor ANOVA test to account for the age differences while studying the difference in vasculature, and while statistical analysis did not show any significant differences, we infer that this could be observed using a larger population sample.

4.3. Effect of imaging modality

CTA and MRA imaging modalities inherently have differences in their imaging datasets due to varying principles and protocols of image acquisition. While CTA is faster, cheaper and more readily available, MRA has high accuracy and reproducibility and fewer artifacts (Ghouri et al., 2019). Also, the skull-stripping problem discussed earlier is prominent in CTA data due to the bright skull pixels along with hardening artifact and bright streaks that can sometimes corrupt CT data. Thus, we investigated the effect of imaging modality in our study to present a comprehensive examination of vascular geometry and subsequent pathology captured by both CTA and MRA. We included the imaging modality as one of the effecting factors in the three-factor ANOVA test to observe differences in the features between the two modalities. The only feature that was significantly different (p < 0.05) was the number of branches. This reveals that there could potentially be differences in the data acquired using imaging modalities and is something to be explored with a larger dataset.

4.4. Limitations

There could be discontinuities in the binary network if the original image dataset itself has inconsistent and poor contrast in some slices where the vessel cross section cannot be seen entirely. In such cases, our algorithm eliminates the corresponding vascular regions which were disconnected from the entire structure, in an attempt to only preserve the completely connected network. With a more comprehensive understanding of human cerebral vasculature, we would be able to implement a method to detect and correct for such discontinuities, especially for geometric feature analysis and CFD studies.

Furthermore, using ‘modality’ as a factor for the ANOVA while comparing healthy and stroke data, we saw that heteroscedasticity is a concern for this data since there is no qualitative/quantitative information on the differences in angiography images from CT and MR in terms of the factors that would impact segmentation accuracy. We plan on studying this in more detail with a large sample of data from both modalities. There are a lot of factors to consider before comparing the modalities (such as, assessing the differences due to the inherent modality and varying protocols) and it would be ideal to utilize data from the same patients, which was outside the scope of this work.

Lastly, a persistent limitation in our method as well as other methods reported in the literature is the imaging resolution and the inability to detect and segment microvasculature which would provide a greater insight into cerebral hemodynamics.

4.5. Conclusion

This method provides a basis for a quantitative tool to study vascular pathology in various underlying cerebrovascular diseases as well as to accurately segment vasculature for visualization and assessment in the efficient diagnosis and treatment of stroke. Moreover, we quantitatively compare healthy and stroke geometries in multi-modality imaging data to study the effects of disease, aging and modality. This part of the work is crucial in studying the vascular morphology and changes caused by (or leading to) cerebrovascular diseases since vascular geometry has the potential to be one of the main biomarkers for prevention and personalized treatment of stroke and other CVD. Apart from these diagnostic and prognostic applications, reconstruction of patient-specific cerebrovascular network is a vital step for computational fluid dynamics (CFD) modeling studies which can analyze cerebral hemodynamics (Steinman et al., 2003, Payne and El-Bouri, 2017) and provide outcomes for various forms of vascular interventions. Important components of CFD studies include 3D reconstruction of the patient’s vascular network and a knowledge of geometric features such as the centerlines, diameters and bifurcations (Hsu et al., 2017, Payne and El-Bouri, 2017).

5. Data and code availability statement

The CTA datasets from healthy subjects and stroke patients were both acquired at 0.43 × 0.43 × 0.62 mm³ resolution using the GE Lightspeed scanner at 100–120 KV. All the CTA data were acquired after bolus injection of 90–120 ml contrast media with the injection rate of 4-5 ml/s. The stroke CTA data was collected at the Centre Hospitalier Universitaire Vaudois, Lausanne, Switzerland and the healthy CTA data as collected at Stanford Healthcare, California, USA. From these datasets, CTA scans of 10 healthy subjects and 10 stroke patients were used for the comparative study. For the MRA study, we utilized data from 10 healthy subjects and 10 stroke patients as well. The MRA scans for healthy subjects were obtained from the MIDAS public database, wherein time of flight (TOF) MRA brain images from healthy volunteers were acquired at 0.5 × 0.5 × 0.8 mm³ and made available by the CASILab at The University of North Carolina at Chapel Hill, and distributed by the MIDAS Data Server at Kitware, Inc. The MRA scans of stroke patients were acquired using the Siemens 1.5T MR scanner with 0.23 × 0.23 × 0.62 mm³ resolution for two subjects, 0.35 × 0.35 × 0.62 mm³ resolution for one subject, and 0.41 × 0.41 × 0.62 mm³ resolution for the remaining subjects at the Centre Hospitalier Universitaire Vaudois, Lausanne, Switzerland.

The data was not specifically obtained for the purpose of this study and is not currently public due to privacy issues of clinical data. Requests can be made to obtain the data via email to the corresponding author and will be shared upon obtaining the necessary permissions from the administering institution.

The code for the segmentation and data analysis was developed in-house by the authors and will eventually be made public via a GitHub repository. Any requests for the code until the public release can be made via email to the corresponding author.

CRediT authorship contribution statement

Aditi Deshpande: Data curation, Methodology, Software, Writing - original draft. Nima Jamilpour: Methodology, Software. Bin Jiang: Data curation, Writing - review & editing. Patrik Michel: Data curation. Ashraf Eskandari: Data curation. Chelsea Kidwell: Writing - review & editing, Validation. Max Wintermark: Data curation, Writing - review & editing, Validation. Kaveh Laksari: Conceptualization, Writing - review & editing, Supervision.

Appendix A. Supplementary data

The following are the Supplementary data to this article: