Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Jan 21;125(4):2276–2286. doi: 10.1021/acs.jpcc.0c10107

First-Principles Study of Na Intercalation and Diffusion Mechanisms at 2D MoS2/Graphene Interfaces

Arianna Massaro †, Adriana Pecoraro †,‡, Ana B Muñoz-García ‡,*, Michele Pavone †,*
PMCID: PMC7876776  PMID: 33584936

Abstract

graphic file with name jp0c10107_0007.jpg

Na-ion batteries (NIBs) are emerging as promising energy storage devices for large-scale applications. Great research efforts are devoted to design new effective NIB electrode materials, especially for the anode side. A hybrid 2D heterojunction with graphene and MoS2 has been recently proposed for this purpose: while MoS2 has shown good reversible capacity as a NIB anode, graphene is expected to improve conductivity and resistance to mechanical stress upon cycling. The most relevant processes for the anode are the intercalation and diffusion of the large Na ion, whose complex mechanisms are determined by the structural and electronic features of the MoS2/graphene interface. Understanding these processes and mechanisms is crucial for developing new nanoscale anodes for NIBs with high performances. To this end, here we report a state-of-the-art DFT study to address (a) the structural and electronic properties of heterointerfaces between the MoS2 monolayers and graphene, (b) the most convenient insertion sites for Na, and (c) the possible diffusion paths along the interface and the corresponding energy barrier heights. We considered two MoS2 polymorphs: 1T and 3R. Our results show that 1T-MoS2 interacts more strongly with graphene than 3R-MoS2. In both cases, the best Na host site is found at the MoS2 side of the interface, and the band structure reveals a proper n-type character of the graphene moiety, which is responsible for electronic conduction. Minimum-energy paths for Na diffusion show very low barrier heights for the 3R-MoS2/graphene interface (<0.25 eV) and much higher values for its 1T counterpart (∼0.7 eV). Analysis of structural features along the diffusion transition states allows us to identify the strong coordination of Na with the exposed S atoms as the main feature hindering an effective diffusion in the 1T case. These results provide new hints on the physicochemical details of Na intercalation and diffusion mechanisms at complex 2D heterointerfaces and will help further development of advanced electrode materials for efficient NIBs.

Introduction

Since the discovery of graphene, 2D-materials have become the focus of intense research for several applications in catalysis, electronics, and optoelectronics.1−3 In the past decade, efficient and low-cost synthetic strategies for large-scale production have been developed, including mechanical or chemical exfoliation into single or few layers.4,5 Transition metal dichalcogenides (TMDCs) have attracted significant attention due to their outstanding properties and natural abundance. Molybdenum disulfide (MoS2) has been widely studied as a largely flexible material, highly performing catalyst toward the hydrogen evolution reaction (HER) and a promising negative electrode in lithium-ion batteries (LIBs).6−9 More recently, the favorable intercalation of Na ions into its structure paved the route toward the use of MoS2 as anode material in Na-ion batteries (NIBs).10 The need for good Na host materials that can replace conventional graphitic anodes has become a major issue when moving from lithium- to sodium-ion batteries.11 Development and optimization of negative electrodes for NIBs have motivated a large amount of research in the energy storage community. While being almost irrelevant for positive electrodes (e.g., layered oxides, phosphate olivines, and polyanionic compounds), the large Na+ radius hinders a convenient reversible storage into the structure of common negative electrodes (e.g., graphite or silicon). TMDCs seem to be well-suited to this end, thanks to the tunable dimensions of interlayer spacing and to the precise nanostructuring that would lead to enhanced ion/electron diffusion kinetics for an improved cell efficiency. Despite showing high theoretical reversible capacity, MoS2 suffers of low electronic conductivity and huge volume variation during sodiation/desodiation processes, leading to quick capacity fading. The combination of MoS2 with conductive carbon matrices has emerged as a promising solution.12,13 The disordered microstructure of hard carbon can provide porous surface area suitable to accommodate active material nanoparticles.14 Still, safety concerns related to electrodeposition of Na metal can limit its applicability.15 Moreover, soft carbon shows a graphite-like layered structure that would be appropriate for Na+ uptake and storage, but the mass loading is generally low due to the limited surface area.16 Lately, the use of graphene has also been considered for several reasons: (i) the electrical conductivity would be significantly enhanced with no need for metallic substrate, conducting additives, and polymeric binders, thus lowering the cell weight; (ii) the volume expansion would be largely restrained; and (iii) the rate capability and cycle stability could be considerably improved because of the nanostructured matrix.17−19 Recently, hybrid MoS2/graphene-based anodes have been tested in Na cells. Both composite20,21 and single-layered22,23 MoS2/graphene electrodes have been produced via easy and low-cost procedures, leading to high-quality and efficient materials (i.e., stable charge capacity and high Coulombic efficiency). Special focus has been placed on the MoS2 polymorphism. In principle, exfoliation of MoS2 can lead to specific monolayered structures differing for both sulfur coordination around Mo atoms and electronic properties: two thermodynamically stable trigonal-prismatic phases showing semiconducting character (2H and 3R, depending on interlayer stacking, the monolayered structure being identical); the metallic octahedral (1T) or distorted octahedral (1T′) phases. While controlled synthesis of monolayered 2H-MoS2 has been well established (large surface area, high quality, number of layers, and vertical and in-plane heterostructures), less is known about direct growth of 1T-MoS2 because of lower thermodynamic stability.24,25 Despite the majority of studies being dedicated to 2H-MoS2/graphene electrodes,20−23,26−29 there is an increasing interest for the 1T counterpart. On one hand, it has been shown that ion intercalation-assisted exfoliation can lead to highly pure products.30,31 On the other hand, 1T-based films seem to limit capacity fading upon charge/discharge processes when tested in both LIBs and NIBs.32,33

Understanding the subtle structure–property relationship underlying MoS2/graphene-based materials is key to boost their application in advanced functional NIB devices.29 Computational modeling can be a powerful tool to this end, since the overall performance rely on charge and mass transfer processes that occur at complex heterogeneous interfaces. Recent theoretical works related to other promising anode materials for NIBs, such as crystalline and amorphous TiO2 or Si-based compounds, have shown that atomistic simulations can provide significant insights for Na intercalation and migration mechanisms.34−38 With regard to hybrid interfaces, their properties cannot be always ascribed to the sum of the single components. For this reason, there is great interest in studying heterojunction from both the theoretical39,40,49,50,41−48 and the experimental51−53 points of view. Hence, here we report a first-principles study of the MoS2/graphene 2D heterostructure. In particular, we focus on the role of MoS2 phase (i.e., 1T and 3R) in determining the activity toward Na+ uptake and diffusion. We apply state-of-the-art density functional theory (DFT) calculations to dissect the structural and electronic features of Na-intercalated compounds at the MoS2/graphene interface. Moreover, we characterize the mechanisms of Na+ migration along the 2D hybrid interface with the climbing-image nudge elastic band (CI-NEB) method. Our results and insights provide important and new design principles for nanostructured NIB anodes.

Methods and Computational Details

Molybdenum disulfide structure consists of MoS6 moieties sharing two S atoms and forming an extended planar layer. Three possible polymorphs of MoS2 can exist (i.e., 1T-, 2H-, and 3R-) showing different structures and properties. This polymorphism arises either from the symmetry on the hexacoordinated Mo center (i.e., octahedral vs trigonal prismatic) and from the stacking of the layers leading to different crystalline packing. On one hand, the metallic 1T-phase shows Oh point group symmetry around the Mo center and belongs to the P3̅m1 space group.54 On the other hand, both 2H- and 3R-phases show D3h point group symmetry around the Mo center but different space groups (P63/mmc and R3m, respectively) and are semiconductors.55 From the 2D-point of view, the 2H- and 3R-phases are identical, so we consider only 1T- and 3R-phases as we are interested in modeling monolayered MoS2. We obtain the 2D-MoS2 layers by cleaving one single layer from the 1T- and 3R- bulk structures optimized at the PBE-D3BJ level of theory (see Figure S1 and Table S1). Geometry optimization of monolayered 1T reveals that this phase undergoes structural distortion and stabilizes in a slightly different geometry, namely the 1T′-phase (see Figures S3 and S4 for additional details), in agreement with the literature.56 For the sake of simplicity, we use the label 1T when referring to this distorted monolayered 1T′-phase from now on. Heterostructures are built by combining a 3 × 3 1T- and 3R-MoS2 monolayer supercell with a 4 × 4 graphene supercell to match the periodicity of both crystalline lattices. The final slab model contains nine formula units of MoS2 for both phases and 32 graphene carbon atoms. The lattice constants have been optimized via an energy scan (Figure S6), where all internal coordinates have been allowed to relax at each point. In the initial configuration, MoS2 and graphene layers have been placed at a distance of 3.5 and 13 Å of vacuum has been added along the c-direction to model a 2D-structure.

We perform spin-polarized DFT calculations with projector-augmented wave (PAW) potentials and plane-wave (PW) basis set, as implemented in the Vienna Ab-initio Simulation Package (VASP) code (ver. 5.4.1).57−59 We use the Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional and add the D3-BJ dispersion correction to account for van der Waals (vdW) interactions at the interface.60−62 A kinetic energy cutoff of 600 eV and a 4 × 4 × 1 Γ-centered k-points sampling mesh are required to converge the PW basis set. Band structures are calculated self-consistently at the PBE-D3BJ level of theory along the Γ-K-M-Γ direction in reciprocal space by considering 10 k-points divisions along each segment.63 Dipole corrections are applied to avoid long-range polarization from the periodic images along the c-direction.64 Atomic positions are relaxed until the maximum forces acting on each atom were below 0.03 eV/Å. For all the calculations, the convergence threshold for energy is set to 10–5 eV. We use the CI-NEB method to determine minimum-energy paths (MEPs) of Na migration and the corresponding energy barrier heights.65 Our approach to model Na diffusion within the interlayer spacing is consistent with recent works focusing on hybrid interfaces as NIB electrodes.66−68

Results and Discussion

MoS2/Graphene Heterointerface

We first focus on the structural and electronic features of monolayer hybrid materials 1T-MoS2/G and 3R-MoS2/G. We must note that 2D heterogeneous materials can have several possible structural configurations. Previous works have addressed how the properties of MoS2/graphene interfaces depend on the stacking configurations. It appears that relevant features (e.g., binding energies and corrugation) are not affected by the relative position of exposed S (MoS2) and C (graphene) atoms.43 In this work, our heterostructure supercell develops from a Mo atom on top of a C atom in the 1T case and from a S atom on top of a C atom in the 3R one. More recently, Hieu and co-workers have reported a slightly more stable configuration with larger interlayer spacing.40 Because the stacking arrangement with the largest interlayer spacing is also the most appropriate structure to model Na intercalation and diffusion, we have considered this feature in our model. The PBE-D3BJ minimum-energy structures and corresponding structural parameters are reported in Figure 1 and Table 1, respectively.

Figure 1.

Figure 1

Open in a new tab

Side and top views of minimum-energy structures for (a) 1T-MoS2/G and (b) 3R-MoS2/G obtained at the PBE-D3BJ level of theory. Mo atoms are depicted in violet, S atoms in yellow, and C atoms in gray.

Table 1. Lattice Constant (a), Interlayer Distance (d), Lattice Mismatch (ε), Binding Energy (ΔEbind), and Adhesion Energy (ΔEadh) of Both 1T-MoS2/G and 3R-MoS2/G Heterostructures Computed at the PBE-D3BJ Level of Theory.

phase a (Å) d (Å) ε/MoS2 ε/G ΔEbind (eV) ΔEadh (eV)
1T-MoS2/G 9.810 3.110 2.17% –0.71% –0.665 –1.649
3R-MoS2/G 9.758 3.350 3.26% –1.25% –0.026 –1.653
Open in a new tab

After geometry optimization, the interlayer distances (considered as the minimum S–C distance) are 3.110 and 3.350 Å for 1T- and 3R-MoS2/G, respectively. These values are within the typical range of vdW-based interactions and seem to be suited for ion intercalation. For both phases, the lattice constant of the heterostructure is closer to graphene than to MoS2 (see Figure S6). This can be related to the stiffness of graphene, which induces larger structural variations in MoS2. We computed the strain that the two materials experience by means of lattice mismatch according to eq 1:

graphic file with name jp0c10107_m001.jpg 1

where apristine is the lattice constant of the pristine material (e.g., monolayered MoS2 and graphene at their minima) and ahybrid is the lattice constant of the heterostructure. ε values are also listed in Table 1.

The MoS2 stretching and the graphene compression are represented by positive and negative values of ε, respectively. The higher absolute values of ε(MoS2) are due to a larger flexibility of MoS2 than graphene. We assessed the thermodynamic stability of these hybrid materials by computing binding and adhesion energy variations. The binding energy is defined as the energy required to form the heterostructure from the pristine materials. The adhesion one represents the energy interaction between the two layers that are faced to each other. These energy variations can be calculated as follows:

graphic file with name jp0c10107_m002.jpg 2a
graphic file with name jp0c10107_m003.jpg 2b

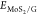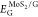where Inline graphic is the total energy of the hybrid material, Inline graphic and EG are the total energies of pristine MoS2 and graphene monolayers, and Inline graphic and Inline graphic are the total energies of the pristine materials at the geometry of the heterostructure. The results reported in Table 1 show a similar adhesion energy for both systems, while 1T-MoS2/G has a more negative binding energy than 3R-MoS2/G, which can be related to the different lattice mismatches.

To elucidate the correlation between the heterostructure formation and the lattice distortion, we have dissected the energy contributions of structural distortion from the adhesion and distortion energies (see the Supporting Information for further details). From the values reported in Table S2, it is evident that higher distortion energy leads to less favorable binding energy, given that adhesion energetics are almost identical for both polymorphs. This result is consistent with what has been observed in different kinds of hybrid materials, where a certain amount of energy is required to allow structural rearrangements (i.e., distortion energies are usually positive).34,69,70 Thus, the formation of 1T-MoS2/G is expected to be thermodynamically favorable and easier than 3R-MoS2/G thanks to the minor strain experienced by both components. On the other hand, adhesion energies are similar, which would suggest that the electronic interaction with graphene is not affected by the MoS2 phase. Because the overall energy variations are negative for both 1T and 3R phases, we can conclude that both phases of MoS2 can be combined with graphene in thermodynamically stable hybrid materials without affecting graphene structural properties.

We have characterized the electronic features of these heterostructures in terms of band structure, projected density of states (pDOS), and charge density difference plot at the PBE-D3BJ level of theory, as depicted by Figure 2.

Figure 2.

Figure 2

Open in a new tab

Electronic structure analysis computed at the PBE-D3BJ level of theory: (from left to right) band structure, atom- and angular momentum-projected density of states, and charge density difference plot of 1T-MoS2/G and 3R-MoS2/G heterostructures (isosurface level: 0.00027 eV/Å3). Color legend: Mo, violet; S, yellow; C, black; green and blue surface densities represent electrons gain and loss, respectively.

Our calculations show that both heterostructures are electronically conductive and that charge transfer occurs from graphene to MoS2. In 3R-MoS2/G, the MoS2 band gap is filled by the graphene states, with a shift of the Dirac cone to higher-energy states.47,71,72 Conversely, in 1T-MoS2/G, both MoS2 and graphene participate to electron conduction, as it can be seen more clearly from the projected band structure in Figure S7, but the same p-type effect is found also in this case. The shift of the Dirac cone in the graphene band structure is commonly related to the presence of an electric field (e.g., electron doping or applied external bias),44,45,48 but it has been observed also when graphene is faced with WS250 or with a single layer of MoS2 upon induced strain.47 These findings point out the importance of considering both mechanical and electronic coupling when dealing with vdW heterostructures.52,53 According to several recent works, the lattice strain also seems to play a role in shifting the 3R-MoS2 CBM from the K to Γ point.47,71,72 This kind of feature in band structures could also arise from the band folding effect occurring when larger cells are considered. In our case, the choice of the supercell dimension is motivated by the need to consider Na intercalation and migration. To the best of our knowledge, there is an open debate in the literature concerning the opening of a band gap in the graphene band structure.40,46 Whether this is due to structural (e.g., strain and stacking) or electronic (e.g., electric field and electron doping) reasons is still unclear. In any case, the band gap is rather small and does not jeopardize the electron conduction in MoS2/graphene interfaces, as observed experimentally. Comparison with band structures of the single components clearly shows that the role of the interface is crucial: the freestanding 1T-MoS2 monolayer, in its more stable distorted structure, shows a small band gap, losing the metallic character typical of the bulk state (see Figures S4 and S5), while the direct band gap of 3R-MoS2 monolayer is centered on the K point (Figure S5). These significant variations corroborate the importance to focus on the heterostructures and not just the pristine materials. With regard to charge density difference plots, we see that the electron depletion at the graphene side (blue blobs) leading to electron accumulation at the MoS2 one (green blobs) mainly involves C and S p states, with a minor contribution of Mo d states in the 1T-MoS2 case. This charge transfer also reflects in the band structures where the p-doping experienced by graphene results in the upward shift of the Dirac cone, as discussed above. We expect that MoS2 is going to play an active role upon cation intercalation since it is the one gathering the electronic charge. In the following section, we discuss this aspect by analyzing the heterostructure behavior upon Na intercalation.

Sodium Intercalation

We model Na intercalation at MoS2/G interfaces by considering a sodium atom placed within the interlayer spacing in the (3 × 3)MoS2/(4 × 4)graphene supercell. The total charge of the model system is equal to zero. Because of the uneven correspondence between atomic sites in both parts of the hybrid system, several intercalation sites can exist with different Na coordination to each material. We have computed the pair distribution functions (PDF) of Na–Mo, Na–S, and Na–C distances (Figure 3) to rationalize all intercalations sites. For the 1T-polymorph, two kinds of coordination sites involve Na and MoS2: (1) those where Na is coordinated to four S atoms with distances around 2.5 Å and to three Mo atoms at ∼3.5 Å labeled as hollow sites and (2) those with a similar Na–S coordination but a peak on the Na–Mo PDF at ∼3 Å, indicating the coordination to one Mo atom and labeled as top sites. Considering coordination of Na with graphene, we can distinghish (1) edge and (2) hollow sites, which differ only in the less intense peaks at ∼2.5 Å for the edge, since Na is coordinated to only two C atoms compared to the six ones for the hollow. From the combination of the two different coordination modes to MoS2 (hollow or top) from one side and the two different coordination modes to graphene on the other side (edge or hollow), all Na sites can be classified into four possible groups (Figure 3a). Also, four coordination sites and similar observations can be identified for 3R-MoS2/G (Figure 3b), except that the Na–S coordination involves three S atoms instead of four. In general, the PDFs computed for the 3R- phase show narrower and more defined peaks, which is representative of a more ordered structure.

Figure 3.

Figure 3

Open in a new tab

Pair distribution function of Na–Mo (purple), Na–S (yellow), and Na–C (gray) distances computed for the four possible intercalation sites at 1T-MoS2/G (a) and 3R-MoS2/G (b) interfaces. Corresponding structural details are shown to the side. Orange labels refer to Na coordination to MoS2, and black labels refer to Na coordination to graphene.

We computed the Na intercalation energy according to eq 3 for each explored configuration:

graphic file with name jp0c10107_m008.jpg 3

where ENa@host and Ehost are the total energies of respectively Na-intercalated systems and the host materials, and ENa is the total energy of sodium metal in the body-centered cubic (bcc) structure (which contains two atoms per cell) computed at the same level of theory.73,74 The results are listed in Table 2.

Table 2. Sodium Intercalation Energies, ΔEint, at Different Intercalation Sites Described in Figure 3 Computed at the PBE-D3BJ Level of Theory According to Eq 3 (Reported Values in eV).

phase top–hollow hollow–hollow top–edge hollow–edge
1T-MoS2/G –1.222 –0.914 –1.105 –1.150
3R-MoS2/G –0.162 –0.131 –0.089 –0.065
Open in a new tab

The overall intercalation energies are negative, suggesting that the formation of Na-intercalated compounds would be favorable for both phases. The 1T-phase seems to be more active toward Na intercalation showing more negative ΔEint values, which is consistent with the experimental evidence of phase stability variation upon ion intercalation.30,31

To see to what extent Na intercalation can modify the electronic structure at the interface, we performed the electronic structure analysis also for the Na-intercalated compounds. Bader charge analysis reveals that the formal charge carried by Na is +0.84 in both 1T- and 3R-MoS2/graphene, which represents a reliable model for the Na+/electrode system. In Figure 4, we report band structures, pDOS, and charge density difference plots computed at the PBE-D3BJ level of theory for the most stable systems. Similar analysis has also been performed at the highest-energy structures along the Na migration coordinate. From the charge density difference plots reported in Figure S8, we can see that Na/interface charge transfers are comparable, thus proving that electronic features are not affected by Na migration. Both band structures (left panel in Figure 4) show the CBM of MoS2 crossing the Fermi level, which is consistent with the desired n-type conductivity for the NIB electrode. Charge density difference plots (Figure 4, right panel) display a consistent polarization of the sulfur and carbon atoms that are coordinating the Na cation. However, the excess electronic charge seems to transfer from the Na to MoS2 side, where the electron density delocalizes along the entire layer.

Figure 4.

Figure 4

Open in a new tab

Electronic structure analysis computed at the PBE-D3BJ level of theory: (from left to right) band structure, atom- and angular momentum-projected density of states, charge density difference plot of Na-intercalated compounds in both 1T-MoS2/G and 3R-MoS2/G heterostructures (isosurface level: 0.002 eV/Å3). Color legend: Mo, violet; S, yellow; C, black; Na, red; green and blue surface densities represent electrons gain and loss, respectively.

In what follows, we explore the possible migration paths and the corresponding energetics to understand how the structural and electronic features of these heterointerfaces can affect the diffusion of the Na ion.

Sodium Migration

In this section, we discuss the mechanism of Na migration through the MoS2/G interface and provide a possible interpretation on the origin of the resulting energy barriers. We have identified two different pathways for each heterostructure, labeled path A and B. For each path, sodium can move along the x-direction, where the sulfur atoms pointing toward the interlayer spacing seem to create a proper diffusion channel (Figure 5a, top). We consider all the intercalation sites lying on a given channel and applied the CI-NEB method to determine the minimum-energy path for Na migration (Figure 5a, bottom). To describe the whole migration mechanism, closed pathways have been selected, with the final structure being the image of the initial one. Figure 5b shows the resulting energetics as a function of the migration coordinate (ξ, Na–Na distance after each Na jump).

Figure 5.

Figure 5

Open in a new tab

(a) Side and top views of Na migration pathways through (left) 1T-MoS2/G and (right) 3R-MoS2/G interfaces and (b) the corresponding energetics computed with the CI-NEB method at the PBE-D3BJ level of theory.

In 3R-MoS2/G, paths A and B (dashed and solid lines, respectively) result to be almost similar, with all the intermediate structures lying very close in energy. All the barriers associated with the Na jump are in the range 0.17–0.22 eV. Contrarily, migration through the 1T-MoS2/G interface is much less regular for both pathways, with larger energy differences among the explored sites. Path A (dashed lines) shows migration barriers going from ∼0.08 to ∼0.70 eV, while ∼0.34 and ∼0.59 eV values are found for path B (solid lines). These values are comparable to Na diffusion barriers that have been obtained with similar approaches for MoS2 bulk (∼0.7 eV),26 freestanding MoS2,27 and graphene sheets (∼0.3 and ∼0.1 eV, respectively)75 and also evaluated as a function of MoS2 interlayer spacing (from 1.2 to 0.2 eV at increasing spacing).28 In general, Na mobility seems to be enhanced when moving from bulk to 2D-like structures. Our computed barrier heights are also directly comparable to those reported by Sun and co-workers on top of graphene-supported MoS2 monolayers (from 0.07 to 1.09 eV):22 while in the work by Sun et al. Na diffusion barriers go up to ∼1.1 eV in certain directions, in our case the highest barriers are 0.7 eV for 1T- and ∼0.3 eV for 3R-MoS2/G, indicating that the interlayer diffusion can be more convenient for Na mobility.

So as to explain the different behaviors among our explored pathways, we focus on the structural features of such intermediates along the migration coordinate. The local coordination of the migrating Na cation indicates that the single jump is more likely to occur (i.e., shows a lower energy barrier) when Na is furthest from the sulfur atoms (as a matter of fact, the hypothetic top-S intercalation site does not represent a stable configuration). To visualize to what extent the sulfur coordination around Na changes when the highest transition state is reached, we have computed the Na–S PDFs at the minimum-energy and highest-energy structures for migration paths A and B. These are shown in orange and red color in Figure 6, respectively.

Figure 6.

Figure 6

Open in a new tab

Pair distribution function of Na–S distance at the highest-energy (red) and minimum-energy structures (orange) along the migration pathways explored for both 1T- and 3R-MoS2/graphene interfaces. Inset: pictorial top-view representations of the short-range Na–S coordination. Na atom at the highest- and minimum-energy structure is represented in red and orange, respectively. Only S atoms from MoS2 are shown for clarity.

From these data, we can conclude that high migration barriers generally arise from the shortening of two Na–S distances below the equilibrium value, as suggested by the left shift of the red peaks around 2.5 Å. In particular, this is more relevant in the case of 1T-MoS2/G (top panels of Figure 6), where the Na–S distance becomes even shorter and leads to ΔEmigr equal to 0.696 and 0.586 eV for paths A and B, respectively. Noteworthy, the interlayer spacing increases upon Na intercalation and migration, with major distortion associated with the 1T-case rather than the 3R-one (the former showing d values increasing from 3.11 to 3.70 Å when going from the minimum- to the highest-energy structure along the migration coordinate, while the latter from 3.35 to 3.76 Å). From these results, we expect that 3R-MoS2/G would allow an easier Na diffusion through the MoS2/graphene interface than its 1T-counterpart. However, considering the more favorable intercalation energies of the 1T-MoS2/G heterostructure, we think that some strategies (e.g., sulfur vacancies, grain boundaries, and/or defect engineering) aiming at lowering the migration barrier at this interface should be developed to boost its application as a promising NIB electrode.

Conclusions

In this work we report an ab initio study of the 2D-MoS2/graphene heterostructure as a promising anode material for Na-ion battery applications. The thermodynamic stability and corresponding electronic features of the monolayered 1T-MoS2/G and 3R-MoS2/G are derived from state-of-the-art first-principles calculations. In particular, we investigated Na intercalation and migration processes through the MoS2/graphene interfaces to unveil the specific roles of MoS2 and graphene in Na+ uptake and diffusion processes. Moreover, we compared the results obtained for the two MoS2 polymorphs: 1T and 3R. The main outcomes are the following:

  • Both single layers of 1T- and 3R-MoS2 can be combined with graphene in thermodynamically stable 2D-hybrid materials, as suggested by the favorable binding and adhesion energies. The smaller lattice mismatch for the 1T-MoS2 accounts for the slightly more favorable binding of this phase to the graphene sheet. Both heterostructures show a moderate charge transfer occurring from graphene to the MoS2 layer and a metallic character in their band structures, thus proving that interfacial effects can completely modify the properties of pristine materials (both 3R- and distorted 1T-monolayers have band gaps).

  • MoS2/graphene can form stable Na-intercalated compounds in both 1T- and 3R-phases, with the 1T-phase showing more favorable Na intercalation energies than 3R. This agrees with 1T-MoS2 becoming more stable in the presence of intercalating alkali ions. MoS2 turns out to be the active material upon Na intercalation since it is the one gaining the electronic charge from Na cation, as shown by the charge density difference plots.

  • Na can easily migrate along the direction parallel to the hybrid interface. We computed minimum-energy paths for Na diffusion and the corresponding energetics with the CI-NEB method at the PBE-D3BJ level of theory. Analysis of the diffusion mechanism shows that the Na migration could be hindered by the sulfur atoms pointing toward the interlayer spacing, thus leading to higher migration barriers in 1T-MoS2/G when Na–S distances along the path become too small. Several strategies, such as introducing sulfur vacancies, can be developed to improve the Na mobility at this hybrid interface.

In conclusion, our results and the new insights at the atomistic level can be very useful to experimental efforts toward the development and optimization of 2D hybrid materials for applications in NIBs. Future works will be devoted at unveiling the roles that defect chemistry and morphology can play in determining the activity of MoS2/G-based electrode materials.

Acknowledgments

A.B.M.-G. and M.P. are deeply grateful to Prof. Emily A. Carter for her mentorship and enduring support, for her inspiring leadership and kindness, and for being such a role model for all women in science. The authors acknowledge the European Union (FSE, PON Ricerca e Innovazione 2014-2020, Azione I.1 “Dottorati Innovativi con caratterizzazione Industriale”) for funding a Ph.D. grant to A.M. Part of this work was performed within the activities “Ricerca Sistema Elettrico” funded through contributions to research and development by the Italian Ministry of Economic Development. The computing resources and the related technical support used for this work have been provided by CRESCO/ENEAGRID High Performance Computing infrastructure and its staff;76 CRESCO/ENEAGRID High Performance Computing infrastructure is funded by ENEA, the Italian National Agency for New Technologies, Energy and Sustainable Economic Development, and by Italian and European research programs. See: http://www.cresco.enea.it/english for information.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcc.0c10107.

  • Structural models and electronic structure analysis of both MoS2 bulk and single 2D components; energy scan, projected band structures, distortion energies of MoS2/graphene heterointerfaces; charge density difference plot of highest-energy structures along the migration coordinate (PDF)

The authors declare no competing financial interest.

Special Issue

Published as part of The Journal of Physical Chemistry virtual special issue “Emily A. Carter Festschrift”.

Supplementary Material

jp0c10107_si_001.pdf (897.6KB, pdf)

References

  1. Novoselov K. S.; Geim A. K.; Morozov S. V.; Jiang D.; Katsnelson M. I.; Grigorieva I. V.; Dubonos S. V.; Firsov A. A. Two-Dimensional Gas of Massless Dirac Fermions in Graphene. Nature 2005, 438 (7065), 197–200. 10.1038/nature04233. [DOI] [PubMed] [Google Scholar]
  2. Geim A. K.; Novoselov K. S. The Rise of Graphene. Nat. Mater. 2007, 6 (3), 183–191. 10.1038/nmat1849. [DOI] [PubMed] [Google Scholar]
  3. Gupta A.; Sakthivel T.; Seal S. Recent Development in 2D Materials beyond Graphene. Prog. Mater. Sci. 2015, 73, 44–126. 10.1016/j.pmatsci.2015.02.002. [DOI] [Google Scholar]
  4. Novoselov K. S.; Fal’Ko V. I.; Colombo L.; Gellert P. R.; Schwab M. G.; Kim K. A Roadmap for Graphene. Nature 2012, 490 (7419), 192–200. 10.1038/nature11458. [DOI] [PubMed] [Google Scholar]
  5. Ren W.; Cheng H. M. The Global Growth of Graphene. Nat. Nanotechnol. 2014, 9 (10), 726–730. 10.1038/nnano.2014.229. [DOI] [PubMed] [Google Scholar]
  6. Bertolazzi S.; Brivio J.; Kis A. Stretching and Breaking of Ultrathin MoS 2. ACS Nano 2011, 5 (12), 9703–9709. 10.1021/nn203879f. [DOI] [PubMed] [Google Scholar]
  7. Radisavljevic B.; Radenovic A.; Brivio J.; Giacometti V.; Kis A. Single-Layer MoS2 Transistors. Nat. Nanotechnol. 2011, 6 (3), 147–150. 10.1038/nnano.2010.279. [DOI] [PubMed] [Google Scholar]
  8. Hwang H.; Kim H.; Cho J. MoS2 Nanoplates Consisting of Disordered Graphene-like Layers for High Rate Lithium Battery Anode Materials. Nano Lett. 2011, 11 (11), 4826–4830. 10.1021/nl202675f. [DOI] [PubMed] [Google Scholar]
  9. Laursen A. B.; Kegnæs S.; Dahl S.; Chorkendorff I. Molybdenum Sulfides - Efficient and Viable Materials for Electro - And Photoelectrocatalytic Hydrogen Evolution. Energy Environ. Sci. 2012, 5 (2), 5577–5591. 10.1039/c2ee02618j. [DOI] [Google Scholar]
  10. Larcher D.; Tarascon J. M. Towards Greener and More Sustainable Batteries for Electrical Energy Storage. Nat. Chem. 2015, 7 (1), 19–29. 10.1038/nchem.2085. [DOI] [PubMed] [Google Scholar]
  11. Wang L. P.; Yu L.; Srinivasan M.; Xu Z. J.; Wang X. Recent Developments in Electrode Materials for Sodium-Ion Batteries. J. Mater. Chem. A 2015, 3 (18), 9353–9378. 10.1039/C4TA06467D. [DOI] [Google Scholar]
  12. Lu Y.; Lu Y.; Niu Z.; Chen J. Graphene-Based Nanomaterials for Sodium-Ion Batteries. Adv. Energy Mater. 2018, 8 (17), 1–21. 10.1002/aenm.201702469. [DOI] [Google Scholar]
  13. Hwang J. Y.; Myung S. T.; Sun Y. K. Sodium-Ion Batteries: Present and Future. Chem. Soc. Rev. 2017, 46 (12), 3529–3614. 10.1039/C6CS00776G. [DOI] [PubMed] [Google Scholar]
  14. Ponrouch A.; Goñi A. R.; Palacín M. R. High Capacity Hard Carbon Anodes for Sodium Ion Batteries in Additive Free Electrolyte. Electrochem. Commun. 2013, 27, 85–88. 10.1016/j.elecom.2012.10.038. [DOI] [Google Scholar]
  15. Jian Z.; Xing Z.; Bommier C.; Li Z.; Ji X. Hard Carbon Microspheres: Potassium-Ion Anode Versus Sodium-Ion Anode. Adv. Energy Mater. 2016, 6 (3), 1–5. 10.1002/aenm.201501874. [DOI] [Google Scholar]
  16. Song L. J.; Liu S. S.; Yu B. J.; Wang C. Y.; Li M. W. Anode Performance of Mesocarbon Microbeads for Sodium-Ion Batteries. Carbon 2015, 95, 972–977. 10.1016/j.carbon.2015.09.032. [DOI] [Google Scholar]
  17. Raccichini R.; Varzi A.; Passerini S.; Scrosati B. The Role of Graphene for Electrochemical Energy Storage. Nat. Mater. 2015, 14 (3), 271–279. 10.1038/nmat4170. [DOI] [PubMed] [Google Scholar]
  18. Wu S.; Ge R.; Lu M.; Xu R.; Zhang Z. Graphene-Based Nano-Materials for Lithium–Sulfur Battery and Sodium-Ion Battery. Nano Energy 2015, 15, 379–405. 10.1016/j.nanoen.2015.04.032. [DOI] [Google Scholar]
  19. Ji L.; Meduri P.; Agubra V.; Xiao X.; Alcoutlabi M. Graphene-Based Nanocomposites for Energy Storage. Adv. Energy Mater. 2016, 6 (16), 1502159. 10.1002/aenm.201502159. [DOI] [Google Scholar]
  20. David L.; Bhandavat R.; Singh G. MoS2/Graphene Composite Paper for Sodium-Ion Battery Electrodes. ACS Nano 2014, 8 (2), 1759–1770. 10.1021/nn406156b. [DOI] [PubMed] [Google Scholar]
  21. Xie X.; Ao Z.; Su D.; Zhang J.; Wang G. MoS2/Graphene Composite Anodes with Enhanced Performance for Sodium-Ion Batteries: The Role of the Two-Dimensional Heterointerface. Adv. Funct. Mater. 2015, 25 (9), 1393–1403. 10.1002/adfm.201404078. [DOI] [Google Scholar]
  22. Sun D.; Ye D.; Liu P.; Tang Y.; Guo J.; Wang L.; Wang H. MoS2/Graphene Nanosheets from Commercial Bulky MoS2 and Graphite as Anode Materials for High Rate Sodium-Ion Batteries. Adv. Energy Mater. 2018, 8 (10), 1–11. 10.1002/aenm.201702383. [DOI] [Google Scholar]
  23. Li G.; Luo D.; Wang X.; Seo M. H.; Hemmati S.; Yu A.; Chen Z. Enhanced Reversible Sodium-Ion Intercalation by Synergistic Coupling of Few-Layered MoS2 and S-Doped Graphene. Adv. Funct. Mater. 2017, 27 (40), 1–8. 10.1002/adfm.201702562. [DOI] [Google Scholar]
  24. Liu L.; Wu J.; Wu L.; Ye M.; Liu X.; Wang Q.; Hou S.; Lu P.; Sun L.; Zheng J.; et al. Phase-Selective Synthesis of 1T′ MoS 2 Monolayers and Heterophase Bilayers. Nat. Mater. 2018, 17 (12), 1108–1114. 10.1038/s41563-018-0187-1. [DOI] [PubMed] [Google Scholar]
  25. Yu Y.; Nam G. H.; He Q.; Wu X. J.; Zhang K.; Yang Z.; Chen J.; Ma Q.; Zhao M.; Liu Z.; et al. High Phase-Purity 1T′-MoS2- and 1T′-MoSe2-Layered Crystals. Nat. Chem. 2018, 10 (6), 638–643. 10.1038/s41557-018-0035-6. [DOI] [PubMed] [Google Scholar]
  26. Su J.; Pei Y.; Yang Z.; Wang X. Ab Initio Study of Graphene-like Monolayer Molybdenum Disulfide as a Promising Anode Material for Rechargeable Sodium Ion Batteries. RSC Adv. 2014, 4 (81), 43183–43188. 10.1039/C4RA06557C. [DOI] [Google Scholar]
  27. Barik G.; Pal S. Defect Induced Performance Enhancement of Monolayer MoS2 for Li- A Nd Na-Ion Batteries. J. Phys. Chem. C 2019, 123 (36), 21852–21865. 10.1021/acs.jpcc.9b04128. [DOI] [Google Scholar]
  28. Shuai J.; Yoo H. D.; Liang Y.; Li Y.; Yao Y.; Grabow L. C. Density Functional Theory Study of Li, Na, and Mg Intercalation and Diffusion in MoS2 with Controlled Interlayer Spacing. Mater. Res. Express 2016, 3 (6), 1–8. 10.1088/2053-1591/3/6/064001. [DOI] [Google Scholar]
  29. Wang L.; Zhang H.; Wang Y.; Qian C.; Dong Q.; Deng C.; Jiang D.; Shu M.; Pan S.; Zhang S. Unleashing Ultra-Fast Sodium Ion Storage Mechanisms in Interface-Engineered Monolayer MoS2/C Interoverlapped Superstructure with Robust Charge Transfer Networks. J. Mater. Chem. A 2020, 8 (30), 15002–15011. 10.1039/D0TA04916F. [DOI] [Google Scholar]
  30. Voiry D.; Salehi M.; Silva R.; Fujita T.; Chen M.; Asefa T.; Shenoy V. B.; Eda G.; Chhowalla M. Conducting MoS2 Nanosheets as Catalysts for Hydrogen Evolution Reaction. Nano Lett. 2013, 13 (12), 6222–6227. 10.1021/nl403661s. [DOI] [PubMed] [Google Scholar]
  31. Sun D.; Huang D.; Wang H.; Xu G. L.; Zhang X.; Zhang R.; Tang Y.; Abd EI-Hady D.; Alshitari W.; Saad AL-Bogami A.; et al. 1T MoS2 Nanosheets with Extraordinary Sodium Storage Properties via Thermal-Driven Ion Intercalation Assisted Exfoliation of Bulky MoS2. Nano Energy 2019, 61 (March), 361–369. 10.1016/j.nanoen.2019.04.063. [DOI] [Google Scholar]
  32. Geng X.; Jiao Y.; Han Y.; Mukhopadhyay A.; Yang L.; Zhu H. Freestanding Metallic 1T MoS2 with Dual Ion Diffusion Paths as High Rate Anode for Sodium-Ion Batteries. Adv. Funct. Mater. 2017, 27 (40), 1702998. 10.1002/adfm.201702998. [DOI] [Google Scholar]
  33. Shu H.; Li F.; Hu C.; Liang P.; Cao D.; Chen X. The Capacity Fading Mechanism and Improvement of Cycling Stability in MoS2-Based Anode Materials for Lithium-Ion Batteries. Nanoscale 2016, 8 (5), 2918–2926. 10.1039/C5NR07909H. [DOI] [PubMed] [Google Scholar]
  34. Massaro A.; Muñoz-García A. B.; Maddalena P.; Bella F.; Meligrana G.; Gerbaldi C.; Pavone M. First-Principles Study of Na Insertion at TiO2anatase Surfaces: New Hints for Na-Ion Battery Design. Nanoscale Adv. 2020, 2 (7), 2745–2751. 10.1039/D0NA00230E. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Bella F.; Muñoz-García A. B.; Colò F.; Meligrana G.; Lamberti A.; Destro M.; Pavone M.; Gerbaldi C. Combined Structural, Chemometric, and Electrochemical Investigation of Vertically Aligned TiO2 Nanotubes for Na-Ion Batteries. ACS Omega 2018, 3 (7), 8440–8450. 10.1021/acsomega.8b01117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Bella F.; Muñoz-García A. B.; Meligrana G.; Lamberti A.; Destro M.; Pavone M.; Gerbaldi C. Unveiling the Controversial Mechanism of Reversible Na Storage in TiO2 Nanotube Arrays: Amorphous versus Anatase TiO2. Nano Res. 2017, 10 (8), 2891–2903. 10.1007/s12274-017-1656-6. [DOI] [Google Scholar]
  37. Majid A.; Hussain K.; Ud-Din Khan S.; Ud-Din Khan S. First Principles Study of SiC as the Anode in Sodium Ion Batteries. New J. Chem. 2020, 44 (21), 8910–8921. 10.1039/D0NJ01311K. [DOI] [Google Scholar]
  38. Arrieta U.; Katcho N. A.; Arcelus O.; Carrasco J. First-Principles Study of Sodium Intercalation in Crystalline Na x Si24 (0 ≤ x ≤ 4) as Anode Material for Na-Ion Batteries. Sci. Rep. 2017, 7 (1), 1–8. 10.1038/s41598-017-05629-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Pandey T.; Nayak A.; Liu J.; Moran S.; Kim J.-S.; Li L.-J.; Lin J.-F.; Akinwande D.; Singh A. Pressure-Induced Charge Transfer Doping of Monolayer Graphene/MoS2 Heterostructure. Small 2016, 12 (30), 4063–4069. 10.1002/smll.201600808. [DOI] [PubMed] [Google Scholar]
  40. Hieu N. N.; Phuc H. V.; Ilyasov V. V.; Chien N. D.; Poklonski N. A.; Van Hieu N.; Nguyen C. V. First-Principles Study of the Structural and Electronic Properties of Graphene/MoS2 Interfaces. J. Appl. Phys. 2017, 122 (10), 104301. 10.1063/1.5001558. [DOI] [Google Scholar]
  41. Jin C.; Rasmussen F. A.; Thygesen K. S. Tuning the Schottky Barrier at the Graphene/MoS2 Interface by Electron Doping: Density Functional Theory and Many-Body Calculations. J. Phys. Chem. C 2015, 119 (34), 19928–19933. 10.1021/acs.jpcc.5b05580. [DOI] [Google Scholar]
  42. Liu B.; Wu L. J.; Zhao Y. Q.; Wang L. Z.; Cai M. Q. First-Principles Investigation of the Schottky Contact for the Two-Dimensional MoS2 and Graphene Heterostructure. RSC Adv. 2016, 6 (65), 60271–60276. 10.1039/C6RA12812B. [DOI] [Google Scholar]
  43. Ma Y.; Dai Y.; Guo M.; Niu C.; Huang B. Graphene Adhesion on MoS2Monolayer: An Ab Initio Study. Nanoscale 2011, 3 (9), 3883–3887. 10.1039/c1nr10577a. [DOI] [PubMed] [Google Scholar]
  44. Baik S. S.; Im S.; Choi H. J. Work Function Tuning in Two-Dimensional MoS2 Field-Effect-Transistors with Graphene and Titanium Source-Drain Contacts. Sci. Rep. 2017, 7 (1), 1–8. 10.1038/srep45546. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Yu L.; Lee Y. H.; Ling X.; Santos E. J. G.; Shin Y. C.; Lin Y.; Dubey M.; Kaxiras E.; Kong J.; Wang H.; et al. Graphene/MoS2 Hybrid Technology for Large-Scale Two-Dimensional Electronics. Nano Lett. 2014, 14 (6), 3055–3063. 10.1021/nl404795z. [DOI] [PubMed] [Google Scholar]
  46. Ebnonnasir A.; Narayanan B.; Kodambaka S.; Ciobanu C. V. Tunable MoS2 Bandgap in MoS2-Graphene Heterostructures. Appl. Phys. Lett. 2014, 105 (3), 031603. 10.1063/1.4891430. [DOI] [Google Scholar]
  47. Singh S.; Alsharari A. M.; Ulloa S. E.; Romero A. H. Proximity-Induced Topological Transition and Strain-Induced Charge Transfer in Graphene/MoS 2 Bilayer Heterostructures. Handb. Graphene 2019, 1–28. 10.1002/9781119468455.ch39. [DOI] [Google Scholar]
  48. Sachs B.; Britnell L.; Wehling T. O.; Eckmann A.; Jalil R.; Belle B. D.; Lichtenstein A. I.; Katsnelson M. I.; Novoselov K. S. Doping Mechanisms in Graphene-MoS2 Hybrids. Appl. Phys. Lett. 2013, 103 (25), 251607. 10.1063/1.4852615. [DOI] [Google Scholar]
  49. Bai H. F.; Xu L. C.; Di M. Y.; Hao L. Y.; Yang Z.; Liu R. P.; Li X. Y. The Intrinsic Interface Properties of the Top and Edge 1T/2H MoS 2 Contact: A First-Principles Study. J. Appl. Phys. 2018, 123 (9), 095301. 10.1063/1.5009701. [DOI] [Google Scholar]
  50. Zhang F.; Li W.; Ma Y.; Tang Y.; Dai X. Tuning the Schottky Contacts at the Graphene/WS2 Interface by Electric Field. RSC Adv. 2017, 7 (47), 29350–29356. 10.1039/C7RA00589J. [DOI] [Google Scholar]
  51. Coy Diaz H.; Addou R.; Batzill M. Interface Properties of CVD Grown Graphene Transferred onto MoS 2(0001). Nanoscale 2014, 6 (2), 1071–1078. 10.1039/C3NR03692H. [DOI] [PubMed] [Google Scholar]
  52. Pierucci D.; Henck H.; Naylor C. H.; Sediri H.; Lhuillier E.; Balan A.; Rault J. E.; Dappe Y. J.; Bertran F.; Fevre P. L.; Johnson A. T. C.; Ouerghi A. Large Area Molybdenum Disulphide- Epitaxial Graphene Vertical Van Der Waals Heterostructures. Sci. Rep. 2016, 6 (1), 1–10. 10.1038/srep26656. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Rao R.; Islam A. E.; Singh S.; Berry R.; Kawakami R. K.; Maruyama B.; Katoch J. Spectroscopic Evaluation of Charge-Transfer Doping and Strain in Graphene/MoS2 Heterostructures. Phys. Rev. B: Condens. Matter Mater. Phys. 2019, 99 (19), 1–25. 10.1103/PhysRevB.99.195401. [DOI] [Google Scholar]
  54. Wypych F.; Schöllhorn R. 1T-MoS2, a New Metallic Modification of Molybdenum Disulfide. J. Chem. Soc., Chem. Commun. 1992, 19, 1386–1388. 10.1039/C39920001386. [DOI] [Google Scholar]
  55. Kam K. K.; Parkinson B. A. Detailed Photocurrent Spectroscopy of the Semiconducting Group VI Transition Metal Dichalcogenides. J. Phys. Chem. 1982, 86 (4), 463–467. 10.1021/j100393a010. [DOI] [Google Scholar]
  56. Kan M.; Wang J. Y.; Li X. W.; Zhang S. H.; Li Y. W.; Kawazoe Y.; Sun Q.; Jena P. Structures and Phase Transition of a MoS2Monolayer. J. Phys. Chem. C 2014, 118 (3), 1515–1522. 10.1021/jp4076355. [DOI] [Google Scholar]
  57. Hohenberg P.; Kohn W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136 (3B), B864–B871. 10.1103/PhysRev.136.B864. [DOI] [Google Scholar]
  58. Kohn W.; Sham L. J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140 (4A), A1133–A1138. 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
  59. Kresse G.; Furthmüller J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54 (16), 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  60. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77 (18), 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  61. Grimme S.; Antony J.; Ehrlich S.; Krieg H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132 (15), 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  62. Barone V.; Casarin M.; Forrer D.; Pavone M.; Sambi M.; Vittadini A. Role and Effective Treatment of Dispersive Forces in Materials: Polyethylene and Graphite Crystals as Test Cases. J. Comput. Chem. 2009, 30 (6), 934–939. 10.1002/jcc.21112. [DOI] [PubMed] [Google Scholar]
  63. Pecoraro A.; Schiavo E.; Maddalena P.; Muñoz-García A. B.; Pavone M. Structural and Electronic Properties of Defective 2D Transition Metal Dichalcogenide Heterostructures. J. Comput. Chem. 2020, 41 (22), 1946–1955. 10.1002/jcc.26364. [DOI] [PubMed] [Google Scholar]
  64. Neugebauer J.; Scheffler M. Adsorbate-Substrate and Adsorbate-Adsorbate Interactions of Na and K Adlayers on Al(111). Phys. Rev. B: Condens. Matter Mater. Phys. 1992, 46 (24), 16067–16080. 10.1103/PhysRevB.46.16067. [DOI] [PubMed] [Google Scholar]
  65. Henkelman G.; Uberuaga B. P.; Jónsson H. A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths. J. Chem. Phys. 2000, 113 (22), 9901–9904. 10.1063/1.1329672. [DOI] [Google Scholar]
  66. Samad A.; Noor-A-Alam M.; Shin Y. H. First Principles Study of a SnS2/Graphene Heterostructure: A Promising Anode Material for Rechargeable Na Ion Batteries. J. Mater. Chem. A 2016, 4 (37), 14316–14323. 10.1039/C6TA05739J. [DOI] [Google Scholar]
  67. Su J.; Li W.; Duan T.; Xiao B.; Wang X.; Pei Y.; Zeng X. C. Graphene/Antimonene/Graphene Heterostructure: A Potential Anode for Sodium-Ion Batteries. Carbon 2019, 153, 767–775. 10.1016/j.carbon.2019.07.053. [DOI] [Google Scholar]
  68. Li J.; Peng Q.; Zhou J.; Sun Z. MoS2/Ti2CT2 (T = F, O) Heterostructures as Promising Flexible Anodes for Lithium/Sodium Ion Batteries. J. Phys. Chem. C 2019, 123 (18), 11493–11499. 10.1021/acs.jpcc.9b01648. [DOI] [Google Scholar]
  69. Rodríguez A. M.; Muñoz-García A. B.; Crescenzi O.; Vázquez E.; Pavone M. Stability of Melamine-Exfoliated Graphene in Aqueous Media: Quantum-Mechanical Insights at the Nanoscale. Phys. Chem. Chem. Phys. 2016, 18 (32), 22203–22209. 10.1039/C6CP04213A. [DOI] [PubMed] [Google Scholar]
  70. González V. J.; Rodríguez A. M.; León V.; Frontiñán-Rubio J.; Fierro J. L. G.; Durán-Prado M.; Muñoz-García A. B.; Pavone M.; Vázquez E. Sweet Graphene: Exfoliation of Graphite and Preparation of Glucose-Graphene Cocrystals through Mechanochemical Treatments. Green Chem. 2018, 20 (15), 3581–3592. 10.1039/C8GC01162A. [DOI] [Google Scholar]
  71. Ahmad S.; Mukherjee S. A Comparative Study of Electronic Properties of Bulk MoS2 and Its Monolayer Using DFT Technique: Application of Mechanical Strain on MoS2 Monolayer. Graphene 2014, 03 (04), 52–59. 10.4236/graphene.2014.34008. [DOI] [Google Scholar]
  72. Peelaers H.; Van de Walle C. G. Effects of Strain on Band Structure and Effective Masses in MoS2. Phys. Rev. B: Condens. Matter Mater. Phys. 2012, 86 (24), 241401. 10.1103/PhysRevB.86.241401. [DOI] [Google Scholar]
  73. Aruja E.; Perlitz H. Neubestimmung Der Gitterkonstante von Natrium. Z. Kristallogr. - Cryst. Mater. 1939, 100, 195. 10.1524/zkri.1939.100.1.195. [DOI] [Google Scholar]
  74. Bai Q.; Yang L.; Chen H.; Mo Y. Computational Studies of Electrode Materials in Sodium-Ion Batteries. Adv. Energy Mater. 2018, 8, 1702998. 10.1002/aenm.201702998. [DOI] [Google Scholar]
  75. Olsson E.; Chai G.; Dove M.; Cai Q. Adsorption and Migration of Alkali Metals (Li, Na, and K) on Pristine and Defective Graphene Surfaces. Nanoscale 2019, 11 (12), 5274–5284. 10.1039/C8NR10383F. [DOI] [PubMed] [Google Scholar]
  76. Ponti G.; Palombi F.; Abate D.; Ambrosino F.; Aprea G.; Bastianelli T.; Beone F.; Bertini R.; Bracco G.; Caporicci M.; Calosso B.; Chinnici M.; Colavincenzo A.; Cucurullo A.; Dangelo P.; Rosa M. D.; Michele P. D.; Funel A.; Furini G.; Gia A. The Role of Medium Size Facilities in the HPC Ecosystem: The Case of the New CRESCO4 Cluster Integrated in the ENEAGRID Infrastructure. Int. Conf. High Perform. Comput. Simul. 2014, 1030–1033. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp0c10107_si_001.pdf (897.6KB, pdf)

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES