MODEL BASED IMAGE RECONSTRUCTION USING DEEP LEARNED PRIORS (MODL)

Abstract

We introduce a model-based image reconstruction framework, where we use a deep convolution neural network (CNN) based regularization prior. We rely on a recursive algorithm, which alternates between a CNN based denoising step and enforcement of data consistency. Unrolling the recursive algorithm yields a deep network that is trained using backpropagation. The unique aspect of this method is the use of the same CNN weights at each iteration, which makes the resulting structure consistent with the model-based formulation. Also, this approach reduces the number of trainable parameters, which hence lower the amount of training data needed. The use of a forward model also reduces the size of the network and enables the exploitation additional prior information available from calibration data. The use of the framework for multichannel MRI reconstruction provides improved reconstructions, compared to other state-of-the-art methods.

1. INTRODUCTION

Model-based reconstruction is a powerful framework for solving a variety of inverse problems in imaging (e.g., MRI, deblurring). The general strategy is to model the measurement scheme numerically, followed by the minimization of a cost function involving the sum of a data consistency and the regularization prior. Carefully engineered priors including total variation [1], adaptive strategies [2], as well as priors learned from exemplary data [3, 4, 5] are widely used. Recently, plug-and-play priors were introduced as a means to harness the power of denoising methods such as block matching with transform-based denoising (BM3D) to regularize inverse problems [6].

Inspired by recent advances in deep learning, several researchers have recently proposed convolutional neural network (CNN) architectures for image recovery. A large majority of these schemes retrained existing architectures (e.g., UNET & ResNet) to recover images from measured data. Surprisingly, this approach yielded better results than pre-designed regularization priors, demonstrating the great potential of these methods. The above strategies rely on a single framework to invert the forward model and to exploit the extensive redundancy in the images. While the ability of such a network to learn the forward model is remarkable, it has some deficiencies compared to model-based frameworks. First of all, large networks with many hyperparameters (e.g., UNET) are often needed to learn the complex inverse model, which requires extensive amounts of training data and significant computational power. Another challenge is that it is often difficult to use a framework trained for a specific image recovery problem to another one when there are differences in the acquisition setting (e.g., variations in coil sensitivities, B0 distortions, phase distortions). For example, most of the current deep learning based MRI recovery schemes [7, 8, 9, 10] are only demonstrated in the single coil setting.

The main focus of this work is to introduce a framework termed MOdel based reconstruction using Deep Learned priors (MoDL), which merges the power of deep learning with model-based image recovery. Specifically, we propose to use a learned CNN architecture to capture the image redundancy as a plug-and-play prior. This approach enables the easy use of side information, often easily available with calibration data, while exploiting image redundancy using CNN. Since we make use of the available forward model, a low-complexity network with a significantly lower number of parameters is sufficient to obtain good recovery, compared to black-box image recovery strategies; this translates to faster training and requires less training data. More importantly, the network is decoupled from the specifics of the acquisition scheme and is only designed to exploit the redundancies in the image data. Hence, the trained network can be reused in a variety of settings, including different coil sensitivities, sampling patterns, and undersampling factors. The resulting framework can be viewed as a recursive network, where the basic building block is a combination of a data-consistency term and a CNN; unrolling the recursive network in the single coil setting yields a linear network that has similarities to the one proposed by [7, 8]. However, the main difference of the proposed scheme is the use of the CNN with exactly the same weights at each iteration, unlike the setting in [7]; In addition to reducing the parameters, the weight reuse strategy yields a structure that is consistent with the model-based framework. More importantly, this approach facilitates its easy use with other regularization terms (e.g., SENSE constraints in parallel MRI acquisition). We demonstrate the utility of the framework in parallel MRI, where we use two regularization priors. The first CNN based prior is learned, while the second prior uses coil sensitivity information that is estimated from calibration scans. The comparison of the proposed framework with state-of-the-art methods demonstrates the benefits.

2. PROPOSED METHOD

We will first explain the plug-and-play CNN model in the single coil mode for simplicity, before generalizing it to the multi-coil setting. We formulate the reconstruction of the image x ∈ Cⁿ as

$$x=\text{arg }\underset{x}{\text{min}}\underset{\text{data consistency}}{\underbrace{\Vert Ax-b{\Vert }_2^2}}+\lambda \underset{\text{regularization}}{\underbrace{{\Vert {\mathcal{N}}_w(x)\Vert }^2}}$$ (1)

Here, A = SF, where S is the sampling operator, and F is the Fourier transform. ${\mathcal{N}}_w$ is a learned CNN estimator of noise and alias patterns, which depends on the learned hyperparameters w. Note that ${\Vert {\mathcal{N}}_w(x)\Vert }^2$ will be high when x is contaminated with noise and alias patterns. The minimization of (1) will yield a solution that is data consistent and is minimally contaminated by noise and alias patterns.

Since ${\mathcal{N}}_w(x)$ is an estimate of the noise and alias terms, one may obtain the denoised estimate as

$${\mathcal{D}}_w(x)=\left(\mathcal{I}-{\mathcal{N}}_w\right)(x)=x-{\mathcal{N}}_w(x).$$ (2)

This reinterpretation shows that ${\mathcal{D}}_w$ can be viewed as a denoising residual learning network, which is a popular deep learning architecture. When ${\mathcal{D}}_w$ is a denoiser, ${\mathcal{N}}_w(x)=x-{\mathcal{D}}_w(x)$ is the residual in x. With this interpretation, (1) can be rewritten as

$$x=\text{arg }\underset{x}{\text{min}}\Vert Ax-b{\Vert }_2^2+\lambda {\Vert x-{\mathcal{D}}_w(x)\Vert }^2$$ (3)

Note that the above formulation is very similar to the plug- and-play prior approach in [6]; the main difference is the denoiser is a deep CNN in our setting, whose weights and the regularization parameters are trained from exemplary data.

2.1. Iterative algorithm & Training

Since ${\mathcal{N}}_w(x)$ is a complex non-linear function of x, we propose to use the iterative strategy to solve (1), where we alternate between the following steps:

$$z[n]={\mathcal{D}}_w(x[n])$$ (4)

$$x[n+1]={\left(A^{H}A+\lambda I\right)}^{-1}\left(A^{H}b+\lambda z[n]\right)$$ (5)

Here, x[n] denotes the solution at the n^th iteration. The algorithm is initialized with z[0] = 0. Note that the above iterative process can be viewed as a cascaded network, which alternates between the data consistency update (5) and the CNN based denoising step (4). The outline of the iterative framework is shown in Fig. 1(a). This iterative form has similarities to the approaches of [7, 11]. However, unlike these works, we use the same denoising ${\mathcal{D}}_w$ operator at each iteration. Since the denoiser and variation priors change from iteration to iteration in [7] and [11], these schemes cannot be viewed as an iterative algorithm to minimize (1).

Fig. 1:

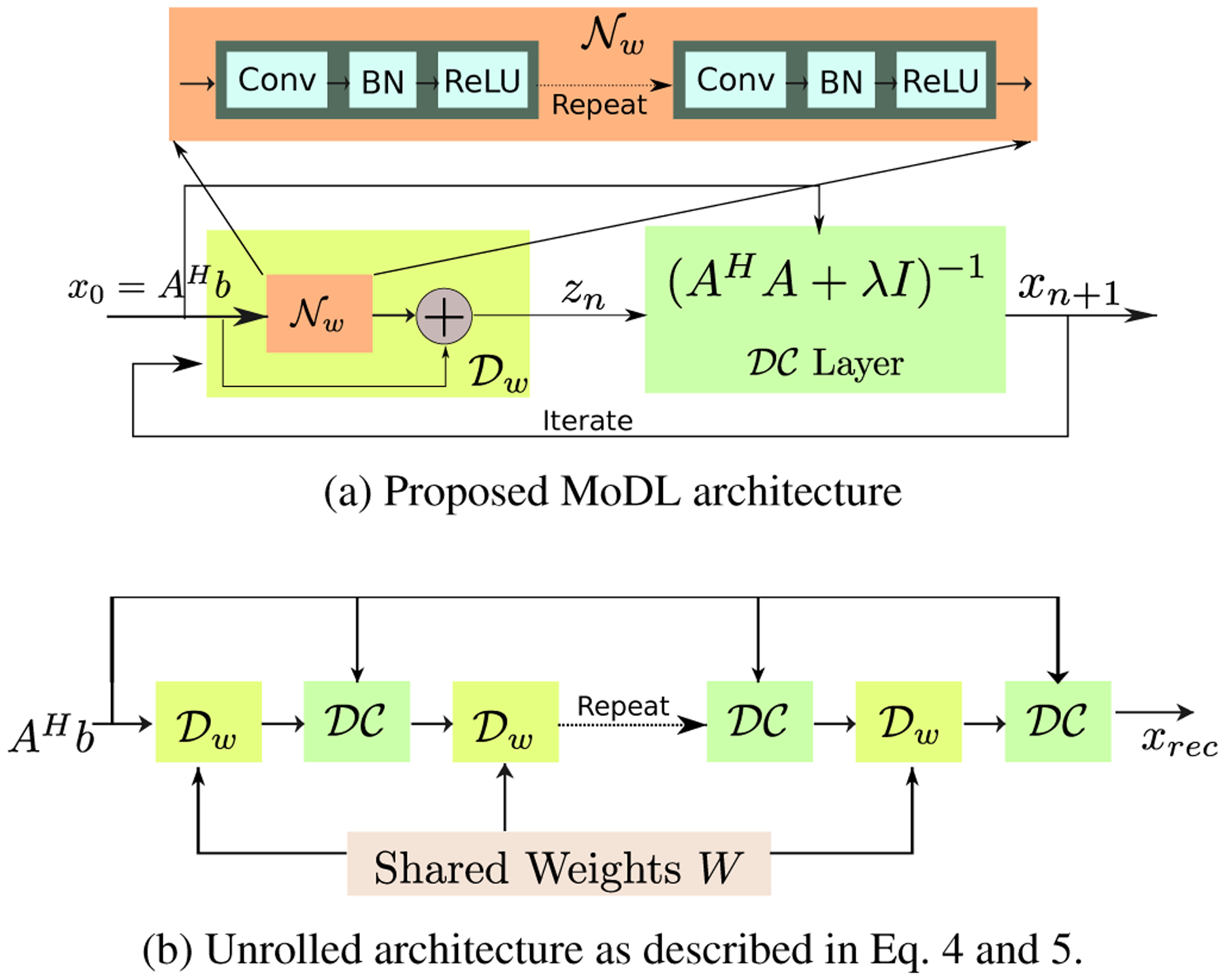
MoDL-CI: Proposed deep learning prior based iterative model architecture for coil-independent (CI) parallel MR image reconstruction. (a) shows the recursive structure, which alternates between the denoiser ${\mathcal{D}}_w$ and the data-consistency (DC) layer. (b) is the unrolled architecture, where the same network parameters are used consistently for the denoisers at all iterations. The parameters of the network, ${\mathcal{D}}_w$, are the same for all the M channels.

Once the number of iterations is fixed, the update rules can be viewed as an unrolled deep linear CNN, as shown in Fig. 1(b), whose weights at different iterations are shared. During the training phase, we update the network parameters specified by w as well as the regularization parameter λ using the ADAM optimization strategy. Note that the data consistency term specified by (5), and hence its gradient, can be computed analytically in the Fourier domain. This allows the computation of the weight gradients using backpropagation. To make the learned network insensitive to changes in acquisition scheme, we use training data with different undersampling patterns.

2.2. Parallel MRI reconstruction

As discussed previously, the main benefit of the model-based approach is the ease in adapting the framework to general image recovery problems. We will now demonstrate the utility of the proposed framework in recovering parallel MRI data. Specifically, we assume that the data is acquired using M coils, whose coil sensitivities are specified by c_i i = 1, … , M. In this work, we assume that the coil sensitivities are estimated from pre-acquired calibration data. We consider the joint recovery of x_i i = 1, … , M from the undersampled measurements b_i = Ax_i We observe that the different coil sensitivity weighted images are restricted to a constraint space

$$\mathcal{C}:x_i=c_i\cdot x;\forall i=1,\dots ,M$$ (6)

where the · operation indicates point by point multiplication of the vectors and x is the coil combined image to be reconstructed. The projection of x_i i = 1, … , M to the above constraint space is specified by

$${\mathcal{P}}_{\mathcal{C}}\left(x_i\right)=\frac{c_i^{*}\cdot x_i}{{\sum }_{i=1}^M{\left|c_i\right|}^2};\forall i=1,\dots ,M$$ (7)

We thus pose the joint recovery of the M coil sensitivity weighted images as a minimization problem, involving the cost function

$$\mathcal{L}=\sum _{i=1}^M\left({\Vert A{x}_i-b_i\Vert }_2^2+{\lambda }_1{\Vert {\mathcal{N}}_w\left(x_i\right)\Vert }^2+{\lambda }_2{\Vert x_i-{\mathcal{P}}_{\mathcal{C}}\left(x_i\right)\Vert }^2\right)$$

Note that the first two terms are separable in x_i, while the last term enforces the constraint $\mathcal{C}$ specified by (6); the constraint will be exactly satisfied as λ₂ → ∞. We minimize the above cost function by alternating between the following steps

$$z_i[n]={\mathcal{D}}_w\left(x_i[n]\right),$$

$$y_i[n]={\mathcal{P}}_{\mathcal{C}}\left(z_i[n]\right),$$

$${\alpha }_i[n]={\lambda }_1{z}_i[n]+{\lambda }_2{y}_i[n],$$

$$x_i[n+1]={\left(A^{H}A+\lambda I\right)}^{-1}\left(A^H{b}_i+{\alpha }_i[n]\right)$$

for all i = 1, … , M. Here λ = λ₁ + λ₂. As with the single channel setting, we set the regularization parameters λ₁ and λ₂ as trainable. We note that the denoising network is the same for all the channels and all the iterations. Since the weights in the unrolled network are all shared, the number of trainable hyperparameters in the multicoil setting is just one more than the single coil setting. The outline of the iterative framework is shown in Fig. 2.

Fig. 2:

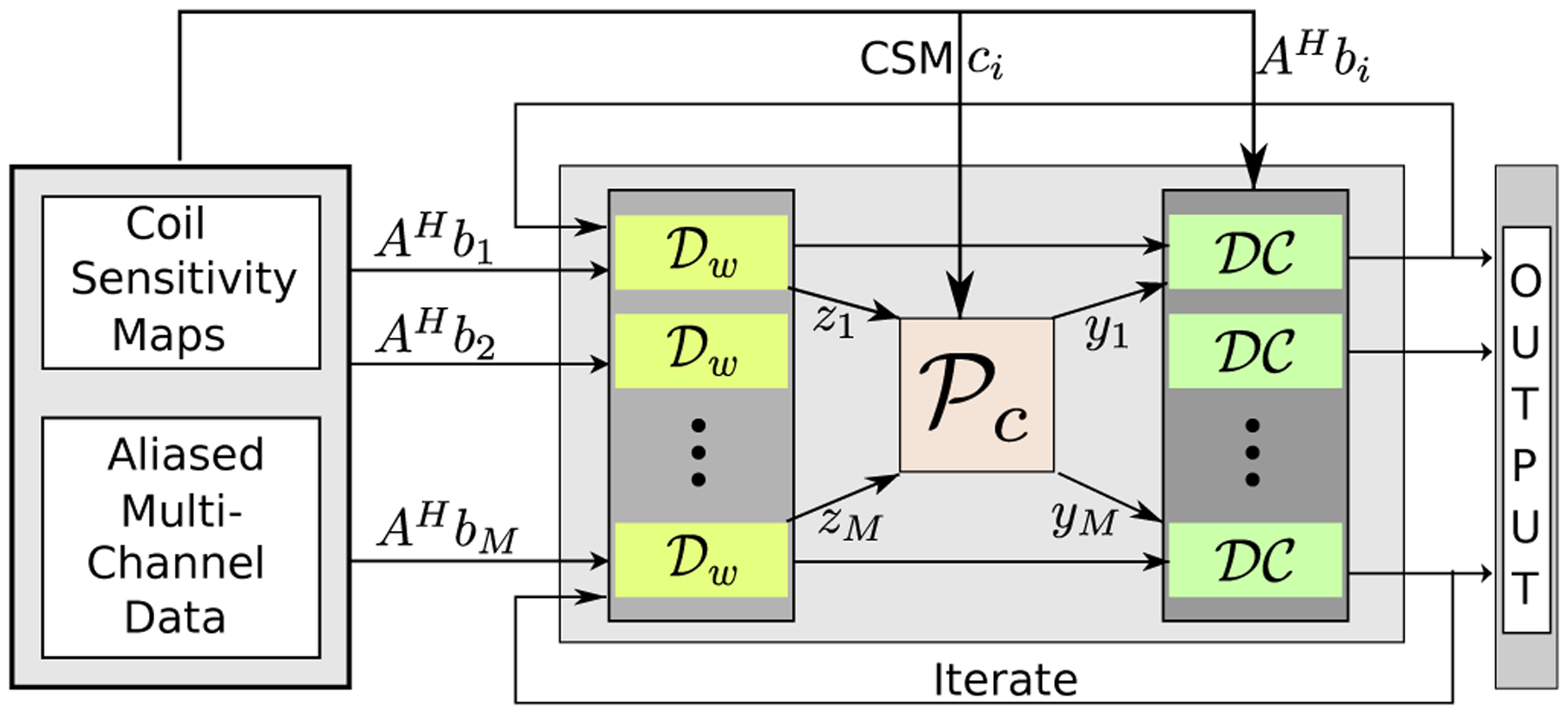
MoDL-CC: extension of the MoDL architecture by incorporating coil-combine (CC) step for parallel MR image recovery. The recursive approach alternates between denoiser ${\mathcal{D}}_i$, projection to coil sensitivity constraints denoted by ${\mathcal{P}}_i$, and data-consistency layer.

3. EXPERIMENTS AND RESULTS

For validation, MRI data was acquired using a 3D T2 CUBE sequence with Cartesian readouts using a 16-channel head coil. The matrix dimensions were 256 × 256 × 208 locations with 1 mm isotropic resolution. Fully sampled multi-channel brain images of five volunteers were collected. We evaluated the inverse Fourier transform of each readout. Out of the 208 slices, we selected around 90 slices that had reliable information for training. Principal component analysis (PCA) based dimensionality reduction was applied to reduce the number of channels from 16 to 4. The coil sensitivity maps were estimated from the central k-space regions of each slice. A total of 380 slices from five subjects were randomly permuted, out of which 300 were used for training the MoDL and the remaining 80 were used during testing.

We used a five-layer model with 64 filters at each layer to implement ${\mathcal{N}}_w$. Each layer consists of convolution (conv) followed by batch normalization (BN) and a non-linear activation function ReLU (rectified linear unit, f(x) = max(0, x)). The proposed recursive model was unrolled assuming 7 iterations and implemented in TensorFlow. Since MR images are complex, the network was trained to recover a tensor of size 256 × 256 × 2 from an input of similar size. The third dimension here corresponds to real and imaginary parts of the images. At each 2D convolution, 64 filters of size 3 × 3 were learned. The analytical form of the data-consistency (DC) update enabled us to implement it as a separate layer, which facilitated the evaluation of the analytical gradients for backpropagation. The training was first performed in the single coil mode; the weights from this training were used to initialize the model in the multi-coil model, which facilitated faster training. The coil-independent model (MoDL-CI) was trained for 1000 epochs using a batch size of 2 for seven hours using an NVIDIA Tesla P100 accelerator card. The coil-combined model (MoDL-CC) was initialized with MoDL-CI and then further trained for 50 epochs within two hours.

Figure 3 shows results obtained from different techniques on a four-fold accelerated data acquisition in the presence of Gaussian noise of σ = 0.01. The reconstruction using coil-independent model followed by coil combination using coil sensitivity maps (MoDL-CI) and the reconstruction where all four coil data were simultaneously fed into the network (MoDL-CC) are shown in the figure. For comparison, a SENSE multichannel reconstruction with Tikhonov regularization and a compressed sensing reconstruction using total variation [1] and a wavelet-based sparsity prior are also provided.

Fig. 3:

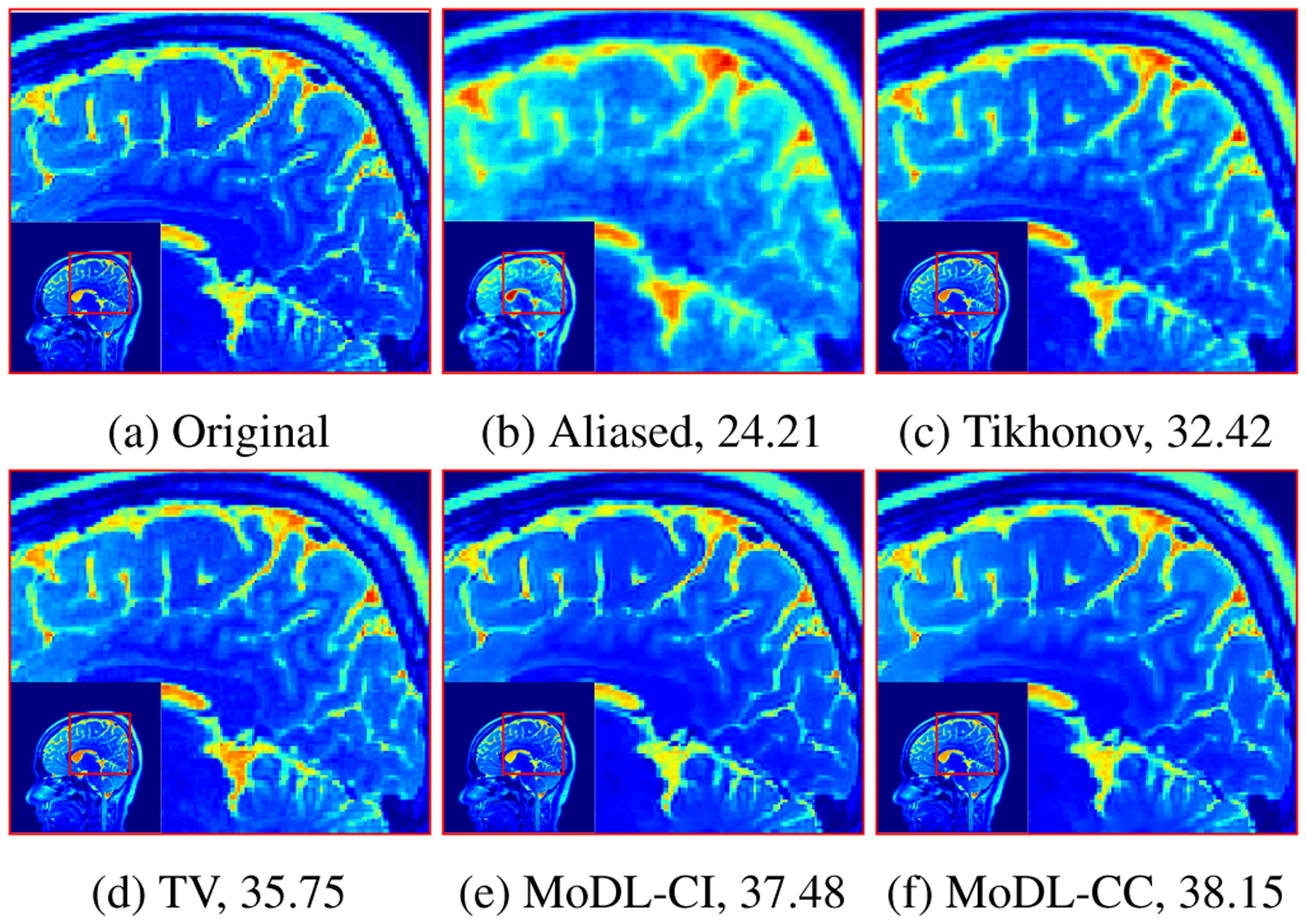
Comparison of proposed MoDL reconstruction with existing techniques for four-fold accelerated case with random noise of σ = 0.01 added in k-space. The numbers in caption represent PSNR in dB.

Figure 4 shows the reconstruction results using the proposed MoDL-CC technique at higher acceleration factors of six and ten. Table 1 shows the result of applying the trained MoDL-CC on a testing data that was 16-fold accelerated with noise of standard deviation σ = 0.03. All the reconstructions in Table 1 were performed using a network trained for 16 fold acceleration. It is evident from the results that the model based framework allows us to use a single trained network for different acceleration factors and different noise levels with minimal degradation in performance.

Fig. 4:

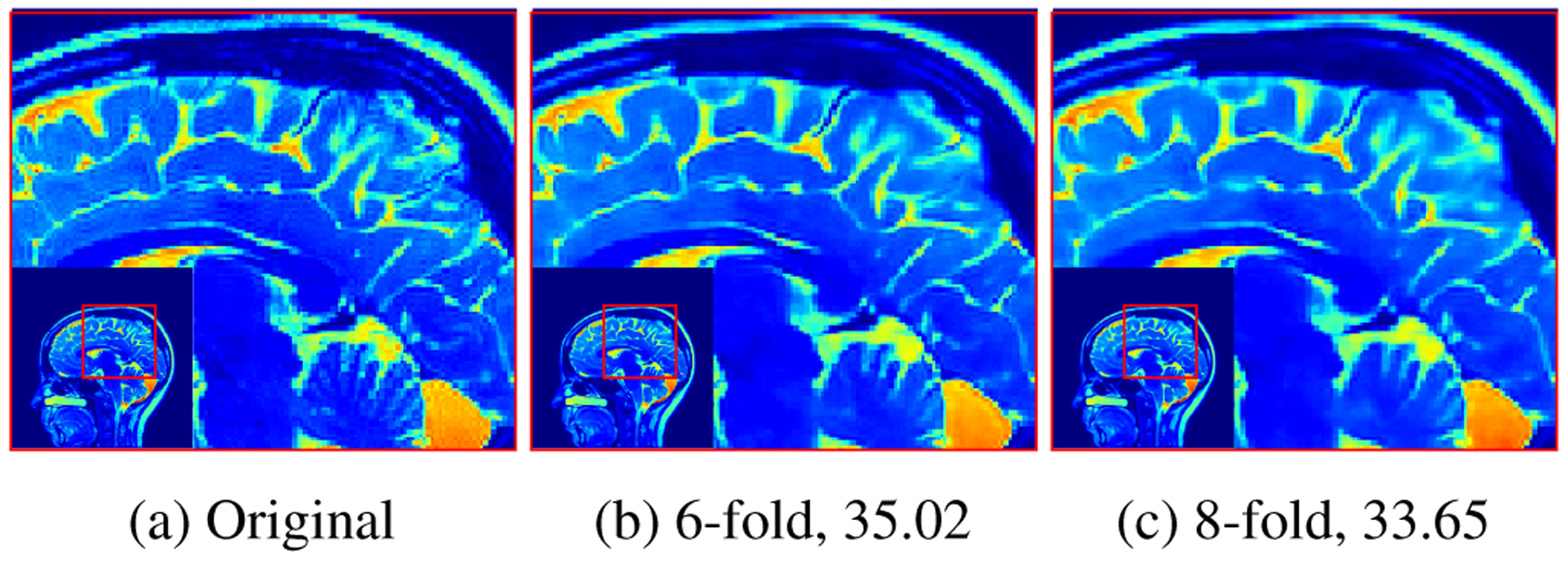
The results obtained by proposed MoDL-CC on 6-fold and 10-fold acceleration in the presence of random noise with σ = 0.01. The numbers in caption represent PSNR.

Table 1:

The average PSNR (dB) values for 80 images obtained using the proposed MoDL-CC for different acceleration factors and noise standard deviation.

Noise (σ)	6-fold	10-fold	16-fold	20-fold
0.00	31.03	31.34	31.04	30.49
0.01	30.97	31.3	31.02	30.46
0.03	30.4	30.89	30.71	30.24
0.05	28.84	29.61	29.88	29.48

4. CONCLUSIONS

In this article, we proposed a model-based approach for image reconstruction using a deep learned prior. With a fixed number of iterations, the MoDL framework can be unrolled as a deep architecture. We use on weight sharing across the CNN networks, thus making it consistent to the model-based framework, and reducing the number of learned parameters; this strategy reduces both the computation time and the amount of training data required. The extended model for parallel imaging has only one extra parameter corresponding to SENSE prior. Experimentally it was found that the learned model is robust to different undersampling ratio and amount of noise. Further, it was observed that increasing the number of iterations of the network helps in better reconstruction.