Modeling the impact of cardio-pulmonary irradiation on overall survival in NRG Oncology trial RTOG 0617

Abstract

Purpose:

To quantitatively predict the impact of cardio-pulmonary dose on overall survival (OS) after radiotherapy for locally-advanced Non-Small Cell Lung Cancer.

Materials and Methods:

We used the NRG Oncology/RTOG 0617 dataset. The model building procedure was pre-registered on a public website. Patients were split between a training and a set-aside validation subset (N=306/131). The 191 candidate variables covered disease, patient, treatment, and dose-volume characteristics from multiple cardiopulmonary substructures (atria, lung, pericardium, and ventricles), including the minimum dose to the hottest x% volume (Dx%[Gy]), mean dose of the hottest x% (MOHx%[Gy]), and minimum, mean Mean[Gy], and maximum dose. The model building was based on Cox regression and given 191 candidate variables, a Bonferroni-corrected p-value threshold of 0.0003 was used to identify predictors. To reduce over-reliance on the most highly correlated variables, stepwise multivariable analysis (MVA) was repeated on 1000 bootstrapped replicates. Multivariable sets selected in ≥10% of replicates were fit to the training subset and then averaged to generate a final model. In the validation subset, discrimination was assessed using Harrell’s c-index, and calibration was tested using risk group stratification.

Results:

Four MVA models were identified on bootstrap. The averaged model included atria D45%[Gy], lung Mean[Gy], pericardium MOH55%[Gy], and ventricles MOH5%[Gy]. This model had excellent performance predicting OS in the validation subset (c=0.89).

Conclusion:

The risk of death due to cardio-pulmonary irradiation was accurately modeled, as demonstrated by predictions on the validation subset, and provides guidance on the delivery of safe thoracic radiotherapy.

Introduction

Although radiotherapy (RT) is an established treatment modality for locally-advanced non-small cell lung cancer (LA-NSCLC), progress has been slow, with patients being deceased on average between one to two years after completion of RT [1]. Long-term results have recently improved fusing RT with immunotherapy checkpoint inhibitors [2], but the exact details of optimal RT remain unclear. Thus, interest continues in understanding and optimizing dose and fractionation parameters in this patient cohort.

In RTOG’s 0617 randomized phase III dose-escalation trial for this patient population, Bradley et al [1] found, unexpectedly, that patients in the accelerated 74 Gy arm were at a higher risk of death than the patients in the conventional 60 Gy arm. In their initial analysis using heart dose-volume characteristics, they found that patients with larger heart volumes irradiated to at least 5 Gy (V5Gy[%]) were at higher risk of death.

Since the publication of the multivariable overall survival (OS) model from the RTOG 0617 trial, at least six cohort studies have presented varying heart and/or lung dose OS models after RT for LA-NSCLC [3–8]. Tucker et al [3] found an association with the mean lung dose, Mean[Gy], but references [4–7] instead established associations with heart dose only: heart V2Gy[%] in [4], the base of the heart in [5], left atrial V63–69Gy[%] in [6], and heart V50Gy[%] in [7]. In contrast, Speirs et al [8] established a simultaneous heart and lung dose association including heart V50Gy[%], heart volume, and lung V5[%]. While the majority of the datasets in [3–8] included a large number of patients (78–1101 patients), these were typically treated at single institutions in which the variability in dose-volume variables is limited given uniform treatment procedures and techniques [9].

The aim of the current study was to generate a predictive model of patient-specific risk of death based on the multi-institutional RTOG 0617 data, addressing a broad range of input data describing dose to a wide range components of the cardio-pulmonary system as well as tumor and individual characteristics. This dataset is valuable for predictive modeling, given the randomization of prescription dose, as well as multi-institutional participation, which reduces correlations due to single institutional treatment approaches [9].

Materials and Methods

To increase rigorousness and promote transparency, the study analysis plan (SAP) was logged on the Open Science Foundation website prior to receipt of the dataset, and is available from that site at the time of this writing [10], as well as in the online Supplementary material. Any departure or addition relative to the SAP is explicitly stated in the following.

Investigated cohort

All patients treated in RTOG 0617 that had complete dose-volume histogram (DVH) data through retrievable treatment plans were included in the present study (437 of 554 patients that were initially enrolled). Characteristics for this cohort are summarized in Table 1. The median follow-up time across all 437 patients was 24 (range: 0.5–97) months. The original study was sponsored by the National Cancer Institute (NCI) and received central institutional review board (IRB) approval under NCI, and the associated ethical guidelines adheres to the Belmont report. All patients read and signed informed consent documents [1].

Table 1.

Summary of the investigated disease, patient and treatment characteristics (n (%) or median (range)) in the whole cohort (left), and separated between training/validation (left/right). The p-value is from a Wilcoxon rank-sum test (exception: comparison of OS curves in which the p-value refers to a log-rank test) between variables in training and validation (Bonferroni-corrected significance level: p=0.003).

	All data (N=437)	Training (N=306)	Validation (N=131)	p
Age [y]	64 (37–83)	64 (37–83)	64 (38–82)	0.86
Cetuximab assigned
Yes (ref)	203 (46)	135 (44)	68 (52)	0.14
No	234 (54)	171 (56)	63 (48)
Concurrent paclitaxel/carboplatin dose
Other (ref)	321 (73)	227 (74)	94 (72)	0.60
85–115%	116 (27)	79 (26)	37 (28)
Consolidation paclitaxel/carboplatin
No (ref)	319 (17)	55 (18)	20 (15)	0.49
Yes	362 (83)	251 (82)	111 (85)
Gender
Male (ref)	179 (41)	122 (40)	56 (43)	0.58
Female	258 (59)	184 (60)	75 (57)
GTV [cm3]	93 (4–1194)	91 (4–1194)	105 (6–959)	0.15
Histology
Adeno (ref)	175 (40)	130 (42)	45 (34)	0.07
SCC (ref)	188 (43)	123 (40)	65 (50)	0.11
Large cell undifferentiated/NSCLC NOS	74 (17)	53 (17)	21 (16)	-
Lymph node group
LLL level 7–10 (ref)	260 (59)	179 (58)	81 (62)	0.52
Other	177 (41)	127 (42)	50 (38)
OS [m]
Alive	118 (27)	82 (27)	36 (27)	0.33
Dead	319 (73)	224 (73)	95 (73)
Median (95%CI) time since randomization*	25 (21–29)	23 (20–28)	26 (21–37)
Prescribed dose
60Gy (ref)	253 (58)	176 (58)	77 (59)	0.81
74Gy	184 (42)	130 (42)	54 (41)
RT technique
3DCRT (ref)	228 (52)	158 (52)	70 (53)	0.73
IMRT	209 (48)	148 (48)	61 (47)
Smoking status
Former (ref)	319 (73)	222 (73)	97 (74)	0.38
Current (ref)	73 (17)	48 (16)	25 (19)	0.75
Tumor inferiority
Upper lobe (ref)	291 (67)	203 (66)	88 (67)	0.21
Lower lobe (ref)	93 (21)	70 (23)	24 (18)	0.87
Tumor laterality
Left (ref)	171 (39)	123 (40)	69 (53)	0.46
Right (ref)	242 (55)	174 (56)	81 (62)	0.79
Tumor stage
IIIA+N2 (ref)	293 (67)	207 (68)	86 (66)	0.68
IIIB+N3	144 (33)	100 (32)	45 (34)
Zubrod Performance
0 (ref)	256 (59)	179 (58)	77 (59)	0.96
1	181 (41)	127 (42)	54 (41)

^*:Based on Kaplan-Meier estimates

Abbreviations: LLL: Left lower lobe; SCC: Squamous cell carcinoma.

Three heart dose-volume thresholds were recommended as treatment planning guidelines in the original trial (Heart V33%<60Gy; V66%<45Gy; V100%<40Gy). These guidelines had the lowest priority among all concerned normal tissues (cf. Appendix 1 in [1]). The cardiac substructures considered (atria, pericardium, and ventricles) were based on the RTOG 1106 organ-at-risk atlas https://www.rtog.org/corelab/contouringatlases/lungatlas.aspx[11]. Segmentation was performed by five physicians following completion of the trial, as part of the analysis effort, and was reviewed by a single physician. As illustrated in the slice-by-slice definitions in [11], the pericardium started ~5–6mm above the superior end of the aortic arch and ended at the diaphragm, and was the envelope of the four chambers, the aorta (primarily the ascending part), the pulmonary artery and vein, the superior vena cava, and the coronary arteries. The inferior boarder of the atria and ventricles (if still appearing; typically, only the left ventricle) were at the last slice of the pericardium while the superior boarder was just below where the pulmonary artery passed the midline (if appearing; typically, only the left side). The left and right atria were fused and so were the left and right ventricle. Other structures analyzed included the gross tumor volume (GTV; prescribed dose and volume only), as well as the non-tumor invaded lung; both obtained from the original treatment planning structure set.

Modeling

There is no universally accepted approach to dose-volume modeling, particularly given multiple potential critical tissues. The goal of our modeling strategy was to deal with the two key challenges of (1) many substructures, which increases the number of potential DVH candidate predictors, as well as (2) a potential over-reliance on predictors with maximum univariate significance, compared to other factors that could have been selected if another dataset were collected. For these reasons, we simulated model OS Cox selection variability on bootstrap. Candidate multivariable models based on bootstrapped datasets were recorded. The final ensemble model was then derived by averaging the coefficients across candidate models, and then validated in the set-aside validation subset.

For the purpose of modeling, the cohort was randomly split into a training and a set-aside validation subset (N=306, 131). However, the split maintained the same fraction of patients in each prescription level arm. Further, the splits were not allowed to be different (at the p≤0.05 level on a Wilcoxon rank-sum test) with respect to: age, systemic therapy (concurrent, consolidation and cetuximab chemotherapy), gender, GTV, histology, lymph node group, OS status, time since randomization, performance status, prescribed dose, RT technique, smoking status, and tumor location and stage (Fig S1; Table 1). This approach aimed at minimizing potential bias between the training and validation subsets since these six variables were previously reported to predict OS in [1] and to further result in a somewhat balanced split also with regards to OS status and time since randomization.

Candidate overall survival models

Within the training process, model building was performed using Cox proportional hazards regression based on a total of 191 variables (19 related to the disease, patient, or treatment, and 43 DVH cut-points and volumes of each of the four structures). Dose was fractionation-corrected using the linear-quadratic equation (assuming α/β=3Gy) and was represented by the minimum and mean dose to the hottest x% volume (Dx%[Gy], MOHx%[Gy]; x was 5–100 in 5% increments) [12], and the mean and max dose (Min[Gy], Mean[Gy], and Max[Gy]). This nomenclature is consistent with TG-263 [13]. The minimum dose to the hottest x% volume, Dx%[Gy], variables, were used rather than VxGy[%] variables, due to preferred statistical properties: as VxGy[%] approaches the prescription dose, many patients have values of zero/close to zero, whereas this is not the case for associated Dx%[Gy].

Candidate predictors were suggested by a p-value≤0.0003 (Bonferroni-corrected for 191 variables), as stated in the SAP. If multiple candidate DVH variables were identified for each structure, the one with the lowest p-value was promoted to multivariable analysis (MVA). The underlying motivation for ‘one best DVH variable per structure choice’ was due to an anticipated strong correlation between DVH variables of the same structure, and parsimonious models are particularly preferred to avoid unnecessary model selection instability. Candidate predictors were then subject to MVA, which was conducted with forward-stepwise variable selection and a retention criterion of p≤0.05 from a likelihood ratio test. Univariable analysis followed by MVA were carried out together on 1000 bootstrapped replicates (with replacement) in which MVA models (selected in ≥10% of the replicates) were considered candidate models, and were subject to validation. As was not clearly stated in the SAP, linear interaction terms between variables in the candidate MVA models were tested and incorporated into the MVA models if adhering to the univariate p-value cut-off, and in addition all regression coefficients were required to be positive given an underlying hypothesis of cardiopulmonary dose leading to worse survival.

Validation of candidate overall survival models

The validation procedure was not described in detail in the SAP, but was carried out as follows as suggested by Royston and Altman [14]: For each candidate MVA model, the validation procedure included calculation of the prognostic index (PI; β₁xVariable₁ + β₂xVariable₂…) using the coefficients obtained in the training subset. The predicted survival curve was obtained combining the PI with the observed survival. The predicted survival curve was assessed both for calibration and discrimination [14, 15]: calibration was assessed in four risk groups (low/moderate/intermediate/high risk: <16^th/16^th-50^th/>50^th-84^th/>84^th percentile of the predicted PI) [14] with the primary focus of comparing the low- to the high-risk group, as suggested in [14]. Discrimination was assessed using Harrell’s c-index, which was independent of the risk group stratification (i.e., assessed using all patients in the validation subset). The model is a TRIPOD type 2b model (one dataset randomly split into a training and validation cohort) [15].

Final ensemble modeling procedure

As noted above, the goal was to propose a modeling procedure that is robust with respect to dataset variability regarding predictor selection. Given the expected distribution of MVA models on bootstrap replication, i.e., more than one candidate MVA model, a subsequent ensemble modeling approach was conducted. This was inspired by the approach proposed by Zhang et al [16], but unlike their Principal Component Analysis method, our generated candidate models were bagged, i.e., the coefficients for each variable were averaged and weighted according to the selection frequency of the associated DVH variable. This leads to a new bagged-based PI in training; the validation procedure was analogous to that described previously.

Results

Candidate overall survival models in the training subset

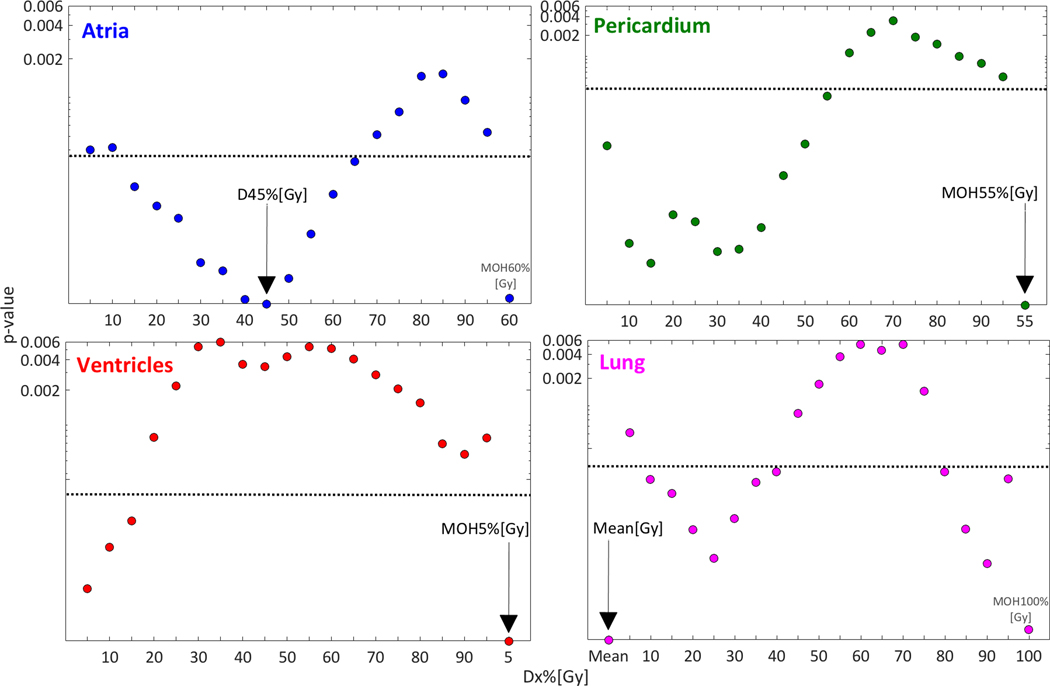
None of the disease or patient characteristics, or structure volume was a candidate predictor (Fig. S2). However, dose to the four investigated structures was, and the best DVH cut-points were Atria D45%[Gy], Pericardium MOH55%[Gy], Ventricles MOH5%[Gy], and Lung Mean[Gy] (Fig. 1; Table S1). These four candidate predictors were passed on to MVA, and resulted in four candidate MVA models (model frequency):

Fig 1.

Univariate p-values (median over all samples) for the investigated Dx%[Gy] variables, and the best MOHx%[Gy] (rightmost data point) for each of the investigated four structures (exception: Mean[Gy] also given for Lung since this was the best DVH predictor). Note: The best DVH predictor for each structure is denoted with a black arrow, the dotted black lines represent the Bonferroni-corrected significance level at p=0.0003, and the y-axis is on a log scale.

1. Atria D45%[Gy] + Pericardium MOH55%[Gy] (18%)

2. Atria D45%[Gy] + Pericardium MOH55%[Gy] + Ventricles MOH5%[Gy] (15%)

3. Atria D45%[Gy] + Pericardium MOH55%[Gy] + Lung Mean[Gy] (14%)

4. Pericardium MOH55%[Gy] +Ventricles MOH5%[Gy]+ Lung Mean[Gy] (10%)

The associated c-index was 0.87 for MVA model 1, followed by 0.84, 0.86, and 0.84 for models 2, 3 and 4, respectively. No interaction term passed the p≤0.0003 criterion (the lowest p-value was observed for the interaction term between Atria D45%[Gy] and Pericardium MOH55%[Gy]; p=0.01), and no such term was, thus, incorporated to any of the MVA models.

Exploration of candidate overall survival models in the validation subset

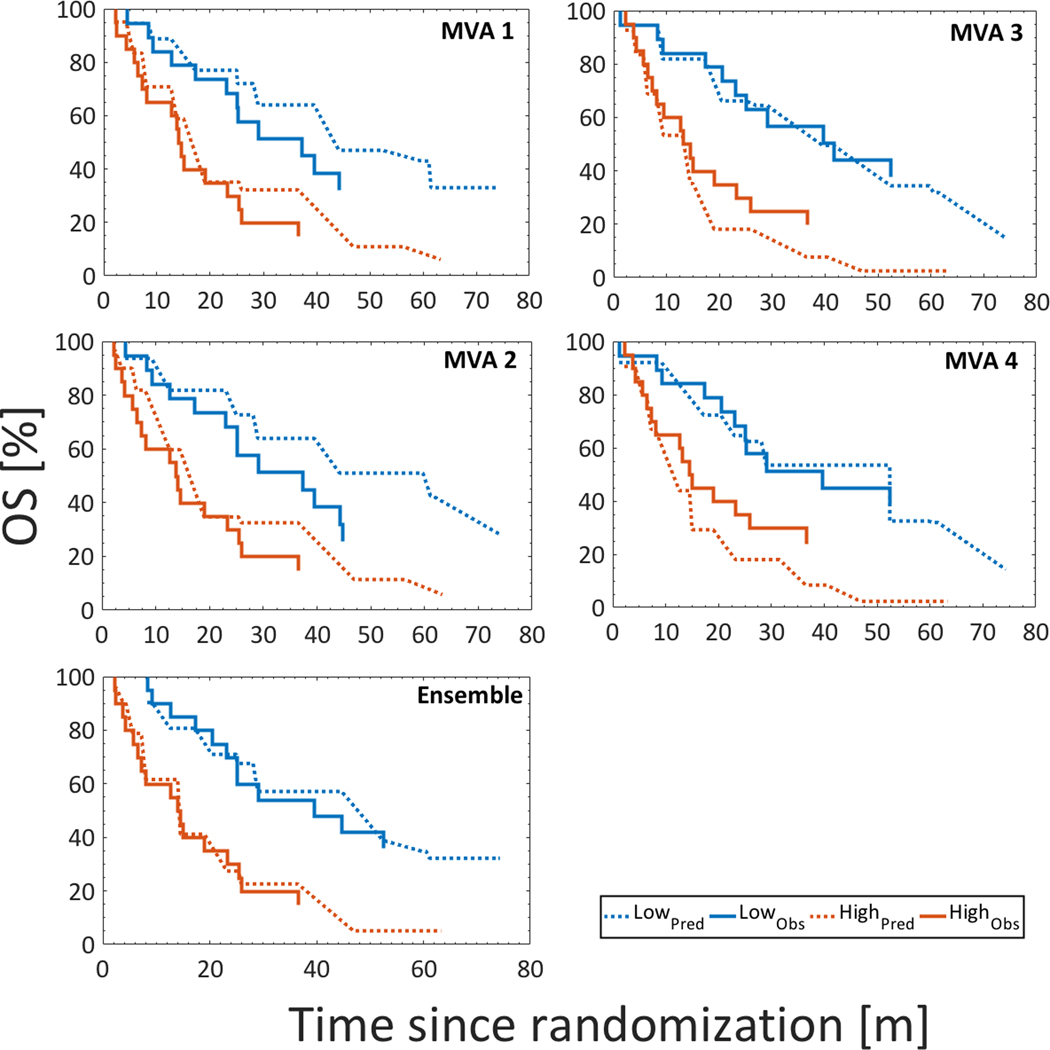
As expected, discrimination of the four MVA models dropped in the validation subset compared to in the training subset (c-index of MVA models 1/2/3/4: 0.80 vs. 0.87/ 0.82 vs. 0.84/ 0.82 vs. 0.86/0.82 vs. 0.84). Also, the PI was slightly lower in validation compared to in training for all models, but not significantly so and was distributed similarly across the subsets (Fig. S3). Calibration was typically satisfactory between the low- and the high risk groups, but somewhat inferior between the moderate- and the intermediate risk groups (Figs. 2, S4). At 18 and 36 months in the high and the low risk groups, the predicted survival rate was higher than the observed survival rate for MVA models 1 and 2, whereas for MVA models 3 and 4 the predicted survival rate was on average lower than the observed survival rate for the corresponding time points and risk groups (Figs. 2 and S4; Table S2).

Fig 2.

Kaplan-Meier curves for the low- and the high risk groups based on MVA models 1–4 and the ensemble model comparing the observed survival rates (solid) vs. the predicted survival rates (dotted) in validation; the latter modifying the observed survival curve in validation based on the PI from training.

Ensemble modeling

Bagging was performed on the four final models, i.e., Atria D45%[Gy]_, Pericardium MOH55%[Gy]_, Ventricles MOH5%[Gy], and Lung Mean[Gy]. The PI in validation was located in between the PIs from MVAs 1–2 and MVAs 3–4 (mean: 0.89 vs. 0.63–0.66, and 1.11–1.11). The associated c-index in validation increased from 0.80–0.82 for the individual MVA models to 0.89 for the bagged model, and in addition, risk group stratification between the high- and the low risk-group was close to perfect (Fig. 2): For the bagged model, the predicted vs. observed survival rate differed in two percentage points (78% vs. 80%) at 18 months and six percentage points (40% vs. 34%) at 36 months in the low risk group. The equivalent difference in the high risk group was one and three percentage points (41% vs. 40%, and 23% vs. 20%). These numbers were considerably smaller compared to the corresponding survival rates for MVA models 1–4 (Table S2) in which the median difference was five and eight percentage points at 18 and 36 months in the low risk group, and 17 and 15 percentage points for the same time points in the high risk group.

In the high risk group, and based on the ensemble model, the population average of Atria D45%[Gy]_, Pericardium MOH55%[Gy]_, Ventricles MOH5%[Gy], and Lung Mean[Gy] were 44Gy, 51Gy, 56Gy and 17Gy (all doses given as the equivalent dose in 2 Gy fractions assuming α/β=3Gy). These could be used as upper limits in the treatment planning of LA-NSCLC. For even more conservative treatments, and if feasible, the upper limits could be defined by combining the intermediate and the high risk group (population average: Atria D45%[Gy]≤30Gy; Pericardium MOH55%[Gy]≤39Gy; Ventricles MOH5%[Gy]≤41Gy; Lung Mean[Gy]≤15Gy). In addition, Fig. S5 provides an overview of the predicted and observed OS using the ensemble model (within two years post-randomization, which was the cohort median follow-up time for OS and also the follow-up time studied in further detail in [1]).

Further, the coefficients behind the PI for the ensemble model (PI_Ensemble: 0.02×Pericardium MOH55%[Gy] + 0.002× Atria D45%[Gy] + 0.002×Ventricles MOH5%[Gy] + 0.03×Lung Mean[Gy]), and the coefficients for all other univariate and multivariable models, are given in Table S1. The ensemble PI can be used to construct predicted survival given the observed survival (alternatively one can use the observed survival provided here if assumed to be similar across cohorts) in external data, e.g., for validation purposes adhering to the procedures used here and as given in more detail in [14].

Discussion

Given the excellent discrimination of survival time based on predictions from the bagged model in the set-aside validation subset (c=0.89), and the use of multi-institutional data from a randomized controlled phase III trial allowing for limited correlations between the investigated variables, this model gives further insights into the unexpected OS findings of RTOG 0617. The present model emphasizes associations between dose to the major blood-carrying structures and OS. Other treatment-related factors such as GTV, prescription dose, and RT technique did not pass even the univariate stage of modeling (p=0.10, 0.27, 0.39).

The bagged model combined the models that emerged on bootstrap: dose to the Atria, Lung, Pericardium, and Ventricles. Previously published studies have predominantly suggested either that dose to cardiac structures [4–6], and/or dose to the lung [3] predicts OS for this patient group. In agreement with the now two previously published OS models based on the same RTOG 0617 data [1, 17], which included heart dose [1], all four candidate MVA models suggested here include dose to the pericardium (through MOH55%[Gy]). The pericardium in this study includes the four chambers, the aorta (primarily the ascending part), the pulmonary artery and vein, the superior vena cava, and the coronary arteries [11]. Also, frequently selected was the Atria D45%[Gy], present in three of the four candidate MVA models together with Pericardium MOH55%[Gy], or with/without Lung Mean[Gy], or Ventricles MOH5%[Gy]. Ventricles MOH5%[Gy] was the only DVH predictor that was related to the higher dose end. While the model suggests striving for Atria D45%[Gy]≤44Gy_, Pericardium MOH55%[Gy]≤51Gy_, Ventricles MOH5%[Gy]≤56Gy, Lung Mean[Gy]≤17Gy, the ranges of these four variables even among patients who survived is wide (Atria D45%[Gy]: 0.2–61Gy_, Pericardium MOH55%[Gy]: 0.6–58Gy_, Ventricles MOH5%[Gy]: 0.4–38Gy, Lung Mean[Gy]: 1.5–17Gy), which indicates the possibility for introducing dose-volume constraints in general also in light of the low priority on dose sparing to the heart in the original 0617 trial (cf. Appendix 1 in [1]).

Others have recently reported associations between dose-volume metrics and OS following RT in LA-NSCLC patients based on primarily single-institutional data from non-randomized trials. Vivekanden et al [6] found that left atrial V63–69Gy[%] predicted OS, and was the only variable significantly doing so in their substructure MVA model (N=78). Stam et al [4] reported an association between OS and heart V2Gy[%] using a contouring-free dose mapping approach focusing only on the heart and lungs (N=469). McWilliam et al [5] also used a ‘contouring-free’ approach (N=1101), and established an association between OS and dose to the base of the heart (aorta, the region of origin of the coronary arteries, and the sinoatrial node). While those three studies found that cardiac dose increases the risk of death, Tucker et al [3] established a similar association (N=468), but instead using Lung Mean[Gy]. However, it should be pointed out that doses to heart substructures were not analyzed. In contrast to [3–8], the current study was based on data from multiple institutions, which includes an inherently broad variability in DVH variables, the modeling approach carefully followed the validation procedures outlined in the anchor publication by Royston and Altman [14] and further also adhered to the TRIPOD statement [15]. In addition, the SAP associated with the current study was pre-registered on a public domain, which allows for analysis transparency.

Perhaps most relevant to our analysis is the OS analysis by Speirs et al [8] (N=416), that includes DVH metrics of both the cardiac and the pulmonary system, resulting in significant variables of heart V50Gy[%], heart volume, and lung V5Gy[%], which is similar to our result. Another closely related result is that of Contreras et al [7], who derived a multivariable Cox model showing that heart V50Gy[%] together with gender, and an elevated blood neutrophil to lymphocyte ratio four months after RT was associated with OS (N=400). They did, however, not exploit dose to any other parts of the blood-carrying tract, and the model was not validated in set-aside data. Taken together, these recent publications, including also the current study, emphasize a role of the heart, lung, and large vessel irradiation on OS.

As stated in in Methods and Materials, only one DVH variable per structure was passed on to multivariable analysis assuming a strong anticipated correlation between DVH variables of the same structure. The intra-structural correlation between each final candidate DVH metric and the other DVH metrics that passed the univariate p-value cut-off (31/43 metrics for Atria, Lung, and Pericardium, and 22/43 Ventricle metrics) for that structure was indeed strong (median Spearman’s rank correlation coefficient, R_s=0.97) for both Atria D45%[Gy] and Pericardium MOH55%[Gy], but was somewhat weaker for Ventricles MOH5%[Gy] and Lung Mean[Gy] (median R_s=0.93, 0.89). For instance, the correlation with Mean[Gy] was typically among the strongest for Atria D45%[Gy], Pericardium MOH55%[Gy], and Ventricles MOH5%[Gy] (R_s=0.97, 0.99, 0.91). The inter-structural correlation between the four final predictors was lower than that of the intra-structural correlation (median R_s=0.69), but not surprisingly of the same magnitude between Pericardium MOH55%[Gy], and either Atria D45%[Gy], or Ventricles MOH5%[Gy] (R_s=0.85, 0.82). In summary, the identified dose regions for all four structures were Mean[Gy] or Median[Gy] alike, but for all four structures correlations were strong throughout most of the investigated dose range. For illustration purposes, which was not specified on the SAP, for each structure the univariate DVH predictor that presented with the weakest correlation with the final predictor for each structure was added to the ensemble model in turn (Atria MOH15%[Gy], Pericardium D5%[Gy], Lung D5%[Gy]: R_s=0.80, 0.63, 0.48 with the final predictor for each structure; Note: No Ventricles DVH variable was included since Ventricles MOH5%[Gy] was strongly correlated with all Ventricle variables (minimum R_s=0.90)). A gain in c-index, as compared to that of the ensemble model, was not observed. A last note regarding correlation: even though the strongest correlations were accounted for, some degree of collinearity will inevitably remain given that the four DVH variables in the final model were derived from the similar region.

A higher cardiopulmonary dose being associated with OS does not necessarily translate into successful estimation of a causal role in mortality, and we would like to emphasize that the current study does not attempt to propose an underlying causal effect. While such a link has been established between heart irradiation and cardiac dysfunction in large breast cancer and Hodgkin’s lymphoma series [18, 19], a similar dose-response for NSCLC has, thus far, only been suggested in two small cohort studies (N=125, 112) [20, 21]. Of the eight available studies (including also the current study) that have analyzed OS after RT for LA-NSCLC and have estimated a relationship with dose to the cardiopulmonary system [1, 3–8], only in [6] and in [7] was an effort made to untie causality from correlation. The approach taken in [6] was to assess cardiac status through electrocardiographic (ECG) measurements, and define abnormality as any new ECG event six months after completed RT relative to baseline. Two MVA models were generated; one based on heart dose, and one based on heart dose as well as dose to cardiac substructures. Heart dose, and ECG changes constituted the former MVA model, while the latter MVA model included only left atrial (LA) dose. A plausible explanation could, e.g., be that ECG changes are associated with damage caused by dose to LA and, thus, LA dose being a proxy for cardiac toxicity, and, therefore, ECG changes did not remain significant. However, an explanation to this was not provided, and given that the analyzed cohort was limited in size in particular for the analysis regarding ECG changes (53/78 patients; Table 2 legend in [6]), this should be explored in an independent, and ideally larger cohort. Another attempt to untangle causality was made in the study by Contreras et al [7] and in the study by Thor et al [22] who found indications of an unprecedented immune suppression explaining OS. Thus far, however, no study has simultaneously explored cardio-pulmonary function and immune suppression in the setting of OS. In summary, the causal etiology of our established dose-response model remains to be further elucidated including, but not limited to, whether it is in the direction of cardiac dysfunction, immunosuppression or both.

None of the investigated non-DVH characteristics were candidate predictors for OS. This included also RT technique (p=0.39) and prescription dose level (p=0.27). A preceding analysis based on the 0617 data neither found an association between RT technique and OS [23]. Also in the same data, prescription dose level was previously found to be a predictor [1], and although this variable was included in the MVA in [1], the original model based on the 0617 data was dominated by Heart V5Gy[%] (p=0.02 vs. 0.004; cf. Appendix 6 in [1]). Of note, even in the entire cohort investigated in the current study the effect of prescription dose level on OS was diminished as opposed to in [1] (p=0.02 vs. 0.004; lower Fig. S6 vs. Figure 2 in [1]). Further, in splitting the training and the validation subsets, the prescription dose level, OS status, and time since randomization were kept as similar as possible and were at least not significantly different. As shown in upper Fig. S6, this splitting approach did not guarantee a preserved pattern in prescription dose level. Although with considerably smaller tumors than in the current study (median: 69 cm³, 35cm³ vs. 93 cm³), the MVA models suggested in [4] and in [5] included tumor volume (p=0.006, <0.001). Tumor volume was also in the MVA model in [3] (median: 128 cm³; p<0.0001). Age was not a predictor here (p=0.27), even though the age distribution was similar across this study and [4] (median (range): 65 (30–87) years vs. 64 (37–83) years) in which the MVA model included age (p=0.001). Age was also present in the MVA model suggested in [5] (median (range): 73 (38–95) years; p=0.04). Lymph node involvement in the left lower lobe, and lower/middle primary tumors only trended towards significance in the current study (p=0.001, 0.02). In the study by Speirs et al [8] bilateral mediastinal lymph node involvement was present in their MVA model (p=0.03), and this was due to tumors being located in the left lower lobe. The MVA model by McWilliam et al [5] included nodal stage (p=0.01).

In conclusion, based on the multi-institutional randomized RTOG 0167 data, we showed that dose to the cardio-pulmonary system (rather than dose to isolated components of this system or other characteristics), above certain levels defined quantitatively by the model, compromises OS after RT for LA-NSCLC. While the causal etiology of this effect remains to be further elucidated the possibility to minimize our model’s suggested DVH cut-points could be explored in standard treatment planning systems.

Translational relevance.

Results of the randomized controlled phase III radiotherapy trial NRG Oncology/RTOG 0617 for locally advanced non-small cell lung cancer showed an unexpected increase in mortality within two years following treatment in the high dose arm. This detailed modeling study, performed according to a pre-registered analysis plan, shows that differential mortality was primarily associated with dose-volume loads on multiple cardio-pulmonary structures. The resulting model, applied to set-aside validation data, shows a strong ability to discriminate risk, as well as good calibration. Although the model does not identify cause, it is a quantitative tool that could be used in treatment planning to reduce mortality risk through adjustment of dose patterns outside the tumor volume.