Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Jan 8;21(2):1083–1089. doi: 10.1021/acs.nanolett.0c04419

Phonon-Assisted Hot Carrier Generation in Plasmonic Semiconductor Systems

Yocefu Hattori †, Jie Meng ‡, Kaibo Zheng ‡,§, Ageo Meier de Andrade ∥, Jolla Kullgren ∥, Peter Broqvist ∥, Peter Nordlander ⊥, Jacinto Sá †,#,*
PMCID: PMC7877730  PMID: 33416331

Abstract

graphic file with name nl0c04419_0006.jpg

Plasmonic materials have optical cross sections that exceed by 10-fold their geometric sizes, making them uniquely suitable to convert light into electrical charges. Harvesting plasmon-generated hot carriers is of interest for the broad fields of photovoltaics and photocatalysis; however, their direct utilization is limited by their ultrafast thermalization in metals. To prolong the lifetime of hot carriers, one can place acceptor materials, such as semiconductors, in direct contact with the plasmonic system. Herein, we report the effect of operating temperature on hot electron generation and transfer to a suitable semiconductor. We found that an increase in the operation temperature improves hot electron harvesting in a plasmonic semiconductor hybrid system, contrasting what is observed on photodriven processes in nonplasmonic systems. The effect appears to be related to an enhancement in hot carrier generation due to phonon coupling. This discovery provides a new strategy for optimization of photodriven energy production and chemical synthesis.

Keywords: Plasmon, hot electron, phonon coupling, ultrafast dynamics

Direct utilization of light for the production of energy and chemicals is essential for a green and sustainable economy. Plasmonic materials have optical cross sections that exceed their geometric size by 10-fold, making them uniquely suitable to convert light into utilizable energy and carriers. Optical excitation of the localized surface plasmon creates hot carriers1−3 that can be exploited to produce chemicals4−9 and electricity.10−12 The energies of the hot carriers are initially equal to the absorbed photon energy13 but rapidly undergo carrier multiplication, resulting in a decrease of their energy.14 The direct utilization of hot carriers, while feasible,15 is limited due to their ultrafast charge relaxation and recombination.13 A popular strategy to extend the lifetime of hot carriers is to inject them into semiconductors,3,12,16,17 an ultrafast process occurring in <300 fs.16,17

Ultrafast transient spectroscopies are powerful tools to study the injection efficiency and lifetimes of photogenerated carriers in hybrid plasmonic/semiconductor systems. Efficient systems are commonly characterized by an ultrafast injection (<1 ps) followed by a slow exponential decay(s) due to charge recombination. Carrier–carrier and carrier–phonon interactions regulate the relaxation of high-energy “hot” carriers,18,19 while the energy level alignment and lifetime of the excited state controls charge injection from sensitizers to the semiconductor.20

Temperature modulates the semiconductor energy levels due to excitation of phonons, which affects electron–phonon coupling and thermal conductance at a metal–semiconductor interface. Recent, ab initio calculations on TiSi2 (metal)–Si (semiconductor) interface revealed that the strength of the coupling between electrons and interfacial joint phonon modes is similar to the strength of electron–phonon coupling in bulk metals and that the thermal conductance can be comparable to the phonon–phonon conductance across the interface. This finding demonstrates the importance of direct coupling of electrons in metals to phonons in adjacent semiconductor and provides a pathway for interfacial thermal transport.21

Classical photosensitizers, such as quantum dots, dyes, low bandgap semiconductors, and organic heterojunctions, are characterized by fixed energy levels that determine their light absorption and injection levels. Excess energy is rapidly dissipated via carrier–phonon coupling (solid-state systems) or vibrational relaxation (molecular systems), which restricts single-junction solar cell efficiency to the Shockley–Queisser limit and narrows the photoredox window for chemical transformation.22 Most photodriven applications operate and/or are subject to variable and/or higher temperatures than room temperature, which in the case of photovoltaics can be detrimental to their application, or as in photoredox processes can be beneficial for the catalytic yield. An increase in temperature increases the number of phonons in the semiconductors and vibration relaxation in molecules, effectively reducing the injection efficiency and lifetime of hot carriers.

Unlike classical photosensitizers, plasmonic materials exhibited larger photocurrents at higher operational temperatures, a phenomenon that remains unexplained.23 Herein, a study of thermal effect on plasmon dynamics and hot electron injection efficiency in hybrid plasmonic/semiconductor systems is presented. Using transient ultrafast infrared spectroscopy, it is shown that an increase in temperature increases the number of hot carriers transferred from the plasmonic material to the semiconductor conduction band. The temperature affected the electron–phonon relaxation in the gold plasmonic, suggesting that the contrasting behavior observed with plasmonic materials is associated with their hot carrier generation properties.24−27 The new physical insights on the role of temperature in hot carrier’s generation provide unique opportunities for photodriven energy production and chemical synthesis.

Au nanoparticles (NPs) were synthesized according to the modified inverse Turkevich method reported by Piella et. al.28 The method yielded Au NPs with a narrow size distribution with an average size of 6.7 ± 2.2 nm, as is shown in the TEM image (Figure 1a). The synthesized Au NPs were then attached to mesoporous TiO2 and ZrO2 films and covered with poly(methyl methacrylate) (PMMA) on top to diminish contact with air, thus mitigating changes in surface moisture and hydroxylation and ensuring signal reversibility and no hysteresis. Blank experiments showed that PMMA itself does not affect the dynamics of the system. The setup used for heating and controlling the temperature is further described in the Supporting Information (SI).

Figure 1.

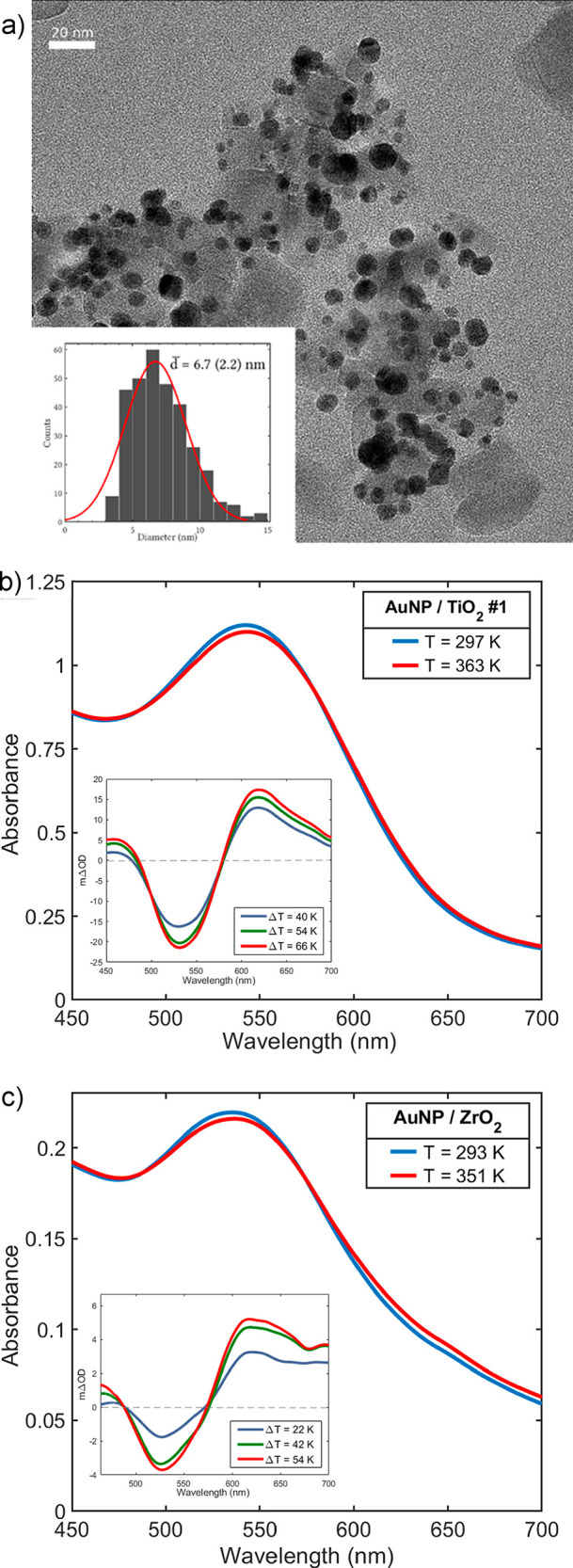
Figure 1

Open in a new tab

Au NP morphology and optical absorbance for different temperatures. (a) TEM image of Au NPs with average size and with inset showing a histogram of size distribution. (b and c) Absorbance spectra of Au NPs attached to TiO2 and ZrO2 for two representative temperatures (inset: difference in absorbance in respect to the one in room temperature).

The static absorbance of Au NPs on TiO2 and ZrO2 (Figure 1b) exhibits a redshift and broadening of the plasmonic peak with a temperature increase. A simple model for the optical properties of metals and the effects caused by the temperature is the Drude model which with the inclusion of an interband transition term εib provides a dielectric permittivity ε(ω) = ε1(ω) + iε2(ω) that can be used to calculate the extinction coefficient of non-interacting spherical metal nanoparticles much smaller than the light wavelength.29 The Drude contribution has the form:

graphic file with name nl0c04419_m001.jpg 1

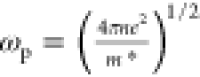where Inline graphic is the bulk plasma frequency, n is the free electron density, m* is the effective mass, and ω is the incident photon frequency. For noble metals, the surface plasmon resonance energy in the nanoparticle can be obtained from ε1(ωsp) = 2εm,29 resulting in

graphic file with name nl0c04419_m003.jpg 2

where εm is the dielectric permittivity of the environment and εib1 is the real part of the interband transition term.

The imaginary term in eq 1 represents the photon absorption by conduction electrons, as described by the average collision frequency Γ which is also known as the plasmon damping. In a bulk-like picture, a photon absorption has to be assisted by a third particle (such as an auxiliary electron, a phonon or a defect) to satisfy energy and momentum conservation. In the absence of defect scattering, the damping term Γ can be split into two contributions, that is, electron–electron (e–e) and electron–phonon (e–ph) scattering terms which depend on ω, the electron gas temperature Te, and the lattice temperature TL:

graphic file with name nl0c04419_m004.jpg 3

In the visible and at room temperature, both the Γe–ph and Γe–e rates are comparable. However, the temperature plays only a minor role for e–e scattering, in contrast to e–ph scattering which can increase by about four times when Au is heated from room temperature to the melting point (∼1340 K). Please see Supporting Information (SI) for details.

In addition to increasing Γe–ph, the thermal expansion of the Au NPs decreases ωsp (eq 2), since the bulk plasma frequency ωp depends on the electron density. Hence, the temperature effect in the absorbance spectra shown in Figure 1b is due to changes in both Γe–ph and electron density. Yeschenko et al.30 analyzed the temperature effect on the surface plasmon resonance of Au NPs in a silica matrix. In their work, they concluded that the plasmon band redshift is caused mainly by thermal expansion, while the broadening is due to the increase in Γe–ph. The change in the dielectric permittivity of the environment εm with temperature was found to be negligible.

To investigate the role of phonons on Au plasmonic hot carrier dynamics and charge transfer at the metal–semiconductor interface, transient absorption spectroscopic studies probing two different spectral regions were performed. These measurements were performed by exciting the sample with a quasi-monochromatic femtosecond pulse at 580 nm, since this wavelength provides a balance between interband transitions excitation31 and variations in Au NPs absorbance change upon external heating (<0.3% variation, inset on Figure 1b). Therefore, the extracted trends with temperature variation can be attributed to temperature and not to changes in sample absorption. A power dependence analysis was also carried out to ensure all the measurements take place within the linear regime, that is, no multiphoton effects.

Ultrafast transient absorption measurements of Au NPs on ZrO2 give rise to the typical features with a bleach region at the absorbance peak and two positives “winglets”17 on its sides both due to e–ph scattering events with a characteristic decay time τe–ph. Zirconium dioxide is an insulator, and no hot electrons can transfer from the Au NP.17 Thus, the hot carrier dynamics on this structure is intrinsic to the Au NP in passive oxide environment. The maximum transient signal intensity reflects the establishment of an electron temperature, which energy is subsequently transferred to the metal lattice through e–ph interactions, leading to thermal equilibrium between the metal electron gas and the lattice.32

Figure 2a shows the time evolution of ΔOD for Au NPs on ZrO2 (AuNPS/ZrO2) probed with a broad light spectrum in the visible region at different laser fluences for T1 = 292 K and T2 = 345 K. The signal decay for each fluence value was fitted with a monoexponential decay function at the bleach peak wavelength (∼540 nm). The derived τe–ph relaxation times for both temperatures versus laser fluence are shown in Figure 2b. The intercepts obtained for T1 and T2 are 0.87 ± 0.16 and 1.31 ± 0.13 ps, respectively. The former is in good agreement with previously reported values for Au NPs at room temperature (∼0.9 ps).33,34

Figure 2.

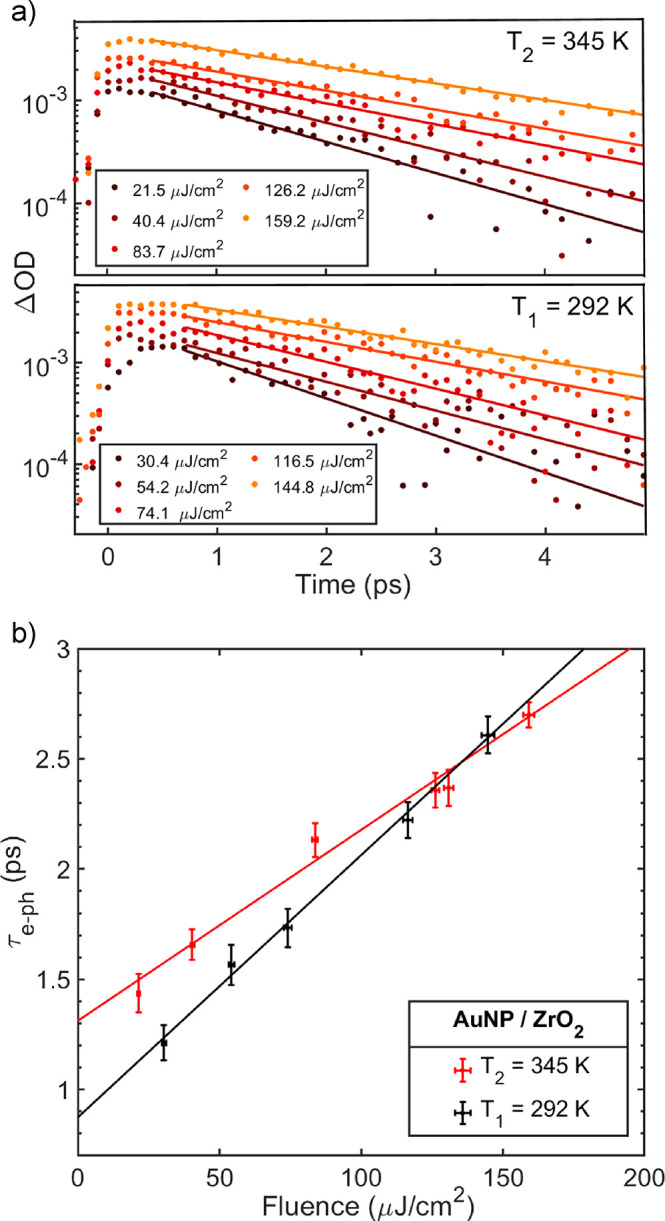
Figure 2

Open in a new tab

Effect of temperature on the transient optical response of Au NPs. (a) Kinetics of the Au/ZrO2 bleach signal at 540 nm for T1 and T2 excited at 575 nm with different fluences. (b) Electron–phonon relaxation time in function of fluence for T1 and T2.

Giri et. al35 have shown that nonthermal electrons significantly alter the e–ph coupling factor G, which quantifies the rate of energy transfer between the electron (thermal and nonthermal) and phonon subsystems. Specifically, at low laser fluences, the e–ph relaxation times are mainly governed by the nonthermal distribution of electrons.

The higher value of τe–ph obtained at T2 in the low fluence limit is a consequence of the reduction of nonthermal electrons owing to the increase in the temperature. In contrast, the shallower slope at T2 reflects a shortened relaxation time compared to T1 at high excitation fluences. In this regime, the population of nonthermal electrons is significantly reduced and τe–ph is smaller than at T1 since the e–ph coupling factor G increases with increasing lattice temperature for a fixed excitation fluence. This can be rationalized as the participation of a broader spectrum of phonon modes enhancing both elastic and inelastic e–ph scattering processes.36

Previous work32−36 focused on the e–ph relaxation dynamics of Au NPs up to room temperature. The present study expands the investigations beyond room temperature but reveals similar behavior, namely that the increase in the temperature leads to faster thermalization of the electrons and subsequent enhancement of the energy-transfer rate between electrons and the lattice. Our limited temporal resolution and probe spectrum range prevent the investigation of the effect of temperature before and during the electron thermalization, which would allow the study of hot carrier generation caused by phonon-assisted plasmon decay.37

Plasmon-induced hot electron injection was investigated through transient infrared absorption spectroscopy (TIRAS). Free carriers have strong absorption in the infrared (IR) spectrum and exhibit a broad featureless signal over the entire mid-IR region38 that decays due to charge recombination. A characteristic temporal profile of TIRAS due to plasmon-induced carrier injection is depicted in the inset of Figure 3a. Figure 3b shows the kinetic trace at 4800 nm for Au/TiO2 and Au/ZrO2, revealing a significant change in IR absorption on the TiO2 upon Au excitation that strongly contrasts with the finding of negligible signal on ZrO2 due to its insulating nature.

Figure 3.

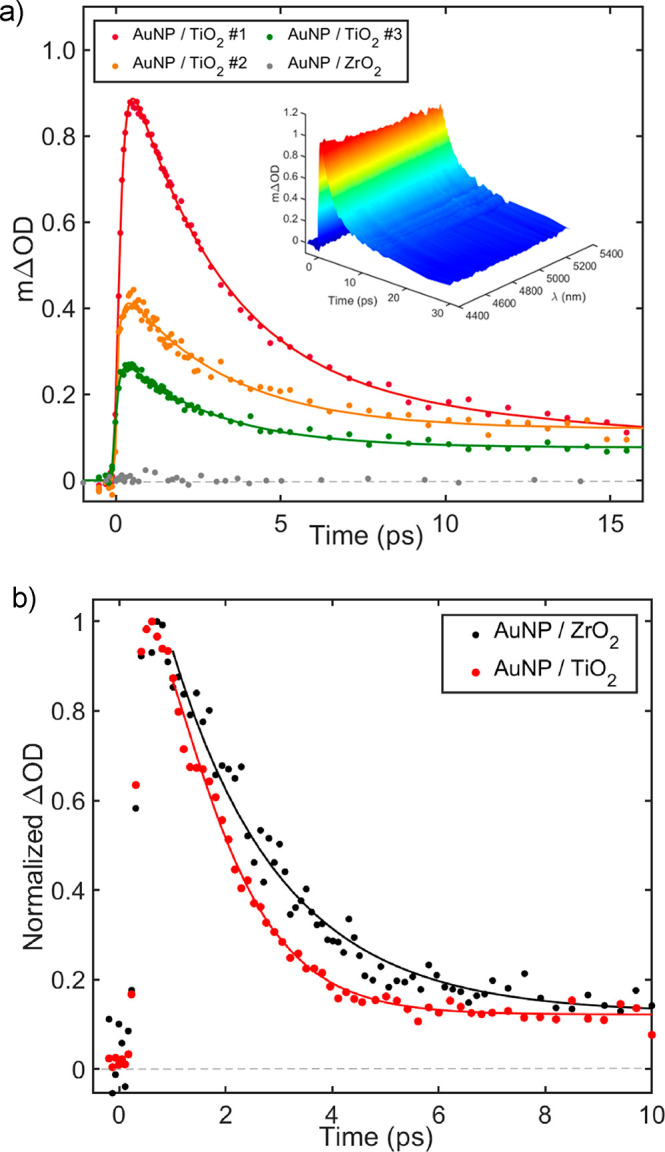
Figure 3

Open in a new tab

Dynamics of hot electron injection into the oxide. (a) TIRAS transient signal extracted at 4800 nm for Au/TiO2 and Au/ZrO2. Inset shows a representative three-dimensional plot of the TIRAS spectra of Au/TiO2 after excitation at 580 nm. (b) Normalized kinetic TAS traces at 540 nm for Au/ZrO2 and for Au/TiO2 excited at 580 nm.

The free carriers detected by TIRAS in the Au/TiO2 system following plasmon excitation can have three origins: (i) plasmonic scattering and trapping; (ii) plasmon-induced energy transformation; and (iii) plasmon-induced hot carrier generation.39,40 Processes (i) and (ii) generate electron–hole pairs directly on the semiconductor, while process (iii) generates hot carriers on the plasmonic structure which subsequently can transfer the semiconductor. The type of injected carrier depends on band alignments which for the present system should be hot electrons injecting into the TiO2 conduction band (CB). Most importantly, processes (i) and (ii) induce electron–hole pair formation directly on the semiconductor. Therefore, if the TIRAS signal is related to the processes (i) and (ii), one should expect some fluorescence related to the radiative recombination of electron–hole pairs created on the semiconductor,41 which we did observe in static and transient mode even when ZnO42 was used instead of TiO2. Additionally, processes (i) and (ii) do not extract charge from the plasmonic structure and consequently should have little to no effect on the TA signal associated with the Au resonance decay. However, as it can be seen in Figure 3b, there is a noticeable difference in the normalized TA signal from Au on an injectable (TiO2) and noninjectable (ZrO2) support, which substantiates the claim that the TIRAS signal originates from the process (iii),that is, injection of plasmon-induced hot carriers into the semiconductor.

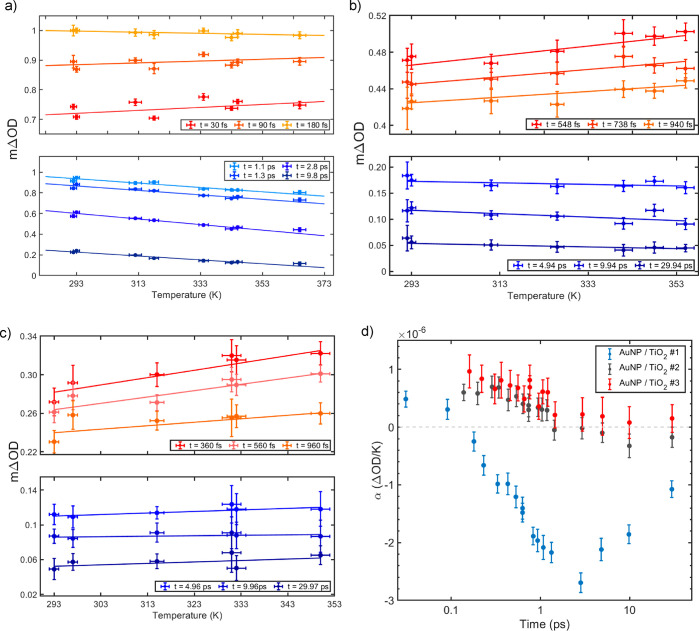
The temporal evolution of the difference in absorption (ΔOD = ODpump – ODunpump) of three samples with different Au NPs loadings is shown in Figure 4. The measurements were taken at a central wavelength of 4800 nm, where a positive signal can be assigned to electrons injected into the CB of TiO2. A linear fitting of the signal as a function of temperature was performed for different time delays (Figure 4). A positive slope α implies a higher number of electrons injected into CB of TiO2 with temperature, and vice versa. An increase in the electron injection in the sample with the highest concentration (#1) is observed only at 30 and 90 fs time delays before recombination becomes important. In contrast, the slope α remains positive for all time delays measured (up to 30 ps) for the lowest Au NPs loading (#3). Note that the values on Figure 4a–c are corrected for time zero after measurement and, therefore, are significant even if the instrument response function is in the order of 95 fs (Figure S1).

Figure 4.

Figure 4

Open in a new tab

TIRAS of Au/TiO2 as a function of temperature. Signal as a function of temperature for different time delays with respect to time-zero of the sample (a) Au/TiO2 #1 (highest loading), (b) Au/TiO2 #2, and (c) Au/TiO2 #3 (lowest loading). (d) Compilation of the slopes α obtained from each sample as a function of time. Positive values of α implies an increase of the number of electrons injected into the CB of TiO2.

The α parameter temporal behavior relates to two distinct photophysical processes, namely electron injection at short time scales and charges recombination of back electrons transfer after 1 ps. With respect to electron injection, it is evident that electron injection increases as gold concentration increases, which is easily understood based on a larger amount of photosensitizer. However, the increase of photosensitizer also increases the density of recombination centers, resulting in a faster decrease of the TIRAS. This becomes even more significant with temperature since increasing the temperature of pure semiconductors will increase the number of conduction electrons and thus increase the conductivity, making it easier for electrons to reach a recombination center, consistent with the kinetics observed in Figure 3a. What is curious is that an increased recombination due to temperature can be significantly suppressed by decreasing the amount of Au NPs, that is, optimizing the number of recombination centers per unit area. Only then the gains in injection due to the increase in operation temperature can be maximized. Note that the reported trends are not related to a difference in local heating due changes in Au NPs concentration because heat release from plasmonic excitation occurs >50 ps (phonon–phonon relaxation time) and dissipates within nanoseconds (phonon–solvent/surrounding relaxation time).7,33 Since we use a 3 kHz system and a pumping scheme that excites only half of the time, the sample is expected to be relaxed every single shot. Moreover, the longer experimental acquisition did not affect signal trends, removing the possibility for low-level local heat-related signals.

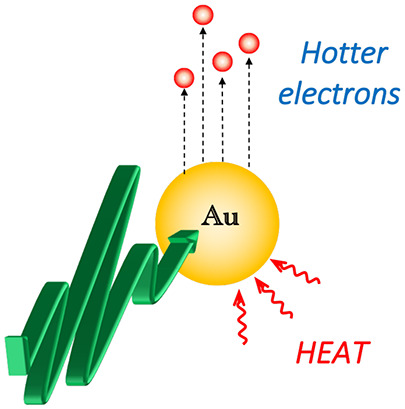
The schematic in Figure 5 shows two possible mechanisms for the observed increase in hot carrier concentration in the semiconductor: (a) phonon-enhanced plasmonic hot carrier generation and (b) phonon-assisted hot carrier transfer across the Au/TiO2 interface barrier. Process (a) can in principle happen because phonon fluctuations increase the phase space for plasmon decay, that is, phonons assist momentum transfer to electrons, thus promoting plasmon decay.24,43−45 The net result is the formation of a higher proportion of injectable charges as the operational temperature increases. Process (b) with phonons transferring energy to already existing hot carriers would promote injection. However, Mahato and Puigdollers46 investigated the effect of temperature on the Schottky barrier of Au–transition-metal oxides in a similar temperature range as here and showed that the Schottky barrier height increases with temperature, thus decreasing the electron injection efficiency. We also noted a negligible temperature dependence of the TiO2 band gap (Figure S12). Theoretical calculations revealed that Schottky barrier is expected to increase with the increase of temperature (Figure S14) consistent with other studies,21 making mechanism (b) less likely. Thus, we believe that the most likely mechanism for the observed increased hot carrier injection is the mechanism (a).

Figure 5.

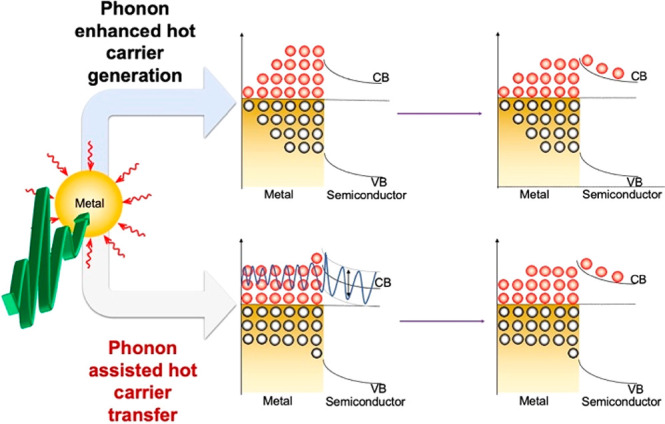
Figure 5

Open in a new tab

Schematic representation of the possible role of phonons for plasmon-induced electron injection. Small red arrows symbolize external heat, and the large green arrow symbolizes the exciting photon that triggers the plasmon.

In conclusion, we have found that an increased temperature results in increased plasmon-induced hot carrier injection into TiO2 in a hybrid Au NP/TiO2 system. Although a definitive experimental validation of the mechanism would require a higher temporal resolution, our combined TAS and TIRAS studies suggest that the origin of this effect is phonon-assisted plasmonic hot carrier formation rather than phonon-promoted hot carrier transfer across the Schottky barrier. This conclusion is further supported by time-domain nonadiabatic molecular dynamics simulations of Au films at different temperatures.35 It is demonstrated that elastic and inelastic e–ph scattering increases with temperature, allowing a larger number of higher-frequency phonon modes to couple to the electronic subsystem. It is further shown that while the inelastic e–ph coupling is largest between near-resonant states, elastic e–ph scattering can be strongest for pairs of electronic states that are energetically distinct. In the context of the emerging interest in plasmon-induced hot carrier applications, our results may be very useful for the development of new strategies to engineer more efficient devices.

Acknowledgments

The authors would like to thank the photovoltaic unit of the Physical Chemistry division, Department of Chemistry-Angstrom, Uppsala University for the access and support using their material preparation systems. The authors would like to thank Uppsala University for financial support. J.S. acknowledges the support by Swedish Research Council (nos. 2015-03764 and 2019-03597). K.Z. acknowledges the support by Danish Council for Independent Research no. 7026-0037B and Swedish Research Council no. 2017-05337. P.N. acknowledges support from the Robert A. Welch Foundation under grant C-1222 and the Air Force Office of Scientific Research (AFOSR) award no. FA9550-15-1-0022.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.0c04419.

  • Detailed description of the sample preparation, structural characterization, transient absorption experiments, and catalytic experiments (PDF)

Author Contributions

J.S. conceived and planned the project in liaison with Y.H. The experimental work was performed by Y.H., J.M., A.M.A., and P.B. Y.H. analyzed and treated the data and prepared the figures in liaison with J.S. The manuscript was drafted by J.S. and Y.H. with input from all authors. The final version was read and agreed on by all the authors.

The authors declare no competing financial interest.

Supplementary Material

nl0c04419_si_001.pdf (1.4MB, pdf)

References

  1. Atwater H.; Polman A. Plasmonics for improved photovoltaic devices. Nat. Mater. 2010, 9, 205–213. 10.1038/nmat2629. [DOI] [PubMed] [Google Scholar]
  2. Brongersma M. L.; Halas N. J.; Nordlander P. Plasmon- induced hot carrier science and technology. Nat. Nanotechnol. 2015, 10, 25–34. 10.1038/nnano.2014.311. [DOI] [PubMed] [Google Scholar]
  3. Sá J.; et al. Direct observation of charge separation on Au localized surface plasmons. Energy Environ. Sci. 2013, 6, 3584–3588. 10.1039/c3ee42731e. [DOI] [Google Scholar]
  4. Linic S.; Christopher P.; Ingram D. B. Plasmonic-metal nanostructures for efficient conversion of solar to chemical energy. Nat. Mater. 2011, 10, 911–921. 10.1038/nmat3151. [DOI] [PubMed] [Google Scholar]
  5. Mubeen S.; et al. An autonomous photosynthetic device in which all charge carriers derive from surface plasmons. Nat. Nanotechnol. 2013, 8, 247–252. 10.1038/nnano.2013.18. [DOI] [PubMed] [Google Scholar]
  6. Pavliuk M. V.; et al. Nano-hybrid plasmonic photocatalyst for hydrogen production at 20% efficiency. Sci. Rep. 2017, 7, 8670. 10.1038/s41598-017-09261-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Pavliuk M. V.; et al. Hydrated electron generation by excitation of copper localized surface plasmon resonance. J. Phys. Chem. Lett. 2019, 10, 1743–1749. 10.1021/acs.jpclett.9b00792. [DOI] [PubMed] [Google Scholar]
  8. DuChene J. S.; et al. Hot hole collection and photoelectrochemical CO2 reduction with plasmonic Au/p-GaN photocathodes. Nano Lett. 2018, 18, 2545–2550. 10.1021/acs.nanolett.8b00241. [DOI] [PubMed] [Google Scholar]
  9. DuChene J. S.; et al. Optical excitation of a nanoparticle Cu/p-NiO photocathode improves reaction selectivity for CO2 reduction in aqueous electrolytes. Nano Lett. 2020, 20, 2348–2358. 10.1021/acs.nanolett.9b04895. [DOI] [PubMed] [Google Scholar]
  10. Garcia de Arquer F. P.; et al. Photoelectric energy conversion of plasmon-generated hot carriers in metal-insulator-semiconductor structures. ACS Nano 2013, 7, 3581–3588. 10.1021/nn400517w. [DOI] [PubMed] [Google Scholar]
  11. Nakamura K.; et al. Properties of plasmons-induced photoelectric conversion on a TiO2/NiO p–n junction with Au nanoparticles. J. Phys. Chem. Lett. 2016, 7, 1004–1009. 10.1021/acs.jpclett.6b00291. [DOI] [PubMed] [Google Scholar]
  12. Hattori Y.; et al. Simultaneous hot electron and hole injection upon excitation of gold surface plasmon. J. Phys. Chem. Lett. 2019, 10, 3140–3146. 10.1021/acs.jpclett.9b01085. [DOI] [PubMed] [Google Scholar]
  13. Lehmann J.; et al. Surface plasmon dynamics in silver nanoparticles studied by femtosecond time-resolved photoemission. Phys. Rev. Lett. 2000, 85, 2921–2924. 10.1103/PhysRevLett.85.2921. [DOI] [PubMed] [Google Scholar]
  14. Tagliabue G.; et al. Quantifying the role of surface plasmon excitation and hot carrier transport in plasmonic devices. Nat. Commun. 2018, 9, 3394. 10.1038/s41467-018-05968-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Hallett-Tapley G. L.; et al. Plasmon-mediated catalytic oxidation of sec-phenethyl and benzyl alcohols. J. Phys. Chem. C 2011, 115, 10784–10790. 10.1021/jp202769a. [DOI] [Google Scholar]
  16. Furube A.; et al. Ultrafast plasmon-induced electron transfer from gold nanodots into TiO2 nanoparticles. J. Am. Chem. Soc. 2007, 129, 14852–14853. 10.1021/ja076134v. [DOI] [PubMed] [Google Scholar]
  17. Tagliabue G.; et al. Ultrafast of hot hole injection modifies hot electron dynamics in Au/p-GaN heterostructures. Nat. Mater. 2020, 19, 1312–1318. 10.1038/s41563-020-0737-1. [DOI] [PubMed] [Google Scholar]
  18. Kahmann S.; Loi M. A. Hot carrier solar cells and the potential of perovskites for breaking the Shockley-Queisser limit. J. Mater. Chem. C 2019, 7, 2471–2486. 10.1039/C8TC04641G. [DOI] [Google Scholar]
  19. Hopper T. R.; et al. Hot Carrier Dynamics in Perovskite Nanocrystal Solids: Role of the Cold Carriers, Nanoconfinement, and the Surface. Nano Lett. 2020, 20, 2271–2278. 10.1021/acs.nanolett.9b04491. [DOI] [PubMed] [Google Scholar]
  20. Myahkostupov M.; et al. Vibrational State Dependence of Interfacial Electron Transfer: Hot Electron Injection from the S1 State of Azulene into TiO2 Nanoparticles. J. Phys. Chem. C 2013, 117, 20485–20493. 10.1021/jp406662n. [DOI] [Google Scholar]
  21. Sadasivam S.; Waghmare U. V.; Fisher T. S. Electron-phonon coupling and thermal conductance at a metal-semiconductor interface: First-principles analysis. J. Appl. Phys. 2015, 117, 134502. 10.1063/1.4916729. [DOI] [Google Scholar]
  22. Shockley W.; Queisser H. J. Detailed Balance Limit of Efficiency of p-n Junction Solar Cells. J. Appl. Phys. 1961, 32, 510–519. 10.1063/1.1736034. [DOI] [Google Scholar]
  23. Nishijima Y.; et al. Plasmon-Assisted Photocurrent Generation from Visible to Near-Infrared Wavelength Using a Au-Nanorods/TiO2 Electrode. J. Phys. Chem. Lett. 2010, 1, 2031–2036. 10.1021/jz1006675. [DOI] [Google Scholar]
  24. Sundararaman R.; et al. Theoretical predictions for hot carrier generation from surface plasmon decay. Nat. Commun. 2014, 5, 5788. 10.1038/ncomms6788. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Wu K.; et al. Efficient hot electron transfer by a plasmon-induced interfacial charge-transfer transition. Science 2015, 349, 632–635. 10.1126/science.aac5443. [DOI] [PubMed] [Google Scholar]
  26. Cushing S. K. Plasmonic hot carriers skip out in femtoseconds. Nat. Photonics 2017, 11, 748–749. 10.1038/s41566-017-0059-2. [DOI] [Google Scholar]
  27. Sykes M. E.; et al. Enhanced generation and anisotropic Coloumb scattering of hot electrons in an ultra-broadband plasmonic nanopatch metasurface. Nat. Commun. 2017, 8, 986. 10.1038/s41467-017-01069-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Piella J.; Bastús N. G.; Puntes V. Size-Controlled Synthesis of Sub-10-nanometer Citrate-Stabilized Gold Nanoparticles and Related Optical Properties. Chem. Mater. 2016, 28, 1066–1075. 10.1021/acs.chemmater.5b04406. [DOI] [Google Scholar]
  29. Kreibig U.; Vollmer M.. Optical Properties of Metal Clusters; Springer: Berlin, 1995. [Google Scholar]
  30. Yeshchenko O. A.; et al. Temperature dependence of the surface plasmon resonance in gold nanoparticles. Surf. Sci. 2013, 608, 275–281. 10.1016/j.susc.2012.10.019. [DOI] [Google Scholar]
  31. Christensen N. E.; Seraphin B. O. Relativistic Band Calculation and the Optical Properties of Gold. Phys. Rev. B 1971, 4, 3321–3344. 10.1103/PhysRevB.4.3321. [DOI] [Google Scholar]
  32. Del Fatti N.; et al. Nonequilibrium electron dynamics in noble metals. Phys. Rev. B: Condens. Matter Mater. Phys. 2000, 61, 16956. 10.1103/PhysRevB.61.16956. [DOI] [Google Scholar]
  33. Logunov S. L.; Ahmadi T. S.; El-Sayed M. A.; Khoury J. T.; Whetten R. L. Electron dynamics of passivated gold nanocrystals probed by sub-picosecond transient absorption spectroscopy. J. Phys. Chem. B 1997, 101, 3713–3719. 10.1021/jp962923f. [DOI] [Google Scholar]
  34. Arbouet A.; et al. Electron-Phonon Scattering in Metal Clusters. Phys. Rev. Lett. 2003, 90, 177401. 10.1103/PhysRevLett.90.177401. [DOI] [PubMed] [Google Scholar]
  35. Giri A.; et al. Experimental evidence of excited electron number density and temperature effects on electron-phonon coupling in gold film. J. Appl. Phys. 2015, 117, 044305. 10.1063/1.4906553. [DOI] [Google Scholar]
  36. Zhou X.; et al. Temperature Dependence of Electron-Phonon Interactions in Gold Films Rationalized by Time-Domain Ab Initio Analysis. J. Phys. Chem. C 2017, 121, 17488–17497. 10.1021/acs.jpcc.7b05211. [DOI] [Google Scholar]
  37. Khurgin J. B. Hot carriers generated by plasmons: where are they generated and where do they go from there?. Faraday Discuss. 2019, 214, 35–58. 10.1039/C8FD00200B. [DOI] [PubMed] [Google Scholar]
  38. Panayotov D. A.; Burrows S. P.; Morris J. Infrared Spectroscopic Studies of Conduction Band and Trapped Electrons in UV-Photoexcited, H-Atom n-Doped, and Thermally Reduced TiO2. J. Phys. Chem. C 2012, 116, 4535–4544. 10.1021/jp2053103. [DOI] [Google Scholar]
  39. Wu N. Plasmonic metal-semiconductor photocatalysts and photoelectrochemical cells: a review. Nanoscale 2018, 10, 2679–2696. 10.1039/C7NR08487K. [DOI] [PubMed] [Google Scholar]
  40. Huang H. J.; et al. Review of Experimental Setups for Plasmonic Photocatalytic Reactions. Catalysts 2020, 10, 46. 10.3390/catal10010046. [DOI] [Google Scholar]
  41. Basheer C. Application of Titanium Dioxide-Graphene Composite Material for Photocatalytic Degradation of Alkylphenols. J. Chem. 2013, 2013, 456586. 10.1155/2013/456586. [DOI] [Google Scholar]
  42. Cieslak A. M.; et al. Ultra long-lived electron-hole separation within water-soluble colloidal ZnO nanocrystals: Prospective applications for solar energy production. Nano Energy 2016, 30, 187–192. 10.1016/j.nanoen.2016.09.045. [DOI] [Google Scholar]
  43. Di Martino G.; et al. Quantum statistics of surface plasmon polaritons in metallic stripe waveguides. Nano Lett. 2012, 12, 2504–2508. 10.1021/nl300671w. [DOI] [PubMed] [Google Scholar]
  44. Besteiro L. V.; Kong X.-T.; Wang Z.; Hartland G.; Govorov A. O. Understanding Hot-Electron Generation and Plasmon Relaxation in Metal Nanocrystals: Quantum and Classical Mechanims. ACS Photonics 2017, 4, 2759–2781. 10.1021/acsphotonics.7b00751. [DOI] [Google Scholar]
  45. Khurgin J. B. Hot carriers generated by plasmons: where are they generated and where do they go from there?. Faraday Discuss. 2019, 214, 35–58. 10.1039/C8FD00200B. [DOI] [PubMed] [Google Scholar]
  46. Mahato S.; Puigdollers J. Temperature dependent current-voltage characteristics of Au/n-Si Schottky barrier diodes and the effect of transition metal oxides as an interface layer. Phys. B 2018, 530, 327–335. 10.1016/j.physb.2017.10.068. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl0c04419_si_001.pdf (1.4MB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES