Non-invasive Prediction of Peak Systolic Pressure Drop across Coarctation of Aorta using Computational Fluid Dynamics

Abstract

This paper proposes a novel method to non-invasively measure the peak systolic pressure difference (PSPD) across coarctation of the aorta for diagnosing the severity of coarctation. Traditional non-invasive estimates of pressure drop from the ultrasound can underestimate the severity and invasive measurements by cardiac catheterization can carry risks for patients. To address the issues, we employ computational fluid dynamics (CFD) computation to accurately predict the PSPD across a coarctation based on cardiac magnetic resonance (CMR) imaging data and cuff pressure measurements from one arm. The boundary conditions of a patient-specific aorta model are specified at the inlet of the ascending aorta by using the time-dependent blood velocity, and the outlets of descending aorta and supra aortic branches by using a 3-element Windkessel model. To estimate the parameters of the Windkessel model, steady flow simulations were performed using the time-averaged flow rates in the ascending aorta, descending aorta, and two of the three supra aortic branches. The mean cuff pressure from one arm was specified at the outlet of one of the supra aortic branches. The CFD predicted PSPDs of 5 patients (n=5) were compared with the invasively measured pressure drops obtained by catheterization. The PSPDs were accurately predicted (mean μ = 0.3mmHg, standard deviation σ = 4.3mmHg) in coarctation of the aorta using completely non-invasive flow and cuff pressure data. The results of our study indicate that the proposed method could potentially replace invasive measurements for estimating the severity of coarctations.

Clinical relevance—

Peak systolic pressure drop is an indicator of the severity of coarctation of the aorta. It can be predicted without any additional risks to patients using non-invasive cuff pressure and flow data from CMR.

I. INTRODUCTION

Coarctation of aorta is a congenital narrowing of the aorta located near or distal to the aortic arch. It represents 5–7 percent [1] of all congenital heart diseases affecting 3 of 10000 newborns every year and occurs with a wide spectrum of severity [2]. Coarctation of the aorta causes increased afterload on the left ventricle, exposure of the upper body to hypertension, flow disturbance in the thoracic aorta, and decreased perfusion to the lower body [2]. If the coarctation is left untreated, it carries the risks of premature coronary artery disease, stroke, endocarditis, aortic dissection and heart failure [3]. Therefore, early diagnosis is crucial to repair the coarctation and prevent accompanied diseases. Typical methods of diagnosis include ultrasound, which can provide limited views of the descending thoracic aorta, and can therefore underestimate the severity or miss the diagnosis of coarctation of the aorta. Cardiac magnetic resonance (CMR) imaging can provide detailed, 3-dimensional images of the aortic arch, but CMR alone cannot assess the pressure drop and therefore cannot judge the severity with accuracy. The gold standard indicator of the severity of coarctation is peak systolic pressure drop (PSPD) across the narrowing which is measured by invasive cardiac catheterization [4] but, this invasive method is associated with several risks to patients [5].

Researchers focused on prediction of pressures and pressure drops in aorta using non-invasive methods. In the study of Shi et al. [4], pressure drop is predicted using magnetic resonance imaging (MRI) flow measurements and Bernoulli equation based friction loss model. However, Bernoulli equation does not include any term that accounts for turbulence which exists in aortic flow and causes additional pressure drop. Other studies investigated computational fluid dynamic (CFD) models to predict pressures in the aorta non-invasively. For example, Zhu et al. [6] utilized CFD based on patient-specific geometry obtained by multidetector computed tomography angiography to predict the peak systolic pressure and peak systolic velocity, then compared these results with invasive pressure measurements and transthoracic echocardiography, respectively. They used lumped parameter model and assumed the same resistance (R) and compliance (C) values for all patients and calculated the peak pressures and velocities in the ascending aorta only. They estimated R and C based on the methods described in [7]–[10] that use pressure curve in the ascending aorta. While the peak pressure and peak velocities in the ascending aorta are important parameters to assess aortic diseases, obtaining the pressure gradient in coarctation cases is crucial [11]. Another study [12] focused on predicting systolic and diastolic pressures and introduced a calibration method for resistance and compliances that are used in the Windkessel models at the inlet and outlets of the model to match systolic and diastolic pressure at the inlet and compared the pressures at various locations calculated by CFD with invasive measurements. The CFD methods that are used in previous studies are based on boundary conditions and/or model parameters obtained invasively. Therefore, defining appropriate conditions at the boundaries estimated using non-invasive methods and developing less complex yet, realistic models are desired.

In this study, we performed CFD analysis of time dependent turbulent flow in the aorta to predict PSPD across a coarctation based on patient-specific aortic geometry, (PC)-CMR flow data, and non-invasive arm cuff pressure measurements. Five patients (n=5) with coarctation of the aorta were included. The systolic and diastolic pressures were measured from one arm of the patients to estimate the mean arterial pressure that is used to specify the boundary condition at the outlet of either the brachiocephalic or left subclavian artery. First, the steady simulations were performed based on time-averaged flows and cuff pressures to predict the mean pressure drop in descending aorta, distal to the coarctation. Unlike previous studies that used invasive pressures to estimate the Windkessel model’s parameters, we used mean pressures obtained from the steady simulations in each branch. Then, transient simulations were run using time-dependent flow rate at the inlet and Windkessel models coupled at the outlets. The contributions of this work include predicting the pressure drop across a coarctation accurately using completely non-invasive data and CFD analysis in multiple cases. We developed a non-invasive PSPD prediction method and validated it by comparing the results with the invasive pressure measurements from five patients.

II. METHODS

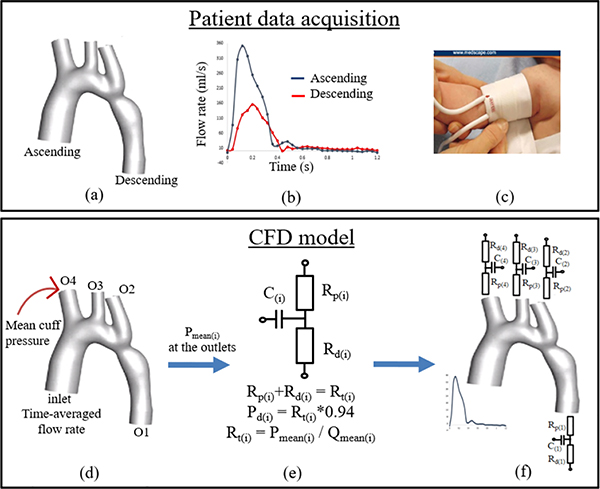
The methodology is summarized in the workflow that is shown in Fig 1. The steps are explained in detail in the subsections.

Fig. 1.

(a) 3-D geometry of aorta after segmentation and smoothing process, (b) time-dependent flow rates in the ascending and descending aorta obtained by CMR, (c) picture of a typical cuff device that is used in infants to measure mean pressure from one arm (right arm in this figure) non-invasively, (d) The model with inlet and outlet (O1, O2, O3, and O4) surfaces where the following boundary conditions are specified: flow rates at the inlet, O1, O2, and O3; and mean cuff pressure at O4 in this example, for steady simulations, (e) schematic of Windkessel model that is used at the outlet boundaries and resistances that are calculated using the mean pressures obtained by steady simulations, and (f) boundary conditions for the transient simulations

A. Patient Data Acquisition

For this study, we selected patients that had a diagnosis of juxtaductal aortic coarctation, with available cardiac MRI (pre-interventional study) and cardiac catheterization pressure measurements (measured during intervention). As a result of selection bias, none of the patients were newborns, as the current clinical standard of care for newborns (those with critical aortic coarctation) is to proceed with surgical repair without any additional diagnostics such as CMR or cardiac catheterization.

1). Geometry:

The geometries of the aortas from 5 patients with coarctations were acquired from CMR imaging data as part of Institutional Review Board (IRB) approved retrospective study. Segmentation of the images to create a three-dimensional (3-D) model was performed using Mimics software (Materialise, Leuven, Belgium). The 3-D aortic geometry shown in Fig. 1(a), included the ascending aorta, aortic arch with three supra aortic branches (brachiocephalic artery, left common carotid artery, and left subclavian artery), and descending aorta. The surface of the model was smoothed after creating the 3-D model to reduce the surface roughness and further smoothing was done using Autodesk Meshmixer software (San Rafael, CA, USA). The format of the aorta models was converted from STL to IGS using Solidworks (Waltham, MA, USA). The boundaries of the models were identified by performing cross-sectional cuts perpendicular to the flow. Lastly, the boundaries were extended between 10 and 30 mm depending on the model to avoid divergence and backflow.

2). Flow:

The time dependent flow rates in the ascending and descending aorta were measured at the cross-sectional planes by 2-D phase-contrast (PC)-CMR. The flow rates in the supra aortic branches were unobtainable. Fig. 1(b) shows an example of flow vs time graph from one of the patients.

3). Non-invasive pressure:

The non-invasive blood pressure measurements were performed using a cuff device right before CMR, as part of routine monitoring. Per clinical standard, in the absence of any significant clinical concern, only one blood pressure measurement was performed per case. Systolic and diastolic pressures from one arm of the patients were measured. Fig. 1(c) shows a cuff device placed on the right arm of an infant. The mean arterial pressure was calculated based on systolic and diastolic pressures [13]. The measured systolic and diastolic arm cuff pressures were 118/71 (left), 103/48 (left), 100/56 (right), 121/72 (right), 97/56 (right) for case 1, 2, 3, 4, and 5, respectively.

B. CFD Model

The 3-D geometries were divided into volumes (Mesh, ANSYS, Canonsburg, PA, USA) with an inflation layer of smaller cells at the aorta walls. The maximum element size was 5×10⁻⁴m and number of inflation layer was 9. ANSYS Fluent was used to solve flow equations written in vector form in (1) and (2) assuming the blood is Newtonian (density=1060 kg/m³, viscosity =0.00371 Pa · s) and the aorta walls are rigid. Spalart-Allmaras turbulence model was chosen to simulate the time-dependent turbulent flow in the aorta. The time step size for the CFD computations was chosen as one fifth of the acquired CMR flow time step size.

$$\frac{\partial \rho }{\partial t}+\nabla (\rho \overrightarrow{u})=0$$ (1)

$$\rho \frac{D\overrightarrow{u}}{Dt}=-\nabla p+\rho \overrightarrow{g}+\nabla {\tau }_{ij}$$ (2)

The blood flow simulations consisted of three steps.

1). Steady simulations:

Steady flow was simulated to calculate mean pressures in ascending aorta and descending aorta. The time-dependent flow rates in the ascending and descending aorta were available from the CMR data, however, flow information in supra aortic branches was unobtainable. Therefore, assumed time-averaged flow splits in previous studies [14] were used to determine the percentage of the inflow that flows out of each supra aortic branch for each model. Mean arterial pressure is obtained via arm cuff measurements. In all of the five patients, coarctations locate distal to the aortic arch. Therefore, we assumed the mean arterial pressure obtained via left arm cuff measurements same as the one in left subclavian artery and can be used as pressure boundary condition at the outlet of left subclavian artery (O2). Similarly, right arm cuff measurements were used to specify pressure boundary condition at the brachiocephalic outlet (O4). All of the five patient datasets that are included in this study had either left or right arm cuff measurement, therefore, only at one outlet, pressure was specified and at other boundaries, flows were specified for steady simulations. Fig. 1(d) shows the boundary conditions for the steady simulations.

2). Estimation of Windkessel model parameters:

The mean pressures were obtained in ascending and descending aorta, and each of the branches from the steady simulations. The pressure differences in ascending aorta and supra aortic branches (O2, O3, and O4) were negligible. The total resistance (R_t) is calculated as the ratio of mean pressure to mean flow rate in each aortic brach [12]. The proximal (R_p) and distal resistances (R_d) that are used in the 3-element Windkessel models at the outlets were estimated as approximately 6 and 94 percent of the R_t [7]. The compliance (C) of each aortic branch were adapted from previous studies [15]. The schematic of the Windkessel model is shown in Fig. 1(e). In the 3-element Windkessel model, the flow and pressure relationship is given by the equation below.

$$P_i=\left(R_{p,i}+R_{d,i}\right)Q_i-R_d{C}_i\frac{d{P}_i}{dt}+R_{p,i}{R}_{d,i}{C}_i\frac{d{Q}_i}{dt}$$ (3)

where i represents each outlet.

3). Transient simulations:

The transient simulations were performed with the time-dependent velocity specified at the ascending aorta inlet and 3-element Windkessel model specified at each outlet. The boundary conditions for transient simulations were shown in Fig. 1(f). Simulations were run until they converge, 5–15 cardiac cycles.

III. EXPERIMENTS AND RESULTS

A. Invasive Measurements

The actual pressure drops across the coarctations were measured by cardiac catheterization. Pressure vs. time curves acquired during the catheterization procedure for the patients within 6 months of the CMR and cuff blood pressures. There is normal human respiratory variation to invasive measurements of blood pressure [16] so, by convention, the lowest peak systolic measurements from the ascending and descending aortas were used to calculate the invasive pressure drop.

B. Validation

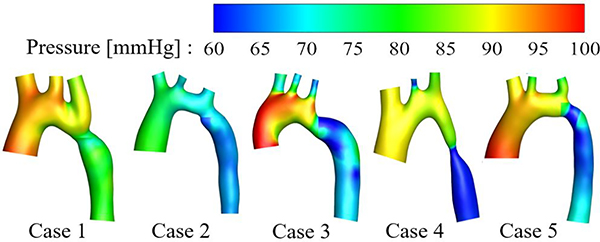
The peak pressure drop between ascending and descending aorta of 5 patients diagnosed with coarctation were obtained by subtracting the peak systolic pressure in the descending aorta from the ascending aorta, as detailed above. The engineer who performed segmentation and who performed CFD analysis were blinded to the invasive pressure measurements before and during the computations. The pressure distributions were shown in Fig 2. The CFD results of PSPD were compared with the invasively measured cardiac catheterization data and shown in Table I. The peak pressures in ascending (AAo) and descending aorta (DAo) were also included in Table I. The PSPD differences between CFD and invasive measurements were less 5.5 mmHg. The mean difference was μ =0.3mmHg and the standard deviation was σ = 4.3mmHg. The peak pressure differences in AAo were less than 12, in DAo were less than 15 percent.

Fig. 2.

Pressure distributions in five aortas with coarctation. Since the peak pressure occurs at different times in AAo and DAo, the pressure distributions of the areas proximal and distal to the coarctation were individually extracted at their respective peak times and juxtaposed for visualization.

TABLE I.

The Comparison of CFD Results and Invasive Measurements of Peak Pressure Drop and Peak Pressure in Ascending and Descending Aorta

		Case 1	Case 2	Case 3	Case 4	Case 5
PSPD (mmHg)	CFD	16.4	15.3	29.0	29.1	26.3
	Invasive	16.8	17.8	25.0	34.0	21.0
	Difference	−0.4	−2.5	4.0	−4.9	5.3
	Difference(%)	2.4	15.1	14.8	15.5	22.4
Peak pressure in AAo (mmHg)	CFD	98.2	81.3	97.6	91.1	98.4
	Invasive	87.6	89.6	98.2	94.0	91.0
	Difference	10.6	−8.3	−0.6	2.9	7.4
	Difference(%)	11.4	9.7	0.6	3.1	7.8
Peak pressure in DAo (mmHg)	CFD	81.8	66.0	68.6	62.0	72.0
	Invasive	70.8	71.8	73.2	60.0	70.0
	Difference	11.0	−5.8	−4.6	2.0	2.0
	Difference(%)	14.4	8.4	6.4	3.2	2.8

IV. DISCUSSION

The flow and cuff pressure measurements were used to obtain the boundary conditions of the CFD model. The CMR flow, invasive pressure, and non-invasive cuff pressure were measured within 6 months, not simultaneously. Invasive pressure measurements were performed while the patients were sedated but the cuff pressure measurements did not require sedation. These may cause the discrepancies between the CFD predicted and invasively measured results shown in Table I. However, CFD predicted peak pressure drops differ less than 5.5 mmHg from the actual measurements.

Additional reason for the discrepancies may be the amplification of the peak pressure moving from aorta to brachial artery [17]. This explains rather large difference in peak pressures in the AAo and DAo. We used cuff pressure measured from the arm (i.e. brachial artery) at one of the outlets for steady simulations to avoid modeling the arterial tree until the arm to simplify the calculations since the purpose was to predict the pressure drop, not the exact pressures in ascending and/or descending aorta.

The cardiac catheterization measurement can vary by 5 – 10 mmHg due to effects of inspiration and expiration; thus measurement variability within this range is considered acceptable. From a clinical standpoint, the widely accepted indication for intervention or re-intervention of the aortic arch is a peak systolic pressure difference greater than 20 mmHg. Thus, in our cases, the CFD results were in clinical agreement with the cardiac catheterization measurements.

Lastly, this study specifically focused on the coarctation cases to demonstrate the use of CFD based on non-invasive cuff pressure measurements and CMR data to predict peak systolic pressure drop. In a future study, we will use this methodology to focus on the management of coarctation in different regions of the aortas.

V. CONCLUSIONS

The goal of this study was to predict the peak systolic pressure drop due to coarctation of the aorta based on non-invasive flow rate and pressure measurements using CFD. Five clinical cases were included. The invasive pressure measurements were available for each case and used only to compare the CFD results.

CFD predicted peak pressure drops showed good agreement with the invasive measurements. The mean prediction accuracy was within 0.3±4.3 mmHg. The differences were less than 5.5 mmHg. The peak pressures in AAo and DAo were also predicted with 11.4 and 14.4 percent accuracy, respectively.

Our findings show that the peak pressure drop across a coarctation can be accurately predicted based on CMR flow and arm cuff pressure data using CFD. This non-invasive PSPD prediction method could potentially replace the invasive measurements that carry additional risks to patients and help doctors to evaluate the severity of the coarctation in order to make a decision of intervention.