Context-aware dimensionality reduction deconvolutes gut microbial community dynamics

Abstract

The translational power of human microbiome studies is limited by high inter-individual variation. We describe a dimensionality reduction tool, compositional tensor factorization (CTF), that incorporates information from the same host, across multiple samples, to reveal patterns driving differences in microbial composition across phenotypes. CTF identifies robust patterns in sparse, compositional datasets, allowing for the detection of microbial changes associated with specific phenotypes that are reproducible across datasets.

Host-associated microbiomes are often host-specific, with the subject driving the majority of the variation. This host-specific variation can obscure microbial changes that are broadly associated with a given phenotype. Collecting multiple samples from the same participant, either longitudinally or from different body sites (i.e., “repeated measures”), is a valid experimental approach to control for inter-individual variation. However, there are multiple challenges to leveraging this type of experimental design due to the nature of microbiome sequencing datasets.

One common way to explore microbiome sequencing data is by performing dimensionality reduction on a distance matrix (e.g. principal coordinates analysis (PCoA)), which describes the relationship among samples, allowing global differences across a dataset to be observed. Nonetheless, when applied to repeated measures, this approach does not account for the inherent temporal or spatial correlation structure. An alternative to analyze repeated measures microbiome data is by using supervised methods, which are focused on generative models inferring the dynamics of these communities (e.g., generalized Lotka Volterra)^1–4. Although these methods account for the correlation structure induced by repeated measures, as well as for sparsity and compositionality, their output does not directly allow clustering of phenotypes by microbial community dynamics.

To address these challenges simultaneously, we developed compositional tensor factorization (CTF), which allows an unsupervised dimensionality reduction for repeated measures data, producing both a traditional beta-diversity analysis as well as a differential feature abundance assessment. In the first step, a two-dimensional matrix is transformed using the robust, centered-log-ratio technique⁵ to account for the inherent sparse and compositional nature of next-generation sequencing datasets⁶ (Fig. 1a). Next, this transformed matrix is restructured into a three-dimensional tensor, which relates microbial sequences, sampled host (or subject), and time or space (Fig. 1b). Decomposition (i.e., factorization) of this tensor provides distinct vectors for subjects (“U”), microbial features (“V”), and timepoints (“W”) (Fig. 1c). Analogous to the concept of reference frames⁷, these vectors are unit-scaled and therefore can be ordered, where their ranking indicates their association to the underlying phenotypic groups. From here on we will refer to the ordering of these vectors as ‘rankings’ (i.e., “feature rankings”). Notably, CTF assumes the data harbors an underlying low-rank structure, where only a few phenotypic factors explain the majority of the variance⁵ (Fig. 1d–g).

Figure 1. Overview of the CTF algorithm.

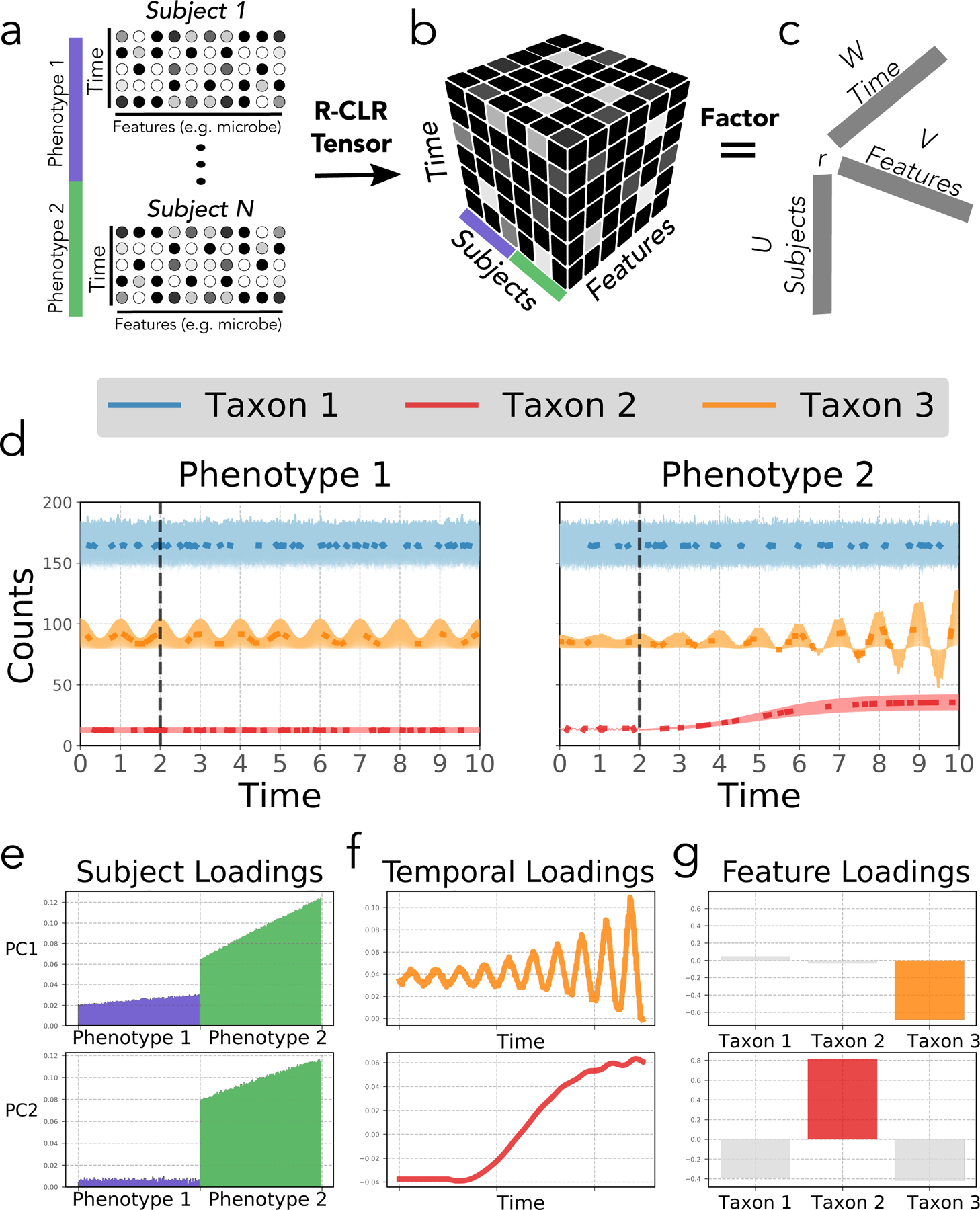
(a) CTF utilizes feature abundance matrices for subjects over time. For each subject with a phenotype of interest, the data is represented as relative abundances of features (abundance gradient represented in grayscale) over time. (b) The matrices are concatenated, robust-centered log-ratio transformed (R-CLR) and structured into a tensor format with modes corresponding to subjects, features and time. (c) The resulting tensor is then factored based only on observed data into loading vectors for each dimension (i.e. subject, timepoint, and feature). (d) Simulated count data is plotted on the y-axis for three taxa with the mean counts in bold and missing values absent from the bold line. Standard deviation of distributions are shaded behind. Two phenotypes are compared; a control unchanging in time (left) and a dynamic phenotype with a perturbation at time point 2 (right). Taxon 1 (blue) is highly abundant and noisy, taxon 2 (red) is lowly abundant but growing exponentially in phenotype 2, and taxon 3 (orange) is oscillatory with increasing amplitude in phenotype 2. The first two principal component axes (i.e. loadings) from CTF (PC1 (top) and PC2 (bottom)) are plotted on the y-axis with the corresponding sample (e), time (f), and feature loadings (g). In PC1, phenotype 2 is linked to the unstable oscillatory waveform of highly loaded taxon 3 (orange, top). Similarly, in PC2, phenotype 2 is linked to the sigmoidal waveform of highly loaded taxon 2 (red, bottom).

To demonstrate the utility of CTF, we applied it to a simulated longitudinal dataset with two phenotypic groups. Simulations were generated based on distributions in real longitudinal 16S data from Halfvarson et al.⁸ while varying the sequencing depth and temporal sampling densities as described by Äijö et al.³ This dataset was chosen because there were strong differences in microbial composition and beta diversity between subjects with and without Crohn’s disease⁸.We compared CTF to state-of-the-art beta-diversity metrics through PCoA including Jaccard⁹, Bray Curtis¹⁰, Aitchison¹¹, unweighted UniFrac¹², and weighted UniFrac¹³. K-nearest neighbor (KNN) classification by disease state in each of our simulations revealed that CTF exhibited higher accuracy than existing methods regardless of sequencing depth or the number of longitudinally collected samples (Fig. 2, Supplementary Table 1, Supplementary Fig. 1). CTF also exhibited higher discriminatory power by PERMANOVA F-statistic across all levels of sequencing depth and at higher sampling densities (≥time points; Fig. 2).

Figure 2. CTF outperforms popular distance metrics in longitudinal in silico data-driven simulations.

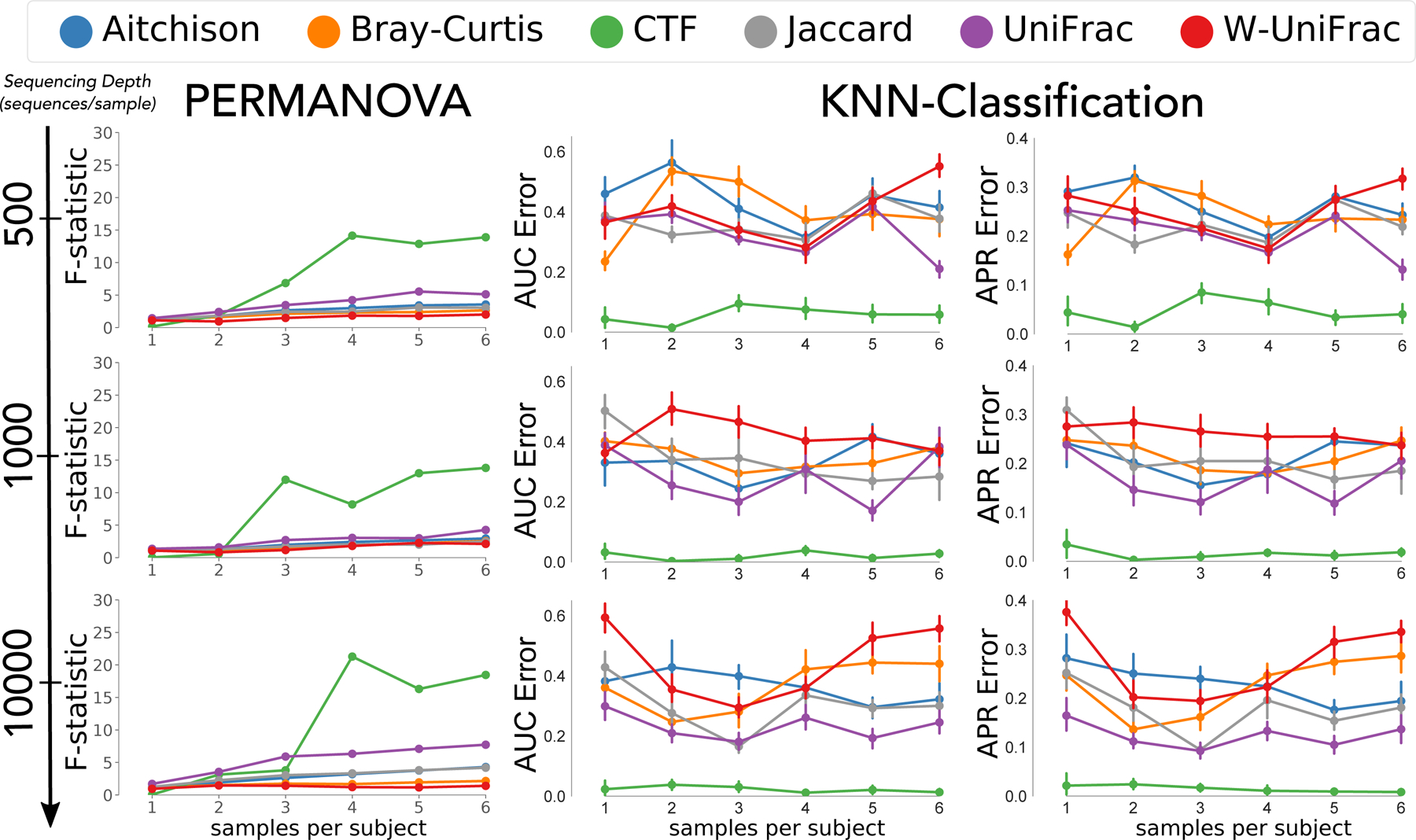
Increasing sequencing depth (500 – 10,000; rows) over differing temporal sampling densities (x-axis) evaluated for PERMANOVA F-statistic as a measure of discriminatory power (left column), in addition to KNN-classification cross-validation by AUC (n=100; middle column), and APR (n=100; right column). Compared among CTF (green) and popular distance metrics Aitchison (blue), Bray-Curtis (orange), Jaccard (grey), unweighted (purple), and weighted (red) UniFrac. Error bars represent standard error of the mean.

We next applied CTF to two published datasets that tracked infant gut development over time. The datasets abbreviated as ECAM (n-subjects=43)¹⁴ and DIABIMMUNE (n-subjects=39)¹⁵ followed infants for the first 2 and 3 years of life, respectively. Both datasets observed that birth mode (i.e., vaginal delivery or caesarean section) differentiated microbial community composition. Similar to our results from the simulated data, CTF is 10-fold better at discriminating vaginally from caesarean born infants compared to state-of-the-art beta-diversity metrics (Supplementary Fig. 2a&b, Supplementary Fig. 3a&b, Supplementary Table 2).

We sought to examine CTF’s ability to reproducibly identify differentially abundant microbes in an unsupervised manner. To this end, we compared the feature rankings between the ECAM and DIABIMMUNE datasets along the first axis of variation and found they were significantly correlated (Pearson correlation; R²=0.974, P<10⁻¹⁰) (Supplementary Fig. 2). While these 2 datasets had <50% overlap at the sOTU level (Supplementary Fig. 2d), highly ranked sOTUs grouped at the genus level were similar across both datasets (Supplementary Fig. 2e). We note that although these datasets were collected and processed using distinct protocols and by different labs, CTF identified the same taxa driving gut microbiome differentiation by birth mode, suggesting a robust microbial structure across infants.

We constructed a birth-mode log-ratio of vaginally to cesarean features using the sOTUs most associated with vaginal and cesarean birth in each dataset (Supplementary Fig. 4; Methods). Samples were significantly separated by birth-mode in both datasets along time (Supplementary Fig. 5, Supplementary Table 3). We note that these birth-mode microbial signatures are not confounded by established differentiators such as antibiotics usage or feeding mode (Supplementary Fig. 5). Nonetheless, we cannot rule out the possibility of unmeasured confounders. We next combined those sOTUs common to both ECAM and DIABIMMUNE birth-mode ratios to create a ‘microbial birth-mode signature’.

To examine the robustness of this microbial birth-mode signature, we tested its discriminatory ability in data from the American Gut Project (AGP, n=8,099), a large cross-sectional dataset¹⁶. We found that this signature significantly differentiated participants under the age of four by birth mode (t-test; p-value=0.042; Supplementary Fig. 6), consistent with our previous findings. The robustness of this microbial signature, across multiple datasets, highlights the ability of CTF to identify differentially abundant features reproducibly associated with a phenotype.

In both the ECAM and DIABIMMUNE datasets we observed that throughout infant development samples from vaginally versus cesarean born infants became less distinct (Supplementary Fig. 2a&b). Similarly, the microbial birth-mode signature no longer differentiated participants by birth mode in samples from participants above the age of four in the AGP dataset (Supplementary Fig. 6).

CTF is the only unsupervised method that allows full utilization of repeated measures while accounting for the inherent properties of microbiome sequencing datasets, namely high-dimensionality, sparsity, and compositionality. In both simulated and real datasets, CTF outperformed the current state-of-the-art beta-diversity metrics. Although CTF can reveal robust microbial signatures, several considerations are necessary when applying this tool. First, CTF relies on an assumption that the underlying data is of low rank. This assumption can be violated, making CTF inappropriate to use, such as when the data are driven by a gradient rather than discrete groupings (for example the 88 Soils dataset¹⁷). Our implementation of CTF estimates the underlying rank and informs the user if the data does not meet this requirement¹⁸. Second, CTF, like other beta-diversity metrics, does not directly account for the presence of confounders that may affect downstream clustering, requiring additional validations similar to the one presented in Supplementary Fig. 5. Finally, although CTF leverages repeated measures to account for inter-individual variation and is optimal in the case of a synchronization event (e.g., treatment, diet), it is permutation invariant and does not take into account the ordering of longitudinal data.

In addition to longitudinal datasets as benchmarked here, CTF could also be used for spatially repeated measurements. This includes studies where samples are collected contemporaneously, for example where multiple body sites are measured (e.g., skin and saliva) or sites with different phenotypes (e.g., lesioned versus adjacent non-lesioned skin). Furthermore, CTF could be used to analyze other types of datasets that contain a high amount of inter-individual variation, such as metabolomics or proteomics. In summary, CTF leverages the power of repeated measures study design to elucidate biological changes while accounting for inter-individual variability. We propose the use of this tool both for the re-analysis of existing datasets and for future microbial community research.

Methods

Preprocessing with robust-clr.

Prior to running tensor factorization, we use the robust centered log-ratio transformation (robust-clr) to center the data around zero and approximate a normal distribution⁵

$$\mathit{\text{rclr}}\left(x\right)=\left[\text{log}\frac{x_1}{g_r\left(x\right)},\cdots ,\text{log}\frac{x_D}{g_r\left(x\right)}\right]$$ (1)

$$g_r\left(x\right)={\left(\prod _{i\in {\mathrm{\Omega }}_x}{x}_i\right)}^{1/\left|{\Omega }_x\right|}$$ (2)

where x_i is the abundance of microbe i, Ω_x set of observed microbes in sample x and g_r(x) is the geometric mean only defined on microbes with abundance > 0. Unlike the traditional clr transformation, the robust-clr handles the high level of sparsity found in microbial datasets without requiring imputation. Furthermore, this transformation has shift invariant properties that allow the restructuring of the matrix into tensor form.

Tensor factorization via alternating least squares minimization.

Here we follow the tensor notations of Lim²² and Anandkumar et al.²³, for a full notation see the Supplementary Discussion. To perform tensor factorization on sparse data we followed a procedure introduced by Jain and Oh²⁴. Due to the high level of sparsity in microbiome datasets we would like to find the minimum rank representation of T that best explains only observed values defined as Ω. We use the projection P_Ω(T)_ijt

$$P_{\mathrm{\Omega }}{\left(T\right)}_{ijt}=f\left(x\right)=\{\begin{array}{ll}{T}_{ij},\hfill & if\left(i,j,t\right)\in \mathrm{\Omega }\hfill \\ 0,\hfill & \mathit{\text{Otherwise}}\hfill \end{array}$$ (3)

The objective function being optimized through alternating least squares minimization (ALS) is given by

$$\underset{\left\{{\sigma }_i,a_i,b_i,c_i\right\}i\in \left[r\right]}{\text{min}}\parallel P_{\mathrm{\Omega }}\left(T\right)-P_{\mathrm{\Omega }}\left(\sum _{i=1}^r\sigma i\left(a_i\otimes b_i\otimes c_i\right)\right){\parallel }_F^2$$ (4)

where a, b, and c are unstructured, orthogonal, and have a Euclidean norm of 1. The low rank representations a, b, and c correspond to loadings for the first, second and third tensor modes respectively. It is important to note that this factorization is permutation invariant, meaning the order of time or space is not a factor in the subsequent loadings of c.

Factorization trajectories.

Here, we focus on the interpretation of tensor factorization for biological data. We are primarily concerned with 3rd-order tensors from studies following multiple subjects over several timepoints. In this tensor the first mode is the subjects or environments sampled. The second mode is biological features such as microbes, metabolites, or genes. The third mode is timepoints where subjects/environments were sampled repeatedly. Of utmost interest is the relation between subject or features and the third mode of time. To obtain easily interpretable loadings we introduce trajectories given by

$$\mathit{\text{Subject}}\mathit{\text{Trajectory}}=a\odot c=\left[a_1\otimes c_1,\cdots a_r\otimes c_r\right]\in {ℝ}^{d^2\times r}$$

$$\mathit{\text{Feature}}\mathit{\text{Trajectory}}=b\odot c=\left[b_1\otimes c_1,\cdots b_r\otimes c_r\right]\in {ℝ}^{d^2\times r}$$

where ⊙ represents the Khatri-Rao product. These trajectories are of the shape (subjects × time, rank) or (features × time, rank) where each rank-1 column has an accompanying singular value σ_r

Log-ratio feature selection.

In order to explore how feature rankings in b or b ⊙ c partitioned subjects we used log-ratios between highly (positive) and lowly (negative) ranked features along the first axis of variation. To avoid the use of pseudo-counts we explore the sum of the minimum number of highly and lowly ranked features summed across all samples, such that no log-ratio contains a zero value. For ECAM 1400 and DIABIMMUNE 750 total features were used and split between numerator and denominator evenly such that no samples were dropped due to zero values (Fig S5). We then used a Linear Mixed Effects (LME) model via statsmodels (v. 0.11.0) to test the if the log-ratio changed over time and in response to birth mode for ECAM and DIABIMMUNE separately. The LME model produced residual R² values of 0.976 and 0.986 for DIABIMMUNE and ECAM respectively. The resulting p-values from the LME were significant (P < .05) by birth mode, time in days, and the interaction of the two (Supplementary Table 3). To produce the microbial birth-mode signature, we used only sequences shared among ECAM, DIABIMMUNE, and the American Gut Project (1,064 features total). We used the ranking structure inferred from ECAM and DIABIMMUNE to evenly divide these shared features into vaginal or cesarean-associated taxa (532 each in the numerator and denominator, respectively). A t-test via SciPy (v. 1.4.1) was used on the microbial birth-mode signature (i.e., log-ratio) to test for significance between birth modes stratified by age or time point for both data sets, respectively.

Data driven simulation benchmarks.

Data driven simulations were designed to benchmark different characteristics of data without making assumptions about microbial dynamics. The IBD dataset was chosen due to its high temporal resolution and two-group (low-rank) comparison. Simulations were generated using a procedure from Äijö et al.³ modified to use a Poisson-lognormal distribution (PLN)²⁵ as opposed to a Poisson-Multinomial distribution. This simulation was repeated for different levels of dispersion, subsampling (i.e. sparsity), sampling density (i.e. number of timepoints) and percentage of randomly missing samples.

Case Study Sequence Processing.

Raw sequences were quality controlled, trimmed at 100 nucleotides, and clustered as amplicon sequence variants (sOTUs) using QIIME 2 release 2019.7 and Deblur (v. 1.1.0)^26,27. The phylogenetic tree was created using SEPP sequence insertion with the Greengenes tree 13.8 release as the reference tree^28,29. Taxonomy assignments were made using a Naive Bayes classifier as implemented in QIIME2 (v. 2019.7). All data preprocessing was conducted on Qiita³⁰ where all the data used here is freely available. All other visualizations were plotted through Matplotlib.

Quantitative comparison of metrics.

All comparisons were made between Jaccard, Bray-Curtis, Weighted UniFrac, Unweighted UniFrac, Aitchison, and CTF distances. All distance metrics were calculated through QIIME2 (v. 2019.7). PERMANOVA on distances between subject groupings (i.e. vaginal vs. caesarean birth mode) was performed through scikit-bio (v. 0.5.5). Dimensionality reduction on distances was performed through PCoA via scikit-bio (v. 0.5.5). The first three components of each dimensionality reduction were evaluated through k-nearest neighbors (KNN) classification via scikit-learn (v. 0.21.2). To assess the classification accuracy, KNN classification was performed with 100-fold 40:60 cross-validation evaluating AUC and APR prediction accuracy at each fold-iteration via scikit-learn (v. 0.21.2).

Basis for simulations.

Halfvarson et al. The IBD cohort used as the introduction example is a previously published dataset by Halfvarson et al. (Qiita ID 1629)⁸. The dataset consists, after filtering as described below, of 23 subjects (14 Crohn’s disease (CD), 9 Control) each with one to eight samples for a total of 134 samples. Samples were filtered from the original data for only CD and Control. For the data-driven simulations, only the first 6 time points were retained to reduce the missing time points across subjects. The resulting data was then run through the data-driven simulation protocol described above for a sequencing depth of 500, 1000, and 10000 mean reads per sample. CTF was performed on each simulated data set through gemelli (v. 0.0.5) with a set rank of 2.

Case study: ECAM.

The ECAM dataset published by Bokulich et al. followed 43 infants (19 c-section, 24 vaginally delivered) from birth over the first year of life with monthly fecal sampling (Qiita ID 10249)¹⁴. Three months (month 6, 15, and 19) were removed for a lack of subjects represented and CTF analysis was run with a set rank of 2. Features with < 5 total counts across samples were filtered. Samples with < 2000 reads per sample were removed.

Case study: DIABIMMUNE.

The DIABIMMUNE dataset, published by Yassour et al., followed 39 infants (4 c-section, 35 vaginally delivered) from the 2nd month after birth over the first three years of life with monthly fecal sampling (Qiita ID 11884)¹⁵. Two months (month 28 and 30) were removed for a lack of subjects represented and CTF analysis was run with a set rank of 4. Features with < 5 total counts across samples were filtered. Samples with < 2000 reads per sample were removed.

Case study: American Gut.

The American Gut Project data and metadata tables were acquired from ftp://ftp.microbio.me/AmericanGut/manuscript-package/ which was provided in McDonald et al.¹⁶. From this data the combined ECAM and DIABIMMUNE log-ratio feature set was used on the subset of the data with age and birth-mode labels provided (8,436 total samples).