Abstract
The x-z cross-sectional profiles of fluorescent objects can be distorted in confocal microscopy, in large part due to mismatch between the refractive index of the immersion medium of typical high numerical aperture objectives and the refractive index of the medium in which the sample is present. Here, we introduce a method to mount fluorescent samples parallel to the optical axis. This mounting allows direct imaging of what would normally be an x-z cross-section of the object, in the x-y plane of the microscope. With this approach, the x-y cross-sections of fluorescent beads were seen to have significantly lower shape-distortions as compared to x-z cross-sections reconstructed from confocal z-stacks. We further tested the method for imaging of nuclear and cellular heights in cultured cells, and found that they are significantly flatter than previously reported. This approach allows improved imaging of the x-z cross-section of fluorescent samples.
Keywords: Nucleus, Refractive index mismatch, Nuclear height, X-z imaging, Vertical cross-section
Introduction
Confocal fluorescence microscopy has been the technique of choice to visualize x-z or axial cross-sectional views (i.e. images in a plane parallel to the optical plane) of microscopic fluorescent objects, using image slices acquired in the focal plane. However, reconstructed x-z cross-sectional profiles of fluorescent objects which are the size of several microns can be distorted in confocal microscopy [1, 2]. These distortions are caused largely by the mismatch between the refractive indices of the medium in which the sample is present and the oil present on typical oil-immersion objectives. The mismatch causes differences between axial travel of the objective relative to the sample and travel of the focal plane in the sample itself, resulting in distortion of the x-z shapes. Also, refractive-index mismatch causes the axial resolution to worsen and peak intensity to decrease with travel into the sample.
Methods to correct for the mismatch have been proposed including the use of water-objective lenses and the calculation of correction factors [1, 3–5]. Other recent approaches include the use of prisms to deflect light in such a way that the x-z cross-section can be directly imaged [6, 7]. Here we developed an approach to image x-z shapes of fluorescent objects, which does not require scaling with correction factors or extra devices like prisms in the light path. We designed an imaging chamber in which samples could be mounted along a plane perpendicular to the focal plane, effectively making what would normally be a measurement in the x-z plane, into a measurement in the x-y plane. Imaging of the x-y cross-sections of spherical polystyrene beads immersed in mounting medium with an oil-immersion objective revealed a substantial reduction in distortion. We further tested the chamber for imaging cells and nuclei.
Results
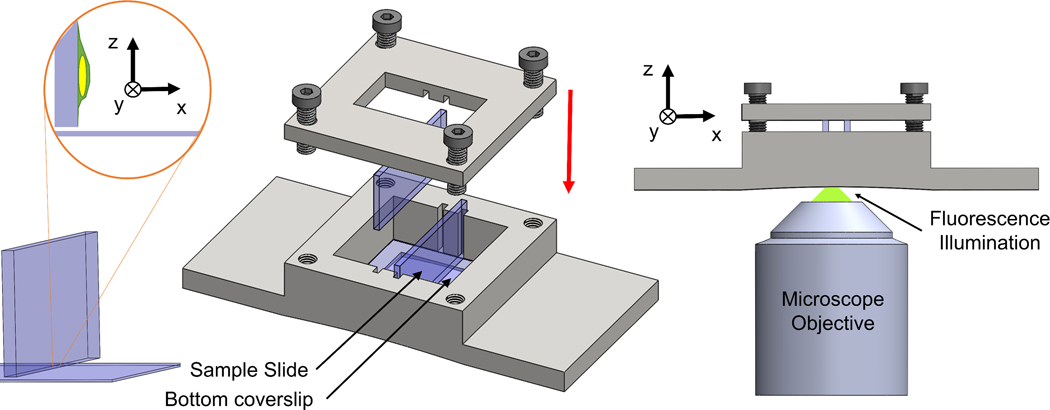
A schematic of our mounting approach is shown in Fig 1. A 3D-printed chamber was designed to hold two glass slides perpendicular to the focal plane. The microscope objective was focused near the bottom edge of the glass slide and the region was scanned to image fluorescent objects. In this setup, the glass slide is held parallel to the optical axis of the microscope, allowing us to image the cross-section orthogonal to the glass slide in the x-y plane (this cross-section would normally be the x-z cross-section reconstructed from confocal z-stacks). The light path in our setup was such that the light from the objective lens passed through the coverslip and into the glycerol-based mounting media before exciting the fluorophores in the sample.
Figure 1. Schematic of the orthogonal imaging chamber.
3D-printed chamber holds slides in an orientation perpendicular to focal plane. Glass slides are slotted vertically in the grooves along the walls of the chamber. A lid is tightened to push the glass slides against the bottom coverslip with threaded screws. A window is provided in the lid to enable transmitted light microscopy. A photo of the imaging chamber (total length = 75 mm) is included.
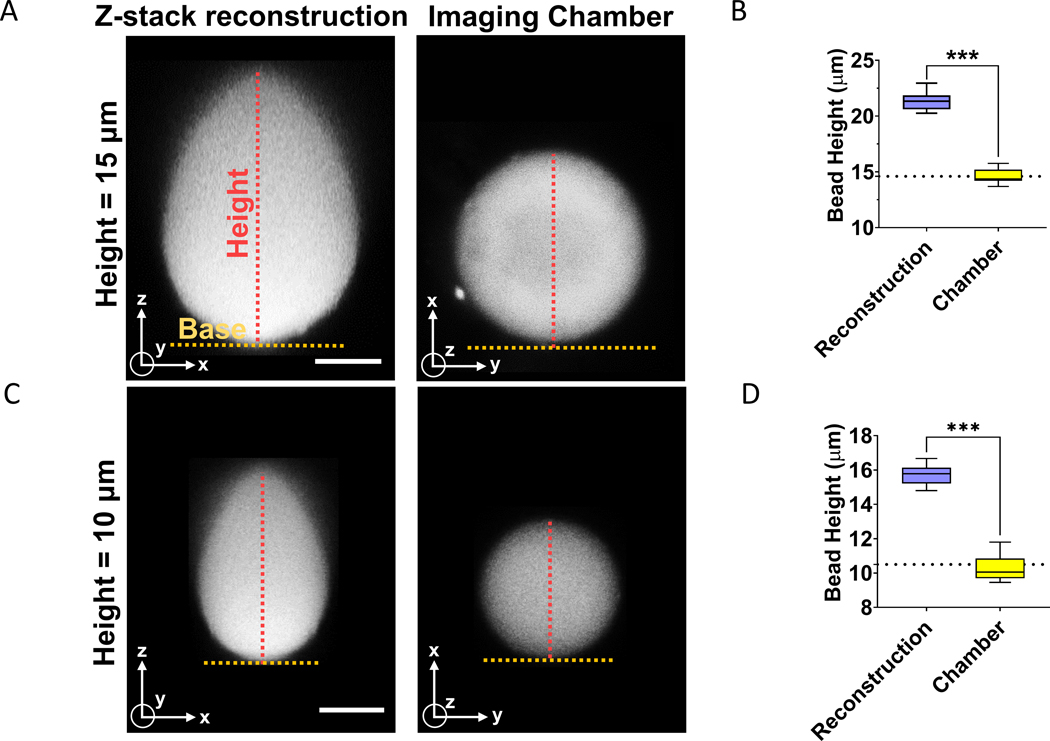
We first reconstructed x-z cross-sections of fluorescent beads of known diameters from confocal z-stacks. We compared these x-z cross-sections to single confocal fluorescent images of x-y cross-sections of fluorescent beads in the orthogonal imaging chamber. All images were acquired on a laser scanning confocal microscope (see methods) using a Nikon CFI Plan Apo Lambda 60X/1.4 NA oil immersion objective lens. Beads were mounted on the glass slides in mounting media with a refractive index of 1.45, while the refractive index of oil was around 1.52. Consistent with previous reports [8], the x-z shapes of 10–15 μm fluorescent beads reconstructed from confocal z-stack imaging resembled a tear-drop shape (Fig 2A and 2C). The average change in the height of the bead was ~ 53 % for the 10 μm beads and ~ 45 % for the 15 μm beads (Fig 2B and 2D). This distortion was measured for confocal z-stacks acquired at a step-size of ~250 nm which is below the Nyquist criterion. Substantially lowering the step size to 50 nm did not decrease the distortion in the beads (Supp Fig 1).
Figure 2. Comparison of x-z shapes reconstructed from confocal sectioning, and corresponding x-y shapes acquired in the orthogonal imaging chamber.
(A) Image of x-z cross-section of fluorescent bead (diameter = 15 μm) reconstructed from confocal z-stacks and acquired with the imaging chamber. Scale bar is 5 μm. (B) The graph shows a quantitative comparison of diameter of beads (d = 15 μm) corresponding to the two imaging methods in (A). Dotted line represents manufacturer’s specification for the mean diameter of the bead. The experiments were performed in triplicates and 20 beads were quantified. “***” signifies statistically significant difference (p < 0.05 by student’s t-test). (C) Image shows x-z cross-section of fluorescent bead (diameter = 10 μm) reconstructed from confocal z-stacks and a single x-y image acquired with the orthogonal imaging chamber. Scale bar is 5 μm. (D) Graph shows a comparison of diameter of beads (d = 10 μm) corresponding to the two imaging methods in (C). Dotted line represents manufacturer’s specification for the mean diameter of the bead. The experiments were performed in triplicates and 20 beads were quantified. “***” signifies statistically significant difference (p < 0.05 by student’s t-test).
In contrast, images of the beads acquired with the orthogonal imaging chamber were not distorted from their circular shapes (Fig 2A and 2C, right). The measured heights were statistically indistinguishable from the diameter specified by the manufacturer (Fig 2B and 2D). These data demonstrate the utility of the orthogonal imaging chamber for reducing distortions in images of shapes captured orthogonal to the mounting surface.
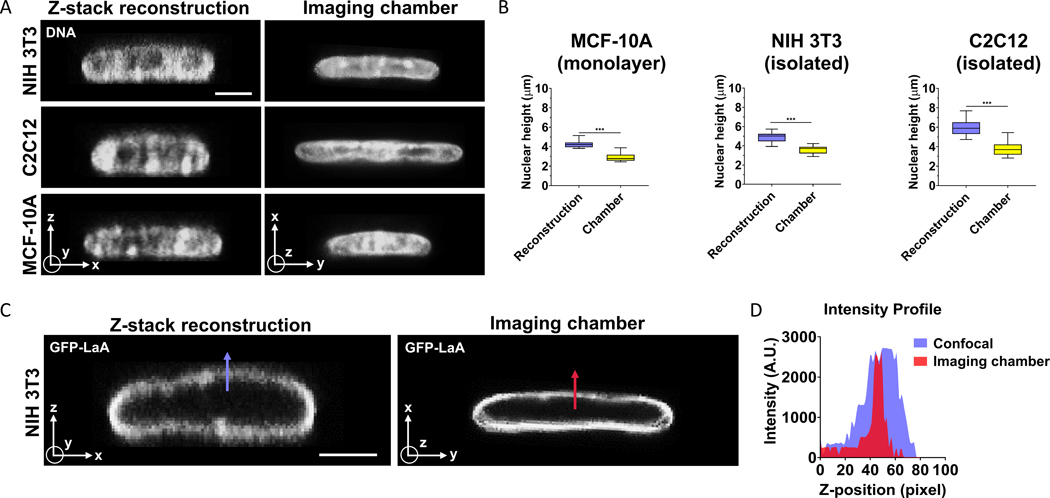
We next evaluated the orthogonal imaging chamber for imaging non-spherical fluorescent structures. The cell nucleus is an example of such a structure as it looks generally circular in the x-y plane but is flattened considerably in the x-z plane such that its three-dimensional shape resembles an ellipsoid [9, 10]. We imaged DNA stained with HOECHST in nuclei of three different cell types - NIH 3T3 fibroblasts, MCF10A mammary epithelial cells and C2C12 myoblasts, by reconstructing x-z cross-sections on a conventional setup, and by direct imaging of x-y cross-sections in the orthogonal imaging chamber. X-y images of nuclei acquired with the imaging chamber, were much flatter than x-z images of nuclei reconstructed from confocal image stacks (Fig 3A, 3B and Table 1). The percentage error in mean nuclear heights was in the range of ~35% to ~62% (Table 1). These results reveal a substantial error in vertical height of the nucleus measured from confocal z-sectioning and reconstruction of the x-z shape. As heights of spread cells in culture are very similar to nuclear heights, these results also suggest that cells are much flatter than suggested by confocal reconstructions.
Figure 3. Difference in nuclear heights measured in x-z reconstructed images and x-y images acquired in the orthogonal imaging chamber.
(A) Hoechst (H33342) stained x-z images of the nucleus in three different cell types reconstructed from confocal z-stacks, and x-y images acquired in orthogonal imaging chamber. Scale bar is 5 μm. (B) Graphs show a quantitative comparison of nuclear heights for NIH 3T3 fibroblasts (left, isolated cells), C2C12 myoblasts (center, isolated cells) and MCF-10A (right, monolayer) for the two imaging conditions in (A). Images were acquired per cell type from at least 15 cells from three independent experiments. “***” signifies statistically significant difference (p < 0.05 by student’s t-test). (C) x-z image of a GFP-lamin A expressing NIH 3T3 fibroblast nucleus reconstructed from z-stack confocal stacks (left) and x-y image of a different nucleus imaged in the orthogonal imaging chamber (right). Scale bar is 5 μm. Blue and red arrows mark the length along which intensity profile was measured (D).
Table 1. Comparisons of nuclear height measured from confocal reconstruction and in the orthogonal imaging chamber.
Nuclear heights measured in three different cell types through reconstruction of the x-z cross-section from confocal z-stacks of HOECHST stained nuclei, or from x-y confocal images acquired in the orthogonal imaging chamber. Data is Mean ± SEM measured from n = 15 cells from three independent experiments.
| Height of Nucleus | |||
|---|---|---|---|
| Cell type | Confocal stacks | Imaging chamber | % Error‡ |
| NIH 3T3 fibroblasts | 4.88 ± 0.11 μm | 3.61 ± 0.10 μm | ~ 35% |
| C2C12 myoblasts | 6.03 ± 0.19 μm | 3.73 ± 0.17 μm | ~ 62% |
| MCF-10A | 4.24 ± 0.09 μm | 2.83 ± 0.08 μm | ~ 50% |
Percentage error was calculated using the formula , where dz = mean height of the nucleus measured from confocal z-stacks and dic = mean height of the nucleus measured by direct x-y imaging in the imaging chamber.
The nucleus is a core-shell structure, with the nuclear lamina (shell) enclosing DNA (core). We compared x-z shapes of the GFP lamin A-labeled lamina in NIH 3T3 fibroblasts acquired from confocal z-stacks in a conventional setup, and x-y shapes captured by direct confocal imaging in the orthogonal imaging chamber. The fluorescence of GFP-lamin A was diffuse in a direction perpendicular to the nuclear periphery in x-z reconstructed images, while it was more localized and less diffuse in x-y images acquired in the orthogonal imaging chamber (Fig 3C and 3D).
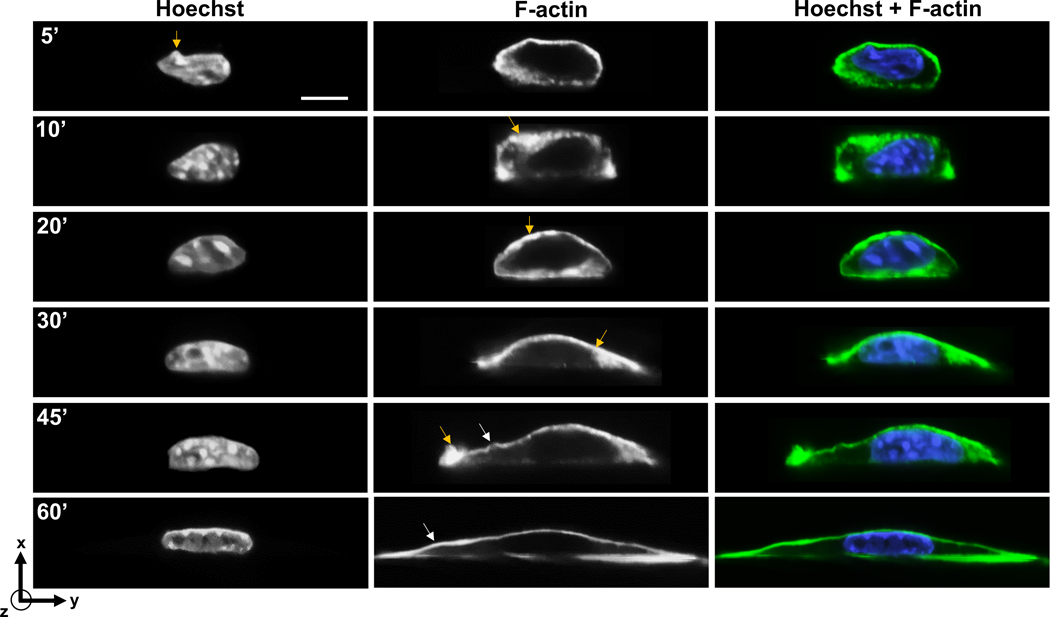
As another example of non-spherical and non-symmetrical structures, we imaged both the cell and the nucleus in the orthogonal imaging chamber. In this experiment, we allowed cells to spread on the glass, and then fixed cells at different times after seeding. This allowed us to capture the F-actin distribution in cells of different shapes and chromatin distribution in nuclei. Cells progressively flattened over 60 minutes of spreading, with the nucleus changing shape from rounder morphologies to flat morphologies (Fig 4). The blue arrows in Figure 4 reveal finer features in the nuclear shape and F-actin distribution. For example, F-actin tended to be enriched in local spots near the apical membrane early in the process of spreading and tended to be spatially inhomogeneous. Upon complete spreading, however, F-actin distribution tended to be less inhomogeneous, and present in relatively uniform, thin structures at the apex and the base. Spatial variations in local curvature of the apical F-actin structure was also evident in the images of cells (marked by white arrowheads in F-actin images at 45’ and 60’ in Figure 4).
Figure 4. X-y imaging of cells fixed at different time points after seeding on to a glass coverslip in the orthogonal imaging chamber.
Chromatin was stained with Hoechst (H33342) and F-actin was stained with phalloidin. Yellow arrows mark local spots of F-actin enrichment, and local nuclear irregularity in image at 5’. White arrowheads mark spatial variations in curvature of apical F-actin. Scale bar is 5 μm.
Discussion
Three-dimensional confocal microscopy is the technique of choice to visualize x-z cross-sections of particles and cellular structures, but these cross-sections are subject to considerable distortions owing largely to the phenomenon of refractive-index mismatch. Here we developed an approach for mounting samples side-ways such that what is normally the x-z cross-section for imaging conventional samples is directly imaged in the x-y plane in the orthogonal imaging chamber. The chamber allows imaging of planes perpendicular to the glass slide with resolution similar to that achieved in XY imaging. Additionally, the reconstruction needed to visualize x-z cross-sections is not required here, as only one image is required of the x-y plane. As such our approach will have better time resolution than approaches that involve reconstruction of confocal z-stacks.
Quantitative measurements of cell and nuclear heights have been performed from x-z cross-sections reconstructed from confocal microscopy of x-y planes captured at different z-positions [6, 9, 11–24]. Such measurements have allowed mechanistic studies of cell spreading and nuclear flattening. Our estimates of error in nuclear heights show that confocal reconstructions significantly overestimate these parameters. Such errors can confound interpretation particularly where treatments or perturbations to cells cause subtle differences in nuclear heights or cellular heights.
One limitation of our approach is that cells can only be imaged close to the edge of the glass slide because of the low working distance of typical 60X or 100X objectives. Nonetheless, for an imaging depth of 70–100 μm with reference to the top surface of the coverslip and an imaging width of 15 mm for our glass slides, the area over which imaging can be performed is 1 – 1.5 mm2, which enables imaging of a substantially large number of micron-sized objects. Further, the area of imaging may also be increased by using objectives that have high working distances. The vertical mounting of cells could potentially impact their shapes due to gravity. However, we have shown that gravity does not affect the shape of cells as they adhere and spread on a surface [9]. This was done by allowing cells to adhere for a short time on a surface, and then inverting it such that gravity acted against the cells. We found no difference in the degree of cell flattening even against gravity. This is consistent with the fact that gravitational forces on cells are very small compared to forces associated with molecular motors that drive cell spreading [25].
Fluorescence intensity drops with distance from the cover slip [26]. This could make it difficult to visualize dimmer samples in the orthogonal imaging chamber. While, the point spread function becomes more diffuse laterally with depth [1], the gross shape of object remains unchanged. Finally, the imaging chamber does not solve the problem of 3-D rendering of objects; any 3D reconstructions will appear elongated in the z direction.
The imaging chamber is compatible with both upright and inverted microscopes, and can be coupled with micromanipulation devices for studying force-deformation relationships of soft particles or cells. Also, it may prove valuable in studying dynamic events in cells in the orthogonal direction, such as apical assembly and disassembly of F-actin structures and microtubules during the process of cell migration. For example, a similar orthogonal mounting approach as ours has been previously used by [24] to study cell migration. The improved resolution and time resolution offered by our approach should be especially useful in this regard.
Conclusions
Orthogonal mounting of fluorescent samples here is a simple but effective method to directly image x-z cross-sections. The approach presented here suggests that cells and nuclei are significantly flatter than evident from reconstructed x-z cross-sections. The improved spatial and time resolution of this method should prove useful for diverse cell biological applications.
Methods
Orthogonal Imaging Chamber.
A 35 × 75 × 11.75mm (W×L×H) chamber was designed to hold two glass slides in an orientation perpendicular to the focal plane as shown in Fig 1 and Supp Fig 2. A 22mm × 22mm × 0.17 mm coverslip (Fisher Scientific, Cat. No. 12-542-B) was adhered to the bottom of the imaging chamber with RTV-108 glue (Momentive RTV Silicone Sealant) to protect the microscope objective from brushing against the edges of the vertical slides. Microscope glass slides (VWR, Cat. No. 26004–422) and coverslips were cut (25mm x 11 mm and 22mm x 11 mm respectively) to enable imaging with a long working distance condenser (Ti-C CLWD, Nikon Instrument Inc.). Two such slides were then inserted in the slotted grooves (8.75 × 1.3 mm with a depth of 1.75 mm) along the walls of the chamber. Once positioned, the vertical slides were pressed against the bottom coverslip by tightening the lid of the imaging chamber (35×35×3 mm) with four threaded screws (Fig 1). An imaging window was provided within the lid to enable simultaneous transmitted light and fluorescence microscopy. All the designs were developed with CAD software (SolidWorks, 3D Assault Systems) and 3D-printed (VeroWhite resin material, 3D printer: Stratasys Objet Eden 260V).
Cell Culture.
Cells were maintained in a humidified incubator at 37°C and 5% CO2. NIH 3T3 fibroblasts stably expressing GFP-Lamin A, a kind gift from Kyle Roux, were cultured in Dulbecco’s Modified Eagle’s Medium (DMEM, 10313–021) with 4.5 g/L glucose (Corning, 25-037-CI), supplemented with 10% v/v donor bovine serum (DBS, Gibco, 16030074) and 1% v/v penicillin/streptomycin (Pen-Strep, Corning, 30-002-CI). C2C12 myoblasts (ATCC CRL-1772) were cultured in Dulbecco’s Modified Eagle’s Medium (DMEM, 10313–021) with 4.5 g/L glucose (Corning, 25-037-CI), supplemented with 10% v/v donor bovine serum (DBS, Gibco, 16030074) and 1% v/v penicillin/streptomycin (Pen-Strep, Corning, 30-002-CI). MCF10A human breast epithelial cells (ATCC CRL-10317) were maintained in DMEM/F12 medium (Invitrogen, 11039–021) supplemented with 20 ng/ml epidermal growth factor (EGF, Peprotech, AF-100-122), 0.5 mg/ml hydrocortisone (Sigma, 50-23-7), 100 ng/ml cholera toxin (Sigma, 9012-63-9), 100 mg/ml insulin (Sigma, 11070-73-8), 1% v/v penicillin-streptomycin mix (Pen-Strep, Corning, 30-002-CI), and 5% v/v horse serum (Invitrogen, 16050–122). Cells were cultured on glass slides, fixed and stained. They were next mounted in glycerol-based mounting medium (Cat #: H-1000, Vectashield, Vector Labs) with a refractive index of 1.45. Because the mounting medium was viscous enough, we did not need to sandwich the cells with a separate glass slide on top.
Immunostaining.
Cells were fixed in 4% paraformaldehyde (Alfa Aesar, J61899) at room temperature for 15 minutes and washed thrice with 1X PBS (Corning, 21-040-CM). Hoechst (H33342, Sigma-Aldrich, 875756-97-1) was used to stain for DNA. Alexa Fluor-488 phalloidin (ThermoFisher Scientific, A12379) was used to stain for actin filaments (f-actin).
Microscopy.
Imaging was performed on a Nikon A1 confocal unit complemented with a 4-channel 15 mW laser light source and mounted on a Nikon Ti2 eclipse microscope (Nikon, Melville, NY). The objective lens was a Nikon CFI Plan Apo Lambda 60X/1.4 NA oil immersion objective lens (MRD01605). We chose a pinhole opening of 1.2 Airy disks and a z-step size of 250 nm, to ensure overlapping z-stacks while sampling at less than half of the depth of focus (which corresponds to ~ 600 nm for 488 nm light) to satisfy Nyquist criterion and minimize photobleaching artifacts [27–31]. Immersion oil Type 37 (Cargille Labs, Cat #: 16237) was used at 37°C (R.I. = 1.52 for λ = 486.1 nm). The microspheres were separated from the immersion oil by a glass coverslip (No. 1.5, R.I. = 1.52).
For confocal reconstruction, images were captured of 100 x-y planes at different z-positions separated by either 100 nm or 250 nm for each 15 μm microsphere. For the 10 μm microsphere, 50 x-y planes were imaged at z-positions separated by 250 nm. When imaging in the orthogonal chamber, we first found a reference focal plane with approximately maximal cross-sectional area. Next, we captured 5 images at x-y planes separated by 0.5 μm at z-positions above and below the reference focal plane. The focal plane with the maximum area was selected as the true cross-section of the object and was quantified.
Polystyrene beads.
We imaged commercially available fluorescent polystyrene microspheres of diameter 14.6 ± 0.146 μm from Molecular Probes, (F8837, λ absorption = 365 nm / λ emission = 415 nm) and of diameter 10.5 ± 0.152 μm from Corpuscular Inc. (Cat #: 141255–05, λ absorption = 480 nm / λ emission = 510 nm). Microspheres were mounted in a mounting medium (Cat #: H-1000, Vectashield, Vector Labs) with a refractive index of 1.45.
Quantitative analysis of images.
Cross-sections of microspheres were reconstructed using NIS-Elements AR 5.02.01 and the maximum intensity projection was applied to the reconstructed images. Intensity profiles along the direction perpendicular to the mounting surface were exported to Origin PRO (OriginLab Corporation). A Gaussian non-linear fit based on Levenberg Marquardt algorithm was applied to the intensity values and top and bottom edges of the objects were determined with the full width at half maximum method (FWHM) [32] function in Origin. The distance between the top and bottom edge was reported as the diameter. A similar analysis was performed on images of nuclei to quantify their heights.
Supplementary Material
Graph shows a comparison between height of the bead (d = 15 μm) from reconstructed z-stacks of 50 nm and 250 nm step size. The experiments were performed in triplicates and 20 beads were quantified for each condition. “n.s.” signifies statistically non-significant difference (p > 0.05 by student’s t-test).
Engineering drawing of orthogonal imaging chamber.
Acknowledgements
The authors would like to acknowledge Matthew C. Mitschelen, Senior Biosystems Applications Manager, Nikon Instruments Inc., Melville, NY, for valuable discussions. PPL acknowledges funding from the Cancer Prevention and Research Institute of Texas (RP170805), the National Institute of General Medical Sciences United States (R01-GM123085), and Texas A&M Engineering Experiment Station. This work was supported by NIH U01 CA225566, a CPRIT established investigator award grant # RR200043 (T.P.L.).
References
- 1.Diaspro A, Federici F, and Robello M, Influence of refractive-index mismatch in high-resolution three-dimensional confocal microscopy. Applied Optics, 2002. 41(4): p. 685–690. [DOI] [PubMed] [Google Scholar]
- 2.Hell S, et al. , Aberrations in confocal fluorescence microscopy induced by mismatches in refractive index. J Microsc, 1993. 169(3): p. 391–405. [Google Scholar]
- 3.Kuypers LC, et al. , A procedure to determine the correct thickness of an object with confocal microscopy in case of refractive index mismatch. J Microsc, 2005. 218(Pt 1): p. 68–78. [DOI] [PubMed] [Google Scholar]
- 4.Van Elburg H, et al. , Improved correction of axial geometrical distortion in index‐mismatched fluorescent confocal microscopic images using high‐aperture objective lenses. 2007. 228(1): p. 45–54. [DOI] [PubMed] [Google Scholar]
- 5.Diel EE, Lichtman JW, and Richardson DS, Tutorial: avoiding and correcting sample-induced spherical aberration artifacts in 3D fluorescence microscopy. Nature Protocols, 2020. 15(9): p. 2773–2784. [DOI] [PubMed] [Google Scholar]
- 6.Feric M, et al. , Coexisting Liquid Phases Underlie Nucleolar Subcompartments. Cell, 2016. 165(7): p. 1686–1697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hobson CM, et al. , Correlating nuclear morphology and external force with combined atomic force microscopy and light sheet imaging separates roles of chromatin and lamin A/C in nuclear mechanics. Molecular Biology of the Cell. 0(0): p. mbc.E20-01-0073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Diaspro A, et al. , Photobleaching, in Handbook of biological confocal microscopy. 2006, Springer; p. 690–702. [Google Scholar]
- 9.Li Y, et al. , Moving cell boundaries drive nuclear shaping during cell spreading. Biophysical Journal, 2015. 109(4): p. 670–686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Neelam S, et al. , Vertical uniformity of cells and nuclei in epithelial monolayers. Scientific Reports, 2016. 6: p. 19689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tocco VJ, et al. , The nucleus is irreversibly shaped by motion of cell boundaries in cancer and non-cancer cells. J Cell Physiol, 2018. 233(2): p. 1446–1454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Neelam S, et al. , Vertical uniformity of cells and nuclei in epithelial monolayers. Sci Rep, 2016. 6: p. 19689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Alam S, et al. , The mammalian LINC complex regulates genome transcriptional responses to substrate rigidity. Sci Rep, 2016. 6: p. 38063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Shiu J-Y, et al. , Nanopillar force measurements reveal actin-cap-mediated YAP mechanotransduction. Nature Cell Biology, 2018. 20(3): p. 262–271. [DOI] [PubMed] [Google Scholar]
- 15.Patteson AE, et al. , Vimentin protects cells against nuclear rupture and DNA damage during migration. J Cell Biol, 2019. 218(12): p. 4079–4092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Katiyar A, et al. , Nuclear size changes caused by local motion of cell boundaries unfold the nuclear lamina and dilate chromatin and intranuclear bodies. Soft Matter, 2019. 15(45): p. 9310–9317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kent IA, et al. , Apical cell protrusions cause vertical deformation of the soft cancer nucleus. Journal of Cellular Physiology, 2019. 234(11): p. 20675–20684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Keeling MC, et al. , Actomyosin and vimentin cytoskeletal networks regulate nuclear shape, mechanics and chromatin organization. Scientific Reports, 2017. 7(1): p. 5219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Versaevel M, et al. , Super-resolution microscopy reveals LINC complex recruitment at nuclear indentation sites. Sci Rep, 2014. 4: p. 7362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lovett DB, et al. , Modulation of Nuclear Shape by Substrate Rigidity. Cellular and Molecular Bioengineering, 2013. 6(2): p. 230–238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hanson L, et al. , Vertical nanopillars for in situ probing of nuclear mechanics in adherent cells. Nature Nanotechnology, 2015. 10(6): p. 554–562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hoffman LM, et al. , Mechanical stress triggers nuclear remodeling and the formation of Transmembrane Actin Nuclear lines with associated Nuclear Pore Complexes. Molecular Biology of the Cell. 0(0): p. mbc.E19-01-0027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Roca-Cusachs P, et al. , Micropatterning of Single Endothelial Cell Shape Reveals a Tight Coupling between Nuclear Volume in G1 and Proliferation. Biophysical Journal, 2008. 94(12): p. 4984–4995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ingram VM, A Side View of Moving Fibroblasts. Nature, 1969. 222(5194): p. 641–644. [DOI] [PubMed] [Google Scholar]
- 25.Howard J, Mechanics of Motor Proteins and the Cytoskeleton. 2001: Sinauer Associates, Publishers. [Google Scholar]
- 26.Sheppard CJR and To P ¨rök, Effects of specimen refractive index on confocal imaging. Journal of Microscopy, 1997. 185(3): p. 366–374. [Google Scholar]
- 27.Wilson T and Tan JB, Three dimensional image reconstruction in conventional and confocal microscopy. Bioimaging, 1993. 1(3): p. 176–184. [Google Scholar]
- 28.Sheppard CJR, Choudhury A, and Gannaway J, Electromagnetic field near the focus of wide-angular lens and mirror systems. IEE Journal on Microwaves, Optics and Acoustics, 1977. 1(4): p. 129–132. [Google Scholar]
- 29.Sheppard CJR, Axial resolution of confocal fluorescence microscopy. Journal of Microscopy, 1989. 154(3): p. 237–241. [Google Scholar]
- 30.North AJ, Seeing is believing? A beginners’ guide to practical pitfalls in image acquisition. J Cell Biol, 2006. 172(1): p. 9–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Sieck GC, Mantilla CB, and Prakash YS, [17] Volume measurements in confocal microscopy, in Methods in Enzymology. 1999, Academic Press; p. 296–315. [DOI] [PubMed] [Google Scholar]
- 32.KUYPERS LC, et al. , A procedure to determine the correct thickness of an object with confocal microscopy in case of refractive index mismatch. Journal of Microscopy, 2005. 218(1): p. 68–78. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Graph shows a comparison between height of the bead (d = 15 μm) from reconstructed z-stacks of 50 nm and 250 nm step size. The experiments were performed in triplicates and 20 beads were quantified for each condition. “n.s.” signifies statistically non-significant difference (p > 0.05 by student’s t-test).
Engineering drawing of orthogonal imaging chamber.