A New Test of a Theory about Old Mosquitoes

Abstract

In vector control, it is widely accepted that killing adult mosquitoes would sharply reduce the proportion of old mosquitoes and cause the greatest changes to malaria transmission. The principle is based on a mathematical model of the sporozoite rate (the proportion of infective mosquitoes) that emphasized changes in mosquito age. Killing adult mosquitoes also reduces mosquito population densities, which are directly proportional to human biting rates (the number of bites, per person, per day). Effect sizes of vector control can be compared using sporozoite rates and human biting rates, which are commonly measured. We argue that human biting rates convey more useful information for planning, monitoring and evaluating vector control, and operational research should focus on understanding mosquito ecology.

Mosquitoes and Malaria Transmission

Human malaria parasites are transmitted by more than 70 species of mosquitoes in the genus Anopheles across many ecological settings [1]. An important challenge for planning malaria control is to understand how mosquito populations would respond to vector control based on measurable differences in their behavior and ecology. A common starting point for understanding these differences has been the Ross-Macdonald model, which describes transmission using a small set of entomological parameters (Box 1) [2, 3]. A general principle derived from the model was that modes of vector control that kill adult mosquitoes, such as indoor residual spraying (IRS, see Glossary), would tend to have a greater effect on malaria transmission than those that do not. The advice comes from Macdonald’s mathematical model for the sporozoite rate (SR, defined as the fraction of mosquitoes found with sporozoites in salivary glands and thus presumed infective, see Glossary) and the accompanying analysis [4]. After becoming infected, a mosquito must survive long enough for parasites to develop into sporozoites, a period that is roughly as long as the typical mosquito lifespan. The parasite’s latent period in the mosquito has been called the extrinsic incubation period (EIP, see Glossary). The analysis showed that since only old mosquitoes could be infective, and since increasing mortality would sharply reduce the fraction of old mosquitoes, then killing adult mosquitoes would have a large effect on transmission [4, 5]. The large, non-linear effect of killing adult mosquitoes to prevent infection and survival through the EIP is often contrasted with a parameter describing mosquito population densities, which has only a linear effect on transmission. In practice, mosquito population densities are rarely measured directly, but the number of mosquitoes per humans is assumed to be directly proportional to the human biting rate (HBR, defined as the number of bites, per person, per day). Recently, several new mathematical models of adult behaviors and ecology have been developed to estimate the effect sizes (see Glossary) of vector control on malaria transmission [6, 7, 8, 9]. Some of these new models consider complex feedbacks and population dynamic thresholds that Macdonald’s analysis ignored, and they show that vector control could have large, non-linear effects on mosquito population densities [5, 10]. There is uncertainty, however, about the ecological factors that affect the population dynamic responses and overall effect sizes of vector control.

Box 1: Macdonald, Sporozoite Rates, and R₀.

Macdonald’s formula for the sporozoite rate had four parameters describing mosquitoes: the ratio of mosquitoes to humans (m), the proportion of mosquitoes surviving each day (p), the extrinsic incubation period (EIP) as a number of days (n), and the human feeding rate (a, thenumber of human blood meals, per mosquito, per day). It also included a parameter describing net infectiousness, the probability a mosquito becomes infected after biting a human (κ).

Though Macdonald presented the formula using p, the original analysis almost certainly used a parameter describing the per-capita mosquito death rate rate (g), where p = e^−g or equivalently g = −ln p, and the probability of surviving the EIP is pⁿ = e^−gn.

Macdonald’s derivation does not appear in his paper, but it most likely borrows from an earlier paper by Sharpe and Lotka [51]. It can be derived from the following system of equations. Changes in the fraction of infected mosquitoes (y) follow the equation:

$$\frac{dy}{dt}=a\kappa (1-y)-gy.$$ (2)

At the steady state:

$$y(\kappa )=\frac{a\kappa }{g+a\kappa }.$$ (3)

Infective mosquitoes appear after a time lag of n days, if they survive. Changes in the proportion infective (z) are described by the equation:

$$\frac{dz}{dt}=a{\kappa }_{t-n}\left(1-y_{t-n}\right)e^{-gn}-gz.$$ (4)

At the steady state, z = ye^−gn, so

$$z(\kappa )=\frac{a\kappa }{g+a\kappa }{e}^{-gn}.$$ (5)

The entomological inoculation rate (EIR, denoted E in equations) is defined as the product of the human biting rate (HBR) and the sporozoite rate (SR, or equivalently z). The HBR is ma so the EIR is:

$$E=maz=\frac{m{a}^2\kappa }{g+a\kappa }{e}^{-gn}.$$ (6)

Macdonald’s formula for R₀ and the formula for vectorial capacity (VC, denoted V in equations) can be derived by considering the EIR as a function of κ and taking a limit of their ratio:

$$V=\underset{\kappa \to 0}{\text{lim}}ma\frac{z(\kappa )}{\kappa }={ma\frac{dz(\kappa )}{d\kappa }|}_{\kappa =0}=\frac{m{a}^2}{g}{e}^{-gn}.$$ (7)

Let b denote the proportion of infective bites that cause an infection and 1 / r the duration of the infectious period for human infections. Macdonald’s formula was equivalent to:

$$R_0=\frac{bV}{r}.$$ (8)

In Macdonald’s notation, the SR was:

$$z=\frac{a\kappa }{-\text{ln}p+a\kappa }{p}^n,$$ (9)

and he used the term Z₀ instead of R₀:

$$R_0=\frac{mb{a}^2}{(-\text{ln}p)r}{p}^n.$$ (10)

We note, as an aside, that without the reconstructed derivation, the units of ln p are problematic. Since g is a rate, the term a/g is a number of human blood meals. Since g = −ln p, the term a/ −ln p must have the same interpretation in the formula for R₀.

Macdonald’s analysis of the SR came with a call to develop better metrics for measuring the age of mosquito populations [4]. There is, however, an easy way of evaluating vector control based on standard metrics. Studies routinely estimate the entomological inoculation rate (EIR, the number of infective bites, per person, per day, see Glossary), which is the product of the HBR and the SR (Box 1). Changes in the age of mosquito populations would affect the SR, while changes in population density would affect the HBR. To test whether there are larger changes in mosquito population age or density, one need only compare changes in the SR to changes in the HBR. Here, we explain the test, apply it, briefly review other supporting evidence, and revisit the standard advice about the importance of old mosquitoes.

Old Mosquitoes

Basic theory for malaria transmission and methods for measuring it were developed by combining entomological and epidemiological research with simple mathematical models [2]. Ross’s research on malaria epidemiology outlined a quantitative roadmap and led to development of metrics to measure malaria, including the EIR [11, 12]. Macdonald’s synthesis of entomological field data presented a mathematical formula for the SR in terms of a few key entomological parameters (Box 1) [4]. Next, Macdonald used the same notation and assumptions to derive a formula for the basic reproductive number for malaria, R₀, which was the basis for a threshold criterion: endemic malaria transmission could not be sustained locally if R₀ < 1 [13]. The parameter set was slightly modified a decade later to include the human blood index (see Glossary) and the mosquito-specific parts of the formula for R₀ were renamed vectorial capacity (VC) [14, 15] (see Glossary).

Macdonald’s analysis of the SR showed that malaria transmission is highly sensitive to changes in mosquito survival, which would affect transmission in two ways [4]. To become infective a mosquito must first become infected, and second survive the EIP. The total reduction in transmission would be measured as a product of effects on these two processes, so the effects of shortening mosquito lifespans could be surprisingly large. The resulting policy advice was encapsulated in a principle and a prejudice. To understand parasite transmission by mosquitoes, it would be important to understand mosquito age. Since only old mosquitoes transmit parasites, programs should strongly prefer interventions that shorten the lifespan of adult mosquitoes.

The Human Biting Rate

When Macdonald extended the model for SR into a formula for R₀ based on the mathematical formula for the EIR, he did not expand the sensitivity analysis to fully consider the effects of adult mosquito mortality on the HBR, so the advice about killing mosquitoes was based exclusively on analysis of changes in the SR (Box 1)[4, 13].

Rewriting the formulas for VC shows that increasing mosquito mortality would also reduce the HBR: holding emergence rates constant, increasing mosquito mortality would reduce mosquito population densities (Box 2) [5]. Killing adult mosquitoes or reducing blood feeding rates would also reduce the number of eggs laid by each adult mosquito and the emergence rate (Box 2) [10], but there is no clear way of knowing the effect size of the population dynamic feedback, defined as the proportional change in mosquito population densities. Since mosquito populations also have thresholds for persistence, adult malaria control could drive local mosquito populations extinct [10, 16]. At the other extreme, mosquito populations that were affected by strong larval competition or by immigration would remain comparatively unchanged [10]. The population dynamic effect size could range from negligible to infinite. Heterogeneity in mosquito ecology is thus an important source of uncertainty both about how to formulate appropriate’ models (e.g. for planning) and the effect size of the population dynamic feedback (e.g. for monitoring and evaluation).

Box 2: Formulas for Vectorial Capacity.

Mathematical models and derived formulae are a means of describing and communicating complex quantitative ideas concisely. With that in mind, we consider the evolution of formulas for VC and extensions of it as cases of a single motivating concept: VC is defined to be the number of infective bites arising from all the mosquitoes biting a single human on a single day, as if the human was perfectly infectious. If appropriate, VC could thus be computed as an expectation for each individual on any day [9].

Garrett-Jones named the formula for VC, which was extracted from Macdonald’s formula for R₀ [15]. He also introduced a new parameter describing the human blood index, which emphasized differences in the human blood feeding habits of mosquitoes [14]. Here, we define f to be the blood feeding rate (the number of blood meals, per mosquito, per day), and Q to be the proportion of bloodmeals taken on humans, such that a = fQ. Otherwise following notation from Box 1, we rewrite the VC:

$$V=\frac{m{f}^2{Q}^2}{g}{e}^{-gn}.$$ (11)

Shortening mosquito lifespan would also reduce mosquito population density (m). A simple model that extends Macdonald’s analysis but is consistent with it assumes a constant emergence rate of adult mosquitoes from aquatic habitats, λ, per human, per day [5],

$$\frac{dm}{dt}=\lambda -gm,$$ (12)

so at the steady state, m = λ/g. The formula for VC could be rewritten:

$$V=\lambda \frac{f^2{Q}^2}{g^2}{e}^{-gn}.$$ (13)

This formula suggests mosquito mortality affects transmission in three ways, which can be interpreted as a reduced probability of surviving long enough to become infected, a reduced probability of surviving the EIP, and a reduced lifespan after becoming infective [5, 10].

Mosquito emergence from aquatic habitats must be related in some way to egg-laying by adult mosquitoes. Lifetime egg production by a female is proportional to the lifetime number of eggs laid, which is proportional to the number of blood meals a mosquito takes over its lifetime, G ∝ f / g. The functional relationship between eggs laid and mosquitoes emerging is not known, but we can imply some relationship in the following formula for the VC:

$$V=\lambda (G)\frac{f^2{Q}^2}{g^2}{e}^{-gn}$$ (14)

In this formula, g affects V in four ways (the three effects identified previously and the effects of reduced egg laying on adult emergence); f in three ways (fewer bloodmeals that could infect a mosquito, fewer bites that could infect a human, and fewer egg batches laid); and Q in two ways. The term that describes mosquito population density (λ) appears only once [10].

The formulas thus continue to support the importance of killing old mosquitoes, consistent with Macdonald’s analysis, but they illustrate two additional effects on the HBR: a direct effect on mosquito population density λ/g; and an effect on eggs laid, G ∝ f/g, which affects adults emerging, λ(G). While λ appears in the formula for VC only once, it may be that killing adult mosquitoes (or other modes of control) would affect mosquito populations, potentially driving them below thresholds for persistence and causing very large changes in λ and thus the HBR [10, 16]. The question is whether large changes in transmission caused by vector control are mainly due to changes in the SR, as described by Macdonald, or changes in the HBR that his formula for R₀ ignored. Should reserarch and entomological surveillance continue to focus on mosquito age, or should a greater emphasis be placed on mosquito ecology?

VC can be written in an even simpler form that tells the story of transmission. The term s = fQ/g describes the expected total number of human bloodmeals over the average mosquito lifespan, and P = e^−gn is the probability the mosquito and parasite survive through the EIP. In this notation,

$$V=\lambda s^{2}P.$$ (15)

In words, after emerging (λ), a mosquito must bite one human to become infected (the first s), survive the EIP (with probability P), and then bite other humans to transmit (the second s) [10].

In an area where there are multiple vector species (or independent populations), then VC is an arithmetic expectation summed over i distinct species (or populations):

$$V=\sum _i{V}_i$$ (16)

Effect sizes can be predicted for individual species (or independent populations) and the total effect size on transmission is computed as a ratio of sums [52].

To address modern needs for planning, monitoring and evaluating vector control, a new generation of models has been developed. These new models are capable of quantifying the effect sizes of several distinct modes vector control in various combinations and at different levels of coverage, but it is not possible to describe VC using simple formulas. The concept of VC and the formulas remain useful as a way of understanding vector control, even if the models are capable of predicting changes in the EIR and malaria outcomes. The VC can be computed numerically, either by directly computing the number of infective bites that would arise from a human on a single day if it were perfectly infectious, or by computing the average values of the statistics that comprise VC and taking their product [9]. VC and its formulas are a useful way of comparing models, making predictions about changes in the parameters that can be measured and tested, and fitting models to data.

In light of potentially large changes in the HBR, the standard interpretation of Macdonald’s original analysis must be reconsidered. On the one hand, the modified sensitivity analysis suggests that malaria transmission intensity is even more sensitive to increased mosquito mortality than Macdonald had predicted [5, 10]. On the other hand, the effects Macdonald had ignored provide an alternative explanation for success or failure of vector control. Changes in transmission caused by vector control could be attributed to massive changes in the age of mosquitoes, or in mosquito population densities, or in both.

A Thought Experiment

At first glance, it might seem difficult to imagine how it would be possible to observe large changes in just the HBR or in just the SR. A simple thought experiment illustrates where the logic of simple models and simple analyses could go wrong.

Suppose the mosquitoes in an area were made up of ten small, comparatively isolated sub-populations loosely coupled by migration. Vector control could respond in two different ways. First, vector control could eliminate nine of those populations, leaving the last one unaffected. In this case, the HBR would decline by 90% leaving the SR unchanged. Second, vector control could be partially effective everywhere, but as mosquitoes laid fewer eggs, there would be less crowding and competition in aquatic populations. With less competition, mosquito populations could respond by increasing emergence of more robust adult mosquitoes. In this case, population densities could remain high, but there would be large changes in the SR.

The differences in these two scenarios point to important factors associated with mosquito ecology that have been overshadowed by the old mosquito hypothesis. Heterogeneity in the responses to vector control can arise from differences in coverage and its spatial pattern, especially large contiguous spatial gaps in coverage. These could interact with mosquito movement and the distribution of adult mosquitoes. The size of the feedback depends, to a large extent, on density dependent and density independent factors in mosquito ecology. These factors probably vary across settings, and the resulting heterogeneity in mosquito ecology translates into operational uncertainty about the outcomes of control. To these, we add consideration of insecticide resistance and differences in contact rates with interventions associated with the mosquitoes’ human biting habits.

A Simple Test

After Macdonald, new research focused on measuring mosquito population age using simple metrics such as the proportion of mosquitoes that were parous (having laid at least one egg batch, see Glossary) [17, 18, 19], which left open questions about the proportion of very old mosquitoes. Macdonald’s model was reframed to support estimation of mosquito bionomic parameters in stable and fluctuating mosquito populations, using the proportion parous as a surrogate for age [24, 25, 26]. Using complex dissection methods, it is possible to estimate parity (see Glossary), the number of egg batches a mosquito has laid, but the methods are laborious and difficult to master [20, 21]. New technologies, such as near infrared spectroscopy, have been explored to measure the chronological age of a mosquito [22, 23]. Scalable methods to measure mosquito age would be valuable for understanding outcomes of vector control, but estimation of mosquito population age is still limited to research settings. Ongoing interest in mosquito age is apparent in the search for new methods to measure it, the search for methods of vector control that would only reduce mosquito age [27], and new mathematical models for the effects of senescence [28, 29].

Despite ongoing interest in mosquito age, emphasis has shifted away from estimating transmission through bionomic parameters, in part, because estimating VC through independent estimates of the bionomic parameters proved challenging. A single estimate of transmission intensity would require 4–5 separate parameter estimates, and there were lingering questions about the accuracy of each parameter and of estimates made by taking their product [30]. Despite advances in measuring parameters [24], the abstract mathematical formulation often seemed far removed from concepts familiar to field entomologists [31, 32]. Partly because of these issues and partly in response to a need for a practical measure of transmission intensity, the WHO later endorsed using the EIR [12].

In fact, the EIR and the VC are very closely related both conceptually and mathematically (Box 3) [5, 33]. The main difference is that the EIR is also affected by the net infectiousness of humans (denoted κ, see Glossary), the probability a mosquito becomes infected after biting a human. The similarity makes it possible to use them interchangeably to test some ideas about the relative importance changes mosquito population age relative to changes in mosquito population densities. The HBR and the SR are frequently measured and they convey relevant information about mosquito population densities and mosquito age. Problematically, changes in the SR are also affected by changes in net infectiousness (κ), but otherwise, the ratios of their formulas effectively isolates the two entomological terms that are of greatest interest: the chances of surviving through the EIP (P) and the emergence rate of adult mosquitoes (λ, see Box 3):

$$\frac{\text{SR}}{\text{HBR}}\approx \frac{P}{\lambda }\kappa .$$ (1)

A useful but imperfect test of whether the non-linear effects of surviving the EIP is larger than the non-linear effect on mosquito population dynamics (see Glossary) is found by comparing the effect size on the HBR to the effect size on the SR, a ratio of ratios. In comparing two ratios, Eq. 1 highlights a problem with the test: changes in the SR could also be due to changes in the net infectiousness (i.e., to κ). If changes in the HBR were larger than changes in the SR, the population dynamic effect size would be clearly larger. If changes in the SR were larger, however, the test would be weakened by the possibility that changes in the SR could either be attributed either to a shift in the proportion of old mosquitoes, or to a change in net infectiousness, or to both. Accurate assessment of changes in the SR would thus require an independent estimate of changes in mosquito age, in net infectiousness, or in both.

Box 3: Vectorial Capacity and Vector Control.

The EIR and the VC are closely related (Box 1). While VC computes the number of infective bites arising from all the mosquitoes blood feeding on a single perfectly infectious human on a single day, EIR is the estimated number of infective bites received by a single person on a single day. The two quantities must balance out, after accounting for net infectiousness, mosquito superinfection, time lags, and mosquito migration [10]. In particular, the formula for VC assumed that humans were “perfectly infectious” to isolate entomological parameters. These are a part of the EIR, so the biggest difference between the EIR and the VC is net infectiousness, κ, the probability a mosquito becomes infected after biting a human. Taking this into account, the following formulas relate the EIR to the VC in four equivalent ways. For estimation, we write:

$$\text{EIR}=\text{HBR}\times \text{SR}.$$ (17)

In Macdonald’s notation, the HBR was ma and the sporozoite rate was z so the EIR was ma×z or

$$E=ma\times \frac{a\kappa }{a\kappa -\text{ln}p}{p}^n.$$ (18)

In the updated notation (Box 2),

$$E=\lambda \frac{fQ}{g}\times \frac{fQ\kappa }{g+fQ\kappa }{e}^{-gn},$$ (19)

or even simpler (Box 2):

$$E=\lambda s\times sP\frac{\kappa }{1+s\kappa }.$$ (20)

These formulas are equivalent at the steady state in the Ross-Macdonald model under a change in notation (Box 2). Under the assumption that 1+sκ is not much larger than 1, we get the approximation:

$$E=V\frac{\kappa }{1+s\kappa }\approx V\kappa =\lambda s\times sP\kappa .$$ (21)

In taking the ratio of the SR to the HBR, the parameter s cancels, leaving Pκ in the numerator and λ in the denominator (Eq. 1).

Another problem arises from the practical concerns about estimating the HBR and the SR accurately, especially when populations fluctuate over time [26]. The SR tends to be around 1–5% [34], so sample sizes required to accurately measure the SR accurately are quite large. The mosquito tissue samples used to measure the SR are usually taken from the trapped mosquitoes used to estimate the HBR. Hence, as the HBR declines, so do the SR sample sizes and confidence in the accuracy of the estimated SR [35].

Applying the Test

A recent study in Nagongera, Tororo District, Uganda measured the HBR and the SR before and after control. The study collected approximately three years of baseline data before the Uganda Ministry of Health started an IRS campaign in Tororo District [36]. IRS and entomological surveillance continued for several years thereafter [35, 37, 38]. Mosquito populations declined sharply, and molecular sub-sampling showed a shift in the An. gambiae s.l. population from An. gambiae s.s. to An. arabiensis. The An. funestus s.l. populations also saw sharp declines, but none of these vector species were locally eliminated [35, 38].

Using archived data from a recent analysis of the entomological data [39], we analyzed changes in the total anopheline mosquito counts to compute an effect size in the HBR and the SR (Figure 1). The crude SR effect size was 3.1, while the crude HBR effect size was approximately 12.8. Measured crudely, the effect size of changes in the HBR were at least 4.1 times larger than changes in the SR.

Figure 1:

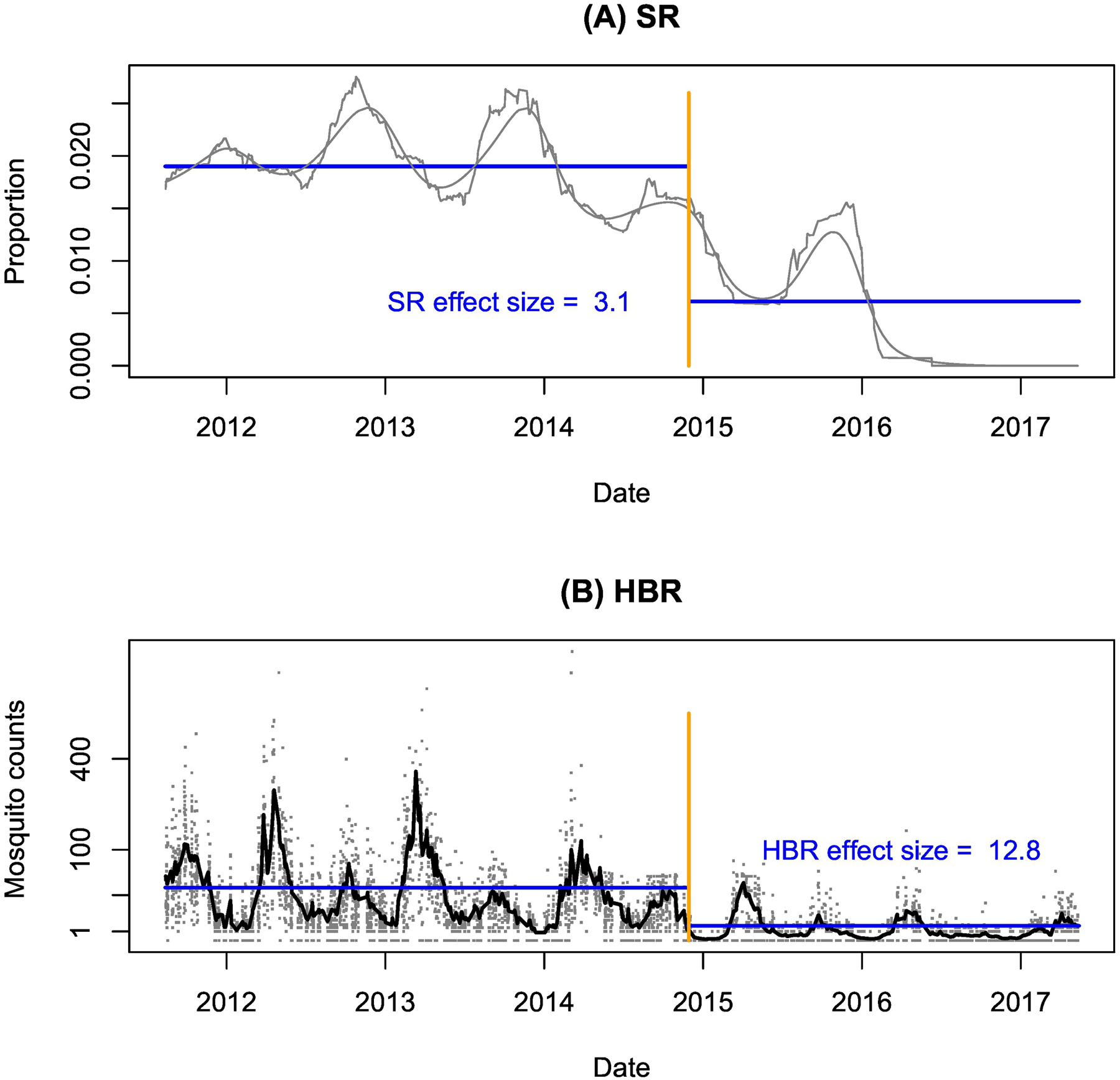
Effects of IRS on the human biting rate and sporozoite rate. During a longitudinal study in Nagongera, Tororo, Uganda, the government implemented an IRS spraying program (the vertical orange line marks the beginning of the first round). The sporozoite rate (shown as smoothed lines in grey) changes seasonally, and it declined sharply after control. a) The average sporozoite rate changed from 1.9% to 0.6%, a factor of approximately 3.1 (blue horizontal lines show the means before and after control). b) Mean mosquito counts declined from 33.9 per day before control to 2.6 per day after control, corresponding to a change in the human biting rate by a factor of 12.8 (blue horizontal lines show the means before and after control). Measured crudely, the effect size on the human biting rate was roughly 4.1 times as large as the effect size on the sporozoite rate.

Notably, the SR continued to decline after the first year of IRS (Fig. 1). An important caveat is that the study did not estimate net infectiousness, so it is not clear how much the declines in the SR were due to a change in mosquito age or in net infectiousness. The study did measure a change in the prevalence of infection by light microscopy from above 30% to below 1%, and slightly less dramatic changes in the prevalence using more sensitive diagnostics [40]. It is possible that each person who remained infected was more infectious in the time period following control [41, 42], but on balance it seems more likely that net infectiousness declined in Nagonera, Tororo. The SR to HBR test thus likely represents a lower bound: the relative importance of the changes in the population density was likely even larger.

Concluding Remarks

The conventional advice arising from Macdonald’s analysis – that killing adult mosquitoes should be disproportionately effective at reducing transmission – remains as well-justified by the mathematical analysis as ever. It may not be true, however, that the biggest effects come through reducing the proportion of old mosquitoes. Scaling up vector control to kill adult mosquitoes drives down mosquito population densities (Fig. 1). In some cases, vector species have been locally eliminated by vector control [16]. In others, responses to vector control have been disappointing. One compelling reason for the heterogeneous responses to vector control is heterogeneity in mosquito ecology, which causes differences in the effect sizes of vector control on mosquito population densities. A focus on sensitivity to mosquito age overlooked a potentially important sensitivity to population dynamics [10]. While research continues to focus on the age of mosquito populations, there is an equally strong case to be made for the importance of mosquito ecology and its role in determining the outcomes of vector control [43].

Macdonald’s elegant mathematical analysis and the concept of sensitivity to parameters have also supported an unwarranted prejudice about the relative importance of the factors affecting transmission intensity. Measured estimates of the EIR range from zero up to more than 1,000 infective bites, per person per year [44], and the factors giving rise to this variability are of great importance for planning vector control. Estimates of the HBR are highly variable across settings, but estimates of the SR are much less variable [34]. For example, the study in Nagongera, Tororo was replicated at two other locations in Uganda using identical protocols, and large differences in the EIR across these three studies were mainly due to differences in the HBR [40, 45]. Mosquito bionomic parameters probably do explain large differences among vector species in their association with high transmission intensity [14], and those species-specific differences are the basis for regional differences in malaria epidemiology [46], but there are even larger differences in the intensity of malaria transmission within these geographical regions [47, 48]. A focus on mosquito age has drawn attention to adult mosquito survival and parasite development rates in relation to temperature, but variables describing ecology tend to be better predictors of the geographical distribution of malaria, including rainfall, topography, hydrology, vector control coverage, and insecticide resistance [49, 50]. To put it another way, after knowing which species are present, most of the variability in local exposure to malaria is due to differences in mosquito population densities, which can be measured through the HBR.

There is a need for more effective guidance about planning, monitoring, and evaluating mosquito populations and vector control based on ecological and other contextual factors (see Outstanding Questions). The ecological context for malaria transmission is one potentially important source of variability and uncertainty in the outcomes of vector control, and there is a need to characterize mosquito ecology and measure and document changes in mosquito population densities. Studies over the past few decades have emphasized estimating the age of mosquitoes, but the HBR is often the dominant source of variability in transmission intensity and responses to vector control. The uncritical application of Macdonald’s incomplete analysis has created a distorted picture of the importance of old mosquitoes. The simple test we have proposed – measuring the EIR before and after an intervention and comparing the HBR effect sizes to the SR effect sizes – is a simple way of assessing some of the local features of the entomological responses to vector control.

Outstanding Questions.

• What fractions of the overall effect sizes of vector control are attributable to changes in the human biting rate vs. changes in the sporozoite rate?

• What are the ecological and operational factors that determine whether the responses to control will be dominated by changes in the sporozoite rate or changes in the human biting rate?

• How much and in what epidemiological settings do changes in net infectiousness offset changes in the sporozoite rate achieved through vector control?

• What ecological factors determine the magnitude of changes in the human biting rate?

• How much does low or heterogeneous coverage affect the outcome of vector control and its effects on the human biting rate and the sporozoite rate?

• What are the spatial scales that characterize mosquito movement and the structure of mosquito populations and responses to control in various ecological and transmission settings?

• How much does spatial heterogeneity in coverage interact with mosquito movement and population structure to determine the measurable outcomes of control?

• What modifiable factors that could be measured through entomological surveillance would predict the outcomes of vector control and help determine the best way to target vector interventions for vector control?

• What are the ecological factors that determine when mosquito populations will be eliminated in response to vector control?

• How well can various modes of vector control be combined for synergistic population dynamic responses?

Highlights.

• Killing adult mosquitoes with vector control is highly effective because it reduces transmission in several ways:

  • Mosquitoes are less likely to become infected and less likely to survive long enough for parasites to become infective, which affect the sporozoite rate (SR);
  • Adult mosquitoes lay fewer eggs so fewer adults emerge, and each emerging mosquito gives fewer bites, which reduce the human biting rate (HBR).

• A simple test of the importance of age vs. density involves comparing changes in the HBR to changes in the SR.

• In some cases, variability in transmission intensity and the success of malaria control is clearly due to variability or changes in the HBR.

• Vector control’s effects on the HBR are unpredictable across ecological settings.

• To reduce uncertainty and improve the outcomes of vector control, entomological surveillance should prioritize measuring the HBR.

Glossary

Effect Size

An effect size is a quantitative measure of an effect. The effect sizes of vector control are often described as proportional change in a quantity relative to a baseline. For example, a 50% decline is an effect size of 2, and a 90% decline is an effect size of 10.

Entomological Inoculation Rate (EIR).

The EIR is defined as the expected number of infective bites received by a single person on a single day. It is estimated as the product of the human biting rate and the sporozoite rate. Mathematical formulas for the EIR are described in Boxes 1 and 3.

Extrinsic Incubation Period (EIP)

The EIP is the number of days required for sporozoites to develop in the mosquito and reach the salivary glands, when a mosquito is presumed infective. Using standard terminology, the EIP is a latent period.

Indoor Residual Spraying (IRS)

IRS is a form of vector control in which insecticides are sprayed on the walls of houses.

Human Biting Rate (HBR)

The HBR is the number of bites by potential vector mosquitoes, per person, per day.

Human Blood Index (HBI)

is defined as the proportion of freshly fed mosquitoes found to contain human blood. It is closely related to a parameter Q defined herein, the fraction of human blood meals among all blood meals. The difference is that some mosquitoes may have blood from multiple blood meals.

Net Infectiousness

The probability a mosquito becomes infected after biting a human.

Parity

For mosquitoes, the number of egg batches that have been laid by a female mosquito.

Parous

A qualitative measure of parity. A female mosquito is parous if she has laid at least one batch of eggs.

Population Dynamics

The mosquito demographic process, including egg laying in aquatic habitats, hatching, and development through larval stages and pupae, and emergence of adults.

Senescence

An increase in mortality rates with age.

Sporozoite Rate (SR)

The proportion of mosquitoes that have sporozoites in their salivary glands. Sporozoite positive mosquitoes are assumed to be infective.

Vectorial Capacity (VC)

The number of infective bites that would eventually arise from all the mosquitoes blood feeding on a single, perfectly infectious human on a single day. Formulas for vectorial capacity are reviewed in Box 2.