Fast Variable Density Poisson-Disc Sample Generation with Directional Variation for Compressed Sensing in MRI

Abstract

We present a fast method for generating random samples according to a variable density poisson-disc distribution. A minimum parameter value is used to create a background grid array for keeping track of those points that might affect any new candidate point; this reduces the number of conflicts that must be checked before acceptance of a new point, thus reducing the number of computations required. We demonstrate the algorithm’s ability to generate variable density poisson-disc sampling patterns according to a parameterized function, including patterns where the variations in density are a function of direction. We further show that these sampling patterns are appropriate for compressed sensing applications. Finally, we present a method to generate patterns with a specific acceleration rate.

1. Introduction

In MRI, multiple coils and compressed sensing have both reduced the number of samples required to generate diagnostic quality images. The multiple coils provide additional spatial encoding that is used to interpolate missing k-space data points (a technique commonly called parallel imaging) [1, 2, 3]. Compressed sensing takes advantage of the a priori knowledge that most of the values of the image are approximately 0 after a sparsifying linear transformation (e.g. a Daubechies Wavelet transform) [4, 5]. When the system matrix satisfies specific properties (e.g. the Restricted Isometry Principal, the Restricted Isometry Principal in Levels, or the Mutual Coherence Conditions) then the error on the final image is bounded [6, 7, 8]. Remarkably, these conditions can often be achieved with a random sampling pattern [9]. Compressed sensing has been used in MRI with great success [4, 10, 11].

When combining multi-coil imaging with compressed sensing, one wants to employ a random sampling pattern to satisfy the compressed sensing requirements, but still keep samples far enough from each other to take advantage of the spatial encoding of the multiple coils. A poisson-disc sampling pattern can be used to simultaneously satisfy these properties in a three-dimensional acquisition with phase encoding in two dimensions [10]; each point of the pattern represents a readout line in the third dimension [12]. It is desirable that the pattern generation algorithm be fast in order to permit investigation of different sampling distributions and determine the advantages and disadvantages of each one. Furthermore, it should accommodate densities that depend on direction to account for different coil configurations. And finally, the sampling pattern should satisfy a desired overall acceleration factor.

The simplest dart throwing algorithm for generating a poisson-disc sampling pattern (randomly choose a point, verify that the point is not too close to any existing point, repeat) is a slow process [13]. Other methods are more efficient, but impose additional requirements (e.g. a mesh defining a surface of interest, or a tiling of the space where the density along the edges of the tiles may be noticeably different) [14]. These are confounding effects that are not required for sample generation in MRI, where the region of k-space of interest is a simple rectangular subset of a Euclidean space. In [15], Bridson described a fast $\mathcal{O}(n)$ algorithm for generating a poisson-disc sampling pattern with a constant density. In [16], Tulleken adapted this algorithm to accommodate a variable density sampling pattern based on a priori knowledge of the largest poisson-disc radius parameter. Tulleken’s method is $\mathcal{O}(n^2)$. Notably, this method cannot accommodate a sampling density that depends on direction.

In many cases of sample generation with MRI, we know the minimum distance between samples a priori. In this paper, we alter the methods of [15, 16] to take advantage of this knowledge. We present a faster method of generating samples according to a variable density poisson-disc distribution in a rectangular subset of a Euclidean space with an arbitrary number of dimensions. We make three novel contributions for generating variable density poisson-disc sampling patterns to be used with compressed sensing in MRI.

• We present a more computationally efficient and faster method than the state of the art.

• We present a computationally efficient method to accommodate rotationally asymmetric sampling density, permitting more acceleration in one direction than another.

• We present an automatic method to generate a sampling pattern with a desired overall acceleration rate, even with an asymmetric sampling density.

2. Methods

2.1. Background

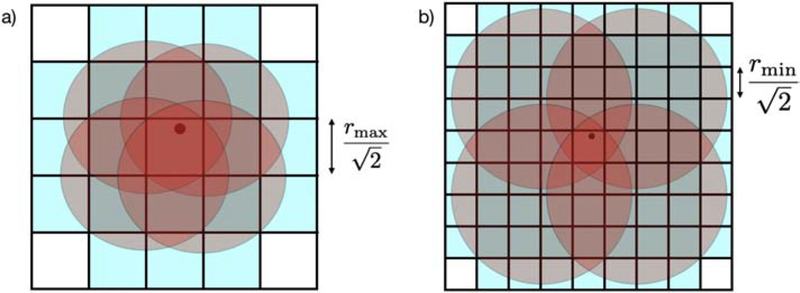
The Bridson method of [15] reduces the computational time dramatically over the dart throwing algorithm by utilizing a background grid. Assuming a fixed poisson-disc parameter r, the method partitions the space into a set of cubes where the edges have length $r/\sqrt{d}$ (where d is the number of dimensions of the space). The cube edge is set to this length so that the cube’s diagonal has length r; thus, each cell can contain at most 1 point. For each new point, then, one need not check the distance to all other points. Instead, only those points that are indexed in grid cells within range (as illustrated in the Fig. 1a, where r = r_max ) need to be checked [16].

Figure 1:

a) For a new point (shown with a black dot), only those cells intersected by the red circles (shaded blue) can contain points close enough to violate the distance threshold. If the point were in n dimensions instead of 2 dimensions, the length of each side of all cubes would be $r_{\max }/\sqrt{n}$. b) A new candidate point y_j with poisson-disc parameter r_j is illustrated with the black dot. In this figure, ceiling(r_j /r_min ) = 4. The red circles have diameter 4r_min and are tangent to the corner of the cell containing y_j. The blue squares are those cells that could contain points that are within r_j of y_j. If the point were in n dimensions instead of 2 dimensions, the length of each side of all cubes would be $r_{\min }/\sqrt{n}$.

Algorithm 1:

Variable Poisson-Disc Sampling

Inputs: rmax, background array, parameter k, N = 0

Select a point at random, add it to the list of points, add index 1 to the active list, and set N = 1

While: active list is not empty

Choose an index i randomly from the active list

Create k new points uniformly at random in the spherical annulus between radii r(xi) and 2r(xi) centered on xi

For each: created point yj

If yj is not within domain bounds, continue

Compute the distance to those points that may be closer than r(yj) with indices listed in the nearby background grid cells as illustrated in Fig. 1a.

If the minimum distance > r(yj)

Add yj to the list of points, add index N + 1 to the active list and the appropriate elements of the background grid, and then increment N by 1.

End If

End For

If none of the k points were valid, remove i from the active list.

End While

Outputs: List of points

When creating candidate points, one must choose points randomly on a spherical annulus. The number of points chosen is denoted by k. In [15], Bridson suggests a value of k =30; we have found that the processing is faster with comparable results in two dimensions when k =10. To choose points in two dimensions, construct a vector with angle (in radians) chosen uniformly at random on [−π, π) and magnitude chosen uniformly at random on [r, 2r]. To sample a point at random in n dimensions, generate a vector with n elements where the value of each element is a realization of a normally distributed random variable. Since the normal distribution is rotationally symmetric, every direction has equal probability density. Then, scale this vector to a magnitude chosen uniformly at random on [r, 2r].

The method by Tulleken of [16], detailed in Alg. 1, accommodates a variable density poisson-disc sampling pattern (meaning that the parameter r changes as a function of location) by altering the background array so that 1) each element of the grid accepts a list of points and 2) the cell size must be computed from the maximum possible parameter value (see Fig. 1a). The index of each new valid point is added to the list of the background grid element that contains the new point.

Though this would result in a realization of the desired sampling pattern, it is inefficient, as the following thought experiment illustrates. Suppose that r is small near the center of the image and increases as the distance from the center increases. In this case, the largest values of r would be attained at the corners of the region. Indeed, this is the most common use case for compressed sensing MRI applications. These values could be so large that the rectangular region of interest would be divided into a small number of large grid cells, meaning that many points would be listed within each grid cell and all of those points would need to be checked with each additional candidate point. The computational cost degenerates to that of the extremely slow dart throwing algorithm. In section 2.2, we explain how to overcome this inefficiency.

2.2. Fast algorithm

For the fast algorithm, it is assumed that a positive minimum bound on r exists: r_min >0. This is almost certainly the case with MRI. The k-space samples need not be closer than the inverse of the field-of-view. Moreover, with compressed sensing, the center region of k-space is often fully sampled (meaning that samples are separated by a distance equal to the inverse of the field-of-view) [12, 10]. With these applications, the density of samples do not vary unless they are located some positive distance from the origin. Thus, for any variable density scheme that reduces the sampling density as distance from the origin increases, the size of the fully-sampled center region can be used to determine r_min.

The region of interest is partitioned into a grid of cubes where the edges all have length $r_{\min }/\sqrt{d}$. (Note that the background grid must be re-defined for different values of r_min.) Grid elements do not contain the indices of points that fall within their boundary. Instead, each grid element contains a list of indices of those points that might have their threshold distance violated by a point in the grid cell. When a new point is considered as a candidate for the sample distribution, its distance is checked against all of those points with indices located in its grid cell. If the candidate point is not too close to any existing points, then its index is added to all of those grid cells where its distance threshold reaches (as illustrated in Fig. 1b). The entire algorithm is specified in Alg. 2.

Algorithm 2:

Fast Variable Density Poisson-Disc Sampling

Inputs: rmin, background array, parameter k

Select a point at random, add it to the list of points, add index 1 to the active list, and set N = 1

While: active list is not empty

Randomly select index i from the active list

Identify the poisson-disc parameter for this point, r(xi)

Create k new points uniformly at random in the spherical annulus between radii r(xi) and 2r(xi) centered on xi

For each: created point yj

If yj is not within domain bounds, continue

Compute the distance to those points with indices in the list of the background grid element that contains yj.

If the minimum computed distance > r(yj)

Add yj to the list of points, add index N + 1 to the active list and the lists of the background grid elements with points that may be within r(yj) according to Fig. 1b, and then increment N by 1.

End If

End For

If none of the k points were valid, remove i from the active list.

End While

Outputs: List of points

We will now prove that there is a computational advantage to the fast algorithm over Alg. 1. We will write the proof for d =1 in hopes that the extension to higher dimensions is clear. The burden comes from the computations of distances between a candidate point and existing points. The slow dart-throwing algorithm computes the distance between each candidate point and all existing points. Both Alg. 1 and Alg. 2 reduce the number of distance computations by taking advantage of a background grid. We will show that the fast algorithm can result in fewer distance computations.

Let z_c be the location (on a line) of a new candidate point; without loss of generality, assume $z_c\in \left[-r_{\max }/2,r_{\max }/2\right]$. With Alg. 1, an existing point at location z_e is compared to the candidate point if $z_e\in \left[-(3/2)r_{\max },(3/2)r_{\max }\right]$, regardless of what the value is for the poisson-disc parameter of the existing point. With the fast algorithm, an existing point at location z_e is only compared to the candidate point if

$$z_e\in \left[r_{\min }\left(\frac{-1}{2}-\lfloor \frac{r_e}{r_{\min }}\rfloor \right),r_{\min }\left(\frac{1}{2}+\lfloor \frac{r_e}{r_{\min }}\rfloor \right)\right],$$

where r_e is the value of the poisson-disc parameter for the existing point. Note that

$$r_{\min }\left(\frac{1}{2}+\lfloor \frac{r_e}{r_{\min }}\rfloor \right)\le \frac{r_{\min }}{2}+r_{\min }\lfloor \frac{r_{\max }}{r_{\min }}\rfloor \le \frac{r_{\min }}{2}+r_{\max }.$$

Since r_min ≤r_max,

$$\left[r_{\min }\left(\frac{-1}{2}-\lfloor \frac{r_e}{r_{\min }}\rfloor \right),r_{\min }\left(\frac{1}{2}+\lfloor \frac{r_e}{r_{\min }}\rfloor \right)\right]\subset \left[-(3/2)r_{\max },(3/2)r_{\max }\right].$$ (1)

It is not necessarily the case that Alg. 2 calculates fewer distances than Alg. 1. For example, if the poisson-disc parameter is constant, the both Alg. 1 and Alg. 2 reduce to the Bridson algorithm. However, by (1), the fast Alg. 2 cannot calculate any more distances than Alg. 1. If the poisson-disc parameter changes significantly over the space, then it will likely calculate fewer, which makes the algorithm more efficient. We show that this is the case for compressed sensing in section 3.

For the results presented in this work, we used the following function for the poisson-disc parameter r (parameterized by γ):

$$r_{\gamma }(x)=\frac{\Vert x{\Vert }_2+0.15}{\gamma },$$ (2)

where ||·||₂ represents the L₂ norm. For this function, r_min = 0.15/γ and r_max = (||x_corner ||₂+0.15)/γ where x_corner is any corner of the sampling domain.

2.3. Sampling density that is based on direction

The rectangular subset of interest in k-space is usually [−0.5, 0.5]^d cube¹. (An exception would be a Homodyne sampling pattern, where the rectangular region is a little more than half of this cube [17].) As discussed, it may be desirable to alter the density distribution of points as a function of direction. That is, in addition to the poisson-disc parameter r being a function of location, it would also be a function of radial direction to take advantage of coil placement geometry. For a general function of radial direction, this is a computationally challenging task since it requires determining the direction between points and evaluating this function. However, in MRI, it is usually the case that we are interested in acceleration rates that differ along the axes of the rectangular region. For example, with a birdcage coil, the spatial encoding of each coil differs significantly in the transverse plane but differs little in the longitudinal direction. Therefore, a higher acceleration is possible in the transverse plane than in the longitudinal direction. An example of this can be seen in Fig. 4a.

Figure 4:

Fully sampled reconstructions of an 8-coil extremity coil. The sensitivities of the coils in the anterior/posterior differ, whereas the sensitivity in the superior/inferior direction are approximately uniform for all coils. a) The fully sampled reconstructions for each of the 8 coils. b) The sum-of-squares reconstruction with fully sampled data. c) The SAKE+L1-ESPIRiT reconstruction of the data retrospectively subsampled with the sampling pattern of figure 2 with γ=125 and undersampling of (3,1).

Since we are interested in acceleration rates that differ along the axes of the rectangular region, a simple trick avoids determining the angle between points and evaluating the parameter function. For simplicity, we will consider a two dimensional case. Suppose one wants to undersample the second dimension by an additional factor of v (meaning the density of samples will be greater in the first dimension than in the second). Then, one can generate a variable density poisson-disc sampling pattern on the region [−0.5, 0.5]×[−0.5/v,0.5/v] quickly with a radially symmetric poisson-disc parameter using Alg. 2. After the points are generated, scale the resulting pattern by v in the second dimension to generate a pattern of points on [−0.5, 0.5]².

2.4. Specifying the Acceleration Rate

The acceleration rate of a sampling pattern is the number of samples acquired divided by the number of samples required for full sampling. It is often convenient to be able to specify an overall acceleration rate and attain a corresponding sampling pattern. In this section, we describe a method to attain this goal.

In order to do so, we require a poisson-disc parameter function $r_{\gamma }:{ℝ}^d\to ℝ$ parameterized by γ ≥ 0 such that r decreases monotonically with increasing γ. (Equivalently, the overall acceleration rate increases with increasing γ.) Note that (2) satisfies this property. Then, with the computational efficiency of Alg. 2, we can now specify an overall acceleration rate α and determine the desired sampling pattern with a binary search algorithm in a reasonable amount of time. (The total computational time is the time of any single iteration multiplied by the number of iterations in Alg. 3.)

In order to use the binary search, one must supply bounds γ_min and γ_max. Since γ is positive, γ_min = 0 is a lower bound. The γ that corresponds to r_min would be γ_max. The complete search is specified in Algorithm 3.

Algorithm 3:

Find Pattern for Specified Acceleration Rate

Inputs: Desired acceleration rate α, bounds γmin and γmax, tolerance tol > 0.

Do:

ε = (γmax − γmin) / 2

γmid = ε + γmin

Determine the sampling pattern P using Algorithm 2 with parameter function $r_{{\gamma }_{\text{mid}}}$

If: Acceleration rate > α

γmax := γmid

Else:

γmin := γmid

While ε > tol

Outputs: Pattern P

3. Results

Figure 2 shows variable density sampling patterns generated with Alg. 2 using the poisson-disc parameter function of (2) for γ∈{50,75,100,125,150} and additional directional undersampling of 3. As expected, as γ increases, the overall acceleration rate (equal to the number of samples divided by the size of the domain) decreases.

Figure 2:

Variable density poisson-disc sampling patterns generated with the fast algorithm of Alg. 2.

Table 1 compares the time required to compute the variable density poisson-disc sampling pattern with Alg. 2 to the time required by Alg. 1 for the sampling patterns shown in Fig. 2. The improvement in run time is between 30–50%. The algorithms were implemented in C on a 2012 Macbook Pro with a 2.5 GHz Intel i7 processor.

Table 1:

Run times for generating variable density poisson-disc sampling patterns with Alg. 1 and Alg. 2. Time is reported in milliseconds. In all cases, Alg. 2 is faster by 30–50%.

	Processing Time (ms): Alg. 2 / Alg. 1
	γ = 50	γ = 75	γ = 100	γ = 125	γ = 150
(3,1)	10 / 20	20 / 40	40 / 70	60 / 110	110 / 150
(1,1)	20 / 30	50 / 80	100 / 140	150 / 220	230 / 340
(1,3)	10 / 20	20 / 40	40 / 70	70 / 110	110 / 150

In Fig. 3, we present a comparison of the results from Alg. 2 to results from Alg. 1 with γ=150 and without any additional directional undersampling. For both, we created a Voronoi partition of the domain and plotted the area of each cell versus distance of the point from the origin in Fig. 3a. The distributions of area versus distance are very similar. In Fig 3b, we show the magnitude of the point spread functions for both algorithms. Again, they are similar; the mean square difference is 1.1×10⁻⁶. The fast algorithm offers a computational benefit without sacrificing quality.

Figure 3:

(a) Area of the Voronoi cell plotted against distance from the origin for each sample point with γ=150 for the fast algorithm (blue) and the Tulleken algorithm (red). The distribution of points of the two algorithms is similar, indicating that they are generating sampling patterns of similar quality. (b) The top row shows the magnitude of the full point spread function and the magnitude of the difference between them. The bottom row zooms in on the region of the white box. There is not a significant difference between the point spread functions of the sampling patterns.

Figures 4 and 5 show how the sampling mask could be used with MRI using knee and ankle data, respectively. The data of Fig. 4 was taken from mridata.org [18]. The data for Fig. 5 was collected with a clinical 3 Tesla scanner and an 8-channel ankle coil. Both of these datasets consist of fully sampled three-dimensional data with two dimensions of phase encodes and a single dimension of readout. An inverse Fast Fourier Transform was applied in the readout direction placing the data in a hybrid space [19, 20]; further processing was only done on a single slice (though multiple slices could also have been reconstructed). The data was retrospectively undersampled with the relevant sampling pattern. The SAKE+L1-ESPIRiT algorithm was used to reconstruct data that was retrospectively subsampled with the variable density poisson-disc sampling masks [22, 22]. Subfigure (a) shows the fully sampled reconstruction from each individual coil, (b) shows the sum-of-squares reconstruction with fully sampled data, and (c) shows the SAKE+L1-ESPIRiT reconstruction from retrospectively subsampled data. The SAKE+L1-ESPIRiT reconstruction is very similar to the fully sampled sum-of-squares reconstruction.

Figure 5:

Fully sampled reconstructions of an 8-coil ankle coil. a) The fully sampled reconstructions for each of the 8 coils. b) The sum-of-squares reconstruction with fully sampled data. c) The SAKE+L1-ESPIRiT reconstruction of the data retrospectively subsampled with the sampling pattern of figure 2 with γ=100 and no directional undersampling.

Figure 6 shows patterns generated with specific accelerations using Alg. 3. Both Alg. 1 and Alg. 2 were used as the underlying method to determine the sampling pattern. A tolerance of 0.01 in the acceleration factor was permitted. Indeed, sampling patterns with the specified acceleration rate were generated. And, the sampling patterns generated with Alg. 1 and Alg. 2 are qualitatively similar.

Figure 6:

Acceleration Patterns

In the spirit of reproducible research, we provide an implementation in C for the algorithms described; the software package can be downloaded from: https://github.com/ndwork/fastVDPD_C.

4. Discussion and Conclusion

In this work, we presented a fast algorithm for generating a variable density poisson-disc sampling pattern, we show how the method can be adapted to permit a further directional undersampling, and we presented a method for generating a sampling pattern with a specific acceleration factor. Having a fast algorithm for creating variable density poisson-disc sampling patterns will empower future researchers to investigate different sampling distributions and determine the advantages and disadvantages of each one. Additionally, different sampling patterns can be generated for different collections, which may be beneficial for some applications.

When selecting candidate points around an existing point, it may be the case that the candidates are unluckily chosen so that they conflict with existing points, but other candidate points could have been created that would not have. Thus, the realized set of samples is not guaranteed to be maximal (where a maximal realization is one where the points are as dense as possible) [23]. However, the probability that the realization is maximal is typically very high (for sufficiently large values of k) [24].

In this paper, we have shown that a simple scaling permits a computationally efficient method for generating patterns with directional undersampling. A more general transformation can be used to create variations with more interesting patterns. For example, an affine transformation (or even any homeomorphism) could be used to generate directional sampling patterns. The applications to MRI of such a technique are not immediately obvious.

It may be possible to further reduce the speed of sample generation by using parallelization to take advantage of multiple processing cores [25]. Additionally, it may be useful to adapt this algorithm to generate samples according to a variable density poisson-disc distribution on a surface [26, 24]. We leave these prospects as possibilities for future work.