MR cell size imaging with temporal diffusion spectroscopy

Abstract

Cytological features such as cell size and intracellular morphology provide fundamental information on cell status and hence may provide specific information on changes that arise within biological tissues. Such information is usually obtained by invasive biopsy in current clinical practice, which suffers several well-known disadvantages. Recently, novel MRI methods such as IMPULSED (imaging microstructural parameters using limited spectrally edited diffusion) have been developed for direct measurements of mean cell size non-invasively. The IMPULSED protocol is based on using temporal diffusion spectroscopy (TDS) to combine measurements of water diffusion over a wide range of diffusion times to probe cellular microstructure over varying length scales. IMPULSED has been shown to provide rapid, robust, and reliable mapping of mean cell size and is suitable for clinical imaging. More recently, cell size distributions have also been derived by appropriate analyses of data acquired with IMPULSED or similar sequences, which thus provides MRI-cytometry. This review summarizes the basic principles, practical implementations, validations, and example applications of MR cell size imaging based on TDS and demonstrates how cytometric information can be used in various applications. In addition, the limitations and potential future directions of MR cytometry are identified including the diagnosis of nonalcoholic steatohepatitis of the liver and the assessment of treatment response of cancers.

1. Introduction

Cell size is a fundamental feature of cells and plays important roles in basic cellular functions. For example, cells monitor cell size and geometry and use this information to control cell division (1,2); Cell shrinkage is a hallmark of programmed cell death (i.e., apoptosis) (3); hepatocytes exhibit ballooning associated with cell swelling in nonalcoholic steatohepatitis; and cancer immunotherapy induces shifts in the mean cell size of a population of cells as small immune cells infiltrate targeted tumors (4). Measurements of cell size and their changes over time can thus have high clinical significance to provide key information at the cellular level, which can lead to more sensitive and specific information on biological tissues. Except for blood analyses of anemia (5,6) or cancer (7), cell size measurements in solid organs are not widely used in routine clinical practice. One major reason is that biopsy is an invasive procedure that has many well-known disadvantages including side effects and an inability to reflect the spatial heterogeneity of whole organs. It is desirable to develop an imaging method that can map cell size non-invasively.

Diffusion MRI (dMRI) is a widely used imaging method that relies on detecting the hindrance and/or restriction to the free diffusion of water molecules in tissues, and which thereby probes tissue microstructure indirectly. Because the degree of restriction depends on the density and spacing of obstacles such as cell membranes, dMRI provides a unique means to probe cell size and density. However, metrics derived from conventional dMRI, particularly the apparent diffusion coefficient (ADC), represent an averaged diffusion property that is influenced by several microstructural features simultaneously. Hence, ADC conveys non-specific information on a variety of tissue properties, including but not limited to sizes of nuclei (5), organelles (6), cells (2), cell membrane permeability (3), intra- and extracellular diffusion coefficients (4), and intracellular volume fraction (5). This sensitivity allows ADC to reflect a variety of pathological variations in biological tissues, but it reduces the specificity to individual tissue properties such as cell size. Moreover, different tissue properties at different length scales may have concurrent, opposing influences on ADC that may cancel out each other, which may result in a reduced sensitivity to pathological variations (7).

Quantitative diffusion modeling is a promising way to disentangle the complex information in dMRI and enhance the specificity to e.g., cell size. Tissues are complex, heterogeneous media containing multiple compartments of water in different microenvironments. These compartments may have different sizes, shapes, connectedness and intrinsic diffusivities, each of which behave differently in their signal changes in response to different diffusion times and diffusion weighting factors (b values). Different compartments may be classified into e.g., intra- and extracellular spaces, based on their particular diffusion and geometrical properties. By using a carefully selected set of data acquisitions and fitting quantitative models to dMRI data, microstructural parameters such as cell size can be obtained. A considerable number of recent studies (8–16) have attempted to derive quantitative indices of tissue microstructure using this strategy. The VERDICT (vascular, extracellular and restricted diffusion for cytometry in tumors) (8–10), IMPULSED (imaging microstructural parameters using limited spectrally edited diffusion) (12,13,17), and POMACE (pulsed and oscillating gradient MRI for assessment of cell size and extracellular space) methods (18) have been developed for mapping mean cell sizes in tumors. Among these methods, VERDICT and IMPULSED have been successfully implemented in patients with prostate (9) and breast (12) cancer, respectively, within clinically feasible scan times. Studies have reported the agreement between VERDICT MRI and 3D histology in fresh and fixed prostate specimens (19), but VERDICT derived cell sizes have not been validated, possibly due to the lack of clear cell boundaries in the haematoxylin and eosin (H&E) stained sections. By contrast, the IMPULSED derived cell size has been comprehensively validated using computer simulations in silico, cells in vitro, and animals in vivo using Na⁺/K⁺-ATPase (ab76020, Abcam) staining for pronounced visualization of cell boundaries (13,17).

However, the above imaging methods report only mean cell sizes of a population, and mean sizes are often inadequate to characterize tissue microstructure. It is well-known that there is significant heterogeneity in cell size particularly in tumors (2). Cell size distributions may provide important additional information on tissue status for diagnosis or monitoring responses to interventions (20–22). Several attempts have been reported to estimate non-parametric compartment size distributions without a priori knowledge of the distribution function in phantoms of glass capillaries (23), fixed tissues ex vivo (24–26), and animal allografts in vivo (27). However, these approaches either used special preclinical hardware or focused on animal applications only. Therefore, there is a need to develop an imaging method for mapping cell size distributions in humans. Recently, an extension of IMPULSED termed MRI-cytometry has been reported to fulfill this requirement (28). With comprehensive validations in preclinical models and demonstrations of applications in breast cancer patients, MRI-cytometry has been shown to be a relatively fast (~ 7 mins) and reliable imaging method suitable for reporting cell size distributions in clinical applications.

Both the IMPULSED and MRI-cytometry approaches are based on Temporal Diffusion Spectroscopy (TDS), which connotes the acquisition of dMRI data with a range of diffusion times expressed in terms of components of a diffusion spectrum. TDS is a general approach which uses different gradient waveforms that have different spectral contents. TDS has been comprehensively reviewed previously (29) so this review will focus on how MR cell size imaging is possible with IMPULSED and MRI-cytometry using the theory of TDS. Briefly, conventional dMRI uses pulsed gradient spin echo (PGSE) sequences that acquire signals after relatively long diffusion times (> 30 ms in practice), corresponding to low frequency components of the diffusion spectrum. TDS also uses oscillating gradient spin echo (OGSE) sequences that can probe much shorter diffusion times, such as 5 ms on regular clinical 3 Tesla MRI scanners (12) and ~1.6 ms on preclinical MRI scanners (13,17) which correspond to higher frequency components of the diffusion spectrum. Because the sensitivity of diffusion to different length scales is dependent on diffusion time (29), using a broader range of diffusion times provides a more comprehensive information on microstructure at different length scales. In particular, the shorter diffusion times achieved with the OGSE sequence increase the sensitivity of acquired signals to intracellular diffusivities, which is usually challenging with the conventional PGSE sequence only. Quantitative measurements of tissue microstructure (e.g., cell sizes and cell densities) are then obtained by fitting a combination of OGSE and PGSE signals to a simple but realistic model of restricted and hindered diffusion in solid tissues. For organs that have dense vasculature (e.g., livers and tumors), the signal decay from Intravoxel Incoherent Motion (IVIM), such as blood in the microcirculation, cannot be ignored. Although measuring perfusion and its related parameters using quantitative IVIM models have been actively investigated (30,31), its clinical values have been questioned (e.g., in need of impractical high SNRs for reliable fittings, and lack of careful assessment and validation of connections between IVIM-theory-based parameters and physiological factors) as to its suitability for tissue characterization (32). Therefore, MR cell size imaging with IMPULSED and MRI-cytometry deliberately remove the influences of IVIM signals prior to the extraction of microstructural parameters.

In this article, we provide a comprehensive review of the theory, development, implementation, validation, and reported applications of MR cell size imaging with IMPULSED and MRI-cytometry. The pulse sequences, recommended acquisition parameters, technical challenges, data analysis strategies, and possible future directions are provided. We aim to provide a detailed handbook from basic theory to advanced applications for implementing MR cell size imaging with IMPULSED and/or MRI-cytometry in research or clinical applications.

2. Theory

2.1. One-compartment model

Diffusion time dependent ADC(t_diff) has long been used to probe the microstructure of porous media and biological tissues (29,33). With the inclusion of OGSE acquisitions, the t_diff range can be significantly extended, so that measurements of the temporal diffusion spectrum ADC(f) provide more comprehensive information, where f is the oscillating gradient frequency. ADC(f) has been fit to either a power law (i.e., ~ e^−θ) (34,35) or a linear function (i.e., ADC = DDR · f + ADC₀) (7,36–39) to obtain the dispersion rate DDR, which has been shown to be correlated with average compartment size in selected media (36,37). To attempt quantification of microstructure over a broader range of t_diff, a simplified one-compartment model of tumors has been considered as (4,40)

$$\text{ADC}(f)={\text{ADC}}_{\mathit{\text{sphere}}}\left(\overline{d},D_{\infty }-D_0\mid f\right)+D_0$$ [1]

where ADC_sphere is the analytical form of ADC of the fluid inside an impermeable sphere at the frequency of f, $\overline{d}$ is the apparent restriction size, and D₀ and D_∞ are ADC values when f → 0 and f → ∞, respectively. Note that $\overline{d}$ is associated with mean cell size and D₀ and D_∞ are mainly determined by the extracellular tortuosity, and intracellular diffusion coefficient, respectively.

Because only a few ADC measurements at different f’s are required, Eq.[1] provides a rapid means to obtain averaged dimension sizes (41), and has been implemented in a few anti-cancer treatment studies (40,42). However, Eq.[1] is an oversimplified one-compartment model so that the measured dimension size reflects but does not equal mean cell size due to e.g., the influence of extracellular water. To better describe complex biological tissues, more realistic and specific multi-compartment models are required.

2.2. General multi-compartment model

The dMRI signal attenuations in biological tissues can be considered consisting of three main components: restricted diffusion in cells, hindered diffusion in the extravascular extracellular space, and dephasing from blood (i.e., the intra-voxel incoherent motion (IVIM) (43)), namely,

$$S\left(TE\mid b,t_{\mathit{\text{diff }}}\right)=\left(1-f_{\mathit{\text{IVIM}}}\right)\times \left(v_{\text{in }}{e}^{-TE/T_{2,in}}{S}_{in}+\left(1-v_{in}\right)e^{-TE/T_{2,ex}}{S}_{ex}\right)+f_{\mathit{\text{IVIM}}}\times e^{-TE/T_{2,\text{ blood }}}{\text{S}}_{\mathit{\text{IVIM}}}$$ [2]

where TE is echo time, b is the diffusion weighting factor, t_diff is the effective diffusion time, S_IVIM is the signal affected by IVIM and f_IVIM is its fraction, T_2,in, T_2,ex, and T_2,blood are T₂ relaxation times in intra-, extra-cellular spaces and the IVIM component (blood in capillaries), respectively. $S_{\mathit{\text{tissue}}}=v_{in}{e}^{-TE/T_{2,in}}{S}_{in}+\left(1-v_{in}\right)e^{-TE/T_{2,ex}}{S}_{ex}$ is the total signal affected by diffusion in tissues, S_in and S_ex are dMRI signals arising from the intra- and extra-cellular spaces, respectively, and v_in is the proton volume fraction of intracellular space. It is usually challenging to directly fit Eq.[2] to dMRI data and hence a simplification is needed. Note that the transcytolemmal water exchange is ignored here for simplicity but its influence should be evaluated (see below).

2.2.1. Influence of IVIM

If the blood volume fraction is small such as in normal brains, f_IVIM ≪ 1 and hence Eq.[2] degenerates to a simple two-compartment model. However, f_IVIM cannot be ignored in tissues with high blood volume fractions such as in some tumors and livers (44). If signals are acquired with only long t_diff values using PGSE sequences only, f_IVIM is much less sensitive to t_diff and hence a three-compartment model can be fit directly including a constant IVIM component (8). However, a broadened t_diff range achieved by using additional OGSE sequences no longer allows the approximation of t_diff-independence because f_IVIM varies significantly with t_diff especially when short t_diff’s are involved (45). For example, a liver study found out that, if the IVIM effect is not removed, a longer t_diff causes a larger signal decay than that of a shorter t_diff, resulting in a patently erroneous conclusion that ADC at long t_diff is larger than the ADC at short t_diff (46).

Based on theory (43), S_IVIM = exp(−b · D*) where D* is the pseudo-diffusion coefficient originated from blood flow and self-diffusion of blood in a randomly orientated blood capillary network. For non-flow-compensated PGSE acquisitions with a relatively long diffusion time, D* is dominated by signal dephasing resulting from blood flow, which is usually 10 – 50 times larger than an intrinsic diffusion coefficient. S_IVIM decays much faster than S_tissue and becomes negligible when b ≥ 0.2 ms/μm². In addition, the Gaussian diffusion approximation is usually valid up to b ⩽ 1 ms/μm². For flow-compensated OGSE acquisitions, D* is dominated by the self-diffusion of blood, which is close to the tissue water diffusion coefficient (47). Therefore, this provides a window of b values in which dMRI signal decays should be mono-exponential. By fitting a mono-exponential model to the data with b values in this window, the y-intercepts obtained by extrapolating the signal curves represent IVIM-weighted S_tissue(b = 0). By normalizing signals with the y-intercepts, the IVIM effect can be removed. We need to emphasize that, because the IVIM effect is t_diff dependent, this procedure should be applied to each diffusion decay curve with the same t_diff. Figure 1 shows a representative case how the IVIM effect was removed in a healthy human liver.

Figure 1.

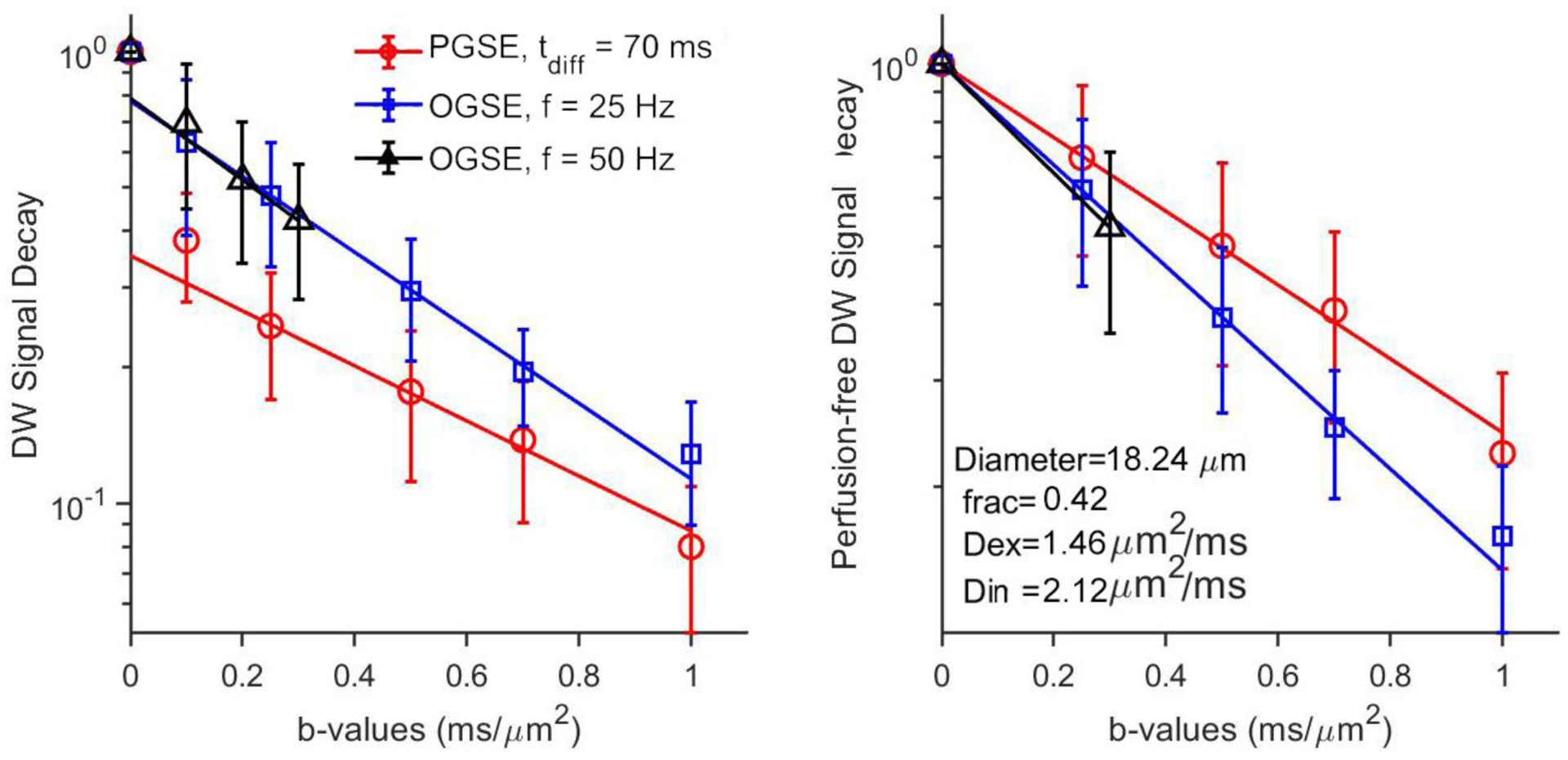
Typical Diffusion-weighted signals for voxels from a single slice of healthy human liver. (A) raw DW signals; (B) Corrected DW signals with the removal of the IVIM effect.

2.2.2. Influence of T₂ relaxation

Most multi-compartment diffusion models ignore the possible differences in relaxation properties between intra- and extracellular spaces (8,17,18). This assumption is particularly relevant in tumors. For example, a quantitative magnetization transfer (qMT) study suggests that the relatively higher transcytolemmal water exchange rate in tumors enables enough proton mixing to yield homogenous T₁ and MT values in the intra- and extracellular spaces (48). Moreover, a multi-echo T₂ spectrum measurement showed that the majority (93.2 ± 6.2%) of total MRI signals arise from a single peak of T₂ (76.4 ± 9.3 ms) in rodent brain tumors at 7 Tesla (49), suggesting small differences between intra- and extracellular spaces in tumors. Therefore, all relaxation terms are considered to be ignored in Eq.[2] for tumors.

2.2.3. Influence of transcytolemmal water exchange

It is well-known that the cell membranes are semipermeable and allow water molecules pass across, producing transcytolemmal water exchange. Early diffusion NMR studies have shown that such water exchange can significantly affect ADC measurements (50) and a recent study suggests transcytolemmal water exchange can be negligible only when the t_diff is at least one order of magnitude smaller than the resident lifetime of intracellular water, which is not the case for most PGSE measurements (51). Moreover, transcytolemmal water exchange is significantly higher in various neural diseases (52,53) and cancer (54), especially in apoptotic regions (55), and hence it should not be ignored in multi-compartment diffusion models.

However, a recent study with both simulations and experiments reported that, although enhanced transcytolemmal water change leads to a remarkable underestimation of intracellular water fraction, it has negligible influences on the estimation of mean cell size at least for t_diff ⩽ 50 ms (56). This is encouraging since our focus is MR cell size imaging and hence the transcytolemmal water exchange can be ignored in our model.

2.3. Simplified two-compartment model

After the removal of the IVIM effect and ignoring relaxation and transcytolemmal water exchange as shown above, the dMRI signal becomes

$$S_{\mathit{\text{tissue}}}=v_{in}{S}_{in}+\left(1-v_{in}\right)S_{ex}$$ [3]

Eq.[3] is a simplified two-compartment model and can be fit regularly. With analytical forms of S_in and S_ex linking to specific microstructural parameters, data can be fit to Eq.[3] to extract microstructural information including cell size. However, it is not a trivial problem to find appropriate analytical forms of S_in and S_ex, particularly due to their strong dependence on t_diff.

2.3.1. Intracellular signal – S_in

The intracellular diffusion-weighted signal S_in reflects the intracellular microenvironment. There are numerous intracellular organelles of varying sizes, so precise descriptions of intracellular diffusion over all time scales are complicated. However, it usually requires very short t_diff to probe variations in diffusion caused by small intracellular structures or specific organelles. For example, it has been shown that t_diff < 0.5 ms (OGSE frequency > 500 Hz) is required detect intracellular diffusion differences in cells at different stages of mitosis (57) and t_diff < 0.14 ms (OGSE frequency > 1800 Hz) is needed to probe specific organelle changes in e.g., cytoskeleton (6). Because usually much longer t_diff values are used in practical dMRI measurements, such as t_diff ⩾ 1.6 ms in animal studies (13,17) and t_diff ⩾ 5 ms in human studies (12,28), the overall intracellular diffusion does not resolve individual contributions (58) arising from within single cells, and can be considered as a membrane-confined “homogenous” fluid with a single intracellular diffusion coefficient D_in.

2.3.2. Extracellular signal – S_ex

Extracellular diffusion has previously been considered as hindered diffusion and described using a constant diffusivity, such as in tumors (8,9). However, other studies have suggested that there is a significant t_diff-dependence in extracellular diffusion. The dependence of extracellular diffusion coefficient D_ex on OGSE gradient frequency f can be described using a power-law as D_ex = D_ex0 + const · f^θ when the effective t_diff is long (34), which has been observed recently in OGSE imaging in healthy human subjects with fitted θ = 0.5 and f up to 60 Hz (59). However, more generally the dependence on t_diff or f may vary. The range of f achievable in OGSE acquisitions is usually limited to a narrow range of f in practice. In such a narrow range, previous studies have suggested the extracellular diffusion coefficient shows an approximately linear dependence on the gradient frequency f, i.e., D_ex = D_ex0 + β_ex · f, where β_ex describes the rate of change of D_ex with f, which is proportional to the inverse of diffusion time (7). This linear approximation has been used extensively in previous pre-clinical cell size imaging studies in tumors (4,13,60).

2.3.3. Analytical forms

The above sections have demonstrated that it is appropriate to assume a simplified dMRI model with practically feasible t_diff ranges that incorporates intracellular dMRI signals S_ex arising from membrane-confined fluid with a single D_in, and extracellular dMRI signals S_ex arising from t_diff-dependent hindered diffusion. However, biological tissues are heterogeneous and contain a variety of cells with different sizes and other microstructures. Two practical approaches, IMPULSED and MRI-cytometry, address the inhomogeneity of cell sizes, D_in’s, and D_ex’s, in different ways and may be used to map mean cell size and cell size distribution, respectively.

2.4. IMPULSED

The variations in size and shape of cells complicate modeling. Although most epithelial tissues show a striking regularity in cell size in normal tissues, cell size heterogeneity occurs during neoplastic growth (2). To simplify the problem while keeping the key microstructural information, numerous studies have assumed cells to be hollow spheres with a cell-volume-weighted mean cell size (diameter) $\overline{d_{vw}}$ (8,12,13,18). For a few regular geometries (i.e., planes, cylinders, and spheres), the analytical expressions that link dMRI signals to the sequence parameters and underlying biophysical properties have been reported for PGSE acquisitions (61) and OGSE acquisitions with sine and cosine waveforms (62), square and general trapezoid-sine waveforms (63), and the trapezoid-cosine waveforms that are widely used in OGSE imaging studies in humans (12). The analytical equations for cosine waveforms (widely used in preclinical imaging) and cosine-modulated trapezoidal waveform with one oscillation n = 1 (widely used in clinical imaging) are provided in the Appendix. Readers are encouraged to refer to the above references for other details. Note that previous studies have suggested the assumption of spherical cells works effectively for non-spherical cells as well to obtain cell sizes of cell-volume-matched spheres (17).

Eq.[3] becomes

$$S=v_{in}s{S}_{in}\left(\overline{d_{vw}},\overline{D_{\mathit{\text{in}}}}\mid t_{\mathit{\text{diff}}},b\right)+\left(1-v_{in}\right)\text{exp}\left[-b\cdot \left(D_{ex0}+{\beta }_{ex}\cdot f\right)\right]$$ [4]

where S_in is given by the appropriate analytical intracellular equation of water diffusion in an impermeable sphere, as reported previously (61) (12,62,63). Eq.[4] can be fit to dMRI data to extract microstructural parameters that are summarized in Table 1. Note that β_ex can be fit reliably in preclinical imaging studies with f up to 150 Hz but not in human imaging studies with f only up to 50 Hz. Therefore, a constant mean extracellular diffusivity $\overline{D_{ex}}$ is usually assumed in human imaging studies on regular clinical MRI scanners to enhance the fitting precision of other metrics (12). Moreover, there are a few other quantities that can be calculated from IMPULSED data, such as the apparent three-dimensional cell density ρ that can be estimated as $\rho =6v_{in}/\pi {\overline{d_{vw}}}^3$ based on a face-centered-cubic packing approximation (13).

Table 1.

Summary of IMPULSED derived metrics and corresponding biophysical features. Note that cell density can be calculated from d and v_in.

IMPULSED metrics	Biophysical features
$\overline{d}$	Mean cell size (cell volume weighted)
vin	Apparent intracellular volume fraction
$\overline{D_{ln}}$	Mean intracellular diffusivity
Dex0	Mean extracellular diffusivity at long tdiff
βex	Mean extracellular diffusivity change rate with tdiff

2.5. MRI-cytometry

Although the IMPULSED method reports the mean cell size, it is well-known that cell sizes are heterogeneous in biological tissues, so it is desirable to map cell size distribution non-invasively. MRI-cytometry has been recently described to fulfill this need (28). Instead of assuming mean values for all fitting metrics, MRI-cytometry considers there are distributions of all microstructural parameters in every image voxel. Each cell has a cell size d and an intracellular diffusion coefficient D_in, both of which can differ from cell to cell. Thus, each image voxel contains cells characterized by P_in (d, D_in), the normalized distribution function of the number of cells with a diameter d and an intracellular diffusivity D_in. Similarly, extracellular space is considered to contain a large number of spin packets that are characterized by P_ex(D_ex0, β_ex), the normalized distribution function of the number of spin packets with D_ex0 and β_ex. Therefore, the dMRI signals can be written as

$$S=\stackrel{\text{intracellular diffusion}}{\overbrace{\underset{D_{in}}{\int }\underset{d}{\int }{\rho }_{in}{P}_{in}\left(d,D_{in}\right)v(d)s_{in}\left(d,D_{in}\right)ddd{D}_{in}}}+\stackrel{\text{ extracellular diffusion }}{\overbrace{\underset{{\beta }_{ex}}{\int }\underset{D_{ex0}}{\int }{\rho }_{ex}{P}_{ex}\left(D_{ex0},{\beta }_{ex}\right)\mathit{\text{exp}}\left[-b\left(D_{ex0}+{\beta }_{ex}f\right)\right]d{D}_{ex0}d{\beta }_{ex}}}$$ [5]

and $S_0=S(b=0)={\int }_{D_{in}}{\int }_d{\rho }_{in}{P}_{in}\left(d,D_{in}\right)v(d)ddd{D}_{in}+{\int }_{{\beta }_{ex}}{\int }_{D_{ex0}}{\rho }_{ex}{P}_{ex}\left(D_{ex0},{\beta }_{ex}\right)d{D}_{ex0}d{\beta }_{ex}$, v(d) = πd³/6 is cell volume, ρ_in and ρ_ex are the T2-weighted intra- and extracellular dMRI signals per unit volume, respectively, and S_in is intracellular signal attenuation of an impermeable spherical cell. The analytical equations for S_in linking geometric features (d and D_in) to dMRI signals (12,62). The marginal distribution P(d) obtained from P(d, D_in) is the cell size distribution. The metrics achievable using IMPULSED, such as $\overline{d_{vw}}$, $\overline{d}$, v_in, and $\overline{D_{in}}$, can all be obtained by MRI-cytometry. For example, the non-cell-volume-weighted mean cell size $\overline{d}=\left({\sum }_{n=1}^N{d}_{(n)}P\left(d_{(n)}\right)\right)/\left({\sum }_{n=1}^{N}P\left(d_{(n)}\right)\right)$ where N is the total number cell sizes discretized in the fittings.

3. Data acquisition

Although IMPULSED and MRI-cytometry make different assumptions and perform different data analyses, both are based on the simplified two-compartment diffusion model (i.e., Eq.[3]) that can be addressed with the same data acquisitions with multiple b values and t_diff values using different pulse sequences.

3.1. Pulse sequences

IMPULSED combines both PGSE and OGSE acquisitions to cover a broader range of t_diff, providing more comprehensive information on tissue microstructure than single measurements of ADC (13,17). Figure 2 shows the typical pulse sequences containing both PGSE and OGSE sequences as implemented on regular clinical MRI scanners (12). G is the gradient strength, δ is the duration of each diffusion gradient, Δ is the separation of two gradients, t_r is the gradient rise time, t_p is the duration time of the first gradient plateau, and for OGSE sequences, t₃ = t_p + t_r/2 and N is the number of cycles in each diffusion gradient. The trapezoid-cosine waveform is the preferred OGSE waveform on clinical MRI scanners because it maximizes the diffusion weighting (64).

Figure 2.

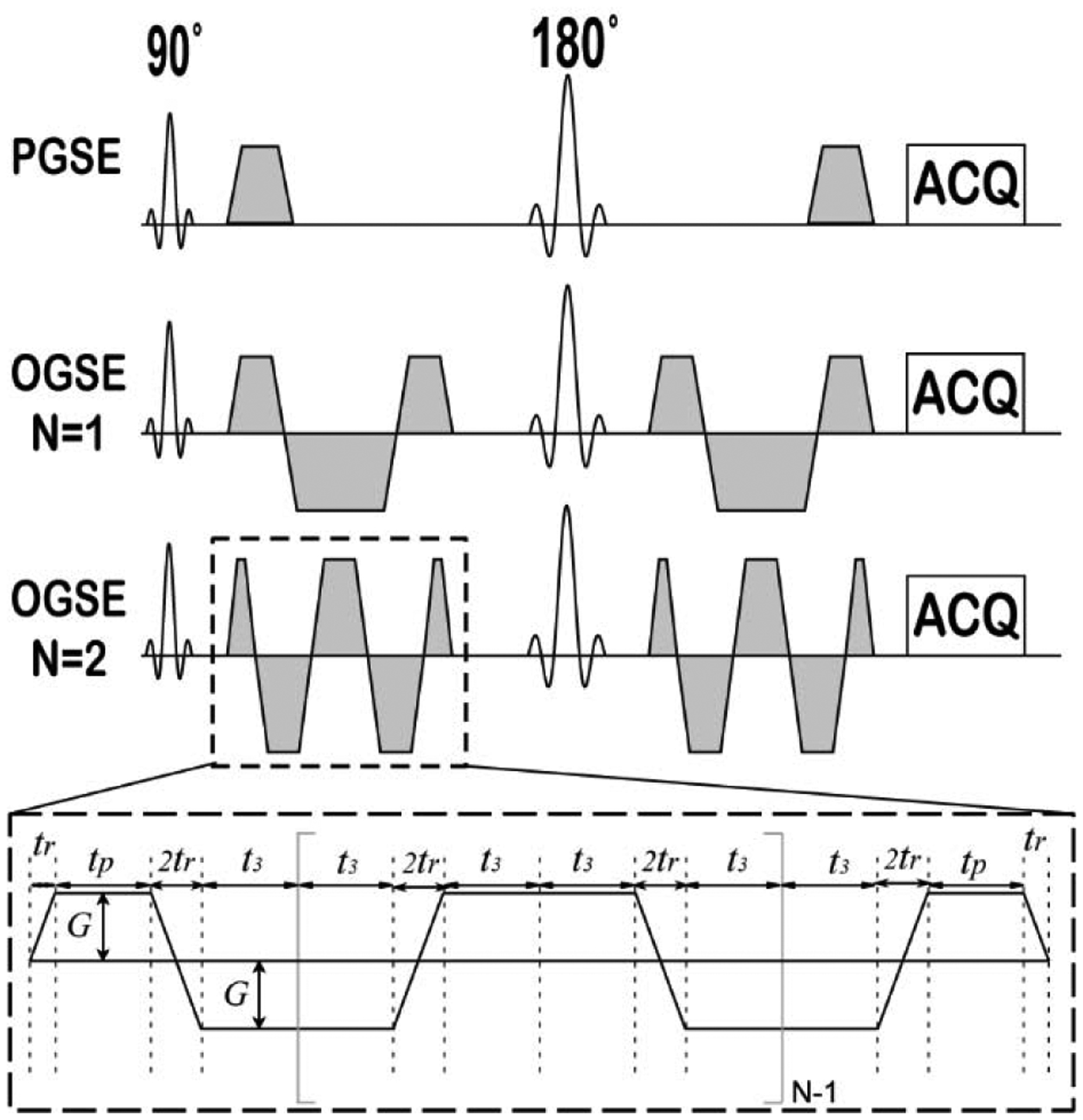
Pulse sequences used in the IMPULSED data acquisitions.

3.2. Imaging parameters

As for typical dMRI, single-shot spin-echo echo-planar imaging (EPI) is usually used for IMPULSED acquisitions but any other dMRI acquisition approaches can be incorporated in the IMPULSED. For example, the recently developed diffusion-prepared 3D gradient spin-echo sequence can reduce the scan time and enhance the SNR of OGSE acquisitions (65).

The maximum gradient strength is a key factor that determines the maximum b values for a specific diffusion time, which thus limits the shortest effective diffusion time, and the highest oscillating frequency, that can be achieved. For example, a gradient strength < 80 mT/m and slew rate ≈ 100 mT/m/sec is commonly achievable for state-of-the-art clinical scanners. With these limitations, the highest oscillating frequency is ~ 50 Hz with a maximum b value of ~300 s/mm². Table 2 lists the typical diffusion parameters used in our previous clinical and preclinical studies, which have proven successful for assessing cell sizes in different types of cancers (4,13,60). Computer simulations suggest the clinical protocol can reliably fit mean cell sizes from 6 to 20 μm (12). Other imaging parameters (e.g., TE, TR, number of b values, number of acquisitions, and acquisition data matrix) should be determined with considerations of the total scan time and SNR obtainable. The SNR requirement for reliable IMPULSED fittings will be discussed later.

Table 2.

Typical diffusion parameters used in the temporal diffusion spectroscopy acquisitions.

		δ /Δ [ms]	N	f [Hz]	b [s/mm2]	Gmax [mT/m]
Clinical (e.g., breast cancer (4))	PGSE	12/74	N/A	N/A	0,250,500,750,1000,1400,1800	80
	OGSE	40/50.5	1	25	0,250,500,750,1000
			2	50	0,100,200,300
Pre-clinical (e.g., xenografts (13))	PGSE	12/48	N/A	N/A	0,375,750,1125,1500	360
	OGSE	20/25	1	50	0,375,750,1125,1500
			2	100	0,375,750,1125,1500
			3	150	0,330,660,990,1321

4. Data analysis

The data analysis procedures of IMPULSED and MRI-cytometry are similar to other quantitative diffusion models. Here we summarize the procedure as below.

4.1. Pre-processing

The following are the pre-processing procedures that have been found useful.

1. Denoising (optional): Diffusion-weighted images can be denoised e.g. using the nonlocal means (NLM) method (66) or the random matrix theory (67), which can significantly enhance SNR for more reliable fittings. For example, the dwidenoise tool in the MRtrix3 software (https://www.mrtrix.org/) performs denoising on DW images (68).

2. Gibbs ringing removal (optional): Gibbs ringing artifacts can be removed to reduce the interactions of e.g., interfaces of CSF (69), such as using the mrdegibbs tool in the MRtrix3 software.

3. Preprocessing: All the DW images can be co-registered with the non-DW (b = 0) image using e.g. the FSL software (70) for correcting any displacement caused by body motions during imaging, eddy current and susceptibility induced image distortions (71).

4. Model selection: Each voxel signal may go through a model selection process using the Bayesian Data-Analysis toolbox (72) to determine which signal model (either constant ADCs across different t_diff, or t_diff dependent TDS model, or just noise) is statistically more justified. Imaging voxels that do not contain apparent cellular structures at length scales that are inside the range to which TDS is sensitive (e.g., edema and necrosis) will be excluded from further TDS parametric mapping.

5. Constraints: All fitting parameters can be constrained with physiologically relevant values. For example, 0 ≤ v_in ≤ 1, $0\le \overline{d_{vw}}\le 25\mu \text{m}$, $0\le \overline{D_{in}},D_{ex}\le D_{\mathit{\text{free}}}$, and 0 ≤ β_ex ≤ 10 μm², where D_free is the diffusivity of free water (=3.07 μm²/ms at 37°C), d ≤ 25 μm because the root-mean-square displacement of free diffusion at 37°C is 21 μm, and β_ex ≤ 10 μm² is determined from numerous studies in vivo (42).

4.2. Data fittings of IMPULSED

Multiple fitting methods have been used in our previous publications, such as traditional nonlinear regression algorithms (13), and Bayesian probability theory-based grid search method (73). The latter has been suggested as the optimal method for making inferences about data (74,75) but at a cost of increased processing time (proportional to mⁿ, where m is the grid number and n is the number of fitting parameters).

4.3. Data fittings of MRI-cytometry

After discretizing d, D_in, D_ex0, and β_ex with N, M, P, and Q possible values, respectively, a regularized non-negative least-squares (NNLS) approach can be used to fit Eq. [5] to dMRI data for MRI-cytometry. Due to the complication caused by v(d), MRI-cytometry used a two-step approach: first fit the cell-volume-weighted P_vw(d, D_in) and then fit the non-cell-volume-weighted P(d, D_in). Specifically, a dictionary containing all possible intra- and extracellular signal forms is constructed and Eq. [5] can be rewritten as

$$S=\left[\begin{array}{c}{S}_1\\ ⋮\\ S_K\end{array}\right]=\stackrel{\text{intracellular }}{\overbrace{[\begin{array}{ccc}{m}_{in(1\mid 1)}& \cdots & m_{in(N\times M\mid 1)}\\ ⋮& \ddots & ⋮\\ m_{in(1\mid K)}& \cdots & m_{in(N\times M\mid K)}\end{array}}}\stackrel{\text{extracellular }}{\overbrace{\begin{array}{ccc}{m}_{ex(1\mid 1)}& \cdots & m_{ex(P\times Q\mid 1)}\\ ⋮& \ddots & ⋮\\ m_{ex}{}_{(1\mid K)}& \cdots & m_{ex(P\times Q\mid K)}\end{array}]}}\times \left[\begin{array}{c}{w}_{in(1)}^{\prime }\\ ⋮\\ w_{in(N\times M)}^{\prime }\\ w_{ex(1)}\\ ⋮\\ w_{ex(P\times Q)}\end{array}\right]=M\cdot w^{\prime }$$ [6]

where $w_{in}^{\prime }={\rho }_{in}{P}_{in}\left(d,D_{in}\right)v(d)\ge 0$, $w_{ex}={\rho }_{ex}{P}_{ex}\left(D_{ex0},{\beta }_{ex}\right)\ge 0$ , M is the basis signal matrix (dictionary) containing both intra- and extracellular signal forms: m_{in (n,m∣k)} = s_in (d_(n), D_in(m)∣b_k, f_k), and m_{ex (p,q∣k)} = exp[−b_k(D_ex0(p) + β_ex(q) · f)]. A regularized non-negative least-square problem formulation is given as

$$\begin{array}{l}\underset{}{\text{argmin}}\hfill \\ w^{\prime }\ge 0\hfill \end{array}\left[\begin{array}{l}M\hfill \\ \xi I\hfill \end{array}\right]w^{\prime }-{\left[\begin{array}{l}S\hfill \\ 0\hfill \end{array}\right]}_2^2,$$ [7]

where I is a unity matrix with a size of N × M + P × Q and ξ is a regularization penalty parameter that is empirically determined as 0.01 in human studies (28). P_vw(d, D_in) and P_ex(D_ex0, β_ex) can be obtained by fitting Eq.[7] using the NNLS approach.

In the second step, the regularized non-negative least-square problem focuses on intracellular signals S_in and the non-cell-volume-weighted P(d, D_in) can be obtained. The details of the data fittings can be found in (28).

5. Validation

Comprehensive validations, including computer simulations in silico, cells in vitro, and animals in vivo, have been performed to validate both IMPULSED and MRI-cytometry in preclinical studies. These validations suggest that IMPULSED and MRI-cytometry can provide reliable mapping of mean cell size and cell size distribution, respectively, in human imaging with short (~ 7 mins) scan time. The following section will focus on the validations of the IMPULSED method. The details of the validations of MRI-cytometry can be found in (28).

5.1. Computer simulations in silico

Computer simulations were performed to investigate the accuracy of IMPULSED measurements in a two-compartment model system mimicking tightly packed cells of diameters ranging from 2.5 to 25 μm with various intracellular volume fractions (43%, 51%, and 62%) (13). As shown in Figure 3, a combination of PGSE (t_diff = 48 ms) and 40, and 80 Hz OGSE acquisitions provided the best accuracy of estimating cell size and intracellular volume fraction when the cell size increased from 2.5 to 25 μm, and such accuracy is not affected by cell densities. Imaging protocols with OGSE acquisitions alone underestimated the sizes of large cells.

Figure 3.

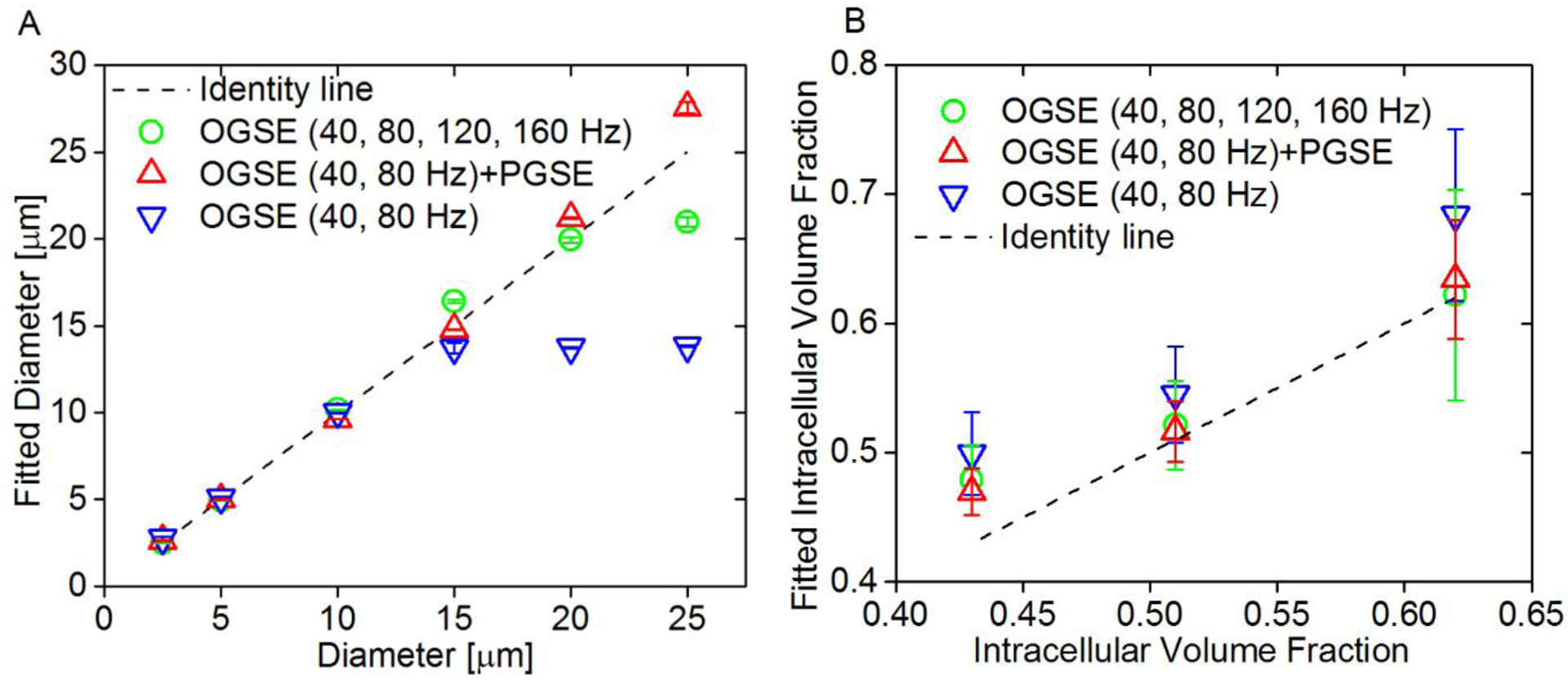
(A) Correlation between fitted diameters and preset diameters in simulations. Fitted diameters generated from three different combinations of OGSE and PGSE signals, mean ± std (n=3, with three different intracellular volume fractions: 43%, 51%, and 62%) vs. preset diameters. The dot line represents the identity line. (B) Fitted intracellular volume fraction generated from three different combinations of OGSE and PGSE signals, mean ± std (n=6, with cell size ranging from 2.5 to 25 μm) vs. preset intracellular volume fractions. The dot line represents the identity line.

5.2. Cultured cells in vitro

Cultured cells (murine erythroleukemia (MEL) and human promyelocytic leukemia K562 cells) of different sizes and at different densities, as well as MDA-MBA-231 cells before and after anti-cancer treatment with Abraxane, were used to validate the IMPULSED method (13). Abraxane is an FDA-approved mitotic inhibitor drug that interrupts cell division during the mitotic (M) phase of the cell cycle when two sets of fully formed chromosomes are supposed to separate into daughter cells. Cells are thereby trapped in the M phase and then undergo apoptosis. Note that cells significantly increase their sizes during the M phase, and hence the cell size can be used as a biomarker to monitor the efficacy of Abraxane treatment. Light microscopy was used to examine the cells. Figure 4 shows the excellent agreement between the sizes derived from experimental IMPULSED and microscopic measurements represented by green bands. Note the derived cell diameters are independent of the cell density, and the estimated intracellular diffusion did not change, while the value of the extracellular diffusion accurately tracked the cell density as expected.

Figure 4.

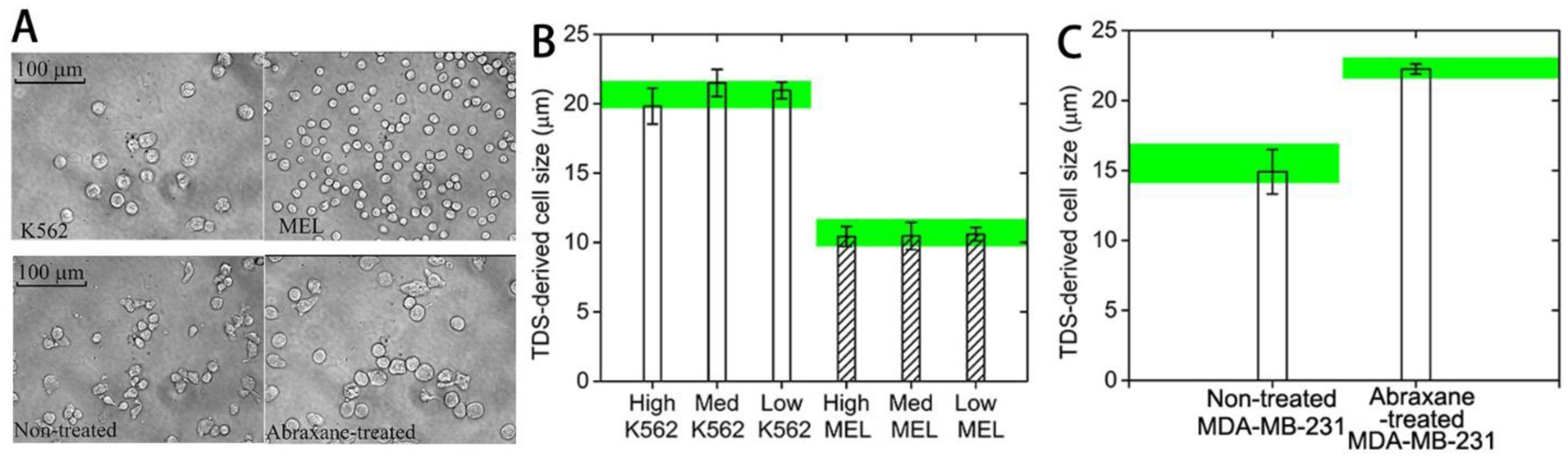
Microscopic pictures of K562, MEL, and MDA-MB-231 before and after anti-mitotic treatment. (B) IMPULSED-derived cell sizes for K562 and MEL at three different cell densities and for MDA-MB-231 before and after anti-mitotic treatment. Noted that the green bands represent the microscopy-derived cell sizes.

5.3. Animal xenografts in vivo

The IMPULSED method was also validated in vivo for mapping mean cell size and cellularities in vivo using three types of human colon cancers (DiFi, HCT116, and SW620). The parametric maps show similar patterns to the H&E stained pictures (Figure 5A). The measured cell sizes were very close to histological results. The IMPULSED-derived cellularity was strongly correlated (Spearman’s correlation coefficient Corr = 0.81, p < 0.001) with histology-derived cellularity and showed heterogeneity within the tumors (Figure 5B).

Figure 5.

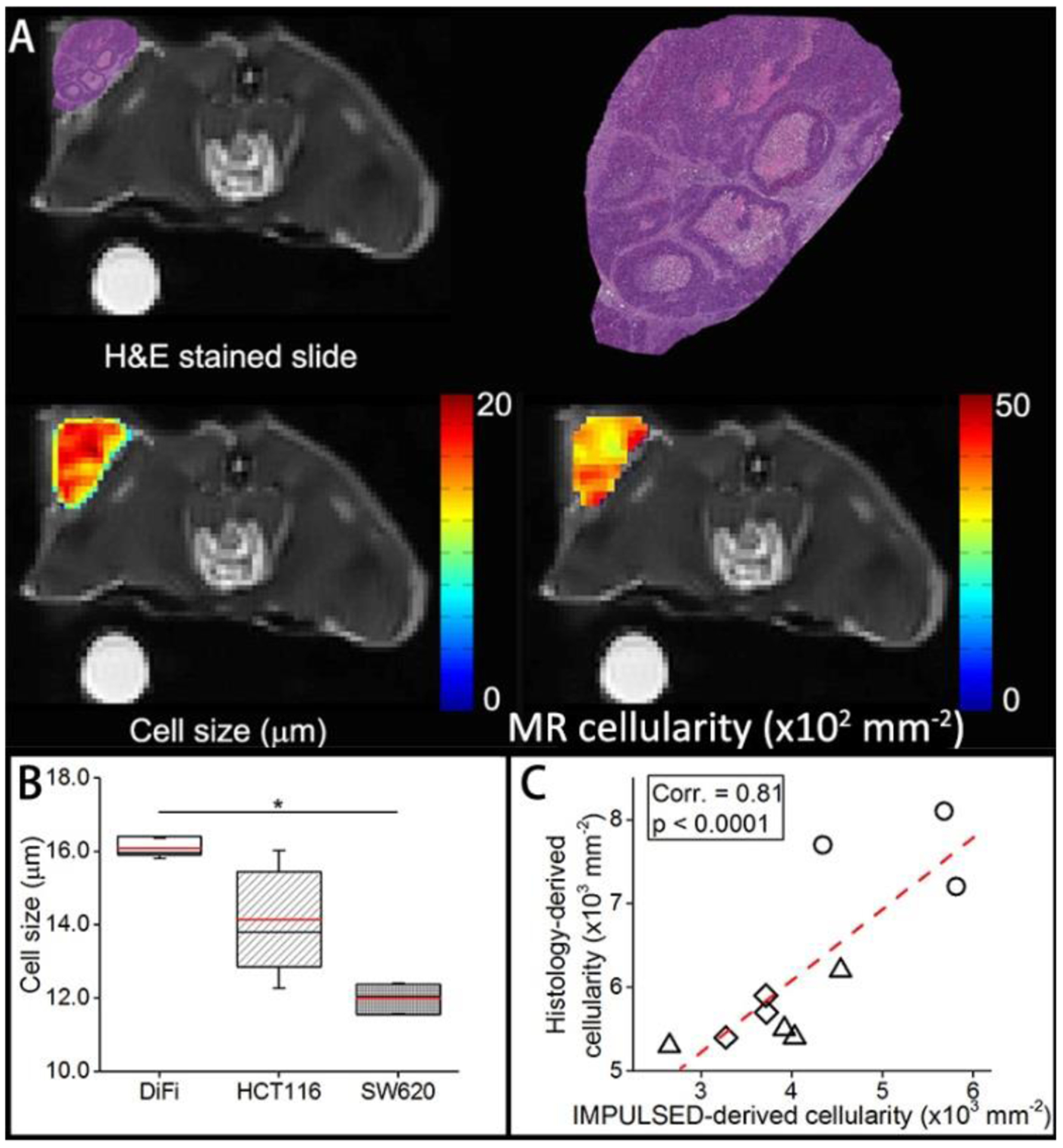
H&E stained histological image, IMPULSED-derived cell size and cell density maps of a representative slice through tumor, overlaid on T2-weighted MR images. (B). Box-and-whisker plot of the fitted cell size for three types of tumors. The 25th-75th percentiles are blocked by the box, the black and red bands inside the box are the median and mean, respectively, and the whiskers mark the SD. C. Correlation between histological-derived cellularities and IMPULSED-derived apparent cellularities for all the tumors.

5.4. Enhanced transcytolemmal water exchange

All the above studies used Eq.[3] that assumes no water exchange. The good agreement between the mean cell size $\overline{d_{vw}}$ obtained from the IMPULSED method and histology in those studies suggests the neglect of exchange is reasonable. However, the above studies were based on intact cells and tumors. Because cell membrane permeability increases after many anti-cancer treatments, it is unclear if such an assumption is still valid with a higher transcytolemmal water exchange rate. This was investigated by Li et al. (56) using both computer simulations and cell experiments in vitro. The computer simulations showed that, over a very broad range of intracellular water lifetimes τ_in (50 – ∞ ms) and mean cell sizes d (5 – 20 μm), transcytolemmal water exchange shows negligible influences on the IMPULSED derived d and D_in, while v_in may be significantly underestimated. This conclusion was confirmed in a cultured cell experiment in vitro by selectively changing cell membrane permeability using different concentrations of saponins while keeping all other cellular microstructure the same. Figure 6 summarizes the dependence of IMPULSED derived d, v_in, and D_in on intracellular water lifetime τ_in and cell membrane permeability P_m. The results suggest mean cell size $\overline{d_{vw}}$ can be reliably fit for a broad range of transcytolemmal water exchange rates, while v_in is significantly underestimated due to this exchange. These findings are consistent with histology results obtained in animals in vivo.

Figure 6.

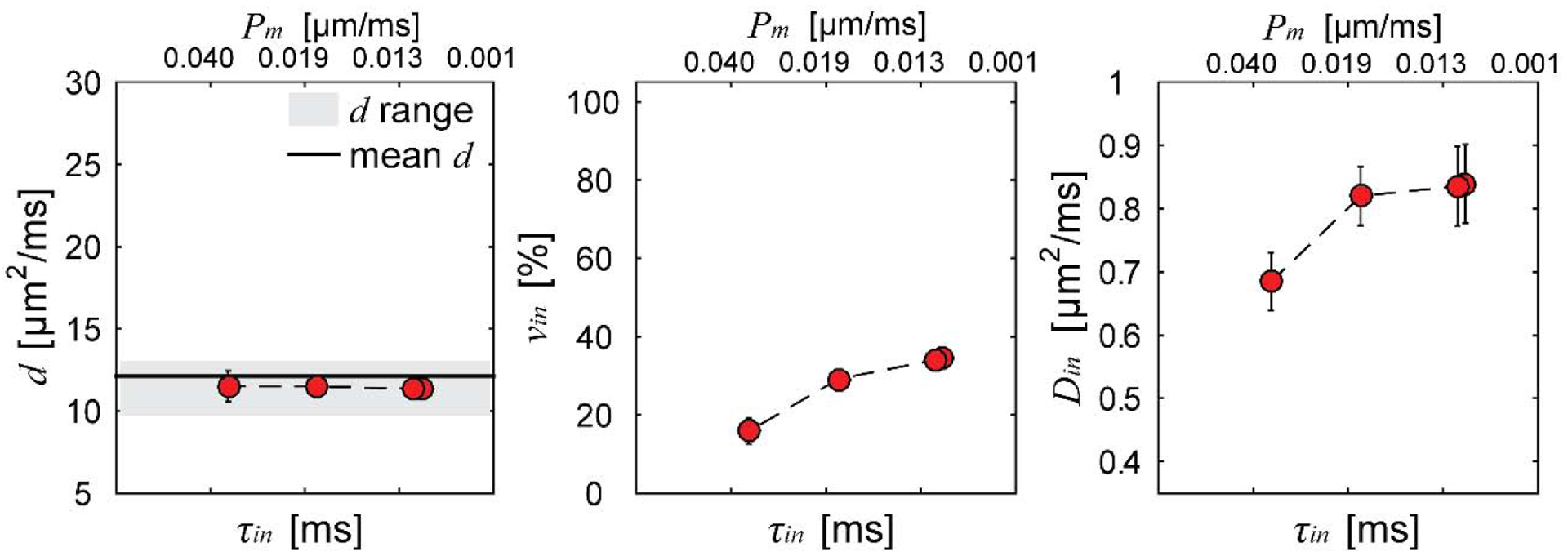
Summary of IMPULSED fitted microstructural parameters versus intracellular water lifetime τ_in and cell membrane permeability P_m. Error bars in each subfigure denote across-sample STD. The $\overline{d_{vw}}$ range indicates histology-derived mean cell diameter ± STD of all cells, and mean d is the volume-weighted cell diameter.

6. Applications in cancer – preclinical proof of concept

One of the potential applications for MR cell size imaging is that cell size could provide earlier and more specific assessments of tumor therapeutic responses to various treatments. Because changes at the cellular level (e.g., cell size) and sub-cellular level (e.g., cytoplasm condensation in apoptosis or organelle duplication during mitosis) are usually early responses of cancer cells to treatment, characterization of cell size and intracellular diffusivity may provide a unique means to assess tumor status. Figure 7 summarizes the recently published studies that use IMPULSED to characterize changes in cell morphology when cells undergo different pathological processes. These cell size changes usually occur earlier than changes in tumor volume, the current gold standard of effective cancer treatments. Three studies that treat tumors by inducing apoptosis (42), mitotic arrest (40), and T cell infiltration (4), respectively, will be highlighted below to show how the IMPULSED method can be used to monitor cell size variations following different treatments.

Figure 7.

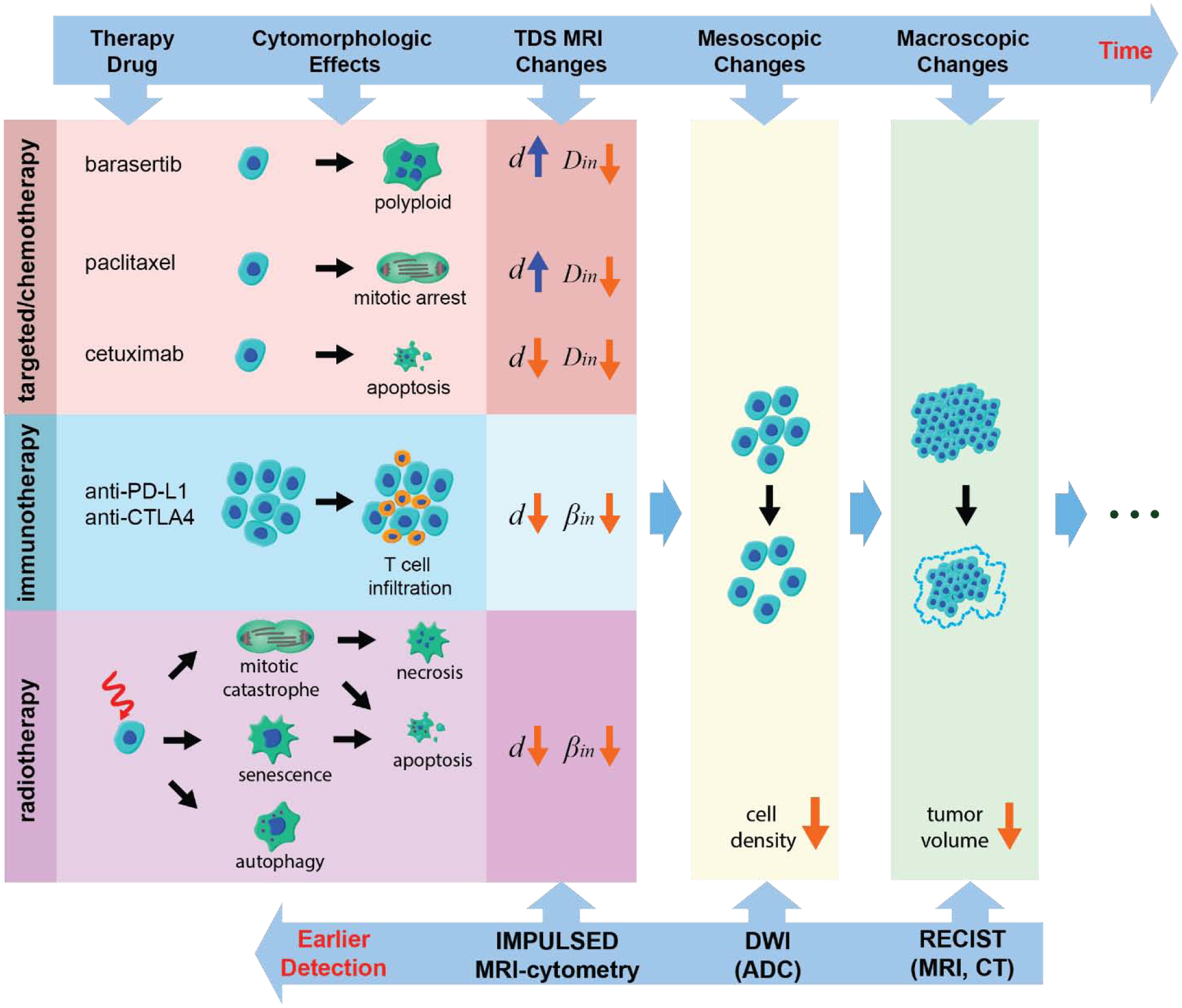
Diagram of various cell morphology changes responding to anti-cancer treatment. All listed therapy approaches and corresponding TDS MRI results are reported previously: barasertib (7), paclitaxel (40), cetuximab (42), anit-PD-L1/anti-CTLA4 (4), and radiation (60)

6.1. Apoptosis

Cell shrinkage, cytoplasm condensation, and DNA fragmentation are hallmarks of cell apoptosis. Their corresponding changes in biophysical features, such as the decrease in mean cell size $\overline{d}$ and the decrease in mean intracellular diffusivity $\overline{D_{ln}}$, can be detected by IMPULSED. This in turns provides a specific means to detect treatment-induced apoptosis in tumors. Two types of human colorectal cell lines, DiFi (responder (76)) and HCT116 (non-responder (77)), were treated with cetuximab, an epidermal growth factor receptor (EGFR) inhibitor used for treatment of colon cancers with wild-type KRAS gene. A one-compartment TDS model was used in this study. The temporal diffusion spectrum was measured using a combination of PGSE (δ/Δ = 4/12 ms) and OGSE (50 to 350 Hz with an interval of 50 Hz) acquisitions. Three parameters were fitted: $\overline{d}$ (averaged dimension size), D₀ (ADC when f → 0), and D_∞ (ADC when f → ∞).

The mean cell size $\overline{d}$ for cetuximab-treated DiFi tumors decreased significantly after the first two treatments and decreased even more after further treatments, indicating apoptotic cell shrinkage. Nuclear condensation and fragmentation slow the water diffusion within the cells, and therefore lowered D_∞ for DiFi tumors after four treatments. D₀ is sensitive to cell density changes as a result of cell death. The combination of these parameters ($\overline{d}$, D_∞, and D₀) may provide a specific in vivo assessment of treatment-induced apoptosis in solid tumors. In addition, changes reported by these parameters occurred earlier than changes in conventional tumor size measurements.

6.2. Mitotic arrest

Paclitaxel is a widely used cytotoxic chemotherapy drug for various cancers. As an inhibitor of microtubule depolymerization, it causes cells to arrest in a mitotic phase and eventually leads to cell death (78). During the mitotic phase, cell size d usually increases significantly and the duplicated intracellular organelles cause more hindrances to water mobility and hence produces significantly decreased D_in. Therefore, measurements of the changes in d and D_in provides a specific means to probe treatment-induced mitotic arrest.

Two types of human ovarian cell lines (OVCAR-8 as a responder to Nab-paclitaxel, and NCI/ADR-RES as a resistant type) were treated with either vehicle (PBS) or Nab-paclitaxel, and treatment responses of both in vitro and in vivo cases were investigated using the one-compartment TDS model. We found that Nab-paclitaxel induced acute cell size increases in responding tumors (confirmed by flow cytometry and light microscopy) in cell culture. Nab-paclitaxel-induced mitotic arrest was quantified histologically by measuring the mitotic index in vivo using a mitosis-specific marker (antiphosphohistone H3). The fitted $\overline{d}$ was able to detect and quantify the increases in tumor cell sizes, which were not detected by ADC using conventional diffusion-MRI. All the MR results had a high degree of consistency with other flow, microscopy, and histological data. Moreover, with an appropriate analysis, the Nab-paclitaxel-responsive tumors in vivo could be easily distinguished from all the other drug-vehicle-treated tumors and Nab-paclitaxel-resistant tumors. This study confirms that TDS detects antimitotic-therapy-induced microstructural variations (notably, increases in cell sizes) in solid tumors in vivo before changes in tissue cellularity or conventional diffusion MRI metrics.

6.3. T-cell infiltration

There is increasing interest of assessing tumor responses to immunotherapy as it has been rapidly adopted as a treatment option for a wide variety of cancers (79–82). However, it takes significantly longer for conventional MRI to characterize successful response to immunotherapy (83). For example, checkpoint inhibitor treatments that block PD1 and CTLA4 receptors lead to cytotoxic T cell infiltration into tumors, which may lead to transient tumor enlargement due to the increased number of T cells, followed by shrinkage or long-term stability of tumor size (84). Because conventional standard-of-care RECIST (version 1.1) (85) criteria are based on tumor volume, this may misdiagnose effective response as disease progression i.e., pseudo-progression (83,86,87). There is a need to develop a specific imaging method to assess tumor response to immunotherapy. T cells are typically 5–10 μm in diameter (88–91), which is significantly smaller than regular cancer cells (10–20 μm) (92). The increased fraction of smaller T cells in tumors during T cell infiltration results in a decrease in the mean cell size, which can be measured by MR cell size imaging. This provides a unique means to detect T cell infiltration without any radiation-sensitive labeling (93).

We began preclinical assessment of immune-checkpoint blockade (ICB) of anti-PD-1 and anti-CTLA4 in a mouse model of colon adenocarcinoma (MC38). This cell line was chosen because MC38 is sensitive to anti-PD-1 alone, while most murine models (of melanoma, lung, and head & neck) are resistant to monotherapy. 34 C57/BL6 mice were subcutaneously injected with 1×10⁶ MC38 cells. After tumors were MRI visible (day 7), mice were imaged at 7, 10, 13, and 16 days. Either dual therapy (200 ug/dose IP, n=19) or mIgG (200 ug/dose IP, n=15) alone were administered after the first 3 imaging sessions on 7, 10, and 13 days. The IMPULSED method was used to measure the mean cell size $\overline{d}$ and other microstructural metrics (see Table 1).

The average cell sizes of ICB responders as measured by IMPULSED are significantly smaller than those of control IgG-treated tumors or ICB non-responders, at 16 days post injection (dpi) (Figure 8B), associated with increasing T cells in ICB responders (Figure 8A). We subsequently validated the MR findings by performing immunohistochemical analyses on tumor tissues collected at 16 dpi. Strong membranous Na⁺/K⁺-ATPase and CD3+ staining in the tumor allows us to segment tumor cells and T cells easily and calculate mean cell sizes and T cell fractions for all the slides (Figure 8C). As shown in Figure 8D, histology-derived mean cell sizes including both tumor cells and T cells have a strong negative correlation (r = −0.9, p < 0.001) with T cell fractions. The mean cell size decreases about 1 μm with a 10% increase of CD3+ T cell fraction. IMPULSED-derived cell sizes show a negative correlation (r = −0.64, p < 0.001) with T cell fractions (Figure 8E). IMPULSED-derived cell sizes show a moderate correlation (r = 0.52, p = 0.008) with histology-derived cell sizes (Figure 8F). All these results suggest that mean cell size is an indicator of immunotherapy-induced T cell infiltration and the IMPULSED method has the potential to assess immunotherapy response via mapping mean cell size.

Figure 8.

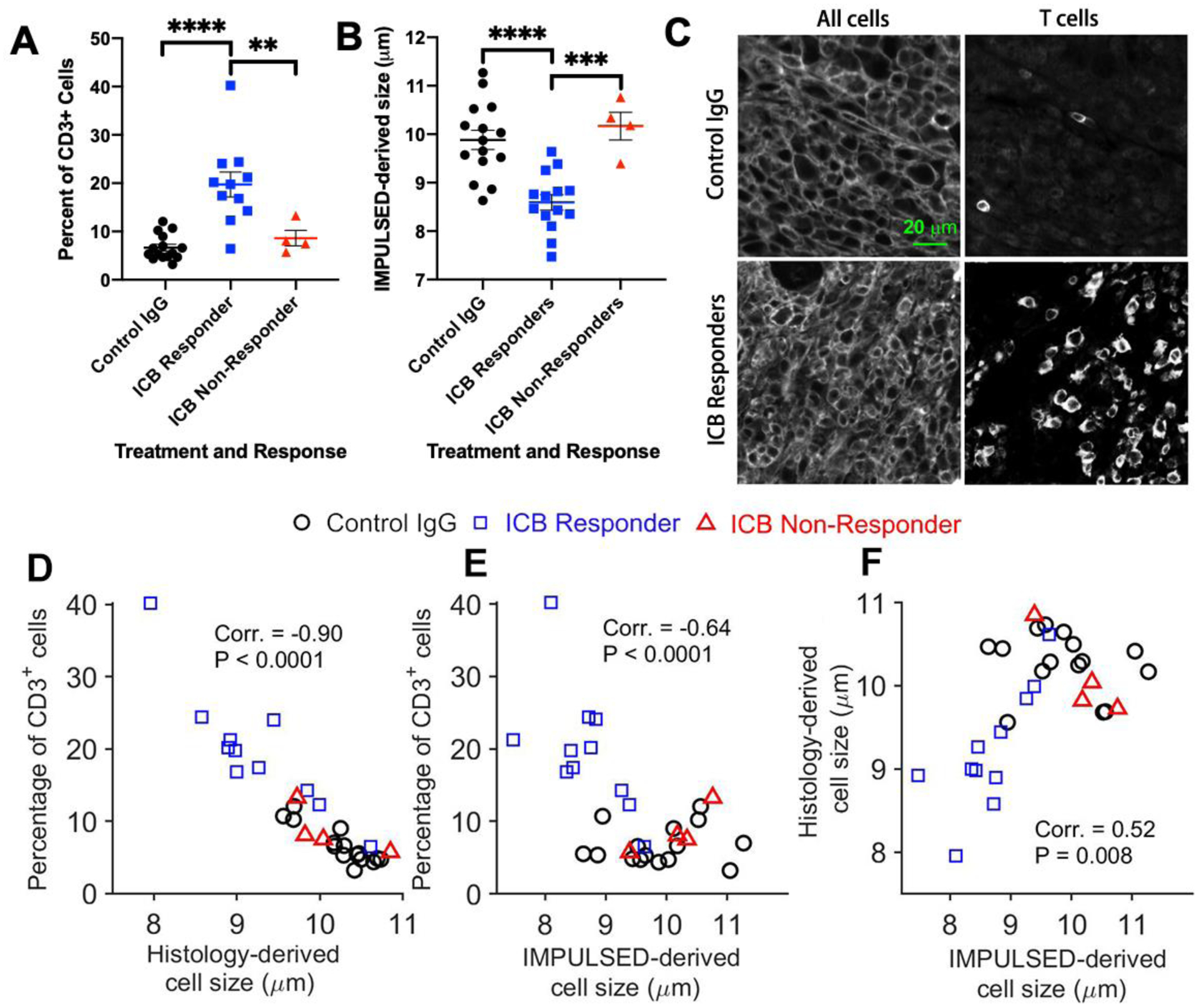
(A) Tumors from ICB responders had a significantly higher percent of CD3+ T cells as measured by immunohistochemistry compared to ICB non-responders and control IgG-treated mice; (B) ICB responding tumors had a significantly smaller mean cell size as measured by IMPULSE than tumors from control or ICB non-responders; (C). Examples of Immunohistochemical analyses of MC38 tumors treated with either control IgG (top) or checkpoint inhibitors (bottom); (D). Validation of IMPULSED-derived cell sizes using histology.

7. Translation to human imaging

The above validation and application studies used animal scanners with fewer hardware restrictions than clinical devices, such as maximum gradient strength G_max up to 360 mT/m. However, G_max is limited ⩽ 80 mT/m on most regular clinical MRI scanners. A few strategies have been used to implement IMPULSED acquisitions on human systems, including

1. use of the cosine-modulated trapezoidal gradient waveform to maximize b values (64);

2. extending gradient durations δ to 40 ms or more to enhance b values;

3. fixing D_in as a constant because of the limited range of t_diff resulting in a decreased sensitivity to intracellular diffusion (12);

4. keeping D_ex as t_diff independent to enhance the fitting accuracy and precision (12).

Another major limitation is the overall scan time, which should be as short as possible for clinical applications. To date, IMPULSED has been implemented for mapping mean cell size in human livers (73) and breast tumors (12). MRI-cytometry has been implemented in breast cancer patients as well (28).

7.1. Breast cancer

IMPULSED was implemented to study breast cancer patients on a Philips 3T scanner. Acquisition sequence parameters were TR/TE = 4500/103ms; FOV = 192×192mm; reconstructed in-plane resolution = 1.3×1.3 mm; 10 or 20 slices; slice thickness = 5 mm; NEX = 2; single-shot EPI; SENSE factor = 3; fat suppression with SPAIR; and dynamic stabilization were used to minimize dMRI signal drifts during scanning. Images were acquired with two opposite diffusion gradient directions for each axis and the geometric means were used as final images to mitigate the cross-terms between diffusion and background gradients. All diffusion sequence parameters were the same as in Table 2. The total scan time ≈ 7 mins.

Figure 9 shows representative IMPULSED-derived parametric maps of d, v_in, and D_ex of a human breast tumor overlaid on a high-resolution anatomical image. As the average SNR of b0 images is ~ 20, the intracellular diffusion coefficient D_in was fixed to 1.58 μm²/ms for improved accuracies of other three parameters (detailed explanation will be given in the discussion). Significantly lower intracellular volume fraction and increased extracellular diffusion coefficients were observed at the center of the tumor, suggesting the presence of a necrotic core. All the fitted values of cell sizes, densities, and diffusion coefficients are within reasonable ranges.

Figure 9.

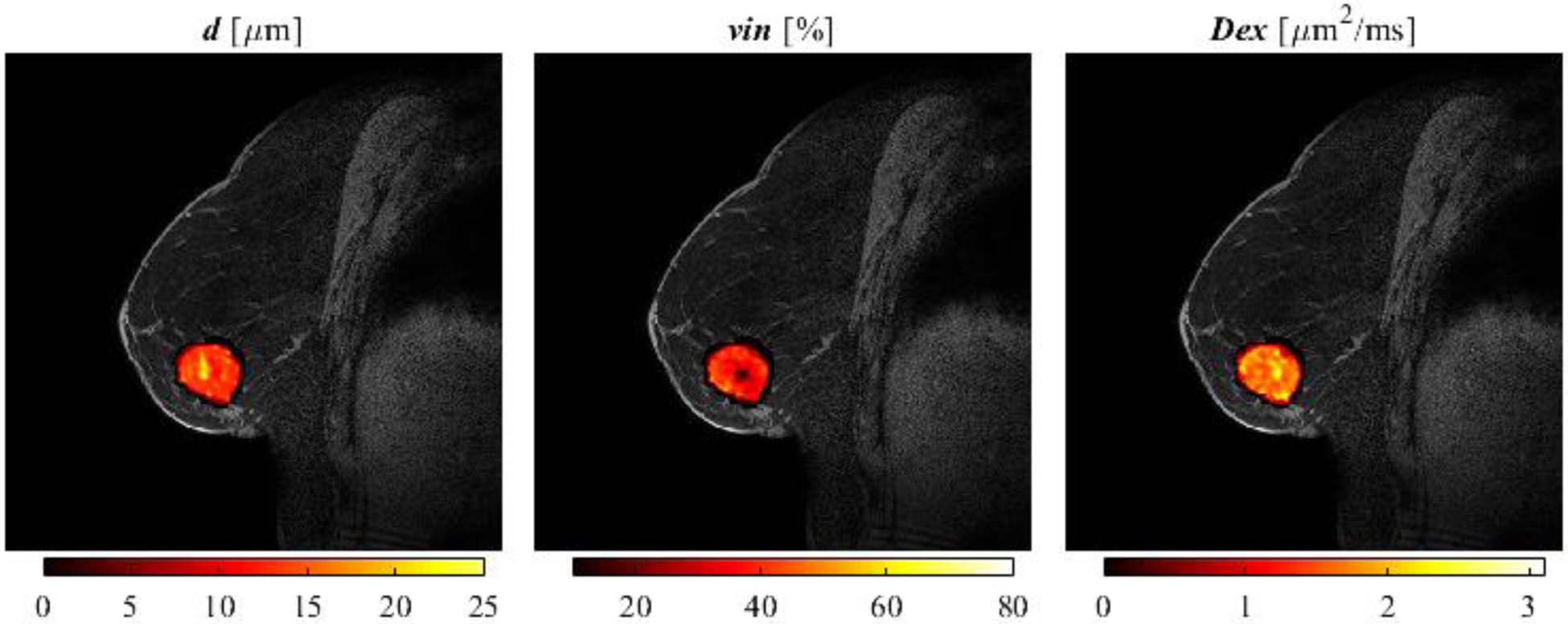
Representative IMPULSED-derived maps of mean cell size d (left), intracellular volume fraction v_in (middle), and extracellular diffusion coefficient D_ex (rigth) overlaid on a high-resolution fat-suppressed anatomical image of a breast cancer patient.

Figure 10 shows representative cell size distributions P(d) and MRI-Cytometry derived v_in and $\overline{d}$ parametric maps of a human breast tumor. SNR was ~45 on T2w b = 0 images. Four examples of cell size distributions from four representative image voxels are provided. For the voxels in the viable tumors (#1, #2, and #4 shown in Figure 10a, e, and g), the shapes of P(d) are similar to each other. However, voxel #2 shows hyperintensity on the T2-weighted b = 0 image and reduced v_in. This might be due to increased extracellular water. By contrast, P(d) appears very differently as a small peak at large cell sizes (> 20 μm) for voxel #3 in the necrotic region. This is because the necrotic core consists of mainly fluid and cell debris with few restrictions. This leads to a small fitted intracellular volume fraction v_in (< 10%) and large fitted cell sizes ≥ 20.5 μm, the root-mean-square-displacement of free water at body temperature 37°. Figure 10d and h demonstrate the MRI-Cytometry derived v_in and $\overline{d}$ parametric maps, which show low v_in and high $\overline{d}$ in the necrotic core compared with viable tumors. Note that transcytolemmal water exchange may be responsible for the underestimation of v_in, but it may have minor influence on $\overline{d}$, as we reported previously (56).

Figure 10.

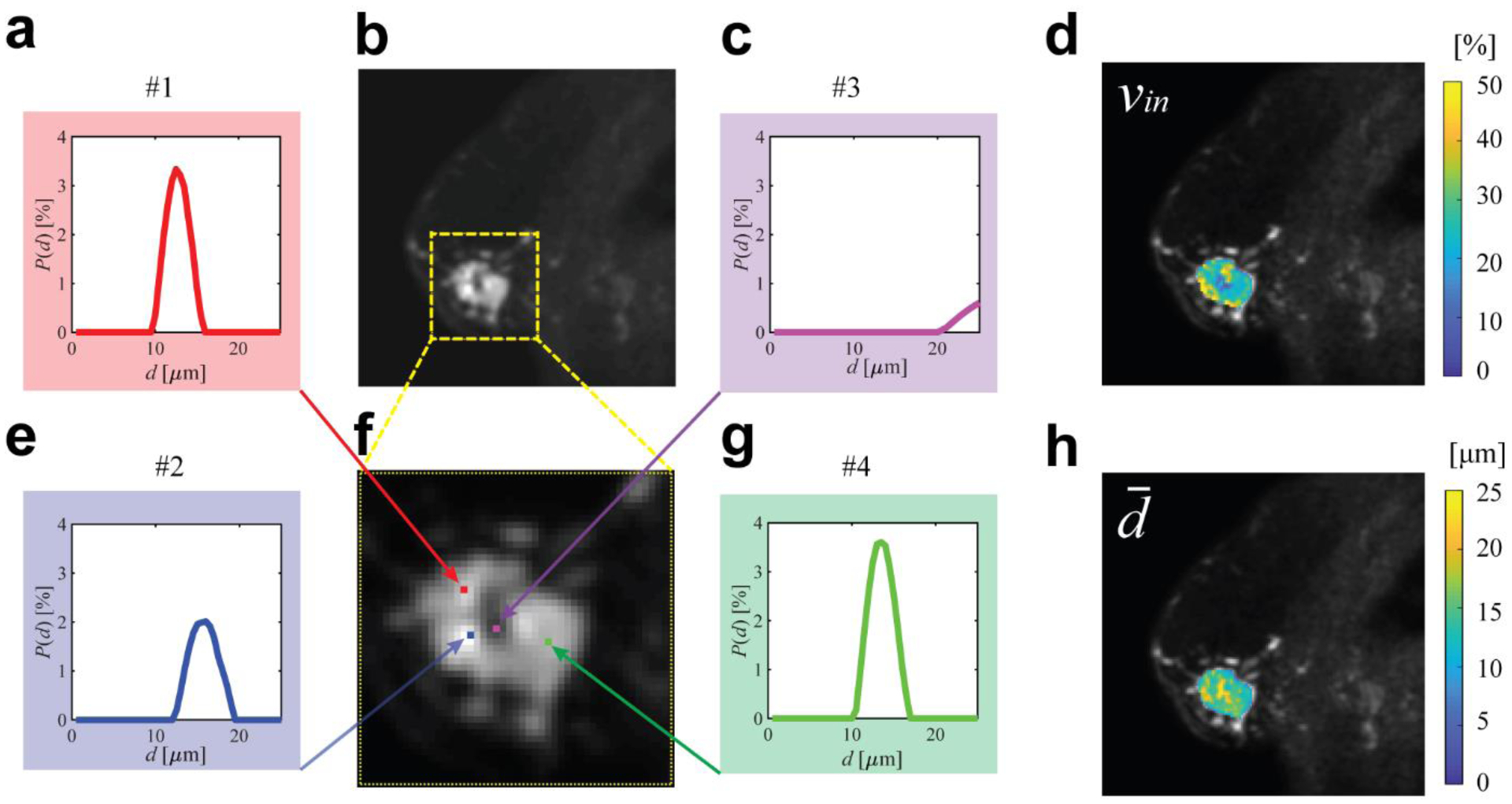
Representative cell size distributions and MRI-Cytometry derived parametric maps of a breast tumor. (b) is T2-weighted b = 0 image of the tumor and (f) is an enlarged view. (a,c,e,g) are four examples of cell size distributions. (d) and (h) are MRI-Cytometry derived v_in and $\overline{d}$ maps of the same tumor.

7.2. Liver

Another reported application of IMPULSED is liver imaging in human subjects. The size and density of hepatocytes, their variations and their changes over time, are fundamental characteristics of liver tissues, and diagnostic biomarkers of several normal and pathological processes. For example, hepatocytes shrink during early apoptosis and they swell during hepatocyte polyploidization; hepatocytes exhibit ballooning associated with cell swelling in nonalcoholic steatohepatitis; inflammation induces shifts in the mean cell size as small immune cells infiltrate the liver. Measurements of hepatocyte sizes and densities can thus have high clinical significance but currently can be obtained only by liver biopsy.

In a recent study, the IMPULSED method was performed for mapping mean cell size d of healthy subject livers shown in Figure 11. MR imaging was performed using a Philips 3T scanner with a dStream TorsoCardiac coil. In addition to the diffusion parameters shown in Table 2, other imaging parameters were: acquired in-plane resolution = 4×4 mm², slice thickness=10 mm; NEX=2; respiratory-gated, single shot EPI; SENSE factor=2; fat suppression with Spectral Attenuated Inversion Recovery (SPAIR). The total scan time ≈ 12 mins. The fitted average cell size for a healthy subject is 17±4.6 μm, consistent with reported human hepatocyte sizes (94,95). The intracellular volume fraction is 37±18.4%, which is smaller than literature values (~ 70%) (96). Underestimation of intracellular volume fraction has been also observed in our previous IMPULSED studies in tumors (13,17). It is due to ignoring water exchange between intra- and extra-cellular spaces as discussed in section 2.2.3.

Figure 11.

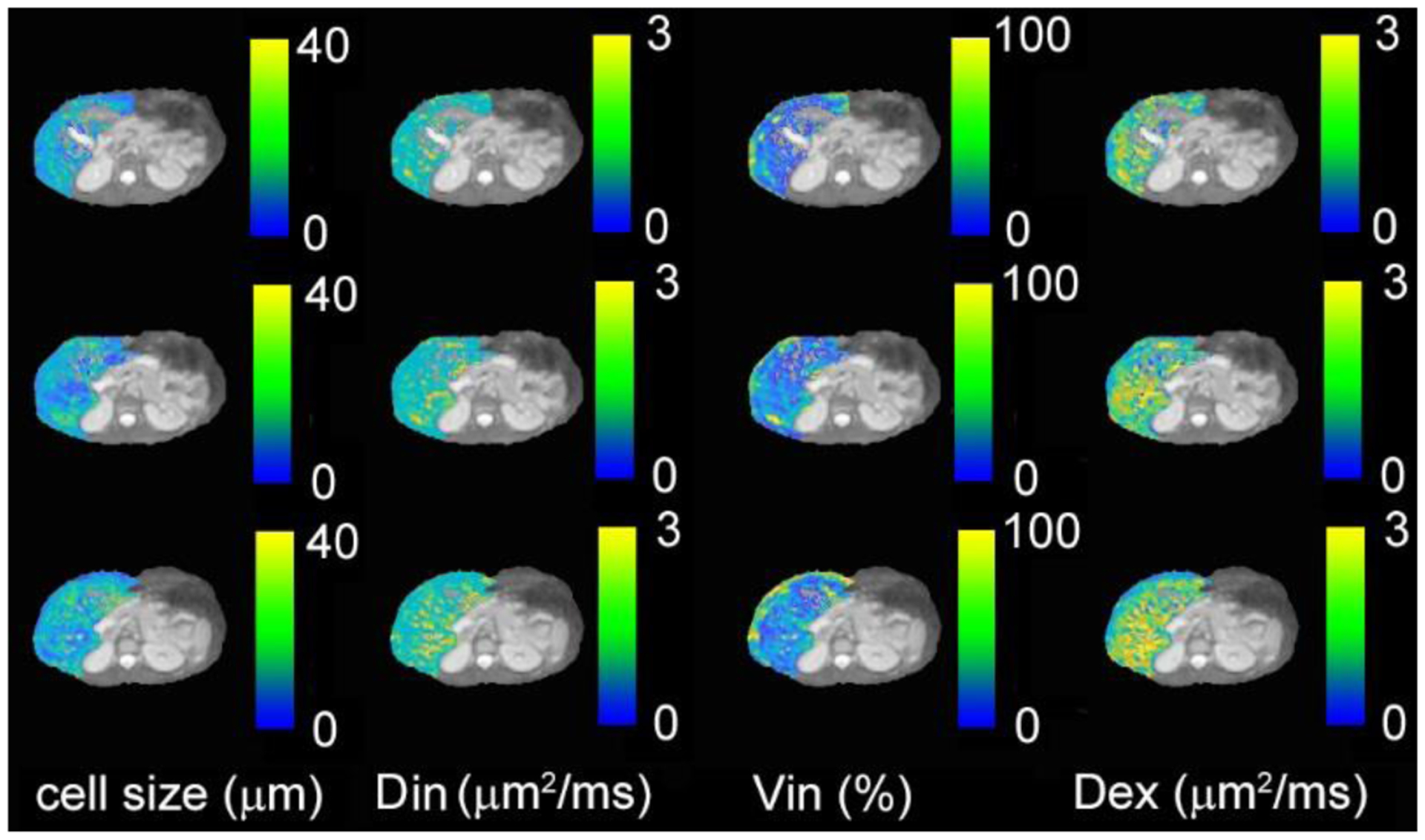
IMPULSED-derived maps of mean cell size d, intracellular diffusion coefficient D_in, apparent intracellular volume fraction v_in, and extracellular diffusion coefficient D_ex overlaid on a high-resolution fat-suppressed anatomical image for three continuous slices of liver from a healthy human subject.

8. Discussion

8.1. Cell density

Cell density is calculated as the quotient of intracellular volume fraction and IMPULSED-derived cell volume. Our previous studies suggest that intracellular volume fraction v_in is intrinsically underestimated by IMPULSED and fitted values decrease rapidly with shorter intracellular water lifetime τ_in, whereas accurate estimates of mean cell diameter may be obtained accurately independent of transcytolemmal water exchange with sufficient SNR (eg, 50). Accordingly, the cell density is likely to be underestimated. The clinical value of such an apparent cell density (including effects from the cell membrane permeability) needs to be further investigated. Future studies should aim to establish a quantitative relationship between the magnitude of membrane permeability and bias of v_in estimates. For example, we can modify the analysis to include water exchange between intra and extracellular spaces, such as using the Karger model (97), or apply another independent measurement of water exchange effects, such as filter exchange imaging (54).

8.2. Intracellular diffusion

Intracellular diffusion is complex due to the existence of cell membranes and a variety of organelles and cytoplasmic contents. Cell membranes are usually believed to dominate the restriction to water diffusion, but organelles have also been reported to affect diffusion measurements significantly. For example, the nucleus, the largest organelle containing chromosomes is bounded by membranes (the nuclear envelope) which restrict water diffusion and allows dMRI to be sensitive to nuclear size and nuclear-to-cytoplasm ratio (5). Changes in individual organelles (6) or overall intracellular microenvironment during cell division (57) have also been shown to contribute to the variations of ADC measurements. All these studies suggest the need for complex modeling of intracellular diffusion. However, based on the theory of IMPULSED, we can adjust t_diff in experiments to tune down the detection sensitivity to intracellular organelles while increasing sensitivity to cell size, which in turn makes it possible to measure cell sizes accurately.

Previous studies assessing intracellular diffusion were achieved with short t_diff ranges such as < 0.5 ms (i.e., f > 500 Hz using OGSE). This is far beyond the shortest t_diff that is achievable on human MRI using current gradient coils (39). For t_diff > 10 ms on current regular clinical MRI scanners, the characteristic length of diffusion measurements is $l=\sqrt{2D{t}_{\mathit{\text{diff }}}}>4.5\mu \text{m}$ if diffusivity D = 2 μm²/ms. For typical cells with size < 10 μm (e.g., red blood cells and T cells) and many cancer cells such as breast cancer cells < 16 μm, this results in a significantly reduced sensitivity to small organelles. Instead, a single diffusion coefficient, D_in, can be defined to represent an averaged diffusion property caused by all organelles and cytoplasm. However, if the cell size is large (e.g., hepatocyte size ~ 20 μm) with a large nuclear size (e.g., 5–7 μm in normal hepatocyte), the approximation of a single D_in is questionable. However, about 7 – 10 % surface area of a nucleus is occupied by nuclear pore complexes (98,99), which allow small proteins and molecules with molecular weight < 40 kDa to translocate between cytoplasm and cell nucleus by passive diffusion (100,101). Therefore, the nuclear membrane has been considered to permit nearly free passage of water molecules between the nucleus and cytosol (101–104). With this assumption, it has been demonstrated in a simulation study that MR diffusion measurements at diffusion times ranging from 1 – 70 ms are not sensitive to variations in the ratio of nuclear volume to cell volume from 0 to 30%, covering the range of nuclear-to-cell-volume ratios reported previously and found in our histology analysis of nuclear size (5). Therefore, for t_diff from 5–70 ms typically used on clinical MRI scanners, it is reasonable to assume a single D_in to describe the overall diffusion inside cells in most applications.

8.3. Extracellular diffusion

To date, the IMPULSED method assumes extracellular diffusion to be linearly dependent on gradient frequency, i.e., D_ex~β_ex · f when f > 50 Hz or D_ex is a constant independent on f when f < 50 Hz. Such assumptions have been used in various studies and gave results consistent with histology. However, the exact t_diff or f dependence of D_ex in tumors or livers is still unclear. In theory, in the short-time range limit t_diff → 0, it is well know that $D_{ex}~\sqrt{t_{\mathit{\text{diff }}}}$ or f^−1/2 (105). In the long-time range, D_ex ~ f^3/2 for short-range disordered media (106). Therefore, there are transitions in the t_diff dependence in the intermediate time range. Because IMPULSED covers a broad range of t_diff (e.g., 5 – 70 ms on regular clinical MRI scanners), the t_diff dependence may vary across different t_diff values. This is particularly important for liver imaging since liver cell size is typically large (~ 20 μm) so that the t_diff range used in the acquisitions may cover both short and intermediate time range. This could complicate the modeling of extracellular diffusion and further investigation is needed.

However, if an even narrower range of f e.g., 25 – 50 Hz is implemented, the dependence of D_ex on f reduces significantly and the assumption of a constant D_ex may work better. In fact, our previous preclinical studies (SNR ~ 50 and oscillating frequency up to 150 Hz) (13) found much larger variations (relative standard deviation ~ 60%) in fitted β maps compared with much smaller variations (relative standard deviation ~ 8%) in the fitted cell size maps. The variation of parametric maps is a combination of tissue inhomogeneities and fitting uncertainties due to multiple factors (e.g., insufficient SNR levels, inefficient fitting algorithms, and insufficient sensitivity to the fitted parameters). The dramatic difference between variations of β_ex and cell size maps from the same tissue strongly suggested that diffusion measurements even with oscillating frequencies up to 150 Hz do not provide enough sensitivity for reliable fitting of the linear dependence of D_ex on f. A direct comparison using simulations showed that D_ex can be treated as a constant for f up to 50 Hz to result in more reliable and accurate fittings of cell size on clinical scanners (4).

9. Conclusion

MR cell size imaging using temporal diffusion spectroscopy provides a reliable and practical means for mapping cell size non-invasively. Because the variation in cell size is usually a part of the first cellular response to diseases or interventions, MR cell size imaging provides a unique and specific means to assess biological tissue status and response to treatments. Towards clinical applications, two approaches have been developed based on TDS, i.e., IMPULSED and MRI-cytometry, for non-invasive mapping of mean cell size and cell size distribution, respectively. Both methods have been comprehensively validated and show promise as useful ways to characterize tissues in a variety of disease models.

12. Appendix

The analytical signal decay of an impermeable structure using the cosine-modulated gradient waveform is derived previously (62) as

$$S=S_0\text{exp}(-2{\gamma }^2{G}^2{\sum }_k\frac{B_k{a}_k^2{D}^2}{{\left(a_k^2{D}^2+4{\pi }^2{f}^2\right)}^2}\{\frac{\left(a_k^2{D}^2+4{\pi }^2{f}^2\right)}{a_{k}D}\left[\frac{\delta }{2}+\frac{\text{sin}(4\pi f\delta )}{8\pi f}\right]-1+\text{exp}\left(-a_{k}D\delta \right)+\text{exp}\left(-a_k\mathit{\text{D}}\Delta \right)\left(1-\text{cosh}\left(a_{k}D\delta \right)\right)\})$$ [A1]

where S₀ is non-diffusion-weighted signal, γ is the gyromagnetic ratio, G is gradient strength, f gradient frequency, D is intra-structural, intrinsic diffusion coefficient, δ gradient duration of a single waveform, and Δ the separation of two gradients. a_k and B_k are structure dependent parameters and have been derived analytically for simple geometries such as planes, cylinders, spheres (107) and spherical shells (62). For diffusion inside an impermeable sphere, $B_k=\frac{2{\left(R/{\mu }_k\right)}^2}{{\mu }_k^2-2}$ and $a_k={\left(\frac{{\mu }_k}{R}\right)}^2$ where R is radius and μ_k is the k^th root of $\mu J_{3/2}^{\prime }(\mu )-\frac{1}{2}{J}_{3/2}(\mu )=0$ and J is a Bessel function of the first kind (μ_k = 2.08, 5.94, 9.21, …).

For the cosine-modulated trapezoidal OGSE sequence with one oscillation n = 1 shown in Figure 2, the analytical signal decay has been derived as (12)

$$S=S_0\text{ exp }\left(-{\gamma }^2{G}^2\sum _k\frac{B_k}{a_k^4{D}^4{t}_r^2}\left\{\begin{array}{l}4\text{exp}\left(-a_{k}D{t}_p\right)-4\text{exp}\left(-a_{k}D{t}_r\right)-4\text{exp}\left(-2a_{k}D{t}_r\right)-8\text{exp}\left(-a_k\mathit{\text{D}}\Delta \right)-12a_{k}D{t}_r+2\text{exp}\left[-a_{k}D\left(\Delta -t_r\right)\right]\hfill \\ \begin{array}{l}+2\text{exp}\left[-a_{k}D\left(\Delta +t_r\right)\right]+2\text{exp}\left[-a_{k}D\left(\Delta +2t_r\right)\right]+2\text{exp}\left[-a_{k}D\left(\Delta -2t_r\right)\right]-2\text{exp}\left[-a_{k}D\left(\Delta -t_p\right)\right]\\ \begin{array}{l}-2\text{exp}\left[-a_{k}D\left(\Delta +t_p\right)\right]-4\text{exp}\left[-a_{k}D\left(t_r+t_p\right)\right]+2\text{exp}\left[-a_{k}D\left(t_r+2t_p\right)\right]-4\text{exp}\left[-a_{k}D\left(2t_r+t_p\right)\right]\hfill \\ \begin{array}{l}+4\text{exp}\left[-a_{k}D\left(3t_r+t_p\right)\right]-4\text{exp}\left[-a_{k}D\left(3t_r+2t_p\right)\right]-4\text{exp}\left[-a_{k}D\left(3t_r+3t_p\right)\right]+4\text{exp}\left[-a_{k}D\left(4t_r+3t_p\right)\right]\\ +2\text{exp}\left[-a_{k}D\left(5t_r+2t_p\right)\right]+4\text{exp}\left[-a_{k}D\left(5t_r+3t_p\right)\right]+2\text{exp}\left[-a_{k}D\left(5t_r+4t_p\right)\right]-4\text{exp}\left[-a_{k}D\left(6t_r+3t_p\right)\right]\\ \begin{array}{l}-4\text{exp}\left[-a_{k}D\left(6t_r+4t_p\right)\right]+2\text{exp}\left[-a_{k}D\left(7t_r+4t_p\right)\right]+6a_k^3{D}^3{t}_r^3+8a_k^3{D}^3{t}_r^2{t}_p+2\text{exp}\left[-a_{k}D\left(\Delta -t_r-t_p\right)\right]\hfill \\ \begin{array}{l}-\text{exp}\left[-a_{k}D\left(\Delta -t_r-2t_p\right)\right]+2\text{exp}\left[-a_{k}D\left(\Delta +t_r+t_p\right)\right]+2\text{exp}\left[-a_{k}D\left(\Delta -2t_r-t_p\right)\right]\\ \begin{array}{l}-\text{exp}\left[-a_{k}D\left(\Delta +t_r+2t_p\right)\right]+2\text{exp}\left[-a_{k}D\left(\Delta +2t_r+t_p\right)\right]-2\text{exp}\left[-a_{k}D\left(\Delta -3t_r-t_p\right)\right]\hfill \\ \begin{array}{l}-2\text{exp}\left[-a_{k}D\left(\Delta +3t_r+t_p\right)\right]+2\text{exp}\left[-a_{k}D\left(\Delta +3t_r+2t_p\right)\right]+2\text{exp}\left[-a_{k}D\left(\Delta -3t_r-2t_p\right)\right]\\ \begin{array}{l}+2\text{exp}\left[-a_{k}D\left(\Delta +3t_r+3t_p\right)\right]+2\text{exp}\left[-a_{k}D\left(\Delta -3t_r-3t_p\right)\right]-2\text{exp}\left[-a_{k}D\left(\Delta +4t_r+3t_p\right)\right]\hfill \\ \begin{array}{l}-2\text{exp}\left[-a_{k}D\left(\Delta -4t_r-3t_p\right)\right]-\text{exp}\left[-a_{k}D\left(\Delta +5t_r+2t_p\right)\right]-\text{exp}\left[-a_{k}D\left(\Delta -5t_r-2t_p\right)\right]\\ \begin{array}{l}-2\text{exp}\left[-a_{k}D\left(\Delta +5t_r+3t_p\right)\right]-2\text{exp}\left[-a_{k}D\left(\Delta -5t_r-3t_p\right)\right]-\text{exp}\left[-a_{k}D\left(\Delta +5t_r+4t_p\right)\right]\hfill \\ \begin{array}{l}-\text{exp}\left[-a_{k}D\left(\Delta -5t_r-4t_p\right)\right]+2\text{exp}\left[-a_{k}D\left(\Delta +6t_r+3t_p\right)\right]+2\text{exp}\left[-a_{k}D\left(\Delta -6t_r-3t_p\right)\right]\\ \begin{array}{l}+2\text{exp}\left[-a_{k}D\left(\Delta +6t_r+4t_p\right)\right]+2\text{exp}\left[-a_{k}D\left(\Delta -6t_r-4t_p\right)\right]-\text{exp}\left[-a_{k}D\left(\Delta +7t_r+4t_p\right)\right]\hfill \\ -\text{exp}\left[-a_{k}D\left(\Delta -7t_r-4t_p\right)\right]+8\hfill \end{array}\end{array}\hfill \end{array}\end{array}\hfill \end{array}\end{array}\hfill \end{array}\end{array}\hfill \end{array}\end{array}\hfill \end{array}\end{array}\hfill \end{array}\right\}\right)$$ [A2]

where t_r is the gradient rise time, t_p is the duration of the first gradient plateau in the gradient waveform, and all other parameters are the same as in Eq.[A1]. Equations for n = 2 and 3 can be found in (12).