Simulation-based optimization of genomic selection scheme for accelerating genetic gain while preventing inbreeding depression in onion breeding

Abstract

Genomic selection (GS) is being increasingly employed in plant breeding programs to accelerate genetic gain of economically important traits. However, its efficiency differs greatly across species, due to differences in reproduction and breeding strategies. Onion (Allium cepa L.) is an out-crossing crop but can be easily self-pollinated. High inbreeding depression occurs, and contamination of self-pollinated seeds is unavoidable in onion breeding. Taking this into consideration, 10-year breeding programs with and without GS were simulated. In addition to general GS, we proposed GS schemes to prevent inbreeding depression by avoiding co-selection of close relatives and combining the shortening of generation time and updating of the prediction model. The results showed that general GS with shortening of generation time yielded the highest genetic gain among the selection schemes in early years. However, inbreeding increased rapidly, reaching very high levels in later years. The proposed GS combining shortening of generation time with updating of the prediction model was superior to the others in later years, as it yielded relatively high genetic gain while maintaining significantly low levels of inbreeding. These results suggested that GS can be beneficial in onion breeding, and an optimal scheme should be selected depending on the selection period.

Introduction

Genomic selection (GS; Meuwissen et al. 2001) is a promising breeding method for improving genetic gain in various plant species. In GS, the genetic ability is predicted based on a model constructed using genome-wide marker genotypic and phenotypic data obtained from a training population. It enables selection of superior individuals among a breeding population without phenotypic evaluation, thereby aiding selection at seedling stages. Previous simulation and empirical studies have shown that GS can achieve a higher genetic gain than conventional phenotypic selection by increasing breeding cycles per unit time (Asoro et al. 2013, Beyene et al. 2015, Krchov and Bernardo 2015, Yabe et al. 2013, 2018). The efficiency of GS is expected to differ greatly across plant species, due to differences in reproduction and breeding strategies (Lin et al. 2014), and the GS breeding scheme needs to be optimized depending on the characteristics of each plant species and target trait.

Onion (Allium cepa L.) is one of the most widely cultivated vegetable crops in tropical, temperate, and boreal regions worldwide. The economic value of onion is derived from its culinary application, nutritional benefits, and health-promoting properties, such as the presence of flavonoid compounds (Griffiths et al. 2002). Onion is a biennial crop, i.e., bulb production occurs in the first year and seed production in the second year. After the juvenile stage, the bulb is formed in response to the lengthening of the photoperiod in late spring/summer of the first year. The bulb overwinters and undergoes vernalization and then flowers and sets seeds in late spring/summer of the second year. Thus, onion breeding programs require more time and greater cost and labor than other annual vegetables. However, it is known that growing plants (seedlings) are vernalized and induced to flower to then produce seeds without going through a bulb stage (Shishido and Saito 1975). This phenomenon is used for seed production systems, called the “seed-to-seed” system, and it can shorten the generation time by half of the normal breeding program. The seed-to-seed system is not popular in conventional breeding programs because it is impossible to select bulbs with desirable qualities and to discard undesirable bulbs. In contrast, this system would be useful to accelerate genetic gain per unit time in GS breeding.

Onion is an out-pollinated crop and exhibits protandry, i.e., the pollen is released by the stamens before the pistils become mature and receptive; however, self-pollination is also feasible. Inbred lines can be produced; however, onion is known to suffer from severe inbreeding depression (Rabinowitch and Currah 2002). Thus, inbred lines are usually produced by selfing only two or three times and maintained by mass seed production to prevent inbreeding depression. Onion possesses small bisexual flowers (florets), and each inflorescence consist of 200 to 600 florets (Brewster 2008). This floral characteristic makes emasculation and hand-crossing much more difficult than in other out-pollinated crops such as maize, which possesses large unisexual floral parts. The necessity for insect pollination, by bees and flies, resulted in more than 30% contamination of self-pollinated seeds in onion breeding (Van Der Meer and Van Bennekom 1972). Controlling inbreeding is very important for the application of GS breeding, because GS can lead to a higher rate of inbreeding than phenotypic selection, due to co-selection of close relatives (Lin et al. 2016). To overcome this problem, various methods have been proposed in animal and plant GS breeding; for instance, genetic relationship information, such as co-ancestry, has been used for selection and mating allocation (Asoro et al. 2013, Gorjanc and Hickey 2018, Lin et al. 2017, Pryce et al. 2012). Although the same or comparable method can be applied in onion GS breeding to prevent inbreeding depression, it is necessary to consider the influence of self-pollination ratio on both genetic gain and inbreeding when employing GS in onion breeding.

In GS, genome-wide molecular marker data of each plant are necessary to construct a prediction model and calculate the prediction values. However, development and utilization of molecular markers in onion breeding have been limited so far. Onion has a huge genome size (16 Gb), over 92% of which is constituted by repetitive elements (Flavell et al. 1974, Fu et al. 2019, Ricroch et al. 2005), and then no reference genomic sequence have been released to date. The practical onion materials have been genotyped using the reference-free genotyping platform (i.e., RAD-seq) or KASP assay whose markers were developed based on the transcriptome sequences (Duangjit et al. 2013, Jo et al. 2017, Scholten et al. 2016). To select the reliable markers by which a single locus is correctly genotyped, expected segregation ratio is useful as a selection criterion. Thus, a segregating population, such as F₂ population, would be appropriate to use as an initial and training population for the practical onion GS breeding in the present state.

In this study, we used simulations to assess different GS schemes, including the setting of self-pollination ratio, to optimize onion breeding. We evaluated the (1) impact of GS on genetic gain and inbreeding, (2) efficiency of the GS procedure to prevent inbreeding depression by avoiding co-selection of close relatives, and (3) efficiency of shortening generation time using the seed-to-seed system and updating the prediction model in GS-based schemes. We evaluated the efficiency of GS by changing the settings of several factors, i.e., the heritability of a trait, number of quantitative trait loci (QTLs), marker density, population size, and self-pollination ratio, assuming the actual scale of an onion breeding program. We sought to identify the optimal GS-based scheme for onion GS breeding.

Materials and Methods

Design of the simulation study

The plant specimens were diploid onions, with 8 pairs of chromosomes (2n = 16). Each chromosome length was set at 120 cM, which was determined by reference to the previous study (Scholten et al. 2016). The positions of QTLs and markers were randomly distributed across the 8 chromosomes. The number of QTLs was set to 30 or 100. The target trait was assumed to be controlled by only additive QTLs, and no dominance and epistatic effects influenced the traits. The effect of each QTL was sampled independently from a standard normal distribution and was standardized so that the genetic variance of the initial population was 1.0. The narrow sense heritability (h²) of the target trait was set at 0.3 and 0.6 in the initial population. Population size was assumed to be 200 to 500 plants. The number of markers was set at 500, 200, and 100. The genotypes of QTLs and markers were defined as 1 (AA), 0 (AB), and –1 (BB). One F₁ plant whose QTL and marker genotypes were heterozygous at all positions was generated, and an F₂ population was produced by selfing this F₁ plant, which was then used as the initial population. The environmental effects on each individual were sampled independently from a normal distribution, and the phenotypic value for each individual was calculated as the sum of the QTLs and environmental effects. In the present study, the influence of inbreeding depression on the phenotypic value was not considered. The self-pollination ratio was set at 0.3, according to a previous study on onion (Van Der Meer and Van Bennekom 1972). The seeds collected from each individual included 30% of self-crossed seeds and 70% of out-crossed seeds. Additionally, for evaluating the effect of self-pollination ratio on the level of genetic gain and inbreeding, the self-pollination ratio was set at 0 and 0.6 under a particular simulation setting in which the population size was 200, the number of QTLs was 100, the prediction model was constructed using 500 markers, and heritability (h²) was 0.3. All simulations were conducted using a custom program developed based on the functions in the R package “Breeding Scheme Language” (Yabe et al. 2017).

Breeding procedure

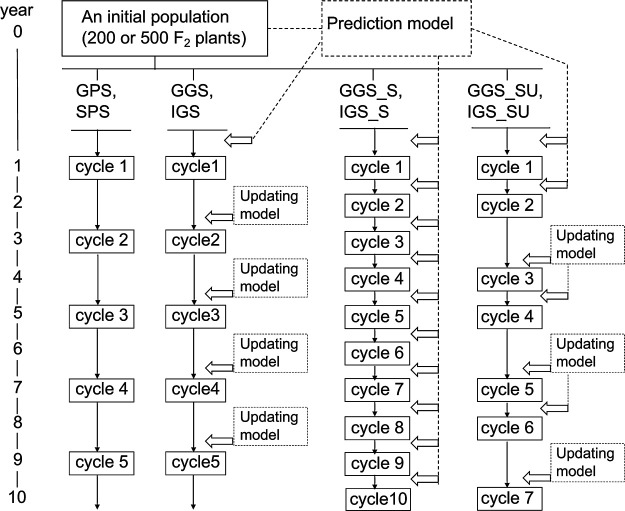
We simulated 10 years of breeding programs to evaluate the efficiency of different selection schemes in onion. Mass selection and inbred line selection are popular in onion breeding (Brewster 2008); therefore, the selection schemes proposed in the present study were designed based on such selection schemes. Four selection schemes, namely general phenotypic selection (GPS), self-crossing phenotypic selection (SPS), general genomic selection (GGS), and inbreeding avoiding genomic selection (IGS), were compared in this study. In GPS and SPS, the top 10 plants were selected based on phenotypic values and used as parents of the next generation. The selected individuals were randomly crossed in GPS, while they were self-crossed in SPS. In GGS, the top 10 plants were selected based on their genomic estimated breeding values (GEBVs). In IGS, to avoid excessive loss of genetic diversity by co-selection of close relatives, the breeding population was divided into 10 groups before selection, and the individual with the highest GEBV was selected from each group (i.e., total 10 individuals). Grouping was achieved using k-means clustering (Hartigan and Wong 1979) in R (R Core Team 2018). Selected individuals were randomly crossed in GGS and IGS. In GS-based schemes, kinship. BLUP in the R package “rrBLUP” (Endelman 2011) was used for calculating GEBVs. In all selection schemes, equal number of seeds were collected from each individual, bulked, and used as the next generation. In GPS, GGS, and IGS, the self-pollinated seeds were contaminated based on the setting of the self-pollination ratio. These selection procedures were continued up to 10 years in each selection scheme, corresponding to five selection cycles, because of the biennial life cycle of onion (Fig. 1). In GGS and IGS, the prediction model was updated (i.e., re-estimated) in every selection cycle with data from that generation and was then used for selection (Fig. 1).

Fig. 1.

Breeding procedures compared in the simulation. GPS: general phenotypic selection, PSP: self-crossing phenotypic selection, GGS: general genomic selection, IGS: inbreeding avoiding genomic selection, GGS_S: GGS with shortening of generation time, IGS_S: IGS with shortening of generation time, GGS_SU: GGS combining shortening of generation time with updating of the prediction model, IGS_SU: IGS combining shortening of generation time with updating of the prediction model. In GGS, IGS, GGS_SU, and IGS_SU, the prediction model was updated (i.e., re-estimated) in generations indicated by “updating model”. The label “cycle” with the numbers in the boxes indicate the breeding population in each selection schemes. The hollow arrows indicate the timing of selection procedure using prediction models.

In GGS and IGS, additional selection procedures, such as shortening of generation time without updating the prediction model (GGS_S and IGS_S) and combined shortening of generation time with updating of the prediction model (GGS_SU and IGS_SU), were also evaluated (Fig. 1). In GGS_S and IGS_S, selection was conducted once per year, using the seed-to-seed system, and a total of 10 cycles were conducted during the selection term. The prediction model constructed with the initial population was used continually during the selection term without updating. In GGS_SU and IGS_SU, the prediction model was updated once per two cycles. In odd-numbered cycles, the generation time was shortened by one year, and individuals were then selected based on the predicted values (i.e., GEBVs) calculated by the prediction model updated in the last selection cycle. In even-numbered cycles, individuals were selected based on GEBVs calculated by the prediction model updated with the data from the same generation, subsequently requiring the normal generation time (i.e., 2 years) due to evaluation of phenotypes. These procedures were continued up to 10 years, corresponding to seven cycles (Fig. 1).

Summarization of simulation results

In the present study, 100 simulations were performed independently, and the mean of simulation replications against each value described below was calculated as summarization. Improvement of genetic gain was evaluated using genetic values, which were calculated for individuals in each breeding population and summarized using the mean and variance of the population in every cycle. The mean of genetic values was treated as “genetic gain”. Inbreeding coefficient in each cycle was calculated as 1- H_cn/H_co, where H_cn is the mean marker heterozygosity in cycle n and H_co is the expected mean marker heterozygosity in cycle 0. In this study, H_co was set at 0.5, because the F₂ population was used as the initial population (i.e., cycle 0), and it was derived from one F₁ plant whose marker genotypes were completely heterozygous. H_cn was calculated from 500 markers in each cycle. Selection accuracy was calculated as the Pearson’s correlation coefficient between prediction values (i.e., GEBVs) and genetic values measured in each cycle. In phenotypic selection (GPS and SPS), the phenotypic values were treated as prediction values. In some simulation replications, the marker genotypes of the breeding population were completely fixed in a particular cycle. In that case, the genetic gain and inbreeding coefficient of the last cycle were continued to be used till the end of the selection term and then used for summarization. The simulation replication in which the marker or QTL genotypes of the breeding population were completely fixed was excluded from the summarization of the selection accuracy after fixation. Response to selection was calculated as the genetic gain per cycle, i.e., the difference between the genetic gain in that cycle and that in the last cycle. Response to selection can also be estimated as irσ_A, where i is selection intensity, r is selection accuracy, and σ_A is the square root of additive genetic variance (Falconer and Mackay 1996). Next, this formula was used to discuss the reason of rapid decline of response to selection in a particular selection scheme. The significance of differences in genetic improvement between selection schemes was analyzed using a matched paired t test for the genetic gain of each breeding population from 100 simulation replications. The P value was adjusted using the Bonferroni method. In t test, populations derived from identical initial populations in each replication were considered as a matched pair. All values presented in figures and supplemental tables indicate the mean of simulation replications.

Results

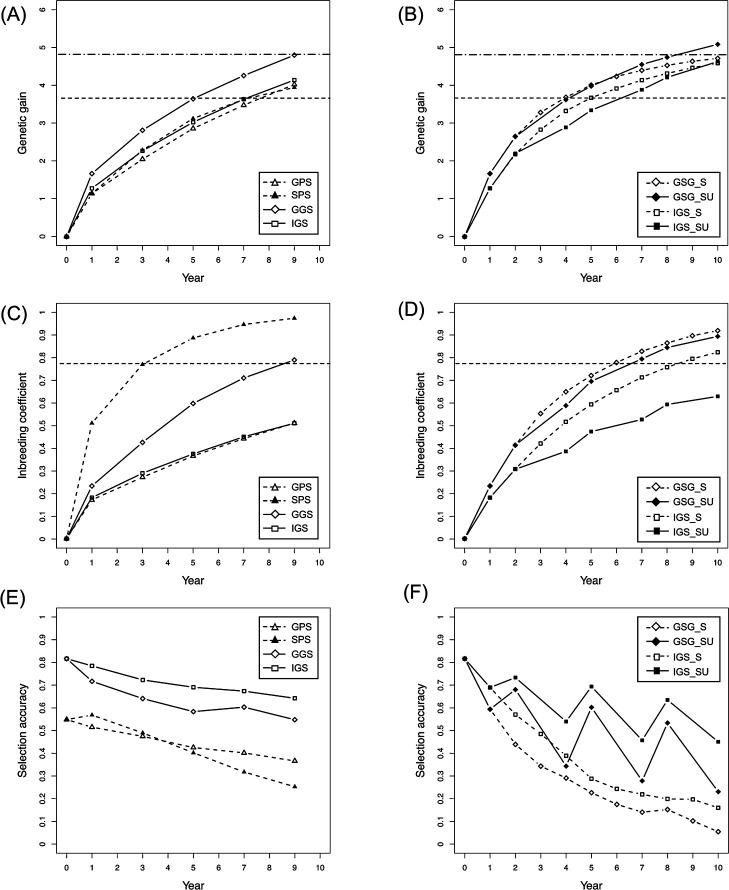
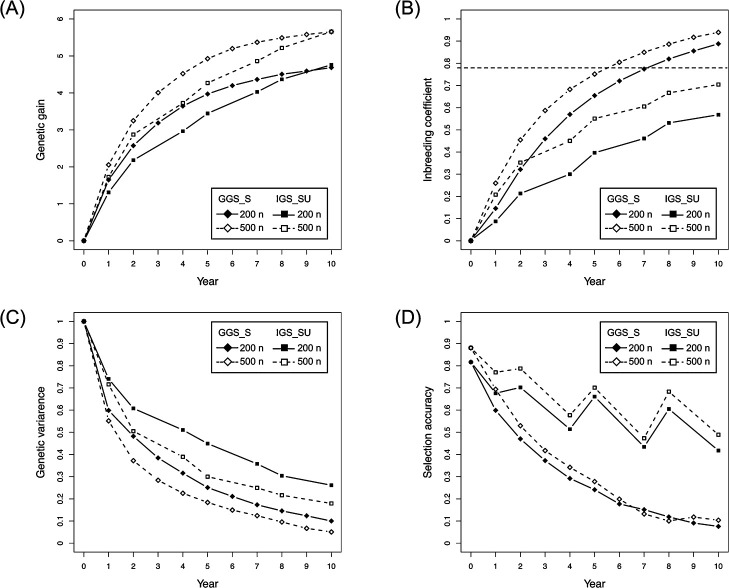
Fig. 2 illustrates the results obtained with the setting where the population size was 200, the number of QTLs was 100, the prediction model was constructed using 500 markers, and heritability (h²) was 0.3 (denoted as “the setting with 200 n, 100 QTLs, 500 markers, and h² = 0.3”). The general GS (GGS) achieved a greater genetic gain than the phenotypic selection schemes (i.e., GPS and SPS) during the selection terms (Fig. 2A; Supplemental Table 1). In contrast, the genetic gain of IGS, which included the selection procedure to avoid co-selection of close relatives, was similar or slightly lower than that of the phenotypic selection schemes (Fig. 2A). GS-based schemes with shortening of generation time (GGS_S and IGS_S) obtained equal or higher genetic gain than selection schemes with ordinary span of breeding generation (i.e., GGS, IGS, PS, and SPS) (Fig. 2B). The difference in genetic gain was remarkable, especially during the early years. The average genetic gain of GGS in year 5 was 3.6 (“horizontal dashed line” in Fig. 2A, 2B), while that in GGS_S and IGS_S was 4.0 and 3.7, respectively (Fig. 2B, Supplemental Table 1). GS-based schemes combining shortening of generation time with updating of the prediction model (i.e., GGS_SU and IGS_SU) did not overperform GGS_S or IGS_S in the early years (Fig. 2B). In contrast, the genetic gain of GGS_SU and IGS_SU was equal or slightly less than that of GGS_S and IGS_S in later years.

Fig. 2.

Comparison of properties among the selection schemes. The panels indicate the changing patterns of genetic gain (A, B), inbreeding coefficient (C, D), and selection accuracy (E, F) during the selection term with the setting of 200 n, 100 QTLs, 500 markers, and h² = 0.3. Horizontal dashed and two-dash lines in (A, B) correspond to the values of GGS in years 5 and 10, respectively. Horizontal dashed lines in (C, D) indicate the values of SPS in year 3 (corresponding to the F₄ generation), which was defined as the threshold for the occurrence of inbreeding depression in this study. The correlation coefficient between the genetic and predicted values was used to indicate the selection accuracy. In phenotype-based selection (i.e., GPS and SPS), the correlation coefficient values between the genetic and phenotypic values represented the selection accuracy.

In the present study, the inbreeding coefficient of phenotypic selection with self-crossing (i.e., SPS) in year 3 (corresponding to the F₄ generation) was defined as the threshold of inbreeding depression, because selfing is limited to two or three times in practical onion breeding. If the inbreeding coefficient exceeded that value, the possibility of inbreeding depression would increase. The inbreeding coefficients in selection schemes with ordinary span of breeding generation (i.e., PS, GGS, and IGS) were lower than the threshold value (“horizontal dashed line” in Fig. 2C, 2D) during the selection terms, except for GS in year 10 (Fig. 2C). The inbreeding coefficients in GS-based schemes including shortening of the generation time (i.e., GGS_S, IGS_S, GGS_SU, and IGS_SU) were lower than the threshold value during the early years but higher at the end of the selection terms, except for IGS_SU (Fig. 2D). IGS_SU maintained significantly low values of inbreeding coefficient during the selection terms.

The accuracy of GS-based schemes with ordinary breeding generation (i.e., GGS and IGS) was higher than that of phenotypic selections (i.e., GPS and SPS) (Fig. 2E). This selection accuracies gradually decreased during selection terms (Fig. 2E). The accuracies of GS-based schemes with shortening of generation time without updating the prediction model (i.e., GGS_S and IGS_S) rapidly decreased, resulting in a very low accuracy at the end of selection (Fig. 2F). The accuracy of GS-based selection schemes combining shortening of generation time cycles with updating of the prediction model (i.e., GGS_SU and IGS_SU) drastically varied depending on years (Fig. 2F). The years with model updating (years 2, 5, and 8) showed high levels of accuracy, while the following years (years 4, 7, and 10) presented low levels of accuracy.

Although the simulation settings, such as the heritability of the target trait, number of QTLs, and population size, were changed, the relationships among selection schemes in each property (i.e., genetic gain and inbreeding coefficient) did not differ from the results presented in Fig. 2 (Supplemental Fig. 1, Supplemental Tables 1–4).

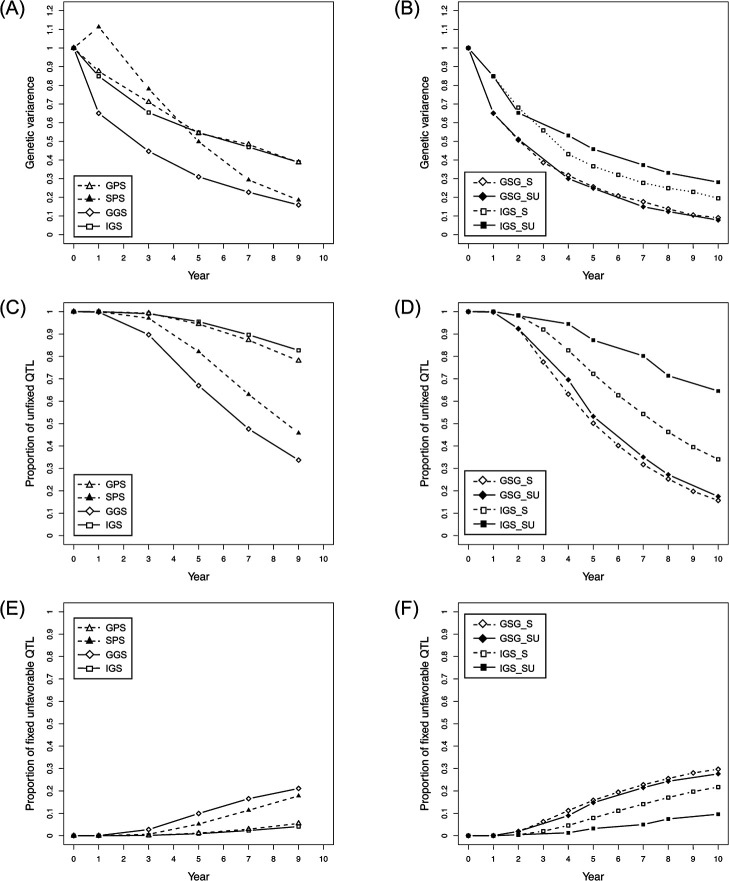
To compare the changing patterns of genetic variation among the selection schemes, the genetic variance, proportion of unfixed QTLs, and fixed unfavorable QTLs (i.e., alleles with a negative effect) were evaluated. Fig. 3 illustrates the results obtained for the setting with 200 n, 100 QTLs, 500 markers, and h² = 0.3. In phenotype-based selections, GPS maintained high levels of genetic variance and proportion of unfixed QTLs, while SPS resulted in a rapid decrease in those values during the selection term (Fig. 3A, 3C). In SPS, the proportion of fixed unfavorable QTLs increased gradually, whereas in GPS, it was maintained at near zero (Fig. 3E). Compared to phenotype-based schemes, GGS led to a rapid decrease in genetic variance and proportion of unfixed QTLs, while increasing the proportion of fixed unfavorable QTLs. In contrast, in IGS, a high level of genetic variance and proportion of unfixed QTLs but a low level of the proportion of fixed unfavorable QTLs were maintained (Fig. 3A, 3C). The relationships of properties between GGS and IGS remained unchanged across the schemes involving shortening of generation time (i.e., GGS_S vs IGS_S) and updating of the prediction model (i.e., GGS_SU vs IGS_SU) (Fig. 3B, 3D, 3F). It was particularly interesting to note that the effects of updating the prediction model differed between GGS- and IGS-based schemes: the properties of GGS_S and GGS_SU were only slightly different, while those of IGS_S and IGS_SU were significantly different (Fig. 3B, 3D, 3F).

Fig. 3.

Comparison of genetic variation among the selection schemes. The panels indicate the changing pattern of genetic variance (A, B), proportion of unfixed QTLs (C, D), and proportion of fixed unfavorable QTLs (i.e., alleles with negative effects) (E, F) in each selection scheme, with the setting of 200 n, 100 QTLs, 500 markers, and h² = 0.3.

Fig. 4 illustrates the results obtained using different number of markers (i.e., 500, 200, and 100) in GGS_S and IGS_SU, which could achieve greater genetic gain while preventing inbreeding depression for short- and long-term selections described above, with the setting of 200 n, 100 QTLs, and h² = 0.3. The relationships among different number of markers remained unchanged across the selection schemes. The smaller the number of markers, the lower the genetic gain, inbreeding coefficient, and selection accuracy (Fig. 4A, 4B, 4D). Genetic variance exhibited an opposite trend, i.e., genetic variance increased with decreasing number of markers (Fig. 4C). The difference was small between selection schemes with 200 and 500 markers but relatively large between schemes with 100 markers and all other schemes.

Fig. 4.

Impact of the number of markers. Comparison of each property between GGS_S and IGS_SU with different number of markers, with the setting of 200 n, 100 QTLs, and h² = 0.3. The panels indicate the mean of the genetic value (A), inbreeding coefficient (B), genetic variance (C), and selection accuracy (D). Horizontal dashed lines in (B) indicate the threshold value of inbreeding depression.

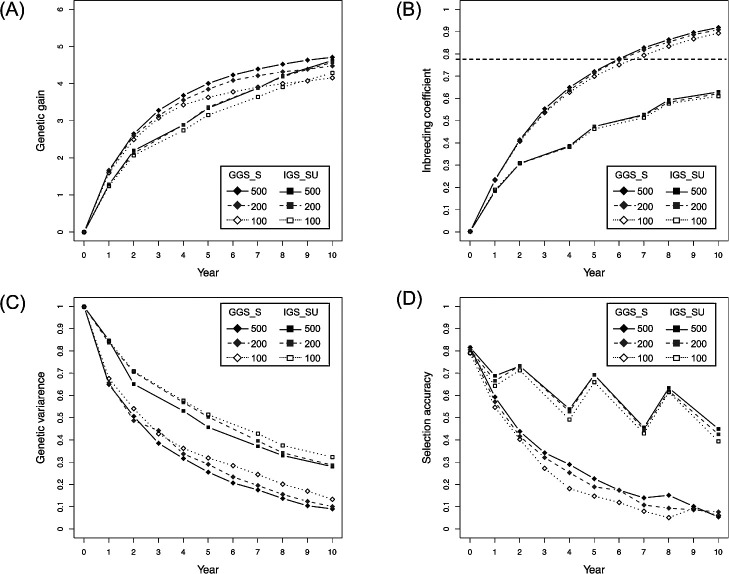
The effect of population size was evaluated by comparing the two settings of population size (i.e., 200 and 500 n). Fig. 5 illustrates the results of GGS_SU and IGS_SU obtained with the setting of 100 QTLs, 500 markers, and h² = 0.3. The relationships between population sizes remained unchanged across selection schemes. Increasing the population size significantly enhanced genetic gain and increased inbreeding coefficient, while decreasing genetic variance (Fig. 5A–5C). The selection accuracy also slightly improved during the early years, although not in the later years (Fig. 5D).

Fig. 5.

Impact of population size. Comparison of each property between GGS_S and IGS_SU with different population sizes, with the setting of 100 QTLs, 500 markers, and h² = 0.3. The panels indicate the mean of the genetic value (A), inbreeding coefficient (B), genetic variance (C), and selection accuracy (D). Horizontal dashed lines in (B) indicate the threshold value of inbreeding depression.

To clarify the effects of self-pollination ratio, each property was compared among different settings of self-pollination ratio (Supplemental Fig. 2). Although genetic gain was only slightly different across different settings, inbreeding coefficients were remarkably enhanced when the self-pollination ratio was increased (Supplemental Fig. 2).

Discussion

Optimal selection schemes for onion GS breeding

It is essential to increase genetic gain while preventing inbreeding depression during onion breeding. In onion breeding, contamination of self-pollinated seeds is unavoidable, and its frequency significantly affects the degree of inbreeding (Supplemental Fig. 2). Thus, considering the self-pollination ratio, a selection scheme that can achieve higher genetic gain while maintaining a lower level of inbreeding during the selection term should be selected as the optimal selection scheme for onion GS breeding. The results of this simulation study revealed that the optimal selection scheme varied depending on the selection term. For short-term selection (i.e., up to 6 years), general GS with shortening of generation time (GGS_S) was superior to the other selection schemes, because GGS_S yielded the highest genetic gain while maintaining the inbreeding coefficient at a value lower than the threshold of inbreeding depression (Fig. 2, Supplemental Fig. 1, Supplemental Tables 1–4). In this study, the threshold was defined as the inbreeding coefficient of SPP in year 3 (corresponding to the F₄ generation), because selfing is limited to two or three times in practical onion breeding. However, the inbreeding coefficient of this selection scheme exceeded the threshold in later years (Fig. 2), suggesting that GGS_S is not suitable for long-term selection. For long-term selection (i.e., 10 years and more), GS with the procedure to avoid co-selection of close relatives, shortening of generation time, and updating of the prediction model (IGS_SU) was superior to the other selection schemes, because IGS_SU could achieve relatively higher genetic gain, while maintaining the inbreeding coefficient at a significantly lower level (Fig. 2, Supplemental Fig. 1, Supplemental Tables 1–4). The standard deviation of genetic gain was relatively larger than that of other properties (Supplemental Tables 1–4). In contrast, significant differences in genetic gain across selection schemes were detected by matched paired t test (Supplemental Tables 5–8). Thus, the large standard deviation of genetic gain may have been caused by differences in settings of the initial population in each simulation replication such as the distribution of QTLs and their effects. The standard deviation of inbreeding coefficient was small (Supplemental Tables 1–4), suggesting that the inbreeding coefficient remained unchanged across simulation replications. These results also support our conclusion. Consequently, breeders should select the appropriate schemes depending on the aim or planned period of their breeding programs, i.e., how much genetic gain is required to improve the target trait and for how long the breeding program would be conducted.

Efficiency of selection schemes for preventing inbreeding depression

In the present study, two GS-based selection schemes were assessed, i.e., GGS and IGS. In GGS, 10 individuals with the highest GEBV were selected as parents for the next selection, which represented the general selection procedure in plant GS breeding. In contrast, in IGS, to avoid excessive loss of diversity by co-selection of close relatives, individuals were selected from each subpopulation constructed using the genetic relationship data of the breeding population. IGS-based selection schemes could successfully maintain lower levels of inbreeding coefficients than the GGS-based selection schemes (Fig. 2). Thus, IGS-based schemes were effective in preventing inbreeding depression. Lin et al. (2017) proposed a method for controlling inbreeding by penalizing both mating group selection and GEBV calculation for individual selection using the genomic relationship matrix (G) of parental candidates. Their proposed method resulted in only one-third of the normal GS inbreeding coefficient (i.e., selected based on only GEBV) without any reduction in genetic gain in the breeding program of ryegrass (out-pollinated crop). Although our proposed method “IGS” is simpler than that proposed by Lin et al. (2017), the concept on which these methods are based, i.e., avoiding co-selection of close relatives, is similar. Moreover, a method similar to IGS was applied in a practical cassava (out-pollinated crop) GS breeding program, and its effectiveness in preventing inbreeding was demonstrated (Ozimati et al. 2019). Due to the simplicity of its implementation, this method would be useful for preventing inbreeding in practical onion GS breeding.

Impact of shortening the generation time and updating the prediction model

In the present study, the GS-based selection schemes with the shortening of generation time (i.e., GGS_S and IGS_S) achieved a higher genetic gain than the GS-based selection schemes with ordinary span of breeding generation (i.e., GGS and IGS) in the early years of selection term (Fig. 2, Supplemental Tables 1–4). In contrast, genetic gain per selection cycle, represented as response to selection, rapidly declined in GGS_S and IGS_S compared to that in GGS and IGS (Supplemental Fig. 3). Thus, high genetic gain of GGS_S and IGS_S was due to the doubled number of selection cycles, because the genetic gain corresponded to the accumulation of response to selection. Bernardo and Yu (2007) suggested that the main advantage of selection based on genetic markers, such as GS, is the gain per unit time, rather than gain per cycle. Accordingly, systems with shortened generation time, such as the seed-to-seed system, would be more efficient in onion GS breeding. In the present study, 10 plants were selected from a breeding population in each selection scheme, when population size was set at 200 and 500. Since the selection intensity was equal among selection schemes with the same population size setting, rapid decline of response to selection in GGS_S and IGS_S was responsible for the decrease in selection accuracy and genetic variance (Figs. 2, 3).

In the later years of selection term, the genetic gain of GGS_S was less than that of GGS_SU, in which the shortening of generation time was combined with the updating of the prediction model during selection terms (Fig. 2). Updating the prediction model enhanced selection accuracy (Fig. 2), while no significant difference in genetic variance was observed between GGS_S and GGS_SU (Fig. 3). Since the response to selection of GGS_SU increased in the cycles after the prediction model was updated (Supplemental Fig. 3), an increase in selection accuracy contributed to higher genetic gain (i.e., the accumulation of response to selection) in GGS_SU in the later years. It was particularly interesting to note that IGS_SU presented a higher selection accuracy and genetic variance than IGS_S during selection cycles (Figs. 2, 3). It is suggested that updating the prediction model contributed to the maintenance of genetic variance in IGS-based schemes but not in GGS-based schemes (Fig. 3). IGS_SU was expected to yield higher genetic gain for selection schemes lasting more than 10 years, due to the maintenance of high levels of response to selection. Although the updating of the prediction model would be useful for onion GS breeding, it requires the evaluation of phenotypes of individuals, and the cost for cultivating and harvesting should be considered in addition to genotyping cost. Taking the high cost into consideration, the timing of updating the prediction model needs to be determined in practical onion breeding programs.

Impact of number of markers and population size

The results of the present study revealed that the genetic gain of the schemes with 500 and 200 markers was not different or only slightly different (Fig. 4A). Because the selection accuracy reached a plateau with lower marker density (i.e., 200 markers), significant genetic gain was not achieved when the marker density was increased (i.e., 500 markers), particularly in IGS_SU. In contrast, the genetic gain and prediction accuracy achieved using 100 markers were less than that achieved using more markers (Fig. 4A, 4D). Thus, we found that at least 200 markers were necessary for efficient onion GS breeding under the settings of our simulation study. Previous studies have suggested that the optimal marker density for GS can be decided based on the range of linkage disequilibrium (LD) in the breeding population (Grattapaglia and Resende 2011, Yabe et al. 2013). In the present study, high levels of LD and large LD blocks were presented in the breeding population, because the F₂ population derived from one F₁ plant was used as the initial population. Therefore, relatively low marker density (i.e., 200 markers) was sufficient. The higher the marker density, the greater the genotyping costs. The simulation study was thus useful to determine optimal marker density.

Increasing the population size greatly enhanced genetic gain in GS-based selection schemes (Fig. 5A). In this study, the selection intensity increased with increasing population size, because the same number of plants (i.e., 10) were selected as parents for the following generations under both settings of the population size (i.e., 200 and 500 n). Greater selection intensity would result in a higher response to selection in a larger population, particularly in the early years. Increasing the population size resulted in a slight increase in inbreeding coefficient; however, the degree of this increment was not critical to inbreeding depression (Fig. 5B). Thus, a larger population size is preferred for onion GS breeding, although the increase in genotyping and phenotyping costs must be considered in practical breeding programs.

Prospects for GS application in practical onion breeding

In GS, genome-wide molecular marker information of each plant is necessary to construct a prediction model and calculate GEBVs. However, development and utilization of molecular markers in onion breeding have been limited, due to insufficient genomic information. Recently, some studies have obtained the genome-wide SNP information using markers developed from transcriptome sequences and genotyping-by-sequence (GBS), in which the reference genome sequence is not required (Duangjit et al. 2013, Jo et al. 2017). These methods would be useful for implementing GS in onion breeding.

In the present study, the GS schemes with shortening of generation time using the seed-to-seed system (e.g., GS_S and IGS_SU) achieved higher genetic gain than the selection schemes with an ordinary generation span (e.g., GPS and GGS) (Fig. 2). These results were consistent with those of previous simulation studies conducted in other plant species, including buckwheat, forest tree, and tall fescue (Iwata et al. 2011, Jighly et al. 2019, Yabe et al. 2013). Yabe et al. (2013) demonstrated that GS with three cycles per year could result in a significantly higher genetic gain than GS with one or two cycles per year in buckwheat. Increasing the number of selection cycles per unit time is indispensable for efficient GS breeding. Although the seed-to-seed system in onion breeding can shorten the generation term by half, it requires about one year per cycle. Recent developments in “speed breeding” protocols have the potential to significantly accelerate selection cycles in many crops by reducing generation time (Ghosh et al. 2018, Ohnishi et al. 2011, Tanaka et al. 2016, Watson et al. 2018). Using these methods, it is possible to increase the number of selection cycles per year by developing such onion breeding systems in future.

In onion, F₁ hybrid cultivars are predominant in regions where onion is grown under the condition of a long-day, while open-pollinated (OP) varieties are predominant in regions with a short-day (Brewster 2008, Khosa et al. 2016). Our proposed GS schemes would be useful for breeding of OP varieties and developing the parental lines of F₁ hybrids. In onion, F₁ hybrids are produced by “three-way cross”, which consist of a pollen donor line and a pair of maternal lines, i.e., male-sterile and maintainer lines (Brewster 2008). The pollen donor and maintainer maternal lines are usually inbred lines, which are developed by selfing two or three times and maintained by mass seed production to prevent inbreeding depression (Brewster 2008). Thus, our proposed GS schemes can be applied instead of such inbreeding selection procedures. The maternal male-sterile line is usually developed by backcrossing with the maintainer line, such that these lines are nearly genetically identical, apart from the presence of the cytoplasmic sterile factor. Since the DNA marker linked to the cytoplasmic sterile factor enables us to select sterile or fertile individuals among a breeding population (Kim et al. 2009), it is also possible to develop both maternal lines simultaneously using our proposed GS schemes. Although the issues of uniformity of phenotypes and prediction of combining ability remain to be addressed, our prosed GS scheme would be partially useful for the development of F₁ hybrid cultivars.

Author Contribution Statement

Conception and design of the study: DS, SY. Development of the simulation program: DS, SY. Drafting of the manuscript: DS, SY.