Optimal Control of Mathematical modeling of the spread of the COVID-19 pandemic with highlighting the negative impact of quarantine on diabetics people with Cost-effectiveness

Abstract

As of November 14, 2020, the number of people infected with the COVID-19 disease has reached more than 54 million people worldwide and more than 1323196 people have died, according to the World Health Organization. This requires many countries to impose a health emergency or quarantine, which has had positive results in reducing the spread of the COVID-19 pandemic, and it has also had negative economic, social and health effects. So, we suggest a mathematical model for the dynamics of how COVID-19 disease is spread, as well as a mathematical modeling for the dynamics of diabetes, then highlight the negative effect of quarantine has on the health of diabetics. Pontryagin’s maximum principle is used to characterize the optimal controls, and the optimality system is solved by an iterative method. Finally, some numerical simulations are performed to verify the theoretical analysis using MATLAB.

1. Introduction

The COVID-19 disease is affecting 217 countries and territories around the world. The COVID-19 disease is considered the most dangerous vis-á-vis other types of corona virus, such as SARS and MERS [1], [2], [3], which spreads rapidly and causes a high number of deaths and infections. According the World Healty Organisation (WHO) [4], [5], [6], [7], [8]

As of November 14, 2020, 17:34 GMT, The number of infections by COVID-19 disease has reached about 54078094, causing the death of more than 1314342. The United States of America is the hardest hit by the coronavirus with more than 11118081 infections and 250383 deaths, followed by India with more than 8797198 infections and 129479 deaths, then Brazil with more than 5819496 infection and 164979 deaths.

The COVID-19 disease is spread through many ways, such as shaking hands with an infected person, sneezing, etc. After infection with the virus, it is transferred to the incubation period, which ranges from two days to 14 days. During this period, patients develop some flu-like symptoms, serious complications, then the collapse and failure of the respiratory system which will eventually lead to death. To reduce the spread of the COVID-19 pandemic. Several countries have taken several precautionary measures to prevent the spread of the pandemic, namely total lockdown. consquently, the ongoing pandemic has, indeed, a non-negligible affect on the global economy.

Quarantine has also had a negative impact on the health of other patients such as diabetes and who have other diseases.

Diabetics are the most affected by the Covid-19 disease, whether they are infected with the virus or not, and they are also the largest number of deaths due to the virus. The quarantine had an effect on diabetics who were not infected with the virus, due to the lack of both exercising and a balanced diet.

According to the International Federation of Diabetics [9], In response to the current COVID-19 epidemic, governments in many countries have restricted the movements of their citizens, confining them to their family environment. General exercise facilities such as gymnasiums, sports centers and swimming pools are closed. Diabetes is attributed to two main factors, genetic or behavioral, economic and social, behavioral manifested by poor nutrition, economic in terms of unemployment or poverty and social manifested by family or practical problems. Who have a main role in diabetic complications such as kidney failure, vision loss and others [10], [11], [12], [13], [14], [15].

Our aim in this paper is to highlight the negative effect of impose of quarantine to reduce the spread of the COVID-19 pandemic on diabetics. In addition to suggesting means and strategies to limit the spread of the COVID-19 pandemic, thus increasing the state of health emergency or quarantine and thus reducing its impact on diabetics and others. With diabetic patients advised to follow medical advice to prevent diabetes complications.

Many mathematical models have been developed to simulate and study the dynamics of tranmission the COVID-19 virus, There are related research, Kouidere et al [16] proposed a mathematical model for the dyanamique of transmission COVID-19 pandemic, and Khajji et al [17] A multi-region discrete time mathematical modeling of the dynamics of COVID-19 disease propagation. kouidere et al [18], [19] introduce a mathematical model of dynamics of population diabetics. In addition, many papers have focused on this and other related topics ([20], [21], [22], [23], [24], [25], [26], [27], [28], [29], [30], [31]).

In this paper, we will study the dynamics of the spread of the COVID-19 pandemic and the modes of transmission, by the suggestion of optimal control strategies to limit the spread of the virus through awareness campaigns (billboards, social network sites...), in addition to the strategy of isolation and health monitoring of infected by COVID-19, the quarantine strategy plays an important role in limiting the spread of the virus.

We will also highlight the negative impact of quarantine on the health of diabetics. This effect on diabetics is reflected in the lack of exercise and the high pressure. In addition, diabetics were the most harmful of the virus infections. The mortality rate of diabetic patients infected by COVID-19 disease is the highest compared to other diseases.

In this regard, we propose a strategy for awareness campaigns to target diabetics through proper and balanced nutrition and exercise during the quarantine period.

These three proposed strategies will play an important role in limiting the spread of the virus, which will include among its results the lifting of quarantine and thus the resumption of sports activities, and reducing the negative impact on diabetics.

For reference, several companies have developed a vaccine to confront the Corona virus, which will play a fundamental role in vaccination against the COVID-19 disease, and the return of life to normal.

In addition to the work mentioned, we will study the dynamics of a mathematical model of the COVID-19 disease with highlighting of the negative impact to apply total quarantine on diabetics patients which contains the following additions:

• - $S$ represented the susceptible people that may be infected with COVID-19 disease.

• - $E$ represented the infected without symptoms which COVID-19 disease in the incubation period.

• - $I$ represented the infected with symptoms.

• - $R$ represented the recovered people after infected with the COVID-19 disease.

• - $Q_T$ represented the people who are not infected with the virus in the quarantine period.

• - $P$ represented the pre-diabetics people.

• - $D$ represented the diabetics without complications.

• - $C$ represented the diabetics with complications.

We noticed that most of researchers about spread of the COVID-19 pandemic focused on continuous and discrete time models and described by differential equations. Recently, more and more attention has been paid to study the control optimal (see [32], [33], [34] and the references mentioned there). this paper is arranged as, in section 2, we combined two mathematicals models: mathematical model of transmission of COVID-19 $SEIR{Q}_T$ and mathematical model of the dyanamics of the population diabetics $PDC$. In section 3, we presented an optimal control problem in our proposed model, some results concerning the existence and characterization of the optimal controls using the Pontryagin’s maximum principle are given. Numerical simulations through MATLAB are given in section 4. Finally we concluded the paper in section 5.

2. Methods

We considered a mathematical model $SEIR{Q}_{T}PDC$ that described the dynamic of spread of COVID-19 pandemic by highliting of the negative impact of applying quarantine total on diabetics people in a given population. We divided the population denoted by N into eight compartments.

• - $S$ represented the susceptible people that may be infected with COVID-19 disease.

• - $E$ represented the infected people without symptoms.

• - $I$ represented the infected people with symptoms.

• - $R$ represented the recovered people after infected with the COVID-19.

• - $Q_T$ represented the people who are not infected with COVID-19 in the quarantine period.

• - $P$ represented the pre-diabetics people.

• - $D$ represented the diabetics without complications.

• - $C$ represented the diabetics with complications.

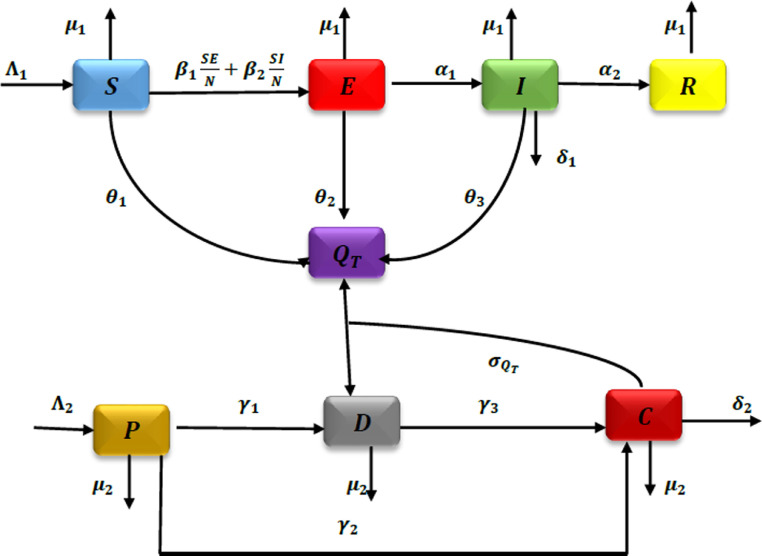
The graphical representation of the proposed model is shown in Figure 1 .

Fig. 1.

Figure compartments model

Hence, we present the COVID-19 mathematical model is governed by the following system of differential equation :

$$\{\begin{array}{c}{\displaystyle \frac{dS\left(t\right)}{dt}={\Lambda }_1-(\mu +{\theta }_1)S\left(t\right)-{\beta }_1\frac{S\left(t\right)E\left(t\right)}{N}-{\beta }_2\frac{S\left(t\right)I\left(t\right)}{N}}\hfill \\ {\displaystyle \frac{dE\left(t\right)}{dt}={\beta }_1\frac{S\left(t\right)E\left(t\right)}{N}+{\beta }_2\frac{S\left(t\right)I\left(t\right)}{N}-(\mu +{\alpha }_1+{\theta }_2)E\left(t\right)}\hfill \\ {\displaystyle \frac{dI\left(t\right)}{dt}={\alpha }_{1}E\left(t\right)-({\alpha }_2+{\theta }_3+\mu +{\delta }_1)I\left(t\right)}\hfill \\ \frac{dR\left(t\right)}{dt}={\alpha }_{2}I\left(t\right)-\mu R\left(t\right)\hfill \\ {\displaystyle \frac{d{Q}_T\left(t\right)}{dt}={\theta }_{1}S\left(t\right)+{\theta }_{2}E\left(t\right)+{\theta }_{3}I\left(t\right)-\mu Q_T\left(t\right)}\hfill \end{array}$$ (1)

where $S\left(0\right)\ge 0,$ E$\left(0\right)\ge 0,$ $I\left(0\right)\ge 0,$ $R\left(0\right)\ge 0$ and $Q_T\left(0\right)\ge 0$ are the initial state.

• - ${\Lambda }_1$: The recruitment rate of susceptible.

• - $\mu$: Natural mortality rate.

• - ${\beta }_1$: The rate of people who were infected by contact with the infected without symptoms.

• - ${\beta }_2$: The rate of people who were infected by contact with the infected with symptoms.

• - ${\alpha }_1$: The rate of people become normaly infected with symptoms.

• - ${\alpha }_2$: The rate of recovered from the virus.

• - ${\theta }_1$: The rate of susceptible who have been in quarantine total.

• - ${\theta }_2$: The rate of infected without symptoms who have been in quarantine total.

• - ${\theta }_3$: The rate of infected with symptoms who have been in quarantine total.

• - ${\delta }_1$: Mortality rate due to complications.

The dynamics of diabetics population with highliting the negative effect of quarantine total is described by:

$$\{\begin{array}{c}{\displaystyle \frac{dP\left(t\right)}{dt}={\Lambda }_2-({\gamma }_1+{\gamma }_2+{\mu }_2)P\left(t\right)}\hfill \\ \frac{dD\left(t\right)}{dt}={\gamma }_{1}P\left(t\right)-({\gamma }_3+{\mu }_2)D\left(t\right)-{\chi }_{Q_T}\left(t\right){\sigma }_{Q}D\left(t\right)\hfill \\ {\displaystyle \frac{dC\left(t\right)}{dt}={\gamma }_{1}P\left(t\right)+{\gamma }_{2}D\left(t\right)-{\mu }_{2}C\left(t\right)+{\chi }_{Q_T}\left(t\right){\sigma }_{Q}D\left(t\right)-{\delta }_{2}C\left(t\right)}\hfill \end{array}$$ (2)

Where

$${\chi }_{Q_T}\left(t\right)=\{\begin{array}{c}1\text{if}{Q}_T\ne 0\\ 0\text{else}\end{array}$$

e.g : $Q_T\ne 0$ : when total quarantine applied where $P\left(0\right)\ge 0,$ $D\left(0\right)\ge 0$ and $C\left(0\right)\ge 0$ are the initial state.

• •${\Lambda }_2$: The recruitment rate of pre-diabetes.
• •${\mu }_2$: natural mortality rate.
• •${\gamma }_1$: the probability of developing diabetes.
• •${\gamma }_2$: the probability of developing diabetes at stage of complications.
• •${\gamma }_3$: the probability of a diabetic person developing a complication.
• •${\sigma }_Q$: the probability of a diabetic person developing a complication due to applying quarantine total.
• •${\delta }_2$: Mortality rate due to complications.

2.1. A MODEL FOR OPTIMAL CONTROL

We consider a mathematical that describe the transmission of COVID-19 with highlighting the negative effect of total quarantine on diabetics.

Hence, we present mathematical model is governed by the following system of differential equation:

$$\{\begin{array}{c}{\displaystyle \frac{dS\left(t\right)}{dt}={\Lambda }_1-(\mu +{\theta }_1)S\left(t\right)-{\beta }_1\frac{S\left(t\right)E\left(t\right)}{N}-{\beta }_2\frac{S\left(t\right)I\left(t\right)}{N}}\hfill \\ {\displaystyle \frac{dE\left(t\right)}{dt}={\beta }_1\frac{S\left(t\right)E\left(t\right)}{N}+{\beta }_2\frac{S\left(t\right)I\left(t\right)}{N}-(\mu +{\alpha }_1+{\theta }_2)E\left(t\right)}\hfill \\ {\displaystyle \frac{dI\left(t\right)}{dt}={\alpha }_{1}E\left(t\right)-({\alpha }_2+{\theta }_3+\mu +{\delta }_1)I\left(t\right)}\hfill \\ {\displaystyle \frac{dR\left(t\right)}{dt}={\alpha }_{2}I\left(t\right)-\mu R\left(t\right)}\hfill \\ {\displaystyle \frac{d{Q}_T\left(t\right)}{dt}={\theta }_{1}S\left(t\right)+{\theta }_{2}E\left(t\right)+{\theta }_{3}I\left(t\right)-\mu Q_T\left(t\right)}\hfill \\ {\displaystyle \frac{dP\left(t\right)}{dt}={\Lambda }_2-({\gamma }_1+{\gamma }_2+{\mu }_2)P\left(t\right)}\hfill \\ {\displaystyle \frac{dD\left(t\right)}{dt}={\gamma }_{1}P\left(t\right)-({\gamma }_3+{\mu }_2)D\left(t\right)-{\sigma }_{Q}D\left(t\right)}\hfill \\ {\displaystyle \frac{dC\left(t\right)}{dt}={\gamma }_{1}P\left(t\right)+{\gamma }_{2}D\left(t\right)-{\mu }_{2}C\left(t\right)+{\sigma }_{Q}D\left(t\right)-{\delta }_{2}C\left(t\right)}\hfill \end{array}$$ (3)

where $S\left(0\right)\ge 0,$ $E\left(0\right)\ge 0,$ $I\left(0\right)\ge 0,$ $R\left(0\right)\ge 0,$ $Q_T\left(0\right)\ge 0,$ $P\left(0\right)\ge 0,$ $D\left(0\right)\ge 0$ and $C\left(0\right)\ge 0$

2.2. Model Basic Properties

2.2.1. Positivity of Solutions

Theorem 1

If $S\left(0\right)\ge 0,$ $E\left(0\right)\ge 0.I\left(0\right)\ge 0,R\left(0\right)\ge 0,Q_T\left(0\right)\ge 0,$ $P\left(0\right)\ge 0,$ $D\left(0\right)\ge 0$ and $C\left(0\right)\ge 0,$ the solutions $S\left(t\right),$ $E\left(t\right),$ $I\left(t\right),$ $R\left(t\right),$ $Q_T\left(t\right),$ $P\left(t\right),$ $D\left(t\right)$ and $C\left(t\right)$ of system (3) are positive for all $t\ge 0$ .

Proof

$$\begin{array}{ccc}\hfill \frac{dS\left(t\right)}{dt}& =& {\Lambda }_1-(\mu +{\theta }_1)S\left(t\right)-{\beta }_1\frac{S\left(t\right)E\left(t\right)}{N}-{\beta }_2\frac{S\left(t\right)I\left(t\right)}{N}\hfill \\ & \ge & -(\mu +{\theta }_1)S\left(t\right)-{\beta }_1\frac{S\left(t\right)E\left(t\right)}{N}-{\beta }_2\frac{S\left(t\right)I\left(t\right)}{N}\hfill \end{array}$$

$$\frac{dS\left(t\right)}{dt}+((\mu +{\theta }_1)+{\beta }_1\frac{E\left(t\right)}{N}+{\beta }_2\frac{I\left(t\right)}{N})S\left(t\right)\ge 0$$

where $F\left(t\right)=\mu$ $+{\theta }_1+{\beta }_1\frac{E\left(t\right)}{N}+{\beta }_2\frac{I\left(t\right)}{N}.$ The both sides in last inequality are multiplied by $\exp \left(\underset{0}{\overset{t}{\int }}F\left(s\right)ds\right).$

We obtain

$$\exp \left(\underset{0}{\overset{t}{\int }}F\left(s\right)ds\right).\frac{dS\left(t\right)}{dt}+F\left(t\right)\exp \left(\underset{0}{\overset{t}{\int }}F\left(s\right)ds\right).S\left(t\right)\ge 0$$

then $\frac{d}{dt}\left(S\left(t\right)\exp \right(\underset{0}{\overset{t}{\int }}F\left(s\right)ds\left)\right)\ge 0$

Integrating this inequality from 0 to $t$ gives:

$$\underset{0}{\overset{t}{\int }}\frac{d}{ds}\left(S\left(s\right)\exp \right(\underset{0}{\overset{t}{\int }}(\mu +{\theta }_1+{\beta }_1\frac{E\left(s\right)}{N}+{\beta }_2\frac{I\left(s\right)}{N})ds\left)\right)ds\ge 0$$

then

$$S\left(t\right)\ge S\left(0\right)\exp \left(\underset{0}{\overset{t}{\int }}(\mu +{\theta }_1+{\beta }_1\frac{E\left(s\right)}{N}+{\beta }_2\frac{I\left(s\right)}{N})ds\right)$$

$⟹S\left(t\right)\ge 0$.

Similarly, we prove that $E\left(t\right)\ge 0I\left(t\right)\ge 0,R\left(t\right)\ge 0$ and $Q_T\left(t\right)\ge 0.$

We have in first equation of system (3) that

$$\begin{array}{ccc}\hfill \frac{dP\left(t\right)}{dt}& =& {\Lambda }_2-({\gamma }_1+{\gamma }_2+{\mu }_2)P\left(t\right)\hfill \\ & \ge & -({\gamma }_1+{\gamma }_2+{\mu }_2)P\left(t\right)\hfill \end{array}$$

$$\frac{dP\left(t\right)}{dt}+({\gamma }_1+{\gamma }_2+{\mu }_2)P\left(t\right)\ge 0$$

Both sides in last inequality are multiplied with $\exp \left(\right({\gamma }_1+{\gamma }_2+{\mu }_2\left)t\right)$ we obtain

$$\begin{array}{ccc}\hfill \exp & & \left(\right({\gamma }_1+{\gamma }_2+{\mu }_2\left)t\right).\frac{dP\left(t\right)}{dt}+({\gamma }_1+{\gamma }_2+{\mu }_2)\hfill \\ \hfill \exp & & \left(\right({\gamma }_1+{\gamma }_2+{\mu }_2\left)t\right).P\left(t\right)\ge 0\hfill \end{array}$$

then

$$\frac{d}{dt}(\exp \left(({\gamma }_1+{\gamma }_2+{\mu }_2)t\right).P\left(t\right))\ge 0$$

Integrating this inequality from 0 to $t$ gives:

$$\underset{0}{\overset{t}{\int }}\frac{d}{ds}(\exp \left(({\gamma }_1+{\gamma }_2+{\mu }_2)s\right).P\left(s\right))ds\ge 0$$

then

$$P\left(t\right)\ge P\left(0\right)\exp \left(\right(\mu +{\theta }_1+{\theta }_2\left)t\right)$$

$⟹P\left(t\right)>0$.

Similarly, we prove that $D\left(t\right)\ge 0$ and $\mathbf{C}\left(t\right)\ge 0.$  □

2.2.2. Invariant region

Theorem 2

The set

$\Omega =\{(S,E,I,R,Q_T,P,D,C)\in {\mathbb{R}}_{+}^6/0\le S+E+I+R+Q_T+P+D+C\le \frac{\Lambda }{\mu }\}$ positively invariant under system (3) with initial conditions, $S\left(0\right)\ge 0,$ $E\left(0\right)\ge 0,$ $I\left(0\right)\ge 0,$ $R\left(0\right)\ge 0,$ $Q_T\left(0\right)\ge 0,$ $P\left(0\right)\ge 0,$ $D\left(0\right)\ge 0$ and $C\left(0\right)\ge 0$ are positive invariants for system (3) .

Proof

Also, one assumes that:

$$\begin{array}{ccc}\hfill \frac{dN}{dt}& =& \Lambda -\mu N-{\delta }_{1}C\le \Lambda -\mu N\hfill \\ & ⟹& N\left(t\right)\le \frac{\Lambda }{\mu }-N\left(0\right)e^{-\mu t}\hfill \end{array}$$

and $\Lambda ={\Lambda }_1+{\Lambda }_2,$ and $N\left(0\right)$ represents the initial values of the total population.

Thus, $\underset{t\to \infty }{lim}\sup N\left(t\right)=\frac{I}{\mu }$. It implies that the region $\Omega$ is a positively invariant set for system (3). So, we only need to consider the dynamics of the system on the set $\Omega$. □

2.2.3. Exictense of solutions

Theorem 3

The system (3) that satisfies a given initial condition

$(S\left(0\right),E\left(0\right).I\left(0\right),R\left(0\right),Q_T\left(0\right),P\left(0\right),D\left(0\right),C\left(0\right))$ has a unique solution.

Proof

Let $X=\left(\begin{array}{c}S\left(t\right)\\ E\left(t\right)\\ I\left(t\right)\\ R\left(t\right)\\ Q_T\left(t\right)\\ P\left(t\right)\\ D\left(t\right)\\ C\left(t\right)\end{array}\right)$ and $\phi \left(X\right)=\left(\begin{array}{c}\frac{dS\left(t\right)}{dt}\\ \frac{dE\left(t\right)}{dt}\\ \frac{dI\left(t\right)}{dt}\\ \frac{dR\left(t\right)}{dt}\\ \frac{d{Q}_T\left(t\right)}{dt}\\ \frac{dP\left(t\right)}{dt}\\ \frac{dD\left(t\right)}{dt}\\ \frac{dC\left(t\right)}{dt}\end{array}\right)$

So the system (3) is rewritten in the following form: $\phi \left(X\right)=AX+B\left(X\right)$ where

$$A=\left(\begin{array}{cccccccc}-(\mu +{\theta }_1)& 0& -0& 0& 0& 0& 0& 0\\ 0& -(\mu +{\alpha }_1+{\theta }_2)& 0& 0& 0& 0& 0& 0\\ 0& {\alpha }_1& A_1& 0& 0& 0& 0& 0\\ 0& 0& {\alpha }_2& -\mu & 0& 0& 0& 0\\ {\theta }_1& {\theta }_2& {\theta }_3& 0& -\mu & 0& 0& 0\\ 0& 0& 0& 0& 0& A_2& 0& 0\\ 0& 0& 0& 0& 0& {\gamma }_1& A_3& 0\\ 0& 0& 0& 0& 0& {\gamma }_1& {\gamma }_2+{\sigma }_Q& -{\mu }_2-{\delta }_2\end{array}\right)$$

Where $A_1=-({\alpha }_2+{\theta }_3+\mu +{\delta }_1),$ $A_2=-({\gamma }_1+{\gamma }_2+{\mu }_2)$ and $A_3=-({\gamma }_3+{\mu }_2+{\sigma }_Q)$ and $B\left(X\right)=\left(\begin{array}{c}{\Lambda }_1-{\beta }_1\frac{S\left(t\right)E\left(t\right)}{N}-{\beta }_2\frac{S\left(t\right)I\left(t\right)}{N}\\ {\beta }_1\frac{S\left(t\right)E\left(t\right)}{N}+{\beta }_2\frac{S\left(t\right)I\left(t\right)}{N}\\ 0\\ 0\\ 0\\ {\Lambda }_2\\ 0\\ 0\end{array}\right)$

$$|B\left(X_1\right)-B\left(X_2\right)|\le M\left(|X_1-X_2|\right)$$

then $\parallel \phi \left(X_1\right)-\phi \left(X_2\right)\parallel \le V.\parallel X_1-X_2\parallel$ where $V=\max (M,\parallel A\parallel )<\infty ,$ and $M$ is constant.

Thus, it follows that the function $\phi$ is uniformly Lipschitz continuous, and the restriction on $S\left(t\right)\ge 0,$ $E\left(t\right)\ge 0$ $I\left(t\right)\ge 0,$ $R\left(t\right)\ge 0,H\left(t\right)\ge 0$ and $R\left(t\right)\ge 0,$ we see that a solution of the system (3) exists [35]. □

2.2.4. Model with controls

As of November 15,2020, several vaccines against the Covid-19 disease have reached late stages in clinical trials in several countries, such as China, the United States of America, Germany and

others, pending approval by the Health and Food Organization. So we suggest the following strategies, there are three controls $u\left(t\right),$ $v\left(t\right)$ and $w\left(t\right)$ for $t\in [0;T]$. The first control can be interpreted as the proportion to be subjected to sensitization and prevention.. So, we note that $u\left(t\right)$ is to diagnosed and awereness program to susceptible people at time $t$. The second control $v\left(t\right)$ is the proportion of quarantine and health monitoring of people with COVID-19 disease and its complications. The third control $w\left(t\right)$ is the proportion awareness program for diabetics without complications for diet tracking and regular diet in the quarantine period at time $t.$

$$\{\begin{array}{c}{\displaystyle \frac{dS\left(t\right)}{dt}={\Lambda }_1-(\mu +{\theta }_1)S\left(t\right)-{\beta }_1(1-u\left(t\right))\frac{S\left(t\right)E\left(t\right)}{N}-{\beta }_2(1-u\left(t\right))\frac{S\left(t\right)I\left(t\right)}{N}}\hfill \\ {\displaystyle \frac{dE\left(t\right)}{dt}={\beta }_1(1-u\left(t\right))\frac{S\left(t\right)E\left(t\right)}{N}+{\beta }_2(1-u\left(t\right))\frac{S\left(t\right)I\left(t\right)}{N}-(\mu +{\alpha }_1+{\theta }_2)E\left(t\right)}\hfill \\ {\displaystyle \frac{dI\left(t\right)}{dt}={\alpha }_{1}E\left(t\right)-({\alpha }_2+{\theta }_3+\mu +{\delta }_1)I\left(t\right)-v\left(t\right)I\left(t\right)}\hfill \\ {\displaystyle \frac{dR\left(t\right)}{dt}={\alpha }_{2}I\left(t\right)-\mu R\left(t\right)+v\left(t\right)I\left(t\right)}\hfill \\ {\displaystyle \frac{d{Q}_T\left(t\right)}{dt}={\theta }_{1}S\left(t\right)+{\theta }_{2}E\left(t\right)+{\theta }_{3}I\left(t\right)-\mu Q_T\left(t\right)}\hfill \\ {\displaystyle \frac{dP\left(t\right)}{dt}={\Lambda }_2-({\gamma }_1+{\gamma }_2+{\mu }_2)P\left(t\right)}\hfill \\ {\displaystyle \frac{dD\left(t\right)}{dt}={\gamma }_{1}P\left(t\right)-({\gamma }_3+{\mu }_2)D\left(t\right)-{\chi }_{Q_T}\left(t\right){\sigma }_Q(1-w\left(t\right))D\left(t\right)}\hfill \\ {\displaystyle \frac{dC\left(t\right)}{dt}={\gamma }_{2}P\left(t\right)+{\gamma }_{3}D\left(t\right)-{\mu }_{2}C\left(t\right)+{\chi }_{Q_T}\left(t\right){\sigma }_Q(1-w\left(t\right))D\left(t\right)-{\delta }_{2}C\left(t\right)}\hfill \end{array}$$ (4)

The problem is to minimize the objective functional

$$J(u,v,w)=E\left(T\right)+I\left(T\right)-D\left(T\right)+\underset{0}{\overset{T}{\int }}[E\left(t\right)+I\left(t\right)-D\left(t\right)+\frac{A}{2}{u}^2\left(t\right)+\frac{B}{2}{v}^2\left(t\right)+\frac{G}{2}{w}^2\left(t\right)]dt$$ (5)

Where $A>0,$ $B>0$ and $G>0$ are the cost coefficients. They are selected to weigh the relative importance of $u\left(t\right),$ $v\left(t\right)$ and $w\left(t\right)$ at time $t,$ $T$ is the final time.

In other words, we seek the optimal controls $u^{*},v^{*}$ and $w^{*}$ such that

$$J(u^{*},v^{*},w^{*})=\underset{u,v,w\in U}{\min }J(u,v,w)$$ (6)

Where $U$ is the set of admissible controls defined by

$$U=\left\{\begin{array}{c}{\displaystyle u,v,w/0\le u_{\min }\le u\left(t\right)\le u_{\max }\le 10\le v_{\min }\le v\left(t\right)\le v_{\max }\le 1}\\ {\displaystyle \text{and}0\le w_{\min }\le w\left(t\right)\le w_{\max }\le 1,t\in [0,T]}\end{array}\right\}$$ (7)

3. The optimal control: existence and characterization

We first show the existence of solutions of the system (4), thereafter we will prove the existence of optimal control [36].

3.1. Existence of an Optimal Control

Theorem 4

Consider the control problem with system (4) .

There exists an optimal control $(u^{*},v^{*},w^{*})\in U$ such that $J(u^{*},v^{*},w^{*})=\underset{u,v,w\in U}{min}J(u,v,w)$

Proof

The existence of the optimal control can be obtained using a result by Fleming and Rishel [36], checking the following steps:

• •It follows that the set of controls and corresponding state variables is nonempty. In Boyce and DiPrima ([37], (Theorem7.1.1))

  To prove that the set of controls and the corresponding state variables is nonempty, we will use a simplified version of an existence result [37]. Let $X_i^{\prime }=F_{X_i}(t;X_1,X_2,\cdots ,X_8)$ with $i=1;\cdots ;8$ where $(X_1,X_2,\cdots ,X_8)=(S,E,I,R,Q_T,P,D,C)$ where $X_1,\cdots ,X_5$ and $X_6$ form the right-hand side of the system of equations (4). Let $u,v$ and $w$ for some constants and since all parameters are constants and $X_1,\cdots ,X_7$ and $X_8$ are continuous, then $F_S,F_E,F_I;F_R;F_{Q_T},F_P;F_{D_T}$ and $F_C$ are also continuous. Additionally, the partial derivatives $\frac{\partial F_{X_i}}{\partial X_i}$ with $i=1;\cdots ;8$ are all continuous. therefore, there exists a unique solution $(S,E,I,R,Q_T,P,D,C)$ that satisfies the initial conditions. Therefore, the set of controls and the corresponding state variables is nonempty and condition 1 is satisfied.

• •$J(u,v,w)=E\left(T\right)+I\left(T\right)-D\left(T\right)+\underset{0}{\overset{T}{\int }}[E\left(t\right)+I\left(t\right)-D\left(t\right)+\frac{A}{2}{u}^2\left(t\right)+\frac{B}{2}{v}^2\left(t\right)+\frac{G}{2}{w}^2\left(t\right)]$$dt$ is convex in $U.$

  Take any controls $u,v\in U$ and $\lambda \in [0,1]$. then $0\le \lambda u+(1-\lambda )v$ additionally, we observe that $\lambda u\le \lambda$ and $(1-\lambda )v\le (1-\lambda ),$ then $\lambda u+(1-\lambda )v\le \lambda +(1-\lambda )=1$ Hence, $0\le \lambda u+(1-\lambda )v\le 1$, for all $u,v\in U$ and $\lambda \in [0,1]$.

• •The control space $U=\left\{\right(u,v,w)/(u,v,w)$ is measurable,$0\le u_{\min }\le u\left(t\right)\le u_{\max }\le 10\le v_{\min }\le v\left(t\right)\le v_{\max }\le 1$ and $0\le w_{\min }\le w\left(t\right)\le w_{\max }\le 1,t\in [0,T-1]\}$. is convex and closed by definition.
• •All the right hand sides of equations of system are continuous, bounded above by a sum of bounded control and state, and can be written as a linear function of $u,v$ and $w$ with coefficients depending on time and state.
• •The integrand in the objective functional, $E\left(t\right)+I\left(t\right)-D\left(t\right)+\frac{A}{2}{u}^2\left(t\right)+\frac{B}{2}{v}^2\left(t\right)+\frac{G}{2}{w}^2\left(t\right)$ is clearly convex on $U$
• •It rest to show that there exists constants ${\zeta }_1,{\zeta }_2,{\zeta }_3,{\zeta }_4>0,$

  and $\zeta$such that $E\left(t\right)+I\left(t\right)-D\left(t\right)+\frac{A}{2}{u}^2\left(t\right)+\frac{B}{2}{v}^2\left(t\right)+\frac{G}{2}{w}^2\left(t\right)$

  satisfies

  $$E\left(t\right)+I\left(t\right)-D\left(t\right)+\frac{A}{2}{u}^2\left(t\right)+\frac{B}{2}{v}^2\left(t\right)+\frac{G}{2}{w}^2\left(t\right)\ge {\zeta }_1+{\zeta }_2{\left|u\right|}^{\zeta }+{\zeta }_3{\left|v\right|}^{\zeta }+{\zeta }_4{\left|w\right|}^{\zeta }.$$
  The state variables being bounded, let ${\zeta }_1=\underset{t\in [0,T]}{inf}\left(E\right(t)+I(t)-D(t\left)\right),{\zeta }_2=\frac{A}{2},{\zeta }_3=\frac{B}{2},{\zeta }_5=\frac{G}{2}$ and $\zeta =2$ then it follows that:

  $$E\left(t\right)+I\left(t\right)-D\left(t\right)+\frac{A}{2}{u}^2\left(t\right)+\frac{B}{2}{v}^2\left(t\right)+\frac{G}{2}{w}^2\left(t\right)\ge {\zeta }_1+{\zeta }_2{\left|u\right|}^{\zeta }+{\zeta }_3{\left|v\right|}^{\zeta }+{\zeta }_4{\left|w\right|}^{\zeta }.$$

  Then from Fleming and Rishel [36], we concluded that there exists an optimal control.

 □

3.2. Characterization of the optimal control

In order to derive the necessary conditions for the optimal control, we applied Pontryagin’s maximum [38] principle to the Hamiltonian $H$ at time $t$ defined by

$$H\left(t\right)=E\left(t\right)+I\left(t\right)-D\left(t\right)+\frac{A}{2}{u}^2\left(t\right)+\frac{B}{2}{v}^2\left(t\right)+\frac{G}{2}{w}^2\left(t\right)+\sum _{i=1}^8{\lambda }_i\left(t\right)f_i(S,E,I,R,Q_T,P,D,C)$$ (8)

where $f_{i,}$ is the right side of the difference equation of the $i^{th}$ state variable.

Theorem 5

Consider the control problem with the system(4). There are three optimal controls$(u^{*},v^{*},w^{*})\in U^3$such that$J(u^{*},v^{*},w^{*})=\underset{u,v,w\in U}{min}J(u,v,w)$

Given the optimal controls$(u^{*},v^{*},w^{*})$and the solutions$S^{*},E^{*},I^{*},R^{*},Q_T^{*},P^{*},D^{*}$and$C^{*}$of the corresponding state system(4), there exists adjoint variables${\lambda }_1,\cdots ,{\lambda }_7$and${\lambda }_8$satisfying:

$${\lambda }_1^{\prime }={\lambda }_1(\mu +{\theta }_1+{\beta }_1(1-u\left(t\right))\frac{E\left(t\right)}{N}+{\beta }_2(1-u\left(t\right))\frac{I\left(t\right)}{N})-{\lambda }_2({\beta }_1(1-u\left(t\right))\frac{E\left(t\right)}{N}+{\beta }_2(1-u\left(t\right))\frac{I\left(t\right)}{N})-{\lambda }_5{\theta }_1$$

$${\lambda }_2^{\prime }=-1+{\lambda }_1{\beta }_1(1-u\left(t\right))\frac{S\left(t\right)}{N}-{\lambda }_2({\beta }_1(1-u\left(t\right))\frac{S\left(t\right)}{N}-\mu -{\alpha }_1)-{\lambda }_3{\alpha }_1-{\lambda }_5{\theta }_2$$

$${\lambda }_3^{\prime }=-1+{\lambda }_1{\beta }_2(1-u\left(t\right))\frac{S\left(t\right)}{N}-{\lambda }_2{\beta }_2(1-u\left(t\right))\frac{S\left(t\right)}{N}+{\lambda }_3({\alpha }_2+{\theta }_3+\mu +{\delta }_1+v\left(t\right))-{\lambda }_4({\alpha }_2+v\left(t\right))-{\lambda }_5{\theta }_3$$

$${\lambda }_4^{\prime }={\lambda }_4\mu$$

$${\lambda }_5^{\prime }={\lambda }_5\mu$$

$$\begin{array}{ccc}\hfill {\lambda }_6^{\prime }& =& {\lambda }_6({\gamma }_1+{\gamma }_2+{\mu }_2)-{\lambda }_7{\gamma }_1-{\lambda }_8{\gamma }_2\hfill \\ \hfill {\lambda }_7^{\prime }& =& 1+{\lambda }_7({\gamma }_3+{\mu }_2-{\sigma }_Q(1-w\left(t\right))-{\lambda }_8({\gamma }_3+{\sigma }_Q(1-w\left(t\right)))\hfill \\ \hfill {\lambda }_8^{\prime }& =& {\lambda }_8({\mu }_2+{\delta }_2)\hfill \end{array}$$

With the transversality conditions at time$T$:${\lambda }_1\left(T\right)=0,{\lambda }_2\left(T\right)=-1,{\lambda }_3\left(T\right)=-1,$${\lambda }_4\left(T\right)=0,{\lambda }_5\left(T\right)=0,{\lambda }_6\left(T\right)=0,{\lambda }_7\left(T\right)=0$and${\lambda }_8\left(T\right)=0.$

Furthermore, for$t\in [0,T],$the optimal controls$u^{*},v^{*}$and$w^{*}$are given by

$$u^{*}=\min (1,\max (0,\frac{({\lambda }_2-{\lambda }_1)}{A}({\beta }_1\frac{S\left(t\right)E\left(t\right)}{N}+{\beta }_2\frac{S\left(t\right)I\left(t\right)}{N})))$$ (9)

$$v^{*}=\min (1,\max (0,\frac{{\lambda }_{3}I\left(t\right)-{\lambda }_{4}I\left(t\right)}{B}))$$ (10)

$$w^{*}=\min (1,\max (0,\frac{({\lambda }_7-{\lambda }_8)}{G}\times {\sigma }_{Q}D\left(t\right)))$$ (11)

Proof

The Hamiltonian $H$ is defined as follows:

$H\left(t\right)=E\left(t\right)+I\left(t\right)-D\left(t\right)+\frac{A}{2}{u}^2\left(t\right)+\frac{B}{2}{v}^2\left(t\right)+\frac{G}{2}{w}^2\left(t\right)+\sum _{i=1}^8{\lambda }_i\left(t\right)f_i(S,E,I,R,Q_T,P,D,C)$ where :

$f_1(S,E,I,R,Q_T,P,D,C)={\Lambda }_1-(\mu +{\theta }_1)S\left(t\right)-{\beta }_1(1-u\left(t\right))\frac{S\left(t\right)E\left(t\right)}{N}-{\beta }_2(1-u\left(t\right))\frac{S\left(t\right)I\left(t\right)}{N}$

$f_2(S,E,I,R,Q_T,P,D,C)={\beta }_1(1-u\left(t\right))\frac{S\left(t\right)E\left(t\right)}{N}+{\beta }_2(1-u\left(t\right))\frac{S\left(t\right)I\left(t\right)}{N}-($$\mu$$+{\alpha }_1+{\theta }_2)E\left(t\right)$

$f_3(S,E,I,R,Q_T,P,D,C)={\alpha }_{1}E\left(t\right)-({\alpha }_2+{\theta }_3+\mu +{\delta }_1)I\left(t\right)-v\left(t\right)I\left(t\right)$

$f_4(S,E,I,R,Q_T,P,D,C)={\alpha }_{2}I\left(t\right)-\mu R\left(t\right)+v\left(t\right)I\left(t\right)$

$f_5(S,E,I,R,Q_T,P,D,C)={\theta }_{1}S\left(t\right)+{\theta }_{2}E\left(t\right)+{\theta }_{3}I\left(t\right)-\mu Q_T\left(t\right)$

$f_6(S,E,I,R,Q_T,P,D,C)={\Lambda }_2-({\gamma }_1+{\gamma }_2+{\mu }_2)P\left(t\right)$

$f_7(S,E,I,R,Q_T,P,D,C)={\gamma }_{1}P\left(t\right)-({\gamma }_3+{\mu }_2)D\left(t\right)-{\sigma }_Q(1-w\left(t\right))D\left(t\right)$

$f_8(S,E,I,R,Q_T,P,D,C)={\gamma }_{2}P\left(t\right)+{\gamma }_{3}D\left(t\right)-({\mu }_2+{\delta }_1)C\left(t\right)+{\sigma }_Q(1-w\left(t\right))D\left(t\right)$

For $t\in [0,T],$ the adjoint equations and transversality conditions can be obtained by using Pontryagin’s maximum principle [38], [39], [40], [41] such that

$$\begin{array}{ccc}\hfill {\lambda }_1^{\prime }& =& -\frac{\partial H}{\partial S}={\lambda }_1(\mu +{\theta }_1+{\beta }_1(1-u\left(t\right))\frac{E\left(t\right)}{N}+{\beta }_2(1-u\left(t\right))\frac{I\left(t\right)}{N})\hfill \\ & & -{\lambda }_2({\beta }_1(1-u\left(t\right))\frac{E\left(t\right)}{N}+{\beta }_2(1-u\left(t\right))\frac{I\left(t\right)}{N})-{\lambda }_5{\theta }_1\hfill \end{array}$$

$${\lambda }_2^{\prime }=-\frac{\partial H}{\partial E}=-1+{\lambda }_1{\beta }_1(1-u\left(t\right))\frac{S\left(t\right)}{N}-{\lambda }_2({\beta }_1(1-u\left(t\right))\frac{S\left(t\right)}{N}-\mu -{\alpha }_1)-{\lambda }_3{\alpha }_1-{\lambda }_5{\theta }_2$$

$${\lambda }_3^{\prime }=-\frac{\partial H}{\partial I}=-1+{\lambda }_1{\beta }_2(1-u\left(t\right))\frac{S\left(t\right)}{N}-{\lambda }_2{\beta }_2(1-u\left(t\right))\frac{S\left(t\right)}{N}+{\lambda }_3({\alpha }_2+{\theta }_3+\mu +{\delta }_1+v\left(t\right))-{\lambda }_4({\alpha }_2+v\left(t\right))-{\lambda }_5{\theta }_3$$

$${\lambda }_4^{\prime }=-\frac{\partial H}{\partial R}={\lambda }_4\mu$$

$${\lambda }_5^{\prime }=-\frac{\partial H}{\partial Q_T}={\lambda }_5\mu$$

$$\begin{array}{ccc}\hfill {\lambda }_6^{\prime }& =& -\frac{\partial H}{\partial P}={\lambda }_6({\gamma }_1+{\gamma }_2+{\mu }_2)-{\lambda }_7{\gamma }_1-{\lambda }_8{\gamma }_2\hfill \\ \hfill {\lambda }_7^{\prime }& =& -\frac{\partial H}{\partial D}=1+{\lambda }_7({\gamma }_3+{\mu }_2-{\sigma }_Q(1-w\left(t\right))-{\lambda }_8({\gamma }_3+{\sigma }_Q(1-w\left(t\right)))\hfill \\ \hfill {\lambda }_8^{\prime }& =& -\frac{\partial H}{\partial C}={\lambda }_8({\mu }_2+{\delta }_2)\hfill \end{array}$$

For $t\in [0,T],$ the optimal controls $u^{*},v^{*}$ and $w^{*}$  can be solved from the optimality condition,

$$\begin{array}{ccc}\hfill -\frac{\partial H}{\partial u}& =& -Au\left(t\right)+({\lambda }_2-{\lambda }_1)({\beta }_1\frac{S\left(t\right)E\left(t\right)}{N}+{\beta }_2\frac{S\left(t\right)I\left(t\right)}{N})=0\hfill \\ \hfill -\frac{\partial H}{\partial v}& =& -Bv\left(t\right)+{\lambda }_{3}I\left(t\right)-{\lambda }_{4}I\left(t\right)=0\hfill \\ \hfill -\frac{\partial H}{\partial w}& =& -Gw\left(t\right)+({\lambda }_7-{\lambda }_8)\times {\sigma }_{Q}D\left(t\right)=0\hfill \end{array}$$

we have

$$u\left(t\right)=\frac{({\lambda }_2-{\lambda }_1)}{A}({\beta }_1\frac{S\left(t\right)E\left(t\right)}{N}+{\beta }_2\frac{S\left(t\right)I\left(t\right)}{N})$$

$$v\left(t\right)=\frac{{\lambda }_3-{\lambda }_4}{B}\times I\left(t\right)$$

$$w\left(t\right)=\frac{({\lambda }_7-{\lambda }_8)}{G}\times {\sigma }_{Q}D\left(t\right)$$

By the bounds in $U$ of the controls, it is easy to obtain $u^{*},v^{*}$ and $w^{*}$ are given in ((9), (10), (11)) the form of system (3). □

4. Results

In this section, we present the results obtained by numerically solving the optimality system. In our control problem, we have initial conditions for the state variables and terminal conditions for the adjoints. That is, the optimality system is a two-point boundary value problem with separated boundary conditions at times step $i=0$ and $i=T$. We solve the optimality system by an iterative method with forward solving of the state system followed by backward solving of the adjoint system. We start with an initial guess for the controls at the first iteration and then before the next iteration, we update the controls by using the characterization. We continue until convergence of successive iterates is achieved. A code is written and compiled in Matlab using the following data.

Different simulations can be carried out using various values of parameters. In the present numerical approach, we use the following parameters values in Table 1 taken from [18] and according to the statistics provided by the World Health Organization [5]:

Table 1.

Parameter values used in numerical simulation

paramter	Description	value in $d^{-1}$
$\mu$	Natural mortality rate	0.02
${\beta }_1$	The rate of people who were infected by contact with the infected without sympt	0.4
${\beta }_2$	The rate of people who were infected by contact with the infected with sympt	0.3
${\alpha }_1$	The rate of people become normaly infected with symptoms	0.4
${\alpha }_2$	The rate of people who recovered from the virus	0.1
${\theta }_1$	The rate of susceptible who have been quarantine total.	$0.9$
${\theta }_2$	The rate of infected without symptoms who have been in quarantine total.	0.2
${\theta }_3$	The rate of infected with symptoms who have been in quarantine total.	0.2
${\delta }_1$	Mortality rate due to complications of COVID-19.	0.1
${\delta }_2$	Mortality rate due to complications of diabete	0.4
$\sigma$	The probability of a diabetic person developing a complication due to quarantine total	0.1
${\Lambda }_1$	The recruitment rate of susceptible.	80000000
${\Lambda }_2$	The recruitment rate of pre-diabetics.	50000
${\gamma }_1$	The probability of developing diabetes	0.2
${\gamma }_2$	The probability of developing diabetes at stage of complications	0.3
${\gamma }_3$	The probability of a diabetic person developing a complication,	0.1

Since control and state functions are on different scales, the weight constant value is chosen as follows: $A=10000,$ $B=10000$ and $G=10000.$ and intial value of compartments $S\left(0\right)=3\times {10}^9,$ $E\left(0\right)=2.5\times {10}^6,$ $I\left(0\right)=6\times {10}^5,$ $R\left(0\right)=5000,$ $Q_T\left(0\right)={10}^{10},$ $P\left(0\right)={10}^6,$ $D\left(0\right)=4\times {10}^5,$ $C\left(0\right)=4\times {10}^4,$

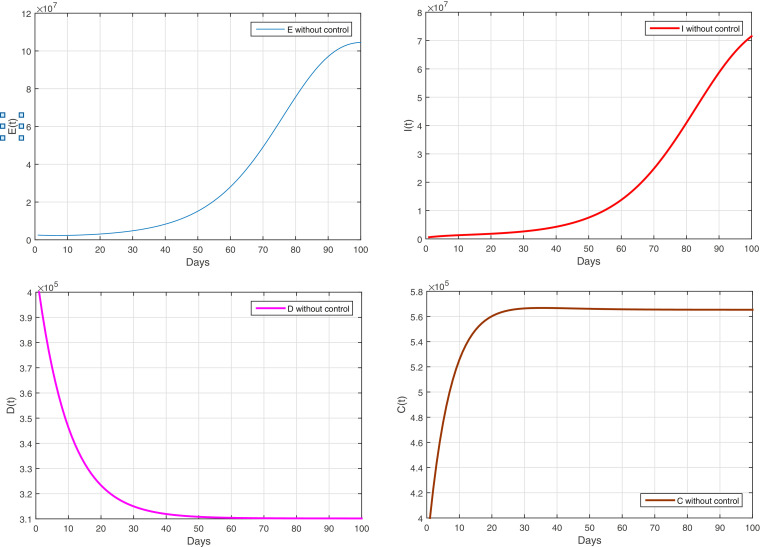
From Figure 2 , we notice an increase in the number of infected without symptoms, which will lead to increase the number of infected with symptoms. Since no preventive measure has been applied to limit the spread of the Covid-19 pandemic. Lead to apply total quarantine in country at all to limit to spread of COVID-19, which will have a negative impact on diabetics, which will increase the risk of complications after lack of exercise due to quarantine and sitting at home leading to obesity.

Fig. 2.

The evolution of the infected and diabetics with and without complications without controls

The proposed control strategy in this work helps to achieve several objectives.

4.1. Strategy A: Sensitization and prevention

We use only the optimal control $u\left(t\right)$

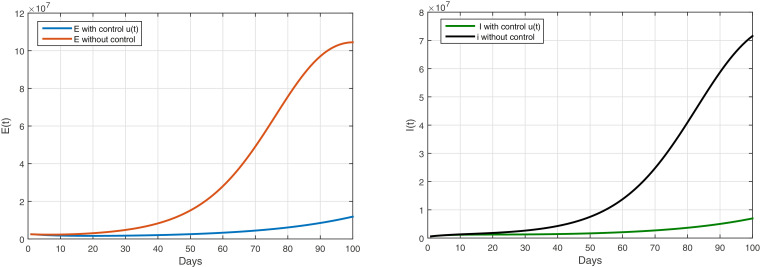
This strategy aims to increase the number of people protected from disease, through the Figure 2, noted that after applying different strategies as awarness program and protected.

According to Figure 3 and Table 2 , the awareness program and prevention strategy has been adopted, through awareness campaigns for all citizens to inform them of the seriousness of the COVID-19 disease, through the media, and to take measures to prevention by avoiding infected people, wash their hands regularly, especially after sneezing and wearing face masks, as well as reducing the spread of the Covid-19 disease. The results of this strategy reduce the number of infected people and lift the complete quarantine, which will lead to reducing the negative impact of the quarantine on the health of diabetics.

Fig. 3.

The evolution of the number of infected with and without symptoms with control $u\left(t\right)$

Table 2.

Percentage of decreasing of number of infected and its types.

Without and with control u(t) after 100 Days	Without control	With control
Infected without symptoms	1.04$\times {10}^8$	$1.18\times {10}^8$
Infected with symptoms	$7.15\times {10}^7$	$6.94\times {10}^6$

4.2. Strategy B: Quarantine

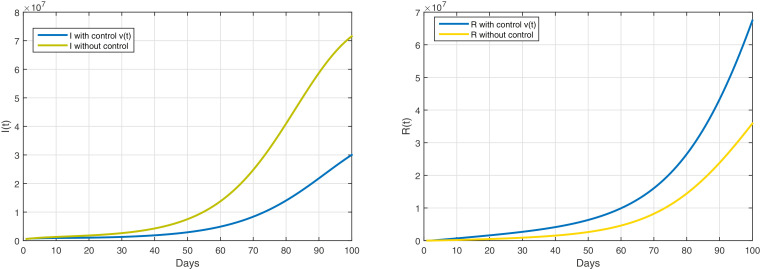
We use only the optimal control $v\left(t\right)$

Based on Figure 4 and Table 3 , a quarantine strategy has been adopted for infected with symptoms as well as infected with serious complications in hospitals with treatment, in order to limit the spread of the COVID-19 pandemic. This strategy plays a very important role in controlling the virus and limiting its spread, which among its consequences will be raising the quarantine in the country. It also reduces the negative impact of quarantine on the health of diabetics. This is explained by Figure 4, by the decrease in the number of infected with symptoms after appliying quarantine strategy.

Fig. 4.

The evolution of the number of infected with and without symptoms with control $v\left(t\right)$

Table 3.

Percentage of decreasing of number of infected with its types.

Without and with control v(t) after 100 Days	Without control	With control
Infected with symptoms	7.15$\times {10}^7$	3$\times {10}^7$
Rocovered	$3.58\times {10}^7$	6.74$\times {10}^7$

4.3. Strategy C: Awareness rogram and Quarantine

We combine the optimal controls $u\left(t\right)$ and $v\left(t\right)$.

In this strategy, the two optimal controls $u\left(t\right)$ and $v\left(t\right)$ are activated at the same time in order to improve the numerical results of case 1.

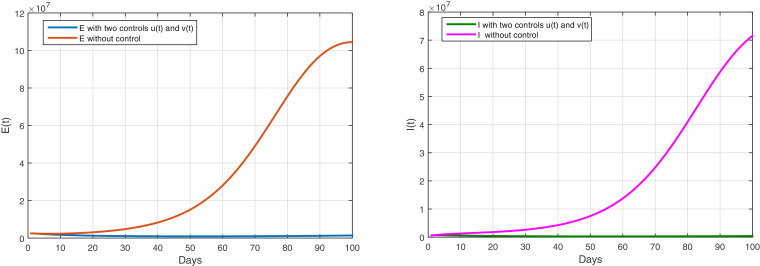
Based on Figure 5 and Table 4 , after applying the two strategies together, the strategy of awareness campaigns about the risks of spreading the virus, in addition to the strategy of quarantining the infected. We got the desired results, with a decrease in 99.43%.

Fig. 5.

The evolution of the number of infected with and without symptoms with controls $u\left(t\right)$ and $v\left(t\right)$

Table 4.

Percentage of decreasing of number of infected with its types.

Infected after 100 Days	Without control	With u(t) and v(t)	Percentage
Infected without symptoms	7.15$\times {10}^7$	3$\times {10}^7$	-98.66%
Infected with symptoms	$3.58\times {10}^7$	6.74$\times {10}^7$	-99.43%

Hence the definitive elimination of the virus and the limitation of the spread of the pandemic under the name of COVID-19.

Conclusion: Based on the observation of the ratios recorded in Table 2, Table 3 and 4, it explains that the implementation of a single strategy is insufficient and will not be sufficient. This means that the joint implementation of the two strategies has produced distinct, satisfactory and excellent results.

4.4. Cost-effectiveness analysis

In this section, we analyze the profitability of the previous three scenarios and strategies by comparing these two control strategies to determine the most profitable strategy. Following the method applied in several studies $[29-31],$ we assess costs using the differential cost-effectiveness (ICER). This ratio used compare the differences between costs and health outcomes of two competing intervention strategies.

The ICER is defined as the quotient of the difference in costs in strategies $i$ and $j,$ by the difference in infected averted in strategies $i$ and $j$ $(i,j\in \{1,2,3,4\left\}\right).$

Given two competing strategies (1) and (2), where strategy (2) has higher effectiveness than strategy (1) $\left(TA\right(2)>TA(1)$), the $ICER$ values are calculated as follow:

$$ICER\left(1\right)=\frac{TC\left(1\right)}{TA\left(1\right)}$$

$$ICER\left(2\right)=\frac{TC\left(2\right)-TC\left(1\right)}{TA\left(2\right)-TA\left(1\right)}$$

Where the total costs $\left(TC\right)$ and the total cases averted $\left(TA\right)$ are defined, during a given period for strategy i for $i=1,2,3$ by:

$$TC\left(i\right)=\underset{0}{\overset{T}{\int }}({\beta }_{1}u\left(t\right)\frac{S\left(t\right)E\left(t\right)}{N}+{\beta }_{2}u\left(t\right)\frac{S\left(t\right)I\left(t\right)}{N}+v\left(t\right)I\left(t\right))dt$$

$$TA\left(i\right)=\underset{0}{\overset{T}{\int }}(E\left(t\right)+I\left(t\right)\left)\right)-(E^{*}\left(t\right)+I^{*}\left(t\right)))dt$$

while $(E^{*}\left(t\right),I^{*}\left(t\right),D^{*}\left(t\right))$ is the optimal solution associated to the optimal control $(u^{*},v^{*},w^{*})$ Using the simulation results and we ranked, in the Table 5 our control strategies in order of increased numbers of averted infections.

Table 5.

Total costs and total averted infections for strategies 1–3

Strategy	Total averted infections (TA)	Total cost (TC)
1	$-6.32\times {10}^8$	$1.24\times {10}^8$
2	$-2.78\times {10}^8$	$2.93\times {10}^8$
3	$-2.45\times {10}^8$	7.55$\times {10}^7$

Strategy 1 is compared with strategy 2 with respect to increased effectiveness, in reference to Table 5. So:

$$ICER\left(1\right)=\frac{TC\left(1\right)}{TA\left(1\right)}=\frac{1.24\times {10}^8}{-6.32\times {10}^8}=-0.1962$$

$$ICER\left(2\right)=\frac{TC\left(2\right)-TC\left(1\right)}{TA\left(2\right)-TA\left(1\right)}=\frac{2.93\times {10}^8-1.24\times {10}^8}{-2.78\times {10}^8+6.32\times {10}^8}=0.4774$$

Since $ICER\left(1\right)<ICER\left(2\right),$ then strategy 2 is less effective than strategy 1. Therefore, strategy 1 is excluded from the set of alternatives.

Next, strategy 1 is compared to strategy 3. The ICER values for strategy 3 and strategy 1 are calculated below:

$$ICER\left(1\right)=\frac{TC\left(1\right)}{TA\left(1\right)}=\frac{1.24\times {10}^8}{-6.32\times {10}^8}=-0.1962$$

$$ICER\left(3\right)=\frac{TC\left(3\right)-TC\left(1\right)}{TA\left(3\right)-TA\left(1\right)}=\frac{7.55\times {10}^7-1.24\times {10}^8}{-2.45\times {10}^8+6.32\times {10}^8}=-0.6951$$

Since $ICER\left(3\right)<ICER\left(1\right),$ then strategy 1 is less effective than strategy 3. Therefore, strategy 3 is excluded from the set of alternatives.

Therefore, the conclusion is that strategy 3 (awarness campaigns to protect potential individuals infected with the virus, prevent contact with people infected with COVID-19 and with hospital quarantine for the infected) is the most effective strategy as previously mentioned by the proportions.

4.5. Strategy D: Awareness rogram

We use only the optimal control $w\left(t\right)$

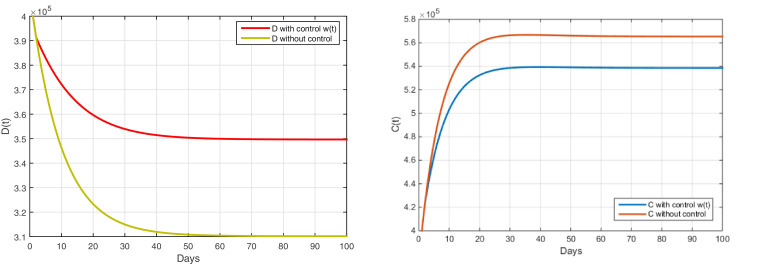
According to Figure 6 and Table 6 , after applying the strategy of awareness campaigns and sensitizing diabetics to the negative effect of not following a medical opinion during this period, applying total quarantine on the country to reduce the COVID-19 pandemic. These tips are in the application of diet and exercise inside the house, in addition to getting away from family problems as much as possible and following an appropriate diet program during this period and the rest of the regular periods.

Fig. 6.

The evolution of the number of diabetics with and without complications with control $w\left(t\right)$

Table 6.

Percentage of decreasing of number of diabetics without and with control.

Without and with control w(t) after 100 Days	Without control	With control
Diabetic without complications	$3.1\times {10}^5$	3.49$\times {10}^5$
Diabetic with complications	5.65$\times {10}^5$	5.38$\times {10}^5$

Remark We can also merge multiple assemblies as $\left(u\right(t),v(t\left)\right)$thus get a variety of results.

5. Conclusion

In this paper, we have compiled two mathematical models, one for the transmission of the COVID-19 disease between people, and the second model for the dynamics of diabetes population. Our objective is to highlight the negative impact of the application of total quarantine on diabetics in particular. We have also proposed several strategies to limit the spread of the COVID-19 pandemic, which leads to the lifting of the quarantine. We have also made recommendations to diabetics who must be followed during a health emergency to avoid complications of diabetes. We also introduced three controls which, respectively, represent Sensitization and prevention, quarantine, awerness program for diabetics people. We applied the results of the control theory and we managed to obtain the characterizations of the optimal controls. The numerical simulation of the obtained results showed the effectiveness of the proposed control strategies. Also, in future papers, we will study the dynamics of transmission of the Covid-19 disease using fractal-fractional Caputo-Fabrizio operator and / or Optimal control of spread of COVID-19 mathematical model using Atangana-Baleanu-Caputo fractional derivative.

CRediT authorship contribution statement

Abdelfatah Kouidere: Writing - original draft, Writing - review & editing. Lahcen EL Youssoufi: Writing - original draft, Writing - review & editing. Hanane Ferjouchia: Writing - original draft, Writing - review & editing. Omar Balatif: Writing - original draft, Writing - review & editing. Mostafa Rachik: Writing - original draft, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.