A standardized framework for testing the performance of sleep-tracking technology: step-by-step guidelines and open-source code

Abstract

Sleep-tracking devices, particularly within the consumer sleep technology (CST) space, are increasingly used in both research and clinical settings, providing new opportunities for large-scale data collection in highly ecological conditions. Due to the fast pace of the CST industry combined with the lack of a standardized framework to evaluate the performance of sleep trackers, their accuracy and reliability in measuring sleep remains largely unknown. Here, we provide a step-by-step analytical framework for evaluating the performance of sleep trackers (including standard actigraphy), as compared with gold-standard polysomnography (PSG) or other reference methods. The analytical guidelines are based on recent recommendations for evaluating and using CST from our group and others (de Zambotti and colleagues; Depner and colleagues), and include raw data organization as well as critical analytical procedures, including discrepancy analysis, Bland–Altman plots, and epoch-by-epoch analysis. Analytical steps are accompanied by open-source R functions (depicted at https://sri-human-sleep.github.io/sleep-trackers-performance/AnalyticalPipeline_v1.0.0.html). In addition, an empirical sample dataset is used to describe and discuss the main outcomes of the proposed pipeline. The guidelines and the accompanying functions are aimed at standardizing the testing of CSTs performance, to not only increase the replicability of validation studies, but also to provide ready-to-use tools to researchers and clinicians. All in all, this work can help to increase the efficiency, interpretation, and quality of validation studies, and to improve the informed adoption of CST in research and clinical settings.

Statement of Significance.

Sleep technology is increasingly used by sleep researchers and clinicians. Wearable sleep trackers are recognized as promising tools for large-scale sleep assessment. However, their level of accuracy is still largely unknown, and the validation process is challenged by the lack of a standardized framework to evaluate the performance of these devices. In our guidelines, we provide step-by-step analytic procedures, an illustrative example, and a set of open-source R functions that can be easily implemented by different laboratories for testing and interpreting the performance of different sleep trackers. The proposed analytical framework can improve the efficiency and reproducibility of validation studies while promoting the informed adoption of sleep trackers for both research and clinical purposes.

Introduction

Sleep-tracking technology, and particularly consumer sleep technology (CST; i.e. multi-sensor wearable sleep trackers such as wristbands, armbands, and smartwatches), is increasingly used by sleep researchers and clinicians to track quality, quantity, and patterns of sleep in an individual’s free-living conditions and for extensive periods [1]. The continuous passive tracking of sleep can generate massive datasets (big data), opening an unprecedented window of opportunity to investigate sleep in relation to a wide range of factors implicated in health and disease [2–4].

The widespread usage of CST by the general population, their limited cost and low level of expertise required are among the main reasons for their growing popularity within the scientific sleep community. Moreover, the recent implementation of miniaturized multisensory systems able to integrate accelerometers with a broad range of other biosensors capturing physiological (e.g. cardiac data) and environmental information (e.g. environmental noise) has further enhanced the potential of CST to deeply explore sleep (sleep composition in addition to sleep/wake patterns) and its physiology (e.g. sleep autonomic function) [2–4]. Consequently, CST is viewed by sleep researchers as a promising cost-effective tool to enable large-scale sleep assessment and advance the field of sleep and circadian science [5].

Despite these advantages, the validity, accuracy, and reliability of CST devices are still poorly supported by empirical data, a crucial and overlooked factor in their adoption (see de Zambotti and colleagues [1]). The unstandardized, undisclosed, and often unvalidated data outcomes and algorithms are among the main challenges the scientific community faces in using CST [1, 5–7]. As recommended by the American Academy of Sleep Medicine (AASM), “further CST data validation regarding device accuracy and application within clinical practice is necessary if these devices are to be considered part of medical evaluation and treatment” [6]. Such a required effort appears to be acknowledged by the CST literature, where an increasing number of validation studies has been reported [3, 8]. Nevertheless, the slow pace of scientific validation and peer-reviewed publication processes is challenged by the relentless pace of the CST industry, with new devices and algorithms being introduced every year, questioning the generalizability of published results and the appropriateness of the term “validation” itself. Consequently, there is a need for more time efficient and standardized validation protocols to continuously update the evidence on the performance (rather than the “validity”) of CST devices [1, 5].

Standardized protocols are also necessary for promoting comparison across studies and better interpretation of CST outcomes. Indeed, CST performance is currently evaluated by a strongly heterogenic and sometimes lax range of methodological and analytical procedures. For instance, Haghayegh and colleagues [9] excluded 50 of the 72 identified articles from their review on the accuracy of Fitbit devices also due to ineligible or insufficiently described method or outcomes, and they reported inconsistencies across multiple aspects such as recording setting, method of reference, and statistical procedures. A similar degree of heterogeneity has been reported by other reviews of CST validation studies [1, 3], including those evaluating the performance of clinical-grade actigraphy [10]. In addition to the diversity in validation protocols, the variety of device features implies important differences in terms of analytical techniques and also in the terminology used to describe their performance. For example, the classic definition of “sensitivity” as the ability to detect sleep (useful in a dichotomic sleep/wake classification) is inadequate to describe the performance of newer devices providing more than two levels of classifications (sleep stages).

In sum, our understanding of CST performance is threatened by heterogeneity at various levels (e.g. data collection procedures, data analysis, device features, and terminology). Such complexity highlights the need for a common framework to aid comparison across studies, devices, and algorithms, to reduce at least some areas of uncertainty.

Initial CST validation guidelines have been introduced by de Zambotti and colleagues [1] and largely supported by a consensus panel report [5] following the Sleep Research Society sponsored workshop “International Biomarkers Workshop on Wearables in Sleep and Circadian Science”, held at the 2018 SLEEP Meeting of the Associated Professional Sleep Societies in Baltimore (Maryland, USA). These efforts highlighted the most up-to-date methodological and analytical requirements to be met by validation studies, with the goal of promoting further development and informed use of CST in the sleep and circadian field.

Here, we aimed to integrate these recommendations by providing step-by-step analytical guidelines to evaluate the performance of sleep trackers compared with reference methods such as PSG. The analytical steps are designed to be simple and easily accessible, to flexibly fit the prototypical datasets used by CST validation studies, and to be applied to any type of sensors providing sleep outcomes. Each step is accompanied by a set of open-source functions [11] based on the R environment [12]. Finally, an empirical sample dataset is used to illustrate the recommended steps, and to describe the essential outputs that should be reported in a validation paper. The analytical pipeline with example code in R matching the step-by-step procedure outlined in the article is available at https://sri-human-sleep.github.io/sleep-trackers-performance/AnalyticalPipeline_v1.0.0.html.

Methods

Step-by-step guidelines for testing the performance of sleep-trackers

The following guidelines target prototypical studies reporting on sleep trackers performance (i.e. comparing the performance of a device in measuring sleep against gold-standard PSG), but they can be generalized to several other cases. For instance, although PSG has been recommended as the gold-standard to evaluate CST [1, 5], we recognize that the comparison of CST devices with other reference methods, including standard actigraphy and subjective sleep reports, can be informative under certain circumstances (e.g. see [13, 14]). Similarly, whereas most sleep trackers are increasingly able to provide information on sleep staging, it is acknowledged that some frequently used devices (including standard actigraphy) can only measure sleep/wake patterns. Thus, the proposed guidelines are designed with a degree of flexibility to generalize to cases where reference methods alternative to PSG are used, or where only the sleep/wake pattern is provided. In the following sections, “device” indicates any sleep tracker under assessment, whereas “reference” refers to any other method against which the device is tested.

Considering the pace of the CST industry, we encourage the use of the term “performance” instead of “validity,” to prevent erroneous interpretation of a device as valid when only limited information is provided (e.g. a single study), and when device functioning can rapidly change as algorithms are updated. Also, “CST validation studies” are typically method comparison studies. Although method comparison has been considered as a special type of validity (i.e. the ability of a measurement to reflect what it is designed to measure), the agreement of a new method with a gold standard should be more correctly referred to its reliability (i.e. the absence of measurement error) [15]. Thus, in the present article “performance” refers to the qualities of a sleep tracker describing its measurement error (reliability and accuracy), as quantified by the agreement with a reference method [16, 17].

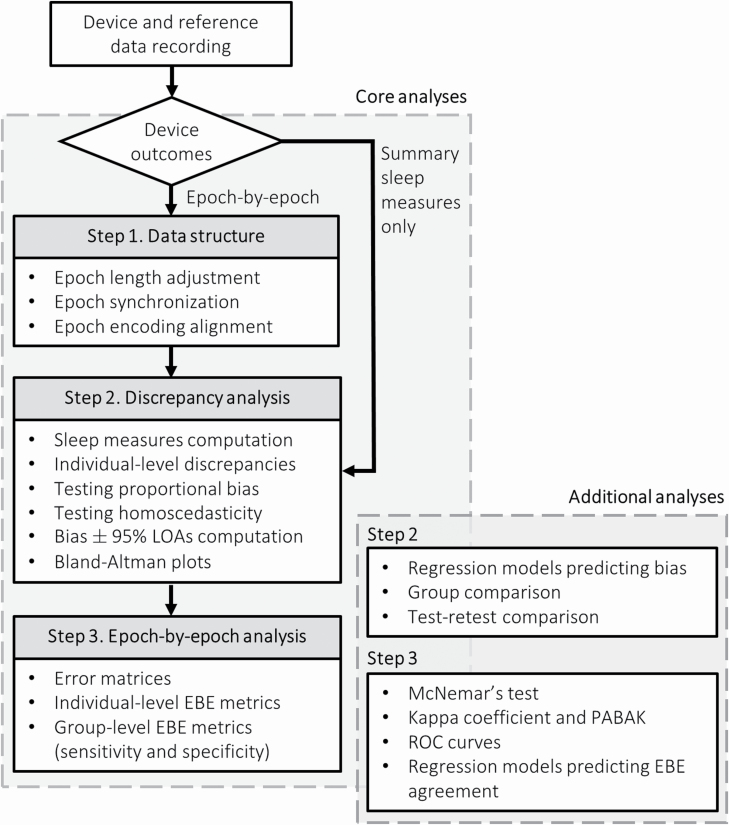
The procedures described below are strictly focused on evaluating such qualities through the computation of the relevant performance metrics on a specific sample of subjects. Group comparison (e.g. insomnia patients vs. healthy sleepers) or measurement precision (i.e. agreement between repeated measurements using the same method) can be addressed with traditional statistical tools (e.g. linear regression, test–retest comparison) to model the variability of the computed metrics (see also [17]). Similarly, common statistical aspects such as data distribution, outlier detection, homoscedasticity, and confidence intervals computation are not discussed in detail but briefly described at the end of each section, and highlighted by the accompanying functions, allowing for informed decision about function parameter settings. A flow chart of the recommended analytical procedures is depicted in Figure 1.

Figure 1.

Analytical flow chart including the core analytical steps to evaluate the performance of sleep trackers. LOAs, limits of agreement; EBE, epoch-by-epoch; PABAK, prevalence-adjusted bias-adjusted kappa; ROC, receiver operating characteristic.

Following the description of the analytical steps, the proposed guidelines are applied to a sample of empirical data, which is used as an example to illustrate the essential recommended analytical steps to be reported in a “validation paper,” and to provide an interpretation of the main outcomes. The data were obtained from a sample of 14 healthy adults (30–53 y, 6 women) recruited from the community of the San Francisco Bay Area, who spent a night at the SRI human sleep lab. All participants gave informed consent and the study was approved by the SRI International Institutional Review Board. Standard laboratory PSG sleep assessment was performed via the Compumedics Grael® HD-PSG system (Compumedics, Abbotsford, Victoria, Australia) while participants were also wearing a Fitbit Charge 2 device (Fitbit Inc.).

Step 1: data structure

The recommended analytical steps rely on minimal methodological assumptions to generate the optimal data structure. First, sleep should be measured simultaneously with the device under assessment and a reference method. Second, both device and reference recordings should have the same epoch length (e.g. 30-s or 1-min). Epoch duration should be adjusted when the epoch length differs between device and reference. For instance, the AASM standards recommend scoring PSG recordings in 30-s epochs [18]. When such length is not allowed by the device, as for CST devices providing 1-min epochs, a conversion should be performed to aggregate PSG epochs, by preferring “wake” score when both sleep and wake are present in either one of the two 30-s epoch of each minute [19]. Importantly, some CST devices do not allow the user to export epoch-by-epoch (EBE) data and instead provide only nightly summary sleep measures. In these cases, assuming that a replicable procedure is used to synchronize the recordings, it is only possible to evaluate the device performance through discrepancy analysis (i.e. by skipping EBE data processing and the analyses described in Step 3).

Third, when EBE data is provided, device and reference recordings should be synchronized on an epoch level. The temporal synchronization between the device and the reference data recordings is critical as lack of synchronization can strongly influence certain outcomes, particularly EBE metrics. Ideally, both recordings should be confined to the period between lights-off and lights-on (i.e. sharing the same time in bed [TIB]), either by synchronizing the starting time before the recording or by aligning the epoch after the recording (post-processing), provided that device and reference share the same timestamps. Several strategies have been proposed to assure the alignment between device and reference starting time (e.g. see [20, 21]). Although lights-off and lights-on are often automatically determined by CST algorithms, their correspondence between device and reference is required for comparing the measures recorded by the two methods.

Fourth, device and reference data should be encoded using the same coding system (e.g. 0 = wake in both device and reference data). The epoch coding system to be used depends on the ability of the device and the reference to provide sleep staging. Conventionally, most CST devices that provide sleep staging information consider PSG-based N1 + N2 sleep as “light sleep” and N3 as “deep sleep.” Checking these specifications with the device manufacturer is recommended. A categorical coding system (e.g. 0 = wake, 1 = N1/N2 or “light” sleep, 2 = N3 or “deep” sleep, 3 = REM sleep) is used when sleep staging is provided, whereas a binary system (e.g. 0 = wake, 1 = sleep) is used when only the sleep/wake pattern is available. Finally, both recordings should not contain any missing data.

Detailed methodological recommendations (e.g. device setting, synchronization, and experimental protocols) in assessing the performance of sleep-tracking technology have been discussed elsewhere [1, 5]. Once the device and reference data have been collected and recoded, the application of the following steps assumes the organization of the dataset in a long format that includes one column for the subject identifier, one column for the epoch identifier, and two columns reporting the device and the reference data, respectively (see section 1 of the analytical pipeline [11]).

Step 2: discrepancy analysis

The analysis of the discrepancies between a new and a reference method is thought to be the main step to evaluate the suitability of the new method as a substitute of the reference.[16] Here, “discrepancy” refers to the difference (bias) and the limits of agreement (LOAs) between any device- and reference-derived numeric measurement (e.g. total sleep time).

Sleep measures computation

Classical overnight sleep parameters (see [18]) can be easily computed from the data structure described at the end of Step 1. Table 1 provides a definition and a computational procedure for each of the main sleep measures to be considered in CST validation studies, including both those derived from sleep/wake dichotomous data (e.g. provided by actigraphy) and those based on sleep staging (e.g. provided by the new generation of multi-sensor CST devices).

Table 1.

Main sleep measures considered in discrepancy analysis

Sleep metric	Definition	Computation
TST	Number of minutes classified as sleep between lights-off and lights-on	Sum of epochs classified as sleep × epoch length (s)/60
SE	Percentage of total sleep time over TIB	TST/TIB
SOL	Number of minutes classified as wake before the first epoch classified as sleep	Sum of epochs classified as wake before the first sleep epoch × epoch length (s)/60
WASO	Number of minutes classified as wake after the first epoch classified as sleep	Sum of epochs classified as wake after the first sleep epoch × epoch length (s)/60
“Light” sleep duration	Number of minutes classified as “light” sleep (the equivalent of PSG N1 + N2 sleep) between lights-off and lights-on	Sum of epochs classified as “light” sleep × epoch length (s)/60
“Deep” sleep duration	Number of minutes classified as “deep” sleep (the equivalent of PSG N3 sleep) between lights-off and lights-on	Sum of epochs classified as “deep” sleep × epoch length (s)/60
REM sleep duration	Number of minutes classified as REM between lights-off and lights-on	Sum of epochs classified as REM sleep × epoch length (s)/60

Sleep measures are defined assuming a recording confined between lights-off and lights-on. TIB, time in bed (assumed to be the same between device and reference); TST, total sleep time; SE, sleep efficiency; SOL, sleep onset latency; WASO, wake after sleep onset; REM, rapid eye movement; PSG, polysomnography. The computation of the latter three measures assumes that sleep staging is provided by both device and reference.

Individual-level discrepancies

After the computation of the relevant sleep measures, data are organized in two columns (device and reference measures) matched by subject and used to compute the difference for each subject in each measure. In contrast with the data structure described in Step 1 (i.e. long form, with one row for each epoch), sleep measures and the corresponding discrepancies are structured in a wide form, with one row for each subject. Specifically, when a device is compared with a reference method, the reference-derived measures are subtracted from device-derived measures (i.e. device − reference), such that positive differences will be interpreted as device’s overestimations, whereas negative differences will be interpreted as device’s underestimations. It is common practice to graphically represent individual-level discrepancies (e.g. Bland–Altman plots, see below), also to highlight potential outliers in the sample (see section 2.2 of the analytical pipeline [11]).

Group-level discrepancies

In a subsequent step, discrepancies computed at the individual level are used to estimate the systematic and the random component of measurement error in the device under assessment. As originally proposed by Altman and Bland [22], the former is quantified by the systematic bias whereas the random error is quantified by the 95% LOAs. Bias and LOAs computation relies on three main assumptions: (1) the bias should be independent from the size of measurement, (2) random error should be uniform over the size of measurement (homoscedasticity), and (3) differences should be normally distributed [16]. A function that automatically tests each assumption and computes the results accordingly is included in 11 (see section 2.3 of the analytical pipeline). Here, we briefly discuss how each assumption is tested, and how bias and LOAs are computed under each circumstance (see also [17]).

Constant bias, homoscedasticity, and normally distributed differences:

When all assumptions are fulfilled, the systematic bias is easily computed as the mean of the differences between each measure obtained with the device and the reference. In this case, the observation of a systematic bias (i.e. significantly higher or lower than zero) simply implies the necessity to adjust for it by subtracting the mean difference (“calibration index”) from device-derived measures. Under the same conditions, LOAs are computed as bias ± 1.96 standard deviations (SD) of the differences [16, 17].

Proportional bias:

Proportional bias indicates a case where the mean difference increases or decreases as a function of the size of measurement (SM), that is the “true magnitude” (i.e. based on the reference) of the considered sleep measure. For instance, it might happen that TST discrepancies are larger for subjects with lower “true TST” compared with subjects with higher TST. Unless a nonlinear relationship between SM and the bias is detected (which is very unlikely to occur), proportional bias for the sleep measure $i$ can be tested and represented using simple linear regression:

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{B}\mathrm{i}\mathrm{a}{\mathrm{s}}_i=b_0+b_1\mathrm{S}{\mathrm{M}}_i.}\end{array}}$$ (1)

A statistical test of the slope b₁, accompanied by the visual inspection of Bland–Altman plots (see below), can be used to decide how to represent the bias: with equation (1) if b₁ is significant, as the mean difference otherwise [16]. When a proportional bias is detected but data are homoscedastic, LOAs are computed as:

$${\displaystyle \begin{array}{l}{\displaystyle 95\mathrm{\%}\mathrm{L}\mathrm{O}\mathrm{A}{\mathrm{s}}_i=\mathrm{B}\mathrm{i}\mathrm{a}{\mathrm{s}}_i\pm 1.96\times \sqrt{\frac{1}{n}{\displaystyle \underset{i=1}{{\displaystyle \sum ^n}}}{[({\mathrm{x}}_{Di}-{\mathrm{x}}_{Ri})-(b_0+b_1\mathrm{S}{\mathrm{M}}_i)]}^2},}\end{array}}$$ (2)

where $n\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{z}\mathrm{e},\mathrm{a}\mathrm{n}\mathrm{d}{\mathrm{x}}_{Di}\mathrm{a}\mathrm{n}\mathrm{d}{\mathrm{x}}_{Ri}$ are the i-th sleep measure obtained with the device and the reference, respectively.

Heteroscedasticity:

Heteroscedasticity indicates a case where the random error (i.e. the SD of the differences) increases or decreases as a function of SM [15]. Similar to what is indicated for proportional bias, heteroscedasticity can be evaluated by visually inspecting the trend of the differences dispersion over SM (Bland–Altman plots) and by applying a linear regression model to the absolute values of the residuals (AR) obtained from the model reported in equation (1):

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{A}{\mathrm{R}}_{\mathrm{i}}={\mathrm{c}}_0+{\mathrm{c}}_1\mathrm{S}{\mathrm{M}}_{\mathrm{i}}.}\end{array}}$$ (3)

If c₁ is significant, data are considered heteroscedastic. To deal with heteroscedasticity, data can be log-transformed before computing LOAs [16, 23]. Alternatively, when log transformation does not remove heteroscedasticity, the SD of the differences can be expressed as a function of SM, using the coefficients estimated with equation (3) [16]. Under the assumption of normality, LOAs are then expressed as:

$${\displaystyle \begin{array}{l}{\displaystyle 95\mathrm{\%}\mathrm{L}\mathrm{O}\mathrm{A}{\mathrm{s}}_i=\mathrm{B}\mathrm{i}\mathrm{a}\mathrm{s}\pm 2.46(c_0+c_1\mathrm{S}{\mathrm{M}}_i).}\end{array}}$$ (4)

Note that in equation (4), the bias is computed depending on the first assumption: as the mean difference if independent from SM, using equation (1) otherwise.

Deviation from normality:

Although departure from normality is thought to be less problematic for LOAs computation compared with other statistical contexts [16], distributions that are very skewed or have long tails should be analyzed with caution. Logarithmic transformation (see above) and nonparametric approaches (e.g. reporting centiles or proportions of differences falling outside cutoff values) have been proposed as strategies to deal with these cases [15, 16]. Only the former is implemented in our functions (see sections 2.3 and 2.4 of the analytical pipeline [11]).

Independently of the specific bias and LOAs computation, confidence intervals (CI) are reported to quantify the uncertainty in each of the estimated discrepancy metrics, and to express bias significance [24, 25]. Alternative approaches such as nonparametric or bootstrap CI should be used when a deviation from normality is detected or when the sample size is small (see [26, 27]). Finally, outliers and influential cases should be carefully evaluated with both graphical (e.g. Bland–Altman plots) and statistical procedures [28]. Excluding such cases is recommended only under specific circumstances that should be clearly explained (e.g. a participant with only 4 h of TST in a sample of good sleepers).

Bland–Altman plots

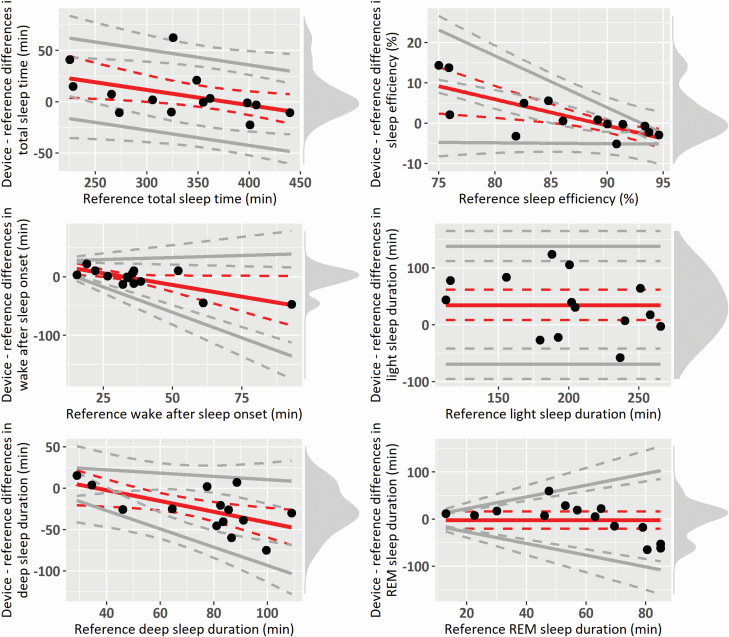
The Bland–Altman plot [22] is widely considered as a core analysis for evaluating the interchangeability between two methods of measurement, and it is the most popular method to measure agreement between continuous medical measurements [29]. The Bland–Altman plot is the graphical representation of what is described in the previous section, in which the differences between device- and reference-derived measures are plotted against SM [16]. In addition to clearly visualizing bias and LOAs, it allows to graphically inspect assumptions of constant bias over SM and homoscedasticity, and to highlight potential outliers. Whereas in the original Bland–Altman plot SM is represented by the mean of the two measurements [22], reference-derived measures (and particularly PSG measures) have been recommended [1, 5] and frequently adopted [30, 31] to represent SM (i.e. on the x-axis). Examples of Bland–Altman plots adjusted for various cases of compliance with assumptions are provided in the illustrative example below (see Figure 2).

Figure 2.

Bland–Altman plots of the sample data. Red solid lines indicate bias, whereas gray solid lines indicate the 95% LOAs, both with their 95% CIs (dotted lines). Black points indicate individual observations, and the density diagram on the right side of each plot represents the distribution of the differences. Plots are adjusted for the specific case of compliance with the assumptions for discrepancy analysis: all fulfilled (“light” sleep duration), proportional bias but homoscedastic differences (total sleep time), constant bias but heteroscedastic differences (REM sleep duration), both proportional bias and heteroscedasticity (sleep efficiency and “deep” sleep duration), and LOAs based on log-transformed differences (wake after sleep onset and REM sleep duration).

Step 3: EBE analysis

The quantification of the agreement between a device and a reference method depends on the nature of the considered data [32]. In the previous step, we discussed the relevant performance metrics for numeric variables (i.e. sleep measures). Here, we discuss the essential procedures to be considered with binary or categorical data, namely, EBE analysis, to be used when the evaluated sleep tracker allows to export EBE data. EBE analysis is the preferred approach to assess the accuracy of a device in sleep and wake classification, compared with a gold standard [1], and it has been widely used to test standard actigraphy against PSG [10, 21]. As in the case of discrepancy analysis, the data structure described at the end of Step 1 is the starting point for analyzing the data on an EBE level.

Error matrices

Error matrices (also referred to as confusion matrices or contingency tables) are cross-tabular representations in which rows and columns indicate the frequency of classification categories for each of the two methods [32]. Importantly, error matrices are the basis of most metrics indicating the performance of binary measurements, including the widely reported sensitivity and specificity. In sleep detection, classic definitions of sensitivity (i.e. ability to correctly classify sleep epochs) and specificity (i.e. ability to correctly classify wake epochs) rely on binary scorings of sleep/wake epochs, as provided by standard actigraphy and other sleep trackers (see [10]). With the increasing capability of CST to perform sleep staging [2], such definitions are updated to generalize to non-binary data (i.e. wake, “light,” “deep,” and REM sleep). In this framework, “sleep-stage sensitivity” refers to the device’s ability to correctly detect a given stage, such as REM sleep, whereas “sleep-stage specificity” is the ability to correctly detect all other considered stages. Careful interpretation of the terminology is necessary when interpreting EBE sleep stage classification, to avoid ambiguity with classic (binary-based) definitions.

Table 2 shows the structure of an error matrix obtained from a device and a reference method providing sleep staging information. Each cell contains the number of epochs in a given condition (e.g. cell C reports the number of epochs scored as “deep” sleep by the device that are scored as wake by the reference). From Table 2, sleep-stage sensitivity is computed as the proportion of epochs classified in a given stage (e.g. REM sleep) by both methods over the total number of epochs classified in that stage by the reference, whereas specificity is computed as the proportion of epochs classified in any of the other stages (e.g. wake and NREM sleep) by both methods over the total number of epochs classified as any of the other stages by the reference. For instance, REM sensitivity is calculated as P/(M + N + O + P), whereas REM specificity is computed as ([A + B + C] + [E + F + G] + [I + J + K])/([A + B + C + D] + [E + F + G + H] + [I + J + K + L]).

Table 2.

Error matrix for evaluating sleep stages detection

		Device
		Wake	“Light”	“Deep”	REM	Total reference
Reference	Wake	A	B	C	D	(A + B + C + D)
	“Light”	E	F	G	H	(E + F + G + H)
	“Deep”	I	J	K	L	(I + J + K + L)
	REM	M	N	O	P	(M + N + O + P)
Total device		(A + E + I + M)	(B + F + J + N)	(C + G + K + O)	(D + H + L + P)	Total number of scored epochs

“Light”, PSG-derived N1 + N2; “deep”, PSG-derived N3; REM, rapid eye movement sleep.

Error matrices can be computed either by considering the total number of epochs in the sample (i.e. “absolute error matrix,” with each cell reporting the sum of epochs in a given classification category, regardless of the subjects) or by accounting for the variability between subjects (see section 3.1 of the analytical pipeline [11]). In the second case, recommended by de Zambotti and colleagues [1], a matrix is generated per each subject (individual-level matrix), and the value in each cell is divided by the corresponding marginal frequency based on the reference (i.e. the “Total reference” column in Table 2), resulting in a “proportional error matrix” that shows the estimated stage-specific sensitivities and specificities per subject. Then, individual-level matrices are averaged to generate a group-level proportional matrix, with each cell reporting the average proportion of epochs in each classification category, with the corresponding SD and 95% CI. The advantage of such representation of EBE performance, in addition to including the essential EBE metrics (described in the following sections), is the immediate interpretation of the nature of device misclassifications (see example in Table 5).

Table 5.

Group-level proportional error matrix of the sample data

		Device
		Wake	“Light”	“Deep”	REM
Reference	Wake	0.62 (0.16) [0.54, 0.70]	0.31 (0.18) [0.22, 0.39]	0.02 (0.02) [0.01, 0.03]	0.06 (0.10) [0.00, 0.10]
	“Light”	0.05 (0.03) [0.04, 0.07]	0.79 (0.10) [0.74, 0.84]	0.06 (0.06) [0.03, 0.09]	0.09 (0.07) [0.06, 0.12]
	“Deep”	0.02 (0.02) [0.00, 0.03]	0.53 (0.24) [0.41, 0.65]	0.44 (0.24) [0.32, 0.56]	0.01 (0.02) [0.00, 0.02]
	REM	0.03 (0.04) [0.00, 0.05]	0.27 (0.29) [0.12, 0.41]	0.02 (0.04) [0.00, 0.04]	0.67 (0.33) [0.52, 0.85]

“Light”, PSG-based N1 + N2; “deep”, PSG-based N3; REM, rapid eye movement sleep. Results are reported as mean (standard deviation) [95% confidence intervals].

Individual-level EBE metrics

Table 3 shows an overview of the most widely reported EBE metrics used to evaluate the performance of CST devices (see also [32, 33]), which can be computed by applying the functions included in our pipeline [11] (sections 3.2 and 3.3) to the data structure described in at the end of Step 1. Although sensitivity and specificity are perhaps the most important metrics, and in most cases they are sufficient to describe a device performance, metrics such as positive predictive value (PPV; sometimes called “precision”) might be useful to provide further details (e.g. to estimate the probability of a given epoch to be in a given stage based on the device classification).

Table 3.

EBE accuracy metrics for sleep/wake and sleep stages detection

EBE metric	Binary definition (sleep/wake)	Categorical definition (sleep staging)
Sensitivity	Proportion of “true” sleep epochs (i.e. based on the reference) that are correctly classified as sleep by the device.	Proportion of epochs classified as a given sleep stage by the reference that are correctly classified as that stage by the device.
Specificity	Proportion of “true” wake epochs (i.e. based on the reference) that are correctly classified as wake by the device.	Proportion of epochs not classified as a given stage by the reference that are correctly not classified as that stage by the device.
Accuracy	Proportion of correctly classified sleep and wake epochs over the total number of epochs.	Proportion of correctly classified epochs for a given stage over the total number of epochs.
PPV	Proportion of epochs classified as sleep by the device that are “true” sleep epochs (i.e. based on the reference).	Proportion of epochs classified as a target stage by the device that are classified as that stage by the reference.
NPV	Proportion of epochs classified as wake by the device that are “true” wake epochs (i.e. based on the reference).	Proportion of epochs not classified as a target stage by the device that are not classified as that stage by the reference.
PI	Proportion of “true” sleep epochs (i.e. based on the reference) over the total number of epochs.	Proportion of epochs classified as a target stage by the reference over the total number of epochs.
BI	Difference in sleep epoch proportion (i.e. sleep epochs over the total number of epochs) between device and reference.	Difference between device and reference in the proportion of epochs classified as a target stage over the total number of epochs.

Metrics are defined based on proportions (generally ranging from 0 to 1), but it is common to report them as percentages, by simply multiplying the result by 100. PPV, positive predictive value; NPV, negative predictive value; PI, Prevalence Index; BI, Bias Index.

Group-level EBE metrics

When considering group-level accuracy metrics, the advantage of evaluating EBE data at an individual level becomes more evident. Indeed, the common practice of considering the total number of epochs regardless of individual differences would result in a single value for each metric (e.g. accuracy = 0.92, specificity = 0.64). However, EBE metrics are sample-based estimates of population parameters, and they should be accompanied by information on their variability (SD) and uncertainty (CI). A function that computes both “absolute” (i.e. based on the total count of epochs in the sample) and “averaged” group-level EBE metrics is included in our pipeline [11] (section 3.1). The second modality is recommended. The same statistical considerations regarding CI computation, sample size, and outliers reported for discrepancy analysis (Step 2) apply also to group-level EBE metrics and error matrices.

Additional EBE analyses

As described in detail by Watson and Petrie [32], binary data can be analyzed with the McNemar’s test [34], which evaluates the significance of systematic differences between proportions of “positive” (e.g. sleep) classifications from the two methods, or the Cohen’s kappa [35], which quantifies the proportion of classification agreement that is not due to chance, ranging from 0 to 1. As is recommended for other metrics, the kappa coefficient should be reported with the corresponding CI. Of note, the kappa coefficient is sensitive to both the number of categories (i.e. the higher the number of categories and the lower the kappa) and the prevalence of each condition. In sleep detection, sleep epochs are usually more prevalent than wake epochs, and this would result in cases of “high agreement but low kappa” [36]. A prevalence-adjusted bias-adjusted kappa (PABAK) has been proposed by Byrt and colleagues [33], and it is recommended for evaluating agreement in sleep detection. Both the McNemar’s test and the kappa coefficient can be applied to both binary (i.e. sleep/wake) and categorical classifications (i.e. sleep staging), with the latter requiring to be dichotomized for each stage before testing. Further analyses might include the receiver operating characteristic (ROC) curve, which consists in plotting sensitivity against (1 – specificity). ROC curves are mainly used to determinate optimal cutoff for diagnostic tests, but they can be also applied to compare the accuracy of two devices (or two algorithms used by the same device) with a reference method [32].

Although we believe that the metrics reported in Table 3 (and particularly sensitivity and specificity) are sufficient for describing the EBE performance of a CST device, these additional analyses can be used to test systematic differences between the two methods, and are provided in our pipeline [11] (section 3.3).

Results

Illustrative example

Here, the proposed guidelines are applied to the sample of empirical data described at the beginning of the previous section, and the core outputs to be reported in publication reports evaluating the performance of sleep tracker devices are depicted.

Data structure

PSG sleep records were scored in 30-s epochs (wake, N1, N2, N3, and REM sleep) according to AASM criteria, and EBE Fitbit data were obtained through Fitabase (Small Steps Labs LLC.). PSG and Fitbit 30-s epochs confined between lights-off and lights-on were matched and organized with the data structure described in Step 1 (see section 1 of the analytical pipeline [11]). In this example, both PSG and Fitbit epochs were encoded as: 0 = wake, 1 = “light” sleep (PSG-based N1 + N2), 2 = “deep” sleep (PSG-based N3), and 3 = REM sleep.

Discrepancy analysis

Results of group-level discrepancy analysis are reported in Table 4. In the sample, “light” sleep duration is overestimated by the device (i.e. bias is positive, with both CI above zero), whereas REM sleep duration does not show a significant bias (i.e. zero is included within the CI). The systematic component of measurement error in “light” sleep duration can be “corrected” by removing 34.54 min (“calibration index”) to all device “light sleep” durations. All other sleep measures show a negative proportional bias, whose magnitude (and significance) depends on SM (expressed as the range of PSG-derived measures). Figure 2 shows the corresponding Bland–Altman plots for some of the considered measures, and it highlights the bias trend over SM. For instance, in the case of WASO and “deep” sleep duration the measure is underestimated by the device for cases showing higher PSG-derived measures (i.e. with PSG-derived WASO higher than 40 min, and N3 duration higher than 60 min), whereas the bias is not significant for lower values. On the contrary, TST and SE are overestimated by the device for subjects with lower PSG-derived measures (i.e. TST lower than about 300 min, SE lower than 85%), whereas the bias is not significant for higher values. In all these cases, the bias is represented as a linear regression with intercept b₀ and slope b₁ (see equation (1) in Step 2 “Group-level discrepancies”), and “corrections” of device-derived measures should be based on SM.

Table 4.

Group-level discrepancies computed on the sample data

Measure	Device mean (SD)	Reference mean (SD)	Bias [95% CI]	Lower LOA [95% CI]	Upper LOA [95% CI]
TST (min)	339.32 (60.61)	332.57 (67.25)	56.42 − 0.15 × ref b0 = [10.03, 104.04] b1 = [−0.28, −0.03]*	Bias − 39.25 [23.06, 62.90]	Bias + 39.25 [23.06, 62.90]
SE (%)	88.07 (4.53)	86.08 (6.90)	58.10 − 0.65 × ref b0 = [31.53, 98.51] b1 = [−1.11, −0.35]*	Bias − 2.46 × (24.90 − 0.26 × ref) c0 = [28.37, 64.51] c1 = [−0.71, −0.30]*	Bias + 2.46 × (24.9 − 0.26 × ref) c0 = [28.37, 64.51] c1 = [−0.71, −0.30]*
SOL (min)	11.36 (14.81)	13.75 (11.60)	7.15 − 0.69 × ref b0 = [2.29, 20.15] b1 = [−2.53, −0.30]*	Bias − 2.46 × (0.82 + 0.53 × ref) c0 = [−12.72, 2.95] c1 = [0.30, 1.54]*	Bias + 2.46 × (0.82 + 0.53 × ref) c0 = [−12.72, 2.95] c1 = [0.30, 1.54]*
WASO (min)	33.82 (12.76)	38.18 (19.79)	26.13 − 0.80 × ref b0 = [8.10, 49.05] b1 = [−1.56, −0.23]*	Bias − ref × 0.94 [0.69, 1.36]	Bias + ref × 0.94 [0.69, 1.36]
“Light” (min)	234.64 (56.85)	200.11 (48.52)	34.54 (52.86) [7.75, 61.43]*	−69.08 [−95.47, −42.25]	138.15 [111.43, 164.29]
“Deep” (min)	50.04 (22.58)	75.61 (23.71)	23.70 − 0.65 × ref b0 = [−3.37, 61.43] b1 = [−1.16, −0.22]*	Bias − 2.46 × (2.66 + 0.18 × ref) c0 = [−37.43, 12.02] c1 = [0.07, 0.71]*	Bias + 2.46 × (2.66 + 0.18 × ref) c0 = [−37.43, 12.02] c1 = [0.07, 0.71]*
REM (min)	54.64 (27.39)	56.86 (23.11)	−2.21 (36.23) [−19.79, 16.21]	Bias − ref × 1.24 [1.04, 1.84]	Bias + ref × 1.24 [1.04, 1.84]

TST, total sleep time; SE, sleep efficiency; SOL, sleep onset latency; WASO, wake after sleep onset; “light”, PSG-derived N1 + N2; “deep”, PSG-derived N3; REM, rapid eye movement sleep; SD, standard deviation; CI, confidence intervals; LOA, limit of agreement; ref, reference-derived measures (i.e. PSG, used to quantify the size of measurement).

*Cases showing a significant bias, proportional bias or heteroscedasticity. When a proportional bias was detected, a linear model predicting the discrepancies by the corresponding PSG measures was specified, and 95% CI were reported for the model’s intercept (b0) and slope (b1), as indicated in equation (1). When heteroscedasticity was detected, a linear model predicting the absolute residuals of the previous model by PSG-derived measures was specified, and 95% CI were reported for the model’s intercept (c0) and slope (c1), as indicated in equation (3).

Data are homoscedastic (the variability of the differences is constant over SM) for both “light” sleep duration and TST, and LOAs are computed as bias ± 1.96 SD of the differences and using equation (2) (i.e. bias ± 1.96 SD of the residuals of the regression model representing the bias), respectively (see Step 2 “Group-level discrepancies”). In both cases, LOAs are represented in Figure 2 as parallel to the bias line.

In contrast, heteroscedasticity was detected for SE, SOL, and “deep” sleep duration, where LOAs were modeled as a function of SM. As in cases of proportional bias, they are expressed as a linear regression with intercept c₀ and slope c₁ (see equation (3) in Step 2 “Group-level discrepancies”). The sign of c₁ determines the direction of heteroscedasticity, with higher random error (i.e. wider LOAs) for higher PSG-derived SOL and “deep” sleep duration, and lower SE. Further cases of heteroscedasticity (WASO) or deviation from normality (REM sleep duration) were addressed by log transforming the measures before computing LOAs. Consequently, LOAs are expressed as a function of SM, which is multiplied by a slope determined based on the log-transformed differences (see [23]). In all these cases, the minimal detectable change depends on SM.

In all cases, bias and LOAs are reported with their 95% CI computed using parametric bootstrap with 10,000 replicates (bootstrap CI were preferred to default classic CI due to small sample size and skewed distributions). When all assumptions are fulfilled (i.e. “light” sleep detection), CI are reported for the mean difference (along with its SD) and LOAs estimates, whereas when a proportional bias and/or heteroscedasticity is detected, CI are reported for the regression intercepts (b₀ and c₀) and slopes (b₁ and c₁). When a log transformation was applied, the LOAs’ CI are reported for the back-transformed slope coefficient [23].

EBE analysis

Table 5 shows the group-level proportional error matrix generated from the sample dataset. As recommended, individual error matrices were computed for each subject, and each cell was divided by the corresponding marginal value for the reference. Thus, each cell includes the average proportion of each classification category over the number epochs classified as the corresponding stage by PSG. Values in the diagonal represent sleep-stage sensitivity, suggesting a better ability of the device to correctly classify “light” sleep (with about 80% of PSG-based N1 + N2 epochs being correctly classified), whereas poorer performance is suggested for “deep” sleep detection (with more than half of PSG-based N3 epochs being erroneously classified as “light” sleep by the device). Similarly, a relevant proportion of PSG-based wake and REM epochs (from 11% to 44%) are considered as “light” sleep by the device, clarifying the results of Step 2 regarding the overestimation of “light” sleep. This pattern of results is also confirmed by stage-specific specificity, which is significantly higher than 90% for all stages but “light” sleep, and by the PABAK coefficient, which is significantly higher than 0.60 for wake and “deep” and REM sleep but lower than 0.45 for “light” sleep (see [11], section 3.3).

Note also that the 95% CI in Table 5 indicate that estimates are more precise for certain categories (e.g. the percentage of “light” sleep considered as wake) compared to other categories (e.g. “deep” and REM sleep sensitivity) which show higher variability between participants (as indicated by the SD), and which should be interpreted with more caution.

Discussion

This work offers a detailed but easily accessible standardized framework and practical tools for analytically testing the performance of sleep-tracking technology against a reference method (e.g. PSG), and is based on recent recommendations for evaluating and using CST [1, 5]. The article is accompanied by an open-source set of R functions (available at https://github.com/SRI-human-sleep/sleep-trackers-performance) [11], and a concrete example of the application of the analytical pipeline on a sample empirical dataset.

We believe this work can increase the time efficiency, quality, and replicability of validation studies, mitigating the excessive degree of heterogeneity in both methodological and statistical procedures currently used in CST validation, with the ultimate goal of improving the informed adoption of CST in research and clinical settings. The generalizability and reproducibility of the proposed analytical steps match with the flexibility of the R functions, which are designed to allow modifications of their arguments to fit specific analytical needs (e.g. logarithmic transformation and bootstrapped CI).

The added value of the recommended analytical steps becomes more evident when their interpretation is compared to less appropriate but widely used analytical techniques. For example, although the correlation between device and reference measures is often used to evaluate CST performance [10], it simply indicates their degree of linear association, with no information on their agreement (e.g. a systematic difference of 50 min is plausible even between two perfectly correlated TST measurements) [22, 32, 37]. Moreover, correlation coefficients are highly sensitive to the range of measurement (the broader the range and the higher the correlation), but insensitive to SM (i.e. proportional bias), and the same applies to intraclass correlation coefficients and t-tests [15, 29, 37].

In contrast, bias and 95% LOAs are sample-based estimates of the agreement between device and reference measurements. Such metrics are independent from the range of measurement, and the relationship between differences and SM (proportional bias) can be easily modeled (equation (1)) [16]. Moreover, they are more immediately interpretable than correlations or t-test outputs, as they separately quantify the most likely difference to occur (systematic bias) and the range within which most differences are expected to lie (random error), both expressed in the original measurement unit (e.g. min). In addition to discrepancy analysis, EBE metrics included in the proportional error matrix (Table 5) allow one to explore more in depth the nature of the observed discrepancies (e.g. high TST discrepancies can be due either to low sensitivity or to low specificity), and stage-specific EBE metrics provide further information on which stages are more accurately detected by the device.

Most importantly, the information provided by bias and LOAs can ultimately be used by sleep researchers and clinicians to potentially “correct” the observed measures based on the results of previous method comparison studies. For example, a constant bias over SM (“calibration index”) can be simply subtracted from device measures in order to reduce systematic over- or underestimations. Differently, a proportional bias implies that differences should be modeled based on SM. However, since only device measures will be available in real practice, they can be used to quantify SM and to estimate the calibration index corresponding to each case.

For instance, in our sample dataset we highlighted a proportional bias for TST, implying that PSG measures are underestimated by the device for subjects/nights with longer TST. Clinicians and researchers could use such information to “correct” the measures collected with the evaluated device under similar conditions and in similar populations as in the reference dataset, in order to obtain more accurate estimates of “true” (reference-derived) measures. As an example, a TST measure of 400 min is likely to be underestimated by the Fitbit Charge 2. Sleep scholars/practitioners can use the information reported in Table 4 for TST (i.e. bias = 56.42 min − 0.15 × ref) to compute the “calibration index” corresponding to the observed measure (bias = 56.42 min − 0.15 × 400 ms = −3.48 min) and apply the correction (TST_corr = 400 min + 3.58 min = 403.58 min). In contrast, the same measures showed a Pearson correlation of 0.94 (almost perfect), an ICC(2,1) of 0.94 (excellent reliability [38]), and a paired t-test indicating no statistically significant differences (t(13) = 1.13, p = 0.28). The latter pattern of results would simply suggest to use the device for obtaining measures almost perfectly associated with those obtainable with the reference, without providing any information on systematic bias, random error and EBE accuracy, and they cannot be used to calibrate future measurements.

Both bias and LOAs should be considered when reporting on a sleep tracker performance, as excessively wide LOAs might suggest a poor performance even in cases where the bias is not significant [1]. When data are homoscedastic, the “minimal detectable change” (i.e. the smallest change detected by a method that exceed measurement error) can be expressed by one-half the difference between the upper and lower LOA [17]. For instance, in our sample dataset we found a minimal detectable change 39.25 min for TST. What “excessively wide” means (i.e. “minimal clinical important change”) strictly depends on the specific application and target population of the device under assessment. Although some general criteria have been proposed for sleep measures (e.g. see [39]), their rationale is still debatable, and interpretation of LOAs should be made on a case-by-case basis [1]. The same applies to EBE metrics, for which there is currently no consensus on threshold values defining a “good” performance. In both cases, the interpretation of the outcomes should be based on the specific application and target population [1, 5].

As a further advantage, the recommended performance metrics can be applied on device-reference comparisons across different samples (e.g. insomnia patients vs. good sleepers) and conditions (e.g. pre-to-post sleep interventions), acknowledging that CST performance can be affected by multiple factors [2, 5]. Individual-level discrepancies can be used as outcome variables in regression models to investigate the role of potential confounders (e.g. sex and age). Critically, the comparison of performance metrics obtained with different firmware/algorithm versions is important to update scientific information on device performance. Similarly, EBE agreement can be used as an outcome variable to model within-night processes (e.g. cardiac activity).

Finally, the advantage of a standardized framework for CST evaluation is particularly evident when comparing results across studies. For instance, the results reported in the last section can be compared with those obtained by de Zambotti and colleagues [20], in which the same device was tested on a different sample, reporting results in the same output format. In line with the previous study, our results suggested higher device specificity for “light” compared to both “deep” and REM sleep, with a large proportion of PSG-derived “deep” sleep epochs being classified as “light” sleep by the device. Such degree of comparability is expected to facilitate replicable evidence, as well as device-specific reviews and meta-analyses.

Of note, the recommended analytical procedures strictly rely on the methodological assumptions summarized in Step 1 and exhaustively discussed in previous guidelines [1, 5]. On the one hand, such best practices (e.g. gold standard comparison, device settings, and recording synchronization), in addition to the analytical steps described in this work, are critical for conducting rigorous validation studies that will advance our knowledge on sleep trackers performance. In this sense, our analytical guidelines should be considered as a first step toward a standardized and time efficient validation pipeline to be integrated with previous recommendations. On the other hand, the implementation of our pipeline per se is not sufficient to guarantee the “validation” of a device. As proposed by Grandner et al.[7], an optimal “validation cycle” would include (1) laboratory-based comparison with PSG, (2) field-based comparison with ambulatory measures, and (3) validation for specific populations. Although the recommended procedures can be applied in each of these phases, methodological assumptions should be adjusted to specific cases. For instance, in ambulatory settings the experimenter cannot directly set lights-on and lights-off times. In such settings, alternative techniques such as self-reported sleep logs should be used to ensure that device and reference recordings are synchronized and that sleep measures are comparable [40]. Moreover, if a CST device classifies motionless wakefulness as sleep, this would probably generalize to diurnal hours [10]. Thus, considering and reporting misclassifications on a 24 h period will be necessary to exhaustively evaluate device performance.

In conclusion, given the increasing interest and use of CST, it is hoped that this article, and the corresponding analytical pipeline, will contribute to the rigor of CST validations and informed use, which is a fundamental step to reach the level of accuracy of these technologies required by research and clinical applications.

Funding

This study was supported by the National Institute on Alcohol Abuse and Alcoholism (NIAAA) grant R21-AA024841. The content is solely the responsibility of the authors and does not necessarily represent the official views the National Institutes of Health.

Disclosure statements

Non-financial disclosure: Authors declared no conflict of interest related to the current work. M.dZ. and F.C.B. have received research funding unrelated to this work from Ebb Therapeutics Inc., Fitbit Inc., International Flavors & Fragrances Inc., and Noctrix Health, Inc.